Page 1 :
GHSS VYTHIRI,WAYANAD, VICTERS CLASS NOTES BASED ON FOCUS POINTS, CHAPTER 1 : ELECTRIC CHARGES AND FIELDS, 1.2 ELECTRIC CHARGE, , SREESHYJU K P,HSST PHYSICS GHSS VYTHIRI,WAYANAD, JIJESH M T ,GVHSS PAYYOLI, , Charge is an intrinsic property of matter like mass. It is, represented by the symbol q or ‘Q’ and unit is Coulomb (C), Properties of charge:, 1. charge is a scalar quantity. There are two types of charges, positive and negative, 2. charge is additive- total charge on any body is sum of, individual charges, 3.Conservation of charge – total charge in an isolated system is, constant, 4.Charg is relativistically invariant-magnitude of charge is, independent of velocity, 5.Quantisation of charge- Total charge on any body is an integral, multiple of fundamental unit of charge, Q = ± ne where n = 1,2,3,…., e= 1.6 ×10-19 C, Qn. A charge of 9.6 ×10-18 C is possible or not?, , Since n = 60, a charge of 9.6 ×10-18 C is possible, Methods of charging:, 1. charging by conduction: when a charged body and an, uncharged body are in direct contact ,, charge flows from charged body to uncharged body, 2.Charging by induction: charging a body without direct contact., 3. Charging by friction – when a body is rubbed with other ,, charge flows from one body to another

Page 4 :
Coulombs law in vector form, , Obeys Newton’s third law of motion

Page 5 :
1.8 ELECTRIC FIELD, The region around a charge where another charge can, experience a force is called electric field, , Since the test charge is small ie q tends to zero, , Super position principle: Electric field at a point due to a system, of charges is the vector sum of electric field due to individual, charges, , Applying superposition principle, , Direction of electric field at a point is the direction of motion of a, positive charge placed at that point

Page 6 :
Expression for electric field due to a point charge, The force on a test charge q placed at a distance r from a, charge Q is, Q, q, r, , 𝐸, , Electric permittivity

Page 8 :
1.9 ELECTRIC FIELD LINES OR ELECTRIC LINES OF FORCE, Electric field lines are imaginary lines drawn to represent an electric, field. It is defined as the path along which a unit positive charge moves if it is, free to do so., Properties of electric field lines, 1.Elecric field lines are straight or curved lines, 2. Tangent drawn at any point on the electric field line gives the direction of, electric field, , 3.Electric field lines starts from positive charge and ends on negative charge., Field lines of a single positive charge are radially outward and while it is, radially inwards for a negative charge, , 4.The magnitude of electric field is proportional to the number of field lines, per unit area, 5.Two electric field lines will never intersect. If they intersect at the point of, intersection electric field is having two different directions , which is not, possible

Page 9 :
6.Electric field lines of a uniform electric field are parallel and equidistant, Fig(1)- towards right , Fig(2)- towards left , Fig(3)- outwards fig(4)- inwards, , 7.Electric field lines never forms closed loops, Sreeshyju. K.P & jijesh.M.T/HSST PHYSICS/GVHSS Payyoli, , Problem:1, Figure shows tracks of three charged particles in a uniform electrostatic, field.(1)Give the signs of three charges. (2)Which particle has the highest, charge to mass ratio( specific charge), , Ans: (1) Charge 1 and 2 are deviated towards positive plate. So they are, negative charges.Charge in track 3 deviated towards negative plate so they, are positive charges., (2) since the deviation from initial path is large for charge 3 , it has large, charge to mass ratio (e/m) (ie y= ut + ½ at2 here u=0 and F=ma or qE=ma, a= eE/m there for, Y=0+ ½ [eE/m]t2 ie y α e/m ), 1.10 ELECTRIC FLUX (φ), Electric flux is a measure of number of field lines passing normally, through an area. It is measured as the product of magnitude of electric field E, and surface area A perpendicular to electric field, Case 1, , Electric field lines are perpendicular to the area. Ie E and A are in same, direction. Therefore electric flux φ = EA, Case 2

Page 10 :
Here component of electric field along the direction of area is Ecosθ .there, for electric flux φ = (Ecosθ) x A = EA cosθ ie φ = 𝑬. 𝑨, Therefor electric flux is also defined as the dot product of electric field vector, and area vector,  Electric flux is a scalar quantity,  Unit of electric flux is Nm2C-1,  Dimension is [φ] = [E][φ]= MLT-3A-1 X L2 = ML3T-3A-1 ( A or I can be used), Problem2, Consider a uniform electric field E= 3x103 𝒊̂ N/C .(a) what is the flux of this, field through a square of 10cm on a side whose side is parallel to the yz plane?, (b) what is the flux through the same square if the normal to its plane makes, a 600 angle with the axes, Ans (a), , Since unit vector is I the direction of electric field is along x axis and the square, is in yz plane the area vector is along x axis .there for E is parallel to A and, θ = 0 , There for φ = EA cosθ =EA cos 0 =EA=3x103 x .12=30Nm2C-1, (b)plane makes an angle θ= 600 with x axis, 𝟏, , φ = EA cosθ= 3x103x .01x cos600= 3x103x .01x = 15 Nm2C-1, 𝟐, , Problem3, What is the net flux of the uniform electric field E= 3x103 𝒊̂ N/C through a, cube of side 20cm oriented so that its faces are parallel to the coordinate, planes, Ans:Net flux over the cube is zero because the nubber of lines of force, entering the cube is same as the number of lines leaving the cube

Page 11 :
1.11 ELECTRIC DIPOLE AND ELECTRIC DIPOLE MOMENT, An electric dipole is a pair of equal and opposite point charges, separated by a distance, ,  The total charge of an electric dipole is zero ( ie –q+q =0),  The field produced by dipole at a point depends on magnitude of, charge , distance of the point and separation between charges, Electric dipole moment is the product of magnitude of the charge and, distance of separation between the charges., ie dipole moment 𝒑 = q x ( 𝟐𝒂 ),  Electric dipole moment is a vector quantity directed from negative, charge to positive charge along the dipole axes ( see fig),  Unit of dipole moment is coulomb- meter (Cm),  Dipole with q tends to infinity and 2a tends to zero and dipole, moment is finite is called a point dipole, Problem:1, A system has two charges qA = 2.5 x 10-7C and qB = - 2.5 x 10-7C, located at point A : (0,0,-15cm) and B = (0,0,+15cm), respectively. What are, the total charge and electric dipole moment of the system, Ans: qA = = 2.5 x 10-7C , qB = - 2.5 x 10-7C charges are equal and opposite, A : (0,0,-15cm) and B = (0,0,+15cm) charges are placed on Z axes, , Total charge = qA + qB = 0, Electric dipole moment p= qx2a, ie p =2.5 x 10-7C x .3m = 7.5 x10-8 Cm direction is from B to A or –Z axes, ELECTRIC FIELD ON THE AXIAL LINE OF A DIPOLE, , Let p is the point on the axial line at distance r from the centre O of an electric dipole, 𝟏, 𝒒, 𝟒𝝅Ɛ𝟎 (𝒓−𝒂)𝟐, , Electric field at p due to +q , 𝑬+ =, , ̂ …………………..(1), 𝒑, , ̂ is the unit vector in the direction of 𝒑, Where 𝒑, Electric field at p due to -q , 𝑬− = −, , 𝟏, 𝒒, 𝟒𝝅Ɛ𝟎 (𝒓+𝒂)𝟐, , ̂ ……………….(2), 𝒑

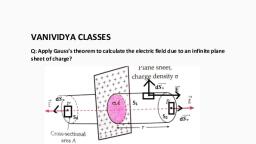
Page 18 :
E=, , 𝝈, ∈𝟎, , x, , 𝑹𝟐, 𝒓𝟐, , …….(6), , CASE 2: INTENSITY AT THE SURFACE OF THE SHELL (r=R), On the surface r=R, Substituting in (4) E =, , 𝟏, 𝟒𝝅∈𝟎, , x, , Also Substituting in (6) E =, , 𝒒, 𝑹𝟐, 𝝈, ∈𝟎, , Note: intensity on the surface of shell > intensity outside the shell, CASE 3: INTENSITY AT A POINT INSIDE THE SHELL (r<R ), , Applying Gauss’s theorem, Ex4πr2 =, , 𝒒, ∈𝟎, , E=0 , since charge enclosed by the Gaussian surface is zero, Graphical representation of variation of intensity with distance, , Problem 1

Page 19 :
Note: intensity of electric field is not always inversely, proportional to square of the distance

Page 20 :
1.FRICTIONAL ELECTRICITY, PROBLEM 1:, , Answer: (a) since polythene piece acquires negative charge it gains, electrons . there for electrons are transferred from wool to polythene ., (b) True. Since polythene has additional electrons its mass, increases = no of electrons transferred x mass of electron (9.11x10 -31kg), 2.COULOMBS LAW, PROBLEM:2

Page 21 :
ANSWER: since charges are like charges the force is repulsive, , PROBLEM 3, , 3.PRINCIPLE OF SUPERPOSITION, PROBLEM 4, , ANSWER:, Y, , X, , Note: this problem can be solved in vector form also

Page 22 :
𝐹 = 𝐹1 + 𝐹2, F= F1 - F2, the direction of net force is same as that of bigger vector F1 ( towards left), 4.ELECTRIC FIELD, PROBLEM 5, , ANSWER: CASE 1, , CASE 2, , 5.ELECTRIC DIPOLE, PROBLEM 6:

Page 25 :
Chapter 2- Electric potential and capacitance, ………………………………………………………………………………, 2.2 ELECTROSTATIC POTENTIAL ( V ), Electrostatic potential at a point is the work done in, bringing a unit positive charge from infinity to that point against, electrostatic force.

Page 28 :
PROBLEM 2, , Ans: Q= 8mC = 8 ×, 10−3 C, q= -2× 10−9 𝐶, OA= 𝑟𝐴= 3 cm=, ), 3x10-2cm, 𝟏, 𝟏, WAB = (-2× 10−9 )x 9×109 x8 × 10−3 x[, ]= 1.2 J, 4x10−2 3x10−2, OB= rB= 4cm =, electrostatic force is conservative, it does not depend on path. So point C is, not relevant, WAB = q (VB- VA), , 2.6 EQUIPOTENTIAL, SURFACES, 𝑸, 𝟏, , WAn, [ - surface is a surface with a constant value of, AB= q (, equipotential, , 𝟒𝝅∈𝟎 𝒓𝑩, 𝟏, potential at all points, , on the surface, ], 𝒓𝑨, PROPERTIES:(1) Potential is constant at all points on this surface or, potential difference between two points on an equipotential, surface is zero, (2) For any charge configuration, equipotential surface is, normal to electric field at that point, (3) Work done to move a charge from one point to another, On an equipotential surface is zero, ie we have , WAB = VB- VA, but VA= VB on an equipotential surface, there for work done WAB = VB- VA = 0, Examples:(1) Equipotential surface for a point charge are, concentric spherical surfaces with charge at centre

Page 29 :
(2)For a uniform electric field, equipotential surface is, perpendicular to the plane i.e. if electric field is along X axes, equipotential surface is planes parallel to YZ plane, Dierection of electric field, , Equipotential surfaces, (3)For an electric dipole, Equipotential surfaces, , (4) for two identical positive charges, , 2.11 CAPACITORS AND CAPACITANCE, Capacitor is a device used to store charge. It consists of two, conductors separated by an insulator, , + +, +Q, +, Conductor1, , -, , -, , -Q, , Conductor 2, Electric field ,from positive plate to negative plate, increases when, charge on the plate increases. When electric field increases, potential increases ie potential difference increases with increase, in charge on the plates, Q∝ V, or Q= CV,, where C is a constant called Capacitance, 𝑸, C=, 𝑽

Page 30 :
Unit of Capacitance, We have, , C=, , 𝑸, , =, , 𝑽, , 𝒄𝒐𝒖𝒍𝒐𝒎𝒃, 𝒗𝒐𝒍𝒕, , = CV-1= Farad (F), , Symbol of capacitor, Fixed capacitance, Variable capacitance, Note:1 The maximum electric field that a dielectric medium can withstand, without breakdown is called dielectric strength, For air it is about 3x 106 Vm-1, Note:2 Total field in region II, , Thus electric field exists only in between the parallel plates having, magnitude E=, , 𝝈, 𝝐𝟎, , and direction from positive plate to negative plate, , 2.12 PARALLEL PLATE CAPACITOR, A parallel plate capacitor consists of two large plane parallel conducting, plates separated by a small distance, Expression for capacitance, , E=, , 𝝈, 𝝐𝟎, , d, Capacitance of a capacitor is, Q= 𝝈𝑨 …….(2), And V= Ed, But E=, , 𝝈, 𝝐𝟎, , ∴ V=, , 𝝈, 𝝐𝟎, , d …….(3), , Substituting (2) and (3) in (1), , C=, , 𝑸, 𝑽, , …….(1)

Page 31 :
C=, C=, , 𝝈𝑨, 𝝈, 𝝐𝟎, , 𝐝, , 𝝐𝟎 𝑨, 𝒅, , Note: Capacitance of a capacitor is, (1) directly proportional to area of plates, (2) inversely proportional to distance between the plates, PROBLEM 1, Find the capacitance of a capacitor of area A= 1m2 and separation 1mm ?, , Answer:, , PROBLEM 2, Find the area of a capacitor of capacitance 1F of separation 1cm (= 102, m) ?, Answer:, We have C=, , Note:, , 𝝐𝟎 𝑨, 𝒅, , For a square plate, , = 30km, ie ,1F Capacitor have plate of 30 km in length and breadth. So farad, is a very big unit and there for we use small units micro farad(1µF= 10 6, F),nano farad (1nF= 10-9F), pico farad (1pF= 10-12F), , 2.14 COMBINATION OF CAPACITORS-SERIES AND PARALLEL

Page 34 :
PROBLEM, , Answer:, C1,C2 and C3 are in series and let the effective capacitance is C’ then, , =3.33𝜇𝐹, C’ is parallel to C4 there fo effective capacitance is Ceff = C’+C4, , Ceff=, Ceff=, 2.15 ENERGY STORED IN A CAPACITOR, , Q’, , V’, +, , 𝛿𝑄, , V, work must be done to move charge from one plate to another of a, capacitor.The work done to charge the cpacitor from zero to maximum, charge Q is stored as energy in capacitor, At an instant let Q’ be the charge and V’ be the potential.Then the, work done to move a small charge 𝜹𝑸 from one plate to another, 𝜹𝒘 = 𝑽′𝜹𝑸 ( since W=qV), But V’=, , 𝑸′, 𝑪

Page 36 :
𝟏, , U= ∈𝟎 E2 v, 𝟐, , ∴ 𝑬𝒏𝒆𝒓𝒈𝒚 𝒅𝒆𝒏𝒔𝒊𝒕𝒚 , 𝒖 =, Energy density, , 𝑼, , 𝒗𝒐𝒍𝒖𝒎𝒆, 𝟏, ,u= ∈𝟎 E2, 𝟐, , =, , 𝑼, 𝒗, , PROBLEM, , ANSWER:, 𝟏, , (a) we have energy U= CV2, 𝟐, , Here C= 500𝝁𝑭 and V= 2V, 𝟏, , U= x 500x 22, 𝟐, , U= 1000J, (b) when a charged capacitor is connected to an uncharged capacitor, charge flows from charged capacitor to uncharged capacitor until the, potential difference across two capacitors become equal. ie here V= 1V, 𝟏, , U= CV2, 𝟐, , U=, , 𝟏, 𝟐, , x500x 12= 250, , Total energy of two capacitors= 250J+250J, U = 500J, Note :, When charge is transferred from a charged capacitor to an uncharged, capacitor, there is a difference in energy of 500J. This difference in energy, is due to radiation loss or heat loss, CHAPTER 3 : CURRENT ELECTRICITY, 3.4 OHMS LAW, Ohms law states that at constant temperature current (I) flowing through a, conductor is proportional to the potential difference ( V)across the ends of, the conductor., ie V ∝ I, or V= IR , where R is called resistance of the conductor ., unit is ohm(𝛀 ), Experimental verification of Ohms Law, Connection diagram, Components, A- Ammeter.V-voltmeter,R – resistance,, Rh- rheostat, E- battery,K- key

Page 37 :
R, , Rh, , E, , Procedure: Moving the slider of the rheostat vary the current and, corresponding voltage is measured, And resistance is calculated in each case., Observatins:, Values of voltages for different values of current are tabulated. Then, 𝑽, , resistance R= is calculated and found to be a constant ( here 10𝛀 ), 𝑰, , A graph can be plotted by taking current along X axis and potential along y, axes .slop of the graph gives resistance, From the above experiment it is clear that, , 𝑽, 𝑰, , is constant or V ∝ I, thus, , ohms law is verified experimentally, , FACTORS AFFECTING THE RESISTANCE OF A CONDUCTOR, Length of the conductor:, Consider a conductor of length l and area of cross section A .Let I is, the current and V is the potential, , 𝑽, , By Ohms law R1 = ……(1), 𝑰, , Let the length of the conductor is doubled, , Then current is same and potential is doubled, Therefor R2 =, , 𝟐𝑽, 𝑰, , ………(2), , Dividing (2) by (1), 𝑹𝟐, 𝑹𝟏, , =, , 𝟐𝑽, 𝑰, , 𝑰, , x =2, , R2 = 2R1, , 𝑽

Page 40 :
PROBLEM 2, , ANSWER :, % change in resistance =, We know that, Δ𝑅, , Given, , 𝑅, 𝚫𝒍, 𝒍, , 𝐱 𝟏𝟎𝟎 =, , 𝚫𝒍, 𝒍, , 𝚫𝑹, 𝑹, , 𝑅, , 𝚫𝒍, 𝒍, , x 100+, , x 100 = 2% and, Δ𝑅, , =, , 𝚫𝑨, 𝑨, , +, , 𝑹, , x 100, , 𝚫𝑨, , 𝚫𝑨, 𝑨, , 𝚫𝑹, , 𝑨, , x 100, , x 100 = 2%, , 𝐱 𝟏𝟎𝟎 = 2% + 2% = 4%, , Percentage change in R is 4%, PROBLEM 3, , ANSWER:, , 3.9 ELECTRICAL ENERGY,POWER, , Consider a conductor AB connected to a battery.V(A) is the potential at A and, V(B) is the potential at B.Let a current I flows through the conductor., The energy used by the battery to maintain the current through the, conductor is called Electrical energy and the time rate of consumption of, electrical energy is calld electric power, The potential difference between A and B, V= V(A)-V(B) > 0, In a time interval ∆t , an amount of charge ∆Q= I∆t flows from A to B, The potential energy of charge at A= QV(A), The potential energy of charge at B= QV(B)

Page 41 :
The change in potential energy, ∆𝑼= Final potential energy- initial potential energy, ∆𝑼 = ∆QV(B) V(B) - ∆QV(A), ∆𝑼 = ∆Q[V(B)- V(A)]= -V∆Q, But ∆Q= I∆t, ∴ ∆𝑼 = - IV∆t < 𝟎, Therefor charges loss their potential energy when current flows from A to B, By conservation of energy total energy is constant, ∴ loss of potential energy= gain in kinetic energy, Or ∆𝑲 = - ∆𝑼= - ( -IV ∆𝒕)= + IV ∆𝒕 >0, Thus when charges are moving freely through a conductor under the action, of an electric field , their kinetic energy increases.This energy gained by the, charges is shared with atoms , they vibrate vigorously and the conductor, heats up, The energy dissipated (by the battery)as heat in the conductor during a, time interval ∆𝒕 is, ∆W= IV ∆𝒕, ( here chemical energy of the battery is converted into electrical energy), Electric Power: It is the time rate of consemption of electrical energy, , Practical Unit of Electrical energy is kilowatt hour (kwh),, 1 kwh= 3.6x106J, Watt is the unit of power ., Practical units of electric power, , Power loss or ohmic loss, The electric power is transmitted from power stations to homes or factories, which may be hundred miles away.So there is a chance for power loss due to, the resistance of the transmission cable.How can we minimise this power, loss?

Page 42 :
Therefor from the above equation, (i) power loss is ∝ Rc ,ie transmission loss can be minimised by using a, transmission cable made by a material of low resistivity, (ii) power loss 𝒊𝒔 ∝, , 𝟏, 𝑽𝟐, , , ie transmition loss can be minimised by increasing, , the voltage.There for electic power is transmitted to large distances by, increasing the voltage using step up transformers, PROBLEM:, , ANSWER:, , = 15,000 J= 15KJ, 3.10 COMBINATION OF RESISTORS- SERIES AND PARALLEL, , (A) SERIES COMBINATION, V2, , 𝑉1, , V, When resistors are connected in series , the current through each resistance, will be same, Consider two resistors R1 and R2 connected in series to a potential, difference V, Potential difference across the combination, V= V1+V2………(1), By ohms law V=IR, Potential difference across R1= V1= IR1

Page 46 :
ANSWER, Two 1 ohm resistors and two 2 ohm resistors are connected in, series in each circuit.The equivalent of these are connected parallel, , 100𝛀 and 200𝛀 series ,equivalent resistance= 300𝛀, 300𝛀 and 300𝛀 parallel , equivalent resistance= 150𝛀, 3.11 CELLS, EMF, INTERNAL RESISTANCE, A cell is a device which supplies electrical energy to all components in a, circuit or it is a device which provides a constant potential difference which, forces the free electrons to move in a closed circuit, A cell consists of a conducting solution called electrolyte eg : dil H2SO4,, AgNO3 and positive and negative electrodes( eg: copper and zinc )

Page 47 :
P, , N, Electrolyte, , Zinc atoms leaves two electrons to zinc rod and moves to electrolyte as Zn2+, ions. There for potential of zinc becomes negative ( - V- ), Copper atom leaves two electrons to electrolyte and copper plate, becomes positive ( +V+ ), When there is no current, , >0, This potential difference is called electro motive force, electro motive force or emf, 𝜺 = 𝑽+ + 𝑽−, , Consider a resistance R Connected across a cell, , Outside the cell, Current flows from positive electrode to negative electrode, through resistor or electrons flows from negative electrode to positive, electrode., Inside the cell, Current flows through the electrolyte from negative, electrode to positive electrode. The electrolyte offers a resistance to the flow, of current inside the cell called internal resistance (r), , Considering internal resistance a cell can be represented as

Page 48 :
Expression For EMF and Current, Consider a cell connected to resistance R . P is positive electrode and N is, negative electrode . A is a point near P and B is a point near N. Current, flows from P to N outside the cell and from N to P inside the cell, , Then Potential difference between P and N is, , This potential difference across the terminals of the cell when, current flows through the external citcuit is called terminal potential, difference, , Where 𝜺 = 𝑽+ + 𝑽− is the emf of the cell and Ir is the potential, drop across the internal resistance of the cell ( negative sign shows that, current flows from lower potential to higher potential inside electrolyte), Therefor, , And I =, , 𝜺, 𝑹+𝒓, , Note:, , 3.13 KIRCHHOFF’S RULES, (A) Kirchhoff’s First Law or Kirchhoff’s junction rule or current law:The algebraic sum of currents at a junction is zero. ie at a junction, ∑𝒊 = 𝟎

Page 49 :
𝐼7, , 𝐼8, , 𝐼1, , 𝐼6, , 𝐼2, , 𝐼5, , 𝐼4, , 𝐼3, , (By convention current entering the junction is positive and current leaving, the junction is negative), Applying Kirchhoff’s junction rule, ∑ 𝒊 = 𝟎, Total current at the junction, I1-I2+I3-I4+I5-I6+I7-I8= 0, Or, I1+I3+I5+I7 = I2+I4+I6+I8, ie Sum of currents entering the junction = Sum of currents leaving the, junction, Note: junction rule and conservation of charge, , I, R, , V, , I, , Fall of potential, , +V, , Rise of potential, , ie total charge is conserved. There is no accumulation or drain of charges, at the junction, (B) Kirchhoff’s Second Law or Kirchhoff’s Loop rule or Voltage law:The algebraic sum of changes in potentials around any closed loop, involving cells and resistors in the loop is zero ie ∑ ∆𝑽 = 𝟎, ( By convention rise of potential is taken as positive and fall of potential, is negative), , -V=-IR, , Applying Kirchhoff’s Voltage law to above closed loop( clockwise, direction) ∑ ∆𝑽 = 𝟎, V + (-V) = 0, V-IR = 0

Page 50 :
Note: The closed path can be taken in clockwise or anti clockwise direction., In the above circuit if take anticlockwise path we get ,–V+IR = 0 which can, be written as V-IR = 0, PROBLEM 1, 𝐼2, I, b, c, 𝐼1, , a, , 3Ω, 9V, , d, , m, I, , g, , 5𝛀, , 3V, , 2V, , f, Find the currents in the network shown, above, , e, , ANSWER, Applying Kirchhoff’s junction rule to junction b and f ,, I = I1 +I2, Applying Kirchhoff’s voltage rule to closed loop abcdefga, -5I2-3+9 = 0, -5I2 +6 = 0……(1), Applying Kirchhoff’s voltage rule to closed loop abmfga, -3I1 +2+9 = 0, -3I1 +11= 0 ……(2), , Substituting ;, I1 =, , 𝟔𝟔, 𝟏𝟖, , = 3.66 A

Page 53 :
I2R4 – I1R3 = 0……(2), , This equation relating four resistors under balanced condition, (IG=0) is called Wheatstone’s Principle, NOTE : Determination of unknown resistance, Let R4 is unknown resistance and R3 is a variable resistance and R1 and, R2 are known resistances, Varying the resistance R3 bridge can be balanced and value of R4 can be, 𝑹, determined as R4 = R3 × 𝟐, 𝑹𝟏, , 3.15 METER BRIDGE, Meter Bridge is an application of Wheatstone’s bridge. It consists of a wire, ( made of consantin,manganin,nichrome etc) of length 1m and of uniform, cross sectional area., , R is the unknown resistance and S is known(standard) resistance ,G is the, galvanometer and it is connected to a jockey . By moving the jockey, through the wire the current through the galvanometer is adjusted to zero, ( bridge is balanced). Let D is the balancing point, Then AD = l and DC = 100 – l, Resistance of length AD=l = Rcml, Resistance of length DC = 100 – l = Rcm(100-l ), Where Rcm is resistance per unit centimetre, Applying Wheatstone’s principle for the balanced bridge

Page 54 :
Or, , 𝑹, 𝑺, , =, , 𝒍, (𝟏𝟎𝟎−𝒍), , Unknown resistance, R= S, , 𝒍, (𝟏𝟎𝟎−𝒍), , Note: By measuring the radius (area A = 𝝅𝒓𝟐 )and length of resistance wire, the resistivity can be determined, 𝑹𝑨, Resistivity 𝝆 =, 𝒍, , ANSWER:, , 3.16 POTENTIOMETER, Potentiometer is a device used to measure potential difference .It consist of, a long piece of uniform resistance wire across which a standard cell is, connected. A rheostat is connected to vary current through the wire

Page 55 :
PRINCIPLE: Since wire is uniform ,potential difference between any, point is directly proportional to distance l, 𝜺( l ) ∝ l, or 𝜺( l ) = ∅ l, where ∅ is the potential per unit length (V/l ) or potential gradient, APPLICATIONS, (1) TO COMPARE THE EMF OF TWO CELLS, , 𝐾2, , Connections are made as shown in figure . Potentiometer AC is connected, to a battery B,Rheostat R and key K1(primary circuit). The cells 𝜺𝟏 and 𝜺𝟐, are connected to point A of the potentiometer.A two way key K2,A, galvenometer G and a jockey is connected to two way key(secondary, circuit., The primary circuit is closed by closing Key K1, The cell 𝜺𝟏 is included in the circuit by closing 1&3 of two way key, K2.cell is is balanced by moving jockey from A to N1 so that the current, through the galvanometer become zero. Let AN1= l1 is the balancing length., Applying Kirchhoffs loop rule to A13GN1A, − 𝜺𝟏 + 0 + ∅ l1 = 0, 𝜺𝟏 = ∅ l1 …….(1), The cell 𝜺𝟐 is included in the circuit by closing 2&3 of two way key K2.cell, is is balanced by moving jockey from A to N2 so that the current through, the galvanometer become zero. Let AN2= l2 is the balancing length, Applying Kirchhoffs loop rule to A23GN2A, -𝜺𝟐 + 0 + ∅ l2 = 0, 𝜺𝟐 = ∅ l2 …….(2), , Note : (1) To find the unknown emf 𝜺𝟏, If emf of the cell 𝜺𝟏 is unknown then by measuring balancing length l1, and l2 then, 𝜺𝟏 = 𝜺𝟐 ×, , 𝒍𝟏, 𝒍𝟐, , where 𝜺𝟐 is known emf

Page 57 :
CHAPTER 4: MOVING CHGARGES AND MAGNETISM, …………………………………………………………………………………………, 4.2 MAGNETIC FORCE, LORENTZ FORCE, , A charged particle q moving in a magnetic field B with a velocity v, experiences a force. This force is given by , 𝑭 mag = q ( 𝒗 × 𝑩 ), The direction of magnetic force is perpendicular to the plane, containing v and B. Force on negative charge is opposite to that of positive, charge, We know that in an electric field E force on a charge q is , 𝑭elec = q𝑬, In an electric and magnetic field total force, 𝑭 = 𝑭elec + 𝑭 mag, 𝑭= q [ 𝑬 + ( 𝒗 × 𝑩 ) ], This force is called Lorentz force, Magnetic Force is given by, 𝑭 mag = q ( 𝒗 × 𝑩 ), F= qvB sin𝜽, (i) Magnetic force is zero if charge is not moving, ie when v =0 ,, , F= 0, , (ii) when particle is moving parallel (𝜽 = 𝟎) or anti parallel (𝜽 = 𝟏𝟖𝟎 ), , In both case , F = 0, ie The magnetic field can not exert a force on the particle if it is at rest or it, moves parallel or antiparallel to the field, (iii) If charged particle moves perpendicular to the field (𝜽 = 𝟗𝟎 )

Page 58 :
Fmax = qvB, SI unit of magnetic field is tesla or (NS/Cm), Definition of 1 Tesla, , CGS unit of Magnetic field is gauss (G), 1G = 10-4T, Magnetic Force On a current Carrying Conductor, , I, , 𝜃, , B, , Consider a rod of uniform cross sectional area A and length l . Let n be, the number density or number of electrons per unit volume of mobile, charge carriers (electrons) Then Volume of the conductor = Al, Total number of charge carriers = Al, Total charge , q= Alne, If we send a current I through this rod the charge carries will get a drift, velocity v, Force on this moving charge carries in a magnetic field is, , Where 𝒍 is a vector in the direction of current

Page 59 :
Magnitude of force on the current carrying conductor is, F = BIl sin 𝜽, Where 𝜽 is the angle between length of the conductor in the, direction of current and magnetic field, The direction of force is given by Flemings left hand rule, Stretch the forefinger , middle finger and thumb of left hand in, mutually perpendicular directions , if forefinger points in the direction of, magnetic field, middle finger points in the direction of current then thumb, gives the direction of magnetic force, , Force, , current, , Force, , PROBLEM 1, , ANSWER:, , F= 0.6 N, , 4.5 MAGNETIC FIELD DUE BTO A CURRENT ELEMENT –BIOT, SAVART LAW, Intensity of magnetic field at a point due to a current element is, (i) directly proportional to current through it, dB α I, (ii) directly proportional to length of the current element, dB α dl, (iii) inversely proportional to the square of the distance between the, current element and the point, dB α, , 𝟏, 𝒓𝟐, , (iv)This magnetic field is perpendicular to the plane of displacement vector, and current element

Page 60 :
x, ie dB ∝, , 𝑰 𝒅𝒍 ×𝒓, 𝒓𝟑, , ( dB is perpndicular to I𝒅𝒍 × 𝒓 ), , dB ∝, dB =, , 𝑰 𝒅𝒍 𝐬𝐢𝐧 𝜽, 𝒓𝟐, 𝝁𝟎 𝑰 𝒅𝒍 𝐬𝐢𝐧 𝜽, 𝟒𝝅, 𝒓𝟐, , where 𝝁𝟎 is called permeability of free space, Comparison of Coulombs Law and Biot- Savart’s Law,  Both these fields are Vectors,  Both the source are linear in the source,  Both these fields have very long range,  Both these fields obey inverse square law,  Both obey super position principle,  Electric field is produced by a scalar source charge but Magnetic, field is produced by a Vector source current element(I𝒅𝒍 ),  Electrostatic field is acting along the displacement vector, but the, magnetic field is perpendicular to the displacement vector,  There is an angular dependence in Biot savarts law which is not, present in Coulombs Law, APPLICATION OF BIO SAVRTS LAW, Magnetic field On the axis of a circular current loop:, , B, Consider a circular loop of radius R carrying a current I. P is a point at a, distance x from the centre O of the loop.

Page 63 :
N=1, Substituting the values, B= 1.88 x 10-4T, Direction into the plane of the paper, (2) magnitude is same B= 1.88 x 10-4T, Direction out of the plane of the paper, , 4.7 &4.8 AMPERES CIRCUITAL LAW, , Applications Of Amper’s Circuital Law, (a) Magnetic Field out Side a long Straight Wire Carrying Current:-, , B, dl, , To find the magnetic field at P due to a infinite straight wire carrying, current I , consider an Amperian loop in the form of a circle of radius r, Applying Ampere’s Circuital theorem, , ∮ 𝒅𝒍 = 2𝝅𝒓, , But, , = 𝛍𝟎 𝑰𝒆𝒏𝒄, , Ienc = I, 𝐁 × 𝟐𝝅𝒓 = 𝛍𝟎 𝑰, B=, PROBLEM 1, , 𝝁𝒐 𝑰, 𝟐𝝅𝒓

Page 64 :
ANSWER, I= 90A and r= 1.5m, B=, , 𝝁𝒐 𝑰, 𝟐𝝅𝒓, , Substituting B = 1.2 x10-5 T, To find the Direction use Right Hand Thumb Rule as follows, , B, Applying Right hand Thumb rule when current flows east to west the, direction of magnetic field will be towards south, (b) Magnetic field due to a Solinoid, A long insulated wire wound in the form of a helix is called a, solenoid. For a long solenoid magnetic field exist only inside the solenoid,, outside magnetic field is zero, , dB, , dl, , To find the magnetic field at P consider an Amperian loop abcd in, the form of a rectangle and applying Amperes circuital Law

Page 67 :
B= 𝝁𝟎 𝒏𝑰, , (a), n=, , 𝑩, 𝝁𝟎 𝑰, , =, , 𝟎.𝟎𝟐𝟕, 𝟒×𝟑.𝟏𝟒×𝟏𝟎−𝟕 ×𝟏𝟐, , = 1791, b) Radius of solenoid = .014 m, Circumference = 2𝝅𝑹= 2x3.14x.014=0.08792, Total number of turns,N= nl = 0.4x1791 m, Total length of wire= .08792x0.4x1791, = 629.8m, 4.10.1 TORQUE ON A RECTANGULAR CURRENT LOOP IN A, UNIFORM MAGNETIC FIELD, , (a) Plane of the coil is along the direction of Magnetic Field :-, , A current carrying Conductor placed in a magnetic, field experience a Force . Rectangular coil can be considered as, made up of four conductors AB,BC,CD and DA ., Force on BC = 0 ( = 0), Force on AD = 0 (𝜽 = 180 ), Force on AB, F1 = IbB, Force on CD, F2 = IbB, Force on AB = Force on CD = IbB, These forces are equal and opposite, but they are not, collinear .There for net force on the loop is zero and loop, experiences a torq

Page 68 :
Torque 𝝉 = one of the force x perpendicular distance, between them, 𝝉 = (IbB)a = IB(ab)= IAB, 𝝉= mB, Where ab = A is the area of the loop and m = IA is the, magnetic moment., (If coil have N turns , m = NIA), (b) Plane of the coil is inclined to the magnetic field :-, , Here the rectangular coil makes an angle with the magnetic, field. Let 𝜽 is the angle between magnetic field and normal to the, plane of the coil., Magnetic moment makes angle 𝜽 with the magnetic field B, Force on BC and DA are equal and opposite and cancels, each other, Force on AB and CD are equal (F1=F2= IbB) and opposite, and not collinear . So loop experiences a torque., Torque 𝝉 = one of the force x perpendicular distance, between them, 𝝉 = (IbB)a sin𝜽

Page 71 :
The galvanometer consists of a coil, with many turns, free to, rotate about a fixed axis in a uniform radial magnetic field. There, is cylindrical soft iron core which not only makes the field radial, but also increases the strength of the magnetic field., A current carrying rectangular coil placed in a magnetic, field experiences a torque. This torque tends to rotates the coil, The deforming torque 𝝉 = NIAB, (since field is radial 𝜽 = 𝟗𝟎 , or sin𝜽 = 1 ), Restoring torque developed in the spring, 𝝉 = k∅, Where ,k, torsional constant or restoring torque per unit twist, ∅, angle of twist, At equilibrium restoring torque = deflecting torque, k∅ = NIAB, or I =(, , 𝒌, 𝑵𝑨𝑩, , )∅, , k, N , A and B are constants, ∴, I∝∅, I= K∅ where K =, , 𝒌, 𝑵𝑨𝑩, , is called galvanometer, , constant, Principle: When a constant current flows through the, galvanometer, due to torque it rotates and the angle of rotation is, directly proportional to current through it, Current sensitivity: Deflection per unit current, ∅, 𝑰, , =, , 𝑵𝑨𝑩, 𝒌, , Current sensitivity can be increased by, (i) increasing the number of turns (N), (ii) increasing the area of the coil (A), (iii) increasing the strength of the magnetic field, (iV) Decreasing the value of k, Voltage sensitivity: Deflection per unit voltage, ∅, 𝑰, ∅, , =, , 𝑰𝑹, , Voltage sensitivity, , 𝑵𝑨𝑩, , =, ∅, 𝑽, , 𝒌, 𝑵𝑨𝑩, 𝒌𝑹, , =, , 𝑵𝑨𝑩, 𝒌𝑹, , Note : voltage sensitivity cannot be increased by increasing the, number of turns because when number of turns is doubled(, increased) the resistance also get doubled and voltage sensitivity, remains same

Page 74 :
Chapter5: MAGNETISM AND MATTER, 5.3 MAGNETISM AND GAUSS,S LAW, , Magnetic flux passing through a closed surface is zero or net magnetic flux, through any closed surface is zero, ie magnetic monopoles do not exist, , 5.4 THE EARTHS MAGNETISM, The strength of the magnetic field varies from place to place on the earths, surface its value is of the order of 10-5T, Cause of earths magnetism:, , MAGNETIC ELEMENTS OF EARTH, Geographic Meridian: A vertical plane passing through geographic north, and geographic south poles, Magnetic Meridian: A vertical plane passing through magnetic north and, magnetic south poles, The elements of earths magnetic field are: 1.Declination (D), 2.Dip or, inclination (I), 3. Horizontal component of earths magnetic Field(HE):, 1.Declination (D):

Page 75 :
Angle between geographic meridian and magnetic meridian is called, declination, , Declination is greater at higher latitudes and smaller near equator, , 2.Dip or inclination (I), The angle between the total magnetic field(BE) and horizontal of a place is, called dip, , 3. Horizontal component of earths magnetic Field(HE):, Resolved component of earths magnetic field in the horizontal direction, ZE= BE sin I ………..(1), HE = BE Cos I……….(2), 𝒁, tan I = 𝑬, 𝑯𝑬, , Squaring and adding(1) and (2) BE = √𝒁𝑬 𝟐 + 𝑯𝟐 𝑬, Qn No:1, , ANSWER:, HE = 0.26 G and I= 600, HE = BE Cos I, 𝑯, Cos 60 = 𝑬, BE =, , 𝑩𝑬, 𝑯𝑬, , 𝒄𝒐𝒔 𝟔𝟎, , =, , 𝟎.𝟐𝟔, 𝟏/𝟐, , = 0.52G, , 5.5 MAGNETISATION AND MAGNETIC INTENSITY, MAGNETISATION (M), Net magnetic moment per unit volume of a sample is called, magnetisation(M)

Page 76 :
M=, , 𝒎𝒏𝒆𝒕, 𝑽, , M is a vector with dimension L-1A and unit Am-1, MAGNETIC INTENSITY OR MAGNETISING FIELD (H), For an air cored solenoid magnetic field, B0= 𝝁𝟎 nI= 𝝁𝟎 𝑯, The term nI=H is called magnetic intensity, Unit of H is Am-1, SUSCEPTIBILITY ( 𝝌 ), Magnetisation M is proportional to magnetic intensity H, ie M ∝ H, M=𝝌H, 𝝌=, , 𝑴, 𝑯, , Ratio of magnetisation and magnetic intensity is called susceptibility ( 𝝌 )., Susceptibility has no unit, Relation between susceptibility and permeability, If the interior of the solenoid is filled with a material with non zero, magnetisation, the field inside the solenoid will be greater than B0, The net magnetic field B in the interior of the solenoid is, B = B0 + Bm, = 𝝁𝟎 𝑯 + 𝝁𝟎 𝑴, But M = 𝝌 H, B = 𝝁𝟎 H ( 1+ 𝝌 )……(1), Also B= 𝝁 H= 𝝁𝟎 𝝁𝒓 H……(2), Where 𝝁 = 𝝁𝟎 𝝁𝒓, From (1) and (2), 𝝁𝒓 = ( 1+ 𝝌 ), , CHAPTER 6, ELECROMAGNETIC INDUCTION, The phenomenon in which electric current is generated by varying a, magnetic field is called electromagnetic induction, , 6.4 FARADAYS LAW OF INDUCTION, It states that the magnitude of induced emf in a circuit is equal to the time, rate of change of magnetic flux through the circuit, 𝜺=-, , 𝒅𝝓𝑩, 𝒅𝒕, , ( The negative sign indicates that the direction of induced emf or current ), If coil is having N turns, , 6.5 LENZ,S LAW AND CONSERVATION OF ENERGY, Lenz’s law states that the polarity of induced emf is such that it tends to, produce a current which opposes the change in magnetic flux that produced it, We have ,induced emf 𝜺 = - N, , 𝒅𝝓𝑩, 𝒅𝒕, , Negative sign represents this effect

Page 77 :
Note- If current is flowing in clockwise direction south pole and if current is, flowing in anticlockwise direction north pole are produced, 𝜺=-N, , 𝒅𝝓𝑩, 𝒅𝒕, , PROBLEM:, , Explanation Of Lenz’s Law:, , When north pole of a magnet is moved towards a circular coil,, magnetic flux increases and according to Lenz’s law the direction, of induced emf is so as to reduce the flux. To oppose the north, pole of the magnet or to reduce the flux North pole must be, developed there.Therefor induced current flows in anticlockwise, direction.

Page 78 :
When north pole of a magnet is moved away from a circular coil,, magnetic flux decreases and according to Lenz’s law the direction, of induced emf is so as to increase the flux. To increase the flux, South pole must be developed there.Therefor induced current, flows in clockwise direction., More examples:, , Lenz’s Law is in accordance with Law of conservtion of Energy:Work done in moving the magnet against the repulsive force is, converted into electrical energy which produces induced electric, current.Thus Lenz’s law is in accordance with law of, conservation of energy., , 6.8 EDDY CURRENTS, , Explanation:, , Consider a pendulum, with metal plate as bob ,oscillating in a magnetic, field produced by a magnet. It is found that the motion of the pendulum is, damped and it comes to rest in a very short time than the pendulum, oscillated without magnetic field ., The reason is that when the pendulum oscillates in the, magnetic field , the magnetic flux linked with the plate changes and an, eddy current is induced in the plate . According to Lenz’s law this induced, current opposes the motion of the plate (bob)

Page 79 :
The eddy current can be minimized by making slots or holes in the plate, .The area available for flow of eddy current is less in this case .Thus, damping is reduced and pendulum oscillates more freely, , Losses due to Eddy current:, (1) unnecessary damping, (2) unnecessary heating eg : in transformers, Methods to Minimize eddy current :, (1) by making slots or holes in the metal plate, (2) use thin sheets instead of metal blocks, (3) laminating the metal sheets, Uses of eddy current:, , 6.9 INDUCTANCE, An electric current can be induced in a coil by flux change, produced by another coil or flux change produced by the same, coil, Flux through a coil is proportional to current

Page 80 :
This constant of proportionality is called inductance, Inductance is a scalar quantity., , MUTUAL INDUCTANCE, , Then corresponding flux linkage with solenoid S1,, , ……….. ( A ), , Then corresponding flux linkage with solenoid S2,

Page 81 :
……….. (B), From A and B , M12 = M21 ie Mutual inductance of first, col with respect to second is equal to mutual inductance of second, coil with respect to first, EMF induced due to mutual induction :-, , It shows that varying current in a coil can induce emf in a, neighbouring coil . This phenomenon is called mutual induction., The magnitude of induced emf depends upon the rate of change, of current and mutual inductance of two coils, SELF INDUCTION, The phenomenon of production of induced emf in a coil due to, the variation of current in the same coil is called self induction

Page 82 :
Back emf, Self induced emf is also called back emf as it opposes any, change in the current in a circuit.self inductance plays the role of, inertia, ENERGY STORED IN AN INDUCTOR

Page 83 :
Note:, , 6.10 AC GENERATOR, Invented by Nicola Tesla.Principle used is electromagnetic induction, , Coil rotates in the magnetic field produced by the magnet and magnetic, flux linked with the coil changes and an emf is induced in it., Expression for induced emf:-, , From the above equation the emf and hence current varies periodically, with time and therefor the current is called alternating current ( ac), Sine 𝝎 = 2𝝅𝝑, 𝜺 = 𝜺𝟎 sin 2𝝅𝝑t

Page 84 :
Graphical Representation, , Step2, , Step1, , Step 4, , Step 3, , Step 5, \, For one complete rotation, , Graph can be plotted11Q11, , as, , Note:1, Depending on mechanical energy required for rotation of armature coil ac, generators can be named as follows, 1. Hydro electric generators- use water falling from a height, 2. Thermal generators- water is heated to produce steam using coal or, other sources, 3. Nuclear power generators- nuclear fuels, Note 2:, Frequency of ac in India is 50 Hz and in USA it is 60Hz, , CHAPTER 7, ALTERNATING CURRENT, 7.2 &7.3 AC VOLTAGE APPLIED TO A RESISTOR, The voltages or current that varies with time are called alternating voltage, or alternating current (ac)

Page 85 :
AC voltage applied to a resistor, , 𝑉𝑚 sin 𝜔𝑡, =0, , i = im 𝑠𝑖𝑛 𝜔𝑡, where im =, , 𝒗𝒎, 𝑹, , is called peak value of current or maximum value of current, , Graphical representation:, , From the graph it is clear that voltage and current are in same phase, Note : phasors

Page 88 :
Where 𝒊𝒎 =, , 𝒗𝒎, 𝑳𝝎, , ,is peak value of current, , Inductive reactance (XL), Inductive reactance is the opposition to the flow of current through an, inductor, , Comparing the above equations, , 𝑋𝐿 ∝ 𝑓, , Phase Relation between voltage and current, , ….. (1), , From (1) and (2), , Graphical Representation of voltage and current, , ….(2)

Page 90 :
7.5 AC voltage applied to a capacitor, , An ac voltage V= 𝒗𝒎 𝐬𝐢𝐧 𝝎𝒕 is applied to a capacitor., Applying, , Current, , Where, , The peak value of current, Capacitive reactance (XC), Opposition to the flow of current through a capacitor is called capacitive, reactance, , We have, , Comparing we get

Page 91 :
SI unit is ohm(𝛀), , Phase Relation between voltage and current, , …… (1), , …… (2), From (1) and (2), , Graphical Representation of voltage and current, , Phasor Diagram, , Power dissipated in the capacitor

Page 92 :
PROBLEM 2, , 7.6 AC VOLTAGE APPLIED TO A SERIES LCR CIRCUIT

Page 93 :
Expression for Impedance ( Z ), An alternating voltage V= 𝒗𝒎 𝐬𝐢𝐧 𝝎𝒕 is applied to an series LCR circuit, , Expression for phase difference ( ∅) using phasor diagram, , Expression for phase difference ( ∅) using impedance triangle, A triangle connecting resistance values of an LCR circuit is called, impedance triangle

Page 96 :
Example:-, , Graph can be plotted as follows, , (i), (ii), , From the graph it is clear that the value of maximum current or, peak current (im) depends on the value of resistance R in the, circuit. When value of resistance increases the peak value, decreases, Application of LCR circuit, Tuning mechanism of a radio or TV set:, Tuner of a radio or TV consists of a series LCR circuit. We vary, the capacitor of LCR circuit to select a particular radio station, such that the resonant frequency of the circuit become nearly, equal to the frequency of radio signal received., Then the amplitude of current will be maximum and a particular, station get selected., Sharpness of resonance

Page 97 :
𝝎𝟏 and 𝝎𝟐 are the frequencies at which the power decreases to, half or current decreases to, , 𝟏, √𝟐, , times the maximum value of, , current., Then, , is called, Then the sharpness of resonance is defined as the ratio of, resonant frequency to band width, , From resonance graph it is clear that, , To Find the band width:, We have, , Solving this equation we get, , Therefor

Page 98 :
Or s =, , =Q, , Sharpness(S) = Quality factor (Q)( numerically), Conclusion:, , For high quality tuning band width should be small and sharpness, should be high, 7.7 POWER IN AC CIRCUIT & POWER FACTOR, We have power, , Or, , or P= 𝑽𝒓𝒎𝒔 𝑰𝒓𝒎𝒔 𝐜𝐨𝐬 ∅, Thus power in an LCR circuit depends not only on V and I but, also on cosine of power factor (∅), Power factor :, , Using impedance triangle, , Power factor,

Page 99 :
Special Cases, , In a resistive circuit voltage and current are in phase ie, , ASSIGNMENT

Page 100 :
CHAPTER 8, ELECTRO MAGNETIC WAVES, Electromagnetic waves are time varying electric and magnetic fields that, propagate in space with a speed of 3× 108 m/s., 8.2 DISPLACEMENT CURRENT, , Consider a capacitor connected to an ac source., , r, Applying amperes circuital theorem ,Magnetic field at p is, ∮ 𝑩 . 𝒅𝒍 = 𝝁𝟎 i(t), 𝑩 ∮ 𝒅𝒍 = 𝝁𝟎 i(t), B. 2𝝅𝒓 = 𝝁𝟎 i(t), B=, , 𝝁𝟎 𝐢(𝐭), 𝟐𝝅𝒓, , Now consider a pot like surface which has same boundary .Applying, Amperes circuital law to such surfaces , we get ∮ 𝑩 . 𝒅𝒍 = 0 ,because no, current passes through the surface 𝝁𝟎 i(t) = 0 , B= 0, r

Page 101 :
But the magnetic field is not zero. This inconsistency is solved by Maxwell, using the concept of Displacement current, The varying electric field between the plates of the capacitor is given by, , Electric flux,, Rate of change of charge, Which is current,, , This current is called Displacement current., Therefor total current, , (Ampere – Maxwell equation), , Using this equation magnetic field, we can find the magnetic field for any, type of surface as Amperian loop.Thus inconsistency in Amperes circuital, theorem is solved by using Ampere – Maxwell equation, , Thus both displacement current and conduction current can produce, magnetic field

Page 102 :
This symmetric nature helped Maxwell to predict the existence of em waves, using Maxwells equations as follows, , PROBLEM, , ANSWER:, (a), , ( b) magnitude of conduction current and displacement current are equal, (c) yes, if conduction current is taken as positive displacement current is negative, There for algebraic sum of current at a plate is zero, Kirchhoffs, junction rule

Page 103 :
8.3 SOURCE OF ELECTRO MAGNETIC WAVES, An oscillating charge ( accelerating charge) produces an oscillating electric, field in space ,which produces an oscillating magnetic field. This oscillating, magnetic field is a source of oscillating electric field and so on.This electric, field and magnetic fields are perpendicular to each other. Thus electric and, magnetic field produced by accelerating charge propagates through space, and electro magnetic waves are produced, , Qn No 1: Is it possible to produce visible light with an oscillating charge?, Ans: No, because frequency of yellow light is ≈ 1014Hz. But we can get, frequency ≈ 1011Hz only., NATURE OF ELECTRO MAGNETIC WAVES, Expression for electric and magnetic field, Let an em wave is propagating along Z axis , with electric field along x axis, and magnetic field along y axis, The electric field and magnetic, field can be represented as, , PROPERTIES OF ELECTROMAGNETIC WAVES, , c

Page 104 :
CHAPTER 9, RAY OPTICS AND OPTICAL INSTRUMENTS, , 9.2 REFLECTION, LAWS OF REFLECTION:, , (1) Incident ray ,reflected ray and the normal at the point of incidence lies, in the same plane, (2) angle of incidence is equal to angle of reflection, i= r, spherical mirrors, A mirror which is the part of a sphere, (1) concave mirror- reflection occurs from inner surface, (2) convex mirror- reflection occurs from outer surface, , Pole (p): center of the spherical surface, Center of curvature (C): center of the sphere of which mirror is a part, Radius of curvature (R): distance between pole and center of curvature, Principal axis : Straight line passing through center of curvature and pole, , Principal axis

Page 105 :
Sign conventions, , (1) All the distances are measured from the pole, (2) distances measured in the same direction of incident light is positive and, distances measured opposite to incident light is negative, (3) All the measurements above x axis ( principal axis) is positive and below, x axis is negative, Notes : image formation, (1) A ray parallel to principal axis after reflection from the mirror passes, through principal focus, , (2) A ray incident at pole at an angle reflects with same angle obeying law, of reflection, , (3) A ray incident at center of curvature reflects through same path, , Eg : image formed by an object at center of curvature, , Focal length (f)

Page 106 :
Rays parallel to principal axis converges to a point on the principal axis in, the case of a concave mirror and appears to diverge from a point on the, principal axis in the case of a convex mirror., This point is called principal focus (F) and distance between pole and, principal focus is called focal length (f), RELATION BETWEEN FOCAL LENGTH (f) AND RADIUS OF, CURVATURE(R) :, , ………. (1), (1), , ……… (2), (2), ASSIGNMENT:, (A) Object is placed beyond C, , Image is formed between C and F . inverted ,real and diminished, (b) object between C and F, , Image is formed beyond C, enlarged , real and, Inverted

Page 107 :
(c) object at F, , image is formed at infinity, , MIRROR EQUATION, Mirror equation is the relation between object distance u, image distance v, and focal length f for a spherical mirror., , From fig right angled triangle A’B’F and MPF are similar., Therefore,, , …………(1), , …………(2), , ………… (3), By applying sign conventions ,we get, B’P= -v, FP = -f, BP= -u, Substituting in 3 we get

Page 108 :
This relation is known as mirror equation, , MAGNIFICATION (m), Magnification(m) is the ratio of height of the image to (h’) to height of the, object(h), , m=, , 𝒉′, 𝒉, , From above ray diagram, , With the use of proper sign convention this equation is applicable for all, types of spherical mirrors, , 9.3 REFRACTION, , When a ray of light travels from one medium to another ,it bends . This, phenomenon is called refraction., LAWS OF REFRACTION, 1. The incident ray ,the refracted ray and the normal at the point of, incidence all lie in the same plane, , 2. Ratio of sine of angle of incidence to sine angle of refraction is a constant, .This law is called Snell’s law

Page 109 :
Refractive index, Refractive index depends on optical density of medium. It is minimum, for air, , If light enders from second medium to first, , Also we have, , From above equations, , Refractive index of second medium with respect to first, medium is the reciprocal of refractive index of first medium, with respect to second, Note: when light travels from rarer medium to denser medium ( eg:, air to water) it bends towards normal and when light travels from, denser medium to rarer medium( eg: water to air) it bends away, from normal, , Note 2: refraction through a glass slab

Page 110 :
Angle of incidence at the air glass interface is equal to angle of emergence ., Incident ray and refracred ray are parallel, eventhough there is a latteral, shift., Note 3: Refraction through three different medium, , Multiplying three equations, , Therefor refractive index of third medium with respect to secondmedium, is equal to refracive index of third medium with respect to fist medium, divided by refractive index of second medium wirth respect first medium, If first medium is air, then we call it as absolute refracrine index, , APPLICATIONS OF REFRACTION, 1. Real depth and apparent depth:, , The bottom of a tank filled with water appears to be raised due to, refraction., , 2.Atmospheric refraction, Sun is visible a little before actual sunrise and until a little, after sun set due to atmospheric refraction.

Page 111 :
9.5 REFRACTION AT SPHERICAL SURFACE, , Consider a spherical surface with center of curvature C , radius of, curvature R and refractive index n2, Image I of a point object O is formed on the principal axes. Consider the, triangles NOM,NCM and NIM., For small angles, , (1), , ..........(2) [From equation(1) ], , …….(3), Applying Snell’s Law, , [From equation(1)

Page 113 :
LENS MAKERS FORMULA and thin lens formula, A lens is a part of two spherical surfaces . We have the equation for, refraction at a spherical surface, , Consider the first surface ABC the above equation becomes, , ……..(1), , Similarly For second surface ADC, , ………(2), Combining these two spherical surface, forms a lens, , Adding equation (1) and (2) we get, , (For a thin lens BI1 = DI1 )

Page 115 :
The first lens A forms image at I1 at a distance V1,then we can write, , ……(1), This image act as object for second lens B and final image is formed at V, , …….(2), Adding equation (1) and (2) we get, , …….(3), , …….(4), From (3) and (4) we get the focal length of combination, , For several lenses of focal length f1,f2,f3…., , And power, , Magnification, Magnification is the ratio of size of image to size of object, , 9.6 REFRACTION THROUGH A PRISMExpression for refractive index of prism, The angle between the emergent ray and the direction of incident, ray is called angle of deviation(𝜹)

Page 119 :
For image formed at near point,, , For image formed at infinity,, , From the equations for magnifications , it is clear that the value of, magnification when image is formed at, infinity is one less than the value of magnification when image, formed at near point., COMPOUND MICROSCOPE, In compound microscope we uses two convex lenses. The lens, near object called objective forms real inverted and magnified, image of the object. The lens near eye called eyepiece which, functions like a simple microscope and produces final image, which is enlarged and virtual., If the image formed by objective is within or near the, principal focus of eyepiece , the final enlarged image is formed at, infinity or near point(D), , L, , N, , 𝐹, , of objective, , From ∆𝑶𝑵𝑭, Tan𝜷 =, , 𝑶𝑵, 𝑶𝑭, , =, , 𝒉, 𝒇𝒐, , ………(1), , he distance between the second focal point of objective and first, focal point of eyepiece (fe) is called tube length(L) of compound, microscope., From∆A’B’F

Page 120 :
Tan𝜷 =, , 𝒉′, , ……….(2), , 𝑳, , From (1) and (2), 𝒉′, 𝑳, , =, , 𝒉′, , mo =, , 𝒉, 𝒇𝒐, , =, , 𝒉, , 𝑳, 𝒇𝒐, , , magnification of objective, , Magnification of eyepiece :, Since eyepiece act as simple microscope we have, me = ( 1+, me = (, , 𝑫, 𝒇𝒆, , 𝑫, 𝒇𝒆, , ) , image formed at near point, , ), image formed at infinity, , Total magnification, m = mo × me, m=, m=, , 𝑳, 𝒇𝒐, 𝑳, 𝒇𝒐, , [1+, [, , 𝑫, , 𝒇𝒆, , 𝑫, 𝒇𝒆, , ], , ], , image formed at near point, image formed at infinity, , Note: To increase magnification, fo and fe should be small. Practically it is, difficult to make focal length small. There for tube length (L) can be, increased to increase the magnification., , CHAPTER 10 :WAVE OPTICS, WAVE FRONT, Wave front is a surface of constant phase. Velocity of a wave front is same, as velocity of wave. Energy of wave travels in a direction perpendicular to, wave front. Light rays are perpendicular to wave front, Light diverging from a point source, , Plane wave front, , Wave front, , Light Ray, , Light emerging out of convex lens, when a point source is placed at its focus, 10.2 HUYGENS WAVE THEORY, According to Huygens principle,each point of wave front is a source of a, secondary disturbance .The wavelets originating from these points( called, secondary wavelets) spread out in all directions with the speed of the wave., The common tangent to all these spheres gives the new wave front., Eg:Propagation of plane wave front

Page 123 :
Let S2P ≈ S1P = D, , Path difference =, If point P is a bright band, , This is the distance of nth bright band from centre O of the screen, Next bright band (n+1)th occurs at, , Difference between these gives fringe width of dark band, , 𝑥𝑛+1, , p, Fringe width, , 𝛽, , 𝑥𝑛, , Band width is incrased by increasing wavelength (𝝀 ), increasing, distance between screen and source (D)and decreasing the, separation of slits (d)., 10.7 POLARISATION OF LIGHT, Light is a transverse wave .The electric field associated with a propagating, light wave is always perpendicular to the direction of propagation., Un polarised light:, If electric field vibrate in all possible directions , then light is called un, polarised light

Page 124 :
Polarised light:, If electric field vibrations are only in one plane, then light is called, polarized light, The phenomenon of restricting the vibration in a particular plane is called, Polarisation, LAW OF MALUS, Case 1- pass axes of polarizer and analyser parallel, , 𝑷𝟏, , 𝑷𝟐, , Case 1- pass axes of polarizer and analyser perpendicular, , Malu’s law states that if 𝜽 is the angle between the pass axes of polarizer, and analyser , the intensity of emergent light is proportional to square of, the cosine of the angle 𝜽 between them, , Polaroids work on the principle of Malus Law. Polaroids are used in sun, glasses, photographic camera, 3D movies etc

Page 125 :
POLARISATION BY SCATTERING, , The unpolarised light from sun undergoes scattering by atmospheric air, molecules.The electrons of atmospheric air molecules vibrates by absorbing, the electric field of sunlight and produces light waves.The electric field of, this light wave is perpendicular to the electric field of sun light.For an, observer standing perpendicular receives polarized light., Indian scientist C V Raman got Nobel prize in 1930 for his study on, Polarisation by scattering, POLARISATION BY REFLECTION, When an un polarized light is incident on a transparent medium, the, refracted light is un polarized and reflected light is partially polarised, , For a particular angle of incidence , the reflected light is completely, polarized , This angle is called Brewster’s angle ( angle of polarization), At Brewster’s angle, the reflected ray and refracted ray are mutually, perpendicular, Brewster’s Law, When light is incident at the boundary of two transparent media at, Brewster’s angle, the tangent of angle of polarization( Brewster’s angle) is, equal to refractive index of the medim.

Page 126 :
𝝁 = 𝐭𝐚𝐧 𝒊𝑩, Proof:, , Note: If light is incident on water, , Qn: State Brewster's law. Prove that if light is incident at the angle of, polarization the reflected and refracted rays are mutually perpendicular.

Page 127 :
CHAPTER 11: Dual nature of radiation & matter, , 11.3 PHOTO ELECTRIC EFFECT, When light of suitable frequency is incident on metal surface, electrons are, emitted.This phenomenon is called photo-electric effect and emitted, electrons are called photoelectrons, Metals like Zinc,Cd,Mn etc responded only to ultraviolet light., However , some alkali metals like Li,Na.K,Cs where sensitive even to, visible light., , Laws of photoelectric effect

Page 128 :
11.6 EINSTEIN’S PHOTOELECTRIC EQUATION, When a photon is incident on a metal surface,it will be absorbed by a single, electron.The electron uses this energy in two ways, (a) One part is used to escape from the metal surface( to provide work, function, ∅𝟎 ), (b) One part is used to increase its kinetic energy, Photon energy (E) = work function + kinetic energy

Page 129 :
Equation (5) can be represented graphically as follows, , NOTE:, Millikan ploted above graph for different metals and calculated the slope, , Since this value of planks constant agree with the actual value, Millikan, proved einsteins photoelectric equation, Explanation Of Laws of photoelecric Effect Based on Einsteins, Photoelectric equation :

Page 130 :
Momentum of photon:

Page 131 :
11.7 PARTICLE NATURE OF LIGHT : THE PHOTON, We can summarise the photon picture of em radiation as follows:

Page 132 :
PROBLEM 1, , CHAPTER 12: ATOMS, 12.4 BOHR ATOM MODEL, Bohr’s postulates are,, , (1), (2)

Page 133 :
(3), , Expression for velocity , Radius , energy of a revolving electron, By Bohr’s postulate the angular momentum of nth orbit is, , Comparing above two equations, , Substituting the values, , Where C is velocity of light, , For first orbit n=1, There for radius of first orbit r1 = 0.5 A0, This radius is called Bohr radius, Also Energy of nth orbit is given by, , SREESHYJU K P,HSST PHYSICS GHSS VYTHIRI,WAYANAD, JIJESH M T ,GVHSS PAY YOLI

Page 134 :
Substituting for rn, , Energy of first orbit , n=1(ground state ), E1 = -13.6 ev, Energy level diagram, ,  The energies of higher level become closer and closer as n increases,  The highest energy state corresponds to n = ∞ and has energy of 0 eV,  The lowest energy state of atom(for n=1,, E= -13.6eV) is called ground state. The minimum energy required to, free an electron from the ground state is 13.6 eV and is called, ionization energy, , Energy of 𝑛𝑡ℎ orbit is

Page 135 :
12.6 De Broglies Explanation of Bohr’s second postulate of quantisation:, According to De Broglie an electron revolving in circular orbit must have, a particle nature and wave nature., , n, , 𝒉, , But 𝝀 = =, n, , 𝒑, , 𝒉, 𝒎𝒗 n, , This is Bohr’s second postulate using From De Broglies concept, Eg: for n= 4, 2𝝅𝒓𝒏 = 4𝝀, LIMITATIONS OF BOHR MODEL, 1. Bohr model is applicable to hydrogenic atoms, 2. Bohr model is unable to explain relative intensities of frequencies in the, spectrum, , CHAPTER 13: NUCLEI, 13.2 ATOMIC MASSES AND COMPOSITION OF NUCLEUS, Protons and Neutrons in a Nucleus are together called Nucleons., The number of protons or electrons in an atom is called Atomic, Number (Z), Sum of protons and neutrons or number of Nucleons in an atom, is called Mass number (A), Number of neutrons in atom is called Neutron number(N), Therefor , A= Z +N, An atom X can be represented as, 𝑨, 𝒁𝑿, Eg : Gold can be represented as 𝟏𝟗𝟕, 𝟕𝟗𝑨𝒖, Number of Neutrons N= A – Z = 197 – 79 = 118, Isotops : Atoms having same atomic number but different mass, number

Page 136 :
Eg: 𝟏𝟏𝑯 ( protium), 𝟐𝟏𝑯 ( Deuterium) , 𝟑𝟏𝑯 ( tritium), Isobars: Atoms having same mass number but different atomic, number, Eg : 𝟑𝟏𝑯 and 𝟑𝟐𝑯𝒆, Isotons: Atoms having same neutron number but different, atomic number, 𝟏𝟗𝟕, 𝒆𝒈: 𝟏𝟗𝟖, 𝟖𝟎𝑯𝒈 and 𝟕𝟗𝑨𝒖 , number of neutrons = 118, Atomic mass unit ( a. m. u ) or (u) : One atomic mass unit is, , 𝟏 th, 𝟏𝟐, , of the mass of Carbon 12 atom, , Charge of a nucleus is + Ze, Mass of neutron mn = 1.00866 u = 1.6749 x 10-27 kg, , 13.3 Size of the Nucleus:, Volume of a nucleus is proportional to its mass number., , MASS – ENERGY RELATION, Mass can be converted into energy., ie E= mc2, where m is the mass and c is velocity of light in vacuum( c= 3x108, m/s ), problem 1:

Page 137 :
Radioactive decay is a nuclear phenomenon in which an unstable nucleus, undergoes a decay., Three types of radioactive decay occur in nature, , NUCLEAR FORCE, The forces acting between the nucleons of a nucleus are called, Nuclear force., , Potential energy versus separation graph:-, , Features of Nuclear forces:, 1.Strongest attractive forces in Nature 2. They are charge, independent 3. They show saturation 4. They are very short range, forces

Page 138 :
Assignment:, , ANSWER

Page 139 :
13.6 Law of Radioactive Decay, This law states that the number of nuclei undergoing decay per unit time is, proportional to total number of nuclei in that sample., If N is the number nuclei in the sample and ∆𝑵 undergo decay in, time ∆𝒕, , Where 𝝀 is a constant called radioactive decay constant or disintegration, constant., Change in number of nuclei in the sample is, dN = - ∆𝑵 in time ∆𝒕 ( negative sign shows that sample is decaying or, decreasing), The rate of change of N is, , Integrating the above equation on both sides, , Where N0 is the number of atoms present at t0 (initial time) and N is the, number of atoms present at time t, t, [ ln N ] N = -𝝀[ t ], 𝑁0, , ln N – ln N0 = -𝝀 (t- t0 ), , 𝒕𝟎, , 𝟏, , [ 𝒔𝒊𝒏𝒄𝒆 ∫ = ln N], 𝑵, , setting t0 = 0, , Since ln A- ln B= ln, N= N0𝒆−𝝀𝒕, This equation is called law of radioactive decay, Then decay rate, , R= (-𝝀) (-N0𝒆−𝝀𝒕 ), , 𝑨, 𝑩

Page 140 :
Activity of a sample (R), , The total decay rate R of a sample of one or more radio nuclides is called, activity of that sample,  SI Unit of radioactivity is Becquerel (Bq), 1 Bq = 1 decay per second,  Another unit is curie, , HALF LIFE PERIOD ( T1/2 ), The time taken by half the number of the atoms of the radio active element, to disintegrate is called Half life, Or it is the time at which both N and R have been reduced to one half of, their initial value, Relation between T1/2 and 𝝀, We have, , Taking reciprocals on both sides, 2= 𝒆𝝀𝑻𝟏/𝟐, , MEAN LIFE (𝝉 ), 𝟏, , It is the time at which both N and R have been reduced to of, 𝒆, , their initial value

Page 141 :
On solving this we get, , Mean life, Relation between half life and mean life, , By substituting, PROBLEM 1, , ALPHA DECAY, When a nucleus undergoes alpha decay (Helium nucleus) , the, atomic number of parent nucleus decreases by two and mass, number decreases by four. ie, , The difference between the initial mass energy and the final mass, energy of the decay product is called the Q value of the process or, disintegration energy, Here mx is mass of parent nucleus ,my is the mass of daughter, nucleus and mHe is the mass of helium nucleus.Eg:, , BETA DECAY, When a nucleus undergoes beta decay an electron( beta minus) or, positron(beta plus) is emitted ., In 𝜷− decay a neutron is converted into proton ,electron and an, anti neutrino( atomic number increases by one and mass number, SREESHYJU K P,HSST PHYSICS GHSS VYTHIRI,WAYANAD, remains same), JIJESH M T ,GVHSS PAYYOLI

Page 142 :
Eg:, , In 𝛃+ decay a proton is converted into nutron,positron and, neutrino, Eg:, , GAMMA DECAY, When a nucleus is in an excited state ,it can make a transition to a, lower energy state by the emission of electromagnetic radiation., As the energy differences between levels in a nucleus are of the, order of MeV, the photons emitted by the nuclei have MeV, energies and are called Gamma rays.Atomic number and mass, number does not change during gamma decay, , CHAPTER 14: SEMICONDUCTOR ELECTRONICS, 14.3 INTRINSIC SEMICONDUCTOR, Eg: germanium,silicon, Semiconductor in pure form( without any impurity) is called, intrinsic semiconductor, A germanium or silicon have four valance electrons. They, form covalent bond by sharing four valance electrons with each, other and have eight electrons in the outermost orbit.

Page 143 :
At room temperature the covalent bond breaks and an electron, become free leaving a hole. These electrons and holes are, responsible for conduction.Therefor total current is sum of, electron current (Ie) and hole current( Ih).ie I= Ie + Ih Number of, electrons and holes are equal in an intrinsic semiconductor, ie ne = nh, , 14.4 EXTRINSIC SEMICONDUCTOR, The conductivity of a semiconductor can be increased by adding, an impurity. This type of semiconductors are called extrinsic, semiconductor. The process of adding impurity is called doping, and impurity atoms are called dopants., N- type semiconductors: When a pentavalent impurity eg:, antimony(Sb),arsenic(As) is added to germanium or silicon ,four, electron of this impurity forms covalent bond with four, germanium and fifth electron become free even at room, temperature.Since arsenic atom donates an electron they are, called donor atom.An electron hole pair can also be produced, intrinsically .The number of electrons are greater than holes ie ne, > nh ,Thus electrons are majority carriers and holes are minority, carriers in an N- type semiconductor

Page 144 :
Note : An N-type semiconductor is neutral ,because an arsenic, atom become a positive ion leaving an electron , there for the, crystal as a whole is neutral, P- type semiconductor: When a trivalent impurity eg:, Aluminium(Al),Boron(B) is added to germanium or silicon ,three, electron of this impurity forms covalent bond with germanium, .But the forth electron leaves a vacancy(hole). Since trivalent, atom has a vacancy and can accept an electron they are called, acceptor atom.An electron hole pair can also be produced, intrinsically ie The number of holes are greater than electrons ie, nh > ne ,Thus holes are majority carriers and electrons are, minority carriers in a P- type semiconductor., , 14.7 RECTIFIER, The process of converting AC into DC is called rectification. Diode, conducts current when it is forward biased and does not conduct when it is, reverse biased, (a)Diode as half wave rectifier: Half wave rectifier Consist of transformer,, diode and load resister(RL)

Page 145 :
Working: During positive half cycle of input ac ,the diode D is forward, biased and it conducts. During negative half cycle diode is reverse biased, and it does not conducts. we get positive half cycle in output and ac input is, converted to dc output, , The out put voltage is still varying , but is restricted only in one, direction. Since rectified output of this circuit is only for half of, input ac ,it is called half wave rectifier., (b)Diode as full wave rectifier:It consists of a center tap transformer, two, diods D1 and D2 and load resistance RL, , C, , Working: During positive half cycle of ac D1 is forward biased D2 is, reverse biased and current flows through D1 and RL( AD1XRLYC). During, negative half cycle D1 is reverse biased and D2 is forward biased and, current flows through D2 and RL (BD2XRLYC). Thus for both half cycle of, input ac we get the out put current in same direction(dc), , The output voltage is unidirectional, but bit is fluctuating. This pulsating, DC can be converted into pure DC voltage by using a filter circuit. A, capacitor connected parallel to load resistance can be used as a filter

Page 146 :
14.9 LOGIC GATES, It is a digital circuit that follows certain logical relationship between input, and output. They are used in computers, calculator, digital watch,, industrial control system etc. Basic logic gates are OR,AND and NOT gate, (1)NOT gate: It has only one input and one output. Out put is the, compliment of input., Truth table, The Boolean relation is Y=Ā, , s, , Symbol, (2)OR gate: It has two or more inputs and a single output. The out put of, OR gate is one if one or more input is one., Truth table, Boolean relation is Y =A+B, , Symbol, (3)ANDgate: It also has two or more inputs and one output. The out Output of, an AND gate is one if both the inputs are one., Truth table, The Boolean relation is Y=A.B, , Symbol, , Combination of gates, (1) NOR gate: The out put of the OR gate is connected to the input of NOT gate, to get NOR gate, Truth table, ( ie OR + NOT=NAND), , Symbol, , (2) NAND gate: The out put of the AND gate is connected to the input of NOT, gate to get NAND gate, ( ie AND + NOT=NAND), , Symbol

Page 147 :
Truth table, , NOR gate and NAND gate as universal gate:, (1) All basic logic gates ( OR , AND &NOT)can be made using NOR gate, .There for NOR gate is called universal gate, , (2) Al l basic logic gates ( OR , AND &NOT)can be made using NAND gate, .There for NAND gate is called universal gate, , SREESHYJU K P,HSST PHYSICS GHSS VYTHIRI,WAYANAD, JIJESH M T ,GVHSS PAYYOLI