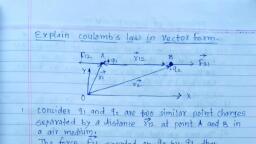
Page 1 :
Yadav Sir ( Sby), , 12.1 Introduction, , 12. Magnetism, , 12.2 Magnetic Lines of Force and Magnetic Field, , 12.3.2 Magnetic Field due to a bar magnet at an arbitrary point, , •, , Magnetic Flux, , 12.4 Gauss Law of Magnetism, , •, , Magnetic Induction, , 12.5 Earths Magnetism, , 12.3 The Bar Magnet, , •, , Magnetic Axis, , •, , Magnetic dipole, , •, , Magnetic Equator, , •, , Fictitious Pole, , •, , Geographic Meridian, , •, , Magnetic Length, , •, , Magnetic Meridian, , •, , Geometric Length, , •, , Magnetic Declination, , •, , Magnetic Axis, , •, , Magnetic inclination or angle of dip, , •, , Magnetic equator, , •, , •, , Earth’s Magnetic Field, , Pole Strength, , •, , Magnetic Maps of the Earth, , •, , Magnetic Dipole Moment, , 12.3.1 Magnetic Field due to, ( a ) A bar magnet at a point along its axis and, ( b ) At a point along its equator

Page 2 :
Yadav Sir ( Sby), , Magnetism : Property of a body by virtue of which it attracts small pieces of iron , is called, magnetism . The body which possesses this attracting property is called magnet., , Freely Suspended Magnet : • For a magnet , north pole (N – pole ) is positive whereas south pole (S – pole ) is negative., • The earth behaves like a huge magnet with its magnetic north pole near geographical south, and magnetic south pole near geographical north., • The earth magnetic field points approximately from geographical south to the north., • Hence , a freely suspended magnet always points in north – south direction., Magnetic poles of Magnet, • The parts of a magnet where there is maximum force of attraction are called magnetic, poles of the magnet., • Each magnet has two poles where attraction is maximum., • Poles are always in pairs i.e. N – pole and S – pole.

Page 3 :
Yadav Sir ( Sby), , ❖ Explain the following terms., Magnetic dipole :-----------------------------------, , N, , S, , 2l, A pair of two magnetic poles of opposite types and equal strength separated by a finite distance is called, magnetic dipole., , Ex :- Bar Magnet , Magnetic needle, Fictitious Pole : S, , N, 2l, , In the case of a magnetic dipole , the two poles cannot be separated from each other . It is not possible to identify, any particular point as the pole of a magnetic dipole., Therefore , a magnetic dipole is supposed to be made up of two fictitious or imaginary poles of equal strength but, opposite in nature, where the entire magnetic property is supposed to be concentrated . One pole is called the north pole (, positive pole ) and the other pole is called the south pole ( negative pole ) .

Page 4 :
Yadav Sir ( Sby), , l, , Magnetic Length : N, , O, -----------------------------------, , S, , 2l, The distance between two poles of a bar magnet is called the magnetic length . It is denoted by 2l , Where l is the, distance of each pole from the center of the magnet., Magnetic length of a bar magnet is given by ,, 5, ---× L, 2l =, 6, Where , L = geometric length of bar magnet., , Geometric length : N, , -----------------------------------, , S, , L, The distance between two ends of a bar magnet is called geometric length., Geometric length of bar magnet is given by ,, 6, L = ---- × 2l, 5

Page 5 :
Yadav Sir ( Sby), , Magnetic axis : ----------------------------------------------------------------S, N, A line passing through the two fictitious poles of a magnet is called the magnetic axis of the magnet., , Magnetic equator : -, , Magnetic equator, , ----------------------------------------------------------------S, N, , A plane passing through the center of a magnetic dipole and perpendicular to its magnetic axis is called, magnetic equator .

Page 6 :
❖ Magnetic lines of force : -, , The path along which a free north pole moves in magnetic field is called magnetic lines of force ., , • Properties of magnetic lines of force : 1. Magnetic lines of force originate from the north pole and end the south pole ., 2. The tangent drawn to a line of force at any point gives the direction of the magnetic field at that point, gives the direction of the magnetic field at that point., 3. Lines of force never intersect each other., 4. In a uniform magnetic field , lines of force are straight lines parallel to each other and are equidistant., 5. The lines of force have a tendency to contract in length . This property explains attractions between, unlike poles., 6. The lines of force exert lateral ; forces of repulsion on each other. This Property explains repulsion, between like poles., , Yadav Sir ( Sby)

Page 7 :
Yadav Sir ( Sby), , ❖ Magnetic Flux : Number of magnetic lines of force passing normally through a given area is called magnetic flux., SI unit : - weber ( Wb ) ., Dimension : - [ L 2 M 1 T -2 A -1 ], ❖ Magnetic Induction : Magnetic induction at a point in a magnetic field is defined as magnetic flux per unit area at that point ., Magnetic induction, , i.e, SI unit, , :-, , Wb/m2, , B, , =, , ϕ, = ------A, , or tesla., , 1 Tesla = 104 Gauss, Dimension : -, , Magnetic flux, --------------Area, , [ L 0 M 1 T -2 A -1 ]

Page 8 :
Yadav Sir ( Sby), , ❖ Pole Strength : -, , ❖ Magnetic Dipole Moment: -, , •, , Pole strength is defined as the concentration of strength, of magnetism at the poles., , •, , It is denoted by (qm )., , •, , For a magnetic dipole , it is given by its magnetic, dipole moment divided by its magnetic length., , •, , m = qm . 2l, m = qm . 2 l, , m, qm = ----, , Where, 2 l is a vector from south pole to north pole., , 2l, , •, , The pole strength of N pole is denoted by ( +m ), and S – pole is denoted by (- m ), , •, , SI unit :-, , •, , Dimension : -, , Am ., [ LA], , The product of pole strength and magnetic length of a magnetic, dipole is called magnetic dipole moment., , •, , SI unit: - Am2

Page 9 :
❖ Magnetic field due to a bar magnet at a point along its axis : M, S, , ------------------------------l, l, , B2, , P, , µ0 2 m, B axis = ---- --------r3, 4π, , B1, , SirS( Sby), Magnitude of magnetic induction at point P dueYadav, to the, –, pole of the magnet is given by ,, , B2, , N, B, r, , Magnetic Induction along its axis, , Consider a bar magnet of magnetic length 2l and the, magnetic dipole moment M, Let P be any point on the axis of the magnet at a distance r, from its center O as shown in figure. We have to find the magnetic, induction at P due to the magnet., NP = r – l, , &, , SP = r + l, , Magnitude of magnetic induction at P due to the N – pole of, the magnet is given by ,, µ0 + qm, B1 = ---- ----4π ( NP ) 2, µ0 + qm, B1 = ---- ----4π ( r - l ) 2, This induction is directed away from the N – pole i.e along NP, or in the same direction as M, , B2, , µ0 - qm, = ---- ----4π ( SP ) 2, µ0 - qm, = ---- ----4π ( r + l ) 2, µ0 qm, = - ---- ----4π ( r + l ) 2, , This induction directed towards the S – pole , i.e along PS or, opposite to M, Thus both B1 and B2 are acting along the axis in opposite, direction., However Since ( r – l ) < ( r + l ) , magnitude of B1 > B2 ., , Therefore the resultant magnetic induction at P due to the, bar magnet is given by,, B = B 1 – B2, As B1 and B2 are along the same line.

Page 11 :
❖ Magnetic field due to a bar magnet at a point along the, equator : -, , Sir ( Sby), We have to find the magnetic induction at P due to Yadav, the bar, magnet, , From fig ,, Q, B1, B, , T, , θ, , P, , θ, , B1cosθ + B2cosθ, , B1Sinθ, , B2, , B2Sinθ, , + qm, , - qm, θ, , S, , θ, , l, , B1, , µ0 + qm, = ---- -------4π ( NP ) 2, , B1, , µ0, + qm, = ---- -------4π ( r 2+ l 2), , This induction is directed away from the N – pole and its, is represented by PQ in the figure ., , R, , r, , NP 2 = SP 2 = r 2 + l 2, , O, , l, , N, , Magnetic induction along the equator, Consider a bar magnet of magnetic moment m having two, poles separated by a distance 2l, Let P be any point on the equator of the magnet , at a, distance r from its Centre O as shown in fig., , Magnetic induction at point P due to S pole is given by ,, µ0, - qm, B2 = ---- ------4π ( SP ) 2, µ0, - qm, = ---- -------4π ( r + l ) 2, This induction is directed towards the S – pole and it is, represented by PR ., , In magnitude, , B 1 = B2, PQ = PR

Page 12 :
Completing the parallelogram PQTR , the diagonal PT, represents the resultant magnetic induction B at the point P due to, the bar magnet., , But 2 qm l = m, , µ, , B, , From fig ,, , = ----0, 4π, , Δ PQT and Δ NPS are Similar ., , µ0, B equator = ---4π, , PT, NS, ---- = ---PQ, NP, NS, ---NP, , PT = PQ, , (1 ), , PQ = B1, , (2), , m, , ------------------( r 2 + l 2 ) 3/2, , The direction of B is along PT, , µ0, B equator = ---4π, , + qm, µ0, = ---- ----4π ( r 2+ l 2), 2, , m, , ------------------( r 2 + l 2 ) 3/2, , If the bar magnet is very short , l << r . Therefore ,, neglecting l 2 in eq ( 2 ) , we get, , Now , PT = B, , NS = 2l, , Yadav Sir ( Sby), , 2, , NP = r + l, , 2, , 2, , NP = ( r + l, , Substituting these value in eq ( 1 ) we get ,, B, , + qm, µ, 2l, = ----0 ---------------------------4π ( r 2+ l 2) ( r 2 + l 2 )1/2, , B, , µ, = ----0, 4π, , 2l qm, ------------------( r 2 + l 2 ) 3/2, , 2 )1/2, , m, , (3), , ------r3, , Eq ( 3 ) represent magnetic induction at a point due to very, short magnet at equatorial point ., In vector form ,, µ0, B equator = - ---4π, , m, , ------r3, , Negative sign shows that direction of B equator is, opposite to direction m

Page 13 :
Yadav Sir ( Sby), , ❖ Show that the magnitude of magnetic induction at a point on the axis of a short bar magnet is twice the magnitude of magnetic, induction at a point on the equator at the same distance., •, , Magnitude of magnetic induction at a point along the axis of a short magnet is given by ,, , •, , µ0, 2 m, B axis = ---- --------r3, 4π, Magnitude of magnetic induction at a point on equatorial line is given by ,, µ0, B equator = ---4π, , m, , ------r3, , Dividing eq (1) by (2), we get, Baxis, =, ----------B equator, , Baxis, ----------- =, B equator, , µ0, 2m, --- --------r3, 4π, ------------------m, µ0, ---------4π, r3, 2, , Baxis = 2 Beq

Page 14 :
❖ Magnetic field due to a bar magnet at an arbitrary, point : -, , Yadav Sir ( Sby), Baxial, , B, Bequator, , α, , Consider a bar magnet of magnetic moment m with Centre, at O as shown in figure., Let P be any point in its magnetic field ., Magnetic moment m is resolved into component along r and, perpendicular to r., , P, r = op, , For the component m cosθ along r , the point P is an axial point ., For the component m sin θ perpendicular to r the point P is an, equatorial point at the same distance r, For point on the axis, µ0, 2 m, B axis = --- --------r3, 4π, µ0, 2 m cos θ, B axis = ---- --------r3, 4π, , θ, , N, , m sin θ, ------B equator =, r3, Directed opposite to m sin θ, µ0, ---4π, , m, , Thus , the magnitude of the resultant magnetic field B , at, point P is given by, ---------- ( 1 ), , B =, , Ba 2 + Beq 2, , Directed along m cos θ, For point an equator, , S, , O, , =, , µ0, ---4π, , 2 m cos θ, ------------r3, , 2, , +, , µ0, ---4π, , m sin θ, ------r3, , 2

Page 16 :
❖ Earth’s Magnetism : -, , Yadav Sir ( Sby), , •, , Magnetic axis : A straight line joining two poles is called magnetic axis, , •, , Magnetic equator : A great circle in the plane perpendicular to magnetic axis is called magnetic equator., , •, , Magnetic Meridian : A plane perpendicular to surface of the earth and passing through the magnetic axis is called magnetic meridian., , •, , Geographic Meridian : A plane perpendicular to the surface of the earth and passing through geographic axis is called geographic, meridian.

Page 17 :
Yadav Sir ( Sby), , ❖ Magnetic Declination, Angle between the geographic and the magnetic meridian at, a place is called magnetic declination (α ) ., , Magnetic Inclination : Angle made by the direction of the resultant magnetic field, with the horizontal at a place is called magnetic inclination or, angle of dip (ϕ)

Page 19 :
Yadav Sir ( Sby), , ❖ Magnetic maps of the earth : •, , Magnetic Maps : Magnetic elements of the earth ( B H , ϕ , α ) vary from place to place also with time. The maps providing, these values at different location are called magnetic maps ., •, , Isomagnetic Charts : Magnetic maps drawn by joining places with the same value of a particular element are called, isomagnetic charts ., •, , Isodynamic lines : Lines joining the places of equal horizontal components ( B H ) on magnetic maps are known as, isodynamic lines ., •, , Isogonic lines : Lines joining the places of equal declination (α) on magnetic maps are called isogonic lines ., , •, , Aclinic lines : Lines joining the place of equal inclination or dip (ϕ ) on magnetic mapes are called aclinic lines .