Page 2 :
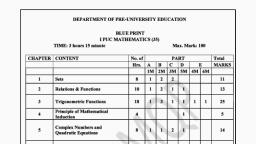
Contents, Foreword, iii, 1., Sets, 1.1, Introduction, 1, Sets and their Representations, The Empty Set, 1.2, 1, 1.3, 5, 1.4, Finite and Infinite Sets, 6., 1.5, Equal Sets, 7, 1.6, Subsets, 9., 1.7, Power Set, 12, 1.8, Universal Set, 12, Venn Diagrams, 1.10 Operations on Sets, 1.11 Complement of a Set, 1.12 Practical Problems on Union and Intersection of Two Sets, 1.9, 13, 14, 18, 2., Relations and Functions, 30, 2.1, Introduction, 30, 2.2, Cartesian Product of Sets, 30, 2.3, Relations, 34, 2.4, Functions, 36, 3., Trigonometric Functions, 49, 3.1, Introduction, 49, 3.2, Angles, Trigonometric Functions, Trigonometric Functions of Sum and Difference of Two Angles, Trigonometric Equations, 49, 3.3, 55, 3.4, 63, 3.5, 74, 4., Principle of Mathematical Induction, 86, 4.1, Introduction, 86, 4.2, Motivation, 87, The Principle of Mathematical Induction, 4.3, 88
Page 3 :
Complex Numbers and Quadratic Equations, Introduction, 5., 97, 5.1, 97, Complex Numbers, Algebra of Complex Numbers, The Modulus and the Conjugate of a Complex Number, 5.5 Argand Plane and Polar Representation, 5.2, 97, 5.3, 98, 5.4, 102, 104, 5.6, Quadratic Equations, 108, Linear Inequalities, Introduction, 6., 116, 6.1, 116, Inequalities, Algebraic Solutions of Linear Inequalities in One Variable, and their Graphical Representation, 6.4 Graphical Solution of Linear Inequalities in Two Variables, Solution of System of Linear Inequalities in Two Variables, 6.2, 116, 6.3, 118, 123, 6.5, 127, 7., Permutations and Combinations, 134, 7.1, Introduction, 134, 7.2, Fundamental Principle of Counting, 134, 7.3, Permutations, 138, 7.4, Combinations, 148, 8., Binomial Theorem, 160, 8.1, Introduction, 160, 8.2, Binomial Theorem for Positive Integral Indices, 160, 8.3, General and Middle Terms, 167, Sequences and Series, Introduction, 9., 177, 9.1, 177, 9.2, Sequences, Series, 177, 9.3, 179, Arithmetic Progression (A. P.), Geometric Progression (G P.), Relationship Between A. M. and G.M., Sum to n terms of Special Series, 9.4, 181, 9.5, 186, 9.6, 191, 9.7, 194, 10. Straight Lines, 10.1 Introduction, 203, 203, 10.2 Slope of a Line, 10.3 Various Forms of the Equation of a Line, 10.4 General Equation of a Line, 10.5 Distance of a Point From a Line, 204, 212, 220, 225, vii
Page 4 :
11. Conic Sections, 236, 11.1 Introduction, 236, 11.2 Sections of a Cone, 236, 11.3 Circle, 239, 11.4 Parabola, 242, 11.5 Ellipse, 11.6 Hyperbola, 247, 255, 12. Introduction to Three Dimensional Geometry, 268, 12.1 Introduction, 268, 12.2 Coordinate Axes and Coordinate Planes in, Three Dimensional Space, 269, 12.3 Coordinates of a Point in Space, 269, 12.4 Distance between Two Points, 271, 12.5 Section Formula, 273, 13. Limits and Derivatives, 281, 13.1 Introduction, 281, 13,2 Intuitive Idea of Derivatives, 281, 13.3 Limits, 284, 13.4 Limits of Trigonometric Functions, 298, 13.5 Derivatives, 303, 14. Mathematical Reasoning, 321, 14.1 Introduction, 321, 14.2 Statements, 321, 14.3 New Statements from Old, 324, 14.4 Special Words/Phrases, 14.5 Implications, 14.6 Validating Statements, 329, 335, 339, 15. Statistics, 347, 15.1 Introduction, 347, 15.2 Measures of Dispersion, 349, 15.3 Range, 349, 15.4 Mean Deviation, 349, 15.5 Variance and Standard Deviation, 361, 15.6 Analysis of Frequency Distributions, 372, ix
Page 5 :
16. Probability, 383, 16.1 Introduction, 383, 16.2 Random Experiments, 384, 16.3 Event, 387, 16.4 Axiomatic Approach to Probability, 394, Appendix 1: Infinite Series, A.1.1 Introduction, 412, 412, A.1.2 Binomial Theorem for any Index, A.1.3 Infinite Geometric Series, 412, 414, A.1.4 Exponential Series, A.1.5 Logarithmic Series, 416, 419, Appendix 2: Mathematical Modelling, A.2.1 Introduction, 421, 421, A.2.2 Preliminaries, 421, A.2.3 What is Mathematical Modelling, 425, Answers, 433