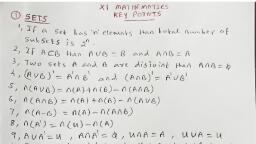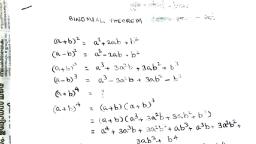Page 1 :
1|Page, , Class 11 Maths Chapter 8 Binomial Theorem, Binomial Theorem for Positive Integer, If n is any positive integer, then, , This is called binomial theorem., Here, nC0, nC1, nC2, … , nno are called binomial coefficients and, n, , Cr = n! / r!(n – r)! for 0 ≤ r ≤ n., , Properties of Binomial Theorem for Positive Integer, (i) Total number of terms in the expansion of (x + a)n is (n + 1)., (ii) The sum of the indices of x and a in each term is n., (iii) The above expansion is also true when x and a are complex numbers., (iv) The coefficient of terms equidistant from the beginning and the end are equal. These, coefficients are known as the binomial coefficients and, n, , Cr = nCn – r, r = 0,1,2,…,n., , (v) General term in the expansion of (x + c)n is given by, Tr + 1 = nCrxn – r ar., (vi) The values of the binomial coefficients steadily increase to maximum and then steadily, decrease .
Page 2 :
2|Page, , (vii), , (viii), (ix) The coefficient of xr in the expansion of (1+ x)n is nCr., (x), (xi) (a), , (b), (xii) (a) If n is odd, then (x + a)n + (x – a)n and (x + a)n – (x – a)n both have the same number of, terms equal to (n +1 / 2)., (b) If n is even, then (x + a)n + (x – a)n has (n +1 / 2) terms. and (x + a)n – (x – a)n has (n / 2), terms., (xiii) In the binomial expansion of (x + a)n, the r th term from the end is (n – r + 2)th term, , from, beginning., , the, , (xiv) If n is a positive integer, then number of terms in (x + y + z) n is (n + l)(n + 2) / 2.
Page 3 :
3|Page, , Middle term in the Expansion of (1 + x)n, (i) It n is even, then in the expansion of (x + a)n, the middle term is (n/2 + 1)th terms., (ii) If n is odd, then in the expansion of (x + a)n, the middle terms are (n + 1) / 2 th term and (n, + 3) / 2 th term., Greatest Coefficient, (i) If n is even, then in (x + a)n, the greatest coefficient is nCn / 2, (ii) Ifn is odd, then in (x + a)n, the greatest coefficient is nCn – 1 / 2 or nCn + 1 / 2 both being equal., Greatest Term, In the expansion of (x + a)n, (i) If n + 1 / x/a + 1 is an integer = p (say), then greatest term is Tp == Tp + 1., (ii) If n + 1 / x/a + 1 is not an integer with m as integral part of n + 1 / x/a + 1, then Tm + 1. is the, greatest term., Important Results on Binomial Coefficients
Page 4 :
4|Page
Page 5 :
5|Page, , Divisibility Problems, From the expansion, (1+ x)n = 1+ nC1x + nC1x2+ … +nCnxn, We can conclude that,, (i) (1+ x)n – 1 = nC1x + nC1x2+ … +nCnxn is divisible by x i.e., it is multiple of x., (1+ x)n – 1 = M(x), , (ii)
Page 6 :
6|Page, , (iii), Multinomial theorem, For any n ∈ N,, , (i), , (ii), (iii) The general term in the above expansion is, , (iv)The greatest coefficient in the expansion of (x1 + x2 + … +, , xm)n is, when n is divided by m., , where q and r are the quotient and remainder respectively,, , (v) Number of non-negative integral solutions of x1 + x2 + … + xn = n is n + r – 1Cr – 1, R-f Factor Relations, Here, we are going to discuss problem involving (√A + B)sup>n = I + f, Where I and n are, positive integers., 0 le; f le; 1, |A – B2| = k and |√A – B| < 1, Binomial Theorem for any Index, If n is any rational number, then
Page 7 :
7|Page, , (i) If in the above expansion, n is any positive integer, then the series in RHS is finite otherwise, infinite., (ii) General term in the expansion of (1 + x)n is Tr + 1 = n(n – 1)(n – 2)… [n – (r – 1)] / r! * xr, (iii) Expansion of (x + a)n for any rational index
Page 8 :
8|Page, , (vii) (1 + x)- 1 = 1 – x + x2 – x3 + …∞, (viii) (1 – x)- 1 = 1 + x + x2 + x3 + …∞, (ix) (1 + x)- 2 = 1 – 2x + 3x2 – 4x3 + …∞, (x) (1 – x)- 2 = 1 + 2x + 3x2 – 4x3 + …∞, (xi) (1 + x)- 3 = 1 – 3x + 6x2 – …∞, (xii) (1 – x)- 3 = 1 + 3x + 6x2 – …∞, (xiii) (1 + x)n = 1 + nx, if x2, x3,… are all very small as compared to x., Important Results, (i) Coefficient of xm in the expansion of (axp + b / xq)n is the coefficient of Tr + l where r = np –, m/p+q, (ii) The term independent of x in the expansion of axp + b / xq)n is the coefficient of Tr + l where, r = np / p + q, (iii) If the coefficient of rth, (r + l)th and (r + 2)th term of (1 + x)n are in AP, then n2 – (4r+1) n, + 4r2 = 2, (iv) In the expansion of (x + a)n, Tr + 1 / Tr = n – r + 1 / r * a / x
Page 9 :
9|Page, , (v) (a) The coefficient of xn – 1 in the expansion of, (x – l)(x – 2) ….(x – n) = – n (n + l) / 2, (b) The coefficient of xn – 1 in the expansion of, (x + l)(x + 2) ….(x + n) = n (n + l) / 2, (vi) If the coefficient of pth and qth terms in the expansion of (1 + x)n are equal, then p + q = n, +2, (vii) If the coefficients of xr and xr + 1 in the expansion of a + x / b)n are equal, then, n = (r + 1)(ab + 1) – 1, (viii) The number of term in the expansion of (x1 + x2 + … + xr)n is n + r – 1C r – 1., (ix) If n is a positive integer and a1, a2, … , am ∈ C, then the coefficient of xr in the expansion of, (a1 + a2x + a3x2 +… + amxm – 1)n is, , (x) For |x| < 1,, (a) 1 + x + x2 + x3+ … + ∞ = 1 / 1 – x, (b) 1 + 2x + 3x2 + … + ∞ = 1 / (1 – x)2, (xi) Total number of terms in the expansion of (a + b + c + d)n is (n + l)(n + 2)(n + 3) / 6., Important Points to be Remembered, (i) If n is a positive integer, then (1 + x)n contains (n +1) terms i.e., a finite number of terms., When n is general exponent, then the expansion of (1 + x)n contains infinitely many terms., (ii) When n is a positive integer, the expansion of (l + x)n is valid for all values of x. If n is, general exponent, the expansion of (i + x)n is valid for the values of x satisfying the condition, |x| < 1.