Page 2 :
The Constitution of India, Chapter IV A, , Fundamental Duties, ARTICLE 51A, Fundamental Duties- It shall be the duty of every citizen of India(a), , to abide by the Constitution and respect its ideals and institutions,, the National Flag and the National Anthem;, , (b), , to cherish and follow the noble ideals which inspired our national, struggle for freedom;, , (c), , to uphold and protect the sovereignty, unity and integrity of India;, , (d), , to defend the country and render national service when called upon, to do so;, , (e), , to promote harmony and the spirit of common brotherhood amongst, all the people of India transcending religious, linguistic and regional, or sectional diversities, to renounce practices derogatory to the, dignity of women;, , (f), , to value and preserve the rich heritage of our composite culture;, , (g), , to protect and improve the natural environment including forests,, lakes, rivers and wild life and to have compassion for living, creatures;, , (h), , to develop the scientific temper, humanism and the spirit of inquiry, and reform;, , (i), , to safeguard public property and to abjure violence;, , (j), , to strive towards excellence in all spheres of individual and, collective activity so that the nation constantly rises to higher levels, of endeavour and achievement;, , (k), , who is a parent or guardian to provide opportunities for education, to his child or, as the case may be, ward between the age of six, and fourteen years.
Page 3 :
The Coordination Committee formed by GR No. Abhyas - 2116/(Pra.Kra.43/16) SD - 4, Dated 25.4.2016 has given approval to prescribe this textbook in its meeting held on, 30.01.2020 and it has been decided to implement it from the educational year 2020-21., , Mathematics and Statistics, (Arts and Science), Part - II, STANDARD - XII, , Maharashtra State Bureau of Textbook Production and Curriculum Research,, Pune - 411 004, Download DIKSHA App on your smartphone. If you scan the Q.R.Code, on this page of your textbook, you will be able to access full text and the, audio-visual study material relevant to each lesson provided as teaching, and learning aids.
Page 5 :
The Constitution of India, , Preamble, WE, THE PEOPLE OF INDIA, having, solemnly resolved to constitute India into a, SOVEREIGN, SOCIALIST, SECULAR, DEMOCRATIC REPUBLIC and to secure to, all its citizens:, JUSTICE, social, economic and political;, LIBERTY of thought, expression, belief, faith, and worship;, EQUALITY of status and of opportunity;, and to promote among them all, FRATERNITY assuring the dignity of, the individual and the unity and integrity of the, Nation;, IN OUR CONSTITUENT ASSEMBLY this, twenty-sixth day of November, 1949, do HEREBY, ADOPT, ENACT AND GIVE TO OURSELVES, THIS CONSTITUTION.
Page 6 :
NATIONAL ANTHEM
Page 7 :
PREFACE, Dear Students,, Welcome to Standard XII, an important milestone in your life., Standard XII or Higher Secondary School Certificate opens the doors of higher, education. Alternatively, you can pursue other career paths like joining the workforce., Either way, you will find that mathematics education helps you considerably. Learning, mathematics enables you to think logically, constistently, and rationally. The curriculum for, Standard XII Mathematics and Statistics for Science and Arts students has been designed, and developed keeping both of these possibilities in mind., The curriculum of Mathematics and Statistics for Standard XII for Science and Arts, students is divided in two parts. Part I deals with topics like Mathematical Logic, Matrices,, Vectors and Introduction to three dimensional geometry. Part II deals with Differentiation,, Integration and their applications, Introduction to random variables and statistical methods., The new text books have three types of exercises for focused and comprehensive, practice. First, there are exercises on every important topic. Second, there are comprehensive, exercises at the end of all chapters. Third, every chapter includes activities that students, must attempt after discussion with classmates and teachers. Additional information has, been provided on the E-balbharati website (www.ebalbharati.in)., We are living in the age of Internet. You can make use of modern technology with, the help of the Q.R. code given on the title page. The Q.R. code will take you to links, that provide additional useful information. Your learning will be fruitful if you balance, between reading the text books and solving exercises. Solving more problems will make, you more confident and efficient., The text books are prepared by a subject committee and a study group. The books, (Paper I and Paper II) are reviewed by experienced teachers and eminent scholars. The, Bureau would like to thank all of them for their valuable contribution in the form of, creative writing, constructive and useful suggestions for making the text books valuable., The Bureau hopes and wishes that the text books are very useful and well received by, students, teachers and parents., Students, you are now ready to study. All the best wishes for a happy learning, experience and a well deserved success. Enjoy learning and be successful., , Pune, Date : 21 February 2020, Bharatiya Saur : 2 Phalguna 1941, , (Vivek Gosavi), Director, Maharashtra State Bureau of Textbook, Production and Curriculum Research, Pune.
Page 8 :
Mathematics and Statistics XII (Part II), Arts and Science, Sr. No, , 1., , 2., , 3., , 4., , Area / Topic, , Sub Unit, , Competency Statement, , The students will be able to, • state and use standard formulas of, derivative of standard functions, • use chain rule of derivatives, Differentiation Differentiation • find derivatives of the logarithm,, implicit, inverse and parametric, functions, • find second and higher order, derivatives., , Applications Applications of, of Derivatives, Derivatives, , Indefinite, Integration, , Definite, Integration, , • find equations of tangents and normal, to a curve, • determine nature of the functionincreasing or decreasing, • find approximate values of the, function, • examine function for maximum and, minimum values, • verify mean value theorems, , Indefinite, Integration, , • understand the relation between, derivative and integral, • use the method of substitution, • solve integrals with the help of, integration by parts, • solve the integrals by the method of, partial fractions, , Definite, Integration, , • understand integral as a limit of sum, • the properties of definite integral, • state the properties of definite integral, and use them to solve problems
Page 9 :
5., , 6., , 7., , 8, , Application, of Definite, Integration, , Differential, Equation, , Probability, Distribution, , Binomial, Distribution, , Application, of Definite, Integration, , • find the area under the curve, bounded, by the curves using definite integrals., , Differential, Equation, , • form a differential equation and find, its order and degree, • solve the first order and first degree, differential equation by various, methods, • apply the differential equations to, study the polpulation, growth and, decay in amount of substance and, physics., , Probability, Distribution, , • understand the random variable and its, types., • find probability mass function and its, probability distribution., • find the expected value, variance and, the standard deviation, • find the probability density function of, continuous random variable, • find distribution function of c.r.v., , Binomial, Distribution, , • understand random experiment with, two or more outcomes., • determine probability distribution of, random experiment with parameters n, and p., • find mean, variance, expected value, and standard deviation for the, binomial distribution.
Page 10 :
INDEX, Sr. No., , Chapter Name, , Page No., , 1, , Differentiation, , 1-64, , 2, , Applications of Derivatives, , 65-94, , 3, , Indefinite Integration, , 95-150, , 4, , Definite Integration, , 151-177, , 5, , Application of Definite Integration, , 178-190, , 6, , Differential Equations, , 191-218, , 7, , Probability Distributions, , 219-244, , 8, , Binomial Distribution, , 245-255, , Answers, , 256-276
Page 11 :
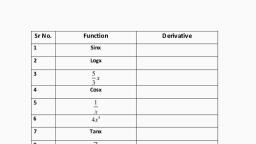
1. DIFFERENTIATION, Let us Study, •, , Derivatives of Composite functions., , •, , Geometrical meaning of Derivative., , •, , Derivatives of Inverse functions, , •, , Logarithmic Differentiation, , •, , Derivatives of Implicit functions., , •, , Derivatives of Parametric functions., , •, , Higher order Derivatives., Let us Recall, , •, , The derivative of f (x) with respect to x, at x = a is given by, , •, , The derivative can also be defined for f (x) at any point x on the open interval as, . If the function is given as y = f (x) then its derivative is written as, ., , •, , For a differentiable function y = f (x) if δx is a small increment in x and the corresponding increment, in y is δy then, , •, , ., , Derivatives of some standard functions., y = f (x), c (Constant), xn, 1, x, 1, xn, , sin x, cos x, tan x, , y = f (x), 0, nxn−1, 1, − 2, x, −, , n, xn+1, , cos x, − sin x, sec2 x, Table 1.1.1, , 1, , sec x, , sec x tan x, , cosec x, , − cosec x cot x, , cot x, , − cosec2 x, , ex, , ex, , ax, , a x log a, , log x, , 1, x, , log a x, , 1, x log a
Page 12 :
Rules of Differentiation :, If u and v are differentiable functions of x such that, (i), , y = u ± v then, , (iii), , y=, , , , (ii), , y = uv then, , u, where v ≠ 0 then, v, , Introduction :, The history of mathematics presents the development of calculus as being accredited to Sir Isaac, Newton (1642-1727) an English physicist and mathematician and Gottfried Wilhelm Leibnitz (16461716) a German physicist and mathematician. The Derivative is one of the fundamental ideas of calculus., It's all about rate of change in a function. We try to find interpretations of these changes in a mathematical, way. The symbol δ will be used to represent the change, for example δx represents a small change in the, variable x and it is read as "change in x" or "increment in x". δy is the corresponding change in y if y is, a function of x., We have already studied the basic concept, derivatives of standard functions and rules of, differentiation in previous standard. This year, in this chapter we are going to study the geometrical, meaning of derivative, derivatives of Composite, Inverse, Logarithmic, Implicit and Parametric functions, and also higher order derivatives. We also add some more rules of differentiation., Let us Learn, 1.1.1 Derivatives of Composite Functions (Function of another function) :, So far we have studied the derivatives of simple functions like sin x, log x, e x etc. But how about, the derivatives of sin, , log sin (x2 + 5) or e tan x etc ? These are known as composite functions. In, this section let us study how to differentiate composite functions., 1.1.2 Theorem : If y = f (u) is a differentiable function of u and u = g (x) is a differentiable function of, x such that the composite function y = f [g (x)] is a differentiable function of x then, , ., , Proof : Given that y = f (u) and u = g (x). We assume that u is not a constant function. Let there be a, small increment in the value of x say δx then δu and δy are the corresponding increments in u and, y respectively., As δx, δu, δy are small increments in x, u and y respectively such that δx ≠ 0, δu ≠ 0 and δy ≠ 0., We have, , ., , Taking the limit as δx → 0 on both sides we get,, , 2
Page 13 :
As δx → 0, we get, δu → 0 (⸪ u is a continuous function of x), , , . . . . . (I), , Since y is a differentiable function of u and u is a differentiable function of x., we have,, and, , , , . . . . . (II), , From (I) and (II), we get, , , . . . . . (III), , The R.H.S. of (III) exists and is finite, implies L.H.S.of (III) also exists and is finite , . Then equation (III) becomes,, , Note:, 1., , The derivative of a composite function can also be expressed as follows. y = f (u) is a differentiable, function of u and u = g (x) is a differentiable function of x such that the composite function, y = f [ g (x)] is defined then, ., , 2., , If y = f (v) is a differentiable function of v and v = g (u) is a differentiable function of u and u = h (x), is a differentiable function of x then, ., , 3., , If y is a differentiable function of u1, ui is a differentiable function of ui+1 for i = 1, 2, ..., n−1 and un, is a differentiable function of x, then, , This rule is also known as Chain rule., , 3
Page 14 :
1.1.3 Derivatives of some standard Composite Functions :, dy, dx, , y, , dy, dx, , n [ f (x)] n−1 ⋅ f '(x), f '(x), , cot [ f (x)], , − cosec2 [ f (x)]⋅ f '(x), , y, [ f (x)] n, , √ f (x), , cosec [ f (x)] − cosec [ f (x)] ⋅ cot [ f (x)] ⋅ f '(x), , 2√ f (x), , 1, [ f (x)]n, , n ⋅ f '(x), , −, , sin [ f (x)], cos [ f (x)], tan [ f (x)], sec [ f (x)], , [ f (x)], cos [ f (x)]⋅ f '(x), − sin [ f (x)]⋅ f '(x), sec2 [ f (x)]⋅ f '(x), sec [ f (x)] ⋅ tan [ f (x)] ⋅ f '(x), n+1, , a f (x), , a f (x) ⋅ log a ⋅ f '(x), , e f (x), , e f (x) ⋅ f '(x), f '(x), , log [ f (x)], , f (x), f '(x), , log a [ f (x)], , f (x) log a, , Table 1.1.2, SOLVED EXAMPLES, Ex. 1 : Differentiate the following w. r. t. x., (i) y =, , √ x2 + 5 (ii), , (iv) log (x5 + 4) , Solution :, , (i) y =, , (v), , y = sin (log x) (iii), 53 cos x − 2 (vi), , y = e tan x, 3, y=, (2x2 − 7)5, , √ x2 + 5, , Method 1 :, , Method 2 :, , Let u = x2 + 5 then y = √ u , where y is, a differentiable function of u and u is a, differentiable function of x then, , , We have y =, , √ x2 + 5, , Differentiate w. r. t. x, , . . . . . (I), [Treat x2 + 5 as u in mind and use the formula, of derivative of √ u ], , Now, y = √ u, Differentiate w. r. t. u, and u = x2 + 5, Differentiate w. r. t. x, du d 2, =, (x + 5) = 2x, dx dx, Now, equation (I) becomes,, , 4
Page 15 :
(ii) y = sin (log x), Method 2 :, , Method 1 :, , We have y = sin (log x), , Let u = log x then y = sin u, where y is, a differentiable function of u and u is a, differentiable function of x then, , , Differentiate w. r. t. x, [sin (log x)], , . . . . . (I), , [Treat log x as u in mind and use the formula, of derivative of sin u], , Now, y = sin u, Differentiate w. r. t. u, = cos u and u = log x, Differentiate w. r. t. x, 1, =, x, Now, equation (I) becomes,, , Note : Hence onwards let's use Method 2., (iii) y = e tan x, , (iv) Let y = log (x5 + 4) , Differentiate w. r. t. x, , Differentiate w. r. t. x, , [log (x5 + 4)], , [e tan x], , (v) Let y = 53 cos x − 2, , (vi) Let y =, , 3, , (2x2 − 7)5, Differentiate w. r. t. x, , Differentiate w. r. t. x, , [53 cos x − 2], dy, = 53 cos x − 2 · log 5 × (3 cos x − 2), dx, dy, = − 3 sin x · 53 cos x − 2 · log 5, dx, , , , , 5
Page 17 :
= (x3 + 2x − 3)4 ⋅3 (x + cos x) 2 ⋅, , (x + cos x) + (x + cos x) 3⋅ 4(x3 + 2x − 3)3 ⋅, , (x3 + 2x − 3), , = (x3 + 2x − 3)4 ⋅3 (x + cos x) 2 (1 − sin x) + (x + cos x) 3 ⋅ 4(x3 + 2x − 3)3 (3x2 + 2), ∴, , dy, = 3(x3 + 2x − 3)4 (x + cos x) 2 (1 − sin x) + 4 (3x2 + 2) (x3 + 2x − 3)3 (x + cos x)3, dx, , (v) y = (1 + cos2 x) 4 × √ x + √tan x, Differentiate w. r. t. x, , , , , , , , , , , , Ex. 3 : Differentiate the following w. r. t. x., (i) y = log3 (log5 x) (ii), , (iii) , , (iv), , (v) , , (vi), , 7
Page 18 :
Solution :, (i) y = log3 (log5 x), , , = log3, , = log3 (log x) - log3 (log 5), , ∴ y =, , - log3 (log 5), , Differentiate w. r. t. x, , , , , , , [Note that log3(log 5) is constant], , , ∴, (ii), , , , [ ⸪ log e = 1], , ∴, Differentiate w. r. t. x, , , , , ∴, , 8
Page 19 :
(iii) , , ∴ , Differentiate w. r. t. x, , , , , , , , , , , ∴ , , (iv), , , , , , ∴, Differentiate w. r. t. x, , 9
Page 20 :
(vi), , (v), , y = a cot x [⸪ alog a f (x) = f (x)], Differentiate w. r. t. x, , , , , (a cot x ), , [⸪ alog a f (x) = f (x)], , , , = sin2 x + cos2 x, ∴, , = a cot x log a ·, , y =1, Differentiate w. r. t. x, , (cot x), , =a cot x log a (− cosec2 x), − cosec2 x· a cot x log a, , Ex. 4, , :, , Solution :, , , If f (x) = √ 7g (x) − 3 , g (3) = 4 and g' (3) = 5, find f ' (3)., Given that : f (x) = √ 7g (x) − 3, Differentiate w. r. t. x, , , ∴, , , For x = 3, we get, , , , =, , 35, 7, =, 2(5) 2, , [Since g (3) = 4 and g' (3) = 5], , 10
Page 22 :
(2) Differentiate the following w.r.t. x, (i), , cos (x2 + a2), , (iii), (v), , (xv), , (ii), (iv), , cot3[log (x3)], , (vii) cosec (√cos x), (ix) e3 sin, , 2 x − 2 cos2 x, , (xvi), , (vi) 5sin, , 3x+3, , (viii) log [cos (x3 − 5)], (x) cos2 [log (x2 + 7)], , (xi) tan [cos (sin x)] (xii) sec[tan (x4 + 4)], (xiii) elog [(log x), , − log x2 ], , (xiv) sin √sin √x, , (xv) log[sec (e )], , (xvi) loge2 (log x), , 2, , x2, , (xvii), , (xvii) [ log [log(log x)]], , (xviii), (xix) y = (25)log5 (sec x) − (16)log4 (tan x), (xx), , 2, , (xviii) sin2 x2 − cos2 x2, , (4) A table of values of f, g, f ' and g' is given, , (3) Differentiate the following w.r.t. x, , (x2 + 4x + 1)3 + (x3 − 5x − 2)4, 5, 8, (ii) (1 + 4x) (3 + x − x2), , x, , f (x), , g(x), , f '(x), , g'(x), , 2, , 1, , 6, , −3, , 4, , 4, , 3, , 4, , 5, , −6, , (iii), , 6, , 5, , 2, , −4, , 7, , (i), , (v), , (iv), , (1 + sin2 x)2 (1 + cos2 x)3, , (i), , If r(x) = f [g(x)] find r' (2)., , (vi) √cos x + √cos √x, , (ii), , If R(x) = g[3 + f (x)] find R' (4)., , (vii) log (sec 3x + tan 3x) (viii), , (iii) If s(x) = f [9 − f (x)] find s' (4)., (iv) If S(x) = g [ g(x) ] find S' (6)., , (ix), (x), , (5) Assume that f ' (3) = − 1, g' (2) = 5, g (2) = 3, (xi), , and y = f [g(x)] then, , (xii) log [tan3 x·sin4 x·(x2 + 7) ], 7, , (6) If, , (xiii), , , f (1) = 4, g (1) = 3,, , f ' (1) = 3, g' (1) = 4 find h' (1)., (7) Find the x co-ordinates of all the points on, the curve y = sin 2x − 2 sin x, 0 ≤ x < 2π, , (xiv), , where, , 12, , 0.
Page 24 :
1.2.2 Derivatives of Inverse Functions :, We know that if y = f (x) is a one-one and onto function then x = f, , ( y) exists. If f −1 ( y) is, differentiable then we can find its derivative. In this section let us discuss the derivatives of some inverse, functions and the derivatives of inverse trigonometric functions., x+2, Example 1 : Consider f (x) = 2x − 2 then its inverse is f −1 (x) =, . Let g(x) = f −1 (x)., 2, 1, d, d, [ f (x)] = 2 and, [g (x)] = ., If we find the derivatives of these functions we see that, 2, dx, dx, These derivatives are reciprocals of one another., −1, , Example 2 : Consider y = f (x) = x2 . Let g = f −1., ∴ g ( y) = x = √ y, ∴ g' ( y) =, Now, , 1, 2√y, , also f ' (x) = 2x, , d, [g ( f (x))] =, dx, , = 1 and g [ f (x)] = x ∴, , At a point ( x, x2 ) on the curve, f ' (x) = 2x and g' ( y) =, , 1, 2√y, , =, , d, d, [g ( f (x))] = (x) = 1, dx, dx, 1, 1, =, ., 2x f '(x), , 1.2.3 Theorem : Suppose y = f (x) is a differentiable function of x on an interval I and y is One-one, onto and, d −1, dx, dy, 1, ≠ 0 on I. Also if f −1( y) is differentiable on f (I ) then, [ f ( y)] =, or, =, dy, dy, dx, f '(x), , where, , dy, ≠ 0., dx, , Proof : Given that y = f (x) and x = f −1 (y) are differentiable functions., Let there be a small increment in the value of x say δx then correspondingly there will be an, increment in the value of y say δy. As δx and δy are increments, δx ≠ 0 and δy ≠ 0., δx δy, We have,, ×, =1, δy δx, δx, δy, ∴, = , where, ≠0, δy, δx, Taking the limit as δx → 0, we get,, , , as δx → 0, δy → 0,, , , , , Since y = f (x) is a differentiable function of x., , 14, , . . . . . (I)
Page 25 :
we have,, , and, , dy, ≠ 0 , dx, , . . . . . (II), , From (I) and (II), we get, , , As, , dy, ≠ 0,, dx, , . . . . . (III), , δx, exists and is finite. ∴ lim, δy→0, δy, , Hence, from (III), , dx, =, dy, , where, , =, , dx, exists and is finite., dy, , dy, ≠0, dx, , An alternative proof using derivatives of composite functions rule., [Identity function], We know that f −1 [ f (x)] = x, Taking derivative on bothe sides we get,, d, d, [ f −1 [ f (x)]] = (x), dx, d dx, i.e. ( f −1)' [ f (x)], [ f (x)] = 1, dx, i.e. ( f −1)' [ f (x)] f ' (x) = 1, 1, ∴ ( f −1)' [ f (x)] =, , . . . . . (I), f ' (x), So, if y = f (x) is a differentiable function of x and x = f −1 ( y) exists and is differentiable then, , ( f −1)' [ f (x)] = ( f −1)' ( y) =, ∴, , (I) becomes, dx, dy, =, where, ≠0, dy, dx, , dx, dy, and f ' (x) =, dy, dx, , SOLVED EXAMPLES, Ex. 1 : Find the derivative of the function y = f (x) using the derivative of the inverse function, x = f −1 ( y) in the following, (i), , (ii), , (iii) y = ln x, , Solution :, (i), We first find the inverse of the function y = f (x), i.e. x in term of y., y3 = x + 4 ∴ x = y3 − 4 ∴ x = f −1 ( y) = y3 − 4, dy, =, =, dx, for x ≠ −4, , , , 15
Page 26 :
(ii), , , We first find the inverse of the function y = f (x), i.e. x in term of y., 2, y2 = 1 + √ x i.e. √ x = y2 − 1, ∴ x = f −1 ( y) = ( y2 − 1), , , , dy, =, dx, , =, , , , , (iii) y = log x, We first find the inverse of the function y = f (x), i.e. x in term of y., y = log x ∴ x = f −1 ( y) = e y, 1, 1, 1, dy, =, =, = y = ln x = ., x, e, e, dx, Ex. 2 : Find the derivative of the inverse of, function y = 2x3 − 6x and calculate its, value at x = −2., Solution : Given : y = 2x3 − 6x, Diff. w. r. t. x we get,, dy, = 6x2 − 6 = 6 (x2 − 1), dx, dx, =, , we have,, dy, ∴, , Ex. 3 : Let f and g be the inverse functions of, each other. The following table lists a, few values of f, g and f ', , 1, 6 ((−2)2 − 1), , =, , 1, 18, , g(x), , f '(x), , −4, , 2, , 1, , 1, 3, , 1, , −4, , −2, , 4, , Solution : In order to find g' (−4), we should first, find an expression for g' (x) for any input, x. Since f and g are inverses we can use, the following identify which holds for, any two diffetentiable inverse functions., 1, g' (x) =, ... [check, how?], f ' [g(x)], , ... [Hint : f [g(x)] = x], , at x = − 2,, , we get, y = 2(−2)3 − 6(−2), , = − 16 + 12 = − 4, , =, , f (x), , find g' (−4)., , dx, 1, =, 2, dy 6 (x − 1), , , , x, , ∴ g' (−4) =, =, , 16, , 1, f '[g (−4)], 1, , f '(1), , =, , 1, 4
Page 27 :
Ex. 4 : Let f (x) = x5 + 2x − 3. Find ( f −1)' (−3)., Solution : Given : f (x) = x5 + 2x − 3, Diff. w. r. t. x we get,, f '(x) = 5x4 + 2, , Note that f (x) = −3 corresponds to x = 0., 1, ∴ ( f −1)' (−3) =, f ' (0), 1, 1, =, =, 5(0) + 2 2, 1.2.4 Derivatives of Standard Inverse trigononmetric Functions :, We observe that inverse trigonometric functions are multi-valued functions and because of this,, their derivatives depend on which branch of the function we are dealing with. We are not restricted to, use these branches all the time. While solving the problems it is customary to select the branch of the, inverse trigonometric function which is applicable to the kind of problem we are solving. We have to, pay more attention towards the domain and range., dy, π, π, 1, ≤ y ≤ then prove that, =, , |x| < 1., dx √1 − x2, 2, 2, π, π, Proof : Given that y = sin−1 x, −1 ≤ x ≤ 1, − ≤ y ≤, 2, 2, ∴ x = sin y , . . . . (I), Differentiate w. r. t. y, dx d, = (sin y), dy dy, dx, = cos y = ± √cos2 y = ± √1 − sin2 y, dy, dx, ∴, = ± √1 − x2, . . . . [⸪ sin y = x], dy, π, π, , But cos y is positive since y lies in 1st or 4th quadrant as − ≤ y ≤, 2, 2, dx, ∴, = √1 − x2, dy, dy, , We have, =, dx, 1., , If y = sin−1 x, −1 ≤ x ≤ 1, −, , dy, 1, =, , |x| < 1, dx √1 − x2, dy, 1, If y = cos−1 x, −1 ≤ x ≤ 1, 0 ≤ y ≤ π then prove that, =−, ., dx, √1 − x2, [As home work for students to prove.], , ∴, 2., , 17
Page 28 :
3., , If y = cot−1 x, x ∈ R, 0 < y < π then, , dy, 1, =−, ., dx, 1 + x2, , Proof : Given that y = cot−1 x, x ∈ R, 0 < y < π, ∴, , x = cot y , . . . . (I), , Differentiate w. r. t. y, dx d, = (cot y), dy dy, dx, = − cosec2 y = − (1 + cot2 y), , dy, dx, ∴, = − (1 + x2) , . . . . [⸪ cot y = x], dy, dy, =, , We have, dx, , , ∴, , 1, dy, =, , dx − (1 + x2), , dy, 1, =−, dx, 1 + x2, , ∴, , dy, π, π, 1, < y < then, =, . [left as home work for students to prove.], dx 1 + x2, 2, 2, dy, π, 1, =, if x > 1, 5. If y = sec−1 x, such that |x| ≥ 1 and 0 ≤ y ≤ π, y ≠ then, dx x√ x2 − 1, 2, dy, 1, =−, if x < − 1, , dx, x√ x2 − 1, π, Proof : Given that y = sec−1 x, |x| ≥ 1 and 0 ≤ y ≤ π, y ≠, 2, ∴ x = sec y , . . . . (I), Differentiate w. r. t. y, dx d, = (sec y), dy dy, dx, = sec y · tan y, dy, dx, = ± sec y ·√tan2 y, ∴, dy, = ± sec y ·√sec2 y − 1, Fig. 1.2.2, dx, ∴, = ± x √ x2 − 1, . . . . . [⸪ sec y = x], dy, We use the sign ± because for y in 1st and 2nd quadrant. sec y · tan y > 0., Hence we choose x √ x2 − 1 if x > 1 and − x √ x2 − 1 if x < − 1, 4., , If y = tan−1 x, x ∈ R, −, , In 1st quadrant both sec y and tan y are positive., In 2nd quadrant both sec y and tan y are negative., ∴ sec y · tan y is positive in both first and second quadrant., , 18
Page 29 :
Also, for x > 0, x √ x2 − 1 > 0, and for x < 0, − x √ x2 − 1 > 0, dx, = x √ x2 − 1 , , when x > 0, |x| > 1, dy, dy, dx, dy, dx, , = − x √ x2 − 1 , , 1, =, , x√ x2 − 1, 1, =−, x√ x2 − 1, , when x < 0, |x| > 1, , i.e. x > 1, i.e. x < − 1, , if x > 1, if x < − 1, , Note 1 : A function is increasing if its derivative is positive and is decreasing if its derivative is, negative., Note 2 : The derivative of sec−1 x is always positive because the graph of sec−1 x is always increasing., dy, π, π, 1, ≤ y ≤ , y ≠ 0 then, =−, if, dx, 2, 2, x√ x2 − 1, dy, 1, if, =, dx x√ x2 − 1, [ Left as home work for students to prove ], , 6., , If y = − cosec x, such that |x| ≥ 1 and −, , Note 3 : The derivative of cosec−1 x is always negative because the graph of cosec, decreasing., , x>1, x<−1, , −1, , x is always, , 1.2.5 Derivatives of Standard Inverse trigonometric Functions :, dy, dx, , y, , sin −1 x, , cos −1 x, , tan −1 x, , cot −1 x, , 1, , |x| < 1, √1 − x2, −, , 1, , |x| < 1, √1 − x2, 1, 1 + x2, −, , 1, 1 + x2, , Conditions, , y, , dy, dx, , Conditions, , 1, for x > 1, x√ x2 − 1, 1, −, for x < − 1, x√ x2 − 1, , |x| ≥ 1, 0≤y≤π, π, y≠, 2, , −1 ≤ x ≤ 1, π, π, − ≤y≤, 2, 2, −1 ≤ x ≤ 1, 0≤y≤π, , sec −1 x, , x∈R, π, π, − <y<, 2, 2, x∈R, 0<y<π, , 1, for x > 1, −, cosec −1 x x√ x2 − 1, 1, for x < − 1, x√ x2 − 1, Table 1.2.1, , 19, , |x| ≥ 1, π, π, − ≤y≤, 2, 2, y≠0
Page 30 :
1.2.6 Derivatives of Standard Inverse trigonometric Composite Functions :, dy, dx, , y, sin, , −1, , [ f (x)], , cos −1 [ f (x)], , f ' (x), , √1 − [ f (x)], , 2, , −, , f ' (x), , √1 − [ f (x)]2, , , | f (x)| < 1, , cot −1 [ f (x)], , , | f (x)| < 1, , sec, , −, , 1 + [ f (x)]2, , f ' (x), , f ' (x), , tan −1 [ f (x)], , dy, dx, f ' (x), , y, , −1, , cosec, , 1 + [ f (x)]2, , [ f (x)], , −1, , [ f (x)], , f (x) √[ f (x)] − 1, 2, , −, , f ' (x), f (x) √[ f (x)] − 1, 2, , , for | f (x)| > 1, , , for | f (x)| > 1, , Table 1.2.2, Some Important Formulae for Inverse Trigonometric Functions :, (1) sin−1 (sin θ) = θ, sin(sin−1 x) = x, (3) tan−1 (tan θ) = θ, tan(tan−1 x) = x, , (2) cos−1 (cos θ) = θ, cos(cos−1 x) = x, (4) cot−1 (cot θ) = θ, cot(cot−1 x) = x, , (5) sec−1 (sec θ) = θ, sec(sec−1 x) = x, , (6) cosec−1 (cosec θ) = θ, cosec(cosec−1 x) = x, , (7) sin−1 (cos θ) = sin−1 sin, , π, −θ, 2, , =, , π, −θ, 2, , (8) cos−1 (sin θ) = cos−1 cos, , π, −θ, 2, , =, , π, −θ, 2, , (9) tan−1 (cot θ) = tan−1 tan, , π, −θ, 2, , =, , π, −θ, 2, , (10) cot−1 (tan θ) = cot−1 cot, , π, −θ, 2, , =, , π, −θ, 2, , (11) sec−1 (cosec θ) = sec−1 sec, , π, −θ, 2, , (12) cosec−1 (sec θ) = cosec−1 cosec, 1, x, , (13) sin−1 (x) = cosec−1, , =, , π, −θ, 2, , π, −θ, 2, =, , π, −θ, 2, 1, x, , (14) cosec−1 (x) = sin−1, , (15) cos−1 (x) = sec−1, , 1, x, , (16) sec−1 (x) = cos−1, , 1, x, , (17) tan−1 (x) = cot−1, , 1, x, , (18) cot−1 (x) = tan−1, , 1, x, , (19) sin−1 x + cos−1 x =, , π, 2, , (22) tan−1 x + tan−1 y = tan−1, , (20) tan−1 x + cot−1 x =, x+y, 1 − xy, , π, 2, , (21) sec−1 x + cosec−1 x =, , (23) tan−1 x − tan−1 y = tan−1, , , In above tables, x is a real variable with restrictions. Table 1.2.3, , 20, , x−y, 1 + xy, , π, 2
Page 31 :
Some Important Substitutions :, Substitutions, , Expression, , √1 − x2, , x = sin θ or x = cos θ, , √1 − x2, , x = tan θ or x = cot θ, , √ x2 + 1, , x = sec θ or x = cosec θ, , 2x, 1 + x2, 1 − x2, , Expression, , a+x, or, a−x, , a−x, a+x, , x = a cos 2θ or x = a cos θ, , 1+x, or, 1−x, , 1−x, 1+x, , x = cos 2θ or x = cos θ, , a + x2, or, a − x2, , a − x2, a + x2, , 1 + x2, 3x − 4x3 or 1 − 2x2, 4x3 − 3x or 2x2 − 1, 3x − x3, 1 − 3x2, 1 − [ f (x)]2, 2 f (x), or, 1 + [ f (x)]2 1 + [ f (x)]2, , x2 = a cos 2θ or x2 = a cos θ, , Substitutions, x = tan θ, x = tan θ, x = sin θ, x = cos θ, x = tan θ, f (x) = tan θ, , Table 1.2.4, SOLVED EXAMPLES, Ex. 1 : Using derivative prove that sin−1 x + cos−1 x =, Solution :, , Let f (x) = sin−1 x + cos−1 x, , . . . . . (I), π, , We have to prove that f (x) =, 2, Differentiate (I) w. r. t. x, d, d, [ f (x)] = [sin−1 x + cos−1 x], dx, dx, 1, 1, f ' (x) =, −, =0, √1 − x2 √1 − x2, , π, ., 2, , f ' (x) = 0 ⇒ f (x) is a constant function., , Let f (x) = c. For any value of x, f (x) must be c only. So conveniently we can choose x = 0,, ∴ from (I) we get,, π π, π, π, f (0) = sin−1 (0) + cos−1 (0) = 0 + = ⇒ c = ∴ f (x) =, 2 2, 2, 2, π, −1, −1, Hence, sin x + cos x = ., 2, Ex. 2 : Differentiate the following w. r. t. x., (i) sin−1 (x3), , , (iv) cot−1, , 1, x2, , (ii) cos−1 (2x2 − x) (iii), (v) cos−1, , 21, , 1+x, (vi), 2, , sin−1 (2x), sin2 (sin−1 (x2))
Page 39 :
y = tan−1 (3x + 2) + tan−1 (2x − 1), Differentiate w. r. t. x., dy, d, =, [tan−1 (3x + 2) + tan−1 (2x − 1)], dx, dx, d, d, =, [tan−1 (3x + 2)] + [tan−1 (2x − 1)], dx, dx, 1, 1, d, d, =, (3x + 2) +, (2x − 1), 2 ·, 2 ·, 1 + (3x + 2) dx, 1 + (2x − 1) dx, 3, 2, dy, ∴, =, 2 +, 1 + (3x + 2), 1 + (2x − 1)2, dx, EXERCISE 1.2, (6) Differentiate the following w. r. t. x., (i) tan−1 (log x), (ii) cosec−1 (e−x ), , (1) Find the derivative of the function y = f (x), using the derivative of the inverse function, x = f −1 ( y) in the following, (i) y = √x, (iii), (v) y = 2x + 3, , (iii) cot−1 (x3), , (ii), (iv), (vi), , y = 2 − √x, y = log (2x − 1), y = ex − 3, x, (vii) y = e2x − 3, (viii) y = log2, 2, (2) Find the derivative of the inverse function of, the following, (i) y = x2·ex, (ii) y = x cos x, (iii) y = x·7x, (iv) y = x2 + log x, (v) y = x log x, (3) Find the derivative of the inverse of the, following functions, and also find their value, at the points indicated against them., (i) y = x5 + 2x3 + 3x, at x = 1, , (v), , tan−1 (√x), , (iv), , cot−1 (4x ), , (vi), , sin−1, 3, , (viii) sin−1 (x 2 ), , (vii) cos−1 (1 − x2), , (ix) cos3 [cos−1 (x3)] (x), , sin4 [sin−1 (√x)], , (7) Differentiate the following w. r. t. x., , (ii) y = ex + 3x + 2,, at x = 0, 2, 3, (iii) y = 3x + 2 log x , at x = 1, (iv) y = sin (x − 2) + x2, at x = 2, (4) If f (x) = x3 + x − 2, find ( f −1)' (0)., (5) Using derivative prove, π, (i) tan−1 x + cot−1 x =, 2, π, (ii) sec−1 x + cosec−1 x = . . . [for | x | ≥ 1], 2, , (i), , cot−1 [cot (ex )], , (ii), , cosec−1, , 2, , 1 + cos x, 2, , (iv) cos−1, , 1 − cos (x2), 2, , (v) tan, , 1 − tan ( 2x ), 1 + tan ( 2x ), , (vi) cosec−1, (vii) tan, , −1, , (viii) cot−1, , 29, , 1, cos (5x), , (iii) cos−1, , −1, , 1 + x2, 2, , 1, 4 cos3 2x − 3 cos 2x, , 1 + cos ( 3x ), sin ( 3x ), sin 3x, 1 + cos 3x
Page 40 :
(ix) tan, , cos 7x, 1 + sin 7x, , (x) tan, , 1 + cos x, 1 − cos x, , −1, , −1, , (v), , (xi) tan (cosec x + cot x), −1, , 1 + sin ( 4x3 ) + 1 − sin ( 4x3 ), , (xii) cot, , −1, , 1 + sin ( 4x3 ) − 1 − sin ( 4x3 ), , cos−1, , (v), , cos, , √3 cos x − sin x, 2, , √2, , (iv) cos−1, −1, , 3 cos 3x − 4 sin 3x, 5, 3 cos (ex) + 2 sin (ex), , √13, , (vi) cosec−1, , 10, 6 sin (2 ) − 8 cos (2x), x, , (9) Differentiate the following w. r. t. x., (i), , cos−1, , 1 − x2, 1 + x2, , (ii) tan−1, , cos−1 (3x − 4x3) (vi) cos−1, , ex − e −x, ex + e −x, 1, , (vii) cos−1, , 1 − 9x, 1 + 9x, , (viii) sin−1, , 4x + 2, 1 + 24x, , (ix) sin−1, , 1 − 25x2, 1 + 25x2, , (x) sin−1, , 1 − x3, 1 + x3, , (xi) tan−1, , 2x 2, 1 − x5, , (xii) cot−1, , 1 − √x, 1 + √x, , (10) Differentiate the following w. r. t. x., , cos √x + sin √x, , (iii) sin−1, , (iv) sin−1 (2x √1 − x2), , 5, , (8) Differentiate the following w. r. t. x., 4 sin x + 5 cos x, (i) sin−1, √41, (ii), , 1 − x2, 1 + x2, , (iii) sin−1, , (i) tan−1, , 8x, 1 − 15x2, , (ii) cot−1, , 1 + 35x2, 2x, , (iii) tan−1, , 2√x, 1 + 3x, , (iv) tan−1, , 2x + 2, 1 − 3(4x), , (v) tan−1, , 2x, 1 + 22x + 1, , (vi) cot−1, , a2 − 6x2, 5ax, , (vii) tan−1, , a + b tan x, b − a tan x, , (viii) tan−1, , 5− x, 6x − 5x − 3, , (ix) cot−1, , 2x, 1 − x2, , 2, , 4 − x − 2x2, 3x + 2, , 1.3.1 Logarithmic Differentiation, The complicated functions given by formulas that involve products, quotients and powers can often, be simplified more quickly by taking the natural logarithms on both the sides. This enables us to use, the laws of logarithms to simplify the functions and differentiate easily. Especially when the functions, are of the form y = [ f (x)]g(x) it is recommended to take logarithms on both the sides which simplifies to, log y = g(x). log [ f (x)], now it becomes convenient to find the derivative. This process of finding the, derivative is called logarithmic differentiation., SOLVED EXAMPLES, Ex. 1 : Differentiate the following w. r. t. x., (i), , (x2 + 3)2, , 3, , (x3 + 5)2, , (2x2 + 1)3, , 2, , , , (ii), , 30, , ex (tan x) 2, x, , 3, , (1 + x2) 2 cos3 x
Page 41 :
3, , 5, , 2, , (iii) (x + 1) 2 (2x + 3) 2 (3x + 4) 3 for x ≥ 0, , (iv), , xa + xx + ax, , (v) (sin x)tan x − xlog x, , Solution :, (x2 + 3)2, , (i) Let y =, , (x3 + 5)2, , 3, , (2x2 + 1)3, , Taking log of both the sides we get,, (x2 + 3)2, , log y = log, , 3, , 2, , (x3 + 5)2, , (x2 + 3)2 (x3 + 5) 3, , = log, , (2x2 + 1)3, , 3, , (2x2 + 1) 2, , 2, , 3, , , = log (x2 + 3)2 (x3 + 5) 3 − log (2x2 + 1) 2, 2, , 3, , , = log (x2 + 3)2 + log (x3 + 5) 3 − log (2x2 + 1) 2, log y = 2 log (x2 + 3) +, Differentiate w. r. t. x., , 2, 3, log (x3 + 5) − log (2x2 + 1), 3, 2, , 2, 3, d, d, (log y) =, 2 log (x2 + 3) + log (x3 + 5) − log (2x2 + 1), 3, 2, dx, dx, d, 2 d, 3 d, 1 dy, , = 2· [log (x2 + 3)] + · [log (x3 + 5)] − · [log (2x2 + 1)], dx, 3 dx, 2 dx, y dx, 2, 3, 2, d, d, d, = 2 · (x2 + 3) + 3, · (x3 + 5) −, ·, (2x2 + 1), 3(x + 5) dx, 2(2x2 + 1) dx, x + 3 dx, 2, 3, 2, dy, 2, = y 2, (2x) +, (3x, ), −, (4x), 3(x3 + 5), 2(2x2 + 1), x +3, dx, (x2 + 3)2 3 (x3 + 5), dy, ∴ , =, dx, (2x2 + 1)3, 2, , (ii) Let y =, , 2, , 2x2, 6x, 4x, +, − 2, 3, 2, x + 3 (x + 5) 2x + 1, , x, , ex (tan x) 2, 3, , (1 + x2) 2 cos3 x, , Taking log of both the sides we get,, 2, , log y = log, , 3, 2 2, , (1 + x ) (cos x)3, , , , , , x, , ex (tan x) 2, , ∴, , 3, , x, , 2, , = log ex (tan x) 2 − log (1 + x2) 2 (cos x)3, x, , 2, , 3, , = log ex + log (tan x) 2 − log (1 + x2) 2 + log (cos x)3, 3, x, log (tan x) − log (1 + x2) − 3 log (cos x), 2, 2, 3, x, log y = x2 + log (tan x) − log (1 + x2) − 3 log (cos x), 2, 2, = x2 log e +, , 31
Page 42 :
Differentiate w. r. t. x., 3, d, d 2 x, (log y) =, x + log (tan x) − log (1 + x2) − 3 log (cos x), 2, 2, dx, dx, d x, d, 3 d, x d, 1 dy, d 2, =, (x ) + · [log (tan x)] + log (tan x), −, [log (1 + x2)] − 3 [log (cos x)], dx 2, dx, 2 dx, 2 dx, y dx dx, 3, d, 1, 3 d, x 1 d, = 2x + ·, · (tan x) + log (tan x) −, · (1 + x2) −, · (cos x), 2, 2 2(1 + x ) dx, cos x dx, 2 tan x dx, 3, 1, 3, x, = 2x + ·(cot x) (sec2 x) + log (tan x) −, ·(2x) −, (− sin x), 2, 2(1 + x ), 2, cos x, 2, 3x, 1, 1, x cos x, =, 2x + ×, ×, +, log, (tan, x), −, + 3 tan x, 1 + x2, 2 sin x cos2 x 2, 3x, 1, x, dy, = y 2x +, + log (tan x) −, + 3 tan x, 1 + x2, 2 sin x cos x 2, dx, 2, , x, , 3x, ex (tan x) 2, 1, dy, ∴ , =, 2x + x cosec 2x + log (tan x) −, + 3 tan x, 3, 1 + x2, 2, dx (1 + x2) 2 cos3 x, 3, , 5, , 2, , (iii) Let y = (x + 1) 2 (2x + 3) 2 (3x + 4) 3, Taking log of both the sides we get,, 3, , 5, , 2, , log y = log (x + 1) 2 (2x + 3) 2 (3x + 4) 3, 3, , 5, , 2, , , = log (x + 1) 2 + log (2x + 3) 2 + log (3x + 4) 3, 3, 5, 2, log (x + 1) + log (2x + 3) + log (3x + 4), 2, 2, 3, Differentiate w. r. t. x., log y =, , 5, 2, d, d 3, (log y) =, log (x + 1) + log (2x + 3) + log (3x + 4), 2, 3, dx, dx 2, 1 dy, 5 d, 2 d, 3 d, ·, = ·, [log (x + 1)] + · [log (3x + 2)] +, · [log (3x + 4)], y dx, 2 dx, 3 dx, 2 dx, d, 5, d, 2, d, 3, =, ·, (x + 1) +, ·, (3x + 2) +, ·, (3x + 4), 2(3x + 1) dx, 3(3x + 4) dx, 2(x + 1) dx, 5, 2, 3, dy, = y, +, (3) +, (3), 3(3x + 4), 2(x + 1) 2(3x + 1), dx, 3, 5, 2, 15, 2, 3, dy, ∴ , = (x + 1) 2 (2x + 3) 2 (3x + 4) 3, +, +, 2(x + 1) 2(3x + 1) 3x + 4, dx, (iv) Let y = xa + xx + ax, Here the derivatives of xa and ax can be found directly but we can not find the derivative of xx, without the use of logarithm. So the given function is split in to two functions, find their derivatives, and then add them., , 32
Page 43 :
Let u = xa + ax and v = xx, ∴ y = u + v, , where u and v are differentiable functions of x., dy du dv, =, + , . . . . . (I), dx dx dx, Now, u = xa + ax, Differentiate w. r. t. x., du d a, d, =, (x ) + (ax), dx dx, dx, du, = axa −1 + ax log a , . . . . . (II), dx, And, v = xx, Taking log of both the sides we get,, log v = log xx, log v = x log x, Differentiate w. r. t. x., d, d, (log v) =, (x log x), dx, dx, 1 dv, d, d, , = x, (log x) + log x (x), v dx, dx, dx, 1, dv, = v x × + log x (1), x, dx, dv, = xx [1 + log x] . . . . . (III), dx, Substituting (II) and (III) in (I) we get,, dy, = axa−1 + ax log a + xx [1 + log x], dx, Let y = (sin x)tan x − xlog x, Let u = (sin x)tan x and v = xlog x, ∴ y = u − v, , where u and v are differentiable functions of x., dy du dv, =, − , . . . . . (I), dx dx dx, Now, u = (sin x)tan x , taking log of both the sides we get,, log u = log (sin x)tan x, ∴, log u = tan x log (sin x), Differentiate w. r. t. x., d, d, (log u) =, [tan x log (sin x)], dx, dx, 1 du, d, d, , = tan x, [log (sin x)] + log (sin x) (tan x), u dx, dx, dx, 1 d, · ·(sin x) + log (sin x)·(sec2), = tan x·, sin x dx, , (v) , , 33
Page 44 :
du, 1, = u tan x·, ·(cos x) + sec2 x·log (sin x), dx, sin x, du, = (sin x)tan x [tan x·cot x + sec2 x·log (sin x)], dx, du, . . . . . (II), = (sin x)tan x [1 + sec2 x·log (sin x)], dx, And, v = xlog x, Taking log on both the sides we get,, log v = log (xlog x), log v = log x log x = (log x)2, Differentiate w. r. t. x., d, d, (log v) =, [(log x)2], dx, dx, d, 1 dv, = 2 log x, (log x), , dx, v dx, dv, 2 log x, 2xlog x log x, , =u, =, , dx, x, x, , . . . . . (III), , Substituting (II) and (III) in (I) we get,, dy, 2xlog x log x, , = (sin x)tan x [1 + sec2 x·log (sin x)] −, dx, x, 1.3.2 Implicit Functions, Functions can be represented in a variety of ways. Most of the functions we have dealt with so far, have been described by an equation of the form y = f (x) that expresses y solely in terms of the variable, x. It is not always possible to solve for one variable explicitly in terms of another. Those cases where it, is possible to solve for one variable in terms of another to obtain y = f (x) or x = g (y) are said to be in, explicit form., If an equation in x and y is given but x is not an explicit function of y and y is not an explicit function, of x then either of the variables is an Implicit function of the other., 1.3.3 Derivatives of Implicit Functions, 1., , Differentiate both sides of the equation with respect to x (independent variable), treating y as a, differentiable function of x., , 2., , Collect the terms containing, , dy, dy, on one side of the equation and solve for ., dx, dx, , 34
Page 59 :
(v) Differentiate 3x w. r. t. logx 3., , (4) (i) Differentiate x sin x w. r. t. tan x., 2x, (ii) Differentiate sin−1, 1 + x2, w. r. t. cos−1, , (vi) Differentiate tan−1, , 1 − x2, ., 1 + x2, , (iii) Differentiate tan−1, , cos x, 1 + sin x, , w. r. t. sec−1 x., (vii) Differentiate xx w. r. t. xsin x., , x, , √ 1 − x2, , (viii) Differentiate tan−1, , 1, w. r. t. sec−1, ., 2x2 − 1, 1 − x2, −1, w. r. t. tan−1 x., (iv) Differentiate cos, 1 + x2, , , , w. r. t. tan−1, , √ 1 + x2 − 1, x, , 2x√ 1 − x2, ., 1 − 2x2, , 1.5.1 Higher order derivatives :, If f (x) is differentiable function of x on an open interval I, then its derivative f ' (x) is also a function, on I, so f ' (x) may have a derivative of its own, denoted as ( f ' (x))' = f '' (x). This new function f '' (x) is, called the second derivative of f (x). By Leibniz notation, we write the second detivative of, d dy, d2 y, y = f (x) as y'' = f '' (x) =, = 2, dx dx, dx, By method of first principle, lim, f ' (x) = h→0, , f (x + h) − f (x), dy, =, and, h, dx, , f '' (x) = lim, h→0, , f ' (x + h) − f ' (x), d2 y, = 2, h, dx, , d, [ f '' (x)] = f ''' (x)., dx, Now the new function f ''' (x) is called the third derivative of f (x). We write the third of y = f (x) as, Further if f '' (x) is a differentiable function of x then its derivative is denoted as, , y ''' = f ''' (x) =, f (4) (x) =, , d4 y, dx4, , d d2 y, d3 y, =, . The fourth derivative, is usually denoted by f (4) (x). Therefore, 2, 3, dx dx, dx, , ., , In general, the nth derivative of f (x), is denoted by f (n) (x) and it obtained by differentiating f (x),, dn y, n times. So, we can write the nth derivative of y = f (x) as y(n) = f (n) (x) = n . These are called higher order, dx, derivatives., Note : The higher order derivatives may also be denoted by y2, y3, . . . , yn., , 49
Page 66 :
dy, dy d2 y, dy 2, 2( 1 − x )· · 2 − 2x, = 2m2y, dx, dx dx, dx, dy, Dividing throughout by 2 we get,, dx, 2, dy, dy, , ( 1 − x2)· 2 − x, = m2y, dx, dx, , , , , 2, , ∴ ( 1 − x2)·, , d2 y, , dy, −, x, − m2y = 0, 2, dx, dx, , 1.5.2 Successive differentiation (or nth order derivative) of some standard functions :, Successive Differentiation is the process of differentiating a given function successively for n times, and the results of such differentiation are called successive derivatives. The higher order derivatives are, of utmost importance in scientific and engineering applications., There is no general formula to find nth derivative of a function. Because each and every function has, it's own specific general formula for it's nth derivative. But there are algorithms to find it., So, here is the algorithm, for some standard functions., Let us use the method of mathematical induction whereever applicable., Step 1 :- Use simple differentiation to get 1st, 2nd and 3rd order derivatives., Step 2 :- Observe the changes in the coefficients, the angles, the power of the function and the signs of, each term etc., Step 3 :- Express the nth derivative with the help of the patterns of changes that you have observed., This will be your general formula for the nth derivative of the given standard function., SOLVED EXAMPLES, Ex. 1 : Find the nth derivative of the following :, (i) xm , , (ii), , , , (v), , (iv) sin x , Solution :, (i) Let y = xm, , 1 , ax + b, cos (ax + b) , , (iii) log x, (vi) eax sin (bx + c), , Differentiate w. r. t. x, d d2 y, d m−2, = m·(m − 1), (x ), 2, dx dx, dx, d3 y, = m·(m − 1)·(m − 2) xm − 3, dx3, In general nth order derivative will be, dn y, = m·(m − 1)·(m − 2)...[m − (n − 1)] xm − n, dxn, dn y, = m·(m − 1)·(m − 2)...[m − n + 1] xm − n, n, dx, , Differentiate w. r. t. x, dy d m, =, (x ) = mxm − 1, dx dx, Differentiate w. r. t. x, d m−1, d dy, =m, x, dx, dx dx, d2 y, 2 = m·(m − 1) xm − 2, dx, , 56
Page 67 :
case (i) :-, , If m > 0 and m > n, then, dn y m·(m − 1)·(m − 2)... [m − (n − 1)] · (m − n)... 2·1 m − n, =, x, dxn, (m − n) · [m − n − 1]... 2·1, dn y m!. xm − n, =, dxn (m − n)!, , case (ii) :-, , If m > 0 and m = n, then, dn y n!. xm − n, n!. x0, =, =, = n!, dxn (n − n)!, 0!, , (ii) Let y =, , case (iii) :-, , 1, ax + b, , If m > 0 and m < n, then, dn y, =0, dxn, , (iii) Let y = log x, Differentiate w. r. t. x, dy d, 1, =, (log x) =, dx dx, x, , Differentiate w. r. t. x, dy d, d, 1, −1, =, =, · (ax + b), 2, dx dx ax + b (ax + b) dx, , Differentiate w. r. t. x, , dy (− 1)·a, =, dx (ax + b)2, , d 1, d dy, =, dx x, dx dx, , Differentiate w. r. t. x, , d2 y, , =, , − 1 (− 1)1, = 2, x2, x, , d, d dy, 1, = (− 1)(a), , dx (ax + b)2, dx dx, , Differentiate w. r. t. x, , dy, d, −2, 2 = (− 1)(a), ·, (ax + b), dx, (ax + b)3 dx, , d d2 y, d 1, = (− 1)1, 2, dx dx, dx x2, , d2 y (− 1)2·2·1·a2, 2 =, dx, (ax + b)3, , d3 y, , dx2, , 2, , dx3, , Differentiate w. r. t. x, , (− 1)2·1·2, −2, =, x3, x3, , In general nth order derivative will be, , d, d dy, 1, 2, 2, =, (−, 1), ·2·1·a, ·, , dx (ax + b)3, dx dx2, 2, , dn y (− 1)n − 1·1·2·3... (n − 1), =, dxn, xn, , d3 y, d, −3, 3 = (− 1)2·2·1·a2·, ·, (ax + b), dx, (ax + b)4 dx, , dn y, dxn, , d y (− 1)3·3·2·1·a3, 3 =, dx, (ax + b)4, 3, , , , = (− 1), , 1, , In general nth order derivative will be, , dn y (− 1)n·n·(n − 1)... 2·1·an, n =, dx, (ax + b)n + 1, dn y (− 1)n·n!·an, n =, dx, (ax + b)n + 1, , 57, , =, , (− 1)n − 1·(n − 1)!, xn
Page 71 :
Let us Remember, ֍, , If a function f (x) is differentiable at x = a then it is continuous at x = a, but the converse is not, true., , Chain Rule : If y is differerentiable function of u and u is differerentiable function of x then y, dy dy du, is differerentiable function of x and, =, ·, dx du dx, ֍ If y = f (x) is a differentiable of x such that the inverse function x = f −1( y) exists then, 1, dy, dy, =, ,, where, ≠0, , dy, dx, dx, dx, ֍, , ֍, , Derivatives of Inverse Trigonometric functions :, f (x), , sin −1 x, , f ' (x), , 1, ,, √1 − x2, |x| < 1, , ֍, , −, , cos −1 x, , tan −1 x, , cot −1 x, , sec −1 x, , 1, ,, √1 − x2, |x| < 1, , 1, 1 + x2, , −, , 1, 1 + x2, x∈R, , 1, x√ x2 − 1, |x| < 1, , x∈R, , cosec −1 x, 1, x√ x 2 − 1, |x| < 1, , −, , This is a simple shortcut to find the derivative of (function) (function), d g, f =f, dx, , g, , g, · f ' + (log f ) · g', f, , If y = f (t ) and y = g (t ) is a differentiable of t such that y is a function of x then, dy, dy, dx, dt, , =, ,, where, ≠0, dx, dx, dt, dt, ֍ Implict function of the form x m y n = (x + y) m + n , m, n ∈ R always have the first order derivative , dy y, d2y, =, and second order derivative 2 = 0, dx x, dx, ֍, , MISCELLANEOUS EXERCISE 1, (I) Choose the correct option from the given alternatives :, 1, 8, (1) Let f (1) = 3, f ' (1) = − , g (1) = − 4 and g' (1) = − . The derivative of √ [ f (x)]2 + [g (x)]2, 3, 3, , w. r. t. x at x = 1 is, 29, 7, 31, 29, (A) −, (B), (C), (D), 15, 3, 15, 15, , 61
Page 72 :
(2), , If y = sec (tan−1 x) then, , (A), (3), , (B), , dy, = ..., dx, x ( x log y − y ), , y ( y log x − x ), , 2 − 4x2, , √ 1 − x2, x, 1 + √ 1 − x2, , x, , √ 1 − x2, , (D) √ 2, , √2, , 4x + 1 log 2, 1 + 42x, , (C), , 4x + 1 log 4, 1 + 44x, , (D), , 22(x + 1) log 2, 1 + 24x, , (B), , y ( y log x − x ), x ( x log y − y ), , dy, = ..., dx, 2 + 4x2, (B), √ 1 − x2, , (C), , (C), , y2 (1 − log x ), x2 (1 − log y ), , 4x2 − 1, , 1−x, dy, , then, = ..., 1+x, dx, , 1 − 2x, , 1 − 2x, , (B), , (C), , √ 1 − x2, , (D), , √ 1 − x2, , + sin 2 tan−1, , (D), , (D), , 2 √ 1 − x2, , y (1 − log x ), x (1 − log y ), , 1 − 2x2, , √ 1 − x2, , 1 − 2x2, , √ 1 − x2, , If y is a function of x and log (x + y) = 2xy, then the value of y' (0) = ..., (B) 0, , (C) −1, , If g is the inverse of a function f and f ' (x) =, , (A) 1 + x7, (9), , 1, , , which of the following is not the derivative of f (x), , 1 + 42x, , (A) 2, (8), , 1+ 24x, , 2·4x log 4, , If y = tan−1, , (A), (7), , 1, , 4x + 2, , If y = sin (2 sin−1 x), then, , (A), (6), , (C), , If x y = y x, then, , (A), (5), , (B) 1, , If f (x) = sin−1, , (A), (4), , 1, 2, , dy, at x = 1, is equal to :, dx, , (B), , 1, 7, 1 + [g(x)], , If x √ y + 1 + y √ x + 1 = 0 and x ≠ y then, , (A), , 1, (1 + x)2, , (10) If y = tan−1, (A), , x, , √ a2 − x2, , (B) −, , 1, (1 + x)2, , (D) 1, , 1, , then the value of g' (x) is equal to :, 1 + x7, 7, , (C) 1 + [g(x)], , (D) 7x6, , (C) (1 + x)2, , (D) −, , dy, = ..., dx, x, x+1, , a−x, dy, , where − a < x < a then, = ..., a+x, dx, (B), , a, , (C) −, , √ a2 − x2, , 62, , 1, 2√ a2 − x2, , (D), , 1, 2√ a2 − x2
Page 73 :
(11) If x = a (cos θ + θ sin θ), y = a (sin θ − θ cos θ) then, (A), , 8 √2, , (B) −, , aπ, , (12) If y = a cos (log x) and A, (A) x2, −x, −y, , d2 y, , 8 √2, , d2 y, dx2, , π, 4, , = ..., , aπ, , (C), , aπ, , θ=, , 8 √2, , (D), , 4 √2, aπ, , dy, + C = 0, then the values of A, B, C are ..., dx, dx, (B) x2, x, y, (C) x2, x, −y, (D) x2, −x, y, 2, , +B, , (II) Solve the following :, (1), , f (x) = −x,, , for −2 ≤ x < 0, , g(x) = 6 − 3x,, 2x − 4, =, ,, 3, , = 2x,, for 0 ≤ x ≤ 2, 18 − x, =, ,, for 2 < x ≤ 7, 4, Let u(x) = f [ g(x)], v(x) = g [ f (x)] and w(x) = g [ g(x)]., , (2), , for 0 ≤ x ≤ 2, for 2 < x ≤ 7, , Find each derivative at x = 1, if it exists i.e. find u' (1), v' (1) and w' (1). if it doesn't exist then, explain why ?, The values of f (x), g(x), f ' (x) and g' (x) are given in the following table., f (x), 3, 2, , x, −1, 2, , g(x), 2, −1, , f ' (x), −3, −5, , g' (x), 4, −4, , Match the following., A Group - Function, d, [ f (g (x))] at x = −1, dx, d, [ g ( f (x) − 1)] at x = −1, (B), dx, d, [ f ( f (x) − 3)] at x = 2, (C), dx, d, [ g ( g (x))] at x = 2, (D), dx, (A), , (3), , B Group - Derivative, 1. −16, 2., , 20, , 3. −20, 4., , 15, , 5., , 12, , Suppose that the functions f and g and their derivatives with respect to x have the following, values at x = 0 and x = 1., x, , f (x), , g(x), , 0, , 1, , 1, , 1, , 3, , −4, , f ' (x) g' (x), 5, −, , 1, 3, , 1, 3, 8, −, 3, , (i) The derivative of f [ g(x)] w. r. t. x at x = 0 is ......, (ii) The derivative of g [ f (x)] w. r. t. x at x = 0 is ......, d 10, (iii) The value of, [x + f (x)]−2, is ......, x=1, dx, (iv) The derivative of f [(x + g(x)] w. r. t. x at x = 0 is ......, , 63
Page 74 :
(4), , Differentiate the following w. r. t. x, , (i) sin 2 tan−1, , 1−x, 1+x, , , , (iii) tan−1, , √ x (3 − x), , 1 − 3x, , (iv) cos−1, , (v) tan−1, , x, 1 − 10x2, −1, +, cot, 1 + 6x2, 7x, , (vi) tan−1, , (5), , 1+x, 1−x, , (ii) sin2 cot−1, , √1 + x − √1 − x, 2, , √ 1 + x2 + x, √ 1 + x2 − x, , y2, − 1., x2, , dy y, (i) If √ y + x + √ y − x = c, then show that, = −, dx x, , 1 − y2, dy, (ii) If x √ 1 − y + y √ 1 − x = 1, then show that, =−, ., 1 − x2, dx, 2, , 2, , dy sin2 (a + y), (iii) If x sin (a + y) + sin a cos (a + y) = 0, then show that, =, ., sin a, dx, dy sin2 (a + y), (iv) If sin y = x sin (a + y), then show that, =, ., sin a, dx, x, y, , (v) If x = e , then show that, , dy, x−y, =, ., dx x log x, , (vi) If y = f (x) is a differentiable function then show that, (6), , (i) Differentiate tan−1, , , , (ii) Differentiate log, , , , (iii) Differentiate tan−1, , d2 x, dy2, , =−, , dy, dx, , √ 1 + x2 − 1 w. r. t. tan−1 2x √ 1 − x2 ., 2, 1 − 2x, , x, , √ 1 + x2 + x, w. r. t. cos (log x)., √ 1 + x2 − x, √ 1 + x2 − 1, , w. r. t. cos−1, , 1 + √ 1 + x2, , ., 2√ 1 + x2, d2 y a2 b2, 2, 2, 2, 2, 2, (7) (i) If y = a cos x + b sin x , show that y + 2 = 3 ., dx, y, 2, d, dy, y, + (4x2 + 3) y = 0., (ii) If log y = log (sin x) − x2 , show that 2 + 4x, dx, dx, d2 y, dy 2, 2, + b2 = 0., (iii) If x = a cos θ, y = b sin θ, show that a y 2 +, dx, dx, x, , (iv) If y = A cos (log x) + B sin (log x), show that x2 y2 + x y1 + y = 0., (v) If y = A emx + B enx, show that y2 − (m + n) y1 + (mn) y = 0., , v, , v, 64, , v, , −3, , ·, , d2 y, ., dx2
Page 75 :
2. APPLICATIONS OF DERIVATIVES, Let us Study, •, , Applications of Drivatives to Tangents and Normals, , •, , Approximations, , •, , Rolle's Theorem and Lagrange's Mean Value Theorem. •, , •, , Maxima and Minima, , •, , Derivative as a rate measure, Increasing and Decreasing Functions, , Let us Recall, •, •, •, •, , Continuous functions., Derivatives of Composite, Inverse Trigonometric, Logarithmic, Parametric functions., Relation between derivative and slope., Higher Order Derivatives., , 2.1.1 Introduction :, In the previous chapter we have studied the derivatives of various functions such as composite, functions, Inverse Trigonometric functions, Logarithmic functions etc. and also the relation between, Derivative and slope of the tangent. In this chapter we are going to study various applications of, differentiation such as application to (i) Geometry, (ii) Rate measure (iii) Approximations (iv) Rolle's, Theorem and Lagrange's Mean Value Therorem (v) Increasing and Decreasing functions and (vi), Maxima and Minima., Let us Learn, 2.1.2 Application of Derivative in Geometry :, In the previous chapter we have studied the relation between derivative and slope of a line or slope, of a tangent to the curve at a given point on it., Let y = f (x) be a continuous function of x representing a curve in XY- plane and P (x1, y1) be any, , point on the curve., Then, , dy, dx, , (x1, y1), , = [ f ' (x)](x , y ) represents slope, also called gradient, of the tangent to the curve at, 1, , 1, , P (x1, y1). The normal is perpendicular to the tangent. Hence, the slope of the normal at P will be the negative, , of reciprocal of the slope of tangent at P. Let m and m' be the slopes of tangent and normal respectively,, , 65
Page 78 :
Ex. 2 : Find points on the curve given by y = x3 − 6x2 + x + 3 where the tangents are parallel to the line, y = x + 5., Solution : Equation of curve is y = x3 − 6x2 + x + 3, Differentiate w. r. t. x, dy d 3, =, (x − 6x2 + x + 3) = 3x2 − 12x + 1, , dx dx, Given that the tangent is parallel to y = x + 5 whose slope is 1., dy, = 1 ⇒ 3x2 − 12x + 1 = 1, ∴ Slope of tangent =, dx, 3x (x − 4) = 0, so, x = 0 or x = 4, When x = 0, y = (0)3 − 6(0)2 + (0) + 3 = 3, When x = 4, y = (4)3 − 6(4)2 + (4) + 3 = −25, So the required points on the curve are (0, 3) and (4, −25)., 2.1.3 Derivative as a Rate measure :, If y = f (x) is the given function then a change in x from x1 to x2 is generally denoted by, δx = x2 − x1 and the corresponding change in y is denoted by δy = f (x2) − f (x1). The difference quotient, f (x2) − f (x1), δy, =, is called the average rate of change with respect to x. This can also be interpreted, x2 − x1, δx, geometrically as the slope of the secant line joining the points P ( x1, f (x1)) and Q ( x2, f (x2)) on the graph, of function y = f (x)., Consider the average rate of change over smaller and smaller intervals by letting x2 to approach x1 and, therefore letting δx to approach 0. The limit of these average rates of change is called the instantaneous, rate of change of y with respect to x at x = x1, which is interpreted as the slope of the tangent to the curve, y = f (x) at P ( x1, f (x1)). Therefore instantaneous rate of change is given by, lim, , δx → 0, , δy, = xlim, →x, δx, 2, , 1, , f (x2) − f (x1), x2 − x1, , We recognize this limit as being the derivative of f (x) at x = x1, i.e. f ' (x1). We know that one, interpretation of the derivative f ' (a) is the instantaneous rate of change of y = f (x) with respect x when, x = a. The other interpretation is f (x) at f ' (a) is the slope of the tangent to y = f (x) at (a, f (a))., SOLVED EXAMPLES, Ex. 1 : A stone is dropped in to a quiet lake and waves in the form of circles are generated, radius of the, circular wave increases at the rate of 5 cm/ sec. At the instant when the radius of the circular, wave is 8 cm, how fast the area enclosed is increasing ?, Solution : Let R be the radius and A be the area of the circular wave., , 68
Page 80 :
Ex. 3 : Water is being poured at the rate of 36 m3/sec in to a cylindrical vessel of base radius 3 meters., Find the rate at which water level is rising., Solution : Let R be the radius of the base, H be the height and V be the volume of the cylindrical vessel, at any time t. R, V and H are functions of t., , V = πR2 H, , , V = π(3)2 H = 9π H, , , , Differentiate w. r. t. t, dV, dH, = 9π, dt, dt, dH 1 dV, = ·, . . . (I), dt 9π dt, , , , , . . . [ Given : R = 3], , Given that,, dV, = 36 m3/sec, . . . (II), dt, 4, dH 1, From (I) we get,, = · (36) =, π, dt 9π, 4, ∴ Water level is rising at the rate of meter/sec., π, Ex. 4 : A man of height 180 cm is moving away from a lamp post at the rate of 1.2 meters per second., If the height of the lamp post is 4.5 meters, find the rate at which (i) his shadow is lengthening., (ii) the tip of the shadow is moving., Solution : Let OA be the lamp post, MN be the man, MB = x be the length of shadow and OM = y be, the distance of the man from the lamp post at time t. Given that man is moving away from, the lamp post at the rate of 1.2 meter/sec. x and y are functions of t., dy, dx, Hence, = 1.2. The rate at which shadow is lengthening = ., dt, dt, , , B is the tip of the shadow and it is at a distance of (x + y) from the post., x+y, x, i.e. 45x = 18x + 18y, i.e. 27x = 18y, =, 4.5, 1.8, 2y, , , ∴, x=, 3, , Differentiate w. r. t. t, dx 2 dy 2, , = ×, = × 1.2 = 0.8 meter/sec., dt 3 dt 3, rate at which the tip of the shadow is moving is given by, d, dx dy, , (x + y) =, +, dt, dt dt, d, (x + y) = 0.8 + 1.2 = 2 meter/sec., ∴, dt, Shadow is lengthening at the rate of 0.8 meter/ sec. and its tip is moving at the rate of 2 meters/sec., , 70
Page 81 :
2.1.4 Velocity, Acceleration and Jerk :, If s = f (t ) is the desplacement function of a particle that moves along a straight line, then f ' (t ) is, the rate of change of the displacement s with respect to the time t. In other words, f ' (t ) is the velocity, of the particle. The speed of the particle is the absolute value of the velocity, that is, | f ' (t )|., The rate of change of velocity with respect to time is valled the acceleration of the particle denoted, by a (t ). Thus the acceleration function is the derivative of the velocity function and is therefore the, second derivative of the position function s = f (t )., dy d 2s, =, i.e. a (t ) = v' (t ) = s'' (t )., Thus, a =, dt dt 2, Let us consider the third derivative of the position function s = f (t ) of an object that moves along a, straight line. s''' (t ) = v'' (t ) = a' (t ) is derivative of the acceleration function and is called the Jerk ( j )., d a d 3s, Thus, j =, =, . Hence the jerk j is the rate of change of acceleration. It is aptly named because, dt dt 3, a jerk means a sudden change in acceleration, which causes an abrupt movement in a vehicle., SOLVED EXAMPLES, Ex. 1 : A car is moving in such a way that the, distance it covers, is given by the equation, s = 4t2 + 3t where s is in meters and t is in, , Ex. 2 : The displacement of a particle at time t, is given by s = 2t3 − 5t2 + 4t − 3. Find the, time when the acceleration is 14 ft/ sec2, the, velocity and the displacement at that time., Solution : Displacement of a particle is given by, s = 2t3 − 5t2 + 4t − 3, . . . (I), Differentiate w. r. t. t., ds d, Velocity, v =, =, (2t3 − 5t2 + 4t − 3), dt dt, ∴ v = 6t2 − 10t + 4, . . . (II), dv, d, Acceleration, a =, =, (6t2 − 10t + 4), dt, dt, ∴ a = 12t − 10, . . . (III), 2, Given : Acceleration = 14 ft/ sec ., , seconds. What would be the velocity and the, acceleration of the car at time t = 20 second ?, Solution : Let v be the velocity and a be the, acceleration of the car., Distance traveled by the car is given by, s = 4t2 + 3t, Differentiate w. r. t. t., ∴ Velocity of the car is given by, ds d, v=, =, (4t2 + 3t ) = 8t + 3, . . . (I), dt dt, and Acceleration of the car is given by, d dv, d, a=, =, (8t + 3 ) = 8 . . . (II), dt dt, dt, Put t = 20 in (I),, ∴ Velocity of the car, vt = 20 = 8(20) + 3 = 163 m/sec., Put t = 20 in (II),, ∴ Acceleration of the car, at = 20 = 8 m/sec2., , ∴, , ∴, ∴, , Note : In this problem, the acceleration is, independent of time. Such a motion is said, to be uniformly accelerated motion., , 71, , 12t − 10 = 14 ⇒ 12t = 24 ⇒ t = 2, So, the particle reaches an acceleration of, 14 ft/ sec2 in 2 seconds., Velocity, when t = 2 is, vt = 2 = 6(2)2 − 10(2) + 4 = 8 ft/ sec., Displacement when t = 2 is, st = 2 = 2(2)3 − 5(2)2 + 4(2) − 3 = 1 foot., Hence the velocity is 8 ft/ sec and the, displacement is 1 foot after 2 seconds.
Page 82 :
EXERCISE 2.1, (1) Find the equations of tangents and normals, to the curve at the point on it., , (9) The surface area of a spherical balloon is, increasing at the rate of 2 cm2/ sec. At what, rate the volume of the balloon is increasing, when radius of the balloon is 6 cm?, , (i) y = x2 + 2e x + 2 at (0, 4), (ii) x3 + y3 − 9xy = 0 at (2, 4), (iii) x2 − √ 3xy + 2y2 = 5 at (√ 3, 2), π, (iv) 2xy + π sin y = 2π at 1,, 2, π π, (v) x sin 2y = y cos 2x at ,, 4 2, , (10) If each side of an equilateral triangle, increases at the rate of √ 2 cm/ sec, find the, rate of increase of its area when its side of, length 3 cm ., (11) The volume of a sphere increase at the rate, of 20 cm3/ sec. Find the rate of change of its, surface area when its radius is 5 cm., , π, (vi) x = sin θ and y = cos 2θ at θ =, 6, 1, (vii) x = √ t , y = t −, at t = 4., √t, , (12) The edge of a cube is decreasing at the rate of, 0.6 cm/sec. Find the rate at which its volume is, decreasing when the edge of the cube is 2 cm., , (2) Find the point on the curve y = √ x − 3 where, the tangent is perpendicular to the line, 6x + 3y − 5 = 0., , (13) A man of height 2 meters walks at a uniform, speed of 6 km/hr away from a lamp post of 6, meters high. Find the rate at which the length, of the shadow is increasing., , (3) Find the points on the curve y = x3 − 2x2 − x, where the tangents are parallel to 3x − y + 1 = 0., (4) Find the equations of the tangents to the, curve x2 + y2 − 2x − 4y + 1= 0 which are, parallel to the X-axis., , (14) A man of height 1.5 meters walks toward a, lamp post of height 4.5 meters, at the rate, 3, of, meter/sec. Find the rate at which, 4, (i) his shadow is shortening. (ii) the tip of the, shadow is moving., , (5) Find the equations of the normals to the, curve 3x2 − y2 = 8, which are parallel to the, line x + 3y = 4., , (15) A ladder 10 meter long is leaning against a, vertical wall. If the bottom of the ladder is, pulled horizontally away from the wall at the, rate of 1.2 meters per second, find how fast the, top of the ladder is sliding down the wall when, the bottom is 6 meters away from the wall., , (6) If the line y = 4x − 5 touches the curve, y2 = ax3 + b at the point (2, 3) find a and b., (7) A particle moves along the curve 6y = x2 + 2., Find the points on the curve at which, y-coordinate is changing 8 times as fast as, the X-coordinate., , (16) If water is poured into an inverted hollow, cone whose semi-vertical angel is 30°, so, that its depth (measured along the axis), increases at the rate of 1 cm/ sec. Find the, rate at which the volume of water increasing, when the depth is 2 cm., , (8) A spherical soap bubble is expanding so, that its radius is increasing at the rate of, 0.02 cm/sec. At what rate is the surface, area is increasing, when its radius is 5 cm?, , 72
Page 83 :
2.2.1 Approximations , If f (x) is a differentiable function of x, then its derivative at x = a is given by, f (a + h) − f (a), , f ' (a) = hlim, →0, h, Here we use ≑ sign for approximation., For a sufficiently small h we have,, , f ' (a) ≑, , , f (a + h) − f (a), h, , i.e. h f ' (a) ≑ f (a + h) − f (a), , ∴, , f (a + h) ≑ f (a) + h f ' (a), , This is the formula to find the approximate value of the function at x = a + h, when f ' (a) exists., Let us solve some problems by using this formula., SOLVED EXAMPLES, Ex. 1 : Find the approximate value of √ 64.1., , Ex. 2 : Find the approximate value of (3.98)3., , Solution :, , Solution :, , Let f (x) = √ x, , Let f (x) = x3, , . . . (I), , , , Differentiate w. r. t. x., 1, . . . (II), f ' (x) =, 2√ x, Let a = 64, h = 0.1, For x = a = 64, from (I) we get, f (a) = f (64) = √ 64 = 8, , , , Differentiate w. r. t. x., , f ' (x) = 3x2, , . . . (II), , Let a = 4, h = − 0.02, For x = a = 4, from (I) we get, f (a) = f (4) = (4)3 = 64, , . . . (III), , . . . (III), , For x = a = 4, from (II) we get, , For x = a = 64, from (II) we get, 1, 1, f ' (a) = f ' (64) =, =, 2√ 64 16, . . . (IV), ∴ f ' (a) = 0.0625, , , . . . (I), , f ' (a) = f ' (4) = 3(4)2 = 48, , , . . . (IV), , We have, f (a + h) ≑ f (a) + h f ' (a), , f [4 + (− 0.02)] ≑ f (4) + (− 0.02)· f ' (4), , We have, f (a + h) ≑ f (a) + h f ' (a), , f (3.98) ≑ 64 + (− 0.02).(48), ..., [From (III) and (IV)], , f (64 + 0.1) ≑ f (64) + (0.1)· f ' (64), , f (3.98) ≑ 64 − 0.96, , f (64.1) ≑ 8 + (0.1)·(0.0625) . . ., , [From (III) and (IV)], , ∴ f (3.98) = (3.98)3 ≑ 63.04, , ≑ 8 + 0.00625, , ∴ f (64.1) = √ 64.1 ≑ 8.00625, , 73
Page 84 :
Ex. 4 : Find the approximate value of tan−1(0.99),, , Ex. 3 : Find the approximate value of, sin (30° 30' ). Given that 1° = 0.0175c, and cos 30° = 0.866., Solution : Let f (x) = sin x . . . (I), Differentiate w. r. t. x., f ' (x) = cos x, 1 °, Now, 30° 30' = 30° + 30' = 30° +, 2, c, π 0.1750, = +, 6, 2, π, , 30° 30' = + 0.00875, . . . (II), 6, π, Let a = , h = 0.00875, 6, π, For x = a = , from (I) we get, 6, 1, π, π, = sin, = = 0.5 . . . (III), f (a) = f, 2, 6, 6, π, For x = a = , from (II) we get, 6, π, π, f ' (a) = f ', = cos, = 0.866 . . . (IV), 6, 6, We have, f (a + h) ≑ f (a) + h f ' (a), f, , Given that π ≑ 3.1416., Solution : Let f (x) = tan−1 x . . . (I), Differentiate w. r. t. x., 1, f ' (x) =, , . . . (II), 1 + x2, Let a = 1, h = −0.01, For x = a = 1, from (I) we get, π, . . . (III), f (a) = f (1) = tan−1 (1) =, 4, For x = a = 1, from (II) we get, 1, = 0.5, . . . (IV), f ' (a) = f ' (1) =, 1 + 12, We have, f (a + h) ≑ f (a) + h f ' (a), , f [(1) + (−0.01)] ≑ f (1) + (−0.01)· f ' (1), π, f (0.99) ≑ − (0.01)·(0.5) . . . [From, 4, (III) and (IV)], π, ≑ − 0.005, 4, 3.1416, − 0.005, ≑, 4, ≑ 0.7854 − 0.005 = 0.7804, , π, π, π, + 0.00875c ≑ f, + (0.00875)· f ', 6, 6, 6, , ∴ f (0.99) = tan−1 (0.99) ≑ 0.7804, , f (30° 30' ) ≑ 0.5 + (0.00875)·(0.866) ..., . . . [From (III) and (IV)], ≑ 0.5 + 0.075775, , ∴ f (30° 30' ) = sin (30° 30' ) ≑ 0.575775, , Ex. 5 : Find the approximate value of e1.005. Given that e = 2.7183., Solution : Let f (x) = e x, Differentiate w. r. t. x., f ' (x) = e x, Let a = 1, h = 0.005, For x = a = 1, from (I) we get, , . . . (I), , , , . . . (II), , f (1 + 0.005) ≑ f (1) + (0.005)· f ' (1), , f (a) = f (1) = e1 = 2.7183, , . . . (III), , f (1.005) ≑ 2.7183 + (0.005) (2.7183) ..., . . . [From (III) and (IV)], f (1.005) ≑ 2.7183 + 0.0135915, ≑ 2.7318915, , For x = a = 1, from (II) we get, f ' (a) = f ' (1) = e1 = 2.7183, , We have, f (a + h) ≑ f (a) + h f ' (a), , f (1.005) = e1.005 ≑ 2.73189, , . . . (IV), , 74
Page 85 :
Ex. 7 : Find the approximate value of, f (x) = x3 + 5x2 − 2x + 3 at x = 1.98., , Ex. 6 : Find the approximate value of, log10 (998). Given that log10 e = 0.4343., log x, Solution : Let f (x) = log10 x =, log 10, f (x) = (log10 e)·log x , ∴ , . . . (I), Differentiate w. r. t. x., log10 e 0.4343, f ' (x) = x =, . . . (II), x, Let a = 1000, h = −2, For x = a = 1000, from (I) we get, f (a) = f (1000) = log10 1000, ∴ f (a) = 3log1010 = 3, , Solution : Let f (x) = x3 + 5x2 − 2x + 3 , . . . (I), Differentiate w. r. t. x., f ' (x) = 3x2 + 10x − 2, . . . (II), Let a = 2, h = −0.02, For x = a = 2, from (I) we get, f (a) = f (2) = (2)3 + 5(2)2 − 2(2) + 3, ∴ f (a) = 27 , For x = a = 2, from (II) we get, , . . . (III), , f ' (a) = f ' (2) = 3(2)2 + 10(2) − 2, , For x = a = 1000, from (II) we get, 0.4343, f ' (a) = f ' (1000) =, 1000, ∴ f ' (a) = 0.0004343, . . . (IV), , , ∴ f ' (a) = 30 , , , f (998) ≑ 3 − (2) (0.0004343) . . ., [From (III) and (IV)], , f (1.98) ≑ 26.4, , ≑ 3 − 0.0008686, , EXERCISE 2.2, , (1) Find the approximate value of given, functions, at required points., , √ 8.95, , (iv) (3.97)4, , 3, , (ii) √ 28 , , We have, f (a + h) ≑ f (a) + h f ' (a), , f (1.98) ≑ 27 − (0.02)·(30) . . . [From, (III) and (IV)], ≑ 27 − 0.6, , f [1000 + (−2)] ≑ f (1000) + (−2) f ' (1000), , (i), , . . . (IV), , f [(2) + (−0.02)] ≑ f (2) + (−0.02)· f ' (2), , We have, f (a + h) ≑ f (a) + h f ' (a), , f (998) = log (998 ) ≑ 2.9991314, , . . . (III), , (3) Find the approximate value of, (ii) cot−1 (0.999), (i) tan−1 (0.999), (iii) tan−1 (1.001), (4) Find the approximate value of, (i) e 0.995, (ii) e 2.1 given that e2 = 7.389, (iii) 3 2.01 given that log 3 = 1.0986, (5) Find the approximate value of, (i) loge (101) given that loge 10 = 2.3026, (ii) loge (9.01) given that log 3 = 1.0986, (iii) log10 (1016) given that log10 e = 0.4343, (6) Find the approximate value of, (i) f (x) = x3 − 3x + 5 at x = 1.99, (ii) f (x) = x3 + 5x2 − 7x + 10 at x = 1.12, , 5, , (iii) √ 31.98, , (v) (4.01)3, , (2) Find the approximate value of, (i) sin (61°) given that 1° = 0.0174c,, √ 3 = 1.732, (ii) sin (29° 30' ) given that 1° = 0.0175c,, √ 3 = 1.732, (iii) cos (60° 30' ) given that 1° = 0.0175c,, √ 3 = 1.732, (iv) tan (45° 40' ) given that 1° = 0.0175c., , 75
Page 86 :
2.3.1 Rolle's Theorem or Rolle's Lemma : , If a real-valued function f is continous on [a, b], differentiable on the open interval (a, b) and f (a), = f (b), then there exists at least one c in the open interval (a, b) such that f ' (c) = 0., Rolle's Theorem essentially states that any real-valued differentiable function that attains equal, values at two distinct points on it, must have at least one stationary point somewhere in between them,, that is, a point where the first derivative (the slope of the tangent line to the graph of the function) is zero., Geometrical Significance :, Let f (x) be a real valued, function defined on [a, b], and it is continuous on [a, b]., This means that we can, draw the graph f (x) between, the values x = a and x = b., Also f (x) is differentiable, on (a, b) which means the, Fig. 2.3.1, graph of f (x) has a tangent, at each point of (a, b). Now the existence of real number c ∈ (a, b) such that f ' (c) = 0 shows that, the tangent to the curve at x = c has slope zero, that is, tangent is parallel to X-axis since f (a) = f (b)., SOLVED EXAMPLES, Ex. 1 : Check whether conditions of Rolle's theorem are satisfied by the following functions., 3, (ii) f (x) = x2 − 2x + 3, x ∈ [1, 4], (i) f (x) = 2x3 − 5x2 + 3x + 2, x ∈ 0,, 2, Solution :, (i) Given that , , f (x) = 2x3 − 5x2 + 3x + 2 . . . (I), 3, 3, f (x) is a polynomial which is continuous on 0, and it is differentiable on 0, ., 2, 2, 3, , Let a = 0, and b = ,, 2, , For x = a = 0 from (I) we get,, , , , , , , , f (a) = f (0) = 2 (0)3 − 5 (0)2 + 3 (0) + 2 = 2, 3, from (I) we get,, For x = b =, 2, 54 45 9, 3, 3 3, 3 2, 3, f (b) = f, =2, −5, +3, +2 =, −, + +2, 8, 4, 2, 2, 2, 2, 2, 54 − 90 + 36, 3, f (b) = f, =, +2=2, 8, 2, 3, =2, So, here f (a) = f (b) i.e. f (0) = f, 2, Hence conditions of Rolle's Theorem are satified., , 76
Page 87 :
(ii) Given that , f (x) = x2 − 2x + 3 , . . . (I), f (x) is a polynomial which is continuous on [1, 4] and it is differentiable on (1, 4)., , , Let a = 1, and b = 4, , , , For x = a = 1 from (I) we get,, , , , f (a) = f (1) = (1)2 − 2(1) + 3 = 2, , , , For x = b = 4 from (I) we get,, , , , f (b) = f (4) = (4)2 − 2(4) + 3 = 11, , , , So, here f (a) ≠ f (b) i.e. f (1) ≠ f (4), , , , Hence conditions of Rolle's theorem are not satisfied., , Ex. 2 : Verify Rolle's theorem for the function, , Ex. 3 : Given an interval [a, b] that satisfies, hypothesis of Rolle's theorem for the, function f (x) = x3 − 2x2 + 3. It is known, , f (x) = x2 − 4x + 10 on [0, 4]., Solution :, Given that, , f (x) = x2 − 4x + 10, , that a = 0. Find the value of b., , . . . (I), , Solution :, , f (x) is a polynomial which is continuous on, [0, 4] and it is differentiable on (0, 4)., , Given that, , . . . (I), , Let g (x) = x3 − 2x2 = x2 (x − 2), , Let a = 0, and b = 4, , From (I),, , For x = a = 0 from (I) we get,, , f (x) = g (x) + 3, , We see that g (x) becomes zero for x = 0 and, x = 2., , f (a) = f (0) = (0)2 − 4(0) + 10 = 10, For x = b = 4 from (I) we get,, , We observe that for x = 0,, , f (b) = f (4) = (4)2 − 4(4) + 10 = 10, So, here f (a) = f (b), , f (x) = x3 − 2x2 + 3, , , , i.e. f (0) = f (4) = 10, , f (0) = g (0) + 3 = 3, , and for x = 2,, , All the conditions of Rolle's theorem are, satisfied., , , ∴, , To get the value of c, we should have, , f (2) = g (2) + 3 = 3, , We can write that f (0) = f (2) = 3, , Now, for x = c,, , It is obvious that the function f (x) is, everywhere continuous and differentiable as, a cubic polynomial. Consequently, it satisfies, all the conditions of Rolle's theorem on the, interval [0, 2]., , f ' (c) = 0 ⇒ 2 (c − 2) = 0 ⇒ c = 2, , So , , f ' (c) = 0 for some c ∈ (0, 4), Differentiate (I) w. r. t. x., f ' (x) = 2x − 4 = 2 (x − 4), , Also c = 2 ∈ (0, 4), Thus Rolle's theorem is verified., , 77, , b = 2.
Page 88 :
Ex. 4 : Verify Rolle's theorem for the function f (x) = ex (sin x − cos x) on, , π 5π, ,, 4 4, , ., , Solution : Given that, f (x) = ex (sin x − cos x) , , . . . (I), , , , We know that ex, sin x and cos x are continuous and differentiable on their domains. Therefore, π 5π, π 5π, f (x) is continuous and differentiable on ,, and ,, respectively. , 4 4, 4 4, π, 5π, , Let a = , and b =, 4, 4, π, , For x = a = from (I) we get,, 4, π, π, 1, 1, π, π, π, = e 4 sin, − cos, = e4, −, =0, , f (a) = f, 4, 4, 4, √2 √2, 5π, , For x = b =, from (I) we get,, 4, 5π, 5π, 1, 1, 5π, 5π, 5π, 4, , f (a) = f, =e, sin, − cos, =e4 −, +, =0, 4, 4, 4, √2 √2, 5π, ., 4, , f (a) = f (b), , , , All the conditions of Rolle's theorem are satisfied., , , , To get the value of c, we should have f ' (c) = 0 for some c ∈, , , , Differentiate (I) w. r. t. x., , , , f ' (x) = e x (cos x + sin x) + (sin x − cos x) e x = 2e x sin x, , , , Now, for x = c, f ' (c) = 0 ⇒ 2e c sin c = 0. As e c ≠ 0 for any c ∈ R, , , , sin c = 0 ⇒ c = 0, ± π, ± 2π, ± 3π, . . ., , , , It is clearly seen that, , , , i.e. f, , π, =f, 4, , , ∴, , π 5π, ,, 4 4, , ., , π 5π, ,, ∴c=π, 4 4, Thus Rolle's theorem is verified., π ∈, , 2.3.2 Lagrange's Mean Value Theorem (LMVT) : , If a real-valued function f is continous on a closed [a, b] and differentiable on the open interval, (a, b) then there exists at least one c in the open interval (a, b) such that, f (b) − f (a), b−a, Lagrange's mean value theorem states, that for any real-valued diffenentiable function which is, continuous at the two end points, there is at least one point at which the tangent is parallel to the the, secant through its end points., f ' (c) =, , 78
Page 89 :
Geometrical Significance :, Draw the curve y = f (x) (see Figure 2.3.2) and take the end, points A (a, f (a)) and B (b, f (b)) on the curve, then, f (b) − f (a), Slope of the chord AB =, b−a, Since by statement of Lagrange's Mean Value., f (b) − f (a), b−a, f ' (c) = Slope of the chord AB., Theorem , , f ' (c) =, , Fig. 2.3.2, , This shows that the tangent to the curve y = f (x) at the point x = c, is parallel to the chord AB., SOLVED EXAMPLES, Ex. 2 : Verify Lagrange's mean value theorem, 1, for the function f (x) = x +, on the, x, interval [1, 3]., 1, Solution : Given that f (x) = x +, . . . (I), x, The function f (x) is continuous on the, closed interval [1, 3] and differentiable, on the open interval (1, 3), so the LMVT, is applicable to the function., Differentiate (I) w. r. t. x., 1, f ' (x) = 1 − 2, . . . (II), x, Let a = 1 and b = 3, 1, From (I), f (a) = f (1) = 1 + = 2, 1, 1 10, f (b) = f (3) = 3 + =, 3, 3, Let c ∈ (1, 3) such that, f (b) − f (a), f ' (c), =, b−a, 10, 1, 3 −2, 1 − 2 =, c, 3−1, , Ex. 1 : Verify Lagrange's mean value theorem, for the function f (x) = √ x + 4 on the, interval [0, 5]., Solution : Given that f (x) = √ x + 4, , . . . (I), , The function f (x) is continuous on the, closed interval [0, 5] and differentiable, on the open interval (0, 5), so the LMVT, is applicable to the function., , , Differentiate (I) w. r. t. x., 1, f ' (x) =, 2√ x + 4, , . . . (II), , Let a = 0 and b = 5, , , From (I),, , f (a) = f (0) = √ 0 + 4 = 2, , f (b) = f (5) = √ 5 + 4 = 3, Let c ∈ (0, 5) such that, , f (b) − f (a), b−a, 1, 3−2 1, , =, =, 2√ c + 4, 5−0 5, 5, 25, 9, ∴ √ c + 4 = ⇒ c + 4 = ∴ c = ∈ (0, 5), 2, 4, 4, Thu s Lagrange's Mean Value Theorem, is verified., , f ' (c), , =, , , , 1, 1− 2, c, , =, , 4, 3, , 2, , =, , 2, 3, , ∴ c2 = 3 ⇒ c = ± √3, ∴ c = √ 3 ∈ (1, 3) and c = − √ 3 ∉ (1, 3), , 79
Page 90 :
EXERCISE 2.3, (1) Check the validity of the Rolle's theorem for, the following functions., (i) f (x) = x2 − 4x + 3, x ∈ [1, 3], (ii) f (x) = e −x sin x, x ∈ [0, π], (iii) f (x) = 2x2 − 5x + 3, x ∈ [1, 3], (iv) f (x) = sin x − cos x + 3, x ∈ [0, 2π], (v) f (x) = x2 if 0 ≤ x ≤ 2, = 6 − x if 2 ≤ x ≤ 6, , (4) If Rolle's theorem holds for the function, f (x) = x3 + px2 + qx + 5, x ∈ [1, 3] with, 1, c=2+, , find the values of p and q., √3, (5) Rolle's theorem holds for the function, f (x) = (x − 2) log x, x ∈ [1, 2], show that the, equation x log x = 2 − x is satisfied by at least, one value of x in (1, 2)., x, (6) The function f (x) = x (x + 3) e− 2 satisfies all, the conditions of Rolle's theorem on [−3, 0]., Find the value of c such that f ' (c) = 0., (7) Verify Lagrange's mean value theorem for, the following functions., (i) f (x) = log x, on [1, e], (ii) f (x) = (x − 1) (x − 2) (x − 3) on [0, 4], 11 13, (iii) f (x) = x2 − 3x − 1, x ∈ − ,, 7 7, , 2, , (vi) f (x) = x 3 , x ∈ [−1, 1], (2) Given an interval [a, b] that satisfies, hypothesis of Rolle's thorem for the function, f (x) = x4 + x2 − 2. It is known that a = − 1., Find the value of b., (3) Verify Rolle's theorem for the following, functions., (i) f (x) = sin x + cos x + 7, x ∈ [0, 2π], x, , x ∈ [0, 2π], (ii) f (x) = sin, 2, (iii) f (x) = x2 − 5x + 9, x ∈ [1, 4], , (iv) f (x) = 2x − x2, x ∈ [0, 1], x−1, (v) f (x) =, on [4, 5], x−3, , 2.4.1 Increasing and decreasing functions :, Increasing functions :, Definition : A function f is said to be a monotonically (or strictly) increasing function on an interval, (a, b) if for any x1, x2 ∈ (a, b) with if x1 < x2 , we have f (x1) < (x2)., Consider an increasing function y = f (x) in (a, b). Let h > 0 be a small increment in x then,, , x < x + h [ x = x1 , x + h = x2 ], , , f (x) < f (x + h), , ∴ , , f (x + h) > f (x) , , [ f (x1) < f (x2)], , ∴ f (x + h) − f (x) > 0, f (x + h) − f (x), > 0 , h, f (x + h) − f (x), ∴ lim, ≥ 0, h→0, h, ∴ , f ' (x) ≥ 0, ∴ , , 80, , Fig. 2.4.1
Page 91 :
If f ' (a) > 0, then in a small δ-neighborhood of a i.e. (a − δ, a + δ), we have f strictly increasing if, f (a + h) − f (a), >0, for |h| < δ, h, Hence if 0 < h < δ, f (a + h) − f (a) > 0 and f (a − h) − f (a) < 0, Thus for 0 < h < δ, f (a − h) < f (a) < f (a + h), Decreasing functions :, , , Definition : A function f is said to be a monotonically (strictly) decreasing function on an interval (a, b), if for any x1, x2 ∈ (a, b) with x1 < x2 , we have f (x1) > (x2)., Consider a decreasing function y = f (x) in (a, b). Let h > 0 be a small increment in x then,, , x + h > x [ x = x1 , x + h = x2 ], , f (x) > f (x + h) [ f (x1) < f (x2)], ∴ , f (x + h) < f (x) , ∴ f (x + h) − f (x) < 0, f (x + h) − f (x), ∴ , < 0 , h, f (x + h) − f (x), ∴ lim, ≤ 0, h→0, h, Fig. 2.4.2, ∴ , f ' (x) ≤ 0, If f ' (a) < 0, then in a small δ-neighborhood of a i.e. (a − δ, a + δ), we have f strictly decreasing, f (a + h) − f (a), <0, for |h| < δ, h, Hence for 0 < h < δ, f (a − h) > f (a) > f (a + h), , because , , , Note : Whenever f ' (x) = 0, at that point the tangent is parallel to X-axis, we cannot deduce that, whether f (x) is increasing or decreasing at that point., SOLVED EXAMPLES, Ex. 2 : Test whether the function, , Ex. 1 : Show that the function f (x) = x3 + 10x + 7, , , f (x) = x3 + 6x2 + 12x − 5 is increasing or, , for x ∈ R is strictly increasing., , decreasing for all x ∈ R., , Solution : Given that f (x) = x3 + 10x + 7, , , Solution : Given that f (x) = x3 + 6x2 + 12x − 5, , Differentiate w. r. t. x., , f ' (x) = 3x2 + 10, , , , Differentiate w. r. t. x., , Here, 3x2 ≥ 0 for all x ∈ R and 10 > 0., , f ' (x) = 3x2 + 12x + 12 = 3(x2 + 4x + 4), , , ∴ 3x2 + 10 > 0 ⇒ f ' (x) > 0, , f ' (x) = 3(x + 2)2, , Thus f (x) is a strictly increasing function., , 3(x + 2)2 is always positive for x ≠ −2, , ∴ f ' (x) ≥ 0 for all x ∈ R, Hence f (x) is an increasing function for all x ∈ R., , 81
Page 92 :
Ex. 3 : Find the values of x, for which the funciton f (x) = x3 + 12x2 + 36x + 6 is (i) monotonically, increasing. (ii) monotonically decreasing., Solution : Given that f (x) = x3 + 12x2 + 36x + 6, , , Differentiate w. r. t. x., , f ' (x) = 3x2 + 24x + 36, , , = 3(x2 + 8x + 12), , f ' (x) = 3(x + 2) (x + 6), (i), , f (x) is monotonically increasing if f ' (x) > 0, i.e. 3(x + 2) (x + 6) > 0, (x + 2) (x + 6) > 0, then either (x + 2) < 0 and (x + 6) < 0 or (x + 2) > 0 and (x + 6) > 0, , Case (I) : x + 2 < 0 and x + 6 < 0, x < − 2 and x < − 6, , , Thus for every x < − 6, (x + 2) (x + 6) > 0, hence f is monotonically increasing., , Case (II) : x + 2 > 0 and x + 6 > 0, x > − 2 and x > − 6, , ∴, , Thus for every x > − 2, (x + 2) (x + 6) > 0 and f is monotonically increasing., From Case (I) and Case (II), f (x) is monotonically increasing if and only if x < − 6 or x > − 2., , Hence, x ∈ (∞,− 6) or x ∈ (− 2, ∞) ⇒ f is monotonically increasing., (ii), , f (x) is said to be monotonically decreasing if f ' (x) = 0, i.e. 3(x + 2) (x + 6) < 0, (x + 2) (x + 6) < 0, then either (x + 2) < 0 and (x + 6) > 0 or (x + 2) > 0 and (x + 6) < 0, , Case (I) : x + 2 < 0 and x + 6 > 0, x < − 2 and x > − 6, , , Thus for x ∈ (− 6, − 2), f is monotonically decreasing., , Case (II) : x + 2 > 0 and x + 6 < 0, x > − 2 and x < − 6, ∴, , This case does not arise. . . . [check. why ?], , 82
Page 93 :
2.4.2 Maxima and Minima :, Maxima of a function f (x) : A function f (x) is said to have a maxima at x = c if the value of the function, at x = c is greater than any other value of f (x) in a δ-neighborhood of c. That is for a small δ > 0 and for, x ∈ (c − δ, c + δ) we have f (c) > f (x). The value f (c) is called a Maxima of f (x). Thus the function f (x), will have maxima at x = c if f (x) is increasing in c − δ < x < c and decreasing in c < x < c + δ., Minima of a function f (x) : A function f (x) is said to have a minima at x = c if the value of the function, at x = c is less than any other value of f (x) in a δ-neighborhood of c. That is for a small δ > 0 and for x, ∈ (c − δ, c + δ) we have f (c) < f (x). The value f (c) is called a Minima of f (x). Thus the function f (x), will have minima at x = c if f (x) is decreasing in c − δ < x < c and increasing in c < x < c + δ., If f ' (c) = 0 then at x = c the function is neither increasing nor decrasing, such a point on the curve, is called turning point or stationary point of the function. Any point at which the tangent to the graph, dy, = 0., is horizontal is a turning point. We can locate the turn points by looking for points at which, dx, At these points if the function has Maxima or Minima then these are called extreme values of the, function., Note : The maxima and the minima of a function are not necessarily the greatest and the least values, of the function in the whole domain. Actually these are the greatest and the least values of the, function in a small interval. Hence the maxima or the minima defined above are known as local, (or relative) maximum and the local (or relative) minimum of the function f (x)., , , To find the extreme values of the function let us use following tests., , 2.4.3 First derivative test :, A function f (x) has a maxima at x = c if, (i), , f ' (c) = 0, , (ii) f ' (c − h) > 0 , , [ f (x) is increasing for values of x < c ], , (iii) f ' (c + h) < 0, , [ f (x) is decreasing for values of x > c ], , where h is a small positive number., A function f (x) has a minima at x = c if, (i), , f ' (c) = 0, , (ii) f ' (c − h) < 0 , , [ f (x) is decreasing for values of x < c ], , (iii) f ' (c + h) > 0 , , [ f (x) is increasing for values of x > c ], , where h is a small positive number., Note : If f ' (c) = 0 and f ' (c − h) > 0, f ' (c + h) > 0 or f ' (c − h) <0, f ' (c + h) < 0 then f (c) in neither, maxima nor minima. In such a case x = c is called a point of inflexion. e.g. f (x) = x3 , f (x) = x5, in [−2, 2]., , 83
Page 94 :
SOLVED EXAMPLES, Ex. 1 : Find the local maxima or local minima of f (x) = x3 − 3x., Solution : Given that f (x) = x3 − 3x . . . (I), Differentiate (I) w. r. t. x., f ' (x) = 3x2 − 3 = 3 (x2 − 1) . . . (II), For extreme values, f ' (x) = 0, 3x2 − 3 = 0, i.e. 3 (x2 − 1) = 0, i.e. x2 − 1 = 0 ⇒ 0 ⇒ x2 = 1 ⇒ x = ± 1, The turning points are x = 1 and x = −1, Let's consider the turning point, x = 1, Let x = 1 − h for a small, h > 0, from (II) we get,, f ' (1 − h) = 3 [(1 − h)2 − 1] = 3 (1 − 2h + h2 − 1) = 3h (h − 2), ∴ f ' (1 − h) < 0 . . . [ since, h > 0, h − 2 < 0 ], ∴, , , ∴, , f ' (x) for x = 1 − h ⇒ f (x) is decreasing for, x > 1., Now for x = 1 + h for a small, h > 0, from (II) we get,, f ' (1 + h) = 3 [(1 + h)2 − 1] = 3 (1 + 2h + h2 − 1) = 3 (h2 + 2h), f ' (1 + h) > 0 . . . [ since, h > 0, h2 + 2h > 0 ], , ∴, ∴, ∴, ∴, , , , ∴, ∴, , f ' (x) < 0 for x = 1 + h ⇒ f (x) is increasing for, x < 1., f ' (x) < 0 for 1 − h < x < 1, f ' (x) > 0 for 1 < x < 1 + h., x = 1 is the point of local minima., Minima of f (x), is f (1) = 13 − 3 (1) = −2, Now, let's consider the turning point, x = −1, Let x = −1 − h for a small, h > 0, from (II) we get,, f ' (−1 − h) = 3 [(−1 − h)2 − 1] = 3 (1 + 2h + h2 − 1) = 3 (h2 + 2h), f ' (−1 − h) > 0 . . . [ since, h > 0, h2 + 2h > 0 ], , ∴, , ∴, ∴, , f ' (x) > 0 for x = −1 − h ⇒ f (x) is increasing for, x < −1., Now for x = −1 + h for a small, h > 0, from (II) we get,, f ' (−1 + h) = 3 [(− 1 + h)2 − 1] = 3 (1 − 2h + h2 − 1) = − 3h (2 − h), f ' (−1 + h) < 0 . . . [ since, h > 0, 2 − h > 0 ], , ∴, ∴, ∴, ∴, , , f ' (x) < 0 for x = − 1 + h ⇒ f (x) is decreasing for, x > −1., f ' (x) > 0 for −1 − h < x < −1, f ' (x) > 0 for −1 < x < −1 + h., x = − 1 is the point of local maxima., Maxima of f (x), is f (−1) = (−1)3 − 3(−1) = −1 + 3 = 2, , , , Hence, Maxima of f (x) = 2 and Minima of f (x) = −2, , 84
Page 95 :
2.4.4 Second derivative test :, A function f (x) has a maxima at x = c if f ' (c) = 0 and f '' (c) < 0, A function f (x) has a minima at x = c if f ' (c) = 0 and f '' (c) < 0, Note : If f '' (c) = 0 then second derivative test fails so, you may try using first derivative test., L2, L1, , L3, , L1, L3, , L2, , Fig. 2.4.4 (a), , Fig. 2.4.4 (b), , Maxima at A : Consider the slopes of the tangents (See Fig 2.4.4a) Slope of L1 is +ve, slope of L2 = 0, and slope of L3 is −ve. Thus the slope is seen to be decreasing if there is a maximum at A., , Minima at A : Consider the slopes of the tangents (See Fig 2.4.4b) slope of L1 is −ve, slope of L2 = 0, and slope of L3 is +ve. Thus the slope is seen to be increasing if there is a minima at A., SOLVED EXAMPLES, Ex. 1 : Find the local maximum and local minimum value of f (x) = x3 − 3x2 − 24x + 5., Solution : Given that f (x) = x3 − 3x2 − 24x + 5 . . . (I), Differentiate (I) w. r. t. x., , f ' (x) = 3x2 − 6x − 24 , , For maximum of f (x), put x = −2 in (I), . . . (II), , , f (−2) = (−2)3 − 3(−2)2 − 24 (−2) + 5 = 33., , For extreme values, f ' (x) = 0, , For x = 4, from (III) we get, , 3x2 − 6x − 24 i.e. 3 (x2 − 2x − 8) = 0, , f '' (4) = 6(4) − 6 = 18 > 0, , i.e. x2 − 2x − 8 = 0 i.e. (x + 2) (x − 4) = 0, , ∴, , At x = 4, f (x) has a minimum value., , , ⇒ x + 2 = 0 or x − 4 = 0 ⇒ x = −2 or x = 4, , For minima of f (x), put x = 4 in (I), , The stationary points are x = −2 and x = 4., , f (4) = (4)3 − 3 (4)2 − 24 (4) + 5 = −75, , Differentiate (II) w. r. t. x., , f '' (x) = 6x − 6 , , ∴, . . . (III), , Local maximum of f (x) is 33 when x = −2, and, Local minimum of f (x) is −75 when x = 4., , For x = −2, from (III) we get,, , f '' (−2) = 6 (−2) − 6 = −18 < 0, ∴ At x = −2, f (x) has a maximum value., , 85
Page 96 :
Ex. 2 : A wire of length 120 cm is bent in the form, of a rectangle. Find its dimensions if the, area of the rectangle is maximum., Solution : Let x cm and y cm be the length and, the breadth of the rectangle. Perimeter of, rectangle = 120 cm., ∴ 2 (x + y) = 120 so, x + y = 60, ∴ y = 60 − x , . . . (I), Let A be the area of the rectangle, ∴ A = xy = x (60 − x) = 60x − x2. . . [From (I)], Differentiate w. r. t. x., dA, = 60 − 2x, . . . (II), dx, dA, =0, For maximum area, dx, i.e. 60 − 2x = 0 ⇒ x = 30, Differentiate (II) w. r. t. x., , Fig. 2.4.5, After leaving the margins, length of the, printing space is (x − 1) m and breadth of, the printing space is ( y − 1.5) m., Let A be the area of the printing space, 24, − 1.5, , A = (x − 1) ( y − 1.5) = (x − 1), x, 24, = 24 − 1.5x −, + 1.5 . . . [ From (I)], x, 24, , A = 25.5 − 1.5x −, . . . (II), x, Differentiate w. r. t. x., 24, dA, = − 1.5 + 2, . . . (III), x, dx, dA, =0, For maximum printing space, dx, 24, i.e. − 1.5x + 2 = 0 ⇒ 1.5x2 = 24 ⇒ x = ± 4, x ≠ −4, x, ∴ x = 4, Differentiate (III) w. r. t. x., 48, d 2A, , = − 3 . . . (IV), 2, x, dx, For, x = 4, from (IV) we get,, 48, d2A, =− 3<0, 2, (4), dx x = 4, When, x = 4 Area of the rectangular, printing space is maximum., 24, =6, Put x = 4 in (I) we get y =, 4, ∴ Area of the printing space is maximum, when width printing space = 4 m. and, length of the printing space = 6 m., , d2A, = − 2 , . . . (III), , dx2, For, x = 30 from (III) we get,, d2A, 2, dx, , x = 30, , =−2<0, , When, x = 30, Area of the rectangle is, maximum., Put x = 30 in (I) we get y = 60 − 30 = 30, ∴ Area of the rectangle is maximum if length, = breadth = 30 cm., Ex. 3 : A Rectangular sheet of paper has it area 24, sq. meters. The margin at the top and the, bottom are 75 cm each and at the sides 50 cm, each. What are the dimensions of the paper,, if the area of the printed space is maximum ?, Solution : Let x m and y m be the width and the, length of the rectangular sheet of paper, respectively. Area of the paper = 24 sq. m., 24, ∴ , xy = 24 ⇒ y =, . . . (I), x, , 86
Page 97 :
Ex. 4 : An open box is to be cut out of piece of, square card coard of side 18 cm by cutting, of equal squares from the corners and, turning up the sides. Find the maximum, volume of the box., Solution : Let the side of each of the small squares, cut be x cm, so that each side of the box to, be made is (18 − 2x) cm. and height x cm., , Ex. 5 : Two sides of a triangle are given, find the, angle between them such that the area of, the triangle is maximum., Solution : Let ABC be a triangle. Let the given, sides be AB = c and AC = b., , Fig. 2.4.7, Let ∆ be the area of the triangle., 1, , ∆ = bc sin A, . . . (I), 2, Differentiate w. r. t. A., d∆ bc, =, cos A, . . . (II), dA 2, d∆, =0, For maximum area, dA, π, bc, i.e. cos A = 0 ⇒ cos A = 0 ⇒ A =, 2, 2, Differentiate (II) w. r. t. A., bc, d2∆, sin A, . . . (III), 2 = −, 2, dA, π, For, A = from (III) we get,, 2, π, bc, bc, d2∆, 2, sin, =, <0, π =−, 2, 2, a, dA A =, , Fig. 2.4.6, Let V be the volume of the box., V = Area of the base × Height, = (18 − 2x)2 x = (324 − 72x + 4x2) x, , V = 4x3 − 72x2 + 324x, . . . (I), Differentiate w. r. t. x, dV, = 12x2 − 144x + 324 . . . (II), dx, dV, =0, , For maximum volume, dx, i.e. 12x2 − 144x + 324 = 0 ⇒ x2 − 12x + 27 = 0, (x − 3) (x − 9) = 0 ⇒ x − 3 = 0 or x − 9 = 0, ∴, x = 3 or x = 9, but x ≠ 9 ∴ x = 3, Differentiate (II) w. r. t. x, d2V, , = 24x − 144, . . . (III), dx2, For, x = 3 from (III) we get,, , 2, , , When, A =, maximum., , d2V, = 24 (3) − 144 = − 72 < 0, 2, dx x = 3, Volume of the box is maximum when x = 3., Maximum volume of the box, = (18 − 6)2 (3) = 432 c.c., , π, Area of the triangle is, 2, , Hence, the area of the triangle is maximum, π, when the angle between the given sides ., 2, π, Note : sin A is maximum (=1), when A =, 2, , 87
Page 98 :
Ex. 6 : The slant side of a right circular cone is l. Show that the semi-vertical angle of the cone of, maximum volume is tan−1 (√ 2 )., Solution : Let x be the height of the cone and r be the radius of the base., So, r2 = l2 − x2, , . . . (I), , Let V be the volume of the cone., π, 1, , V = πr2x = (l2 − x2) x , 3, 3, π, ∴ V = (l2 x − x3), 3, Differentiate w. r. t. x, dV π, = (l2 − 3x2), . . . (II), dx 3, dV, =0, , For maximum volume, dx, π, l2, i.e. (l2 − 3x2) = 0 ⇒ x2 =, 3, 3, l, l, l, l, l, , x=±, ⇒x=, or x = −, is the stataionary point but, x ≠ −, ∴ x=, √3, √3, √3, √3, √3, Differentiate (II) w. r. t. x, d2V, 2 = − 2πx, . . . (III), dx, l, from (III) we get,, For, x =, √3, d2V, 2πl, 2, <0, l =−, dx x = √ 3, √3, Volume of the cone is maximum when height of the cone is x =, Put x =, , l, in (I) we get, r =, √3, , l2 −, , l, ., √3, , l 2 l √2, =, √3, √3, , Let α be the semi-vertical angle., r, Then tan α = =, x, , l √2, √3, l, √3, , = √2, , ∴ α = tan−1 (√ 2 ), Ex. 7 : Find the height of a covered box of fixed volume so that the total surface area of the box is, minimum whose base is a rectangle with one side three times as long as the other., Solution : Given that, box has a rectangular base with one side three times as long as other., Let x and 3x be the sides of the rectangular base., Let h be the height of the box and V be its volume., , 88
Page 100 :
(4) Find the values of x for which the function, f (x) = x3 − 12x2 − 144x + 13, (a) Increasing, (b) Decreasing, , (14) Find the largest size of a rectangle that can be, inscribed in a semi circle of radius 1 unit, So, that two vertices lie on the diameter., , (5) Find the values of x for which, , (15) An open cylindrical tank whose base is a, circle is to be constructed of metal sheet so, as to contain a volume of πa3 cu. cm of water., Find the dimensions so that sheet required is, minimum., , f (x) = 2x3 − 15x2 − 144x − 7 is, (a), (b), , strictly increasing, strictly decreasing, , (6) Find the values of x for which f (x) =, (a), (b), , strictly increasing, strictly decreasing, , x, is, x2 + 1, , (16) The perimeter of a triangle is 10 cm. If one of, the side is 4 cm. What are the other two sides, of the triangle for its maximum area ?, , 1, increasing in, 3x, 1, 1 1, , 1 and decreasing in, ,, ., 3, 9 3, , (17) A box with a square base is to have an open, top. The surface area of the box is 192 sq.cm., What should be its dimensions in order that, the volume is largest ?, , (7) Show that f (x) = 3x +, , (8) Show that f (x) = x − cos x is increasing for, all x., , (18) The profit function P (x) of a firm, selling x, items per day is given by, , (9) Find the maximum and minimum of the, following functions (i), , y = 5x3 + 2x2 − 3x, , (ii), , f (x) = 2x3 − 21x2 + 36x − 20, , P (x) = (150 − x)x − 1625. Find the number, of items the firm should manufacture to get, maximum profit. Find the maximum profit., (19) Find two numbers whose sum is 15 and when, the square of one multiplied by the cube of, the other is maximum., , (iii) f (x) = x − 9x + 24x, 16, (iv) f (x) = x2 + 2, x, 3, , 2, , (20) Show that among rectangles of given area,, the square has the least perimeter., , log x, x, (10) Divide the number 30 in to two parts such, that their product is maximum., (v), , f (x) = x log x, , (vi) f (x) =, , (21) Show that the height of a closed right circular, cylinder of a given volume and least surface, area is equal to its diameter., , (11) Divide that number 20 in to two parts such, that sum of their squares is minimum., , (22) Find the volume of the largest cylinder that, can be inscribed in a sphere of radius 'r' cm., 2x, (23) Show that y = log (1 + x) −, , x > −1 is, 2+x, an increasing function on its domain., 4 sin θ, (24) Prove that y =, − θ is an increasing, 2 + cos θ, π, function of θ ∈ 0,, ., 2, , (12) A wire of length 36 meters is bent in the form, of a rectangle. Find its dimensions if the area, of the rectangle is maximum., (13) A ball is thrown in the air. Its height at any, time t is given by h = 3 + 14t − 5t2. Find the, maximum height it can reach., , 90
Page 101 :
Let us Remember, ֍, , Equations of tangent and Normal at P (x1, y1) respectively are given by, y − y1 = m (x − x1) where m =, , dy, dx, , y − y1 = m' (x − x1) where m' = −, ֍, ֍, , ֍, , ֍, , (x1, y1), , dy, dx, , 1, , , if, , dy, dx, , (x1, y1), , ≠0, (x1, y1), , Approximate value of the function f (x) at x = a + h is given by f (a + h) ≑ f (a) + h f ' (a), , Rolle's theorem : If real-valued function f is continous on a closed [a, b], differentiable on the, open interval (a, b) and f (a) = f (b), then there exists at least one c in the open interval (a, b), such that f ' (c) = 0., Lagrange's Mean Value Theorem (LMVT) : If a real-valued function f is continous on a, closed [a, b] and differentiable on the open interval (a, b) then there exists at least one c in the, f (b) − f (a), f ' (c) =, open interval (a, b) such that, b−a, Increasing and decreasing functions :, (i), , A function f is monotonically increasing if f ' (x) > 0., , (ii), , A function f is monotonically decreasing if f ' (x) < 0., , (iii) A function f is increasing if f ' (x) ≥ 0., (iv) A function f is decreasing if f ' (x) ≤ 0., First Derivative test :, A function f (x) has a maxima at x = c if, (i) f ' (c) = 0, (ii) f ' (c − h) > 0, [ f (x) is increasing for values of x < c ], (iii) f ' (c + h) < 0, [ f (x) is decreasing for values of x > c ], where h is a small positive number., A function f (x) has a minima at x = c if, (i) f ' (c) = 0, (ii) f ' (c − h) < 0, [ f (x) is decreasing for values of x < c ], (iii) f ' (c + h) > 0, [ f (x) is increasing for values of x > c ], where h is a small positive number., (ii) Second Derivative test :, , A function f (x) has a maxima at x = c if f ' (c) = 0 and f " (c) < 0., , ֍, , (i), , , , A function f (x) has a minimum at x = c if f ' (c) = 0 and f " (c) > 0., , 91
Page 102 :
MISCELLANEOUS EXERCISE 2, (I) Choose the correct option from the given alternatives :, (1), , If the function f (x) = ax3 + bx2 + 11x − 6 satisfies conditions of Rolle's theorem in [1, 3] and, 1, = 0, then values of a and b are respectively., f ' 2 +, √3, (A) 1, −6, (B) −2, 1, (C) −1, −6, x2 − 1, (2) If f (x) = x2 + 1 , for every real x, then the minimum value of f is -, , (D) −1, 6, , (A) 1, , (D) 2, , (3), , (B) 2, , (C) 2.5, , (D) 3, , Let f (x) and g (x) be differentiable for 0 < x < 1 such f (0) = 0, g (0) = 0, f (1) = 6. Let there, exist a real number c in (0, 1) such that f ' (c) = 2g' (c), then the value of g (1) must be, , (A) 1, (5), , (C) −1, , A ladder 5 m in length is resting against vertical wall. The bottom of the ladder is pulled along, the ground away from the wall at the rate of 1.5 m/ sec. The length of the higher point of, ladder when the foot of the ladder is 4.0 m away from the wall decreases at the rate of, , (A) 1, (4), , (B) 0, , (B) 3, , (C) 2.5, , (D) −1, , Let f (x) = x3 − 6x2 + 9x + 18, then f (x) is strictly decreasing in -, , (A) (−∞, 1), , (B) [3, ∞), , (C) (−∞, 1] U [3, ∞), , If x = − 1 and x = 2 are the extreme points of y = α log x + βx2 + x then, 1, 1, 1, (B) α = −6, β = −, (C) α = 2, β = −, (A) α = −6, β =, 2, 2, 2, , (D) (1, 3), , (6), , (7), , (D) α = 2, β =, , 1, 2, , The normal to the curve x2 + 2xy − 3y2 = 0 at (1, 1), , (A) Meets the curve again in second quadrant. (B) Does not meet the curve again., , (8), , (C) Meets the curve again in third quadrant. (D) Meets the curve again in fourth quadrant., x, , The equation of the tangent to the curve y = 1 − e 2 at the point of intersection with Y-axis is, , (A) x + 2y = 0, (9), , (B) 2x + y = 0, , (C) x − y = 2, , (D) x + y = 2, , If the tangent at (1, 1) on y2 = x (2 − x)2 meets the curve again at P then P is, , (A) (4, 4), , (B) (−1, 2), , (C) (3, 6), , (D), , 9 3, ,, 4 8, , (10) The appoximate value of tan (44° 30' ) given that 1° = 0.0175., (A) 0.8952, , (B) 0.9528, , (C) 0.9285, , 92, , (D) 0.9825
Page 103 :
(II) (1), , If the curves ax2 + by2 = 1 and a' x2 + b' y2 = 1 intersect orthogonally, then prove that, 1, 1, 1, 1, −, =, − ., , b, a' b', a, (2) Determine the area of the triangle formed by the tangent to the graph of the function y = 3 − x2, drawn at the point (1, 2) and the cordinate axes., (3), , Find the equation of the tangent and normal drawn to the curve y4 − 4x4 − 6xy = 0 at the, point M (1, 2)., (4), , A water tank in the form of an inverted cone is being emptied at the rate of 2 cubic feet per, second. The height of the cone is 8 feet and the radius is 4 feet. Find the rate of change of the, water level when the depth is 6 feet., , (5), , Find all points on the ellipse 9x2 + 16y2 = 400, at which the y-coordinate is decreasing and the, x-coordinate is increasing at the same rate., 2, on [−1, 1]., e + e− x, , (6), , Verify Rolle's theorem for the function f (x) =, , (7), , The position of a particle is given by the function s(t ) = 2t2 + 3t − 4. Find the time t = c in the, interval 0 ≤ t ≤ 4 when the instantaneous velocity of the particle equals to its average velocity, in this interval., , (8), , Find the approximate value of the function f (x) = √ x2 + 3x at x = 1.02., , x, , 2, = 1.1547., √3, (10) Find the intervals on which the function y = xx, (x > 0) is increasing and decreasing., , (9), , Find the approximate value of cos −1 (0.51) given π = 3.1416,, , (11) Find the intervals on the which the function f (x) =, , x, , is increasing and decreasing., log x, , (12) An open box with a square base is to be made out of a given quantity of sheet of area a2, Show, a3, ., the maximum volume of the box is, 6√ 3, (13) Show that of all rectangles inscribed in a given circle, the square has the maximum area., (14) Show that a closed right circular cyclinder of given surface area has maximum volume if its, height equals the diameter of its base., (15) A window is in the form of a rectangle surmounted by a semi-circle. If the perimeter be 30 m,, find the dimensions so that the greatest possible amount of light may be admitted., (16) Show that the height of a right circular cylinder of greatest volume that can be inscribed in a, right circular cone is one-third of that of the cone., (17) A wire of length l is cut in to two parts. One part is bent into a circle and the other into a, square. Show that the sum of the areas of the circle and the square is least, if the radius of the, circle is half the side of the square., , 93
Page 104 :
(18) A rectangular Sheet of paper of fixed perimeter with the sides having their length in the ratio, 8 : 15 converted in to an open rectangular box by folding after removing the squares of equal, area from all corners. If the total area of the removed squares is 100, the resulting box has, maximum valume. Find the lengths of the rectangular sheet of paper., (19) Show that the altitude of the right circular cone of maximum volume that can be inscribed in, 4r, a shpere of radius r is, ., 3, (20) Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of, 2R, radius R is, . Also find the maximum volume., √3, (21) Find the maximum and minimum values of the function f (x) = cos2 x + sin x., , v, , v, , 94, , v
Page 105 :
3. INDEFINITE INTEGRATION, Let us Study, •, , Definition and Properties, , •, , Different Techniques : 1. by substitution 2. by parts 3. by partial fraction, , Introduction :, In differential calculus, we studied differentiation or derivatives of some functions. We saw that, derivatives are used for finding the slopes of tangents, maximum or minimum values of the function., Now we will try to find the function whose derivative is known, or given f (x). We will find g (x), such that g' (x) = f (x). Here the integration of f (x) with respect to x is g (x) or g (x) is called the primitive, d 3, of f (x). For example, we know that the derivative of x3 w. r. t. x is 3x2. So, x = 3x2 ; and integral of, dx, 2, 3, 3x w. r. t. x is x . This is shown with the sign of integration namely '�'. We write �3x2 · dx = x3., In this chapter we restrict ourselves only to study the methods of integration. The theory of, integration is developed by Sir Isaac Newton and Gottfried Leibnitz., �f (x)·dx = g (x), read as an integral of f (x) with respect to x, is g (x). Since the derivative of constant, function with respect to x is zero (0), we can also write, �f (x)·dx = g (x) + c , where c is an arbitarary constant and c can take infinitely many values., , For example :, , f (x) = x2 + c represents familly of curves for, different values of c., f ' (x) = 2x gives the slope of the tangent to , f (x) = x2 + c., In the figure we have shown the curves, y = x2 , y = x2 + 4, y = x2 − 5., Note that at the points (2, 4), (2, 8) (2, −1), respectivelly on those curves, the slopes of tangents, are 2 (2) = 4., Fig. 3.1.1, , 95
Page 106 :
3.1.1 Elementary Integration Formulae, d xn+1, dx n + 1, , (i), , =, , (n + 1) x n, (n + 1), , , n ≠ −1, , =, , xn , , ⇒ ∴, , d (ax + b) n + 1, , dx (n + 1) · a, , , =, =, , (n + 1) (ax + b) n, (n + 1), (ax + b) n, , �xn · dx =, , , , ⇒, , xn+1, +c, n+1, , ∴ �(ax + b) n· dx =, , This result can be extended for n replaced by any rational, d, dx, , ax, = ax, a > 0, log a, , (ax + b) n + 1 1, · +c, a, n+1, , p, ., q, , ax, (ii), ⇒ ∴ �a · dx =, +c, log a, Aax + b 1, ax + b, �A · dx =, · +c,A>0, log A a, d x x , (iii), e =e, ⇒, �e x · dx = e x + c, dx, 1, �e ax + b· dx = e ax + b · + c, a, d, (iv), sin x = cos x, ⇒, �cos x · dx = sin x + c, dx, 1, �cos (ax + b)· dx = sin (ax + b)· + c, a, d, (v), cos x = − sin x, ⇒, �sin x · dx = − cos x + c, dx, 1, �sin (ax + b)· dx = − cos (ax + b)· + c, a, d, (vi), tan x = sec2 x, ⇒, �sec2 x · dx = tan x + c, dx, 1, �sec2 (ax + b)· dx = tan (ax + b)· + c, a, d, (vii), sec x = sec x · tan x, ⇒, �sec x · tan x · dx = sec x + c, dx, 1, �sec (ax + b)· tan (ax + b)·dx = sec (ax + b)· + c, a, d, (viii), cosec x = − cosec x · cot x ⇒, �cosec x · cot x · dx = − cosec x + c, dx, 1, �cosec (ax + b)· cot (ax + b) · dx = − cosec (ax + b)· + c, a, d, (ix), cot x = − cosec2 x, ⇒, �cosec2 x · dx = − cot x + c, dx, 1, �cosec2 (ax + b)· dx = − cot (ax + b)· + c, a, 1, d, 1, (x), log x = , x > 0, ⇒ � dx = log x + c, x ≠ 0., x, dx, x, 1, 1, ∴ also�, · dx = log (ax + b)· + c, a, (ax + b), x, , We assume that the trigonometric functions and logarithmic functions are defined on the, respective domains., , 96
Page 114 :
Corollary I :, If �f (x) · dx = g (x) + c, , then �f (ax + b) · dx = g (ax + b), , Proof : Let I = �f (ax + b) · dx, , Corollary II :, [ f (x)]n + 1, �[ f (x)] · f ' (x)·dx =, + c, n ≠ −1, n+1, n, , 1, +c, a, , Proof : Let I = �[ f (x)]n + 1 · f ' (x)·dx, put f (x) = t, , put ax + b = t, , Differentiating both the sides, f ' (x)·dx = dt, , Differentiating both the sides, 1, a · dx = 1 · dt ⇒ dx = dt, a, 1, I = �f (t) · · dt, a, 1, = · �f (t) · dt, a, 1, = · g (t) + c, a, 1, = · g (ax + b) + c, a, 1, ∴ �f (ax + b) · dx = g (ax + b) + c, a, , I, , = � [t]n · dt, t n+1, =, +c ,, n+1, [ f (x)]n + 1, =, +c, n+1, ∴, , (sin −1 x)4, , =, +c, 4, , :, , f ' (x), ·dx = log ( f (x) ) + c, f (x), , Proof : Consider �, , f ' (x), ·dx, f (x), , For example : �cot x · dx, , put f (x) = t, , = �, , Differentiating both the sides, f ' (x)·dx = dt, I, , =�, , 1, · dt, t, , = �, , d, dx sin, , x, · dx, sin x, , = log (sin x) + c, , = log ( f (x)) + c, �, , cos x, · dx, sin x, , d, sin x = cos x, dx, , = log (t) + c, , ∴, , (sin −1 x)3, · dx, √ 1 − x2, , , = �[(sin −1 x)3] ·, , For example : �sec (5x − 4) · dx, 1, , = tan (5x − 4) + c, 5, , �, , [ f (x)]n + 1, �[ f (x)] · f ' (x)·dx =, +c, n+1, n, , For example : �, , 2, , Corollary III, , n ≠ −1, , f ' (x), ·dx = log ( f (x)) + c, f (x), , 104, , 1, · dx, √ 1 − x2
Page 115 :
Corollary IV, �, , f ' (x), , √ f (x), , :, ·dx = 2 √ f (x) + c, , Proof : Consider �, , f ' (x), , √ f (x), , For example : �, , ·dx, , put f (x) = t, , = �, , Differentiating both the sides, f ' (x)·dx = dt, I, , =�, , 1, , √t, , = 2 · �, , = �, , · dt, 1, , 2√ t, = 2 √ t + c, , 1, · dx, x√ log x, 1, x, , √ log x, , · dx, , d, dx, , log x, · dx, √ log x, , = 2 √ log x + c, , · dt, , = 2 √ f (x) + c, ∴, , �, , f ' (x), , √ f (x), , ·dx = 2 √ f (x) + c, , f ' (x), Using corollary III, �, ·dx = log, f (x), functions., , ( f (x)), , + c we find the integrals of some trigonometric, , 3.2.2 Integrals of trignometric functions :, Activity :, , 1. �tan x · dx, , Solution :, I =, , =, =, , log (sec x) + c, , =, , Solution :, , �tan x · dx, , sin x, · dx, cos x, − sin x, −�, · dx, cos x, , =, , 2. �cot (5x − 4) · dx, , �, , I =, , =, , − log (cos x) + c, , �, , ............., , sin (5x − 4), , · dx, , 5 cos (5x − 4), 1, �, · dx, ............., ....., , d, (.............) = ............., dx, =, , 105, , 1, log [sec (5x − 4)] + c, 5
Page 116 :
Activity :, , 3. �sec x · dx = log (sec x + tan x) + c, Solution :, , (sec x) (sec x + tan x), · dx, sec x + tan x, sec2 x + sec x · tan x, �, =, · dx, sec x + tan x, sec x · tan x + sec2 x, �, =, · dx, sec x + tan x, d, (sec x + tan x) = sec x · tan x + sec2 x, dx, , =, , ⸪, ∴, , 4., , Let I = �sec x · dx, , �, , Solution :, =, , �, , �, =, �, =, , Let I = �cosec x · dx, , (cosec x) ( . . . . . . . . . . ), · dx, (..........), ................, · dx, ........, − cosec x · cot x + cosec2 x, · dx, ........, , d, (cosec x − cot x), dx, , �sec x · dx = log (sec x + tan x) + c, Also,, , x, π, �sec x · dx = log tan, +, 2, 4, , �cosec x · dx = log (cosec x − cot x) + c, , +c, ∴, , =, , . . . . . . . .. . . . . . . ., , =, , log (cosec x − cot x) + c, , �cosec x · dx = log (cosec x − cot x) + c, , Also,, , �cosec x · dx = log tan, , x, 2, , +c, , SOLVED EXAMPLES, Ex. :, , Evaluate the following functions :, , cot (log x), · dx, x, cot (log x), Solution : Let I =�, · dx, x, put log x = t, , cos √ x, · dx, √x, cos √ x, Solution : Let I = �, · dx, √x, put √ x = t, 1, ∴, · dx = 1 · dt, 2√ x, 1, ∴, · dx = 2 · dt, √x, , 1. �, , ∴, , 2. �, , 1, · dx = 1 · dt, x, , = �cot t · dt, , = log (sin t ) + c, , = 2 · �cos t · dt, , = log (sin log x) + c, , = 2 · sin t + c, , = 2 · sin √ x + c, , 106
Page 118 :
8. �, , Solution :, , 1, · dx, 3x + 7x−n, , 1, Consider �, · dx, 3x + 7x−n, =�, , 1, , · dx = �, , 7, 3x + n, x, n, x, = � n+1, · dx, 3x + 7, , 3x, , 9. � (3x + 2) √ x − 4 · dx, 1, , n+1, , +7, , Solution : put x − 4 = t, ∴ x = 4 + t, Differentiate, 1· dx = 1· dt, , · dx, , =, , xn, , =, , put 3xn+1 + 7 = t, Differentiate w. r. t. x, 3(n + 1) xn · dx = dt, 1, ∴ xn · dx =, dt, 3(n + 1), , =, , =, , =�, =�, =�, , =, , =, , 3, , 5, , 3, 5, 28, 6, (x − 4) 2 +, (x − 4) 2 + c, 3, 5, , 1, · log (3xn+1 + 7) + c, 3(n + 1), , sin (x + a), · dx, cos (x − b), , Solution :, , , , 1, , � 14t 2 + 3t 2 · dt, 3, , = � 3(n + 1) · dt, t, 1, =, · log ( t ) + c, 3(n + 1), , 10. �, , 1, , � (14 + 3t ) · t 2 · dt, , t2, t2, = 14 3 + 3 5 · dx, 2, 2, , 1, , =, , � [ 3(4 + t ) + 2 ]·√ t· dt, , sin [(x − b) + (a + b)], · dx, cos (x − b), sin (x − b) · cos (a + b) + cos (x − b) · sin (a + b), · dx, cos (x − b), sin (x − b) · cos (a + b) cos (x − b) · sin (a + b), +, cos (x − b), cos (x − b), , �[cos (a + b) · tan (x − b) + sin (a + b)] · dx, , cos (a + b) · log (sec (x − b)) + x·sin (a + b) + c, , 108
Page 119 :
11. �, , ex + 1, ex − 1, , Solution :, I, , = �, , = �, , 12. �, , · dx, , e −1+2, · dx, ex − 1, , I, , 2, ex − 1, + x, · dx, x, e −1 e −1, , =�, , = �, , 2, · dx, ex − 1, 2, = � dx + � x, · dx, e (1 − e−x), e−x, �, = � 1dx + 2, · dx, 1 − e−x, , =, , put (1 − e−x) = t, , = x + 2 log (1 − e−x ) + c, ex − 1, , cos x, 1, 1, cos x −, cos x, √2, √2, √2, , · dx, , cos x, 1, �, · dx, π, √ 2 cos cos x − sin π sin x, 4, 4, , 1, cos x, �, · dx, √ 2 cos x + π, 4, π, π, put x + = t ∴ x = t −, 4, 4, Differentiating both sides, 1·dx = 1·dt, , = x + 2 · log ( t ) + c, , �, , 1, · dx, sin x, 1−, cos x, , =, , e−x · dx = 1 dt, 1, I = � 1dx + 2 � · dt, t, , ∴, , · dx, , cos x, cos x − sin x, , = �, , Differentiate w. r. t. x, −(e−x) (−1) · dx = 1 dt, , ex + 1, , 1 − tan x, , Solution :, , x, , = � 1 +, , , , 1, , =, , · dx = x + 2 log (1 − e−x ) + c, , 1, �, √2, , 1, =, �, √2, , cos t −, cos t, cos t·cos, , π, 4, , · dt, , π, π, + sin t·sin, 4, 4, · dt, cos t, , 1, 1, 1, �, +, tan t · dt, √2, √2 √2, 1, 1, =, ·, [ t + log (sec t )] + c, √2 √2, =, , =, , To evaluate the integrals of type �, , a cos x + b sin x, , 1, π, π, x + + log sec x +, 2, 4, 4, , +c, , · dx, express the Numerator as, c cos x + d sin x, Nr = λ (Dr) + µ (Dr)' , find the constants λ & µ by compairing the co-efficients of like terms and then, integrate the function., , 109
Page 120 :
EXERCISE 3.2 (A), I., , Integrate the following functions w. r. t. x :, (log x) n, , 1., , 2., , x, 1+x, x·sin (x + log x), , 3., , 6., , e +1, 3x, , ex · log (sin ex), , 7., , sin4 x·cos3 x, , √ tan3 (x2), (x2 + 2), (x + 1), , 10., , 2, , · a x + tan, , −1, , 1., , x, , e2x + 1, , 3., , e2x − 1, 1, 4x + 5x−11, , 4., , 12. e3 log x·(x4 + 1), , 5., , 2, , 13., , √ tan x, sin x·cos x, , 14., , 15., , 2 sin x·cos x, 3 cos2 x + 4 sin2 x, , 16., , 10 x9 + 10x·log 10, 10x + x10, , 19. (2x + 1)√ x + 2, , 18., , (x − 1), , 7., , 2, , (x2 + 1), 1, , 9., , √ x + x3, xn − 1, , −, , 21. (5 − 3x) (2 − 3x), , 1, 2, , 22., , 2, , x (x3 − 1), , 1, x·log x·log (log x), , cos 3x − cos 4x, sin 3x + sin 4x, , 2., , cos x, sin (x − a), , sin (x − a), cos (x + b), 1, sin x·cos x + 2 cos2x, sin x + 2 cos x, 3 sin x + 4 cos x, 4 e x − 25, , 6., 8., , 2 ex − 5, 3 e 2x + 5, , 1, 2 + 3 tan x, 20 + 12 e x, 3 ex + 4, , 10. cos8 x·cot x, , 4 e 2x − 5, , 12. cos7 x, , 14. sin5 x·cos8 x, , 7 + 4x + 5x2, (2x +, , √ 9 − x6, , 1, , 13. tan 3x·tan 2x·tan x, , 20. x ·√ a + x, 2, , 24., , 11. tan5 x, , √ 1 + 4x n, 5, , x2, , II. Integrate the following functions w. r. t. x :, , −1, , 11. x9·sec2 (x10), , 17., , 25., , x·sec2 (x2), , 8., , tan (ex), , 9., , √ 1 − x2, , 4., , e3x, , 5., , 23., , 3, −1, (sin x) 2, , 16., , 3, 3) 2, , 15. 3cos x·sin 2x, 2, , sin 6x, sin 10x·sin 4x, , 17., , sin x·cos3 x, 1 + cos2x, , 3.2.3 Some Special Integrals, 1., 3., 5., 7., , �, , �, , �, , �, , 1, x +a, 2, , 2, , · dx =, , x, 1, tan−1, +c, a, a, , 2., , 1, , a+x, 1, ·, dx, =, log, +c, a2 − x2, a−x, 2a, 1, , · dx = log ( x + √ x2 − a2 ) + c, , √x − a, 2, , 2, , 1, x√ x − a, 2, , 4., , 2, , · dx =, , 6., , x, 1, sec−1, +c, a, a, , 110, , �, , �, , �, , 1, x −a, 2, , 2, , · dx =, , 1, , √ a2 − x2, 1, , √ x + a2, 2, , x−a, 1, log, +c, x+a, 2a, , · dx = sin−1, , x, +c, a, , · dx = log ( x + √ x2 + a2 ) + c
Page 124 :
3.2.4, In order to evaluate the integrals of type �, we can use the following steps., , (1) Write ax2 + bx + c as, a x2 +, (2), , x2 +, , b, x or, a, , 1, ax + bx + c, 2, , · dx and �, , 1, , √ ax + bx + c, 2, , · dx, , b, c, x+, , a > 0 and take a or √ a out of the integral sign., a, a, , b, x − x2 is expressed by the method of completing square by adding and, a, , 2, 1, subtracting, coefficient of x ., 2, (3) Express the quadractic expression as a sum or difference of two squares, , i.e. ((x + β)2 ± α2) or (α2 − (x + β)2), (4) We know that, , � f (x) dx = g (x) + c, , � f (x + β) dx = g (x + β) + c, 1, � f (αx + β) dx = g (αx + β) + c, α, (5) Use the standard integral formula and express the result in terms of x., ⇒, , 3.2.5, In order to evaluate the integral of type �, we can use the following steps., , 1, a sin2 x + b cos2 x + c, , · dx, , (1) Divide the numerator and denominator by cos2 x or sin2 x., (2) In denominator replace sec2 x by 1 + tan2 x and /or cosec2 x by 1 + cot2 x, if exists., 1, (3) Put tan x = t or cot x = t so that the integral reduces to the form � 2, · dt, at + bt + c, (4) Use the standard integral formula and express the result in terms of x., , 3.2.6, To evaluate the integral of the form �, x, = t., 2, x, If tan = t, 2, , 1, a sin x + b cos x + c, , · dx , we use the standard substitution, , tan, , then (i), , (ii), , x 1, · ·dx = 1·dt, 2 2, 2 dt, 2, 2, i.e. dx =, x ·dt =, x ·dt = 1 + t2, 1 + tan2, sec2, 2, 2, x, 2 tan, 2t, 2, sin x =, =, x, 1 + t2, 1 + tan2, 2, , sec2, , 114
Page 125 :
x, 1 − t2, 2, (iii) cos x =, x = 1 + t2, 1 + tan2, 2, 1 − tan2, , We put tan x = t for the integral of the type �, therefore, , , and, , dx, , =, , sin 2x, , =, , cos 2x, , =, , 1, a sin 2x + b cos 2x + c, , · dx, , 1, ·dt, 1 + t2, 2t, ·dt, 1 + t2, 1 − t2, ·dt, 1 + t2, , With this substitution the integral reduces to the form �, , integral formula and express the result in terms of x., , 1, ax2 + bx + c, , · dx. Now use the standard, , SOLVED EXAMPLES, Ex. :, , Evaluate :, , 1. �, , 1, 4x2 + 11, , Solution : I =, , =, , ⸪, , �, , 1, x +a, 2, , I, , 2, , �, , =, , 1, 11, 4 x2 +, 4, , 1, ·�, 4, , · dx =, , =, , 2. �, , · dx, , x2 +, , √ 11, 2, , 2, , x, √ 11, 2, , �, , · dx, 1, b2, , a, − x2, b2, 2, , · dx, , 1, 1, ·�, · dx, 2, a 2, b, − x2, b, 1, a+x, 1, ·, dx, =, log, +c, ⸪ � 2, a − x2, a−x, 2a, a, +x, 1, 1, b, I =, ·, · log a, +c, b2, a, −x, 2, b, b, a, +x, 1, 1, b, =, ·, · log a, +c, b2, a, −, x, 2, b, b, 1, a + bx, =, ·log, +c, 2ab, a − bx, =, , · dx, , x, 1, tan−1, +c, a, a, , 1, 1, ·, · tan−1, 4 √ 11, 2, , a − b2 x2, , Solution : I =, , · dx, , 1, , 1, 2, , +c, , 1, 2x, tan−1, +c, 2 √ 11, √ 11, , 115
Page 126 :
3. �, , 1, , √ 3x2 − 7, �, , Solution : I =, , �, , =, , ⸪, , �, , 1, , √ x2 − a2, , 1, , · dx, , 7, 3 x2 −, 3, 1, , 2, , √7, x2 −, √3, , √3 ·, , 1, ·�, √3, , =, , 4. �, , · dx, , 2, , √7, x2 −, √3, , · dx = log | x + √ x − a, 2, , 2, , =, , √7, x2 −, √3, , =, , 1, ·log x +, √3, , x2 −, , 5. �, Solution :, , ⸪, =, , =, , =, , 1, , √ 3x2 − 4x + 2, =, , �, , 7, 3, , 1, ·�, √3, 1, ·�, √3, , �, , 1, , ∴, , +c, , �, , x2 + 8x + 16 − 4, , · dx, , 1, · dx, (x + 4)2 − (2)2, , x−a, 1, ·, dx, =, log, +c, x2 − a2, x+a, 2a, =, , =, , 2, , 1, , 1, (x + 4) − 2, ·log, 2(2), (x + 4) + 2, 1, x+2, ·log, 4, x+6, , 1, x + 8x + 12, 2, , · dx =, , +c, , +c, , 1, x+2, ·log, 4, x+6, , +c, , +c, , 1, 4, 2, 3 x2 − x +, 3, 3, 2, , · dx, , 1, 4, −, 2, 3, , =, , 1, , √3 ·, , �, , · dx, , · dx, , 1, coefficient of x, �, 2, �, , =, , I, , |+c, , 1, ·log x +, √3, , I, , �, , ⸪, · dx, , x2 + 8x + 12, , Solution : I =, , · dx, , 1, , 1, , 4, 4 4 2, x2 − x + − +, 3, 9 9 3, , · dx, , 1, 4, 2 4, 4, x2 − x +, +, −, 3, 3 9, 9, 1, 2, , 2, √2, x−, +, 3, 3, , 2, , 2, , 2 2 4, = −, =, �, 3, 9, , ⸪, , · dx, , �, , 1, , √ x + a2, , 1, ·log, =, √3, , · dx, , =, , 116, , 1, ·log, √3, , 2, , · dx = log | x + √ x2 + a2 | + c, , 2, x−, +, 3, x−, , 2, +, 3, , 2, x−, 3, x2 −, , 2, , √2, +, 3, , 4, 2, x+, 3, 3, , 2, , +c, +c
Page 127 :
6. �, , 1, 3 − 10x − 25x2, , Activity :, , · dx, , 7. �, , Solution :, I, , �, , =, , �, , =, , ⸪, , =, , =, , 3, 2, − x2 + x, 25, 25, 5, , �, , , , =, , 1, 1, ·�, · dx, 25, 3, 2, 1, 1, − x2 − x +, −, 25, 5, 25 25, , =, , �, , 1, 1, ·�, · dx, 25, 3, 2, 1, 1, 2, − x − x+, +, 25, 5, 25, 25, , I =, , 1, 2, , 2, 5, , 2, , =, , 1, 1, =, �, 5, 25, , 1, a −x, 2, , =, , =, , 2, , · dx =, , 1, ·, 25, , 2, , ⸪, , · dx, , I, , · dx, , a+x, 1, log, +c, a−x, 2a, , 1, · log, 2, 2, 5, , 2, + x−, 5, 2, − x−, 5, , �, , 1, 5, 1, 5, , +c, , 1, 1 + 5x, ·log, +c, 5, 3 − 5x, , 117, , 2, , 2, 1, 1 2 1, (− 1) = −, = �, 2, 2, 4, , 1, , 1 1, 1 − x2 − x + −, 4 4, , · dx, , 1, , · dx, , 1− ................, 1, , �, , 2, , 1, √5, − x−, 2, 2, , 1, , √a − x, 2, , · dx, , 1− ..........., , 1, coefficient of x, �, 2, , �, , 1, 1, ·�, 2, 25, 2, 1, − x−, 5, 5, , =, , ⸪, , · dx, , · dx, 1, , I = �, , =, , 2, , √ 1 + x − x2, , Solution :, , 2, , 1, 1, ·�, 25, 4, 2, 1, − x2 − x +, 25, 5, 25, , =, , I, , 1, , 1, �, coefficient of x, 2, , , =, , ⸪, , 1, · dx, 3, 10, 25, −, x − x2, 25 25, , 1, , 2, , · dx = sin−1, , 2, , · dx, , x, +c, a, , =, , ................, , =, , ................
Page 128 :
x, , sin 2x, · dx, 3 sin4 x − 4 sin2 x + 1, sin 2x, Solution : I = �, · dx, 2, 3 (sin2 x) − 4 (sin2 x) + 1, , e2, 9. � −x, · dx, √ e − ex, , 8. �, , put sin2 x = t, , ∴ 2 sin x·cos x·dx = 1·dt, , =, , 2, , ⸪, =, I, , =, , =, , =, , =, , ∴, , 1, coefficient of t, �, 2, , 1, ·�, 3, , 2 2 4, = −, = �, 3, 9, , 1, · dt, 4, 4 4 1, 2, t − t+ − +, 3, 9 9 3, , 1, ·�, 3, 1, ·�, 3, 1, ·, 3, , 1, 4, 4, 1, t2 − t +, −, 3, 9, 9, 1, 2, t−, 3, , 2, , 1, −, 3, , 1, · log, 1, 2, 3, , 2, , =, , �, , =, , �, , =, , �, , =, , · dx, , 1 − (e x)2, ex, , √ ex, 1 − (e x)2, √ ex, , √ ex · √ ex, 1 − (e x)2, ex, 1 − (e x)2, , · dx, , · dx, · dx, , e x·dx = 1·dt, = �, , I, , 1, 1 − t2, , · dt, , =, , sin−1 (t ) + c, , =, , sin−1 (e x ) + c, , +c, , x, , ∴�, , +c, +c, , sin 2x, · dx, 3 sin4 x − 4 sin2 x + 1, 3 sin2 x − 3, 3 sin2 x − 1, , √ ex, , ex = t, , ∴, , · dt, , 1, 2, −, 3, 3, 1, 2, t−, +, 3, 3, , 1, 3 sin2 x − 3, ·log, 2, 3 sin2 x − 1, , 1, ·log, 2, , �, , put, , · dt, , t−, , 1, 3t − 3, ·log, 2, 3t − 1, , =, , 2, , =, , 2, , 1, 4, −, 2, 3, , =, , �, , I, , 1, · dt, 3t − 4t + 1, 1, �, · dt, 4, 1, 3 t2 − t +, 3, 3, �, , √ ex, · dx, 1, x, −e, ex, , = �, , sin 2x·dx = 1·dt, , ∴, =, , Solution :, , +c, , 118, , e2, , √e − e, −x, , x, , · dx = sin−1 (e x ) + c
Page 131 :
Activity : 14., , I, , sin x = . . . . . . . ., , and, , 1, , 2, 1 + t2, , =, , =, , =, =, , =, , =, , =, , =, =, =, , =, , �, , 1+t, ...., 1 + t2, , 2, , ·�, , √3, 1, , a, a2 − b2, , ∴I =, , · dt, t, , 2, 1, ·, ·log, √ 3 2 (...), ·log, , +c, +c, , x, 1, 2, ·log, x, 2, 3 − √ 3 tan, 2, , and, , cos θ =, , b, a2 − b2, , = 2·sin (x − θ), , 2, , 1 + √ 3 tan, , sin θ =, , = √ 1 + 3 (cos θ·sin x − sin θ·cos x), , · dt, 1 1, 1 − t2 −, t+ −, 3 3, √3, 1, 2, ·�, · dt, 1, 1, 2, √3, 1 − t2 −, t+, +, 3, 3, √3, 1, 2, ·�, 2 · dt, 1, √3, .... − t− 3, √, 1, 2, ·�, · dt, ( . . . ) 2 − ( . . . )2, √3, , √3, , · dx, , Using this we express sin x − √ 3 cos x, , · dt, , 2, , √3 1 − t −, , sin x − √ 3 cos x, , = 2·sin x −, , ........, , 2, , · dt, , · dt, , 2, , 2, , 1, , Solution : For any two positive numbers a and b,, we can find an angle θ, such that, ∴, , 2, , �, , 14. �, , cos x = . . . . . . . ., , . . . . . . . . + √3 . . . . . . . ., 2, , �, , �, , Alternative method :, , · dx, , sin x − √ 3 cos x, x, put tan = t, ∴ dx = . . . . . . . ., 2, , Solution :, ∴, , 1, , �, , +c, , 121, , �, , π, 3, 1, , π, 2·sin x −, 3, , · dx, , =, , 1, π, ·�cosec x −, · dx, 2, 3, , =, , 1, π, π, ·log cosec x −, − cot x −, 2, 3, 3, , =, , 1, x π, ·log tan, +, + c, 2, 2 6, , +c
Page 139 :
For example :, , �x·e x·dx = x�e x·dx − �, , d(x) x, ·�e ·dx ·dx, dx, , = x·e x − �(1)·e x·dx, , , , = x·e x − �e x·dx, , , , = x·e x − e x + c, , , , now let us reverse the choise of u and v, �e x·x·dx = e x·�x 1·dx − �, , ∴, , , , = ex ·, , , , =, , x2, 2, , − �e x·, , d x, ·e �x·dx·dx, dx, , x2, 2, , ·dx, , 1, 1, ·e x·x2 − ·�e x·x2·dx, 2, 2, , We arrive at an integral �e x·x2·dx which is more difficult, but it helps to get �e x·x2·dx, , Thus it is essential to make a proper choise of the first function and the second function. The first, function to be selected will be the one, which comes first in the order of L I A T E., , , L, , Logarithmic function., , , , I, , Inverse trigonometric function., , , , A, , Algebric function., , , , T, , Trigonometric function., , , , E, , Exponential function., , For example :, , �sin x·x·dx, , = �x·sin x·dx . . . . . by LIATE, = x·�sin x·dx − �, , d, ·x·�sin x·dx·dx, dx, , = x·(− cos x) − �(1) (− cos x)·dx, = − x·cos x + �cos x·dx, = − x·cos x + sin x + c, , 129
Page 142 :
Activity :, Prove the following results., (i) �eax· sin (bx + c)·dx, , =, , eax, ·[a sin (bx + c) + b cos (bx + c)] + c, a2 + b2, , eax, ·[a sin (bx + c) − b cos (bx + c)] + c, (ii) �e · cos (bx + c)·dx = 2, a + b2, ax, , 5., , � log (log x) +, , Solution :, , I, , 1, , (log x)2, , ·dx, , = �log (log x)·1·dx + �, , = log (log x)·�1·dx − �, = log (log x)·x − �, = log (log x)·x − �, , 1, , 1, (log x)2, , ·dx, , d, 1, · log (log x) �1·dx + �, ·dx, dx, (log x)2, , 1, 1, · ·(x)·dx + �, ·dx, log x x, (log x)2, 1, , log x, , ·dx + �, , 1, , (log x)2, , = log (log x)·x − �(log x)−1·1·dx + �, , ·dx, , 1, (log x)2, , = log (log x)·x − �(log x)−1·�1·dx + �, , ·dx, , d, 1, · (log x)−1 ·�1·dx·dx � + �, ·dx, dx, (log x)2, , 1, 1, = log (log x)·x − �(log x)−1·x − � − 1(log x)−2· ·x·dx � + �, ·dx, (log x)2, x, = log (log x)·x − (log x)−1·x − �(log x)−2·dx + �, = x·log (log x) −, ∴ � log (log x) +, , 1, (log x)2, , 1, , (log x)2, , ·dx, , x, 1, 1, �, −�, ·dx, +, ·dx, log x, (log x)2, (log x)2, , ·dx = x·log (log x) −, , x, +c, log x, , Note that :, , To evaluate the integrals of type �sin−1 x·dx; �tan−1 x·dx ; �sec−1 x·dx; �log x·dx, take the second function, (v) to be 1 and then apply integration by parts., �√ a2 − x2 ·dx ; �√ a2 + x2 ·dx ; �√ x2 − a2 ·dx, , 132
Page 145 :
11. �√ 4 + 3x − 2x2 ·dx, , �√ 4 − 2x2 + 3x ·dx, , Solution : I =, , 3, x · dx, 2, , =, , � 4 − 2 x2 −, , =, , �√ 2 · 2 − x2 −, , 3, x · dx, 2, ⸪, , I, , =, , √ 2 ·� 2 − x2 −, , =, , √ 2 ·� 2 − x2 −, 2, , √ 41, , =, , √ 2 ·�, , ⸪, , �√ a − x ·dx =, , =, , 2, , 4, , 2, , 1, 3, −, =, 2, 2, , 9, 9, 3, x+, +, · dx, 16, 16, 2, , 3, − x−, 4, , 2, , · dx, , x, a2, x, 2, 2, ·√ a − x + ·sin−1, 2, 2, a, , 2, , 3, x−, 4, √2 ·, 2, , 9, 9, 3, x+, −, · dx, 16 16, 2, , 1, coefficient of x, �, 2, , ·, , √ 41, 4, , 2, , − x−, , 3, 4, , +c, , √ 41, , 2, , +, , 4, 2, , 2, , x−, ·sin−1, , 3, 4, , √ 41, , +c, , 4, , =, , √2, , 4x − 3, 8, , ·, , ∴ �√ 4 + 3x − 2x2 ·dx =, , Note that :, , 2+, , 4x − 3, 41, 3, x − x2 +, · sin−1, 32, 2, √ 41, , +c, , 4x − 3, 41, 4x − 3, · √ 4 + 3x − 2x2 +, · sin−1, +c, 8, 16 √ 2, √ 41, , 3.3.2 :, To evaluate the integral of type �( px + q) √ ax2 + bx + c . dx, , d, (ax2 + bx + c) + B, . . . for constants A, B., dx, Then the integral will be evaluated by the useual known methods., we express the term px + q = A ·, , 135, , 2, , 3 2 9, = −, =, �, 4, 16
Page 146 :
3.3.3 Integral of the type �e x [ f (x) + f ' (x)] · dx = e x · f (x) + c, Let e x · f (x) = t, , Differentiating w. r. t. x, e x [ f ' (x) + f (x)] =, , dt, dx, , dt, dx, By definition of integration,, , e x [ f (x) + f ' (x)] =, , ∴, ∴, , �e x [ f (x) + f ' (x)] · dx = t + c, , �e x [ f (x) + f ' (x)] · dx = e x · f (x) + c, , e.g. �e x [ tan x + sec2 x] · dx = e x · tan x + c, , ⸪, , d, tan x = sec2 x, dx, , SOLVED EXAMPLES, 1., , �e x, , 2 + sin 2x, ·dx, 1 + cos 2x, , 2., , =, , �e x, , =, , �e x, , =, =, , 2 + 2 sin x·cos x, ·dx, 2·cos2 x, , I, , sin x·cos x, 1, +, ·dx, cos2 x, cos2 x, , �e x [ tan x + sec2 x ]·dx, , = �e x, , ∴ �e x, , x+3−1, ·dx, (x + 3)2, −1, x+3, +, ·dx, 2, (x + 3) (x + 3)2, 1, −1, +, ·dx, x + 3 (x + 3)2, , ∴ f (x) =, , f ' (x) = sec x, 2, , ∴ �e x [ f (x) + f ' (x)] · dx = e x · f (x) + c, , =, , = �e x, = �e x, , �e x [ sec2 x + tan x ]·dx, , ∴ f (x) = tan x ⇒, , I, , x+2, ·dx, (x + 3)2, , Solution :, , Solution :, I, , �e x, , −1, 1, ⇒ f ' (x) =, (x + 3)2, x+3, , ∴ �e x [ f (x) + f ' (x)] · dx = e x · f (x) + c, , e x · tan x + c, , 2 + sin 2x, ·dx = e x · tan x + c, 1 + cos 2x, , ∴, , 136, , 1, +c, x+3, , =, , ex ·, , =, , ex, +c, x+3, , �e x, , x+2, ex, ·dx, =, +c, (x + 3)2, x+3
Page 147 :
3., , �e, , tan−1 x, , Solution :, , 4., , put tan−1 x = t, , Solution :, , ∴ x = tan t, , =, =, =, , I, , = �e x, = �e x, , �e t ·[ tan t + (1 + tan2 t )]·dt, �e t ·[ tan t + sec2 t ]·dt, f (t ) = tan t , , ⇒, , f ' (t ) = sec t, , = �e x, , 2, , =, , e t · f (t ) + c, , =, , e · tan t + c, , =, , e tan, , t, , tan−1 x, , −1 x, , (x + 1)2, , = �e x, , �e t ·[ 1 + tan t + tan2 t ]·dt, , Here, , ∴ �e, , �, , I, , differentiating w. r. t. x, 1, ∴, ·dx= 1·dt, 1 + x2, I, , (x2 + 1)·e x, , 1 + x + x2, ·, ·dx, 1 + x2, , x2 + 1, ·dx, (x + 1)2, x2 − 1 + 2, ·dx, (x + 1)2, 2, x2 − 1, +, ·dx, (x + 1)2 (x + 1)2, 2, x−1, +, ·dx, x + 1 (x + 1)2, , Here f (x) =, , x−1, x+1, , ⇒ f ' (x) =, , 2, (x + 1) (1) − (x − 1)(1), =, 2, (x + 1)2, (x + 1), , ⸪, , ·x+c, , 1 + x + x2, −1, ·, ·dx = e tan x · x + c, 1 + x2, , ·dx, , �[ f (x) + f ' (x)] · dx = e x · f (x) + c, , I, , = ex ·, , ∴, , �, , x−1, +c, x+1, , (x2 + 1)·e x, (x + 1), , 2, , ·dx = e x ·, , x−1, +c, x+1, , EXERCISE 3.3, I. Evaluate the following :, 1., 4., 7., 10., 13., 16., 19., , �x2·log x·dx, , 2., , �x2·sin 3x·dx, , �x2·tan−1 x·dx, , 5., , � e2x · cos 3x·dx, , 11. �x·sin−1 x·dx, , � sec3 x·dx, , �, , log (log x), ·dx, x, , � sin θ·log (cos θ)·dθ, , �, , log x, ·dx, x, , 8., , �x3·tan−1 x·dx, �x·sin2 x·dx, , 14. �, , t·sin−1 t, , √ 1 − t2, , ·dt, , 17. �x·cos x·dx, 3, , 20. �x·sin 2x·cos 5x·dx, , 137, , 3., 6., 9., , �x·tan−1 x·dx, , �(log x)2 ·dx, �x3·log x·dx, , 12. �x2·cos−1 x·dx, , 15. �cos √ x·dx, 18. �, , sin (log x)2, x, , ·log·x·dx, , 21. �cos ( 3 x )·dx
Page 148 :
II. Integrate the following functions w. r. t. x :, 1., , e2x·sin 3x, , 2., , e−x·cos 2x, , 3., , sin (log x), , 4., , √ 5x2 + 3, , 5., , x2·√ a2 − x6, , 6., , √ (x − 3)(7 − x), , 7., , √ 4x(4x + 4), , 8., , (x + 1)√ 2x2 + 3, , 9., , x √ 5 − 4x − x2, , 10., , sec2 x·√ tan2 x + tan x − 7, , 11. √ x2 + 2x + 5, , 12. √ 2x2 + 3x + 4, , III. Integrate the following functions w. r. t. x :, 1., 4., , (2 + cot x − cosec2 x)·ex, x, ·ex, (x + 1)2, e sin, , 9., , cosec (log x) [ 1 − cot (log x)], , −1 x, , ·, , x + √ 1 − x2, , 7., , √1 − x, , 2, , 2., , 1 + sin x, ·ex, 1 + cos x, , 5., , ex, [x (log x)2 +2 (log x)], x, , 8., , log (1 + x) (1 + x), , 3., , ex ·, , 1, 1, − 2, x, x, , 6., , e 5x ·, , 5x · log x + 1, x, , 3.4 Integration by partial fraction :, If f (x) and g (x) are two polynomials then, , f (x), , g (x) ≠ 0 is called a rational algebric function., g (x), , f (x), is called a proper rational function provided degree of f (x) < degree of g (x) ; otherwise it is, g (x), called improper rational function., If degree of f (x) ≥ degree of g (x) i.e., the form Quotient +, , f (x), is an improper rational function then express it as in, g (x), , Remainder, Remainder, , g (x) ≠ 0 where, is proper rational function., g (x), g (x), , Lets see the three different types of the proper rational function, , f (x), , g (x) ≠ 0 where the, g (x), , denominator g (x) is expressed as, (i), , a non-repeated linear factors, , (ii), , repeated Linear factors and, , (iii), , product of Linear factor and non-repeated quadratic factor., , 138
Page 149 :
No., (i), , Rational form, px2 + qx + r, (x − a) (x − b) (x − c), , Partial form, B, C, A, +, +, (x − a) (x − b) (x − c), , (ii), , px2 + qx + r, (x − a)2 (x − b), , B, C, A, +, +, 2, (x − c), (x − a) (x − a), , (iii), , px2 + qx + r, (x − a) (x2 + bx + c), , Bx + C, A, + 2, (x − a) x + bx + c, , Type (i) : �, , px2 + qx + r, (x − a) (x − b) (x − c), , · dx i.e. denominator is expressed as non-repeated Linear factors., , SOLVED EXAMPLES, , 1., , �, , 3x2 + 4x − 5, (x2 − 1) (x + 2), , Solution : I =, Consider,, , �, , ·dx, 3x2 + 4x − 5, , (x − 1) (x + 1) (x + 2), , 3x2 + 4x − 5, , (x − 1) (x + 1) (x + 2), , =, , =, ∴, , ·dx, A, , (x − 1), , +, , B, (x + 1), , +, , C, (x + 2), , A (x + 1) (x + 2) + B (x − 1) (x + 2) + C (x − 1) (x + 1), (x − 1) (x + 1) (x + 2), , 3x2 + 4x − 5 = A (x + 1) (x + 2) + B (x − 1) (x + 2) + C (x − 1) (x + 1), , at x = 1,, , at x = −1,, , 3 (1)2 + 4 (1) − 5, , = A (2) (3) + B (0) + C (0), 1, 2 = 6A, ⇒ A =, 3, 2, 3 (−1) + 4 (−1) − 5 = A (0) + B (−2)(1) + C (0), −6 = −2B ⇒ B = 3, , at x = − 2,, , 3 (−2)2 + 4 (−2) − 5 = A (0) + B (0) + C (−3) (−1), 1, −1 = 3C, ⇒ C =−, 3, 1, 1, −, 3, 3, 3x2 + 4x − 5, 3, Thus,, =, +, +, (x − 1) (x + 1) (x + 2), (x − 1) (x + 1) (x + 2), 1, 1, −, 3, 3, 1, 3, 1, ∴I =�, +, +, ·dx, = log (x − 1) + 3 log (x + 1) − log (x + 2) + c, 3, 3, (x − 1) (x + 1) (x + 2), =, , 1, (x − 1) (x + 1)9, log, 3, (x + 2), , + c , , ∴�, , 3x2 + 4x − 5, , (x2 − 1) (x + 2), , 139, , ·dx =, , 1, log, 3, , (x − 1) (x + 1)9, (x + 2), , +c
Page 150 :
2., , �, , 2x2 − 3, (x2 − 5) (x2 + 4), , Solution :, , ·dx, , Consider,, , 2x2 − 3, (x2 − 5) (x2 + 4), , Let, , x2 = m, =, , ∴ , , 2m − 3, (m − 5) (m + 4), , Now,, ∴, , 2m − 3, . . . proper rational function., (m − 5) (m + 4), =, , A, (m − 5), , +, , B, (m + 4), , =, , A (m + 4) + B (m − 5), (m − 5) (m + 4), , 2m − 3 = A (m + 4) + B (m − 5), , at m = 5,, , 2(5) − 3, , = A (9) + B (0), 7, ⇒ A =, 9, = A (0) + B (−9), , 7 = 9A, at m = −4,, , 2(−4) − 3, , −11 = −9B ⇒, , Thus,, , B =, 7, 9, , 11, 9, 11, 9, , 2m − 3, =, +, (m − 5) (m + 4) (m − 5) (m + 4), 7, 9, , ∴I =�, , x2 − 5, , +, , 11, 9, , 2x2 − 3, i.e. 2, (x − 5) (x2 + 4), , ·dx, , x2 + 4, , =, , 1, 1, 7, 11, ·� 2, ·dx, +, ·�, ·dx, 9, 9, x − (√ 5)2, x2 + (2)2, , =, , x − √5, 11 1, x, 7, 1, ·, ·log, + · ·tan−1, +c, x + √5, 9 2, 2, 9 2(√ 5), , ∴I =, , ∴�, , 7, 18(√ 5), , ·log, , x − √5, 11, x, +c, + · tan−1, x + √5, 18, 2, , 2x2 − 3, (x2 − 5) (x2 + 4), , ·dx =, , 7, 18(√ 5), , ·log, , x − √5, 11, x, + · tan−1, +c, x + √5, 18, 2, , 140, , =, , 7, 9, x2 − 5, , +, , 11, 9, x2 + 4
Page 151 :
3., , 1, , �, , (sin θ) (3 + 2 cos θ), �, , Solution : I =, , ·dθ, 1, , (sin θ) (3 + 2 cos θ), , =�, , ·dθ, , = �, put cos θ = t ∴, , sin θ, ·dθ , (1 − cos θ) (3 + 2 cos θ), 2, , sin θ, ·dθ , (1 − cos θ) (1 + cos θ) (3 + 2 cos θ), , − sin θ·dθ = 1·dt, , ∴ sin θ·dθ = − 1·dt, −1, A, B, C, Consider,, =, +, +, (1 − t ) (1 + t ) (3 + 2t ), (1 − t ) (1 + t ) (3 + 2t ), A (1 + t ) (3 + 2t ) + B (1 − t ) (3 + 2t ) + C (1 − t ) (1 + t ), (1 − t ) (1 + t ) (3 + 2t ), , =, ∴, , − 1 = A (1 + t ) (3 + 2t ) + B (1 − t ) (3 + 2t ) + C (1 − t ) (1 + t ), , at t = 1,, , at t = −1,, , at t = −, , 3, ,, 2, , − 1 = A (2) (5) + B (0) + C (0), 1, − 1 = 10A ⇒ A = −, 10, − 1 = A (0) + B (2)(1) + C (0), 1, − 1 = 2B, ⇒ B =−, 2, , −1=−, , −, , =−, , =, , 5, C, 4, , ⇒ C=, , −1, (1 − t ) (1 + t ) (3 + 2t ), , Thus,, , ∴I =�, , 5, 2, , − 1 = A (0) + B (0) + C +, , 1, 10, , (1 − t ), , −, +, , 1, 2, , (1 + t ), , +, , 4, 5, (3 + 2t ), , −, , 1, 2, , 4, 5, −, =, , 1, 10, , (1 − t ), , −, +, , 1, 2, , (1 + t ), , +, , 4, 5, (3 + 2t ), , ·dt, , 1, 4, 1, 1, 1, log (1 − t )·, − log (1 + t ) + log (3 + 2t )· + c, 5, 2, (−1) 2, 10, , 1, 4, 1, log (1 − cos θ ) − log (1 + cos θ ) +, log (3 + 2 cos θ ) + c, 2, 10, 10, , (1 − cos θ) (3 + 2 cos θ)4, 1, =, log, + c , (1 + cos θ)5, 10, , ⸪ log am = m·log a, , 141
Page 152 :
4., , �, , 1, 2 cos x + sin 2x, , Solution : I = �, =, , ·dx, 1, , 2 cos x + sin 2x, , (1 − t ) (1 + t )2, , =, , A, , (1 − t ), , +, , B, , (1 + t ), , 1 = A (2)2 + B (0) + C (0), , , , 1 = 4A ⇒ A =, , at t = −1,, , 1 = A (0) + B (0) + C (2), , ·dx, , +, , C, , (1 + t )2, , A (1 + t )2 + B (1 − t ) (1 + t ) + C (1 − t ), (1 − t ) (1 + t )2, , =, , 1, 4, , 1 = 2C ⇒ C =, , at t = 0,, , , 1 =A+B+C, 1, 1, , 1= +B+, 4, 2, , ⇒ B=, , 1, 4, , 1, 4, , 1, 4, , 1, 2, , 1, =, +, +, (1 − t ) (1 + t )2, (1 − t ), (1 + t ), (1 + t )2, , Thus,, , ∴I =�, , �, , 2 (cos x) (1 + sin x), , 1, 2, 1 = A (1)2 + B (1) (1) + C (1), , , , ∴, , 1, , cos x·dx = 1·dt, , at t = 1,, , =, , =�, , 1 = A (1 + t )2 + B (1 − t ) (1 + t ) + C (1 − t ), , ∴, , =, , 2 cos x + 2 sin x·cos x, , ·dx, , 1, 1, 1, 1, 1, 1, �, �, ·�, ·dt, =, ·, ·dt, =, ·, ·dt, (1 − t ) (1 + t ) (1 + t ), 2, 2 (1 − t ) (1 + t )2, 2 (1 − t 2 ) (1 + t ), 1, , Consider,, , 1, , cos x, cos x, 1, 1, ·� 2, ·dx = ·�, ·dx, 2, 2 cos x (1 + sin x), 2 (1 − sin x) (1 + sin x), , put sin x = t , ∴, =, , =�, , ·dx , , 1, 2, , 1, 4, (1 − t ), , +, , 1, 4, (1 + t ), , +, , 1, 2, (1 + t )2, , ·dt =, , 1 1, 1, 1 (−1), 1, log (1 − t )·, + log (1 + t ) + ·, +c, 2 4, 2 (1 + t ), (−1) 4, , 1, 1, 1 −1, 1, log (1 − t )·, + log (1 + t ) + ·, +c, 4, 2 1+t, (−1) 4, , 1, 1, 1 + sin x, 2, 2, − log (1 − sin x) + log (1 + sin x) −, +c =, log, +c, −, 8, 8, 1 − sin x, 1 + sin x, 1 + sin x, 1, , 2 cos x + sin 2x, , ·dx =, , 1, 1 + sin x, 2, log, −, +c, 8, 1 − sin x, 1 + sin x, , 142
Page 154 :
∴, , I1, , =−, , 1, 1, ·�, ·dx, 3 1+x, , =−, =−, , ∴, , I2, , =, , I3, , =, , 1, ·�, 2, , 1, = ·, 2, , x −x+, 2, , 1, x−, 2, 1, √3, 2, , 1, 1, , 4, 1, 2, , −, , · dx , , 1, , √3, +, 2, , · tan−1, , 1, 2 tan θ − 1, tan−1, √3, √3, , �, , 2, , =, , 2, 1, 1 2 1, (−1) = −, = �, 2, 2, 4, , · dx, , 1, 2 + c , 3, √, 2, , =, , ∴, , 2, , 1, �, coefficient of x, 2, , . . . (VI), , x−, , 1, 2x − 1, tan−1, +c, √3, √3, , I3, , ⸪, , +1, , 4, , =, ∴, , . . . (V), , 1, log ( tan2 θ − tan θ + 1 ) , 6, , 3, 1, ·� 2, ·dx, x −x+1, 6, , 1, = ·�, 2, =, , 1, log ( 1 + tan θ ) , 3, , 1, 2x − 1, 1, ·� 2, ·dx = [ log (x2 − x + 1)], 6, x −x+1, 6, , =, ∴, , 1, [ log (1 + x)], 3, , . . . (VII), , + c , , 1, 1, tan θ + tan3 θ, 1, 2 tan θ − 1, ·dθ = − log ( 1 + tan θ ) + log ( tan2 θ − tan θ + 1 ) +, tan−1, +c, 3, 6, 3, 1 + tan θ, √3, √3, , EXERCISE 3.4, I. Integrate the following w. r. t. x :, 1., , x2 + 2, (x − 1) (x + 2) (x + 3), , 2., , x2, (x2 + 1) (x2 − 2) (x2 + 3), , 144, , 3., , 12x + 3, 6x + 13x − 63, 2
Page 156 :
Let us Remember, ֍, , We can always add arbitarary constant c to the integration obtained :, , d, · g (x) = f (x), ⇒, �f (x) · dx = g (x) + c, dx, f (x) is integrand, g (x) is integral of f (x) with respect to x, c is arbitarary constant., (I), , i.e., , (II), , �f (ax + b) · dx = g (ax + b) ·, , 1, +c, a, , [ f (x)]n + 1, (III) (1) �[ f (x)] · f ' (x)·dx =, + c (2), n+1, n, , (3) �, , f ' (x), , √ f (x), , ·dx = 2 √ f (x) + c, , (IV) (1) �xn · dx =, , xn+1, n+1, , +c, , (2), , (3) �constant (k) · dx = kx + c, , (4), , (7) �sin x · dx = − cos x + c, , (8), , (5) �e x · dx = e x + c, , (6), , (9) �tan x · dx = log (sec x) + c, , (10), , (11) �sec x · dx = log (sec x + tan x) + c (12), = log tan, , , , x π, +, 2 4, , (15) �sec x · tan x · dx = sec x + c , , (19) �, (21) �, , (16), , 1, , · dx = sin−1 x + c , √ 1 − x2, 1, 1 + x2, , �, , (18), , √x, , �cos x · dx = sin x + c, , �cot x · dx = log (sin x) + c, , �cosec x·dx = log (cosec x − cot x) + c, = log tan, , x, 2, , +c, , �cosec2 x · dx = − cot x + c, , �cosec x · cot x · dx = − cosec x + c, �, �, , · dx = sec−1 x + c, , (22), , �, , 146, , ax, +c, log a, , 1, � · dx = log (x) + c, x, , (20), , x · √ x2 − 1, , · dx = 2 √ x + c, , �ax · dx =, , · dx = tan−1 x + c , , 1, , f ' (x), ·dx = log ( f (x)) + c, f (x), , 1, , + c , , (13) �sec2 x · dx = tan x + c (14), (17) �, , �, , −1, · dx = cos−1 x + c, √ 1 − x2, −1, · dx = cot−1 x + c, 1 + x2, , −1, · dx = cosec−1 x + c, 2, x · √x − 1
Page 157 :
(23) �, (25) �, (27) �, (29) �, , 1, x +a, 2, , 2, , 1, a −x, 2, , 2, , · dx =, , x, 1, tan−1, +c, a, a, , · dx =, , a+x, 1, log, +c, a−x, 2a, , 1, 2, , 1, x√ x − a, 2, , (26) �, , · dx = log | x + √ x2 − a2 | + c (28) �, , √x − a, 2, , (24) �, , 2, , · dx =, , (30) �√ a2 − x2 · dx =, (31) �√ a2 + x2 · dx =, , 1, x −a, 2, , 2, , 1, , √a − x, 2, , 2, , 1, , √ x + a2, 2, , (V), , (VI), , x−a, 1, log, +c, x+a, 2a, , · dx = sin−1, , x, +c, a, , · dx = log | x + √ x2 + a2 | + c, , x, 1, sec−1, +c, a, a, , x, x, a2, 2, 2, a, −, x, +, sin−1, +c, √, 2, a, 2, x, a2, 2, 2, a, +, x, +, log ( x + √ x2 + a2 ) + c, √, 2, 2, , x, a2, 2, 2, (32) �√ x − a · dx = √ x − a − log ( x + √ x2 − a2 ) + c, 2, 2, 2, , · dx =, , 2, , d, If u and v are differentiable functions of x then �u·v·dx = u·�v·dx − �, ·u, dx, where u·v follows the L I A T E order., �e x [ f (x) + f ' (x)] · dx = e x · f (x) + c, , (VII) For the integration of type �, , (�v·dx)·dx, , f (x), f (x), · dx, g (x) ≠ 0 where, proper rational function., g (x), g (x), , (i) non-repeated linear factors, (ii) repeated Linear factors and, (iii) product of Linear factor and non-repeated quadratic factor., 1, �, 1, ·dx, 1, �, ·dx, a, sin, x, +, b, cos, x, +, c, (VIII) � 2, ·, dx, 2, ax + bx + c, x + a2, x, Method of completing, put tan, =t, 2, 1, square, � 2, · dx, px + q, x − a2, �, · dx, ax2 + bx + c, 1, �, 1, ·dx, d, � 2, · dx, a sin2 x + b cos2 x + c, px + q = A (ax2 + bx + c) + B, 2, a −x, dx, Divide Nr and Dr by cos2 x, (VIII) �, , 1, , · dx, √ x2 + a2, 1, � 2, · dx, √ x − a2, 1, � 2, · dx, √ a − x2, , �, �, , 1, , √ ax + bx + c, 2, , ·dx, , px + q, ·dx, √ ax2 + bx + c, , 147
Page 158 :
MISCELLANEOUS EXERCISE 3, (I) Choose the correct option from the given alternatives :, (1), , �, , 1 + x + √ x + x2, ·dx =, √x + √1 + x, , (A), (2), , �, , 1, √x + 1+ c, 2, , (B), , 1, x4, �, ·dx, =, f, (x), +, c, ,, then, ·dx =, x + x5, x + x5, , (A) log x − f (x) + c, (3), , �, , 3, 2, (x + 1) 2 + c, 3, , (B) f (x) + log x + c, , 3, , (C) √ x + 1 + c, , (D) 2 (x + 1) 2 + c, , (C) f (x) − log x + c, , (D), , 1, x5 f (x) + c, 5, , log (3x), ·dx =, x log (9x), , (A) log (3x) − log (9x) + c , , (B) log (x) − (log 3)·log (log 9x) + c, , (C) log 9 − (log x)·log (log 3x) + c, , (D) log (x) + (log 3)·log (log 9x) + c, , (4), , �, , sinm x, ·dx =, cosm + 2 x, , (A), (5), , tanm + 1 x, +c, m+1, , � tan (sin−1 x)·dx =, 1, , 2 − 2, , (A) (1 − x ), (6), , �, , If f (x) =, , (B) (1 − x ), , 1, 2, , +c, , x, +c, 2, sin−1 x, , (B) − x cot, , x, +c, 2, , (C), , tanm x, +c, m, , tanm x, (C), +c, √ 1 − x2, , (C) cot, , √1 − x, , , g (x) = esin x, then � f (x)· g (x)·dx =, , · (sin−1 x − 1) + c , , (B) esin, , −1 x, , · (sin−1 x + 1) + c , , (D) esin, , (C) esin, , If �tan3 x·sec3 x·dx =, , (A) (5, 3), , x, +c, 2, , (D) (m + 1) tanm + 1 x + c, , (D) − √ 1 − x2 + c, , (D) x tan, , −1, , 2, , −1 x, , (A) esin, , (8), , +c, , 2, , x − sin x, ·dx =, 1 − cos x, , (A) x cot, (7), , (B) (m + 2) tanm + 1 x + c, , −1 x, , · (1 − sin−1 x) + c, , −1 x, , · (sin−1 x − 1) + c, , 1, 1, secm x −, secn x + c , then (m, n) =, m, n, 1 1, (B) (3, 5), (C), ,, 5 3, , 148, , (D) (4, 4), , x, +c, 2
Page 159 :
(9), , �, , 1, ·dx =, cos x − cos2 x, , (A) log (cosec x − cot x) + tan, (C) log (sec x + tan x) − cot, (10) �, , x, +c, 2, , (D) cos 2x − sin x + c, , (B) −2 √ cot x + c, , (C), , ex, (B) 2 + c, x, , (C), , e x (x − 1), ·dx =, x2, , ex, (A), +c, x, (12) � sin (log x)·dx =, , x, [sin (log x) − cos (log x)] + c, 2, x, (C), [cos (log x) − sin (log x)] + c, 2, (13) � x x (1 + log x)·dx =, , 1, (1 + log x)2 + c, 2, , (A), , (14) � cos, , −, , 3, 7, , (A) log ( sin, (C) −, (15) 2�, , −, , 11, 7, , −, , 4, 7, , x·sin, , 7, −, tan, 4, , 4, 7, , 1, √ cot x + c, 2, , x−, , 1, ex + c, x, , (D) √ cot x + c, , (D) xe −x + c, , x, [sin (log x) + cos (log x)] + c, 2, x, (D), [cos (log x) − sin (log x)] + c, 4, , (A), , (B), , (B) x 2x + c, , (C) x x log x + c, , (D) x x + c, , x·dx =, 4, 4, (B), tan 7 x + c, 7, , x ) + c , , 3, , (D) log ( cos 7 x ) + c, , x + c , , cos2 x − sin2 x, ·dx =, cos2 x + sin2 x, , (A) sin 2x + c, (16) �, , (B) sin 2x − cos x + c, , √ cot x, ·dx =, sin x ·cos x, , (A) 2 √ cot x + c, (11) �, , x, +c, 2, , (B) cos 2x + c, , (C) tan 2x + c, , (D) 2 sin 2x + c, , dx, ·dx =, cos x √ sin2 x − cos2 x, , (A) log ( tan x − √ tan2 x − 1 ) + c, , (B) sin−1 (tan x) + c, , (C) 1 + sin−1 (cot x) + c , , (D) log ( tan x + √ tan2 x − 1 ) + c, , 149
Page 160 :
log x, ·dx =, (log ex)2, x, (A), +c, 1 + log x, (17) �, , (B) x (1 + log x) + c, , (18) � [sin (log x) + cos (log x)]·dx =, , (A) x cos (log x) + c, (19) �, , cos 2x − 1, cos 2x + 1, , (C), , 1, +c, 1 + log x, , (D), , 1, +c, 1 − log x, , (B) sin (log x) + c, , (C) cos (log x) + c, , (D) x sin (log x) + c, , (B) x + tan x + c, , (C) x − tan x + c, , (D) − x − cot x + c, , ·dx =, , (A) tan x − x + c, e 2x + e −2x, ·dx =, ex, 1, (A) e x − 3x + c, 3e, (20) �, , 1, +c, 3e 3x, , (B) e x +, , 1, +c, 3e 3x, , (C) e −x +, , (II) Integrate the following with respect to the respective variable :, x7, 2, (1) (x − 2) √ x, (2), x+1, 3, t, 3 − 2 sin x, (4), (5), 2, (t + 1), cos2 x, cos 7x − cos 8x, (7) cos 3x · cos 2x · cos x, (8), 1 + 2 cos 5x, , (D) e −x − , , 1, +c, 3e 3x, , 3, , (3) (6x + 5) 2, sin6 θ + cos6 θ, sin2 θ · cos2 θ, 1 + sin x, (9) cot −1, cos x, (6), , (III) Integrate the following :, (1), , (1 + log x)3, x, 3, , (2) cot −1 (1 − x + x2), 3, , (4) √ x sec (x 2 )· tan (x 2 ), , (5) log (1 + cos x) − x· tan, , 1, x · sin2 (log x), x2, (6), √ 1 − x6, 1, (9), 2 cos x + 3 sin x, (3), , x, 2, , (7), , 1, (1 − cos 4x) (3 − cot 2x), , (8) log (log x) + (log x)−2, , (10), , 1, x3 · √ x2 − 1, , (11), , 3x + 1, √ − 2x2 + x + 3, , (12) log (x2 + 1), , (13) e 2x · sin x · cos x, , (14), , x2, (x − 1) (3x − 1) (3x − 2), , (15), , 1, sin x + sin 2x, , (16) sec2 x · √ 7 + 2 tan x − tan2 x, , (17), , x+5, x3 + 3x2 − x − 3, , (18), , 1, x · (x5 + 1), , (19), , √ tan x, sin x · cos x, , (20) sec4 x ·cosec2 x, , v, , v, 150, , v
Page 161 :
4. DEFINITE INTEGRATION, Let us Study, •, , Definite integral as limit of sum., , •, , Fundamental theorem of integral calculus., , •, , Methods of evaluation and properties of definite integral., , 4. 1 Definite integral as limit of sum :, In the last chapter, we studied various methods of finding the primitives or indefinite integrals of, b, , given function. We shall now interprete the definite integrals denoted by f (x) dx, read as the integral, a, , from a to b of the function f (x) with respect to x. Here a < b, are real numbers and f (x) is definited on, [a, b]. At present, we assume that f (x) ≥ 0 on [a, b], and f (x) is continuous., b, , f (x) dx is defined as the area of the region, , a, , bounded by y = f (x), X-axis and the ordinates x = a, and x = b. If g (x) is the primitive of f (x) then the area, is g (b) − g (a)., The reason of the above definition will be clear, from the figure 4.1. and the discussion that follows, here. We are using the mean value theorem learnt, earlier. Divide the interval [a, b] into a equal parts, by, , Fig. 4.1, , a = x0 < x1 < x2 < . . . < xn −1< xn = b., Draw the curve y = f (x) in [a, b] and divide the interval [a, b] into n equal parts by, a = x0 < x1 < x2 < . . . < xn −1< xn = b., Divide the region whose area is measured into their strips as above., Note that, the area of each strip can be approximated by the area of a rectangle Mr Mr + 1 QP as, shown in the figure 4.1, which is (xr −1 − xr) × f ( T ) where T is a point on the curve y = f (x) between P, and Q., , 151
Page 162 :
The mean value theorem states that if g (x) is the primitive of f (x),, g (xr + 1) − g (xr) = (xr + 1 − xr) · f (tr), , where xr < tr < xr + 1., , Now we can replace f ( T ) by f (tr) given here and express the approximation of the area of the, shaded region as, , n=1, r=0, , (xr + 1 − xr) · f (tr) where xr < tr < xr + 1., , Now we can replace f ( T ) by f (tr) given here and express the approximation of the area of the, shaed region as, n=1, r=0, , (xr + 1 − xr) · f (tr) =, , n=1, r=0, , g (xr + 1) − g (xr) = g (b) − g (a), , Thus taking limit as n → ∞, = lim, n→∞ � (xr + 1 − xr) · f (tr), , g (b) − g (a), , = lim, n→∞ Sn, b, , = f (x) dx, a, , The word 'to integrate' means 'to find the sum of'. The technique of integration is very useful in, finding plane areas, length of arcs, volume of solid revolution etc..., SOLVED EXAMPLES, Ex. 1 :, , 2, , (2x + 5) dx, , 1, , Solution :, , 2, , b, , 1, , a, , Given, (2x + 5) dx = f (x) dx, , , , f (x) = 2x + 5, , , , ⇒, , a=1;b=2, , f (a + rh) = f (1 + rh), , and, =, 2(1 + rh) + 5 , , b, , n, , a, , r=1, , We know f (x) dx = lim, n→∞, , h · f (a + rh), , 152, , ∴, , b−a, n, , 2−1, n, nh = 1, h=, , , = 2 + 2rh + 5 , , = 7 + 2rh , , h=
Page 166 :
n, , ∴, , r=1, , sin rh, , =, , cos, , h, h, + sin, 2, 2, h, 2 sin, 2, , Now from I,, π⁄2, 0, , sin x · dx = lim, n→∞, , n, r=1, , h · sin rh, , h, h, + sin, 2, 2, = lim, n→∞ h ·, h, 2 sin, 2, π, 1, ⸪, nh =, as n→∞ ⇒ h→0, →0, 4, n, cos, , lim, , cos, , = n→∞, h→0, , h, h, + sin, 2, 2, h, 2·sin, 2, h, , cos 0 + sin 0, =, , 1, 2, 1+0, =, , 1, 2·, 2, π⁄2, , ∴, , =1, , sin x · dx = 1, , 0, , EXERCISE 4.1, I., , Evaluate the following integrals as limit of sum., (1), , 3, , (3x − 4)·dx, , (2), , 1, , (4), , 2, , x ·dx , 2, , 0, , (3x − 1)·dx, 2, , 0, , 4, , (5), , 3, , (3), , 2, 0, , x3·dx , , 1, , 156, , e x·dx
Page 167 :
4.2 Fundamental theorem of integral calculus :, Let f be the continuous function defined on [a, b] and if f (x) dx = g (x) + c, then, , b, , f (x) dx =, , g (x) + c, , a, , b, , Ex. :, , a, , , = [( g (b) + c ) − ( g (a) + c )], , = g (b) + c − g (a) − c, , b, , x3 x2, −, 3, 2, , (x − x) dx =, 2, , 2, , 5, 2, , 53 52, 23 22, −, −, −, 3, 2, 3, 2, , =, , 4, 125 25 8, −, −, +, 2, 3, 2, 3, 117 21 234 − 83, =, −, =, 3, 2, 6, 5, 151, ∴, (x2 − x) dx =, 3, , , = g (b) − g (a), Thus, , 5, , =, , f (x) dx = g (b) − g (a), , a, , 2, , b, , In f (x) dx, , a is called as a lower limit and b is called as an upper limit., , a, , Now let us discuss some fundamental properties of definite integration., These properties are very useful in evaluation of the definite integral., 4.2.1, a, a, , a, , ∴, , Let, , f (x) dx = g (x) + c, , Let, , b, , a, , a, , b, , Property II : f (x) dx = − f (x) dx, , Property I : f (x) dx = 0, , f (x) dx = g (x) + c, , b, , f (x) dx =, , g (x) + c, , a, , ∴ f (x) dx =, , a, , a, , a, , , = [( g (a) + c ) − ( g (a) + c )], , = 0, , g (x) + c, , b, a, , , , =, , [( g (b) + c ) − ( g (a) + c )], , , , =, , g (b) − g (a), , , , =, , − [ g (a) − g (b) ], , , , =, , − f (x) dx, , a, b, , Thus, , b, , a, , f (x) dx = − f (x) dx, , a, , Ex., , 3, , x dx, , =, , 1, , , , =, , x2, 2, , 3, , Ex., , 1, , x dx, , b, , =, , 3, , 1, , 32 12 9, 1, − =, − =4, 2, 2, 2, 2, , , , 157, , =, , x2, 2, , 1, 3, , 12 32, 1, 9, −, =, −, =−4, 2, 2, 2, 2
Page 168 :
b, , b, , a, , a, , Property III : f (x) dx =, Let, , f (t ) dt, , Ex., , b, a, , b, a, , = [( g (b) + c ) − ( g (a) + c )], , , , = g (b) − g (a) . . . . . (i), , b, a, , a, , = [( g (b) + c ) − ( g (a) + c )], , , , = g (b) − g (a) . . . . . (ii), , f (x) dx =, , a, , i.e. definite integration is independent of the, variable., b, , c, , a, , a, , Let, , =, , √3 − 1, 2, , f (x) dx +, , b, , π⁄3, , π⁄3, , cos t · dt, , =, , sin t, , = sin, , f (t ) dt, , Property IV : f (x) dx =, , f (x) dx, , Consider R.H.S. :, , f (x) dx +, , a, , =, , √3 − 1, 2, , where a < c < b i.e. c ∈ [a, b], , f (x) dx, , c, c, , b, , , , = g (x) + c, , , , = [( g (c) + c ) − ( g (a) + c )] + [( g (b) + c ) − ( g (c) + c )], , , , = g (c) + c − g (a) − c + g (b) + c − g (c) − c, , , , = g (b) − g (a), , , , = g (x) + c, , , , b, , =, , a, , + g (x) + c, , c, , b, a, , f (x) dx : L.H.S., , a, , Thus, , b, a, , f (x) dx =, , c, a, , f (x) dx +, , b, , f (x) dx, , π, π, − sin, 3, 6, , √3, 1, −, 2, 2, , c, , b, , where a < c < b, , c, , 158, , π⁄6, , =, , f (x) dx = g (x) + c, c, , π, π, − sin, 3, 6, , π⁄6, , a, , π⁄6, , √3, 1, −, 2, 2, , Ex., , from (i) and (ii), b, , sin x, , =, , b, , , , b, , cos x · dx =, , = sin, , , , R.H.S. : f (t ) dt = g (t ) + c, , π⁄3, , π⁄6, , f (x) dx = g (x) + c, , L.H.S. : f (x) dx = g (x) + c, , π⁄3
Page 170 :
a, , a, , 0, , 0, , Property VI : f (x) dx = f (a − x) dx, Let, , Ex. :, , Consider R.H.S. :, , Let, , f (a − x) dx, , put a − x = t i.e., , a, , =, , f (t ) (−dt ), =, , 0, , f (t ) dt ..., , =, , a, , b, , f (x ) dx, , ..., , 0, , =, , a, , f (x) dx = − f (x) dx, , a, , 0, , b, , =, , as definite, integration is, independent of, the variable., , π⁄4, , π⁄4, , π⁄4, , =, , π⁄4, , π, −x, 4, , π, − tan x, 4, log 1 +, · dx, π, 1 + tan ·tan x, 4, log 1 +, , 1 − tan x, · dx, 1 + tan x, , log, , 1 + tan x + 1 − tan x, · dx, 1 + tan x, , log, , 2, · dx, 1 + tan x, , 0, , [log 2 − log (1 + tan x)] · dx, , 0, , =, , π⁄4, , (log 2) · dx −, , 0, , Thus, , 0, , . . . (i), , tan, , 0, , = L. H. S., , a, , log 1 + tan, , 0, , a, , =, , π⁄4, 0, , = − f (t ) dt, a, , π⁄4, 0, , x=a−t, , As x varies from 0 to a, t varies from a to 0, therefore I =, , log (1 + tan x) · dx, , I =, , − dx = dt ⇒ dx = − dt, 0, , π⁄4, 0, , 0, , ∴, , log (1 + tan x) · dx, , 0, , f (x) dx = g (x) + c, a, , π⁄4, , I = (log 2), , a, , π⁄4, , log (1 + tan x) · dx, , 0, π⁄4, , 1 · dx − I, , . . .by eq. (i), , 0, , f (x) dx = f (a − x) dx, , π⁄4, , 0, , I + I = (log 2) x, 2I = (log 2), ∴, , I =, , 0, , π, −0, 4, , π, (log 2), 8, , Thus, π⁄4, 0, , 160, , log (1 + tan x) · dx =, , π, (log 2), 8
Page 171 :
Property VII :, 2a, , Property VIII :, , a, , a, , a, , 0, , −a, , f (x) dx = f (x) dx + f (2a − x) dx, , 0, , R.H.S. :, , a, , 0, , a, , =0, , 0, , = I1 + I2, , and f (x) odd function if f (− x) = − f (x), , Consider I2 = f (2a − x) dx, , a, , 0, , put 2a − x = t i.e., , x = 2a − t, , I, f (t ) dt, , 2a, , f (t ) dt ..., , 2a, , =, , b, , f (x) dx ..., , ∴ f (x) dx =, 0, , b, , 2a, , =, , b, , f (x) dx = f (t ) dt, , a, , f (x) dx, , a, , a, , 2a, , 0, , 0, , 0, , =, , 2a, , a, , a, , 0, , 0, , −, , 0, , f (−t ) dt, , a, b, , f (−t ) dt ..., , a, , f (x) dx = − f (x) dx, , a, , f (−x) dx ..., , b, , b, b, , f (x) dx = f (t ) dt, , a, , a, , =, , a, 0, a, , a, , f (−x) dx + f (x) dx, 0, , [ f (−x) + f (x)] dx, , 0, , f (x) dx, , If f (x) is odd function then f (−x) = − f (x), hence, a, , f (x) dx : L.H.S, , f (x) dx = 0, , −a, , 0, , Thus,, , 0, , f (x) dx, , , =, , f (x) dx + f (2a − x) dx = f (x) dx +, , 2a, , 0, a, , −a, , 0, , 0, , a, a, , f (−t ) (−dt ) =, , Equation (i) becomes, , a, , from eq. (i), a, , 0, , 0, , b, , a, , 0, a, , =, , a, , f (x) dx = − f (x) dx, , a, , 0, , f (x) dx, , =, , 2a, , =, , 0, , −a, , 2a, , = −, , . . . (i), , ∴ dx = −dt, put x = − t, As x varies from − a to 0, t varies from a to 0, , f (t ) (− dt), a, , a, , f (x) dx + f (x) dx, , −a, 0, , Consider, , As x varies from 0 to 2a, t varies from 2a to 0, a, , 0, , f (x) dx =, , −a, , −1 dx = 1 dt ⇒ dx = − dt, , =, , , if f (x) is odd function, , f (x) even function if f (− x) = f (x), , . . . (i), , a, , I, , 0, , f (x) dx + f (2a − x) dx, , 0, , ∴, , a, , f (x) dx = 2 · f (x) dx , if f (x) even function, , If f (x) is even function then f (−x) = f (x), hence, a, , f (x) dx = f (x) dx + f (2a − x) dx, , f (x) dx, , a, , = 2 · f (x) dx, , −a, , 0, , Hence :, a, , a, , f (x) dx = 2 · f (x) dx , if f (x) even function, , −a, , 0, , =0, , 161, , , if f (x) is odd function
Page 172 :
Ex. :, 1., , π⁄4, , x3 · sin4 x · dx, , −π⁄4, , f (x) = x3 · sin4 x, , Let, , f (−x) = (−x)3 · [sin (−x)]4 = −x3 · [− sin x]4 = −x3 · sin4 x, = −f (x), f (x) is odd function., , , , ∴, , π⁄4, , x3 · sin4 x · dx = 0, , −π⁄4, 1, , 2., , −1, , 1, , x2, · dx, 1 + x2, , Let, , f (−x) =, , =, , 2, , , , =, , 2, , , , =, , 2, , , , =, , 2 x − tan x, , , , =, , , , =, , 2 �(1 − tan−1x) − (0 − tan−1x)�, , , , =, , −1, , x2, f (x) =, 1 + x2, (−x)2, 1 + (−x)2, , , , x2, =, 1 + x2, , , , = f (x), , f (x) is even function., , 1, , ∴, , −1, , SOLVED EXAMPLES, Ex. 1 :, , 3, 1, , 0, 1, 0, 1, 0, , x2, · dx, 1 + x2, 1 + x2 − 1, · dx, 1 + x2, 1−, , 3, 1, , 3, 1, , 1, √2 + x + √x, , √2 + x − √x, ·dx, 2+x−x, , =, , 1 3, =, · (√ 2 + x − √ x )·dx, 2, 1, , 3, , 3, , 1 (2 + x) 2 x 2, ·, −, =, 2, 3, 3, 2, 2, , 3, , 4−π, x2, 2 · dx =, 2, 1+x, , 1, , 1, , 162, , 3, 1, , 3, 3, 3, 3, 1, � (2 + 3) 2 − (3) 2 − (2 + 1) 2 − (1) 2 �, 3, , 3, , ∴, , 0, , π, − 0�, 4, π, 4−π, =, 2 1−, 4, 2, , 3, 3, 3, 3, 1, �5 2 − 3 2 − 3 2 + 1 2 �, 3, 3, 3, 1, =, �5 2 − 2(3) 2 + 1�, 3, , =, , 1, , 2 �1 −, , 3, 3, 1, =, · (2 + x) 2 − (x) 2, 3, , √2 + x − √x, ·dx, √2 + x − √x, , 1, · dx, 1 + x2, −1, , 1, ·dx, √2 + x + √x, , Solution : =, =, , 1, , x2, · dx, 1 + x2, , 3, 3, 1, 1, dx =, 5 2 − 2(3) 2 + 1, 3, √2 + x + √x
Page 173 :
Ex. 2 :, , π⁄2, , Ex. 3 :, , √ 1 − cos 4x · dx, , 0, , Solution : Let I =, , π⁄2, , π⁄2, , cos3 x · dx, , 0, , Solution : Let I =, , √ 1 − cos 4x · dx, , 0, , , I=, √ 2 sin2 2x · dx, , π⁄2, , − cos 2x, = √2 ·, 2, , , , ∴, , π⁄2, , , , =, , 1, 4, , π, π, 1, sin 3 + 3 sin, −, 2, 2, 3, 1, sin 3 (0) + 3 sin (0), 3, , , , =, , 1, 4, , 3π, π, 1, sin, + 3 sin −, 2, 2, 3, 1, sin 0 + 3 sin 0, 3, 1, (− 1) + 3 (1) − 0, 3, , 0, , π, =, · cos 2 − cos 0, 2, 2, √2, = −, · [cos π − cos 0], 2, √2, · (− 1 − 1) = √ 2, = −, 2, , , , √ 1 − cos 4x · dx = √ 2, , π⁄4, , , , =, , 1, 4, , , , =, , 1, 1, 1, − +3 =, 4, 3, 4, , 0, , Solution : Let I =, , π⁄4, 0, , ∴ sec2 x ·dx = 1·dt, π, As x varies from 0 to, 4, t varies from 0 to 1, 1, 1, · dt, =, 2t2 + 4t + 1, 0, 1, ·, =, 2, , 1, , 1, ·, 2, , 1, , 1, ·, 2, , 1, , =, =, , 0, , 0, , 0, , 1, , 1 · dt, t + 2t +, 2, 1, , =, , =, , · dt, 1, t + 2t + 1 − 1 +, 2, 1, · dt, 1 2, 2, (t + 1) −, √2, , 1, ·, 2, , 1, 1, 2, √2, , √2, log, 4, , 2, 8, =, 3, 3, , 2, 3, , 1, (t + 1) −, √2, log, 1, (t + 1) +, √2, √2 t + √2 − 1, √2 t + √2 + 1, , 0, , 1, , 1, , 0, , 0, , =, , √2, √ 2 (1) + √ 2 − 1, √ 2 (0) + √ 2 − 1, log, − log, 4, √ 2 (1) + √ 2 + 1, √ 2 (0) + √ 2 + 1, , =, , √2, 2 √2 − 1, √2 − 1, log, − log, 4, 2 √2 + 1, √2 + 1, , =, , √2, log, 4, , 2 √2 − 1, √2 − 1, ÷, 2 √2 + 1, √2 + 1, , =, , √2, log, 4, , 3 + √2, 3 − √2, , 2, , 2, , cos3 x · dx =, , 0, , sec2 x, · dx, 2 tan2 x + 5 tan x + 1, , put tan x = t, , π⁄2, , ∴, , sec2 x, · dx, 2 tan2 x + 5 tan x + 1, , π⁄2, , =, , π⁄2, , √2, , 1, [ cos 3x + 3 cos x ] · dx, 4, , 1, 1, sin 3x· + 3 sin x, 4, 3, , 0, , Ex. 4 :, , =, , π⁄2, 0, , sin 2x · dx, , 0, , , , , , A, ⸪ 1 − cos A = 2 sin2, 2, , = √2 ·, , cos3 x · dx, , 0, , π⁄2, 0, , π⁄2, , 163
Page 174 :
Ex. 5 :, , 2, 1, , log x, · dx, x2, 2, , 1, ·dx, x2, , Solution : Let I = (log x), 1, , , , , , , 1, = (log x)· 2 ·dx, x, , 2, 1, , 1, d, log x · 2 ·dx·dx, x, 1 dx, , 1, = (log x)· −, x, , 2, , 2, , 2, , 2, , 1, log x, x, , = −, , 1, log x, = −, x, , −, 1, , +, 1, 2, 1, , 2, , −, , 1, , 1, 1, · −, ·dx, x, 1 x, , 1, ·dx, x2, 2, , 1, + −, x, , 1, , 1, 1, log 2 − − log 1, 2, 1, , =, , −, , , , =−, , 1 1, 1, 1, log 2 − 0 − + 1 = − log 2, 2 2, 2, 2, , ∴, , 2, 1, , Ex. 6 :, , log x, · dx, x2, π⁄2, 0, , =, , −, , 1, 1, − −, 2, 1, , , , +, , ⸪ log 1 = 0 , , 1, 1 − log 2, 2, , cos x, · dx, 1 + cos x + sin x, , Solution : Let I, , =, , π⁄2, 0, , , , =, , =, , π⁄2, , 2 cos, , cos, , , , =, , 0, , 2, , x, x, − sin, 2, 2, x, 2 cos, 2, , 0, , π⁄2, , x, x, − sin2, 2, 2, x, x, x, + 2 sin, ·cos, 2, 2, 2, , cos2, , π⁄2, 0, , , , cos x, · dx, 1 + cos x + sin x, , cos, , cos, , · dx, , x, x, + sin, 2, 2, , · dx, , x, x, cos, + sin, 2, 2, , x, x, − sin, 2, 2, x, cos, 2, , · dx =, , π⁄2, 0, , 164, , 1 − tan, , x, 2, , · dx
Page 176 :
Ex. 8 :, , 2, , 2x, , 0, , 2x (1 + 4x ), , Solution : Let I =, , · dx, , 2, , 2x, , 0, , 2x (1 + 4x ), , · dx, , put 2x = t , , ∴ 2x · log 2 ·dx = 1·dt, As x varies from 0 to 2, t varies from 1 to 4, 1, log 2, · dt, t (1 + t 2 ), , 4, , =, , 1, , 4, , =, , 1, ·, log 2, , 4, , =, , 1, ·, log 2, , =, =, , 1, · dt, t (1 + t 2 ), , 1, , 1 + t2 − t2, t (1 + t 2 ), , 1, , =, , 1, ·, log 2, , · dt, , =, , 4, , =, , 1, ·, log 2, 1, ·, log 2, , =, Ex. 9 :, , 1, , 2, , =, , 1, t, −, · dt, t, 1 + t2, , 1, 4, 1, , 4, , 1, 1, · dt −, 2, t, , 1, , 1, , Solution : Let I =, , ∴, , 2t, · dt, 1 + t2, , | 5x − 3 |, , = (5x − 3) for (5x − 3) > 0 i.e. x >, 1, , 3⁄5, −1, , 3, 5, , 1, log 2, 2, , log 1 = 0, 1, 4 √2, · log, log 2, √ 17, , 2, , 2x, , 0, , 2x (1 + 4x ), , · dx =, , 1, 4 √2, · log, (log 2), √ 17, , = log2, , 4 √2, √ 17, , 3, 5, , | 5x − 3 |· dx + | 5x − 3 |· dx , , = − 5, 3, , 3⁄5, , =, , 3⁄5, , x2, 2, 3, 5, , 3⁄5, , − 3x, 5, −, 2, , +, , 5, , −1, , 3, 5, , 2, , x2, 2, , −1, , 1, , − 3x, , 3⁄5, , , , 5, − 3 (−1) −, (−1)2, 2, , 166, , − (5x − 3)· dx +, , 5 2, 3x −, x, 2, , =, +, , 1, , 1, log 17 −, 2, , | 5x − 3 |· dx, , = − (5x − 3) for (5x − 3) < 0 i.e. x <, , 4, , 1, 1, 1, · log 4 − log 17 + log 2, log 2, 2, 2, , , , −1, , =, , log 4 −, , | 5x − 3 |· dx, , −1, , =, , ⸪, , t, 1+t, · dt, −, 2, t (1 + t ) t (1 + t 2 ), 2, , 1, , 1, ·, log 2, , log 1 −, , may be solved by method of partial fraction, 4, , 1, 1, · log (t ) − log (1 + t 2 ), log 2, 2, , 1, 3⁄5, , (5x − 3)· dx, , 3⁄5, , 5 2, +, x − 3x, 2, −1, , 5, (1)2 − 3 (1) −, 2, , 5, 2, , 3, 5, , 1, 3⁄5, 2, , −3, , 3, 5
Page 177 :
9, 5, 9, −, − −3−, 2, 5 10, , =, , 9, 9, 5, 5, 9 9, −, +3+, +, −3− +, = 2, 5 10, 2, 2, 10 5, , =, ∴, , 1, , Ex. 10 :, , π⁄2, , 1, 3, , 1 + tan x, , 0, , Solution : Let I =, π⁄2, , 1+, , 0, , =, , π⁄2, , 3, 3, , 0, , 18 − 9 +25, 5, , = 2, , =, , 34, 5, , · dx, , π⁄2, , 1, 3, , 1 + tan x, , 0, , 1, , 9, 5, 9, −, +, 5 10 2, , 34, 5, , | 5x − 3 |· dx =, , −1, , =, , 9, 5, 9, −3 −, −, 2, 10 5, , +, , · dx, , · dx, , 3, , sin x, , 3, , cos x, 3, , 0, , 0, , I =, , 3, , 3, , cos x + sin x, , a, , π⁄2, 0, , cos x, , a, , By property f (x) dx = f (a − x) dx, , · dx . . . (i), =, , π⁄2, 0, , π, −x, 2, , π, π, cos, − x + 3 sin, −x, 2, 2, 3, , 3, , cos, , sin x, 3, , sin x + cos x, , · dx, , · dx . . . (ii), , adding (i) and (ii), I+I =, , π⁄2, , 3, 3, , 0, , 2I =, , 3, , cos x + sin x, , π⁄2 3, , cos x + sin x, , 3, , cos x + sin x, , 0, , 2I =, , π⁄2, , 3, , π⁄2, , x, , 0, , 1, 3, , 0, , 3, 3, , 0, , sin x, 3, , sin x + cos x, , · dx, , · dx, , 1 · dx, , 1, I =, 2, ∴ , , · dx +, , π⁄2, , 3, , 0, , π⁄2, , cos x, , 1 + tan x, , =, , 1, 2, , π, π, −0 =, 4, 4, , · dx =, , π, , 4, , with the help of the above solved/ illustrative example verify whether the following examples, π, evaluates their definite integrate to be equal to / as, 4, π⁄2, , π⁄2, , π⁄2, , π⁄2, , 1, , · dx ;, 3, 0 1 + cot x, , 0, , sin4 x, · dx ;, sin4 x + cos4 x, , 0, , 0, , sin x, · dx ;, sin x + cos x, 5, cosec 2, , 5, cosec 2, , x+, , x, , 5, sec 2, , 167, , x, , π⁄2, 0, , · dx , , sec x, · dx ;, sec x + cosec x
Page 178 :
Ex. 11 :, , 2, , 8, , (11 − x), , 3, , x2 + (1 − x), , · dx, , 2, , Solution : Let I =, b, , By property, , 2, , 8, , (11 − x), , 3, , x2 + (1 − x), , 2, , · dx , , . . . (i), , b, , f (x) dx = f (a + b − x) dx, , a, , a, , 8, [11− (8 + 3 − x)] 2, [11− (11 − x)] 2, · dx =, · dx, I =, 2, 2, 2, 2, [, 8, +, 3, −, x, ], +, [, 11, −, (8, +, 3, −, x), ], (, 11, −, x, ), +, [, 11, −, (11, −, x), ], 3, 3, 8, , =, , 8, , x2, , 3, , (11 − x)2 + x 2, , · dx , , adding (i) and (ii), 8, , I+I =, , 3, , 2, , 8, , (11 − x), , x2 + (1 + x), , 2, , · dx +, , 3, , x2, , · dx, , (11 − x)2 + x 2, , 8, , (11 − x)2 + x 2, · dx, 2I =, 2, 3 x 2 + (11 − x), 1, I =, 2, 1, I =, 2, ∴ , , 8, 3, , 1 · dx, 8, , x, , =, , 3, , 1, 5, [8 − 3] =, 2, 2, , 2, , 8, , (11 − x), , 3, , x2 + (1 + x), , 2, , Note that : In general , , · dx =, , 5, 2, , b, , f (x), , a, , f (x) + f (a + b − x), , 1, (b − a), 2, , · dx =, , verify the generalisation for the following examples :, 2, , √x, · dx ;, 1 √3 − x + √x, , x3, · dx, 3, 3, (9, −, x), +, x, 2, 7, , , , 1, , 9, , , 4, , x4, , (13 − x), , π⁄3, , , , π⁄6, , 1, 4, , +, , 1, x4, , 1, 1 + √ cosec x, , · dx , , π⁄3, π⁄6, , · dx , , 168, , 1, 1 + √ cot x, , · dx, , ;, , . . . (ii)
Page 183 :
Note that :, To evaluate the integrals of the type, , π⁄2, , sinn x · dx and, , 0, , π⁄2, , cosn x · dx, the results used are known as, , 0, , 'reduction formulae' which are stated as follows :, π⁄2, , sinn x · dx =, , 0, , , π⁄2, , =, , cosn x · dx =, , 0, , (n − 1) (n − 3) (n − 5), 4 2, ·, ·, ···, ,, n, (n − 2) (n − 4), 5 3, , if n is odd., , (n − 1) (n − 3) (n − 5), 3 1 π, ·, ·, ···, · ,, n, (n − 2) (n − 4), 4 2 2, , if n is even., , π⁄2, , π, cos, −x, 2, , 0, , , , =, , π⁄2, 0, , , , =, , π⁄2, , n, , · dx , , n, , [ sin x ] · dx, sinn x · dx, , 0, π⁄2, , sin7 x · dx =, , 0, , (7 − 1) (7 − 3) (7 − 5), ·, ·, 7, (7 − 2) (7 − 4), , , , =, , (7 − 1)·(7 − 3)·(7 − 5), 7·(7 − 2)·(7 − 4), , , , =, , 6 · 4 · 2 16, =, 7 · 5 · 3 35, , π⁄2, , cos8 x · dx =, , 0, , , , =, , , , =, , , , =, , (8 − 1) (8 − 3) (8 − 5) (8 − 7) π, ·, ·, ·, ·, 8, (8 − 2) (8 − 4) (8 − 6) 2, (8 − 1)·(8 − 3)·(8 − 5) ·(8 − 7) π, ·, 2, 8·(8 − 2)·(8 − 4)·(8 − 6), 7·5·3·1 π, ·, 8·6·4·2 2, 35π, 256, , 173, , . . . by property
Page 184 :
Let us Remember, n=1, , ֍, r=0, , (xr + 1 − xr) · f (tr) =, , n=1, r=0, , g (xr + 1) − g (xr) = g (b) − g (a), , Thus taking limit as n → ∞, b, , lim, = lim, n→∞ � (xr + 1 − xr) · f (tr) = n→∞ Sn = f (x) dx, , g (b) − g (a), ֍, , a, , b, , Fundamental theorem of integral calculus : f (x) dx = g (b) − g (a), a, , a, , Property I : f (x) dx = 0, a, b, , a, , a, , b, , Property II : f (x) dx = − f (x) dx, b, , b, , a, , a, , b, , c, , Property III : f (x) dx =, Property IV : f (x) dx =, a, , f (t ) dt, f (x) dx +, , a, , b, , b, , a, , a, , b, , f (x) dx, , where a < c < b i.e. c ∈ [a, b], , c, , Property V : f (x) dx = f (a + b − x) dx, a, , a, , 0, , 0, , Property VI : f (x) dx = f (a − x) dx, Property VII :, , 2a, , a, , a, , f (x) dx = f (x) dx + f (2a − x) dx, , 0, , 0, a, , Property VIII :, , 0, a, , f (x) dx = 2 · f (x) dx, , −a, , , if f (x) even function, , 0, , =, 0, , , if f (x) is odd function, , f (x) even function if f (− x) = f (x) and f (x) odd function if f (− x) = − f (x), ֍, , 'Reduction formulae' which are stated as follows :, π⁄2, , sinn x · dx =, , 0, , , π⁄2, 0, , =, , cos x · dx =, n, , (n − 1) (n − 3) (n − 5), 4 2, ·, ·, ···, ,, n, (n − 2) (n − 4), 5 3, , if n is odd., , (n − 1) (n − 3) (n − 5), 3 1 π, ·, ·, ···, · ,, (n − 2) (n − 4), n, 4 2 2, , if n is even., , π⁄2, 0, , π, cos, −0, 2, , n, , · dx =, , π⁄2, 0, , 174, , n, , [ sin x ] · dx =, , π⁄2, 0, , sinn x · dx
Page 185 :
MISCELLANEOUS EXERCISE 4, (I) Choose the correct option from the given alternatives :, 3, , dx, =, 3, 2 x (x − 1), 208, 1, (A), log, 189, 3, (1), , (2), , π⁄2, 0, , (C) log, , (B), , π−4, 2, , (C) 4 −, , 208, 189, , (D) log, , 189, 208, , 4−π, 2, , π, 2, , (D), , 4+π, 2, , log 5 x, e √ ex, , −1, ·dx =, e +3, x, , 0, , (A) 3 + 2π, (4), , 189, 1, log, 208, 3, , sin2 x·dx, =, (1 + cos x)2, , (A), (3), , (B), , π⁄2, , (B) 4 − π, , (C) 2 + π, , (D) 4 + π, , sin6 x cos2 x·dx =, , 0, , (A), , 7π, 256, , (B), , 3π, 256, , (C), , 5π, 256, , (D), , −5π, 256, , 1, , k, dx, = , then k is equal to, 3, 0 √1 + x − √x, √2, (A) √ 2 (2√ 2 − 2), (B), (2 − 2√ 2 ), 3, (5), , If, , 2, , (6), , 1, , e, , If, , 2√ 2 − 2, 3, , (D) 4√ 2, , 1 1x, e ·dx =, x2, , (A) √ e + 1, (7), , (C), , 2, , (B) √ e − 1, , √e − 1, , (C) √ e (√ e − 1), , (D), , (C) a = −e, b = 2, , (D) a = −e, b = −2, , (C) I1 = 2I2, , (D) I1 = I2, , e, , 1, 1, b, −, ·dx, =, a, +, , then, log x (log x)2, log 2, , (A) a = e, b = −2, e2, , (B) a = e, b = 2, 2, , dx, ex, (8) Let I1 =, and I2 =, ·dx, then, e log x, 1 x, 1, (A) I1 = I2, (B) I1 + I2 = 0, 3, , 175
Page 187 :
(IV) Evaluate the following :, a, , (1), , π⁄2, , If √ x·dx = 2a· sin x·dx then find the value of, 0, , a+1, , 3, , 0, , x·dx., , a, , k, , π, 1, ·dx = . Find k., 2, 16, 0 2 + 8x, , (2), , If, , (3), , If f (x) = a + bx + cx , show that, , 1, 2, , 0, , f (x) =, , v, , 1, 6, , v, , 177, , f (0) + 4 f, , v, , 1, + f (1) ., 2
Page 188 :
5. APPLICATION OF DEFINITE INTEGRATION, Let us Study, •, , Area under the curve, •, , Area bounded by the curve, axis and given lines, , •, , Area between two curves., Let us Recall, , •, , In previous chapter, we have studied definition of, definite integral as limit of a sum. Geometrically, b, , � f (x)·dx gives the area A under the curve y = f (x) with, , a, , f (x) > 0 and bounded by the X−axis and the lines x = a,, , x = b ; and is given by, b, , � f (x) dx = φ (b) − φ (a), , Fig. 5.1, , a, , where � f (x) dx = φ (x), , This is also known as fundamental theorem of integral calculus., We shall find the area under the curve by using definite integral., 5.1 Area under the curve :, For evaluation of area bounded by certain curves, we need to know the nature of the curves and, their graphs. We should also be able to draw sketch of the curves., 5.1.1 Area under a curve :, The curve y = f (x) is continuous in [a, b] and, f (x) ≥ 0 in [a, b]., 1. The area shaded in figure 5.2 is bounded by the curve, y = f (x), X−axis and the lines x = a, x = b and is given by, x=b, , the definite integral � ( y)·dx, x=a, , A = area of the shaded region., b, , A = � f (x)·dx, , Fig. 5.2, , a, , 178
Page 189 :
2. The area A, bounded by the curve x = g (y), Y axis, and the lines y = c and y = d is given by, d, , A = � x·dy, y=c, , y=d, , = � g ( y)·dx, y=c, , Fig. 5.3, SOLVED EXAMPLE, Ex. 1 : Find the area bounded by the curve y = x2, the, Y axis the X axis and x = 3., Solution :, A, , 3, , The required area A = � y·dx, = � x2·dx, 0, , x3, =, 3, Fig. 5.4, , x=0, , 3, , 3, 0, , A = 9 − 0, = 9 sq.units, , 5.1.2 Area between two curves :, Let y = f (x) and y = g (x) be the equations of the two, curves as shown in fig 5.5., Let A be the area bounded by the curves y = f (x), and y = g (x), , , A =, , |A, , 1, , − A2, , |, , where, , A1 = Area bounded by the curve y = f (x), X-axis and, x = a, x = b., Fig. 5.5, , A2 = Area bounded by the curve y = g (x), X-axis and, x = a, x = b., , 179
Page 190 :
The point of intersection of the curves y = f (x) and y = g (x) can be obtained by solving their, equations simultaneously., ∴ The required area , , A=, , SOLVED EXAMPLES, , b, , | � f (x) dx, a, , b, , − � g (x) dx, a, , |, , Ex. 1 : Find the area of the region bounded by the curves y2 = 9x and x2 = 9y., Solution :, , The equations of the curves are, , , , y2 = 9x . . . . . (I) , , and, , x2 = 9y . . . . . (II), , , , Squaring equation (II), , , , x4 = 81y2, , , , x4 = 81 (9x) . . . by (1), , , , x4 = 729 x, , ∴, , x (x3 − 93) = 0, , i.e., , x (x3 − 93) = 0, , ⇒, , x = 0 , , or, , x=9, , From equation (II), y = 0 , , or, , y=9, , ∴, ∴, , Fig. 5.6, , The points of intersection of the curves are (0, 0), (9, 9)., Required area A, , =, , , =, , 9, , 9, , � √9x dx − �, , 0, , 0, , 3, 2, 3 · · x2, 3, , 2 · 9 2 − 27, , , , 54 − 27, , =, , =, , 9, 0, , 1 x3, −, ·, 9 3, , 9, 0, , 3, , =, A, , x2, dx, 9, , 27 sq.units, , Now, we will see how to find the area bounded by the curve y = f (x), X-axis and lines x = a, x = b, if f (x) is negative i.e. f (x) ≤ 0 in [ a, b ]., , 180
Page 191 :
Ex. 2 : Find the area bounded by the curve y = − x2 , X−axis and lines x = 1 and x = 4., Solution :, , Let A be the area bounded by the curve y = − x2 , X−axis and 1 ≤ x ≤ 4., The required area, , A, , 4, , � y dx, , =, , 1, 4, , � − x2 dx, , =, , 1, , , =, , x3, , −, , 3, , 4, 1, , 64 1, +, 3, 3, A, = − 21,, But we consider the area to be positive., =, , Fig. 5.7, , |, , −, , |, , ∴ A = −21 sq.units = 21 square units., Thus, if f (x) ≤ 0 or f (x) ≥ 0 in [ a, b ] then the area enclosed between y = f (x) , X−axis and, , |, , b, , |, , x = a, x = b is � f (x)·dx ., a, , If the area A is divided into two parts A1 and A2 such that, A1 is the part of a ≤ x ≤ t where f (x) ≤ 0 and, A2 is the part of a ≤ x ≤ t where f (x) ≥ 0, then in A1, the required area is below the X−axis, and in A2, the required area is above the X-axis., Now the total area A, , Fig. 5.8, , = A1 + A2, , |, , t, , b, , | | � f (x) dx |, , = � f (x) dx +, a, , t, , Ex. 3 : Find the area bounded by the line y = x, X axis and the lines x = −1 and x = 4., Solution :, , Consider the area A, bounded by straight line y = x , X axis and x = −1, x = 4., From figure 5.9, A is divided into A1 and A2, The required area, , A1, , =, , , =, =, Fig. 5.9, , , , 181, , A1, , =, , 0, , � y dx, , −1, , x, 2, , 2, , 0, , −1, , 0, , = � x dx, −1, , 1, 0−, 2, 1, − square units., 2
Page 192 :
But area is always positive., ∴, , A1 =, , | − 12 |sq.units = 12 square units., , ∴, , 4, , =, , 42, = 8 square units., 2, , Required area A = A1 + A2 =, , 1, 17, + 8 =, sq.units, 2, 2, , x2, A2 = � y dx = � x dx =, 2, 0, 0, 4, , 4, , 0, , Ex. 4 : Find the area enclosed between the X-axis and the curve y = sin x for values of x between, 0 to 2π., Solution : The area enclosed between the curve and the X-axis, consists of equal area lying alternatively above and, below X-axis which are respectively positive and, negative., 1), , Area, , A1, , =, , =, , area lying above the X-axis, π, , � sin x · dx, , 0, , =, , − cos x, , π, 0, , , , =, , − [cos π − cos 0] =, , A1, , =, , 2, , 2), , =, , area lying below the X-axis = � sin x dx = − cos x, , Area, , A2, , =, A2 =, ∴, , Fig. 5.10, , − (−1 − 1), 2π, , π, , − [−1 − (− 1)], , 2π, π, , = [− cos 2π − cos π], , −2, , Total area = A1 + | A2 | = 2 + | (− 2) | = 4 sq.units., , Activity :, Ex. 5 : Find the area enclosed between y = sin x and X-axis between 0 and 4π., Ex. 6 : Find the area enclosed between y = cos x and X-axis between the limits :, π, , 2, , (i), , 0≤x≤, , (ii), , π, ≤x≤π, 2, , , , (iii) 0 ≤ x ≤ π, , 182
Page 193 :
SOLVED EXAMPLES, Ex. 1 : Using integration, find the area of the region bounded by the line 2y + x = 8 , X−axis and the, lines x = 2 and x = 4., Solution :, , The required region is bounded by the lines 2y + x = 8, and x = 2, x = 4 and X−axis., ∴, , y=, , , , 1, (8 − x) and the limits are x = 2, x = 4., 2, Required area = Area of the shaded region, , =, =, , 4, , � y dx, , x=2, 4, , �, , 2, , 1, x2, 8x −, 2, 2, , 4, , =, , 1, 2, , 42, , =, , 5 sq. units., , , =, Fig. 5.11, , 1, (8 − x) dx, 2, , 8·(4) −, , 2, , 2, , − 8·(2) −, , 22, 2, , Ex. 2 : Find the area of the regions bounded by the following curve, the X−axis and the given lines :, (i) y = x2 , x = 1, x = 2 , , (ii), , y2 = 4x , x = 1, x = 4, y ≥ 0, , π, π, ,x=, 2, 2, Let A be the required area, , (iii) y = sin x, x = −, Solution :, , (i) A =, =, =, =, A =, Fig. 5.12, , 183, , 3, , � y dx, , 1, 3, , � x2 dx, , 1, , 1 3, x, 3, , 3, 1, , 1, [27 − 1], 3, 26, sq. units., 3
Page 194 :
(ii) A =, =, =, =, A =, (iii) A =, , 4, , � y dx, , 1, 4, , � 2√ x dx, , 1, , 1, , 4, , 2 � x 2 dx, 1, , 4, , 3, 2, x2, 2·, 3, , 3, 4, 42 − 1, 3, , =, 1, , Fig. 5.13, , 28, sq. units., 3, π⁄2, , y dx, , −π⁄2, , =, , π⁄2, , sin x dx, , −π⁄2, , | sin x · dx |+ | sin x · dx|, =| − cos x, |+| − cos x |, π, π, + | − cos, = | − cos 0 − cos, |, 2, 2, 0, , π⁄2, , =, , −π⁄2, , 0, , π, 2, , 0, , −, , =, A =, , π, 2, , 0, , + cos 0, , |, Fig. 5.14, , | [−1 − 0] + [ 0 + 1 ] = 1 + 1, 2 sq. units., , Ex. 3 : Find the area of the region bounded by the parabola y2 = 16x and the line x = 4 ., Solution :, A =, , y2 = 16x, , Area POCP + Area QOCQ, , =, , 2 (Area POCP), , =, , 2 � y · dx, , =, A =, A =, , y = ± 4 √x, , ⇒, , 4, , 0, 4, , 2 � 4 √ x· dx, 0, , 3, 2, x2, 8·, 3, , 4, , , , 0, , =, , 16, ×8, 3, Fig. 5.15, , 128, sq. units., 3, , 184
Page 195 :
Ex. 4 : Find the area of the region bounded by the curves x2 = 16y, y = 1, y = 4 and the Y-axis, lying in, the first quadrant., Solution : , , Required area =, A =, =, =, , 4, , � x dy, , 1, 4, , � √16 y dy, , 1, , 4, , 4 � √ y · dy, 1, , 2 3, 4·, ·y2, 3, , 4, , , 1, , =, , 8, ×[8−1], 3, , A =, , 56, sq. units., 3, , Fig. 5.16, x2 y2, Ex. 5 : Find the area of the ellipse 2 + 2 = 1., a, b, , Solution : By the symmetry of the ellipse, required area of the ellipse is 4 times the area of the region, OPQO. For this region the limit of integration are x = 0, and x = a., x2 y2, From the equation of ellipse 2 + 2 = 1, a, b, 2, 2, y, x, =, 1, −, b2, a2, a2 − x2, y2 = b2 ·, a2, b, y =, · √ a2 − x2, , In first quadrant, y > 0, a, Fig. 5.17, , , A, , =, , a, , 4 � y dx, a, , =, , �, , 0, , x=0, , b, · √ a2 − x2 dx, a, , x, x, a2, 4b, 2, 2, ·, sin−1, =, √a − x +, a, 2, a, a, , , , =, A, , =, , 4b a π, ·, · −0, 2 2, a, 2, , a, 0, , πab sq. units, , 185, , a, 0
Page 197 :
Ex. 8 : Find the area of sector bounded by the circle x2 + y2 = 16 and the line y = x in the first quadrant., Solution :, , Required area A = A (∆OCB) + A (region ABC), To find,, , =, =, , x2 + y2 = 16 . . . (I), , and line , , y=x, , Substitute (II) in (I), x2 + x2 = 16, 2x2 = 16, x2 = 8, x = ± 2√ 2 ,, The point of intersection is B (2√ 2, 2√ 2), , Fig. 5.20, , A =, , The point of intersection of, , 2√2, , 0, , 0, , 2√2, , � x · dx + � √16 − x · dx, , =, , 2, , 1 2, x, 2, , 2√2, 0, , x, x, 16, +, sin−1, √ 16 − x2 +, 2, 4, 2, , . . . (II), , y = ± 2√ 2, , 4, 2√2, , 2√ 2, 1, 1, · (2√ 2)2 + 8 sin−1 1 −, √ 8 + 8 sin−1, 2, 2, 2, 4+8·, , π, π, −4− 8·, 4, 2, , Note that, the required area is, , ∴, , A = 2π sq. units., , 1, times the area of the circle given., 8, EXERCISE 5.1, , (1) Find the area of the region bounded by the, following curves, X- axis and the given lines:, , (2) Find the area of the region bounded by the, parabola :, , (i), , y = 2x, x = 0, x = 5, , (i), , y2 = 16x and its latus rectum., , (ii), , x = 2y, y = 0, y = 4, , (ii), , y = 4 − x2 and the X-axis, , (iii) x = 0, x = 5, y = 0, y = 4, (iv) y = sin x, x = 0, x =, (v), , xy = 2, x = 1, x = 4, , (3) Find the area of the region included between:, , π, 2, , (i), , y2 = 2x, line y = 2x, , (ii), , y2 = 4x, line y = x, , (vi) y2 = x, x = 0, x = 4, , (iii) y = x2 and the line y = 4x, , (vii) y2 = 16x and x = 0, x = 4, , (iv) y2 = 4ax and the line y = x, (v), , 187, , y = x2 + 3 and the line y = x + 3
Page 198 :
Let us Remember, ֍, , The area A, bounded by the curve y = f (x), X-axis and the lines x = a and x = b is given by, b, , x=b, , a, , x=a, , A = � f (x)·dx = � f ( x)·dx, , If the area A lies below the X-axis, then A is negative and in this case we take | A |., , ֍, , The area A of the region bounded by the curve x = g ( y), the Y axis, and the lines y = c and, y = d is given by, d, , A= �, , y=c, , ֍, , y=d, , f (x)·dx = � g ( y)·dx, y=c, , Tracing of curve :, (i), , X-axis is an axis of symmetry for a curve C, if (x, y) ∈ C ⇔ (x, −y) ∈ C., , (ii), , Y-axis is an axis of symmetry for a curve C, if (x, y) ∈ C ⇔ (−x, y) ∈ C., , (iii) If replacing x and y by −x and −y respectively, the equation of the curve is unchanged, then the curve is symmetric about X-axis and Y-axis., MISCELLANEOUS EXERCISE 5, (I) Choose the correct option from the given alternatives :, (1), , The area bounded by the region 1 ≤ x ≤ 5 and 2 ≤ y ≤ 5 is given by, , (A) 12 sq. units, , (B) 8 sq. units, , (C) 25 sq. units, (D) 32 sq. units, 1, (2) The area of the region enclosed by the curve y = , and the lines x = e, x = e2 is given by, x, 3, 5, 1, sq. unit, (C), sq. units, (D), sq. units, (A) 1 sq. unit, (B), 2, 2, 2, The area bounded by the curve y = x3 , the X-axis and the lines x = − 2 and x = 1 is, 15, 17, 15, sq. units, (C), sq. units, (D), sq. units, (A) − 9 sq. units, (B) −, 4, 4, 4, (3), , The area enclosed between the parabola y2 = 4x and line y = 2x is, 1, 1, 2, sq. units, (B), sq. units, (C), sq. units, (A), 3, 4, 3, (4), , (5), , (D), , 3, sq. units, 4, , The area of the region bounded between the line x = 4 and the parabola y2 = 16x is, , (A), , 128, sq. units, 3, , (B), , 108, sq. units, 3, , 188, , (C), , 118, sq. units, 3, , (D), , 218, sq. units, 3
Page 199 :
(6), , The area of the region bounded by y = cosx,Y-axis and the lines x = 0, x = 2π is, , (A) 1 sq. unit, (7), , 31, sq. units, 3, , (D) 4 sq. units, , (B), , 32, sq. units, 3, , (C), , 32√2, 3, , sq. units, , (D), , 16, sq. units, 3, , The area under the curve y = 2√x , enclosed between the lines x = 0 and x = 1 is, , (A) 4 sq. units, (9), , (C) 3 sq. units, , The area bounded by the parabola y2 = 8x the X-axis and the latus rectum is, , (A), (8), , (B) 2 sq. units, , (B), , 3, sq. units, 4, , (C), , 2, sq. units, 3, , (D), , 4, sq. units, 3, , The area of the circle x2 + y2 = 25 in first quadrant is, , (A), , 25π, 3, , sq. units, , (B) 5π sq. units, , (C) 5 sq. units, , x2 y2, +, = 1 is, a2 b2, π, (B) πab sq. units, (C), sq. units, ab, , (D) 3 sq. units, , (10) The area of the region bounded by the ellipse, (A) ab sq. units, , (D) πa2 sq. units, , (11) The area bounded by the parabola y2 = x and the line 2y = x is, (A), , 4, sq. units, 3, , (B) 1 sq. units, , (C), , 2, sq. units, 3, , (12) The area enclosed between the curve y = cos 3x , 0 ≤ x ≤, (A), , 1, sq. units, 2, , (B) 1 sq. units, , (C), , (D), , 1, sq. units, 3, , π, and the X-axis is, 6, , 2, sq. units, 3, , (D), , 1, sq. units, 3, , (13) The area bounded by y = √ x and line x = 2y + 3, X-axis in first quadrant is, 34, sq. units, 3, x y, x2 y2, (14) The area bounded by the ellipse 2 + 2 = 1 and the line + = 1 is, a, b, a b, πab ab, (A) π ab − 2 ab, (B), −, (C) π ab − ab, 4, 2, , (A) 2√ 3 sq. units, , (B) 9 sq. units, , (C), , (15) The area bounded by the parabola y = x2 and the line y = x is, 1, 1, 1, (B), (C), (A), 3, 6, 2, , (D) 18 sq. units, , (D) πab, , (D), , 1, 12, , (D), , 4, 3, , (16) The area enclosed between the two parabolas y2 = 4x and y = x is, (A), , 8, 3, , (B), , 32, 3, , (C), , 189, , 16, 3
Page 200 :
(17) The area bounded by the curve y = tan x, X-axis and the line x =, (A), , 1, log 2, 3, , (B) log 2, , (C) 2 log 2, , π, is, 4, (D) 3·log 2, , (18) The area of the region bounded by x2 = 16y, y = 1, y = 4 and x = 0 in the first quadrant, is, (A), , 7, 3, , (B), , 8, 3, , (C), , 64, 3, , (D), , 56, 3, , (19) The area of the region included between the parabolas y2 = 4ax and x2 = 4ay, (a > 0) is given by, 16 a2, (A), 3, , 8 a2, (B), 3, , 4 a2, (C), 3, , 32 a2, (D), 3, , (20) The area of the region included between the line x + y = 1 and the circle x2 + y2 = 1 is, (A), , π, −1, 2, , (B) π − 2, , (C), , π 1, −, 4 2, , (D) π −, , 1, 2, , (II) Solve the following :, (1), , , Find the area of the region bounded by the following curve, the X-axis and the given lines, (i) 0 ≤ x ≤ 5, 0 ≤ y ≤ 2 , , (ii), , y = sin x , x = 0, x = π , , (2), , Find the area of the circle x2 + y2 = 9, using integration., , (3), , Find the area of the ellipse, , (4), , Find the area of the region lying between the parabolas., , (iii) y = sin x , x = 0, x =, , π, 3, , x2 y2, +, = 1 using integration., 25 16, , (i) y2 = 4x and x2 = 4y (ii), , 4y2 = 9x and 3x2 = 16y , , (iii) y2 = x and x2 = y, , (5), , Find the area of the region in first quadrant bounded by the circle x2 + y2 = 4 and the x axis, and the line x = y√ 3 ., , (6), , Find the area of the region bounded by the parabola y2 = x and the line y = x in the first, quadrant., , (7), , Find the area enclosed between the circle x2 + y2 = 1 and the line x + y = 1, lying in the first, quadrant., , (8), , Find the area of the region bounded by the curve ( y − 1)2 = 4 (x + 1) and the line y = (x − 1)., , (9), , Find the area of the region bounded by the straight line 2y = 5x + 7, X−axis and x = 2, x = 5., , (10) Find the area of the region bounded by the curve y = 4x2, Y-axis and the lines y = 1, y = 4., , v, , v, 190, , v
Page 201 :
6. DIFFERENTIAL EQUATIONS, Let us Study, •, , Differential Equation, , •, , Order and degree of differential equation, , •, , Formation of differential equation, , •, , Solution of differential equation, , •, , Types of differential equation., , •, , Application of differential equation., , Let us Recall, •, , The differentiation and integration of functions and the properties of differentiation and integration., Let us Learn, , 6.1.1 Introduction :, In physics, chemistry and other sciences we often have to build mathematical models which involves, differential equations. We need to find functions which satisfy those differential equations., 6.1.2 Differential Equation :, Equation which contains the derivative of a function is called a differential euqation. The following, are differential equations., dy, dw, d2 y, d2 w, 2, (i), = cos x , (ii), +, k, y, =, 0 , (iii), − x2, +w=0, 2, 2, dx, dx, dx, dx, (iv), (v), , d2 y, dt2, d3 y, dx, , 3, , +, , d2 x, dt2, , +x, , = x, here x and y are functions of 't '., , dy, − 4xy = 0, here x is a function of y., dx, , (vi), , r, , dr, + cos θ = 5, dθ, , 6.2 Order and degree of the differential equation :, The order of a differential equation is the highest order of the derivative appearing in the equation., The degree of differential equation is the power of the highest ordered derivative present in the, equation. To find the degree of the differential equation, we need to have a positive integer as the index, of each derivative., , 191
Page 206 :
Ex. 4 : A particle is moving along the X-axis. Its acceleration at time t is proportional to its velocity at, that time. Find the differential equation of the motion of the particle., Solution : Let s be the displacement of the particle at time 't'., Its velocity and acceleration are, , ds, d2 s, and 2 respectively. , dt, dt, , , , ds, d2 s, Here 2 ∝, dt, dt, , , , ds, d2 s, =, k, ,, dt, dt2, , ∴, , (where k is constant ≠ 0), , is the required differential equation., EXERCISE 6.2, (1) Obtain the differential equations by eliminating arbitrary constants c1 , c2 , A and B., (i), , x3 + y3 = 4ax, , (ii), , Ax2 + By2 = 1, , (iii) y = A cos (log x) + B sin (log x), , (iv), , y2 = (x + c)3, , (v), , (vi), , ( y − a)2 = 4 (x − b), , y = Ae5x + Be−5x, , (vii) y = a +, , a, x, , (viii) y = c1 e 2x + c2 e 5x, , (ix) c1 x 3 + c2 y 2 = 5, , (x), , y = e−2x (A cos x + B sin x), , (2) Form the differential equation of family of lines having intercepts a and b on the co-ordinate axes, respectively., (3) Find the differential equation of all parabolas having length of latus rectum 4a and axis is parallel, to the X-axis., (4) Find the differential equation of an ellipse whose major axis is twise its minor axis., (5) Form the differential equation of family of lines parallel to the line 2x + 3y + 4 = 0, (6) Find the differential equations of all circles having radius 9 and centre at point A (h, k)., (7) Form the differential equation of all parabolas whose axis is the X-axis., , 196
Page 207 :
6.4 Solution of differential equation :, Verify that, y = a sin x and y = b cos x, are solutions of the differential equation, where a and b are any constants., Also y = a sin x + b cos x is a solution of the equation., Here sin x and cos x are particular solutions where as a sin x + b cos x is the general solution which, describes all possible solutions., A solution which can be otained from the general solution by giving particular values to the, arbitarary constants is called a particular solution. , Therefore the differential equation has infinitely many solutions., SOLVED EXAMPLES, Ex. 1 : Verify that : y sec x = tan x + c, , Ex. 2 : Verify that : y = log x + c, , is a solution of the differential equation, , is a solution of the differential equation, , dy, + y tan x = sec x., dx, , x, , Solution :, , Solution :, , Here, , y sec x = tan x + c, , Differentiate w. r. t. x, we get, y sec x tan x + sec x, ∴, , d2 y, dx2, , +, , dy, = 0., dx, , Here, , y = log x + c, , Differentiate w. r. t. x, we get, dy 1, =, dx x, , dy, = sec2 x, dx, , dy, + y tan x = sec x, dx, , ∴ x, , Hence y sec x = tan x + c, , dy, =1, dx, , Differentiate w. r. t. x, we get, , is a solution of the differential equation, , x, , dy, + y tan x = sec x, dx, , ∴ x, , d2 y, dx2, d2 y, dx2, , +, , dy, ×1=0, dx, , +, , dy, =0, dx, , y = log x + c is the solution of, x, , 197, , d2 y, dx2, , +, , dy, = 0., dx
Page 209 :
(ii), , dx x log x, =, t, dt, , ∴, , dx, dt, =, x log x, t, Integrating both sides, we get, , ∴, , �, , dx, dt, =�, x log x, t, , log ( log x ) = log ( t ) + log c, , ∴, , log ( log x ) = log ( tc ), , ∴, , log x = ct, , ∴, , e ct = x, , Ex. 2 : Find the particular solution with given initial conditions :, π, dy, = e 2ycos x when x = , y = 0 , 6, dx, Solution :, dy, (i), = e 2ycos x, dx, (i), , ∴, , dy, = cos x·dx, e 2y, , ∴, , e −2y·dy = cos x·dx, , (ii), , y − 1 x − 1 dy, +, ·, = 0, when x = y = 2, y + 1 x + 1 dx, , (ii), , y − 1 x − 1 dy, +, ·, =0, y + 1 x + 1 dx, , ∴, , x+1, y+1, ·dx +, ·dy = 0, x−1, y−1, , ∴, , Integrating both sides, we get, , ∴, ∴, , ∴, ∴, , ∴, ∴, ∴, , �e −2y·dy = �cos x·dx, , ∴, , e −2y, = sin x + c, . . . (I), −2, π, When x = , y = 0. So eq. (1), becomes, 6, , (x − 1) + 2, x−1, 1+, , ·dx +, , ( y − 1) + 2, y−1, , ·dy = 0, , 2, 2, ·dx + 1 +, ·dy = 0, x−1, y−1, , Integrating , we get, , π, 1 1, e0, = sin + c ∴ − = + c, 6, 2 2, −2, 1 1, − − =c, ∴ c = −1, 2 2, (Given initial condition determines the value, of c), Put in eq. (1), we get, , �dx + 2 �, , dx, dy, + �dy + 2 �, =0, x−1, y−1, , ∴, , x + 2 log ( x − 1 ) + y + 2 log ( y − 1 ) = c, , ∴, , x + y + 2 log [(x − 1) ( y − 1)] = c, , . . . (I), , When x = 2, y = 2. So eq. (I), becomes, , e −2y, = sin x − 1, −2, − e −2y = 2sin x − 2, 2y, , e (2sin x − 2) + 1 = 0 is the required particular, solution., , 199, , ∴, , 2 + 2 + 2 log [(2 − 1) (2 − 1)] = c, , ∴, , 4 + 2 log (1 × 1) = c, , ∴, , 4 + 2 log 1 = c, , ∴, , 4 + 2 (0) = c, , ∴, , c=4, , ∴, , x + y + 2 log [ (x − 1) ( y − 1)] = 4 is required, particular solution., , Put in eq. (I), we get
Page 214 :
6.4.2 Linear Differential Equation :, The differential equation of the type,, , dy, + Py = Q (where P, Q are functions of x.), dx, , is called linear differential equation., ∫Pdx, , To get the solution of equation, multiply the equation by e, , , which is helping factor here., , We get,, , Note that,, ∴, ∴, Hence,, , dy, + Py = Q·e∫Pdx, dx, d, dy, [, y·e∫Pdx ] =, + y·P · e∫Pdx, dx, dx, d, [ y·e∫Pdx] = Q·e∫Pdx, dx, , e, , ∫Pdx, , �Q·e∫Pdx ·dx = y·e∫Pdx, , y·e∫Pdx = �Q·(e∫Pdx) dx + c, , is the solution of the given equation, , Here e∫Pdx is called the integrating factor. (I.F.), Note :, , For the linear differential equation., dx, + py = Q, (where P, Q are constants or functions of y) the general solution is, dy, x (I.F.) = �Q·(I.F.) dy + c , where I.F. (integrating factor) = e∫Pdy, , SOLVED EXAMPLES, Ex. 1:, , Solve the following differential equations :, dy, dy, + y = e−x , (ii) x sin, + (x cos x + sin y) = sin x, (i), dx, dx, , (iii) (1 + y2) dx = (tan−1 y − x) dy, Solution :, (i), , dy, + y = e−x , dx, , . . . (I), , eq. (II) becomes,, , This is linear differential equation of the form, dy, + Py = Q where P = 1, Q = e−x, dx, , ∴, ∴, , It's Solution is, y (I.F.) = �Q·(I.F.) dx + c, , where, , ∴, , . . . (II), , ∴, , I.F. = e∫Pdx = e∫dx = ex, , 204, , y·ex = �e−x × ex·dx + c, y·ex = �e−x + x·dx + c, , y·ex = �e0·dx + c, , y·ex = �dx + c, , y·ex = x + c is the general solution.
Page 215 :
(ii) x sin x, , dy, + (x cos x + sin x) y = sin x, dx, , (iii) (1 + y2) dx = (tan−1 y − x) dy, , divide by x sin x, we get, 1, 1, dy, + cot x +, y=, x, x, dx, , ∴, . . . (I), , ∴, , It is the linear differential equation of the type, , This is linear differential equation of the type, , 1, where, P = cot x + ,, x, 1, Q =, x, dy, + Py = Q, dx, , dx, 1, tan−1 y, + Px = Q where P =, ,Q=, dy, 1 + y2, 1 + y2, Its solution is , , Its solution is, y (I.F.) = �Q·(I.F.) dx + c, , where, , I.F. = e, , ∫Pdx, , ∫(cot x +, , =e, , x (I.F.) = �Q·(I.F.) dy + c, , . . . (II), , where, , 1, ) dx, x, , dx, x, , , , I.F. = e∫cot x dx + ∫, , , , I.F. = elog | sin x | + log x, , , , I.F. = x sin x, , ∴, , eq. (II) becomes,, 1, y·x sin x = � × x sin x·dx + c, x, xy·sin x = − cos x + c, , ∴, , xy·sin x + cos x = c is the general solution., , dx (tan−1 y − x), =, dy, (1 + y2), dx, 1, tan−1 y, +, x, =, dy, 1 + y2, 1 + y2, , , , . . . (II), , 1, , I.F. = e∫Pdy = e∫ 1 + y, , 2, , dy, , −1 y, , I.F. = etan, , eq. (II) becomes,, tan−1 y, , x·e, , =�, , tan−1 y, 1+y, , 2, , −1, , ·etan y·dy + c . . . (III), , tan−1 y = t, , in R.H.S. Put, , differentiate w. r. t. x, we get, dy, = dt, 1 + y2, , ∴, eq. (III) becomes, −1 y, , x·etan, , = �t·et·dt + c, , = t�et·dt − �[1× et ] dt + c, , = t·et − �et·dt + c, = t·et − et + c, −1 y, , x·etan, , 205, , −1, , −1 y, , = tan−1 y·etan y− etan, c, , ∴, , x = tan−1 y − 1 +, , ∴, , x + 1 − tan y = c·e− tan, −1, , +c, , tan−1 y, , e, , −1 y, , is the solution.
Page 217 :
(ix) ydx + (x − y2) dy = 0, (xi) (1 + x2), , (x), , (1 − x2), , dy, −1, + y = etan x, dx, , 1, dy, + 2xy = x (1 − x2) 2, dx, , (2), , Find the equation of the curve which passes through the origin and has slope x + 3y − 1 at any point, (x, y) on it., , (3), , Find the equation of the curve passing through the point, , 3, , √ 2 having slope of the tangent to, √2, , 4x, ., 9y, The curve passes through the point (0, 2). The sum of the co-ordinates of any point on the curve, exceeds the slope of the tangent to the curve at that point by 5. Find the equation of the curve., , the curve at any point (x, y) is −, (4), (5), , If the slope of the tangent to the curve at each of its point is equal to the sum of abscissa and the, product of the abscissa and ordinate of the point. Also the curve passes through the point (0, 1)., Find the equation of the curve., , 6.5 Application of differential Equations :, There are many situations where the relation in the rate of change of a function is known. This gives, a differential equation of the function and we may be able to solve it., 6.5.1 Population Growth and Growth of Bacteria :, It is known that a number of bacteria in a culture increase with time. It means there is growth in the, number of bacteria. It the population P increases at time t then the rate of change of P is proportional to, the population present at that time., dP, , ∴, ∝P, dt, , , ∴, , dP, = k·P ,, dt, , , , ∴, , dP, = kdt, P, , (k > 0), , on integrating, , , , dP, = �kdt, P, , , , ∴, , , , ∴, , log P = kt + c1, , , , ∴, , P = c·ekt, , �, , where c = ec, , 1, , which gives the population at any time t., , 207
Page 218 :
SOLVED EXAMPLES, Ex. 1 : The population of a town increasing at, a rate proportional to the population at that, time. If the population increases from 40, thousands to 60 thousands in 40 years, what, will be the population in another 20 years., , Ex. 2 : Bacteria increase at the rate proporational, to the number of bacteria present. If the, original number N doubles in 3 hours, find, in how many hours the number of bacteria, will be 4N?, , 3, = 1·2247 ., 2, , Given, , Solution : Let x be the number of bacteria at time t., Since the rate of increase of x is proporational, x, the differential equation can be written as :, dx, = kx , dt, where k is constant of proportionality., , Solution : Let P be the population at time t. Since, rate of increase of P is a proportional to P, itself, we have,, dP, = k·P, . . . (1), dt, where k is constant of proportionality., , Solving this differential equation we have, x = c1·ekt, where c1 = ec, , Solving this differential equation, we get, kt, , Given that x = N when t = 0, , c, , P = a·e , where a = e . . . (2), , ∴, , Initially P = 40,000 when t = 0, ∴, , ∴, , From equation (2), we have, , ∴, , c1 = N, , 40,000 = a·1, , ∴, , x = N·ekt, , ∴ a = 40,000, , P = 40,000·ekt, , . . . (3), , ∴, , From equation (2), we have, , Again given that P = 60,000 when t = 40, , 2N = N·e3k, , From equation (3),, , e3k = 2, , 60,000 = 40,000·e40k, , Now we have to find t, when x = 4 N, , 3, . . . (4), 2, Now we have to find P when t = 40 + 20, = 60 years, From equation (3), we have, P, , ∴, , kt, , 3k, , i.e. 4 = e = (e, ∴, , 3, , ∴, , = 40,000·e60k= 40,000 (e40k ) 2, , 3 2, = 40,000, = 73482, 2, Required population will be 73482., , ∴, , 208, , . . . (3), , From equation (2), we have, 4 N = N·ekt, , 3, , ∴, , . . . (2), , Again given that x = 2N when t = 3, , e40k =, , ∴, , From equation (1) we get, N = c1·1, , eq. (2) becomes, ∴, , . . . (1), , t, 3, 2, , t, 3, ), , 2 =, . . . by eq. (3), t, =2, 3, t=6, Therefore, the number of bacteria will be 4N, in 6 hours., 2
Page 219 :
6.5.2 Radio Active Decay :, We know that the radio active substances (elements) like radium, cesium etc. disintegrate with time., It means the mass of the substance decreases with time., The rate of disintegration of such elements is always proportional to the amount present at that time., If x is the amount of any material present at time t then, dx, , = − k·x, dt, where k is the constant of proportionality and k > 0. The negative sign appears because x decreases, as t increases., Solving this differential equation we get, x = a·ekt, , where a = ec (check!) . . . (1), , If x0 is the initial amount of radio active substance at time t = 0, then from equation (1), x0 = a·1, , ∴, a = x0, , ∴, x = x0 e−kt, , . . . (2), , This expression gives the amount of radio active substance at any time t., Half Life Period :, Half life period of a radio active substance is defined as the time it takes for half the amount/mass, of the substance to disintegrate., Ex. 3 : Bismath has half life of 5 days. A sample originally has a mass of 800 mg. Find the mass, remaining after 30 days., Solution : Let x be the mass of the Bismath present at time t., dx, Then, = − k·x , where k > 0, dt, Solving the differential equation, we get, ∴ From equation (2), we have, x = c·e−kt , , . . . (1), , where c is constant of proporationality., Given that x = 800, when t = 0, , ∴, , 400 = 800 e−5k, 400 1, e−5k =, =, . . .(3), 800 2, Now we have determine x, when t = 30,, , ∴, , From equation (2), we have, , using these values in euqation (1), we get, 800 = c·1 = c, ∴, , x = 800 e−30k = 12·5 (verify !), . . . (2), Since half life is 5 days, we have x = 400, ∴ The mass after 30 days will be 12·5 mg., when t = 5,, Now let us discuss another application of differential equation., x = 800 e−kt, , 209
Page 220 :
6.5.3 Newton's Law of Cooling :, Newton's law of cooling states that the rate of change of cooling heated body at any time is, proporational to the difference between the temperature of a body and that of its surrounding medium., Let θ be the temperature of a body at time t and θ0 be the temperature of the medium., dθ, is the rate of change of temperature with respect to time t and θ - θ0 is the difference of, Then, dt, temperature at time t. According to Newton's law of cooling., dθ, , ∴ , ∝ (θ - θ0), dt, dθ, , ∴ , = -k (θ - θ0) , . . . (1), dt, where k is constant of proportionality and negative sign indicates that difference of temperature is, decreasing., dθ, Now , = -k (θ - θ0), , dt, dθ, , ∴ , = -k dt, (θ - θ0), ∴Integrating and using the initial condition viz., , , ∴ , , θ = θ1 , , , , ∴ , , θ = θ0 + (θ1 - θ0) e−kt (verify), , when t = 0, we get, . . . (2), , Thus equation (2) gives the temperature of a body at any time t., Ex. 4 : Water at 100°c cools in 10 minutes to 88°c in a room temperature of 25°c. Find the temperature, of water after 20 minutes., Solution : Let θ be the temperature of water at time t. Room temperature is given to be 25°c. Then, according to Newton's law of cooling. we have, ∴ From equation (1) we have, dθ, ∝ (θ - 25) , dt, θ = 25 + 75·e−20k, dθ, 2, = -k (θ - 25),, where k > 0, = 25 + 75 (e−20k), dt, After integrating and using initial condition., dy 2, −kt, . . . by (2), = 25 + 75, We get θ = 25 + 75·e , . . . (1), dx, But given that θ = 88°c when t = 10, , ∴, , 75 × 21 × 21, 25 × 25, 1323, = 25 +, = 77·92, 25, Therefore temperature of water after 20, minutes will be 77·92°c., , , , From equation (1) we get, 88 = 25 + 75·e−10k, , ∴, , 63 21, =, . . . (2), 75 25, Now we have to find θ, when t = 20,, , 63 = 75·e−10k ∴ e−10k =, , 210, , =, , 25 +
Page 221 :
6.5.4 Surface Area :, Knowledge of a differential equation is also used to solve problems related to the surface area. We, consider the following examples :, Ex. 5 : Water is being poured into a vessel in the form of an inverted right circular cone of semi vertical, angle 45°c in such a way that the rate of change of volume at any moment is proporational to the, area of the curved surfaces which is wet at that moment. Initially, the vessel is full to a height of , 2 cms. And after 2 seconds the height becomes 10 cm. Show that after 3.5 seconds from that start,, the height of water will be 16 cms., Solution : Let the height of water at time t seconds be h cms., , Fig. 6.2, , We are given that initial height is 2 cms. and after 2 seconds, the height is 10 cms., ∴, , h = 2 when t = 0, , . . . (1), , and h = 10 when t = 2, , . . . (2), , Let v be the volume, r be the radius of the water surface and l be that slant height at time t seconds., ∴, , Area of the curved surface at this moment is πrl., But the semi vertical angle is 45°., tan 45° =, , r, =1, h, , , , ∴, , , , ∴ , , r, , = h, , and, , l2, , = r2 + h2 = 2h2, , ∴ , , l, , = √2 h, , , , , ∴, , Area of the curved surface, , = πrl = π·h·√ 2 h, , , = √ 2 πh2, , 211
Page 222 :
Since rate of change of volume is proporational to this area, we get, dv, ∝ √ 2 πh2, dt, dv, , ∴ , = c·√ 2 πh2, dt, where c is constant of proportionality., Let, , , c√ 2 π = k, dv, = kh2, ∴ , dt, , . . . (3), , where k is constant, 1, π r2 h, Now, v =, 3, 1, 1, , =, π r2·h = πh3, (since r = h), 3, 3, , , , ∴, , Differentiating with respect to t, we get, , Equating, , ∴ , , dv, from (3) and (4) we get, dt, , , , , πh2, , ∴ , , where a is constant., , dh, dv, = πh2, dt, dt, , . . . (4), , dh, = kh2, dt, dh, k, =, = a (say), dt, π, , integrating we get, , h = at + b, using (1) we have, , 2, , = a.0 + b, , . . . (5), ∴, , b=2, , ∴, , a=4, , ∴ Equation (5) becomes, , h = at + 2, Now using (2) we get, 10 =, 2a + 2, using the values of a and b in equation (5), we have, , , ∴ , , h, , = 4t + 2, , ∴ , , h, , = 4 × 3·5 + 2, , Now put t = 3·5, , , = 14 + 2 = 16 cm, Therefore, height of water after 3·5 seconds will be 16 cms., , 212
Page 223 :
EXERCISE 6.6, 1., , In a certain culture of bacteria the rate of increase is proportional to the number present. If it is found, that the number doubles in 4 hours, find the number of times the bacteria are increased in 12 hours., , 2., , If the population of a country doubles in 60 years, in how many years will it be triple (treble) under, the assumption that the rate of increase is proporational to the number of inhabitants?, [Given log 2 = 0·6912, log 3 = 1·0986], , 3., , If a body cools from 80°c to 50°c at room temperature of 25°c in 30 minutes, find the temperature, of the body after 1 hour., , 4., , The rate of growth of bacteria is proportional to the number present. If initially, there were 1000, 1, bacteria and the number double in 1 hour, find the number of bacteria after 2 hours., 2, [Take √ 2 = 1·414], , 5., , The rate of disintegration of a radio active element at any time t is proportational to its mass at that, time. Find the time during which the original mass of 1·5 gm. will disintegrate into its mass of 0·5 gm., , 6., , The rate of decay of certain substance is directly proporational to the amount present at that instant., Initially, there are 25 gms of certain substance and two hours later it is found that 9 gms are left., Find the amount left after one more hour., , 7., , Find the population of a city at any time t, given that the rate of increase of population is proporational, to the population at the instant and that in a period of 40 years the population increased from 30,000, to 40,000., , 8., , A body cools according to Newton's law from 100°c to 60°c in 20 minutes. The temperature of the, surrounding being 20°c how long will it take to cool down to 30°c?, , 9., , A right circular cone has height 9 cms and radius of the base 5 cms. It is inverted and water is, π, poured into it. If at any instant the water level rises at the rate of cms/ sec. where A is the area of, A, water surface at that instant, show that the vessel will the full in 75 seconds., , 10. Assume that a spherical raindrop evaporates at a rate proporational to its surface area. If its radius, originally is 3mm and 1 hour later has been reduced to 2mm, find an expression for the radius of, the raindrop at any time t., 11. The rate of growth of the population of a city at any time t is proportional to the size of the population., For a certain city it is found that the constant of proportionality is 0.04. Find the population of the, city after 25 years if the initial population is 10,000. [Take e = 2·7182], 12. Radium decomposes at the rate proportional to the amount present at any time. If p percent of, amount disappears in one year, what percent of amount of radium will be left after 2 years ?, , 213
Page 224 :
Let us Remember, ֍, , Equation which contains the derivative of a function is called a differential equation., , ֍, , The order of a differential equation is the highest order of the derivative appearing in the, equation., , ֍, , The degree of the differential equation is the power of the highest ordered derivative present in, the equation., , ֍, , Order and degree of a differential equation are always positive integers., , ֍, , Solution of a differential equation in which number of arbitary constants is equal to the order, of a differential equation is the general solution of the differential equation., , ֍, , Solution obtained from the general solution by giving particular values to the arbitrary constants, is the particular solution of the differential equation., , ֍, , The most general form of a linear differential equation of the first order is :, where P and Q are functions of x or constant., , ֍, , ֍, , dy, + Py = Q, dx, , Its solution is given by : y (I.F.) = �Q·(I.F.) dx + c , where I.F. (integrating factor) = e∫Pdx, , dx, = kx is in the form x = a·ekt where a is initial value of x., dt, Further, k > 0 represents growth and k > 0, represents decay., Solution of a differential equation, , Newton's law of cooling is θ = θ0 + (θ1 - θ0) e−kt., MISCELLANEOUS EXERCISE 6, , (I) Choose the correct option from the given alternatives :, (1), , The order and degree of the differential equation, , (A) 2, 1, (2), , (B) 1, 2, , The differential equation of y = c2 +, , (A) x4, , dy, dx, , 2, , (C) x3, , dy, dx, , 2, , c, is . . ., x, , dy, 1+, dx, , d2 y, =, dx2, , 3, 2, , are respectively . . ., , (C) 3, 2, , -x, , dy, = y , dx, , (B), , +x, , dy, = y , dx, , (D), , 214, , 2, , d2 y, dx, , 2, , d2 y, dx, , 2, , (D) 2, 3, , +x, +, , dy, +y=0, dx, , dy, -y=0, dx
Page 225 :
(3), , x2 + y2 = a2 is a solution of ..., , (A), , d2 y dy, +, -y=0, dx2 dx, , (B) y = x 1 +, , dy, dy, (C) y = x, +a 1+, dx, dx, (4), , (5), , 2, , + a2y, , d2 y, dy, (D), = (x + 1), 2, dx, dx, , 2, , The differential equation of all circles having their centers on the line y = 5 and touching the, X-axis is, , (A) y2 1 +, , , dy, dx, , dy, = 25, dx, , (C) ( y − 5)2 + 1 +, , dy, dx, , 2, , = 25, , The differential equation y, (A) circles, , (B) ( y − 5)2 1 +, , dy, dx, , 2, , (D) ( y − 5)2 1 −, , dy, dx, , 2, , = 25, = 25, , dy, + x = 0 represents family of . . ., dx, , (B) parabolas, , 1 dy, The solution of · = tan−1 x is ..., x dx, x2 tan−1 x, (A), +c=0, 2, , (C) ellipses, , (D) hyper bolas, , (6), , , , (B) x tan−1 x + c = 0, , (C) x − tan−1 x = c , , (D) y =, , x2 tan−1 x, 2, , −, , 1, (x − tan−1 x) + c, 2, , dy, (7) The solution of (x + y)2, = 1 is ..., dx, (A) x = tan−1 (x + y) + c, , (B) y tan−1, , (C) y = tan−1 (x + y) + c , , (D) y + tan−1 (x + y) = c, , (8), , The solution of, (A) sin−1, (C) sin, , x, =c, y, , y +√ x2 − y2, dy, =, is . . ., dx, 2, , y, = 2 log | x | + c, x, , (B) sin−1, , x, = log | x | + c, y, , (D) sin, , y, = log | x | + c, x, y, = log | y | + c, x, , dy, + y = cos x − sin x is . . ., dx, (A) y e x = cos x + c, , (B) y e x + e x cos x = c, , (C) y e x = e x cos x + c , , (D) y2 e x = e x cos x + c, , (9), , The solution of, , 215
Page 226 :
dy, + 2y = x2 log x is . . ., dx, 1, (C) 2, (D) x2, n, , (10) The integrating factor of linear differential equation x, (A), , 1, x, , (B) k, , (11) The solution of the differential equation, (A) y sec x + tan x = c , (C) sec x + y tan x = c, (12) The particular solution of, (A) e x − y = x + 1, , dy, = sec x − y tan x is, dx, (B) y sec x = tan x + c, (D) sec x = y tan x + c, , dy, = xe y − x, when x = y = 0 is . . ., dx, (B) e x + y = x + 1, (C) e x + e y = x + 1, , (D) e y − x = x − 1, , x2 y2, (13) 2 − 2 = 1 is a solution of . . ., a, b, dy, (A), + yx +, 2, dx, dx, d2 y, , (C) y, , dy, d2 y, +2, 2, dx, dx, , = 0 , , dy, (B) xy 2 + 2, dx, dx, , + y = 0 , , (D) xy, , 2, , 2, , d2 y, , 2, , −y, , dy, dx, , =0, , dy, d2 y, +y 2 =0, dx, dx, , (14) The decay rate of certain substance is directly proporational to the amount present at that, instant. Initially there are 27 grams of substance and 3 hours later it is found that 8 grams left., , , , The amount left after one more hour is..., 2, 1, (A) 5 grams, (B) 5 grams, 3, 3, , (C) 5·1 grams, , (D) 5 grams, , (15) If the surrounding air is kept at 20°c and a body cools from 80°c to 70°c in 5 minutes, the, temparature of the body after 15 minutes will be..., (A) 51·7°c, , (B) 54·7°c, , (C) 52·7°c, , (D) 50·7°c, , (II) Solve the following :, (1), , Determine the order and degree of the following differential equations :, , (i), , d2 y, dx, , 2, , +5, , (iii) 3 1 +, (v), , d4 y, dx4, , dy, + y = x3 , dx, , dy, dx, , + sin, , 2, , =, , (ii), , d2 y, , (iv), , dx2, , dy, =0, dx, , 216, , d3 y, dx3, , 2, , =5 1+, , dy, dx, , dy, dy, = 3y + 4 1 + 5, dx, dx, , 2
Page 228 :
(6) Find the particular solution of the following differential equations :, dy, (1) y (1 + log x) = (log x x ) , when y (e) = e 2, dx, dy, = y, when x = 2, y = 1, (2) (x + 2y2), dx, π, dy, − 3y cot x = sin 2x, when y, =2, (3), 2, dx, (4), , (x + y) dy + (x − y) dx = 0, when x = 1 = y, , (5), , 2e y dx + y − 2xe y dy = 0, when y (0) = 1, , x, , x, , y2 + y + 1, dy, = 2, is given by, (7) Show that the general solution of the differential equation, dx, x +x+1, (x + y + 1) = c (1 − x − y − 2xy), (8) The normal lines to a given curve at each point (x, y) on the curve pass through (2, 0). The curve, passes through (2, 3). Find the equation of the curve., (9) The volume of spherical balloon being inflated changes at a constant rate. If initially its radius is , 3 units and after 3 seconds it is 6 units. Find the radius of the balloon after t second., (10) A person's assets start reducing in such a way that the rate of reduction of assets is proportional to, the square root of the assets existing at that moment. If the assets at the begining are ` 10 lakhs and, 2, they dwindle down to ` 10,000 after 2 years, show that the person will be bankrupt in 2 years, 9, from the start., , v, , v, , 218, , v
Page 229 :
7. PROBABILITY DISTRIBUTIONS, Let us Learn, •, , Random variables, , •, , Types of random variables, , •, , Probability distribution of random variable., , , , • Discrete random variable, , • Continuous random variable, , , , • Probability mass function , , • Probability density function, , , , • Expected values and variance , , • Cumulative distribution function, , Let us Recall, •, , A random experiment and all possible outcomes of an experiment, , •, , The sample space of a random experiment, Let us Study, , 7.1 Random variables :, We have already studied random experiments and sample spaces corresponding to random, experiments. As an example, consider the experiment of tossing two fair coins. The sample space, corresponding to this experiment contains four elements, namely {HH, HT,TH,TT}. We have already, learnt to construct the sample space of any random experiment. However, the interest is not always, in a random experiment and its sample space. We are often not interested in the outcomes of a random, experiment, but only in some number obtained from the outcome. For example, in case of the experiment, of tossing two fair coins, our interest may be only in the number of heads when two coins are tossed., In general, it is possible to associate a unique real number to every possible outcome of a random, experiment. The number obtained from an outcome of a random experiment can take different values, for different outcomes. This is why such a number is a variable. The value of this variable depends on, the outcome of the random experiment, therefore it is called a random variable., A random variable is usually denoted by capital letters like X, Y, Z, . . ., , 219
Page 230 :
Consider the following examples to understand the concept of random variables., (i) When we throw two dice, there are 36 possible outcomes, but if we are interested in the sum of the, numbers on the two dice, then there are only 11 different possible values, from 2 to12., (ii) If we toss a coin 10 times, then there are 210 = 1024 possible outcomes, but if we are interested in the, number of heads among the 10 tosses of the coin, then there are only 11 different possible values,, from 0 to 10., (iii) In the experiment of randomly selecting four items from a lot of 20 items that contains 6 defective, items, the interest is in the number of defective items among the selected four items. In this case,, there are only 5 different possible outcomes, from 0 to 4., In all the above examples, there is a rule to assign a unique value to every possible outcome of the, random experiment. Since this number can change from one outcome to another, it is a variable. Also,, since this number is obtained from outcomes of a random experiment, it is called a random variable., A random variable is formally defined as follows., Definition :, A random variable is a real-valued function defined on the sample space of a random experiment., In other words, the domain of a random variable is the sample space of a random experiment, while its, co-domain is the set of real numbers., Thus X : S → R is a random variable., We often use the abbreviation r.v. to denote a random variable. Consider an experiment where three, seeds are sown in order to find how many of them germinate. Every seed will either germinate or will, not germinate. Let us use the letter Y when a seed germinates and the letter N when a seed does not, germinate. The sample space of this experiment can then be written as, S = �YYY, YYN, YNY, NYY, YNN, NYN, NNY, NNN�, and n (S) = 23 = 8., , None of these outcomes is a number. We shall try to represent every outcome by a number. Consider, the number of times the letter Y appears in a possible outcome and denote it by X. Then, we have, X (YYY ) = 3, X (YYN ) = X (YNY) = X (NY Y) = 2, X (YNN) = X (NYN) = X (NNY ) = 1, X (NNN ) = 0., The variable X has four possible values, namely 0, 1, 2, and 3. The set of possible values of X is, called the range of X. Thus, in this example, the range of X is the set �0, 1, 2, 3� ., , A random variable is usually denoted by a capital letter, like X or Y . A particular value taken by, the random variable is usually denoted by the small letter x. Note that x is always a real number and, the set of all possible outcomes corresponding to a particular value x of X is denoted by the event, [X = x]., , 220
Page 231 :
For example, in the experiment of three seeds, the random variable X takes four possible values,, namely 0, 1, 2, 3. The four events are then defined as follows., [X = 0] = �NNN �,, , [X = 1] = �YNN, NYN, NNY �,, [X = 2] = �YYN, YNY, NYY �,, , [X = 3] = �YYY�., , Note that the sample space in this experiment is finite and so is the random variable defined on it., , A sample space need not always be finite. For example, the experiment of tossing a coin until a head, is obtained. The sample space for this experiment is S = �H, TH, TTH, TTTH, . . . �., , Note that S contains an unending sequence of tosses required to get a head. Here, S is countably, infinite.The random variable X : S → R, denoting the number of tosses required to get a head, has the, range �1, 2, 3, . . . � which is also countably infinite., , 7.2 Types of Random Variables :, , There are two types of random variables, namely discrete and continuous., 7.2.1 Discrete Random Variables :, Definition : A random variable is said to be a discrete random variable if the number of its possible, values is finite or countably infinite., The values of a discrete random variable are usually denoted by non-negative integers, that is,, �0, 1, 2, . . . �., , Examples of discrete random variables include the number of children in a family, the number of, patients in a hospital ward, the number of cars sold by a dealer, number of stars in the sky and so on., Note : The values of a discrete random variable are obtained by counting., 7.2.2 Continuous Random Variable :, Definition : A random variable is said to be a continuous random variable if the possible values of this, random variable form an interval of real numbers., A continuous random variable has uncountably infinite possible values and these values form an, interval of real numbers., Examples of continuous random variables include heights of trees in a forest, weights of students, in a class, daily temperature of a city, speed of a vehicle, and so on., , 221
Page 232 :
The value of a continuous random variable is obtained by measurement. This value can be measured, to any degree of accuracy, depending on the unit of measurement. This measurement can be represented, by a point in an interval of real numbers., The purpose of defining a random variable is to study its properties. The most important property, of a random variable is its probability distribution. Many other properties of a random variable are, obtained with help of its probability distribution. We shall now learn about the probability distribution, of a random variable. We shall first learn the probability of a discrete random variable, and then learn, the probability distribution of a continuous random variable., 7.3 Probability Distribution of Discrete Random Variables :, Let us consider the experiment of throwing two dice and noting the numbers on the upper-most, faces of the two dice. The sample space of this experiment is, S = �(1, 1), (1, 2),.....(6, 6)� and n (S) = 36., , Let X denote the sum of the two numbers in any single throw., Then �2, 3, · · · , 12� is the set of possible values of X. Further,, [X = 2] = �(1, 1)�,, , [X = 3] = �(1, 2), (2, 1)�,, . . ., . . ., [X = 12] = �(6, 6)�., , Next, all of these 36 possible outcomes are equally likely if the two dice are fair, that is, if each of, the six faces have the same probability of being uppermost when the die is thrown., 1, As the result, each of these 36 possible outcomes has the same probability =, 36, This leads to the following results., 1, P [X = 2] = P �(1, 1)� = ,, 36, P [X = 3] = P �(1, 2), (2, 1)� =, , 2, ,, 36, , P [X = 4] = P �(1, 3), (2, 2), (3, 1)� =, and so on., , 222, , 3, ,, 36
Page 233 :
The following table shows the probabilities of all possible values of X., x, P (x), , 2, , 3, , 4, , 5, , 6, , 7, , 8, , 9, , 10, , 11, , 12, , 1, 36, , 2, 36, , 3, 36, , 4, 36, , 5, 36, , 6, 36, , 5, 36, , 4, 36, , 3, 36, , 2, 36, , 1, 36, , Table 7.1, Such a description giving the values of the random variable X along with the corresponding, probabilities is called the probability distribution of the random variable X., In general, the probability distribution of a discrete random variable X is defined as follows., Definition : The probability distribution of a discrete random variable X is defined by the following, system of numbers. Let the possible values of X be denoted by x1 , x2 , x3 , . . . , and the corresponding, , probabilities be denoted by p1 , p2 , p3 , . . . , where pi = P [X = xi ] for i = 1, 2, 3, . . . ., , Note : A discrete random variable can have finite or infinite number of possible values, but they are, countable., Sometimes, the probability distribution of a discrete random variable is presented in the form of, ordered pairs of the form (x1 , p1 ), (x2 , p2 ), (x3 , p3 ), . . . A common practice is to present the probability, , distribution of a discrete random variable in a tabular form as shown below., xi, , x1, , x2, , x3, , ..., , P [X = xi ], , p1, , p2, , p3, , ..., , Table 7.2, Note : If xi is a possible value of X and pi = P [X = xi ], then there is an event [ Ei ] in the sample, , space S such that pi = P [ Ei ]. Since xi is a possible value of X, pi = P [ X = xi ] > 0. Also, all possible, values of X cover all sample points in the sample space S, and hence the sum of their probabilities is 1., That is, pi ≥ 0, for all i and, , i, , pi = 1., , 7.3.1 Probability Mass Function (p. m. f.) :, Sometimes the probability pi of X taking the value xi is a function of xi for every possible value of, , X. Such a function is called the probability mass function (p. m. f.) of the discrete random variable X., , For example, consider the coin-tossing experiment where the random variable X is defined as the, number of tosses required to get a head. Let probability of getting head be ‘t’ and that of not getting head, be 1 − t. The possible values of X are given by the set of natural numbers, 1, 2, 3, . . . and, P [ X = i ] = (1 − t ), , 223, , i−1, , t , for i = 1, 2, 3, . . .
Page 234 :
This result can be verified by noting that if head is obtained for the first time on the i th toss, then, the first i − 1 tosses have resulted in tail. In other words, X = i represents the event of having i − 1 tails, followed by the first head on the toss., We now define the probability mass function (p. m. f.) of a discrete random variable., Definition : Let the possible values of a discrete random variable X be denoted by x1 , x2 , x3 , . . . ,, with the corresponding probabilities pi = P [X = xi ], i = 1, 2, . . . If there is a function f such that, pi = P [X = xi ] = f (xi ) for all possible values, of X, then f is called the probability mass function, n, pi = 1, (p. m. f.) of X, if (i) pi ≥ 0 , i = 1,2,... n and (ii), i=1, , For example, consider the experiment of tossing a coin 4 times and defining the random variable, X as the number of heads in 4 tosses. The possible values of X are 0, 1, 2, 3, 4, and the probability, distribution of X is given by the following table., x, P [X = x ], , 0, 1, 16, , 1, 1, 4, , 2, 3, 8, , 3, 1, 4, , 4, 1, 16, , Table 7.3, Note that : P [X = x] =, where, , 4, x, , 4, x, , 1, 2, , 4, , , x = 0, 1, 2, 3, 4, . . ., , is the number of ways of getting x heads in 4 tosses., , 7.3.2 Cumulative Distribution Function (c. d. f. ) :, The probability distribution of a discrete random variable can be specified with help of the p. m., f. It is sometimes more convenient to use the cumulative distribution function (c.d.f.) of the random, variable. The cumulative distribution function (c. d. f.) of a discrete random variable is defined as, follows., Definition : The cumulative distribution function (c. d. f.) of a discrete random variable X is denoted, by F and is defined as follows., F (x) = P [X ≤ x], , =, , =, =, , xi < x, , xi < x, , xi < x, , P [X = xi ], pi , f ( xi ), , where f is the probability mass function (p. m. f.) of the discrete random variable X., , 224
Page 235 :
For example, consider the experiment of tossing 4 coins and counting the number of heads., We can form the next table for the probability distribution of X., x, f (x) = P [X = x], F (x) = P [X ≤ x], , 0, 1, 16, 1, 16, , 1, 1, 4, 5, 16, , 2, 3, 8, 11, 16, , 3, 1, 4, 15, 16, , 4, 1, 16, 1, , Table 7.4, For example, consider the experiment of tossing a coin till a head is obtained. The following table, shows the p. m. f. and the c. d. f. of the random variable X, defined as the number of tosses required for, the first head., ..., x, 1, 2, 3, 4, 5, f (x), F (x), , 1, 2, 1, 2, , 1, 4, 3, 4, , 1, 8, 7, 8, , 1, 16, 15, 16, , 1, 32, 31, 32, , ..., ..., , Table 7.5, It is possible to define several random variables on the same sample space. If two or more random, variables are defined on the same sample space, their probability distributions need not be the same., For example, consider the simple experiment of tossing a coin twice. The sample space of this, experiment is S = �HH, HT, TH, TT�., Let X denote the number of heads obtained in two tosses. Then X is a discrete random variable and, its value for every outcome of the experiment is obtained as follows., X (HH ) = 2, X (HT ) = X (TH ) = 1, X (TT ) = 0., Let Y denote the number of heads minus the number of tails in two tosses. Then Y is also a discrete, random variable and its value for every outcome of the experiment is obtained as follows., Y (HH ) = 2, Y (HT ) = Y (TH) = 0, Y (TT ) = −2., Number of heads, Let, Z=, Number of tails + 1, Then Z is also a discrete random variable and its values for every outcome of the experiment is, 1, obtained as follows. , Z (HH) = 2, Z (HT ) = Z (TH ) =, , Z (TT ) = 0., 2, These example show that it is possible to define many distinct random variables on the same sample, space. Possible values of a discrete random variables can be positive or negative, integer or fraction., , 225
Page 236 :
SOLVED EXAMPLES, Ex. 1 : Two persons A and B play a game of tossing a coin thrice. If the result of a toss is head, A gets, ` 2 from B. If the result of a toss is tail, B gets ` 1.5 from A. Let X denote the amount gained, or lost by A. Show that X is a discrete random variable and show how it can be defined as a, function on the sample space of the experiment., Solution : X is a number whose value depends on the outcome of a random experiment., Therefore, X is a random variable. Since the sample space of the experiment has only 8, possible outcomes, X is a discrete random variable. Now, the sample space of the experiment is, S = �HHH, HHT, HTH, THH, HTT, THT, TTH, TTT�., , , The values of X in rupees corresponding to these outcomes of the experiment are as, follows., X (HHH) = 2 × 3 = ` 6, X (HHT) = X (HTH) = X (THH) = 2 × 2 − 1.50 × 1 = ` 2.50, X (HTT) = X (THT) = X (TTH) = 2 × 1 − 1.50 × 2 = ` − 1.00, X (TTT) = − 1.50 × 3 = ` − 4.50, , Here, a negative amount shows a loss to player A. This example shows that X takes a, unique value for every element of the sample space and therefore X is a function on the sample, space. Further, possible values of X are 4.50, 1, 2.50, 6., Ex. 2 : A bag contains 1 red and 2 green balls. One ball is drawn from the bag at random, its colour is, noted, and then ball is put back in the bag. One more ball is drawn from the bag at random and, its colour is also noted. Let X denote the number of red balls drawn from the bag as described, above. Derive the probability distribution of X., Solution : Let the balls in the bag be denoted by r, g1 , g2 . The sample space of the experiment is then, given by S = �r r, r g1, r g2, g1 r, g2 r, g1 g1 , g1 g2 , g2 g1 , g2 g2 �., , Since X is defined as the number of red balls, we have, X ({r r}) = 2,, , X ({r g1}) = X (r g2) = X (g1 r) = X (g2 r)= 1,, X ({g1 g1}) = X (g1 g2) = X (g2 g1) = X (g2 g2) = 0., Thus, X is a discrete random variable that can take values 0, 1, and 2., , , The probability distribution of X is then obtained as follows :, x, P [X = x], , 0, 4, 9, , 226, , 1, 4, 9, , 2, 1, 9
Page 237 :
Ex. 3 : Two cards are randomly drawn, with replacement, from a well shuffled deck of 52 playing, cards. Find the probability distribution of the number of aces drawn., Solution : Let X denote the number of aces among the two cards drawn with replacement., , Clearly, 0, 1, and 2 are the possible values of X. Since the draws are with replacement, the, outcomes of the two draws are independent of each other. Also, since there are 4 aces in the deck, of 52 cards,, 4, 1, 12, P [ ace ] =, =, and P [non-ace] =, . Then, 52 13, 13, 12 12 144, P [X = 0] = P [non-ace and non-ace] =, ×, =, ,, 13 13 169, P [X = 1] = P [ace and non-ace] + P [non-ace and ace], =, , 1, 12 12, 1, 24, ×, +, ×, =, ,, 13 13 13 13 169, , 1, 1, 1, ×, =, ., 13 13 169, The required probability distribution is then as follows., , and P [X = 2] = P [ace and ace] =, , , 0, 144, 169, , x, P [X = x], , 1, 24, 169, , 2, 1, 169, , Ex. 4 : A fair die is thrown. Let X denote the number of factors of the number on the upper face. Find, the probability distribution of X., Solution : The sample space of the experiment is S = �1, 2, 3, 4, 5, 6� . The values of X for the possible, outcomes of the experiment are as follows., X(1) = 1, X(2) = 2, X(3) = 2, X(4) = 3, X(5) = 2, X(6) = 4. Therefore,, 1, p1 = P [X = 1] = P [{1}] =, 6, 3, p2 = P [X = 2] = P [{2, 3, 5}] =, 6, 1, p3 = P [X = 3] = P [{4}] =, 6, 1, p4 = P [X = 4] = P [{6}] =, 6, The probability distribution of X is then as follows., x, P [X = x], , 1, 1, 6, , 2, 3, 6, , 227, , 3, 1, 6, , 4, 1, 6
Page 238 :
Ex. 5 : Find the probability distribution of the number of doublets in three throws of a pair of dice., Solution : Let X denote the number of doublets. Possible doublets in a pair of dice are (1, 1), (2, 2),, (3, 3), (4, 4), (5, 5, ), (6, 6)., Since the dice are thrown thrice, 0, 1, 2, and 3 are possible values of X. Probability of getting a, 1, 1, 5, doublet in a single throw of a pair of dice is p =, and q = 1 −, = ., 6, 6, 6, 5, 5, 5 125, P [X = 0] = P [ no doublet] = qqq =, ×, ×, =, ., 6, 6, 6 216, 75, P [X = 1] = P [one doublet] = pqq + qpq + qqp = 3pq2 =, ., 216, 15, P [X = 2] = P [two doublets] = ppq + pqp + qpp = 3p2q =, ., 216, 1, P [X = 3] = P [three doublets] = ppp =, ., 216, Ex. 6 : The probability distribution of X is as follows :, , , x, , 0, , 1, , 2, , 3, , 4, , P [X = x], , 0·1, , k, , 2k, , 2k, , k, , Find (i) k, (ii) P [X < 2], (iii) P [X ≥ 3], (iv) P [1 ≤ X < 4], (v) F(2)., Solution : The table gives a probability distribution and therefore, P [X = 0] + P [X = 1] + P [X = 2] + P [X = 3] + P [X = 4] = 1., That is, 0·1 + k + 2k + 2k + k = 1., That is, 6k = 0·9. Therefore k = 0·15., (i) k = 0·15., (ii) , , P [X < 2] = P [X = 0] + P [X = 1] = 0·1 + k = 0·1 + 0.15 = 0·25, , (iii) , , P [X ≥ 3] = P [X = 3] + P [X = 4] = 2k + k = 3(0·15) = 0·45, , (iv) , , P [1 ≤ X < 4], , = P [X = 1] + P [X = 2] + P [X = 3], , = k + 2k + 2k = 5k, , = 5(0·15) = 0·75., (v) , , F (2) = P [X ≤ 2] = P [X = 0] + P [X = 1] + P [X = 2], , = 0·1 + k + 2k = 0·1 + 3k, , = 0·1 + 3(0·15) = 0·1 + 0·45 = 0·55., 7.3.3 Expected value and Variance of a random variable :, In many problems, it is desirable to describe some feature of the random variable by means, of a single number that can be computed from its probability distribution. Few such numbers are, mean, median, mode and variance and standard deviation. In this section, we shall discuss mean and, variance only. Mean is a measure of location or central tendency in the sense that it roughly locates a, middle or average value of the random variable., , 228
Page 239 :
Definition : Let X be a random variable whose possible values x1 , x2 , x3 , . . . , xn occur with probabilities, p1 , p2 , p3 , . . . , pn respectively. The expected value or arithmetic mean of X, denoted by E (X ) or µ is, defined by, n, , E(X ) = µ =, xi pi = x1 p1 + x2 p2 + x3 p3 + . . . + xn pn, i=1, , In other words, the mean or expectation of a random variable X is the sum of the products of all, possible values of X by their respective probabilities., Definition : Let X be a random variable whose possible values x1 , x2 , x3 , . . . , xn occur with probabilities, 2, , p1 , p2 , p3 , . . . , pn respectively. The variance of X, denoted by Var (X ) or σx is defined as, 2, σx, , The non-negative number σx =, , n, , = Var (X ) =, , i=1, , (xi − µ)2 pi, , Var (X ) is called the standard deviation of the random, , variable X., We can also use the simplified form of, n, , Var (X ) =, , n, , xi pi −, 2, , i=1, , i=1, , Var (X ) = E(X ) − [E(X )], 2, , 2, , xi pi, , 2, , n, , where, , SOLVED EXAMPLES, , i=1, , xi2 pi = E(X 2 ), , Ex. 1 : Three coins are tossed simultaneously, X is the number of heads. Find expected value and, variance of X., Solution : S = �HHH, HHT, HTH, THH, HTT, THT, TTH, TTT� and X = � 0 , 1 , 2 , 3 �, X = xi P = pi, 0, 1, 2, 3, , 1, 8, 3, 8, 3, 8, 1, 8, , xi pi, , xi2 pi, , 0, , 0, , 3, 8, 6, 8, 3, 8, , 3, 8, 12, 8, 9, 8, , n, , xi pi =, , i=1, n, , Then E (X), , =, , i=1, , xi pi =, , 12, 8, , =, , i=1, , n, , xi pi −, 2, , i=1, , xi2 pi =, , 229, , 24, 8, , 12, = 1·5, 8, , n, , Var (X ), , n, , i=1, , xi pi, , 2, , =, , 24, − (1·5)2 = 3 − 2·25 = 0·75, 8
Page 240 :
Ex. 2 : Let a pair of dice be thrown and the random variable X be the sum of the numbers that appear, on the two dice. Find the mean or expectation of X and variance of X., Solution : The sample space of the experiment consists of 36 elementary events in the form of ordered, pairs (xi , yi ), where xi = 1, 2, 3, 4, 5, 6 and yi = 1, 2, 3, 4, 5, 6., , , The random variable X i.e. the sum of the numbers on the two dice takes the values 2, 3, 4, 5, 6,, 7, 8, 9, 10, 11 or 12., X = xi P = pi, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, , 1, 36, 2, 36, 3, 36, 4, 36, 5, 36, 6, 36, 5, 36, 4, 36, 3, 36, 2, 36, 1, 36, , xi pi, , xi2 pi, , 2, 36, 6, 36, 12, 36, 20, 36, 30, 36, 42, 36, 40, 36, 36, 36, 30, 36, 22, 36, 12, 36, , 4, 36, 18, 36, 48, 36, 100, 36, 180, 36, 294, 36, 320, 36, 324, 36, 300, 36, 242, 36, 144, 36, , 252, =7, 36, , n, i=1, , xi pi =, , n, i=1, , xi2 pi =, , 1974, = 54·83, 36, , n, , Then E (X), , =, , i=1, , xi pi = 7, , n, , Var (X ), , =, , n, , xi pi −, 2, , i=1, , , =, 54·83 − 49, = 5·83, , 230, , i=1, , xi pi, , 2, , = 54·83 − (7)2
Page 241 :
Ex. 3 : Find the mean and variance of the number randomly selected from 1 to 15., Solution : The sample space of the experiment is S = � 1, 2, 3, …, 15 �., , Let X denote the number selected., , Then X is a random variable which can take values 1, 2, 3, …, 15. Each number selected is, equiprobable therefore, 1, P(1) = P(2) = P(3) = … = P(15) =, 15, n, 1, 1, 1, 1, µ = E(X ) =, xi pi = 1 ×, +2 ×, +3×, + … + 15 ×, i=1, 15, 15, 15, 15, 1, 1, 15 × 16, = (1 + 2 + 3 + … + 15) ×, =, ×, =8, 15, 15, 2, n, n, 2, 1, 1, 1, 1, Var (X ) =, xi2 pi −, xi pi, = 12 ×, + 22 ×, + 32 ×, + … + 152 ×, − (8)2, i=1, i=1, 15, 15, 15, 15, 1, , = (12 + 22 + 32 + … + 152 ) ×, − (8)2, 15, 1, 15 × 16 × 31, =, ×, − (8)2, 15, 6, , = 82·67 − 64 = 18·67, Ex. 4 : Two cards are drawn simultaneously (or successively without replacement) from a well shuffled, pack of 52 cards. Find the mean, variance and standard deviation of the number of kings drawn., Solution : Let X denote the number of kings in a draw of two cards. X is a random variable which can, assume the values 0, 1 or 2., 48, C2 48 × 47 188, Then , P (X = 0) = P ( no card is king) = 52 =, =, C2 52 × 51 221, C1 × 48C1, , 4, , , , P (X = 1) = P ( exactly one card is king) =, , Then , , C2, 1, 4×3, P (X = 2) = P ( both cards are king) = 52 =, =, C2 52 × 51 221, , C2, , 52, , =, , 4 × 48 × 27 32, =, 221, 52 × 51, , Then , , 4, , , , n, , µ = E(X ) =, , i=1, , xi pi = 0 ×, , 188, 32, 1, 34, +1 ×, +2×, =, 221, 221, 221 221, , 34, 188, 32, 1, + 12 ×, + 22 ×, −, i=1, i=1, 221, 221, 221, 221, 1156, 6800, 36, =, −, =, = 0·1392, 221 48841 48841, , σ = Var (X ) = √ 0·1392, n, , Var (X ), , =, , n, , xi pi −, 2, , xi pi, , 2, , = 02 ×, , 231, , 2
Page 242 :
EXERCISE 7.1, 1., , Let X represent the difference between number of heads and number of tails obtained when a coin, is tossed 6 times. What are possible values of X ?, , 2., , An urn contains 5 red and 2 black balls. Two balls are drawn at random. X denotes number of black, balls drawn. What are possible values of X ?, , 3., , State which of the following are not the probability mass function of a random variable. Give, reasons for your answer., (i), , (ii), X, , 0, , 1, , 2, , X, , 0, , 1, , 2, , 3, , 4, , P (X ), , 0·4, , 0·4, , 0·2, , P (X ), , 0·1, , 0·5, , 0·2, , –0·1, , 0·2, , (iii), , (iv), X, , 0, , 1, , 2, , Z, , 3, , 2, , 1, , 0, , –1, , P (X ), , 0·1, , 0·6, , 0·3, , P (Z ), , 0·3, , 0·2, , 0·4, , 0, , 0·05, , (v), , (vi), Y, , –1, , 0, , 1, , X, , 0, , –1, , –2, , P (Y ), , 0·6, , 0·1, , 0·2, , P (X ), , 0·3, , 0·4, , 0·3, , 4, , Find the probability distribution of (i) number of heads in two tosses of a coin. (ii) Number of tails, in the simultaneous tosses of three coins. (iii) Number of heads in four tosses of a coin., , 5., , Find the probability distribution of the number of successes in two tosses of a die, where a success, is defined as number greater than 4 appears on at least one die., , 6., , From a lot of 30 bulbs which include 6 defectives, a sample of 4 bulbs is drawn at random with, replacement. Find the probability distribution of the number of defective bulbs., , 7., , A coin is biased so that the head is 3 times as likely to occur as tail. If the coin is tossed twice, find, the probability distribution of number of tails., , 8., , A random variable X has the following probability distribution :, X, , 0, , 1, , 2, , 3, , 4, , 5, , 6, , 7, , P (X ), , 0, , k, , 2k, , 2k, , 3k, , k2, , 2k2, , 7k2 + k, , Determine : (i) k , 9., , (ii) P (X < 3) , , (iii) P ( X > 4), , Find expected value and variance of X for the following p.m.f., X, , –2, , –1, , 0, , 1, , 2, , P (X ), , 0·2, , 0·3, , 0·1, , 0·15, , 0·25, , 232
Page 243 :
10. Find expected value and variance of X ,where X is number obtained on uppermost face when a fair, die is thrown., 11. Find the mean number of heads in three tosses of a fair coin., 12. Two dice are thrown simultaneously. If X denotes the number of sixes, find the expectation of X., 13. Two numbers are selected at random (without replacement) from the first six positive integers. Let, X denote the larger of the two numbers obtained. Find E (X )., 14. Let X denote the sum of the numbers obtained when two fair dice are rolled. Find the standard, deviation of X., 15. A class has 15 students whose ages are 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 and 20, years. One student is selected in such a manner that each has the same chance of being chosen and, the age X of the selected student is recorded. What is the probability distribution of the random, variable X ? Find mean, variance and standard deviation of X., 16. In a meeting, 70% of the members favour and 30% oppose a certain proposal. A member is selected, at random and we take X = 0 if he opposed, and X = 1 if he is in favour. Find E (X ) and Var (X )., 7.4 Probability Distribution of a Continuous Random Variable :, A continuous random variable differs from a discrete random variable in the sense that the possible, values of a continuous random variable form an interval of real numbers. In other words, a continuous, random variable has uncountably infinite possible values., For example, the time an athlete takes to complete a thousand-meter race is a continuous random, variable., We shall extend what we learnt about a discrete random variable to a continuous random variable., More specifically, we shall study the probability distribution of a continuous random variable with, help of its probability density function (p. d. f.) and its cumulative distribution function (c. d. f.). If, the possible values of a continuous random variable X form the interval [a, b], where a and b are real, numbers and a < b, then the interval [a, b] is called the support of the continuous random variable X., The support of a continuous random variable is often denoted by S., In case of a discrete random variable X that takes finite or countably infinite distinct values,, the probability P [X = x] is determined for every possible value x of the random variable X. The, probability distribution of a continuous random variable is not defined in terms of probabilities of, possible values of the random variable since the number of possible values are unaccountably infinite., Instead, the probability distribution of a continuous random variable is characterized by probabilities, of intervals of the form [ c, d ], where c < d. That is, for a continuous random variable, the interest is, in probabilities of the form P [c < X < d], where a ≤ c < d ≤ b., , 233
Page 244 :
This probability is obtained by integrating a function of X over the interval [c, d]. Let us first, define the probability density function (p.d.f.) of a continuous random variable., 7.4.1 Probability Density Function (p. d. f.) :, Let X be a continuous random variable defined on interval S = (a , b). A non-negative integrable, function f (x) is called the probability density function (p. d. f.) of X if it satisfies the following, conditions., 1. f (x) is positive or zero every where in S, that is, f (x) ≥ 0, for all x ∈ S., 2. The area under the curve y = f (x) over S is 1. That is, � f (x) dx = 1, S, , 3. The probability that X takes a value in A, where A is some interval, is given by the integral of, f (x) over that interval. That is, P [X ∈ A] = � f (x) dx, A, , 7.4.2 Cumulative Distribution Functions (c. d. f.) :, , The cumulative distribution function for continuous random variables is just a straightforward, extension of that of the discrete case. All we need to do is replace the summation with an integral., Definition : The cumulative distribution function (c. d. f.) of a continuous random variable X is, , defined as :, x, F (x) = � f (t) dt for a < x < b., a, , You might recall, for discrete random variables, that F (x) is, in general, a non-decreasing step, function. For continuous random variables, F (x) is a non-decreasing continuous function., SOLVED EXAMPLES, , Ex. 1 : Let X be a continuous random variable whose probability density function is f (x) = 3x2 ,, for 0 < x < 1. note that f (x) is not P [X = x]., , , For example, f (0.9) = 3(0.9)2 = 2·43 > 1, which is clearly not a probability. In the continuous, case, f (x) is the height of the curve at X = x, so that the total area under the curve is 1. Here it is, areas under the curve that define the probabilities., , Solution : Now, let’s start by verifying that f (x) is a valid probability density function., , , For this, note the following results., , 1., , f (x) = 3x2 ≥ 0 for all x ∈ [0, 1]., , , , 2., , , , � f (x) = � 3x2 dx = 1, , Therefore, the function f (x) = 3x2, for 0 < x < 1 is a proper probability density function., , 1, , 1, , 0, , 0, , 234
Page 245 :
Also, for real numbers c and d such that 0 ≤ c < d ≤ 1, note that, d, , d, , d, , c, , c, , c, , P [c < X < d] = � f (x) dx = � 3x2 dx = x3 = d 3 – c 3 > 0, , ● , , What is the probability that X falls between, , 1, 1, and 1? That is, what is P, <X<1 ?, 2, 2, , 1, and d = 1 in the above integral to obtain, 2, 1, 7, 1, 1 3, P, < X < 1 = 13 –, =1–, = ., 8, 8, 2, 2, , Substitute c =, , ● , , , 1, ?, 2, See that the probability is 0 . This is so because, , What is P X =, d, , � f (x) dx =, c, , 1⁄2, , x3 dx = 1 – 1 = 0., , 1⁄2, , The ordinate AB, with A, , , 1, 1 1, , 0 and B, ,, is degenerate case of rectangle and has area 0, 2, 2 8, , As a matter of fact, in general, if X is a continuous random variable, then the probability that X, takes any specific value x is 0. That is, when X is a continuous random variable, then, , P [X = x] = 0 for every x in the support., Ex. 2 : Let X be a continuous random variable whose probability density function is f (x) =, , x3, , for an, 4, interval 0 < x < c. What is the value of the constant c that makes f (x) a valid probability density, function?, , Solution : Note that the integral of the p. d. f. over the support of the random variable must be, , , , , c, , That is, � f (x) dx = 1., 0, , c x3, x4, x3, dx = 1. But, �, dx =, That is, �, 16, 4, 4, 0, 0, c, , we have, , c4, , 16, , c, , =, 0, , c4, 16, , . Since this integral must be equal to 1,, , = 1, or equivalently c 4 = 16, so that c = 2 since c must be positive., , Ex. 3 : Let's return to the example in which X has the following probability density function :, f (x) = 3x2, , , for 0 < x < 1. What is the cumulative distribution function F (x) ?, , Solution : F (x) =, , x, −0, , x, , x, , 0, , 0, , f (x) dx = 3x2 dx = x3, , = x3, , 235
Page 246 :
Ex. 4 : Let's return to the example in which X has the following probability density function :, x3, f (x) =, for 0 < x < 4. What is the cumulative distribution function X ?, 4, x, x, x 3, 1 x4, 1, x4, x, Solution : F (x) = f (x) dx =, dx =, =, = [x 4 – 0] =, 4 4 0 16, 16, 0, 0 4, Ex. 5 : Suppose the p.d.f. of a continuous random variable X is defined as:, f (x) = x + 1 , for –1 < x < 0, and , f (x) = 1 – x , for 0 ≤ x < 1., Find the c.d.f. F(x)., Solution : If we look the p.d.f. it is defined in two steps, Now for the other two intervals :, For –1 < x < 0 and 0 < x < 1., x, , F (x) =, , (x + 1) dx, , −1, , x2, +x, =, 2, , Fig. 7.1, , =, , =, , 1, 2, For 0 < x < 1, , x2, 2, , +x+, , x, , 1, x2, +x –, –1, 2, 2, , =, −1, , 1 x2 + 2x + 2, =, 2, 2, , (x + 1)2, 2, , F (0) =, , , F (x) = P (0 < x < 1) = P (–1 < x < 0) + P (0 < x < 1) =, , 0, , (x + 1) dx +, , x, 0, , −1, x, , 1, = + (1 – x ) dx, 2 0, 1, x2, = + x +, 2, 2, F (x) = 0, for x ≤ –1, 1, F (x) = (x + 1)2, for –1 < x ≤ 0, 2, 1, x2, = + x – , for 0 < x < 1 , 2, 2, , , 236, , (1 – x ) dx
Page 247 :
b, , If probability function f (x) is defined on (a , b) with f (x) ≥ 0 and � f (x) dx = 1, then we can, a, extend this function to the whole of 1R as follows., , For x ≤ a and x ≥ b, define f (x) = 0., , , Then note that, , t, , � f (x) = 0 , for t ≤ a and for x ≥ b, , −∞, t, , a, , b, , t, , −∞, , −∞, , a, , b, , � f (x) dx = � f (x) dx + � f (x) dx + � f (x) dx = 0 + 1 + 0, Thus F(t ) = 0, for t ≤ a and F(t ) = 1, for t ≥ b, , Ex. 6 : Verify if the following functions are p.d.f. of a continuous r.v. X., (i), , f (x) = e –x, for 0 < x < ∞ and = 0, otherwise., , (ii) f (x) =, , x, , for –2 < x < 2 and = 0, otherwise., 2, , Solution : (i) e –x is ≥ 0 for any value of x since e > 0,, ∴, , e –x > 0, for 0 < x < ∞, , ∞, , ∞, , ∞, , 0, , 0, , 0, , � f (x) dx = � e –x dx = – e –x =, , , , , 1, – e 0 = –(0 – 1) = 1, e∞, , Both the conditions of p.d.f. are satisfied f (x) is p.d.f. of r.v., , (ii) f (x) < 0 i.e. negative for –2 < x < 0 therefore f(x) is not p.d.f., Ex. 7 : Find k if the following function is the p.d.f. of r.v. X., f (x) = kx2(1 – x),, , for 0 < x < 1 and = 0, otherwise., , Solution : Since f (x) is the p.d.f. of r.v. X, 1, , kx2 (1 – x ) dx = 1, 0, 1, , ∴ , , k (x2 – x3 ) dx = 1, , 0, , ∴ , ∴ , ∴ , , x3 x4, –, k, 3, 4, , 1, , = 1 , 0, , 1 1, –, – (0)� = 1 , 3 4, 1, k×, = 1 , 12, k�, , ∴, , k = 12, , 237
Page 248 :
Ex. 8 : For each of the following p.d.f. of r.v. X, find (a) P ( X < 1) and (b) P ( | X | < 1 ), x2, (i) f (x) = , , for –3 < x < 3 and = 0, otherwise., 18, x+2, (ii) f (x) =, , for –2 < x < 4 and = 0, otherwise., 18, Solution :, (i) (a), , (b), , P ( X < 1) , , 2, , =, , 1, 1, 28 14, [1 – (–3)3] =, (1 + 27) =, =, 54, 54, 54 27, , −3, , 1 3, (x ), x, dx = 18, P ( | X | < 1) = P (–1 < x < 1) =, −1 18, 3, 1, , 1, [1 – (–1)3], , =, 54, (ii) (a), , 1, , 1 3, (x ), x, dx = 18, =, −3 18, 3, 1, , P ( X < 1) , , =, , 1, −2, , =, , 2, , 1, , −1, , 1, 2, 1, (1 + 1) =, =, 54, 54 27, , 1 x2, x+2, dx =, + 2x, 18 2, 18, , 1, , −2, , 1 5, 1 9 1, 1, 1, (–2)2, �, +2 –, + 2 (–2) � =, � + 2� =, × =, , =, 18 2, 18 2 4, 18 2, 2, (b), , P ( | X | < 1) = P (–1 < x < 1) =, , 1, , −1, , 1 x2, x+2, dx =, + 2x, 18 2, 18, , 1, , −1, , 1 5 3, 1, 2, 1, 1, 1, �, +2 –, –2 �=, � + �=, ×4=, , =, 18 2 2, 18, 9, 18 2, 2, Ex. 9 : Find the c.d.f. F(x) associated with p.d.f. f (x) of r.v. X where, , f (x) = 3 (1 – 2x2), , for 0 < x < 1 and = 0, otherwise., , Solution : Since f (x) is p.d.f. of r.v. therefore c.d.f. is, x, x, 2x3, = [ 3x – 2x3 ] = 3x – 2x3, F (x) = 3 (1 – 2x2) dx = 3 x –, 3, 0, 0, , EXERCISE 7.2, 1., , Verify which of the following is p.d.f. of r.v. X :, π, (i) f (x) = sin x,, for 0 ≤ x ≤, (ii), f (x) = x, for 0 ≤ x ≤ 1 and = 2 – x for 1 < x <2, 2, (iii) f (x) = 2,, for 0 ≤ x ≤ 1, , 238
Page 249 :
x, , for 0 < x < 4 and = 0 otherwise, 8, Find (a) P (x < 1·5 ) (b) P ( 1 < x < 2 ) (c) P( x > 2 ), , 2., , The following is the p.d.f. of r.v. X : f (x) =, , 3., , It is known that error in measurement of reaction temperature (in 0° c) in a certain experiment is, continuous r.v. given by, x2, f (x) = , for –1 < x < 2 and = 0 otherwise, 3, (i) Verify whether f (x) is p.d.f. of r.v. X., (ii) Find P( 0 < x ≤ 1 ), (iii) Find probability that X is negative., , 4., , Find k if the following function represent p.d.f. of r.v. X., (i), (ii), , 5., , 3, 1, <x<, ., 2, 4, 1, 1, 1, f (x) = kx (1 – x), for 0 < x < 1 and = 0 otherwise, Also find P, <x<, ,P x<, ., 2, 2, 4, , f (x) = kx, for 0 < x < 2 and = 0 otherwise, Also find P, , Let X be amount of time for which a book is taken out of library by randomly selected student and, suppose X has p.d.f., f (x) = 0·5x, for 0 ≤ x ≤ 2 and = 0 otherwise., Calculate: (i) P (X ≤ 1), , 6., , (iii) P ( x ≥ 1·5), , Suppose that X is waiting time in minutes for a bus and its p.d.f. is given by, 1, f (x) = , for 0 ≤ x ≤ 5 and = 0 otherwise., 5, Find the probability that (i) waiting time is between 1 and 3, , , 7., , (ii) P (0·5 ≤ x ≤ 1·5), , (ii) waiting time is more than 4 minutes., , Suppose error involved in making a certain measurement is continuous r.v. X with p.d.f., f (x) = k (4 – x2), for –2 ≤ x ≤ 2 and = 0 otherwise., Compute : (i) P(x > 0), , 8., , 9., , (ii) P(–1 < x < 1), , (iii) P(–0·5 < x or x > 0·5), , The following is the p.d.f. of continuous r.v., x, f (x) = , for 0 < x < 4 and = 0 otherwise., 8, (i) Find expression for c.d.f. of X , (ii) Find F(x) at x = 0·5 , 1.7 and 5., x2, Given the p.d.f. of a continuous r.v. X , f (x) = , for –1 < x < 2 and = 0 otherwise, 3, Determine c.d.f. of X hence find P( x < 1) , P( x < –2) , P( X > 0) , P(1 < x < 2), , 10. If a r.v. X has p.d.f.,, c, f (x) = , for 1 < x < 3, c > 0, Find c, E(X) and Var (X)., x, , 239
Page 250 :
Let us Remember, ֍, , A random variable (r.v.) is a real-valued function defined on the sample space of a random, experiment., The domain of a random variable is the sample space of a random experiment, while its codomain is the real line., Thus X : S → R is a random variable., There are two types of random variables, namely discrete and continuous., , ֍, , Discrete random variable : Let the possible values of discrete random variable X be denoted, by x1 , x2 , x3 , . . . , and the corresponding probabilities be denoted by p1 , p2 , p3 , . . . , where, pi = P [X = xi ] for i = 1, 2, 3, . . . . If there is a function f such that pi = P [X = xi ] = f (xi ) for, all possible values of X, then f is called the probability mass function (p. m. f.) of X., Note : If xi is a possible value of X and pi = P [X = xi ], then there is an event Ei in the sample, space S such that pi = P [Ei ]. Since xi is a possible value of X, pi = P [X = xi ] > 0. Also, all, possible values of X cover all sample points in the sample space S, and hence the sum of their, probabilities is 1. That is, pi > 0 for all i and Σ pi = 1., , ֍, , c.d.f (F(x)) : The cumulative distribution function (c. d. f.) of a discrete random variable X is, denoted by F and is defined as follows., , , , F (x) = P [X ≤ x], , =, , =, =, ֍, , xi < x, , xi < x, , xi < x, , P [X = xi], pi , f ( xi ), , Expected Value or Mean of Discrete r. v. : Let X be a random variable whose possible values, x1 , x2 , x3 , . . . , xn occur with probabilities p1 , p2 , p3 , . . . , pn respectively. The expected value, or arithmetic mean of X, denoted by E (X ) or µ is defined by, n, , , , E(X ) = µ =, , i=1, , xi pi = x1 p1 + x2 p2 + x3 p3 + . . . + xn pn, , In other words, the mean or expectation of a random variable X is the sum of the products of, all possible values of X by their respective probabilities., , 240
Page 251 :
֍, , Variance of Discrete r. v. : Let X be a random variable whose possible values x1 , x2 , x3 , . ., . , xn occur with probabilities p1 , p2 , p3 , . . . , pn respectively. The variance of X, denoted by, Var (X ) or σx2 is defined as, 2, σx, , n, , = Var (X ) =, , i=1, , (xi − µ)2 pi, , The non-negative number σx = Var (X ), is called the standard deviation of the random variable X., Another formula to find the variance of a random variable. We can also use the simplified form of, n, , Var (X ) =, , n, , xi pi −, 2, , i=1, , i=1, , xi pi, , 2, , 2, , Var (X ) = E(X 2 ) − [E(X )] , ֍, , n, , where, , i=1, , xi2 pi = E(X 2 ), , Probability Density Function (p. d. f.) : Let X be a continuous random variable defined on, interval S = (a , b). A non-negative integrable function f (x) is called the probability density, function (p. d. f.) of X if it satisfies the following conditions., 1. f (x) is positive every where in S, that is, f (x) > 0, for all x ∈ S., 2. The area under the curve f (x) over S is 1. That is, � f (x) dx = 1, S, , 3. The probability that X takes a value in A, where A is some interval, is given by the integral, of f (x) over that interval. That is, P [X ∈ A] = � f (x) dx, A, , ֍, , The cumulative distribution function (c. d. f.) of a continuous random variable X is defined, as :, x, , F (x) = � f (t) dt for a < x < b., a, , MISCELLANEOUS EXERCISE 7, (I) Choose the correct option from the given alternatives :, (1), , P.d.f. of a.c.r.v X is f (x) = 6x (1 − x), for 0 ≤ x ≤ 1 and = 0, otherwise (elsewhere), , If P (X < a) = P (X > a), then a =, 1, (A) 1, (B), 2, , (C), , 241, , 1, 3, , (D), , 1, 4
Page 252 :
(2), , , If the p.d.f of a.c.r.v. X is f (x) = 3 (1 − 2x2), for 0 < x < 1 and = 0, otherwise (elsewhere), then the c.d.f of X is F(x) =, , (A) 2x − 3x2, , (B) 3x − 4x3, (C) 3x − 2x3, (D) 2x3 − 3x, x2, (3) If the p.d.f of a.c.r.v. X is f (x) =, , for −3 < x < 3 and = 0, otherwise, 18, then P (| X | < 1) =, 1, 1, 1, 1, (A), (B), (C), (D), 27, 28, 29, 26, (4) If a d.r.v. X takes values 0, 1, 2, 3, . . . which probability P (X = x) = k (x + 1)·5 −x, where k is, a constant, then P (X = 0) =, 16, 7, (B), (A), 25, 25, (5), , (C), , 18, 25, , (D), , 19, 25, , (5 Cx), If p.m.f. of a d.r.v. X is P (X = x) =, , for x = 0, 1, 2, 3, 4, 5 and = 0, otherwise, 25, , If a = P (X ≤ 2) and b = P (X ≥ 3), then E (X ) =, (A) a < b, , (C) a = b, (D) a + b, x, , for x = 1, 2, 3, . . ., n and = 0, otherwise, (6) If p.m.f. of a d.r.v. X is P (X = x) =, n (n + 1), , then E (X ) =, n 1, n 1, n 1, n 1, +, (B), +, (C), +, (D), +, (A), 3 6, 2 5, 1 3, 1 2, c, (7) If p.m.f. of a d.r.v. X is P (x) = 3 , for x = 1, 2, 3 and = 0, otherwise (elsewhere), x, , then E (X ) =, 294, 297, 294, 343, (B), (C), (D), (A), 251, 294, 297, 297, (8), , (B) a > b, , If the a d.r.v. X has the following probability distribution :, X, , −2, , −1, , 0, , 1, , 2, , 3, , P (X = x), , 0·1, , k, , 0·2, , 2k, , 0·3, , k, , , , then P (X = −1) =, 2, 3, 1, (B), (C), (A), 10, 10, 10, (9) If the a d.r.v. X has the following probability distribution :, , , , (D), , 4, 10, , X, , 1, , 2, , 3, , 4, , 5, , 6, , 7, , P (X = x), , k, , 2k, , 2k, , 3k, , k2, , 2k2, , 7k2 + k, , then k =, , (A), , 1, 7, , (B), , 1, 8, , (C), , 242, , 1, 9, , (D), , 1, 10
Page 253 :
(10) The expected value of X for the following p.m.f., X, , –2, , –1, , 0, , 1, , 2, , P (X ), , 0·3, , 0·4, , 0·2, , 0·15, , 0·25, , (A) 0·85, , (B) – 0·35, , (C) 0·15, , (D) – 0·15, , (II) Solve the following :, (1) Identify the random variable as either discrete or continuous in each of the following. Write, down the range of it., , (i) An economist is interested the number of unemployed graduate in the town of population, 1 lakh., , (ii) Amount of syrup prescribed by physician., , (iii) The person on the high protein diet is interested gain of weight in a week., , (iv) 20 white rats are available for an experiment. Twelve rats are male. Scientist randomly, selects 5 rats number of female rats selected on a specific day., , (v) A highway safety group is interested in studying the speed (km/hrs) of a car at a check, point., (2), , , (3), , The probability distribution of discrete r.v. X is as follows, X=x, , 1, , 2, , 3, , 4, , 5, , 6, , P (X = x), , k, , 2k, , 3k, , 4k, , 5k, , 6k, , (i) Determine the value of k. , , , (5), , X=x, , –3, , –2, , –1, , 0, , 1, , 2, , 3, , P (X = x), , 0·05, , 0·1, , 0·15, , 0·20, , 0·25, , 0·15, , 0.1, , (ii) X is non negative. (iii) X is odd., , (iv) X is even., , (5 Cx), The p.m.f. of a r.v. X is given by P (X = x) =, , for x = 0, 1, 2, 3, 4, 5 and = 0, otherwise., 25, Then show that P (X ≤ 2) = P (X ≥ 3)., In the p.m.f. of r.v. X, 1, x, , 2, , 3, , 4, , 5, , 1, 20, , 3, 20, , a, , 2a, , 1, 20, , P (X), , (6), , Find P (X ≤ 4) , P (2 < X < 4) , P ( X ≥ 3)., , The following probability distribution of r.v. X, , , Find the probability that, (i) X is positive. , (4), , (ii), , Find a and obtain c.d.f. of X., A fair coin is tossed 4 times. Let X denotes the number of heads obtained write down the, probability distribution of X. Also find the formula for p.m.f. of X., , 243
Page 254 :
(7), , Find the probability distribution of the number of successes in two tosses of a die, where a, success is defined as (i) number greater than 4 (ii) six appears on at least one die., , (8), , A random variable X has the following probability distribution., , , , X, , 0, , 1, , 2, , 3, , 4, , 5, , 6, , 7, , P (X ), , 0, , k, , 2k, , 2k, , 3k, , k2, , 2k2, , 7k2 + k, , Determine (i) k, , (9), , , , (ii) P (X > 6), , (iii) P (0 < X < 3), , The following is the c.d.f. of r.v. X, X, , –3, , –2, , –1, , 0, , 1, , 2, , 3, , 4, , F (X ), , 0·1, , 0·3, , 0·5, , 0·65, , 0·75, , 0·85, , 0·9, , 1, , Find p.m.f. of X., , (i) P (–1 ≤ X ≤ 2), , (ii) P (X ≤ 3/ X > 0), , (10) Find the expected value, variance and standard deviation of r.v. X whose p.m.f. are given, below., (i), , (iii), , X=x, , 1, , 2, , 3, , P (X = x), , 1, 5, , 2, 5, , 2, 5, , (ii), , X=x, , 1, , 2, , 3, , ..., , n, , P (X = x), , 1, n, , 1, n, , 1, n, , ..., , 1, n, , (iv), , X=x, , –1, , 0, , 1, , P (X = x), , 1, 5, , 2, 5, , 2, 5, , X=x, , 0, , 1, , 2, , 3, , 4, , 5, , P (X = x), , 1, 32, , 5, 32, , 10, 32, , 10, 32, , 5, 32, , 1, 32, , (11) A player tosses two coins he wins ` 10 if 2 heads appears , ` 5 if 1 head appears and ` 2 if no, head appears. Find the expected winning amount and variance of winning amount., 3–x, , for x = –1, 0, 1, 2 and = 0, otherwise, (12) Let the p.m.f. of r.v. X be P (x) =, 10, Calculate E(X ) and Var (X )., (13) Suppose error involved in making a certain measurement is continuous r.v. X with p.d.f., f (x) = k (4 – x2) , for –2 ≤ x ≤ 2 and = 0 otherwise., , , Compute (i) P ( X > 0), , (ii) P (–1 < x < 1), (iii) P ( X < 0.5 or X > 0.5), 1, (14) The p.d.f. of r.v. X is given by f (x) = , for 0 < x < 2a and = 0, otherwise., 2a, a, 3a, =P X>, ., , Show that P X <, 2, 2, k, (15) The p.d.f. of r.v. of X is given by f (x) = , for 0 < x < 4 and = 0, otherwise., √x, Determine k . Determine c.d.f. of X and hence P (X ≤ 2) and P (X ≤ 1)., , v, , v, 244, , v
Page 255 :
8. BINOMIAL DISTRIBUTION, Let us Study, •, , Bernoulli Trial, , •, , Binomial distribution, , •, , Mean and variance of Binomial Distribution., Let us Recall, , •, , Many experiments are dichotomous in nature. For example, a tossed coin shows a ‘head’ or ‘tail’,, A result of student ‘pass’ or ‘fail’, a manufactured item can be ‘defective’ or ‘non-defective’, the, response to a question might be ‘yes’ or ‘no’, an egg has ‘hatched’ or ‘not hatched’, the decision is, ‘yes’ or ‘no’ etc. In such cases, it is customary to call one of the outcomes a ‘success’ and the other, ‘not success’ or ‘failure’. For example, in tossing a coin, if the occurrence of the head is considered, a success, then occurrence of tail is a failure., Let us Learn, , 8.1.1 Bernoulli Trial :, Each time we toss a coin or roll a die or perform any other experiment, we call it a trial. If a coin, is tossed, say, 4 times, the number of trials is 4, each having exactly two outcomes, namely, success or, failure. The outcome of any trial is independent of the outcome of any other trial. In each of such trials,, the probability of success or failure remains constant. Such independent trials which have only two, outcomes usually referred to as ‘success’ or ‘failure’ are called Bernoulli trials., Definition:, Trials of a random experiment are called Bernoulli trials, if they satisfy the following conditions :, (i), , Each trial has exactly two outcomes : success or failure., , (ii) The probability of success remains the same in each trial., Throwing a die 50 times is a case of 50 Bernoulli trials, in which each trial results in success (say, an even number) or failure (an odd number) and the probability of success ( p) is same for all 50, throws. Obviously, the successive throws of the die are independent trials. If the die is fair and has, six numbers 1 to 6 written on six faces, then, , , p=, , 1, and q = 1 − p , 2, , 245, , ∴q=, , 1, 2
Page 256 :
For example :, Consider a die to be thrown 20 times. if the result is an even number, consider it a success, else it is, 1, as there are 3 even numbers in the possible outcomes., a failure. Then p =, 2, 1, If in the same experiment, we consider the result a success if it is a multiple of 3, then p = as there, 3, are 2 multiples of 3 among the six possible outcomes. Both above trials are Bernoulli trials., SOLVED EXAMPLE, Ex. 1 : Six balls are drawn successively from an urn containing 7 red and 9 black balls. Tell whether, or not the trials of drawing balls are Bernoulli trials when after each draw the ball drawn is, , , (i) replaced, , (ii) not replaced in the urn., , Solution :, (i) The number of trials is finite. When the drawing is done with replacement, the probability of, 7, which is same for all six trials (draws). Hence, the drawing of, 16, balls with replacements are Bernoulli trials., , success (say, red ball) is p =, , (ii) , , , , When the drawing is done without replacement, the probability of success (i.e. red ball) in first, 7, 6, 7, trial is, in second trial is, if first ball drawn is red and is, if first ball drawn is black, 16, 15, 15, and so on. Clearly probability of success is not same for all trials, hence the trials are not, Bernoulli trials., , 8.2 Binomial distribution:, Consider the experiment of tossing a coin in which each trial results in success (say, heads) or, failure (tails). Let S and F denote respectively success and failure in each trial. Suppose we are interested, in finding the ways in which we have one success in six trials. Clearly, six different cases are there as, listed below:, SFFFFF, FSFFFF, FFSFFF, FFFSFF, FFFFSF, FFFFFS., 6!, = 15 combinations., 4!×2!, But as n grows large, the calculation can be lengthy. To avoid this the number for certain probabilities, can be obtained with Bernoullis formula.For this purpose, let us take the experiment made up of three, Bernoulli trials with probabilities p and q = 1 – p for success and failure respectively in each trial. The, sample space of the experiment is the set, Similarly, two successes and four failures can have, , S = �SSS, SSF, SFS, FSS, SFF, FSF, FFS, FFF�, , 246
Page 257 :
The number of successes is a random variable X and can take values 0, 1, 2, or 3.The probability, distribution of the number of successes is as below :, P (X = 0), , = P (no success), , = P (�FFF�) = P(F )·P(F )·P(F ) , since trials are independent., , = q · q · q = q3, P (X = 1), , = P (one success), , = P (�SFF, FSF, FFS�), , = P (�SFF�) + P (�FSF�) + P (�FFS�), , = P (S)·P(F )·P(F) + P(F)·P(S)·P(F) + P(F)·P(F)·P(S), = p·q·q + q·p·q + q·q·p = 3pq2, P (X = 2), , = P (two success), , = P (�SSF, SFS, FSS�), , = P (�SSF�) + P (�SFS�) + P (�FSS�), , = P(S)·P(S)·P(F) + P(S)·P(F)·P(S) + P(F)·P(S)·P(S), = p·p·q + p·q·p + q·p·p = 3p2q, and , , P (X = 3), , = P (three successes), , = P (�SSS�), , = P(S)·P(S)·P(S), = p3, Thus, the probability distribution of X is, X, , 0, , 1, , 2, , 3, , P (X ), , q3, , 3q2p, , 3qp2, , p3, , Also, the binominal expansion of, (q + p)3 is q3 + 3q2 p + 3 qp2 + p3, Note that the probabilities of 0, 1, 2 or 3 successes are respectively the 1st, 2nd, 3rd and 4th term in the, expansion of (q + p)3., Also, since q + p = 1, it follows that the sum of these probabilities, as expected, is 1.Thus, we may, conclude that in an experiment of n-Bernoulli trials, the probabilities of 0, 1, 2,..., n successes can be, , 247
Page 258 :
obtained as 1st, 2nd, 3rd , . . . , (n + 1)th terms in the expansion of (q + p)n . To prove this assertion (result),, let us find the probability of x successes in an experiment of n-Bernoulli trials., Clearly, in case of x successes (S), there will be (n – x) failures (F ). Now x successes (S ) and (n – x), n!, failures (F) can be obtained in, ways., x ! (n – x) !, In each of these ways the probability of x successes and (n – x) failures, = P (x successes)· P ((n – x) failures), = (P (S)·P (S). . . P (S) x times)·(P (F )·P(F))· . . . ·(P(F)·(n – x) times), = ( p·p·p. . . p x times) (q·q·q. . . q (n – x) times), = px·qn – x, Thus probability of getting x successes in n-Bernoulli trial is, P (x successes out of n trials) =, , n!, × px × qn – x = nCx px × qn – x, x ! (n – x) !, , Clearly, P (x successes), i.e. nCx px qn – x is the (x + 1)th term in the binomial expansion of (q + p)n ., Thus, the probability distribution of number of successes in an experiment consisting of n-Bernoulli, trials may be obtained by the binomial expansion of (q + p)n . Hence, this distribution of number of, successes X can be written as, 0, , X, P (X ), , n, , C0 p0 × qn, , 1, , 2, , C1 p1 × qn – 1 nC2 p2 × qn – 2, , n, , ..., ..., , x, , ..., , Cx px × qn – x, , ..., , n, , n, n, , Cn pn × q0, , The above probability distribution is known as binomial distribution with parameters n and p,, because for given values of n and p, we can find the complete probability distribution. It is represented, X~B (n, p) as read as X follows binomial distribution with parameters n, p, The probability of x successes P (X = x) is also denoted by P (x) and is given by, n, P (x) = Cx·qn – x × p x, x = 0, 1, . . . , n, (q = 1 – p), , This P (x) is called the probability function of the binomial distribution., A binomial distribution with n-Bernoulli trials and probability of success in each trial as p, is, denoted by B (n, p) or X~B (n, p)., Lets Note :, , (i) The number of trials should be fixed., , , , (ii) The trials should be independent., , 248
Page 259 :
SOLVED EXAMPLES, Ex. 1 : If a fair coin is tossed 10 times, find the probability of getting, , , (i) exactly six heads , , (ii) at least six heads, , (iii) at most six heads, , Solution : The repeated tosses of a coin are Bernoulli trials. Let X denote the number of heads in an, experiment of 10 trials., 1, 1, 1, Clearly, X ~ B (n, p) with n = 10 and p = , q = 1 − p = 1 −, ∴ q=, 2, 2, 2, P (X = x) = nCx px × qn – x, 1 x, 1 n–x, ×, 2, 2, Exactly six successes means x = 6, , = 10Cx, (i) , , P (X = 6) = 10C6, , 1, 2, , 6, , 1, 2, , ×, , 10 – 6, , =, , 1, 10 !, ×, 2, 6 ! (10 – 6) !, , 6, , ×, , 1, 2, , , (ii) , , 4, , =, , 1, 10 × 9 × 8 × 7, ×, 2, 4×3×2×1, , =, , 105, 512, , At least six successes means x ≥ 6, , 10, , P (X ≥ 6) = [P (X = 6) + P (X = 7) + P (X = 8) + P (X = 9) + P (X = 10)], = 10C6, =, , 1, 2, , 6, , ×, , 1 4 10, 1 7 1, + C7, ×, 2, 2, 2, , 1, 10 × 9 × 8 × 7, ×, 2, 4×3×2×1, , 10, , +, , 3, , 1 8 1, ×, 2, 2, , + 10C8, , 1, 10 × 9 × 8, ×, 2, 3×2×1, , = (210 + 120 + 45 + 10 + 1) ×, , 10, , +, , 2, , + 10C9, , 1 9 1 1 10, 1, ×, + C10, 2, 2, 2, , 1, 10 × 9, ×, 2, 2×1, , 10, , + 10, , 1, 2, , 10, , +, , 1, 2, , 10, , 10, , 1, 1024, , 386, 193, =, 1024 512, At most six successes means x ≤ 6, , =, (iii) , , P (X ≤ 6) = 1 – (P (X > 6), , , = 1 – [P (X = 7) + P (X = 8) + P (X = 9) + P (X = 10)], , , , =1–, , 10, , C7, , 1 7 1, ×, 2, 2, , 3, , 1, 10 × 9 × 8, = 1 –, ×, 2, 3×2×1, = 1 –, , + C8, 10, , 10, , 1 8 1, ×, 2, 2, , 2, , 1, 10 × 9, +, ×, 2, 2×1, , (120 + 45 + 10 + 1) ×, , 1, 1024, , + C9, 10, , 10, , =1–, , 249, , 1 9 1 1 10, 1, ×, + C10, 2, 2, 2, , 1, + 10, 2, , 1, ×, 2, , 10, , 10, , 1, ×, 2, , 0, , 10, , 176, 88, 512 – 88 424 53, =1–, =, =, =, 1024, 512, 512, 512 64, , ×, , 1, 2, , 0
Page 260 :
Ex. 2 : Ten eggs are drawn successively with replacement from a lot containing 10% defective eggs., Find the probability that there is at least one defective egg., Solution : Let X denote the number of defective eggs in the 10 eggs drawn., Since the drawing is done with replacement, the trials are Bernoulli trials., 1, Probability of success =, 10, 1, 1, 9, , p = , , q =1−p=1−, ∴ q=, 10, 10, 10, n = 10, 1, 10, , , , X~B, , , , P (X = x) = 10Cx, , , , Here X ≥ 1, , , , P (X ≥ 1) = 1 − 10C0, , 10,, , 1, 10, , x, , 1, 10, , , , = 1 − 1 × 1×, , , =1−, , 9, 10, , ×, , 9, 10, , 10 – x, , 0, , 9, 10, , ×, , 9, 10, , 10, , 10, , 10, , 8.3 Mean and Variance of Binomial Distribution ( Formulae without proof ) :, Let X~ B (n, p) then mean or expected value of r.v. X is denoted by µ or E (X ) and given by, µ = E (X ) = np., The variance is denoted by Var (X ) and given by Var (X ) = npq., Standard deviation of X is denoted by SD (X ) or σ and given by SD (X ) = σx = Var (X ), For example : If X~B ( 10 , 0·4 ) then find E (X) and Var (X )., Solution : Here n = 10, p = 0·4,, q=1−p, , q = 1 − 0·4 = 0·6, , E (X ) = np, = 10 × 0·4 = 4, , , Var (X ) = npq, , = 10 × 0·4 × 0·6, = 2.4, , 250
Page 261 :
SOLVED EXAMPLES, Ex. 1 : Let the p.m.f. of r.v. X be, 5 x, 4, P (X = x) = 4Cx, ×, 9, 9, then find E (X) and Var (X )., , 4–x, , , for x = 0, 1, 2, 3, 4., , Solution : P (X = x) is binomial distribution with n = 4 , p =, , , E (X ) = np, , = 4 ×, , , Var (X ) = npq, , = 4 ×, , 5, 4, and q =, 9, 9, , 20, 5, =, 9, 9, 80, 5, 4, ×, =, 81, 9, 9, , Ex. 2 : If E (X ) = 6 and Var (X ) = 4·2, find n and p., Solution : E(X ) = 6 therefore np = 6 and Var (X ) = 4·2 therefore npq = 4·2, npq 4·2 , =, ∴ q = 0·7, 6, np, , ∴ p = 1 − q = 1 − 0·7, ∴ p = 0·3, np = 6 , 6, ∴ n × 0·3 = 6 , ∴ n=, = 20, 0·3, EXERCISE 8.1, (1) A die is thrown 6 times. If ‘getting an odd number’ is a success, find the probability of, (i) 5 successes, (ii) at least 5 successes, (iii) at most 5 successes., (2) A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of, two successes., (3) There are 5% defective items in a large bulk of items. What is the probability that a sample of 10, items will include not more than one defective item?, (4) Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards. find the, probability that, (i) all the five cards are spades, (ii) only 3 cards are spades, (iii) none is a spade., (5) The probability that a bulb produced by a factory will fuse after 150 days of use is 0·05. Find the, probability that out of 5 such bulbs, (i) none, (ii) not more than one, (iii) more than one, (iv) at least one, will fuse after 150 days of use., , 251
Page 262 :
(6) A bag consists of 10 balls each marked with one of the digits 0 to 9. If four balls are drawn, successively with replacement from the bag, what is the probability that none is marked with the, digit 0?, (7) On a multiple choice examination with three possible answers for each of the five questions, what, is the probability that a candidate would get four or more correct answers just by guessing?, (8) A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is 1/100., find the probability that he will win a prize, (i) at least once, (ii) exactly once, (iii) at least twice, (9) In a box of floppy discs it is known that 95% will work. A sample of three of the discs is selected at, random. Find the probability that, (i) none, (ii) 1, (iii) 2 , (iv) all 3 of the sample will work., (10) Find the probability of throwing at most 2 sixes in 6 throws of a single die., (11) It is known that 10% of certain articles manufactured are defective. What is the probability that in, a random sample of 12 such articles, 9 are defective?, (12) Given that X~ B (n, p), (i) If n = 10 and p = 0·4, find E (X ) and Var (X ) (ii) If p =0·6 and E(X ) = 6, find n and Var (X )., (iii) If n = 25 , E(X ) = 10 find p and SD(X )., , (iv) If n = 10, E(X ) = 8, find Var (X )., , Let us Remember, ֍, , Trials of a random experiment are called Bernoulli trials, if they satisfy the following, conditions :, (i), , Each trial has exactly two outcomes : success or failure., , (ii) The probability of success remains the same in each trial., Thus probability of getting x successes in n-Bernoulli trial is, P (x successes out of n trials) =, , n!, x ! (n – x) !, , × px × qn – x = nCx px × qn – x, , Clearly, P (x successes), i.e. nCx px qn – x is the (x + 1)th term in the binomial expansion of, (q + p)n ., ֍, , Let X~ B (n, p) then mean of expected value of r.v. X is denoted by µ., E (X ) and given by µ = E (X ) = np., The variance is denoted by Var (X ) and given by Var (X ) = npq., Standard deviation of X is denoted by SD (X ) or σ and given by SD (X ) = σx = Var (X ), , 252
Page 263 :
MISCELLANEOUS EXERCISE 8, (I) Choose the correct option from the given alternatives :, (1), , A die is thrown 100 times. If getting an even number is considered a sucess, then the standard, deviation of the number of successes is, , (A) √ 50, (2), , (C) 25, , (D) 10, , The mean and the variance of a binomial distribution are 4 and 2 respectively. Then the, probablity of 2 successes is, , (A), (3), , (B) 5, , 128, 256, , (B), , 219, 256, , (C), , 37, 256, , (D), , 28, 256, , For a binomial distribution, n = 5. If P (X = 4) = P (X = 3) then p = . . ., 3, 2, 1, (B), (C) 1, (D), 4, 3, 3, In a binomial distribution, n = 4. If 2 P (X = 3) = 3 P (X = 2) then p = . . ., , (A), (4), , (A), (5), , 4, 13, , (B), , If X~ B (4, p) and P (X = 0) =, , (A), , 1, 16, , (B), , 5, 13, , (C), , 9, 13, , (D), , 6, 13, , (D), , 1, 8, , 16, , then P (X = 4) = . . ., 81, 1, 81, , (C), , 1, 27, , 3, ., 4, How many minimum number of times must he fire so that the probability of hitting the target, at least once is more than 0·99 ?, (6), , The probability of a shooter hitting a target is, , (A) 2, (7), , (B) 3, , (C) 4, , (D) 5, , If the mean and variance of a binomial distribution are 18 and 12 respectively, then n = ..., , (A) 36, , (B) 54, , (C) 18, , (D) 27, , (ii) P (X ≥ 1), , (iii) P (X ≤ 8)., , (II) Solve the following :, (1), , Let X~ B (10, 0·2), Find (i) P (X = 1), , (2), , Let X~ B (n, p), , , (3), , , (i) If n = 10 , E (X ) = 5, find p and Var (X )., (ii) If E (X )= 5 and Var (X ) = 2·5 , find n and p., , If fair coin is tossed 10 times find the probability that it shows heads, (i) 5 times., , (ii) in the first four tosses and tail in last six tosses., , 253
Page 264 :
(4), , Probability that bomb will hit target is 0·8. Find the probability that out of 10 bombs dropped, exactly 2 will miss the target., , (5), , The probability that a mountain-bike rider travelling along a certain track will have a tyre, burst is 0·05. Find the probability that among 17 riders : (i) exactly one has a burst tyre, , , , (ii) at most three have a burst tyre (iii) two or more have burst tyres., , (6), , Probability that a lamp in a classroom will burnt out will be 0·3. Six lamps are fitted in the, classroom. If it is known that the classroom is unusable if the number of lamps burning in it, is less than four, find the probability that classroom can not used at random occasion., , (7), , Lot of 100 items contains 10 defective items. Five items are selected at random from the, lot and sent to the retail store. What is the probability that the store will receive at most one, defective item?, , (8), , A large chain retailer purchases certain kind of electric device from manufacturer. The, manufacturer indicates that the defective rate of the device is 3% . The inspector of the retailer, picks 20 items from a shipment. What is the probability that the store will receive at most one, defective item?, , (9), , The probability that the certain kind of component will survive a check test is 0·6. Find the, probability that exactly 2 of the next 4 components tested survive., , (10) An examination consists of 10 multiple-choice questions, in each of which a candidate has, to deduce which one of five suggested answers is correct. A completely unprepared student, guesses each answer completely randomly. What is the probability that this student gets 8 or, more questions correct? Draw the appropriate moral !, (11) The probability that a machine will produce all bolts in a production run within specification, is 0·998. A sample of 8 machines is taken at random. Calculate the probability that, , , (i) all 8 machines , , (ii) 7 or 8 machines, , , , (iii) at least 6 machines will produce all bolts within specification, , (12) The probability that a machine develops a fault within the first 3 years of use is 0·003. If 40, machines are selected at random, calculate the probability that 38 or more will not develop, any faults within the first 3 years of use., (13) A computer installation has 10 terminals. Independently, the probability that any one terminal, will require attention during a week is 0·1. Find the probabilities that, , , (i) 0, , (ii) 1, , (iii) 2, , , , (iv) 3 or more, terminals will require attention during the next week., , 254
Page 265 :
(14) In a large school, 80% of the pupils like mathematics. A visitor to the school asks each of, 4 pupils, chosen at random, whether they like mathematics., , , (i) Calculate the probabilities of obtaining an answer yes from 0, 1, 2, 3, 4 of the pupils, , , , (ii) Find the probability that the visitor obtains the answer yes from at least 2 pupils:, , , , (a) when the number of pupils questioned remains at 4, , , , (b) when the number of pupils questioned is increased to 8., , (15) It is observed that, it rains on 12 days out of 30 days. Find the probability that, , , (i) it rains exactly 3 days of week., , (ii) it will rain on at least 2 days of given week., , (16) If probability of success in a single trial is 0·01. How many trials are required in order to have, probability greater than 0·5 of getting at least one success?, (17) In binomial distribution with five Bernoulli's trials, probability of one and two success are, 0·4096 and 0·2048 respectively. Find probability of success., , v, , v, , 255, , v
Page 267 :
(xv) − sec x, (xvi) 2 log 4 +, (xvii) 2x −, , 9x2, 3x, −, x2 + 5 2 (2x3 − 4), , (xviii) − sin x log a −, (xx), , 6x, x2 − 3, , −, , 1, x log x, , x(x2 + 2)3 (7x2 + 38), (x2 +, , (4) (i) −16, , (ii) 35 (iii) −20, , (8) e 2x + 6ex + 14, e, , x2, , +5, , 2, , 1, , 2, , (vi), , (vii) 2e2x − 3, , (viii), , 1, (2) (i), (ii), x, x·e (x + 2), 1, (iii) x, (iv), 7 (x log 7 + 1), (v), (3) (i), 1, 4, (5) (i), , (ii), , 3 √x, 2 √ 1 − x3, , (x), , 2x, , 2, , 2xex, , ex, , 1, x log 2, 1, cos x − x sin x, x, 2x2 + 1, , (iii), , 1, 12, , (iv), , − 5x log 5 (iii), , 1, 6, 1, −, 2, , 1, 2, 3, (viii) −, 2, 1, (xi) −, 2, , 1, , (ii), , (iv) 3, , (v), , (v), , 3, , (v), , −, , (vii), , 2·3x log 3, 1 + 32x, , √1 − x2, , −, , 1, 2, , (vi) −6, (ix) −, , 7, 2, , (xii), , 2, 3, , 1, , (iii), , 1, 2 √x, , ex, , (vi) 2x log 2, , 2, 1 + x2, 2, (iv) ±, √1 − x2, 2ex, (vi) −, 1 + e2x, (ii), , 1, , 4x + 2 log 4, 2·4x log 4, (viii), or, 1 + 42x, 1 + 42x, (ix) −, , 1, 4, , (ii), , (9) (i), , 1, 1 + log x, 1, 14, , (viii), , 2, 1 + x2, 2, (iii) −, 1 + x2, , 4 √x 2 − √x, 1, 2, (iii), ,, for, x, >, 2 , (iv), 3, 2x − 1, 3 (x − 2)2, (v), , 2, √ 2 − x2, , (8) (i), , (ii) −, , 2√ x, , (vii), , (x), , EXERCISE 1.2, 1, , x, √ 1 − x4, , (vii) −, , 2e2x + 6ex, 8, g' [ f (x)]· f ' (x), 2xe x +5, − 2e6., , (1) (i), , (vi), , (iv) − x, , , 2x, ex, f ' [g(x)]·g' (x),, , (iv), , 4x log 4, −, 1 + 42x, , 1, 2√ x (1 + x), , (7) (i), , (iv) 28, , ex, √1 − e2x, , (v), , (ix) 9x8, , 3, 5) 2, , 2π, (7) x = 0 or, or 2π, 3, , 12, (6), 5, , (5) −5 , , 3x2, (iii) −, 1 + x6, , 6, 2, +, 5 − 4x 7 − 6x, , (xix) 0, , 1, (ii), x [ 1 + (log x)2], , (6) (i), , 1, 5, , (xi), , (4), , (10) (i), and (ii) derivative proved., , 257, , 10, 1 + 25x2, , 5x√x, 1 + x5, , (x) −, (xii), , 5, 3, +, 1 + 9x2 1 + 25x2, , 3√x, 1 + x3, , 1, 2 √ x (1 + x)
Page 268 :
(ii), , 7, 5, −, 1 + 49x2 1 + 25x2, , (vi), , (iii), , 1, 2√x, , (viii), , 1, 3, −, 1 + 9x 1 + x, , 1, 3, (iv) 2 log 2, +, 2x, 1 + 9(2 ) 1 + 22x, , (ix), , x, , (v) 2x log 2, , 3a, 2a, +, , a2 + 9x2 a2 + 4x2, 2, , −, , 2, , 1 + (2x + 1), 2, 2, , 1 + (2x + 3), , +, , (vii) 1, 3, , 1 + (3x − 4)2, 1, , 1 + (x − 1)2, , 1, 2, −, 2x, 1 + 4(2 ) 1 + 22x, , EXERCISE 1.3, (1) (i), (ii), , 3, 4, 2, (x + 1)2, −, −, (x + 3)3 (x + 3)4 x + 1 x + 2 x + 3, 1, 3, , 3, , 2, 4, 4, 4x − 1, −, +, 2 4x − 1, 2x + 3 5 − 2x, (2x + 3) (5 − 2x), 3, , (iii) (x2 + 3) 2 ·sin3 2x·2x2, 3, , (iv), (v), , (x2 + 2x + 2) 2, , (√ x + 3)3 (cos x)x, , [x cot x + log (sin x)] , , ex e −1 + e x + x x (1 + log x), , (iii) (log x) x, (iv) x e · e x, x, , (v), , 3, 3(x +1), −, + x tan x − log (cos x), x2 + 2x + 2 2√ x (√ x + 3), , x5·tan3 4x 5, + 24 cosec 8x − 6 cot 3x , sin2 3x, x, , (vii) sinx x, (2) (i), , 3x, + 6 cot 2x + 2x log 2, x +3, 2, , −1, , (vi) xtan, , x, , log x, tan−1 x, +, 1 + x2, x, , (viii) cos (xx) · xx (1 + log x), , (ii) x x · x x · log x 1 + log x +, , 1, , x, , x log x, , + e x · x x (1 + log x), x, , 1, + log (log x) + (cos x) cot x [1 + cosec2 x log (cos x)], log x, 1, sin x, + log x + (log x) sin x, + cos x log (log x), x, x log x, , sec2 x · etan x + (log x) tan x, , tan x, + sec2 x log (log x), x log x, , (vi) (sin x)tan x [1 + sec2 x log (sin x)] + (cos x) cot x [1 + cosec2 x log (cos x)], (vii) 10 x x x log 10 (1 + log x) + x x ·x 9 (1 + 10 log x) + x 10 ·10 x, x, , 10, , x, , (viii) 2, , 258, , 1, + log x·log 10, x
Page 269 :
y, x, (ii) −, x, y, 3x2 + 2xy + y2, √ y (2 √ x + √ y ), (iii) −, (iv) − 2, x + 2xy + 3y2, √ x (2 √ y + √ x ), e y + yex, y, (v) −, (vi) − x, e + xey, x, 1 + y sin (xy), sin (x − y) + e x + y, (vii), (viii), −, 1 + x sin (xy), sin (x − y) − e x + y, , (3) (i), , (ix), (x), , EXERCISE 1.5, , −, , (1) (i), (ii), , (iii) − e 4x (9 cos 5x + 40 sin 5x ), 1 + log x, (iv) x (5 + 6 log x ) (v) −, (x log x)2, (iv) x x − 1 + x x (1 + log x)2, , y (1 − xe x − y), x (1 − ye x − y), , (2) (i), , sin (x − y) − cos (x + y) − 1, sin (x − y) + cos (x + y) − 1, , 1, t, , (ii), , (iv) sec3 θ (v), , y ( t + 1) log a, axt, 3√ 3, , (vii) −, , (ii) − √ 3, , 2, , (iii), , (4) (i), , 2, √ a2 + m2, , , , b, θ, tan, a, 2, , 2, , (vi), (2) (i), , b, cos θ, a, , 1, 2, , (viii), , (iii) −, , , , 1, 3, , (ii), , π, 6, , x cos x + sin x, , sec2 x, , (iii) −, , 1, 2, , (vi) −, , x √ x2 − 1, 2, , (iv) 2, , (v), , (v), (ii) 1 , , (iv) −, , dny, dx, , =, n, , dny, dx n, dny, dx, , n, , (ii) −, , 1, 4at3, , 2√ 2 b, a2, , m ! an (ax + b) m − n, if m > 0, m > n ,, (m − n) !, , = 0 if m > 0, m < n, = n ! a n if m > 0, m = n, , (− 1) n n !, (iii) a ne ax + b, n+1, x, , nπ, (− 1) n − 1 (n − 1) ! a n, (vi), cos, +x, 2, (ax + b) n, , nπ, + ax + b, 2, nπ, (viii) (− 2) n cos, + 3 − 2x, 2, (− 1) n − 1 (n − 1) ! 2 n, (ix), (2x + 3) n, (vii) a n sin, , − x (log x)2·3x, , (1 + log x)· xx + 1 − sin x, (vii), sin x + x cos x·log x, (viii), , 1, θ, cosec4, , 4a, 2, , (iv) p na px + q (log a) n, , (iv) 1 − √ 2 (v) 3 + π, (4) (i), , −, , (iii) 6, , EXERCISE 1.4, (1) (i), , 12, x4, 2e 2x (1 + tan x) ·(2 + tan x + tan2 x), , 40x3 − 24x −, , (x), , √ 1 − x2, , (− 1) n · n ! · 3 n, (3x − 5) n + 1, n, , (xi) e ax (a2 + b2) 2 ·cos bx + c + n tan−1, , 4(1 + x ), 2, , (xii) e 8x·(10)n cos 6x + 7 + n tan−1, , 259, , 3, 4, , b, a
Page 270 :
MISCELLANEOUS EXERCISE 1, (I), 1, D, (II) (1), , 2, C, 3, 4, , 3, C, , 4, B, , (ii) Does not exist, , 5, A, , (A) 3, (B) 5, (C) 4, (D) 1., , (3), , (i) −, , 1, 9, , (iv) −, , 4, 9, , , (4), , , (i) −, , 40, 3, , (iii) −, , 29, 96, , 8, C, (iv) −, , 10, C, 1, , 2·√ 1 − x2, , 11, A, , 12, B, , [Hint : x = cos 2θ], , 5, 3, +, 1 + 9x2 1 + 25x2, , (vi), , 1, [Hint : x = tan θ], 2 (1 + x2), , (6), , [Hint : x = cos 2θ], √ 1 − x2, , 9, B, , (v), , x, , , , 1, (ii) − [Hint : x = cos 2θ], 2, , (iii), , 7, D, , , (iii) −2, , (2), , (ii) −, , 6, C, , (i), , √ 1 − x2, 4 (1 + x2), , (ii) −, , 2x, , √ 1 + x2. sin (log x), , (iii) 1, , 3, [Hint : √ x = tan θ], 2√ x (1 + x), , 2. APPLICATIONS OF DERIVATIVES, EXERCISE 2.1, (1) (i), (ii), , (3) (2, −2) −, , 2x − y + 4 = 0, x + 2y − 8 = 0, 4x − 5y + 12 = 0, 5x + 4y − 26 = 0,, , (6) a = 2, b = − 7 (7) (4, 11) and − 4, −, (8) 0.8 π cm2/sec., , (iv) πx + 2y − 2π = 0,, , (v), , (4) y = 0 and y = 4, , (5) x + 3y − 8 = 0, x + 3y + 8 = 0, , (iii) y = 2, x =√ 3, , , , 14, 2, ,−, 27, 3, , 3 √6, , 4x − 2πy + π2 − 4 = 0, , (10), , 2x − y = 0, 4x + 8y − 5π = 0, , (12) 7.2 cm3/ sec, , (vi) 4x + 2y − 3 = 0, 2x − 4y + 1 = 0, , 2, , (9), , 6 cm3/ sec., , cm2/ sec. (11) 8 cm2/ sec, (13) 3 km/hr, , 9, 3, meter/sec. (ii), meter/sec., 8, 8, 4π, (16), (15) 0.9 meter/sec., cm3/ sec, 3, , (14) (i), , (vii) 17x − 4y − 20 = 0, 8x + 34y − 135 = 0, (2) (4, 1), , 260, , 31, 3
Page 271 :
EXERCISE 2.2, (1) (i) 2.9168, , (ii) 3.03704, , EXERCISE 2.4, (iii) 1.9997, , (1) (i) Increasing ∀ x ∈ R, , (iv) 248.32 (v) 64.48, , (ii) Decreasing∀ x ∈ R, , (ii) 0.42423, , (2) (i) 0.953, , (iii) Increasing ∀ x ∈ R, , (iii) 0.4924, , (2) (i) x < −1 and x > 2 , , (iv) 1.02334, (3) (i) 0.7845, , (ii) 0.7859, , (5) (i) 4.6152, , (ii) 2.1983, , (6) (i) 6.91, , (ii) 9.72, , (iii) x < −2 and x > 6, , (iii) 0.7859, , (4) (i) 2.70471 (ii) 8.1279, , (3) (i) −1< x < 2 , , (iii) 9.09887, , Valid, , (4) (a) (−∞, −4] ∪ [12, ∞), (b) −4 ≤ x ≤ 12 i.e. [−4, 12], , (ii), , Valid , , (iii) Invalid, , (iv), , Valid, , (v), , (vi), , Invalid, , Invalid, , (5) (a) x < −3 and x > 8, , (b) −3 < x < 8, , (6) (a) −1 < x < 1 , , (b) (−∞, −1) ∪ (1, ∞), , (9) (i), (ii), , (2) b = 1, π, 5π, (3) (i), or, , 4, 4, , (ii), , 5, c = π (iii) c =, 2, , (4) p = −6, q = 11, , (6), , c = −2, , (7) (i) e − 1, (iv), , 1, 2, , (ii) 2 ±, , (ii) (−5, 5) − {0}, , (iii) x ∈ (2, 4), , (iii) 3.006049, , EXERCISE 2.3, (1) (i), , (ii) R − {1}, , 2, √3, , (iii), , Max =, , 36, 16, , Min = −, 25, 27, , Max = − 3, Min = − 128, , (iii) Max = 20, Min = 16 (iv) Min = 8, (v) Min = −, (10) 15, 15, , 1, 7, , 1, e, , (11) 10, 10, , (14) l = √ 2 and b =, , (v) 3 + √ 2, , , , (vi) Max =, (12) 9 , , 1, e, , (13) 12.8, , 1, √2, , (15) Radius = Height = a , , (16) 3, 3, , (17) Side of square base = 8 cm, Height = 4 cm, (18) x = 75, P = 4000 , (22), , 4πr 3, 3 √3, , (19) 6, 9, , cm3, , MISCELLANEOUS EXERCISE 2, (I), 1, A, , 2, C, , 3, B, , 4, B, , 5, D, , 261, , 6, C, , 7, D, , 8, A, , 9, D, , 10, D
Page 272 :
(II) (2) 4, , (11) Increasing in [e, ∞), Decreasing in (1, e], , (3) 14x − 13y + 12 = 0, 13x + 14y − 41 = 0, , 60, 30, 30, ,b=, ,r=, π+4, π+4, π+4, , 2, (4), ft/sec , 9π, , 16, 16, (5), ,3 , −, ,−3, 3, 3, , (15) l =, , (6) c = 0 , , (7), , (17) Side =, , c = 2 (8) 2.025, , (9) 1.03565 , 1, (10) Decreasing in 0,, and, e, 1, , Increasing in , ∞, e, , l, l, x, , Radius =, =, π+4, 2(π + 4) 2, , (18) 24, 45 , , 5, , Min = 1, 4, , (21) Max =, , 3. INDEFINITE INTEGRATION, 3, , (iv), , EXERCISE 3.1, (1) (i), , x4, 4, , +, , x3, 3, , −, , x2, 2, , + x + c (ii), , x2, 4, 6, (v), 5, , 3, , − 2x2 + 4x + c, , (v), , − 7x + c, √x, 1, 5x2, −, + 3 log x − 4 + c, x, 2, 10, x2 √ x − 4√ x −, +c, √x, , (iii) 3 tan x − 4 log x −, (iv), , 2, , x3, , (2) (i) tan x − x + c, (iii) sec x + c, , 2 (x + 5) 2, 3, , − 14 √ x + 5 + c, , 3, 1, 13, (4x − 1) 2 −, √ 4x − 1 + c, 12, 4, , (vi) − cos 2x + c, (vii), , 2, 5x, 5x, sin, − cos, +c, 5, 2, 2, , (viii), , 1, (2x + sin 2x) + c, 4, , (ii) − 2 cos x + c, (ix) −, , (iv) − cot x − 2x + c, , (v) − cot x − tan x + x + c, , (x), , (vi) sec x − tan x + x + c, (vii) sec x − tan x + x + c, , 3, 3, 2, (7x − 2) 2 + (7x − 5) 2, 21, , (4) f (x) =, , (viii) sin x − cos x + c (ix) − √ 2 cos x + c, 1, 1, (x) −, cos 7x − cos x + c, 14, 2, , 3, 4 3, x 2 + (x + 3) 2 + c, 9, , x2, 2, , +, , +c, , 3, 7, +, 2, 2x, 2, , EXERCISE 3.2 (A), , (3) (i) x − 2 log ( x + 2) + c, , I., , 1, log (2x + 1) + c, 2, 5, 26, (iii) x −, log (3x − 4) + c, 3, 9, (ii) 2x +, , 1., , (log x) n + 1, +c, n+1, , 2., , 5, 2, (sin −1 x) 2 + c, 5, , 3. log (cosec (x + log x ) − cot (x + log x)) + c, 4., , 262, , −1, +c, √ tan (x2), , 5., , 1 3x, (e + 1) + c, 3
Page 273 :
1, · a x + tan x + c, log a, 2, 1, [log (sin ex)] + c, 7., 2, 8. log (ex − e−x ) + c, 1, 1, 9., sin5 x − sin7 x + c, 5, 7, 1, 10., 1og (4x12 + 5) + c, 48, 1, 1, tan x10 + c, 12. log (x4 + 1) + c, 11., 4, 10, 1, 14. tan−1 x + 2, +c, 13. 2 √ tan x + c, x +1, 15. log (3 cos2 x + 4 sin2 x) + c, 6., , −1, , 16. 2 tan−1√ x + c, , 7., , 5x − 3 log | 2e x − 5 | + c, , 8., , − 5x − log | 3e x − 4 | + c, , 9., , −x+, , 8, , 3., , cos (a + b)·log (sec (x + b)) −, log (tan x + 2) + c, , 5., , 11, 2, x+, log (3 sin x + 4 cos x) + c, 75, 25, , 6, , +, , cos4 x, 4, , +, , cos2 x, 2, , +, , 1, log (cos2 x − 1) + c, 2, , 1, 1, 1, cos11 x − cos9 x +, cos13 x + c, 6, 9, 13, , 14., , 1, 2, · 3cos x + c, log 3, , 15. −, 16., , 1, sin5 4x, log, +c, 20, sin2 10x, , 17., , 1, log [(1 + cos2x) − cos2x] + c, 2, , EXERCISE 3.2 (B), I. 1., 2., , (sin (a + b))·x + c, 4., , cos6 x, , 1, (sec 3x)2, log, +c, 13., 6, (sec 2x)3 (sec x)6, , 1, x3 − 1, 25. log, +c, 3, x3, , 2., , +, , tan4 x tan2 x, −, + log (sec x) + c, 4, 2, 3, 1, 12. sin x − sin3 x + sin5 x − sin7 x + c, 5, 7, , 24. log (log (log x)) + c, II. 1., , cos8 x, , 11., , 17. log (10x + x10) + c, , x, +c, 2·log sec, 2, cos a·log (sin (x − a)) − (sin a) x + c, , 7, log | 4e 2x − 5 | + c, 8, , , , 3, 1, 49, 5, 11, 2, 22., (2x + 3) − (2x + 3) 2 −, +c, 12, 2, 4 √ 2x + 3, , 1, x3, sin−1, +c, 3, 3, , 3, 2x, +, log (2 cos x + 3 sin x) + c, 13 13, , 10., , √ 1 + 4x n, 18., +c, 2n, 5, 3, 4, 2, (x + 2) − 2 (x + 2) 2 + c, 19., 5, 7, 1, 4a2 2 2 5 2a4 2 2 3, 20. (a2 + x2) 2 −, (a + x ) 2 + (a + x ) 2 + c, 7, 5, 3, 3, 2, 21. − 2 √ 2 − 3x − (2 − 3x) 2 + c, 9, , 23., , 6., , 3., 4., , 263, , 1, 4√ 3, , log, , 1, log, 30, 1, , √ 14, 1, , √3, , tan−1, , 2x − √ 3, +c, 2x + √ 3, 5 + 3x, 5 − 3x, , +c, , √ 2x, +c, √7, , log x +, , x2 +, , 8, 3, , +c
Page 274 :
5., 6., , 2x, 1, sin−1, +c, 2, √ 11, 1, , √2, , 2., , 5, x −, 2, , log x +, , 3. √ 2 tan−1, , +c, , 2, , tan, , 7. 9 sin−1, , x, − √ 9 − x2 + c, 9, , 4. tan−1 2 tan, , 8. 2 sin, , −1, , x, − √ 4 − x2 + c, 2, , 5., , 9. 2 sin, , −1, , x, 1, − (√ 100 − x2 ) + c, 10, 2, , 6. −, , x+2, 1, log, +c, x+6, 4, , 10., 11., 12., 13., , 1, , √5, , √ 5 − 1 + 2x, +c, √ 5 + 1 − 2x, , log, , 1, , 8√ 2, , log, , 1, , 2√ 19, , 7., , log, , 2x − 5 − 2 √ 2, 2x − 5 + 2 √ 2, , +c, , 3x + 2 + √ 19, 3x + 2 − √ 19, , +c, , 5, 14., log x + +, 6, √3, , 5, 7, x2 + x +, 3, 3, , 1, , 1, , √2, , log x −, , 17. log x −, 18., 19., 20., II. 1., , 1, , 2√ 7, 1, , √2, , 2√ 3, √5, , x2 −, , 2 tan x, √7, , log, , +c, , tan−1, , 2 tan, , √5, , +2, , x, +1 +c, 2, , tan−1 (√ 5 tan x ) + c, , 1, , √5, 1, , 2√ 11, , tan−1, , 3 tan x − 2, +c, √5, , log, , √ 11 − 2 + tan x, +c, √ 11 + 2 − tan x, , 9., , π, π, 1, log sec x +, + tan x +, 4, 4, 2, , +c, +c, , x+1, 3, 5, log (x2 + 6x + 5) −, log, +c, x+5, 2, 4, , 2. log (x2 + 4x − 5) −, , 3, x+4 +c, 2, , 3., , 1, log, 2, , +c, , 4., , x−1, +c, x+5, , 1, 3, log (2x2 + 3x − 1) +, ·, 2, 2√ 17, log, , 4x + 3 − √ 17, +c, 4x + 3 + √ 17, , 3, 5, ·, √ 2x2 + 2x + 1 +, 2, 2√ 2, log x +, , √ 3 + tan x, +c, √ 3 − tan x, x, 2, , −1, +c, √2, , π, π, 1, log sec x +, + tan x +, 4, 4, √2, , 1, + √ x2 − x − 6 + c, 2, , tan−1, , √5, , x, 2, , 8., , I. 1., , tan−1 (√ 2 tan x) + c, , 1, 2, , 3, +, 4, , 1, , −1, +c, +1, , EXERCISE 3.2 (C), , 15. log (x + 4 + √ x2 − 8x − 20 ) + c, 16., , x, 2, x, 2, , 1, 3 tan, log, 3, 3 tan, , 1, 1, + x2 + x +, 2, 2, , +c, , x−1, 2, , +c, , 5. − 7 √ 3 + 2x − x2 + 10·sin−1, , +c, , 264
Page 275 :
6. √ x2 − 16x + 63 +, log �(x − 8) + √ x2 − 16x + 63� + c, 2x − 9, 9, sin−1, +c, 9, 2, , 7. √ 9x − x2 +, 8., , 3, , log, , 4√ 2, , 2., 3., 4., 5., , x3, , x2, , −, , 3, , cos 3x +, , 1, 1, log (sec x + tan x) + sec x·tan x + c, 2, 2, , 11., 12., , 1, cos (log x)2 + c, 2, 1, −, (log x)2 + c, 2, x, 1, 1, sin 3x +, cos x −, x sin 7x, 6, 18, 14, 1, −, cos 7x + c, 98, , 20., , 13, x2, , 2, , (3x 3, , 21., , e2x, , II. 1., , 13, e−x, , 3., , √5, , 4., , 6., , 1, 1, sin x + x √ 1 − x2 − sin−1 x + c, 4, 4, 2, 3, 3, x, 1, 1, −1, 2, 2 2, cos x − √ 1 − x + (1 − x ) + c, 3, 9, 3, , 14., , − (sin−1 t ) √ 1 − t2 + t + c, , x, 2, , x2 +, , 3, +, 5, +c, , x3, a2, x3, ·√ a2 − x6 +, sin−1, +c, a, 6, 2, x−5, x−5, (x − 3) (7 − x) + 2 sin−1, +c, √, 2, 2, , 5., , −1, , (log x) [log (log x) − 1 ] + c, , [ 2 sin 3x − 3 cos 3x ] + c, , 3, 3, log x + x2 +, 10, 5, , [2 cos 3x + 3 sin 3x] + c, , 13., , − 6) sin 3 x + 6 3 x cos 3 x + c, , [ − cos x + 2 sin 2x ] + c, 5, x, [ sin (log x) − cos (log x) ] + c, 2, , 2., , 1, 1 2, x − x·sin 2x −, cos 2x + c, 2, 4, x4, x4, log x −, +c, 4, 16, e2x, , 1, x, sin 3x +, cos 3x + 3x sin x, 9, 3, , −, , 19., , 1, x, tan−1 x −, (x − tan−1 x) + c, 2, 2, 3, x2 1, x, tan−1 x −, +, log (1 + x2) + c, 6, 3, 6, x, 1, (tan−1 x) (x4 − 1) − (x3 − 3x) + c, 12, 4, , 7., , 10., , 1, 4, , 2, , x [(log x)2 − 2 (log x) + 2 ] + c, , 9., , 17., , 2, 2, x sin 3x + cos 3x + c, 9, 27, , 6., , 8., , (cos θ)·[1 − log (cos θ)] + c, , 18., , (3·log x − 1) + c, , 9, , 16., , + 3 cos x + c, , EXERCISE 3.3, 1., , 2 [√ x·sin √ x + cos √ x ] + c, , 2√ 2 sin x + √ 2 − 2, +c, 2√ 2 sin x + √ 2 + 2, , 9. √ e2x − 1 − log (ex + √ e2x − 1) + c, , I., , 15., , 1, 2x, � √ 4x + 4 + 2 log (2x + √ 4x + 4)� + c, log 2 2, 3, 1, 8., (2x2 + 3) 2 +, 6, , 7., , √2, 265, , x, 2, , x2 +, , 3, 3, 3, +, log x + x2 +, 2, 4, 4, , +c
Page 276 :
9., 10., 11., 12., III. 1., 5., 8., , −, , 3, x+2, 1, (5 − 4x − x2) 2 − (x + 2) √ 5 − 4x − x2 − 9 sin−1, +c, 3, 3, , (1 + 2 tan x), 29, 1, tan2 x + tan x − 7 −, log � + tan x + √ tan2 x + tan x − 7 � + c, √, 4, 8, 2, x+1, √ x2 + 2x + 5 + 2 log �x + 1 + √ x2 + 2x + 5 � + c, 2, , √2 �, , 4x + 3, 8, , x2 +, , ex (2 + cot x ) + c, , 3, 23, x+2 +, log, 2, 16 √ 2, x, 2. ex · tan + c, 2, , x+, , 3, 4, , + x2 +, , 3. e x ·, , 1, +c, x, , 3, x+2 �+c, 2, 4. ex ·, , e x ·(log x)2 + c, , 6. e 5x · log x + c, , 7. e sin, , (1 + x)2, , 1, 2, , 9. x·cosec (log x) + c, , 2, , log (1 + x) −, , +c, , −1 x, , 1, +c, x+1, , ·x + c, , EXERCISE 3.4, I., , 1., , 1, 11, log (x − 1) − 2 log (x + 2) +, (x + 3) + c, 4, 4, , 2., , 1, 1, tan−1 x +, log, 6, 15√ 2, , 3., 5., , x − √2, x + √2, , −, , x, √3, tan−1, +c, 10, √3, , 51, 31, 8, 2, log (2x + 9) +, log (3x − 7) + c 4. −, log (x + 4) −, log (x − 1) + c, 41, 41, 5, 5, 5, log (3x + 1) + log (x − 1) + c, x − log (x + 3) + log (x − 2) + c , 6. x2 + 3x +, 3, , 7., , x5, 2x + 1, 1, 1, x, 11 −1 x, 9, log, + 3 log (x + 3) + c 8., log 5, + c 9., tan, − tan−1, +c, x +1, 2x − 1, 2, 5, 2, 2, 2, √5, , 10., , 2 log, , 12., , 2x − 4, 1, log x, +c, 2 +1, 5·log 2, , 14., , 9, 6·log x − log (x + 1) −, +c, x+1, , 16., , 1, 1, 1, log (x − l) −, log (x2 + x + l) −, tan−1, 3, 6, √3, , x+1, 5, +, log, x−1, 2√ 2, , x + √2, x − √2, , +c, , 11. log, 13., , 266, , 5, 2, , 2 + x2, +c, 3 + x2, 1, x+1, 11, +, log, +c, x+1, x+3, 4, , x6 (x3 + 3), 1, 15., log, +c, (3x3 + 1)3, 8, 2x + 1, +c, √3
Page 277 :
4, +c, sin x − 2, , 17., , 3·log (sin x − 2) −, , 18., , 1, 2, 1, log (cos x + 1) +, log (cos x − 1) −, log (2 cos x + 1) + c, 6, 3, 2, , 19., , 1, cos x − 1, 1, log, +, +c, 4 · (cos x + 1), cos x + 1, 8, , 21., , 1, 2, 1, log (1 − cos x) −, log (1 + cos x) +, log (3 + 2 cos x) + c, 2, 5, 10, , 22., , ex+ 1, ex, 1, 1, 1 +, log, tan−1, +c, 3, 6, 2, (e 2x + 9) 2, , (1 + 2 sin x)4, 1, 20., log, +c, (1 − sin x) (1 + sin x)3, 6, , 23., , (3 log x + 2)2, 11, 5, log, +, tan−1 (log x) + c, 2, 26, √ (log x) + 1 26, , MISCELLANEOUS EXERCISE 3, , (I), , (II) (1), (2), , 1, B, , 2, A, , 3, B, , 4, A, , 5, D, , 6, B, , 7, A, , 8, A, , 9, C, , 10, B, , 11, A, , 12, A, , 13, D, , 14, C, , 15, A, , 16, D, , 17, A, , 18, D, , 19, C, , 20, A, , 8 5 8 3, 2 7, x2 −, x2−, x2 + c, 5, 3, 7, x7, 7, , −, , x6, 6, , +, , x5, 5, , −, , x4, 4, , +, , x3, 3, , −, , x2, 2, , + x − log (x + 1) + c, , (3), , 5, 1, (6x + 5) 2 + c, 15, , (4), , 1, t2, − 2t + 3·log (t + 1) +, +c, t+1, 2, , (5), , 3 tan x − 2 sec x + c , , (6), , tan θ − cot θ − 3 θ + c, , (7), , 1, (2 sin 6x + 3 sin 4x + 6 sin 2x + 12 x) + c, 48, , (8), , 1, 1, sin 2x −, sin 3x + c, 2, 3, , (9), , π, 1, x − x2 + c, 4, 4, , (III) (1), (2), (3), , 1, (1 + log x)4 + c , 4, 1, 1, log (1 + x2) − (1 − x) tan−1(1 − x) +, log (x2 −2x + 2) + c, (tan−1 x) x −, 2, 2, 3, 2, sec x 2 + c, − cot (log x) + c , (4), 3, , 267
Page 278 :
(5), , x log (1 + cos x) + c, , (6), , 1, sin−1 (x3 ) + c, 3, , (7), , 1, log (3 − 2 cot x) + c, 4, , (8), , x· log (log x) −, , (10), , 1, 2√ x2 − 1, 2 sec−1 x +, +c, 4, x2, , (9), , 2, , √ 13, , (11) −, , tan, , −1, , x, 2, , 2 tan, , −3, , √ 13, , +c, , 3, 2x − 1, 7, sin−1, +c, √ − 2x2 + x + 3 +, 2, 4√ 2, √7, , 1, +c, log x, , (12) x· log (x2 + 1) − 2 [ x − tan−1 x ] + c, , (13), , 1, e 2x · [ sin 2x − cos 2x ] + c, 4, , (14), , 1, 1, 4, log (3x − 1) +, log (x − 1) −, log (3x − 2) + c, 18, 2, 9, , 1, (cos x − 1)(cos x + 1)3, (15), log �, �+c, 6, (2 cos x + 1)4, , tan x − 1, tan x − 1, +c, √ 7 + 2 tan x − tan2 x + 4 sin−1, 2√ 2, 2, , (16), , 1, (x − 1)3 (x + 3), (17), log �, �+c, 4, (x + 1)4, , 1, (18), log, 5, , (19) 2 √ tan x + c , , (20), , x5, x5 + 1, , +c, , 1, 2, +, − cot x + c, 3, 3 cot x cot x, , 4. DEFINITE INTEGRATION, EXERCISE 4.1, I., , (1), , 4, , (2), , 64, 3, , (3) e 2 − 1, , (4), , 6, , (5) 20, , EXERCISE 4.2, I., , (1), , 64, 3, , (5), , 1, 3π, [13√ 13 + 7√ 7 − 3√ 3 − 27] (6) 1 −, 18, 4, , (10), , 1, 3, , (2) log, , tan−1, , 4, 2, + tan−1, 3, 3, , 25, , 24, , (11) π, , (3) − 1 +, , (12), , 268, , (7), π, 6, , π, 4, , 4, 7√ 2, (13) 1, , (4) 2, (8) 1 (9), (14), , 3π, 16, , π 1, −, 4 2, , (15) 1
Page 279 :
II. (1), , π 1, − log 2, 4 2, , (4) 0, (7) log, , 4, 3, , (14), , π, π, +1 −, +1, 4, 2, , π, 4, , (5), , 2, 1, tan−1, 3, 3, , (6), , 1, log, 4, , (8), , 1, tan−1, ab, , ae, − tan−1, b, , 0, , (6) 0, , (7), , 0, , 1 + √5, , 2, , 2 √2 + 1, 2 √2 − 1, , a, be, (11), , π, −1, 2, , (15) sin (log 3), , (2), , (11) 4 log, , (3), , (10), , π, 4, , III. (1), , 1, log 2, 2, , 4, 3, π, (13), −1, 2, , π, 4, 8, (12), 3, , (9), , π, e4, , (2), , (3), , 0, , π2, 6 √3, 16, (13), 105, (8), , (12) 0, , 7, 16, (3) 2, 77, , (4) 0, , (5), , (9) 0, , (10) 0, , (14), , π, 3, , (15), , π, 1, log, 2, 2, , MISCELLANEOUS EXERCISE 4, , (I), 1, A, (II) (1), , 2, A, , 3, C, , 1, (3 − log 3) (2), 10, , 4, C, , 5, D, , 6, C, , 7, A, , 8, D, 1, 8, , 2 − √2, , (3), , 6 − 4 log 2, , (4), , 1, log 2, 3, , (8), , π, 5, , (9) 0, , (6) π − 2, , (7), , π2, (2), 16, π, (5), − log 2, 2, , 7, 7 + 3 √5, 2, 1, tan−1, (3), log, , 5, 2, √ 35, √5 a, 1 π, π, (6), − log √ 2 , (7) − log 2, 2 4, 2, , (III) (1), , (9) log, (IV) (1), , 5 + 3 √3, , 1 + √3, , 1, 9, when a = 0 ; when a = 4, 2, 2, , (10), , 17, 2, , (2), , k=, , 269, , 1, 2, , 9, B, , 10, A, , 1, 21, π, (10), 2, , (5), , (4), , π, 20, , (8), , π3, 6
Page 280 :
5. APPLICATION OF DEFINITE INTEGRAL, EXERCISE 5.1, (1) (i), , 25, , (iv) 1, , (ii) 16, , (iii) 20, , (v) 2 log 4, , 32, (vi), 3, , 128, sq. units, 3, , (vii), , 16, 3, 8, (ii), 3, 1, (v), 6, , 128, 3, 1, (3) (i), 12, a2, (iv) 8, 3, , (ii), , (2) (i), , (iii), , 32, 3, , MISCELLANEOUS EXERCISE 5, (I), 1, A, , 2, A, , 3, C, , 4, B, , 5, A, , 6, D, , 7, B, , 8, D, , 9, A, , 10, B, , 11, A, , 12, D, , 13, B, , 14, B, , 15, C, , 16, C, , 17, A, , 18, D, , 19, A, , 20, C, , (II), 1., , (i), , 10, , 2., , 9π , , 4., , (i), , 16, , 3, , (ii) 2, , (iii), , 3., , 20π, , (ii), , 8, , 3, , (iii), , 1, 2, , 5., 8., , 1, 3, , π, , 3, 56, , 3, , 6., , 1, 6, , 9., , 36, , π 1, −, 4 2, 7, 10., 3, 7., , 3, 4, , 6. DIFFERENTIAL EQUATIONS, EXERCISE 6.1, (1) (i), , 2, 1, , (ii) 2, 3, , (iii) 1, 2, , (iv) 3, 1, , (v) 2, 1, , (vi) 3, 2, , (vii) 2, not definded, (ix) 3, 3, , d2 y, − 25y = 0, (v), dx2, , (viii) 2, 2, , (ii), , (vi) 2, , d2 y, dx2, , 3, , +, , − 27y = 0, dy, dx, , 3, , =0, , dy, dy, d2 y, + 10y = 0, (vii) (x + xy) + y = 0 (viii) 2 − 7, dx, dx, dx, , (x) 2, 1, , 2, , EXERCISE 6.2, (1) (i), , dy, dy, d2 y, +, x, +, y, =, 0, (iv), 8, dx, dx, dx2, , (iii) x2, , (ix) xy, , dy, 2x3 + 3xy2, − y3 = 0, dx, dy 2, dy, d2 y, xy 2 + x, −y, =0, dx, dx, dx, , (x), , 270, , d2 y, dx, , d2 y, dx2, , 2, , +x, , +4, , dy, dx, , 2, , − 2y, , dy, + 5y = 0, dx, , dy, =0, dx
Page 283 :
7. PROBABILITY DISTRIBUTIONS, EXERCISE 7.1, 1., , { −6, −4, −2, 0, 2, 4, 6 }, , 4., , (i), , 2. { 0, 1, 2 }, 3., , (i), , p.m.f. , , (ii), , Not p.m.f, , (iii) p.m.f , , (iv) Not p.m.f , , (v), , (iv) p.m.f , , Not p.m.f., , X, , 0, , 1, , 2, , P (X ), , 1, 4, , 1, 2, , 1, 4, , (ii), X, , 0, , 1, , 2, , 3, , P (X ), , 1, 8, , 3, 8, , 3, 8, , 1, 8, , (iii), , 5., X, , 0, , 1, , 2, , X, , 0, , 1, , 2, , 3, , 4, , P (X ), , 2, 3, , 2, 9, , 1, 9, , P (X ), , 1, 16, , 1, 4, , 3, 8, , 1, 4, , 1, 16, , 6., X, , 0, , P (X ), , 4, 5, , 1, 4, , 4, 5, , 2, 3, , 1, 5, , 4, 5, , 0, , 1, , 2, , P (X ), , 9, 16, , 3, 8, , 1, 16, , 1, 5, , 2, , 4, 5, , 8., , (i), , 1, 10, , 1, 5, , 4, 3, , 1, 5, , (ii), , 15. 17·53, 4·9, 2·21 , , 16. 0·7, 0·21, , EXERCISE 7.2, 1., , (i), , p.d.f. , , (ii), , 4, , 3, 1, , (iii), 10, 5, 7 524, 9. –0·05, 2·2475 10. ,, 11. 1·5, 3 54, 1, 12. , 13. 4·67, 14. 2·41, 3, , 7., X, , 2, , 3, , Not a p.d.f, , (iii) Not a p.d.f , , 273, , 2., , (a), , 3., , (i), , 2·25, ,, 16, p.d.f., , 3, ,, 16, 1, (ii), 9, (b), , (c), (iii), , 3, 4, , 1, 9
Page 284 :
4., , (i), , 5., , (i), , 6., , (i), , 7., , (i), , 1 35, ,, 2 64, 1, 4, 2, 5, 1, 2, , (ii) 6,, (ii), , 1, , 2, , (ii), , 1, 5, , (ii), , 11, , 16, , 11 1, ,, 32 2, (iii), , 7, 16, , x2, , 8., , (i), , 9., , 8 7, 2, , 0, , , 9 9, 9, , 10., , 4, 1, ,, ,, log 3 log 3, , (ii), , 16, , 1, , 0·18, 1, 64, , 4 (log 3 – 1), (log 3)2, , (iii) 0·6328, , MISCELLANEOUS EXERCISE 7, (I), 1, B, , 2, C, , 3, A, , 4, B, , 5, C, , 6, B, , 7, B, , 8, A, , 9, D, , 10, B, , (II) Solve the following :, (1), , (2), (5), , (i) Discrete {1, 2, 3, ..., 100000}, , (ii), , Continuous. , , (iv) Discrete {0, 1, 2, 3, 4, 5 }, 1, 10 1 6, (i), (ii) , ,, 21, 21 7 7, 1, 4, , (v), , Continuous, , (3), , (i) 0·5 , , (iii), , (ii) 0·7, , Continuous., , (iii) 0·55, , (iv) 0·45, , 1, , 2, , 3, , 4, , 5, , 1, 20, 1, 20, , 3, 20, 1, 5, , 1, 4, 9, 20, , 1, 2, 19, 20, , 1, 20, , X, , 0, , 1, , 2, , 3, , 4, , P (X), , 1, 16, , 1, 4, , 3, 8, , 1, 4, , 1, 16, , x, P (X), F (x ), , 1, , (6), , 4, C, x, 4, 2, (7) (i) , , (ii), , X, , 0, , 1, , 2, , X, , 0, , 1, , 2, , P (X ), , 4, 9, , 4, 9, , 1, 9, , P (X ), , 25, 36, , 10, 36, , 1, 36, , 274
Page 285 :
(8), , (i), , 1, 10, , (ii), , 17, 3, (iii), 100, 10, , (9), X, , –3, , –2, , –1, , 0, , 1, , 2, , 3, , 4, , F (X ), , 0·1, , 0·3, , 0·5, , 0·65, , 0·75, , 0·85, , 0·9, , 1, , P (x ), , 0·1, , 0·2, , 0·2, , 0·15, , 0·10, , 0·10, , 0·05, , 0·10, , (i) 0·55, (10) (i), , (ii) 0·25, , 11 14 √ 14, , ,, 5 25 5, , (ii), , (11) ` 5·5, 8·25, (15) k =, , 1 14 √ 14, , ,, 5 25 5, , (12) 0, 1, , (iii), , n + 1 n2 – 1, ,, ,, 2, 12, , (13), , (i), , 1, , 2, , n2 – 1, 12, (ii), , 5 5 √5, , ,, 2 4 2, , (iv), , 11, , 16, , (iii), , , , (ii) 50, , 81, 128, , √x 1 1, 1, 1 1, , (16) k = , F (x) = ,, ,, 2 √2 2, 4, θ e, , 8. BINOMIAL DISTRIBUTION, EXERCISE 8.1, 3, 25, , 7, 26, , (i), , 2., , 25, , 216, , 4., , (i), , 5., , (i) (0·95)5 , , (ii) (1·2) (0·95)4, , (iii) 1 – (1·2) (0·95)4, , (iv) 1 – (0·95)5, , 6., , 9, 10, , (ii), , 4, , 199, 2010, , 3. 29, , 1, , 1024, , 7., , (iii), , 63, 64, , 1., , (ii), , 8., , 99, (i) 1 –, 100, (iii) 1 – 149, , 45, 1024, , 11, 243, , 9., , (i), , 10., , 7, 3, , 50, , 9949, 10050, , 19, 192, 1, (ii), 3, (iii), 3, 203, 203, 203, 5, 6, , 5, , 9949, 10050, , 11., , 22, , (iv), , 93, 1011, , 12. (i) 4, 2·4 (ii) 10, 2·4 (iii), , 2, 8, ; √ 6 (iv), 5, 5, , MISCELLANEOUS EXERCISE 8, (I), 1, B, , 2, D, , 3, D, , 4, C, , 275, , 5, B, , 6, C, , 19, 20, , 7, B, , 3
Page 286 :
(II) Solve the following :, (1), , , (i) 2 × (0·8)9, , (11) (i) (0·998)8 , (ii) 1 − (0·8)10, , (iii) 1 − (8·2) (0·2), , (iii) 1 − 1·014 × (0·998)7, , 9, , (12) 775·44 × (0·003)38, , 1, , Var (X ) = 2·5, 2, 1, (ii) n = 10, p =, 2, 63, 105, (3) (i), (ii), 256, 512, (2), , (i) p =, , 45, , (5), , (i) 0·65 × (0·95)16, , , , (13) (i) 0·910, (iii) 0·45 × (0·9)8, , , , (iv) 1 − 2·16 × (0·9)8, 1 16 96 256 256, ,, ,, ,, , 4, 54 5 4 5 4 5 4, 5, , 608, , 54, 81, (15) (i) 35 × 8 × 7 , 5, log 0·5, (16) (i), , log 0·99, 1, (17), 5, , (ii) (a), , (ii) (2·0325) × (0·95)14, , (iii) 1 − (1·6) × (0·95)16, (6), , 0·2114 , (7) 1·4 × (0·9)4, , (8), , 6·97 × (0·97)19, , (9), , 0·3456 (10), , 30·44, 58, , v, , (ii) 0·99, , , , (14) (i), , 226, 210, , (4), , (ii) 1·014 × (0·998)7, , v, , 276, , v, , 33, 58, 12393, (ii) 1 −, 57, (b) 1 −
Page 287 :
Practical Notebook for Standard XII, , Practical Notebook Cum Journal - Mathematics, •, , English, Medium, , •, , •, , Price, ` 57.00, , •, •, •, , Based on Government approved, syllabus and textbook, Inclusion of practicals based on, all chapters as per Evaluation, scheme., With full of various activities,, pictures, figures/ diagrams, etc., Inclusion of objective/multiple, choice questions, Inclusion of useful questions for, oral examination, More questions for practice and, separate space for writing, answers, , Practical notebooks are available for sale in the regional depots of, the Textbook Bureau., (1) Maharashtra State Textbook Stores and Distribution Centre, Senapati Bapat Marg, Pune 411004 25659465, (2) Maharashtra State Textbook Stores and Distribution Centre, P-41, Industrial Estate, Mumbai - Bengaluru, Highway, Opposite Sakal Office, Kolhapur 416122 2468576 (3) Maharashtra State Textbook Stores and, Distribution Centre, 10, Udyognagar, S. V. Road, Goregaon (West), Mumbai 400062 28771842, (4) Maharashtra State Textbook Stores and Distribution Centre, CIDCO, Plot no. 14, W-Sector 12, Wavanja, Road, New Panvel, Dist. Rajgad, Panvel 410206 274626465 (5) Maharashtra State Textbook Stores and, Distribution Centre, Near Lekhanagar, Plot no. 24, 'MAGH' Sector, CIDCO, New Mumbai-Agra Road, Nashik, 422009 2391511 (6) Maharashtra State Textbook Stores and Distribution Centre, M.I.D.C. Shed no. 2 and 3,, Near Railway Station, Aurangabad 431001 2332171 (7) Maharashtra State Textbook Stores and Distribution, Centre, Opposite Rabindranath Tagore Science College, Maharaj Baug Road, Nagpur 440001, 2547716/2523078 (8) Maharashtra State Textbook Stores and Distribution Centre, Plot no. F-91, M.I.D.C.,, Latur 413531 220930 (9) Maharashtra State Textbook Stores and Distribution Centre, Shakuntal Colony,, Behind V.M.V. College, Amravati 444604 2530965, , E-learning material (Audio-Visual) for Standards One to, Twelve is available through Textbook Bureau, Balbharati..., • Register your demand by scanning the Q.R. Code, given alongside., • Register your demand for E-learning material by using, Google play store and downloading ebalbharati app., www.ebalbharati.in, www.balbharati.in, ebalbharati