Page 1 :
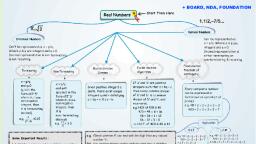
JEE(Adv.)-Mathematics, , Sequence & Series, , SEQUENCE & SERIES, &, 1., 1.1, , DEFINITION OF SEQUENCE & SERIES :, Sequence :, A succession of terms a1, a2, a3, a4........ formed according to some rule or law., Examples are : 1, 4, 9, 16, 25, –1, 1, –1, 1,........, , x x2 x3 x4, , , , , ......, 1! 2! 3! 4!, , 1.1.1 Real Sequence, e.g., , A sequence whose range is a subset of R is called a real sequence., (i), 2, 5, 8, 11, ......................., (ii), 4, 1, – 2, – 5, ......................, (iii), 3, –9, 27, – 81, ........................, , Note : A finite sequence has a finite (i.e. limited) number of terms, as in the first example above. An infinite, sequence has an unlimited number of terms, i.e. there is no last term, as in the second and third examples., , S OLVED E XAMPLE, Example # 1 :, , Write down the sequence whose nth term is, (i), , Solution :, , (i), , 2n, n, , 3 + ( -1)n, , (ii), , 3n, , 2n, n, put n = 1, 2, 3, 4, .............. we get, Let tn =, , t1 = 2, t2 = 2, t3 =, , 8, ,t =4, 3 4, , so the sequence is 2, 2,, (ii), , Let tn =, , 3 + ( -1)n, , 3n, put n = 1, 2, 3, 4, ......, , so the sequence is, , 1.2, , 8, , 4, ........, 3, , 2 4 2, 4, , ,, ,............, ,, 3 9 27 81, , Series :, The indicated sum of the terms of a sequence. In the case of a finite sequence a 1, a2, a3,................,, n, , an the corresponding series is a1 + a2 + a3 + ........ + an =, , åa, k =1, , k, , . This series has a finite or limited number, , of terms and is called a finite series., e.g., (i), 1 + 2 + 3 + 4 + .................... + n, (ii), 2 + 4 + 8 + 16 + ................., (iii), – 1 + 3 – 9 + 27 – .............., , E, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 1

Page 2 :
JEE(Adv.)-Mathematics, , Sequence & Series, , &, 2., , ARITHMETIC PROGRESSION (A.P.) :, A.P. is a sequence whose terms differ by a fixed number. This fixed number is called the common difference., If a is the first term & d the common difference, then A.P. can be written as, a, a + d, a + 2d, .............., a + (n – 1) d , .........., (a), , nth term of AP Tn = a + (n – 1)d , where d = tn – tn–1, , (b), , The sum of the first n terms : S n =, , n, n, [a + l] = [2a + (n - 1)d], 2, 2, , where l is nth term., Note :, (i), , nth term of an A.P. is of the form An + B i.e. a linear expression in 'n', in such a case the coefficient, of n is the common difference of the A.P. i.e. A., , (ii), , Sum of first 'n' terms of an A.P. is of the form An2 + Bn i.e. a quadratic expression in 'n', in such case, the common difference is twice the coefficient of n2. i.e. 2A, , (iii), , Also nth term, , Tn = Sn – Sn–1, , S OLVED E XAMPLE, Example # 2 : Find the number of terms in the sequence 4, 12, 20, ........,108., Solution :, , a = 4, d = 8, Þ, , so, , 108 = 4 + (n – 1)8, , n = 14, , Example # 3 : If (x + 1), 3x and (4x + 2) are first three terms of an A.P. then find its 5th term, Solution :, , (x + 1), 3x, (4x + 2) are in AP, Þ, , 3x – (x + 1) = (4x + 2) – 3x, , Þ, , x=3, , \, , a = 4, d = 9 – 4 = 5, , Þ, , T5 = 4 + (4)5 = 24, , Example # 4 : The sum of first four terms of an A.P. is 56 and the sum of it's last four terms is 112. If its first term, is 11 then find the number of terms in the A.P., Solution :, , a + a + d + a + 2d + a + 3d = 56, 4a + 6d = 56, 44 + 6d = 56, , (as a = 11), , 6d = 12, , hence d = 2, , Let total number of terms = n, Now sum of last four terms., , 2, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 3 :
JEE(Adv.)-Mathematics, , Sequence & Series, , a + (n – 1)d + a + (n – 2)d + a + (n – 3)d + a + (n – 4)d = 112, Þ, , 4a + (4n – 10)d = 112, , Þ, , 44 + (4n – 10)2 = 112, , Þ, , 4n – 10 = 34, , Þ, , n = 11, , Example # 5 : Find the sum of all the three digit natural numbers which on division by 7 leaves remainder 3., Solution :, , All these numbers are 101, 108, 115, ........, 997, 997 = 101 + (n – 1) 7, Þ, , n = 129, , Example # 6 : The sum of n terms of two A.Ps. are in ratio, Solution :, , 7n + 1, . Find the ratio of their 11, 1th terms., 4n + 27, , Let a1 and a2 be the first terms and d1 and d2 be the common differences of two A.P.s respectively,, n, [ 2a1 + (n - 1)d1], 7n + 1, 2, then, =, n, 4n + 27, [2a 2 + (n - 1)d2 ], 2, , æ n - 1ö, a1 + ç, ÷ d1, 7n + 1, è 2 ø, =, æ n - 1ö, 4n + 27, a2 + ç, ÷ d2, è 2 ø, , Þ, , For ratio of 11th terms, n -1, = 10, 2, , Þ, , n = 21, , so ratio of 11th terms is =, , 7(21) + 1, 4, 148, =, =, 4(21) + 27, 3, 111, , Example # 7 : If sum of n terms of a sequence is given by Sn = 2n2 + 3n, find its 50th term., Solution :, , Let tn is nth term of the sequence so tn = Sn – Sn – 1., = 2n2 + 3n – 2(n – 1)2 – 3(n – 1), = 4n + 1, so, , E, , t50 = 201., Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 3

Page 4 :
JEE(Adv.)-Mathematics, , Sequence & Series, , Problems for Self Practice -1:, Write down the sequence whose nth terms is, , (2), (3), , For an A.P, show that tm + t2n + m = 2tm + n, If the sum of p terms of an A.P. is q and the sum of its q terms is p, then find the sum of its (p + q), term., Which number of term of the sequence 2005, 2000, 1995, 1990, 1985, ............. is the first negative, term, , (4), (5), , Find the maximum sum of the A.P. 40 + 38 + 36 + 34 + 32 + .............., , Answers : (1), , 2.1, , 2n, n, , (1), , 2 4 8 16, , , , ,....... ,, 1 2 3 4, , (3), , –(p + q), , (4), , 403, , (5), , 420, , Properties of A.P. :, (a), , If each term of an A.P. is increased, decreased, multiplied or divided by the some nonzero number,, then the resulting sequence is also an A.P., In general assume, Three numbers in A.P. :, a – d, a, a + d, Four numbers in A.P., :, a – 3d, a – d, a + d, a + 3d, Five numbers in A.P., :, a – 2d, a – d, a, a + d, a + 2d, The common difference can be zero, positive or negative., kth term from the last = (n – k +1)th term from the beginning (If total number of terms = n)., The sum of the two terms of an AP equidistant from the beginning & end is constant and equal to, the sum of first & last terms. Þ Tk + Tn–k+1 = constant = a + l., Any term of an AP (except the first ) is equal to half the sum of terms which are equidistant from it., , (b), , (c), (d), (e), (f), , a n = (1 / 2 ) (a n - k + a n + k ), k < n, For, (g), , k = 1, a n = (1/ 2)(a n -1 + a n +1 ) ; For k = 2, a n = (1/ 2)(a n -2 + a n +2 ) and so on., , If a, b, c are in AP, then 2b = a + c., , S OLVED E XAMPLE, 5, , Example # 8 :, , Solution :, , If a1, a2, a3, a4, a5 are in A.P. with common difference ¹ 0, then find the value of, , å a , when, i, , i= 1, , a3 = 2., As a1, a2, a3, a4, a5 are in A.P., we have a1 + a5 = a2 + a4 = 2a3., 5, , Hence, , åa, i=1, , i, , = 10., , Example # 9 :, , If, , 1, 1, 1, ,, ,, are in A.P., prove that a2, b2, c2 are also in A.P.., b+c c +a a+b, , Solution :, , Q, , 1, 1, 1, ,, ,, are in A.P.., b+c c +a a+b, , Þ, , 4, , 1, 1, 1, 1, –, =, –, c+a, b+c, a+b, c+a, Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 5 :
JEE(Adv.)-Mathematics, Þ, , b+c -c -a, c +a-a-b, =, (c + a )(b + c ), (a + b )(c + a), , Þ, , b-a, c -b, =, b+c, a+b, , Þ, , b2 – a2 = c2 – b2, , Þ, , a2, b2, c2 are in A.P., , Example # 10 : If, , Solution :, , Sequence & Series, , b+c -a c +a-b a+b-c, 1 1 1, ,, ,, are in A.P., then prove that , ,, are also in A.P., a, b, c, a b c, , Given, , b+c -a c +a-b a+b-c, ,, ,, are in A.P.., a, b, c, , Add 2 to each term, b+c +a c +a+b a+b+c, ,, ,, are in A.P.., a, b, c, , Þ, , divide each by a + b + c Þ, , 1 1 1, , ,, are in A.P.., a b c, , Example # 11 : Four numbers are in A.P. If their sum is 20 and the sum of their squares is 120, then find the middle, two terms, Solution :, Let the numbers are a – 3d, a – d, a + d, a + 3d, given, a – 3d + a – d + a + d + a + 3d = 20, Þ, 4a = 20 Þ a = 5, and, (a – 3d)2 + (a – d)2 + (a + d)2 + (a + 3d)2 = 120 Þ, 4a2 + 20d2 = 120, Þ, 4 × 52 + 20d2 = 120, Þ, d2 = 1 Þ d = ± 1, Hence numbers are 2, 4, 6, 8, or, 8, 6, 4, 2 Þ Ans is 4 & 6, Example # 12 : If a1, a2, a3,...........,an are in A.P. where ai > 0 for all i, show that :, , 1, 1, 1, (n - 1), +, + ...... +, =, a1 + a 2, a2 + a3, a n -1 + a n, a1 + a n, 1, Solution :, , L.H.S. =, , a1 + a 2, , 1, , +, , a2 + a3, , + ...... +, , 1, a n -1 + a n, , =, , 1, 1, 1, +, + ...... +, a 2 + a1, a3 + a2, a n + a n -1, , =, , a - a2, a 2 - a1, a - a n -1, + 3, + ...... + n, a n - a n -1, ( a 2 - a1 ) ( a 3 - a 2 ), , Let 'd' is the common difference of this A.P., then a2 – a1 = a3 – a2 = ....... = an – an–1 = d, Now L.H.S., =, , =, , E, , 1, d, , d, , {, (, , } 1d {, , a 2 - a1 + a 3 - a 2 + ...... + a n -1 - a n -2 + a n - a n -1 =, , a n - a1, a n + a1, , ), , =, , a1 + (n - 1)d - a1, d, , (, , a n + a1, , ), , =, , a n - a1, , }, , 1 (n - 1)d, n -1, =, = R.H.S., d ( a n + a1 ), a n + a1, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 5

Page 6 :
JEE(Adv.)-Mathematics, , Sequence & Series, , Problems for Self Practice -2:, (1), Find the sum of first 24 terms of the A.P. a1, a2, a3......, if it is know that, a1 + a5 + a10 + a15 + a20 + a24 = 225., (2), Find the number of terms common to the two A.P.'s 3, 7, 11, ...... 407 and 2, 9, 16, ......, 709, Answers :, (1), 900, (2), 14, , 2.2, , Arithmetic Mean :, If three terms are in A.P. then the middle term is called the A.M. between the other two, so if a, b, c are in, A.P., b is A.M. of a & c. So A.M. of a and c =, , a+c, =b., 2, , Let a1, a2,........ ,an be n positive real numbers, then we define their arithmetic mean (A) as, A=, , a1 + a 2 + ..... + a n, n, , n-Arithmetic means Between Two Numbers :, If a,b be any two given numbers & a, A1, A2, .........., An, b are in AP, then A1, A2,........An are the 'n' A.M’s, between a & b then. A1 = a + d , A2 = a + 2d ,......, An= a + nd or b – d, where d =, Þ A1 = a +, , b-a, n +1, , b-a, 2(b - a), , A2 = a +, ,......., n +1, n +1, , Note : Sum of n A.M's inserted between a & b is equal to n times the single A.M. between a & b, n, , i.e., , åA, r =1, , r, , = nA where A is the single A.M. between a & b., , S OLVED E XAMPLE, Example # 13 : Between two numbers whose sum is, , 13, , an even number of A.M.s is inserted, the sum of these, 6, , means exceeds their number by unity. Find the number of means., Solution :, , Let a and b be two numbers and 2n A.M.s are inserted between a and b, then, 2n, (a + b) = 2n + 1., 2, 13 ù, é, êgiven a + b = 6 ú, ë, û, , æ 13 ö, n ç ÷ = 2n + 1., è 6 ø, , Þ, \, , n = 6., Number of means = 12., , Example # 14 : Insert 20 A.M. between 2 and 86., Solution :, Here 2 is the first term and 86 is the 22nd term of A.P. so 86 = 2 + (21)d, Þ, d=4, so the series is 2, 6, 10, 14,......., 82, 86, \, required means are 6, 10, 14,...,82., , 6, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 7 :
JEE(Adv.)-Mathematics, , Sequence & Series, , Problems for Self Practice -3:, (1), (2), , If A.M. between pth and qth terms of an A.P. be equal to the A.M. between rth and sth terms of the A.P.,, then prove that p + q = r + s., If n A.M.s are inserted between 20 and 80 such that first mean : last mean = 1 : 3, find n., , (3), , For what value of n,, , Answers :, , (2), , a n +1 + b n +1, an + b n, , n = 11, , , a ¹ b is the A.M. of a and b., (3), , n=0, , &, 3., , GEOMETRIC PROGRESSION (G.P.) :, G.P. is a sequence of non zero numbers each of the succeeding term is equal to the preceeding term, multiplied by a constant. Thus in a GP the ratio of successive terms is constant. This constant factor is, called the COMMON RATIO of the sequence & is obtained by dividing any term by the immediately previous, term. Therefore a, ar, ar2, ar3, ar4 , .......... is a GP with 'a' as the first term & 'r' as common ratio., , 3.1, , (a), , nth term ; Tn = a r n–1, , (b), , Sum of the first n terms; Sn =, , (c), , Sum of infinite G.P. , S¥ =, , a(r n - 1), , if r ¹ l, r -1, , a, ; 0 < r <1, 1- r, , Properties of GP :, (a), , If each term of a G.P. be multiplied or divided by the some non-zero quantity, then the resulting, sequence is also a G.P., , (b), , In general assume, Three consecutive terms of a GP : a/r, a, ar ;, Four consecutive terms of a GP :, a/r3, a/r, ar, ar3 & so on., , (c), (d), , If a, b, c are in G.P. then b2 =ac., If in a G.P, the product of two terms which are equidistant from the first and the last term, is constant, and is equal to the product of first and last term. Þ Tk. Tn–k+1 = constant = a.l, , (e), , If each term of a G.P. be raised to the same power, then resulting sequence is also a G.P., , (f), (g), (h), , In a G.P., Tr2 = Tr–k. Tr+k, k < r, r ¹ 1, If the terms of a given G.P. are chosen at regular intervals, then the new sequence is also a G.P., If a1, a2, a3.....an is a G.P. of positive terms, then log a1, log a2,.....log an is an A.P. and, vice-versa., , (i), , If a1, a2, a3..... and b1, b2, b3..... are two G.P.'s then a1b1, a2b2, a3b3..... &, , a1 a 2 a 3, , , .......... is also, b1 b2 b3, , in G.P., , E, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 7

Page 8 :
JEE(Adv.)-Mathematics, , Sequence & Series, , S OLVED E XAMPLE, Example # 15 : If a, b, c, d and p are distinct real numbers such that, , (a, , 2, , ), , (, , (A) A.P., Solution :, , ), , + b 2 + c 2 p 2 - 2p ( ab + bc + cd ) + b 2 + c 2 + d 2 £ 0 then a, b, c, d are in, (B) G.P., , (, , (C) H.P., , Here, the given condition a + b + c, 2, , 2, , 2, , )p, , 2, , (D) none of these, , - 2p ( ab + bc + ca ) + b 2 + c 2 + d 2 £ 0, , Þ ( ap - b ) + ( bp - c ) + ( cp - d ) £ 0, 2, , 2, , 2, , Q a square can not be negative, \ ap - b = 0, bp - c = 0, cp - d = 0 Þ p =, , b c d, = = Þ a, b, c, d are in G.P.. Ans. (B), a b c, , Example # 16 : If a, b, c are in G.P., then the equations ax + 2bx + c = 0 and dx + 2ex + f = 0 have a common, 2, , root if, , d e f, , , are in a b c, , (A) A.P., Solution :, , 2, , (B) G.P., , (C) H.P., , (D) none of these, , a, b, c are in G.P Þ b = ac, 2, , 2, , 2, Now the equation ax + 2bx + c = 0 can be rewritten as ax + 2 acx + c = 0, , Þ, , (, , ax + c, , ), , 2, , =0Þx=-, , c, c, ,a, a, , If the two given equations have a common root, then this root must be, , Thus d, , d f 2e c, 2e, 2e, c, c, + =, =, =, - 2e, +f =0 Þ, a c c a, ac b, a, a, , Þ, , -, , c, ., a, , d e f, , , are in A.P.. Ans. (A), a b c, , Example # 17 : A number consists of three digits which are in G.P. the sum of the right hand and left hand digits, exceeds twice the middle digit by 1 and the sum of the left hand and middle digits is two third of the, sum of the middle and right hand digits. Find the numbers., Solution :, Let the three digits be a, ar and ar2 then number is, 100a + 10ar + ar2, ....(i), Given, a + ar2 = 2ar +1, or, a(r2 – 2r + 1) = 1, or, a(r – 1)2 = 1, ....(ii), Also given a + ar =, , 8, , 2, (ar + ar2), 3, , Þ, \, , 3 + 3r = 2r + 2r2 Þ 2r2 – r – 3 = 0 Þ (r + 1)(2r – 3) = 0, r = –1, 3/2, , for, , r = –1, a =, , 1, 1, = ÏI, 2, (r - 1), 4, , \ r ¹ –1, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 9 :
JEE(Adv.)-Mathematics, for, , Sequence & Series, , r = 3/2, a =, , 1, æ3 ö, ç - 1÷, è2 ø, , 2, , =4, , From (i), number is 400 + 10.4., , {from (ii)}, , 3, 9, + 4. = 469 Ans., 2, 4, , Example # 18 : Find the value of 0.32 58, Solution :, , Let R = 0.32 58 Þ R = 0.32585858...., ......... (i), Here number of figures which are not recurring is 2 and number of figures which are recurring is, also 2., then 100 R = 32.585858......, ..........(ii), and, 10000 R = 3258.5858....., ..........(iii), Subtracting (ii) from (iii) , we get, 1613, 4950, Aliter Method : R = .32 + .0058 + .0058 + .000058 +..........., , 9900 R = 3226 Þ R =, , = .32 +, , 58 æ, 1, 1, ö, 1+, +, + .........¥ ÷, 104 çè 102 104, ø, , æ, ö, 58 ç 1 ÷, = .32 + 4 ç, ÷, 1 ÷, 10 ç, 1, ç, ÷, è 100 ø, =, , 32, 58, 3168 + 58 3226 1613, +, =, =, =, 100 9900, 9900, 9900 4950, , Problems for Self Practice -4:, (1), If the pth, qth, rth terms of a G.P. be a, b, c respectively, prove that aq – r br – p cp – q = 1., (2), The sum of infinite number of terms of a G.P. is 4, and the sum of their cubes is 192, find the series., (3), Find a three digit number whose consecutive digits form a G.P. If we subtract 792 from this number,, we get a number consisting of the same digits written in the reverse order. Now, if we increase the, second digit of the required number by 2, then the resulting digits will form an A.P., (4), If a, b, c are respectively the p th , q th and r th terms of the given G.P., then show that, (q – r) log a + (r – p) log b + (p – q)log c = 0, where a, b, c > 0., (5), Find three numbers in G.P., whose sum is 52 and the sum of whose products in pairs is 624., (6), A G.P. consist of 2n terms. If the sum of the terms occupying the odd places is S1 and that of the, terms occupying the even places is S2 , then find the common ratio of the progression., (7), The sum of three numbers in G.P. is 70, if the two extremes be multiplied each by 4 and the mean, by 5, the products are in A.P. Find the numbers., (8), , 111 ..........1, If a = 14243 , b = 1 + 10 + 102 + 103 + 104 and c = 1 + 105 + 1010 + ..... + 1050, then prove that, 55, , (i), Answers :, , E, , ‘a’ is a composite number, (2) 6, – 3,, , 3, ,........, 2, , (3) 931, , (ii), , a = bc., (5) 4, 12, 36, , (6), , S2, S1, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , (7) 10, 20, 40, , 9

Page 10 :
JEE(Adv.)-Mathematics, 3.2, , Sequence & Series, , Geometric Mean :, If a, b, c are in G.P., then b is the G.M. between a & c, b2 = ac. So G.M. of a and c = ac = b, Let a1, a2,........ ,an be n positive real numbers, then we define their geometric mean (G) as, G = (a1 a2...........an)1/n, n-Geometric Means Between Two Numbers :, If a, b are two given positive numbers & a, G1, G2, ........, Gn, b are in G.P. Then G1, G2, G3 ,.......Gn are, 'n' G.Ms between a & b. where b = arn+1 Þ r = (b/a)1/n+1, , G1 = a(b / a)1/ n +1 ,, , G 2 = a(b / a) 2 / n +1 ................,, , = ar,, , = ar2, ................, , G n = a(b / a) n / n +1, = arn = b/r, , Note : The product of n G.Ms between a & b is equal to nth power of the single G.M. between a & b i.e., n, , P G r = (G) n where G is the single G.M. between a & b, r =1, , S OLVED E XAMPLE, Example # 19 : Insert 4 G.M.s between 2 and 486., 1, , Solution :, , æ b ö n+1, Common ratio of the series is given by r = ç ÷, = (243)1/5 = 3, èaø, , Hence four G.M.s are 6, 18, 54, 162., Example # 20 : If the third term of G.P. is 4, then find the product of first five terms., Solution :, T1T2T3T4T5 = (T3)5 = 45 = 1024, , &, 4., , HARMONIC PROGRESSION (H.P.) :, A sequence is said to be in H.P. if the reciprocal of its terms are in AP., If the sequence a1, a2, a3, ......., an is an HP then 1/a1, 1/a2,........., 1/an is an AP . Here we do not have the, formula for the sum of the n terms of an HP. The general form of a harmonic progression is, , 1 1, 1, 1, ,, ,, ,........., a a + d a + 2d, a + ( n - 1) d, Note : No term of any H.P. can be zero., (i), , If a, b, c are in HP, then b =, , 2ac, a a-b, or =, a+c, c b-c, , S OLVED E XAMPLE, Example # 21 : If m th term of H.P. is n, while nth term is m, find its (m + n)th term., Solution :, , Given Tm = n or, , 1, = n; where a is the first term and d is the common difference of the, a + (m - 1) d, , corresponding A.P., so, , 10, , a + (m – 1)d =, , 1, n, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 11 :
JEE(Adv.)-Mathematics, , Sequence & Series, , and, , a + (n – 1) d =, , or, , d=, , 1, m, , 1, mn, , Hence T(m + n) =, , Þ, , (m – n)d =, , so, , a=, , m-n, mn, , 1, (m - 1), 1, –, =, n, mn, mn, , 1, mn, mn, =, =, ., a + (m + n - 1) d, 1+ m + n - 1 m + n, , Example # 22 : If pth, qth, rth terms of an H.P. be a, b, c respectively, prove that, (q – r)bc + (r – p) ac + (p – q) ab = 0, Solution :, Let 'x' be the first term and 'd' be the common difference of the corresponding A.P.., so, , 1, = x + (p – 1)d, a, , ...........(i), , 1, = x + (q – 1) d, b, , ..........(ii), , 1, = x + (r – 1) d, c, , ..........(iii), , (i) - (ii), Þ, ab(p – q)d = b – a, (ii) - (iii), Þ, bc (q – r)d = c – b, (iii) - (i), Þ, ac (r – p) d = a – c, (iv) + (v) + (vi) gives, bc (q – r) + ac(r – p) + ab (p – q) = 0., , ..........(iv), ..........(v), ..........(vi), , Example # 23 : The sum of three numbers are in H.P. is 37 and the sum of their reciprocals is 1/4. Find the, numbers., Solution :, Three numbers are in H.P. can be taken as, , 1 1 1, , ,, a-d a a+d, then, , 1, 1, 1, = 37, + +, a-d a a+d, , and, , a–d+a+a+d =, , from (i),, , ........(i), , 1, 1, Þ a=, 4, 12, , 12, 12, 12, 12, + 12 +, = 37 Þ, +, = 25, 1 - 12d, 1 + 12d, 1 - 12d 1 + 12d, , Þ, , 24, 24, 1, = 25 Þ 1 - 144d 2 =, Þ d2 =, 2, 25 ´ 144, 1 - 144d, 25, , \, , d=±, , \, , a – d, a, a + d are, , 1, 60, 1 1 1, 1 1 1, , ,, or, ,, ,, 15 12 10, 10 12 15, , Hence, three numbers in H.P. are 15, 12, 10 or 10, 12, 15 Ans., , E, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 11

Page 12 :
JEE(Adv.)-Mathematics, , Sequence & Series, , Example # 24 : Suppose a is a fixed real number such that, , a -x a -y a -z, =, =, px, qy, rz, , If p, q, r are in A.P., then prove that x, y, z are in H.P., Solution :, , Q, \, Þ, , given, , p, q, r are in A.P., q–p=r–q, p – q = q – r = k (let), , ........ (i), , a, a, -1 a -1, -1, a -x a -y a -z, y, =, =, =, =z, Þ x, px, qy, rz, p, q, r, , Þ, , æa ö æa ö æa ö æa ö, ç - 1÷ - ç - 1÷ ç - 1÷ - ç - 1÷, è x ø è y ø è y ø è z ø (by law of proportion), =, p-q, q-r, , Þ, , a a a a, x y y z, =, k, k, , Þ, , 1 1 1 1, æ1 1ö, æ1 1ö, aç - ÷ = aç - ÷ Þ - = x y y z, èx yø, èy zø, , \, , 2 1 1, = +, y x z, , \, , 1 1 1, , , are in A.P.., x y z, , {from (i)}, , Hence x, y, z are in H.P., Problems for Self Practice -5 :, (1), If the 7th term of a H.P. is 8 and the 8th term is 7. Then find the 28th term., (2), In a H.P., if 5th term is 6 and 3rd term is 10. Find the 2nd term., , q -r r -p p-q, +, +, =0., a, b, c, , (3), , If the pth, qth and rth terms of a H.P. are a,b,c respectively, then prove that, , (4), (5), , If a, b, c be in H.P., show that a : a – b = a + c : a – c., If the ratio of H.M. between two positive numbers 'a' and 'b' (a > b) is to their G.M. as 12 to 13, prove, that a : b is 9 : 4., , (6), , If H be the harmonic mean of a and b, then find the value of, , H, H, +, – 1., 2a, 2b, , (7), If a, b, c, d are in H.P., then show that ab + bc + cd = 3ad, Answers :, (1), 2, (2), 15, (6), 0, , 12, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 13 :
JEE(Adv.)-Mathematics, 4.1, , Sequence & Series, , Harmonic Mean :, If a, b, c are in H.P., then b is H.M. between a & c. So H.M. of a and c =, , 2ac, = b., a+c, , Let a 1, a 2,........ ,a n be n positive real numbers, then we define their harmonic mean (H) as, H=, , n, 1, 1, 1ö, æ1, ç a + a + a + .... a ÷, è 1, 2, 3, n ø, , Insertion of 'n' HM's between a and b :, a, H1, H2, H3 ,........, Hn, b ® H.P, 1 1 1 1, 1 1, , ,, ,, ,.......... , ® A.P., a H1 H 2 H 3, Hn b, , 1 1, 1 1, = + (n + 1)D Þ D = b a, b a, n+1, æ 1 1ö, ç - ÷, 1, 1, = + nç b a ÷, Hn a, è n+1 ø, , S OLVED E XAMPLE, 2, 2, and, ., 3, 13, Let 'd' be the common difference of corresponding A.P.., , Example # 25 : Insert 4 H.M between, Solution :, , so, , 13 3, d = 2 2 = 1., 5, , \, , 1, 3, 5, +1=, =, H1, 2, 2, , or, , H1 =, , 2, 5, , 1, 3, 7, +2=, =, H2, 2, 2, , or, , H2 =, , 2, 7, , 1, 3, 9, +3=, =, H3, 2, 2, , or, , H3 =, , 2, 9, , 1, 3, 11, =, +4=, H4, 2, 2, , or, , H4 =, , 2, ., 11, , Problems for Self Practice -6:, (1), , an + bn, is the G.M. between a & b then find the value of 'n'., If n -1, a + b n -1, , (2), , If b is the harmonic mean between a and c, then prove that, , Answers : (1), , E, , 1, 1, 1 1, +, = + ., b-a b-c a c, , 1, 2, Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 13

Page 14 :
JEE(Adv.)-Mathematics, , Sequence & Series, , &, 5., , ARITHMETICO-GEOMETRIC SERIES :, A series, each term of which is formed by multiplying the corresponding term of an A.P. & G.P. is called the, Arithmetico-Geometric Series , e.g. 1+ 3x + 5x 2 + 7x3 + ........., Here 1, 3, 5, ........ are in A.P. & 1, x, x 2, x3 ............. are in G.P., (a), Sum of n terms of an Arithmetico-Geometric Series :, Let Sn = a + (a + d)r + (a + 2d)r + .......... + [a + (n - 1)d]r, 2, , n -1, , a, dr(1 - r n -1 ) [a + (n - 1)d] r n, +, , r ¹1, then Sn =, 1- r, (1 - r)2, 1- r, (b), , Sum to infinity :, r, If 0 < r < 1 & n ® ¥ , then nLim, ®¥, , n, , = 0, S¥ =, , a, 1– r, , +, , dr, (1 – r), , 2, , S OLVED E XAMPLE, Example # 26 : Find the sum of the series 1 +, , Solution :, , Let, , S=1+, , 7, 10, 4, + 2 + 3 + ...... to n terms., 5, 5, 5, , 7, 10, 3n - 2, 4, + 2 + 3 + ...... + n-1, 5, 5, 5, 5, , ..........(i), , 4, 7, 3n - 5, 3n - 2, æ 1ö, 1, ç ÷ S=, + 2 + 3 + ....... + n-1 +, 5, 5, 5, 5, 5, 5n, è ø, , ..........(ii), , (i) – (ii) Þ, , 3, 3, 3, 3n - 2, 4, 3, ., S=1+, + 2 + 3 + ....... + n -1 –, 5, 5, 5, 5, 5, 5n, 3 æç æ 1 ö, 1- ç ÷, ç è5ø, 5, 4, è, S=1+, 1, 5, 15, , =, , 12n + 7, 7, \, –, 4.5n, 4, , n -1 ö, , ÷, ÷, ø, , S =, , –, , 3n - 2, 5, , n, , =1+, , 1, 3n - 2, 3, 3, –, × n -1 –, 5, 5n, 4, 4, , (12n + 7), 35, ., –, 16 . 5n-1, 16, , Example # 27 : Evaluate 1 + 2x + 3x2 + 4x3 + ......... upto infinity, where | x | < 1., Solution :, Let S = 1 + 2x + 3x2 + 4x3 + ....., ........(i), xS = x + 2x2 + 3x3 + ........., ........(ii), (i) - (ii) Þ (1 – x) S = 1 + x + x 2 + x3 + .........., or, , 14, , S =, , 1, (1 - x )2, Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 16 :
JEE(Adv.)-Mathematics, , Sequence & Series, , Problems for Self Practice -7:, (1), (2), , Evaluate : 1.2 + 2.22 + 3.23 + ...... + 100. 2100, Evaluate : 1 + 3x + 6x 2 + 10x3 + ...... upto infinite term, where | x | < 1., , (3), , 1ö, 1ö, æ, æ, Sum to n terms of the series : 1 + 2 ç1 + ÷ + 3 ç1 + ÷ + ......, n, n, ø, è, è, ø, , (4), , Find sum to n terms of the series 3 + 5 ´, , (5), , If the sum to the infinity of the series 3 + 5r + 7r2 + .......... is, , (6), , If the sum to infinity of the series 3 + ( 3 + d ) ., , 2, , Answers :, , (2), , 1, 1, + 7 ´ 2 + ........, 4, 4, , 44, , then find the value of r.., 9, , 44, 1, 1, then find d., + ( 3 + 2d ) . 2 + ......... is, 9, 4, 4, , 1, , (1), , 99.2101 + 2., , (4), , 8æ, 1 ö æ 2n + 1 ö, 4 + ç 1 - n -1 ÷ - ç, ÷, 9 è 4 ø è 3 ´ 4 n -1 ø, , (1 - x )3, , (3), , n2, , (5), , 1, 4, , (6), , 2, , &, 6., , RELATION BETWEEN MEANS, (i), (ii), , If A, G, H, are respectively A.M., G.M., H.M. between two positive number a & b then, (a) G2 = AH (A, G, H constitute a GP), (b) A ³ G ³ H, (c) A = G = H Û a = b, Let a1, a2,........ ,an be n positive real numbers, then we define their arithmetic mean (A), geometric, mean (G) and harmonic mean (H) as A =, , G = (a1 a2...........an)1/n and H =, , a1 + a 2 + ..... + a n, n, , n, 1 ö, æ1 1 1, ç a + a + a + .... a ÷, è 1, 2, 3, n ø, , It can be shown that A ³ G ³ H. Moreover equality holds at either place if and only if, a1 = a2 =......= an, , S OLVED E XAMPLE, Example # 31 : If a, b, c > 0, prove that, Solution :, , a, b, c, +, +, ³3, b, c, a, , Using the relation A.M. ³ G.M. we have, 1, a b c, + +, a b c, 3, a, b, c, æ, ö, b c a ³ ç . . ÷ Þ + +, ³3, b c a, èb c aø, 3, , 16, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 17 :
JEE(Adv.)-Mathematics, , Sequence & Series, , æ 1 1 1ö, Example # 32 : If x,y,z are positive, then prove that (x + y + z) çç x + y + z ÷÷ ³ 9, ø, è, , Solution :, , Using the relation A.M. ³ H.M., 3, x+y+z, ³ 1 1 1 Þ (x + y + z), 3, + +, x y z, , Example # 33 : If ai > 0 " i Î N such that, , n, , Õa, , i, , æ 1 1 1ö, çç + + ÷÷ ³ 9, èx y zø, , = 1 , then prove that (1 + a1) (1 + a2) (1 + a3) ........(1 + an) ³ 2n, , i =1, , Solution :, , Using A.M. ³ G.M., 1 + a1 ³ 2 a1, 1 + a2 ³ 2 a 2, M, , 1 + an ³ 2 an, Þ, , (1 + a1) (1 + a2) .........(1 + an) ³ 2n (a1a 2 a 3 ......a n )1/ 2, As a1 a2 a3 ..... an = 1, Hence (1 + a1) (1 + a2) .......... (1 + an) ³ 2n., , Example # 34 : If n > 0, prove that 2n > 1 + n 2n-1, Solution :, , Using the relation A.M. ³ G.M. on the numbers 1, 2, 22, 23,..........., 2n–1 , we have, , 1 + 2 + 2 2 + ....... + 2n-1, > (1.2. 22. 23. ......... .2n–1)1/n, n, Equality does not hold as all the numbers are not equal., 1, , 2n - 1, Þ, >n, 2 -1, , ( n-1), ( n-1), æ ( n-1) n ö n, ç2 2 ÷, n, n, 2, 2, 2, Þ, 2, >, 1, +, n., 2, Þ, 2, –, 1, >, n., ç, ÷, è, ø, , Example # 35 : Find the greatest value of xyz for positive value of x, y, z subject to the condition xy + yz + zx = 12., Solution :, Using the relation A.M. ³ G.M., xy + yz + zx, ³ (x2 y2 z2)1/3 Þ 4 ³ (x y z)2/3 Þ xyz £ 8, 3, , Example # 36 : If a, b, c are in H.P. and they are distinct and positive, then prove that an + cn > 2bn, Solution :, , Let an and cn be two numbers, then, , an + cn, > (an cn)1/2, 2, an + cn > 2 (ac)n/2, Also G.M. > H.M., i.e., , ...........(i), , ac > b, (ac)n/2 > bn, , ...........(ii), , hence from (i) and (ii), we get a + cn > 2bn, n, , E, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 17

Page 18 :
JEE(Adv.)-Mathematics, , Sequence & Series, , Problems for Self Practice -8:, (1), , If a, b, c are real and distinct, then show that a2 (1 + b2) + b2 (1 + c2) + c2 (1 + a2) > 6abc, , (2), , If a, b, c, d be four distinct positive quantities in G.P., then show that, (i), , a+d>b+c, , (ii), , 1, 1 ö, æ 1, 1, 1, +, ÷, +, >2 ç, ab, cd, è bd ac ad ø, , (3), , Prove that DABC is an equilateral triangle iff tan A + tan B + tan C = 3 3, , (4), , If a, b, c > 0, prove that [(1 + a) (1 + b) (1 + c)]7 > 77 a4 b4 c4, , &, SIGMA NOTATIONS ( S ), , 7., , Theorems :, n, , å (a, , (a), , r =1, , n, , n, , n, , r ± br ) = å a r ± å br, r =1, , (b), , r =1, , åka, r =1, , n, , r, , = kå ar, r =1, , n, , å k = nk, , (c), , 7.1., , r =1, , ; where k is a constant., , Results, n, , år =, , (a), , r =1, , n, , n(n + 1), (sum of the first n natural numbers), 2, n(n + 1)(2n + 1), (sum of the squares of the first n natural numbers), 6, , (b), , år, , (c), , n 2 (n + 1) 2 é n ù, r, =, = ê å r ú (sum of the cubes of the first n natural numbers), å, 4, r =1, ë r =1 û, , 2, , r =1, , n, , =, , 2, , 3, , Note :, If nth term of a sequence is given by Tn = an3 + bn2 + cn + d where a, b, c, d are constants,, then sum of n terms Sn = STn = aSn3 + bSn2 + cSn + Sd, This can be evaluated using the above results., , S OLVED E XAMPLE, Example # 37 : Find the sum of the series to n terms whose general term is 2n + 1., Solution :, , 18, , Sn = STn = å(2n + 1) = 2Sn + S1 =, , 2(n + 1) n, + n = n2 + 2n, 2, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 19 :
JEE(Adv.)-Mathematics, , Sequence & Series, n, , Example # 38 : Tk = k2 + 2k , then find, n, , Solution :, , å, , n, , Tk, , =, , k =1, , å, , k2 +, , n, , å, , åT, , ., , 2k =, , n (n + 1) (2n + 1), n (n + 1) (2n + 1), 2(2n - 1), +, + 2n + 1 – 2., =, 6, 6, 2 -1, , k, , k =1, , k =1, , k =1, , n, , Example # 39 : Find the value of the expression, , i, , j, , ååå, , 1, , i = 1 j = 1k = 1, , n, , Solution :, , i, , n, , j, , ååå, , 1, , =, , i = 1 j = 1k =1, , i, , åå, , i =1 j =1, , n, i (i + 1), 1 éê, i2 +, =, 2, 2, ê, i =1, ëi = 1, , n, , j, , ù, 1 é n (n + 1) ( 2n + 1) + n (n + 1) ù, iú =, ê, 6, 2 úû, 2 ë, i =1 ú, û, n, , =, , å, , =, , n (n + 1) (n + 2), n (n + 1), [2n + 1 + 3] =, ., 6, 12, , å, , å, , 13 13 + 2 3 13 + 23 + 33, +, +, + ....., Example # 40: Find the sum up to 16 terms of the series, 1, 1+3, 1+ 3 + 5, , Solution :, , ïì n ( n + 1) ïü, í, ý, 2, îï, þï, , 2, , 13 + 23 + 33 + .... + n 3, tn =, =, =, n, 1 + 3 + 5 + .... (2n - 1), {2 + 2 ( n - 1)}, 2, , \, , S n = St n =, , \, , S16 =, , n 2 ( n + 1), 4, n2, , 2, , =, , ( n + 1), 4, , 2, , n2 n 1, ==, + +, 4 2 4, , 1 2 1, 1, 1 n ( n + 1)( 2n + 1) 1 n ( n + 1) 1, Sn + Sn + S1 = ., + ., + .n, 4, 2, 4, 4, 6, 2, 2, 4, , 16.17.33 16.17 16, +, +, = 446, 24, 4, 4, , Problems for Self Practice -9:, Find the sum of the series upto n terms 1 +, , (2), , Find the sum of 'n' terms of the series whose nth term is tn = 3n2 + 2n., , Answers : (1), , E, , 1+ 2 1+ 2 + 3 1+ 2 + 3+ 4, +, +, + ..........., 2, 3, 4, , (1), , n(n + 3), 4, , (2), , n(n + 1)(2n + 3), 2, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 19

Page 20 :
JEE(Adv.)-Mathematics, , Sequence & Series, , &, 8., , METHOD OF DIFFERENCE FOR FINDING Tn ( NTH TERM):, Some times the nth term of a sequence or a series can not be determined by the method, we have discussed, earlier. So we compute the difference between the successive terms of given sequence for obtained the nth, terms., If T1, T2, T3,........,Tn are the terms of a sequence then some times the terms T2– T1, T3– T2,......... constitute, an AP/GP. nth term of the series is determined & the sum to n terms of the sequence can easily be obtained., Case 1 :, (a), If difference series are in A.P., then, Let Tn = an2 + bn + c, where a, b, c are constant, (b), If difference of difference series are in A.P., Let Tn = an3 + bn2 + cn + d, where a, b, c, d are constant, Case 2 :, (a), If difference are in G.P., then, Let Tn = arn + b, where r is common ratio & a, b are constant, (b), If difference of difference are in G.P., then, Let Tn = arn + bn + c, where r is common ratio & a, b, c are constant, Determine constant by putting n = 1, 2, 3 ....... n and putting the value of T 1, T2, T3 ...... and sum of, series (Sn) = å Tn, , Note : The above method can be generalised as follows :, Let u1, u2, u3, ......... be a given sequence., The first differences are D1u1, D1u2, D1u3, ........ where D1u1 = u2 – u1, D1u2 = u3 – u2 etc., The second differences are D2u1, D2u2, D2u3, ......., where D2u1 = D1u2 – D1u1, D2u2 = D1u3 – D1u2 etc., This process is continued untill the kth differences Dku1 , Dku2 , ........ are obtained, where the kth differences, are all equal or they form a GP with common ratio different from 1., Case - 1 :, , The kth differences are all equal., In this case the nth term, un is given by un = a0nk + a1nk–1 + .....+ ak , where a0, a1, ...., ak are, calculated by using first 'k + 1' terms of the sequence., , Case - 2 :, , The kth differences are in GP with common ratio r (r ¹ 1), The nth term is given by un = l rn – 1 + a0 nk–1 + a1 nk–2 + ..... + ak–1, , S OLVED E XAMPLE, Example # 41 : Find the sum of n terms of the series 3 + 7 + 14 + 24 + 37 + .........., Solution :, Clearly here the differences between the successive terms are, 7 – 3, 14 – 7, 24 – 14, ........ i.e. 4, 7, 10, 13,........., which are in A.P., Let, S = 3 + 7 + 14 + 24 + ........ + Tn, S = 3 + 7 + 14 + ....... + T n – 1 + Tn, Subtracting, we get, 0 = 3 + [4 + 7 + 10 + 13 +........ (n –1) terms] – Tn, \, Tn = 3 + Sn – 1 of an A.P. whose a = 4 and d = 3., \, , 20, , 6 + (n - 1)(3n + 2), æ n - 1ö, 1, 2, ÷ (2.4 + (n - 2)3) =, Tn = 3 + ç, or, Tn = ( 3n - n + 4 ), è 2 ø, 4, 2, Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 23 :
JEE(Adv.)-Mathematics, , Sequence & Series, , Example # 45 : Sum to n terms of the series, , Solution :, , 4, 5, 6, +, +, + ........., 1. 2 . 3, 2.3.4, 3.4.5, , r +3, 1, 3, =, +, r(r + 1)(r + 2), (r + 1)(r + 2), r(r + 1)(r + 2), , Let Tr =, , ù, 1 ù, 1, é 1, 3 é 1 = ê, +, ú, ê, ú, ër + 1 r + 2 û, 2 ë r(r + 1) (r + 1)(r + 2) û, ù, 1 ù, 1, é1, 3 é1 S= ê ú, ê, ú +, 2, n, +, 2, 2, (, n, +, 1, )(, n, +, 2, ), ë, û, 2 ë, û, , \, , n, , åT, , Example # 46 : If, Solution :, , r, , r =1, , Q, , =, , n, (n + 1)(n + 2)(n + 3) , then find, 8, , n -1, , åT - åT, r =1, , Tn =, , Þ, , 3 ù, 1, 5, 1 é1 +, 5, [2n + 5], –, –, ê, ú =, 2(n + 1)(n + 2), 4, n + 2 ë 2(n + 1) û, 4, , r, , r, , 1, , r =1, , r, , ., , r =1, , n(n + 1)(n + 2)(n + 3) (n - 1)n(n + 1)(n + 2) n(n + 1)(n + 2), =, [(n + 3) - (n - 1)], 8, 8, 8, , =, , n(n + 1)(n + 2), n(n + 1)(n + 2), (4) =, 8, 2, , 1, 2, (n + 2) - n, 1, 1, =, =, =, Tn n(n + 1)(n + 2) n(n + 1)(n + 2) n(n + 1) (n + 1)(n + 2), , Let Vn =, , \, , n, , åT, , T n = Sn – S n – 1, n, , =, , =, , ......... (i), , 1, n(n + 1), , 1, = Vn - Vn +1, Tn, , Putting n = 1, 2, 3, .... n, , E, , Þ, , 1 1, 1, 1, +, +, + ....... +, = (V1 - Vn +1 ), T1 T2 T3, Tn, , Þ, , åT, , n, , 1, , r =1, , r, , =, , n2 + 3n, 2(n + 1)(n + 2), , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 23

Page 24 :
JEE(Adv.)-Mathematics, , Sequence & Series, , Problems for Self Practice -10:, (1), , Sum to n terms the following series, (i), , 4 + 14 + 30 + 52 + 80 + 114 + .........., , (ii), , 2 + 5 + 12 + 31 + 86 + ..............., , (iii), , 3, , 1, , +, , 1+ 2, 3, , 1 +2, , 3, , +, , 1+ 2 + 3, 3, , 1 + 23 + 3 3, , + ........., , (iv), , 1, 1, 1, +, +, + ........., 1. 3 . 5, 3.5.7, 5.7.9, , (v), , 1 . 5 . 9 + 2 . 6 . 10 + 3 . 7. 11 + ........., , Answers :, , 24, , 1, , (1), , (i), , n(n + 1)2, , (ii), , 3n + n2 + n - 1, 2, , (iii), , 2n, n+1, , (iv), , ù, 1, 1 é1 ê, ú, 4 ë 3 (2n + 1)(2n + 3) û, , (v), , n, (n + 1) (n + 8) (n + 9), 4, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 25 :
JEE(Adv.)-Mathematics, , Sequence & Series, , PART-I : SUBJECTIVE QUESTIONS, Section (A) : Arithmetic Progression, k, + 9., 7, , A-1., , Find the sum of first 48 terms of the series whose kth term is, , A-2., , Find the sum of all those integers between 100 and 800 each of which on division by 16 leaves the, remainder 7., , A-3., , Find the number of integers between 100 & 1000 that are not divisible by 13, , A-4., , If the sum of first 10 terms of an A.P. is 140 and the sum of first 16 terms is 320, find the sum of n terms, , A-5., , Find the sum of the series (a + b)2 + (a2 + b2) + (a – b)2 + ..... + to n terms., , A-6., , If x > 0, and log2 x + log2, , A-7., , If pth, qth and rth terms of an A.P are a,b,c respectively than prove that a(q – r) + b(r – p) + c(p – q) = 0, , A-8., , The sum of three consecutive numbers in A.P. is 27, and their product is 504, find them., , A-9., , If a, b, c are in A.P., then show that:, , ( x ) + log ( x ) + log ( x ) + log ( x ) + ...... = 4, then find x., 2, , 4, , 8, , 2, , 16, , 2, , (i) b + c - a, c + a - b, a + b - c are in A.P., (ii) a +, , (iii), , 1, 1, 1, ,b+, ,c+, are in AP, bc, ca, ab, , 1, ,, b+ c, , 1, ,, c+ a, , 1, are in AP, a+ b, , (iv) a2 (b + c), b2 (c + a), c2 (a + b) are also in A.P., A-10. The fourth power of the common difference of an arithmetic progression with integer entries is added to the, product of any four consecutive terms of it. Prove that the resulting sum is the square of an integer., , an + bn, A-11. If n–1, is the A.M. between a and b (where a ¹ b) then find the value of n, a + b n–1, A-12. There are 11 AMs between 28 and 10. Find the number of integral AMs, A-13. If a, b, c, d, e, f are AMs between 2 and 12 then find thesum a + b + c +d + e + f, , Section (B) : Geometric Progression, , E, , B-1., , A boy agrees to work at the rate of one rupee the first day, two rupees the second day, four rupees the third day,, eight rupees the fourth day and so on in the month of April. How much would he get on the 20th of April., , B-2., , The seventh term of a G.P. is 8 times the fourth term. Find the G.P. when its 5th term is 48, , B-3., , The sum of three numbers which are consecutive terms of an A.P. is 21. If the second number is reduced by 1, & the third is increased by 1, we obtain three consecutive terms of a G.P., find the numbers., , B-4., , If the pth, qth & rth terms of an AP are in GP. Find the common ratio of the GP., , B-5., , The sum of infinite number of terms of a G.P. is 4 and the sum of their cubes is 192. Find the series., Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 25

Page 26 :
JEE(Adv.)-Mathematics, B-6., B-7., B-8., , The third term of a G.P. is the square of the first term. If the second term is 8, find its sixth term., The continued product of three numbers in G.P. is 216, and the sum of the products of them in pairs is 156; find, the numbers, If a, b, c, d are in G.P., prove that :, (i) (a2 - b2), (b2 - c2), (c2 - d2) are in G.P., (ii), , B-9., , Sequence & Series, , 1, 2, , a +b, , 2, , ,, , 1, 2, , b +c, , 2, , ,, , 1, 2, , c + d2, , are in G.P.., , In a set of four numbers, the first three are in G.P. and the last three are in A.P. with a common difference of 6., If the first number is same as the fourth find the four number., , B-10. If G is the geometric mean between two distinct positive numbers a and b, then show that, , 1, 1, 1, +, =, G-a G-b G, , ., B-11. If a is the A.M. of b and c and GMs inserted between b and c are G1, G2 then prove that G13 + G 32 = 2abc, , Section (C) : Harmonic and Arithmetic Geometric Progression, C-1., , If mth term of a H.P. be n and nth term be m then find the (mn)th term, , C-2, , If a, b, c are in H.P. and a > c > 0, then prove that, , C-3., , If b is the harmonic mean between a and c, then prove that, , 1, 1, is positive, b-c a-b, 1, 1, 1 1, +, = + ., b-a, b-c, a c, , a –2 – d –2, C-4. If a, b, c, d are in H.P. then find the value of –2, b – c –2, C-6., C-7., , If the first and (2n + 1)th term of a A.P, G.P and H.P (consisting of positive terms) are equal and their (n + 1)th, terms are a, b, c respectively then prove that a, b, c are in G.P., If a be a positive real number and A.M of a and 2a exceed their HM by 2, then find a, , C-8., , The H.M. between two numbers is, , C-9., , If 9 AMs A1, ....A9 and 9HMs H1, H2, ...... H9 are inserted between 2 and 3 alternatively then find the value of, Ai +, , 16, , their A.M. is A and G.M. is G. If 2A + G2 = 26, then find the numbers., 5, , 6, Hi, , C-10. Sum the following series 1 +, , 3, 4, 2, + 2 + 3 + ........ to n terms., 2, 2, 2, , C-11. Find the sum of n terms of the series the rth term of which is (2r + 1)2r., C-12. Find the sum :, , 26, , 3 5, 7, 9, –, +, –, + ......... ¥, 2 6 18 54, Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 27 :
JEE(Adv.)-Mathematics, , Sequence & Series, , Section (D) : Means, Inequalities A.M. ³ G.M. ³ H.M, D-1., D-2., , If the product of three positive real numbers say a, b, c be 27, then find the minimum value of ab + bc + ca, Using the relation A.M. ³ G.M. prove that, (x2y + y2z + z2x) (xy2 + yz2 + zx 2) ³ 9x2 y2 z2. (x, y, z are positive real number), , D-3, , If a, b, c are three positive real numbers, then the minimum value of the expression, , D-4., , If x > 0, then find greatest value of the expression, , D-5., , If xi > 0, i = 1, 2, ..., 50 and x 1 + x2 + .. + x50 = 50, then find the minimum value of, , D-6., , If a, b, c are positive real numbers and sides of the triangle, then prove that, (a + b + c)3 ³ 27 (a + b – c) (c + a – b) (b + c – a), If a, b, c be three unequal positive quantities in H.P. then prove that an + cn > 2bn, If abc = 8 and a, b, c > 0, then find the minimum value of (2 + a) (2 + b) (2 + c), Using the relation A.M. ³ G.M. prove that (a + b) . (b + c) . (c + a) > abc ; if a, b, c are positive real numbers, , D-7., D-8, D-9, , x100, 1 + x + x 2 + x 3 + ..... + x 200, , b+c c+a a+b, +, +, a, b, c, , ., 1, 1, 1, +, + .....+, ., x1, x2, x 50, , Section (E) : Summation of series, k, , å, , k, , tn ., , E-1., , (i) If tn = 3 – 2 then find, , E-2., , Find the sum of the series 313 + 323 + ...... + 503, , E-3., , If Sn =, , n, , n, , n, , E-4., , åt, , r, , r =1, , =, , n=1, , (ii) If tn = n(n + 2) then find, , 1, n (2n2 + 9n + 13 ) , then, 6, , Find the sum of n terms :, , ¥, , å, , r =1, , 1, r . tr, , åt, n=1, , n, , ., , equals, , 13 13 + 23 13 + 23 + 33, + ........., +, +, 1, 1+ 3, 1+3+ 5, , Section (F) : Method of difference and Vn Method, F-1., F-2., , Sum to n terms : 3 + 15 + 35 + 63 + ......, Find the sum to n-terms of the sequence : 1 + 5 + 13 + 29 + 61 + ........, , F-3., , Find the sum to n-terms of the sequence :, , F-4., , Find the sum, , ¥, , å, , r=2, n, , F-5, , F-6., , E, , If Sn =, , å, r =1, , 1, 1, 1, +, +, + ...., 1.3.5, 3.5.7, 5.7.9, , 1, r -1, 2, , Tr = n(n + 1)(n + 2)(n + 3) then find, , r+2, 1, × r +1 , then find, If tr =, r(r + 1) 2, , 10, , 1, , r =1, , r, , åT, , n, , åt, , r, , r =1, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 27

Page 28 :
JEE(Adv.)-Mathematics, , Sequence & Series, , PART-II : OBJECTIVE QUESTIONS, Section (A) : Arithmetic Progression, A-1., , A-2., , A-3., , A-4., , If a1, a2 , ......., an are distinct terms of an A.P., then, (A) a1+ 2a2 + a3 = 0, (B) a1 - 2a2 + a4 = 0, (C) a1 + 3a2 - 3a3 - a4 = 0, (D) a1 - 4a2 + 6a3 - 4a4 + a5 = 0, If the sum of the first 2n terms of the A.P. 2, 5, 8, ....., is equal to the sum of the first n terms of the, A.P. 57, 59, 61, ..., then n equals, (A) 10, (B) 12, (C) 11, (D) 13, The sum of integers from 1 to 100 that are divisible by 2 or 5 is, (A) 2550, (B) 1050, (C) 3050, (D) none of these, Let a1, a2, a3,..... be terms of an AP. If, , (A), A-5., A-6., , A-7., , A-8., , 7, 2, , (B), , a1 + a 2 + ...... + ap, a1 + a 2 + ...... + a q, , 2, 7, , (C), , =, , p2, q, , 2, , , p ¹ q, then, , 11, 41, , a6, equals :, a 21, , (D), , 41, 11, , The sum of four integers in A.P. is 24 and their product is 945. The common difference of A.P. is, (A) ± 1, (B) ± 2, (C) ± 3, (D) ± 4, If a1, a2, a3,........ are in A.P. such that a1 + a5 + a10 + a15 + a20 + a24 = 225, then, a1 + a2 + a3 + ..... + a23 + a24 is equal to, (A) 909, (B) 75, (C) 750, (D) 900, A person is to count 4500 currency notes. Let an denote the number of notes he counts in the nth minute. If, a1 = a2 = .....= a10 = 150 and a10, a11,....are in an AP with common difference –2, then the time taken by him to, count all notes is, (A) 34 minutes, (B) 125 minutes, (C) 135 minutes, (D) 24 minutes, th, There are n A.M's between 3 and 54, such that the 8th mean: (n - 2) mean:: 3: 5. The value of n is., (A) 12, (B) 16, (C) 18, (D) 20, , Section (B) : Geometric Progression, B-1., , B-2., , The third term of a G.P is 4. The product of the first five terms is, (A) 43, (B) 45, (C) 44, For a sequence {an}, a1 = 2 and, , (A), B-3., , B-4., , 20, [4 + 19 × 3], 2, , an, , =, , 1, . Then, 3, , 1 ö, æ, (B) 3 ç1 - 20 ÷, è 3 ø, , 20, , åa, r =1, , r, , is, , (C) 2 (1 – 320), , 1 ö, æ, (D) ç1 - 20 ÷, è 3 ø, , One side of an equilateral triangle is 24 cm. The mid-points of its sides are joined to form another triangle, whose mid - points are in turn joined to form still another triangle. This process continues indefinitely. Then the, sum of the perimeters of all the triangles is, (A) 144 cm, (B) 212 cm, (C) 288 cm, (D) 172 cm, If S is the sum to infinity of a G.P. whose first term is ‘a’, then the sum of the first n terms is, aö, æ, (A) S ç1 - ÷, S, è, ø, , 28, , an + 1, , (D) 4, , n, , n, é æ, aö ù, ê, ú, 1, 1, ÷, ç, (B) S, Sø ú, êë è, û, , n, é æ, aö ù, (C) a ê1 - ç1 - ÷ ú, Sø ú, êë è, û, , n, é æ, Sö ù, ê, ú, 1, 1, ç, (D) S, a ÷ø ú, êë è, û, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 29 :
JEE(Adv.)-Mathematics, B-5, , B-6, , Sequence & Series, , If y, x, z are in A.P., then, (A) x + y, y + z, z + x are in G.P., (C) 3x, 3y, 3z are in G.P., The real values of x for which y = 1 +, , B-8, , B-9, , If, , 1, ,, b+ c, , 2 4 8 16, + + + + K ¥ is finite is, x x2 x3 x4, (B) (–¥ , –2) È (2, ¥), (D) none of these, , (A) (–2, 2), (C) (2, ¥), B-7, , (B) 2x+y, 2y+z, 2z + x are in G.P., (D) none of these, , 1, ,, c+ a, , 1, are in A.P. then 9ax + 1, 9bx+1, 9cx+1 (where x Î R) are in, a+ b, , (A) G.P., (B) G.P. only if x < 0, (C) G.P. only if x > 0, (D) none of these, A G.P. consists of even number of terms. If the sum of all the terms is 5 times the sum of the terms occupying, odd places, then its common ratio is, (A) 2, (B) 3, (C) 4, (D) 5, If k1, k2, k3 and k4 are GM's between a and b, then roots of the equation k 2k 3 x2 (A) One positive, one negative, (C) Both positive, , k2, x - k1k 4 = 0 are, k1 + k 3, , (B) Both negative, (D) Imaginary, , Section (C) : Harmonic and Arithmetic Geometric Progression, C-1., C-2., , C-3., , C-4, , log45 , log205, log1005 are in, (A) A.P., (B) G.P., (C) H.P., (D) none of these, Let the positive numbers a, b, c, d be in A.P. Then abc, abd, acd, bcd are:, (A) not in A.P./G.P./H.P., (B) in A.P., (C) in G.P., (D) in H.P., Statement 1 : 3,6,12 are in G.P., then 9,12,18 are in H.P., Statement 2 : If three consecutive terms of a G.P. are positive and if middle term is added in these terms, then, resultant will be in H.P., (A) STATEMENT-1 is true, STATEMENT-2 is true and STATEMENT-2 is correct explanation for, STATEMENT-1, (B) STATEMENT-1 is true, STATEMENT-2 is true and STATEMENT-2 is not correct explanation for, STATEMENT-1, (C) STATEMENT-1 is true, STATEMENT-2 is false, (D) STATEMENT-1 is false, STATEMENT-2 is true, If ai Î R and a1, a2, a3 are in A.P., a2, a3, a4 are in G.P. and a3, a4, a5 are in H.P. then, , (A), C-5, , E, , a1, a3, , (B), , a3, a1, , (C), , a5, a1, , a1 - a3, a3 - a5 is equal to, , (D) 1, , The harmonic mean of two numbers is 4 and their arithmetic mean and geometric mean satisfy the relation, 2A + G2 = 27. The numbers are, (A) 6, 3, (B) 5, 4, (C) 5, -5/2, (D) -3, 1, Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 29

Page 30 :
JEE(Adv.)-Mathematics, C-6., , If 3 +, , 1, 1, (3 + d) + 2 (3 + 2d) +...... + upto ¥ = 8, then the value of d is, 4, 4, , (A) 9, C-7., , (B) 5, , The sum of the series 1 +, , (A), , C-8., , Sequence & Series, , 8, 3, , (C) 1, , (D) 4, , 7, 15, 31, 3, +, +, +, + ..... to infinity is, 16, 64, 256, 4, , (B), , 4, 3, , (C) 2, , (D) 3, , If A, G & H are respectively the A.M., G.M. & H.M. of three positive numbers a, b, & c, then the equation whose, roots are a, b, & c is given by:, (A) x3 - 3 Ax2 + 3 G3x - G3 = 0, , (B) x3 - 3 Ax2 + 3 (G3/H)x - G3 = 0, , (C) x3 + 3 Ax2 + 3 (G3/H) x - G3 = 0, , (D) x3 - 3 Ax2 - 3 (G3/H) x + G3 = 0, , Section (D) : Inequality A.M. ³ G.M. ³ H.M, D-1., , If a, b, c, d are positive real numbers such that a + b + c + d = 2, then M = (a + b) (c + d) satisfies the relation:, (A) 0 £ M £ 1, , D-2., , (B) 1 £ M £ 2, , (D) 3 £ M £ 4, , If x Î R, the numbers 51+x + 51–x, a/2, 25x + 25–x form an A.P. then 'a' must lie in the interval:, (A) [1, 5], , D-3., , (C) 2 £ M £ 3, , (B) [2, 5], , (D) [12, ¥), , (C) [5, 12], 2 3 2, , If a + b + c = 3 and a > 0, b > 0, c > 0, the greatest value of a b c ., (A), , 310.2 4, 77, , (B), , 3 9.2 4, , (C), , 77, , 3 9.25, , (D), , 77, , 310.25, 77, , D- 4. If x, y, z are positive numbers then minimum value of xln y -ln z + yln z -ln x + zln x -ln y is, (A) 1, D-5, , (B) 2, , (D) 4, , If 2x + 3y + 5z = 10 and 81xyz = 100, where x, y, z Î R+, then number of ordered triplet (x, y, z) is, (A) 0, , D-6, , (C) 3, , (B) 1, , (C) infinite, , (D) none of these, , Let p, q, r Î R and 27pqr ³ (p + q + r) and 3p + 4q + 5r = 12 then p + q + r5 is equal to, +, , (A) 3, , 3, , (B) 6, , 3, , (C) 2, , 4, , (D) none of these, , Section (E) : Summation of series, E-1., , Sum of the series S = 12 – 22 + 32 – 42 + .... – 20022 + 20032 is, (A) 2007006, , E-2., , If Hn = 1 +, (A) 2n – Hn, , 30, , (B) 1005004, , (C) 2000506, , (D) none of these, , 1, 5, 1, 1, 3, 2n - 1, +, + ...........+ , then value of 1 +, +, + ......... +, is, 3, 3, 2, n, 2, n, , (B) 2n + Hn, , (C) Hn – 2n, , (D) Hn + n, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 31 :
JEE(Adv.)-Mathematics, , Sequence & Series, 10, , E-3., , Given that a1, a2, a3, .....an form an A.P. find then following sum, , a iai +1ai + 2, , å a +a, i=1, , i, , i+ 2, , Given that a1 = 1 ; a2 = 2, (A), E-4., , 495, 2, , (B), , 415, 2, , (C) 112, , (D) 115, , If the sum of first n terms of an A.P. is cn2, then the sum of squares of these n terms is, (A), , n( 4n 2 - 1) c 2, 6, , (B), , n( 4n 2 + 1) c 2, 3, , (C), , n( 4n 2 - 1) c 2, 3, , (D), , n( 4n 2 + 1) c 2, 6, , Section (F) : Method of difference and Vn Method, F-1., , Statement 1 : The sum of the first 30 terms of the sequence 1,2,4,7,11,16, 22,...... is 4520., Statement 2 : If the successive differences of the terms of a sequence form an A.P., then general term, sequence is of the form an2 + bn + c., , of, , (A) STATEMENT-1 is true, STATEMENT-2 is true and STATEMENT-2 is correct explanation for, STATEMENT-1, (B) STATEMENT-1 is true, STATEMENT-2 is true and STATEMENT-2 is not correct explanation for, STATEMENT-1, (C) STATEMENT-1 is true, STATEMENT-2 is false, (D) STATEMENT-1 is false, STATEMENT-2 is true, , r 3 + (r 2 + 1)2, is equal to, å, 4, 2, 2, r =1 (r + r + 1)(r + r), ¥, , F-2., , (A), , 3, 2, , (B) 1, , (C) 2, , 2n, , F-3., , If H1, H2, H3, ……, H2n + 1 are in H.P., then, (A) 2n - 1, , F-4., , E, , æ Hi + Hi+1 ö, ÷ is equal to, i, i +1 ø, , å ( -1) çè H - H, i=1, , i, , (B) 2n + 1, , (C) 2n, , (D) 2n + 2, , If a1, a2, ...., an are in HP, then the expression a1a2 + a2a3 +......+ an – 1 an is equal to :, (A) (n – 1) (a1 – an), , F-5., , (D) infinite, , (B) na1an, , (C) (n – 1) a1an, , Find the sum to ten terms of the sequence : 1 . 3 ., , 22, , (A) 11.12 .13 .23, , (B) 10.11 .12 .23, , (C) 10.12 .13 .23, , (D) None of these, , +2.4., , 32, , +3.5., , (D) n (a1 – an), 42, , + ...., , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 31

Page 32 :
JEE(Adv.)-Mathematics, , Sequence & Series, , PART - III : MATCH THE COLUMN, 1., , Column-I, (A), , (B), , Column-II, , The cofficient of x 49 in the product, (x – 1) (x – 3) (x – 5) (x – 7) ....... (x – 99), , (p), , –2500, , Let Sn denote sum of first n terms of an A.P. If S2n = 3Sn,, , (q), , 9, , (r), , 3, , (s), , 6, , then, , S3n, is, Sn, , 12, 16, 8, + 2 + 3 + - - - is, 3, 3, 3, , (C), , Sum of infinite series 4 +, , (D), , The length,breadth, height of a rectangular box are in G.P., (length > breadth > height) The volume is 27, the total surface, area is 78. Then the length is, , 2., , Column-I, (A), , Column-II, , The value of xyz is 15/2 or 18/5 according as the series, , (p), , 2, , a, x, y, z, b are in an A.P. or H.P. then 'a + b' equals, where a, b are positive integers., , 1, , 1, , 1, , (B), , The value of 2 4 . 4 8 . 8 16 - - - ¥ is equal to, , (q), , 1, , (C), , If x, y, z are in A.P., then, , (r), , 3, , (s), , 4, , (x + 2y – z) (2y + z – x) (z + x – y) = kxyz,, where k Î N, then k is equal to, (D), , There are m A.M. between 1 and 31. If the ratio of the, 7th and (m –1)th means is 5 : 9, then, , 32, , m, is equal to, 7, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 33 :
JEE(Adv.)-Mathematics, , Sequence & Series, , PART-I : OBJECTIVE, 1., , If 1, 2, 3 ... are first terms; 1, 3, 5 .... are common differences and S 1, S2, S3 .... are sums of n terms of given, p AP’s; then S1 + S2 + S3 + ... + Sp is equal to, (A), , 2., , (B), , n(np + 1), 2, , (C), , np(p + 1), 2, , If a, b and c are three terms of an A.P. such that a ¹ b, then, (A), , 3., , np(np + 1), 2, , (B), , 2, , 3, , (D), , np(np - 1), 2, , b-c, may be equal to, a-b, , (C) 1, , (D) None of these, , Sum of the first n terms of an A.P (having positive terms) is given by S n = (1 + 2Tn) (1 – Tn), where Tn is the, nth term of the series, then the value of T22 is, , (A), , 2 +1, 2 2, , (B), , (C), , 1, 2 2, , (D) none of these, , 4., , If the sum of n terms of a G.P. (with common ratio r) beginning with the pth term is k times the sum of an equal, number of terms of the same series beginning with the qth term, then the value of k is:, (A) rp/q, (B) rq/p, (C) r p - q, (D) rp + q, , 5., , Suppose a, b, c are in A.P. and a2, b2, c2 are in G.P. if a < b < c and a + b + c =, (A), , 1, , (B), , 2 2, , 1, 2 3, , (C), , 1, 1, –, 3, 2, , 3, , then the value of a is, 2, , (D), , 1, 1, –, 2, 2, , 6., , Area of the triangle with vertices (a, b), (x 1, y1) and (x2, y2) where a, x1, x2 are in G.P. with common ratio r and, b, y1, y2 are in G.P. with common ratio s is, (A) ab(r – 1)(s – 1) (s – r), (B) ab(r + 1)(s + 1)(s – r), (C) ab(r – 1) (s – 1) (s – r), (D) ab (r + 1)(s + 1)(r – s), , 7., , Let S =, , (A), 8., , 4 44 444, +, +, + .......¥ . Then S is equal to, 19 192 193, , 38, 81, , (B), , é3, ë4, , 9., , 4, 19, , (C), , 36, 171, , (D) none of these, , If three distinct real numbers a, b, c are in G.P and a + b + c = ax, then, , ö, ø, , (A) x Î ê , ¥ ÷ – {1, 3}, , E, , 2 -1, 2 2, , (B) x Î R+, , (C) x Î (–1, ¥), , (D) none of these, , If a, b, c are in A.P a, x, b are in G.P and b, y, c are in G.P., then x 2, b2, y2 are in, (A) A.P., (B) G.P., (C) H.P., (D) None of these, Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 33

Page 34 :
JEE(Adv.)-Mathematics, ¥, , 10., , If x =, , å, n=0, , an , y =, , ¥, , å, n=0, , Sequence & Series, , bn , z =, , ¥, , åc, , n, , n=0, , where a,b,c are in AP and |a| < 1, |b| < 1, |c| < 1, then x,y,z are in :, , (A) HP, (C) AP, 11., , (B) Arithmetico–Geometric Progression, (D) GP, , Given the sequence of numbers x1, x2, x3, ...... x2013 which satisfy, , =, , x 2013, , nature of the sequence is, x 2013 + 4025, , (A) A.P., 12., , x3, x1, x2, = ......., =, =, x1 + 1, x2 + 3, x3 + 5, , If, , (B) G.P., , (C) H.P., , (D) A.G.P., , 1, 1, 1, 1, +, + +, = 0 and a, b, c are not in A.P, then, a a - 2b c c - 2b, , (A) a, b, c are in G.P, , (C) a,, , (B) a,, , b, , c are in H.P, 2, , b, , c are in A.P, 2, , (D) a, 2b, c are in H.P, , 13., , If 3x 2 - 2( a -d) x + (a2 + 2( b2 +c2) +d2) = 2(ab +bc + cd), then, (A) a, b, c, d are in G .P., (B) a, b, c, d are in H .P., (C) a, b, c, d are in A .P., (D) none of these, , 14., , If x, y, z are real numbers such that x 2 + 18y2 + 81z2 = 6xy + 54yz, then x, y, z are in, (A) A.P., (B) G.P., (C) H.P., (D) A.G.P., , 15., , The sum of the first n-terms of the series 12 + 2.22 + 32 + 2.42 + 52 + 2.62 + .......... is, , n(n + 1)2, , when n is even., 2, , When n is odd, the sum is, (A), 16., , n(n + 1)2, 4, , (B), , n2 (n + 2), 4, , (C), , n 2 (n + 1), 2, , (D), , n(n + 2)2, 4, , Let Tr and Sr be the rth term and sum up to rth term of a series respectively. If for an odd number n, Sn = n and, Tn =, , (A), 17., , Tn-1, n2, 2, 1 + m2, , then Tm (m being even) is, , (B), , 2m 2, 1 + m2, , (C), , (m + 1)2, 2 + (m + 1)2, , (D), , 2(m + 1)2, 1 + (m + 1)2, , Consider the sequence 2, 3, 5, 6, 7, 8, 10, 11, ..... of all positive integer, then 2011th term of this sequence is, (A) 2056, (B) 2011, (C) 2013, (D) 2060, If a1, a2, a3, ........., an are positive real numbers whose product is a fixed number c, then the minimum value of, a1 + a2 + a3 + .... + an – 1 + 2an is, (A) n(2c)1/n, (B) (n + 1) c1/n, (C) 2nc1/n, (D) (n + 1)(2c)1/n, , 18., , 34, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 35 :
JEE(Adv.)-Mathematics, 19., , Sequence & Series, , If 12 + 22 + 32 + ....... + 20032 = (2003) (4007) (334) and, (1) (2003) + (2) (2002) + (3) (2001) + ..... + (2003) (1) = (2003) (334) (x)., then x equals, (A) 2005, , 20., , If, , (B) 2004, , (C) 2003, , 1, p2, 1, 1, 1, 1, 1, +, +, +......, upto, ¥, =, , then 2 + 2 + 2 +...... =, 2, 2, 2, 1, 6, 1, 2, 3, 3, 5, , (A) p2/12, , (B) p2/24, , (C) p2/8, 2, , 21., , (D) p2/4, , 3, , 7 æ1ö, 9 æ1ö, 11 æ 1 ö, +, The sum of, + ... upto 10 terms is equal to, ç ÷ +, ç, ÷, 2 ´ 3 è 3 ø 3 ´ 4 è 3 ø 4 ´ 5 çè 3 ÷ø, (A), , 1, 1, 2 12 ´ 310, , (B), , n, , 22., , (D) 2001, , The value of, , 1, 1, 3 12 ´ 310, , 1, 1, 2 10 ´ 310, , (D) none of these, , å (a + r + ar)(-a) is equal to, r, , r =0, , (A) ( -1)n [(n + 1)an+1 - a], n, (C) ( -1), , (C), , (n + 2)an+1, 2, , (B) ( -1)n (n + 1)an+1, n, (D) ( -1), , nan, 2, , PART-II : NUMERICAL QUESTIONS, 1., , A man arranges to pay off a debt of Rs. 3600 by 40 annual installments which form an arithmetic series. When, 30 of the installments are paid he dies leaving a third of the debt unpaid. Find the value of the first installment., , 2., , If the common difference of the A.P. in which T7 = 9 and T1T2T7 is least, is ‘d’ then 20d is–, , 3., , The number of terms in an A.P. is even ; the sum of the odd terms is 24, sum of the even terms is 30, and the, last term exceeds the first by 10½; find the number of terms., , 4., , If, , a+b, b+c, , b,, are in A.P. and a, b be the roots of equation 2acx 2 + 2abcx + (a + c) = 0 then, 1 - ab, 1 - bc, , (1 + a) (1 + b) is equal to (a, b, c ¹ 0), 5., , If S denote the sum to infinity and Sn the sum of n terms of the series 1 +, , S - Sn <, 6., , 1, , then find the least value of n, 300, , In a circle of radius R a square is inscribed, then a circle is inscribed in the square, a new square in the circle, and so on for n times. If the ratio of the limit of the sum of areas of all the circles to the limit of the sum of areas, of all the squares as n ® ¥ is k, then find the value of, , E, , 1 1 1, + + + ... such that, 3 9 27, , 4k, ., p, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 35

Page 36 :
JEE(Adv.)-Mathematics, 7., , Sequence & Series, , Find the sum of the infinitely decreasing G.P. whose third term, three times the product of the first and fourth, term and second term form an A.P. in the indicated order, with common difference equal to 1/8., If a, b, c are in GP, a – b, c – a, b – c are in HP, then the value of a + 4b + c is, Given that a, g are roots of the equation Ax 2 - 4 x + 1 = 0 and b, d the roots of the equation, B x2 - 6 x + 1 = 0, then find value of (A + B), such that a, b, g & d are in H.P., a, a1, a2, a3,..., a2n , b are in A.P. and a, g1, g2, g3,.....g2n, b are in G.P. and h is the harmonic mean of a and b,, , 8., 9., 10., , if, 11., , a 2 + a 2n - 1, an + a n + 1, a1 + a 2n, Kn, + g g, , then find value of K., +, ..., +, is, equal, to, g, g, g1g2n, 20h, 2 2n - 1, n n +1, , If the arithmetic mean of two numbers a & b (0 < a < b) is 6 and their geometric mean G and harmonic mean, H satisfy the relation G2 + 3 H = 48. Then find the value of (2a – b), If a1 , a2 , a3 , a4 are positive real numbers such that a1 + a2 + a3 + a4 = 16 then find maximum value of, (a1 + a2)(a3 + a4)., , 12., , a, b, c, +, +, b +c -a c +a-b a+b-c, , 13., , If a, b, c are the sides of a triangle, then find the minimum value of, , 14., , Find the number of solutions of equation x a, , 15., , If S1 , S2, S3 are the sums of first n natural numbers, their squares, their cubes respectively, then, , 1/ x, , +, , 1 x, a = 2 a, a ³ 1, x, S 3 (1 + 8S1 ), S 22, , is equal to, 2, , 2, 25, = 12 k, 5, , 16., , If, , 17., , If S =, , 1, , If, , å, , 32, 4 2 52 6 2, +, +........ ¥, then find the value of k, 52 53 5 4 55, 2, , 3, , +........¥, then find the value of 14S., +, 2, 4 +, 1 + 32 + 34, 1 + 12 + 14 1 + 2 + 2, , n, , 18., , +, , tr =, , r =1, , n(n + 1)(n + 2)(n + 3 ), , then, 8, , ¥, , 4, , r =1, , r, , åt, , equals, , PART - III : ONE OR MORE THAN ONE CORRECT, 1., , The interior angles of a polygon are in A.P. If the smallest angle is 120º & the common difference is 5º, then the, number of sides in the polygon is:, (A) 7, (B) 9, (C) 16, (D) 5, If 1, logy x, logz y, –15 logx z are in A.P., then, (A) z3 = x, (B) x = y–1, (C) z–3 = y, (D) x = y–1 = z3, Consider an infinite geometric series with first term 'a' and common ratio r. If the sum is 4 and the second term, is 3/4, then:, , 2., 3., , (A) a =, , 36, , 7, 3, ,r=, 4, 7, , (B) a = 2, r =, , 3, 8, , (C) a =, , 3, 1, ,r=, 2, 2, , (D) a = 3, r =, , 1, 4, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 37 :
JEE(Adv.)-Mathematics, 4., , Sequence & Series, , Three numbers a, b, c between 2 and 18 are such that, (i) their sum is 25, (ii) the numbers 2, a, b, are in A.P., (iii) the number b, c, 18 are in G.P., then which of the following options are correct., (A) a = 5, , 5., , (B) b = 8, , (B) n = 5, , 5 + 1, 2, , 10., , (B) 0 < r < 1, , If a satisfies the equation a, , 2017, , (C), , 2, , i, , = 126 then, , i=1, , ak +1, =4, ak, , (D), , 5 +1, , (C) r = 3.5, , 2, 5-1, , (D) r = 5.2, , – 2a + 1 = 0 and S = 1 + a + a + ..... + a, 2, , (B) 2018, , . then posible value(s) of S is/are, , 2016, , (C) 2017, , (D) 2, , Which of the following numbers is/are composite, (A) 1111......1 (91 digits), , (B) 1111......1 (81 digits), , (C) 1111......1 (75 digits), , (D) 1111......1 (105 digits), , If the arithmetic mean of two positive numbers a & b (a > b) is twice their geometric mean, then a: b is:, (A) 2 + 3 : 2 - 3, , 11., , (D), , åa, , If b1, b2, b3 (bi > 0) are three successive terms of a G.P. with common ratio r, the value of r for which the, inequality b3 > 4b2 – 3b1 holds is given by, , (A) 2016, 9., , 5 - 1, 2, , (B), , (A) r > 3, 8., , ak +1, (C) a = 2, k, , n, , The sides of a right triangle form a G.P. The tangent of the smallest angle is, (A), , 7., , (D) a + b + c = 25, , ak +1, is constant for every k ³ 1. If n > m Þ an > am and a1 + an = 66, a2an–1 = 128 and, If, ak, , (A) n = 6, 6., , (C) b + c = 20, , (B) 7 + 4 3 : 1, , (C) 1: 7 - 4 3, , (D) 2:, , 3, , Which of the following is/are TRUE, (A) Equal numbers are always in A.P. , G.P. and H.P., (B) If a, b, c be in H.P., then a -, , b b, b, , ,cwill be in AP, 2 2, 2, , (C) If G1 and G2 are two geometric means and A is the arithmetic mean inserted between two positive numbers,, then the value of, , G12 G22, +, is 2A., G2 G1, , (D) Let general term of a G.P. (with positive terms) with common ratio r be Tk + 1 and general term of another G.P., (with positive terms) with common ratio r be T¢k + 1, then the series whose general term T¢¢k + 1 = Tk + 1 + T¢k + 1 is, also a G.P. with common ratio r., 12., , Let a, x, b be in A.P; a, y, b be in G.P and a, z, b be in H.P. If x = y + 2 and a = 5z, then, (A) y2 = xz, , E, , (B) x > y > z, , (C) a = 9, b = 1, , (D) a = 1/4, b = 9/4, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 37

Page 38 :
JEE(Adv.)-Mathematics, , Sequence & Series, , If ak ak–1 + ak–1 ak–2 = 2ak ak–2 , k ³ 3 and a1 = 1, here Sp =, , 13., , 1, a2016, , p, , 1, , k =1, , k, , åa, , S2p, and given that S does not depend on p then, p, , may be, , (A) 4031, (B) 1, (C) 2016, (D) 2017/2, First three terms of the sequence 1/16, a, b, 1/6 are in geometric series and last three terms are in harmonic, series if, , 14., , (A) a =, , 1, 1, ,b=, 9, 12, , (C) a = 1, b = -, , (B) a =, , 1, 4, , 1, 1, ,b=, 9, 12, , (D) a = -, , 1, ,b=1, 4, , æ, 1 ö æ, 1ö æ, 1 ö, For the series 2 + ç 2 +, ÷ + ç (2 2 - 1) + ÷ + ç 3 2 – 2 +, ÷ + ....., 2ø è, 2ø è, 2 2ø, è, , (, , 15., , (A) Sn =, , 2, , (, , æ, ç, 2 + n -1 - n + ç, çç, è, , ), , n/ 2, , (, , æ, ç, n, (C) Sn =, 3 + (n - 1) 2 - n + ç, 2, çç, è, , (, , 16., , ö, ÷, ÷, n-1, ÷, 2, 2 - 1 2 ÷ø, , (2, , ), , (, , ), , -1, , ), , ö, ÷, ÷, n-1, ÷÷, 2, 2 -1 2, ø, , (2, , n/ 2, , ), , -1, , ), , ), , (B) Tn =, , (, , (, , If, , n, , å r(r + 1) (2r + 3) = an, , 4, , ), , n-1, 2, , n, 1, 3 + (n - 1) 2 - n + æç ö÷, (D) Sn =, 2, è 2ø, , The roots of the equation x 4 – 8x3 + ax2 – bx + 16 = 0, are positive, if, (A) a = 24, (B) a = 12, (C) b = 8, , 17., , ), , æ 1ö, 2 2 + n -1 - n + ç ÷, è2ø, , n -1, 2, , (D) b = 32, , + bn3 + cn2 + dn + e, then, , r =1, , (A) a + c = b + d, (C) a, b – 2/3, c – 1 are in A.P., n, , 18., , The value of, , å, r =1, , (A), , (C), , 38, , n, a + a + nx, , a + nx - a, x, , 1, a + r x + a + (r - 1) x, , (B) e = 0, (D) c/a is an integer, is, , (B), , (D), , n, a - a + nx, , a + a +nx, x, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , E

Page 39 :
JEE(Adv.)-Mathematics, , Sequence & Series, , PART - IV : COMPREHENSION, Comprehension - 1, Let Vr denotes the sum of the first r terms of an arithmetic progression (A.P.) whose first term is r and the, common difference is (2r – 1). Let, Tr = Vr + 1 – Vr – 2 and Qr = Tr + 1 – Tr for r = 1, 2, ......, 1., , 2., , 3., , The sum V1 + V2 + .... + Vn is, (A), , 1, n(n + 1) (3n2 – n + 1), 12, , (B), , 1, n(n + 1) (3n2 + n + 2), 12, , (C), , 1, n(2n2 – n + 1), 2, , (D), , 1, (2n3 – 2n + 3), 3, , Tr is always, (A) an odd number, , (B) an even number, , (C) a prime number, , (D) a composite number, , Which one of the following is a correct statement ?, (A) Q1, Q2, Q3,...... are in A.P. with common difference 5, (B) Q1, Q2, Q3,...... are in A.P. with common difference 6, (C) Q1, Q2, Q3,..... are in A.P. with common difference 11, (D) Q1 = Q2 = Q3 = ......, , Comprehension - 2, In a sequence of (4n + 1) terms the first (2n + 1) terms are in AP whose common difference is 2, and the last, (2n + 1) terms are in GP whose common ratio 0.5. If the middle terms of the AP and GP are equal, then, 4., , Middle term of the sequence is, (A), , 5., , 2n - 1, , (B), , n . 2n + 1, 2 2n - 1, , (C) n . 2n, , (D) None of these, , First term of the sequence is, (A), , E, , n . 2n + 1, , 4n + 2n . 2n, 2n - 1, , (B), , 4n - 2n . 2n, 2n - 1, , (C), , 2n - n . 2n, 2n - 1, , (D), , 2n + n . 2n, 2n - 1, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 39

Page 40 :
JEE(Adv.)-Mathematics, , Sequence and Series, , PART - I : JEE (ADVANCED) / IIT-JEE PROBLEMS (PREVIOUS YEARS), 1., , Let Sk, k = 1, 2, ........, 100, denote the sum of the infinite geometric series whose first term is, , 100 2, 1, common ratio is . Then the value of, +, 100!, k, , 2., , 100, , å (k, k =1, , 2, , - 3k + 1)Sk is, , k -1, and the, k!, , [IIT-JEE -2010, Paper-1, (3, 0), 84], , Let a1, a2, a3, ....., a11 be real numbers satisfying a1 = 15, 27 – 2a2 > 0 and ak = 2ak–1 – ak–2 for k = 3, 4, ...., 11., If, , 2, a1 + a 2 + ... + a11, a12 + a 22 + .... + a11, is equal to, = 90, then the value of, 11, 11, , [IIT-JEE - 2010, Paper-2, (3, 0), 79], p, , 3., , Let a1, a2, a3,....., a100 be an arithmetic progression with a1 = 3 and Sp =, , å a , 1 £ p £ 100., i, , i=1, , Sm, For any integer n with 1 £ n £ 20, let m = 5n. If S does not depend on n, then a2 is, n, , [IIT-JEE 2011, Paper-1, (4, 0), 80], The minimum value of the sum of real numbers a–5, a–4, 3a–3, 1, a8 and a10 where a > 0 is, , 4., , [IIT-JEE 2011, Paper-1, (4, 0), 80], 5., , Let a1, a2, a3,.... be in harmonic progression with a1 = 5 and a20 = 25. The least positive integer n for which, an < 0 is, , [IIT-JEE 2012, Paper-2, (3, –1), 66], , (A) 22, , (B) 23, , (C) 24, , (D) 25, 4n, , 6., , Let Sn =, , 7., , å, , (–1), , k =1, , k(k +1), 2, , k2 . Then Sn can take value(s), , (A) 1056, , (B) 1088, , (C) 1120, , (D) 1332, , [JEE (Advanced) 2013, Paper-1, (4, – 1)/60], , A pack contains n card numbered from 1 to n. Two consecutive numbered card are removed from the pack and, the sum of the numbers on the remaining cards is 1224. If the smaller of the numbers on the removed cards is, k, then k – 20 =, , 40, , [JEE (Advanced) 2013, Paper-1, (4, – 1)/60], Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522

Page 41 :
JEE(Adv.)-Mathematics, 8., , Let a,b,c be positive integers such that, , Sequence and Series, b, is an integer. If a,b,c are in geometric progression and the arithmetic, a, , mean of a,b,c is b + 2, then the value of, , 9., , a 2 + a – 14, is, a +1, , [JEE (Advanced) 2014, Paper-1, (3, 0)/60], , Suppose that all the terms of an arithmetic progression (A.P.) are natural numbers. If the ratio of the sum of the, first seven terms to the sum of the first eleven terms is 6 : 11 and the seventh term lies in between 130 and 140,, then the common difference of this A.P. is, , 10., , 11., , The least value of a Î R for which 4ax2 +, , [JEE (Advanced) 2015, P-2 (4, 0) / 80], 1, ³ 1 , for all x > 0, is, x, , (A), , 1, 64, , (B), , 1, 32, , (C), , 1, 27, , (D), , 1, 25, , Let bi > 1 for i = 1, 2, ....., 101. Suppose logeb1, logeb2,.....,logeb101 are in Arithmetic Progression (A.P.) with the, com mon diff erence log e 2. Suppose a 1, a 2 ,......, a 101 are in A.P. such that a 1 = b 1 and, a51 = b51. If t = b1 + b2 + ..... + b51 and s = a1 + a2 + .... + a51 then, , [JEE(Advanced)-2016, 3(–1)], , (A) s > t and a101 > b101, (B) s > t and a101 < b101, (C) s < t and a101 > b101, (D) s < t and a101 < b101, 12., , The sides of the right angled triangle are in arithmetic progression. If the triangle has area 24, then what is the, length of its smallest side ?, , 13., , [JEE(Advanced)-2017, 3], , Let X be the set consisting of the first 2018 terms of the arithmetic progression 1, 6, 11, ..... , and Y be the set, consisting of the first 2018 terms of the arithmetic progression 9, 16, 23, ..... Then, the number of elements in, the set X È Y is ______, , 14., , [JEE(Advanced)-2018, 3], , Let AP(a, d) denote the set of all the terms of an infinite arithmetic progression with first term a and common, difference d > 0. If AP (1, 3) Ç AP(2, 5) Ç AP (3,7) = AP (a, d) then a + d equals ......, [JEE(Advanced)-2019, Paper-1, (3, 0), 62], , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 41

Page 42 :
JEE(Adv.)-Mathematics, , Sequence and Series, , PART - II : JEE(MAIN) / AIEEE PROBLEMS (PREVIOUS YEARS), 1., , A man saves Rs. 200 in each of the first three months of his service. In each of the subsequent months his, saving increases by Rs. 40 more than the saving of immediately previous month. His total saving from the start, of service will be Rs. 11040 after :, (1) 18 months, , [AIEEE 2011, I, (4, –1), 120], , (2) 19 months, 100, , 2., , Let an be the nth term of an A.P. If, , å, , (3) 20 months, , (4) 21 months, , 100, , a 2r = a and, , r =1, , åa, , 2r -1, , = b , then the common difference of the A.P. is :, , r =1, , [AIEEE 2011, II, (4, –1), 120], (1) a – b, 3., , (2), , a -b, 100, , (3) b – a, , (4), , The sum of first 20 terms of the sequence 0.7, 0.77, 0.777,....., is, , 4., , (1), , 7, (179 – 10–20), 81, , (2), , 7, (99 – 10–20), 9, , (3), , 7, (179 + 10–20), 81, , (4), , 7, (99 + 10–20), 9, , a -b, 200, , [AIEEE - 2013, (4, –1),360], , If (10)9 + 2(11)1 (10)8 + 3(11)2 (10)7 + . . . . . . . . + 10 (11)9 = k(10)9, then k is equal to, [JEE(Main) 2014, (4, – 1), 120], (1) 100, , 5., , (2) 110, , (3), , 121, 10, , (4), , 441, 100, , Three positive numbers form an increasing G.P. If the middle term in this G.P. is doubled, the new numbers are, in A.P. Then the common ratio of the G.P. is, (1) 2 –, , 6., , 3, , (2) 2 +, , 3, , [JEE(Main) 2014, (4, – 1), 120], (3), , 2+ 3, , (4) 3 +, , 2, , If m is the A. M. of two distinct real numbers l and n(l, n > 1) and G1, G2 and G3 are three geometric means, between l and n, then G14 + 2 G 42 + G34 equals :, (1) 4 l2 mm, , (2) 4 lm2 n, , [JEE(Main) 2015, (4, – 1), 120], (3) 4 lmn2, , (4) 4 l2m2n2, , 13 + 2 3, 13 + 2 3 + 3 3, 13, +, +, + ......... is :, The sum of first 9 terms of the series, 1+ 3, 1+ 3 + 5, 1, , 7., , [JEE(Main) 2015, (4, – 1), 120], (1) 71, , 42, , (2) 96, , (3) 142, , (4) 192, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522

Page 43 :
JEE(Adv.)-Mathematics, 8., , Sequence and Series, , If the 2nd, 5th and 9th terms of a non-constant A.P. are in G.P., then the common ratio of this G.P. is:[JEE(Main) 2016, (4, – 1), 120], , (1), , 7, 4, , (2), , 8, 5, , (3), , 4, 3, , 2, , 9., , 2, , 2, , 2, , 16, æ 3ö æ 2ö æ 1ö, 2 æ 4ö, m, then m is equal, If the sum of the first ten terms of the series ç 1 ÷ + ç 2 ÷ + ç 3 ÷ + 4 + ç 4 ÷ + ..., is, 5, è 5ø è 5ø è 5ø, è 5ø, to :-, , [JEE(Main) 2016, (4, – 1), 120], , (1) 99, 10., , (4) 1, , (2) 102, , (3) 101, , (4) 100, , If, for a positive integer n, the quadratic equation,, x(x + 1) + (x + 1) (x + 2) + ..... + (x + n – 1) (x + n) = 10n, , 11., , has two consecutive integral solutions, then n is equal to :, , [JEE(Main) 2017, (4, – 1), 120], , (1) 11, , (4) 10, , (2) 12, , (3) 9, , For any three positive real numbers a, b and c, 9(25a2 + b2) + 25(c2 – 3ac) = 15b(3a + c)., Then :, , [JEE(Main) 2017, (4, – 1), 120], , (1) a, b and c are in G.P., (2) b, c and a are in G.P., (3) b, c and a are in A.P., (4) a, b and c are in A.P., 12., , Let a, b, c Î R. If f(x) = ax 2 + bx + c is such that a + b + c = 3 and f(x + y) = f(x) + f(y) + xy, " x, y Î R, then, 10, , å f(n), , is equal to :, , [JEE(Main) 2017, (4, – 1), 120], , n =1, , (1) 255, , (2) 330, , (3) 165, , (4) 190, , 12, , 13., , Let a1, a2, a3, ..... , a49 be in A.P. such that, , k =0, , then m is equal to(1) 68, 14., , å a 4k +1 = 416 and a9 + a43 = 66. If a12 + a 22 + ...... + a172 = 140m,, , (2) 34, , [JEE(Main) 2018, (4, – 1), 120], (3) 33, , (4) 66, , Let A be the sum of the first 20 terms and B be the sum of the first 40 terms of the series, 12 + 2·22 + 32 + 2·42 + 52 + 2·62 + ...... . If B – 2A = 100l, then l is equal to :, [JEE(Main) 2018, (4, – 1), 120], (1) 248, , 15., , (2) 464, , (3) 496, , (4) 232, , If a, b and c be three distinct real numbers in G. P. and a + b + c = xb, then x cannot be :, [JEE(Main) 2019, 09-01-19, P-1, (4, – 1), 120], (1) 4, , (2) –3, , (3) –2, , (4) 2, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 43

Page 44 :
JEE(Adv.)-Mathematics, , Sequence and Series, 15, , 30, , 16., , Let a1, a2,.........,a30 be an A. P., S =, , åa, i =1, , i, , and T =, , å a(, i=1, , a10 is equal to :, , . If a5 = –27 and S – 2T = 75, then, , [JEE(Main) 2019, 09-01-19, P-1, (4, – 1), 120], , (1) 57, 17., , 2i -1), , (2) 47, , (3) 42, , (4) 52, , The sum of the follwing series, , 1+6 +, , (, , 9 12 + 22 + 32, 7, , ) + 12 (1, , 2, , + 2 2 + 32 + 4 2, 9, , ) + 15 (1, , 2, , + 22 + .... + 52, 11, , ) + .... up to 15 terms, is :, , [JEE(Main) 2019, 09-01-19, P-2, (4, – 1), 120], (1) 7820, 18., , (2) 7830, , (3) 7520, , (4) 7510, , Let a, b and c be the 7th, 11th and 13th terms respectively of a non-constant A.P. If these are also the three, consecutive terms of a G.P., then, , (1), , 7, 13, , (2) 2, , a, is equal to:, c, , [JEE(Main) 2019, 09-01-19, P-2, (4, – 1), 120], , (3), , 1, 2, , (4) 4, , Five numbers are in A.P., whose sum is 25 and product is 2520. If one of these five numbers is -, , 19., , greatest number amongst them is :, (1), 20., , 21, 2, , (2) 27, , 1, , then the, 2, , [JEE(Main) 2020, 07-01-20, P-1, (4, – 1), 100], (3) 16, , (4) 7, , If the sum of the first 40 terms of the series, 3 + 4 + 8 + 9 + 13 + 14 + 18 +19 +… is (102)m, then m is equal, to :, [JEE(Main) 2020, 07-01-20, P-2, (4, – 1), 100], (1) 20, , (2) 5, , (3) 10, , (4) 25, 9, , 21., , Let a1, a2, a3,… be a G.P. such that a1 < 0, a1 + a2 = 4 and a3 + a4 = 16. If, , åa, i =1, , i, , = 4l , then l is equal to :, , [JEE(Main) 2020, 07-01-20, P-2, (4, – 1), 100], (1) –171, , 44, , (2) 171, , (3), , 511, 3, , (4) –513, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522

Page 45 :
JEE(Adv.)-Mathematics, , Sequence and Series, , SECTION-(F), , Exercise # 1, PART - I, SECTION-(A), A-1., A-4., A-6., A-8., A-12., , 1020 A-2., n2 + 4n A-5., 4, 4, 9, 14, 5, , 19668 A-3., 830, n(a2 + b2) + nab(3 – n), A-11., A-13., , 1, 42, , F-1., , n, (4n2 + 6n –1), 3, , F-3., , 1, 1, –, F-4., 4(2n + 1)(2n + 3), 12, , 3, 4, , F-5, , 65, 1056, , (n + 1)2n - 1, 2n+1(n + 1), , F-2., , F-6., , 2n + 2 – 3n – 4, , SECTION-(B), PART - II, , B-2., , 3, 6, 12, 24, ....., , B-3., , 3, 7, 11 or 12, 7, 2, , B-4., , q-r, p-q, , B-5., B-7., , 6, –3, 3/2, ......, 2, 6, 18 or 18, 6, 2, , B-6., B-9., , 128, 8, , SECTION-(A), A-1., A-3., A-5., A-7., , SECTION-(C), C-1., C-7., , 1, 12, , C-4., C-8., , 3, 2, 8, , C-9., , 5, , C-10., , 4–, , C-11., , n.2n + 2 – 2n + 1 + 2., , C-12., , 15, 16, , (D), (C), (A), (A), , 2+n, 2n-1, , B-1., B-3., B-5, B-7, B-9, , (B), (A), (B), (A), (A), , 27, , D-3, , 6, , D-4., , 1, 201, , D-5., , 50, , D-8, , 64, , C-1., C-3., C-5, C-7., , (C), (A), (A), (A), , 1, , E-4., , n(2n 2 + 9n + 13), 24, , (B), (B), (B), (C), , 1, (ii) k(k + 1) (2k + 7), 6, , C-2., C-4, C-6., C-8., , (D), (A), (A), (B), , SECTION-(D), , SECTION-(E), , E-3., , B-2., B-4., B-6, B-8, , SECTION-(C), , D-1., , E-1., , (C), (C), (D), (B), , SECTION-(B), , SECTION-(D), , 1 k+1, (i), (3 + 1) – 2k+1, 2, , A-2., A-4., A-6., A-8., , D-1., D-3., D-5., , (A), (A), (B), , D-2., D-4., D-6., , (D), (C), (A), , SECTION-(E), E-1., E-3, , (A), (A), , E-2., E-4., , (A), (C), , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 45

Page 46 :
JEE(Adv.)-Mathematics, , Sequence and Series, , SECTION-(F), F-1., F-3, F-5, , (D), (C), (A), , F-2, F-4, , PART - IV, , (A), (C), , 1., 3., 5., , (B), (B), (B), , 2., 4., , (D), (A), , PART - III, , Exercise # 3, , (A) ® (p), (B) ® (s), (C) ® (q), (D) ® (q), (A) ® (s), (B) ® (p), (C) ® (s), (D) ® (p), , 1., 2., , Exercise # 2, PART - I, 1., 3., 5., 7., 9., 11., 13., 15., 17., 19., 21., , (A), (B), (D), (A), (A), (A), (C), (C), (A), (A), (A), , 2., 4., 6., 8., 10., 12., 14., 16., 18., 20., 22., , (C), (C), (C), (A), (A), (D), (B), (D), (A), (C), (B), , 51, 8, 6, 2, 11, 0, 3, 9, 7, , 2., 4., 6., 8., 10., 12., 14., 16., 18., , 1., 3., , 4., 6., 8., 10., 12., 14., , 3, 2., 0, 3 or 9, both 3 and 9 (The common difference of, the arithmatic progression can be either 0 or 6,, and accordingly the second term can be either 3,, or 9 ; thus the answers 3, or 9, or both 3 and 9, are acceptable.), 8, 5., (D), (A,D), 7., 5, 4, 9., 9, (C), 11., (B), 6, 13., 3748, 157, , PART - II, , PART - II, 1., 3., 5., 7., 9., 11., 13., 15., 17., , PART - I, , 33, 1, 2, 0, 40, 64, 1, 54, 2, , 1., 3., 5., 7., 9., , (4), (3), (2), (2), (3), , 2., 4., 6., 8., 10., , (2), (1), (2), (3), (1), , 11., , (3), , 12., , (2), , 13., 15., 17., 19., 21., , (2), (4), (1), (3), (1), , 14., 16., 18., 20., , (1), (4), (4), (1), , PART - III, 1., 3., 5., 7., 9., 11., 13., 15., 17., , (B), (D), (A, C), (A,B,C,D), (A,B,C,D), (C,D), (A,B), (B,C), (A,B,C,D), , 46, , 2., 4., 6., 8., 10., 12., 14., 16., 18., , (A,B,C,D), (A,B,C,D), (B,C), (C,D), (A,B,C), (A,B,C), (B,D), (A,D), (A,C), Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522

Page 47 :
JEE(Adv.)-Mathematics, , Sequence and Series, , 1., , If a, b are two distinct numbers such that a, A1, A2,…., An, b are in A.P. and a, H1, H2, ……, Hn, b are in H.P. then, prove that Ar > Hr where r = 1, 2, ….,n., , 2., , If x, y, z are distinct positive real numbers satisfying x + y + z = 1, then prove that ç, , æ 1 öæ 1 öæ 1 ö, + 1÷çç + 1÷÷ç + 1÷ is, è x øè y øè z ø, , always greater than 24 3 ., 3., , Three positive distinct numbers x, y, z are three terms of geometric progression in an order, and the numbers, x + y, y + z, z + x are three terms of arithmetic progression in that order. Prove that x xyyzz = xyyzzx., , 4., , Find the value of n, such that the coefficient of x n–2 in the expression, (x – 1)(x – 2)(x – 22) …… (x – 2n–1) for all n Î I, is 290., , 5., , If a1, a2, a3, ……, a2n are 2n positive real numbers in G.P, prove that, , a1a 2 + a3a 4 + a5a6 + ... + a 2n-1a2n = a1 + a 3 + a 5 + ... + a 2n-1 a 2 + a 4 + a 6 + ... + a 2n, 6., , Find the sum in the nth group of sequence,, (i) (1), (2, 3); (4, 5, 6, 7); (8, 9,........, 15); ............, (ii) (1), (2, 3, 4), (5, 6, 7, 8, 9),........, , 7., , If a, b, c are positive real numbers, then prove that, (i) b2c2 + c2a2 + a2b2 ³ abc (a + b + c)., , (iii), 8., , (ii), , a, b, c, 3, +, +, ³, b+c, c+a, a+b, 2, , 2, 2, 2, 9, +, +, ³, a+b, b+c, c+a, a+b+c, , If the sum of the first m terms of an A.P. is equal to the sum of either the next n terms or the next p terms, then, æ 1 1ö, æ 1 1ö, prove that (m + n) çç - ÷÷ = (m + p) ç - ÷ ., m, p, èm nø, ø, è, , 9., , a, b, c, d are four distinct real numbers and they are in A.P. If, 2(a - b) +x (b - c)2 + (c - a)3 = 2(a - d) + (b - d)2 + (c - d)3 then find the permissible values of x., , 10., , Let a, b, c, d, e are positive numbers such that abcd = e4. Show that (1 + a)(1 + b)(1 + c)(1 + d) ³ (1 + e)4., , 11., , If positive and distinct numbers a, b, c are in H.P., prove that, , 12., , Find sum of the series, , a+b, c +b, +, >4 ., 2a - b 2c - b, , n, n -1, n-2, +, +, + . . . . up to n terms.., 1. 2 . 3 2 . 3 . 4 3 . 4 . 5, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 47

Page 48 :
JEE(Adv.)-Mathematics, , Sequence and Series, , 13., , Let a1, a2,........, be positive real numbers in geometric progression. For each n, let An, Gn, Hn be respectively, the arithmetic mean, geometric mean & harmonic mean of a1, a2,......, an. Find an expression for the geometric, mean of G1, G2,......, Gn in terms of A1, A2, ........, An, H1, H2, ......., Hn., , 14., , Let a1, a2, ........an, be real numbers such that, a1 + a 2 - 1 + a 3 - 2 + ...... + an - (n - 1) =, , 1, n(n - 3), (a1 + a2 + ......+ an) –, 2, 4, , 100, , then find the value of, , åa, , i, , i=1, , r, p, + ., p, r, , 15., , If a, b, c are in A.P., p, q, r are in H.P. and ap, bq, cr are in G.P., then find, , 16., , Let {an} and {bn} are two sequences given by an = ( x )1/ 2 + ( y )1/ 2 and bn = ( x )1/ 2 – ( y )1/ 2 for all n Î N. Then, , n, , n, , n, , n, , find a1a2a3........an., 17., , In an A.P. of which ‘a’ is the Ist term, if the sum of the Ist ' p ' terms is equal to zero, show that the sum of the, next ' q ' terms is -, , a (p + q ) q, ., p -1, , n, æ n-1 2 ö, æ n -1, ö, 2, If ai Î R, i = 1, 2, 3, .......n and all ai 's are distinct such that ç a i ÷ + 6ç ai ai+1 ÷ + 9 a i £ 0, ç, ÷, ç, ÷, i= 2, è i=1 ø, è i =1, ø, , å, , 18., , å, , å, , and a1 = 8 then find the sum of first five terms., 19., , If a, b, c are in H.P.; b, c, d are in G.P.; and c, d, e are in A.P. such that (ka – b)2 e = ab2 then value of k., , 20., , Prove that, , 21., , The value of x + y + z is 15 if a, x, y, z, b are in AP while the value of (1/x) + (1/y) + (1/z) is 5/3 if, a, x, y, z, b are in HP. Find a and b., , 2, 3 , 5 cannot be terms of a single A.P.., , n, , å (5, , 3n . 5n, , 22., , Find the value of Sn =, , 23., , If n is a root of the equation x² (1 - ac) - x (a² + c²) - (1 + ac) = 0 and if n HM’s are inserted between a and c, show, that the difference between the first and the last mean is equal to ac(a - c)., , 24., , Circles are inscribed in the acute angle a so that every neighbouring circles touch each other. If the radius of, the first circle is R, then find the sum of the radii of the first n circles in terms of R and a., , 25., , Solve the equation (2 + x 1 + x2 + x3 + x4)5 = 6250 x1 x2 x3 x4 .where x1, x2, x3, x4 > 0., , 26., , Let A, G, H be A.M., G.M. and H.M. of three positive real numbers a, b, c respectively such that, G2 = AH, then prove that a, b, c are terms of a GP., , 48, , n =1, , n, , - 3 n )(5n+1 - 3 n+1 ), , and hence S¥., , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522

Page 49 :
JEE(Adv.)-Mathematics, 27., , Sequence and Series, , If sum of first n terms of an A.P. (having positive terms) is given by Sn = (1 + 2Tn) (1 – Tn) where Tn is the nth term, of series, then T22 =, , a- b, , (a Î N, b Î N), then find the value of (a + b), 4, , 3, 4, 5, 6, + 4 + 6 + 7 + ......, 3, 2, 2 ×3 2 ×3 2 ×5, , 28., , Sum the series upto infinite terms :, , 29., , If 1.0! + 3.1! + 7.2! + 13.3! + 21.4! + …. upto (n+1) terms = 4000. (4000!), then find the value of n., , 30., , Show that éë (n + 1)( 2n + 1) ùû > ( n!), n, , ¥, , 31., , Find, , ¥, , 1, , åå a × a, i= 0 j= 0, , i, , j, , 2, , , where i ¹ j and a > 1., , sin 2 x, sin x, sin 3x, +, +, + ............, cos x + cos 2 x cos x + cos 4 x cos x + cos 6 x, , 32., , Find the sum of n terms of the series, , 33., , If a, b, c are three distinct positive real numbers in G.P., then prove that c2 + 2ab > 3ac., , 34., , Evaluate the sum to n terms of the series, , 35., , If the equation x 2 – 3x – ai = 0 has integral roots for all ai Î N and ai £ 300, then find, , 4., 9., , No value, x Î (– ¥, –8] È [16, ¥)., , 8 16 24, +, +, + …….., 5 65 325, , 6., , (i) 2n - 2 (2n + 2n - 1 - 1); (ii) (n - 1)3 + n3, , 12., , n(n + 1), 4(n + 2), , 13., , 16., , 14., , 5050, , 15., , a, c, +, c, a, , 19., , 2, , 21., , (, , ), , 24., , a n, é, ù, R 1 - sin a, 2 êæ 1 + sin 2 ö, ú, ç, ÷, 1, êç 1 - sin a ÷, ú 27., 2 sin a, 2, 2, è, ø, ë, û, , 32., , 1, x, cosec, 4, 2, , x, xù, é, ê sec(2n + 1) 2 - sec 2 ú, ë, û, , n, , G=, , Õ, , åa ., i, , 1, , ( A k Hk ) 2n, , K =1, , x-y, bn, , 18., , 488, 81, , a = 1, b = 9 OR b = 1, a = 9, , 22., , 3, 4, , 6, , 1/2, , 29., , 3999., , 1, ù, 2n + 2n + 1úû, , 35., , 1600, , 34., , 28., , é, ë, , 2 ê1 -, , 2, , Corporate Office : Reliable Institute, A-10 Road No.1, IPIA, Kota-324005 (Rajasthan) INDIA, visit us at: www.reliablekota.com, ( +91-7427056522, 7568756522, 7425906522, , 49