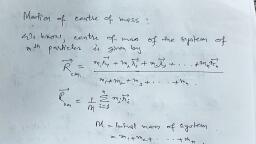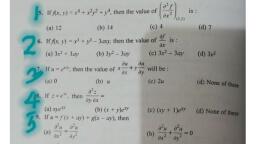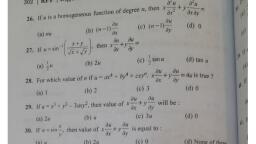Page 1 :
a PRL! NG Pos . a #, = tao eas ————— errr SS, , Baap 6 — DIFFERENTIATION, 6.1. DIFFE " ;, RENTIAL COEFFICIENT OR DERIVATIVE OF A FUNCTION, , SS eg EO, T), te differential coefficient or derivative of variable y with respect to variable x is defined as, , the instantaneous rate of change of y w.r.t. x. It Is denoted by °, , , , Let y be a function of x, Le, y = f(x), , value of Ries, Oe variable and y is the dependent variable, Therefore, by changing Cie, ; x be increased ent in x, Let the correspon ing, increment in y be A y. Then, by a small amount A x, called increment in x, Le py, , ytAysf(+ Ax) 5 Aye(yt Ay -yat er dx)-S), , 6 Ay _ LUtaese) AD), Ax Ax, , te eg RSE germane) are TI ces ot, , rder to obtain, , A, > atio in the value of the function f (x). In 0, , Here a. is the average change or increment, x, the instantaneous rate of change of y with respect to %,, , Ay f(xtAx)-fO), Ax30 Ax Ax70 Ax, , Ay as Ax — 9, , we calculate the limit of, Ax, , The quantity Lt Ay is represented by 2 and is called differential coefficient or derivative of y, x, , Ax30 Ax, w.rt. x. This differential coefficient or derivative of variable y w.r.t. variable x is the instaneous rate of, , +Ax)—-f &, change of y w.r-t. x. Hence, ay ta i flat d= fO |, dx Ax 30 Ax, , d, , Note. 1. The symbol ¢. should not be taken as quotient of dy and dx., ie, , , , 6.2. GEOMETRICAL INTERPRETATI, , Let the function ; y =f (x) be represented graphically, by a curve AB (Fig, 0.14). Take two close points P (x, y) | seat, , and Q (x + Ax, y + Ay) on this curve. Join P and Q, we get, a chord PQ. Let o be the angle which the chord PQ makes, with the positive x-axis. Draw a perpendicular PS on the, straight line QQ,. From the figure, it is clear that, , PS = P,Q, = OQ, - OP, = (x + Ax) — x= Oe, Similarly, OS = Ay, , ‘, }, i, , f, , Slope of chord PQ = tan % = =, , Ap, 1 (yt hy) zy _ f@t+An-f@, , ~ Ax Ax Ax, , As point Q approaches point FP, both A x and A y decrease continuously. In the limiting case, when the, point Q will almost coincide with point P, the chord PQ becomes almost a tangent to the curve at P, Let the, , estab |
Page 3 :
: ., ~ é ou “4% 5 £ _ war F- *, , , , , , Tua im eae es i, fos, eats NEA LAGI i ey, , , , 615. DERIVATIVES OF TRIGONOMETRIGAL FUNCTIONS, 12. If yesine dy _d d, y= sin x, then ae eae (sinx)@cosx. 13. 1f y = cos x, then = © Ae (cos x) =~—sin x., eye d, 14. If y= tan x, then & = © (tan x) =sec? x. 15. If y = cot x, then aT 4 (cot x) =—cosec” x., Oe dx, 16, If y = sec x, then 22 6 “(seo x) wtan veec x, Gx’ ax, 17. If y = cosec x dy _d, sec x, then —- = — (cosec x) =—cot x cosec x, dx dx, 6.6. DERIVATIVES OF LOGARITHMIC AND EXPONENTIAL FUNCTIONS, 18. If y = log, x, then ok woe = dy 2 d (u), e* Hd i ee Ue ba: 19. If y = log, u, then ~~ ie ae!, ly d, 20. If y = e%, then 2 =e} = at - &Y = ae™, We Og, c=". 21. If y = e™, then eo, , 6.7. CONDITIONS FOR MAXIMA OR MINIMA, If y =f (x), then for maximum or minimum value of y for a value of x the first differential coefficient, , of y w.r.t. x Should be zero, i.e., “ = 0). Find the value of x from here., , , , 2, Now, find the second derivative of y w.r.t. x, i.e., a and put the value of x., , d?, (i) If the value of oe is negative, then y is maximum for a given value of x., , d?, (ii) If the value of a is positive, then y is minimum for a given value of x., wy, , , , ‘Exarnpie fl) Differentiate the following w.rt. x. (i) 2002 (ii) e™* (ili) 1., Solution. Since these are constant quantities, so (i) <. (2002) = 9 (ii) < (e7!) =0 (iii) =) =iOe, , Example P Differentiate the following with respect to x., , 1, (yx i) itt) Vx, , *o| >, , Solution. (i) y=2°; < =6x9! =6x° (ii) y=, , | ; i, ger xi ‘ dy l ia 1 Py col, (iii) y Vx = x2 | 5 pa rJx, , , , , , ee et OE ABN EN