Page 1 :
C, T,, , ER, , G, AN, A, , TE, LA, N
Page 2 :
G, AN, A, , Learning Outcomes, , The learner, Energized Text Books facilitate the students in understanding the concepts clearly, accurately and effectively., Content in the QR Codes can be read with the help of any smart phone or can as well be presented on the Screen with, LCD projector/K-Yan projector. The content in the QR Codes is mostly in the form of videos, animations and slides,, and is an additional information to what is already there in the text books., , •, , This additional content will help the students understand the concepts clearly and will also help the teachers in, making their interaction with the students more meaningful., , generalizes properties of numbers and relations among them studied earlier to evolve results,, such as Euclid’s division algorithm, Fundamental Theorem of Arithmetic and applies them to solve, problems related to real life contexts., , •, , derives proofs for irrationality of numbers by applying logical reasoning., , At the end of each chapter, questions are provided in a separate QR Code which can assess the level of learning, outcomes achieved by the students., , •, , identifies exponential or logarithmic form, derives proofs for properties of logarithms and solves, problems using them., , •, , identifies sets among collections and classify them like finite set, infinite set etc., , Let us know how to use QR codes, , •, , analyses sets by representing them in the form of Venn diagrams., , In this textbook, you will see many printed QR (Quick Response) codes, such as, , •, , develops a relationship between algebraic and graphical methods of finding the zeroes of a, polynomial., , •, , finds solutions of pairs of linear equations in two variables using graphical and different algebraic, methods., , •, , demonstrates strategies of finding roots and determining the nature of roots of a quadratic, equation., , •, , develops strategies to apply the concept of A.P., G.P. to daily life situations., , •, , derives formulae to establish relations for geometrical shapes in the context of a coordinate plane,, such as, finding the distance between two given points, to determine the coordinates of a point, between any two given points, to find the area of a triangle, etc., , •, , works out ways to differentiate between congruent and similar figures., , •, , establishes properties for similarity of two triangles logically using different geometric criteria, established earlier such as, Basic Proportionality Theorem, etc., , •, , constructs a triangle similar to a given triangle as per a given scale factor., , •, , examines the steps of geometrical constructions and reason out each step, , •, , derives proofs of theorems related to the tangents of circles, , •, , constructs a pair of tangents from an external point to a circle and justify the procedures., , •, , examines the steps of geometrical constructions and reason out each step, , •, , determines all trigonometric ratios with respect to a given acute angle (of a right triangle), , •, , establishes the relation among trigonometric ratios of acute angles, , •, , uses trigonometric ratios in solving problems in daily life contexts like finding heights of different, structures or distance from them., , •, , finds surface areas and volumes of objects in the surroundings by visualising them as a combination, of different solids like cylinder and a cone, cylinder and a hemisphere, combination of different, cubes, etc., , •, , demonstrates strategies for finding surface area etc. when a solid is converted from one shape to, the other., , •, , calculates mean, median and mode for different sets of data related with real life contexts., , •, , determines the probability of an event and applies the concept in solving daily life problems., , •, , solves problems that are not in the familiar context of the child using above learning. These, problems should include the situations to which the child is not exposed earlier., , We expect the students and the teachers to use the content available in the QR Codes optimally and make their, class room interaction more enjoyable and educative., , TE, LA, N, , Use your mobile phone or tablet or computer to see interesting lessons, videos, documents, etc. linked to the QR code., , Step Description, A. Use Android mobile phone or tablet to view content linked to QR Code:, 1. Click on Play Store on your mobile/ tablet., 2. In the search bar type DIKSHA., 3., , will appear on your screen., 4. Click Install, 5. After successful download and installation, Click Open, 6. Choose your prefered Language - Click English, 7. Click Continue, 8. Select Student/ Teacher (as the case may be) and Click on Continue, On the top right, click on the QR code scanner icon, printed in your book, OR, , and scan a QR code, , T,, , 9., , C, , ER, , Click on the search icon, and type the code printed below the QR code,, in the search bar (, ), 10. A list of linked topics is displayed, 11. Click on any link to view the desired content, B. Use Computer to view content linked to QR code:, 1. Go to https://diksha.gov.in/telangana, 2. Click on Explore DIKSHA-TELANGANA, 3. Enter the code printed below the QR code in the browser search bar (, ), 4. A list of linked topics is displayed, 5. Click on any link to view the desired content
Page 4 :
© Government of Telangana, Hyderabad., , First Published 2014, , G, AN, , All rights reserved., , A, , New Impressions 2015, 2016, 2017, 2018, 2019, 2020, 2021, , AN, , No part of this publication may be reproduced,, stored in a retrieval system, or transmitted, in any, form or by any means without the prior permission in, writing of the publisher, nor be otherwise circulated, in any form of binding or cover other than that in, which it is published and without a similar condition, including this condition being imposed on the subsequent purchaser., , T,, TE, L, , The copy right holder of this book is the Director, of School Education, Hyderabad, Telangana., , SC, ER, , This Book has been printed on 70 G.S.M. Maplitho, Title Page 200 G.S.M. White Art Card, , Free distribution by T.S. Government 2021-22, , Printed in India, at the Telangana Govt. Text Book Press,, Mint Compound, Hyderabad,, Telangana., (ii)
Page 6 :
Foreword, , A, , Education is a process of human enlightenment and empowerment. Recognizing, the enormous potential of education, all progressive societies have committed themselves, to the Universalization of Elementary Education with a strong determination to provide, quality education to all. As a part of its continuation, universalization of Secondary, Education has gained momentum., , AN, , G, AN, , In the secondary stage, the beginning of the transition from functional mathematics, studied upto the primary stage to the study of mathematics as a discipline takes place., The logical proofs of propositions, theorems etc. are introduced at this stage. Apart from, being a specific subject, it is connected to other subjects involving analysis and through, concomitant methods. It is important that children finish the secondary level with the, sense of confidence to use mathematics in organising experience and motivation to, continue learning in High level and become good citizens of India., I am confident that the children in our state Telangana learn to enjoy mathematics,, make mathematics a part of their life experience, pose and solve meaningful problems,, understand the basic structure of mathematics by reading this text book., , T,, TE, L, , For teachers, to understand and absorb critical issues on curricular and pedagogic, perspectives duly focusing on learning in place of marks, is the need of the hour. Also, coping with a mixed class room environment is essentially required for effective transaction, of curriculum in teaching learning process. Nurturing class room culture to inculcate, positive interest among children with difference in opinions and presumptions of life style,, to infuse life in to knowledge is a thrust in the teaching job., , SC, ER, , The afore said vision of mathematics teaching presented in State Curriculum Frame, work (SCF -2011) has been elaborated in its mathematics position paper which also, clearly lays down the academic standards of mathematics teaching in the state. The text, books make an attempt to concretize all the sentiments., The State Council for Education Research and Training Telangana appreciates the, hard work of the text book development committee and several teachers from all over the, state who have contributed to the development of this text book. I am thankful to the, District Educational Officers, Mandal Educational Officers and head teachers for making, this possible. I also thank the institutions and organizations which have given their time in, the development of this text book. I am grateful to the office of the Commissioner and, Director of School Education for extending co-operation in developing this text book. In, the endeavor to continuously improve the quality of our work, we welcome your comments, and suggestions in this regard., Place : Hyderabad, Date, , Director, , : 17 October, 2013, , SCERT, Hyderabad, (iv)
Page 7 :
Preface, , G, AN, , A, , With this Mathematics book, children would have completed the three years of, learning in the elementary classes and one year of secondary class. We hope that, Mathematics learning continues for all children in class X also however, there may be, some children for whom this would be the last year of school. It is, therefore, important, that children finish the secondary level with a sense of confidence to use Mathematics in, organizing experience and motivation to continue learning., , T,, TE, L, , AN, , Mathematics is essential for everyone and is a part of the compulsory program for, school education till the secondary stage. However, at present, Mathematics learning does, not instill a feeling of comfort and confidence in children and adults. It is considered to be, extremely difficult and only for a few. The fear of Mathematics pervades not just children, and teachers but our entire society. In a context where Mathematics is an increasing part, of our lives and is important for furthering our learning, this fear has to be removed. The, effort in school should be to empower children and make them feel capable of learning, and doing Mathematics. They should not only be comfortable with the Mathematics in the, classroom but should be able to use it in the wider world by relating concepts and ideas of, Mathematics to formulate their understanding of the world., , SC, ER, , One of the challenges that Mathematics teaching faces is in the way it is defined., The visualization of Mathematics remains centered around numbers, complicated, calculations, algorithms, definitions and memorization of facts, short-cuts and solutions, including proofs. Engaging with exploration and new thoughts is discouraged as the, common belief is that there can be only one correct way to solve a problem and that, Mathematics does not have possibilities of multiple solutions., Through this book we want to emphasize the need for multiple ways of attempting, problems, understanding that Mathematics is about exploring patterns, discovering, relationships and building logic. We would like all teachers to engage students in reading, the book and help them in formulating and articulating their understanding of different, concepts as well as finding a variety of solutions for each problem. The emphasis in this, book is also on allowing children to work with each other in groups and make an attempt, to solve problems collectively. We want them to talk to each other about Mathematics and, create problems based on the concepts that have learnt. We want everybody to recognize, that Mathematics is not only about solving problems set by others or learning proofs and, methods that are developed by others, but is about exploration and building new arguments., Doing and learning Mathematics is for every person coming up with her own methods and, own rules., (v)
Page 8 :
G, AN, , A, , Class X is the final year of secondary level students and their have already dealt, about the consolidation of initiations. They have already learnt also to understand that, Mathematics consists of ideas that are applied in life situations but do not necessarily, arise from life. We would also like children to be exposed to the notion of proof and recognize, that presenting examples is not equivalent to proof with modeling aspects., , T,, TE, L, , AN, , The purpose of Mathematics as we have tried to indicate in the preface as well as, in the book has widened to include exploring mathematization of experiences. This means, that students can begin to relate the seemingly abstract ideas they learn in the classrooms, to their own experiences and organize their experiences using these ideas. This requires, them to have opportunity to reflect and express both their new formulations as well as, their hesitant attempt on mathematizing events around them. We have always emphasized, the importance of language and Mathematics interplay. While we have tried to indicate at, many places the opportunity that has to be provided to children to reflect and use language., We would emphasise the need to make more of this possible in the classrooms. We, have also tried to keep the language simple and close to the language that the child normally, uses. We hope that teachers and those who formulate assessment tasks would recognize, the spirit of the book. The book has been developed with wide consultations and I must, thank all those who have contributed to its development. The group of authors drawn from, different experiences have worked really hard and together as a team. I salute each of, them and look forward to comments and suggestions of those who would be users of this, book., , SC, ER, , Text Book Development Committee, , (vi)
Page 9 :
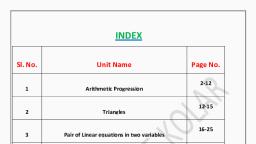
Mathematics, , Class-X, , NO. OF SYLLABUS TO BE, PERIODS COVERED DURING, , 01, , Real Numbers, , 15, , 02, , Sets, , 08, , 03, , Polynomials, , 04, , Pair of Linear Equations in, Two Variables, , 05, , Quadratic Equations, , 06, , Progressions, , 07, , Coordinate Geometry, , 08, , June, , PAGE, NUMBER, , A, , CONTENTS, , 1 - 28, , G, AN, , CHAPTER, NUMBER, , June, , 29 - 50, , 08, , July, , 51 - 76, , 15, , September, , 12, , October, , 105 - 128, , 11, , January, , 129 - 162, , 12, , November, , 163- 194, , Similar Triangles, , 18, , July, August, , 195 - 228, , 09, , Tangents and Secants to a Circle, , 15, , November, , 229 - 248, , 10, , Mensuration, , 10, , December, , 249 - 272, , 11, , Trigonometry, , 15, , August, , 273 - 297, , 12, , Applications of Trigonometry, , 08, , September, , 298 - 308, , 13, , Probability, , 10, , January, , 309 - 326, , 14, , Statistics, , 15, , July, , 327 - 356, , 08, , January, , 357 - 369, , SC, ER, , T,, TE, L, , AN, , 77 - 104, , Appendix Mathematical Modelling, Answers, , 370 - 388, , Revision, , February, , (vii)
Page 11 :
1, , A, , Real Numbers, , G, AN, , 1.1 INTRODUCTION, , "God made the integers. All else is the work of man" - Leopold Kronecker., , AN, , Life is full of numbers. Imagine the moment you were born. Your parents probably noted, the time you were born, your weight, your length and the most important thing: counted your, fingers and toes. After that, numbers accompany you throughout life., What are the other contexts where you deal with numbers?, , T,, TE, L, , We use the numbers to tell our age to keep track of our income and to find the savings after, spending certain amount money. Similarly, we measure our wealth also., In this chapter, we are going to explore the notion of the numbers. Numbers play a, fundamental role within the realm of mathematics. We will come to see the richness of numbers, and delve into their surprising traits. Some collection of numbers fit so well together that they, actually lead to notions of aesthetics and beauty., , SC, ER, , For that, let us look in to a puzzle., , In a garden, a swarm of bees are settling in equal number on same flowers. When they, settle on two flowers, one bee will be left out. When they settle on three flowers, two bees will be, left out. When they settle on four flowers, three bees will be left out. Similarly, when they settle on, five flowers, no bee will be left out. If there are at most fifty bees, how many bees are there in the, swarm?, Let us analyse and solve this puzzle., Let the number of bees be 'x'. Then working backwards we see that x < 50., , If the swarm of bees is divided into 5 equal groups no bee will be left, which translates to, x = 5a + 0 for some natural number 'a'.
Page 12 :
2, , Class-X Mathematics, , If the swarm is divided in to 4 equal groups 3 bees will be left out and it translates to, x = 4b + 3 for some natural number b., If the swarm is divided into 3 equal groups 2 bees will be left out and it translates to, x = 3c + 2 for some natural number c., , A, , If the swarm is divided into 2 equal groups 1 bee will be left out and it translates to, x = 2d + 1 for some natural number d., , G, AN, , That is, in each case we have a positive integer y (in this example y takes values 5, 4, 3, and 2 respectively) which divides x and leaves remainder 'r' (in our case r is 0, 3, 2 and 1, respectively), that is smaller than y. In the process of writing above equations, we have used, division algorithm unknowingly., , AN, , Getting back to our puzzle. We must look for the multiples of 5 that satisfy all the conditions., Hence x = 5a + 0., , T,, TE, L, , If a number leaves remainder 1 when it is divided by 2, we must consider odd multiples, only. In this case, we have 5, 15, 25, 35 and 45. Similarly, if we check for the remaining two, conditions on these numbers we will get 35 as the only possible number., Therefore, the swarm of bees contains 35 bees., Let us verify the answer., , When 35 is divided by 2, the remainder is 1. That can be written as, 35 = 2 ´ 17 + 1, , SC, ER, , When 35 is divided by 3, the remainder is 2. That can be written as, 35 = 3 ´ 11 + 2, , When 35 is divided by 4, the remainder is 3. That can be written as, 35 = 4 ´ 8 + 3, , and when 35 is divided by 5, the remainder is '0'. That can be written as, 35 = 5 ´ 7 + 0, , Let us generalise this. For each pair of positive integers a and b (dividend and divisor, respectively), we can find the whole numbers q and r (quotient and remainder respectively), satisfying the relation, a = bq + r, 0 < r < b, , Free Distribution by T.S. Government 2021-22
Page 13 :
Real Numbers, , 3, , D O T HIS, Find q and r for the following pairs of positive integers a and b, satisfying a = bq + r., (i) a = 13, b = 3, , (ii) a = 80, b = 8, , (iii) a = 125, b = 5, , G, AN, , A, , (iv) a = 132, b = 11, , T HINK & D ISCUSS, , In questions of above "DO THIS", what is the nature of q and r?, , AN, , Theorem-1.1 : (Division Algorithm) : Given positive integers a and b, there exist unique pair, of whole numbers q and r satisfying a = bq + r, 0 < r < b., , T,, TE, L, , This result was first recorded in Book VII of Euclid's Elements. Euclid's algorithm is, based on this division algorithm., Further, Euclid's algorithm is a technique to compute the Highest Common Factor (HCF), of two given integers. Recall that the HCF of two positive integers a and b is the greatest positive, integer d that divides both a and b., , SC, ER, , Let us find the HCF of 60 and 100, through the following activity., , ACTIVITY, , Take two paper strips of equal width and having lengths 60 cm, and 100 cm. Our task is, , to find the maximum length of a strip which can measure both the strips completely, Take 60 cm strip and measure the 100 cm strip with it. Cut off the left over 40 cm. Now,, , take this 40 cm strip and measure the 60 cm strip with it. Cut off the left over 20 cm. Now,, take this 20 cm strip and measure the 40 cm with it., Since nothing is left over, we may conclude that 20 cm strip is the longest strip which can, measure both 60 cm and 100 cm strips without leaving any part., , Free Distribution by T.S. Government 2021-22
Page 14 :
Class-X Mathematics, , 4, , Let us link the process we follwed in the "Activity" to Euclid's algorithm to get HCF of 60, and 100., When 100 is divided by 60, the remainder is 40, 100 = (60 ´ 1) + 40, , A, , Now consider the division of 60 with the remainder 40 in the above equation and apply, , G, AN, , the division algorithim, 60 = (40 ´ 1) + 20, , Now consider the division of 40 with the remainder 20, and apply the division lemma, , AN, , 40 = (20 ´ 2) + 0, , Notice that the remainder has become zero and we cannot proceed any further. We claim, that the HCF of 60 and 100 is the divisor at this stage, i.e. 20. (You can easily verify this by listing, , T,, TE, L, , all the factors of 60 and 100.) We observe that it is a series of well defined steps to find HCF of, 60 and 100. So, let us state Euclid's algorithm clearly., , To obtain the HCF of two positive integers, say c and d with c > d, follow the steps below:, Step 1 : Apply Euclid's Division Lemma, to c and d. So, we find unique pair of whole numbers,, q and r such that c = dq + r, 0 < r < d., , Step 2 : If r = 0, d is the HCF of c and d. If r ¹ 0, apply the division lemma to d and r., , SC, ER, , Step 3 : Continue the process till the remainder is zero. The divisor at this stage will be the, required HCF., , This algorithm works because HCF (c, d) = HCF (d, r) where the symbol HCF (m, n), , denotes the HCF of any two positive integers m and n., , DO THIS, , Find the HCF of the following by using Euclid algorithm., (i) 50 and 70, , (ii) 96 and 72, , (iii), , 300 and 550, , (iv) 1860 and 2015, , Free Distribution by T.S. Government 2021-22
Page 15 :
Real Numbers, , 5, , T HINK & D ISCUSS, Can you find the HCF of 1.2 and 0.12 by using Euclid division algorithm? Justify your, answer., , G, AN, , A, , Euclid's algorithm is useful for calculating the HCF of very large numbers, and it was one of, the earliest examples of an algorithm that a computer had been programmed to carry out., Remarks :, , Euclid's algorithm and division algorithm are so closely interlinked that people often call, former as the division algorithm also., , 2., , Although division algorithm is stated for only positive integers, it can be extended for all, integers a and b where b ¹ 0. However, we shall not discuss this aspect here., , AN, , 1., , T,, TE, L, , Division algorithm has several applications related to finding properties of numbers. We, give some examples of these applications below:, Example 1 : Show that every positive even integer is of the form 2q, and that every positive odd, integer is of the form 2q + 1, where q is some integer., Solution : Let a be any positive integer and b = 2. Then, by division algorithm, a = 2q + r, for, some integer q > 0, and r = 0 or r = 1, because 0 < r < 2. So, a = 2q or 2q + 1., , SC, ER, , If a is of the form 2q, then a is an even integer. Also, a positive integer can be either even, or odd. Therefore, any positive odd integer is of the form 2q + 1., , Example 2 : Show that every positive odd integer is of the form 4q + 1 or 4q + 3, where q is, some integer., , Solution : Let a be a positive odd integer, and b = 4. We apply the division algorithm for a and, b = 4., We get a = 4q +r, for q > 0 and 0 < r < 4. The possible remainders are 0, 1, 2 and 3., , That is, a can be 4q, 4q + 1, 4q + 2, or 4q + 3, where q is the quotient. However, since, a is odd, a cannot be 4q which equals 2 (2q) or 4q + 2 which equals 2(2q+1) (since they are, both divisible by 2)., Therefore, any odd integer is of the form 4q + 1 or 4q + 3., , Free Distribution by T.S. Government 2021-22
Page 16 :
Class-X Mathematics, , 6, , EXERCISE - 1.1, 1., , Use Euclid's algorithm to find the HCF of, (i) 900 and 270, , (ii) 196 and 38220, , (iii) 1651 and 2032, , Use division algorithm to show that any positive odd integer is of the form 6q + 1,, or 6q + 3 or 6q + 5, where q is some integer., , 3., , Use division algorithm to show that the square of any positive integer is of the form, 3p or 3p + 1., , 4., , Use division algorithm to show that the cube of any positive integer is of the form 9 m,, 9m + 1 or 9m + 8., , 5., , Show that one and only one out of n, n + 2 or n + 4 is divisible by 3, where n is any, positive integer., , AN, , G, AN, , A, , 2., , T,, TE, L, , 1.2 THE FUNDAMENTAL THEOREM OF ARITHMETIC, , We know from division algorithm that for given positive integers a and b there exist, unique pair of whole numbers q and r satifying, a = bq + r,, , 0<r<b, , T HINK & D ISCUSS, , SC, ER, , If r = 0, then what is the relationship between a, b and q in a = bq + r ?, , From the above discussion you might have concluded that if a = bq, 'a' is divisible by, , 'b' then we can say that 'b' is a factor of 'a'., , For example we know that 24 = 2 ≥ 12, 24 = 8 ≥ 3, = 2≥2≥2≥3, We know that, if 24 = 2 ≥ 12 then we can say that 2 and 12 are factors of 24. We can, also write 24 = 2 ≥ 2 ≥ 2 ≥ 3 and you know that this is the prime factorisation of 24., , Free Distribution by T.S. Government 2021-22
Page 17 :
Real Numbers, , 7, , Let us take any collection of prime numbers, say 2, 3, 7, 11 and 23. If we multiply some, or all of these numbers, allowing them to repeat as many times as we wish, we can produce, infinitely many large positive integers. Let us observe a few :, 7 ≥ 11 ≥ 23 = 1771, , 3 ≥ 7 ≥ 111 ≥ 23 = 5313, , 2 ≥ 3 ≥ 7 ≥ 111 ≥ 23 = 10626, , 23 ≥ 3 ≥ 73 = 8232, , 22 ≥ 3 ≥ 7 ≥ 111 ≥ 23 = 21252, , A, , 2 ≥ 3 ≥ 11 = 66, , G, AN, , Now, let us suppose collection of all prime numbers. When we take two or more primes, from this collection and multiply them, do we get prime number again? or do we get composite, number? So, if we multiply all these primes in all possible ways, we will get an infinite collection, of composite numbers., , AN, , Now, let us consider the converse of this statement i.e. if we take a composite number, can it be written as a product of prime numbers? The following theorem answers the question., , T,, TE, L, , Theorem-1.2 : (Fundamental Theorem of Arithmetic) : Every composite number can be, expressed (factorised) as a product of primes and this factorization is unique, apart, from the order in which the prime factors occur., This gives us the Fundamental Theorem of Arithmetic which says that every composite, number can be factorized as a product of primes. Actually, it says more. It says that any given, composite number can be factorized as a product of prime numbers in a ‘unique’ way, except, for the order in which the primes occur. For example, when we factorize 210, we regard 2 ≥ 3, , SC, ER, , ≥ 5 ≥ 7 as same as 3 ≥ 5 ≥ 7 ≥ 2, or any other possible order in which these primes are, written. That is, given any composite number there is one and only one way to write it as a, , product of primes, as long as we are not particular about the order in which the primes occur., , In general, given a composite number x, we factorize it as x = p1.p2.p3 .....pn, where, p1, p2, p3...., pn are primes and written in ascending order, i.e., p1 £ p2 £ ... £ pn. If we express, all these equal primes in simplified form, we will get powers of primes. Once we have decided, that the order will be ascending, then the way the number is factorised, is unique. For example,, 27300 = 2 ≥ 2 ≥ 3 ≥ 5 ≥ 5 ≥ 7 ≥ 13 = 22 ≥ 3 ≥ 52 ≥ 7 ≥ 13, , DO THIS, Express 2310 as a product of prime factors. Also see how your friends have, factorized the number. Have they done it in the same way? Verify your final product with your, friend’s result. Try this for 3 or 4 more numbers. What do you conclude?, , Free Distribution by T.S. Government 2021-22
Page 18 :
Class-X Mathematics, , 8, , Let us apply Fundamental Theorem of Arithmetic, Example 3. Consider the numbers of the form 4n where n is a natural number. Check whether, there is any value of n for which 4n ends with zero?, , G, AN, , A, , Solution : If 4n is to end with zero for a natural number n, it should be divisible by 2 and 5. This, means that the prime factorisation of 4n should contain the prime number 5 and 2. But it is not, possible because 4n = (2)2n. So 2 is the only prime in the factorisation of 4n. Since 5 is not present, in the prime factorization, there is no natural number 'n' for which '4n' ends with the digit zero., You have already learnt how to find the HCF (Highest Common Factor) and LCM, (Lowest Common Multiple) of two positive integers using the prime factorization method. Let, us recall this method through the following example., Example-4. Find the HCF and LCM of 12 and 18 by the prime factorization method., , T,, TE, L, , AN, , 12 = 2 ≥ 2 ≥ 3 = 22 ≥ 31, 18 = 2 ≥ 3 ≥ 3 = 21 ≥ 32, Note that HCF (12, 18) = 21 ≥ 31 = 6 = Product of the smallest power of each, common prime factor of the, numbers., , Solution : We have, , LCM (12, 18) = 22 ≥ 32 = 36, , = Product of the greatest power of each, prime factor of the numbers., , SC, ER, , From the example above, you might have noticed that HCF (12, 18) ≥ LCM [12, 18], = 12 ≥ 18. In fact, we can verify that for any two positive integers a and b,, HCF (a, b) ≥ LCM [a, b] = a ≥ b. We can use this result to find the LCM of two positive, integers, if we have already found the HCF of the two positive integers., , D O T HIS, , Find the HCF and LCM of the following given pairs of numbers by prime factorisation, method., (i) 120, 90, (ii) 50, 60, (iii) 37, 49, , TRY THIS, 3n ´ 4m cannot end with the digit 0 or 5 for any natural numbers ‘n’and 'm'. Is it, true? Justify your answer., , Free Distribution by T.S. Government 2021-22
Page 19 :
Real Numbers, , 9, , E XERCISE - 1.2, 1. Express each of the following numbers as a product of its prime factors., (i) 140, , (ii) 156, , (iii) 3825, , (iv) 5005, , (v) 7429, , (ii) 17, 23, and 29, , (iv) 72 and 108, , (v) 306 and 657, , (iii) 8, 9 and 25, , G, AN, , (i) 12, 15 and 21, , A, , 2. Find the LCM and HCF of the following integers by the prime factorization method., , n, , 3. Check whether 6 can end with the digit 0 for any natural number n., , 4. Explain why 7 ≥ 11 ≥ 13 + 13 and 7 ≥ 6 ≥ 5 ≥ 4 ≥ 3 ≥ 2 ≥ 1 + 5 are composite, numbers., , AN, , 5. How will you show that (17 ≥ 11 ≥ 2) + (17 ≥ 111 ≥ 5) is a composite number?, Explain., 100, , T,, TE, L, , 6. Which digit would occupy the units place of 6 ., , Now, let us use the Fundamental Theorem of Arithmetic to explore real numbers further., First, we apply this theorem to find out when the decimal form of a rational number is terminating, and when it is non-terminating and repeating. Second, we use it to prove the irrationality of many, numbers such as, 1. 2. 1, , 2 , 3 and 5 ., , RATIONAL, , NUMBERS AND THEIR DECIMAL EXPANSIONS, , SC, ER, , In the previous classes, we have discussed some properties of integers. How can you find, the preceding or the succeeding integers for a given integer? You might have recalled that the, difference between an integer and its preceding or succeeding integer is 1. You might have found, successor or predecessor by adding or subtracting 1 from the given numbers., In class IX, you learnt that the rational numbers would either be in a terminating decimal, form or a non-terminating repeating decimal form. In this section, we are going to consider a, rational number, say, , p, p, (q ¹ 0) and explore exactly when the number, is a terminating, q, q, , decimal form and when it is a non-terminating repeating (or recurring) decimal form. We do so, by considering certain examples, Let us consider the following terminating decimal numbers., (i) 0.375, , (ii) 1.04, , (iii) 0.0875, , Free Distribution by T.S. Government 2021-22, , (iv) 12.5
Page 20 :
Class-X Mathematics, , (i) 0.375 <, , p, form., q, , 375 375, <, 1000 103, , (iii) 0.0875 <, , 875, 875, < 4, 10000 10, , (ii) 1.04 <, , 104 104, <, 100 10 2, , (iv) 12.5 <, , 125 125, < 1, 10, 10, , A, , Now, let us express them in, , p, form, q, , G, AN, , 10, , We see that all terminating decimal numbers taken by us can be expressed in, , whose denominators are powers of 10. Let us now factorize the numerator and denominator and, then express them in the simplest form :, , (ii), , 1.04 <, , AN, , (i), , 375 3≥53, 3 3, < 3 3< 3<, 3, 10, 2 ≥5, 2, 8, , 104 23 ≥13 26 26, <, <, <, 102 22 ≥52 52 25, , T,, TE, L, , Now, , 0.375 <, , (iii), , 875 53 ≥ 7, 7, 7, 0.0875 < 4 < 4 4 < 4, <, 10, 2 ≥5, 2 ≥5 80, , (iv), , 12.5 <, , 125, 53, 25, <, <, 10, 2≥5, 2, , Have you observed any pattern in the denominators of the above numbers? It appears, , SC, ER, , that when the decimal number is expressed in its simplest rational form, p and q are coprimes, , and the denominator (i.e., q) has only powers of 2, or powers of 5, or both. This is because 2, , and 5 are the only prime factors of powers of 10., From the above examples, you have seen that any rational number that terminates in its, , decimal form can be expressed in a rational form whose denominator is a power of 2 or 5 or, both. So, when we write such a rational number in, , p, form, the prime factorization of q will be in, q, , 2n5m, where n, m are some non-negative integers., , Free Distribution by T.S. Government 2021-22
Page 21 :
Real Numbers, , 11, , We can state our result formally as below:, Theorem-1.3 : Let x be a rational number whose decimal form terminates. Then x can, be expressed in the form of, , p, , where p and q are coprime, and the prime factorization, q, , A, , of q is of the form 2n5m, where n, m are non-negative integers., , G, AN, , D O T HIS, , p, Write the following terminating decimals in the form of , q ¹ 0 and p, q are, q, co-primes, (i) 15.265, , (ii) 0.1255, , (iii) 0.4, , (iv) 23.34, , AN, , And also write the denominators in 2n5m form., , (v) 1215.8, , p, and the prime factorization of q is of, q, p, the form 2n5m, where n, m are non-negative integers, then does have a terminating decimal, q, expansion?, , T,, TE, L, , Now, if we have a rational number in the form of, , So, it seems to make sense to convert a rational number of the form, form 2n5m, to an equivalent rational number of the form, back to our examples above and work backwards., , 3 3, 3≥53, 375, < 3 < 3 3 < 3 < 0.375, 8 2, 2 ≥5, 10, , SC, ER, (i), , (iii), , (ii), , p, , where q is of the, q, , a, , where b is a power of 10. Let us go, b, , 26 26 13≥ 23 104, <, <, <, < 1.04, 25 52 22 ≥52 102, , 7, 7, 7 ≥53, 875, 25, 53, 125, < 4, < 4 4 < 4 < 0.0875 (iv), <, <, < 12.5, 80 2 ≥5 2 ≥5, 10, 2, 2≥5 10, , p, So, these examples show us how we can convert a rational number of the form ,, q, a, where q is of the form 2n5m, to an equivalent rational number of the form , where b is a power, b, of 10. Therefore, the decimal forms of such a rational number terminate. We find that a rational, p, number of the form , where q is a power of 10, is a terminating decimal number.., q, So, we conclude that the converse of Theorem 1.3 is also true which can be formally, stated as :, , Free Distribution by T.S. Government 2021-22
Page 22 :
Class-X Mathematics, , 12, , p, be a rational number, such that the prime factorization of q is, q, of the form 2n5m, where n and m are non-negative integers. Then x has a decimal, expansion which terminates., Theorem 1.4 : Let x =, , D O T HIS, , 1.2.2 N O N - T ER M I N AT I N G ,, , G, AN, , A, , Write the denominator of the following rational numbers in 2n5m form where n and m, are non-negative integers and then write them in their decimal form, 3, 7, 51, 14, 80, (i), (ii), (iii), (iv), (v), 4, 25, 64, 25, 100, R E C U R R I N G D E C I M A LS I N R AT I O N A L, , NUMBERS, , AN, , Let us now consider rational numbers whose decimal expansions are, non-terminating and recurring., , T,, TE, L, , 1, Let us look at the decimal form of ., 7, , 1, = 0.1428571428571 ..... which is a non-terminating and recurring, 7, , decimal number. Notice that the block of digits '142857' is repeating in the quotient., Notice that the denominator i.e., 7 can't be written in the form 2n5m., , SC, ER, , D O T HIS, , Write the following rational numbers in the decimal form and find out, the block of repeating digits in the quotient., (i), , 1, 3, , (ii), , 2, 7, , (iii), , 5, 11, , (iv), , 10, 13, , 0.1428571, 7 1.0000000, 7, 30, 28, 20, 14, 60, 56, 40, 35, 50, 49, 10, 7, 30, , From the 'Do this' exercise and from the example taken above, we can, formally state as below:, p, Theorem-1.5 : Let x = be a rational number, such that the prime factorization of q is, q, not of the form 2n5m, where n and m are non-negative integers. Then, x has a decimal, expansion which is non-terminating repeating (recurring)., From the above discussion, we can conclude that the decimal form of every rational, number is either terminating or non-terminating repeating., , Free Distribution by T.S. Government 2021-22
Page 23 :
Real Numbers, , 13, , Example-5. Using the above theorems, without actual division, state whether decimal form of the, following rational numbers are terminating or non-terminating, repeating decimals., 16, 25, 100, 41, (ii), (iii), (iv), (i), 125, 32, 81, 75, 16, 16, 16, <, < 3 has a terminating decimal form., 125 5≥5≥5 5, , (ii), , 25, 25, 25, <, < 5 has a terminating decimal form., 32 2≥ 2≥ 2≥ 2≥ 2 2, , (iii), , 100, 100, 100, <, < 4 has a non-terminating repeating decimal form., 81 3≥3≥3≥3 3, , (iv), , 41, 41, 41, <, <, has a non-terminating repeating decimal form., 75 3≥5≥5 3≥52, , G, AN, , A, , (i), , AN, , Solution :, , Example-6. Write the decimal form of the following rational numbers without actual division., (i), , 35, 50, , (i), , 35, 7 ≥5, 7, 7, <, <, < 1 < 0.7, 50 2≥5≥5 2 ≥5 10, , 21, 25, , T,, TE, L, , (ii), , Solution :, , 7, 8, , (iii), , 21, 21, 21≥ 22, 21≥ 4, 84, <, <, < 2 2 < 2 < 0.84, (ii), 2, 25 5≥5 5≥5≥ 2, 5 ≥2, 10, , SC, ER, , 7, 7, 7, 7 ≥ 53, 7 ≥125, 875, <, <, <, <, <, < 0.875, (iii), 3, 3, 8 2≥ 2≥ 2 2, ∋23 ≥53 ( ∋2≥5( ∋10(3, , EXERCISE - 1.3, , 1. Write the following rational numbers in their decimal form and also state which, are terminating and which are non-terminating repeating decimal form., (i), , 3, 8, , 229, 400, , (ii), , (iii), , 4, , 1, 5, , (iv), , 2, 11, , (v), , 8, 125, , 2. Without performing division, state whether the following rational numbers will, have a terminating decimal form or a non-terminating repeating decimal form., (i), , 13, 3125, , (ii), , (vi), , 23, 2 × 52, , (vii), , 3, , 11, 12, , (iii), , 64, 455, , 129, 9, (viii), 7, 5, 2 ×5 ×7, 15, 2, , Free Distribution by T.S. Government 2021-22, , (iv), (ix), , 36, 100, , 15, 1600, , (x), , (v), 77, 210, , 29, 343
Page 24 :
Class-X Mathematics, , 14, , 3. Write the following rational numbers in decimal form using Theorem 1.4., 13, 25, , (ii), , 15, 16, , (iii), , 23, (iv), 23.52, , 4. Express the following decimal numbers in the form of, , 7218, 32.52, , (iii) 43.12, , NUMBERS, , (iv) 0.63, , G, AN, , 1.3 I RRATIONAL, , (ii) 0.120112001120001..., , 143, 110, , p, and write the prime factors of, q, , q. What do you observe?, (i) 43.123, , (v), , A, , (i), , AN, , In class IX, you were introduced irrational numbers and some of their properties. You, studied about their existence and how the rationals and the irrationals together made up the real, numbers. You even studied how to locate irrationals on the number line. However, we did not, , T,, TE, L, , prove that they were irrationals. In this section, we will prove that 2, 3, 5 and p in, general is irrational, where p is a prime. One of the theorems, we use in our proof, is the, fundamental theorem of Arithmetic., , p, , where p, q, and q are integers and q ¹ 0. Some examples of irrational numbers, with which you are already, familiar, are :, Recall, a real number is called irrational if it cannot be written in the form, , 2, 3, 15, ο, 0.10110111011110…, etc., , SC, ER, , Before we prove that 2 is irrational, we will look at a theorem, the proof of, which is based on the Fundamental Theorem of Arithimetic., , Theorem-1.6 : Let p be a prime number. If p divides a2, (where a is a positive integer),, then p divides a., , Proof : Let the prime factorization of a be as follows :, a = p1 p2 … pn, where p1, p2, …., pn are primes, not necessarily distinct., Therefore a2 = (p1p2 … pn) (p1p2 … pn) = p21p22 … p2n., , Now, we are given that p divides a2. Therefore, from the Fundamental Theorem of, Arithmetic, it follows that p is one of the prime factors of a2. However, using the uniqueness part, of the Fundamental Theorem of Arithmetic, we realise that the only prime factors of a2 are, p1 , p2 ,… pn. So p is one of p1, p2, … pn., Now, since a = p1p2 … pn,, , p divides a. Hence the result., , Free Distribution by T.S. Government 2021-22
Page 25 :
Real Numbers, , 15, , D O T HIS, Verify the theorem proved above for p= 2, p=3, p = 5 and p=7 for a2 = 1, 4, 9, 25, 36,, 49, 64 and 81., Now, we prove that, , Solution : Let us assume that, , 2 is rational., , A, , 2 is irrational., , G, AN, , Example 7. Show that, , 2 is irrational. We will use a method called proof by contradiction., , If it is rational, then there must exist two integers r and s (s ¹ 0) such that, , r, 2 = s., , If r and s have a common factor other than 1, then, we divide r and s by their highest, a, 2 = b , where a and b are co-prime. So, b 2 = a., , AN, , common factor to get, , On squaring both sides and rearranging, we get 2b2 = a2. Therefore, 2 divides a2., , T,, TE, L, , Now, by Theorem 1.6, it follows that since 2 is dividing a2, it also divides a., So, we can write a = 2c for some integer c. On squaring, we get a2 = (2c)2, Substituting for a2, we ge 2b2 = (2c)2 so that 2b2 = 4c2, that is, b2 = 2c2., This means that 2 divides b2, so 2 divides b also (again using Theorem 1.6 with p= 2)., Therefore, both a and b have 2 as a common factor., But this contradicts the fact that a and b are co-prime., , SC, ER, , This contradiction has arisen because of our assumption that, , assumption is false. So, we conclude that, In general, it can be shown that, , 2 is rational. Thus our, , 2 is irrational., d is irrational whenever d is a positive integer, , which is not the square of another integer. As such, it follows that, are all irrational numbers., , 6, 8, 15, , 24 etc., , In class IX, we mentioned that :, , •, , the sum or difference of a rational and an irrational number is irrational, , •, , the product or quotient of a non-zero rational and an irrational number is irrational., We prove some of these particular cases here., , Free Distribution by T.S. Government 2021-22
Page 26 :
Class-X Mathematics, , 16, , Example-8. Show that 5 – 3 is irrational., Solution : Let us assume that 5 – 3 is rational., That is, we can find coprimes a and b (b ¹ 0) such that 5 –, , we get, , 3, , A, , a, =, b, , a, 3 = 5 ,b, , Since a and b are integers (b ¹ 0), 5 ,, , G, AN, , Therefore, 5 –, , a, 3 = b., , a, is rational and, b, , 3 is also rational., , AN, , But this contradicts the fact that 3 is irrational number.., , This contradiction has arisen because of our assumption that 5 – 3 is rational., So, we conclude that 5 – 3 is irrational., , T,, TE, L, , Example-9. Show that 3 2 is irrational., , Solution : Let us assume, the contrary that 3 2 is rational., a, i.e., we can find co-primes a and b (b ¹ 0) such that 3 2 = ., b, a, 2 = 3b ., , SC, ER, , we get, , Since 3, a and b are integers,, , a, is rational and so, 3b, , But this contradicts the fact that, So, we conclude that 3, , Example-10. Prove that, , Therefore,, , 2 +, , 2 is irrational., , 2 is irrational., , 2 + 3 is irrational., , Solution : Let us suppose that, Let, , 2 is rational., , 2 +, , 3 is rational., , a, 3 = b , where a, b are integers and b ¹ 0, , a, 2= b– 3 ., , Free Distribution by T.S. Government 2021-22
Page 27 :
Real Numbers, , 17, , Squaring on both sides, we get, , a2, a, ∗ 3, 2, 2, b, b, Rearranging, 2<, , 3, , A, , 2a, a2, 3 < 2 ∗ 3, 2, b, b, a2, ∗1, b2, a 2 ∗ b2, 3<, 2ab, , a 2 ∗ b2, is rational and so 3 is rational., 2ab, , AN, , Since a, b are integers,, , G, AN, , <, , This contradicts the fact that, , 3 is irrational. Hence, , Note :, , The sum of two irrational numbers need not be irrational., , T,, TE, L, , 1., , For example, if a =, which is rational., 2., , 2 ∗ 3 is irrational., , 2 and b = , 2 , then both a and b are irrational, but a + b = 0, , The product of two irrational numbers need not be irrational., For example, a = 2 and b = 3 2 , where both a and b are irrational, but, ab = 6 which is rational., , SC, ER, , EXERCISE - 1.4, , 1., , Prove that the following are irrational., (i), , 2., , 1, 2, , Prove that, , (ii), , 3 +, , (iii) 6 +, , 5, , 2, , (iv), , 5, , (v) 3 + 2 5, , p ∗ q is an irrational, where p, q are primes., , 1.4 E XPONEN TIAL S R EVIST ED, We know the power 'an' of a number 'a' with natural exponent 'n' is the product of 'n', n, × a4, × a244, ×× ×××3, ×a, i.e a = a14, , factors each of which is equal to 'a', , n - factors, , 2 , 2 , 2 , 2 .............. are powers of 2, 30, 31, 32, 33 ............... are powers of 3, 0, , 1, , 2, , 3, , Free Distribution by T.S. Government 2021-22
Page 28 :
Class-X Mathematics, , 18, , We also know that when 81 is written as 34, it is said to be in exponential form. The, number '4' is the 'exponent' or 'index' and 3 is the 'base'. We read it as " 81 is the 4th power of, base 3"., Recall the laws of exponents, , m, , n, , m+n, , ;, , am, æaö, (iii) ç ÷ = m, b, èbø, , (ii) (ab) = a .b, m, , m, , m, , G, AN, , (i) a . a = a, m, , (iv) (am)n = amn, (v) a0 = 1, , (vi) a–m =, , 1, am, , AN, , DO THIS, 1. Evaluate, , 2, , æ5ö, æ 1ö, (ii) (4.73) (iii) 0 (iv) (–1) (v) (0.25) (vi) ç ÷ (vii) ç 1 ÷, è4ø, è 4ø, , 2, , T,, TE, L, , (i) 2, , 1, , A, , If a, b are real numbers, where a ¹ 0, b ¹ 0 and m, n are integers, then, , 0, , 3, , 4, , –1, , 2. (a) Express 10, 100, 1000, 10000, 100000 is exponential form, (b) Express the following products in simplest exponential form, (i) 16 ´ 64, , (ii) 25 ´ 125, , (iii) 128 ¸ 32, , SC, ER, , EXPONENTIAL AND LOGARITHIMS, Let us Observe the following, , 2x = 4 = 22 gives x = 2, 3y = 81 = 34 gives y = 4, 10z = 100000 = 105 gives z = 5, , Can we find the values of x for the following?, 2x = 5,, , 3x = 7 ,, , 10x = 5, , If so, what are the values of x?, For 2x = 5, What should be the power to which 2 must be raised to get 5?, Therefore, we need to establish a new relation between x and 5., , Free Distribution by T.S. Government 2021-22
Page 29 :
Real Numbers, , 19, , In such situation, a new logarithm relation is introduced., Consider y = 2x , we need that value of x for which y becomes 5 from the facts that if, x = 1 then y = 21 = 2, if x = 2 then y = 22 = 4 , if x = 3 then y = 23 = 8, we observe that x, lies between 2 and 3., We will now use the graph of y=2x to locate such a 'x' for which 2x = 5., Let us draw the graph of y = 2x, , G, AN, , A, , GRAPH OF EXPONENTIAL 2X, , For this we compute the value of 'y' by choosing some values for 'x'., –3, , –2, , –1, , 0, , 1, , 2, , y=2x, , 1, 8, , 1, 4, , 1, 2, , 1, , 2, , 4, , 3, , 8, , AN, , x, , We plot the points and connect them in a smooth curve., Note that as x increases, the, value of y = 2x increases. As 'x', decreases the value of, y = 2x decreases very close to 0, but, never attains the value 0., , Y', , T,, TE, L, , 9, , Let us think, if y = 2x then, for which value of x, y becomes 5?, , SC, ER, , We know that, in the graph, Y- axis represents the value of 2x and, X- axis represents the value of x., Locate the value of 5 on Y - axis,, and represent it as a corresponding X', point "P" on Y- axis. Draw a line, parallel to X- axis through P, which, meets the graph at the point Q., , 7, , P, , The Curve comes, closer to the X-axis,, but neither touches nor, cut the X-axis., , Q, , 5, , 3, , 1, -5, , -3, , -1, , O, , 1, , R, , 3, , 5, , X, , Y', , Now draw QR perpendicular to X - axis. Can we find the length of OR approximately, from the graph? or where does it lie? Thus, we know that the x coordinate of the point R is the, required value of x, for which 2x=5., This value of x is called the logarithm of 5 to the base 2, written as log25., , Free Distribution by T.S. Government 2021-22
Page 30 :
Class-X Mathematics, , 20, , It has been difficult to find x when 2x = 5 or 3x = 7 or 10x = 5. Then we have following, solutions to the above equations., If 2x = 5 then x is "logarithm of 5 to the base 2" and it is written as log25, , A, , If 3x = 7 then x is "logarithm of 7 to the base 3" and it is written as log37, , G, AN, , If 10x = 5 then x is "logarithm of 5 to the base 10" and it is written as log105, , In general, a and N are positive real numbers such that a ¹ 1 we define, logaN = x Û ax = N., , x, , –2 –1, , 0, , 1 2, , 3, , y = 2x, , 1, 4, , 1, , 2 4, , 8, , 1, 4, , 1, 2, , 1, , 2, , 4, , 8, , x = log2 y –2, , –1, , 0, , 1, , 2, , 3, , y, , T,, TE, L, , 1, 2, , AN, , Let us compare the following two values., , Observe the graph y = 2x in the light of our definition of logarithm, y=, , 1, ; x=–2, 4, , i.e., , 2–2 =, , 1, 4, , and, , –2 = log2, , 1, 4, , y=, , 1, ; x = –1, 2, , i.e., , 2–1 =, , 1, 2, , and, , –1 = log2, , 1, 2, , SC, ER, , If, , y=2, , ; x=1, , i.e., , 21 = 2, , and, , 1 = log22, , y=4, , ; x =2, , i.e., , 22 = 4, , and, , 2 = log24, , y=8, , ; x=3, , i.e., , 23 = 8, , and, , 3 = log28, , Let us consider one more example :, If 10 y = 25 then it can be represented as y = log1025 or y = log 25,, Logarithms of a number to the base 10 are also called common logarithms. In this case,, , we generally omit the base i.e. log1025 is also written as log 25., , Free Distribution by T.S. Government 2021-22
Page 31 :
Real Numbers, , 21, , D O T HIS, (1) Write the following in logarithmic form., (i) 7 = 2x, , (ii) 10 = 5b, , (iii), , 1, = 3c, 81, , (iv) 100 = 10z (iv), , 1, = 4a, 257, , (ii) log525 = 2, , (iii) log22 = 1 (iv) x = log 92, , (ii) log5625 = y, , (iii) log1010000 = z, , G, AN, , (i) log10100 = 2, , A, , (2) Write the following in exponential form., , T RY T HIS, Solve the following, (i) log232 = x, , AN, , Can we say "exponential form and logarithmic form" are inverses of one another?, , T,, TE, L, , Also, observe that every positive real number has a unique logarithmic value because, any horizontal line intersects the graph at only one point., , T HINK & D ISCUSS, , (1) Does log20 exist? Give reasons., (2) Prove, (i) logbb = 1 (ii) logb1 = 0, (iv) if logx16 = 2 then x2 = 16, , P ROPERTIES, , OF, , (iii) logbbx = x, , Þ x = ± 4 , Is it correct or not?, , L OGARITHMS, , SC, ER, , Logarithms are important in many applications and also in advanced mathematics. We will, now establish some basic properties useful in manipulating expressions involving logarithms., (i) The Product Rule, The properties of exponents correspond to properties of logarithms. For example when, we multiply with the same base, we add exponents, i.e., , ax. ay = ax+y, , This property of exponents coupled with an awareness that a logarithm is an exponent, suggest the Product Rule., Theorem: (Product Rule) Let a, x and y be positive real numbers with a ¹ 1., Then loga xy = loga x + loga y, i.e., The logarithm of a product is the sum of the logarithms, Proof: Let loga x = m and loga y = n then we have am = x and an = y, , Free Distribution by T.S. Government 2021-22
Page 32 :
Class-X Mathematics, , 22, , Now, xy = am an = am+n, \ logaxy = m + n = logax + logay, , TRY THIS, , G, AN, , A, , We know that log10100000 = 5, Show that you get the same answer by writing 100000 = 1000 ´ 100 and then using, the product rule. Verify the answer., , D O T HIS, , AN, , Express the logarithms of the following as the sum of the logarithm, (i) 35 ´ 46, (ii) 235 ´ 437 (iii) 2437 ´ 3568, (ii) The Quotient Rule, When we divide with the same base, we subtract exponents, , ax, = a x- y, y, a, This property is called the quotient rule., Theorem: (Quotient Rule) Let a, x and y be positive real numbers where a ¹ 1., , T,, TE, L, , i.e., , æ xö, , SC, ER, , Then loga ç ÷ = logax– logay, è yø, Proof: Let loga x = m and loga y = n then we have am = x and an = y, Now, , x, am, = n = am-n, y, a, , \, , æ xö, loga ç ÷ = m–n = log x– log y, a, a, è yø, æ xö, loga ç ÷ = logax– logay, è yø, , D O T HIS, Express the logarithms of the following as the difference of logarithms, (i), , 23, 373, (ii), 34, 275, , (iii) 4325 ¸ 3734, , (iv) 5055 ¸ 3303, , Free Distribution by T.S. Government 2021-22
Page 33 :
Real Numbers, , 23, , T HINK & D ISCUSS, We know that (am)n = amn, Let am = x then m = log ax, n, , A, , xn = amn then log ax = mn, , (iii), , G, AN, , = n log ax (why?), The Power Rule, , When an exponential expression is raised to a power, we multiply the exponents, i.e., , (am)n = am.n, , This property is called the power rule., , then,, , logaxn = n logax, , T,, TE, L, , T RY T HIS, , AN, , Theorem: (Power Rule) Let a and x be positive real numbers with a ¹ 0 and n, be any real number, , We have log232 = 5. Show that we get the same result by writing 32 = 25 and then using, power rules. Verify the answer., Can we find the value of x such that 2x = 35? In such cases we find the value of, 35 = 243. Then we can evaluate the value of x, for which the value of 2x equals to 243., Applying the logarithm and using the formula log a x n = n log a x , easily we can find the, , SC, ER, , values of 325, 333 etc., 2x = 35, Taking logarithms to the base 2 on both sides, we get., x, , 5, , log 22 = log 23, , x log 22 = 5log 2 3, x = 5 log2 3, , (Q loga xn = n loga x and log aa = 1), , We observe that the value of x is the product of 5 and the value of log 2 3., , D O T HIS, Using logaxn = n logax, expand the following, (i) log2725, , (ii) log5850, , (iii) log 523, , Note: log x = log10x, , Free Distribution by T.S. Government 2021-22, , (iv) log1024
Page 36 :
Class-X Mathematics, , 26, , 3. Evaluate each of the following in terms of x and y, if it is given that x = log23 and, y = log25, (i) log2 15, , (ii) log27.5, , (iii) log260, , (iv) log26750, , 4. Expand the following., , x3, y2, , A, , æ p2 q3 ö, æ 128 ö÷, ç, 2 3 4, ÷, (ii) log çç, (iii) logx y z (iv) log ç r 4 ÷ (v) log, è 625 ø÷, è, ø, , G, AN, , (i) log1000, , 5. If x2 + y2= 25xy, then prove that 2 log(x + y) = 3log3 + logx + logy., æ x ∗ y ÷ö 1, x y, 6. If log çç, ÷ < (log x ∗ log y ) , then find the value of ∗ ., èç 3 ÷ø 2, y x, , 1 1, , ., x y, , AN, , 7. If (2.3)x = (0.23)y = 1000, then find the value of, , T,, TE, L, , 8. I f 2x+1 = 31-x then find the value of x., , 9. Is (i) log 2 rational or irrational? Justify your answer., (ii) log 100 rational or irrational? Justify your answer., , O PTIONAL E XERCISE, , [For extensive learning], , Can the number 6n, n being a natural number, end with the digit 5? Give reason., , 2., , Is 7 ≥ 5 ≥ 3 ≥ 2 + 3 a composite number? Justify your answer.., , 3., , Prove that, , SC, ER, , 1., , ∋2, , (∋, , ∋2, , 3∗ 5, , (, , (, , is an irrational number. Also check whether, , 3 ∗ 5 2 3 , 5 is rational or irrational., , 4., , If x2 + y2 = 6xy, prove that 2 log (x + y) = logx + logy + 3 log 2, , 5., , Find the number of digits in 42013, if log10 2 = 0.3010., , Free Distribution by T.S. Government 2021-22
Page 37 :
Real Numbers, , 27, , Suggested Projects, Note, : Ask, your teacher about integral part and decimal part of the logarithm of a number., Euclid, Algorithm, Find the H.C.F by Euclid Algorithm by using colour ribbon or grid paper., , WE HAVE DISCUSSED, , G, AN, , WHAT, , A, , l, , Division Algorithm: Given positive integers a and b, there, exist whole numbers q and r satisfying a = bq + r, 0 < r < b., , 2., , The Fundamental Theorem of Arithmetic states that every, composite number can be expressed (factorized) as a product of its primes and this, factorization is unique, apart from the order in which the prime factors occur., If p is a prime and p divides a2, where a is a positive integer, then p divides a., Let x be a rational number whose decimal expansion terminates. Then we can express x, , 3., 4., , AN, , 1., , T,, TE, L, , p, , where p and q are coprime and the prime factorization of q is of the, q, form 2n5m, where n and m are non-negative integers., , in the form of, , 5., , SC, ER, , 6., , p, be a rational number such that the prime factorization of q is of the form 2n5m,, q, where n and m are non-negative integers. Then x has a decimal expansion which, terminates., p, Let x =, be a rational number such that the prime factorization of q is not of the form, q, 2n5m, where n and m are non-negative integers. Then x has a decimal expansion which, is non-terminating and repeating (recurring)., We define loga x = n, if an = x, where a and x are positive numbers and a ¹ 1., Laws of logarithms :, If a, x and y are positive real numbers and a ¹ 1, then, x, (i), loga xy = loga x + loga y, (ii), loga = loga x , loga y, y, loga N, m, (iii), loga x = m loga x, (iv), =N, (v), loga1 = 0, a, (vi), loga a = 1, Let x =, , 7., 8., , 9., , Logarithms are used for calculations in engineering, science, business and economics., , Free Distribution by T.S. Government 2021-22
Page 38 :
2, 2.1 I NTRODUCTION, , G, AN, , When you are asked to describe a person, how would you do it?, , A, , Sets, , Let us see some examples., , Ramanujan was a mathematican, interested in number theory., Dasarathi was a telugu poet and also a freedom fighter., , AN, , Albert Einstein was a physicist who proposed theory of relativity., , Maryam Mirzakhan is the only woman mathematican to win Fields medal., , T,, TE, L, , We classify the individuals first as a member of larger recognizable group then with, specific character and interest. People classify and categorize the world around them, in order to, make sense of their environment and their relationships to others., Books in the library are arranged according to the subject, so that we can find them, quickly., , In chemistry the elements are categorized in groups and classes to study their general, properties, Your mathematics syllabus for tenth class has been divided into 14 chapters under, different headings., , SC, ER, , DENTAL FORMULA, , Observe the set of human teeth. It is, classified into 4-types according to, their functions., (i) Incisors, , (ii) Canines, , (iii) Premolars and (iv) Molars, The teeth set is classified into Incisors,, Canines, Premolars and Molars on, the basis of chewing method. Formula, of this teeth set is called 'Dental, formula' and it is 2, 1, 2, 3.
Page 39 :
29, , Mathematics in this manner is no different from other subjects, it needs to place elements, into meaningful groups., A few examples of such groups of numbers we commonly use in mathematics are, , ¥ = Collection of natural numbers 1, 2, 3...., , G, AN, , I or ¢ = Collection of Integers 0, ± 1, ± 2, ± 3, ......, , A, , W = Collection of whole numbers 0, 1, 2, 3....., , ¤ = Collection of rational numbers i.e the numbers that can be written in, , where p, q are integers and q ¹ 0, , p, form, q, , AN, , ¡ = Collection of real numbers i.e. the numbers which have decimal expansion., , DOTHIS, , T,, TE, L, , Identify and write the “common property” to make meaningful group of the following, collections., 1) 2,4,6,8,…, 2) 2,3,5,7,11,…, 3) 1,4,9,16,…, 4) January, February, March, April,…, 5) Thumb, index finger, middle finger, ring finger, little finger., , T HINK, , AND, , D ISCUSS, , SC, ER, , Observe the following collections and prepare as many generalized statements as, possible by describing their properties., 1) 2,4,6,8,…, , 2.2, , 2) 1,4,9,16,…, , SET, , A set is a well-defined collection of distinct objects. The objects in a set are, called elements. Sets are written by enclosing all of its elements between the brackets { }., For example, when we want to write a set of the first five prime numbers, it can be, written as {2,3,5,7,11} and set of incisors = {central incisor, lateral incisor}
Page 40 :
Class-X Mathematics, , 30, , DOTHIS, Write the following sets., 1) Set of the first five positive integers., , A, , 2) Set of multiples of 5 which are more than 100 and less than 125, 4) Set of digits in the Ramanujan number, , 2.2.1 R OSTER, , FORM AND, , S ET, , BUILDER FORM, , G, AN, , 3) Set of first five cubic numbers., , It is difficult to express a set in a long sentence. Therefore, sets are generally denoted by, , AN, , capital letters of English alphabet A, B, C....., For example, M is the set of molars of our teeth., , We can write this set as M={first molar, second molar, third molar}., , T,, TE, L, , Let us look at another example. Q is the set of quadrilaterals with at least two equal, sides. Then, we can write this set as, , Q ={square, rectangle, rhombus, parallelogram, kite, isosceles trapezium}, Here, we are writing a set by listing the elements in it. In such case, the set is said to be, written in the “roster form”., , SC, ER, , In the above two examples, let us discuss belongingness of the elements and its representation. Suppose, if we want to say “second molar is in the set of molars”, then we can represent this as “second molar Î M”. And we read this as "second molar belongs to set M", Can we say “rhombus Î Q” in the above example of set of quadrilaterals? How do you, , read this?, , Does “square” belong to the set M in the above examples?, Then, how do we denote this? When we say “ square is not in the set M”, we denote as, , “square Ï M”. And we read this as "square does not belong to the set M"., Recall from the classes you have studied earlier that we denote natural numbers by, ¥, set of integers by ¢, set of rational numbers by ¤, and set of real numbers by ¡ ., , Free Distribution by T.S. Government 2021-22
Page 41 :
Sets, , 31, , D O T HIS, , THINK, , AND, , G, AN, , A, , Some numbers are given below. Decide which number sets they belong to and do not, belong to and express using correct symbols., 5, i) 1, ii) 0, iii) -4, iv), v) 1.3, 6, vi) 2, vii) log 2, viii) 0.03, ix) p, x) -4, , DISCUS, , Can you write the set of rational numbers in roster form?, , T,, TE, L, , AN, , You might have concluded that like natural numbers or integers it is not possible to write, the set of rational numbers also by showing list of elements in it. You might have also concluded, p, that all the rational numbers are written in the form of (q ¹ 0 and p,q are integers)., q, When we write a set by defining its elements with a “common property”, we can say that, the set is in the “set builder form”. Set builder form should follow some syntax. Let us know it by, observing an example., Suppose A is a set of multiples of 3 less than 20. Then, A={3,6,9,12,15,18} is the roster, form of the set A.When we write its set builder form, it is, A={x : x is a multiple of 3, x < 20} and we A={ x : x is a multiple of 3 and x<20}, , SC, ER, , read this as “A is the set of elements x such, , that x is a multiple of 3 and x is less than 20. the set of all x such that x is a multiple of 3 and x<20, p, Similarly, we can express the rational numbers set as ¤ ={x : x = , p, q are integers and q ¹ 0}, q, In the example,, Note : (i), , In roster form, the order in which the elements are listed is immaterial. Thus,, the set of digits in the Ramanujam number can be written as- {7, 2, 1, 9}, {1, 2,, 7, 9} or {1, 7, 2, 9} etc., , (ii), , While writing the elements of a set in roster form, an element is not repeated. For, example, the set of letters forming the word “SCHOOL” is {s, c, h, o, l} and not, {s, c, h, o, o, l}. Therefore a set contains distinct elements., , Free Distribution by T.S. Government 2021-22
Page 42 :
Class-X Mathematics, , 32, , Let us observe "roster form" and "set builder form" of some sets., Roster form, , Set builder form, V = {x : x is a vowel in the english alphabet}, , A = {-2,-1,0,1,2}, , A = {x : -2 £ x £ 2, x Î ¢ }, , 1 1 1 1, B = {1, , , , }, 2 3 4 5, , 1, B = {x : x = , n Î ¥ , n £ 5}, n, , C = {2,5,10,17}, , C = {x : x = n 2 + 1, n Î ¥, n £ 4 }, , G, AN, , D O T HIS, , 2., , G = {all the factors of 20}, , (ii), , F = {the multiples of 4 between 17 and 61 which are divisible by 7}, , (iii), , S = {x : x is a letter in the word 'MADAM'}, , (iv), , P = {x : x is a whole number between 3.5 and 6.7}, , AN, , (i), , Write the following sets in the roster form., (i), , B is the set of all months in a year having 30 days., , (ii), , P is the set of all prime numbers smaller than 10., , (iii), , X is the set of the colours of the rainbow, , A is the set of factors of 12. Represent which one of the following is a member of A and, which is not?, (A) 1, (B) 4, (C) 5, (D) 12, , SC, ER, , 3., , List the elements of the following sets., , T,, TE, L, , 1., , A, , V = {a, e, i, o, u}, , TRY THIS, , 1., , Write some sets of your choice, involving algebraic and geometrical ideas., , 2., , Match roster forms with the set builder form., (i), , {p, r, i, n, c, a, l}, , (a), , {x : x is a positive integer and is a divisor of 18}, , (ii), , {0}, , (b), , {x : x is an integer and x2 – 9 = 0}, , (iii), , {1, 2, 3, 6, 9, 18}, , (c), , {x : x is an integer and x + 1 = 1}, , (iv), , {3, -3}, , (d), , {x : x is a letter of the word PRINCIPAL}, , Free Distribution by T.S. Government 2021-22
Page 43 :
Sets, , 33, , EXERCISE - 2.1, Which of the following are sets? Justify your answer., (i), The collection of all the months of a year begining with the letter “J”., (ii), The collection of ten most talented writers of India., (iii), A team of eleven best cricket batsmen of the world., (iv), The collection of all boys in your class., (v), The collection of all even integers., If A={0, 2, 4, 6}, B = {3, 5, 7} and C = {p, q, r}, then fill the appropriate symbol,, Î or Ï in the blanks., (i), 0 ….. A, (ii) 3 ….. C, (iii) 4 ….. B, (iv), 8 ….. A, (v) p ….. C, (vi) 7 ….. B, Express the following statements using symbols., (i), The element ‘x’ does not belong to ‘A’., (ii), ‘d’ is an element of the set ‘B’., (iii), ‘1’ belongs to the set of Natural numbers., (iv), ‘8’ does not belong to the set of prime numbers P., State whether the following statements are true or false. Justify your answer, (i), 5 Ï set of prime numbers, (ii), S = {5, 6, 7} implies 8 Î S., , 4., , AN, , 3., , (iii), (iv), , -5 Ï W where‘W’ is the set of whole numbers, 8, Î ¢ where ‘ ¢ ’ is the set of integers., 11, , Write the following sets in roster form., (i), B = {x : x is a natural number smaller than 6}, (ii), C = {x : x is a two-digit natural number such that the sum of its digits is 8}., (iii), D = {x : x is a prime number which is a divisor of 60}., (iv), E = {x : x is an alphabet in BETTER}., Write the following sets in the set-builder form., (i), {3, 6, 9, 12}, (ii), {2, 4, 8, 16, 32}, (iii), {5, 25, 125, 625}, (iv), {1, 4, 9, 16, 25, ….. 100}, Write the following sets in roster form., (i), A = {x : x is a natural number greater than 50 but smaller than 100}, (ii), B = {x : x is an integer, x2 = 4}, (iii), D = {x : x is a letter in the word “LOYAL”}, , SC, ER, , 5., , T,, TE, L, , 2., , G, AN, , A, , 1., , 6., , 7., , (iv), , E = {x : x = 2n2 + 1, –3 £ n £ 3, n Î Z }, , Free Distribution by T.S. Government 2021-22
Page 44 :
Class-X Mathematics, , 34, , Match the roster form with set builder form., (a) {x : x is prime number and a divisor of 6}, , (ii) {2, 3}, , (b) {x : x is an odd natural number smaller than 10}, , (iii) {m, a, t, h, e, i, c, s}, , (c) {x : x is a natural number and divisor of 6}, , (iv) {1, 3, 5, 7, 9}, , (d) {x : x is a letter of the word MATHEMATICS}, , A, , (i) {1, 2, 3, 6}, , 2.3 EMPTY SET, Let us consider the following examples of sets:, , G, AN, , 8., , A = {x : x is a natural number smaller than 1}, , (ii), , D = {x : x is an odd number divisible by 2}, , AN, , (i), , T,, TE, L, , How many elements are there in sets A and D? We find that there is no natural number, which is smaller than 1. So set A contains no elements or we can say that A is an empty set., Similarly, there are no odd numbers that are divisible by 2. So, D is also an empty set., A set which does not contain any element is called an empty set, or a Null set, or a void, set. Empty set is denoted by the symbol f or { }., Here are some more examples of empty sets., , A = {x : 1 < x < 2, x is a natural number}, , (ii), , B = {x : x2 – 2 = 0 and x is a rational number}, , SC, ER, , (i), , Note : f and {0} are two different sets. {0} is a set containing an element 0 while f has no, elements (null set)., , D O T HESE, , 1., , Which of the following are empty sets? Justify your answer., (i), , Set of integers which lie between 2 and 3., , (ii), , Set of natural numbers that are smaller than 1., , (iii), , Set of odd numbers that leave remainder zero, when divided by 2., , Free Distribution by T.S. Government 2021-22
Page 45 :
Sets, , 35, , TRY THIS, Which of the following sets are empty sets? Justify your answer., (i), , A = {x : x2 = 4 and 3x = 9}., , (ii), , The set of all triangles in a plane having the sum of their three angles less, , A, , 1., , G, AN, , than 180., , 2.4 UNIVERSAL S ET, , teeth set, , incisors, , AN, , Consider the teeth set that we had discussed in the begining, of the chapter. You had classified the whole teeth set into four smaller, sets namely incisors, canines, premolars and molars., , But, are teeth in the set of molars also members of the whole teeth pre-molars, set? or not?, , canines, , molars, , T,, TE, L, , Here, whole teeth set is the "universal set" of above said four teeth sets., Consider the teeth set as universal set and canines, incisors, are two sets within it. Then we can represent this as shown in, the adjacent diagram also., , m, canines, , incisors, , Observe the diagram. What does the remaining empty, part of the diagram represents?, , SC, ER, , Let us see some more examples of universal sets:, , (i), , If we want to study the various groups of people of our state (may be according to, income or work or caste), universal set is the set of all people in Telangana., , (ii), , If we want to study the various groups of people in our country, universal set is the set of, all people in India., , The universal set is generally denoted by 'm' and sometimes by U. The Universal set is, usually represented by rectangles to show in the form of a figure., Let us consider the set of natural numbers,, 1. When we say " if x<3, then x<4",, ¥ ={1,2,3,4...}.Then set of even numbers is, we denote as "x<3 Þ x<4"., 2., When we say "x-2 =5 if and only if x=7",, formed by some elements of ¥ . Then ¥ is, we write this as "x-2 = 5 Û x=7", universal set for the smaller set of even numbers., Is ¥ also universal set for the set of odd numbers?, , Free Distribution by T.S. Government 2021-22
Page 46 :
Class-X Mathematics, , 36, , 2.4.1 S U BSET, Consider a set from A = {1,2,3}. How many sets can you form by taking as many elements, as you wish from set A?, , G, AN, , A, , Now, {1},{2},{3},{1,2},{2,3},{1,3} and {1,2,3} are the sets you can form. Can you, form any other sets? These sets are called subsets of A. If we want to say {1,2} is subset of A,, then we denote it as {1,2} Ì A. When we consider the subsets of A, we should say {1,2,3} is, also as a subset of A., If all elements of set A are present in B, then A is said to be subset of B denoted by A Í B., Then we can write as A Í B Û "a Î A Þ a Î B", where A and B are two sets., Let us consider the set of real numbers ¡ . It has many subsets., , AN, , For example, the set of natural numbers ¥ = {1, 2, 3, 4, 5, ……},, the set of whole numbers W = {0, 1, 2, 3, ......},, , ¡, , ¥, , T,, TE, L, , the set of integers ¢ = {…., -3, -2, -1, 0, 1, 2, 3, …..}, , The set of irrational numbers ¤ ' is composed of all real numbers which are not rational., Consider a null set f and a non empty set A. Is f a subset of A? If not f should have an, element which is not an element of A. For being an empty set f has no such element, thus f Ì A., Null set is a subset of every set., , Is A Í A? All elements of LHS set A are also elements of RHS set A. Thus … ., , SC, ER, , Every set is a subset of itself., , Thus, ¤ ' = {x : x Î ¡ and x Ï ¤ } i.e., all real numbers that are not rational. e.g., , 5 and p., , W, , Similarly, the set of natural numbers, ¥ is a subset of the set of, , ¥, , whole numbers W and we can write ¥ Ì W. Also W is a subet of ¡ ., , That is, , Z Ì W and W Ì ¡, Þ, , 2,, , ¡, , ¥, , ¥ Ì WÌ ¡, , W, , Some of the obvious relations among these subsets are, , ¥ Ì ¢ Ì ¤ Ì ¡ and ¤ ' Ì ¡ , and ¥ Ë ¤ '., , Free Distribution by T.S. Government 2021-22
Page 47 :
Sets, , 37, , Consider the set of vowels, V = {a, e, i, o, u}. Also consider the set A, of all letters in the, English alphabet. A = {a, b, c, d, ….., z}. We can see that every element of set V is also an, element A. But there are elements of A which are not a part of V. In this case, V is called the, proper subset of A., , A, , In other words V Ì A. Since, whenever a Î V, then a Î A It can also be denoted by, , G, AN, , V Í A and is read as V is the subset of A. The symbol Ì is used to denote proper subset and Í, is used to denote subset., , D O T HIS, A = {1, 2, 3, 4},, , B = {2, 4},, , Fill in the blanks with Ì or Ë ., A ….. B, , (ii), , (iv), , A ….. C, , (v), , F = { }., , C ….. A, , (iii), , B ….. A, , B ….. C, , (vi), , f ….. B, , T,, TE, L, , 2., , (i), , C = {1, 2, 3, 4, 7},, , AN, , 1., , State which of the following statement are true., (i) { } = f, , (ii), , f =0, , (iii), , 0={0}, , TRY THIS, , A = {set of quadrilaterals}, B = {square, rectangle, trapezium, rhombus}. State whether, , SC, ER, , 1., , A Ì B or B Ì A. Justify your answer., , 2., , If A = {a, b, c, d}. Write all the subsets of set A., , 3., , P is the set of factors of 5, Q is the set of factors of 25 and R is the set of factors of 125., Which one of the following is false? Explain., , (A) P Ì Q, , 4., , (B) Q Ì R, , (C) R Ì P, , (D) P Ì R, , A is the set of prime numbers less than 10, B is the set of odd numbers less than 10 and, C is the set of even numbers less than 10. Which of the following statements are true?, (i) A Ì B, , (ii) B Ì A, , (iii) A Ì C, , (iv) C Ì A, , (v) B Ì C, , (vi) f Ì A, , Free Distribution by T.S. Government 2021-22
Page 48 :
Class-X Mathematics, , 38, , 2.5 V ENN, , DIAGRAMS, , We have already seen different ways of representing sets using diagrams. Let us learn, about Venn-Euler diagram or simply Venn-diagram. It is one of the ways of representing the, relationships between sets. These diagrams consist of rectangles and closed curves usually circles., , (i), , Consider that m = {1, 2, 3, …., 10} is the universal set, , 1, , Venn-diagram is as:, , m = {1, 2, 3, …., 10} is the universal set of which, A, , 5, , A, , 1, , also B Ì A. Then, the Venn-diagram is :, , 4, 6, , B, , AN, , = {2, 4, 6, 8, 10} and B = {4, 6} are subsets and, , 9, , 2, , a, , Then we illustrate these sets with a Venn diagram as, , 2.6 B ASIC O PERATIONS, , ON, , m, , 3, 7, m, , B, , A, , L et A = { a, b, c, d} and B = {c, d, e, f }., , 7, , 5, , 10, , 8, , T,, TE, L, , (iii), , 3, , 2, 4, 8 6, 10, , 9, , (ii), , m, , A, , G, AN, , of which, A = {2, 4, 6, 8, 10} is a subset. Then the, , A, , As mentioned earlier in the chapter, the universal set is usually represented by a rectangle., , c, , e, f, , b, , S ETS, , We know that arithmetics has operations of addition, subtraction, multiplication and division, on numbers. Similarly, we define the operation of union, intersection and difference of sets., OF, , S ETS, , SC, ER, , 2.6.1 UNION, , Let us consider m , the set of all students in your school., , Suppose A is the set of students in your class who, were absent on Tuesday and B is the set of students who, were absent on Wednesday. Then,, , A, , B, , m, , Let A = {Roja, Ramu, Ravi} and, Let B = {Ramu, Preethi, Haneef}, , AÈB, Now, we want to find K, the set of students who were, absent on either Tuesday or Wednesday. Then, does Roja Î K? Ramu Î K? Ravi Î K?, Haneef Î K? Preethi Î K? Akhila Î K?, Roja, Ramu, Ravi, Haneef and Preethi all belong to K but Akhila does not who is always, present., Hence, K = {Roja, Ramu, Ravi, Haneef , Preethi}, , Free Distribution by T.S. Government 2021-22
Page 49 :
Sets, , 39, , Here, the set K is the called the union of sets A and B. The union of A and B is the set, which consists of all the elements of A or B. The symbol ‘È’ is used to denote the union., Symbolically, we write A È B and usually read as ‘A union B’., A È B = {x : xÎA or xÎB}, , A, , Example-1. Let A = {2, 5, 6, 8} and B = {5, 7, 9, 1}. Find A È B., , = {2, 5, 6, 8, 5, 7, 9, 1}, = {1, 2, 5, 6, 7, 8, 9}., , G, AN, , Solution : We have A È B = {2, 5, 6, 8} È {5, 7, 9, 1}, , Note that the common element 5 was taken only once while writing A È B., Example-2. Let A = {a, e, i, o, u} and B = {a, i, u}. Show that A È B = A., , AN, , Solution : We have A È B = {a, e, i, o, u} È {a, i, u}, = {a, e, i, o, u, a, i, u}, = {a, e, i, o, u} = A., , T,, TE, L, , This example illustrates that union of a set A and its subset B is the set A itself., i.e, if B Ì A, then A È B = A., , Example-3. If A = {1, 2, 3, 4} and B = {2, 4, 6, 8}. Find A È B., Solution : A = {1, 2, 3, 4} and B = {2, 4, 6, 8}, then A È B = {1, 2, 3, 4}È {2, 4, 6, 8}, = {1, 2, 3, 4, 2, 4, 6, 8}, , A, , 1, , B, , 6, , 2, 4, , 3, , m, 8, , SC, ER, , = {1, 2, 3, 4, 6, 8}, , 2. 6. 2 I NTERSECTION, , OF, , S ETS, , A È B = {1, 2, 3, 4, 6, 8}, , Let us again consider the example of students who were absent. Now let us find the set L, that represents the students who were absent on both Tuesday and Wednesday. We find that, L = {Ramu}., Here, the set L is called the intersection of sets A and B., , A, , In general, the intersection of sets A and B is the set of all, elements which are common in both A and B. i.e., those elements, which belong to A and also belong to B. We denote intersection, symbolically by as A Ç B (read as “A intersection B”)., i.e., A Ç B = {x : x Î A and x Î B}, , Free Distribution by T.S. Government 2021-22, , AÇB, , B, , m
Page 50 :
Class-X Mathematics, , 40, , The intersection of A and B can be illustrated using the Venn-diagram as shown in the, shaded portion of the figure, given below, for Example 5., Example-4. Find A Ç B when A = {5, 6, 7, 8} and B = {7, 8, 9, 10}., Solution : The common elements in both A and B are 7 and 8., (common elements), , Example-5. If A = {1, 2, 3} and B = {3, 4, 5}, then represent, A Ç B in Venn-diagrams., , A, , 1, 2, , 4, 5, , 3, , G, AN, , Solution : The intersection of A and B can be represented in, the Venn-diagram as shown in the adjacent figure., , m, , B, , A, , \ A Ç B = {5, 6, 7, 8} Ç {7, 8, 9, 10} = {7, 8}, , A Ç B = {3}, , D ISJOINT S ETS, , A, , 1 3, 5 7, , B, , 2, , 4, , 6, , 8, , m, , AÇB= f, , T,, TE, L, , AN, , Suppose A = {1, 3, 5, 7} and B = {2, 4, 6, 8}. We see, that there are no common elements in A and B. Such sets are, known as disjoint sets. The disjoint sets can be represented, by means of the Venn-diagram as shown in the adjacent figure:, , D O T HIS, , Let A = {2, 4, 6, 8, 10, 12} and B = {3, 6, 9, 12, 15}. Find A È B and A Ç B, , 2., , If A = {6, 9, 11}; B = { }, find A È f ., , 3., , A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; B = {2, 3, 5, 7}. Find A Ç B., , SC, ER, , 1., , 4., , If A = {4, 5, 6}; B = {7, 8} then show that A È B = B È A., , TRY THIS, , 1., , Write some sets A and B such that A and B are disjoint., , 2., , If A = {2, 3, 5}, find A È f and f È A and comment on results., , 3., , If A = {1, 2, 3, 4} and B = {1, 2, 3, 4, 5, 6, 7, 8}, then find A È B and A Ç B. What, do you notice from the result?, , 4., , Let A = {1, 2, 3, 4, 5, 6} and B = {2, 4, 6, 8, 10}. Find the intersection of A and B., , Free Distribution by T.S. Government 2021-22
Page 51 :
Sets, , 41, , T HINK & D ISCUSS, The intersection of any two disjoint sets is a null set. Justify your answer., OF, , S ETS, , A, , 2. 6. 3 DIFFERENCE, , G, AN, , Suppose A is the set of all odd numbers less than 10 and B is the set of prime numbers less, than 10. If we consider the set of odd numbers less than 10 which are not prime, then the, elements in the set belong to set A, but not to the set B. This set is represented by A - B and read, it as A difference B., \ A - B = {1, 9}., , A, , T,, TE, L, , A – B = {x : x Î A and x Ï B}., , B, , AN, , Now we define the difference set of sets A and B, as the set of elements which belong to A but do not, belong to B. We denote the difference of A and B by, A – B or simply “A minus B”., , Example-6. Let A = {1, 2, 3, 4, 5}; B = {4, 5, 6, 7}. Find A – B., Solution : Given A = {1, 2, 3, 4, 5} and B = {4, 5, 6, 7}. Only the elements which are in A but, not in B should be taken., A – B = {1, 2, 3, 4, 5} – {4, 5, 6, 7} = {1, 2, 3}, , SC, ER, , \ A – B = {1, 2, 3}. Since 4, 5 are the elements in B they are taken away from A., Similarly for B – A, the elements which are only in B are taken., B – A = {4, 5, 6, 7} – {1, 2, 3, 4, 5} = {6, 7}, , \ B – A = {6, 7} (4, 5 are the elements in A and so they are taken away from B)., , Note that A – B ¹ B – A, The Venn diagram of A – B and B – A are shown below., , A, , 1, 2, , 3, , m, , B, 4, 5, , 6, 7, , A – B = {1, 2, 3}, , Free Distribution by T.S. Government 2021-22, , A, 1, 2, , 3, , m, , B, 4, 5, , 6, , B – A = {6, 7}, , 7
Page 52 :
Class-X Mathematics, , 42, , D O T HIS, If A = {1, 2, 3, 4 ,5} and B = {4, 5, 6, 7}, then find A – B and B – A. Are they equal?, , 2., , If V = {4, 5, 6, 7, 8, 9} and B = {1, 4, 9, 16, 25}, find V – B and B – V., , A, , 1., , G, AN, , T HINK & D ISCUSS, , The sets A – B, B – A and A Ç B are mutually disjoint sets. Use examples to observe, if this is true., , AN, , E XERCISE - 2.2, , If A = {1, 2, 3, 4} and B = {1, 2, 3, 5, 6}, then find A Ç B and B Ç A. Are they equal?, , 2., , If A = {0, 2, 4}, find A Ç f and A Ç A. What did you notice from the result?, , 3., , If A = {2, 4, 6, 8, 10} and B = {3, 6, 9, 12, 15}, find A – B and B – A., , 4., , If A and B are two sets such that A Ì B then what is A È B? Explain by giving an, example., , 5., , Let A = {x : x is a natural number}, B = {x : x is an even natural number}, , T,, TE, L, , 1., , C = {x : x is an odd natural number} and D = {x : x is a prime number}, , SC, ER, , Find A Ç B, A Ç C, A Ç D, B Ç C, B Ç D and C Ç D., , 6., , 7., , If A = {3, 6, 9, 12, 15, 18, 21},, , B = {4, 8, 12, 16, 20},, , C = {2, 4, 6, 8, 10, 12, 14, 16} and, , D = {5, 10, 15, 20}, find, , (i) A – B, , (ii) A – C, , (iii) A – D, , (iv) B – A, , (v) C – A, , (vi) D – A, , (vii) B – C, , (viii) B – D, , (ix) C – B, , (x) D – B, , State whether each of the following statements is true or false. Justify your answers., (i), , {2, 3, 4, 5} and {3, 6} are disjoint sets., , (ii), , {a, e, i, o, u} and {a, b, c, d} are disjoint sets., , (iii), , {2, 6, 10, 14} and {3, 7, 11, 15} are disjoint sets., , (iv), , {2, 6, 10} and {3, 7, 11} are disjoint sets., , Free Distribution by T.S. Government 2021-22
Page 53 :
Sets, , 43, , 2.7 E QUAL S ETS, Consider the following sets., A = {Sachin, Dravid, Kohli}, B = {Dravid, Sachin, Dhoni}, , A, , C = {Kohli, Dravid, Sachin}, , G, AN, , What do you observe in the above three sets A, B and C? All the players that are in A are, in C. Also, all the players that are in C are in A. Thus, A and C have same elements but some, elements of A and B are different. So, the sets A and C are equal sets but sets A and B are not, equal., , Two sets A and C are said to be equal if every element in A belongs to C (i.e.A Í C) and, every element in C belongs to A (i.e.C Í A)., , AN, , If A and C are equal sets, then we write A = C. Thus, we can also write that C Í A and, A Í C Û A = C. [Here Û is the symbol for two way implication and is usually read as, if and, only if (briefly written as “iff”], , T,, TE, L, , Example-7. If A = {p, q, r} and B = {q, p, r}, then check whether A=B or not., Solution : Given A = {p, q, r} and B = {q, p, r}., , In the above sets, every element of A is also an element of B. \ A Í B., Similarly every element of B is also in A., , \ B Í A., , Then from the above two relations, we can say A=B., , SC, ER, , Examples-8. If A = {1, 2, 3, ….} and ¥ is the set of natural numbers, then check whether A, and ¥ are equal?, , Solution : The elements are same in both the sets. Therefore, A Í ¥ and ¥ Í A., Therefore, both A and N are the set of Natural numbers. Therefore the sets A and N are, , equal sets i.e. A = N., , Example-9. Consider the sets A = {1, 2, 3} and B = {1, 2, 3, 4}. Are they equal?, Solution : A Í B but B Ë A then A ¹ B., , Free Distribution by T.S. Government 2021-22
Page 54 :
Class-X Mathematics, , 44, , Example-10. Let A be the set of prime numbers smaller than 6 and B be the set of prime, factors of 30. Check if A and B are equal., Solution : The set of prime numbers less than 6, A = { 2,3,5}, The prime factors of 30 are 2, 3 and 5. So, P = { 2,3,5}, P are equal. i.e A Í B , B Í A Þ A = B, , G, AN, , Example-11. Show that the sets C and B are equal, where, , A, , Since the elements of A are the same as the elements of P and vice versa therefore, A and, , C = {x : x is a letter in the word ‘ASSASSINATION’}, B = {x : x is a letter in the word STATION}, , Solution : Given that C = {x : x is a letter in the word ‘ASSASSINATION’}, , AN, , The roster form of the set C = {A,S,I,N,T,O}, since elements in a set cannot be repeated., Also given that B = {x : x is a letter in the word STATION}, , T,, TE, L, , ‘B’ can also be written as B = {A,S,I,N,T,O}, So, the elements of C and B are same and C = B., i.e. C Í B, B Í C Þ C=B, , Example-12. Consider the sets f , A = {1, 3}, B = {1, 5, 9}, C = {1, 3, 5, 7, 9}. Insert the, symbol Ì or Ë between each of the following pair of sets., (ii) A ….. B, , (iii) A ….. C, , (iv) B ….. C, , SC, ER, , (i) f ….. B, Solution :, , (i), , f Ì B, as f is a subset of every set., , (ii), , A Ë B, as 3 Î A but 3 Ï B., , (iii), , A Ì C as 1, 3 ÎA also belong to C., , (iv), , B Ì C as every element of B is also an element of C., , E XERCISE - 2.3, , 1., , Which of the following sets are equal?, A = {x : x is a letter in the word FOLLOW}, B = {x : x is a letter in the word FLOW}, and C = {x : x is a letter in the word WOLF}, , Free Distribution by T.S. Government 2021-22
Page 55 :
Sets, 2., , 45, , Consider the following sets and fill up the blanks with = or ¹ so as to make the statement, true., , D = {d, c, a, b}, , E = {a, e, i, o, u};, , F = {set of vowels in English Alphabet}, , 5., , G, AN, , A, , C = {a, b, c, d};, , A .... B, , (ii), , A .... E, , (iii), , C .... D, , (iv), , D .... F, , (v), , F .... A, , (vi), , D .... E, , (vii), , F .... B, , AN, , (i), , In each of the following, state whether A = B or not., (i), , A = {a, b, c, d}, , B = {d, c, a, b}, , (ii), , A = {4, 8, 12, 16}, , B = {8, 4, 16, 18}, , (iii), , A = {2, 4, 6, 8, 10}, , B = {x : x is a positive even integer and x < 10}, , (iv), , A = {x : x is a multiple of 10} B = {10, 15, 20, 25, 30, …}, , State the reasons for the following :, , SC, ER, , 4., , B = {The first three natural numbers}, , T,, TE, L, , 3., , A = {1, 2, 3};, , (i), , {1, 2, 3, …., 10}, , ¹, , {x : x Î N and 1 < x < 10}, , (ii), , {2, 4, 6, 8, 10}, , ¹, , {x : x = 2n+1 and x Î N}, , (iii), , {5, 15, 30, 45}, , ¹, , {x : x is a multiple of 15}, , (iv), , {2, 3, 5, 7, 9}, , ¹, , {x : x is a prime number}, , List all the subsets of the following sets., (i) B = {p, q}, , (ii) C = {x, y, z}, , (iv) E = {1, 4, 9, 16} (v) F = {10, 100, 1000}, , Free Distribution by T.S. Government 2021-22, , (iii) D = {a, b, c, d}
Page 56 :
Class-X Mathematics, , 46, , 2.8, , FINITE, , AND, , I NFINITE, , SETS, , Now consider the following sets:, (i), , A = {the students of your school}, , (ii), , L = {2,3,5,7}, , (iii), , B = {x : x is an even number}, , (iv), , J = {x : x is a multiple of 7}, , A, , Can you list the number of elements in each of the sets given above? In (i), the number of, , G, AN, , elements will be the number of students in your school. In (ii), the number of elements in set L is, 4. We find that it is possible to express the number of elements of sets A and L in definite whole, numbers. Such sets are called finite sets., , Now, consider (iii), the set B of all even numbers. Can we count the number of elements in, set B? We see that the number of elements in this set is not finite. We find that the number of, , AN, , elements in B is infinite. And, the set J also has infinite number of elements. Such sets are called, infinite sets., , T,, TE, L, , We can draw infinite number of straight lines passing though a given point. So, this set of, straight lines is infinite. Similarly, it is not possible to find out the last number among the collection, of all integers. Thus, we can say the set of integers is infinite., Consider some more examples :, , Let ‘W’ be the set of the days of the week. Then W is finite., , (ii), , Let ‘S’ be the set of solutions of the equation x2 – 16 = 0. Then S is finite., , (iii), , Let ‘G’ be the set of points on a line. Then G is infinite., , SC, ER, , (i), , Example-13. State which of the following sets are finite or infinite., (i), , {x : x Î ¥ and (x - 1) (x - 2) = 0}, , (ii), , {x : x Î ¥ and x2 = 4}, , (iii), , {x : x Î ¥ and 2x - 2 = 0}, , (iv), , {x : x Î ¥ and x is prime}, , (v), , {x : x Î ¥ and x is odd}, , Solution :, (i), , x can take the values 1 or 2 in the given case. The set is {1,2}. Hence, it is finite., , (ii), , x2 = 4, implies that x = +2 or -2. But x Î ¥ or x is a natural number so the set, is{2}. Hence, it is finite., , Free Distribution by T.S. Government 2021-22
Page 57 :
Sets, , 47, , (iii), , In the given set x = 1 and 1 Î ¥ . Hence, it is finite., , (iv), , The given set is the set of all prime numbers. There are infinitely many prime numbers., Hence, set is infinite., , 2.9, , Since there are infinite number of odd numbers, hence the set is infinite., , C ARDINALITY, , OF A FINITE SET, , A, , (v), , G, AN, , Now, consider the following finite sets :, , A = {1, 2, 4}; B = {6, 7, 8, 9, 10}; C = {x : x is a alphabet in the word "INDIA"}, Here, Number of elements in set A = 3. Number of elements in set B = 5., , Number of elements in set C is 4 (In the set C, the element ‘I’ repeats twice. We know, , AN, , that the elements of a given set should be distinct. So, the number of distinct elements in set C is 4)., The number of elements in a finite set is called the cardinal number of the set or the, cardinality of the set., , T,, TE, L, , The cardinal number or cardinality of the set A is denoted as n(A) = 3., Similarly, n(B) = 5 and n(C) = 4., , For finite set cardinality is a whole number., , We will learn cardinality of infinite sets in higher classes., Note : There are no elements in a null set. The cardinal number of that set is n( f ) = 0, , SC, ER, , D O T HESE, , 1., , State which of the following sets are finite and which are infinite. Give reasons for your, answer., (i), , 2., , A = {x : x Î N and x < 100}, 2, , 2, , 2, , (iii), , C = {1 , 2 , 3 , …..}, , (v), , {x : x is a day of the week}., , (ii), , B = {x : x Î N and x < 5}, , (iv), , D = {1, 2, 3, 4}, , Tick the set which is infinite, (A) The set of whole numbers < 10, , (B) The set of prime numbers < 10, , (C) The set of integers < 10, , (D) The set of factors of 10, , Free Distribution by T.S. Government 2021-22
Page 58 :
48, , Class-X Mathematics, , T HINK & D ISCUSS, An empty set is a finite set. Is this statement true or false? Why?, , G, AN, , The set of lines passing through a given point., , (ii), , Set of odd natural numbers divisible by 2., , (iii), , {x : x is a natural number, x < 5 and x > 7}, , (iv), , {x : x is a common point to any two parallel lines}, , (v), , Set of even prime numbers., , AN, , (i), , State whether the following sets are finite or infinite., (i), , The set of months in a year., , (ii), , {1, 2, 3, …, 99, 100}, , (iii), , The set of prime numbers smaller than 99., , (iv), , The set of letters in the English alphabet., , (v), , The set of lines that can be drawn parallel to the X-Axis., , (vi), , The set of numbers which are multiples of 5., , (vii), , The set of circles passing through the origin (0, 0)., , SC, ER, , 2., , State which of the following sets are empty and which are not?, , T,, TE, L, , 1., , A, , EXERCISE - 2.4, , Example-14. If A = {1, 2, 3,4,5}; B = {2,4,6,8} then find n(A È B)., Solution :, , The set A contains five elements \ n(A) = 5, and the set B contains four elements \ n(B) = 4, But A È B={1,2,3,4,5,6,8} does not contain 9 elements and it contains 7 elements, , only. Why?, , Free Distribution by T.S. Government 2021-22
Page 59 :
Sets, T HINK &, , 49, , DISCUSS, , 1. What is the relation between n(A), n(B), n(A Ç B) and n(A È B)?, , A, , 2. If Aand B are disjoint sets, then how can you find n(A È B)?, , l, , G, AN, , Suggested Projects, , Conduct a survey in your classroom. Ask your classmates whether they like circket or, badminton (or choose any other two games)., By using sets, find out, , How many are interested in game1/ newspaper1/ TV channel1?, , (ii), , How many are interested in game2/ newspaper2/ TV channel2?, , (iii), , How many are interested in both? and, , AN, , (i), , T,, TE, L, , (iv) How many are interested in neither?, , Extension:, We can extend the above survey for three games/ newspapers/, TV channels etc., , WHAT WE H AVE D ISCUSSED, , A set is a collection of distinct objects. A well defined set, means that:, , SC, ER, , 1., , (i) there is a universe of objects which are taken into, consideration., (ii) any object in the universe is either an element or is not an element of the set., , 2., , An object belonging to a set is known as an element of the set. We use the symbol 'Î' to, denote membership of an element and read as belongs to., , 3., , Sets can be written in the roster form where all elements of the set are written, separated, by commas, within curly brackets(braces)., , 4., , Sets can also be written in the set-builder form. Where the elements are difined using a, common property., , Free Distribution by T.S. Government 2021-22
Page 60 :
50, , Class-X Mathematics, , A set which does not contain any element is called an empty set, or a Null set, or a void, set., , 6., , A set is called a finite set if its cordinality/ cardinal number is a whole number., , 7., , We can say that a set is infinite if it is not finite., , 8., , The number of elements in a finite set is called the cardinal number/ cardinality of the set., , 9., , The universal set is denoted by 'm' or U. The universal set is usually represented by, rectangles., , 10., , A is a subset of B if 'a' is an element of A implies that 'a' is also an element of B. This is, written as A Í B if a ÎA Þ a Î B, where A, B are two sets., , 11., , Two sets, A and B are said to be equal if every element in A belongs to B and every, element in B belongs to A., , 12., , A union B is written as A È B = {x : x Î A or x Î B}., , 13., , A intersection B is written as A Ç B = {x : x Î A and x Î B}, , 14., , The difference of two sets A, B is defined as A - B, , T,, TE, L, , AN, , G, AN, , A, , 5., , A - B = {x : x Î A and x Ï B}, , Venn diagrams are a convenient way of showing operations between sets., , SC, ER, , 15., , Free Distribution by T.S. Government 2021-22
Page 61 :
3, , A, , Polynomials, , G, AN, , 3.1 I NTRODUCTION, , We have already learnt about Polynomials in class IX. We will do some more work with, them. Let us observe the following two situations., A flower bed in a garden is in the shape of a triangle. The longest side is 3 times the, smallest side and the smallest side is 2 units shorter than the intermediate side. Let P, represent the length of the smallest side. Then what is the perimeter in terms of P?, , AN, , 1., , There is an "unknown" in the above situation. Let this unknown "the smallest side" is, given as ‘P’ units., , Perimeter, 2., , T,, TE, L, , Since, Perimeter of triangle = sum of all sides, , P, , P+2, , = P + 3P + P + 2, 3P, = 5P + 2, The length of a rectangular dining hall is twice its breadth. Let x represents the breadth of, the hall. What is the area of the floor of the hall in terms of x?, , In this, the length is given as twice the breadth., , SC, ER, , So, if breadth = x, then length = 2x, , Since area of rectangle = lb, , Area = (2x) (x), = 2 x2, , 2 x2, , x, , 2x, As we know, the perimeter, 5P + 2 of the triangle and the area 2x2 of the rectangle are in, the form of polynomials of different degrees.
Page 62 :
Class-X Mathematics, , 52, , 3.2 W HAT, , ARE, , P OLYNOMIALS?, , A polynomial in x is an expression containing the sum of a finite number of terms of the, form axn for a real number a, where a ¹ 0 and a whole number n., Not polynomials, 1, 2, , 4x, , 1, x-4, 3, , 3x2 + 4x-1 + 5, , G, AN, , 2x, , A, , Polynomials, , 4+, , x2 - 2x - 1, , D O T HIS, , 1, x, , OF A, , P OLYNOMIAL, , T,, TE, L, , 3. 2. 1 D EGREE, , AN, , State which of the following are polynomials and which are not? Give reasons., 1, 1, 2, (iii) 4 z ∗, (iv) m2 , 2 m ∗ 2 (v) P ,2 ∗ 1, (i) 2x3 (ii) ,1∋ x ÷ 0(, x, 7, , Recall that if p(x) is a polynomial in x, the highest power of x in p(x) is called the degree, of the polynomial p(x). For example, 3x + 5 is a polynomial in the variable x. It is a polynomial, of degree 1 and is called a linear polynomial. 5x, 2y∗5 ,, , 1, P, m + 1 etc. are some more linear, 3, , SC, ER, , polynomials., A polynomial of degree 2 is called a quadratic polynomial. For example, x2 + 5x + 4 is, a quadratic polynomial in the variable x. 2x2 + 3x -, , 1 2, y, , p -1, 3 – z – z2, y2 - +, 2, 3, , 2 are some, , examples of quadratic polynomials., The expression 5x3–4x2+x–1 is a polynomial in the variable x of degree 3, and is called, , a cubic polynomial. Some more examples of cubic polynomials are 2 – x3, p3, l3 – l2 – l + 5., 6 can be written as 6 ´ x0. As the index of x is 0, it is a polynomial of 0 degree., , TRY THIS, Write 3 different quadratic, cubic and 2 linear polynomials with different number of terms., We can write polynomials of any degree., 3, 7 u 6– u 4 + 4 u 2 – 8 is polynomial of degree 6 and x10 – 3x8 + 4x5 + 2x2 -1 is a, 2, polynomial of degree 10., , Free Distribution by T.S. Government 2021-22
Page 63 :
Polynomials, , 53, , We can write a polynomial in a variable x of a degree n where n is any whole number., Generally, we say, p(x) = a0 xn + a1 xn-1 + a2 xn-2 + …….. + an-1 x +an is a polynomial of nth degree, invariable x, where a0, a1, a2….. an-1, an are real coefficients of x and a0 ¹ 0, , G, AN, , A, , For example, the general form of a linear polynomial (degree 1) in one variable x is ax+b,, where a and b are real numbers and a ¹ 0., , TRY THIS, , Write the general form of a quadratic polynomial and a cubic polynomial in variable x., , 2., , Write a general polynomial q(z) of degree n with coefficients that are b0, b1, b2, ..... bn., What are the conditions on b0, b1, b2, ..... bn?, , 3.2.2 V ALUE, , OF A, , P OLYNOMIAL, , AN, , 1., , T,, TE, L, , Now, consider the polynomial p(x) = x2 – 2x – 3. What is the value of the polynomial at, any value of x? For example, what is its value at x = 1? Substituting x = 1, in the polynomial,, we get p(1) = (1)2 – 2(1) – 3 = –4. The value – 4, is obtained by replacing x by 1 in the given, polynomial p(x). –4 is the value of x2 – 2x – 3 at x = 1., Similarly, p(0) = –3, then, –3 is the value of p(x) at x = 0., , SC, ER, , Thus, if p(x) is a polynomial in x, and if k is a real number, then the value obtained by, substituting x = k in p(x) is called the value of p(x) at x = k and is denoted by p(k)., , D O T HIS, , (i), , If p(x) = x2 – 5x – 6, then find the values of p(1), p(2), p(3), p(0), p(–1), p(–2), p(–3)., , (ii), , If p(m) = m2 – 3m + 1, then find the value of p(1) and p(–1)., , 3. 2. 3 ZEROES, , OF A, , P OLYNOMIAL, , What are the values of p(x) = x2 – 2x – 3 at x = 3, –1 and 2?, We have,, , p(3) = (3)2 – 2(3) – 3 = 9 – 6 – 3 = 0, , also, , p(-1) = (–1)2 – 2(–1) – 3 = 1 + 2 – 3 = 0, , and, , p(2) = (2)2 – 2(2) – 3 = 4 – 4 – 3 = –3, , Free Distribution by T.S. Government 2021-22
Page 64 :
Class-X Mathematics, , 54, , We see that p(3) = 0 and p(-1) = 0. 3 and –1 are called Zeroes of the polynomial, p(x) = x2 – 2x -3., 2 is not zero of p(x), since p(2) ¹ 0, More generally, a real number k is said to be a zero of a polynomial p(x), if p(k) = 0., , A, , D O T HIS, , G, AN, , (i) Let p(x) = x2 – 4x + 3. Find the value of p(0), p(1), p(2), p(3) and obtain zeroes of the, polynomial p(x)., (ii) Check whether -3 and 3 are the zeroes of the polynomial x2 – 9., , 1., , AN, , EXERCISE - 3.1, , In p(x) = 5x7 – 6x5 + 7x-6, what is the, , (iii) constant term., , State which of the following statements are true and which are false? Give reasons for, your choice., , 2 x2– 3x + 1 is 2 ., , (i), , The degree of the polynomial, , (ii), , The coefficient of x2 in the polynomial p(x) = 3x3 – 4x2 + 5x + 7 is 2., , (iii), , The degree of a constant term is zero., 1, is a quadratic polynomial., 2, x , 5x ∗ 6, , SC, ER, , 2., , (ii) degree of p(x), , T,, TE, L, , (i) coefficient of x5, , (iv), (v), , The degree of a polynomial is one more than the number of terms in it., , 3., , If p(t) = t3 – 1, find the values of p(1), p(–1), p(0), p(2), p(–2)., , 4., , Check whether –2 and 2 are the zeroes of the polynomial x4 – 16., , 5., , Check whether 3 and –2 are the zeroes of the polynomial p(x) when p(x) = x2 – x – 6., , 3.3 W ORKING, , WITH, , P OLYNOMIALS, , You have already learnt how to find the zeroes of a linear polynomial., ,5, For example, if k is a zero of p(x) = 2x + 5, then p(k) =0 gives 2k +5 = 0 \ k =, ., 2, , Free Distribution by T.S. Government 2021-22
Page 65 :
Polynomials, , 55, , In general, if k is a zero of p(x) = ax+b (a ¹ 0), then p(k) = ak + b = 0,, ,b, ,b, , or the zero of the linear polynomial ax + b is, ., Therefore k =, a, a, Thus, the zero of a linear polynomial is related to its coefficients, including the constant term., OF THE, , Z EROES, , OF A, , P OLYNOMIAL, , A, , 3.4 G EOMETRICAL M EANING, , You know that a real number k is a zero of the polynomial p(x) if p(k) = 0. Let us see the, , G, AN, , graphical representations of linear and quadratic polynomials and the geometrical meaning of, their zeroes., 3.4.1. G RAPHICAL, , REPRESENTATION OF A LINEAR POLYNOMIAL, , Consider first a linear polynomial ax + b (a ¹ 0). You have studied in Class-IX that the graph of, , AN, , y = ax + b is a straight line. For example, the graph of y = 2x + 3 is a straight line intersecting, the Y-axis at (0, 3) and it also passes through the points (–2, –1) and (2, 7)., , T,, TE, L, , Table 3.1, x, , –2, , –1, , 0, , 2, , y = 2x + 3, , –1, , 1, , 3, , 7, , (–2, –1), , (–1, 1), , (0, 3), , (2, 7), , (x, y), , SC, ER, , In the graph, you can see that, the graph of y = 2x+3 intersects, the X-axis between x = –1 and, x = –2, that is, at the point, , (2, 7), , 6, 5, 4, , -3, æ -3 ö, çè , 0÷ø . So, x = 2 is the zero, 2, of the polynomial 2x + 3. Thus,, , the zero of t he po lynomial, 2x + 3 is the x-coordinate of the, po int where the graph of, y = 2x + 3 intersects the X-axis., , Y, 7, , 3, æ -3 ö, ç 2 ,0÷, è, ø, , X', , (0, 3), , 2, 1, , 0, -7 -6 -5 -4 -3 -2 -1, -1, (-2, -1), -2, -3, -4, -5, -6, -7, Y', , Free Distribution by T.S. Government 2021-22, , X, 1, , 2, , 3, , 4, , 5, , 6, , 7
Page 66 :
Class-X Mathematics, , 56, , D O T HIS, Draw the graph of (i) y = 2x + 5, (ii) y = 2x – 5, (iii) y = 2x and find the point of, intersection on X-axis. Is the x-coordinate of these points also the zero of the polynomials?, , G, AN, , A, , In general, for a linear polynomial ax + b, a ¹ 0, the graph of y = ax + b is a straight line, ,b, which intersects the X-axis at exactly one point, namely, ( ,0) ., a, , Therefore, the linear polynomial ax + b, a ¹ 0, has exactly one zero, namely, the, x-coordinate of the point where the graph of y = ax + b intersects the X-axis. This point of, , 3.4.2. G RAPHICAL R EPRESENTATION, , -b, a, , AN, , intersection of the straight line with X-axis, as we know is, OF A, , Q UADRATIC P OLYNOMIAL, , T,, TE, L, , Now, let us look for the geometrical meaning of a zero of a quadratic polynomial. Consider, the quadratic polynomial x2 – 3x – 4. Let us see how the graph of y = x2 – 3x – 4 looks like. Let, us list a few values of y = x2 – 3x – 4 corresponding to a few values for x as given in Table 3.2., , SC, ER, , Table 3.2, x, –2, –1, 0, 1, 2, 3, 4, 5, 2, y = x – 3x – 4, 6, 0, –4, –6, –6, –4, 0, 6, (x, y), (– 2, 6) (– 1, 0) (0, -4) (1, – 6) (2, – 6) (3, – 4) (4, 0) (5, 6), We locate the points listed above on a, Y, graph paper and join the points with a, 7, smooth curve., (-2, 6), (5, 6), 6, 2, Is the graph of y = x – 3x – 4 a, 5, straight line? No, it is like a, shaped, 4, 3, curve. It is intersecting the X-axis at, 2, two points., 1, In fact, for any quadratic polynomial, (4, 0), (-1, 0), X', X, 2, 0, ax + bx + c,a ¹ 0, the graph of, -7 -6 -5 -4 -3 -2 -1, 1 2 3 4 5 6 7, -1, the corresponding equat ion, y = ax2 + bx + c. ( a ¹ 0 ) either opens, upwards like, or downwards like, . This depends on whether a > 0 or, a < 0. (The shape of such curves are, called parabolas.), , -2, -3, , (0, -4) -4, -5, -6, -7, , (3, -4), , (1, -6), , (2, -6), , Y', , Free Distribution by T.S. Government 2021-22
Page 67 :
Polynomials, , 57, , From the table, we observe that -1 and 4 are zeroes of the quadratic polynomial. From, the graph, we see that -1 and 4 are also x- coordinates of points of intersection of the parabola, with the X-axis. Zeroes of the quadratic polynomial x2 – 3x – 4 are the x-coordinates of the, points where the graph of y = x2 – 3x – 4 intersects the X-axis., , A, , For the polynomial p(x) = y = x2 – 3x – 4; the curve intersects the X-axis at (-1, 0), which means p(–1)=0 and since p(4)=0 the curve intersects the X-axis at (4, 0)., , G, AN, , In general for polynomial p(x) if p(a)=0, its graph intersects X-axis at (a, 0)., , This is true for any quadratic polynomial, i.e., the zeroes of a quadratic polynomial, ax2 + bx + c,, , ( a ¹ 0), , are precisely the x-coordinates of the points where the parabola, , AN, , representing y = ax2 + bx + c ( a ¹ 0 ) intersects the X-axis., , TRY THIS, , T,, TE, L, , Draw the graphs of (i) y = x2 – x – 6 (ii) y = 6 – x – x2 and find zeroes in each case., What do you notice?, From our earlier observation about the shape of the graph of y = ax2 + bx + c, ( a ¹ 0 ), the following three cases arise., , Case (i) : The curve cuts X-axis at two distinct points A and A¢ . In this case, the x-coordinates, of A and A¢ are the two zeroes of the quadratic polynomial ax2+bx +c irrespective of whether, the parabola opens upward or downward., , SC, ER, , Y, , X', , A, , O, , A', , X, , X', , Y', , (i), , Free Distribution by T.S. Government 2021-22, , Y, , A', , O, , Y', , (ii), , A, , X
Page 68 :
58, , Class-X Mathematics, , Case (ii) : Here, the curve touches X-axis at exactly one point, i.e., at two coincident points. So,, the two points A and A¢ of Case (i) coincide here to become one point A., , A, , Y', , (i), , X, , X', , G, AN, , O, , AN, , X', , Y, , A, , Y, , O, , A, , X, , Y', , (ii), , T,, TE, L, , In this case, the x-coordinate of A is the only zero for the quadratic polynomial ax2 + bx + c., Case (iii) : Here, the curve is either completely above the X-axis or completely below the, X-axis without intersecting X-axis., , SC, ER, , Y, , X', , O, , X, , X', , Y', , Y, , O, , X, , Y', , (i), , (ii), , So, the quadratic polynomial ax2 + bx + c has no zero in this case., So, you can see geometrically that a quadratic polynomial can have either two distinct zeroes or, two equal zeroes (i.e., one zero), or no zero. This also means that a polynomial of degree 2 has, atmost two zeroes., , Free Distribution by T.S. Government 2021-22
Page 69 :
Polynomials, , 59, , TRY THIS, 1. Write three quadratic polynomials that have 2 zeroes each., 2. Write one quadratic polynomial that has one zero., , A, , 3. How will you verify if a quadratic polynomial has only one zero?, , G, AN, , 4. Write three quadratic polynomials that have no zeroes., , T HINK & D ISCUSS, , 1 2, x , y = x2 and y =, 2, 2x2. Try to plot some more graphs for y = x2+1 , y = 2x2+1. Comment on your, observations., , AN, , Observe the curves in the graph given below. They represent y =, , T,, TE, L, , 9, 8, , y = x2, , y = 2 x2, , 1, y = x2, 2, , 7, 6, , SC, ER, , 5, , -4, , -3, , 4, 3, 2, 1, -2, , -1, , 0, -1, -2, , 1, , 2, , 3, , 4, , Scale: X-axis : 1cm = 1unit, Y-axis : 1cm = 1 unit, , Free Distribution by T.S. Government 2021-22
Page 70 :
Class-X Mathematics, , 60, , 3. 4. 3 G EOMETRICAL M EANING, , OF, , Z EROES, , OF A, , C UBIC P OLYNOMIAL, , What do you expect the geometrical meaning of the zeroes of a cubic polynomial to be?, Let us find out. Consider the cubic polynomial x3 – 4x. To see how the graph of y = x3 – 4x, , Table 3.3, –2, , –1, , 0, , 3, , (–2, 0), , (–1, 3), , y = x3 – 4x, (x, y), , 1, , 2, , 0, , –3, , (0, 0), , 0, , (1, –3), , (2, 0), , Y, , We see that the graph of, y = x3– 4x looks like the one, given in the figure., , Scale: X-axis: 1 cm = 1 unit., Y-axis 1 cm = 1 unit., 6, , AN, , 7, 5, , (-1, 3), , T,, TE, L, , We see from the table above, that –2, 0 and 2 are zeroes of, the cubic polynomial x3 – 4x., –2, 0 and 2 are the, x-coordinates of the points, where the graph of y = x3 – 4x, intersects the X-axis. So this, polynomial has three zeros., , 0, , G, AN, , x, , A, , looks like, let us list a few values of y corresponding to a few values for x as shown in Table 3.3., , 3, 2, 1, , (-2, 0), , (2, 0), , 0, -7 -6 -5 -4 -3 -2 -1, -1, , 1, , 2, , 3, , X, 4, , 5, , 6, , 7, , -2, -3, (1, -3), , -4, , SC, ER, , X', , 4, , -5, -6, -7, Y', , Let us take a few more examples. Consider the cubic polynomials x3 and x3 – x2 respectively., See Table 3.4 and 3.5., Table 3.4, x, , –2, , –1, , 0, , 1, , 2, , y = x3, , –8, , –1, , 0, , 1, , 8, , (x, y), , (–2, –8), , (–1, –1), , (0, 0), , (1, 1), , (2, 8), , Free Distribution by T.S. Government 2021-22
Page 71 :
Polynomials, , 61, , Table 3.5, –2, , –1, , 0, , 1, , 2, , y = x3 – x2, , –12, , –2, , 0, , 0, , 4, , (–2, –12), , (–1, –2), , (0, 0), , (1, 0), , (2, 4), , (x, y), Y, , Y, , (2, 8), , 7, 6, 5, , 5, , 3, , 3, 2, , (-2, -8), , (1, 1), 1, , 2, , AN, , 2, , X, , 3, , 4, , X', , -4, , T,, TE, L, , -4, , 1, (0,(0,, 0) 0), 0, -3 -2-2 -1-1, -1 -1, (-1, -1), -2 -2, , (2, 4), , 4, , 4, , X', , Scale:, X=axis: 1 cm=1 unit, Y=axis: 1 cm=1 unit, , G, AN, , Scale:, 7, X=axis: 1 cm=1 unit, 6, Y=axis: 1 cm=1 unit, , A, , x, , 1, , 0, -1, -1, (-1, -2), -2, , -3 -2, , -3 -3, , -3, , -4 -4, , -4, , -5 -5, , -5, , -6 -6, , -6, , -7 -7, Y' Y', , -7, , SC, ER, , y = x3, , X, , (1, 0), 1, , 2, , 3, , 4, , Y', , y = x3 – x2, , In y = x3, you can see that 0 (zero) is the x-coordinate of the only point where the graph, of y = x3 intersects the X-axis. So, the polynomial has only one zero. Similarly, 0 and 1 are the, x-coordinates of the only points where the graph of y = x3 – x2 intersects the X-axis. So, the, cubic polynomial has two distinct zeroes., From the examples above, we see that there are at most 3 zeroes for any cubic polynomial., In other words, any polynomial of degree 3 can have at most three zeroes., , TRY THIS, Find the zeroes of cubic polynomials (i) – x3 (ii) x2 – x3 (iii) x3 – 5x2 + 6x without drawing, the graph of the polynomial., , Free Distribution by T.S. Government 2021-22
Page 72 :
Class-X Mathematics, , 62, , Remark : In general, given a polynomial p(x) of degree n, the graph of y = p(x) intersects the, X-axis at at most n points. Therefore, a polynomial p(x) of degree n has at most n zeroes., , O, , X, , O, , X', , Y', , (i), , O, , X, , X', , X, , Y', , (ii), , (iii), , Y, , Y, , O, , X', , O, , Y', , T,, TE, L, , Y, , X, , X', , O, , X, , X, , Y', , Y', , Y', , (iv), , (v), , (vi), , SC, ER, , X', , Y, , AN, , X', , Y, , G, AN, , Y, , A, , Example-1. Look at the graphs in the figures given below. Each is the graph of y = p(x), where, p(x) is a polynomial. In each of the graphs, find the number of zeroes of p(x) in the given range, of x., , Solution : In the given range of x in respective graphs :, (i) The number of zeroes is 1 as the graph intersects the X-axis at one point only., (ii) The number of zeroes is 2 as the graph intersects the X-axis at two points., (iii) The number of zeroes is 3. (Why?), (iv) The number of zeroes is 1. (Why?), (v) The number of zeroes is 1. (Why?), (vi) The number of zeroes is 4. (Why?), , Free Distribution by T.S. Government 2021-22
Page 73 :
Polynomials, , 63, , Example-2. Find the number of zeroes of the given polynomials. And also find their values., (i) p(x) = 2x + 1, , (ii) q(y) = y2 – 1, , (iii) r(z) = z3, , Solution : We will do this without plotting the graph., , A, , (i) p(x) = 2x + 1 is a linear polynomial. It has only one zero., , Let p(x) = 0, So, 2x+1=0, ,1, 2, , The zero of the given polynomial is, , ,1, ., 2, , AN, , Therefore x =, , G, AN, , To find zeroes,, , T,, TE, L, , (ii) q(y) = y2 – 1 is a quadratic polynomial., It has at most two zeroes., , To find zeroes, let q(y) = 0, Þ y2 – 1 = 0, , Þ (y + 1) (y – 1) = 0, , SC, ER, , Þ y = -1 or y = 1, , Therefore the zeroes of the polynomial are -1 and 1., , (iii) r(z) = z3 is a cubic polynomial. It has at most three zeroes., Let r(z) = 0, , Þ z3 = 0, , Þz=0, , So, the zero of the polynomial is 0., , Free Distribution by T.S. Government 2021-22
Page 74 :
Class-X Mathematics, , 64, , E XERCISE – 3.2, 1., , The graphs of y = p(x) are given in the figures below, for some polynomials p(x). In each, case, find the number of zeroes of p(x)., Y, , Y, , O, , X, , X', , Y', , X, , X', , Y', , SC, ER, , (iv), , 2., , 3., , X', , O, , (iii), , Y, , Y, , O, , X, , Y', , (v), , X', , X, , Y', , (ii), , T,, TE, L, , Y, , O, , X, , Y', , (i), , X', , O, , AN, , X', , G, AN, , A, , Y, , O, , X, , Y', , (vi), , Find the zeroes of the given polynomials., (i) p(x) = 3x, , (ii) p(x) = x2 + 5x + 6, , (iii) p(x) = (x+2) (x+3), , (iv) p(x) = x4 – 16, , Draw the graphs of the given polynomial and find the zeroes. Justify the answers., (i) p(x) = x2 – x – 12, , (ii) p(x) = x2 – 6x + 9, , (iii) p(x) = x2 – 4x + 5, , (iv) p(x) = x2 + 3x – 4, , (v) p(x) = x2 – 1, 4., , Check whether 1, –1 and, , 1, are zeroes of the polynomial p(x) = 4x2 + 3x – 1., 4, , Free Distribution by T.S. Government 2021-22
Page 75 :
Polynomials, 3.5 R ELATIONSHIP, , BETWEEN, , Z EROES, , AND, , C OEFFICIENTS, , OF A, , 65, , P OLYNOMIAL, , b, . Are the zeroes, a, of higher degree polynomials also related to their coefficients? Think about this and discuss with, , You have already seen that the zero of a linear polynomial ax + b is –, , A, , friends. We will now try to explore the relationship between zeroes and coefficients of a quadratic, polynomial. For this, let us take the quadratic polynomial p(x) = 2x2 – 8x + 6., , G, AN, , In Class-IX, we have learnt how to factorise quadratic polynomials by splitting the, middle term. So, we split the middle term ‘–8x’ as a sum of two terms, whose product is, 6 × 2x2 = 12 x2. So, we write, 2x2 – 8x + 6 = 2x2 – 6x – 2x + 6, = 2x(x – 3) – 2(x – 3), , AN, , = (2x – 2) (x – 3) = 2(x – 1) (x – 3), , T,, TE, L, , p(x) = 2x2 – 8x + 6 is zero when x – 1 = 0 or x – 3 = 0, i.e., when x = 1 or x = 3. So,, the zeroes of 2x2 – 8x + 6 are 1 and 3. We now try and see if these zeroes have some relationship, to the coefficients of terms in the polynomial. The coefficient of x2 is 2; of x is –8 and the, constant is 6, which is the coefficient of x0. (i.e. 6x0 = 6), We see that the sum of the zeroes = 1 + 3 = 4 =, Product of the zeroes = 1 × 3 = 3 =, , ,(,8) ,(coefficient of x), = coefficient of x2, 2, , constant term, 6, = coefficient of x 2, 2, , Let us take one more quadratic polynomial: p(x) = 3x2 + 5x – 2., , SC, ER, , By splitting the middle term we see,, , 3x2 + 5x – 2 = 3x2 + 6x – x – 2 = 3x(x + 2) – 1(x + 2), = (3x – 1) (x + 2), , 3x2 + 5x – 2 is zero when either 3x – 1 = 0 or x + 2 = 0, , i.e., when x =, , 1, or x = –2., 3, , The zeroes of 3x2 + 5x – 2 are, , 1, and –2. We can see that the :, 3, , Sum of its zeroes, , =, , 1, ,5 ,(coefficient of x), + (-2) =, = coefficient of x2, 3, 3, , Product of its zeroes, , =, , 1, ,2, constant term, × (-2) =, =, 3, 3, coefficient of x 2, , Free Distribution by T.S. Government 2021-22
Page 76 :
Class-X Mathematics, , 66, , D O T HIS, Find the zeroes of the quadratic polynomials given below. Find the sum and product, of the zeroes and verify relationship to the coefficients of terms in the polynomial., p(x) = x2 – x – 6, , (ii) p(x) = x2 – 4x + 3, (iv) p(x) = x2 + 2x + 1, , G, AN, , (iii) p(x) = x2 – 4, , A, , (i), , In general, suppose a and b are the zeroes of the quadratic polynomial p(x) = ax2 + bx + c,, where a ¹ 0, then (x – a) and (x – b) are the factors of p(x)., , Therefore, ax2 + bx + c = k (x – a) (x – b), where k is a constant, , AN, , = k[x2 – (a + b) x + ab], , = k x2 – k (a + b) x + k a b, , T,, TE, L, , Comparing the coefficients of x2, x and constant terms on both the sides, we get, a = k, b = – k(a+b) and c = kab., This gives a + b =, ab =, , ,b, ,, a, c, a, , SC, ER, , Note : a and b are Greek letters pronounced as ‘alpha’ and ‘beta’ respectively. We will, use one more letter ‘g’ pronounced as ‘gamma’., Sum of zeroes for a quadratic polynomial ax2 + bx + c, ,(coefficient of x), ,b, =a+b=, = coefficient of x2, a, Product of zeroes for a quadratic polynomial ax2 + bx + c, constant term, c, = ab =, = coefficient of x 2, a, Let us consider some examples., , Free Distribution by T.S. Government 2021-22
Page 77 :
Polynomials, , 67, , Example-3. Find the zeroes of the quadratic polynomial x2 + 7x + 10 and verify the relationship, between the zeroes and the coefficients., Solution : We have, x2 + 7x + 10 = (x + 2) (x + 5), , A, , So, the value of x2 + 7x + 10 is zero when x + 2 = 0 or x + 5 = 0,, , G, AN, , i.e., when x = –2 or x = –5., Therefore, the zeroes of x2 + 7x + 10 are –2 and –5., Now, sum of the zeroes= –2 + (–5) = – (7) =, , constant term, 10, = coefficient of x 2, 1, , AN, , Product of the zeroes = –2 × (–5) = 10 =, , ,(7) ,(coefficient of x), = coefficient of x2, 1, , Example-4. Find the zeroes of the polynomial x2 – 3 and verify the relationship between the, zeroes and the coefficients., , T,, TE, L, , Solution : Recall the identity a2 – b2 = (a – b) (a + b)., Using it, we can write: x2 – 3 = (x –, , 3 ) (x +, , So, the value of x2 – 3 is zero when x =, , SC, ER, , 3 or x = –, , 3., , 3 and – 3 ., , Therefore, the zeroes of x2 – 3 are, Sum of the zeroes =, , 3), , ,(coefficient of x), 3 + (– 3 ) = 0 = coefficient of x2, , Product of zeroes = ( 3 ) × (–, , 3)=–3=, , constant term, ,3, = coefficient of x 2, 1, , Example-5. Find the quadratic polynomial, whose sum and product of the zeroes are – 3 and 2, respectively., Solution : Let the quadratic polynomial be ax2 + bx + c and its zeroes be a and b. We have, a+b=–3=, , ,b, c, and ab = 2 = ., a, a, , If we take a = 1, then b = 3 and c = 2, So, one quadratic polynomial which fits the given conditions is x2 + 3x + 2., , Free Distribution by T.S. Government 2021-22
Page 78 :
68, , Class-X Mathematics, , Similarly, we can take 'a' to be any real number. Let us say it is k. This gives, , -b, = -3, k, , c, = 2 or c = 2k. Substituting the values of a, b and c, we get the polynomial is, k, kx2 + 3kx + 2k., ,1, ., 3, , G, AN, , Example-6. Find the quadratic polynomial whose zeroes are 2 and, , A, , or b = 3k and, , Solution : Let the quadratic polynomial be ax2 + bx + c, a ¹ 0 and its zeroes be a and b., Here a = 2, b =, , ,1, 3, , æ ,1ö÷ ,2, çç ÷ =, çè 3 ø÷, 3, , T,, TE, L, , Product of the zeroes = (ab) = 2, , AN, , æ , 1ö 5, Sum of the zeroes = (a + b) = 2 + çççè ø÷÷÷ =, 3, 3, , Therefore the quadratic polynomial ax2 + bx + c is, k[x2 – (a + b)x + a b], where k is a constant and k ¹ 0, i.e. k [x2 –, , 5, 2, x– ], 3, 3, , SC, ER, , We can take different values for k., , When k = 3, the quadratic polynomial will be 3x2 – 5x – 2., , and when k = 6, the quadratic polynomial will be 6x2 – 10x – 4., , TRY THIS, , 1, ., 3, , (i), , Find a quadratic polynomial with zeroes -2 and, , (ii), , What is the quadratic polynomial the sum of whose zeroes is, of the zeroes is -1., , -3, and the product, 2, , Free Distribution by T.S. Government 2021-22
Page 79 :
Polynomials, , 69, , 3.6 C UBIC P OLYNOMIALS, Let us now look at cubic polynomials. Do you think similar relation holds between the, zeroes of a cubic polynomial and its coefficients as well?, Let us consider p(x) = 2x3 – 5x2 – 14x + 8., , A, , 1, ., 2, , G, AN, , We see that p(x) = 0 for x = 4, – 2,, , Since p(x) can have at most three zeroes, these are the zeroes of 2x3 – 5x2 – 14x + 8., Sum of its zeroes, , 1 5 ,(,5) ,(coefficient of x2 ), = 4 + (–2) +, = =, = coefficient of x3, 2 2, 2, , Product of its zeroes, , = 4 × (–2) ×, , AN, , 1, ,8 ,(constant term), =–4=, = coefficient of x3, 2, 2, , T,, TE, L, , However, there is one more relationship here. Consider the sum of the products of the, zeroes taken two at a time. We have:, ìï, 1 üï ìï 1 üï, = {4≥ (,2)} ∗ íï(,2) ≥ ýï ∗ íï ≥ 4ýï, 2 þï îï 2 þï, îï, , =–8–1+2=–7=, , constant of x, ,14, = coefficient of x 3, 2, , SC, ER, , In general, it can be proved that if a, b, g are the zeroes of the cubic polynomial, ax3 + bx2 + cx + d,, , ax3 + bx2 + cx + d is a polynomial with zeroes a, b, g ., , Let us see how a, b, g relate to a, b, c, d., , Since a, b, g are the zeroes, the polynomial can be written as ( x - a ) ( x -b) ( x - g ), = x3 - x 2 ( a + b + g ) + x (ab + bg + ag ) - abg, , To compare with the polynomial, we multiply by 'a' and get, ax3 - x 2 a (a + b + g ) + xa (ab + bg + ag ) - aabg ., , \ b = - a (a + b + g ), c = a (ab + bg + ag ), d = - aabg, a+b+g=, , ,b, ,, a, , ab + bg + ga =, , c, a, , and a b g =, , Free Distribution by T.S. Government 2021-22, , ,d, ., a
Page 81 :
Polynomials, , 71, , E XERCISE – 3.3, , (ii) 4s2 – 4s + 1, , (iii) 6x2 – 3 – 7x, , (iv) 4u2 + 8u, , (v) t2 – 15, , (vi) 3x2 – x – 4, , A, , (i) x2 – 2x – 8, , Find the quadratic polynomial in each case with the given numbers as the sum and product, of its zeroes respectively., (i), , 1, ,–1, 4, , (ii) 2,, , (iv) 1, 1, , 1, 3, , 1 1, ,, 4 4, , (iii) 0,, , 5, , (vi) 4, 1, , Find the quadratic polynomial for the zeroes a, b given in each case., (i) 2, –1, , (ii), , 3,– 3, , (iii), , 1, ,–1, 4, , T,, TE, L, , 3., , (v) –, , G, AN, , 2., , Find the zeroes of the following quadratic polynomials and verify the relationship between, the zeroes and the coefficients., , AN, , 1., , (iv), , 1 3, ,, 2 2, , 4., , Verify that 1, –1 and +3 are the zeroes of the cubic polynomial x3 – 3x2 – x + 3 and, check the relationship between zeroes and the coefficients., , 3.7, , DIVISION ALGORITHM, , FOR, , P OLYNOMIALS, , SC, ER, , You know that a cubic polynomial has at most three zeroes. However, if you are given, only one zero, can you find the other two? For example, let us consider the cubic polynomial, x3 + 3x2 – x – 3. If one of its zeroes is 1, then you know that this polynomial is divisible by, x – 1. Therefore, we would get the quotient x2 – 2x – 3 on dividing by x – 1., We get the factors of x2 – 2x – 3 by splitting the middle term. The factors are (x + 1) and, , (x – 3). This gives us, , x3 – 3x2 – x + 3 = (x – 1) (x2 – 2x – 3), = (x – 1) (x + 1) (x – 3), , So, the three zeroes of the cubic polynomial are 1, – 1, 3., Let us discuss the method of dividing one polynomial by another in detail. Before doing, the steps formally, consider an example., , Free Distribution by T.S. Government 2021-22
Page 82 :
72, , Class-X Mathematics, , Example-8. Divide 2x2 + 3x + 1 by x + 2., Solution : Note that we stop the division process when either the, remainder is zero or its degree is less than the degree of the divisor. So,, here the quotient is 2x – 1 and the remainder is 3., , 2 x ,1, x ∗ 2 2 x 2 ∗ 3x ∗ 1, ,, , Let us verify division algorithm., , , x ∗1, , ,x ,2, ∗ ∗, , G, AN, , i.e., 2x2 + 3x + 1 = (x + 2) (2x – 1) + 3, , ,, , A, , (2x – 1) (x + 2) + 3 = 2x2 + 3x – 2 + 3 = 2x2 + 3x + 1, , 2x2 ∗ 4 x, , Therefore, Dividend = Divisor × Quotient + Remainder, , 3, , Let us now extend this process to divide a polynomial by a, quadratic polynomial., , AN, , Example-9. Divide 3x3 + x2 + 2x + 5 by 1 + 2x + x2., , x 2 ∗ 2 x ∗ 1 3 x3 ∗ x 2 ∗ 2 x ∗ 5, , T,, TE, L, , Solution : We first arrange the terms of the dividend, and the divisor in the decreasing order of their exponents., (Arranging the terms in this order is termed as writing, the polynomials in its standard form). In this example,, the dividend is already in its standard form and the divisor, in standard form, is x2 + 2x + 1., , Step 1 : To obtain the first term of the quotient, divide, the highest degree term of the dividend (i.e., 3x3) by the, highest degree term of the divisor (i.e., x2). This is 3x., Then carry out the division process. What remains is –5x2 –x+5., , SC, ER, , 3x , 5, , ,, , 3 x3 ∗ 6 x 2 ∗ 3x, ,, , ,, , , 5x 2 , x ∗ 5, , , 5 x 2 ,10 x , 5, , ∗, , ∗, , ∗, , 9 x ∗ 10, , Step 2 : Now, to obtain the second term of the quotient, divide the highest degree term of the, new dividend (i.e., – 5x2) by the highest degree term of the divisor (i.e., x2). This gives – 5., , Step 3 : What remains is 9x + 10. Now, the degree of 9x + 10 is less than the degree of the, divisor x2 + 2x + 1. So, we cannot continue the division any further. Why?, , So, the quotient is 3x – 5 and the remainder is 9x + 10. Also,, (x2 + 2x + 1) × (3x – 5) + (9x + 10), , = (3x 3 + 6x 2 + 3x – 5x 2 – 10x – 5 + 9x + 10), = 3x 3 + x2 + 2x + 5, , Here, again we see that, Dividend = Divisor × Quotient + Remainder, , Free Distribution by T.S. Government 2021-22
Page 83 :
Polynomials, , 73, , We are applying here an algorithm called division algorithm., This says that, If p(x) and g(x) are any two polynomials with g(x) ¹ 0, then we can find polynomials, q(x) and r(x) such that, , A, , p(x) = g(x) × q(x) + r(x),, , G, AN, , where either r(x) = 0 or degree of r(x) < degree of g(x) if r(x) ¹ 0, This result is known as the Division Algorithm for polynomials., Now, we have the following results from the above discussions, , If g(x) is a linear polynomial, then r(x) = r is a constant., , (ii), , If degree of g(x) = 1, then degree of p(x) = 1 + degree of q(x)., , (iii), , If p(x) is divided by (x – a), then the remainder is p(a)., , AN, , (i), , T,, TE, L, , (iv), If r = 0, we say q(x) divides p(x) exactly or q(x) is a factor of p(x)., Let us now take some examples to illustrate its use., Example-10. Divide 3x2 – x3 – 3x + 5 by x – 1 – x2, and verify the division algorithm., Solution : Note that the given polynomials are not in standard form. To carry out division, we, first write both the dividend and divisor in decreasing orders of their degrees., So,, , dividend = – x3 + 3x2 – 3x + 5 and, divisor = – x2 + x – 1., , SC, ER, , Division process is shown on the right side., , We stop here since degree of the remainder is, less than the degree of the divisor i.e. (–x2 + x – 1)., So, quotient = x – 2, remainder = 3., , Now,, , Dividend = Divisor × Quotient + Remainder, = (–x2 + x – 1) (x – 2) + 3, = – x3 + x2 – x + 2x2 – 2x + 2 + 3, = – x3 + 3x2 – 3x + 5, , In this way, the division algorithm is verified., , Free Distribution by T.S. Government 2021-22, , x ,2, ,x2 ∗ x ,1 , x3 ∗3x2 ,3x ∗5, , x3 ∗ x2 , x, , ∗, , ,, , ∗, , 2x2 ,2x ∗5, , 2x2 ,2x ∗ 2, , , ∗, 3, , ,
Page 85 :
Polynomials, 2., , 75, , Check in which case the first polynomial is a factor of the second polynomial by dividing, , t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12, , (ii), , x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2, , (iii), , x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1, , Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are, , G, AN, , 3., , (i), , A, , the second polynomial by the first polynomial :, , 5, 5, ., and ,, 3, 3, 4., , On dividing x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were, , Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm, and, , T,, TE, L, , 5., , AN, , x – 2 and – 2x + 4, respectively. Find g(x)., , (i) deg p(x) = deg q(x), , (ii) deg q(x) = deg r(x), , (iii) deg r(x) = 0, , O PTIONAL E XERCISE, [For extensive learning], , Verify that the numbers given alongside the cubic polynomials below are their zeroes., Also verify the relationship between the zeroes and the coefficients in each case:, , SC, ER, , 1., , (i) 2x3 + x2 – 5x + 2 ; (, , 1, , 1, –2), 2, , (ii) x3 – 3x2 + 3x – 1 ; (1, 1, 1), , 2., , Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a, time, and the product of its zeroes as 2, –7, –14 respectively., , 3., , If the zeroes of the polynomial x3 – 3x2 + x + 1 are a – b, a, a + b find a and b., , 4., , If two zeroes of the polynomial x4 – 6x3 – 26x2 + 138x – 35 are 2 ± 3 , find the other, zeroes., , 5., , If the polynomial x4 – 6x3 – 16x2 + 25x + 10 is divided by another polynomial, x2 – 2x + k, the remainder comes out to be x + a, find k and a., , Free Distribution by T.S. Government 2021-22
Page 86 :
Class-X Mathematics, , 76, , Suggested Projects, Quadratic polynomial - Zeroes of the polynomial - geometrical meaning/ graphs., Draw graphs for quadratic polynomial ax2 + bx + c for various conditions., (i) a > 0, , (ii) a < 0, , (iv) b > 0, , and comment on the graphs, , WHAT WE H AVE D ISCUSSED, , (v) b < 0, , A, , (vi) b = 0, , (iii) a = 0, , G, AN, , l, , Polynomials of degrees 1, 2 and 3 are called linear,, quadratic and cubic polynomials respectively., , 2., , A quadratic polynomial in x with real coefficients is of the form ax2 + bx + c, where a, b,, c are real numbers with a ¹ 0., , 3., , The zeroes of a polynomial p(x) are the x-coordinates of the points where the graph of, y = p(x) intersects the X-axis., , 4., , A quadratic polynomial can have at most 2 zeroes and a cubic polynomial can have at, most 3 zeroes., , 5., , If a and b are the zeroes of the quadratic polynomial ax2 + bx + c, a ¹ 0, then, , T,, TE, L, , AN, , 1., , a+b=–, , b, c, , ab = ., a, a, , If a, b, g are the zeroes of the cubic polynomial ax3 + bx2 + cx + d, a ¹ 0, then, , SC, ER, 6., , a+b+g=, , ,b, ,, a, , c, ,, a, ,d, abg =, ., a, , ab + bg + ga =, and, , 7., , The division algorithm states that given any polynomial p(x) and any non-zero polynomial, g(x), there exist polynomials q(x) and r(x) such that, p(x) = g(x) q(x) + r(x),, where either r(x) = 0 or degree r(x) < degree g(x) if r(x) ¹ 0., , Free Distribution by T.S. Government 2021-22
Page 87 :
4.1 I NTRODUCTION, , AN, , G, AN, , One day, Siri went to a book shop with her father and bought 3 notebooks, and 2 pens. Her father paid `80 for them. Her friend Laxmi liked the notebooks, and pens. So, she too bought 4 notebooks and 3 pens of the same kind for, `110. Now her classmates Rubina liked the pens whereas Joseph liked the, notebooks. They asked Siri the cost of the pen and the notebook separately., But, Siri did not know the costs separately. How will they find the costs of, these items?, , A, , 4, , Pair of Linear Equations, in Two Variables, , T,, TE, L, , In this example, the cost of a notebook and a pen are not known. These are unknown, quantities. We come across many such situations in our day-to-day life., , T HINK & D ISCUSS, , Two situations are given below:, , (i) The cost of 1kg potatoes and 2kg tomatoes was `30 on a certain day. After two days,, the cost of 2kg potatoes and 4kg tomatoes was found to be `66., , SC, ER, , (ii) The coach of a cricket team of M.K.Nagar High School buys 3 bats and 6 balls for, `3900. Later he buys one more bat and 2 balls for `1300., Identify the unknowns in each situation. We observe that there are two unknowns in each, case., , 4.1.1 HOW D O WE FIND U NKNOWN QUANTITIES?, , In the introduction, Siri bought 3 notebooks and 2 pens for `80. How can we find the cost, of a notebook or the cost of a pen?, , Rubina and Joseph tried to guess. Rubina said that price of each notebook could be `25., Then three notebooks would cost `75 and the two pens would cost `5. In that case each pen, could be for `2.50., Joseph felt that `2.50 for one pen was too less. In his opinion, it should be at least `16., Then the price of each notebook would also be `16.
Page 88 :
78, , Class-X Mathematics, , We can see that there can be many possible values for the price of a notebook and of a pen, so that the total cost is `80. So, how do we find the price at which Siri and Laxmi bought them?, By using only Siri's situation, we cannot find the costs. We have to use Laxmi's situation also., 4.1.2 U SING B OTH E QUATIONS T OGETHER, , (i), , Cost of 3 notebooks + 2 pens = `80., , (ii), , Cost of 4 notebooks + 3 pens = `110., , G, AN, , So, we have two situations which can be represented as follows:, , A, , Laxmi also bought the same types of notebooks and pens as Siri. She paid `110 for 4, notebooks and 3 pens., , Does this help us find the cost of a pen and a notebook?, , AN, , Consider the prices mentioned by Rubina. If the price of one notebook is `25 and the, price of one pen is `2.50 then,, The cost of 4 notebooks would be, , :, , 4 × 25 = `100, , And the cost for 3 pens would be, , :, , 3 × 2.50 = `7.50, , T,, TE, L, , If Rubina is right then Laxmi should have paid ` 100 + ` 7.50 = ` 107.50 but she paid `110., Now, consider the prices mentioned by Joseph., , The cost of 4 notebooks, if one is for `16, would be, , :, , 4 × 16 = ` 64, , And the cost for 3 pens, if one is for `16, would be, , :, , 3 × 16 = ` 48, , If Joseph is right then Laxmi should have paid `64 + `48 = `112 but this is more than the, price she paid., , SC, ER, , So what do we do? How to find the exact cost of the notebook and the pen?, , If we have only one equation but two unknowns (variables), we can find many solutions., So, when we have two variables, we need at least two independent equations to get a unique, solution. One way to find the values of unknown quantities is by using the Model method. In this, method, rectangles or portions of rectangles are often used to represent the unknowns. Let us, look at the first situation using the model method:, Step-1 : Represent a notebook by, , and a pen by, , Siri bought 3 books and 2 pens for `80., , ., D80, , Laxmi bought 4 books and 3 pens for `110., D110, , Free Distribution by T.S. Government 2021-22
Page 89 :
Pair of Linear Equations in Two Variables, , 79, , Step-2 : Increase (or decrease) the quantities in proportion to make one of the quantities equal in, both situations. Here, we make the number of pens equal., (3 books × 3) 9 books, , (2 pens × 3) 6 pens, , D240, , (4 books × 2) 8 books, , (3 pens × 2) 6 pens, , A, , (3×D80), , G, AN, , D220, (2×D110), , In Step 2, we observe a simple proportional reasoning., , Since, Siri bought 3 books and 2 pens for `80, so for 9 books and 6 pens:, , AN, , 3 × 3 = 9 books and 3 × 2 = 6 pens, the cost will be 3 × 80 = `240, , (1), , Similarly, Laxmi bought 4 books and 3 pens for `110, so:, , 2 × 4 = 8 books and 2 × 3 = 6 pens will cost 2 × 110 = `220, , (2), , T,, TE, L, , After comparing (1) and (2), we can easily observe that 1 extra book costs, `240 - ` 220 = `20. So one book cost is `20., , Siri bought 3 books and 2 pens for `80. Since each book costs `20, 3 books cost ` 60., So the cost of 2 pens become ` 80 - ` 60 = ` 20., So, cost of each pen is `20 ÷ 2 = `10., , SC, ER, , Let us try these costs in Laxmi's situation. 4 books will cost ` 80 and three pens will cost, ` 30 for a total of ` 110, which is true., From the above discussion and calculation, it is clear that to get exactly one solution (unique, solution) we need at least two independent linear equations in the same two variables., In general, an equation of the form ax + by + c = 0, where a, b, c are real numbers and, , where at least one of a or b is not zero i.e. a 2 + b 2 ¹ 0 , is called a linear equation in two, variables x and y., , TRY THIS, , Mark the correct option in the following questions:, 1., , Which of the following equations is not a linear equation?, a) 5 + 4x = y+ 3, 2, , c) 3 - x = y + 4, , b) x+2y = y - x, d) x + y = 0, , Free Distribution by T.S. Government 2021-22
Page 90 :
Class-X Mathematics, , 80, , 2. Which of the following is a linear equation in one variable?, a) 2x + 1 = y - 3, , b) 2t - 1 = 2t + 5, , c) 2x - 1 = x2, , d) x2 - x + 1 = 0, , 3. Which of the following numbers is a solution for the equation 2(x + 3) = 18?, b) 6, , c) 13, , d) 21, , A, , a) 5, , a) 4.5, , b) 3, , c) 2.25, , G, AN, , 4. The value of x which satisfies the equation 2x - (4 - x) = 5 - x is, d) 0.5, , 5. The equation x - 4y= 5 has, , b) unique solution, , c) two solutions, , d) infinitely many solutions, , 4.2 S OLUTIONS, , OF, , P AIRS, , OF, , AN, , a) no solution, , L INEAR EQUATIONS, , IN, , TWO V ARIABLES, , T,, TE, L, , In the introductory example of notebooks and pens, how many equations did we have?, We had two equations or a pair of linear equations in two variables. What do we mean by the, solution for a pair of linear equations?, A pair of values of the variables x and y which together satisfy each one of the equations, is called a solution for a pair of linear equations., 4.2.1 GRAPHICAL METHOD, , OF, , FINDING SOLUTION, , OF A, , PAIR, , OF, , LINEAR EQUATIONS, , SC, ER, , What will be the number of solutions for a pair of linear equations in two variables? Is the, number of solutions infinite or unique or none?, In an earlier section, we used the model method for solving the pair of linear equations., Now, we will use graphs to solve the equations., Let: a1x + b1y + c1 = 0, (a12 + b12 ¹ 0) and a2x + b2y + c2 = 0; (a22 + b22 ¹ 0) form a pair, , of linear equation in two variables., , The graph of a linear equation in two variables is a straight line. Ordered pairs of real, numbers (x, y) representing points on the line are solutions of the equation and ordered pairs of, real numbers (x, y) that do not represent points on the line are not solutions., If we have two lines in the same plane, what can be the possible relations between them?, What is the significance of this relation?, , Free Distribution by T.S. Government 2021-22
Page 91 :
Pair of Linear Equations in Two Variables, , 81, , When two lines are drawn in the same plane, only one of the following three situations is, possible:, i), The two lines may intersect at one point., The two lines may not intersect i.e., they are parallel., , iii), , The two lines may be coincident., (actually both are same), , G, AN, , A, , ii), , Let us write the equations in the first example in terms of x and y, where x is the cost of a, notebook and y is the cost of a pen. Then, the equations are 3x + 2y = 80 and 4x + 3y = 110., For the equation 3x + 2y = 80, , 0, , y=, , 10, , y=, , 20, , y=, , 30, , y=, , 80 - 3x, 2, 80 - 3(0), = 40, 2, 80 - 3(10), = 25, 2, 80 - 3(20), = 10, 2, 80 - 3(30), = -5, 2, , 110 - 4 x, 3, 110 - 4( -10), -10 y =, = 50, 3, 110 - 4(20), 20 y =, = 10, 3, 110 - 4(50), 50 y =, = -30, 3, , (x, y), (0, 40), (10, 25), , x, , y=, , (x, y), , AN, , y=, , (-10, 50), (20, 10), , T,, TE, L, , x, , For the equation 4x + 3y = 110, , (20, 10), (30, -5), , SC, ER, , Y, , 60, , 55, , 50, , 45, , 40, 35, 30, 25, 20, 15, (20, 10), , 10, 5, I, , X, , -10, , 0, , 5, , 10, , 15, , 20, , 25, , 30, , 35, , 40, , 45, , 50, , 55, , -5, , +, 4x, , -10, , -20, , |, , Y, , 0, 11, , 80, , -25, -30, , =, 3y, , -15, , =, 2y, , Free Distribution by T.S. Government 2021-22, , -5, , +, 3x, , After plotting the above points in the, Cartesian plane, we observe that the two, straight lines are intersecting at the point, (20, 10)., Substituting the values of x and y in, the equations, we get 3(20) + 2(10) = 80, and 4(20) + 3(10) = 110. Thus both the, equations are satisfied., Thus, as determined by the graphical, method, the cost of each book is `20 and, of each pen is `10. Recall that we got the, same solution using the model method., Since (20, 10) is the common point,, there is only one solution for this pair of linear, equations in two variables. Such equations, are known as consistent and independent, pair of linear equations. They will always, have a unique solution., , (50, -30), , X
Page 92 :
Class-X Mathematics, , 82, , Now, let us look at the first example from the ‘think and discuss section’. We want to find, the cost of 1kg of potatoes and the cost of 1 kg of tomatoes each. Let the cost of 1kg potatoes, be `x and cost of 1kg of tomatoes be `y. Then, the equations will become 1x+2y=30 and, 2x+4y=66., , 0, , y=, , 2, , y=, , 4, , y=, , 6, , y=, , 30 - x, 2, 30 - 0, 2, 30 - 2, 2, 30 - 4, 2, 30 - 6, 2, , (x, y), , x, , y=, , = 15, , (0, 15), , 1, , y=, , = 14, , (2, 14), , 3, , = 13, , (4, 13), , 5, , = 12, , (6, 12), , 66 - 2 x, 4, 66 - 2(1), 4, 66 - 2(3), 4, 66 - 2(5), 4, 66 - 2(7), 4, , y=, y=, , 7, , y=, , Here, we observe that the situation is, , = 16, , (1, 16), , 17, , T,, TE, L, , 16, , the lines do not intersect, the equations have no, , 15, , common solution. This means that the cost of the, , 14, 13, , potato and tomato was different on different days., , 12, , We see this in real life also. We cannot expect the, , = 15, , (3, 15), , = 14, , (5, 14), , = 13, , (7, 13), , Scale, x axis: 1 cm=1 unit, 2yxaxis: 1 cm = 1 unit, +4, y=, 66, x+, 2y, =3, 0, , Y, , represented graphically by two parallel lines. Since, , 11, 10, , same price of vegetables every day; it keeps changing., , 9, , Also, the change is independent., , SC, ER, , (x, y), , G, AN, , y=, , AN, , x, , For the equation 2x + 4y = 66, , A, , For the equation x + 2y = 30, , 8, 7, , Such pairs of linear equations which have no, , 6, 5, , solution are known as inconsistent pairs of linear, , 4, , equations., , 3, 2, , In the second example, from the “think and, , discuss” section, let the cost of each bat be ` x and, , each ball be ` y. Then we can write the equations as, , 3x + 6y = 3900 and x + 2y = 1300., , 1, X, , I, , -2, , -1, , 0, , 2, , 3, , 4, , 5, , 6, , 7, , 8, , X, , -2, Y, , For the equation 3x + 6y = 3900, 3900 - 3x, x y=, (x, y), 6, 3900 - 3(100), = 600 (100, 600), 100 y =, 6, , 1, , -1, , |, , For the equation x + 2y = 1300, 1300 - x, x y=, (x, y), 2, 1300 - 100, 100 y =, = 600 (100, 600), 2, , Free Distribution by T.S. Government 2021-22
Page 93 :
Pair of Linear Equations in Two Variables, , 1300 - 200, = 550 (200, 550), 2, 1300 - 300, 300 y =, = 500 (300, 500), 2, 1300 - 400, 400 y =, = 450 (400, 450), 2, , 200 y =, , The equations are geometrically shown, by a pair of coincident lines. If the solutions of, the equations are given by the common points,, then what are the common points in this case?, , Scale, x axis: 1 cm=100 units, y axis: 1 cm = 100 units, , Y, , A, , 3900 - 3(200), = 550 (200, 550), 6, 3900 - 3(300), 300 y =, = 500 (300, 500), 6, 3900 - 3(400), 400 y =, = 450 (400, 450), 6, , 200 y =, , 83, , G, AN, , 700, 600, , 500, 400, 300, 200, , 100, , AN, , From the graph, we observe that every, point on the line is a common solution to both, the equations. So, they have infinitely many, solutions as both the equations are equivalent., Such pairs of equations are called consistent, and dependent pair of linear equations in two, variables. This system of equations that has, solution are known as ‘consistent equations’., , I, , -200 -100 0, , 100 200 300 400 500 600, , X, , -100, -200, , T,, TE, L, , T RY, , X, , Y, , |, , THIS, , In the example given above, can you find the cost of each bat and ball?, , T HINK &, , DISCUSS, , SC, ER, , Is a dependent pair of linear equations always consistent. Why or why not?, , DO, , THIS, , 1. Represent the following systems of equations graphically and comment on solutions:, i) x - 2y = 0, ii) x + y = 2, iii) 2x - y = 4, 3x + 4y = 20, 2x + 2y = 4, 4x - 2y = 6, 2. Represent the pair of linear equations x + 2y - 4 = 0 and 2x + 4y- 12 = 0 graphically and, comment on solutions., , 4.2.3 R ELATION BETWEEN C OEFFICIENTS, , AND, , N ATURE, , OF, , S YSTEM, , OF, , E QUATIONS, , Let a1, b1, c1 and a2, b2, c2 denote the coefficients of a given pair of linear equations in two, a, , b, , c, , 1, 1, 1, variables. Then, let us write and compare the values of a , b and c in the above examples., 2, 2, 2, , Free Distribution by T.S. Government 2021-22
Page 94 :
Class-X Mathematics, , 84, , a1, a2, , 3, 4, , 1. 3x+2y–80=0, , b1, b2, , 2, 3, , c1, c2, , -80, -110, , Comparison, , Algebraic, , of ratios, , interpretation representation, , a1, b, ¹ 1, a2, b2, , Consistent and Intersecting One, , 4x+3y–110=0, 2, 4, , -30, -66, , a1, b, c, = 1 ¹ 1 Inconsistent Parallel, a2, b2, c2, , 2x+4y–66=0, 3. 3x+6y=3900, , solution, , Independent, , 1, 2, , Solutions, , No, , G, AN, , 2. 1x+2y–30=0, , Graphical, , A, , Pair of lines, , solution, , 3, 1, , 6, 2, , 3900, 1300, , a1, b, c, = 1 = 1 Consistent, a2, b2, c2, , Coincident Infinitely, , and, dependent, , many, solutions, , AN, , x+2y=1300, Let us look at examples., , T,, TE, L, , Example-1. Check whether the given pair of equations represent intersecting or parallel or, coincident lines. Find the solution if the lines are intersecting., 2x + y - 5 = 0, 3x - 2y - 4 = 0, Solution :, a1, , a1, 2, =, a2, 3, b1, , c1, -5, =, c2, -4, , b1, 1, =, b2, -2, , SC, ER, , Since a ¹ b , therefore they are intersecting lines and hence, it is a consistent pair of linear, 2, 2, equation., For the equation 2x + y = 5, , For the equation 3x - 2y = 4, , x, , y = 5 - 2x, , (x, y), , x, , y=, , 4 - 3x, -2, , (x, y), , 0, , y = 5 - 2 (0) = 5, , (0, 5), , 0, , y=, , 4 - 3(0), = -2, -2, , (0, -2), , 1, , y = 5 - 2(1) = 3, , (1, 3), , 2, , y=, , 4 - 3(2), =1, -2, , (2, 1), , 2, , y = 5 - 2(2) = 1, , (2, 1), , 4, , y=, , 4 - 3(4), =4, -2, , (4, 4), , 3, 4, , y = 5 - 2(3) = -1, y = 5 - 2(4) = -3, , (3, -1), (4, -3), , Free Distribution by T.S. Government 2021-22
Page 95 :
Pair of Linear Equations in Two Variables, The unique solution of, this pair of equations, is (2,1)., , 85, , Scale, x axis: 1 cm=1 unit, y axis: 1 cm = 1 unit, , Y, 8, 7, 6, , 4, , G, AN, , 3x, , 3, , A, , -2, y=, , 4, , 5, , 2, (2, 1), , 1, X, , I, , -2, , -1, , 0, , 1, , 2, , 5, , 4, , 2x, , -1, , 3, , 6, , 7, , 8, , X, , +y, , =5, , AN, , -2, -3, Y|, , T,, TE, L, , Example-2. Check whether the following pair of equations is consistent., 3x + 4y = 2 and 6x + 8y = 4. Verify by a graphical representation., Solution : 3x + 4y - 2 = 0, 6x+8y - 4 = 0, a1, 3 1, b1, 4 1, c1, -2 1, = =, = =, =, =, a2 6 2, b2 8 2, c2, -4 2, a1, b1, c1, Since a = b = c , therefore, they are coincident lines. So, the pair of linear equations, 2, 2, 2, , SC, ER, , are consistent and dependent and have infinitely many solutions., For the equation 3x + 4y = 2, , x, , y=, , 2 - 3x, 4, , (x, y), , 0, , y=, , 2 - 3(0), 1, =, 4, 2, , (0,, , 2, , y=, , 2 - 3(2), = -1, 4, , (2, -1), , 4, , y=, , 6, , y=, , For the equation 6x + 8y = 4, x, , y=, , 4 - 6x, 8, , (x, y), , 0, , y=, , 4 - 6(0), 1, =, 8, 2, , (0,, , 2, , y=, , 4 - 6(2), = -1, 8, , (2, -1), , 2 - 3(4), = -2.5 (4, -2.5), 4, , 4, , y=, , 4 - 6(4), = -2.5, 8, , (4, -2.5), , 2 - 3(6), = -4, 4, , 6, , y=, , 4 - 6(6), = -4, 8, , (6, -4), , 1, ), 2, , (6, -4), , Free Distribution by T.S. Government 2021-22, , 1, ), 2
Page 96 :
Class-X Mathematics, , 86, , Scale, x axis: 1 cm=1 unit, y axis: 1 cm = 1 unit, , Y, 4, 3, , 1, -2, , -1, , 0, , 1, , -1, , Scale, 5, 3, 4, x axis: 1 cm=1 unit, y axis: 1 cm = 1 unit, 2, , -2, -3, , 7, , 8, , X, , AN, , -4, , 6, , G, AN, , XI, , A, , 2, , |, , Y, , T,, TE, L, , Example-3. Check whether the system of equations 2x-3y = 5 and 4x-6y = 15 are consistent., Also verify by graphical representation., Solution : 4x-6y - 15 = 0, 2x-3y - 5 = 0, , b1, -6 2, =, =, b2, -3 1, , c1 - 15 3, =, =, c2, -5 1, , a1, b, c, = 1 ¹ 1, a2, b2, c2, , SC, ER, , a1, 4 2, = =, a2 2 1, , So the equations are inconsistent. They have no solutions and their graph is of parallel lines., For the equation 4x - 6y = 15, , For the equation 2x - 3y = 5, , x, , y=, , 15 - 4 x, -6, , (x, y), , x, , y=, , 5 - 2x, -3, , (x, y), , 0, , y=, , 15 - 0 - 5, =, -6, 2, , (0, -2.5), , 1, , y=, , 5 - 2(1), =-1, -3, , (1, -1), , 3, , y=, , 15 - 4(3) - 1, =, -6, 2, , (3, -0.5), , 4, , y=, , 5 - 2(4), =1, -3, , (4, 1), , 6, , y=, , 15 - 4(6) 3, =, -6, 2, , (6, 1.5), , 7, , y=, , 5 - 2(7), =3, -3, , (7, 3), , Free Distribution by T.S. Government 2021-22
Page 97 :
Pair of Linear Equations in Two Variables, , 4, 3, 2, 1, X, , -2, , -1, , 0, , 1, , 2, , 3, , 4, , 5, , -1, -2, -3, -4, , D O T HIS, , |, , 7, , 8, , X, , AN, , Y, , 6, , G, AN, , 5, , A, , Scale, x axis: 1 cm=1 unit, y axis: 1 cm = 1 unit, =5, y, -3, 2x, 9, y=, 6, 4x, , Y, , I, , 87, , T,, TE, L, , Check each of the given system of equations to see if it has a unique solution, infinite, solutions or no solution. Solve them graphically., (i) 2x+3y = 1, (ii) x + 2y = 6, (iii) 3x + 2y = 6, 3x-y = 7, 2x + 4y = 12, 6x + 4y = 18, , TRY THIS, , For what value of 'p' the following pair of equations has a unique solution., 2x + py = - 5 and 3x + 3y = - 6, 2. Find the value of 'k' for which the pair of equations 2x - ky + 3 = 0, 4x + 6y - 5 =0, represent parallel lines., 3. For what value of 'k', the pair of equations 3x + 4y + 2 = 0 and 9x + 12y + k = 0, represents coincident lines., 4. For what positive values of 'p', the following pair of linear equations have infinite solutions?, px + 3y - (p - 3) = 0, 12x + py - p = 0, , SC, ER, , 1., , Let us look at some more examples., Example-4. In a garden there are some bees and flowers. If one bee sits on each flower then, one bee will be left. If two bees sit on each flower, one flower will be left. Find the number of, bees and number of flowers., Solution : Let the number of bees = x and, the number of flowers = y, If one bee sits on each flower then one bee will be left. So, x = y + 1, , Free Distribution by T.S. Government 2021-22
Page 98 :
or, , Class-X Mathematics, x-y-1=0, , ... (1), , If two bees sit on each flower, one flower will be left. So, y =, or, , x - 2y+2 = 0, For the equation x - y - 1 = 0, , x, + 1 then x = 2(y- 1), 2, , ... (2), For the equation x - 2y + 2 = 0, , y=x-1, , (x, y), , x, , y=, , 0, , y = 0 - 1 = -1, , (0, -1), , 0, , y=, , 1, , y=1-1=0, , (1, 0), , 2, , 2, , y=2-1=1, , (2, 1), , 4, , 3, , y=3-1=2, , (3, 2), , 4, , y=4-1=3, , (4, 3), , x+2, 2, 0+ 2, 2, 2+2, 2, 4+2, 2, 6+ 2, 2, , y=, , AN, , y=, , T,, TE, L, , 6, , y=, , Y, , 5, , 4, 3, 2, , (x, y), , =1, , (0, 1), , G, AN, , x, , A, , 88, , Scale, (4, 3), x axis: 1 cm=1 unit, y axis: 1 cm = 1 unit, , x-, , 2y, , =, +2, , =2, , (2, 2), , =3, , (4, 3), , =4, , (6, 4), , 0, , XI, , -1, , 0, , 1, , 2, , 3, , 4, , 5, , 6, , 7, , 8, , X, , -1, , Scale, x axis: 1 cm=1 unit, y axis: 1 cm = 1 unit, , x, , -y, , SC, ER, , -1, , -2, , =, , 0, , 1, , -2, -3, -4, Y|, , In the graph, (4, 3) is the point of intersection. Therefore, there are 4 bees and 3 flowers., Example-5. The perimeter of a rectangular plot is 32m. If the length is increased by 2m and the, breadth is decreased by 1m, the area of the plot remains the same. Find the length and breadth, of the plot., Solution : Let length and breadth of the rectangular land be l and b respectively. Then,, area = lb, and, Perimeter = 2(l + b) = 32 m, Then, l + b = 16 which implies l + b - 16 = 0, ... (1), , Free Distribution by T.S. Government 2021-22
Page 99 :
Pair of Linear Equations in Two Variables, , 89, , G, AN, , A, , If length is increased by 2 m, then new length is l + 2. Also breadth is decreased by 1m; so, new breadth is b - 1., Then, area = (l + 2) (b - 1), Since there is no change in the area,, (l + 2) (b - 1) = lb, lb - l +2b - 2 = lb, or lb - lb = l - 2b + 2, l - 2b + 2 = 0, ... (2), For the equation l + b - 16 = 0, For the equation l - 2b + 2 = 0, l, , b = 16 - l, , (l, b), , l, , b=, , 6, , b = 16 - 6 = 10, , (6, 10), , 6, , 8, , b = 16 - 8 = 8, , (8, 8), , 8, , 10, , b = 16 - 10 = 6, , (10, 6), , 10, , b=, , 12, , b = 16 - 12 = 4, , (12, 4), , 12, , b=, , 14, , b = 16 - 14 = 2, , (14, 2), , 14, , b=, , b=, , T,, TE, L, , AN, , b=, , l+2, 2, 6+ 2, =4, 2, 8+2, =5, 2, 10 + 2, =6, 2, 12 + 2, =7, 2, 14 + 2, =8, 2, , (l, b), , (6, 4), (8, 5), (10, 6), (12, 7), (14, 8), , SC, ER, , So, original length of the plot is 10m and its breadth is 6m., Taking measures of length on X-axis and measure of breadth on Y-axis, we get the graph, Scale, Y, x axis: 1 cm=1 unit, 14, y axis: 1 cm = 1 unit, , XI, , -2, , 12, 10, , l-, , 6, , (10, 6), , l+, , 4, 2, -1, , 2b, , 8, , 0, , 2, , 4, , 6, , 8, , 10, , -1, -2, -3, -4, Y|, , Free Distribution by T.S. Government 2021-22, , 12, , b, , =, +2, , -1, , 14, , 6, , =, 16, , 0, , 0, , 18, , X
Page 100 :
Class-X Mathematics, , 90, , E XERCISE - 4.1, a1, , c1, , b) 9x+3y + 12 = 0, 18x+6y + 24 = 0, , c) 6x - 3y + 10 = 0, 2x - y + 9 = 0, , A, , a) 5x- 4y + 8 = 0, 7x+6y-9 = 0, , Check whether the following equations are consistent or inconsistent. Solve them graphically., a) 3x+2y=5, , b) 2x - 3y = 8, , 2x - 3y=7, d) 5x-3y = 11, -10x+6y = -22, , e), , 4, x +2y = 8, 3, , 3x-3y = 16, , c), , h) 2x + y-6 = 0, , 3, 5, x+ y = 7, 2, 3, , 9x - 10y = 12, , f) x + y = 5, , 2x+3y = 12, , T,, TE, L, , g) x - y = 8, , 4x - 6y = 9, , G, AN, , 2., , b1, , By comparing the ratios a , b , c , state whether the lines represented by the following, 2, 2, 2, pairs of linear equations intersect at a point / are parallel / are coincident., , AN, , 1., , i), , 4x-2y- 4 = 0, , 2x+2y = 10, 2x-2y - 2 = 0, 4x-4y- 5 = 0, , Form equations for the following situations and solve them graphically., 3., , Neha went to a shop to purchase some pants and skirts. When her friend asked her how, many of each she had bought, she answered, "the number of skirts are two less than twice, the number of pants purchased and the number of skirts is four less than four times the, number of pants purchased.", , SC, ER, , Help her friend to find how many pants and skirts Neha bought., , 4., , 10 students of Class-X took part in a mathematics quiz. If the number of girls is 4 more, than the number of boys, then find the number of boys and the number of girls who took, part in the quiz., , 5., , 5 pencils and 7 pens together cost `50 whereas 7 pencils and 5 pens together cost D46., Find the cost of one pencil and that of one pen., , 6., , Half the perimeter of a rectangular garden is 36 m. If the length is 4m more than its width,, then find the dimensions of the garden., , 7., , We have a linear equation 2x + 3y - 8 = 0. Write another linear equation in two variables, x and y such that the graphical representation of the pair so formed is intersecting lines., Now, write two more linear equations so that one forms a pair of parallel lines and the, second forms coincident line with the given equation., , Free Distribution by T.S. Government 2021-22
Page 101 :
Pair of Linear Equations in Two Variables, , 91, , The area of a rectangle gets reduced by 80 sq units, if its length is reduced by 5 units and, breadth is increased by 2 units. If we increase the length by 10 units and decrease the, breadth by 5 units then the area will be increased by 50 sq units. Find the length and, breadth of the rectangle., , 9., , In a class, if three students sit on each bench, one student will be left. If four students sit on, each bench, one bench will be left. Find the number of students and the number of benches, in that class., OF, , FINDING, , THE, , SOLUTIONS, , FOR A, , PAIR, , OF, , LINEAR, , G, AN, , 4.3 ALGEBRAIC METHODS, EQUATIONS, , A, , 8., , We have learnt how to solve a pair of linear equations graphically. But, the graphical method, is not convenient in all cases where the point representing the solution has no integral co-ordinates., , T,, TE, L, , AN, , 4 1, For example, when the solution is of the form ( 3 , 2 7 ), (- 1.75, 3.3), ( ,, ) etc. There, 13 19, is every possibility of making mistakes while plotting such co-ordinates on graph. Is there any, alternative method of finding a solution? There are several other methods, some of which we, shall discuss now., , 4.3.1 S UBSTITUTION M ETHOD, , This method is useful for solving a pair of linear equations in two variables where one, variable can easily be written in terms of the other variable. To understand this method, let us, consider it step-wise., Step-1 : In one of the equations, express one variable in terms of the other variable. Say y in, terms of x., , SC, ER, , Step-2 : Substitute the value of y obtained in step 1 in the second equation., , Step-3 : Simplify the equation obtained in step 2 and find the value of x., , Step-4 : Substitute the value of x obtained in step 3 in either of the equations and solve it for y., , Step-5 : Check the obtained solution by substituting the values of x and y in both the original, equations., , Example-6. Solve the given pair of equations using substitution method., 2x - y = 5, 3x + 2y = 11, Solution : 2x - y = 5, (1), 3x + 2y = 11, (2), Equation (1) can be written as, y = 2x - 5, Substituting in equation (2) we get, , Free Distribution by T.S. Government 2021-22
Page 102 :
Class-X Mathematics, , 92, , 3x + 2(2x - 5) = 11, 3x + 4x - 10 = 11, 7x = 11 + 10 = 21, x = 21/7 = 3., Substitute x =3 in equation (1), , A, , 2(3) - y = 5, , G, AN, , y=6-5=1, , Substituting the values of x and y in equation (2), we get 3(3) + 2(1) = 9 + 2 = 11, Both the equations are satisfied by x = 3 and y = 1., Therefore, the required solution is x = 3 and y = 1., , AN, , D O T HIS, , Solve each pair of equation by using the substitution method., , 4) x +, , 6, =6, y, , 3x -, , 2) x+2y = - 1, 2x - 3y = 12, , 3) 2x+3y = 9, 3x+4y = 5, , 5) 0.2x + 0.3y = 13, , 6), , T,, TE, L, , 1) 3x - 5y = -1, x-y=-1, , 8, =5, y, , 0.4x + 0.5y = 2.3, , 2x + 3y = 0, 3x - 8 y = 0, , 4.3.2 E LIMINATION M ETHOD, , SC, ER, , In this method, first we eliminate (remove) one of the two variables by equating its coefficients., This gives a single equation which can be solved to get the value of the other variable. To understand, this method, let us consider it stepwise., Step-1 : Write both the equations in the form of ax + by = c., , Step-2 : Make the coefficients of one of the variables, say 'x', equal by multiplying each equation, by suitable real numbers., Step-3 : If the variable to be eliminated has the same sign in both equations, subtract one equation, from the other to get an equation in one variable. If they have opposite signs then add., Step-4 : Solve the equation for the remaining variable., Step-5 : Substitute the value of this variable in any one of the original equations and find the, value of the eliminated variable., Example-7. Solve the following pair of linear equations using elimination method., 3x + 2y = 11, 2x + 3y = 4, , Free Distribution by T.S. Government 2021-22
Page 103 :
Pair of Linear Equations in Two Variables, , 93, , 3x + 2y = 11, (1), 2x + 3y = 4, (2), Let us eliminate 'y' from the given equations. The coefficients of 'y' in the given equations are 2, and 3. L.C.M.of 2 and 3 is 6. So, multiply equation (1) by 3 and equation (2) by 2., 9x + 6y = 33, , Equation (2) × 2, , 4x + 6y = 8, , (-) (-) (-), 5x, = 25, 25, x=, =5, 5, Substitute x = 5, in equation (1), 3(5) + 2y = 11, -4, = -2, 2, , AN, , 2y = 11 - 15 = - 4 Þ y =, , G, AN, , Equation (1) × 3, , A, , Solution :, , T,, TE, L, , Therefore, the required solution is x = 5, y = - 2., , D O T HIS, , Solve each of the following pairs of equations by the elimination method., 1. 8x+ 5y = 9, 3x+2y = 4, , 2. 2x + 3y = 8, 4x + 6y = 7, , 3. 3x + 4y = 25, 5x - 6y = -9, , SC, ER, , TRY THIS, , Solve the given pair of linear equations, , (a - b)x + (a + b)y = a2 - 2ab - b2, (a + b) (x + y) = a2 + b2, , Let us see some more examples:, , Example-8. Rubina went to the bank to withdraw `2000. She asked the cashier to give the, cash in `50 and `100 notes only. She got 25 notes in all. Can you tell how many notes each of, `50 and `100 she received?, , Solution :, , Let the number of `50 notes be x;, Let the number of `100 notes be y;, then, x + y = 25, and, 50x + 100y = 2000, Method I: Solution through the substitution method:, , Free Distribution by T.S. Government 2021-22, , (1), (2)
Page 104 :
Class-X Mathematics, , 94, , From equation (1), , x = 25 -y, , Substituting in equation (2), , 50 (25 - y) + 100y = 2000, 1250 - 50y + 100y = 2000, , y=, , 750, = 15, 50, , G, AN, , x = 25 - 15 = 10, , A, , 50y = 2000 - 1250 = 750, , Hence, Rubina received ten `50 notes and fifteen `100 notes., Method II: Solution through the elimination method:, Equation (1) × 50 :, , 50x + 50y = 1250, , Equation (2) × 1, , 50x + 100y = 2000, , :, , (-), , (-), , (-), , same sign, so subtract, , T,, TE, L, , -50y = -750, , AN, , In the equations, coefficients of x are 1 and 50 respectively. So,, , or, , y=, , -750, = 15, -50, , Substitute y in equation (1) x + 15 = 25, , x = 25 - 15 = 10, , Hence Rubina received ten D50 notes and fifteen D100 rupee notes., , SC, ER, , Example-9. In a competitive exam, 3 marks were awarded for every correct answer and 1, mark was deducted for every wrong answer. Madhu scored 40 marks in this exam. Had 4, marks been awarded for each correct answer and 2 marks deducted for each incorrect answer,, Madhu would have scored 50 marks. If Madhu had attempted all questions, how many questions, were there in the test?, Solution :, , Let the number of correct answers be x, and the number of wrong answers be y., , When 3 marks are given for each correct answer and 1 mark deducted for each wrong, answer, his score is 40 marks., So, 3x - y = 40, , (1), , His score would have been 50 marks if 4 marks were given for each correct answer and 2, marks deducted for each wrong answer., Thus, 4x - 2y = 50, , (2), , Free Distribution by T.S. Government 2021-22
Page 105 :
Pair of Linear Equations in Two Variables, , 95, , Substitution method, From equation (1),, , y = 3x - 40, , Substituting in equation (2), , 4x - 2 (3x - 40) = 50, 4x - 6x + 80 = 50, -30, =15, -2, , Substitute the value of x in equation (1), 3(15) - y = 40, 45 - y = 40, y = 45 - 40 = 5, , AN, , \ Total number of questions = 15 + 5 = 20, , G, AN, , x=, , A, , - 2x = 50 - 80 = -30, , D O T HIS, , T,, TE, L, , Use the elimination method to solve the example-9., , Example-10. Mary told her daughter, "Seven years ago, I was seven times as old as you were, then. Also, three years from now, I shall be three times as old as you will be." Find the present, age of Mary and her daughter., Solution :, , Let Mary's present age be x years and her daughter's age be y years., , Then, seven years ago Mary's age was x - 7 and daughter's age was y - 7., , SC, ER, , x - 7 = 7(y - 7), x - 7 = 7y - 49, , x - 7y + 42 = 0, , (1), , Three years hence, Mary's age will be x + 3 and daughter's age will be y + 3., x + 3 = 3 (y + 3), x + 3 = 3y + 9, x - 3y - 6 = 0, (2), , Elimination method, Equation 1, , x - 7y = - 42, , Equation 2, , x - 3y = 6, (-) (+) (-), -4y = -48, , same sign for x, so subtract., , Free Distribution by T.S. Government 2021-22
Page 106 :
Class-X Mathematics, , 96, , y=, , -48, = 12, -4, , Substitute the value of y in equation (2), x-3 (12) - 6 = 0, , A, , x = 36 + 6 = 42, , D O T HIS, Solve example-10 by the substitution method., , The point which corresponds to, how much money you have to earn, through sales in order to equal the, money you spent in production is, break even point., , T,, TE, L, , AN, , Example-11. A publisher is planning to produce a new, textbook. The fixed costs (reviewing, editing, typesetting, and so on) are ` 320000. Besides that, he also spends, another ` 31.25 in producing each book. The wholesale, price (the amount received by the publisher) is ` 43.75, per book. How many books must the publisher sell to, break even, i.e., so that the cost of production will equal, revenues?, , G, AN, , Therefore, Mary's present age is 42 years and her daughter's age is 12 years.`, , Solution : The publisher breaks even when costs equal revenues. If x represents the number of, books printed and sold and y be the breakeven point, then the cost and revenue equations for the, publisher are, (1), (2), , SC, ER, , Cost equation is given by, y = 320000 + 31.25x, Revenue equation is given by, y = 43.75x, Using the second equation to substitute for y in the first equation, we have, 43.75x = ` 320000 + 31.25x, , 12.5x = ` 320000, , x=, , 32 0 0 00, = 25,600, 1 2 .5, , Thus, the publisher will break even when 25,600 books are printed and sold., , E XERCISE - 4.2, Form a pair of linear equations for each of the following problems and find their solution., 1., , The ratio of incomes of two persons is 9 : 7 and the ratio of their expenditures is 4 : 3. If, each of them manages to save `2000 per month then find their monthly income., , Free Distribution by T.S. Government 2021-22
Page 107 :
Pair of Linear Equations in Two Variables, , 97, , The sum of a two digit number and the number obtained by reversing the digits is 66. If the, digits of the number differ by 2, find the number. How many such numbers are there?, , 3., , The larger of two supplementary angles exceeds the smaller by 18°. Find the angles., , 4., , The taxi charges in Hyderabad have two components: fixed and per kilometer charge., Upto first 3 km you will be charged a certain minimum amount. From there onwards you, have to pay additionally for every kilometer travelled. For the first 10 km, the charge paid, is `166. For a journey of 15 km. the charge paid is `256., What are the fixed charges and charge per km?, , G, AN, , i., , A, , 2., , ii. How much does a person have to pay for travelling a distance of 25 km?, , 4, if 1 is added to both numerator and denominator. If, however,,, 5, 1, 5 is subtracted from both numerator and denominator the fraction will be equal to ., 2, What is the fraction?, , A fraction will be equal to, , 6., , Places A and B are 100 km apart on a highway. One car starts from point A and another, from point B at the same time at different speeds. If the cars travel in the same direction,, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the, speeds of the two cars?, , 7., , Two angles are complementary. The larger angle is 3° less than twice the measure of the, smaller angle. Find the measure of each angle., , 8., , A dictionary has a total of 1382 pages. It is broken up into two parts. The second part of the, book has 64 pages more than the first part. How many pages are in each part of the book?, , 9., , A chemist has two solutions of hydrochloric acid in stock. One is 50% solution and the, other is 80% solution. How much of each should be used to obtain 100ml of a 68%, solution., , SC, ER, , T,, TE, L, , AN, , 5., , 10., , You have `12,000/- saved amount, and wants to invest it in two schemes yielding 10%, and 15% interest. How much amount should be invested in each scheme so that you, should get overall 12% interest., , 4.4 EQUATIONS R EDUCIBLE, VARIABLES, , TO A, , P AIR, , OF, , L INEAR E QUATIONS, , IN, , TWO, , Now we shall discuss the solution of pairs of equations which are not linear but can be, reduced to linear form by making suitable substitutions. Let us see an example:, 2 3, + = 13, Example-12. Solve the following pair of equations., x y, 5 4, - = -2, x y, Solution : Observe the given pair of equations. They are not linear equations. (Why?), , Free Distribution by T.S. Government 2021-22
Page 108 :
Class-X Mathematics, , 98, , (1), , æ1ö, æ1ö, 5 ç ÷ - 4 ç ÷ = -2, èxø, è yø, , (2), , A, , æ1ö, æ1ö, We have 2 ç ÷ + 3 ç ÷ = 13, èxø, è yø, , G, AN, , 1, 1, = p and, = q, we get the following pair of linear equations:, y, x, , If we substitute, , 2p + 3q = 13, , (3), , 5p - 4q = -2, , (4), , Coefficients of q are 3 and 4 and their LCM is 12. Using the elimination method:, 8p + 12q = 52, , Equation (4) × 3, , 15p - 12q = -6 'q' terms have opposite sign, so we add the two equations., 23p= 46, 46, =2, 23, , T,, TE, L, , p=, , AN, , Equation (3) × 4, , Substitute the value of p in equation (3), 2(2) +3q = 13, , 3q = 13 - 4 = 9, 9, =3, 3, , SC, ER, , q=, , But,, , 1, =p=2, x, , Þx=, , 1, 2, , 1, =q=3, y, , Þy=, , 1, 3, , Example-13. Kavitha thought of constructing 2 more rooms in her house. She enquired about, the labour and time estimates. She came to know that 6 women and 8 men could finish this work, in 14 days. But she wished to complete that work in only 10 days. When she enquired elsewhere,, she was told that 8 women and 12 men could finish the work in 10 days. Find out how much, time would be taken to finish the work if one man or one woman worked alone., Solution : Let the time taken by one woman to finish the work = x days., , Free Distribution by T.S. Government 2021-22
Page 109 :
Pair of Linear Equations in Two Variables, , 99, , 1, x, , The portion of work done by one woman in one day, , =, , Let the time taken by one man to finish the work, , = y days., , The portion of work done by one man in one day, , =, , A, , 1, y, , G, AN, , Now, 8 women and 12 men can finish the work in 10 days., So the portion of work done by 8 women and 12 men in one day, , =, , 1, 10, , 1, ., x, , =, , 8, x, , Also, the portion of work done by 8 women in one day is 8 ×, , 1, 12, =, y, y, , Total portion of work done by 8 women and 12 men in one day, , =, , T,, TE, L, , AN, , Similarly, the portion of work done by 12 men in one day is 12 ×, , SC, ER, , Equating equations (1) and (2), , 8 12, +, x y, , (1), , (2), , æ 8 12 ö 1, ç + ÷=, è x y ø 10, æ 8 12 ö, 10 ç + ÷ = 1, èx y ø, , 80 120, +, = 1 (3), x, y, , Also, 6 women and 8 men can finish the work in 14 days., The portion of work done by 6 women and 8 men in one day =, , Þ, , 6 8 1, + =, x y 14, æ6 8ö, 14 ç + ÷ = 1, èx yø, æ 84 112 ö, ç +, ÷ =1, y ø, è x, , Free Distribution by T.S. Government 2021-22, , (4)
Page 110 :
Class-X Mathematics, , 100, , Observe equations (3) and (4). Are they linear equations? How do we solve these equations?, We can convert them into linear equations by substituting, , 1, 1, = u and = v., y, x, , 80u + 120v = 1, , (5), , Equation (4) becomes, , 84u + 112v = 1, , (6), , L.C.M. of 80 and 84 is 1680. Using the elimination method,, (21 × 80)u + (21 × 120)v = 21, , Equation (4) × 20, , (20 × 84)u + (20 × 112)v = 20, , G, AN, , Equation (3) × 21, 1680u+2520v = 21, 1680u+2240v = 20, (-), (-) (-), , Same sign for u, so subtract, , AN, , 280v = 1, 1, 280, , 1, =1, 280, , T,, TE, L, , v=, , A, , Equation (3) becomes, , Substitute in equation (5), , 80u + 120 ×, 80u = 1 -, , 3, 7-3 4, =, =, 7, 7, 7, , 1, , 4, 1, 1, u=, ´, =, 7, 80, 140, 20, , SC, ER, , So one woman alone can finish the work in 140 days and one man alone can finish the, work in 280 days., Example-14. A man travels 370 km partly by train and partly by car. If he covers 250 km by, train and the rest by car, it takes him 4 hours. But if he travels 130 km by train and the rest by car,, it takes 18 minutes more. Find the speed of the train and that of the car., Solution : Let the speed of the train be x km per hour and that of the car be y km per hour. Also,, , we know that time =, , Distance, Speed, , In situation 1, time spent travelling by train =, , 250, hrs, x, , And time spent travelling by car, , 120, hrs, y, , =, , Free Distribution by T.S. Government 2021-22
Page 111 :
Pair of Linear Equations in Two Variables, So, total time taken = time spent in train + time spent in car =, , 101, , 250 120, +, x, y, , But, total time of journey is 4 hours, so, , ® (1), , G, AN, , 125 60, +, =2, x, y, , A, , 250 120, +, =4, x, y, , Again, when he travels 130 km by train and the rest by car, Time taken by him to travel 130 km by train =, , 130, hrs, x, , 130, 240, +, x, y, , T,, TE, L, , Total time taken =, , 240, hrs, y, , AN, , Time taken by him to travel 240 km (370 - 130) by car =, , But, it is given that the time of journey is 4 hrs 18 min i.e., 4, , 130, 240, 43, +, =, x, y, 10, , So,, , 18, 3, hrs = 4 hrs, 10, 60, 10, , (2), , 1, 1, = a and = b in equations (1) and (2), y, x, , SC, ER, , Substitute, , ®, , 3, , 125a + 60b = 2, , ®, , (3), , 130a+ 240b = 43/10, , ®, , (4), , For 60 and 240, LCM is 240. Using the elimination method,, Equation (3) × 4, , 500a+240b= 8, , Equation (4) × 1, , 130a+240b =, (-) (-), , 370a = 8 -, , 43, (Same sign, so subtract), 10, , (-), , 43 80 - 43 37, =, =, 10, 10, 10, , Free Distribution by T.S. Government 2021-22
Page 112 :
Class-X Mathematics, , 102, , a=, , 1, 1, 37, ´, =, 10, 370, 100, 10, , Substitute a =, , 1, in equation (3), 100, , 3, 1, 1, ´, =, 4, 80, 60, 20, , So a =, , 1, 1, and b =, 100, 80, , 1, 1, 1, 1, =, =, and, y, 80, x 100, , T,, TE, L, , So, , G, AN, , b=, , 5 8-5, 3, =, =, 4, 4, 4, , AN, , 60b = 2 -, , A, , æ 5, ö, 1, ç 125 ´, ÷ + 60b = 2, 100 ÷, çè, 4 ø, , x = 100 km/hr and y = 80 km/hr., , So, speed of the train was 100 km/hr and speed of the car was 80 km/hr., , SC, ER, , EXERCISE - 4.3, , Solve each of the following pairs of equations by reducing them to a pair of linear equations., , i), , 5, 1, +, =2, x -1, y-2, 6, 3, =1, x -1 y - 2, , iii), , 2, 3, +, x, y =2, 4, 9, x, y = -1, , ii), , x+ y, =2, xy, x- y, =6, xy, , iv), , 6x+3y = 6xy, 2x + 4y = 5xy, , Free Distribution by T.S. Government 2021-22
Page 113 :
Pair of Linear Equations in Two Variables, v), , 5, 2, = -1, x+ y x- y, , vi), , 15, 7, +, = 10, x+ y, x- y, 10, 2, +, =4, x+ y, x- y, , 5 4, = -2, x y, viii), , 1, 1, 3, +, =, 3x + y, 3x - y, 4, , 1, 1, -1, =, 2 ( 3 x + y ) 2(3x - y ), 8, , G, AN, , 15, 5, = -2, x+ y x- y, 2., , 2, 3, +, = 13, x, y, , A, , vii), , 103, , Formulate the following problems as a pair of equations and then find their solutions., A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours it can, go 40 km upstream and 55 km downstream. Determine the speed of the stream and, that of the boat in still water., , AN, , i., , ii. Rahim travels 600 km to his home partly by train and partly by car. He takes 8 hours, if he travels 120 km by train and rest by car. He takes 20 minutes more if he travels, 200 km by train and rest by car. Find the speed of the train and the car., , T,, TE, L, , iii. 2 women and 5 men can together finish an embroidery work in 4 days while 3 women, and 6 men can finish it in 3 days. Find the time to be taken by 1 woman alone and 1, man alone to finish the work., , O PTIONAL E XERCISE, [For extensive learning], , Solve the following equations:-, , SC, ER, , 1., , (i), , 2x, y, +, =2, a, b, , (ii), , x -1, y +1, +, =9, 3, 2, , x y, =4, a b, , (iii), , x, y, +, =5, 7, 3, , (iv), , x y, =6, 2 9, , (v), , ax by, =a+b, b, a, , x +1, y -1, +, =8, 2, 3, , 3x + 2 y = 3, 5x + 3 y = 3, , (vi), , ax - by = 2ab, , Free Distribution by T.S. Government 2021-22, , 2x + 3y = 17, 2x+2 - 3y+1 = 5
Page 114 :
Class-X Mathematics, , 104, , 2., , Animals in an experiment are to be kept on a strict diet. Each animal is to receive among, other things 20g of protein and 6g of fat. The laboratory technicians purchased two food, mixes, A and B. Mix A has 10% protein and 6% fat. Mix B has 20% protein and 2% fat., How many grams of each mix should be used?, , Suggested Projects, , A, , Construct some pairs of linear equations from daily life situations and find solutions of the, equations by using graphs., , WHAT WE H AVE D ISCUSSED, , 3., , The graph of a pair of linear equations in two variables is represented by two lines., i. If the lines intersect at a point then the point gives the unique solution of the two equations., In this case, the pair of equations is consistent and independent., ii. If the lines coincide, then there are infinitely many solutions - each point on the line, being a solution. In this case, the pair of equations is consistent and dependent., iii. If the lines are parallel then the pair of equations has no solution. In this case, the pair, of equations is inconsistent., We have discussed the following methods for finding the solution(s) of a pair of linear, equations., i. Model Method., ii. Graphical Method, iii. Algebraic methods - Substitution method and Elimination method., , SC, ER, , 4., , AN, , 2., , Two linear equations in the same two variables are called a pair, of linear equations in two variables., a1x + b1y + c1 = 0 (a12 + b12 ¹ 0), a2x + b2y + c2 = 0 (a22 + b22 ¹ 0), where a1, a2, b1, b2, c1, c2 are real numbers., A pair of linear equations in two variables can be solved by using various methods., , T,, TE, L, , 1., , G, AN, , l, , 5., , There exists a relation between the coefficients and nature of system of equations., a, , b, , 1, 1, If a ¹ b then the pair of linear equations is consistent., 2, 2, a, b, c, ii. If 1 = 1 ¹ 1 then the pair of linear equations is inconsistent., a2 b2, c2, , i., , iii. If, 6., , a1, b, c, = 1 = 1 then the pair of linear equations is dependent and consistent., a2, b2, c2, , There are several situations which can be mathematically represented by two equations, that are not linear to start with. But we can alter them so that they will be reduced to a pair, of linear equations., , Free Distribution by T.S. Government 2021-22
Page 115 :
I NT RO DU CT I O N, , G, AN, , 5.1, , A, , 5, , Quadratic Equations, , AN, , 16 m., , 16+2x m., , Sports committee of Dhannur High School wants to construct a Kho-Kho court of, dimensions 29 m × 16 m. This is to be, x, laid in a rectangular plot of area 558 m2., They want to leave space of equal width, all around the court for the spectators., x, What would be the width of the space, for spectators? Would it be enough?, Suppose, the width of the space is, x meter. So, according to the figure the, length of the plot would be (29 + 2x), meter., , T,, TE, L, , 29 m., , 29+2x m., , And, breadth of the rectangular plot would be, , = (16 + 2x) m., , Therefore, area of the rectangular plot, , = length × breadth, = (29 + 2x) (16 + 2x), , = 558 m2, , \ (29 + 2x) (16 + 2x), , = 558, , SC, ER, , Since the area of the plot is, 2, , = 558, , 2, , =0, , 2, , =0, , \ 4x + 90x + 464, 4x + 90x - 94, , 2x + 45x - 47, , 2x2 + 45 x - 47 = 0, , (dividing by 2), , ..... (1), , In the previous class we solved the linear equations of the form ax + b = c to find the value, of ‘x’. Similarly, the value of x from the above equation will give the possible width of the space, for spectators., Can you think of more such examples where we have to find the quantities, like in the, above example using equations., Let us consider another example:, Rani has a square metal sheet. She removed squares of side 9 cm from each corner of this, sheet. Of the remaining sheet, she turned up the sides to form an open box as shown. The, capacity of the box is 144 cm3. Can we find out the original dimensions of the metal sheet?
Page 116 :
Class-X Mathematics, , 106, , Suppose the side of the square piece of metal sheet, be ‘x’ cm., Then, the dimensions of the box are, , 9 cm., , 9 cm., , 9 cm., , 9 cm., , x cm., , 9 cm × (x–18) cm × (x–18) cm, 9 (x–18) (x–18) = 144, , x cm., , ..... (2), , Are they quadratic polynomials?, , AN, , Let us observe the L.H.S of equation (1) and (2), , 2, , 9 cm., , 8, , x2 – 36x + 308 = 0, , x - 18, , -1, , So, the side ‘x’ of the metal sheet has to satisfy the, equation., , x, , x2 – 36x + 308 = 0, , G, AN, , (x–18) 2 = 16, , A, , Since volume of the box is 144 cm3, , T,, TE, L, , We have studied quadratic polynomials of the form ax + bx + c,, a ¹ 0 in one of the previous chapters., Since, the LHS of the above equations are quadratic polynomials and the RHS is 0 they, are called quadratic equations., In this chapter we will study quadratic equations and methods to find their roots., , 5.2 Q UADRATI C E Q UAT I O N S, , SC, ER, , A quadratic equation in the variable x is an equation of the form ax2 + bx + c = 0, where a,, b, c are real numbers and a ¹ 0. For example, 2x2 + x - 300 = 0 is a quadratic equation,, Similarly, 2x2 - 3x + 1 = 0, 4x - 3x2 + 2 = 0 and 1 - x2 + 300 = 0 are also quadratic equations., , In fact, any equation of the form p(x) = 0, where p(x) is a polynomial of degree 2, is a, quadratic equation. When we write the terms of p(x) in descending order of their degrees, then, we get the standard form of the equation. That is, ax2 + bx + c = 0, a ¹ 0 is called the standard, form of a quadratic equation and y = ax2 + bx + c is called a quadratic function., , T RY T HIS, , Check whether the following equations are quadratic or not ?, (i) x2 - 6x - 4 = 0, , (ii) x3 - 6x2 + 2x - 1 = 0, , (iii) 7x = 2x 2, , (iv) x 2 +, , (v) (2x + 1) (3x + 1) = b(x - 1) (x - 2), , 1, = 2 (x ¹ 0), x2, (vi) 3y2 = 192, , Free Distribution by T.S. Government 2021-22
Page 117 :
Quadratic Equations, , 107, , There are various situations described by quadratic functions. Some of them are:When a rocket is fired upward, then the path of the rocket is defined by, a ‘quadratic function.’, , 2., , Shapes of the satellite dish, reflecting mirror in a telescope, lens of the, eye glasses and orbits of the celestial objects are defined by the quadratic, functions., , G, AN, , A, , 1., , Reflecting Mirror, Artificial, Satellite, , Earth, , T,, TE, L, , Earth, , Lens of Spectacles, , AN, , Satellite Dish, , Sun, , SC, ER, , 3. The path of a projectile is defined by a quadratic, function., , 4. When the brakes are applied to a vehicle, the stopping distance is calculated by using, a quadratic equation., , Example-1. Represent the following situations with suitable mathematical equations., i., , Sridhar and Rajendar together have 45 marbles. Both of them lost 5 marbles each,, and the product of the number of marbles they now have is 124. We would like to find, out how many marbles each of them had previously., , Solution :, , i. Let Sridhar has x marbles., Then, the number of marbles with Rajendar will be = 45 – x (Why?)., The number of marbles left with Sridhar, when he lost 5 marbles = x – 5, , Free Distribution by T.S. Government 2021-22
Page 118 :
Class-X Mathematics, , 108, , G, AN, , A, , The number of marbles left with Rajendar, when he lost 5 marbles = (45 – x) – 5, = 40 – x, Therefore, their product = (x – 5) (40 – x), = 40x – x2 – 200 + 5x, = – x2 + 45x – 200, So, – x2 + 45x – 200 = 124 (Given that product = 124), i.e., – x2 + 45x – 324 = 0, i.e., x2 – 45x + 324 = 0, (Multiply by -1), , Therefore, the number of marbles Sridhar had i.e. ‘x’, should satisfy the quadratic, equation, x2 – 45x + 324 = 0, , which is the required representation of the problem., , AN, , ii. The hypotenuse of a right triangle is 25 cm. We know that the difference in lengths of, the other two sides is 5 cm. We would like to find out the length of the two sides?, Solution:Let the length of the smaller side be x cm, , T,, TE, L, , Then length of the longer side = (x + 5) cm, Given length of the hypotenuse = 25 cm, We know that in a right angled triangle, = (25)2, , x2 + x2 + 10x + 25 = 625, 2, , SC, ER, , 2x + 10x - 600, x2 + 5x - 300, , =0, , x+5 cm., , So, x2 + (x + 5)2, , (hypotenuse)2 = (side)2 + (height)2, , =0, , 25, , cm, ., , x, , Value of x from the above equation will give the possible value of length of sides of the, given right angled triangle., Example-2. Check whether the following are quadratic equations:, i., , (x – 2)2 + 1 = 2x – 3, , iii. x (2x + 3) = x2 + 1, Solution :, , i., , ii. x(x + 1) + 8 = (x + 2) (x – 2), iv. (x + 2)3 = x3 – 4, , LHS = (x – 2)2 + 1 = x2 – 4x + 4 + 1 = x2 – 4x + 5, Therefore, (x – 2)2 + 1 = 2x – 3 can be written as, x2 – 4x + 5 = 2x – 3, , i.e., x2 – 6x + 8 = 0, , Free Distribution by T.S. Government 2021-22
Page 119 :
Quadratic Equations, , 109, , It is in the form of ax2 + bx + c = 0., Therefore, the given equation is a quadratic equation., ii. Here, and, , LHS = x(x + 1) + 8 = x2 + x + 8, RHS = (x + 2)(x – 2) = x2 – 4, , A, , Therefore, x2 + x + 8 = x2 – 4, , i.e., x + 12 = 0, , G, AN, , x2 + x + 8 - x2 + 4 = 0, It is not in the form of ax2 + bx + c = 0, (a ¹ 0), , Therefore, the given equation is not a quadratic equation., iii. Here, LHS = x (2x + 3) = 2x2 + 3x, , AN, , So, x (2x + 3) = x2 + 1 can be rewritten as, 2x2 + 3x = x2 + 1, , T,, TE, L, , Therefore, we get x2 + 3x – 1 = 0, , It is in the form of ax2 + bx + c = 0., , So, the given equation is a quadratic equation., iv. Here, LHS = (x + 2)3 = (x + 2)2 (x + 2), , = (x2 + 4x + 4) (x + 2), , SC, ER, , = x3 + 2x2 + 4x2 + 8x + 4x + 8, , = x3 + 6x2 + 12x + 8, , Therefore, (x + 2)3 = x3 – 4 can be rewritten as, x3 + 6x2 + 12x + 8 = x3 – 4, , i.e., 6x2 + 12x + 12 = 0, , or, x2 + 2x + 2 = 0, , It is in the form of ax2 + bx + c = 0., , So, the given equation is a quadratic equation., , Remark : In (ii) above, the given equation appears to be a quadratic equation, but it is not a, quadratic equation., In (iv) above, the given equation appears to be a cubic equation (an equation of degree, 3) and not a quadratic equation. But it turns out to be a quadratic equation. As you can see, often, we need to simplify the given equation before deciding whether it is quadratic or not., , Free Distribution by T.S. Government 2021-22
Page 120 :
Class-X Mathematics, , 110, , EXERCISE - 5.1, Check whether the following are quadratic equations :, , 2., , (x + 1)2 = 2(x – 3), , x2 – 2x = (–2) (3 – x), , iii. (x – 2)(x + 1) = (x – 1)(x + 3), , iv., , (x – 3)(2x +1) = x(x + 5), , v. (2x – 1)(x – 3) = (x + 5)(x – 1), , vi., , x2 + 3x + 1 = (x – 2)2, , vii. (x + 2)3 = 2x (x2 – 1), , viii., , x3 – 4x2 – x + 1 = (x – 2)3, , A, , ii., , i., , G, AN, , 1., , Represent the following situations in the form of quadratic equations :, i., , The area of a rectangular plot is 528 m2. The length of the plot is one metre more than, twice its breadth. We need to find the length and breadth of the plot., , AN, , ii. The product of two consecutive positive integers is 306. We need to find the integers., iii. Rohan’s mother is 26 years older than him. The product of their ages after 3 years will, be 360 years. We need to find Rohan’s present age., , T,, TE, L, , iv. A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h, less, then it would have taken 3 hours more to cover the same distance. We need to, find the speed of the train., , 5.3 S OLUTION, , OF A, , Q UADRATIC E QUATION, , BY, , F ACTORISATION, , SC, ER, , We have learned to represent some of the daily life situations in the form of quadratic, equation with an unknown variable ‘x’., Now, we need to find the value of x., , Consider the quadratic equation 2x2 – 3x + 1 = 0. If we replace x by 1. Then, we get, (2 × 12) – (3 × 1) + 1 = 0 = RHS of the equation. Since 1 satisfies the equation , we say that 1, is a root of the quadratic equation 2x2 – 3x + 1 = 0., \ x = 1 is a solution of the quadratic equation., , In general, a real number a is called a root of the quadratic equation ax2 + bx + c = 0,, if aa2 + b a + c = 0. We also say that x = a is a solution of the quadratic equation, or, a satisfies the quadratic equation., Let’s discuss the method of finding roots of a quadratic equation., , Free Distribution by T.S. Government 2021-22
Page 121 :
Quadratic Equations, , 111, , Example-3. Find the roots of the equation 2x2 – 5x + 3 = 0, by factorisation., Solution : Let us first split the middle term. We need to find p and q,, Such that b = p + q = –5 and ac = p × q = 6, For this we have to list out all possible pairs of factors of 6. They are (1, 6), (–1, –6);, , A, , (2, 3); (–2, –3). From the list, it is clear that the pair (–2, –3) will satisfy our condition, , G, AN, , p + q = –5 and p × q = 6., , The middle term ‘–5x’ can be written as ‘–2x – 3x’., , So, 2x2 – 5x + 3 = 2x2 – 2x – 3x + 3 = 2x (x – 1) –3(x – 1) = (2x – 3)(x – 1), Now, 2x2 – 5x + 3 = 0 can be rewritten as (2x – 3)(x – 1) = 0., , AN, , So, the values of x for 2x2 – 5x + 3 = 0 are the same for (2x – 3)(x – 1) = 0,, , T,, TE, L, , i.e., either 2x – 3 = 0 or x – 1 = 0., 3, Now, 2x – 3 = 0 gives x = or x – 1 = 0 gives x = 1., 2, 3, So, x = or x = 1 are the solutions of the equation., 2, 3, In other words, 1 or are the roots of the equation 2x2 – 5x + 3 = 0., 2, , DO THIS, , SC, ER, , Find the roots of the following equations using factorisation method., (i) x2 + 5x + 6 = 0, , (ii), , x2 - 5x + 6= 0, , (iii) x2 + 5x - 6 = 0, , (iv), , x2 - 5x – 6= 0, , TRY THIS, , Find the roots of the equation 2x2 – 5x + 3 = 0 and verify whether 1 and, , of the equation., , 3, are the roots, 2, , Note that we have found the roots of 2x2 – 5x + 3 = 0 by factorising 2x2 – 5x + 3, into two linear factors and equating each factor to zero., , Free Distribution by T.S. Government 2021-22
Page 122 :
Class-X Mathematics, , 112, , Example 4 : Find the roots of the equation x–, , 1, 1, = (x ¹ 0), 3x 6, , 1, 1, = Þ 6x2 – x – 2 = 0, 3x, 6, 6x2 – x – 2 = 6x2 + 3x – 4x – 2, = 3x (2x + 1) – 2 (2x + 1), = (3x – 2)(2x + 1), 2, The roots of 6x – x – 2 = 0 are the values of x for which (3x – 2)(2x + 1) = 0, Therefore, 3x – 2 = 0 or 2x + 1 = 0,, 2, 1, i.e., x =, or x = 3, 2, 2, 1, Therefore, the roots of 6x2 – x – 2 = 0 are, and - ., 3, 2, 2, 1, We verify the roots, by checking that and - satisfy 6x2 – x – 2 = 0., 3, 2, Example-5. Find the width of the space for spectators discussed in section 5.1., , AN, , G, AN, , A, , Solution : We have x-, , T,, TE, L, , Solution : In Section 5.1, we found that if the width of the space for spectators is x m, then x, satisfies the equation 2x2 + 45x – 47 = 0. Applying the factorisation method we write this, equation as:2x2 – 2x + 47x – 47 = 0, , 2x (x – 1) + 47 (x – 1) = 0, i.e., (x – 1) (2x + 47) = 0, , SC, ER, , So, the roots of the given equation are x = 1 or x =, , -47, . Since ‘x’ is the width of space, 2, , of the spectators it cannot be negative., Thus, the width is 1 m. So it is not enough for spectators., , E XERCISE - 5.2, , 1., , Find the roots of the following quadratic equations by factorisation:, i., , x2 – 3x – 10 = 0, , 2, iv. 2 x - x +, , 1, =0, 8, , vii. 3x2 – 5x + 2 = 0, , ii. 2x2 + x – 6 = 0, , iii., , v. 100x2 – 20x + 1 = 0, , vi. x(x + 4) = 12, , viii. x -, , 3, = 2 (x ¹ 0), x, , 2 x2 + 7 x + 5 2 = 0, , ix. 3(x – 4)2 – 5(x – 4) = 12, , Free Distribution by T.S. Government 2021-22
Page 123 :
Quadratic Equations, , 113, , Find two numbers whose sum is 27 and product is 182., , 3., , Find two consecutive positive integers, sum of whose squares is 613., , 4., , The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the, other two sides., , 5., , A cottage industry produces a certain number of pottery articles in a day. It was observed, on a particular day that the cost of production of each article (in rupees) was 3 more than, twice the number of articles produced on that day. If the total cost of production on that, day was D90, find the number of articles produced and the cost of each article., , 6., , Find the dimensions of a rectangle whose perimeter is 28 meters and whose area is 40, square meters., , 7., , The base of a triangle is 4cm longer than its altitude. If the area of the triangle is 48 sq.cm, then find its base and altitude., , 8., , Two trains leave a railway station at the same time. The first train travels towards west and, the second train towards north. The first train travels 5 km/hr faster than the second train., If after two hours they are 50 km. apart, find the average speed of each train., , 9., , In a class of 60 students, each boy contributed money equal to the number of girls and, each girl contributed money equal to the number of boys. If the total money then collected, was D1600. How many boys were there in the class?, , 10., , A motor boat heads upstream a distance of 24 km in a river whose current is running at 3, km per hour. The trip up and back takes 6 hours. Assuming that the motor boat maintained, a constant speed, what was its speed in still water?, , SC, ER, , T,, TE, L, , AN, , G, AN, , A, , 2., , 5.4 S OLUTION, , OF A, , Q UADRATIC E QUATION, , BY, , C OMPLETING, , THE, , S QUARE, , In the previous section, we have learnt method of factorisation for obtaining the roots of a, quadratic equation. Is method of factorisation applicable to all types of quadratic equation? Let, us try to solve x2 + 4x - 4 = 0 by factorisation method, To solve the given equation x2 + 4x - 4 = 0 by factorisation method., , We have to find ‘p’ and ‘q’ such that, , p + q = 4 and, p × q = -4, , We have no integers p, q satisfying above equation. So by factorisation method it is difficult, to solve the given equation., Therefore, we shall try another method., , Free Distribution by T.S. Government 2021-22
Page 124 :
Class-X Mathematics, , 114, , Consider the following situation, The product of Sunita’s age (in years) two years ago and her age four years hence is one, more than twice her present age. What is her present age?, To answer this, let her present age be x years. Her age two years ago was x – 2 and her, age after four years will be x + 4. So, the product of both the ages is (x – 2)(x + 4)., x2 + 2x – 8 = 2x + 1, , i.e.,, , x2 – 9 = 0, , i.e.,, , A, , (x – 2)(x + 4) = 2x + 1, , G, AN, , Therefore,, , So, Sunita’s present age satisfies the quadratic equation x2 – 9 = 0., , We can write this as x2 = 9. Taking square roots, we get x = 3 or x = – 3. Since the age is, a positive number, x = 3., , AN, , So, Sunita’s present age is 3 years. It is easy to solve this equation because it is x2=9, , T,, TE, L, , Now, consider another quadratic equation (x + 2)2 – 9 = 0. To solve it, we can write it as, (x + 2)2 = 9. Taking square roots, we get x + 2 = 3 or x + 2 = – 3., Therefore,, , x = 1 or x = –5, , So, the roots of the equation (x + 2)2 – 9 = 0 are 1 and – 5., In both the examples above, the term containing x is inside a square, and we found the, roots easily by taking the square roots. But, what happens if we are asked to solve the equation, x2 + 4x – 4 = 0, which cannot be solved by factorisation also., , SC, ER, , So, we now introduce the method of completing the square. The idea behind this, method is to adjust the left side of the quadratic equation so that it becomes a perfect, square of the first degree polynomial and the RHS without x term., The process is as follows:, x2 + 4x – 4 = 0, , Þ, , x2 + 4x = 4, , x2 + 2. x . 2 = 4, , Now, the LHS is in the form of a2 + 2ab. If we add b2 it becomes as a2 + 2ab + b2 which, is perfect square. So, by adding b2 = 22 = 4 to both sides we get,, x2 + 2.x.2 + 22 = 4 + 4, Þ, , (x + 2)2 = 8 Þ x + 2 = ± 8, , Þ, , x = –2 ± 2 2, , Free Distribution by T.S. Government 2021-22
Page 125 :
Quadratic Equations, , 115, , Now consider the equation 3x2 – 5x + 2 = 0. Note that the coefficient of x2 is not 1. So, we divide the entire equation by 3 so that the coefficient of x2 is 1, 5, 2, x2 - x + = 0, 3, 3, , Þ, , 5, -2, x2 - x =, 3, 3, , Þ, , x 2 - 2.x., , Þ, , 5 æ5ö, -2 æ 5 ö, x - 2.x. + ç ÷ =, +ç ÷, 6 è6ø, 3 è6ø, , 5 -2, =, 6, 3, 2, , 2, , 2, , æ, çç add, è, , 5ö, (12 ´ -2) + ( 25 ´ 1), æ, çè x - ÷ø =, 6, 36, , T,, TE, L, , 2, , 2, ö, æ5ö, ç ÷ both side ÷÷, è6ø, ø, , AN, , 2, , 5ö, -2 25, æ, +, çx- ÷ =, 6ø, 3 36, è, , G, AN, , A, , \, , 2, , 5ö, -24 + 25, æ, çè x - ÷ø =, 6, 36, 2, , 5ö, 1, æ, çx- ÷ =, 6ø, 36, è, 5, 1, = ±, 6, 6, , SC, ER, , x-, , So, x =, , 5 1, 5 1, +, or x = 6 6, 6 6, , Therefore, x = 1 or x =, i.e.,, , (take square root of both sides), , 4, 6, , x = 1 or x =, , 2, 3, , Therefore, the roots of the given equation are 1 and, , 2, ., 3, , From the above examples we can deduce the following algorithm for completing the square., Algorithm : Let the quadratic equation be ax2 + bx + c = 0 (a ¹ 0), Step-1 : Divide each side by ‘a’, , Free Distribution by T.S. Government 2021-22
Page 126 :
Class-X Mathematics, , 116, , Step-2 : Rearrange the equation so that constant term c/a is on the right hand side (RHS)., 2, , é 1 æ b öù, Step-3 : Add ê ç ÷ ú to both sides to make LHS, a perfect square., ë 2 è a øû, , Step-4 : Write the LHS as a square and simplify the RHS., , A, , Step-5 : Solve it., , G, AN, , Example-6. Find the roots of the equation 5x2 – 6x – 2 = 0 by the method of completing the, square., Solution : Given : 5x2 – 6x – 2 = 0, Now, we follow the Algorithm, , AN, , 6, 2, 2, Step-1 : x - x - = 0 (Dividing both sides by 5), 5, 5, , T,, TE, L, , 6, 2, 2, Step-2 : x - x =, 5, 5, , 2, , 6, 2 æ 3ö, æ3ö, Step-3 : x - x + ç ÷ = + ç ÷, 5, 5 è5ø, è5ø, 2, , 2, , æ, çç Adding, è, , 2, ö, æ3ö, ç ÷ to both sides ÷÷, è5ø, ø, , 2, , 3ö, 2 9, æ, Step-4 : ç x - ÷ = +, 5ø, 5 25, è, 2, , SC, ER, , 3 ö 19, æ, Step-5 : ç x - ÷ =, 5ø, 25, è, , x-, , 3, 19, =±, 5, 25, , x=, , 3, 19, 3, 19, +, or x = 5, 5, 5, 5, , \ x=, , 3 + 19, 3 - 19, or x =, 5, 5, , Free Distribution by T.S. Government 2021-22
Page 127 :
Quadratic Equations, , 117, , Example-7. Find the roots of 4x2 + 3x + 5 = 0 by the method of completing the square., , 3, 5, x+ = 0, 4, 4, , x2 +, , 3, -5, x=, 4, 4, 2, , 3, -5 æ 3 ö, æ 3ö, x + x+ç ÷ = +ç ÷, 4, 4 è8ø, è8ø, , 2, , G, AN, , x2 +, , A, , Solution : Given 4x2 + 3x + 5 = 0, , 2, , 2, , 2, , 3ö, -71, æ, <0, çx+ ÷ =, 8ø, 64, è, 2, , AN, , 3ö, -5 9, æ, +, çx+ ÷ =, 8ø, 4 64, è, , T,, TE, L, , 3ö, æ, But ç x + ÷ cannot be negative for any real value of x (Why?). So, there is no real value, 8ø, è, of x satisfying the given equation. Therefore, the given equation has no real roots., , DO THIS, , SC, ER, , Solve the equations by completing the square, (i) x2 - 10x + 9 = 0, , (ii), , x2 - 5x + 5= 0, , (iii) x2 + 7x - 6 = 0, , We have solved several examples with the use of the method of ‘completing the square.’, Now, let us apply this method in standard form of quadratic equation ax2+bx+c=0 (a¹0)., , Step 1 : Dividing the equation by ‘a’ we get, x2 +, , Step 2 : x 2 +, , b, c, x+ = 0, a, a, , b, c, x=a, a, , Free Distribution by T.S. Government 2021-22
Page 129 :
Quadratic Equations, x=, , -1 ± 1 + 4(2)(528), -1 ± 4225 -1 ± 65, =, =, 4, 4, 4, , i.e.,, , x=, , -66, 64, or x =, 4, 4, , i.e.,, , x = 16 or x = -, , A, , 33, 2, , 119, , G, AN, , Since x cannot be negative. So, the breadth of the plot is 16 metres and hence, the length, of the plot is (2x + 1) = 33m., , You should verify that these values satisfy the conditions of the problem., , AN, , T HINK & D ISCUSS, , T,, TE, L, , We have three methods to solve a quadratic equation. Among these three, which, method would you like to use? Why?, Example-9. Find two consecutive positive odd integers, sum of whose squares is 290., Solution : Let the first positive odd integer be x. Then, the second integer will be x + 2. According, to the question,, x2 + (x + 2)2 = 290, , x2 + x2 + 4x + 4 = 290, , i.e.,, , 2x2 + 4x – 286 = 0, , SC, ER, , i.e.,, , i.e.,, , x2 + 2x – 143 = 0, , which is a quadratic equation in x., , -b ± b 2 - 4ac, Using the quadratic formula x =, 2, we get, x =, , i.e.,, , -2 ± 4 + 572 -2 ± 576 -2 ± 24, =, =, 2, 2, 2, , x = 11 or x = – 13, , But x is given to be positive odd integer. Therefore, x ¹ – 13., Thus, the two consecutive odd integers are 11 and (x + 2) = 11 + 2 = 13., Check : 112 + 132 = 121 + 169 = 290., , Free Distribution by T.S. Government 2021-22
Page 130 :
120, , Class-X Mathematics, , Example-10. A rectangular park is to be designed whose breadth is 3 m less than its length. Its, area is to be 4 square metres more than the area of a park that has already been made in the, shape of an isosceles triangle with its base as the breadth of the rectangular park and of altitude, 12 m. Find its length and breadth., Solution : Let the breadth of the rectangular park be x m., , A, , So, its length = (x + 3) m., , Therefore, its area =, , 1, × x × 12 = 6 x m2., 2, , x2 + 3x = 6x + 4, i.e.,, , x2 – 3x – 4 = 0, , Using the quadratic formula, we get, 3 ± 25 3 ± 5, =, = = 4 or – 1, 2, 2, , T,, TE, L, , x=, , AN, , According to our requirements,, , 12, , x+3, , Now, base of the isosceles triangle = x m., , G, AN, , Therefore, the area of the rectangular park = x(x + 3) m2 = (x2 + 3x) m2., , But x ¹ – 1 (Why?). Therefore, x = 4., , x, , So, the breadth of the park = 4m and its length will be x + 3 = 4 + 3 = 7m., Verification : Area of rectangular park = l × b = 7m × 4m = 28 m2,, 1, 1, × b × h = × 4m × 12m = 24 m2, 2, 2, Difference between area of rectangular park and triangular park = (28–24) m2, , SC, ER, , Similarly, area of triangular park =, , = 4 m2, Example-11. Find the roots of the following quadratic equations, if they exist., (i) x2 + 4x + 5 = 0, Solution :, , (ii) 2x2 – 2 2 x + 1 = 0, , (i) x2 + 4x + 5 = 0. Here, a = 1, b = 4, c = 5. So, b2 – 4ac = 16 – 20 = – 4 < 0., , Since the square of a real number cannot be negative, therefore b2 - 4ac will not, have any real value., So, there are no real roots for the given equation., (ii) 2x2 – 2 2 x + 1 = 0. Here, a = 2, b = -2 2 , c = 1., , Free Distribution by T.S. Government 2021-22
Page 131 :
Quadratic Equations, , 121, , So, b2 – 4ac = 8 – 8 = 0, , 1, 2 2± 0, 2, ., =, ± 0 i.e., x =, 2, 4, 2, , A, , 1, 1, ,, ., 2, 2, , So, the roots are, , Example-12. Find the roots of the following equations:, (i) x +, , 1, = 3, x ¹ 0, x, , G, AN, , Therefore, x =, , (ii), , Solution :, , 1, 1, = 3, x ¹ 0, 2, x x-2, , x2 + 1 = 3x, Here,, , T,, TE, L, , x2 – 3x + 1 = 0, which is a quadratic equation., , i.e.,, , So,, , AN, , 1, (i) x + = 3 . Multiplying both sides of equation by x, we get, x, , a = 1, b = – 3, c = 1, , b2 – 4ac = 9 – 4 = 5 > 0, 3± 5, (why ?), 2, , x=, , So, the roots are, , 3+ 5, 3- 5, ., and, 2, 2, , SC, ER, , Therefore,, , (ii), , 1, 1, = 3, x ¹ 0, 2., x x-2, , As x ¹ 0, 2, multiplying the equation by x (x – 2), we get, (x – 2) – x = 3x (x – 2), = 3x2 – 6x, , So, the given equation reduces to 3x2 – 6x + 2 = 0, which is a quadratic equation., Here, a = 3, b = – 6, c = 2. So, b2 – 4ac = 36 – 24 = 12 > 0, Therefore,, , x=, , 6 ± 12, 6± 2 3, 3± 3, =, =, ., 6, 6, 3, , Free Distribution by T.S. Government 2021-22
Page 132 :
Class-X Mathematics, , 122, , So, the roots are, , 3+ 3, 3- 3, ., and, 3, 3, , Example-13. A motor boat whose speed is 18 km/h in still water. It takes 1 hour more to go, 24 km upstream than to return downstream to the same spot. Find the speed of the stream., , A, , Solution : Let the speed of the stream be x km/h., , The time taken to go upstream =, , G, AN, , Therefore, the speed of the boat upstream = (18 – x) km/h and the speed of the boat, downstream = (18 + x) km/h., , distance, 24, =, hours., speed, 18 - x, 24, hours., 18 + x, , AN, , Similarly, the time taken to go downstream =, According to the question,, , i.e.,, i.e.,, , T,, TE, L, , 24, 24, =1, 18 - x, 18 + x, , 24(18 + x) – 24(18 – x) = (18 – x) (18 + x), x2 + 48x – 324 = 0, , Using the quadratic formula, we get, , SC, ER, , -48 ± 482 + 1296, -48 ± 3600, x=, =, 2, 2, =, , -48 ± 60, = 6 or -54, 2, , Since x is the speed of the stream, it cannot be negative. So, we ignore the root x = – 54., Therefore, x = 6 gives the speed of the stream as 6 km/h., , E XERCISE - 5.3, , 1., , Find the roots of the following quadratic equations, if they exist., i., , 2x2 + x – 4 = 0, , iii. 5x2 - 7x - 6 = 0, , ii., , 4 x 2 + 4 3x + 3 = 0, , iv. x2 + 5 = -6x, , Free Distribution by T.S. Government 2021-22
Page 133 :
Quadratic Equations, , 123, , 2., , Find the roots of the quadratic equations given in Q.1 by applying the quadratic formula., , 3., , Find the roots of the following equations:, 1, (i) x - = 3, x ¹ 0, (ii), x, , 1, 1, 11, = , x ¹ -4, 7, x + 4 x - 7 30, , The sum of the reciprocals of Rehman’s ages, (in years) 3 years ago and 5 years from now, 1, is . Find his present age., 3, , 5., , In a class test, the sum of Moulika’s marks in Mathematics and English is 30. If she got 2, marks more in Mathematics and 3 marks less in English, the product of her marks would, have been 210. Find her marks in the two subjects., , 6., , The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer, side is 30 metres more than the shorter side, find the sides of the field., , 7., , The difference of squares of two numbers is 180. The square of the smaller number is 8, times the larger number. Find the two numbers., , 8., , A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would, have taken 1 hour less for the same journey. Find the speed of the train., , 9., , Two water taps together can fill a tank in 9, , 10., , An express train takes 1 hour less than a passenger train to travel 132 km between Mysore, and Bengaluru (without taking into consideration the time they stop at intermediate stations)., If the average speed of the express train is 11km/h more than that of the passenger train,, find the average speed of the two trains., , T,, TE, L, , AN, , G, AN, , A, , 4., , SC, ER, , 3, hours. The tap of larger diameter takes 10, 8, hours less than the smaller one to fill the tank separately. Find the time in which each tap, can separately fill the tank., , 11., , Sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24 m, find, the sides of the two squares., , 12., , An object is thrown upwards with an initial velocity of 16 ft/sec from a building with a, height of 96 feet. It is at a height of S = 96 + 16t – 16t2 from the ground after a flight of, ‘t’ seconds. Find the time taken by the object to touch the ground., , 13., , If a polygon of ‘n’ sides has, , 1, n (n-3) diagonals. How many sides are there in a polygon, 2, with 65 diagonals? Is there a polygon with 50 diagonals?, , Free Distribution by T.S. Government 2021-22
Page 134 :
Class-X Mathematics, , 124, , 5.5 N ATURE, , OF, , ROOTS, , In the previous section, we have seen that the roots of the equation ax2 + bx + c = 0 are, given by, -b ± b 2 - 4ac, 2a, , Now, let us try to study the nature of roots of a quadratic equation., , A, , x=, , G, AN, , Remember that zeroes are those points where value of polynomial becomes zero or we, can say that the curve of quadratic polynomial cuts the X-axis., Similarly, roots of a quadratic equation are those points where the curve cuts the X-axis., Case-1 : If b2 - 4ac > 0;, , AN, , -b + b 2 - 4ac -b - b 2 - 4ac, ,, We get two distinct real roots, 2a, 2a, , T,, TE, L, , In such case if we draw corresponding graph for the given quadratic equation we get the, following types of figures., , Figure shows that the corresponding curve of the quadratic equation cuts the X-axis at two, distinct points, Case-2 : If b2 - 4ac = 0, -b + 0, 2a, , SC, ER, , x=, , So, x =, , -b -b, ,, 2a 2a, , Figure shows that the curve of the quadratic equation touches X-axis at one point., , Case-3 : If b2 - 4ac < 0, , There are no real roots. Roots are imaginary., , Free Distribution by T.S. Government 2021-22
Page 135 :
Quadratic Equations, , 125, , In this case, the curve neither intersects nor touches the X-axis at all. So, there are no real, roots., Since, b2 – 4ac determines whether the quadratic equation ax2 + bx + c = 0 (a ¹ 0) has, real roots or not, b2 – 4ac is called the discriminant of the quadratic equation., So, a quadratic equation ax2 + bx + c = 0 (a ¹ 0) has, ii. two equal real roots, if b2 – 4ac = 0,, iii. no real roots, if b2 – 4ac < 0., Let us consider some examples., , A, , two distinct real roots, if b2 – 4ac > 0,, , G, AN, , i., , AN, , Example-14. Find the discriminant of the quadratic equation 2x2 – 4x + 3 = 0, and hence find, the nature of its roots., Solution : The given equation is in the form of ax2 + bx + c = 0, where a = 2, b = – 4 and, c = 3. Therefore, the discriminant, , T,, TE, L, , b2 – 4ac = (– 4)2 – (4 × 2 × 3) = 16 – 24 = – 8 < 0, So, the given equation has no real roots., , Example-15. A pole has to be erected at a point on the boundary of a circular park of diameter, 13 metres in such a way that the difference of its distances from two diametrically opposite fixed, gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from, the two gates should the pole be erected?, , SC, ER, , Solution : Let us first draw the diagram., , Let P be the required location of the pole. Let the distance of the, pole from the gate B be x m, i.e., BP = x m. Now the difference of the, distances of the pole from the two gates = AP – BP (or, BP – AP)= 7 m., Therefore, AP = (x + 7) m., Now, AB = 13m, and since AB is a diameter,, ÐBPA = 900, 2, , 2, , (Why?), 2, , Therefore,, , AP + PB = AB, , i.e.,, , (x + 7)2 + x2 = 132, , i.e.,, , x2 + 14x + 49 + x2 = 169, , i.e.,, , (By Pythagoras theorem), , 2x2 + 14x – 120 = 0, , Free Distribution by T.S. Government 2021-22, , B, 13, , A, , m, , x, P, , x +7
Page 136 :
Class-X Mathematics, , 126, , So, the distance ‘x’ of the pole from gate B satisfies the equation, x2 + 7x – 60 = 0, So, it would be possible to place the pole if this equation has real roots. To see if this is so or not,, let us consider its discriminant. The discriminant is, , A, , b2 – 4ac = 72 – 4 × 1 × (– 60) = 289 > 0., , G, AN, , So, the given quadratic equation has two real roots, and it is possible to erect the pole on, the boundary of the park., Solving the quadratic equation x2 + 7x – 60 = 0, by the quadratic formula, we get, x=, , -7 ± 289 -7 ± 17, =, 2, 2, , AN, , Therefore, x = 5 or – 12., , Since x is the distance between the pole and the gate B, it must be positive., Therefore, x = – 12 will have to be ignored. So, x = 5., , T,, TE, L, , Thus, the pole has to be erected on the boundary of the park at a distance of 5m from the, gate B and 12m from the gate A., , TRY THIS, , 1. Explain the benefits of evaluating the discriminant of a quadratic equation before attempting, to solve it. What does its value signify?, , SC, ER, , 2. Write three quadratic equations, one having two distinct real solutions, one having no, real solution and one having exactly one real solution., , Example-16. Find the discriminant of the equation 3 x 2 - 2 x +, , 1, = 0 and hence find the nature, 3, , of its roots. Find them, if they are real., Solution : Here a = 3, b = – 2 and c =, , 1, 3, , Therefore, discriminant b 2 - 4ac = (-2) 2 - 4 ´ 3 ´, , 1, = 4 - 4 = 0., 3, , Hence, the given quadratic equation has two equal real roots., The roots are, , -b -b, 2 2, 1 1, ,, , i.e., , , i.e., , ., 2a 2a, 6 6, 3 3, , Free Distribution by T.S. Government 2021-22
Page 137 :
Quadratic Equations, , 127, , EXERCISE - 5.4, 1., , Find the nature of the roots of the following quadratic equations. If real roots exist, find, them:, (i) 2x2 – 3x + 5 = 0, , (ii), , 3x2 - 4 3x + 4 = 0, , Find the values of k for each of the following quadratic equations, so that they have two, equal roots., , G, AN, , 2., , A, , (iii) 2x2 – 6x + 3 = 0, , (i) 2x2 + kx + 3 = 0, , (ii), , kx (x – 2) + 6 = 0 (k ¹ 0), , Is it possible to design a rectangular mango grove whose length is twice its breadth, and the, area is 800 m2? If so, find its length and breadth., , 4., , The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in, years was 48. Is the above situation possible? If so, determine their present ages., , 5., , Is it possible to design a rectangular park of perimeter 80 m and area 400 m2? If so, find, its length and breadth. Comment on your answer., , T,, TE, L, , AN, , 3., , O PTIONAL E XERCISE, , [For extensive Learning], , Some points are plotted on a plane such that any three of them are non collinear. Each, point is joined with all remaining points by line segments. Find the number of points if the, number of line segments are 10., , 2., , A two digit number is such that the product of its digits is 8. When 18 is added to the, number the digits interchange their places. Determine the number., , 3., , A piece of wire 8 m. in length is cut into two pieces, and each piece is bent into a square., Where should the cut in the wire be made if the sum of the areas of these squares is to be, 2 m2?, , SC, ER, , 1., , 2, 2, 2, 2, é, ù, æ xö æ y ö, æ xö æ 8 - xö, =, 2, ê Hint : x + y = 8, ç ÷ + ç ÷ = 2 Þ ç ÷ + ç, ú., è 4ø è 4 ø, è 4 ø è 4 ÷ø, úû, ëê, , 4., , Vinay and Praveen working together can paint the exterior of a house in 6 days. Vinay by, himself can complete the job in 5 days less than Praveen. How long will it take Vinay to, complete the job?, , 5., , Show that the sum of roots of a quadratic equation ax2 + bx + c = 0 (a ¹ 0) is, , Free Distribution by T.S. Government 2021-22, , -b, ., a
Page 138 :
128, , Class-X Mathematics, , 6., , Show that the product of the roots of a quadratic equation ax2 + bx + c = 0 (a ¹ 0) is, , 7., , If the sum of the fraction and its reciprocal is 2, , c, ., a, , 16, , find the fraction., 21, , l, , G, AN, , Solving quadratic equations by geometrical methods., , A, , Suggested Projects, Take two or three quadratic equations of the form ax2 + bx + c = 0, where a ¹ 0, for, different situations like a > 0, a < 0, b = 0 and solve them by graphical methods., , AN, , WHAT WE H AVE D ISCUSSED, , Standard form of quadratic equation in variable x is, ax2 + bx + c = 0, where a, b, c are real numbers and a ¹ 0., , 2., , A real number a is said to be a root of the quadratic equation, ax2 + bx + c = 0, if aa2 + ba + c = 0., , 3., , If we can factorise ax2 + bx + c, a ¹ 0, into a product of two linear factors, then the roots, of the quadratic equation ax2 + bx + c = 0 can be found by equating each factor to zero., , 4., , A quadratic equation can also be solved by the method of completing the square., , 5., , Quadratic formula: The roots of a quadratic equation ax2 + bx + c = 0 (a ¹ 0) are given, by, , SC, ER, , T,, TE, L, , 1., , -b ± b 2 - 4ac, , provided b2 – 4ac > 0., 2a, , 6., , A quadratic equation ax2 + bx + c = 0 (a ¹ 0) has, (i) two distinct real roots, if b2 – 4ac > 0,, , (ii) two equal roots (i.e., coincident roots), if b2 – 4ac = 0, and, , (iii) no real roots, if b2 – 4ac < 0., , Free Distribution by T.S. Government 2021-22
Page 139 :
6, , A, , Progressions, , G, AN, , 6.1 I NTRODUCTION, , You might have observed that in nature, many things follow a certain pattern such as the, petals of a sunflower, the cells of a honeycomb, the grains on a maize cob, the spirals on a, pineapple and on a pine cone etc., , T,, TE, L, , AN, , Can you see a pattern in each of the above given example? We can see the natural, patterns have a repetition which is not progressive. The identical petals of the sunflower are, equidistantly grown. In a honeycomb identical hexagonal shaped cells are arranged symmetrically, around each hexagonal cell. Similarly, you can find out other natural patterns in spirals of, pineapple...., You can look for some other patterns in nature. Some examples are:, (i), , List of the last digits (digits in unit place) taken from the values of 4, 42, 43, 44, 45, 46 ..... is, 4, 6, 4, 6, 4, 6, ......, , Mary is doing problems on patterns as a part of preparing for a bank exam. One of them, is “find the next two terms in the following pattern”., , SC, ER, , (ii), , 1, 2, 4, 8, 10, 20, 22 ......., , (iii), , Usha applied for a job and got selected. She has been offered a job with a starting, monthly salary of D 8000, with an annual increment of D500. Her salary (in rupees) for, 1st, 2nd, 3rd ... years will be 8000, 8500, 9000 ..... respectively., , (iv), , The lengths of the rungs of a ladder decrease uniformly by 2 cm from bottom to top. The, bottom rung is 45 cm in length. The lengths (in cm) of the 1 st, 2nd, 3rd, .... 8th rung from, the bottom to the top are 45, 43, 41, 39, 37, 35, 33, 31 respectively., Can you see any relationship between the terms in the pattern of numbers written above?, , Pattern given in example (i) has a repetitive pattern where 4 and 6 are repeating, alternatively.
Page 140 :
Class-X Mathematics, , 130, , Now try to find out the pattern in example (ii). In examples (iii) and (iv), the relationship, between the numbers in each list is constantly progressive. In the given list 8000, 8500, 9000, ...., each succeeding term is obtained by adding 500 to the preceding term., , (b), , G, AN, , A, , Where as in 45, 43, 41, ..... each succeeding term is obtained by adding ‘-2’ to each, preceding term. Now we can see some more examples of progressive patterns., 5, (a), In a savings scheme, the amount becomes times of itself after 3 years., 4, The maturity amount (in Rupees) of an investment of D8000 after 3, 6, 9 and 12 years, will be 10000, 12500, 15625, 19531.25 respectively., The number of unit squares in squares with sides 1, 2, 3, .... units are respectively,, , T,, TE, L, , AN, , 12, 22, 32, ...., , Hema put ` 1000 into her daughter’s money box when she was one year old and increased, the amount by ` 500 every year. The amount of money (in `) in the box on her 1st, 2nd,, 3rd, 4th ........ birthday would be 1000, 1500, 2000, 2500, ..... respectively., , (d), , The fraction of first, second, third ..... shaded regions of the squares in the following, figure will be respectively., , SC, ER, , (c), , 1 1 1, 1, , ,, ,, , ...., 4 16 64 256, , Free Distribution by T.S. Government 2021-22
Page 141 :
Progressions, (e), , 131, , A pair of rabbits are too young to produce in their first month. In the second, and every, subsequent month, they produce a new pair. Each new pair of rabbits produce a new, pair in their second month and in every subsequent month (see the figure below). Assuming, no rabbit dies, the number of pairs of rabbits at the start of the 1st, 2nd, 3rd, ....., 6th, month, respectively are :, , A, , 1, 1, 2, 3, 5, 8, , G, AN, , 1, 1, , AN, , 2, , 5, 8, , T,, TE, L, , 3, , In the examples above, we observe some patterns. In some of them, we find that the, succeeding terms are obtained by adding a fixed number and in others by multiplying with a, fixed number. In another, we find that they are squares of consecutive numbers and so on., , SC, ER, , In this chapter, we shall discuss some of these patterns in which succeeding terms are, obtained by adding a fixed number to the preceding term or multiplying the preceding term by a, fixed number. These patterns are called as arithmetic and geometric progressions respectively., We shall also see how to find their nth term and the sum of n consecutive terms for a general value, , of ‘n’ and use this knowledge in solving some daily life problems., History : Evidence is found that by 400 BCE, Babylonians knew of Arithmetic and geometric, progressions. According to Boethins (570 CE), these progressions were known to early, Greek writers. Among the Indian mathematicians, Aryabhatta (470 CE) was the first to give, formula for the sum of squares and cubes of natural numbers in his famous work Aryabhatiyam, written around 499 CE. He also gave the formula for finding the sum of n terms of an Arithmetic, Progression starting with pth term. Indian mathematician Brahmagupta (598 CE), Mahavira, (850 CE) and Bhaskara (1114-1185 CE) also considered the sums of squares and cubes., , Free Distribution by T.S. Government 2021-22
Page 142 :
Class-X Mathematics, , 132, , 6.2 A RITHMETIC P ROGRESSIONS, Consider the following lists of numbers :, (i) 1, 2, 3, 4, . . ., (iii) – 3, –2, –1, 0, . . ., , (ii), , 100, 70, 40, 10, . . ., , (iv), , 3, 3, 3, 3, . . ., , G, AN, , Each of the numbers in the pattern is called a term., , A, , (v) –1.0, –1.5, –2.0, –2.5, . . ., , Can you write the next term in each of the patterns above? If so, how will you get it?, Perhaps by following a pattern or rule, let us observe and write the rule., In (i), each term is 1 more than the term preceding it., In (ii), each term is 30 less than the term preceding it., , AN, , In (iii), each term is obtained by adding 1 to the term preceding it., , In (iv), all the terms in the list are 3 , i.e., each term is obtained by adding (or subtracting) 0 to the, term preceding it., , T,, TE, L, , In (v), each term is obtained by adding – 0.5 to (i.e., subtracting 0.5 from) the term preceding it., In all the lists above, we can observe that successive terms are obtained by adding or, subtracting a fixed number to the preceding terms. Such list of numbers is said to form an Arithmetic, Progression ( A.P. )., , TRY THIS, , Which of these are Arithmetic Progressions and why?, , SC, ER, , (i), , (a) 2, 3, 5, 7, 8, 10, 15, ......, , (b), , 2, 5, 7, 10, 12, 15, ......, , (c) -1, -3, -5, -7, ......, , (ii) Write 3 more Arithmetic Progressions., , 6.2.1 WHAT, , IS AN, , A RITHMETIC PROGRESSION ?, , We observe that an Arithmetic progression is a list of numbers in which each, term, except the first term is obtained by adding a fixed number to the preceding term., This fixed number is called the common difference of the A.P.., , Let us denote the first term of an A.P. by a1, second term by a2, . . ., nth term by an and the, common difference by d. Then the A.P. becomes a1, a2, a3, . . ., an., So, a2 – a1 = a3 – a2 = . . . = an – an – 1 = d., , Free Distribution by T.S. Government 2021-22
Page 143 :
Progressions, , 133, , Let us see some more examples of A.P. :, Heights ( in cm ) of some students of a school standing in a queue in the morning assembly, are 147 , 148, 149, . . ., 157., , (b), , Minimum temperatures ( in degree celsius ) recorded for a week, in the month of January, in a city, arranged in ascending order are, – 3.1, – 3.0, – 2.9, – 2.8, – 2.7, – 2.6, – 2.5, , (c), , The balance money ( in D) after paying 5% of the total loan of D1000 every month is, 950, 900, 850, 800, . . ., 50., , (d), , Cash prizes ( in D ) given by a school to the toppers of Classes I to XII are 200, 250,, 300, 350, . . ., 750 respectively., , (e), , Total savings (in D) after every month, for 10 months when ` 50 are saved each month, are 50, 100, 150, 200, 250, 300, 350, 400, 450, 500., , T HINK, , D ISCUSS, , 4., , Think how each of the list given above form an A.P.. Discuss with your friends., Find the common difference in each pattern above? Think when is it positive?, Write an arithmetic progression in which the common difference is a small positive, quantity., Make an A.P. in which the common difference is big(large) positive quantity., , 5., , Make an A.P. in which the common difference is negative., , T,, TE, L, , 1., 2., 3., , AND, , AN, , G, AN, , A, , (a), , General form of an A.P. : An A.P. can be written as, , SC, ER, , a, a + d, a + 2d, a + 3d, . . ., , This is called general form of an A.P where ‘a’ is the first term and ‘d’ is the common, difference, For example in 1, 2, 3, 4, 5, ...., The first term is 1 and the common difference is also 1., In 2, 4, 6, 8, 10 ....., what is the first term and what is the common difference?, , A CTIVITY, (i), , Make the following figures with match sticks, , Free Distribution by T.S. Government 2021-22
Page 144 :
Class-X Mathematics, , 134, , (ii) Write down the number of match sticks required for each figure., (iii) Can you find a common difference in members of the list?, (iv) Does the list of these numbers form an A.P.?, 6.2.2 P ARAMETERS, , OF, , A RITHMETIC P ROGRESSIONS, , THIS, , AN, , DO, , G, AN, , A, , Note that in examples (a) to (e) above, in section 6.2.1 there are only a finite number of, terms. Such an A.P. is called a finite A.P.. Also note that each of these Arithmetic Progressions, (A.P.s) has a last term. The A.P.s in examples (i) to (v) in the section 6.2, are not finite A.P.s and, so they are called infinite Arithmetic Progressions. Such A.P.s are never ending and do not, have a last term., , Write three examples for finite A.P. and three for infinite A.P.., , T,, TE, L, , Now, to know about an A.P., what is the minimum information that you need? Is it enough, to know the first term? Or, is it enough to know only the common difference?, We can see that we need to know both – the first term a and the common difference d., These two parameters are sufficient for us to complete the Arithmetic Progression., For instance, if the first term a is 6 and the common difference d is 3, then the A.P. is, 6, 9,12, 15, . . ., , and if a is 6 and d is – 3, then the A.P. is, , SC, ER, , 6, 3, 0, –3, . . ., , Similarly, when, , a = – 7, d = – 2,, , the A.P. is – 7, – 9, – 11, – 13, . . ., , a = 1.0, d = 0.1,, , the A.P. is 1.0, 1.1, 1.2, 1.3, . . ., , a = 0,, , a = 2,, , 1, ,, 2, d = 0,, , d=1, , 1, 1, , 3, 4 , 6, . . ., 2, 2, the A.P. is 2, 2, 2, 2, . . ., , the A.P. is 0, 1, , So, if you know what a and d are, you can list the A.P.., Let us try the other way. If you are given a list of numbers, how can you say whether it is, an A.P. or not?, For example, for any list of numbers :, 6, 9, 12, 15, . . . ,, , Free Distribution by T.S. Government 2021-22
Page 145 :
Progressions, , 135, , We check the difference of the succeeding terms. In the given list we have a2 – a1 = 9 – 6 = 3,, a3 – a2 = 12 – 9 = 3,, a4 – a3 = 15 – 12 = 3, We see that a2 - a1 = a3 - a2 = a4 - a3 ... = 3, , G, AN, , For the list of numbers : 6, 3, 0, – 3, . . .,, , A, , Here, the difference of any two consecutive terms in each case is 3. So, the given list is an, A.P. whose first term a is 6 and common difference d is 3., a2 – a1 = 3 – 6 = – 3,, , a3 – a2 = 0 – 3 = – 3, a4 – a3 = –3 – 0 = –3, , a2 - a1 = a3 - a2 = a4 - a3 = -3, , AN, , Similarly, this is also an A.P. whose first term is 6 and the common difference is –3., So, we see that if the difference between any two consecutive terms is constant, then it is, an Arithmetic Progression., , T,, TE, L, , In general, for an A.P. a1, a2, . . ., an, we can say, d = ak + 1 – ak where k Î N; k > 1, , where ak + 1 and ak are the (k + 1)th and the kth terms respectively., Consider the list of numbers 1, 1, 2, 3, 5, . . . . By looking at it, you can tell that the, difference between any two consecutive terms is not the same. So, this is not an A.P.., , SC, ER, , Note : To find d in the A.P. : 6, 3, 0, – 3, . . ., we have subtracted 6 from 3 and not 3 from 6., We have to subtract the kth term from the (k + 1) th term even if the (k + 1)th term is smaller and, to find ‘d’ in a given A.P., we do not need to find all of a2 - a1, a1 - a2 .... . It is enough to find, only one of them, , D O T HIS, , 1., , Take any Arithmetic Progression., , 2., , Add a fixed number to each and every term of A.P.. Write the resulting numbers as a list., , 3., , Similarly subtract a fixed number from each and every term of A.P.. Write the resulting, numbers as a list., , 4., , Multiply or divide each term of A.P. by a fixed number and write the resulting numbers, as a list., , 5., , Check whether the resulting lists are A.P. in each case., , 6., , What is your conclusion?, , Free Distribution by T.S. Government 2021-22
Page 146 :
Class-X Mathematics, , 136, , Let us consider some examples, 1 -1 -3 -5, ,, ,, ,, ........, write the first term a and the common, 4 4 4 4, difference d. Find the 7th term, , Example-1. For the A.P. :, , A, , 1, -1 1 -1, - =, ; d=, 4, 4 4 2, , G, AN, , Solution : Here, a =, , Remember that we can find d using any two consecutive terms, once we know that the, numbers are in A.P.., The seventh term would be, , -5 1 1 1 -11, - - - =, 4 2 2 2, 4, , AN, , Example-2. Which of the following forms an A.P.? If they form an A.P., then write the next, two terms?, , (iv), , 4, 10, 16, 22, . . . (ii) 1, – 1, – 3, – 5, . . . (iii) – 2, 2, – 2, 2, – 2, . . ., , T,, TE, L, , (i), , 1, 1, 1, 2, 2, 2, 3, 3, 3, . . ., , (v) x, 2x, 3x, 4x ......, , Solution : (i) We have a2 – a1 = 10 – 4 = 6, a3 – a2 = 16 – 10 = 6, , a4 – a3 = 22 – 16 = 6, , ak + 1 – ak is same every time., , SC, ER, , i.e.,, , So, the given list of numbers forms an A.P. with the common difference d = 6., The next two terms are: 22 + 6 = 28 and 28 + 6 = 34., , (ii) a2 – a1 = – 1 – 1 = – 2, a3 – a2 = – 3 – ( –1 ) = – 3 + 1 = – 2, , a4 – a3 = – 5 – ( –3 ) = – 5 + 3 = – 2, , i.e., ak + 1 – ak is same every time., So, the given list of numbers forms an A.P. with the common difference d = – 2., The next two terms are:, – 5 + (– 2 ) = – 7 and – 7 + (– 2 ) = – 9, , Free Distribution by T.S. Government 2021-22
Page 147 :
Progressions, , 137, , (iii) a2 – a1 = 2 – (– 2) = 2 + 2 = 4, a3 – a2 = – 2 – 2 = – 4, As a2 – a1 ¹ a3 – a2, the given list of numbers does not form an A.P.., (iv) a2 – a1 = 1 – 1 = 0, a3 – a2 = 1 – 1 = 0, Here, a2 – a1 = a3 – a2 ¹ a4 – a3., So, the given list of numbers does not form an A.P.., (v) We have, , a2 – a1 = 2x – x = x, a3 – a2 = 3x – 2x = x, , i.e., ak+1 – ak is same every time., \ So, the given list form an A.P.., , AN, , a4 – a3 = 4x – 3x = x, , G, AN, , A, , a4 – a3 = 2 – 1 = 1, , T,, TE, L, , The next two terms are 4x + x = 5x and 5x + x = 6x., , E XERCISE - 6.1, 1., , In which of the following situations, the list of numbers involved forms an arithmetic, progression? why?, The minimum taxi fare is ` 20 for the first km and there after ` 8 for each, additional km., , SC, ER, , (i), , (ii), , The amount of air present in a cylinder when a vacuum pump removes, , air remaining in the cylinder at a time., , (iii), , The cost of digging a well, after every metre of digging, when it costs ` 150 for, the first metre and rises by ` 50 for each subsequent metre., , The amount of money in the account at the end of each year, when `10000 is, deposited at compound interest at 8 % per annum., Write first four terms of the A.P., when the first term a and the common difference d are, given as follows:, (iv), , 2., , 1, of the, 4, , (i), , a = 10, d = 10, , (ii) a = –2, d = 0, , (iii), , a = 4, d = – 3, , (iv) a = – 1, d =, , (v), , a = – 1.25, d = – 0.25, , Free Distribution by T.S. Government 2021-22, , 1, 2
Page 148 :
Class-X Mathematics, , 138, , For the following A.P.s, write the first term and the common difference:, (i), (iii), , (ii) – 5, – 1, 3, 7, . . ., , 1 5 9 13, , , , ,...., 3 3 3 3, , (iv) 0.6, 1.7, 2.8, 3.9, . . ., , A, , Which of the following are A.P.s ? If they form an A.P., find the common difference d and, write the next three terms., 5 7, (ii) 2, ,3, ,...., 2 2, , (iii), , – 1.2, – 3.2, – 5.2, – 7.2, . . ., , (iv) – 10, – 6, – 2, 2, . . ., , (v), , 3, 3 + 2,3 + 2 2,3 + 3 2,...., , (vi) 0.2, 0.22, 0.222, 0.2222, . . ., , (vii), , 0, – 4, – 8, –12, . . ., , (ix), , 1, 3, 9, 27, . . ., , (xi), , a, a2, a3, a4, . . ., , (xiii), , G, AN, , 2, 4, 8, 16, . . ., , (i), , 1 1 1 1, (viii) - , - , - , - ,...., 2 2 2 2, , AN, , 4., , 3, 1, – 1, – 3, . . ., , (x) a, 2a, 3a, 4a, . . ., , (xii), , 2, 8, 18, 32,....., , T,, TE, L, , 3., , 3, 6, 9, 12,....., , 6.3 nth T ERM, , OF AN, , A RITHMETIC PROGRESSION, , Usha who applied for a job and got selected. Let us consider the offer made to her. She, has been offered a starting monthly salary of ` 8000, with an annual increment of ` 500. What, would be her monthly salary in the fifth year?, , SC, ER, , To answer this, let us first see what her monthly salary for the second year would be., It would be ` (8000 + 500) = ` 8500., , In the same way, we can find the monthly salary for the 3rd, 4th and 5th year by adding, ` 500 to the salary of the previous year., So, the salary for the 3rd year = `(8500 + 500), = ` (8000 + 500 + 500), = ` (8000 + 2 × 500), = ` [8000 + (3 – 1) × 500], , (for the 3rd year), , = ` 9000, Salary for the 4th year, , = ` (9000 + 500), = ` (8000 + 500 + 500 + 500), , Free Distribution by T.S. Government 2021-22
Page 149 :
Progressions, , 139, , = ` (8000 + 3 × 500), = ` [8000 + (4 – 1) × 500], , (for the 4th year), , = ` 9500, Salary for the 5th year, , = ` (9500 + 500), , A, , = ` (8000+500+500+500 + 500), = ` (8000 + 4 × 500), = ` 10000, Observe that we are getting a list of numbers, , (for the 5th year), , G, AN, , = ` [8000 + (5 – 1) × 500], , 8000, 8500, 9000, 9500, 10000, . . ., , AN, , These numbers are in Arithmetic Progression., , T,, TE, L, , Looking at the pattern above, can we find her monthly salary in the 6th year? The 15th year?, And, assuming that she is still working at the same job, what would be her monthly salary in the, 25th year? Here, we can calculate the salary of the present year by adding ` 500 to the salary of, previous year. Can we make this process shorter? Let us see. You may have already got some, idea from the way we have obtained the salaries above., Salary for the 15th year, , = Salary for the 14th year + ` 500, , SC, ER, , é, ù, + 500 +24444, 500 + ... + 500, = ` ê8000 + 500, 14444, 3 ú + `500, êë, úû, 13 times, , i.e.,, , = ` [8000 + 14 × 500], , = ` [8000 + (15 – 1) × 500] = ` 15000, First salary + (15 – 1) × Annual increment., , In the same way, her monthly salary for the 25th year would be, ` [8000 + (25 – 1) × 500] = ` 20000, = First salary + (25 – 1) × Annual increment, , This example has given us an idea about how to write the 15th term, or the 25th term. By using, the same idea, now let us find the nth term of an A.P.., Let a1, a2, a3, . . . be an A.P. whose first term a1 is a and the common difference is d., Then,, the second term a2 = a + d = a + (2 – 1) d, , Free Distribution by T.S. Government 2021-22
Page 150 :
Class-X Mathematics, , 140, , the third term a3 = a2 + d = (a + d) + d = a + 2d = a + (3 – 1) d, the fourth term a4 = a3 + d = (a + 2d) + d = a + 3d = a + (4 – 1) d, ........, ........, Looking at the pattern, we can say that the nth term an = a + (n – 1) d., , G, AN, , an is also called the general term of the A.P.., , A, , So, the nth term of an A.P. with first term a and common difference d is given by, an = a + (n – 1) d., If there are m terms in the A.P., then am represents the last term which is sometimes, also denoted by l., Finding terms of an A.P. : Using the above formula we can find different terms of an, arithemetic progression., , AN, , Let us consider some examples., , Example-3. Find the 10th term of the A.P. : 5, 1, –3, –7 . . ., , T,, TE, L, , Solution : Here, a = 5, d = 1 – 5 = – 4 and n = 10., We have an = a + (n – 1) d, , So, a10 = 5 + (10 – 1) (–4) = 5 – 36 = –31, , Therefore, the 10th term of the given A.P. is – 31., , Example-4. Which term of the A.P. : 21, 18, 15, . . . is – 81?, Is 0 a term of this A.P.? Give reason for your answer., , SC, ER, , Solution : Here, a = 21, d = 18 – 21 = – 3 and if an = – 81, we have to find n., , As, , an = a + ( n – 1) d,, , we have, , – 81 = 21 + (n – 1)(– 3), , So,, , – 81 = 24 – 3n, – 105 = – 3n, , n = 35, , Therefore, the 35th term of the given A.P. is – 81., , Next, we want to know if there is any n for which an = 0. If such n is there, then, 21 + (n – 1) (–3) = 0,, i.e.,, i.e.,, , 3(n – 1) = 21, n=8, , So, the eighth term is 0., , Free Distribution by T.S. Government 2021-22
Page 151 :
Progressions, , 141, , Example-5. Determine the A.P. whose 3rd term is 5 and the 7th term is 9., Solution : We have, , and, , a3 = a + (3 – 1) d = a + 2d = 5, , (1), , a7 = a + (7 – 1) d = a + 6d = 9, , (2), , A, , Solving the pair of linear equations (1) and (2), we get, , Hence, the required A.P. is 3, 4, 5, 6, 7, . . ., , G, AN, , a = 3, d = 1, , Example-6. Check whether 301 is a term of the list of numbers 5, 11, 17, 23, . . ., Solution : We have :, , AN, , a2 – a1 = 11 – 5 = 6, a3 – a2 = 17 – 11 = 6, a4 – a3 = 23 – 17 = 6, , As (ak + 1 – ak) is the same for k = 1, 2, 3, etc., the given list of numbers is an A.P.., Now, for this A.P. we have a = 5 and d = 6., , We know, , T,, TE, L, , We choose to begin with the assumption that 301 is nth term of this A.P.. We will see if an, ‘n’ exists for which an = 301., an = a + (n – 1) d, , So, for 301 to be a term we must have, 301 = 5 + (n – 1) × 6, 301 = 6n – 1, , SC, ER, , or, , So,, , n=, , 302 151, =, 6, 3, , But n should be a positive integer (Why?)., , So, 301 is not a term of the given list of numbers., , Example-7. How many two-digit numbers are divisible by 3?, Solution : The list of two-digit numbers divisible by 3 is :, 12, 15, 18, . . . , 99, Is this an A.P. ? Yes it is. Here, a = 12, d = 3, an = 99., , As, , an = a + (n – 1) d,, , Free Distribution by T.S. Government 2021-22
Page 152 :
Class-X Mathematics, , 142, , we have, , 99 = 12 + (n – 1) × 3, , i.e.,, , 87 = (n – 1) × 3, 87, = 29, 3, n = 29 + 1 = 30, , n–1=, , i.e.,, , (So, 99 is the 30th term), , So, there are 30 two-digit numbers divisible by 3., , A.P. : 10, 7, 4, . . ., – 62., Solution : Here, a = 10, d = 7 – 10 = – 3, l = – 62,, where, , l = a + (n – 1) d, , G, AN, , Example-8. Find the 11th term from the last of the A.P. series given below :, , A, , i.e.,, , – 62 = 10 + (n – 1)(–3), , i.e.,, , – 72 = (n – 1)(–3), , i.e.,, , n – 1 = 24, , or, , n = 25, , T,, TE, L, , So,, , AN, , To find the 11th term from the last term, we will find the total number of terms in the A.P., , So, there are 25 terms in the given A.P., , The 11th term from the last will be the 15th term of the A.P. (Note that it will not be the 14th, term. Why?), So,, , a15 = 10 + (15 – 1)(–3) = 10 – 42 = – 32, , SC, ER, , i.e., the 11th term from the end is – 32., , Note : The 11th term from the last is also equal to 11th term of the A.P. with first term – 62 and, the common difference 3., , Example-9. A sum of ` 1000 is invested at 8% simple interest per year. Calculate the interest, at the end of each year. Do these interests form an A.P.? If so, find the interest at the end of 30, years., Solution : We know that the formula to calculate simple interest is given by, , Simple Interest =, , P´R ´T, 100, , So, the interest at the end of the 1st year = `, The interest at the end of the 2nd year = `, , 1000 ´ 8 ´ 1, = ` 80, 100, , 1000 ´ 8 ´ 2, = ` 160, 100, , Free Distribution by T.S. Government 2021-22
Page 153 :
Progressions, The interest at the end of the 3rd year =, , 143, , 1000 ´ 8 ´ 3, = ` 240, 100, , Similarly, we can obtain the interest at the end of the 4th year, 5th year, and so on. So, the, interest (in Rupees) at the end of the 1st, 2nd, 3rd, . . . years, respectively are, , A, , 80, 160, 240, . . ., It is an A.P. and the difference between the consecutive terms in the list is 80,, d = 80. Also, a = 80., , G, AN, , i.e.,, , So, to find the interest at the end of 30 years, we shall find a30., Now,, , a30 = a + (30 – 1) d = 80 + 29 × 80 = 2400, , So, the interest at the end of 30 years will be ` 2400., , AN, , Example-10. In a flower bed, there are 23 rose plants in the first row, 21 in the second, 19 in, the third, and so on. There are 5 rose plants in the last row. How many rows are there in the, flower bed?, , T,, TE, L, , Solution : The number of rose plants in the 1st, 2nd, 3rd, . . ., rows are 23, 21, 19, . . ., 5, It forms an A.P. (Why?)., , Let the number of rows in the flower bed be n., Then a = 23, d = 21 – 23 = – 2, an = 5, As,, , an = a + (n – 1) d, , We have, 5 = 23 + (n – 1)(– 2), , i.e.,, , – 18 = (n – 1)(– 2), , i.e., n = 10, , SC, ER, , So, there are 10 rows in the flower bed., , E XERCISE - 6.2, , 1., , Fill in the blanks in the following table, given that a is the first term, d the common, difference and an the nth term of the A.P.:, , S. No., , a, , d, , n, , an, , (i), , 7, , 3, , 8, , ..., , (ii), , – 18, , ..., , 10, , 0, , (iii), , ..., , –3, , 18, , –5, , (iv), , – 18.9, , 2.5, , ..., , 3.6, , (v), , 3.5, , 0, , 105, , ..., , Free Distribution by T.S. Government 2021-22
Page 154 :
144, , 2., , Class-X Mathematics, , Find the, (i) 30th term of the A.P. 10, 7, 4 ......, (ii) 11th term of the A.P. : -3,, , (i) a1 = 2, a3 = 26 find a2, (iii) a1 = 5, a4 = 9, , 1, find a2, a3, 2, , A, , Find the respective terms for the following A.P.s., (ii), , a2 = 13, a4 = 3 find a1, a3, , (iv), , a1 = -4, a6 = 6 find a2, a3, a4, a5, , G, AN, , 3., , -1, , 2,....., 2, , (v) a2 = 38, a6 = -22 find a1, a3, a4, a5, 5., , Which term of the A.P. : 3, 8, 13, 18, . . . ,is 78?, , AN, , 4., , Find the number of terms in each of the following A.P.s :, 7, 13, 19, . . . , 205, , (ii), , 18, 15, , T,, TE, L, , (i), , 1, , 13, ..., -47, 2, , Check whether, –150 is a term of the A.P. : 11, 8, 5, 2 . . ., , 7., , Find the 31st term of an A.P. whose 11th term is 38 and the 16th term is 73., , 8., , If the 3rd and the 9th terms of an A.P. are 4 and – 8 respectively, which term of this A.P., is zero?, , 9., , The 17th term of an A.P. exceeds its 10th term by 7. Find the common difference., , 10., , Two A.P.s have the same common difference. The difference between their 100 th terms, is 100. What is the difference between their 1000th terms?, , SC, ER, , 6., , 11., , How many three-digit numbers are divisible by 7?, , 12., , How many multiples of 4 lie between 10 and 250?, , 13., , For what value of n, are the nth terms of two A.P.s: 63, 65, 67, . .. and 3, 10, 17, . . ., equal?, , 14., , Determine the A.P. whose third term is 16 and the 7th term exceeds the 5th term by 12., , 15., , Find the 20th term from the end of the A.P. : 3, 8, 13, . . ., 253., , 16., , The sum of the 4th and 8th terms of an A.P. is 24 and the sum of the 6th and 10th terms, is 44. Find the first three terms of the A.P.., , 17., , Subba Rao started his job in 1995 at a monthly salary of ` 5000 and received an, increment of ` 200 each year. In which year did his salary reach ` 7000?, , Free Distribution by T.S. Government 2021-22
Page 155 :
Progressions, 6.4 SUM, , OF, , F IRST n T ERMS, , IN, , 145, , A RITHMETIC P ROGRESSION, , AN, , G, AN, , Here, the amount of money (in Rupees) put in the money, box on her first, second, third, fourth . . . birthday were respectively, 1000, 1500, 2000, 2500, . . . till her 21st birthday. To find the, total amount in the money box on her 21st birthday, we will have, to write each of the 21 numbers in the list above and then add, them up. Don’t you think it would be a tedious and time consuming, process? Can we make the process shorter?, , A, , Let us consider the situation again given in Section 6.1 in which Hema put ` 1000 in the, money box when her daughter was one year old, ` 1500 on her second birthday, ` 2000 on her, third birthday and will continue in the same way. How much money will be collected in the money, box by the time her daughter is 21 years old?, , T,, TE, L, , This would be possible if we can find a method for getting, this sum. Let us see., 6.4.1 H OW ‘GAUSS ’, , FOUND THE SUM OF TERMS, , We consider the problem given to Gauss, to solve when he was just 10 years old. He was, asked to find the sum of the positive integers from 1 to 100. He replied that the sum is 5050. Can, you guess how could he do it?, Let S = 1 + 2 + 3 + . . . + 99 + 100, , SC, ER, , And then, reverse the numbers to write, , S = 100 + 99 + . . . + 3 + 2 + 1, , When he added these two, term by term he got,, , 2S = (100 + 1) + (99 + 2) + . . . + (3 + 98) + (2, + 99) + (1 + 100), = 101 + 101 + . . . + 101 + 101 (100 times), (check this out and discuss), So,, , S=, , 100 ´ 101, = 5050,, 2, , i.e., the sum = 5050., , Free Distribution by T.S. Government 2021-22, , Carl Fredrich Gauss, (1777-1855) was a great, German Mathematician
Page 156 :
Class-X Mathematics, , 146, , 6.4.2 S UM, , OF, , n, , TERMS OF AN, , A.P.., , We will now use the same technique that was used by Gauss to find the sum of the first n, terms of an A.P. : a, a + d, a + 2d, . . ., The nth term of this A.P. is a + (n – 1) d., , A, , Let Sn denote the sum of the first n terms of the A.P., \ Sn = a + (a + d ) + (a + 2d ) + ... + a + ( n - 1) d, Sn = [a + (n - 1) d ] + [ a + ( n - 2) d ] + ... + a, Adding term by term, , G, AN, , By writing Sn in two different orders, we get, , = n[2a + (n - 1)d ], , n times, , AN, , 2Sn = [2a + (n - 1)d ] + [2a + (n - 1)d ] + .... + [2a + (n - 1)d ], , T,, TE, L, , n, n, n, n, \ Sn = [2a + ( n - 1) d ] = [ a + {a + ( n - 1) d }] = [first term + nth term] = ( a + an ), 2, 2, 2, 2, , If the first and last terms of an A.P. are given and the common difference is not given then, Sn =, , n, n, ( a + an ) is very useful to find Sn or Sn = ( a + l ) where ‘l’ is the last term., 2, 2, , SC, ER, , Now, we return to the example (c) in the introduction 6.1. The amount of money (in, Rupees) in the money box of Hema’s daughter on 1 st, 2nd, 3rd, 4th birthday, . . ., were 1000,, 1500, 2000, 2500, . . ., respectively., This is an A.P.. We have to find the total money collected on her 21st birthday, i.e., the sum, of the first 21 terms of this A.P.., Here, a = 1000, d = 500 and n = 21. Using the formula :, n, Sn = [2a + ( n - 1) d ],, 2, 21, [2 ´ 1000 + (21 - 1) ´ 500], we have, S =, 2, 21, [2000 + 10000], 2, 21, [12000] = 126000, =, 2, So, the amount of money collected on her 21st birthday is ` 1,26,000., , =, , Free Distribution by T.S. Government 2021-22
Page 157 :
Progressions, , 147, , We use Sn in place of S to denote the sum of first n terms of the A.P. so that we know how many terms we, have added. We write S20 to denote the sum of the first 20 terms of an A.P.. The formula for the sum of the first n, terms involves four quantities Sn, a, d and n. If we know any three of them, we can find the fourth., , A, , Remark : The nth term of an A.P. is the difference of the sum of first n terms and the sum of first, (n – 1) terms of it, i.e., an = Sn – Sn – 1., , G, AN, , D O T HIS, Find the sum of indicated number of terms in each of the following A.P.s, (i) 16, 11, 6 .....; 23 terms, , -0.5, -1.0, -1.5, .....; 10 terms, , 1 3, , ....., 10 terms, 4 2, , Let us consider some examples., , AN, , (iii) -1,, , (ii), , Example-11. If the sum of the first 14 terms of an A.P. is 1050 and its first term is 10, find the 20th term., , T,, TE, L, , Solution : Here, Sn = 1050; n = 14, a = 10, n, Sn = [2a + ( n - 1) d ], 2, 14, 1050 = [2(10) +13d ] = 140 + 91d, 2, 910 = 91d, \ d = 10, , SC, ER, , \ a20 = 10 + (20 -1) 10 = 200, , Example-12. How many terms of the A.P. : 24, 21, 18, . . . must be taken so that their sum is 78?, Solution : Here, a = 24, d = 21 – 24 = –3, Sn = 78. Let the number of terms of A.P. be n, then, we need to find n., n, We know that, Sn = [2a + ( n - 1) d ], 2, n, n, 78 = [48 + ( n - 1)(-3)] = [51 - 3n], So,, 2, 2, 2, or, 3n – 51n + 156 = 0, or, n2 – 17n + 52 = 0, or, , (n – 4)(n – 13) = 0, , or, , n = 4 or 13, , Both values of n are admissible. So, the number of terms is either 4 or 13., , Free Distribution by T.S. Government 2021-22
Page 158 :
148, , Class-X Mathematics, , Remarks :, In this case, the sum of the first 4 terms = the sum of the first 13 terms = 78., , 2., , Two answers are possible because the sum of the terms from 5th to 13th will be zero., This is because a is positive and d is negative, so that some terms are positive and some, are negative, and will cancel out each other., , Example-13. Find the sum of :, the first 1000 natural numbers (ii) the first n natural numbers, , G, AN, , (i), , Solution :, (i), , Let S = 1 + 2 + 3 + . . . + 1000, , S1000 =, , n, (a + l ) for the sum of the first n terms of an A.P., we have, 2, , AN, , Using the formula Sn =, , A, , 1., , 1000, (1 + 1000) = 500 × 1001 = 500500, 2, , (ii), , T,, TE, L, , So, the sum of the first 1000 positive integers is 500500., Let Sn = 1 + 2 + 3 + . . . + n, , Here a = 1 and the last term l is n., Therefore, Sn =, , n(1 + n), n( n + 1), (or) Sn =, 2, 2, , SC, ER, , The sum of first n positive integers is given by Sn =, , n(n + 1), 2, , Example-14. Find the sum of first 24 terms of the list of numbers whose nth term is given by, an = 3 + 2n, , Solution : As, so,, , an = 3 + 2n,, a1 = 3 + 2 = 5, , a2 = 3 + 2 × 2 = 7, , a3 = 3 + 2 × 3 = 9, ..., List of numbers becomes 5, 7, 9, 11, . . ., , Free Distribution by T.S. Government 2021-22
Page 159 :
Progressions, , 149, , Here, 7 – 5 = 9 – 7 = 11 – 9 = 2 and so on., So, it forms an A.P. with common difference, d = 2., , Therefore,, , S24 =, , 24, [2 ´ 5 + (24 - 1) ´ 2] = 12(10 + 46) = 672, 2, , G, AN, , So, the sum of first 24 terms of the list of numbers is 672., , A, , To find S24, we have n = 24, a = 5, d = 2., , Example-15. A manufacturer of TV sets produced 600 sets in the third year and 700 sets in the, seventh year. Assuming that the production increases uniformly by a fixed number every year,, find :, the production in the 1st year, , (iii), , the total production in first 7 years, , (ii), , the production in the 10th year, , AN, , (i), , T,, TE, L, , Solution : (i) Since the production increases uniformly by a fixed number every year, the number, of TV sets manufactured in 1st, 2nd, 3rd, . . ., years will form an A.P.., Let us denote the number of TV sets manufactured in the nth year by an., Then,, or,, , a + 2d = 600, , a + 6d = 700, , SC, ER, , and, , a3 = 600 and a7 = 700, , Solving these equations, we get d = 25 and a = 550., Therefore, production of TV sets in the first year is 550., , (ii), , Now, , a10 = a + 9d = 550 + 9 × 25 = 775, , So, production of TV sets in the 10th year is 775., , (iii), , Also,, , S7 =, =, , 7, [2 ´ 550 + (7 - 1) ´ 25], 2, 7, [1100 + 150] = 4375, 2, , Thus, the total production of TV sets in first 7 years is 4375., , Free Distribution by T.S. Government 2021-22
Page 160 :
Class-X Mathematics, , 150, , E XERCISE - 6.3, 2, 7, 12, . . ., to 10 terms., , (ii), , –37, –33, –29, . . ., to 12 terms., , (iii), , 0.6, 1.7, 2.8, . . ., to 100 terms., , (iv), , 1 1 1, , , , .....,to 11terms., 15 12 10, , A, , Find the sums given below :, (i), , 1, 7 + 10 + 14 + .... + 84, 2, , (iii), , –5 + (–8) + (–11) + . . . + (–230), , (ii), , In an A.P.:, (i), (ii), (iii), (iv), (v), (vi), (vii), , G, AN, , 3., , (i), , 34 + 32 + 30 + . . . + 10, , given a = 5, d = 3, an = 50, find n and Sn., given a = 7, a13 = 35, find d and S13., given a12 = 37, d = 3, find a and S12., given a3 = 15, S10 = 125, find d and a10., given a = 2, d = 8, Sn = 90, find n and an., given an = 4, d = 2, Sn = –14, find n and a., given l = 28, S = 144, and there are total 9 terms, find a., , AN, , 2., , Find the sum of the following A.P.s:, , T,, TE, L, , 1., , The first and the last terms of an A.P. are 17 and 350 respectively. If the common, difference is 9, how many terms are there and what is their sum?, , 5., , Find the sum of first 51 terms of an A.P. whose second and third terms are 14 and 18, respectively., , 6., , If the sum of first 7 terms of an A.P. is 49 and that of 17 terms is 289, find the sum of first, n terms., , 7., , Show that a1, a2, . . ., an, . . . form an A.P. where an is defined as below :, , SC, ER, , 4., , (i), , an = 3 + 4n, , (ii), , an = 9 – 5n, , Also find the sum of the first 15 terms in each case., , 8., , If the sum of the first n terms of an A.P. is 4n – n2, what is the first term (note that the first, term is S1)? What is the sum of first two terms? What is the second term? Similarly, find, the 3rd, the 10th and the nth terms., , 9., , Find the sum of the first 40 positive integers divisible by 6., , 10., , A sum of ` 700 is to be used to give seven cash prizes to students of a school for their, overall academic performance. If each prize is ` 20 less than its preceding prize, find the, value of each of the prizes., , Free Distribution by T.S. Government 2021-22
Page 161 :
Progressions, , 151, , 11., , Students of a school decided to plant trees in and around the school to reduce air pollution., It was decided that the number of trees, that each section of each class will plant, will be, the same as the class, in which they are studying, e.g., a section of Class I will plant 1, tree, a section of Class II will plant 2 trees and so on till Class XII. There are three, sections of each class. How many trees will be planted by the students?, , 12., , A spiral is made up of successive, semicircles, with centres alternately at A, and B, starting with centre at A, of radii, 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, . . . as, shown in Figure. What is the total length, of such a spiral made up of thirteen, 22, consecutive semicircles? (Take p = ), 7, , A, , l3, , G, AN, , l1, A, , B, , l2, , l4, , AN, , [Hint : Length of successive semicircles is, l1, l2, l3, l4, . . . with centres at A, B, A, B, . . ., respectively.], , 200 logs are stacked in the following manner: 20 logs in the bottom row, 19 in the row, above, 18 in the row above it and so on. In how many rows are the 200 logs placed and, how many logs are in the top row?, , 14., , In a bucket and ball race, a bucket is placed at the starting point, which is 5 m from the, first ball, and the other balls are placed 3 m apart in a straight line. There are ten balls in, the line., , SC, ER, , T,, TE, L, , 13., , 5m, , 3m, , 3m, , A runner starts from the bucket, picks up the nearest ball, runs back with it, drops it in, the bucket, runs back to pick up the next ball, runs to the bucket to drop it in, and she, continues in the same way until all the balls are in the bucket. What is the total distance, the runner has to run?, , [Hint : To pick up the first ball and the second ball, the total distance (in metres) run by, a runner is 2 × 5 + 2 × (5 + 3)], , Free Distribution by T.S. Government 2021-22
Page 162 :
152, , Class-X Mathematics, , 6.5 G EOMETRIC P ROGRESSIONS, Consider the following patterns, 30, 90, 270, 810 ....., , (ii), , (iii), , 30, 24, 19.2, 15.36, 12.288, , 1 1 1, 1, , , ,, ....., 4 16 64 256, , Can we write the next term in each of the patterns above?, , G, AN, , In (i), each term is obtained by multiplying the preceding term by 3., , A, , (i), , In (ii), each term is obtained by multiplying the preceding term by, , 1, ., 4, , In (iii), each term is obtained by multiplying the preceding term by 0.8., , AN, , In all the lists given above, we see that successive terms are obtained by multiplying the, preceding term by a fixed number. Such a list of numbers is said to form Geometric Progression, (G.P.)., This fixed number is called the common ratio ‘r’ of G.P. So in the above example (i), (ii),, 1, , 0.8 respectively.., 4, , T,, TE, L, , (iii) the common ratios are 3,, , Let us denote the first term of a G.P. by a and common ratio r. To get the second term, according to the rule of Geometric Progression, we have to multiply the first term by the common, ratio r, where a ¹ 0, r ¹ 0 and r ¹ 1, \ The second term = ar, , Third term = ar . r = ar2, , SC, ER, , \ a, ar, ar2 ..... is called the general form of a G.P., , In the above G.P. the ratio between any term (except first term) and its preceding term is ‘r’, , i.e.,, , ar ar 2, =, = .......... = r, a, ar, , If we denote the first term of GP by a1, second term by a2 ..... nth term by an, , then a2 = a3 = ...... = an = r, a1 a2, an -1, , \ A list of numbers a1, a2, a3 .... an ... is called a geometric progression (G.P.), if each, term is non zero and, an, = r (r ¹ 1), an -1, where n is a natural number and n > 2., , Free Distribution by T.S. Government 2021-22
Page 163 :
Progressions, , 153, , D O T HIS, Find which of the following are not GPs, 6, 12, 24, 48, ....., , 2., , 1, 4, 9, 16, ......, , 3., , 1, -1, 1, -1, ....., , 4., , -4, -20, -100, -500, ....., , A, , 1., , (i), , A person writes a letter to four of his friends. He asks each one of them to copy the letter, and give it to four different persons with same instructions so that they can move the, chain ahead similarly. Assuming that the chain is not broken the number of letters at first,, second, third ... stages are, , The total amount at the end of first , second, third .... year if ` 500/- is deposited in the, bank with annual interest rate of 10% compounded annually is, , T,, TE, L, , 550, 605, 665.5 ......, , A square is drawn by joining the mid points of the sides, of a given square. A third square is drawn inside the, second square in the same way and this process, continues indefinitely. If a side of the first square is, 16cm then the area of first, second, third ..... square, will be respectively., , SC, ER, , (iii), , AN, , 1, 4, 16, 64, 256 .............. respectively., (ii), , G, AN, , Some more example of GP are :, , 256, 128, 64, 32, ....., , (iv), , Initially a pendulum swings through an arc of 18 cm., On each successive swing the length of the arc is 0.9th of the, previous length. So the length of the arc at first, second, third......., swing will be resepectively (in cm)., 18, 16.2, 14.58, 13.122......, , T HINK - D ISCUSS, 1., , Explain why each of the lists above is a G.P., , 2., , To know about a GP, what is the minimum information that we need?, , Free Distribution by T.S. Government 2021-22
Page 164 :
154, , Class-X Mathematics, , Now, let us learn how to construct a G.P. when the first term ‘a’ and common ratio ‘r’, are given. And also learn how to check whether the given list of numbers is a G.P., Example-16. Write the G.P. if the first term, a = 3, and the common ratio, r = 2., Solution : Since ‘a’ is the first term, the G.P. can easily be written., , G, AN, , A, , We know that in G.P. every succeeding term is obtained by multiplying the preceding, term with common ratio ‘r’. So, we have to multiply the first term a = 3 by the common ratio, r = 2 to get the second term., (Q First term × common ratio), , \ Second term = ar = 3 × 2 = 6, , Similarly, the third term = second term × common ratio, = 6 × 2 = 12, , 3, 6, 12, 24,..... ., , AN, , If we proceed in this way, we get the following G.P., , -1, 2, , T,, TE, L, , Example-17. Write the G.P. if a = 256, r =, , Solution : General form of G.P. = a, ar, ar2, ar3, ....., , 2, , 3, , æ -1 ö, æ -1 ö, æ -1 ö, = 256, 256 ç ÷ , 256 ç ÷ , 256 ç ÷, è 2 ø, è 2 ø, è 2 ø, , SC, ER, , = 256,, , -256 256 -256, ,, ,, ,..., 2, 4, 8, , = 256, -128, 64, -32 ......, , Example-18. Find the common ratio of the G.P. 25, -5, 1,, , -1, ., 5, , Solution : We know that if the first, second, third .... terms of a G.P. are a1, a2, a3 .... respectively, , the common ratio r =, , a2 a3, =, = ....., a1 a2, , Here a1 = 25, a2 = -5, a3 = 1., So common ratio r =, , -5, 1 -1, =, = ., 25 -5 5, , Free Distribution by T.S. Government 2021-22
Page 165 :
Progressions, , 155, , Example-19. Which of the following lists of numbers form G.P.?, (i), 3, 6, 12, ....., (ii), 64, -32, 16,, 1 1 1, ,, , ,......, 64 32 8, Solution : (i)We know that a list of numbers a1, a2, a3, .....an ..... is called a G.P. if each term is, , (iii), , Here all the terms are non zero. Further, , a3 12, =, =2, a2, 6, a2 a3, =, = 2, a1 a2, , i.e.,, , So, the given list of number forms a G.P. with the common ratio 2., All the terms are non zero., , T,, TE, L, , (ii), , AN, , 6, a2, = = 2 and, a1, 3, , G, AN, , A, , a2 a3, an, non zero and a = a = ..... a = r, 1, 2, n -1, , a2 -32 -1, =, =, a1, 64, 2, a3, 16, -1, =, =, a1 -32, 2, , and, , a2 a3 -1, =, =, a1 a2, 2, , SC, ER, , \, , So, the given list of numbers form a G.P. with common ratio, , (iii), , All the terms are non zero., 1, a2, = 32 = 2, and, 1, a1, 64, , Here, , 1, a3, = 8 =4, 1, a2, 32, , a2, a, ¹ 3, a1 a2, , So, the given list of numbers does not form G.P., , Free Distribution by T.S. Government 2021-22, , -1, ., 2
Page 166 :
Class-X Mathematics, , 156, , EXERCISE - 6.4, , 2., , In which of the following situations, does the list of numbers involved is in the form of a G.P.?, Salary of Sharmila: when her salary is ` 5,00,000 for the first year and expected, to receive yearly increment of 10% ., , (ii), , Number of bricks needed to make each step: if the stair case has total 30 steps,, provided that bottom step needs 100 bricks and each successive step needs 2, bricks less than the previous step., , (iii), , Perimeter of the each, triangle: when the mid, points of sides of an, equilateral triangle, whose side is 24 cm are, joined to form another, triangle, whose mid, points in turn are joined, to form still another, triangle and the process, continues indefinitely., , AN, 24 cm, , 24 cm, , 24 cm, , Write three terms of the G.P. when the first term ‘a’ and the common ratio ‘r’ are given?, a = 4;, , r=3, , SC, ER, , (i), (iii), , 3., , G, AN, , A, , (i), , T,, TE, L, , 1., , a = 81; r =, , -1, 3, , (ii), , a= 5; r=, , (iv), , a=, , 1, 5, , 1, ; r=2, 64, , Which of the following are G.P.? If they are in G.P. write next three terms?, (i) 4, 8, 16 ....., , (iii) 5, 55, 555, ...., (v), , 1 1 1, , , ....., 2 4 6, , (vii) x, 1,, , 1, ,....., ( x ¹ 0), x, , (iv), , 1 -1 1, ,, , ....., 3 6 12, -2, -6, -18 ....., , (vi), , 3, -32, 33, ....., , (ii), , (viii), , 1, , - 2, 4 2....., 2, , (ix) 0.4, 0.04, 0.004, ....., 4., , Find x so that x, x + 2, x + 6 are consecutive terms of a geometric progression., , Free Distribution by T.S. Government 2021-22
Page 167 :
Progressions, 6.6 nth, , TERM OF A, , 157, , G.P., , Let us examine a problem. The number of bacteria in a certain petri dish culture triples, every hour. If there were 30 bacteria present in the petri dish originally, then what would be the, number of bacteria in fourth hour?, , Since for every hour it triples, = 3 × 30 = 30 × 31, = 30 × 3(2-1), = 90, , = 3 × no.of bacteria in second hour, = 3 × 90, = 30 × 32, , = 30 × 3(3-1), , T,, TE, L, , = 270, , = 30 × (3×3), , AN, , No.of bacteria in third hour, , G, AN, , No.of bacteria in Second hour = 3 × no.of bacteria in first hour, , A, , To answer this, let us first see what the number of bacteria in second hour would be., , No.of bacteria in fourth hour = 3 × no.of bacteria in third hour, = 3 × 270, , = 30 × (3×3×3), , = 30 × 33, , = 30 × 3(4-1), , = 810, , Observe that we are getting a list of numbers, 30, 90, 270, 810, ...., , SC, ER, , These numbers are in GP (why ?), , Now looking at the pattern formed above, can you find number of bacteria in 20th hour?, , You may have already got some idea from the way we have obtained the number of, bacteria as above. By using the same pattern, we can compute that number of bacteria in 20 th, hour., The number of bacteria in 20 th hour = 30 ´ (3 ´ 3 ´ ... ´ 3), 14, 4244, 3, 19 terms, , = 30 × 319 = 30 × 3(20-1), This example would have given you some idea about how to write the 25th term, 35th, term and more generally the nth term of the G.P., Let a1, a2, a3 ..... be in GP whose ‘first term’ a1 is ‘a’ and the common ratio is ‘r’., , Free Distribution by T.S. Government 2021-22
Page 168 :
158, , Class-X Mathematics, , then the second term a2 = ar = ar(2-1), the third term a3 = a2×r = (ar) × r = ar2 = ar(3-1), the fourth term a4 = a3×r = ar2 × r = ar3 = ar(4-1), ................................................, Looking at the pattern we can say that nth term an = arn-1, , A, , ................................................, , Let us consider some examples, , 5 5 5, , , ......., 2 4 8, , AN, , Example-20. Find the 20th and nth term of the G.P., , G, AN, , So nth term of a G.P. with first term ‘a’ and common ratio ‘r’ is given by an = arn-1., , T,, TE, L, , 5, 5, 1, Solution : Here a = and r = 4 =, 5 2, 2, 2, a20 = ar 20-1 =, , Then, , an = ar n-1 =, , SC, ER, , and, , 5 æ 1ö, ç ÷, 2 è 2ø, , 5æ1ö, ç ÷, 2è 2ø, , 19, , =, , n -1, , =, , 5, 220, , 5, 2n, , Example-21. Which term of the G.P. : 2, 2 2 , 4 ..... is 128 ?, , Solution : Here a = 2 r =, , 2 2, = 2, 2, , Let 128 be the nth term of the G.P., , Then, , an = arn-1 = 128, 2.( 2) n-1 = 128, , ( 2) n-1 = 64, n-1, (2) 2, , = 26, , Free Distribution by T.S. Government 2021-22
Page 169 :
Progressions, Þ, \, , 159, , n -1, =6, 2, , n = 13., , Hence 128 is the 13th term of the G.P., , a3 = ar2 = 24, , ...(1), , a6 = ar5 = 192, , ...(2), , G, AN, , Solution : Here, , A, , Example-22. In a GP the 3rd term is 24 and 6th term is 192. Find the 10th term., , 5, Dividing (2) by (1) we get ar = 192, 24, ar 2, , r3 = 8 = 23, , Þ, , r =2, , AN, , Þ, , Substituting r = 2 in (1) we get a = 6., , T,, TE, L, , \ a10 = ar9 = 6(2)9 = 3072., , E XERCISE -6.5, , For each geometric progression given below, find the common ratio ‘r’, and then find an, (i), , 3,, , 3 3 3, , , ........., 2 4 8, , (ii), , 2, -6, 18, -54, , (iii), , -1, -3, -9, -27 ...., , (iv), , 4 8, 5, 2, , ........., 5 25, , SC, ER, , 1., , 2., , Find the 10th and nth term of G.P. : 5, 25, 125, ....., , 3., , Find the indicated term of each Geometric Progression, (i), , 4., , 1, a1 = 9; r = ; find a7, 3, , (ii), , 1, a1 = -12; r = ; find a6, 3, , (ii), , 3, 3, 3 3 ...... is 729 ?, , Which term of the G.P., (i), , 2, 8, 32, ..... is 512 ?, , (iii), , 1 1 1, 1, , , ..... is, ?, 3 9 27, 2187, , Free Distribution by T.S. Government 2021-22
Page 170 :
160, , Class-X Mathematics, , 5., , Find the 12th term of a G.P. whose 8th term is 192 and the common ratio is 2., , 6., , The 4th term of a geometric progression is, , 2, 16, and the seventh term is, . Find the, 3, 81, , geometric series., If the geometric progressions 162, 54, 18 ..... and, , 2 2 2, ,, , .... have their nth term, 81 27 9, , A, , 7., , O PTIONAL E XERCISE, [For extensive Learning], Which term of the A.P. : 121, 117, 113, . . ., is, the first negative term?, [ Hint : Find n for an < 0], , AN, , 1., , G, AN, , equal. Find the value of n., , 25 cm, , The sum of the third and the seventh terms of an, A.P. is 6 and their product is 8. Find the sum of, first sixteen terms of the A.P.., , 3., , A ladder has rungs 25 cm apart. The rungs, decrease uniformly in length from 45 cm at the, bottom to 25 cm at the top. If the top and the, , T,, TE, L, , 2., , 2, , 1, m, 2, , SC, ER, , 1, bottom rungs are 2 m apart, what is the length, 2, of the wood required for the rungs?, , [Hint : Number of rungs =, , 4., , 250, +1], 25, , 25 cm, , The houses of a row are numbered consecutively, 45 cm, from 1 to 49. Show that there is a value of x such, that the sum of the numbers of the houses preceding, the house numbered x is equal to the sum of the numbers of the houses following it. And, find this value of x., [Hint : Sx – 1 = S49 – Sx], , 5., , The sitting area around a football ground comprises of 15 steps, each of which is 50 m, long and built of bricks., , Free Distribution by T.S. Government 2021-22
Page 171 :
Progressions, Each step has a rise of, , 161, , 1, 1, m and a tread of m. (see Fig. 5.8). Calculate the total volume, 4, 2, , of the sitting area., 1 1, 3, ´ ´ 50 m ], 4 2, , G, AN, , A, , [Hint : Volume of the first step =, , 6., , AN, , 1, m, 4, , 50 m, , 1, m, 2, , 150 workers were engaged to finish a piece of work in a certain number of days. Four, , T,, TE, L, , workers dropped from the work on the second day. Four workers dropped on third, day and so on. It took 8 more days to finish the work. Find the number of days in which, the work was completed., , [Let the no.of days to finish the work be ‘x’ then, 150 x =, , x+8, [2 ´ 150 + ( x + 8 - 1)(-4)] ], 2, , SC, ER, , [Ans. x = 17 Þ x + 8 = 17 + 8 = 25], , 7., , 1, A machine costs ` 5,00,000. If its value depreciates 15% in the first year, 13 % in the, 2, second year, 12% in the third year and so on. What will be its value at the end of 10, years, when all the percentages will be applied to the original cost?, , 1, [Total depreciation = 15 + 13 +12+....10 terms., 2, Sn =, , 10, [30 - 13.5] = 82.5% ], 2, , \ after 10 year original cost =100 - 82.5 = 17.5 i.e., 17.5% of 5,00,000, , Free Distribution by T.S. Government 2021-22
Page 172 :
162, , Class-X Mathematics, , Suggested Projects, 1. Write down a sequence and verify whether it is an A.P. or not, using a grid paper., , G, AN, , WHAT WE H AVE D ISCUSSED, , A, , 2. Find the sum of n terms in an A.P. using grid paper., , In this chapter, you have studied the following points :, , An arithmetic progression (A.P.) is a list of numbers in which each term is obtained by, adding a fixed number d to the preceding term, except the first term. The fixed number d, is called the common difference., , AN, , 1., , The terms of A.P. are a, a + d, a + 2d, a + 3d, . . ., , A given list of numbers a1, a2, a3, . . . is an A.P., if the differences a2 – a1, a3 – a2, a4 –, a3, . . ., give the same value, i.e., if ak + 1 – ak is the same for different values of k., , 3., , In an A.P. with first term a and common difference d, the nth term (or the general term), is given by an = a + (n – 1) d., , 4., , The sum of the first n terms of an A.P. is given by :, , T,, TE, L, , 2., , n, S = [2a + ( n - 1) d ], 2, , If l is the last term of the finite A.P., say the nth term, then the sum of all terms of the A.P., is given by :, , SC, ER, , 5., , S=, , 6., , n, (a + l ) ., 2, , A Geometric Progression (G.P.) is a list of numbers in which first term is non-zero each, succeeding term is obtained by multiplying preceding term with a fixed non zero number, ‘r’ except first term. This fixed number is called common ratio ‘r’., , The general form of GP is a, ar, ar2, ar3 ...., , 7., , If the first term and common ratio of a GP are a and r respectively then nth term, an = arn-1., , Free Distribution by T.S. Government 2021-22
Page 173 :
7, , A, , Coordinate Geometry, , G, AN, , 7.1 I NTRODUCTION, , You know that in chess, the Knight moves in ‘L’ shape or two and a half steps (see figure)., It can jump over other pieces too. A Bishop moves, diagonally, as many steps as are free in front of it., 8, , AN, , Find out how other pieces move. Also locate 7, Knight, Bishop and other pieces on the board and see 6, how they move., 5, , T,, TE, L, , Consider the position of Knight. It can move in 4, directions as shown by dotted lines in the figure. Suppose,, it is at B then its position will be expressed as f 6. Find, the coordinates of its position after the various moves, shown in the figure., , H, , A, , B, , C, , 4, 3, , G, , 2, , D, F, , E, , 1, a, , b, , c, , d, , e, , f, , g, , h, , DO T HIS, , From the figure write coordinates of the points A, B, C, D, E, F, G, H., , ii., , Find the distance covered by the Knight in each of its 8 moves i.e. find the distance of A,, B, C, D, E, F, G and H from its original position., , SC, ER, , i., , iii. What is the distance between two points H and C? Also find the distance between two, points A and B, , 7.2 D ISTANCE B ETWEEN T WO P OINTS, The two points (2, 0) and (6, 0) lie on the X-axis as shown in figure., It is easy to see that the distance between two points A and B as 4 units., , We can say the distance between points lying on X-axis is the difference between the, x-coordinates.
Page 174 :
Class-X Mathematics, Y, 9, 8, 7, 6, 5, 4, 3, 2, 1, , What is the distance between, (-2, 0) and (-6, 0)?, The difference in the value of, x-coordinates is, (-6) - (-2) = -4 (Negative), , Therefore, the distance, = | (- 6) - (-2)| = |-4| = 4 units., , -9 -8 -7 -6 -5 -4 -3 -2 -1 O, -1, -2, -3, -4, -5, -6, -7, -8, -9, , T,, TE, L, , So, in general for the points, A(x1, 0) and B(x2, 0) that lie on the, X-axis, the distance between A and B is, |x2 - x1|., Similarly, if two points lie on, Y-axis, then the distance between the, points A and B would be the difference, between their y coordinates of the points., , SC, ER, , The distance between two points, (0, y1) and (0, y2) would be |y2 - y1|., , For example, let the points, be A(0, 2) and B(0, 7), Then, the distance between A and, , A(2, 0), , 1, , B(6, 0), , 1 2 3 4 5 6 7 8 9, , X, , G, AN, , So, we will take absolute value of, the difference., , X, , AN, , We never say the distance in, negative values., , Scale, X-axis : 1 cm = 1 unit, Y-axis : 1 cm = 1 unit, , A, , 164, , X, , Y, , 1, , Y, 9, 8, B (0, 7) 7, 6, 5, 4, 3, A (0, 2) 2, 1, , Scale, X-axis : 1 cm = 1 unit, Y-axis : 1 cm = 1 unit, , 1, , -9 -8 -7 -6 -5 -4 -3 -2 -1 O, -1, -2, -3, -4, -5, -6, -7, -8, -9, , 1 2 3 4 5 6 7 8 9, , Y, , X, , 1, , B is |7 - 2| = 5 units., , DO, , THIS, , 1. Where do points (-4, 0), (2, 0), (6, 0) and (-8, 0) lie on coordinate plane?, 2. Find the distance between points (i) (-4, 0) and (6, 0); (ii) (–4, 0) and (–8, 0)?, , Free Distribution by T.S. Government 2021-22
Page 175 :
Coordinate Geometry, TRY, , 165, , THIS, , 1. Where do points (0, -3), (0, -8), (0, 6) and (0, 4) lie on coordinate plane?, , A, , 2. Find the distance between points (i) (0, -3) and (0, 6); (ii) (0, –3) and (0, –8)?, , G, AN, , T HINK & D ISCUSS, , How will you find the distance between two points in which x or y coordinates are, same but not zero, like (2, 4) and (2, 9)?, , D ISTANCE B ETWEEN T WO POINTS, C OORDINATE A XES ., , ON A, , LINE PARALLEL, , TO THE, , AN, , 7.3, , Consider the points A(x1, y1) and B(x2, y1). Since the y-coordinates are equal, points lie, on a line, parallel to X-axis., , T,, TE, L, , AP and BQ are drawn perpendicular to X-axis., Observe the figure. APQB is a rectangle., Therefore, AB = PQ., , Y, , PQ = |x2 - x1| (i.e., The modulus, , SC, ER, , of difference between x coordinates), , Similarly, line joining two points, A( x 1,y1) B(x2,y1), , A(x1, y1) and B(x1, y2) is parallel to, , (x2 - x1), , Y-axis. Then the distance between these, two points is |y2 - y1| (It is read as, , X¢, , O, , P, , (x2 - x1), , modulus of the difference of y, coordinates)., , Example-1. What is the distance, between A (4,0) and B (8, 0)., Solution : The absolute value of the, difference in the x coordinates is |x2 - x1| = |8 - 4| = 4 units., , Free Distribution by T.S. Government 2021-22, , Q, , Y¢, , X
Page 176 :
Class-X Mathematics, , 166, , Example-2. A and B are two points given by (8, 3), (-4, 3). Find the distance between, A and B., Solution : Here x1 and x2 are lying in two different quadrants and y-coordinate are equal., Distance AB = |x2 - x1| = |-4 - 8| = |-12| = 12 units, , G, AN, , Find the distance between the following points., , A, , DO T HIS, i. (3, 8), (6, 8) ii. (-4,-3), (-8,-3) iii. (3, 4), (3, 8), , B (0,, , Then distance AB = ?, , Hence, by using Pythagorean, theorem, AB2 = AO2 + OB2, AB2 = 42 + 32, , X, , -9 -8 -7 -6 -5 -4 -3 -2 -1 O, -1, -2, -3, -4, -5, -6, -7, -8, -9, , A (4, 0), 1 2 3 4 5 6 7 8 9, , Y, , X, , 1, , SC, ER, , AB = 16 + 9 = 25 = 5 units, is the distance between A and B., , Scale, X-axis : 1 cm = 1 unit, Y-axis : 1 cm = 1 unit, , 1, , T,, TE, L, , The DAOB is a right angle triangle., From the figure, OA = 4 units (x-coordinate), OB = 3 units (y-coordinate), , Y, 9, 8, 7, 6, 5, 4, 3) 3, 2, 1, , AN, , Let A and B denote the points, (4, 0) and (0, 3) and ‘O’ be the, origin., , (iv) (-5, -8), (-5, -12), , DO T HIS, , Find the distance between the following points, (i) A (2, 0) and B(0, 4), (ii) P(0, 5) and Q(12, 0), , TRY THIS, Find the distance between points O (origin) and A (7, 4)., , Free Distribution by T.S. Government 2021-22
Page 178 :
Class-X Mathematics, , 168, , Example-3., , Find the distance between two points A(4, 3) and B(8, 6), , Solution : Compare these points with (x1, y1), (x2, y2), x1 = 4, x2 = 8, y1 = 3, y2 = 6, Using distance formula, , A, , distance AB =, , ( x2 - x1 )2 + ( y2 - y1 )2, , (8 - 4)2 + (6 - 3)2 = 42 + 32, , = 16 + 9 =, , G, AN, , d=, , 25 = 5 units., , AN, , DO T HIS, , Find the distance between the following pair of points, (ii), , (-8, 6) and (2, 0), , T,, TE, L, , (i) (7, 8) and (-2, 3), , TRY THIS, , Find the distance between A(1, -3) and B(-4, 4) and round it off to two decimal places., , SC, ER, , T HINK & D ISCUSS, , Sridhar calculated the distance between T(5, 2) and R(-4, -1) to the nearest decimal, as 9.5 units., Now, find the distance between P(4, 1) and Q(-5, -2). What do you observe in these, two results?, , Example-4. Show that the points A (4, 2), B (7, 5) and C (9, 7) are three points lying on a same, line., Solution : Let us find the distances AB, BC, AC by using distance formula,, d=, , ( x2 - x1 )2 + ( y2 - y1 ) 2, So, AB =, , (7 - 4) 2 + (5 - 2)2 = 32 + 32 = 9 + 9 = 18 = 9 ´ 2 = 3 2 units., , Free Distribution by T.S. Government 2021-22
Page 179 :
Coordinate Geometry, , 169, , BC =, , (9 - 7)2 + (7 - 5) 2 = 22 + 22 = 4 + 4 = 8 = 2 2 units, , AC =, , (9 - 4)2 + (7 - 2)2 = 52 + 52 =, , =, , 25 + 25 = 50, , 25 ´ 2 = 5 2 units., , A, , Now AB + BC = 3 2 + 2 2 = 5 2 = AC. Therefore, the three points (4, 2), (7, 5) and (9,, , G, AN, , 7) lie on a straight line., , Note: Points that lie on the same line are called collinear points., Example-5. Do the points (3, 2), (-2, -3) and (2, 3) form a triangle?, , Solution : Let us apply the distance formula to find the lengths PQ, QR and PR, where, , PQ =, , ( -2 - 3)2 + ( -3 - 2 )2, , QR =, , ( 2 - ( -2) ) + ( 3 - ( -3) ), , PR =, , ( 2 - 3 )2 + ( 3 - 2 ) 2, , 2, , ( -5 )2 + ( -5 )2, , ( 4 )2 + ( 6 )2, , =, , = 25 + 25 = 50 = 7.07 units (approx), = 52 = 7.21 units (approx), , T,, TE, L, , 2, , =, , AN, , P(3, 2), Q(-2, -3) and R(2, 3) are the given points., , =, , ( -1)2 + 12, , = 2 = 1.41 units (approx), , Since the sum of any two of these lengths is greater than the third length, the points P, Q, and R form a triangle and all the sides of triangle are unequal., , SC, ER, , Example-6. Show that the points (1, 7), (4, 2), (-1, -1) and (-4, 4) are the vertices of a, square., Solution : Let A(1, 7), B(4, 2), C(-1, -1)and D(-4, 4) be the given points., , One way of showing that ABCD is a square is to use the property that all its sides should, be equal and both its diagonals should also be equal. Now, the sides are, AB = (1 - 4)2 + (7 - 2)2 = 9 + 25 = 34 units, BC =, , (4 + 1)2 + (2 + 1)2 = 25 + 9 = 34 units, , CD = (-1 + 4)2 + (-1 - 4)2 = 9 + 25 = 34 units, DA =, , ( -4 - 1) + ( 4 - 7 ), 2, , 2, , =, , Free Distribution by T.S. Government 2021-22, , 25 + 9 = 34 units
Page 180 :
Class-X Mathematics, , 170, , and diagonal are, , (1 + 1)2 + (7 + 1)2 = 4 + 64 = 68 units, , AC =, , BD = (4 + 4)2 + (2 - 4)2 = 64 + 4 = 68 units, , A, , Since AB = BC = CD = DA and AC = BD. So all the four sides of the quadrilateral, ABCD are equal and its diagonals AC and BD are also equal. Therefore, ABCD is a square., , G, AN, , Example-7. The figure shows the arrangement of desks in a class room. Madhuri, Meena,, Pallavi are seated at A(3, 1), B(6, 4) and C(8, 6) respectively. Do you think they are seated in a, line? Give reasons for your answer., 10, 9, , Solution : Using the distance formula, we have, , 8, 7, , ( 6 - 3) + ( 4 - 1), , BC=, , (8 - 6 ), , 2, , 2, , 2, , = 9 + 9 = 18 = 3 2 units, , + (6 - 4) =, 2, , C, , 6, , AN, , AB=, , 4 + 4 = 8 = 2 2 units, , 5, , B, , 4, 3, , AC=, , T,, TE, L, , 2, , (8 - 3) + ( 6 - 1), 2, , 2, , = 25 + 25 = 50 = 5 2 units, , A, , 1, 0, , 1, , 2, , 3, , 4, , 5, , 6, , 7, , 8, , 9, , 10, , Since, AB + BC = 3 2 = 2 2 = 5 2 = AC, we can say that the points A, B and C are, collinear. Therefore, they are seated in a line., , SC, ER, , Example-8. Find the relation between x and y such that the point (x , y) is equidistant from the, points (7, 1) and (3, 5)., , Solution : Given P(x, y) be equidistant from the points A(7, 1) and B(3, 5)., \ AP = BP., , So, AP2 = BP2, , i.e., (x – 7)2 + (y – 1)2 = (x – 3)2 + (y – 5)2, , i.e., (x2 – 14x + 49) + (y2 – 2y + 1) = (x2 – 6x + 9) + (y2 – 10y + 25), , (x2 + y2 - 14x - 2y + 50) - (x2 + y2 - 6x - 10y + 34) = 0, -8x + 8y = -16 (Dividing both sides by –8), i.e., x – y = 2 which is the required relation., , Free Distribution by T.S. Government 2021-22
Page 181 :
Coordinate Geometry, , 171, , Example-9. Find a point on the Y-axis which is equidistant from both the points A(6, 5) and, B(– 4, 3)., Solution : We know that a point on the Y-axis is of the form (0, y). So, let the point, P(0, y) be equidistant from A and B. Then PA = PB, PA =, , ( 6 - 0), , PB =, , ( -4 - 0 ) + ( 3 - y ), , 2, , 2, , A, , + (5 - y ), , G, AN, , 2, , 2, , PA2 = PB2, So, (6 – 0)2 + (5 – y)2 = (– 4 – 0)2 + (3 – y)2, , AN, , i.e., 36 + 25 + y2 – 10y = 16 + 9 + y2 – 6y, i.e., 4y = 36, , T,, TE, L, , i.e., y = 9, So, the required point is (0, 9)., , Let us check our solution :, , AP =, , (6 - 0)2 + (5 - 9)2 = 36 + 16 = 52, , BP =, , (-4 - 0)2 + (3 - 9)2 = 16 + 36 = 52, , SC, ER, , So (0, 9) is equidistant from (6, 5) and (4, 3)., , E XERCISE 7.1, , 1. Find the distance between the following pairs of points, (i), , (2, 3) and (4, 1), , (ii), , (-5, 7) and (-1, 3), , (iii), , (-2, -3) and (3, 2), , (iv), , (a, b) and (-a, -b), , 2. Find the distance between the points (0, 0) and (36, 15)., 3. Verify whether the points (1, 5), (2, 3) and (-2, -1) are collinear or not., , 4. Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle., 5. Show that the points A(a, 0), B(-a, 0), C(0, a 3 ) form an equilateral triangle., , Free Distribution by T.S. Government 2021-22
Page 182 :
Class-X Mathematics, , 172, , 6. Prove that the points (-7, -3), (5, 10), (15, 8) and (3, -5) taken in order are the corners, of a parallelogram., 7. Show that the points (-4, -7), (-1, 2), (8, 5) and (5, -4) taken in order are the vertices of, a rhombus. Find its area., , A, , 1, ´ product of its diagonals), 2, , G, AN, , (Hint : Area of rhombus =, , 8. Name the type of quadrilateral formed, if any, by the following points, and give reasons for, your answer., (-1, -2), (1, 0), (-1, 2), (-3, 0), , (iii), , (4, 5), (7, 6), (4, 3), (1, 2), , (ii) (-3, 5), (3, 1), (1, -3), (-5, 1), , AN, , (i), , 9. Find the point on the X-axis which is equidistant from (2, -5) and (-2, 9)., 10. If the distance between two points (x, 7) and (1, 15) is 10, find the value of x., , units., , T,, TE, L, , 11. Find the values of y for which the distance between the points P(2, -3) and Q(10, y) is 10, , 12. Find the radius of the circle whose centre is (3, 2) and passes through (-5, 6)., 13. Can you draw a triangle with vertices (1, 5), (5, 8) and (13, 14) ? Give reason., 14. Find a relation between x and y such that the point (x, y) is equidistant from the points, , SC, ER, , (-2, 8) and (-3, -5), , 15. In a class room, 4 friends are seated at the points, , 10, , A, B, C and D as shown in Figure. Jarina and Phani, , 9, , walk into the class and after observing for a few, , 8, , B, , 7, , minutes Jarina asks Phani “Don’t you notice that, , 6, , ABCD is a square?” Phani disagrees. Using distance, , 5, , formula, decide who is correct and why?, , 4, , A, , C, , 3, 2, , D, , 1, 1, , 2, , 3, , 4, , 5, , 6, , 7, , 8, , 9, , 10, , 16. Find a relation between x and y such that the point (x, y) is equidistant from the points, (7, 1) and (3, 5)., , Free Distribution by T.S. Government 2021-22
Page 183 :
Coordinate Geometry, , 173, , 7.5 S ECTION F ORMULA, Y, , AN, , G, AN, , A, , A and B are two towns. To reach B, B(36, 15), from A, we have to travel 36 km East and, 15 km North from there (as shown in the, figure). Suppose a telephone company, wants to position a relay tower at P, (x, y) P, C 15 km, between A and B in such a way that the, 36-x, y, y, distance of the tower from B is twice its, A, x, distance from A. If P lies on AB, it will, X, 36-x, O, D, divide AB in the ratio 1 : 2 (See figure). If, 36 km, we take A as the origin O, and 1 km as, one unit on both the axes, the coordinates, of B will be (36, 15). In order to know the position of the tower, we must know the coordinates, of P. How do we find these coordinates?, , T,, TE, L, , Let the coordinates of P be (x, y). Draw perpendiculars from P and B to the X-axis, meeting it in, D and E, respectively. Draw PC perpendicular to BE. Then, by the AA similarity criterion,, studied earlier, DPOD and DBPC are similar., OD OP 1, PD OP 1, =, =, =, =, Therefore,, and, PC PB 2, BC PB 2, y, 1, x, 1, = ., So,, =, 15 - y 2, 36 - x 2, 2x = (36 - x), , 2y = 15 - y, , 3x = 36, , 3y = 15, , x = 12, , y=5, , SC, ER, , These equations give x = 12 and y = 5., , You can check that P(12, 5) meets the condition that OP : PB = 1 : 2., Consider any two points A(x1, y1) and B(x2, y2), Y, and assume that P (x, y) divides AB internally in the, (x, y ) m, ratio m1 : m2,, P, , AP m1, i.e.,, =, PB m2, (See figure)., , m1, , ..... (1), , Draw AR, PS and BT perpendicular to the Xaxis. Draw AQ and PC parallel to the X-axis. Then,, by the AA similarity criterion,, DPAQ ~ DBPC, , Free Distribution by T.S. Government 2021-22, , A, , 2, , B(x2,y2), C, , Q, , (x1,y1), O, , R, , S, , X
Page 185 :
Coordinate Geometry, , 175, , Special Case : Let A (x1, y1) and B (x2, y2) be any two points. Then the midpoint of the line, segment AB divides the line segment in the ratio 1 : 1. Therefore, the coordinates of the midpoint P are, , Let us solve few examples based on the section formula., , A, , æ 1.x1 + 1. x2 1. y1 + 1. y2 ö æ x1 + x2 y1 + y2 ö, ,, ,, ç, ÷ =ç, ÷., 1+1 ø è 2, 2 ø, è 1+1, , G, AN, , Example-10. Find the coordinates of the point which divides the line segment joining the points, (4, -3) and (8, 5) in the ratio 3 : 1 internally., Solution : Let P(x, y) be the required point. Using the section formula, , 3(8) + 1(4) 24 + 4 28, =, =, = 7,, 3+1, 4, 4, 3(5) + 1( -3) 15 - 3 12, =, =, =3, 3 +1, 4, 4, , T,, TE, L, , x=, , AN, , æ m x + m2 x1 m1 y 2 + m2 y1 ö, P( x, y ) = ç 1 2, ,, ÷, m1 + m2 ø , we get, è m1 + m2, , y=, , P(x, y) = (7, 3) is the required point., , Example-11. Find the midpoint of the line segment joining the points (3, 0) and (-1, 4), Solution : The midpoint M(x, y) of the line segment joining the points (x1, y1) and (x2, y2)., , SC, ER, , æ x1 + x2 y1 + y2 ö, ,, M(x, y) = ç, ÷, 2 ø, è 2, , \ The mid point of the line segment joining the points (3, 0) and (-1, 4) is, æ 3 + (-1) 0 + 4 ö æ 2 4 ö, ,, M(x, y) = ç, ÷ = ç , ÷ = (1, 2) ., 2 ø è2 2ø, è 2, , DO T HIS, 1 Find the point which divides the line segment joining the points (3, 5) and (8, 10) in the, ratio 2 : 3 internally., 2. Find the midpoint of the line segement joining the points (2, 7) and (12, -7)., , Free Distribution by T.S. Government 2021-22
Page 186 :
Class-X Mathematics, , 176, , 7.6 T RISECTIONAL P OINTS, , OF A, , LINE, , The points which divide a line segment into 3 equal parts are said to be the trisectional, points., , A, , Example-12. Find the coordinates of the points of trisection of the line segment joining the, points A(2,-2) and B(-7, 4)., , G, AN, , Solution : Let P and Q be the points of trisection of AB i.e., AP=PQ=QB (see figure below)., Therefore, P divides AB in the ratio 1 : 2 internally., , A, (2, -2), , P, , Q, , B, (-7, 4), , Therefore, the coordinates of P are (by applying the section formula), , æ 1(-7) + 2(2) 1(4) + 2( -2) ö, ,, ç, ÷, 1+ 2, 1+ 2, è, ø, , T,, TE, L, , =, , AN, , æ m x + m2 x1 m1 y 2 + m2 y1 ö, P( x, y ) = ç 1 2, ,, ÷, m1 + m2 ø, è m1 + m2, , =, , æ - 7 + 4 4 - 4 ö æ -3 0 ö, ,, ç, ÷ = ç , ÷ = ( -1, 0 ), 3 ø è 3 3ø, è 3, , Now, Q also divides AB in the ratio 2:1 internally., So,the coordinates of Q are, , SC, ER, , æ 2(-7) + 1(2) 2(4) + 1( -2) ö, =ç, ,, ÷, 2 +1, 2 +1, è, ø, , æ -14 + 2 8 - 2 ö æ -12 6 ö, ,, , ÷ = ( -4, 2 ), =ç, ÷ =ç, 3 ø è 3 3ø, è 3, , Therefore, the coordinates of the points of trisection of the line segment are P(-1, 0) and, Q(-4, 2), , DO T HIS, , 1. Find the trisectional points of line segment joining (2, 6) and (-4, 8)., 2. Find the trisectional points of line segment joining (-3, -5) and (-6, -8)., , Free Distribution by T.S. Government 2021-22
Page 189 :
Coordinate Geometry, , 179, , We should verify that the ratio satisfies the y-coordinate also., , =, , -8 ´, , 2, + 10, 7, , 2, +1, 7, , -16, + 10, 7, -16 + 70 54, =, =, =, =6, 9, 9, 9, 7, , A, , -8m1 + 10m2, =, m1 + m2, , G, AN, , Now,, , m1, + 10, m2, (Dividing throughout by m2), m1, +1, m2, , -8, , Therefore, the point (-4, 6) divides the line segment joining the points A(-6, 10) and, , T,, TE, L, , T HINK - D ISCUSS, , AN, , B (3, -8) in the ratio 2 : 7., , The line segment joining points A(6, 9) and B(-6, -9) is given, (a) In what ratio does the origin divide AB ? And what is it called for AB ?, (b) In what ratio does the point P(2, 3) divide AB ?, (c) In what ratio does the point Q(-2, -3) divide AB ?, , SC, ER, , (d) In how many equal parts is AB divided by P and Q?, (e) What do we call P and Q for AB ?, , Example-15. Find the ratio in which the y-axis divides the line segment joining the points, (5, -6) and (-1, -4). Also find the point of intersection., Solution : Let the ratio be K : 1. Then by the section formula, the coordinates of the point which, divides AB in the ratio K : 1 are, æ K( -1) + 1(5) K( -4) + 1( -6) ö, ,, ç, ÷, K +1, K +1, è, ø, æ - K + 5 -4K - 6 ö, ,, i.e., ç, ÷, K +1 ø, è K +1, , Free Distribution by T.S. Government 2021-22
Page 190 :
Class-X Mathematics, , 180, , This point lies on the Y-axis, and we know that on the Y-axis the abscissa is 0., Therefore,, , -K + 5, =0, K +1, , Putting the value of K = 5, we get the point of intersection as, , A, , -K + 5 = 0 Þ K = 5., So, the ratio is K : 1 = 5 : 1, , G, AN, , -20 - 6 ö æ, -26 ö æ -13 ö, æ -5 + 5 -4(5) - 6 ö æ, ,, =ç, ÷ = ç 0,, ÷ = ç 0,, ÷ = ç 0,, ÷, 5 +1 ø è, 6 ø è, 6 ø è, 3 ø, è 5 +1, , Example-16. Show that the points A(7, 3), B(6, 1), C(8, 2) and D(9, 4) taken in that order are, vertices of a parallelogram., Solution : Let the points A(7, 3), B(6, 1), C(8, 2) and D(9, 4) be vertices of a parallelogram., , AN, , We know that the diagonals of a parallelogram bisect each other., , \ So the midpoint of the diagonals AC and DB should be same., , T,, TE, L, , æ x1 + x2 y1 + y2 ö, ,, Now, we find the mid points of AC and DB by using ç, ÷ formula., 2 ø, è 2, æ 7 + 8 3 + 2 ö æ 15 5 ö, ,, midpoint of AC = ç, ÷=ç , ÷, 2 ø è 2 2ø, è 2, æ 9 + 6 4 + 1 ö æ 15 5 ö, ,, midpoint of DB = ç, ÷=ç , ÷, 2 ø è 2 2ø, è 2, , D(9, 4), , A(7,3), , C(8, 2), , B(6, 1), , Hence, midpoint of AC and midpoint of DB is same., , SC, ER, , Therefore, the points A, B, C, D are vertices of a parallelogram., , Example-17. If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a, parallelogram, taken in order, find the value of p., Solution : We know that diagonals of parallelogram bisect each other., So, the coordinates of the midpoint of AC = Coordinates of the midpoint of BD., i.e.,, , æ 6 + 9 1+ 4ö æ 8 + p 5ö, ,, , ÷, çè, ÷ =ç, 2, 2 ø è 2, 2ø, æ 15 5 ö æ 8 + p 5 ö, , ÷ then, çè , ÷ø = çè, 2 2, 2, 2ø, , 15 8 + p, =, 2, 2, , 15 = 8 + p Þ p = 7., , Free Distribution by T.S. Government 2021-22
Page 191 :
Coordinate Geometry, , 181, , E XERCISE - 7.2, 1. Find the point which divides the line segment joining the points (-1, 7) and (4, -3) in the, ratio 2 : 3., , A, , 2. Find the points of trisection of the line segment joining (4, -1) and (-2, -3)., , G, AN, , 3. Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by, (-1, 6)., 4. If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find, x and y., , AN, , 5. Find the point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4)., 6. If A and B are (-2, -2) and (2, -4) respectively, find the P on AB such that AP =, , 3, AB., 7, , parts., , T,, TE, L, , 7. Find the points which divide the line segment joining A(-4, 0) and B(0, 6) into four equal, 8. Find the points which divides the line segment joining A(-2, 2) and B(2, 8) into four equal, parts., 9. Find the point which divides the line segment joining the points (a + b, a - b) and (a - b,, a + b) in the ratio 3 : 2 internally., , SC, ER, , 10. Find the centroid of the triangles with vertices:, i., , (-1, 3), (6, -3) and (-3, 6), , iii., , (1, -1), (0, 6) and (-3, 0), , ii., , (6, 2), (0, 0) and (4, -7), , 11. Find the point A (x, y) when C divides AB in the ratio 2:3. Points B and C are given as, (–5, 8) and (3, 6)., , 12. The line segment AB meets the coordinate axes in points A and B. If point P (3, 6) divides, AB in the ratio 2:3, then find the points A and B., , Free Distribution by T.S. Government 2021-22
Page 192 :
Class-X Mathematics, , 182, , 7.8 AREA, , OF THE, , TRIANGLE, , Consider the points A(0, 4) and B(6, 0) which form a triangle with origin O on a plane as, shown in the figure., 4 units, , What is the area of the DAOB?, , =, , O 6 units B(6, 0), , G, AN, , \ Area of DAOB =, , A, , DAOB is a right angle triangle with the base as 6 units (i.e.,, x coordinate) and height as 4 units (i.e., y coordinate)., , A(0, 4), , 1, ´ base ´ height, 2, , 1, ´ 6 ´ 4 =12 square units., 2, , AN, , TRY THIS, , T,, TE, L, , Take a point A on X-axis and B on Y-axis and find area of the triangle AOB. Discuss, with your friends how to find the area of the triangle?, , T HINK - D ISCUSS, , Y, A, , Let A(x1, y1), B(x2, y2), C(x3, y3) be three points., , SC, ER, , Then find the area of the following triangles and, , X', , discuss with your friends in groups about the area of, , C, , X, , B, , that triangle., , (i), Y', , Y, , A, , X, , C, , B, , X', , C, , X, , (iii), , (ii), Y', , B, , X', , C, , Y', , A, , A, , B, , X', , Y, , Y, , X, , (iv), Y', , Free Distribution by T.S. Government 2021-22
Page 194 :
Class-X Mathematics, , 184, , Example-18. Find the area of a triangle whose vertices are (1, -1), (-4, 6) and (-3, -5)., Solution : Area of the triangle = D =, , 1, x1 ( y2 - y3 ) + x2 ( y3 - y1 ) + x3 ( y1 - y2 ), 2, , =, , 1, 1(6 + 5) + ( -4) ( -5 + 1) + ( -3)(-1 - 6), 2, 1, 11 + 16 + 21 = 24, 2, , So, the area of the triangle is 24 square units., , G, AN, , D =, , A, , The area of the triangle formed by the vertices A(1, -1), B(-4, 6) and C(-3, -5), by using, the formula, , AN, , Example-19. Find the area of a triangle formed by the points A(5, 2), B(4, 7) and C(7, -4)., , D=, =, , T,, TE, L, , Solution : The area of the triangle formed by the vertices A(5, 2), B(4, 7) and C(7, -4) is given, by, 1, 5(7 + 4) + 4( -4 - 2) + 7(2 - 7), 2, 1, -4, 55 - 24 - 35 =, = -2 = 2, 2, 2, , Therefore, the area of the triangle = 2 square units., , SC, ER, , D O T HIS, , Find the area of the triangle whose vertices are, 1., , (5, 2) (3, -5) and (-5, -1), , 2., , (6, -6), (3, -7) and (3, 3), , Example-20. If A(-5, 7), B(-4,-5), C(-1, -6) and D(4,5) are the vertices of a quadrilateral,, then, find the area of the quadrilateral ABCD., , Solution : By joining B to D, you will get two triangles ABD, and BCD., The area of DABD, =, , 1, -5(-5 - 5) + ( -4)(5 - 7) + 4(7 + 5), 2, , Free Distribution by T.S. Government 2021-22
Page 195 :
Coordinate Geometry, 106, 1, = 50 + 8 + 48 =, = 53 square units, 2, 2, , 185, , A, , D, , Also, the area of DBCD, , B, , C, , A, , =, , 1, -4(-6 - 5) - 1(5 + 5) + 4( -5 + 6), 2, , 1, 44 - 10 + 4 = 19 Square units, 2, , G, AN, , =, , So, the area of quadrilateral ABCD = Area of DABD + area of DBCD, , TRY THIS, , AN, , 53+19 = 72 square units., , T,, TE, L, , Find the area of the square formed by (0, -1), (2, 1) (0, 3) and (-2, 1) as vertices., , T HINK & D ISCUSS, , Find the area of the triangle formed by the following points, (i) (2, 0), (1, 2), (1, 6), , (ii) (3, 1), (5, 0), (1, 2), , SC, ER, , (iii) (-1.5, 3), (6, 2), (-3, 4), , •, , What do you observe?, , •, , Plot these points on three different graphs. What do you observe now?, , •, , Can we have a triangle with area as zero square units? What does it mean?, , 7.8.1. C OLLINEARITY, , We know that the points that lie on the same line are called collinear points., Suppose the points A(x1, y1), B(x2, y2) and C(x3, y3) are collinear i.e. they are lying on a, line. Then, they can not form a triangle. i.e. area of DABC is zero., Similarly, when the area of a triangle formed by three points A, B and C is zero, then these, three points are said to be collinear points., , Free Distribution by T.S. Government 2021-22
Page 196 :
Class-X Mathematics, , 186, , Example-21. The points (3, -2) (-2, 8) and (0, 4) are three points in a plane. Show that these, points are collinear., Solution : By using area of the triangle formula, 1, 3(8 - 4) + (-2)(4 - (-2)) + 0(( -2) - 8), 2, 1, = 12 - 12 = 0, 2, , G, AN, , A, , D=, , The area of the triangle is 0. Hence the three points are collinear i.e., they lie on the same, line., , Example-22. Find the value of ‘b’ for which the points A(1, 2), B(-1, b) and C(-3, -4) are, collinear., Then x1 = 1, y1 = 2;, , x2 = -1, y2 = b;, , x3 = -3, y3 = -4, , 1, x1 ( y2 - y3 ) + x2 ( y3 - y1 ) + x3 ( y1 - y2 ), 2, , T,, TE, L, , We know, area of D =, , AN, , Solution : Let the given points A(1, 2), B(-1, b) and C(-3, -4), , 1, area of DABC = 1(b + 4) + ( -1)( -4 - 2) + ( -3)(2 - b) = 0 (Q The given points are collinear), 2, |b + 4 + 6 - 6 + 3b| = 0, , |4b + 4| = 0, 4b + 4 = 0, , SC, ER, , \ b = -1, , DO T HIS, , Verify whether the following points are collinear, , (i) (1, -1), (4, 1), (-2, -3), , (ii) (1, -1), (2, 3), (2, 0), , (iii) (1, -6), (3, -4), (4, -3), , 7.8.2. A REA, , OF A, , T RIANGLE - ‘H ERON’ S F ORMULA ’, , We know the formula for area of the triangle is, , 1, ´ base ´ height ., 2, , Any given triangle may be a right angled triangle, equilateral triangle or an isosceles triangle., How do we calculate its area?, , Free Distribution by T.S. Government 2021-22
Page 197 :
Coordinate Geometry, , 187, , If we know the base and height directly, we apply, the above formula to find the area of a triangle., , G, AN, , For this Heron, an Ancient Greek mathematician,, derived a formula for a triangle whose lengths of sides a, b, and c are known. The formula is:, a+b+c, A = s( s - a)(s - b)( s - c) , where s =, 2, , A, , However, if the height (h) is not known, how do we, find its area?, , For example, we find the area of the triangle whose lengths of sides are 12m, 9m, 15m by, using Heron’s formula we get, , 12 + 9 + 15 36, =, =18m, 2, 2, , s=, , T,, TE, L, , s=, , a+b+c, 2, , AN, , A = s(s - a )( s - b)( s - c) , where, , Then s - a = 18 - 12 = 6m, s - b = 18 - 9 = 9m, , s - c = 18 - 15 = 3m, , SC, ER, , A = 18(6)(9)(3) = 2916 = 54 square meters., , DO T HIS, , (i) Find the area of the triangle the lengths of whose sides are 7m, 24m, 25m (use, Heron’s Formula)., , (ii) Find the area of the triangle formed by the points (0, 0), (4, 0), (4, 3) by using, Heron’s formula., , Free Distribution by T.S. Government 2021-22
Page 198 :
Class-X Mathematics, , 188, , EXERCISE - 7.3, 1. Find the area of the triangle whose vertices are, (i) (2, 3) (-1, 0), (2, -4), (ii), (iii) (0, 0), (3, 0) and (0, 2), , (-5, -1), (3, -5), (5, 2), , G, AN, , A, , 2. Find the value of ‘K’ for which the points are collinear., (i) (7, -2) (5, 1) (3, K), (ii), (8, 1), (K, -4), (2, -5), (iii) (K, K) (2, 3) and (4, -1)., , 3. Find the area of the triangle formed by joining the mid-points of the sides of the triangle, whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the, given triangle., , AN, , 4. Find the area of the quadrilateral whose vertices taken in order are (-4, -2), (-3, -5),, (3, -2) and (2, 3)., , T,, TE, L, , 5. Find the area of the triangle formed by the points (2, 3), (6, 3) and (2, 6) by using Heron’s, formula., , 7.9 S TRAIGHT LINES, , Bharadwaj and Meena are trying to find solutions for a linear equation in two variable., Bharadwaj : Can you find solutions for 2x + 3y = 12, Meena : Yes, I have found some of them., 2x+3y = 12, , SC, ER, , In general,, , 3y = 12 - 2x, y=, , 12 - 2 x, 3, , Meena : Can you write these solutions, in ordered pairs?, , Bharadwaj : Yes, (0, 4), (3, 2), (6, 0),, (-3, 6), Meena, can you plot these points, on the coordinate plane?, Meena : I have done like this., Bharadwaj : What do you observe?, , X, , x, , 0, , 3, , 6, , -3, , y, , 4, , 2, , 0, , 6, , Y, 9, Scale, 8, X-axis : 1 cm = 1 unit, 7, D(-3,6), Y-axis : 1 cm = 1 unit, 6, 5, A(0,4), 4, 3, B(3,2), 2, 1, , C(6,0), , 1, , -9 -8 -7 -6 -5 -4 -3 -2 -1 O, -1, -2, -3, -4, -5, -6, -7, -8, -9, , 1 2 3 4 5 6 7 8 9, , Y, , X, , 1, , Free Distribution by T.S. Government 2021-22
Page 199 :
Coordinate Geometry, , 189, , What does this figure represent?, Meena : It is a straight line., Bharadwaj : Can you identify some more points on this line?, Can you help Meena to find some more points on this line?, , A, , ..................., ..................., ..................., ..................., And in this line, what is AB called ?, , G, AN, , AB is a line segment., , D O T HIS, , Plot these points on the coordinate plane and join them:, 2. P(3, -5) Q(5, -1), R(2, 1), S(1, 2), , AN, , 1. A(1, 2), B(-3, 4), C(7, -1), , T,, TE, L, , Which one is a straight line? Which is not? Why?, , T HINK & D ISCUSS, , Does y = x + 7 represent a straight line? Draw the line on the coordinate plane., At which point does this line intersect Y-axis?, 7.9.1 S LOPE, , OF THE STRAIGHT LINE, , SC, ER, , You might have seen a slide in a park. Two slides have been shown here. On which of, them can you slide faster?, , Obviously your answer will be second. Why?, Observe these lines., , Free Distribution by T.S. Government 2021-22
Page 200 :
Class-X Mathematics, , 190, , m, l, , X, , X, , O, , A, , O, , Which line makes greater angle with OX ?, , G, AN, , Since, the line “m” makes a greater angle with OX than line ‘l’,, , line ‘m’ has a greater “slope” than line ‘l’. We may also term the “Steepness” of a line as, its slope., , AN, , How can we measure the slope of a line?, , A CTIVITY, , Consider the line given in the figure identify the points on the line and fill the table below., 0, , 1, , 2, , y coordinate, , 0, , 2, , 4, , 3, , 4, , 6, , 8, , T,, TE, L, , x coordinate, , We can observe that y coordinates change when x coordinates change., When y coordinate increases from, y1 = 0 to y2 = 2,, So the change in y is = ........................, , SC, ER, , Then corresponding change in ‘x’ is = ..., \, , change in y, = .................., change in x, , When y coordinate increases from, y1 = 2 to y3 = 4,, , the change in y is = .................., the corresponding change in x is ............, So,, , change in y, = ..............., change in x, , Y, , 9, Scale, X-axis : 1 cm = 1 unit 8, Y-axis : 1 cm = 1 unit 7, , X, , 6, 5, 4, 3, 2, 1, , 1, , -9 -8 -7 -6 -5 -4 -3 -2 -1 O, -1, -2, -3, -4, -5, -6, -7, -8, -9, , 1 2 3 4 5 6 7 8 9, , Y, , X, , 1, , Then, can you try other points on the line? Choose any two points and fill in the table., , Free Distribution by T.S. Government 2021-22
Page 201 :
Coordinate Geometry, , 191, , Change in x, , Change in y, Change in x, , 2, , 1, , 2, =2, 1, , What do you conclude from the above activity?, , G, AN, , A, , Change in y, , Therefore, the ratio of change in y to change in x, on a line, has a relation with the angle, made by the line with X-axis. Let us discuss about this relationship now., OF A LINE JOINING, , TWO P OINTS, , AN, , 7.9.2 S LOPE, , Slope will be denoted by ‘m’ and the line ‘l’, makes the angle q with X-axis., , Y, , 2 ,y, 2), , T,, TE, L, , Let A(x1, y1) and B(x2, y2) be two points on a line ‘l’ not parallel to Y-axis as shown in the, figure., change in y, The slope of a line = change in x, y2 - y1, Slope of AB = m = x - x, 2, 1, , \, , tan q =, , \ tan q =, , x, B(, , =, X¢, , BC, y -y, = 2 1, AC, x2 - x1, , 1 ,y, 1), , Opposite side of angle q, adjacent side of angle q, , A, (x, , SC, ER, , So, AB line segment makes the same angle q with, AC also., , q, , y2 - y1, =m, x2 - x1, , Hence \ m = tanq =, , y2 - y1, x2 - x1, , It is the formula to find slope of line segment AB, which is having end points as (x1, y1), (x2, y2)., If q is angle made by the line with X-axis, then m = tan q., , Free Distribution by T.S. Government 2021-22, , Y¢, , y2 - y1, , x2 - x1 C, , X
Page 202 :
Class-X Mathematics, , 192, , Example-22. The end points of a line segment are (2, 3) and (4, 5). Find the slope of the line segment., Solution : The end points of the line segment are (2, 3) and (4, 5), the slope of the line segment is, m=, , y2 - y1 5 - 3 2, =, = =1, x2 - x1 4 - 2 2, , A, , Slope of the given line segment is 1., , G, AN, , D O T HIS, Find the slope of AB , where, A(4, -6), B(7, 2), , 3., , A(-2, -5), B(1, -7), , 2., , A(8, -4), B(-4, 8), , AN, , 1., , TRY THIS, , T,, TE, L, , suur, Find the slope of AB , where, 1., A(2, 1), B(2, 6), 2., A(-4, 2), B(-4, -2), 3., A(-2, 8), B(-2, -2), suur, 4., Justify that the line AB formed by points given in the above three examples is, parallel to Y-axis. What can you say about the slope in each case? Why?, , SC, ER, , T HINK & D ISCUSS, , suur, Find the slope of AB passing through A(3, 2) and B(-8, 2), suur, Is the line AB parallel to X-axis ? Why?, , Think and discuss with your friends in groups., , Example-23. Determine x so that 2 is the slope of the line passing through P(2, 5) and Q(x, 3)., , Solution : Slope of the line passing through P(2, 5) and Q(x, 3) is 2., Here, x1 = 2, y1 = 5,, Slope of PQ =, , x2 = x,, , y2 = 3, , y2 - y1 3 - 5, -2, -2, =, =, Þ, =2, x2 - x1 x - 2 x - 2, x-2, , Þ -2 = 2x - 4, , Þ 2x = 2, , Þ x=1, , Free Distribution by T.S. Government 2021-22
Page 203 :
Coordinate Geometry, , 193, , EXERCISE - 7.4, (4, -8) and (5, -2), , (ii), , (0, 0) and ( 3,3), , (iii), , (2a, 3b) and (a, -b), , (iv) (a, 0) and (0, b), (v), , A(-1.4, -3.7) and B(-2.4, 1.3), , 1ö, æ 1 ö, æ, (vii) Aç -3 , 3÷ and Bç -7, 2 ÷, 2ø, è 2 ø, è, , T,, TE, L, , (viii) A(0, 4) and B(4, 0), , AN, , (vi) A(3, -2) and B(-6, -2), , G, AN, , (i), , A, , 1. Find the slope of the line passing through the given two points, , O PTIONAL E XERCISE, [For extensive learning], , 1. Centre of a circle Q is on the Y-axis. The circle passes through the points (0, 7) and, (0, -1). If it intersects the positive X-axis at (p, 0), what is the value of ‘p’?, , SC, ER, , 2. DABC is formed by the points A(2, 3), B(-2, -3), C(4, -3). What is the point of intersection, of the side BC and the bisector of angle A?, 3. The side BC of an equilateral triangle DABC is parallel to X-axis. Find the slopes of the, lines along sides BC, CA and AB., , 4. Find the centroid of the triangle formed by the line 2x + 3y - 6 = 0, with the coordinate, axes., , Free Distribution by T.S. Government 2021-22
Page 205 :
8, , A, , Similar Triangles, , 8.1 I NTRODUCTION, , G, AN, , D, , T,, TE, L, , AN, , There is a tall tree in the, backyard of Snigdha’s house., A, She wants to find out the height, of that tree but she is not sure, how to find it. Meanwhile, her, uncle arrives at home. Snigdha, requests her uncle to help her to, B, E, C, find the height of the tree. He, thinks for a while and then asks her to bring a mirror. He places it on the ground at a certain, distance from the base of the tree. He then asked Snigdha to stand on the otherside of the mirror, at such a position from where she is able to see the top of the tree in that mirror., When we draw the figure from (AB) girl to the mirror (C) and mirror to the tree (DE) as, above, we observe triangles DABC and DDEC. Now, what can you say about these two, triangles? Are they congruent? No, because although they have the same shape their sizes are, different. Do you know what we call the geometrical figures which have the same shape, but are, not necessarily of the same size? They are called similar figures., How do we know the height of a tree or a mountain?, , •, , How do we know the distances of far away objects such as Sun or Moon?, , SC, ER, , •, , Do you think these can be measured directly with the help of a measuring tape? The fact is that, all these heights and distances have been found out using the idea of indirect measurements which, is based on the principle of similarity of figures., , 8.2 S IMILAR F IGURES, , (i), , (ii), , (iii), , Observe the object (car) in the figure (i)., If breadth of the figure is kept the same and the length is doubled, it appears as in fig.(ii).
Page 206 :
Class-X Mathematics, , 196, , If the length in fig.(i) is kept the same and its breadth is doubled, it appears as in fig.(iii)., Now, what can you say about fig.(ii) and (iii)? Do they resemble fig.(i)? We find that the, figure is distorted. Can you say that they are similar? No, they have same shape, yet they are not, similar., , (i), , T,, TE, L, , AN, , G, AN, , A, , Think what a photographer does when she prints photographs of different sizes from the, same film (negative) ? You might have heard about stamp size, passport size and post card size, photographs. She generally takes a photograph on a small size film, say 35 mm., and then, enlarges it into a bigger size, say 45 mm (or 55 mm). We observe that every line segment of the, smaller photograph is enlarged in the ratio of 35 : 45 (or 35 : 55). Further, in the two photographs, of different sizes, we can see that the corresponding angles are equal. So, the photographs are, similar., , (ii), , (iii), , Similarly, in geometry, two polygons of the same number of sides are similar if their, corresponding angles are equal and their corresponding sides are in the same ratio or proportion., A polygon in which all sides and angles are equal is called a regular polygon., The ratio of the corresponding sides is referred to as scale factor (or representative factor)., In real life, blue prints for the construction of a building are prepared using a suitable scale factor., , D ISCUSS, , SC, ER, , T HINK, , AND, , Give some more examples from your daily life where scale factor is used., , All regular polygons having the same number of sides are always similar. For example, all, squares are similar, all equilateral triangles are similar and so on., Circles with same radius are, congruent and those with different radii are, not congruent. But, as all circles have same, shape and different size, they are all similar., We can say that all congruent figures, are similar but all similar figures need not, be congruent., , Similar, Squares, , Similar equilateral, triangles, , Similar, Circles, , Free Distribution by T.S. Government 2021-22
Page 207 :
Similar Triangles, , 197, , To understand the similarity of figures more clearly, let us perform the following activity., , A CTIVITY, , the roof. Fix a glowing bulb at the point of suspension. Then, a shadow, of quadrilateral ABCD is cast on the table. Mark the outline of the, , A, , Suspend a transparent plastic sheet horizontally from the ceiling of, A, , D, , G, AN, , shadow as quadrilateral A ¢ B¢ C¢ D¢ ., , B, , Now, this quadrilateral A ¢ B¢ C¢ D¢ is enlargement or magnification, , A’, D’, , C, , B’, C’, , same shape but of different sizes., , AN, , of quadrilateral ABCD. Further, A ¢ lies on ray OA where ‘O’ is the, uuur, uuur, uuur, bulb, B¢ on OB , C¢ on OC and D¢ on OD . Quadrilaterals ABCD and A ¢ B¢ C¢ D¢ are of the, , A¢ corresponds to vertex A and we denote it symbolically as A ¢ « A. Similarly B¢ « B,, , T,, TE, L, , C¢ « C and D¢ « D., , By actually measuring angles and sides, you can verify, (i) ÐA = ÐA¢ , ÐB = ÐB¢ , ÐC = ÐC¢ , ÐD = ÐD¢, (ii), , and, , AB, BC, CD, DA ., =, =, =, A¢ B¢, B¢C¢ C¢D¢ D¢A¢, , This emphasises that two polygons with the same number of sides are similar if, , SC, ER, , (i) All the corresponding angles are equal and, , (ii) All the lengths of the corresponding sides are in the same ratio (or in proportion), Is a square similar to a rectangle? In both the figures, corresponding angles are equal but, , their corresponding sides are not in the same ratio. Hence, they are not similar. For similarity of, polygons only one of the above two conditions is not sufficient, both have to be satisfied., , T HINK, , AND, , D ISSUSS, , •, , Can you say that a square and a rhombus are similar? Discuss with your friends., , •, , Are any two rectangles similar? Justify your answer., , Free Distribution by T.S. Government 2021-22
Page 208 :
Class-X Mathematics, , 198, , D O T HIS, 1., , Fill in the blanks with similar / not similar., (i) All squares are ........................, (ii) All equilateral triangles are ........................, , A, , (iii) All isosceles triangles are ........................, , G, AN, , (iv) Two polygons with same number of sides are ........................ if their corresponding, angles are equal and corresponding sides are equal., (v) Reduced and Enlarged photographs of an object are ........................, (vi) Rhombus and squares are ........................ to each other., 2. Write True / False for the following statements., , AN, , (i) Any two similar figures are congruent., (ii) Any two congruent figures are similar., , (iii) Two polygons are similar if their corresponding angles are equal., , T,, TE, L, , 3. Give two different examples of pair of, (i) Similar fgures, , 8.3 S IMILARITY, , OF, , (ii) Non similar figures, , T RIANGLES, , In the example of finding a tree’s height by Snigdha, we had drawn two triangles which, showed the property of similarity. We know that, two triangles are similar if their, , SC, ER, , (i) Corresponding angles are equal and, , (ii) Lengths of the corresponding sides are in the same ratio (in proportion), In DABC and DDEC in the introduction,, ÐA = ÐD , ÐB = ÐE , ÐACB = ÐECD, , Also, , DE, EC, DC, =, =, = K (scale factor), AB, BC, AC, , D, A, , B, , C, , E, , thus DABC is similar to DDEC., , Symbolically we write DABC ~ DDEC, (Symbol ‘~’ is read as “Is similar to”), As we have stated that K is a scale factor, So, if K > 1, we get enlarged figures,, K = 1, we get congruent figures and, K < 1, we get reduced (or diminished) figures, , Free Distribution by T.S. Government 2021-22
Page 209 :
Similar Triangles, Further, in triangles DABC and DDEC, corresponding angles, are equal. So, they are called equiangular triangles. The ratio of any, two corresponding sides in two equiangular triangles is always the, same. For proving this, Basic Proportionality theorem is used. This, is also known as Thales Theorem., , 199, , Basic proportionality, theorem?, , G, AN, , A, , To understand Basic proportionality theorem or Thales theorem,, let us do the following activity., , A CTIVITY, , A, , Take any ruled paper and draw a triangle on it with base on, one of the lines. Several lines will cut the triangle ABC. Select, any one line among them and name the points where it meets the, sides AB and AC as P and Q., , Q, , AN, , P, , AP, AQ, B, C, and, . What do you observe?, PB, QC, The ratios will be equal. Why ? Is it always true? Try for different lines intersecting the, triangle. We know that all the lines on a ruled paper are parallel and we observe that every, time the ratios are equal., , T,, TE, L, , Find the ratio of, , So in DABC, if PQ || BC then, , AP, AQ, =, ., PB, QC, , This is known as the result of basic proportionality theorem., , SC, ER, , 8.3.1 B ASIC P ROPORTIONALITY T HEOREM (T HALES T HEOREM ), Theorem-8.1 : If a line is drawn parallel to one side of a triangle to intersect the other two sides, in distinct points, then the other two sides are divided in the same ratio., Given : In DABC, DE || BC, and DE intersects sides AB and AC at D and E respectively., , RTP:, , AD AE, =, DB EC, , Construction : Join B, E and C, D and then draw, , A, , DM ^ AC and EN ^ AB., Proof : Area of DADE =, , 1, ´ AD ´ EN, 2, , Area of DBDE =, , 1, ´ BD ´ EN, 2, , Free Distribution by T.S. Government 2021-22, , N, D, , B, , M, E, , C
Page 211 :
Similar Triangles, , 201, , Similarly, joining B2C2, B3C3 and B4C4, you see that, AB2 AC 2 2, and, =, =, B2 B C 2 C 3, , Y, C4, C3, C2, C1, , AB3 AC3 3, and, =, =, B3 B C3C 2, , B1 B2 B3 B4, , B, , X, , A, , A, , C, , G, AN, , AB4 AC 4 4, and, =, =, B4 B C 4 C 1, , check whether C1B1 || C2B2 || C3B3 || C4 B4 || CB?, , From this we obtain the following theorem called converse of the Thales theorem, , AN, , Theorem-8.2 : If a line divides two sides of a triangle in the same ratio, then the line is parallel to, the third side., , RTP : DE || BC, , AD AE, =, DB EC, , T,, TE, L, , Given : In DABC, a line DE is drawn such that, , A, , Proof : Assume that DE is not parallel to BC then draw the line, DE1 parallel to BC, So, , D, , E, , (why ?), , AE AE ¢, =, (why ?), EC E¢C, , B, , SC, ER, , \, , AD AE ¢, =, DB E¢C, , 1, , E, , Adding 1 to both sides of the above, you can see that E and E¢ must coincide (why ?), , TRY THIS, , 1. In DPQR, E and F are points on the sides PQ and PR respectively. For each of the, following, state whether EF ||QR or not?, (i) PE = 3.9 cm EQ = 3 cm PF = 3.6 cm and FR = 2.4 cm, (ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm., (iii) PQ = 1.28 cm PR = 2.56 cm PE = 1.8 cm and PF = 3.6 cm, , Free Distribution by T.S. Government 2021-22, , C
Page 212 :
202, , Class-X Mathematics, , 2. In the following figures DE || BC., , D, , E, , 7.2, , 3c, , m., , C, , B, , C, , A, , ., cm, m., , cm, , ., , E, , c, 5.4, , B, , m., , 1.5, , Find AD, , m., , D, , (ii), , c, 1.8, , Find EC, , 1c, , (i), , A, , A, , G, AN, , Construction : Division of a line segment (using Thales theorem), , 8, 7, 6, , Take a sheet of paper from a lined note book., Number the lines by 1, 2, 3, ... starting with the bottom, line numbered ‘0’., Take a thick cardboard paper (or file card or chart, strip) and place it against the given line segment AB, and transfer its length to the card. Let A1 and B1 denote, the points on the file card corresponding to A and B., , B1, , 5, , 4, , 3, , T,, TE, L, , ACTIVITY, , 9, , AN, , Madhuri drew a line segment. She wants to divide it, in the ratio of 3 : 2. She measured it by using a scale and, divided it in the required ratio. Meanwhile, her elder sister, came. She saw this and suggested Madhuri to divide the, line segment in the given ratio without measuring it. Madhuri, was puzzled and asked her sister for help to do it. Then her, sister explained. You may also do it by the following activity., , P1, , 2, , 1, 0, , A1, , A, 1, A, , B, B1, , SC, ER, , Now, place A1 on the zeroeth line of the lined, paper and rotate the card about A1 unitl point B1, falls on the 5th line (3 + 2)., Mark the point where the third line touches the file card, by P1., Again, place this card along the given line segment and transfer this point P1 and denote, it with ‘P’., So, ‘P’ is the required point which divides the given line segment in the ratio 3:2., Now, let us learn how this construction can be done., Given a line segment AB. We want to divide it in, A, B, the ratio m : n where m and n are both positive integers., Let us take m = 3 and n = 2., Steps :, 1. Draw a ray AX through A making an acute angle, with AB., , X, , Free Distribution by T.S. Government 2021-22
Page 213 :
Similar Triangles, 2. With ‘A’ as centre and with any length draw an arc, on ray AX and label the point A1., B, A1, , A2, , A3, , A4, , A5, , A, , B, , A1, 3. Using the, same compass, setting and with, X A as centre draw another arc and locate A ., 1, 2, , X, , A, , A, , 203, , G, AN, , 4. Like this, locate 5 points (=m + n) A1, A2, A3, A4, A5, such that AA1 = A1A2 = A2A3 = A3A4 = A4A5, , C, , 3, , A, , 2, , B, , A, , 5. Join A5B. Now through point A3(m = 3) draw a line parallel to 1 A2, A3, A5B (by making an angle equal to ÐBA 5A ) intersecting AB at C, A4, A5 X, and observe that AC : CB = 3 : 2., , Example-1. In DABC, DE || BC,, , AD 3, = and AC = 5.6cm. Find AE., DB 5, , T,, TE, L, , Solution : In DABC, DE || BC, Þ, , AN, , Now, let us solve some example problems using Thales theorem and its converse., , AD AE, =, (by Thales theorem), DB EC, , D, , A, , E, , AD 3, AE 3, =, =, So, DB 5, EC 5, , but, , SC, ER, , Given AC = 5.6 and AE : EC = 3 : 5., AE, 3, =, AC - AE 5, , AE, 3, =, (cross multiplication), 5.6 - AE, 5, , 5AE = (3 ´ 5.6) - 3AE, , 8AE = 16.8, AE =, , 16.8, = 2.1cm., 8, , Free Distribution by T.S. Government 2021-22, , B, , C
Page 214 :
Class-X Mathematics, , 204, , B, , Example-2. In the given figure, LM || AB, AL = x - 3, AC = 2x, BM = x - 2, M, , and BC = 2x + 3 find the value of x, Solution : In DABC, LM || AB, AL BM, Þ, =, (by B.P.T), LC MC, , C, , A, G, AN, , x -3, x-2, =, 2 x - ( x - 3) (2 x + 3) - ( x - 2), x-3 x-2, =, (cross multiplication), x+3 x+5, , (x - 3) (x + 5) = (x - 2) (x + 3), , AN, , x2 + 2x - 15 = x2 + x - 6, 2x - x = - 6 + 15, x=9, , T,, TE, L, , D O T HIS, , C, , Find the value(s) of x in the given figures., , D, , 1. In DABC, DE || AB, AD = 8x + 9, CD = x + 3, , C, , BE = 3x + 4, CE = x., , A, , E, B, , E, , In DABC, DE || BC. AD = x, DB = x - 2,, , SC, ER, , 2., , A, , L, , AE = x + 2 and EC = x - 1., , A, , D, , B, , Example-3. The diagonals of a quadrilateral ABCD intersect each other at point ‘O’ such that, AO CO, =, . Prove that ABCD is a trapezium., BO DO, , Solution : Given : In quadrilateral ABCD ,, , AO, CO, =, ., BO, DO, , RTP : ABCD is a trapezium., Construction : Through ‘O’ draw a line parallel to AB which meets DA at X., Proof : In DDAB, XO || AB, Þ, , DX, DO, =, XA, OB, , (by construction), (by basic proportionality theorem), , Free Distribution by T.S. Government 2021-22
Page 215 :
Similar Triangles, ..... (1), , AO, CO, =, BO, DO, , (given), , AO, BO, =, CO, OD, , ..... (2), , X, O, B, , A, , G, AN, , From (1) and (2), AX, AO, =, XD, CO, AX AO, =, XD OC, , AN, , In DADC, XO is a line such that, Þ XO || DC, , C, , D, , A, , again, , AX, BO, =, XD, OD, , 205, , (by converse of the basic the proportionality theorem), , Þ AB || DC, , T,, TE, L, , In quadrilateral ABCD, AB || DC, Þ ABCD is a trapezium, , (by definition), , Hence proved., , Example-4. In trapezium ABCD, AB || DC. E and F are points on non-parallel sides AD and, , SC, ER, , BC respectively such that EF || AB. Show that, , AE BF, ., =, ED FC, , Solution : Let us join A, C to intersect EF at G., AB || DC and EF || AB (given), Þ EF || DC (Lines parallel to the same line are parallel to each other), , In DADC, EG || DC, , So, , AE AG, =, (by BPT), ED GC, , E, , ...(1), , Similarly, In DCAB, GF || AB, CG CF, AG BF, =, =, (by BPT) i.e.,, GA FB, GC FC, , B, , A, , D, , ...(2), , From (1) & (2) AE = BF ., ED FC, , Free Distribution by T.S. Government 2021-22, , G, , F, C
Page 216 :
Class-X Mathematics, , 206, , P, , E XERCISE - 8.1, 1. In DPQR, ST is a line such that, , PS PT, and, =, SQ TR, , S, , T, , A, , also ÐTSP = ÐPRQ ., Prove that DPQR is an isosceles triangle., Q, , R, , G, AN, , B, M, , 2. In the given figure, LM || CB and LN || CD, A, , C, , L, , Prove that, , A, , AN, , N, , AM AN, =, AB, AD, , D, , 3. In the given figure, DE || AC and DF || AE, , D, , T,, TE, L, , BF BE, Prove that, ., =, FE EC, , B, , F, , C, , E, , 4. Prove that a line drawn through the mid-point of one side of a triangle parallel to another, side bisects the third side (Using basic proportionality theorem)., , SC, ER, , 5. Prove that a line joining the midpoints of any two sides of a triangle is parallel to the third, side. (Using converse of basic proportionality theorem), P, , 6. In the given figure, DE || OQ and DF || OR. Show, that EF || QR., , D, E, , P, , Q, , A, , 7., , O, B, Q, , C, R, , F, , O, R, , In the adjacent figure, A, B and C are points on OP, OQ, and OR respectively such that AB || PQ and AC||PR., Show that BC || QR., , Free Distribution by T.S. Government 2021-22
Page 217 :
Similar Triangles, , 207, , 8. ABCD is a trapezium in which AB||DC and its diagonals intersect each other at point ‘O’., Show that AO = CO ., BO DO, , ABD, , D ISCUSS, , G, AN, , T HINK, , A, , 9. Draw a line segment of length 7.2 cm and divide it in the ratio 5 : 3. Measure the two parts, and verify the results., , Discuss with your friends that in what way similarity of triangles is different from, similarity of other polygons?, , 8.4 C RITERIA, , FOR, , S IMILARITY, , OF, , T RIANGLES, , T,, TE, L, , AN, , We know that two triangles are similar if corresponding angles are equal and corresponding, sides are proportional. For checking the similarity of two triangles, we should check for the, equality of corresponding angles and equality of ratios of their corresponding sides. Let us make, an attempt to arrive at certain criteria for similarity of two triangles. Let us perform the following, activity., , A CTIVITY, , Use a protractor and ruler to draw two non congruent triangles so that each triangle, should have 40° and 60° angle. Check the figures made by you by measuring the third angles, of two triangles., It should be each 80° (why?), , SC, ER, , Measure the lengths of the sides of the triangles and compute the ratios of the lengths of the, corresponding sides., Are the triangles similar?, , B, , °, 40, , P, A, , 60, , °, , C, , Q, , 40°, , 60°, , This activity leads us to the following criterion for similarity of two triangles., , Free Distribution by T.S. Government 2021-22, , R
Page 218 :
Class-X Mathematics, , 208, , 8.4.1 AAA CRITERION FOR SIMILARITY OF TRIANGLES, Theorem-8.3 : In two triangles, if corresponding angles are equal, then their corresponding, sides are in proportion and hence the triangles are similar., A, , Given : In triangles ABC and DEF, ÐA = ÐD , ÐB = ÐE and ÐC = ÐF, AB BC, AC, =, =, DE EF, DF, B, Construction : If AB<DE and AC<DF, locate points P and Q on DE and DF, , C, , D, , G, AN, , respectively, such that AB = DP and AC = DQ. Join PQ., , A, , RTP :, , Proof : DABC @ DDPQ (why ?), , T,, TE, L, , AN, , This gives ÐB = ÐP = ÐE and PQ || EF (How ?), P, Q, DP DQ, AB, AC, \, =, =, (why ?), (why ?) i.e.,, PE QF, DE, DF, AB, BC, AB, BC, AC, E, F, =, =, =, . Hence proved., Similarly, and So, DE, EF, DE, EF, DF, In the above construction, if AB=DE or AB>DE, what will you do?, Note : If two angles of a triangle are respectively equal to the two angles of another triangle, then, by the angle sum property of a triangle, third angles will also be equal., So, AA similarity criterion is stated as if two angles of one triangle are respectively equal to, the two angles of anther triangle, then the two triangles are similar., What about the converse of the above statement?, , If the sides of a triangle are respectively proportional to the sides of another triangle, is it, true that their corresponding angles are equal? Let us exercise it through an activity., , SC, ER, , A CTIVITY, , Draw two triangles ABC and DEF such that AB = 3 cm, BC = 6 cm, CA = 8 cm,, DE = 4.5 cm, EF = 9 cm and FD = 12 cm., D, , A, , B, , C, , E, , F, , AB, BC, CA 2, =, =, = ., DE, EF, FD 3, Now, measure the angles of both the triangles. What do you observe? What can you, say about the corresponding angles? They are equal, so the triangles are similar. You can, verify it for different triangles., , So you have, , From the above activity, we can write the following criterion for similarity of two triangles., , Free Distribution by T.S. Government 2021-22
Page 219 :
Similar Triangles, , 209, , 8.4.2. SSS Criterion for Similarity of Triangles, Theorem-8.4 : In two triangles, if corresponding sides are proportional, then their corresponding, angles are equal and hence the triangles are similar., A, , AB, BC, CA, =, =, (< 1), DE, EF, FD, , RTP : ÐA = ÐD , ÐB = ÐE , ÐC = ÐF, , G, AN, , B, , A, , Given : DABC and DDEF are such that, , C, , Construction : Let DE > AB. Locate points P and Q on DE and DF respectively, D, , Proof :, , AN, , such that AB = DP and AC = DQ. Join PQ., DP, DQ, and PQ || EF (why ?), =, PE, QF, , P, , Q, , \, , So,, , T,, TE, L, , So, ÐP = ÐE and ÐQ = ÐF (why ?), DP, DQ, PQ, =, =, DE, DF, EF, , E, , F, , DP, DQ, BC, =, =, (why ?), DE, DF, EF, , SC, ER, , So, BC = PQ (Why ?), , DABC @ DDPQ (why ?), , So, ÐA = ÐD , ÐB = ÐE and ÐC = ÐF (How ?), , We studied that for similarity of two polygons any one condition is not sufficient. But for, , the similarity of triangles, there is no need for fulfillment of both the conditions as one automatically, implies to the other. Now, let us look for SAS similarity criterion. For this, let us perform the, following activity., , Free Distribution by T.S. Government 2021-22
Page 221 :
Similar Triangles, , 211, , TRY THIS, 1. Are triangles formed in each figure similar? If so, name the criterion of similarity. Write, the similarity relation in symbolic form., L, F, , (i), , P, , (ii), , I, , Y, 3, , B, , cm, , 4 cm., , A, , (viii), , ., , R, , 6 cm ., , 5 cm., , 6, , P, , 60°, , 60° 80°, , B, , CQ, , 2 cm., , 40°, , P, , 70°, , 70°, , 80°, , 40°, , C Q, , 2.5 cm., , B, , P, , 3c, m, ., , 31, 3, , C, , AN, , O, , (vi), , T,, TE, L, , 2 cm., , A, , J, , A, , P, , Q, , 2, , B, , C, , A, , 3, , P, , 5, , B, , (v), , G, AN, , (iv), , 2, , X, 3, , (vii), , A, , A, 2, , R, , Q, , K, , (iii), , A, , H, G, , N, , M, , Q, 10, c, , 5c, , R, , m., R, , m., , B, , C, , 2. If pairs of the triangles are similar and then find the value of x., , SC, ER, , (i), , P S, , 4.5, , 5, , x, , 3, , °x, 10, 70°, 1, B, 3 Q 3, R, , R L, , A, , (iii), , x, , 24, , Dx, , A, 2, , E, , S, , P, , 9, , B, T, , x, , X, , 4, M, , (v), Q, , 5, 15, , C, , 6, , (iv), , 14, , C, , 22, B, , A, , (ii), , P, , 5, , Q, , T, , x, , N, x, , A, , (vi), R, , 7.5, , Z, , 18, , B, , 12, , Y, , Free Distribution by T.S. Government 2021-22, , C
Page 222 :
Class-X Mathematics, , 212, , A, , E, A, , 1.6 cm, , (vii), , D, 3cm, , 1.5 cm C, , D, 15cm, , B, , 4cm E, , C, , x, , A, , B, , (viii)5cm, , x, , G, AN, , Construction : To construct a triangle similar to a given triangle as per given scale factor., a) Construct a triangle similar to a given triangle ABC with its sides equal to, sides of DABC (scale factor, , 3, ), 4, , 3, of corresponding, 4, , A, , AN, , Steps : 1. Draw a ray BX, making an acute angle with BC on the side, opposite to vertex A., , 2. Locate 4 points B1, B2, B3 and B4 on BX so that BB1 = B1B2 =, B2B3 = B3B4., , 1, , A, , 1, , C, , B, , T,, TE, L, , 3. Join B4C and draw a line through B3 which is parallel to B4C, intersecting BC at C¢ ., 4. Draw a line through C¢ parallel to CA to intersect AB at A¢ ., , B1, , B2, , B3, , C, , B4, X, , So D A¢BC¢ is the required triangle., , Let us take some examples to illustrate the use of these criteria., , SC, ER, , Example-5. A person 1.65m tall casts 1.8m shadow. At the same instance, a lamp post casts, a shadow of 5.4 m. Find the height of the lamppost., P, , A, , h m., , 1.65 m., , B, , 1.8 m., , C, , Q, , 5.4 m., , R, , Solution: After representing in the form of a figure, In DABC and DPQR, ÐB = ÐQ = 900., , ÐC = ÐR (AC || PR, all sun’s rays are parallel at any instance), DABC ~ DPQR ( by AA similarity), , AB BC, =, (corresponding parts of Similar triangles), PQ QR, , Free Distribution by T.S. Government 2021-22
Page 223 :
Similar Triangles, , 213, , 1.65 1.8, =, PQ, 5.4, PQ =, , 1.65 ´ 5.4, = 4.95m, 1.8, , A, , The height of the lamp post is 4.95m., , G, AN, , Example-6. A man sees the top of a tower in a mirror which is at a distance of 87.6m from the, tower. The mirror is on the ground facing upwards. The man is 0.4m away from the, mirror and his height is 1.5m. How tall is the tower?, Solution : After representing in the form of a figure, In DABC & DEDC, ÐCBA = ÐEDC = 90°, ÐACB = ÐDCE (Complements of the, angle of incidence and angle of reflection, are congruent), , AN, , AB BC, 1.5, 0.4, =, Þ, =, ED CD, h, 87.6, h=, , h, , 1.5 m., , T,, TE, L, , DABC ~ DEDC (by AA similarity), , A, , E, , B, , 0.4 m. C, , 87.6 m, , Mirror, , D, Tower, , 1.5 ´ 87.6, = 328.5m, 0.4, , Hence, the height of the tower is 328.5m., , SC, ER, , Example7. Gopal is worrying that his neighbour can peep into his living room from the top floor, of his house. He has decided raise the height of the fence that is high enough to block the, view from his neighbour’s top floor window. What should be the height of the fence? The, measurements are given in the figure., Solution : After representing in the form of a figure, In DABD & DACE, ÐB = ÐC = 90°, , E, , ÐA = ÐA (common angle), 1.2 m., DABD ~ DACE, (by AA similarity), C, , AB, BD, 2, BD, =, Þ, =, AC, CE, 8, 1.2, BD =, , 2 ´ 1.2 2.4, =, = 0.3m, 8, 8, , 1.5 m., R, , D, B, 1.5 m., Q, 8 m., , A, 1.5 m., P, 2m., , Total height of the fence required is 1.5 m. + 0.3 m. = 1.8m to block the neighbour’s view., , Free Distribution by T.S. Government 2021-22
Page 224 :
Class-X Mathematics, , 214, , E XERCISE - 8.2, , A, , 1. In the given figure, ÐADE = ÐCBA, (i) Show that DABC ~ DADE, (ii) If AD = 3.8 cm, AE = 3.6cm,, , D, , E, , BE = 2.1 cm and BC = 4.2 cm,, , B, , A, , C, , find DE., , G, AN, , 2. The perimeters of two similar triangles are 30 cm and 20 cm respectively. If one side of, the first triangle is 12 cm, determine the corresponding side of the second triangle., A, , 3. In the given figure, AB || CD || EF., given that AB=7.5 cm, DC= y cm, , m, , m, xc, y cm, , EF = 4.5 cm and BC = x cm, find, the values of x and y., , E, , T,, TE, L, , B, , AN, , 3c, , m, , C, , 4.5, c, , 7.5, , cm, , F, , D, , 4. A girl of height 90 cm is walking away from the base of a lamp post at a speed of, 1.2 m/sec. If the lamp post is 3.6m above the ground, find the length of her shadow after, 4 seconds., 5. Given that DABC ~ DPQR, CM and RN are respectively the medians of DABC and, C, DPQR. Prove that, (i) DAMC ~ DPNR, , R, , SC, ER, , CM AB, =, (ii), RN PQ, , (iii) DCMB ~ DRNQ, , A, , M, , P, , N, , Q, , 6. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the, point ‘O’. Using the criterion of similarity for two triangles, show that, , 7. AB, CD, PQ are perpendicular to BD., If AB = x, CD = y and PQ = z, , OA OB, =, ., OC OD, , A, C, , 1 1 1, prove that + = ., x y z, B, , P, z, , y, , Q, , D, , Free Distribution by T.S. Government 2021-22
Page 225 :
Similar Triangles, , 215, , 8. A flag pole 4m tall casts a 6 m shadow. At the same time, a nearby building casts a shadow, of 24m. How tall is the building ?, 9. CD and GH are respectively the bisectors of ÐACB and ÐFGE such that D and H lie, on sides AB and FE of DABC and DFEG respectively. If DABC ~ DFEG, then show that, CD AC, =, (ii), DDCB ~ DHGE, (iii) DDCA ~ DHGF, (i), GH FG, , G, AN, , A, , 10. AX and DY are altitudes of two similar triangles DABC and DDEF. Prove that AX : DY =, AB : DE., , 11. Construct a DABC with your own measurements. Construct another triangle similar to, 5, of the corresponding sides of the triangle ABC., 3, 12. Construct a triangle of sides 4cm, 5 cm and 6 cm. Then, construct a triangle similar to it,, , DABC, with its sides equal to, , 2, of the corresponding sides of the first triangle., 3, , AN, , whose sides are, , 13. Construct an isosceles triangle whose base is 8cm and altitude is 4 cm. Then, draw another, , 8.5 A REAS, , T,, TE, L, , 1, triangle whose sides are 1 times the corresponding sides of the isosceles triangle., 2, OF, , SIMILAR T RIANGLES, , SC, ER, , For two similar triangles, ratios of, their corresponding sides is the same. Do, you think there is any relationship between, the ratios of their areas and the ratios of, their corresponding sides ? Let us do the, following activity to understand this., , ACTIVITY, , Make a list of pairs of similar, polygons in this figure., Find, , (i) the ratio of similarity (scale factor), and, (ii) the ratio of areas., You will observe that ratio of areas is the square of the ratio of their corresponding sides., Let us prove it like a theorem., , Free Distribution by T.S. Government 2021-22
Page 228 :
218, , Class-X Mathematics, , DAOB ~ DCOD (by AA similarity), ar(DAOB) AB2, =, ar( DCOD) DC 2, , E XERCISE - 8.3, , G, AN, , \ ar(DAOB) : ar(DCOD) = 4 : 1., , A, , (2DC) 2 4, =, =, (DC)2 1, , AN, , 1. D, E, F are mid points of sides BC, CA, AB of DABC. Find the ratio of areas of DDEF, and DABC., 2. In DABC, XY || AC and XY divides the triangle into two parts of equal area. Find, , AX, ., XB, , T,, TE, L, , 3. Prove that the ratio of areas of two similar triangles is equal to the square of the ratio of, their corresponding medians., 4. DABC ~ DDEF. BC = 3cm, EF = 4cm and area of DABC = 54 cm2. Determine the area, of DDEF., , SC, ER, , 5. ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm,, 1, BP = 3cm, AQ = 1.5 cm and CQ = 4.5 cm, prove that area of DAPQ =, (area of, 16, DABC)., 6. The areas of two similar triangles are 81cm2 and 49 cm2 respectively. If the altitude of the, bigger triangle is 4.5 cm. Find the corresponding altitude of the smaller triangle., , 8.6 P YTHAGORAS T HEOREM, You are familar with the Pythagoras theorem. You had verified this theorem through some, , activities. Now, we shall prove this theorem using the concept of similarity of triangles. For this,, we make use of the following result., Theorem-8.7 : If a perpendicular is drawn from the vertex of the right angle of a right triangle to, , the hypotenuse, then the triangles on both sides of the perpendicular are similar to the whole, triangle and to each other., , Free Distribution by T.S. Government 2021-22
Page 229 :
Similar Triangles, , 219, , Proof: ABC is a right triangle, right angled at B. Let BD be the perpendicular to hypotenuse AC., B, , In DADB and DABC, ÐA = ÐA, , So DADB ~ DABC (how?), , ...(1), , Similarly, DBDC ~ DABC (how?), , ...(2), , A, , A, , and ÐBDA = ÐABC (why?), C, , G, AN, , So from (1) and (2), triangles on both sides of the perpendicular BD are similar to the, triangle ABC., Also since DADB ~ DABC, DBDC ~ DABC, , (Transitive Property), , This leads to the following theorem., AND, , D ISCUSS, , T,, TE, L, , T HINK, , AN, , So DADB ~ DBDC, , For a right angled triangle with integer sides atleast one of its measurements must be, an even number. Why? Discuss this with your friends and teachers., 8.6.1 P YTHAGORAS T HEOREM (B AUDHAYANA T HEOREM ), Theorem-8.8 : In a right triangle, the square of length of the hypotenuse is equal to the sum of, the squares of lengths of the other two sides., B, , SC, ER, , Given: DABC is a right triangle right angled at B., RTP : AC2 = AB2 + BC2, , Construction : Draw BD ^ AC., Proof : DADB ~ DABC, Þ, , AD AB, =, AB AC, , AD . AC = AB2, , A, , (sides are proportional), ...(1), , Also, DBDC ~ DABC, Þ, , CD BC, =, BC AC, , CD . AC = BC2, , ...(2), , Free Distribution by T.S. Government 2021-22, , C
Page 230 :
220, , Class-X Mathematics, , On adding (1) & (2), AD . AC + CD . AC = AB2 + BC2, AC (AD + CD) = AB2 + BC2, AC . AC = AB2 + BC2, , A, , AC 2 = AB2 + BC2, , G, AN, , The above theorem was earlier given by an ancient Indian mathematician Baudhayana, (about 800 BC) in the following form., “The diagonal of a rectangle produces by itself the same area as produced by its both sides, (i.e. length and breadth).” So, this theorem is also referred to as the Baudhayana theorem., What about the converse of the above theorem ?, We prove it like a theorem, as done earlier also., , T,, TE, L, , Given : In DABC, AC2 = AB2 + BC2, , AN, , Theorem-8.9 : In a triangle, if square of the length of one side is equal to the sum of squares of, the lengths of the other two sides, then the angle opposite to the first side is a right angle and the, triangle is a right angled triangle., A, , P, , RTP : ÐB = 900., Construction : Construct a right, angled triangle DPQR right, angled at Q such that PQ = AB, and QR = BC., , C, , SC, ER, , Proof : In DPQR, PR2 = PQ2, + QR2 (Pythagorean theorem as, ÐQ = 900), , PR2 = AB2 + BC2 (by construction), , but AC2 = AB2 + BC2 (given), , B, , R, , Q, , ...(1), ...(2), , \ AC = PR from (1) & (2), , Now In DABC and DPQR, AB = PQ (by construction), BC = QE (by construction), AC = PR (proved), \ DABC @ DPQR (by SSS congruency), \ ÐB = ÐQ (by cpct), , Free Distribution by T.S. Government 2021-22
Page 233 :
Similar Triangles, , 223, , C, , 3. In the given fig. if AD ^ BC, Prove that AB2 + CD2 = BD2 + AC2., , D, , B, , A, , Solution : Let the shortest side be x m., , G, AN, , A, , Example-14. The hypotenuse of a right triangle is 6m more than twice of the shortest side. If, the third side is 2 m. less than the hypotenuse, then find the sides of the triangle., Then hypotenuse = (2x + 6)m and third side = (2x + 4)m., By Pythagores theorem, we have, (2x + 6)2 = x2 + (2x + 4)2, x2 - 8x - 20 = 0, (x - 10) (x + 2) = 0, , T,, TE, L, , x = 10 or x = -2, , AN, , 4x2 + 24x + 36 = x2 + 4x2 + 16x + 16, , But, x can’t be negative as it is a side of a triangle., \ x = 10, , Hence, the sides of the triangle are 10m, 26m and 24m., , SC, ER, , Example-15. ABC is a right triangle right angled at C. Let BC = a, CA = b, AB = c and let p, 1, 1 1, be the length of perpendicular from C on AB. Prove that (i) pc = ab (ii) 2 = 2 + 2 ., p, a b, Solution :, A, , (i) CD ^ AB and CD = p., 1, ´ AB ´ CD, 2, 1, = cp ., 2, 1, also area of DABC = ´ BC ´ AC, 2, 1, = ab, 2, 1, 1, cp = ab, 2, 2, cp = ab, ...(1), , Area of DABC =, , Free Distribution by T.S. Government 2021-22, , c D, b, p, , B, , a, , C
Page 234 :
Class-X Mathematics, , 224, , (ii) Since DABC is a right triangle right angled at C., AB2 = BC2 + AC2, c2 = a2 + b2, 2, , G, AN, , A, , æ ab ö, 2, 2, ç ÷ = a +b, è p ø, 1 a 2 + b2, 1, 1, = 2 2 = 2 + 2., 2, p, ab, a, b, , E XERCISE - 8.4, , A, , 1. Prove that the sum of the squares of the sides of a rhombus, is equal to the sum of the squares of its diagonals., , D, , AN, , 2. ABC is a right triangle right angled at B. Let D and E be, any points on AB and BC respectively., Prove that AE2 + CD2 = AC2 + DE2., , B, , C, , E, , T,, TE, L, , 3. Prove that three times the square of any side of an, equilateral triangle is equal to four times the square of the altitude., 4. PQR is a triangle right angled at P and M is a point on QR such that PM ^ QR ., Show that PM2 = QM × MR., , 5. ABD is a triangle right angled at A and AC ^ BD, , C, , Show that (i) AB2 = BC × BD., , SC, ER, , (ii) AC2 = BC × DC, , (iii) AD2 = BD × CD., , A, , B, 2, , 2, , 6. ABC is an isosceles triangle right angled at C. Prove that AB = 2AC ., , 7. ‘O’ is any point in the interior of a triangle ABC., , A, , If OD ^ BC, OE ^ AC and OF ^ AB, show that, (i) OA2+OB2+OC2-OD2-OE2-OF2 = AF2+BD2+CE2, , (ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2., , E, , F, O, B, , D, , C, , 8. A 24m long wire is attached to a vertical pole of height 18m. And it has a stake attached to, the other end. How far from the base of the pole should the stake be driven so that the, wire will be taut?, 9. Two poles of heights 6m and 11m stand on a plane ground. If the distance between the, feet of the poles is 12m find the distance between their tops., , Free Distribution by T.S. Government 2021-22
Page 235 :
Similar Triangles, 10. In an equilateral triangle ABC, D is a point on side BC such that BD =, 9AD2 = 7AB2., , 225, , 1, BC. Prove that, 3, , A, , 11. In the given figure, ABC is a triangle right angled at, B. D and E are ponts on BC trisect it., , G, AN, , A, , Prove that 8AE2 = 3AC2 + 5AD2., , B, , E, , C, D, , A, , E, , AN, , 12. ABC is an isosceles triangle right angled, at B. Similar triangles ACD and ABE, are constructed on sides AC and AB., Find the ratio between the areas of, DABE and DACD., , D, , B, , C, , T,, TE, L, , 13. Equilateral triangles are drawn on the three sides of a right angled triangle. Show that the, area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the, other two sides., 14. Prove that the area of the equilateral triangle described on the side of a square is half the, area of the equilateral triangles described on its diagonal., , 8.7 D IFFERENT, , FORMS OF THEORITICAL STATEMENTS, , 1. Negation of a statement :, , SC, ER, , We have a statement and if we add “Not” in the statement, we will get a new statement;, which is called negation of the statement., , For example take a statement “DABC is a equilateral”. If we denote it by “p”, we can, write like this., p : Triangle ABC is equilateral and its negation will be “Triangle ABC is not equilateral”., Negation of statement p is denoted by ~p; and read as negation of p. the statement ~p, negates the assertion that the statement p makes., When we write the negation of the statements, we would be careful that there should not, be any confusion in understanding the statement., Observe this example carefully, , p : All irrational numbers are real numbers. We can write negation of p like this., ~p : All irrational numbers are not real numbers., , Free Distribution by T.S. Government 2021-22
Page 236 :
226, , Class-X Mathematics, , How do we decide this negation is true or false? We use the following criterion “Let p be, a statement and ~p its negation. Then ~p is false whenever p is true and ~p is true whenever, p is false., For example, , s : 2 + 2 = 4 is True, , G, AN, , 2. Converse of a statement :, , A, , ~ s : 2 + 2 ¹ 4 is False, , A sentence which is either true or false is called a simple statement. If we combine two, simple statements, then we will get a compound statement. Connecting two simple statements, with the use of the words “If and then” will give a compound statement which is called, , AN, , implication (or) conditional., , Combining two simple statements p & q using if and then, we get p implies q which can be, denoted by p Þ q. In this p Þ q, suppose we interchange p and q we get q Þ p. This, , T,, TE, L, , is called its converse., , Example : p Þ q : In DABC, if AB = AC then ÐC = ÐB, Converse q Þ p : In DABC, if ÐC = ÐB then AB = AC, , 3. Proof by contradiction :, , In this proof by contradiction, we assume that the negation of the statement as true; which, , SC, ER, , we have to prove. In the process of proving, we get contradiction somewhere. Then, we, realize that this contradiction occurs because of our wrong assumption that the negation is, true. Therefore, we conclude that the original statement is true., , O PTIONAL E XERCISE, T, , [For extensive learning], , 1. In the given figure,, , P, , QT QR and Ð1 = Ð2 , prove that DPQS ~ DTQR., =, PR, QS, Q 1, , 2, R, , Free Distribution by T.S. Government 2021-22
Page 237 :
Similar Triangles, 2. Ravi is 1.82m tall. He wants to find the height, of a tree in his backyard. From the tree’s base, he walked 12.20 m. along the tree’s shadow, to a position where the end of his shadow, exactly overlaps the end of the tree’s shadow., He is now 6.10m from the end of the shadow., , 227, , E, C, 1.82 m., A, , 6.10 m., , 12.20 m., , B, , A, , How tall is the tree ?, , D, , 4. DABC and DAMP are two right triangles right, , C, , M, , AN, , angled at B and M respectively., Prove that (i) DABC ~ DAMP and, CA BC, =, (ii), ., PA MP, , G, AN, , 3. The diagonal AC of a parallelogram ABCD intersects DP at the point Q, where ‘P’ is any, point on side AB. Prove that CQ ´ PQ = QA ´ QD., , A, , P, , 1, 1 hour?, 2, , T,, TE, L, , B, 5. An aeroplane leaves an airport and flies due north, at a speed of 1000 kmph. At the same time, another aeroplane leaves the same airport and, flies due west at a speed of 1200 kmph. How far apart will the two planes be after, , 6. In a right triangle ABC right angled at C, P and Q are points on sides AC and CB respectively, which divide these sides in the ratio of 2 : 1., , SC, ER, , Prove that (i) 9AQ2 = 9AC2 + 4BC2, (ii) 9BP2 = 9BC2 + 4AC2, , (iii) 9(AQ2 + BP2) = 13AB2, , Suggested Projects, l, , Find the height of a tree/ tower/ temple etc. using the properties of similar triangles, use, the procedure discussed in ‘Introduction of Similar Triangles’, chapter., , W HAT WE H AVE D ISCUSSED, 1. Two figures having the same shape with all parts in proportion are, called similar figures., , Free Distribution by T.S. Government 2021-22
Page 238 :
228, , Class-X Mathematics, , 2. All the congruent figures are similar but the converse is not true., 3. Two polygons of the same number of sides are similar,, if, (i) their corresponding angles are equal and, (ii) their corresponding sides are in the same ratio (i.e. proportion), 4. If a line is drawn parallel to one side of a triangle to intersect the other two sides at distinct, points then the other two sides are divided in the same ratio., , G, AN, , A, , 5. If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the, third side., , 6. In two triangles, if corresponding angles are equal, then their corresponding sides are in the, same ratio and hence the two triangles are similar (AAA similarity), 7. If two angles of a triangle are equal to the two angles of another triangle, then third angles, of both triangles are equal by angle sum property of triangle., , AN, , 8. In two triangles, if corresponding sides are in the same ratio, then their corresponding, angles are equal and hence the triangles are similar. (SSS similar), 9. If one angle of a triangle is equal to one angle of another triangle and the including sides of, these angles are in the same ratio, then the triangles are similar. (SAS similarity), , T,, TE, L, , 10. The ratio of areas of two similar triangles is equal to the square of the ratio of their, corresponding sides., 11. If a perpendicular is drawn from the vertex of the right angle to the hypotenuse in a right, angle triangle, then the triangles formed on both sides of the perpendicular are similar to the, whole triangle and also to each other., 12. In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the, other two sides (Pythagorean Theorem)., , SC, ER, , 13. In a triangle, if square of one side is equal to the sum of the squares of the other two sides,, then the angle opposite to the first side is a right angle., , Puzzle, , Draw a triangle. Join the mid-point of the sides of the triangle. You get 4 triangles again, join the mid-points of these triangles. Repeat this process. All the triangles drawn are, similar triangles. Why ? Think and discuss with your friends., , Free Distribution by T.S. Government 2021-22
Page 239 :
9, , A, , Tangents and Secants, to a Circle, , G, AN, , 9.1 I NTRODUCTION, , We have seen that two lines in a plane may intersect at a point or may not intersect. In, some situations, they may coincide with each other., O, , T,, TE, L, , AN, , Similarly, what are the possible relative positions of a curve and a line given in a plane? A, curve may be a parabola as you have seen in polynomials or a simple closed curve like a “circle”, which is a collection of all those points on a plane that are at a constant distance from a fixed, point., Y, X, , SC, ER, , You might have seen circular objects rolling on a plane creating a path. For example;, bicycle wheel on a sandy field, wheels of train on the track etc., where a circle as well as a line, are involved., Let us observe the relative positions of a circle and a line are given in a plane., , 9.1.1 A LINE, , AND, , A CIRCLE, , You are asked to draw a circle and a line on a paper. Abhiram argues that there can only, be 3 possible ways of presenting them on a paper., Consider a circle with centre ‘O’ and a line PQ. The three possibilities are given in the, P, P, following figures., P, A, , O, , (i), , O, B, , Q, , (ii) Q, , O, , A, , (iii), , Q
Page 240 :
Class-X Mathematics, , 230, , In Fig.(i), the line PQ and the circle have no common point. In this case, PQ is a nonintersecting line with respect to the circle., In Fig.(ii), the line PQ intersects the circle at two points A and B. It forms a chord AB, with its end points A and B on the circle. In this case, the line PQ is a secant of the circle., , A, , In Fig.(iii), there is only one point A, common to the line PQ and the circle. This line is, called a tangent to the circle., , G, AN, , You can see that there cannot be any other position of the line with respect to the circle., We will study the existence of tangents to a circle and also study their properties and constructions., Do you know?, , The word ‘tangent’ comes from the latin word ‘tangere’, which means to touch and was, introduced by Danish mathematician Thomas Fineke in 1583., , Draw a circle with any radius. Draw four tangents at different, points. How many more tangents can you draw to this circle?, , T,, TE, L, , i., , AN, , D O T HIS, , ii. How many tangents can you draw to a circle from a point away, from it?, , p, , q, , l, m, , O, , iii. In the adjacent figure, which lines are tangents to the circle?, , 9.2 TANGENTS, , OF A, , CIRCLE, , We can see that tangent to a circle can be drawn at any point on the circle. How many, tangents can be drawn at any point on the circle?, , SC, ER, , To understand this let us consider the following activity., , ACTIVITY, , A, , Take a circular wire and attach a straight wire AB at a point P of, the circular wire, so that the system can rotate about the point P in a, P, O, B, plane., The, circular, wire, represents, a, circle, 11, 1, A, A, A, and the straight wire AB represents a line, Q, intersects the circle at point P., 1, Place the system on a table and gently rotate the wire AB about, Q, 2, the point P to get different positions of the straight wire as shown, O, P, in the figure. The wire intersects the circular wire at P and at one, Q, B, 3, of the points Q1, Q2 or Q3 etc. So while it generally intersects, circular wire at two points one of which is P in one particular, 11, 1, B, B, position, it intersects the circle only at the point P (See position, , Free Distribution by T.S. Government 2021-22
Page 241 :
Tangents and Secants to a Circle, , 231, , A¢ B¢ of AB). This is the position of a tangent at the point P to the circle. You can check that, in all other positions of AB, it will intersect the circle at P at another point. Thus A¢ B¢ is a, tangent to the circle at P., , We see that there is only one tangent to the circle at point P., , G, AN, , A, , Moving wire AB in either direction from this position makes it cut the circular wire in two, points. All these are therefore secants. Tangent is a special case of a secant where the two, points of intersection of a line with a circle coincide., , D O T HIS, , P, , Draw a circle and a secant PQ to the circle on a paper as shown, in the figure. Draw various lines parallel to the secant on both sides of it., , What happens to the length of chord coming closer and closer, A, to the centre of the circle?, , AN, , What is the longest chord?, , O, , How many tangents can you draw to a circle, which are parallel, to each other ?, , T,, TE, L, , Q, , The common point of a tangent and the circle is called the point of contact and the tangent, is said to touch the circle at the common point., , SC, ER, , Observe the tangents to the circle in the figures given below:, , How many tangents can you draw to a circle at a point on it? How many tangents can, you draw to the circle in all? See the points of contact. Draw radii from the points of contact. Do, you see anything special about the angle between the tangents and the radii at the points of, contact. All appear to be perpendicular to the corresponding tangents. We can also prove it. Let, us see how., Theorem-9.1 : The tangent at any point of a circle is, perpendicular to the radius through the point of contact., Given : A circle with centre ‘O’ and a tangent XY to the, , A, , O, , circle at a point P and OP radius., To prove : OP is perpendicular to XY., P, , Free Distribution by T.S. Government 2021-22, , Y
Page 242 :
232, , Class-X Mathematics, , suur, Proof : Take a point Q on XY other than P and join O and Q., The point Q must lie outside the circle (why?) (Note that if Q, , lies inside the circle, XY becomes a secant and not a tangent to, , A, , O, , the circle), P, , Q Y, , A, , Therefore, OQ is longer than the radius OP of the circle [Why?], i.e., OQ > OP., , G, AN, , This must happen for all points on the line XY. It is therefore true that OP is the shortest of, all the distances of the point O to the XY., , As a perpendicular is the shortest in length among all line segments drawn from a point to, the line (Activity 5.3 of 7th class). Therefore OP is perpendicular to XY., i.e., OP ^ XY, , T,, TE, L, , AN, , Hence, proved., Note : The line containing the radius through the point of contact is also called the ‘normal to, the circle at the point’., , TRY THIS, , How can you prove the converse of the above theorem., “If a line in the plane of a circle is perpendicular to the radius at its endpoint on the circle,, then the line is tangent to the circle”., We can find some more results using the above theorem, , SC, ER, , (i) Since there can be only one perpendicular OP at the point P, it follows that one and only, one tangent can be drawn to a circle at a given point on the circle., , (ii) Since there can be only one perpendicular to XY at the point P, it follows that the, perpendicular to a tangent to a circle at its point of contact passes through the centre., Think about these. Discuss these among your friends and with your teachers., , 9.2.1 C ONSTRUCTION, , OF, , T ANGENT, , TO A, , C IRCLE, , How can we construct a line that would be tangent to a circle at a given point on it? We use, what we just found i.e. the tangent has to be perpendicular to the radius at the point of contact., To draw a tangent through the point of contact we need to draw a line prependicular to the radius, at that point. To draw this radius we need to know the center of the circle. Let us see the steps for, this construction., , Free Distribution by T.S. Government 2021-22
Page 243 :
Tangents and Secants to a Circle, , 233, , Construction : Construct a tangent to a circle at a given point on it, when the centre of the circle, is known., We have a circle with centre ‘O’ and a point P anywhere on its circumference. Then, we have to, construct a tangent through P., Let us observe steps of construction to draw a tangent., , O, , P, , 1. Draw a circle with centre ‘O’ and mark, a point ‘P’ anywhere on it. Join O and P., , G, AN, , X, , A, , Steps of Construction :, , P, , O, , 2. Draw a perpendicular line through the, point P and name it as XY, as shown in, the figure., , Y, , AN, , 3. XY is the required tangent to the given circle passing through P., Can you draw one more tangent through P ? give reason., , T,, TE, L, , TRY THIS, , How can you draw the tangent to a circle at a given point when the, centre of the circle is not known?, Hint : Draw equal angles ÐXPQ and ÐPRQ . Explain the, construction., 9.2.2 F INDING L ENGTH, , OF THE, , X, , Q, R, , P, , Y, , T ANGENT, , SC, ER, , Can we find the length of the tangent to a circle from a given point?, , Example : Find the length of the tangent to a circle with centre ‘O’ and radius = 6 cm. from a, point P such that OP = 10 cm., Solution : Tangent is perpendicular to the radius at the point of contact (Theorem 9.1), Here, PA is tangent segment and OA is radius of circle, \ OA ^ PA Þ ÐOAP = 90°, Now, in DOAP, OP2 = OA2 + PA2 (pythagoras theorem), 102 = 62 + PA2, 100 = 36 + PA2, PA2 = 100 - 36, = 64, \ PA = 64 = 8 cm., , Free Distribution by T.S. Government 2021-22, , A, 6, O, , P, 10
Page 244 :
Class-X Mathematics, , 234, , E XERCISE - 9.1, 1. Fill in the blanks, (i) A tangent to a circle touches it in ................ point (s)., (ii) A line intersecting a circle in two points is called a ............., , A, , (iii) Number of tangents can be drawn to a circle parallel to the given tangent is ......, (iv) The common point of a tangent to a circle and the circle is called ..............., , G, AN, , (v) We can draw ............. tangents to a given circle., , (vi) A circle can have ................ parallel tangents at the most., , 2. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at, a point Q so that OQ = 13 cm. Find length of PQ., , 9.3, , T,, TE, L, , AN, , 3. Draw a circle and two lines parallel to a given line drawn outside the circle such that one, is a tangent and the other, a secant to the circle., 4. Calculate the length of tangent from a point 15 cm away from the centre of a circle of, radius 9 cm., 5. Prove that the tangents to a circle at the end points of a diameter are parallel., , N UMBER, , OF TANGENTS TO A CIRCLE FROM ANY POINT, , To get an idea of the number of tangents from a point on a circle, let us perform the, following activity., , A CTIVITY, , SC, ER, , (i) Draw a circle on a paper. Take a point, P inside it. Can you draw a tangent to, the circle through this point ? You will, find that all the lines through this point, intersect the circle in two points. What, are these ? These are all secants of a, circle. So, it is not possible to draw, any tangent to a circle through a point, inside it. (See the adjacent figure), , (ii) Next, take a point P on the circle and, draw tangents through this point. You, have observed that there is only one, tangent to the circle at a such a point., (See the adjacent figure), , P, O, , (i), , P, , O, , (ii), , Free Distribution by T.S. Government 2021-22
Page 245 :
Tangents and Secants to a Circle, (iii) Now, take a point P outside the circle, , 235, , A, , and try to draw tangents to the circle, from this point. What do you observe?, You will find that you can draw exactly, two tangents to the circle through this, , O, , B, , A, , (iii), , G, AN, , point (See the adjacent figure), Now, we can summarise these facts as follows :, , P, , Case (i): There is no tangent to a circle passing through a point inside the circle., Case(ii): There is one and only one tangent to a circle at a point on the circle., , Case(iii): There are exactly two tangents to a circle through a point outside the circle. In, this case, A and B are the points of contacts of the tangents PA and PB, respectively., , AN, , The length of the segment from the external point P and the point of contact with the, circle is called the length of the tangent from the point P to the circle., , T,, TE, L, , Note that in the above figure (iii), PA and PB are the length of the tangents from P to the, circle. What is the relation between lengths PA and PB?, Theorem-9.2 : The lengths of tangents drawn from an external point to a circle are equal., Given : A circle with centre O, P is a point outside the circle and PA and PB are two tangents, to the circle from P. (See figure), To prove : PA = PB, , Proof : Join O, A , O, B and O, P., , SC, ER, , ÐOAP = ÐPBO = 90 0, between radii and tangents is, Now, in the two right triangles (Angle, 0, 90 according to theorem 9.1), DOAP and DOBP,, OA = OB (radii of same circle), A, OP = OP (Common), Therefore, by R.H.S. Congruency axiom,, O, DOAP @ DOBP, This gives PA = PB, (CPCT), , Hence proved., , B, , TRY THIS, Use Pythagoras theorem to write a proof of the above theorem., , Free Distribution by T.S. Government 2021-22, , P
Page 246 :
Class-X Mathematics, , 236, , 9.3.1. C ONSTRUCTION, , OF, , T ANGENTS, , TO A, , CIRCLE, , FROM AN, , E XTERNAL, , POINT, , You have seen that if a point lies outside the circle, there will be exactly two tangents to the, circle from this point. We shall now see how to draw these tangents., Construction : To construct the tangents to a circle from a point outside it., , A, , Given : We are given a circle with centre ‘O’ and a point P outside it. We have to construct two, tangents from P to the circle., , G, AN, , Steps of construction :, Step(i) : Join PO and draw a perpendicular, bisector of it. Let M be the midpoint, of PO., , T,, TE, L, , Step (iii) : Join PA and PB. Then PA and PB, are the required two tangents., , Proof : Now, Let us see how this construction, is justified., , P, , O, , M, , AN, , Step (ii) : Taking M as centre and PM or MO, as radius, draw a circle. Let it intersect, the given circle at the points A and B., , P, , A, , O, , M, , Join OA. Then ÐPAO is an angle in, the semicircle and,, , B, , therefore, ÐPAO = 90°., , A, , SC, ER, , Can we say that PA ^ OA ?, , Since, OA is a radius of the given circle,, PA has to be a tangent to the circle (By, converse theorem of 9.1), , P, , O, , M, , Similarly, PB is also a tangent to the, circle., , B, , Hence proved., , Some interesting statements about tangents and secants and their proof:, Statement-1 : The centre of a circle lies on the bisector of the angle between two tangents drawn, from a point outside it. Can you think how we can prove it?, Proof : Let PQ and PR be two tangents drawn from a point P outside of the circle with centre O, Join O, Q and O, R, triangles OQP and ORP are congruent because,, , Free Distribution by T.S. Government 2021-22
Page 247 :
Tangents and Secants to a Circle, , 237, , Q, , ÐOQP = ÐPRO = 90o (Theorem 9.1), OQ = OR (Radii), OP is common., , O, , P, , This means ÐQPO = ÐOPR (CPCT), Therefore, OP is the bisector angle of ÐQPR ., , A, , R, , G, AN, , Hence, the centre lies on the bisector of the angle between the two tangents., , Statement-2 : In two concentric circles, the chord of the bigger circle, that touches the smaller, circle is bisected at the point of contact with the smaller circle., , Join OP., , AN, , Proof : Consider two concentric circles C1 and C2 with centre O, and a chord AB of the larger circle C1, touching the smaller circle, C2 at the point P (See the figure). We need to prove that AP = PB., , O, , Then, AB is a tangent to the circle C2 at P and OP is its radius., , A, , T,, TE, L, , Therefore, by Theorem 9.1,, , C1, , C, 2, , B, , P, , OP ^ AB, , Now, DOAP and DOBP are congruent. (Why?) This means AP = PB. Therefore, OP is, the bisector of the chord AB, as the perpendicular from the centre bisects the chord., Statement-3 : If two tangents AP and AQ are drawn to a circle with centre O from an external, point A, then ÐQAP = 2ÐQPO = 2 ÐOQP ., , SC, ER, , Proof : We are given a circle with centre O, an external point A and two tangents AP and AQ to, the circle, where P, Q are the points of contact (See figure)., We need to prove that, , P, , ÐQAP = 2 ÐQPO, , Let ÐQAP = q, , A, , q, , O, , Now, by Theorem 9.2, AP = AQ., So DAPQ is an isoscecles triangle, , Therefore,, , ÐAPQ + ÐPQA + ÐQAP = 180° (Sum of three angles), , Þ ÐAPQ = ÐPQA =, , 1, (180° - q), 2, , 1, = 90° - q, 2, , Free Distribution by T.S. Government 2021-22, , Q
Page 248 :
Class-X Mathematics, , 238, , Also, by Theorem 9.1, ÐOPA = 90°, So, ÐOPQ = ÐOPA - ÐAPQ, 1 ù 1, 1, é, = 90° - ê90 - qú = q = ÐPAQ, 2 û 2, 2, ë, , A, , 1, ÐPAQ ., 2, , G, AN, , This gives ÐOPQ =, , \ ÐPAQ = 2 ÐOPQ. Similarly ÐPAQ = 2ÐOQP, , Statement-4 : If a quadrilateral ABCD is drawn to circumscribe a circle, then AB+CD=AD+BC., Proof : Since, the circle touches the sides AB, BC, CD and DA of quadrilateral ABCD at the, , AN, , points P, Q, R and S respectively as shown, AB, BC, CD and DA are tangents to the circle., Since, the two tangents to a circle drawn from a point outside it are equal, by theorem 9.2., , BP = BQ, DR = DS, , T,, TE, L, , AP = AS, , R, , C, , D, Q, , S, , and CR = CQ, , On adding, we get, , A, , P, , B, , SC, ER, , AP + BP + DR + CR = AS + BQ + DS + CQ, or, , (AP + PB) + (CR + DR) = (BQ + QC) + (DS + SA), , or, , AB + CD = BC + DA., , Example-1. Draw a pair of tangents to a circle of radius 5cm which are inclined to each other, at an angle 60°., Solution : To draw the circle and the two tangents we need to see how we proceed. We only, have the radius of the circle and the angle between the tangents. We do not know the distance of, the point from where the tangents are drawn to the circle and we do not know the length of the, tangents either. We know only the angle between the tangents. Using this, we need to find out the, distance of the point outside the circle from which we have to draw the tangents., , Free Distribution by T.S. Government 2021-22
Page 249 :
Tangents and Secants to a Circle, , 239, , To begin, let us consider a circle with centre ‘O’ and radius 5cm. Let PA and PB are two, tangents drawn from a point ‘P’ outside the circle and the angle between them is 60o. In this, ÐAPB = 60o. Join OP.., As we know,, A, , OP is the bisector of ÐAPB,, , sin 30o =, , 5 cm., O, , 60°, , 5 cm., , Opp. side OA, =, Hyp, OP, , P, , A, , Now ln DOAP,, , 60 o, =30o (Q DOAP @ DOBP), 2, , G, AN, , ÐOAP= ÐOPB=, , B, , 1, 5, =, (From trigonometric ratio), 2, OP, , T,, TE, L, , AN, , OP = 10 cm., Now we can draw a circle of radius 5 cm with centre ‘O’., We then mark a point at a distance of 10 cm from the centre, of the circle. Join OP and complete the construction as given, in construction 9.2. Hence PA and PB are the required pair, of tangents to the given circle., You can also try this construction without using, trigonometric ratio., , A, , 10 cm., M, , O, , P, , B, , In DOAP; ÐA = 90°, ÐP = 30°, ÐO = 60° and OA=5, cm. Construct DAOP to get P.., , TRY THIS, , SC, ER, , Draw a pair of radii OA and OB in a circle such that ÐBOA = 120o. Draw the bisector, of ÐBOA and draw lines perpendiculars to OA and OB at A and B. These lines meet on, the bisector of ÐBOA at a point which is the external point and the perpendicular lines are, the required tangents. Construct and Justify., , E XERCISE - 9.2, , 1., , Choose the correct answer and give justification for each., , (i) The angle between a tangent to a circle and the radius drawn at the point of contact is, (a), , 60°, , (b) 30°, , (c) 45°, , (d) 90°, , (ii) From a point Q, the length of the tangent to a circle is 24 cm. and the distance of Q from, the centre is 25 cm. The radius of the circle is, (a), , 7cm, , (b) 12 cm, , (c) 15cm, , Free Distribution by T.S. Government 2021-22, , (d) 24.5cm
Page 250 :
Class-X Mathematics, , 240, , A, , (iii) If AP and AQ are the two tangents a circle with centre O so that, ÐQOP = 110°, then ÐPAQ is equal to, (a), , 60°, , (b), , 70°, , (c), , 80°, , (d), , P, 110°, , 90°, , Q, , O, , (iv) If tangents PA and PB from a point P to a circle with centre O are, inclined to each other at angle of 80°, then ÐPOA is equal to, 50°, , (b), , 60°, , (c), , 70°, , (d), , ÐBOA =, , (a), , 80°, , G, AN, , (v) In the figure, XY and X1Y1 are two parallel tangents to, a circle with centre O and another tangent AB with point, of contact C intersecting XY at A and X1Y1 at B then, , 80°, , A, , (a), , X, , A, , O, , (b), , 100°, , (c), , 90°, , (d), , Y, , C, , 60°, , B, , AN, , 2. Two concentric circles of radii 5 cm and 3cm are drawn., Find the length of the chord of the larger circle which, touches the smaller circle., , X1, , 1, , Y, , A, , T,, TE, L, , 3. Prove that the parallelogram circumscribing a circle is a rhombus., 4. A triangle ABC is drawn to circumscribe a circle of radius 3 cm., such that the segments BD and DC into which BC is divided by, the point of contact D are of length 9 cm. and 3 cm. respectively, (See adjacent figure). Find the sides AB and AC., , O, , B, , 9 cm., , D, , 3cm., , C, , 5. Draw a circle of radius 6cm. From a point 10 cm away from its centre, construct the pair, of tangents to the circle and measure their lengths. Verify by using Pythogoras Theorem., , SC, ER, , 6. Construct a tangent to a circle of radius 4cm from a point on the concentric circle of radius, 6cm and measure its length. Also verify the measurement by actual calculation., 7. Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair, of tangents from this point to the circle and measure them. Write your conclusion., 8. In a right triangle ABC, a circle with a side AB as diameter, is drawn to intersect the hypotenuse AC in P. Prove that, the tangent to the circle at P bisects the side BC., 9. Draw a tangent to a given circle with center O from a, point ‘R’ outside the circle. How many tangents can be, drawn to the circle from that point?, , Hint : The distance of two points to the point of contact, is the same., , A, , O, , B, , P, , Q, , C, , Free Distribution by T.S. Government 2021-22
Page 251 :
Tangents and Secants to a Circle, 9.4 SEGMENT, , 241, , OF A CIRCLE FORMED BY A SECANT, , We have seen a line and a circle. When a line meets a, circle in only one point, it is a tangent. A secant is a line which, intersects the circle at two distinct points and the line segment, between the points is a chord., , A, , B, , A, , Here, ‘l’ is the secant and AB is the chord., , l, , AN, , G, AN, , Shankar is making a picture by sticking, pink and blue paper. He makes many pictures. One picture he makes is of a, washbasin. How much paper does he need to make this picture? This picture, can be seen in two parts. There is a rectangle below, but what is the remaining, part? It is the segment of a circle. We know how to find the area of rectangle., How do we find the area of the segment? In the following discussion, we will, try to find this area., , T,, TE, L, , D O T HIS, , Shankar made the following pictures also., , To find area of a figure, identify what are the shapes involved in it?, , SC, ER, , Make some more pictures and think of the shapes they can be divided into different, parts., , T RY T HIS, , Name the shapes involved in the following figure., D, , A, , C, D, , C, , 2 cm, , A, , 10 cm., , B, , Free Distribution by T.S. Government 2021-22, , O, , 3.5 cm, , B
Page 252 :
Class-X Mathematics, , 242, , Lets us recall the formulae of the area of the following geometrical figures as given in the table., S.No., , Figure, , 1., b, , Dimensions, , Area, , length = l, , A = lb, , breadth = b, A = s2, , Side = s, , s, s, , height=h, h, , 3., , base = b, , b, , r, , A=, , 1, bh, 2, , A = pr2, , radius = r, , AN, , 4., , G, AN, , 2., , A, , l, , T,, TE, L, , 9.4.1., FINDING THE A REA OF SEGMENT OF A CIRCLE, Swetha made the segments by drawing secants to the circle., , A, , B, , l, , A, , B, , (i), , l, , B, l, , A, , (ii), , (iii), , SC, ER, , As you know, a segment is a region bounded by an arc and a chord. The area that is, shaded (, ) in fig.(i) is a minor segment, a semicircle in fig.(ii) and a major segment in fig.(iii)., How do we find the area of a segment? Do the following activity., , Take a small circular paper and fold it along a chord and shade the, smaller part as shown in the figure. What do we call this smaller part? It, is a minor segment (APB). What do we call the unshaded portion of the, circle? Obviously it is a major segment (AQB)., , O, , x, , A, , O, , You have already come across the sectors and A, segments in earlier classes. The portion of some, P, unshaded part and shaded part (minor segment), is a sector which is the combination of a triangle and a segment., , Q, , r, , Q, , r, B, , B, , Let OAPB be a sector of a circle with centre O and radius ‘r’ as shown, in the figure. Let the measure of ÐAOB be ‘x’., , P, , Free Distribution by T.S. Government 2021-22
Page 253 :
Tangents and Secants to a Circle, , 243, , You know that the area of a circle is pr2 and the angle measured at the centre is 360°., So, when the degree measure of the angle at the centre is 1°, then area of the corresponding, 1°, sector is, ×pr2., 360°, Therefore, when the degree measure of the angle at the centre is x°, the area of the sector, x°, ×pr2., 360°, , A, , is, , G, AN, , Now let us take the case of the area of the segment APB of a circle with centre ‘O’ and, radius ‘r’. You can see that, Area of the segment APB = Area of the sector OAPB - Area of DOAB, x°, × pr2 - area of DOAB, 360°, , AN, , =, , TRY THIS, , T,, TE, L, , How can you find the area of a major segment using area of the corresponding minor segment?, , D O T HIS, 1., , 120°, , The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand, in 10 minutes., , SC, ER, , 2., , Find the area of sector, whose radius is 7 cm. with the given angle:, i., 60°, ii., 30°, iii. 72°, iv. 90°, v., , Now, we will see an example to find area of segment of a circle., , Example-1. Find the area of the segment AYB shown in the adjacent figure. It is given that the, , radius of the circle is 21 cm and Ð AOB = 1200 (Use p =, , 22, and, 7, , 3 = 1.732), A, , Solution : Area of the segment AYB, , 120 0 22, Now, area of the sector OAYB =, ´ ´ 21 ´ 21 cm2, 0, 7, 360, = 462 cm2, , Y, , 120°, , = Area of sector OAYB - Area of DOAB, , 21 cm., , 21 cm., , ...(1), , B, , For finding the area of DOAB, draw OM ^ AB as shown in the figure:Note OA = OB. Therefore, by RHS congruence,DAMO @ DBMO., , Free Distribution by T.S. Government 2021-22, , O
Page 254 :
Class-X Mathematics, , 244, , 1, 0, 0, So, M is the midpoint of AB and Ð AOM = Ð BOM = ´ 120 = 60, 2, , Let, OM = x cm, OM, = cos 600., OA, , So, OM =, , 21, cm, 2, , AM, = sin 60°, OA, , AN, , Also,, , G, AN, , or,, , B, , 1ö, æ, 0, çQ cos 60 = ÷, 2ø, è, , x, 1, =, 21 2, 21, x=, 2, , or,, , 21 cm., 60°, M, O, 60°, 21 cm., , A, , So, from DOMA ,, , A, , æ, 3ö, 0, çQ sin 60 = 2 ÷, è, ø, , T,, TE, L, , AM, 3, =, 21, 2, , So, AM =, , 21 3, cm., 2, , Therefore, AB = 2AM =, , SC, ER, , So, Area of DOAB =, , 2 ´ 21 3, cm. = 21 3 cm, 2, , 1, ´ AB ´ OM, 2, , =, , 1, 21, cm2., ´ 21 3 ´, 2, 2, , =, , 441, 2, 3 cm ., 4, , ...(2), , 441 ö 2, æ, 3 ÷ cm ., Therefore, area of the segment AYB = ç 462 4, è, ø, , (Q from (1), (2) ], =, , (, , ), , 21, 88 - 21 3 cm 2, 4, , = 271.047 cm2, , Free Distribution by T.S. Government 2021-22
Page 255 :
Tangents and Secants to a Circle, , 245, , Example-2. Find the area of the segments shaded in figure, if PQ = 24 cm., PR = 7 cm. and, QR is the diameter of the circle with centre O (Take p=, , 22, ), 7, , Solution : Area of the segments shaded = Area of sector OQPR - Area of triangle PQR., Since QR is diameter, ÐQPR = 90° (Angle in a semicircle), = PQ2 + PR2, , G, AN, , QR2, , In DQPR,, , A, , So, using Pythagoras Theorem, = 242 + 72, , Q, , = 625, 625 = 25 cm., , =, , 1, QR, 2, , 1, 25, (25) =, cm., 2, 2, , T,, TE, L, , Then, radius of the circle =, , R, , AN, , QR, , O, , m., , 24, , P, , 7c, , = 576 + 49, , ., cm, , =, , Now, area of semicircle OQPR =, , SC, ER, , =, , 1, pr2, 2, , 1 22 25 25, ´ ´ ´, 2 7 2 2, , = 245.53 cm2 ..... (1), , Area of right angled triangle QPR =, =, , 1, × PR × PQ, 2, 1, × 7 × 24, 2, , = 84 cm2, , ..... (2), , From (1) and (2),, , Area of the shaded segments, , = 245.53 - 84, = 161.53 cm2, , Example-3. A round table top has six equal designs as shown in the figure. If the radius of the, table top is 14 cm., find the cost of making the designs with paint at the rate of D5 per cm2. (use, 3 = 1.732), , Free Distribution by T.S. Government 2021-22
Page 256 :
246, , Class-X Mathematics, , Solution : We know that the radius of circumscribing circle of a regular hexagon is equal to the, length of its side., \ Each side of regular hexagon = 14 cm., Therefore, Area of six design segments = Area of circle - Area of the regular hexagon., Now, Area of circle, = pr2, , Area of regular hexagon = 6 ×, =6×, , 3 2, a, 4, , ., cm, 4, 1 r, , 3, × 14 × 14, 4, , ..... (2), , AN, , = 509.2 cm2, Hence, area of six designs, , ..... (1), , A, , 22, × 14 × 14 = 616 cm2, 7, , G, AN, , =, , = 616 - 509.21 (from (1), (2), = 106.79 cm2., , T,, TE, L, , Therefore, cost of painting the design at the rate of D5 per cm2, = D106.79 × 5, = D533.95, , E XERCISE - 9.3, 1., , In a circle of radius 10 cm, a chord subtends a right angle at the centre. Find the area of the, corresponding: (use p = 3.14), Minor segment, , SC, ER, , i., , 2., , ii. Major segment, , In a circle of radius 12 cm, a chord subtends an angle of 120° at the centre. Find the area, of the corresponding minor segment of the circle (use p = 3.14 and 3 = 1.732), , 3., , A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm, sweeping through an angle of 115°. Find the total area cleaned at each sweep of the, 22, D, C, blades. (use p = ), 7, , 4., , Find the area of the shaded region in the adjacent figure, where, ABCD is a square of side 10 cm and semicircles are drawn with, each side of the square as diameter (use p = 3.14), A, , 10 cm., , B, , Free Distribution by T.S. Government 2021-22
Page 257 :
Tangents and Secants to a Circle, Find the area of the shaded region in figure, if ABCD is a square, of side 7 cm. and APD and BPC are semicircles. (use p =, A, , 6. In the figure, OACB is a, quadrant of a circle with centre, O and radius 3.5cm. If, OD=2cm, find the area of the, , C, , 2 cm, , shaded region. (use p =, , A, , B, , 22, ), 7, , ., , O, , AB and CD are respectively arcs of two concentric circles of radii, 21 cm and 7 cm with centre O (See figure). If ÐAOB = 30°, find, , C, , 22, ), 7, , T,, TE, L, , 10 cm., A, , D, , C, , AN, , the area of the shaded region. (use p =, D, , 30°, , ., 21 cm, , 7., , B, , 3.5 cm, , P, , 7 cm, , O, , 22, ), 7, , C, , G, AN, , D, , 7 cm., , D, , A, , 5., , 247, , B, , A, , 8. Calculate the area of the designed region in figure, common, between the two quadrants of the circles of radius 10 cm each., (use p = 3.14), , 10 cm., , B, , SC, ER, , O PTIONAL E XERCISE, , [For extensive Learning], , 1. Prove that the angle between the two tangents drawn from an external point to a circle is, supplementary to the angle subtended by the line segment joining the points of contact at, the centre., 2. PQ is a chord of length 8cm of a circle of radius 5cm. The, tangents at P and Q intersect at a point T (See figure). Find, O, m., the length of TP., 5c, 8 cm., P, Q, 3. Prove that opposite sides of a quadrilateralcircumscribing a circle, subtend supplementary angles at the centre of the circle., 4. Draw a line segment AB of length 8cm. Taking A as centre,, draw a circle of radius 4cm and taking B as centre, draw, another circle of radius 3cm. Construct tangents to each circle, from the centre of the other circle., T, , Free Distribution by T.S. Government 2021-22
Page 258 :
248, , Class-X Mathematics, , 5. Let DABC be a right triangle in which AB = 6 cm, BC = 8 cm and ÐB = 900. BD is the, perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents, from A to this circle., 6. Find the area of the shaded region in the figure, in which two, circles with centres A and B touch each other at the point C, where, AC = 8 cm and AB = 3 cm., , A, , A, B, , C, , 14 cm., , B, , AN, , A, , 7. ABCD is a rectangle, with AB = 14 cm and BC, C, = 7 cm. Taking DC, BC, and AD as diameters, three semicircles are, drawn as shown in the figure. Find the area of, the shaded region., , G, AN, , D, , WHAT WE HAVE DISCUSSED, , T,, TE, L, , In this chapter, we have studied the following points., , 1. A tangent to a circle is a line which touches the circle at only one point., 2. The tangent at any point of a circle is perpendicular to the radius through the point of, contact., 3. The lengths of the two tangents from an external point to a circle are equal., , SC, ER, , 4. We learnt, , a) to construct a tangent to a circle at a given point when the centre of the circle is known., b) to construct the pair of tangents from an external point to a circle., , 5. A secant is a line which intersects the circle at two distinct points and the line segment, between the points is a chord., 6. Area of segment of a circle = Area of the corresponding sector - Area of the corresponding, triangle., , Free Distribution by T.S. Government 2021-22
Page 259 :
Mensuration, , A, , 10, , G, AN, , 10.1 I NTRODUCTION, , TRY THIS, , Consider the following situations. In each situation, find out whether you need to find, volume or surface area and why?, i., , T,, TE, L, , 1., , AN, , In classes VIII and IX, we have learnt about surface area and volume of regular solid, shapes. We use them in real life situations to identify what we need and what is to be measured, or estimated. For example, to find the quantity of paint required to white wash a room, we need, the surface area and not the volume. To find the number of boxes that would contain a quantity, of grain, we need the volume and not the area., , Quantitiy of water inside a bottle., , iii. Number of bags inside the lorry., , ii., , Canvas needed for making a tent., , iv., , Gas filled in a cylinder., , v. Number of match sticks that can be put in the match box. (vi) Paper for gift pack, State 5 more such examples and ask your friends to choose what they need?, , SC, ER, , 2., , We see so many things of different shapes (combination of two or more regular solids), around us. Houses stand on pillars, storage water tanks are cylindrical and are placed on cuboidal, foundations, a cricket bat has a cylindrical handle and a flat main body, etc. Think of different, objects around you. Some of these are shown below:
Page 260 :
Class-X Mathematics, , 250, , TRY THIS, 1. Break the pictures in the previous figure into solids of known shapes., 2. Think of 5 more objects around you that can be seen as a combination of shapes. Name, the shapes that combined to make them., , G, AN, , A, , You have learnt how to find the surface area and volume of single regular solids only. We, can however see that other objects can be seen as combinations of the solid shapes. So, we now, have to find their surface area and volumes. The table of the solid shapes, their areas and volumes, are given below., Let us recall the surface areas and volumes of different solid shapes., , 1., , Figure, , Cuboid, b, , 3., , Right, prism, , 4a2, , a, , a, , a, , Volume, , Nomenclature, , lbh, , l:length, , 2(lb+bh+hl), , T,, TE, L, , Cube, , 2h(l+b), , h, l, , 2., , Lateral / Curved Total surface, surface area, area, , AN, , S. Name of, No. the solid, , b:breadth, h:height, , 6a2, , a3, , a:side of, the cube, , Perimeter of base, , Lateral surface, , area of base, , ´ height, , area+2(area of, , ´ height, , -, , the end surface), , 4., , Regular, circular, , 5., , Right, , pyramid, , 6., , height, , h, , cone, , 7., , slant, height, , 1, 2, , (perimeter of, , h:height, , Lateral surfaces, , base) ´ slant, height, , area+area of, the base, , prl, , pr(l+r), , Hemisphere, , area of, , r, , r, , -, , the base, ´ height, 1, 3, , pr2h, , l, , r:radius of, the base, h:height, l:slant height, , 4pr2, , 4pr2, , 4, 3, , pr3, , r:radius, , 2pr2, , 3pr2, , 2, 3, , pr3, , r:radius, , r, , 8., , 1, 3, , r, , Sphere, , r:radius of, the base, , r, , Right, , circular, , pr2h, , 2pr(r+h), , h, , SC, ER, , Cylinder, , 2prh, , Free Distribution by T.S. Government 2021-22
Page 261 :
Mensuration, , 251, , Now, let us see some examples to illustrate the method of finding CSA (Curved Surface, Area), TSA (Total Surface Area) of the shapes given in the table., Example-1. The radius of a conical tent is 7m and its height is 10 meters. Calculate the length, , G, AN, , Solution : The radius of conical tent is (r) = 7m and height (h) = 10m., , A, , 22 ù, é, of canvas used in making the tent, if the width of canvas is 2m. ê Use p = ú, 7û, ë, , \ So, the slant height of the cone l2 = r2 + h2 Þ l =, =, , r 2 + h2, , 49 + 100, , Now, surface area of the tent = prl, , 22, ´ 7 ´ 12.2 m 2, 7, , T,, TE, L, , =, , AN, , = 149 = 12.2 m., , = 268.4 m2., , Area of canvas used = 268.4m2, , 10 m, , It is given that the width of the canvas = 2m, , 7m, , Area, 268.4, =, = 134.2m, Length of canvas used =, width, 2, , SC, ER, , Example-2. An oil drum is in the shape of a cylinder having the following dimensions: diameter, is 2 m. and height is 7 m. The painter charges ` 3 per m2 to paint the drum. Find the total, charges to be paid to the painter for 10 drums ?, Solution : It is given that diameter of the cylinder (oil drum) = 2 m., d 2, = =1 m, 2 2, Total surface area of a cylindrical drum = 2pr(r + h), , Radius of cylinder =, , = 2´, , 22, ´ 1(1 + 7 ), 7, , 7m, , 22, =2 ´, ´8, 7, , =, , 352 2, m . = 50.28 m2, 7, , Free Distribution by T.S. Government 2021-22, , 2m
Page 262 :
Class-X Mathematics, , 252, , The total surface area of a drum, , = 50.28 m2, , Painting charge per 1m2, , = `3., , Cost of painting of 10 drums, , = 50.28 ´ 3 ´ 10, = `1508.40, , G, AN, , Solution : Let r be the common radius of a sphere, a cone and cylinder., , A, , Example-3. A sphere, a cylinder and a cone are of the same radius and same height. Find the, ratio of their curved surface areas., Height of sphere = its diameter = 2r., , Then, the height of the cone = height of cylinder = height of sphere., , The slant height of cone l = r 2 + h 2, , AN, , = 2r., , = r 2 + (2r )2 = 5r, , T,, TE, L, , S1 = Curved surface area of sphere = 4pr2, , S2 = Curved surface area of cylinder, 2prh = 2pr ´ 2r = 4pr2, S3 = Curved surface area of cone = prl = pr ´, , 5r=, , 2, , 5 pr, , \ Ratio of curved surface area is, , S1 : S2 : S3 = 4pr2 : 4pr2 :, , SC, ER, , =4:4:, , 2, , 5 pr, , 5, , Example-4. A company wants to manufacture 1000 hemispherical basins from a thin steel, sheet. If the radius of each basin is 21 cm., find the area of steel sheet required to manufacture the, above hemispherical basins?, Solution : Radius of the hemispherical basin (r) = 21 cm, Surface area of a hemispherical basin = 2pr2, = 2´, , 22, ´ 21 × 21 = 2772 cm2., 7, , Hence, area of the steel sheet required for one basin = 2772 cm2, Total area of steel sheet required for 1000 basins = 2772 × 1000 = 2772000 cm2, = 277.2 m2, , Free Distribution by T.S. Government 2021-22
Page 263 :
Mensuration, , 253, , Example-5. A right circular cylinder has base radius 14cm and height 21cm., Find its (i) area of base (or area of each end), , (ii) curved surface area, , (iii) total surface area and, , (iv) volume., , A, , Solution : Radius of the cylinder (r) = 14cm, , Now (i) Area of base(area of each end) pr2 =, = 616 cm2, (ii) Curved surface area = 2prh = 2 ´, , 22, (14)2, 7, , 22, ´ 14 ´ 21, 7, , 21 cm, , 14 cm, , AN, , = 1848cm2., , G, AN, , Height of the cylinder (h) = 21cm, , (iii) Total surface area = 2 ´ area of the base + curved surface area, , T,, TE, L, , = 2 ´ 616 + 1848 = 3080 cm2., , (iv) Volume of cylinder = pr2h = area of the base ´ height, = 616 ´ 21 = 12936 cm3., , Example-6. Find the volume and surface area of a sphere of radius 2.1cm (p =, , 22, ), 7, , Solution : Radius of sphere (r) = 2.1 cm, , SC, ER, , Surface area of sphere = 4pr2, = 4´, , =, , Volume of sphere =, , 22, 22 21 21, ´ (2.1) 2 = 4 ´ ´ ´, 7, 7 10 10, , 1386, = 55.44 cm 2, 25, 4 3 4 22, pr = ´ ´ (2.1) 3, 3, 3 7, =, , 4 22, ´ ´ 2.1´ 2.1 ´ 2.1 = 38.808 cm3., 3 7, , Free Distribution by T.S. Government 2021-22, , 2.1 cm
Page 264 :
254, , Class-X Mathematics, , Example-7. Find the volume and the total surface area of a hemisphere of radius 3.5 cm., Solution : Radius of sphere (r) is 3.5 cm =, 2 3, pr, 3, 2 22 7 7 7 539, ´ ´ ´ ´ =, = 89.83 cm3, 3 7 2 2 2, 6, , Total surface area = 3pr2, , EXERCISE - 10.1, , 22 7 7, 231, ´ ´ =, = 115.5 cm2, 7 2 2, 2, , AN, , = 3´, , A, , =, , 3.5 cm, , G, AN, , Volume of hemisphere =, , 7, cm, 2, , T,, TE, L, , 1. A joker’s cap is in the form of right circular cone whose base radius is 7cm and height is, 24 cm. Find the area of the sheet required to make 10 such caps., 2. A sports company was ordered to prepare 100 paper cylinders for packing shuttle cocks., The required dimensions of the cylinder are 35 cm length /height and its radius is 7 cm., Find the required area of thick paper sheet needed to make 100 cylinders?, 3. Find the volume of right circular cone with radius 6 cm. and height 7cm., , SC, ER, , 4. The lateral surface area of a cylinder is equal to the curved surface area of a cone. If their, bases are the same, find the ratio of the height of the cylinder to the slant height of the cone., 5. A self help group wants to manufacture joker’s caps of 3cm. radius and 4 cm. height. If, the available paper sheet is 1000 cm2, then how many caps can be manufactured from that, paper sheet?, , 6. A cylinder and cone have bases of equal radii and are of equal heights. Show that their, volumes are in the ratio of 3:1., 7. The shape of solid iron rod is cylinderical. Its height is 11 cm. and base diameter is 7cm., Then find the total volume of 50 such rods., 8. A heap of rice is in the form of a cone of diameter 12 m. and height 8 m. Find its volume?, How much canvas cloth is required to cover the heap ? (Use p = 3.14), , 9. The curved surface area of a cone is 4070 cm2 and its diameter is 70 cm. What is its slant, height?, , Free Distribution by T.S. Government 2021-22
Page 265 :
Mensuration, 10.2 S URFACE A REA, , OF THE, , C OMBINATION, , OF, , 255, , S OLIDS, , G, AN, , Lets take another example, an oil-tanker /, water-tanker. Is it a single shaped object? You, may guess that it is made up of a cylinder with, two hemispheres at it ends., , A, , We have seen solids which are made up of combination of solids known like, sphere, cylinder and cone. We can observe in our real life also like wooden things,, house items, medicine capsules, bottles, oil-tankers etc. We eat ice-cream in our daily, life. Can you tell how many solid figures are there in it? It is usually made up of cone, and hemisphere., , AN, , If you want to find the surface areas or, volumes or capacities of such objects, how would, you do it? We cannot classify these shapes under any of the solids you have already studied., , T,, TE, L, , As we have seen, the oil-tanker was made up of a cylinder with two hemispheres stuck at, either end. It will look like the following figure:, , SC, ER, , If we consider the surface of the newly formed, object, we would be able to see only the curved, surfaces of the two hemispheres and the curved surface, of the cylinder., , TSA of new solid = CSA of one hemisphere + CSA of cylinder + CSA of other hemisphere, , Here ,TSA and CSA stand for ‘total surface area’ and ‘curved surface area’ respectively., Now let us look at another example., , T HINK, , AND, , D ISCUSS, , Saniya prepared a toy. She mounted a cone on a cylinder whose circular, radii are same. She told to Archana that the total surface area of the toy is the, sum of the total surface ara of the cone and cylinder. Do you agree with this?, Justify your answer., , Free Distribution by T.S. Government 2021-22
Page 266 :
Class-X Mathematics, , 256, , Suppose, we want to make a toy by putting together a hemisphere and a cone. Let us see, the steps that we should be going through., , Step-2, , AN, , Step-1, , G, AN, , A, , First, we should take a cone and hemisphere of equal radii and bring their flat faces together., Here, of course, we should take the base radius of the cone equal to the radius of the hemisphere,, for the toy to have a smooth surface. So, the steps would be as shown below:, , Step-3, , At the end, we got a nice round-bottomed toy. Now, if we wants to find how much paint, , T,, TE, L, , we are required to colour the surface of the toy, for this we need to know the total surface area, of the toy, which consists of the CSA of the hemisphere and the CSA of the cone., TSA of the toy = CSA of hemisphere + CSA of cone, Is this formula stated above true for all the objects made by combination of various regular, solids? Discuss with your firiends., , SC, ER, , T RY T HIS, , - Use known solid shapes and make as many objects (by combining more than two) as, possible that you come across in your daily life., [Hint : Use clay, or balls, pipes, paper cones, boxes like cube, cuboid etc], , T HINK, , AND, , D ISCUSS, , A sphere is inscribed in a cylinder., •, , What is the ratio of total surface areas of cylinder and sphere?, , •, , What is the ratio of volumes of cylinder and sphere?, What have you observed?, , Free Distribution by T.S. Government 2021-22
Page 267 :
Mensuration, , 257, , Example-8. Koushik got a playing top as his birthday present, which surprisingly had no colour, on it. He wanted to colour it with his crayons. The top is shaped like a cone surmounted by a, hemisphere. The entire top is 5cm. in height and the diameter of the top is 3.5cm. Find the area, , A, , 22 ö, æ, he has to colour. ç Take p = ÷, 7 ø, è, , Solution : This top is exactly like the object, that the combination of a, , G, AN, , cone and hemisphere having equal radii of circular base., , i.e. TSA of the toy = CSA of hemisphere + CSA of cone, , =, , 1, 4p r 2 ) = 2p r 2, (, 2, , 5 cm, , AN, , Now, the curved surface area of the hemisphere, , 3.5 cm, , 22 3.5 3.5 ö, æ, 2, ´, = ç 2´ ´, ÷ = cm, 7, 2, 2, è, ø, , T,, TE, L, , Also, the height of the cone = height of the top – height (radius) of the hemispherical part, 3.5 ö, æ, = ç5 ÷ = cm = 3.25cm, 2 ø, è, , So, the slant height of the cone, , 2, , æ 3.5 ö, 2, l = r +h = ç, ÷ + (3.25) cm = 3.7cm, è 2 ø, 2, , (approx.), , SC, ER, , 2, , æ 22 3.5, ö, ´ 3.7 ÷ cm 2, Therefore, (SA of cone = p rl = ç ´, 2, è 7, ø, , this gives the surface area of the top as, 22 3.5 3.5 ö 2 æ 22 3.5, æ, ö, ´, ´ 3.7 ÷ cm 2, = ç 2´ ´, ÷ cm + ç ´, 7, 2, 2 ø, 2, è, è 7, ø, , =, , 22 3.5, 11, ´, ( 3.5 + 3.7 ) cm 2 = ´ (3.5 + 3.7)cm 2, 7, 2, 2, , = 39.6cm2 (approx.), Note: You may not that total surface area of the top is not the sum of the total surface area of the, cone and hemisphere., , Free Distribution by T.S. Government 2021-22
Page 268 :
Class-X Mathematics, , 258, , Example-9. A wooden toy rocket is in the shape of a cone mounted on a cylinder as shown in, the adjacent figure. The height of the entire rocket is 26 cm, while the height of the conical part is, 6cm. The base of the conical position has a diameter of 5 cm, while the base diameter of the, cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical, portion is to be painted yellow, find the area of the rocket painted with each of these color (Take, , A, , p = 3.14), , G, AN, , Solution : Let ‘r’ be the radius of the base of the cone and its slant height be ‘l’. Further, let r1, be the radius of cylinder and h1 be its height, We have,, , AN, , r = 2.5 cm., h = 6 cm., r1 = 1.5 cm. h1 = 20 cm., Now, l = r 2 + h 2, l=, , T,, TE, L, , Þ l = (2.5)2 + 62, , Base of cylinder, , 6.25 + 36 = 42.25 = 6.5, , Now, area to be painted in orange =, , 3 cm, , CSA of the cone + base area of the cone base area of the cylinder, , Base of cone, , SC, ER, , = prl + pr2 - pr12, , = p{(2.5 × 6.5) + (2.5)2 – (1.5)2} cm2, , = p(20.25) cm2 = 3.14 × 20.25 cm2, = 63.585 cm2, , Area to be painted yellow, , = Curved surface area of the cylinder + Area of the base of the cylinder, = 2pr1h1 + pr12, = pr1 (2h1 + r1), = 3.14 × 1.5 (2×20+1.5) cm2, , Free Distribution by T.S. Government 2021-22
Page 269 :
Mensuration, , 259, , = 3.14 ´ 1.5 ´ 41.5 cm2, = 4.71 ´ 41.5 cm2, = 195.465 cm2., , A, , Therefore, area to be painted yellow = 195.465 cm2, , G, AN, , EXERCISE - 10.2, , 1. A toy is in the form of a cone mounted on a hemisphere of the same diameter. The diameter, of the base and the height of the cone are 6 cm and 4 cm respectively. Determine the, surface area of the toy. [use p = 3.14], , AN, , 2. A solid is in the form of a right circular cylinder with a hemisphere at one end and a cone at, the other end. The radius of the common base is 8 cm. and the heights of the cylindrical, and conical portions are 10 cm and 6 cm respectivly. Find the total surface area of the, solid. [use p = 3.14], , T,, TE, L, , 3. A medicine capsule is in the shape of a cylinder with two, hemispheres stuck to each of its ends. The length of the, capsule is 14 mm. and the thickness is 5 mm. Find its, surface area., , 4. Two cubes each of volume 64 cm3 are joined end to end together. Find the surface area, of the resulting cuboid., , SC, ER, , 5. A storage tank consists of a circular cylinder with a hemisphere stuck on either end. If the, external diameter of the cylinder be 1.4 m. and its length be 8 m, then find the cost of, painting it on the outside at rate of `20 per m2., , 6. A sphere, a cylinder and a cone have the same radius and same height. Find the ratio of, their volumes., [Hint : Diameter of the sphere is equal to the heights of the cylinder and the cone.], , 7. A hemisphere is cut out from one face of a cubical wooden block such that, the diameter of the hemisphere is equal to the side of the cube. Determine, the total surface area of the remaining solid., 8. A wooden article was made by scooping out a hemiphere from each end of, a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm., and its radius of the base is of 3.5 cm, find the total surface area of the, article., , Free Distribution by T.S. Government 2021-22
Page 270 :
Class-X Mathematics, , 260, , 10.3 V OLUME, , OF, , COMBINATION, , OF, , SOLIDS, , G, AN, , Suresh runs an industry in a shed which is in the, shape of a cuboid surmounted by a half cylinder. The base, of the shed is of dimensions 7 m. ´ 15 m. and the height of, the cuboidal portion is 8 m. Find the volume of air that the, shed can hold? Further, suppose the machinery in the, shed occupies a total space of 300 m3 and there are 20, workers, each of whom occupies about 0.08 m3 space, on an average. Then how much air is in the shed ?, , A, , Let us understand volume of a combined solid, through an example., , T,, TE, L, , AN, , The volume of air inside the shed (when there are, neither people nor machinery) is given by the volume of, air inside the cuboid and inside the half cylinder taken, together. The length, breadth and height of the cuboid are, 15 m., 7 m. and 8 m. respectively. Also the diameter of the half cylinder is 7 m. and its height is, 15 m., So, the required volume= volume of the cuboid +, , 1, volume of the cylinder.., 2, , 1 22 7 7, é, ù, = ê15 ´ 7 ´ 8 + ´ ´ ´ ´ 15ú m3, 2 7 2 2, ë, û, , = 1128.75m3., , Next, the toal space occupied by the machinery = 300 m3., , SC, ER, , And the total space occupied by the workers, , = 20 ´ 0.08 m3, , = 1.6m3, , Therefore, the volume of the air, inside the shed when there are machinery and workers, = 1128.75 - (300.00 + 1.60), = 1128.75 - 301.60 = 827.15 m3, , Note : In calculating the surface area of combination of solids, we can not add the surface areas, of the two solids because some part of the surface areas disappears in the process of joining, them. However, this will not be the case when we calculate the volume. The volume of the solid, formed by joining two basic solids will acutally be the sum of the volumes of the constituents as, seen in the example above., , Free Distribution by T.S. Government 2021-22
Page 271 :
Mensuration, , 261, , TRY THIS, 1. If the diameter of the cross - section of a wire is decreased by 5%, by what percentage, should the length be increased so that the volume remains the same ?, , A, , 2. Surface areas of a sphere and cube are equal. Then find the ratio of their volumes., , G, AN, , Let us see some more examples., , 22 ö, æ, ç Use p = ÷ ., 7 ø, è, , AN, , Example-10. A solid toy is in the form of a right circular cylinder with hemispherical shape at, one end and a cone at the other end. Their common diameter is 4.2 cm and the height of the, cylindrical and conical portions are 12cm and 7cm respectively. Find the volume of the solid toy., , Solution : Let height of the conical portion h1 = 7cm, , The height of cylindrical portion h2 = 12 cm, 4.2, 21, = 2.1 =, cm, 2, 10, , T,, TE, L, , Radius (r) =, , Volume of the solid toy, , = Volume of the Cone+Volume of the Cylinder+Volume of the Hemisphere., =, , 1 2, 2, pr h1 + pr 2 h2 + pr 3, 3, 3, , SC, ER, , 2 ù, 2 é1, = pr ê h1 + h2 + r ú, 3 û, ë3, 22, =, 7, , cm, h1, r, , 2, , 2 21 ù, æ 21 ö é 1, ´ ç ÷ ´ ê ´ 7 + 12 + ´ ú, 3 10 û, è 10 ø ë 3, , =, , 22 441 é 7 12 7 ù, ´, ´ + +, 7 100 êë 3 1 5 úû, , =, , 22 441 é 35 + 180 + 21 ù, ´, ´, ú, 7 100 êë, 15, û, , =, , 22 441 236 27258, ´, ´, =, = 218.064 cm3 ., 7 100 15, 125, , Free Distribution by T.S. Government 2021-22, , h2, , cm, , cm
Page 272 :
Class-X Mathematics, , 262, , Example-11. A cylindrical container is filled with ice-cream whose diameter is 12 cm and, height is 15 cm. The whole ice cream is distributed to 10 children by filling in equal cones, and forming hemispherical tops. If the height of the conical portion is twice the diameter of, its base, find the diameter of the ice cream cone., Solution : Let the radius of the base of conical ice cream = x cm, , A, , \ diameter = 2x cm, , G, AN, , Then, the height of the conical ice cream, = 2 (diameter) = 2(2x) = 4x cm, Volume of ice cream cone, , = Volume of conical portion + Volume of hemispherical portion, , 1 2, 2, px (4 x ) + px3, 3, 3, , =, , 4px 3 + 2px3, 6px 3, =, 3, 3, , x cm, , T,, TE, L, , =, , AN, , x cm, , 1, 2, = pr2h +, pr3, 3, 3, , = 2px3 cm3, , Diameter of cylindrical container = 12 cm, , Its height (h) = 15 cm, , SC, ER, , \ Volume of cylindrical container = pr2h, , = p(6)2 15, = 540p cm3, , Number of children to whom ice cream is given = 10, Volume of cylindrical container, = 10, Volume of one ice cream cone, , Þ, , 540p, = 10, 2px 3, , 2px3 × 10 = 540p, Þ, , x3 =, , 540, = 27, 2 ´ 10, , Free Distribution by T.S. Government 2021-22
Page 273 :
Mensuration, Þ, , x3 = 27, , Þ, , x3 = 33, , Þ, , x=3, , 263, , \ Diameter of ice cream cone 2x = 2(3) = 6cm, , G, AN, , A, , Example-12. A solid consisting of a right circular cone standing on a hemisphere, is placed, upright in a right circular cylinder full of water and touching the bottom. Find the volume of, water left in the cylinder, given that the radius of the cylinder is 3 cm. and its height is 6cm., The radius of the hemisphere is 2 cm. and the height of the cone is 4 cm., 22 ö, æ, ç Take p = ÷ ., 7 ø, è, , AN, , Solution : In the figure drawn here,, , ABCD is a cylinder, LMN is a hemisphere and OLM is a cone, , T,, TE, L, , We know that when a solid is immersed in the water, then water, displaced equal to the volume of the solid., 2, , 2, , 3, , Volume of the cylinder = pr h = p ´ 3 ´ 6 = 54 p cm, Volume of the hemisphere =, , Volume of the solid figure, , 16, 16, π+, π, =, 3, 3, , =, , 4, L, A, , 32, π, 3, , Volume of water left in the cylinder, = Volume of Cylinder - Volume of solid figure immersed, = 54p =, , C, , 2 3 2, 16, pr = ´ p´ 23 = p cm3, 3, 3, 3, , 1 2, 1, 16, pr h = ´ p´ 22 ´ 4 = p cm 3, 3, 3, 3, , SC, ER, , Volume of the cone =, , O, , D, , 32p, 3, , 162p - 32p 130p, =, 3, 3, , Free Distribution by T.S. Government 2021-22, , 2, 3, , 2, N, , M, , 2, 3, , B
Page 274 :
264, , Class-X Mathematics, =, , 130 22 2860, ´, =, = 136.19 cm3, 3, 7, 21, , A, , Example-13. A cylindrical pencil is sharpened to produce a perfect cone at one end with no, over all loss of its length. The diameter of the pencil is 1cm and the length of the conical, portion is 2cm. Calculate the volume of the peels that are obtained after sharpening pencil., , ., , 2 cm, , G, AN, , 355 ù, é, Give your answer correct to two places if it is in decimal ê use p =, ., 113 úû, ë, , Solution : Diameter of the pencil = 1cm, So, radius of the pencil (r) = 0.5 cm, Length of the conical portion = h = 2cm, , AN, , Volume of peels = Volume of cylinder of length 2 cm and base radius 0.5 cm., - volume of the cone formed by this cylinder, , T,, TE, L, , 1 2, 2 2, 2, = pr h - pr h = pr h, 3, 3, , 2 355, ´ (0.5) 2 ´ 2 cm3 = 1.05 cm 3, = ´, 3 113, , 1 cm., , E XERCISE -10.3, , SC, ER, , 1. An iron pillar consists of a cylindrical portion of 2.8 m height and 20 cm in diameter and, a cone of 42 cm height surmounting it. Find the weight of the pillar if 1 cm3 of iron weighs, 7.5 g., , 2. A toy is made in the form of hemisphere surmounted by a right cone whose circular base is, joined with the plane surface of the hemisphere. The radius of the base of the cone is 7 cm, and its volume is, , 3, of the hemisphere. Calculate the height of the cone and the surface, 2, , 1ö, æ, area of the toy correct to 2 places of decimal ç Take p = 3 ÷ ., 7ø, è, , 3. Find the volume of the largest right circular cone that can be cut out of a cube whose edge, is 7 cm., , Free Distribution by T.S. Government 2021-22
Page 275 :
Mensuration, , 265, , 4. A cylinderical mug of radius 5cm and height 9.8 cm is full of water. A solid in the form of, 3 cm., right circular cone mounted on a hemisphere is, immersed into the mug. The radius of the hemisphere, 4 cm., is 3.5 cm and height of conical part 5 cm. Find the, , A, , 22 ö, æ, volume of water left in the tub ç Take p = ÷ ., 7 ø, è, , G, AN, , 5. In the adjacent figure, the height of a solid cylinder is, 10 cm and diameter is 7cm. Two equal conical holes, of radius 3cm and height 4 cm are cut off as shown, the figure. Find the volume of the remaining solid., , 4 cm., 3 cm., , AN, , 6. Spherical marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7, cm, which contains some water. Find the number of marbles that should be dropped in to, the beaker, so that water level rises by 5.6 cm., , SC, ER, , T,, TE, L, , 7. A pen stand is made of wood in the shape of cuboid with three conical depressions to hold, the pens. The dimensions of the cuboid are 15cm by 10 cm by 3.5 cm. The radius of each, of the depression is 0.5 cm and the depth is 1.4cm. Find the volume of wood in the entire, stand., , 10.4 CONVERSION, , OF, , S OLID, , FROM, , O NE S HAPE, , TO, , A NOTHER, , A women self help group (DWACRA) prepares candles by melting, down cuboid shape wax. In gun factories, spherical bullets are made, by melting solid cube of lead, goldsmith prepares various ornaments, by melting cubiod gold biscuts. In all these cases, the shapes of, solids are converted into another shapes. In this process, the volume, always remains the same., How does this happen? If you want a candle of any special shape,, you have to heat the wax in metal container till it is completely melted., Then, you pour it into another container which has the special shape, that you wanted., , Free Distribution by T.S. Government 2021-22
Page 276 :
Class-X Mathematics, , 266, , T HINK, , AND, , D ISCUSS, , AN, , G, AN, , A, , For example, lets us take a candle in the shape of solid cylinder, melt it and pour whole of, the molten wax into another container shaped like a sphere. On cooling, you will obtain a candle, in the shape of the sphere. The volume of the new candle will be the same as the volume of the, earlier candle. This is what we have to remember when we come across objects which are, converted from one shape to another, or when a type of liquid which originally filled a container, of a particular shape is poured into another container of a different shape or size as you observe, in the following figures., , T,, TE, L, , Which barrel shown in the adjacent figure, can hold more water? Discuss with your friends., , 4cm, 1cm, 1cm, , 2cm, , To understand what has been discussed, let us consider some examples., , SC, ER, , Example-14. A cone of height 24cm and radius of base 6cm is made up of modelling clay., A child moulds it in the form of a sphere. Find the radius of the sphere., Solution : Volume of cone =, , 1, ´ p´ 6 ´ 6 ´ 24 cm 3, 3, , If r is the radius of the sphere, then its volume is, , 4 3, pr, 3, , Since, the volume of clay in the form of the cone and the sphere remains the same, we have, 4 3, 1, pr = π × 6 × 6 × 24, 3, 3, , r3 = 3 ´ 3 ´ 24 = 3 × 3 × 3 × 8, r3 = 33 ´ 23, r=3 ´ 2=6, Therefore, the radius of the sphere is 6cm., , Free Distribution by T.S. Government 2021-22
Page 277 :
Mensuration, , 267, , D O T HIS, 1. A copper rod of diameter 1 cm. and length 8 cm. is drawn into a wire of length 18m of, uniform thickness. Find the thickness of the wire., , G, AN, , A, , 2. Pravali’s house has a water tank in the shape of a cylinder on the roof. This is filled by, pumping water from a sump (an under ground tank) which is in the shape of a cuboid. The, sump has dimensions 1.57 m. ´ 1.44 m. ´ 1.5 m. The water tank has radius 60 cm. and, height 95 cm. Find the height of the water left in the sump after the water tank has been, completely filled with water from the sump which had been full of water. Compare the, capacity of the tank with that of the sump. (p = 3.14), , AN, , Example-15. The diameter of the internal and external surfaces of a hollow hemispherical shell, are 6 cm. and 10 cm. respectively. It is melted and recast into a solid cylinder of diameter 14 cm., Find the height of the cylinder., Solution : Outer radius of hollow hemispherical shell R =, , T,, TE, L, , Internal radius of hollow hemispherical shell (r) =, , 10, = 5 cm., 2, , 6, = 3 cm., 2, , Volume of hollow hemispherical shell = External volume - Internal volume, 2, 2, p R3 - p r3, 3, 3, , =, , 2, p (R 3 - r 3 ), 3, , SC, ER, , =, , =, , 2, p (125 - 27), 3, , 2, 196p 3, p´ 98 cm 3 =, cm, 3, 3, , 6 cm., , r, , 2, = p (53 - 33 ), 3, =, , 10 cm., , r, , ...(1), , Since, this hollow hemispherical shell is melted and recast into a solid cylinder. So their, volumes must be equal, Diameter of cylinder = 14 cm. (Given), So, radius of cylinder = 7 cm., , Free Distribution by T.S. Government 2021-22
Page 278 :
Class-X Mathematics, , 268, , Let the height of cylinder = h, \ volume of cylinder = pr2h, = p ´ 7 ´ 7 ´ h cm3 = 49ph cm3, , ...(2), , According to given condition, , 196, p = 49 ph, 3, h=, , G, AN, , Þ, , [From equatiion (1) and (2)], , A, , volume of hollow hemispherical shell = volume of solid cylinder, , 196, 4, = cm., 3 ´ 49 3, , Hence, height of the cylinder = 1.33 cm., , T,, TE, L, , 2 3, pr, 3, , AN, , Example-16. A hemispherical bowl of internal radius 15 cm contains a liquid. The liquid is to, be filled into cylindrical bottles of diameter 5 cm and height 6 cm. How many bottles are, necessary to empty the bowl ?, Solution : Volume of hemisphere =, , Internal radius of hemisphere r = 15 cm, , \ Volume of liquid contained in hemispherical bowl, , SC, ER, , =, , 2, p(15)3 cm3, 3, , = 2250 p cm3., , This liquid is to be filled in cylindrical bottles and the height of each bottle (h) = 6 cm., , and radius (R) =, , 5, cm, 2, , \ Volume of 1 cylindrical bottle = pR2h, 2, , æ5ö, = p´ ç ÷ ´ 6, è2ø, = π´, , 25, 75, ´ 6 cm 3 =, π cm3 ., 4, 2, , Free Distribution by T.S. Government 2021-22
Page 279 :
Mensuration, Number of cylindrical bottles required, , 269, , Volume of hemispherical bowl, = Volume of 1 cylindrical bottle, 2 ´ 2250, 2250p, = 60 ., =, 75, 75, p, 2, , A, , =, , Solution : Diameter of metallic sphere = 6cm, , AN, , \ Radius of metallic sphere = 3cm, , G, AN, , Example-17. The diameter of a metallic sphere is 6cm. It is melted and drawn into a long wire, having a circular cross section of diameter as 0.2 cm. Find the length of the wire., , 0.2 cm., , T,, TE, L, , 6 cm., , Now, diameter of cross section of cylindrical wire = 0.2 cm., \ Radius of cross section of cylinder wire = 0.1 cm., Let the length of wire be l cm., , Since the metallic sphere is converted into a cylidrical shaped wire of length h cm., , SC, ER, , Volume of the metal used in wire = Volume of the sphere, p´ (0.1) 2 ´ h =, , 4, ´ p´ 33, 3, , 2, , 4, æ 1 ö, p´ ç ÷ ´ h = ´ p´ 27, 3, è 10 ø, π´, , 1, ´ h = 36π, 100, , h=, , 36p´ 100, cm, p, , = 3600 cm = 36 m, Therefore, the length of the wire is 36 m., , Free Distribution by T.S. Government 2021-22
Page 280 :
Class-X Mathematics, , 270, , Example-18. How many spherical balls can be made out of a solid cube of lead whose edge, measures 44 cm and each ball being 4 cm. in diameter., Solution : Side of lead cube = 44 cm., 4, cm. = 2 cm., 2, 4 3, pr, 3, , A, , Now volume of a spherical ball =, , G, AN, , Radius of spherical ball =, , =, , 4 22 3, ´ ´ 2 cm3, 3 7, , =, , 4 22, ´, ´ 8 cm 3, 3 7, , AN, , Let the number of balls be ‘x’., , 4 22, ´, ´ 8 ´ x cm 3, 3 7, It is clear that volume of x spherical balls = Volume of lead cube, , T,, TE, L, , Volume of x spherical ball =, , Þ, , 4 22, ´, ´ 8 ´ x = (44)3, 3, 7, , Þ, , 4 22, ´, ´ 8 ´ x = 44 ´ 44 ´ 44, 3 7, , Þ x=, , 44 ´ 44 ´ 44 ´ 3 ´ 7, 4 ´ 22 ´ 8, , SC, ER, , x = 2541, , Hence, total number of spherical balls = 2541., , Example-19. A women self help group (DWACRA) is supplied a rectangular solid (cuboid, shape) of wax block with dimensions 66 cm, 42 cm, 21 cm, to prepare cylindrical candles each, 4.2 cm in diameter and 2.8 cm of height. Find the number of candles prepared using this solid., Solution : Volume of wax in the rectangular solid = lbh, = (66 ´ 42 ´ 21) cm3., 4.2, cm. = 2.1 cm., 2, Height of cylindrical candle = 2.8 cm., , Radius of cylindrical candle =, , Free Distribution by T.S. Government 2021-22
Page 281 :
Mensuration, , 271, , Volume of candle = pr2h, 22, ´ (2.1) 2 ´ 2.8, 7, Let x be the number of candles, , =, , 22, ´ 2.1´ 2.1´ 2.8 ´ x, 7, Q Volume of x cylindrical candles = volume of wax in rectangular shape, , = 1500, , G, AN, , 22, ´ 2.1 ´ 2.1 ´ 2.8 ´ x = 66 ´ 42 ´ 21, 7, 66 ´ 42 ´ 21´ 7, x =, 22 ´ 2.1 ´ 2.1´ 2.8, , A, , Volume of x cylindrical wax candles =, , EXERCISE - 10.4, , AN, , Hence, the number of cylindrical wax candles that can be prepared is 1500., , SC, ER, , T,, TE, L, , 1. A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of, radius 6cm. Find the height of the cylinder., 2. Three metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted together to, form a single solid sphere. Find the radius of the resulting sphere., 3. A 20m deep well of diameter 7 m is dug and the earth got by digging is evenly spread out, to form a rectangular platform of base 22 m ´ 14 m. Find the height of the platform., 4. A well of diameter 14 m is dug 15 m deep. The earth taken out of it has been spread, evenly to form circular embankment all around the well of width 7 m. Find the height of the, embankment., 5. A container shaped a right circular cylinder having diameter 12 cm and height 15 cm is full, of ice cream. The icecream is to be filled into cones of height 12 cm and diameter, 6 cm, making a hemispherical shape on the top. Find the number of such cones which can, be filled with ice cream., 6. How many silver coins, 1.75 cm in diameter and thickness 2 mm, need to be melted to, form a cuboid of dimensions 5.5 cm ´ 10 cm ´ 3.5 cm?, 7. A vessel is in the form of an inverted cone. Its height is 8 cm. and the radius of its top is, 5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of, 1, radius 0.5cm are dropped into the vessel, of the water flows out. Find the number of, 4, lead shots dropped into the vessel., 8. A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller, 2, cones, each of diameter 4 cm and height 3cm. Find the number of cones so formed., 3, , Free Distribution by T.S. Government 2021-22
Page 282 :
Class-X Mathematics, , 272, , O PTIONAL E XERCISE, [For extensive Learning], 1., , A golf ball has diameter equal to 4.1 cm. Its surface has 150 dimples each of radius 2 mm., Calculate total surface area which is exposed to the surroundings. (Assume that the dimples, , G, AN, , 2., , A, , 22 ù, é, are all hemispherical) êp = ú, 7û, ë, , A cylinder of radius 12 cm contains water to a depth of 20 cm. When a spherical iron ball, is dropped in to the cylinder, the level of water is raised by 6.75 cm. Find the radius of the, 22 ù, é, ball. êp = ú, 7û, ë, , 4., 5., , AN, , A solid toy is in the form of a right circular cylinder with a hemispherical shape at one end, and a cone at the other end. Their common diameter is 4.2 cm. and heights of the cylindrical, and concial portion are 12 cm. and 7 cm. respectively. Find the volume of the solid, 22 ù, é, toy. êp = ú, 7û, ë, Three metal cubes with edges 15 cm., 12 cm. and 9 cm. respectively are melted together, and formed into a single cube. Find the diagonal of this cube., , T,, TE, L, , 3., , A hemispherical bowl of internal diameter 36 cm. contains a liquid. This liquid is to be filled, in cylindrical bottles of radius 3 cm. and height 6 cm. How many bottles are required to, empty the bowl?, , SC, ER, , Suggested Projects, , Make an open box from a 20cm by 20cm piece of cardboard by cutting out four squares, from corners folding the flaps. What is the biggest volume of box you can make in this way?, Can you find a relation between the size of paper and the size of the square cutout that, produces the maximum volume., Extension: You can extend this by taking a rectangular sheet of paper instead of a square, sheet of paper., , W HAT WE H AVE D ISCUSSED ., , 1., , The volume of the solid formed by joining two or more basic solids, is the sum of the volumes of the constituents., , 2., , In calculating the surface area of a combination of solids, we can, not add the surface area of the two constituents because some, part of the surface area disappears on joining them., , Free Distribution by T.S. Government 2021-22
Page 283 :
11, , A, , Trigonometry, , G, AN, , 11.1 I NT RO DU CT I O N, We have learnt about triangles and their properties in previous, classes. There, we observed different daily life situations where triangles, are used., Let’s again look at some of the daily life examples., Electric poles are present everywhere. They are usually setup, by using a metal wire. The pole, wire and the ground form a, triangle. But, if the length of the wire decreases, what will be, the shape of the triangle and what will be the angle of the wire, with the ground ?, , l, , T,, TE, L, , AN, , l, , q, A person is whitewashing a wall with the help of a ladder which, is kept as shown in the adjacent figure on, left. If the person wants to paint at a higher position, what will the, person do? What will be the change in angle of the ladder with the, ground ?, , In the temple at Jainath in Adilabad district, which was built in, 13 century, the first rays of the Sun fall at the feet of the Idol of, Suryanarayana Swami in the month of December. There is a relation, between distance of Idol from the door, height of the hole on the, door from which Sun rays are entering and angle of sun rays in that, month. Can you think of the relation between them?, , SC, ER, , l, , q, , l, , th, , In a play ground, children like to, slide on a slider and slider is on a, defined angle from earth. What, will happen to the slider if we, change the angle? Will children, still be able to play on it?, , q
Page 284 :
Class-X Mathematics, , 274, , The above examples are geometrically showing the application part of triangles in our daily, life and we can measure the heights, distances and slopes by using the properties of triangles., These types of problems are part of ‘trigonometry’ which is a branch of mathematics., Now, look at the example of a person who is white washing the wall with the help of a, , A, , ladder as shown in the previous figure. Let us observe the following conditions., , G, AN, , We denote the foot of the ladder by A and top of it by C and the point of intersection of, the wall and line through base of the ladder as B. Therefore, DABC is a right angled triangle with, right angle at B. Let the angle between ladder and base be q., 1., , If the person wants to white, walll, , What happens to the angle, , T,, TE, L, , made by the ladder with the, , AN, , wash at a higher point on the, , C, , ground?, l, , What will be the change in, the distance AB?, , 2., , If the person wants to white, , wash at a lower point on the, , q, , B, , SC, ER, , wall-, , A, , l, , What happens to the angle made by the ladder with the ground?, , l, , What will be the change in the distance AB?, , We have observed in the above example of a person who was white washing. When he, , wants to paint at higher or lower points, he should change the position of ladder. So, when ‘q’ is, , increased, the height also increases and the base decreases. But, when q is decreased, the height, also decreases and the base increases. Do you agree with this statement?, Here, we have seen a right angled triangle D ABC. Now, let’s name the sides again, because trigonometric ratios of angles are based on sides only., , Free Distribution by T.S. Government 2021-22
Page 285 :
Trigonometry, 11.1.1 NAMING THE SIDES, , IN A, , 275, , RIGHT T RIANGLE, , Let’s take a right triangle ABC as show in the figure., In triangle ABC, we can consider Ð BAC as A where angle A is an acute angle. Since, AC is the longest side, it is called “hypotenuse”., Here, you observe the position, of side BC with respect to angle A. It is, opposite to angle A and we can call it as, “opposite side of angle A”. And the, remaining side AB can be called as, “Adjacent side of angle A”, AC = Hypotenuse, BC = Opposite side of angle A, , q, , A, , B, , AN, , AB = Adjacent side of angle A, , G, AN, , A, , C, , D O T HIS, , For angle R, P, , 2., , (i) For angle X, (ii) For angle Y, , SC, ER, , 1., , T,, TE, L, , Identify “Hypotenuse”, “Opposite side” and “Adjacent side” for the given angles in, the given triangles., , Q, , R, , Z, , X, , Y, , TRY THIS, , Write lengths of “Hypotenuse”, “Opposite side” and, “Adjacent side” for the given angles in the given triangles., 1., , For angle C, , 2., , For angle A, , C, , B, , A, , What do you observe? Is there any relation between the opposite side of the angle A and, adjacent side of angle C? Like this, suppose you are setting up a pole by giving support of strong, ropes. Is there any relationship between the length of the rope and the length of the pole? Here,, we have to understand the relationship between the sides and angles we will study this under the, section called trigonometric ratios., , Free Distribution by T.S. Government 2021-22
Page 286 :
Class-X Mathematics, , 276, , 11.2 T RIGONOMETRIC R ATIOS, We have seen some examples in the beginning of the chapter which are related to our daily, life situations. Let’s know about the trigonometric ratios and how they are defined., , A, , A CTIVITY, Draw a horizontal line on a paper., , 2., , Let the initial point be A and mark other points B, C, D and E at a distance, of 3cm, 6cm, 9cm, 12 cm respectively from A., , G, AN, , 1., , S, , Y, , R, , 5., , Then join AP, PQ, QR and RS., Find lengths ofAP, AQ, AR and, AS., , Q, , P, , AN, , 4., , Draw the perpendiculars BP, CQ, DR and ES of, lengths 4cm, 8cm, 12cm, 16cm from the points, B, C, D and E respectively., q, , A, , B, , T,, TE, L, , 3., , Name of, , Name of, , Length of, , Length of, , Length of, , triangle, , the angle, , hypotenuse opposite side adjacent side, , DABP, , ÐBAP = q, , C, , D, , E, , X, , Opposite side, , Adjacent side, , Hypotenuse, , Hypotenuse, , SC, ER, , DACQ ÐCAQ = q, , DADR, DAES, , Then find the ratios, , BP CQ DR, ES, ,, ,, and, ., AP AQ AR, AS, , Did you get the same ratio as, , 4, ?, 5, , AB AC AD, AE, ,, ,, and, ? What do you observe?, AP AQ AR, AS, Are these ratios constant for this fixed angle (q) even though the sides are different?, Similarly try to find the ratios, , Free Distribution by T.S. Government 2021-22
Page 287 :
Trigonometry, , 277, , 11.2.1 D EFINING T RIGONOMETRIC R ATIOS, In the above activity, when we observe right angled triangles ABP, ACQ, ADR and AES,, Ð A is common, Ð B, Ð C, Ð D and Ð E are right angles and Ð P,, Ð Q, Ð R and Ð S are, , A, , also equal. Hence, we can say that triangles ABP, ACQ, ADR and AES are similar triangles., When we observe the ratio of opposite side of angle A and hypotenuse in a right angled triangle, , angled triangles ABP, ACQ, ADR and AES. The ratios, , G, AN, , and the ratio of similar sides in another triangle, it is found to be constant in all the above right, , BP CQ DR, ES, ,, ,, and, are named as, AP AQ AR, AS, , “sine A” or simply “sin A” in those triangles. If the value of angle A is ‘q’, then the ratio would, , AN, , be “sin q”., , Hence, we can conclude that the ratio of opposite side of an angle (measure of the angle), , T,, TE, L, , and length of the hypotenuse is constant in all similar right angled triangles. This ratio will, be named as “sine” of that angle., , AB AC AD, AE, ,, ,, and, , it is also found to be, AP AQ AR, AS, constant. And these are the ratios of the adjacent sides of the angle A and hypotenuses in right, Similarly, when we observe the ratios, , angled triangles ABP, ACQ, ADR and AES. So, the ratios, , AB AC AD, AE, ,, ,, and, will be, AP AQ AR, AS, , SC, ER, , named as “cosine A” or simply “cos A” in those triangles. If the value of the angle A is “q”, then, , the ratio would be “cos q”, , Hence, we can also conclude that the ratio of the adjacent side of an angle (measure of the, angle) and length of the hypotenuse is constant in all similar right triangles. This ratio, will be named as “cosine” of that angle., Similarly, the ratio of opposite side and adjacent side of an angle is constant and it can be, named as “tangent” of that angle., , Free Distribution by T.S. Government 2021-22
Page 288 :
Class-X Mathematics, , 278, , L ET ’S DEFINE RATIOS, , IN A, , C, , RIGHT A NGLE TRIANGLE, , Consider a right angled triangle ABC having right angle at B as shown, in the adjacent figure. Then, trigonometric ratios of the angleAin right angled, , Length of the side opposite to angle A BC, =, Length of hypotenuse, AC, , Length of the side adjacent to angle A AB, =, Length of hypotenuse, AC, , tangent of Ð A = tan A =, , Length of the side opposite to angle A BC, =, Length of the side adjacent to angle A AB, , AN, , cosine of Ð A = cos A =, , D O T HIS, , 2., , SC, ER, , 3., , C, Find (i) sin C (ii) cos C and, (iii) tan C in the adjacent triangle., In a triangle DXYZ, Ð Y is right angle,, XZ = 17 m and YZ = 15 cm, then find, (i) sin X (ii) cos Z (iii) tan X, A, B, In a triangle DPQR, with right angle at Q, the value of Ð P is x, PQ = 7 cm and QR, = 24 cm, then find sin x and cos x., , T,, TE, L, , 1., , B, , G, AN, , sine of Ð A = sinA =, , A, , A, , triangle ABC are defined as follows :, , T RY T HIS, , In a right angled triangle DABC, right angle is at C. BC + CA = 23 cm and, BC - CA = 7cm, then find sin A and tan B., , T HINK, , AND, , D ISCUSS, , Discuss among your friends, 4, (i), Does sin x = exist for some value of angle x? How can you say?, 3, (ii), The value of sin A and cos A is always less than 1. Why?, (iii), , Is tan A product of tan and A? Justify your answer., , Free Distribution by T.S. Government 2021-22
Page 289 :
Trigonometry, , 279, , There are three more ratios defined in trigonometry which are considered as multiplicative, inverses of the above three ratios., Multiplicative inverse of “sine A” is “cosecant A”, simply written as “cosec A”, it is also, some times written as cscA i.e., cosecA =, , 1, sinA, , A, , Similarly, multiplicative inverse of “cos A” is secant A” (simply written as “sec A”) and, , 1, 1, and cot A =, cosA, tanA, , i.e., secA =, , How can you define ‘cosecA’ in terms of sides?, , Opposite sideof the angle A, ,, Hypotenuse, , AN, , If sinA =, , G, AN, , that of “tan A” is “cotangent A” (simply written as cot A), , T,, TE, L, , Hypotenuse, then cosecA = Opposite sideof the angle A, , T RY T HIS, , Express secA and cos A in terms of sides of right angled triangle., , T HINK, , Is, , D ISCUSS, , sinA, = tan A ?, cosA, , SC, ER, , l, , AND, , l, , cos A, Is sin A = cot A ?, , Let us see some examples, 3, Example-1. If tan A = , then find the other trigonometric ratio of angle A., 4, 3, Solution : Given tan A =, 4, Opposite side 3, Hence tan A =, =, Adjacent side 4, Therefore, opposite side : adjacent side = 3:4, , A, , For angle A, opposite side = BC = 3k, Adjacent side = AB = 4k (where k is any positive number), , Free Distribution by T.S. Government 2021-22, , C, , B
Page 290 :
Class-X Mathematics, , 280, , Now, we have in triangle ABC (by Pythagoras theorem), AC2 = AB2 + BC2, = (3k)2 + (4k)2 = 25k2, AC, , =, , 25k 2, , G, AN, , A, , = 5k = Hypotenuse, Now, we can easily write the other ratios of trigonometry, , 3k 3, 4k 4, = , cos A =, =, 5k 5, 5k 5, 1, 5, 1, 4, 1, 5, = , sec A =, = ., = , cot A =, Hence cosec A =, sin A 3, tan A 3, cos A 4, , AN, , sin A =, , Example-2. If Ð A and Ð P are acute angles such that sin A = sin P then prove that Ð A = Ð P, , T,, TE, L, , Solution : Given sin A = sin P, we have sin A =, and sin P =, , BC, AC, , QR, PQ, , Let,, , A, , R, , B P, , BC QR, =, AC PQ, , SC, ER, , Then, , Q, , C, , BC QR, =, =k, AC PQ, , .....(1), , By using Pythagoras theorem, , AB, AC2 - BC2, =, =, PR, PQ 2 - QR 2, , AC 2 - k 2AC2, PQ 2 - k 2 PQ2, , =, , ( ), (1 - k ), , AC 2 1 - k 2, PQ 2, , 2, , =, , AC, PQ (From (1)), , Hence, AC = AB = BC then DABC : DPQR, PQ PR QR, Therefore, ÐA = ÐP, , Free Distribution by T.S. Government 2021-22
Page 291 :
Trigonometry, , 281, , Example-3. Consider a triangle DPQR, right angled at R, in which PQ = 29 units, QR = 21, units and Ð PQR = q, then find the values of, Q, , (i) cos2q + sin2q and (ii) cos2q - sin2q, Solution : ln DPQR, we have, , PR = PQ 2 - QR 2 = (29)2 - (21)2, 400 = 20 units, , PR 20, =, PQ 29, QR 21, =, cos q =, PQ 29, , sin q =, , 2, , 441 + 400, æ 21 ö æ 20 ö, =1, (i) cos q + sin q = ç ÷ + ç ÷ =, 841, è 29 ø è 29 ø, 2, , 2, , 2, , AN, , Now, , R, , P, , 2, , 21, , G, AN, , =, , q, , A, , 29, , 2, , 41, æ 21 ö æ 20 ö, (ii) cos q - sin q = ç ÷ - ç ÷ =, 841, è 29 ø è 29 ø, 2, , T,, TE, L, , 2, , EXERCISE - 11.1, , In right angled triangle ABC, 8 cm, 15 cm and 17 cm are the lengths of AB, BC and CA, respectively. Then, find sin A, cos A and tan A., , 2., , The sides of a right angled triangle PQR are PQ = 7 cm, PR = 25 cm and ÐQ = 90o, respectively. Then find, tan P - tan R., , 3., , In a right angled triangle ABC with right angle at B, in which a = 24 units, b = 25 units, and Ð BAC = q. Then, find cos q and tan q., , 4., , If cos A =, , 5., , If 3 tan A = 4, then find sin A and cos A., , 6., , In DABC and DXYZ, if Ð A and Ð X are acute angles such that cos A = cos X then, , SC, ER, , 1., , 12, , then find sin A and tan A (A<90o)., 13, , show that Ð A = Ð X., 7., , 7, (1 ∗ sin q) (1, sin q), Given cot q = , then evaluate (i), 8, (1 ∗ cos q) (1, cos q), , 8., , In a right angled triangle ABC, right angle is at B. If tan A =, (i) sin A cos C + cos A sin C, , Free Distribution by T.S. Government 2021-22, , (ii), , (1 ∗ sin q), cos q, , 3 , then find the value of, , (ii) cos A cos C - sin A sin C
Page 292 :
Class-X Mathematics, , 282, , 11.3 T RIGONOMETRIC R ATIOS, , OF SOME SPECIFIC ANGLES, , We already know about isosceles right angled triangle and right angled triangle with angles, 30º, 60º and 90º., Can we find sin 30o or tan 60o or cos 45o etc. with the help of these triangles?, , OF, , 45, , O, , G, AN, , 11.3.1 T RIGONOMETRIC R ATIOS, , A, , Does sin 0o or cos 0o exist?, , In isosceles right angled triangle ABC right angled at B, Ð A = Ð C = 45o (why ?) and BC = AB (why ?), , AN, , Let’s assume the length of BC = AB = a, , A, , Then, AC2 = AB2 + BC2 (by Pythagoras theorem), = a2 + a2 = 2a2,, , T,, TE, L, , Therefore, AC = a 2, , B, , C, , Using the definitions of trigonometric ratios,, , Length of the oppositeside to angle 45o BC, a, 1, =, =, =, sin 45 =, Length of hypotenuse, AC a 2, 2, o, , Length of theadjacent side to angle 45o AB, a, 1, =, =, =, cos 45 =, Length of hypotenuse, AC a 2, 2, , SC, ER, , o, , Length of theopposite side to angle 45o BC a, =, = =1, tan 45 =, Length of the adjacent side to angle 45o AC a, o, , Similarly, you can determine the values of cosec 45 o, sec 45o and cot 45o., , 11.3.2 T RIGONOMETRIC R ATIOS, , OF, , 30, , O, , AND, , 60, , O, , Let us now calculate the trigonometric ratios of 30o and 60o., , A, 30º 30º, , Consider an equilateral triangle ABC. Since each angle is, o, 60 in an equilateral triangle, we have Ð A = Ð B = Ð C = 60o 2a, , 2a, , and let the sides of equilateral t riangle be, AB = BC = CA = 2a units., Draw the perpendicular line AD from vertex A to, BC as shown in the adjacent figure., , B, , 60º, , 60º, a, , D, , a, , C, , Free Distribution by T.S. Government 2021-22
Page 294 :
284, , Class-X Mathematics, , 11.3.3 T RIGON OMETRIC R ATIOS, , OF, , 0, , O, , AND, , 90, , O, , Till now, we have discussed trigonometric ratios of 30 o, 45o and 60o. Now let us, determine the trigonometric ratios of angles 0o and 90o., Suppose a segment AC of length r is, making an acute angle with ray AB. Height of C, from B is BC. When AC leans more on AB so, that the angle made by it decreases, then what, happens to the lengths of BC and AB ?, , C, , G, AN, , A, , r, , q, , AN, , As the angle A decreases, the height of A, B, C from AB ray decreases and foot B is shifted, from B to B1 and B2 and gradually when the angle becomes zero, height (i.e. opposite side of the, angle) will also become zero (0) and adjacent side would be equal to AC i.e. length equal to r., C, , A, , T,, TE, L, , C, , A, , B, , Step (i), , C, , B, , Step (ii), , SC, ER, , Let us look at the trigonometric ratios, sin A =, , BC, AB, and cos A =, AC, AC, , If A = 0o then BC = 0 and AC = AB = r., , Thus, sin 0o =, , 0, r, = 0 and cos 0o = = 1., r, r, , We know that tan A =, So, tan0o =, , sin A, cos A, , sin 0o 0, = =0, cos 0o 1, , Free Distribution by T.S. Government 2021-22
Page 295 :
Trigonometry, , 2., 3., , Discuss with your friends about the following conditions:, 1, ? Is it defined? Why?, What can you say about cosec 0o =, sin 0º, 1, . Is it defined? Why?, What can you say about cot 0o =, tan 0º, sec 0o = 1. Why?, , G, AN, , 1., , D ISCUSS, , AND, , A, , T HINK, , 285, , T,, TE, L, , AN, , Now, let us see what happens when angle made by AC, with ray AB increases. When angle A is increased, height of point, C increases and the foot of the perpendicular shifts from B to X, and then to Y and so on. In other words, we can say that the height, BC increases gradually, the angle on C gets continuous increment, and at one stage the angle reaches 90o. At that time, point B reaches, A and AC equal to BC., , SC, ER, , Step (i), So, when the angle becomes 90o, base (i.e. adjacent side, of the angle) would become zero (0), the height of C from AB ray increases and it would be, equal to AC and that is the length equal to r., , Step (ii), Now let us see trigonometric ratios, sin A =, , BC, AB, and cos A =, ., AC, AC, , If A = 90o then AB = 0 and AC = BC = r., Then , sin 90o =, , r, 0, = 1 and cos 90o = = 0., r, r, , Free Distribution by T.S. Government 2021-22, , Step (iii)
Page 296 :
Class-X Mathematics, , 286, , TRY THIS, Find the values for tan 90o, cosec 90o, sec 90o and cot 90o., , 30o, , 45o, , 60o, , 1, 2, , 1, 2, 1, 2, , 3, 2, 1, 2, , 0, , sin A, , 0, , cos A, , 1, , tan A, , 0, , cot A, , not defined, , 3, , sec A, , 1, , 2, 3, , 1, , AN, , 3, , 1, 3, , 1, , T,, TE, L, , cosec A, , 3, 2, 1, 3, , T HINK, , not defined, , AND, , 2, , 90o, , G, AN, , o, , ÐA, , A, , Now, let us observe the change in values of trigonometric ratios of all the above discussed, angles in the form of a table., Table 11.1, , 2, , 2, , 2, 3, , 2, , 1, 0, , not defined, 0, , not defined, 1, , D ISCUSS, , SC, ER, , Observe the above table, , What can you say about the values of sin A and cos A, as the value of angle A increases, from 0o to 90o?, If A > B, then sin A > sin B. Is it true ?, If A > B, then cos A > cos B. Is it true ? Discuss., , Example-4. In DABC, right angle is at B, AB = 5 cm and Ð ACB = 30o. Determine the lengths, of the sides BC and AC., A, , 5 cm, , Solution : Given AB=5 cm and Ð ACB=30o. To find the length of, side BC, we will choose the trignometric ratio involving BC and the, given side AB. Since, BC is the side adjacent to angle C and AB is, the side opposite to angle C., , B, , Free Distribution by T.S. Government 2021-22, , C
Page 297 :
Trigonometry, , 287, , AB, = tan C, BC, 1, 5, i.e., = tan 30o =, 3, BC, , Therefore,, , which gives BC = 5 3 cm, , 5, AC, , G, AN, , sin 30o =, , A, , Now, by using the trigonometric ratios in DABC, , 1, 5, =, 2 AC, , AN, , AC = 10 cm, , T,, TE, L, , Example-5. A chord of a circle of radius 6cm is making an angle 60o at the centre. Find the, length of the chord., Solution : Given that the radius of the circle is OA = OB = 6cm and Ð AOB = 60o., OC is height from ‘O’ upon AB and it is an angle, bisector., Then, Ð COB = 30o., Consider DCOB, , BC, OB, , SC, ER, sin 30o =, , O, , 1 BC, =, 2 6, , BC =, , 6, = 3., 2, , A, , C, , B, , But, length of the chord AB = 2BC, = 2 ´ 3 = 6 cm, \ Therefore, length of the chord = 6 cm., , Free Distribution by T.S. Government 2021-22, , The first use of, the idea of ‘sine’, the way we use, it today was, given in the book, Aryabhatiyam, by Aryabhatta,, in 500 C.E., Aryabhatta used, the word ardhajya for the halfchord, which was shortened to jya or, jiva in due course. When the, Aryabhatiyam was translated into, Arabic, the word jiva was retained, as it is. The word jiva was translated, into sinus, which means curve, when, the Arabic version was translated into, Latin. Soon the word sinus, also used, as sine, became common in, mathematical texts throughout, Europe. An English Professor of, astronomy Edmund Gunter (1581–, 1626), first used the abbreviated, notation ‘sin’.
Page 298 :
Class-X Mathematics, , 288, , Example-6. In DPQR, right angle is at Q, PQ = 3 cm and PR = 6 cm. Determine Ð QPR and, Ð PRQ., P, , Solution : Given PQ = 3 cm and PR = 6 cm, PQ, = sin R, PR, 3 1, or sin R = =, 6 2, , G, AN, , and therefore, Ð QPR = 60o (why?), AND, , R, , Q, , So, Ð PRQ = 30o, , T HINK, , A, , Therefore,, , D ISCUSS, , AN, , If one of the sides and any other part (either an acute angle or any side) of a right angled, triangle is known, the remaining sides and angles of the triangle can be determined. Do, you agree? Explain with an example., 1, 1, , cos (A + B) = , where 0o < A + B < 90o and A > B, find A and B., 2, 2, 1, Solution : Since, sin (A - B) = , therefore, A - B = 30o (why?), 2, 1, Also, since cos (A + B) = , therefore, A + B = 60o (why?), 2, , T,, TE, L, , Example-7. If sin (A - B) =, , Solving the above equations, we get : A = 45o and B = 15o. (How?), , SC, ER, , EXERCISE - 11.2, , 1., , 2., , Evaluate the following., o, , o, , (i), , sin 45 + cos 45, , (iii), , sin 30o + tan45o - cosec 60o, cot 45o + cos 60o - sec 30o, , (v), , sec2 60o - tan 2 60o, sin 2 30o + cos 2 30o, , (ii), , cos 45o, sec 30o + cosec 60o, , (iv), , 2 tan245o + cos230o - sin2 60o, , Choose the right option and justify your choice(i), , 2 tan 30o, =, 1 + tan 2 45o, , (a) sin 60o, , (b) cos 60o, , (c) tan 30o, , (d) sin 30o, , Free Distribution by T.S. Government 2021-22
Page 299 :
Trigonometry, 1 - tan 2 45o, =, 1 + tan 2 45o, , (a) tan 90o, (iii), , (b) 1 (c), , sin 45o (d), , (b) sin 60o, , (c), , 0, , 2 tan 30o, =, 1 - tan 2 30o, , tan 60o (d), , sin 30o, , G, AN, , (a) cos 60o, , A, , (ii), , 289, , Evaluate sin 60o cos 30o + sin 30o cos 60o. What is the value of sin(60o + 30o). What, can you conclude ?, , 4., , Is it right to say that cos(60o + 30o) = cos 60o cos30o - sin 60o sin 30o., , 5., , In right angled triangle DPQR, right angle is at Q, PQ = 6cm and Ð RPQ = 60o., Determine the lengths of QR and PR., , 6., , In DXYZ, right angle is at Y, YZ = x, and XZ = 2x. Then, determine Ð YXZ and, Ð YZX., , 7., , Is it right to say that sin (A + B) = sin A + sin B? Justify your answer., , T,, TE, L, , AN, , 3., , 11.4 T RIGONOMETRIC R ATIOS, , OF, , C OMPLEMENTARY, , ANGLES, , We already know that two angles are said to be complementary, if their sum is equal to 90o., Consider a right angled triangle ABC with right angle at B. Are there any complementary angles, in this triangle?, C, , SC, ER, , Since, angle B is 90o, sum of other two angles must be 90o., (Q Sum of angles in a triangle 180o), Therefore, Ð A + Ð C = 90o. Hence Ð A and Ð C are, complementary angles., , Let us assume that Ð A = x, then for angle x, BC is, A, opposite side and AB is adjacent side., sin x =, , BC, AC, , cosec x =, , AC, BC, , cos x =, , AB, AC, , tan x =, , BC, AB, , sec x =, , AC, AB, , cot x =, , AB, BC, , Free Distribution by T.S. Government 2021-22, , B
Page 301 :
Trigonometry, , 291, , Example-9. If cos 7A = sin(A - 6o), where 7A is an acute angle, find the value of A., Solution : Given cos 7A = sin(A - 6o), , ...(1), , sin (90 - 7A) = sin (A - 6o), since, (90 - 7A) & (A - 6o) are both acute angles,, , A, , therefore, 90o - 7A = A - 6o, 8A = 96o, , G, AN, , which gives A = 12o., , Example-10. If sin A = cos B, then prove that A + B = 90º., Solution : Given that sin A = cos B, , ...(1), , We can write (1) as, sin A = sin (90o - B), , AN, , We know cos B = sin (90o - B)., , T,, TE, L, , Since A, B are acute angles, A = 90o - B, o, Þ A + B = 90 ., , Example-11. Express sin 81o + tan 81o in terms of trigonometric ratios of angles between, 0o and 45o., Solution : We can write sin 81o = sin(90o - 9o) = cos 9o, , SC, ER, , and tan 81o = tan(90o - 9o) = cot 9o, , Then, sin 81o + tan 81o = cos 9o + cot 9o, , Example-12. IfA, B and C are interior angles of triangle ABC, then show that sin (, , B+C, A, ) = cos, 2, 2, , Solution : Given A, B and C are angles of triangle ABC then A + B + C = 180 o., On dividing the above equation by 2 on both sides, we get, A B+C, +, = 90o, 2, 2, B+C, A, = 90o 2, 2, , Free Distribution by T.S. Government 2021-22
Page 304 :
Class-X Mathematics, , 294, , 2, , 2, , æ AB ö, æ BC ö, æ AC ö, ç, ÷ +ç, ÷ =ç, ÷, è AB ø, è AB ø, è AB ø, , i.e., 1 + tan2 A = sec2A, , 2, , (A¹90°), , Similarly, on dividing (1) by BC2, we get cot 2A + 1 = cosec2A. (A¹0°), , T HINK, , AND, , D ISCUSS, , G, AN, , A, , By using above identities, we can express each trigonometric ratio in terms of another ratio., If we know the value of a ratio, we can find all other ratios by using these identities., , Are these identities true only for 00 < A< 900 ? If not, for which other values ofAthey are true?, sec2 A - tan2A = 1, , l, , D O T HIS, , 15, , then find cos C., 17, , If sin C =, , (iii), , If cosec q =, , (ii) If tan x =, , T,, TE, L, , (i), , cosec2A - cot2A = 1, , AN, , l, , 5, , then find sec x., 12, , 25, , then find cot q., 7, , TRY THIS, , SC, ER, , Evaluate the following and justify your answer., (i), , sin 2 15o + sin 2 75o, cos 2 36o + cos 2 54o, , (iii), , sec 16o cosec 74o - cot 74o tan 16o., , (ii), , sin 5o cos 85o + cos5o sin 85o, , Example-13. Show that cot q + tan q = sec q cosec q. (0°<q<90°), , Solution : LHS = cot q + tan q, =, , cos q sin q, +, sin q cos q, , =, , cos 2 q + sin 2 q, sin q cos q, , (why ?), , Free Distribution by T.S. Government 2021-22
Page 305 :
Trigonometry, =, , 1, sin q cos q, , =, , 1, 1, = cosecq sec q, sin q cos q, , 295, , (why ?), , (Why ?), (Why ?), , = sec4q - sec2q = R.H.S, , 1 + cos q, 1 - cos q, , (multiply numerator and denominator by, , T,, TE, L, , Solution : LHS =, , 1 + cos q, = cosec q + cot q; (0°<q<90°), 1 - cos q, , AN, , Example-15. Prove that, , G, AN, , Solution : L.H.S. = tan2q + tan4q, = tan2q (1 + tan2q), = tan2q . sec2q, = (sec2q - 1) sec2q, , A, , Example-14. Show that tan2q + tan4q = sec4q - sec2q (q¹90°), , 1 + cos q 1 + cos q, ., 1 - cos q 1 + cos q, , =, , (1 + cos q)2, 1 - cos2 q, , =, , (1 + cos q)2, sin 2 q, , (Why ?), , SC, ER, , =, , =, , =, , 1 + cos q, sin q, , 1, cos q, +, = cosecq + cot q = R.H.S., sin q sin q, , E XERCISE 11.4, , 1., , Evaluate the following :, (i), , (1 + tan q + sec q) (1 + cotq - cosec q), , (ii), , (sin q + cos q)2 + (sin q - cos q)2, , (iii), , (sec2q - 1) (cosec2q -1), , Free Distribution by T.S. Government 2021-22, , (1 + cos q) )
Page 306 :
Class-X Mathematics, , 296, , 1 - cos q, ., 1 + cos q, , 2., , Show that (cosec q - cot q)2 =, , 3., , Show that, , 4., , 1 - tan 2 A, = tan 2 A (0°<q<90°)., Show that, 2, cot A - 1, , 5., , Show that, , 6., , Simplify secA (1 - sinA) (secA + tanA)., , 7., , Prove that (sinA + cosec A)2 + (cosA + secA)2 = 7 + tan2A + cot2A., , 8., , Simplify (1 - cos q) (1 +cosq) (1 + cot2q)., , 9., , If secq + tan q = p, then what is the value of secq - tan q ?, , 10., , If cosec q + cot q = k, then prove that cos q =, , AN, , G, AN, , 1, - cos q = tan q.sin q (0°<q<90°)., cos q, , A, , 1 + sin A, = sec A + tan A (0°<q<90°)., 1 - sin A, , T,, TE, L, , k2 - 1, ., k2 + 1, , O PTIONAL E XERCISE, , [For extensive Learning], , Prove that cot q - cos q = cos ecq - 1 ., cot q + cos q cos ecq + 1, , sin q - cos q + 1, 1, [use the identity sec2 q = 1 + tan2 q]., =, sin q + cos q - 1 s ecq - tan q, , SC, ER, , 1., , 2., , Prove that, , 3., , Prove that (cosec A - sin A) (sec A - cos A) =, , 4., , Prove that, , 5., , æ 1 + tan 2 A ö æ 1 + tan A ö 2, =ç, = tan 2 A ., ÷, Show that ç, 2, ÷, è 1 + cot A ø è 1 - cot A ø, , 6., , Prove that, , 1, ., tan A + cot A, , 1 + sec A, sin 2 A, ., =, sec A, 1 - cos A, , (sec A ,1), (1, cos A), ., <, (sec A ∗ 1), (1 ∗ cos A), , Free Distribution by T.S. Government 2021-22
Page 307 :
Trigonometry, , 297, , WHAT WE H AVE D ISCUSSED, In a right angled triangle ABC, with right angle at B,, , Side opposite to angle A , cos A = Side adjacent to angle A, Hypotenuse, Hypotenuse, , A, , sin A =, , G, AN, , 1., , 1, 1, sin A, 1, ; s ecA =, ; tan A =, ; tan A =, sin A, cos A, cos A, cot A, , 2., , cosec A =, , 3., , If one of the trigonometric ratios of an acute angle is known, the remaining trignometric, , AN, , ratios of the angle can be determined., , The values of the trigonometric ratios for angle 0o, 30o, 45o, 60o and 90o., , 5., , The value of sin A and cos A never exceeds 1, whereas the value of sec A (A¹90°) and, , T,, TE, L, , 4., , cosec A (A¹0°) is always greater than or equal to 1., 6., , sin (90o- A) = cos A, cos (90o- A) = sin A, , tan (90o- A) = cot A, cot (90o- A) = tan A, , SC, ER, , sec A (90o- A) = cosec A, cosec (90o- A) = sec A, , 7., , sin2 A + cos2 A = 1, sec2 A - tan2 A = 1 for 0o < A < 90o, , cosec2 A - cot2 A = 1 for (0o < A < 90o), , Free Distribution by T.S. Government 2021-22
Page 308 :
Class-X Mathematics, , 12, , Applications of, Trigonometry, , A, , 298, , G, AN, , 12.1 I NTRODUCTION, , You have studied in social studies that the highest mountain peak in the world is Mount, Everest and its height is 8848 meters. Kuntala waterfall in Adilabad district is the highest natural, waterfall in Telangana. Its height is 147 feet., Is it possible to measure these heights by using measring tape?, , AN, , How were these heights measured?, , SC, ER, , T,, TE, L, , Can you measure the height of your school building or the tallest tree in or around your, school?, , Let us understand through some examples. Vijaya wants to find the height of a palm tree., She tries to locate the top most point of the tree. She also, imagines a line joining the top most point and her eye., , Here, “the line of sight”, “horizontal line” and “the tree”, form a right angle triangle., To find the height of the tree, she needs to find a side, and an angle in this triangle., “The line of sight is above the horizontal line and angle, between the line of sight and the horizontal line is called angle, of elevation”., , Line, of si, ght, , This line is called “line of sight”. She also imagines a, horizontal line, from her eye to the tree., , Angle of, elevation, , q, , Free Distribution by T.S. Government 2021-22
Page 309 :
Applications of Trigonometry, , 299, , Horizontal line, , Suppose, you are, standing on the top of your, school building and you want to, find the distance of borewell, from the building on which you, are standing. For that, you have, to observe the base of the, borewell., , q Angle of depressio, n, fs, igh, t, , G, AN, , A, , Li, ne, o, , Then, the line of sight from, your eye to the base of borewell is below the horizontal line from your eye., , Here, “the angle between the line of sight and horizantal line is called angle of depression.”, , T,, TE, L, , AN, , Trigonometry has been used by surveyors for centuries. They use Theodolites to measure, angles of elevation or depression in the process of survey. In nineteenth century, two large, Theodolites were built by British India for the surveying project “great trigonometric survey”., During the survey in 1852, the highest mountain peak in the world was discovered in the, Himalayas. From the distance of 160 km, the peak was observed from six different, stations and the height of the peak was calculated. In 1856, this peak was named after Sir, George Everest, who had commissioned and first used the giant Theodolites. Those, theodolites are kept in the museum of the Survey of India in Dehradun for display., , TO, , S OLVE P ROBLEMS, , SC, ER, , 12.2 D RAWING F IGURES, , When we want to solve the problems of heights and distances, we should consider the, following:, (i), , All the objects such as towers, trees, buildings, ships, mountains etc. shall be considered, as linear for mathematical convenience., , (ii), , The angle of elevation or angle of depression is considered with reference to the horizontal, line., , (iii), , The height of the observer is neglected, if it is not given in the problem., , When we try to find heights and distances at an angle of elevation or depression, we need, to visualise geometrically. To find heights and distances, we need to draw figures and with the, help of these figures we can solve the problems. Let us see some examples., , Free Distribution by T.S. Government 2021-22
Page 310 :
Class-X Mathematics, , 300, , Example-1. The top of a clock tower is observed at angle of elevation of a and the foot of the, tower is at the distance of d meters from the observer. Draw the diagram for this data., Solution : The diagrams are as shown below :, , a, , B, , d, , G, AN, , A, , A, , a, , C, , d, , AN, , Example-2. Rinky observes a flower on the ground from the balcony of the first floor of a, building at an angle of depression b. The height of the first floor of the building is x meters. Draw, the diagram for this data., , T,, TE, L, , Solution :, , D, , b, , b, , b, , A, x, , b, C, , B, , SC, ER, , Here ÐDAC = ÐBCA = b (why?), , Example-3. A large balloon has been tied with a rope and it is floating in the air. A person has, observed the balloon from the top of a building at angle of elevation of q1 and foot of the rope at, an angle of depression of q2. The height of the building is h feet. Draw the diagram for this data., , Solution : We can see that ÐADB = ÐDAE. (Why?), , q1, , D, , q2, , C, , q1, , B, , q2, , h, , q2, , E, , q2, A, , Free Distribution by T.S. Government 2021-22
Page 311 :
Applications of Trigonometry, , 301, , D O T HIS, Draw diagram for the following situations :, A person is flying a kite at an angle of elevation a and the length of thread, from his hand to kite is ‘l’., , (ii), , A person observes two banks of a river at angles of depression q1 and q2, (q1 < q2 ) from the top of a tree of height h which is at a side of the river. The, width of the river is ‘d’., , T HINK, , AND, , D ISCUSS, , You are observing top of your school building at an angle of elevation a from a point, which is at d meter distance from foot of the building., , AN, , 1., , A, , (i), , G, AN, , 1., , Which trigonometric ratio would you like to consider to find the height of the building?, A ladder of length x meter is leaning against a wall making angle q with the ground., Which trigonometric ratio would you like to consider to find the height of the point on, the wall at which the ladder is touching?, , T,, TE, L, , 2., , Till now, we have discussed how to draw diagrams as per the situations given. Now, we, shall discuss how to find heights and distances., Example-4. A boy observed the top of an electric pole at an angle of elevation of 60º when the, observation point is 8 meters away from the foot of the pole. Find the height of the pole., , SC, ER, , Solution : From the figure, in triangle DOAB, , A, , OB = 8 meters and, ÐAOB = 60º., , Let height of the pole = AB = h meters, , (we know the adjacent side and we need to find the opposite side of, ÐAOB in the triangle DOAB. Hence we need to consider the trigonometric, ratio “tangent” to solve the problem)., AB, tan 60º =, OB, h, 3=, h = 8 3m., 8, , Free Distribution by T.S. Government 2021-22, , h, , 60°, O, , 8m, , B
Page 312 :
Class-X Mathematics, , 302, , Example-5. From a helicopter, Rajender observes a person standing on the ground at an angle, of depression 45º. If the helicopter is flying at a height of 500 m from the ground, what is the, distance of the person from Rajender?, Solution : From the figure, in triangle DOAB, , P, , 45º, , O, , OA = 500 m and, , OB = distance of the person from Rajender = x., , G, AN, , x, , B, , 45º, , 500 m, , A, , ÐPOB = ÐABO = 45º (why ?), , A, , sin 45º =, , OA, OB, , T,, TE, L, , 1, 500, =, x, 2, , AN, , (we know the opposite side of ÐABO and we need to find hypotenuse OB in the triangle, OAB. Hence, we need to consider the ratio “sine”.), , x = 500 2 m, , (The distance from the person to Rajendar is 500 2 m), , EXERCISE - 12.1, , A tower stands vertically on the ground. From a point which is 15 meter away from the, foot of the tower, the angle of elevation of the top of the tower is 45º. What is the height, of the tower?, , SC, ER, , 1., , 2., , A tree was broken due to storm and the broken part bends so that the top of the tree, touches the ground by making 30º angle with the ground. The distance between the foot, of the tree and the top of the tree on the ground is 6m. Find the height of the tree before, falling down., , 3., , A contractor wants to set up a slide for the children to play in the park. He wants to set, it up at the height of 2 m and by making an angle of 30º with the ground. What should be, the length of the slide?, , 4., , Length of the shadow of a 15 meter high pole is 15 3 meters at 8 O’clock in the, morning. Then, what is the angle of elevation of the Sun rays with the ground at the time?, , 5., , You want to setup a pole of height 10 m vertically with the support of three ropes. Each, rope has to make an angle 30º with the pole. What should be the length of the rope?, , Free Distribution by T.S. Government 2021-22
Page 313 :
Applications of Trigonometry, , 303, , Suppose, you are shooting an arrow from the top of a building at an height of 6 m to a, target on the ground at an angle of depression of 60º. What is the distance between you, and the object?, , 7., , An electrician wants to repair an electric connection on a pole of height 9 m. He needs, to reach 1.8 m below the top of the pole to do repair work. What should be the length, of the ladder he should use, when it makes an angle of 60º with the ground? What will, be the distance between foot of the ladder and foot of the pole?, , 8., , A boat has to cross a river. It crosses the river by making an angle of 60º with the bank, of the river due to the stream of the river and travels a distance of 600m to reach the, another side of the river. What is the width of the river?, , 9., , An observer of height 1.8 m is13.2 m away from a palm tree. The angle of elevation of, the top of the tree from his eye, B, is 45º. What is the height of the, palm tree?, , 10., , In the adjacent figure, AC = 6, cm, AB = 5 cm and ÐBAC =, 30º. Find the area of the, triangle., A, , AN, , G, AN, , A, , 6., , 5c, , m, , T,, TE, L, , 30º, , 12.3 S OLUTION, , FOR, , C, 6 cm, , T WO TRIANGLES, , We have discussed the solution of a one triangle problem. What will be the solution if there, D, are two triangles?, , SC, ER, , Suppose, you are standing in, front of a tree. You want to find the, height of the tree observing the tree, from different points of observation, in the same line with the tree., , How can yo u do this?, Suppose you are observing the top, of the palm tree at an angle of, elevation 45º. The angle of elevation, changes to 30º when you move, 11 m away from the earlier point., , A, , 30º, , 45º, B, , E, , Free Distribution by T.S. Government 2021-22, , C, , E1
Page 314 :
Class-X Mathematics, , 304, , D, , Let us see how we can find height of the tree., From figure, we have, AB = 11 m, ÐCAD = 30º, , ÐCBD = 45º, , h, , From triangle BDC,, , 30º, , A, , DC, tan 45º =, BC, , 11 m, , F, , h, Þ x<h, x, From triangle ADC,, 1<, , 45º, , B, , C, E, , AN, , ...(1), , DC, AC, , T,, TE, L, , tan 30º =, , G, AN, , and length of BC = x., Then AC = 11 + x., , A, , L et the height of the palm tree CD = h meters, , 1, h, =, 3 11 + x, 11 + x, 3, , h=, , 11, h, +, 3, 3, , SC, ER, , h=, , h-, , h, , (, , h =, , h, 11, =, 3, 3, , ) = 11, , 3 -1, 3, , (, , 3, , 11, , ), , 3 -1, , m., , The height of the palm tree is, , (, , 11, , ), , 3 -1, , m, , Note : Total height of the palm tree is CD + CE where CE = AF, which is the height of the girl., , Free Distribution by T.S. Government 2021-22
Page 315 :
Applications of Trigonometry, , 305, , Example-6. Two men on either side of a temple of 30 meter height observe its top at the angles, of elevation 30º and 60º respectively. Find the distance between the two men., Solution : Height of the temple BD = 30 meter., Angle of elevation of one person ÐDAB = 30º, Angle of elevation of another person ÐBCD = 60º, , BD, AB, , 1, 30, <, x, 3, , tan 60º =, , BD, d, , 30, 3<, d, , d<, , 30º, x, , D, , 60º, d, , C, , 30, .......... (2), 3, , T,, TE, L, , x < 30 3 .......... (1), , A, , G, AN, , tan 30º =, , B, , From DBCD, , AN, , From DBAD, , A, , Let the distance between the first person and the temple, AD = x and distance between the, second person and the temple, CD = d, , from (1) and (2) distance between the persons = BC + BA = x + d, , < 30 3 ∗, , 30 30≥ 4 120, <, <, < 40 3 m, 3, 3, 3, , The required distance is 40 3 m, , SC, ER, , Example-7. A straight highway leads to the foot of a tower. Ramaiah standing at the top of the, tower observes a car at an angle of depression 30º. The car is approaching the foot of the tower, with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60º., Find the time taken by the car to reach the foot of the tower from this point., Solution :, , Let the distance travelled by the car in 6 seconds = AB = x meters, Heights of the tower, , CD = h meters, , The remaining distance to be travelled by the car BC = d meters, , and AC = AB + BC = (x + d) meters, ÐADP = ÐDAB = 30º (why?), ÐBDP = ÐDBC = 60º (why?), From DBCD, , Free Distribution by T.S. Government 2021-22
Page 316 :
Class-X Mathematics, , 60º, , h, d, , h=, , 3d, , 30º, , h, , ...(1), , From DACD, , B, , d, , A, , AN, , 1, h, =, 3 (x + d ), h=, , 30º, , 60º, , C, , CD, tan 30º =, AC, , A, , 3=, , P, , D, , CD, tan 60º =, BC, , G, AN, , 306, , (x + d ), 3, , ...(2), , T,, TE, L, , From (1) & (2), we have, , x+d, = 3d, 3, x + d = 3d, , x = 2d, x, 2, , SC, ER, , d=, , Time taken to travel ‘x’ meters = 6 seconds., Time taken to travel the distance of ‘d’ meters, i.e.,, , x, meters is 3 seconds., 2, , EXERCISE - 12.2, , 1., , A TV tower stands vertically on the side of a road. From a point on the other side, directly opposite to the tower, the angle of elevation of the top of tower is 600. From, another point 10 m away from this point, on the line joining this point to the foot of the, tower, the angle of elevation of the top of the tower is 30º. Find the height of the tower, and the width of the road., , Free Distribution by T.S. Government 2021-22
Page 317 :
Applications of Trigonometry, , 307, , A 1.5 m tall boy is looking at the top of a temple which is 30 meter in height from a point, at certain distance. The angle of elevation from his eye to the top of the crown of the, temple increases from 30º to 60º as he walks towards the temple. Find the distance he, walked towards the temple., , 3., , A statue stands on the top of a 2m tall pedestal. From a point on the ground, the angle, of elevation of the top of the statue is 60º and from the same point, the angle of elevation, of the top of the pedestal is 45º. Find the height of the statue., , 4., , From the top of a building, the angle of elevation of the top of a cell tower is 60º and the, angle of depression to its foot is 45º. If distance of the building from the tower is 7m,, then find the height of the tower., , 5., , A wire of length 18 m had been tied with electric pole at an angle of elevation 30º with, the ground. Because it was covering a long distance, it was cut and tied at an angle of, elevation 60º with the ground. How much length of the wire was cut?, , 6., , The angle of elevation of the top of a building from the foot of the tower is 30º and the, angle of elevation of the top of the tower from the foot of the building is 60º. If the tower, is 30 m high, find the height of the building., , 7., , Two poles of equal heights are standing opposite to each other on either side of the road,, which is 120 feet wide. From a point between them on the road, the angles of elevation, of the top of the poles are 60º and 30º respectively. Find the height of the poles and the, distances of the point from the poles., , 8., , The angles of elevation of the top of a tower from two points at a distance of 4 m and, 9 m from the base of the tower and in the same straight line with it are complementary., Find the height of the tower., , 9., , The angle of elevation of a jet plane from a point A on the ground is 60º. After a flight of, 15 seconds, the angle of elevation changes to 30º. If the jet plane is flying at a constant, , SC, ER, , T,, TE, L, , AN, , G, AN, , A, , 2., , height of 1500 3 meter, find the speed of the jet plane., , 10., , ∋, , (, , 3 < 1.732, , The angle of elevation of the top of a tower from the foot of a building is 30º and the, angle of elevation of the top of the building from the foot of the tower is 60º. What is the, ratio of heights of tower and building., , O PTIONAL E XERCISE, [For extensive learning], , 1., , A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of, 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at, an instant is 60º. After some time, the angle of elevation reduces to 30º. Find the distance, travelled by the balloon during that interval., , Free Distribution by T.S. Government 2021-22
Page 318 :
308, , Class-X Mathematics, , The angles of elevation of the top of a lighthouse from 3 boats A, B and C in a straight line, of same side of the light house are a, 2a, 3a respectively. If the distance between the boats, A and B and the boats B and C are x and y respectively find the height of the light house?, , 3., , Inner part of a cupboard is in the cuboidical shape with its length, breadth and height in, the ratio 2 : 1 : 1. What is the angle made by the longest stick which can be inserted, in the cupboard with its base inside., , 4., , An iron spherical ball of volume 232848 cm3 has been melted and converted into a solid, cone with the vertical angle of 120o. What are its height and diameter of the base of the, cone?, , 5., , Show that the area of an Isosceles triangle is A = a2 Sin q Cos q, where a is the length of one of the two equal sides and q is the measure, of one of two equal angles, , G, AN, , A, , 2., , a, , q, , q, , AN, , A right circular cylindrical tower with height ‘h’ and radius ‘r’, stands, on the ground. Let ‘p’ be a point in the horizontal plane ground and ABC be the semicircular edge of the top of the tower such that B is the point in it nearest to p. The angles, of elevation of the points A and B are 45 o and 60o respectively. Show that, h, 3(1 + 3), ., =, r, 2, , T,, TE, L, , 6., , a, , Suggested Projects, , Find the heights and distances, , Using clinometer - find the height of a tower/ tree/ building., , SC, ER, , l, , W HAT W E H AVE D ISCUSSED, , In this chapter, we have studied the following points :, , 1., , (i), , (ii), , (iii), , 2., , The line of sight is the line drawn from the eye of an observer to a point on the object, being viewed by the observer., The angle of elevation of the object viewed, is the angle formed by the line of sight, with the horizontal when it is above the horizontal level, i.e., the case when we raise, our head to look at the object., The angle of depression of an object viewed, is the angle formed by the line of sight, with the horizontal when it is below the horizontal level, i.e., the case when we lower, our head to look at the object., , The height or length of an object or the distance between two distant objects can be, determined with the help of trigonometric ratios., , Free Distribution by T.S. Government 2021-22
Page 319 :
Probability, , A, , 13, , G, AN, , 13.1 I NTRODUCTION, Kumar and Sudha were walking together to play a carroms match:, Kumar : Do you think that we would win?, , Sudha : There are 50 percent chances for that. We may win., Kumar : How do you say 50 percent?, Is her chance of wining 50%?, , AN, , Do you think Sudha is right in her statement?, , T,, TE, L, , In this chapter, we study about such questions. We also discuss words like ‘probably’,, ‘likely’, ‘possibly’, etc. and how to quantify these. In class IX we studied about events that are, extremely likely and in fact, are almost certain and those that are extremely unlikely and hence, almost impossible. We also talked about chance, luck and the fact that an event occurs once, does not mean that it would happen each time. In this chapter, we try to learn how the likelihood, of an event can be quantified., This quantification into a numerical measure is referred to as finding 'Probability'., IS, , P ROBABILITY, , SC, ER, , 13.1.1 W HAT, , Consider an experiment: A normal coin was tossed 1000 times. Head turned up 455 times, and tail turned up 545 times. If we try to find the likelihood of getting heads we may say it is 455, out of 1000 or, , 455, or 0.455., 1000, , This estimation of probability is based on the results of an actual, experiment of tossing a coin 1000 times. These estimates are called experimental, or empirical probabilities. In fact, all experimental probabilities are based on, the results of actual experiments and an adequate recording of what happens, in each of the events. These probabilities are only 'estimations'. If we perform, the same experiment for another 1000 times, we may get slightly different, data, giving different probability estimate.
Page 320 :
310, , Class-X Mathematics, , Many persons from different parts of the world have done this kind of experiment and, recorded the number of heads that turned up., For example, the eighteenth century French naturalist Comte de Buffon, tossed a coin, 4040 times and got 2048 times heads. The experimental probability of getting a head, in this, 2048, i.e., 0.507., 4040, , A, , case, was, , probability of getting a head, in this case, was, , G, AN, , J.E. Kerrich, from Britain, recorded 5067 heads in 10000 tosses of a coin. The experimental, 5067, = 0.5067. English Statistician Karl Pearson, 10000, , spent some more time, making 24000 tosses of a coin. He got 12012 times heads, and thus, the, , AN, , experimental probability of a head obtained by him was 0.5005., , Now, suppose we ask, 'What will be the experimental probability of getting a head, if the, experiment is carried on up to, say, one million times? Or 10 million times? You would intuitively, , T,, TE, L, , feel that as the number of tosses increases, the experimental probability of a head (or a tail) may, 1, settle down closer and closer to the number 0.5 , i.e., . This matches the ‘theoretical probability’, 2, of getting a head (or getting a tail), about which we will learn now., This chapter is an introduction to the theoretical (also called classical) probability of an, event. Now we discuss simple problems based on this concept., , SC, ER, , 13.2 P ROBABILITY - A T HEORETICAL A PPROACH, Let us consider the following situation: Suppose a ‘fair’ coin is tossed at random., When we speak of a coin, we assume it to be 'fair', that is, it is symmetrical so that there is, , no reason for it to come down more often on one side than the other. We call this property of the, coin as being 'unbiased'. By the phrase 'random toss', we mean that the coin is allowed to fall, freely without any bias or interference. These types of experiments are random experiments, (Here we dismiss the possibility of its 'landing' on its edge, which may be possible, for example,, if it falls on sand). We refer to this by saying that the outcomes, head and tail, are equally likely., Outcomes in an experiment are “equally likely” when chances of getting them are equal., For basic understanding of probability, in this chapter, we will assume that all the experiments, have equally likely outcomes., , Free Distribution by T.S. Government 2021-22
Page 321 :
Probability, , 311, , D O T HIS, Outcomes of which of the following experiments are equally likely?, 1. Getting a digit 1, 2, 3, 4, 5 or 6 when a dice is rolled., 2. Selecting a different colour ball from a bag of 5 red balls, 4 blue balls and 1 black, ball., 3. Winning in a game of carrom., 4. Units place of a two digit number selected may be 0, 1, 2, 3, 4, 5, 6, 7, 8 or 9., 5. Selecting a different colour ball from a bag of 10 red balls, 10 blue balls and 10, black balls., 6. Raining on a particular day of July., Are the outcomes of every experiment equally likely?, Give examples of 5 experiments that have equally likely outcomes and five more examples, that do not have equally likely outcomes., , AN, , b., c., , G, AN, , A, , a., , (i), , T,, TE, L, , ACTIVITY, , Take any coin, toss it 50 times, 100 times and 150 times and count the number of times, a head and a tail come up seperately. Record your observations in the following table:Number of, experiments, , 1., , 50, , 2., , 100, , Number of, heads, , Probability of, head, , Number of, tails, , Probability of, tails, , SC, ER, , S., No., , 3., , 150, , What do you observe? Obviously, as the number of experiments increases, probability, 1, of head or tail reaches 50% or . This empirical interpretation of probability can be applied, 2, to every event associated with an experiment that can be repeated a large number of times., , Now, we know that the experimental or empirical probability P(E) of an event E is, P(E) =, , Number of trials in which the event happened, Total number of trials, , “The assumption of equally likely outcomes” (which is valid in many experiments, as in two, of the examples seen, of a coin and of a dice) is one of the assumption that leads us to the, following definition of probability of an event., , Free Distribution by T.S. Government 2021-22
Page 322 :
Class-X Mathematics, , 312, , Probability and Modelling, , G, AN, , A, , The requirement of repeating an experiment has some limitations, as it may be very, expensive or unfeasible in many situations. Of course, it worked well in the experiments of, tossing the coin or throwing a dice. But, how about repeating the experiment of launching a, satellite in order to compute the empirical probability of its failure during launching, or the, repetition of the phenomenon of an earthquake to compute the empirical probability of a, multi-storeyed building getting destroyed in an earthquake? For finding these probabilities we, calculate models of behaviour and use them to estimate behaviour and likely outcomes. Such, models are complex and are validated by predictions and outcomes. Forecast of weather,, result of an election, population demography, earthquakes, crop production etc. are all based, on such models and their predictions., , P(T) =, , AN, , The theoretical probability (also called classical probability) of an event T, written as P(T),, is defined as, Number of outcomes favourable to T, Number of all possible outcomes of the experiment, , T,, TE, L, , where we assume that the outcomes of the experiment are equally likely. We usually simply, refer to theoretical probability as Probability., The definition of probability was given by Pierre Simon Laplace, in 1795., , SC, ER, , Probability theory had its origin in the16th century when an Italian, physician and mathematician J. Cardan wrote the first book on the subject,, The Book on Games of Chance. James Bernoulli (1654 -1705), A. De, Moivre (1667-1754), and Pierre Simon Laplace are among those who, made significant contributions to this field. In recent years, probability, has been used extensively in many areas such as biology, economics,, genetics, physics, sociology etc., , Pierre Simon Laplace, (1749 – 1827), , 13.3 MUTUALLY EXCLUSIVE EVENTS, If a coin is tossed, we get a head or a tail, but not both. Similarly, if we select a student of, a high school that he/ she may belong to one of either 6, 7, 8, 9 or 10 classes, but not to any two, or more classes. In both these examples, occurrence of an event prevents the occurrence of, other events. Such events are called mutually exclusive events., Two or more events of an experiment, where occurence of an event prevents occurences, of all other events, are called Mutually Exclusive Events. We will discuss this in more detail, later in the chapter., , Free Distribution by T.S. Government 2021-22
Page 323 :
Probability, , 313, , 13.4.1 F INDIN G P ROBABILITY, , G, AN, , A, , How do we find the probability of events that are equally likely? We consider the tossing, of a coin as an event associated with experiments where the equally likely assumption holds. In, order to proceed, we recall that there are two possible outcomes each time. This set of outcomes, is called the sample space. We can say that the “sample space” of one toss is {H, T}. For the, experiment of drawing out a ball from a bag containing red, blue, yellow and white ball, the, sample space is {R, B, Y, W}. What is the sample space when a dice is thrown?, , D O T HIS, , Think of 5 situations with equally likely events and find the sample space., , AN, , Let us now try to find the probability of equally likely events that are mutually exclusive., Example-1. Find the probability of getting a head when a coin is tossed once. Also find the, probability of getting a tail., , T,, TE, L, , Solution : In the experiment of tossing a coin once, the number of possible outcomes is two Head (H) and Tail (T). Let E be the event 'getting a head'. The number of outcomes favourable, to E, (i.e., of getting a head) is 1. Therefore,, Number of outcomes favourable to E 1, P(E) = P (head) =, =, Number of all possible outcomes, 2, Similarly, if F is the event 'getting a tail', then, 1, (Guess why?), 2, , SC, ER, , P(F) = P(tail) =, , Example-2. A bag contains a red ball, a blue ball and an yellow ball, all the balls being of the, same size. Manasa takes out a ball from the bag without looking into it. What is the probability, that she takes a (i) yellow ball? (ii) red ball? (iii) blue ball?, Solution : Manasa takes out a ball from the bag without looking into it. So, it is equally likely, that she takes out any one of them., Let Y be the event 'the ball taken out is yellow', B be the event 'the ball taken out is blue',, and R be the event 'the ball taken out is red'., Now, the number of possible outcomes = 3., (i) The number of outcomes favourable to the event Y = 1., So, P(Y) =, , 1, 1, 1, . Similarly, P(R) = and P(B) =, 3, 3, 3, , Free Distribution by T.S. Government 2021-22
Page 324 :
Class-X Mathematics, , 314, , Remarks, , 2. In Example 1, we note that : P(E) + P(F) = 1, In Example 2, we note that : P(Y) + P(R) + P(B) = 1., , A, , 1. An event having only one outcome in an experiment is called an elementary event. In, Example 1, both the events E and F are elementary events. Similarly, in Example 2, all, the three events, Y, B and R are elementary events., , G, AN, , If we find the sum of the probabilities of all the elementary events, we would get the, total as 1., , AN, , 3. In events like a throwing a dice, probability of getting less than 3 and of getting a 3 or, more than three are not elementary events of the possible outcomes. In tossing two, coins {HH}, {HT}, {TH} and {TT} are elementary events., Example-3. Suppose we throw a dice once. (i) What is the probability of getting a number, greater than 4? (ii) What is the probability of getting a number less than or equal to 4?, Sample space, , T,, TE, L, , Solution : (i) In rolling an unbaised dice, S, , = {1, 2, 3, 4, 5, 6}, , No. of outcomes, , n(S) = 6, , Favourable outcomes for, , E, , = {5, 6}, , number greater than 4, , n(E) = 2, , Probability, , P(E) =, , SC, ER, , No. of favourable outcomes, , 2, 1, =, 6, 3, , (ii) Let F be the event 'getting a number less than or equal to 4'., Sample space, , S, , = {1, 2, 3, 4, 5, 6}, , No. of outcomes, , n(S) = 6, , Favourable outcomes for, , F, , = {1, 2, 3, 4}, , number less or equal to 4, , No. of favourable outcomes, , n(F) = 4, , Probability, , P(F) =, , 4, 2, =, 6, 3, , Note : Are the events E and F in the above example elementary events?, No, they are not elementary events. The event E has 2 outcomes and the event F has 4, outcomes., , Free Distribution by T.S. Government 2021-22
Page 325 :
Probability, 13.4.2 C OMPLEMENTARY E VENTS, , AND, , 315, , P ROBABILITY, , In the previous section, we read about elementary events. Then in example-3, we calculated, probability of events which are not elementary. We saw,, 1, 2, + =1, 3, 3, , G, AN, , Here, F is the same as 'not E' because there are only two events., , A, , P(E) + P(F) =, , We denote the event 'not E' by E . This is called the complement event of event E., So, P(E) + P(not E) = 1, , i.e., P(E) + P( E ) = 1, which gives us P( E ) = 1 - P(E)., , ) = 1 – P(E), , AN, , In general, it is true that for an event E, P(, , T,, TE, L, , D O T HIS, (i), , Is ‘getting a head’ complementary to ‘getting a tail’? Give reasons., , (ii), , In case of a dice is getting a 1 complementary to events getting 2, 3, 4, 5, 6? Give, reasons for your answer., , (iii), , Write of any five pair of events that are complementary., AND, , C ERTAIN E VENTS, , SC, ER, , 13.4.3 I MPOSSIBLE, , Consider the following about the throws of a dice with sides marked as 1, 2, 3, 4, 5, 6., , (i), , What is the probability of getting a number 7 in a single throw of a dice?, , We know that there are only six possible outcomes in a single throw of this dice. These, outcomes are 1, 2, 3, 4, 5 and 6. Since, no face of the dice is marked 7, there is no outcome, favourable to 7, i.e., the number of such outcomes is zero. In other words, getting 7 in a single, 0, =0, 6, That is, the probability of an event which is impossible to occur is 0. Such an event is, , throw of a dice, is impossible. Suppose E = outcome of geeting 7. So, P(E) =, called an impossible event., , Free Distribution by T.S. Government 2021-22
Page 326 :
Class-X Mathematics, , 316, , (ii), , What is the probability of getting 6 or a number less than 6 in a single throw of a dice?, , G, AN, , A, , Since, every face of a dice is marked with 6 or a number less than 6, it is sure that we will, always get one of these when the dice is thrown once. So, the number of favourable outcomes is, the same as the number of all possible outcomes, which is 6. Suppose E = (getting 6 or a number, less than 6), 6, Therefore, P(E) = = 1, 6, So, the probability of an event which is sure (or certain) to occur is 1. Such an event is, called a sure event or a certain event., , AN, , Note : From the definition of probability P(E), we see that the numerator (number of outcomes, favourable to the event E) is always less than or equal to the denominator (the number of all, possible outcomes). Therefore, 0 £ P(E) £ 1., , T RY T HIS, , T,, TE, L, , 1. A child has a dice whose six faces show the letters A, B, C, D, E and F. The dice is, thrown once. What is the probability of getting (i) A? (ii) D?, 2. Which of the following cannot be the probability of an event?, (a), , 2.3, , AND, , -1.5, , (c), , 15%, , (D), , 0.7, , D ISCUSS, , SC, ER, , THINK, , (b), , 1. Why is tossing a coin considered to be a fair way of deciding which team should get the, ball at the beginning of any game?, 7, 2. Can be the probability of an event? Explain., 2, 3. Which of the following arguments are correct and which are not correct? Give reasons., i) If two coins are tossed simultaneously there are three possible outcomes - two heads,, 1, two tails or one of each. Therefore, for each of these outcomes, the probability is ., 3, ii)If a dice is thrown, there are two possible outcomes - an odd number or an even, 1, number. Therefore, the probability of getting an odd number is ., 2, , Free Distribution by T.S. Government 2021-22
Page 327 :
Probability, 13.5 D ECK, , OF, , C ARDS, , AND, , 317, , PROBABILITY, , Have you seen a deck, of playing cards?, , G, AN, , A, , A deck of playing, cards consists of 52 cards, which are divided into 4, suits of 13 cards each. They, are black spades (ª), red, hearts (© ), red diamonds, (¨) and black clubs (§)., , AN, , The cards in each suit are Ace, King, Queen, Jack, 10, 9, 8, 7, 6, 5, 4, 3 and 2. Kings,, Queens and Jacks are called face cards. Many games are played with this deck of cards. Some, games are played with part of the deck and some with two decks even. The study of probability, has a lot to do with card and dice games as it helps players to estimate possibilities and predict, how the cards could be distributed among players., , T,, TE, L, , Example-4. One card is drawn from a well-shuffled deck of 52 cards. Calculate the probability, that the card will (i) be an ace, (ii) not be an ace., Solution : Well-shuffling ensures equally likely outcomes., (i), , There are 4 aces in a deck., , Let E be the event 'the card is an ace'., , The number of outcomes favourable to E = 4, , SC, ER, , The number of possible outcomes = 52 (Why ?), 4, 1, =, Therefore, P(E) =, 52 13, , (ii), , Let F be the event 'card drawn is not an ace'., The number of outcomes favourable to the event F = 52 - 4 = 48 (Why?), The number of possible outcomes = 52, Therefore, P(F) =, , 48 12, =, 52 13, , Alternate Method : Note that F is nothing but E ., Therefore, we can also calculate P(F) as follows:, 1, 12, =, P (F) = P( E ) = 1 - P(E) = 1 13 13, , Free Distribution by T.S. Government 2021-22
Page 328 :
Class-X Mathematics, , 318, , TRY THIS, What is the probability that the card drawn will be a queen?, , 2., , What is the probability that it is a face card?, , 3., , What is the probability it is a spade?, , 4., , What is the probability that is the face card of spades?, , 5., , What is the probability it is not a face card?, , 13.6 U SE, , OF, , P ROBABILITY, , G, AN, , 1., , A, , You have a single deck of well shuffled cards. Then,, , T,, TE, L, , AN, , Let us look at some more occasions where probability may be useful. We know that in, sports some countries are strong and others are not so strong. We also know that when two, players are playing it is not that they win equal times. The probability of winning of the player or, team that wins more often is more than the probability of the other player or team. We also, discuss and keep track of birthdays. Sometimes it happens that people we know have the same, birthdays. Can we find out whether this is a common event or would it only happen occasionally., Classical probability helps us do this., Example-5. Sangeeta and Reshma, play a tennis match. It is known that the probability of, Sangeeta winning the match is 0.62. What is the probability of Reshma winning the match?, Solution : Let S and R denote the events that Sangeeta wins the match and Reshma wins the, match, respectively., , SC, ER, , The probability of Sangeeta's winning chances = P(S) = 0.62 (given), The probability of Reshma's winning chances = P(R) = 1 - P(S), = 1 -0.62 = 0.38 [R and S are complementary], , Example-6. Sarada and Hamida are friends. What is the probability that both will have, (i) different birthdays? (ii) the same birthday? (ignoring a leap year)., Solution : Out of the two friends, one girl, say, Sarada's birthday can be any day of the year., Now, Hamida's birthday can also be any day of 365 days in the year. We assume that these 365, outcomes are equally likely., (i) If Hamida's birthday is different from Sarada's, the number of favourable outcomes for her, birthday is 365 - 1 = 364, So, P (Hamida's birthday is different from Sarada's birthday) =, , 364, 365, , Free Distribution by T.S. Government 2021-22
Page 329 :
Probability, , 319, , (ii) P(Sarada and Hamida have the same birthday) = 1 - P (both have different birthdays), = 1-, , 364, 1, [ Using P( E ) = 1 - P(E)] =, 365, 365, , G, AN, , A, , Example-7. There are 40 students in Class X of a school of whom 25 are girls and 15 are, boys. The class teacher has to select one student as a class representative. She writes the name, of each student on separate cards, the cards being identical. Then she puts cards in a box and, stirs them thoroughly. She then draws one card from the box. What is the probability that the, name written on the card is the name of (i) a girl? (ii) a boy?, Solution : There are 40 students, and only one name card has to be chosen., The number of all possible outcomes is 40, (i), , The number of outcomes favourable for a card with the name of a girl = 25 (Why?), , (ii), , 25, 5, =, 40, 8, , AN, , \ P (card with name of a girl) = P(Girl) =, , The number of outcomes favourable for a card with the name of a boy = 15 (Why?), 15, 3, =, 40, 8, 5, 3, P(Boy) = 1 - P(not Boy) = 1 - P(Girl) = 1 - =, 8 8, , or, , T,, TE, L, , Therefore, P(card with name of a boy) = P(Boy) =, , EXERCISE - 13.1, 1., , Complete the following statements:, , (i) Probability of an event E + Probability of the event 'not E' = ______________, , SC, ER, , (ii) The probability of an event that cannot happen is__________., Such an event is called __________, , (iii) The probability of an event that is certain to happen is __________., Such an event is called______, , (iv) The sum of the probabilities of all the elementary events of an experiment is_________, (v) The probability of an event is greater than or equal to __________ and less than or, equal to _______, , 2., , Which of the following experiments have equally likely outcomes? Explain., (i) A driver attempts to start a car. The car starts or does not start., (ii) A player attempts to shoot a basketball. She/he shoots or misses the shot., , Free Distribution by T.S. Government 2021-22
Page 330 :
320, , Class-X Mathematics, , (iii) A trial is made to answer a true-false question. The answer is right or wrong., (iv) A baby is born. It is a boy or a girl., If P(E) = 0.05, what is the probability of 'not E'?, , 4., , A bag contains lemon flavoured candies only. Malini takes out one candy without looking, into the bag. What is the probability that she takes out, (i) an orange flavoured candy? (ii) a lemon flavoured candy?, Rahim removes all the hearts from the cards. What is the probability of, i. Getting an ace from the remaining pack., ii. Getting a diamonds., iii. Getting a card that is not a heart., , AN, , iv. Getting the Ace of hearts., , G, AN, , 5., , A, , 3., , 6., , It is given that in a group of 3 students, the probability of 2 students not having the same, birthday is 0.992. What is the probability that the 2 students have the same birthday?, , 7., , A dice is rolled once. Find the probability of getting, , T,, TE, L, , (i) a prime number (ii) a number lying between 2 and 6 (iii) an odd number., 8., , What is the probability of selecting a red king from a deck of cards?, , 9., , Make 5 more problems of this kind using dice, cards or birthdays and discuss with friends, and teacher about their solutions., , 13.7 M ORE A PPLICATIONS, , OF, , P ROBABILITY, , SC, ER, , We have seen some examples of using probability. Think about the contents and ways, probability has been used in these. We have seen again that probability of complementary events, add to 1. Can you identify in the examples and exercises given above, and those that follow,, complementary events and elementary events? Discuss with teachers and friends. Let us see, more uses., Example-8. A box contains 3 blue, 2 white, and 4 red marbles. If a marble is selected at, random from the box, what is the probability that it will be, (i) white?, , (ii) blue?, , (iii) red?, , Solution : Saying that a marble is drawn at random means all the marbles are equally likely to be, drawn., \ The number of possible outcomes = 3 +2 + 4 = 9 (Why?), Let W denote the event 'the marble is white', B denote the event 'the marble is blue' and R, denote the event 'marble is red'., , Free Distribution by T.S. Government 2021-22
Page 331 :
Probability, , 321, , (i) The number of outcomes favourable to the event (W = 2), 2, 9, , Similarly, (ii) P(B) =, , 3 1, 4, = and (iii) P(R) =, 9, 3, 9, , A, , So, P(W) =, , G, AN, , Note that P(W) + P(B) + P(R) = 1., , Example-9. Harpreet tosses two different coins simultaneously (say, one is of D1 and other of, D2). What is the probability that she gets at least one head?, , AN, , Solution : We write H for 'head' and T for 'tail'. When two coins are tossed simultaneously, the, possible outcomes are (H, H), (H, T), (T, H), (T, T), which are all equally likely. Here, (H, H), means heads on the first coin (say on D1) and also heads on the second coin (D2). Similarly, (H, T) means heads up on the first coin and tail up on the second coin and so on., The outcomes favourable to the event E, 'at least one head' are (H, H), (H, T) and (T, H)., , \P(E) =, , T,, TE, L, , So, the number of outcomes favourable to E is 3., , 3, [Since the total possible outcomes = 4], 4, , i.e., the probability that Harpreet gets at least one head is, Check This, , 3, 4, , SC, ER, , Did you observe that in all the examples discussed so far, the number of possible outcomes, in each experiment was finite? If not, check it now., There are many experiments in which the outcome is number between two given numbers,, or in which the outcome is every point within a circle or rectangle, etc. Can you count the number, of all possible outcomes in such cases? As you know, this is not possible since there are infinitely, many numbers between two given numbers, or there are infinitely many points within a circle. So,, the definition of theoretical probability which you have learnt so far cannot be applied in the, present form., What is the way out? To answer this, let us consider the following example:, , Free Distribution by T.S. Government 2021-22
Page 332 :
322, , Class-X Mathematics, , Example-10. In a musical chair game, the person playing the music has been advised to stop, playing the music at any time within 2 minutes after she starts playing. What is the probability that, the music will stop within the first half-minute after starting?, , 1, 2, , 2, , 1, , G, AN, , 0, , A, , Solution : Here, the possible outcomes are all the numbers between 0 and 2. This is the portion, of the number line from 0 to 2, , AN, , Let E be the event that 'the music is stopped within the first half-minute'., 1, The outcomes favourable to E are points on the number line from 0 to, 2, 1 1, The distance from 0 to 2 is 2, while the distance from 0 to is, 2 2, , Since all the outcomes are equally likely, we can argue that, of the total distance is 2 and, 1, 2, , T,, TE, L, , the distance favourable to the event E is, , 1, Distance favourable to the event E, 1, So, P(E) =, = 2=, Total distance in which outcomes can lie, 2 4, We now try to extend this idea for finding the probability as the ratio of the favourable area, to the total area., 6 km., Lake, , Solution : The helicopter is equally likely, to crash anywhere in the region. Area of the, entire region where the helicopter can crash, = (4.5 × 9) km2 = 40.5 km2, , 2 km., , 4.5 km., , SC, ER, , Example-11. A missing helicopter is, reported to have crashed somewhere in the, rectangular region as shown in the figure., What is the probability that it crashed inside, the lake shown in the figure?, , 9 km., , Area of the lake = (2.5 × 3) km2 = 7.5 km2, Therefore, P (helicopter crashed in the lake) =, , 7.5, 5, =, = 0.185, 40.5, 27, , Free Distribution by T.S. Government 2021-22
Page 333 :
Probability, , 323, , Example-12. A carton consists of 100 shirts of which 88 are good, 8 have minor defects and 4, have major defects. Jhony, a trader, will only accept the shirts which are good, but Sujatha,, another trader, will only reject the shirts which have major defects. One shirt is selected at, random from the carton. What is the probability that, (i) it is acceptable to Jhony?, (ii) it is acceptable to Sujatha?, , A, , Solution : One shirt is selected at random from the carton of 100 shirts. Therefore, there are, 100 equally likely outcomes., , Therefore, P (shirt is acceptable to Jhony) =, , G, AN, , (i) The number of outcomes favourable (i.e., acceptable) to Jhony = 88 (Why?), 88, = 0.88, 100, , (ii) The number of outcomes favourable to Sujatha = 88 + 8 = 96 (Why?), 96, = 0.96, 100, , AN, , So, P (shirt is acceptable to Sujatha) =, , T,, TE, L, , Example-13. Two dice, one red and one yellow, are thrown at the same time. Write down all, the possible outcomes. What is the probability that the sum of the two numbers appearing on the, top of the dice is (i) 8 (ii) 13 (iii) less than or equal to 12?, , SC, ER, , Solution : When the red dice shows '1', the, yellow dice could show any one of the, numbers 1, 2, 3, 4, 5, 6. The same is true, when the red dice shows '2', '3', '4', '5' or, '6'. The possible outcomes of the experiment, are shown in the figure; the first number in, each ordered pair is the number appearing, on the red dice and the second number is, that on the white dice., , 1, , 1, 1, 1, , 2, 1, 2, , 3, 1, 3, , 4, 1, 4, , 5, 1, 5, , 6, 1, 6, , 2, , 2, 1, , 2, 2, , 2, 3, , 2, 4, , 2, 5, , 2, 6, , 3, , 3, 1, , 3, 2, , 3, 3, , 3, 4, , 3, 5, , 3, 6, , 4, , 4, 1, , 4, 2, , 4, 3, , 4, 4, , 4, 5, , 4, 6, , 5, , 5, 1, , 5, 2, , 5, 3, , 5, 4, , 5, 5, , 5, 6, , 6, , 6, 1, , 6, 2, , 6, 3, , 6, 4, , 6, 5, , 6, 6, , Note that the pair (1, 4) is different from (4, 1). (Why?), So, the number of possible outcomes n(S) = 6 × 6 = 36., , (i), , The outcomes favourable to the event 'the sum of the two numbers is 8' denoted by E, are:, (2, 6), (3, 5), (4, 4), (5, 3), (6, 2) (See figure), i.e., the number of outcomes favourable to E is n(E) = 5., Hence, P(E) =, , (ii), , 5, n(E), =, n(S) 36, , As there is no outcome favourable to the event F, 'the sum of two numbers is 13',, So, P(F) =, , 0, =0, 36, , Free Distribution by T.S. Government 2021-22
Page 334 :
324, , Class-X Mathematics, , (iii) As all the outcomes are favourable to G, 'sum of two numbers is 12',So, P(G) =, , 36, =1, 36, , EXERCISE - 13.2, A bag contains 3 red balls and 5 black balls. A ball is selected at random from the bag., What is the probability that the ball selected is (i) red ? (ii) not red?, , 2., , A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken, out of the box at random. What is the probability that the marble taken out will be (i) red?, (ii) white ? (iii) not green?, , 3., , A Kiddy bank contains hundred 50p coins, fifty D1 coins, twenty D2 coins and ten D5, coins. If it is equally likely that one of the coins will fall out when the bank is turned upside, down, what is the probability that the coin (i) will be a 50 p coin? (ii) will not be a D5 coin?, , 4., , Gopi buys a fish from a shop for his aquarium. The shopkeeper takes, out one fish at random from a tank containing 5 male fish and 8 female, fish (See figure). What is the probability that the fish taken out is a, male fish?, , 5., , A game of chance consists of spinning an arrow which comes to rest, pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (See figure), and, these are equally likely outcomes. What is the probability that it will, point at, (i) 8 ?, , T,, TE, L, , AN, , G, AN, , A, , 1., , SC, ER, , (iii) a number greater than 2?, 6., , 7., , (ii) an odd number?, (iv) a number less than 9?, , 8, , 1, , 7, , 2, , 6, , 3, 5, , 4, , One card is selected from a well-shuffled deck of 52 cards. Find the probability of getting, (i) a king of red colour, , (ii) a face card, , (iii) a red face card, , (iv) the jack of hearts, , (v) a spade, , (vi) the queen of diamonds, , Five cards-the ten, jack, queen, king and ace of diamonds, are well-shuffled with their, face downwards. One card is selected at random., (i) What is the probability that the card is the queen?, , (ii) If the queen is selected and put aside (without replacement), what is the probability that, the second card selected is (a) an ace? (b) a queen?, 8., , 12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look, at a pen and tell whether or not it is defective. One pen is taken out at random from this lot., Determine the probability that the pen taken out is a good one., , Free Distribution by T.S. Government 2021-22
Page 335 :
Probability, , 325, , A lot of 20 bulbs contain 4 defective ones. One bulb is selected at random from the lot., What is the probability that this bulb is defective? Suppose the bulb selected in previous, case is not defective and is not replaced. Now one bulb is selected at random from the, rest. What is the probability that this bulb is not defective?, , 10., , A box contains 90 discs which are numbered from 1 to 90. If one disc is selected at, random from the box, find the probability that it bears (i) a two-digit number (ii ) a perfect, 3 m., square number (iii) a number divisible by 5., , 11., , Suppose you drop a die at random on the rectangular region, shown in figure. What is the probability that it will land inside, the circle with diameter 1m?, , 12., , A lot consists of 144 ball pens of which 20 are defective, and the others are good. The shopkeeper draws one pen, at random and gives it to Sudha. What is the probability that (i) She will buy it? (ii) She will, not buy it ?, , 13., , Two dice are rolled simultaneously and counts are added (i) complete the table given, below:, , Probability, , 1, 36, , 3, , AN, , 2, , 4, , 5, , 6, , T,, TE, L, , Event : 'Sum on 2 dice', , 2 m., , G, AN, , A, , 9., , 7, , 8, , 5, 36, , 9, , 10, , 11, , 12, 1, 36, , (ii) A student argues that 'there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and, 1, 12. Therefore, each of them has a probability . Do you agree with this argument? Justify, 11, your answer., A game consists of tossing a one rupee coin 3 times and noting its outcome each time., Deskhitha wins if all the tosses give the same result i.e., three heads or three tails, and loses, otherwise. Calculate the probability that she will lose the game., , 15., , A dice is thrown twice. What is the probability that (i) 5 will not come up either time? (ii) 5, will come up at least once? [Hint : Throwing a dice twice and throwing two dice, simultaneously are treated as the same experiment]., , SC, ER, , 14., , O PTIONAL E XERCISE, , [For extensive Learning], 1., , Two customers Shyam and Ekta are visiting a particular shop in the same week (Tuesday, to Saturday). Each is equally likely to visit the shop on any day as on another day. What is, the probability that both will visit the shop on (i) the same day? (ii) consecutive days? (iii), different days?, , Free Distribution by T.S. Government 2021-22
Page 336 :
326, , Class-X Mathematics, , A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is, double that of a red ball, determine the number of blue balls in the bag., , 3., , A box contains 12 balls out of which x are black. If one ball is drawn at random from the, box, what is the probability that it will be a black ball? If 6 more black balls are put in the, box, the probability of drawing a black ball is now double of what it was before. Find x., , 4., , A jar contains 24 marbles, some are green and others are blue. If a marble is drawn at, random from the jar, the probability that it is green is 23 . Find the number of blue marbles, in the jar., , WHAT WE H AVE D ISCUSSED, , 3., 4., 5., 6., 7., , SC, ER, , 8., , The theoretical (classical) probability of an event E, written as P(E), is defined as, Number of outcomes favourable to E, P (E) =, Total number of all possible outcomes of the experiment, where we assume that the outcomes of the experiment are equally likely., The probability of a sure event (or certain event) is 1., The probability of an impossible event is 0., The probability of an event E is a number P(E) such that 0 £ P (E) £ 1, An event having only one outcome is called an elementary event. The sum of the probabilities, of all the elementary events of an experiment is 1., For any event E, P (E) + P ( E ) = 1, where E stands for 'not E'. E and E are called, complementary events., Some more terms used in the chapter are given below:, , AN, , 2., , In this chapter, you have studied the following points:, We have dealt with experimental probability and theoretical, probability., , T,, TE, L, , 1., , G, AN, , A, , 2., , Random experiment, , : For random experiments, the results are known well in advance,, but the result of the specific performance cannot be predicted., Equally likely events, : Two or more events are said to be equally likely if each one of, them has an equal chance of occurrance., Mutually Exclusive events : Two or more events are mutually exclusive if the occurrence of, each event prevents the every other event., Exhaustive events, : Two or more events are said to be exhaustive, if the union of, their outcomes is the entire sample space., Complementary events, : Two events are said to be complementary, if they are mutually exclusive, and also exhaustive. (OR) Two events are said to be complementary, if occurrence of an event prevents the occurrence of the other and the, union of their outcomes is the entire sample space., Sure events, : An event which will definitely occur is called a sure event. The, collection of all outcomes of a sure event is the entire sample space., Impossible event, : An event which cannot occur on any account is called an, impossible event., , Free Distribution by T.S. Government 2021-22
Page 338 :
Class-X Mathematics, , 328, , Ganesh prepared the following table to understand the performance of his class:, Number of children, , 0 - 33, , 4, , 34 - 50, , 6, , 51 - 75, , 10, , 76 - 100, , 6, , A, , Marks, , G, AN, , Is the data given in the above table grouped or ungrouped?, , He showed this table to his teacher and the teacher appreciated him for organising the, data to be understood easily. We can see that most children have got marks between 51-75. Do, you think that Ganesh should have used smaller range? Why or why not?, , UNGROUPED D ATA, , T,, TE, L, , 14.2 M EAN, , AN, , In the previous class, you had learnt about the difference between grouped and ungrouped, data as well as how to present this data in the form of tables. You had also learnt to calculate the, mean value for ungrouped data. Let us recall this learning and then learn to calculate the mean,, median and mode for grouped data., OF, , SC, ER, , We know that the mean (or average) of observations is the ratio of sum of the values of, all the observations divided by the total number of observations. Let x1, x2,. . ., xn be observations, with respective frequencies f1, f2, . . ., fn. This means that observation x1 occurs f1 times, x2, occurs f2 times, and so on., Now, the sum of the values of all the observations = f1x1 + f2x2 + . . . + fnxn, and the, number of observations = f1 + f2 + . . . + fn., So, the mean x of the data is given by, f x ∗ f 2 x2 ∗ ... ... ... ∗ f n xn, x< 1 1, f1 ∗ f 2 ∗ ... ... ... ∗ f n, Recall that we can write this in short, using the Greek letter å (read as sigma) which, , means summation i.e., x < å fi xi, å fi, Example-1. The marks obtained in mathematics by 30 students of Class X of a certain school, are given in table the below. Find the mean of the marks obtained by the students., Marks obtained (xi ), , 10, , 20, , 36, , 40, , 50, , 56, , 60, , 70, , 72, , 80, , 88, , 92, , 95, , Number of student ( fi), , 1, , 1, , 3, , 4, , 3, , 2, , 4, , 4, , 1, , 1, , 2, , 3, , 1, , Free Distribution by T.S. Government 2021-22
Page 339 :
Statistics, , 329, , Solution : Let us re-organize this data and find the sum of all observations., Number of, students ( fi), 1, , 10, , 20, , 1, , 20, , 36, , 3, , 108, , 40, , 4, , 160, , 50, , 3, , 150, , 56, , 2, , 112, , 60, , 4, , 240, , 70, , 4, , 280, , 72, , 1, , 80, , 1, , 88, , 2, , AN, , G, AN, , 10, , 72, 80, , T,, TE, L, , 176, , 92, , 3, , 276, , 95, , 1, , 95, , å f i =30, , Total, , So,, , fi xi, , x<, , A, , Marks, obtained (xi ), , å f i xi = 1779, , å fi xi 1779, <, < 59.3, å fi, 30, , SC, ER, , Therefore, the mean marks are 59.3., , In most of our real life situations, data is usually so large that to make a meaningful study,, it needs to be condensed as a grouped data. So, we need to convert ungrouped data into, grouped data and derive some method to find its mean., , Let us convert the ungrouped data of Example 1 into grouped data by forming classintervals of width, say 15. Remember that while allocating frequencies to each class-interval,, students whose score is equal to in any upper class-boundary would be considered in the next, class, e.g., 4 students who have obtained 40 marks would be considered in the class-interval, 40-55 and not in 25-40. With this convention in our mind, let us form a grouped frequency, distribution table., Class interval, Number of students, , 10-25, , 25-40, , 40-55, , 55-70, , 70-85, , 85-100, , 2, , 3, , 7, , 6, , 6, , 6, , Free Distribution by T.S. Government 2021-22
Page 340 :
Class-X Mathematics, , 330, , Now, for each class-interval, we require a point which would serve as the representative, of the whole class. It is assumed that the frequency of each class-interval is centred, around its mid-point. So, the mid-point of each class can be chosen to represent the, observations falling in that class and is called the class mark. Recall that we find the class mark by, finding the average of the upper and lower limit of the class., , A, , Upper class limit + Lower class limit, 2, , G, AN, , Class mark =, , 10 ∗ 25, =17.5. Similarly, we can find the class, 2, marks of the remaining class intervals. We put them in the table. These class marks serve as our, xi’s. We can now proceed to compute the mean in the same manner as in the previous example., , For the class 10 -25, the class mark is, , Number of, students ( fi), , 25-40, 40-55, 55-70, 70-85, 85-100, , 17.5, , f ix i, , 35.0, , 3, , 32.5, , 97.5, , 7, , 47.5, , 332.5, , 6, , 62.5, , 375.0, , 6, , 77.5, , 465.0, , 6, , 92.5, , 555.0, , å fi =30, , SC, ER, , Total, , 2, , T,, TE, L, , 10-25, , Class, Marks (xi ), , AN, , Class, interval, , å fi xi =1860.0, , The sum of the values in the last column gives us å fi xi . So, the mean x of the given, data is given by, x<, , å fi xi 1860, <, < 62, å fi, 30, , This new method of finding the mean is known as the Direct Method., We observe that in the above cases we are using the same data and employing the same, formula for calculating the mean but the results obtained are different. In example (1), 59.3 is the, exact mean and 62 is the approximate mean. Can you think why this is so?, , Free Distribution by T.S. Government 2021-22
Page 341 :
Statistics, T HINK, , 331, , AND DISCUSS, , 1. The mean value can be calculated from both ungrouped and grouped data. Which one, do you think is more accurate? Why?, , A, , 2. When is it more convenient to use grouped data for analysis?, , G, AN, , Sometimes when the numerical values of xi and fi are large, finding the product of xi and fi, becomes tedious and time consuming. So, for such situations, let us think of a method of reducing, these calculations., , AN, , We can do nothing with the fi's, but we can change each xi to a smaller number so that our, calculations become easy. How do we do this? How about subtracting a fixed number from each, of these xi's? Let us try this method for the data in example 1., The first step is to choose one among the xi's as the assumed mean, and denote it by 'a'., Also, to further reduce our calculation work, we may take 'a' to be that xi which lies in the centre, of x1, x2, ..., xn. So, we can choose a = 47.5 or a = 62.5. Let us choose a = 47.5., as di, i.e.,, , T,, TE, L, , The second step is to find the deviation of ‘a’ from each of the xi's, which we denote, di = xi – a = xi – 47.5, , The third step is to find the product of di with the corresponding fi, and take the sum of all, the fi di’s. These calculations are shown in table given belowClass, , Class, , di < xi , 47.5, , fi di, , di < xi , a, , students ( fi), , Marks (xi ), , 10-25, , 2, , 17.5, , -30, , -60, , 25-40, , 3, , 32.5, , -15, , -45, , 40-55, , 7, , 47.5 (a), , 0, , 0, , 55-70, , 6, , 62.5, , 15, , 90, , 70-85, , 6, , 77.5, , 30, , 180, , 85-100, , 6, , 92.5, , 45, , 270, , SC, ER, , interval, , Number of, , Total, , å fi =30, , So, from the above table, the mean of the deviations, d <, Now, let us find the relation between d and x ., , Free Distribution by T.S. Government 2021-22, , å f i d i = 435, å fi di, å fi
Page 342 :
Class-X Mathematics, , 332, , d<, , å fi di, å fi, , So,, , d<, , å fi ( xi , a ), å fi, å fi xi å fi a, ,, å fi, å fi, , = x ,a, , d = x ,a, x < a∗, , Therefore, , å fi, å fi, , AN, , =, , G, AN, , Mean of deviations,, , A, , Since, in obtaining di we subtracted ‘a’ from each xi so, in order to get the mean x we, need to add ‘a’ to d . This can be explained mathematically as:, , å fi di, å fi, , T,, TE, L, , Substituting the values of a, å fi di and å fi from the table, we get, x < 47.5 ∗, , 435, < 47.5 ∗ 14.5 < 62, 30, , Therefore, the mean of the marks obtained by the students is 62., The method discussed above is called the Assumed Mean Method., , SC, ER, , ACTIVITY, , Consider the data given in example 1 and calculate the arithmetic mean by deviation, method by taking successive values of xi i.e., 17.5, 32.5, ... as assumed means. Now discuss, the following:, , 1. Are the values of arithmetic mean in all the above cases equal?, 2. If we take the actual mean as the assumed mean, how much will å fi di be?, 3. Reason about taking any mid-value (class mark) as assumed mean?, , Observe that in the table given below the values in Column 4 are all multiples of 15. If, we divide all the values of Column 4 by 15, we would get smaller numbers which we then, multiply with fi. (Here, 15 is the class size of each class interval.), So, let ui <, , xi , a, , where a is the assumed mean and h is the class size., h, , Free Distribution by T.S. Government 2021-22
Page 344 :
Class-X Mathematics, , 334, , æ å f u ö÷, i i÷, x < a ∗ ççç, ´h, å, fi ø÷÷, è, , or, , Substituting the values of a, å fi ui h and å fi from the table, we get, 29, ´15, 30, , A, , x < 47.5 ∗, , G, AN, , = 47.5 + 14.5 = 62, So, the mean marks obtained by a student are 62., , The method discussed above is called the Step-deviation method., We note that:, , The step-deviation method will be convenient to apply if all the di’s have a common, , AN, , l, , factor., , The mean obtained by all the three methods is same., , l, , The assumed mean method and step-deviation method are just simplified forms of the, , T,, TE, L, , l, , direct method., l, , The formula x < a ∗ h u still holds if a and h are not as given above, but are any nonzero numbers such that ui <, , xi , a, ., h, , Let us apply these methods in more examples., , SC, ER, , Example-2. The table below gives the percentage distribution of female teachers in the primary, schools of rural areas of various states and union territories (U.T.) of India. Find the mean, percentage of female teachers using all the three methods., Percentage of female teachers, , Number of States/U.T., , 15 - 25, , 25 - 35, , 35 – 45, , 45 - 55, , 6, , 11, , 7, , 4, , 55 - 65, , 65 - 75 75 – 85, , 4, , 2, , 1, , Source : Seventh All India School Education Survey conducted by NCERT, Solution : Let us find the class marks xi of each class, and arrange them in a table., , Here, we take a = 50 and h = 10., Then di = xi – 50 and ui =, , xi , 50, ., 10, , Free Distribution by T.S. Government 2021-22
Page 345 :
Statistics, , 335, , Now find di and ui and write them in the table, , of female, , States/U.T., , teachers C.I, , fi, , 15 – 25, , 6, , 25 – 35, 35 – 45, 45 – 55, 55 – 65, 65 – 75, 75 – 85, , 11, 7, 4, 4, 2, 1, , Total, , 35, , xi , 50, , ui <, xi , 50, 10, , 20, , -30, , -3, , 120, , -180, , -18, , 30, 40, 50, 60, 70, 80, , -20, -10, 0, 10, 20, 30, , -2, -1, 0, 1, 2, 3, , 330, 280, 200, 240, 140, 80, , -220, -70, 0, 40, 40, 30, , -22, -7, 0, 4, 4, 3, , -360, , -36, , xi, , di <, , fi xi, , fi di, , fi ui, , A, , Number of, , G, AN, , Percentage, , 1390, , Using the direct method, x <, , AN, , From the above table, we obtain å fi < 35, å fi xi < 1390, å fi di < ,360, å f i ui < ,36 ., å fi xi 1390, <, < 39.71 ., å fi, 35, , å fi di, ,360, < 50 ∗, < 50 ,10.29 < 39.71 ., å fi, 35, , T,, TE, L, , Using the assumed mean method x < a ∗, , æ å f u ö÷, ,36, i i÷, ´ h < 50 ∗, ´10 < 39.71 ., Using the step-deviation method x < a ∗ çç, ÷, çè å fi ø÷, 35, , Therefore, the mean percentage of female teachers in the primary schools of rural areas is 39.71., AND, , D ISCUSS, , SC, ER, , T HINK, , 1. Is the result obtained by all the three methods same?, 2. If xi and fi are sufficiently small, then which method is an appropriate choice?, , 3. If xi and fi are numerically large numbers, then which methods are appropriate to use?, , Even if the class sizes are unequal, and xi are large numerically, we can still apply the, step-deviation method by taking h to be a suitable divisor of all the di’s., , Example-3. The below distribution shows the number of wickets taken by bowlers in one-day, cricket matches. Find the mean number of wickets by choosing a suitable method. What does, the mean signify?, Number of wickets 20 - 60 60 - 100 100 - 150 150 - 250 250 - 350 350 – 450, Number of bowlers, , 7, , 5, , 16, , Free Distribution by T.S. Government 2021-22, , 12, , 2, , 3
Page 346 :
Class-X Mathematics, , 336, , Solution : Here, the class size varies, and the xi's are large. Let us still apply the step deviation, method with a = 200 and h = 20. Then, we obtain the data as given in the table., , wickets, , Number of, , xi , a, h, (h = 20), , di <, , xi, , ui <, , xi , a, , bowlers ( fi ), 7, , 40, , -160, , -8, , 60 – 100, , 5, , 80, , -120, , -6, , 100 – 150, , 16, , 125, , -75, , 150 – 250, , 12, , 200 (a), , 250 – 350, , 2, , 300, , 100, , 350 – 450, , 3, , 400, , 200, , 45, , -30, , -3.75, , -60, , 0, , 0, , 5, , 10, , 10, , 30, , AN, , Total, , -56, , G, AN, , 20 – 60, , fi ui, , A, , Number of, , -106, , 0, , T,, TE, L, , æ å f u ÷ö, ,106, i i÷, ´ h < 200 ∗, ´ 20 < 200 , 47.11 < 152.89, So x < a ∗ ççç, ÷, 45, è å fi ÷ø, Thus, the average number of wickets taken by these 45 bowlers in one-day cricket is 152.89., Classroom Project :, , Collect the marks obtained by all the students of your class in Mathematics in the recent, examination conducted in your school. Form a grouped frequency distribution of the, data obtained. Do the same regarding other subjects and compare. Find the mean in, each case using a method you find appropriate., , SC, ER, , 1., , 2., , Collect the daily maximum temperatures recorded for a period of 30 days in your city., Present this data as a grouped frequency table. Find the mean of the data using an, appropriate method., , 3., , Measure the heights of all the students of your class and form a grouped frequency, distribution table of this data. Find the mean of the data using an appropriate method., , E XERCISE - 14.1, , 1., , A survey was conducted by a group of students as a part of their environment awareness, programme, in which they collected the following data regarding the number of plants in, 20 houses in a locality. Find the mean number of plants per house., , Number of plants, , 0-2, , 2-4, , 4–6, , 6-8, , Number of houses, , 1, , 2, , 1, , 5, , 8 - 10 10 - 12, 6, , 2, , 12 – 14, 3, , Free Distribution by T.S. Government 2021-22
Page 347 :
Statistics, 2., , 337, , Consider the following distribution of daily wages of 50 workers of a factory., Daily wages in Rupees 200 - 250, Number of workers, , 250 - 300, , 12, , 300 - 350 350 - 400, , 14, , 8, , 400– 450, , 6, , 10, , Daily pocket, 11 - 13, allowance(in Rupees), Number of children, 4., , 13 - 15, , 15 - 17, , 6, , 9, , 7, , 17 - 19, , 19 - 21, , 21 - 23, , 23 - 25, , f, , 5, , 4, , 13, , Thirty women were examined in a hospital by a doctor and their heart beats per minute, were recorded and summarised as shown. Find the mean heart beats per minute for, these women, choosing a suitable method., 68-71 71-74 74-77, , T,, TE, L, , Number of heart beats/minute 65-68, Number of women, 5., , G, AN, , The following distribution shows the daily pocket allowance of children of a locality. The, mean pocket allowance is ` 18. Find the missing frequency f., , AN, , 3., , A, , Find the mean daily wages of the workers of the factory by using an appropriate method., , 2, , 4, , 3, , 77-80, , 8, , 80-83 83-86, , 7, , 4, , 2, , In a retail market, fruit vendors were selling oranges kept in packing baskets. These, baskets contained varying number of oranges. The following was the distribution of, oranges., 10-14, , 15–19, , 20-24, , 25-29, , 30–34, , Number of baskets, , 15, , 110, , 135, , 115, , 25, , SC, ER, , Number of oranges, , Find the mean number of oranges kept in each basket. Which method of finding the, mean did you choose?, , 6., , The table below shows the daily expenditure on food of 25 households in a locality., , Daily expenditure (in Rupees) 100-150, Number of house holds, , 150-200, , 200-250, , 250-300, , 300-350, , 5, , 12, , 2, , 2, , 4, , Find the mean daily expenditure on food by a suitable method., , 7., , To find out the concentration of SO2 in the air (in parts per million, i.e., ppm), the data, was collected for 30 localities in a certain city and is presented below:, Concentration of SO2 in ppm, Frequency, , 0.00-0.04 0.04-0.08, 4, , 0.08-0.12, , 9, , Find the mean concentration of SO2 in the air., , Free Distribution by T.S. Government 2021-22, , 9, , 0.12-0.16, 2, , 0.16-0.20 0.20-0.24, 4, , 2
Page 348 :
Class-X Mathematics, , 338, , 8., , A class teacher has the following attendance record of 40 students of a class for the, whole term. Find the mean number of days a student was present out of 56 days in the, term., , Number of days, , 38-41, , 41-44, , 44-47, , 47-50, , 50-53, , 53-56, , 1, , 3, , 4, , 4, , 7, , 10, , 11, , A, , Number of students, , 35-38, , The following table gives the literacy rate (in percentage) of 35 cities. Find the mean, literacy rate., , G, AN, , 9., , Literacy rate in %, , 45–55, , 55-65, , 65-75, , 75-85, , 85-95, , Number of cities, , 3, , 10, , 11, , 8, , 3, , AN, , 14.3 MODE, , A mode is that value among the observations which occurs most frequently., , T,, TE, L, , Before learning, how to calculate the mode of grouped data, let us first recall how we, found the mode for ungrouped data through the following example., Example-4. The wickets taken by a bowler in 10 cricket matches are as follows: 2, 6, 4, 5, 0,, 2, 1, 3, 2, 3. Find the mode of the data., Solution : Let us arrange the observations in order i.e., 0, 1, 2, 2, 2, 3, 3, 4, 5, 6, Clearly, 2 is the number of wickets taken by the bowler in the maximum number of matches, (i.e., 3 times). So, the mode of this data is 2., , SC, ER, , D O T HIS, , 1., , Find the mode of the following data., a), , 5, 6, 9, 10, 6, 12, 3, 6, 11, 10, 4, 6, 7., , b), , 20, 3, 7, 13, 3, 4, 6, 7, 19, 15, 7, 18, 3., , c), , 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6., , 2., , Is the mode always at the centre of the data?, , 3., , Does the mode change, if another observation is added to the data in example?, Comment., , 4., , If the maximum value of an observation in the data in Example 4 is changed to 8,, would the mode of the data be affected? Comment., , Free Distribution by T.S. Government 2021-22
Page 349 :
Statistics, , 339, , In a grouped frequency distribution, it is not possible to determine the mode by looking, at the frequencies. Here, we can only locate a class with the maximum frequency, called the, modal class. The mode is a value inside the modal class, and is given by the formula., , A, , where,, , æ f1 , f 0 ö÷, ÷÷´ h, Mode < l ∗ ççç, è 2 f1 , f0 , f 2 ø÷, l = lower boundary of the modal class,, , G, AN, , h = size of the modal class interval,, f1 = frequency of the modal class,, , f0 = frequency of the class preceding the modal class,, , f2 = frequency of the class succeeding the modal class., , Let us consider the following examples to illustrate the use of this formula., , Family size, , 7, , 3-5, , 5-7, , 7-9, , 9-11, , 8, , 2, , 2, , 1, , T,, TE, L, , Number of families, , 1-3, , AN, , Example-5. A survey conducted on 20 households in a locality by a group of students resulted, in the following frequency table for the number of family members in a household., , Find the mode of this data., , Solution : Here the maximum class frequency is 8, and the class corresponding to this frequency, is 3-5. So, the modal class is 3-5., Now,, , modal class = 3-5, boundary limit (l) of modal class = 3, class size (h) = 2, , SC, ER, , frequency of the modal class (f1) = 8,, , frequency of class preceding the modal class (f0) = 7,, frequency of class succeeding the modal class (f2) = 2., , Now, let us substitute these values in the formula-, , æ f1 , f 0 ö÷, ÷´ h, Mode < l ∗ çç, çè 2 f1 , f0 , f 2 ø÷÷, , æ 8,7, ÷ö´ 2 < 3 ∗ 2 < 3.286, < 3 ∗ çç, çè 2´8 , 7 , 2 ÷÷ø, 7, , Therefore, the mode of the data above is 3.286., Example-6. The marks distribution of 30 students in a mathematics examination are given in the, adjacent table. Find the mode of this data. Also compare and interpret the mode and the mean., , Free Distribution by T.S. Government 2021-22
Page 350 :
Class-X Mathematics, Number of, students ( fi), , 10-25, 25-40, 40-55, 55-70, 70-85, , 2, 3, 7, 6, 6, , 85-100, , 6, , Class Marks (xi ), 17.5, 32.5, 47.5, 62.5, 77.5, , 35.0, 97.5, 332.5, 375.0, 465.0, , 92.5, , å fi = 30, , Total, , f i xi, , A, , Class interval, , G, AN, , 340, , 555.0, , å fi xi = 1860.0, , Solution : Since the maximum number of students (i.e., 7) have got marks in the interval, 40-65, the modal class is 40 - 55., , AN, , The lower boundary ( l ) of the modal class = 40,, the class size ( h) = 15,, the frequency of modal class ( f1 ) = 7,, , T,, TE, L, , the frequency of the class preceding the modal class ( f0 ) = 3 and, the frequency of the class succeeding the modal class ( f2 ) = 6., Now, using the formula:, , æ f1 , f 0 ö÷, ÷, Mode < l ∗ çç, çè 2 f , f , f ø÷÷´ h, 1, 0, 2, , SC, ER, , æ 7 , 3 ÷ö, < 40 ∗ çç, ´15 < 40 ∗12 < 52, çè 2´7 , 6 , 3÷÷ø, , Interpretation : The mode marks is 52. Now, from Example 1, we know that the mean marks, is 62. So, the maximum number of students obtained 52 marks, while on an average a student, obtained 62 marks., , T HINK, , 1., , AND, , D ISCUSS, , It depends upon the demand of the situation whether we are interested in finding the, average marks obtained by the students or the marks obtained by most of the students., a. What do we find in the first situation?, b. What do we find in the second situation?, , 2., , Can mode be calculated for grouped data with unequal class sizes?, , Free Distribution by T.S. Government 2021-22
Page 351 :
Statistics, , 341, , EXERCISE - 14.2, The following table shows the ages of the patients admitted in a hospital on a particular day:, Age (in years), , 5-15, , 15-25, , 25-35, , 35-45, , 45-55, , 55-65, , 6, , 11, , 21, , 23, , 14, , 5, , Number of patients, , A, , 1., , The following data gives the information on the observed life times (in hours) of 225, electrical components :, , Lifetimes (in hours) 0 - 20, Frequency, , 20 - 40, , 10, , 40 - 60, , 60 - 80, , 80 - 100, , AN, , 2., , G, AN, , Find the mode and the mean of the data given above. Compare and interpret the two, measures of central tendency., , 35, , 52, , 61, , 100 - 120, , 38, , 29, , 3., , T,, TE, L, , Determine the modal lifetimes of the components., , The following data gives the distribution of total monthly household expenditure of 200, families of Gummadidala village. Find the modal monthly expenditure of the families., Also, find the mean monthly expenditure :, , Expenditure, (in rupees), , 24, , SC, ER, , Number of families, , 1000- 1500- 2000- 2500- 3000- 3500- 4000- 45001500 2000 2500 3000 3500 4000 4500 5000, , 4., , 33, , 28, , 30, , 22, , 16, , 7, , The following distribution gives the state-wise, teacher-student ratio in higher secondary, schools of India. Find the mode and mean of this data. Interpret the two measures., , Number of students, Number of States, , 5., , 40, , 15-20 20-25 25-30 30-35 35-40 40-45 45-50 50-55, 3, , 8, , 9, , 10, , 3, , 0, , 0, , 2, , The given distribution shows the number of runs scored by some top batsmen of the, world in one-day international cricket matches., , Runs, , 3000- 4000- 5000- 6000- 7000- 8000- 9000- 100004000 5000 6000 7000 8000 9000 10000 11000, , Number of batsmen, , 4, , 18, , 9, , 7, , Find the mode of the data., , Free Distribution by T.S. Government 2021-22, , 6, , 3, , 1, , 1
Page 352 :
Class-X Mathematics, , 342, , 6., , A student noted the number of cars passing through a spot on a road for 100 periods,, each of 3 minutes, and summarised this in the table given below., , Number of cars 0 - 10 10 - 20 20 - 30 30 - 40, Frequency, , 7, , 14, , 13, , 40 - 50 50 - 60 60 - 70 70 - 80, , 12, , 20, , 11, , 15, , 8, , OF, , G ROUPED DATA, , G, AN, , 14.4 MEDIAN, , A, , Find the mode of the data., , Median is a measure of central tendency which gives the value of the middle-most, observation in the data. Recall that for finding the median of ungrouped data, we first arrange the, data values or the observations in ascending order., , AN, , æ n ∗1ö÷th, ÷ observation and, Then, if n is odd, the median is the ççç, è 2 ø÷, , T,, TE, L, , th, æ n ö÷th, æ n ö÷, ç, ç, if n is even, then the median will be the average of the çç ÷÷ and çç ∗1÷÷ observations., è 2ø, è2 ø, , Suppose, we have to find the median of the following data, which is about the marks, out of, 50 obtained by 100 students in a test :, Marks obtained, , 20, , 29, , 28, , 33, , 42, , 38, , 43, , 25, , Number of students, , 6, , 28, , 24, , 15, , 2, , 4, , 1, , 20, , First, we arrange the marks in ascending order and prepare a frequency table as follows :, , SC, ER, , Marks obtained, , Number of students (frequency), , 20, , 6, , 25, , 20, , 28, , 24, , 29, , 28, , 33, , 15, , 38, , 4, , 42, , 2, , 43, , 1, , Total, , 100, , Free Distribution by T.S. Government 2021-22
Page 353 :
Statistics, , 343, , æ n ö÷th, Here n = 100, which is even. The median will be the average of the ççç ÷÷ and the, è 2ø, th, , æ n ÷öth, çç ∗1÷, çè 2 ÷ø, , st, , observations, i.e., the 50 and 51 observations. To find the position of these middle values, we, construct cumulative frequency., Number of students, 6, , 6, , G, AN, , 20, , Cumulative frequency, , A, , Marks obtained, , 6 + 20 =, , 26, , 26, , upto 28, , 26 + 24 = 50, , 50, , upto 29, , 50 + 28 = 78, , 78, , upto 33, upto 38, , 78 + 15 = 93, , 93, , 93 + 4 =, , 97, , 97, , 97 + 2 =, , 99, , 99, , 99 + 1 = 100, , 100, , T,, TE, L, , upto 42, , AN, , upto 25, , upto 43, , Now we add another column depicting this information to the frequency table above and name it, as cumulative frequency column., From the table above, we see that :, th, , 50 observation is 28 (Why?), , SC, ER, , st, , 51 observation is 29, Median =, , 28 ∗ 29, < 28.5 marks, 2, , Remark : The above table is known as Cumulative, Frequency Table. The median marks 28.5 conveys, the information that about 50% students obtained, marks less than 28.5 and another 50% students, obtained marks more than 28.5., Consider a grouped frequency distribution of, marks obtained, out of 100, by 53 students, in a certain, examination, as shown in adjacent table., , Free Distribution by T.S. Government 2021-22, , Marks, 0-10, 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80, 80-90, 90-100, , Number of students, 5, 3, 4, 3, 3, 4, 7, 9, 7, 8
Page 354 :
344, , Class-X Mathematics, , From the table, try to answer the following questions :, , (Cumulative frequency), 5, , Less than 20, , 5+3=8, , Less than 30, , 8 + 4 = 12, , Less than 40, , 12 + 3 = 15, , Less than 50, , 15 + 3 = 18, , Less than 60, , 18 + 4 = 22, , Less than 70, , 22 + 7 = 29, , Less than 80, , 29 + 9 = 38, , Less than 90, , 38 + 7 = 45, , Less than 100, , 45 + 8 = 53, , A, , Less than 10, , T,, TE, L, , Similarly, we can compute the cumulative, frequencies of the other classes, i.e., the, number of students with marks less than, 30, less than 40, ..., less than 100., , Number of students, , G, AN, , How many students have scored less than, 20 marks? Observe that the number of, students who have scored less than 20, include the number of students who have, scored marks from 0-10 as well as the, number of students who have scored, marks from 10-20. So, the total number, of students with marks less than 20 is 5 +, 3, i.e., 8. We say that the cumulative, frequency of the class 10-20 is 8. (As, shown in table 14.11), , Marks obtained, , AN, , How many students have scored marks, less than 10? The answer is clearly 5., , This distribution is called the cumulative frequency distribution of the less than type. Here 10, 20,, 30, ..., 100, are the upper boundaries of the respective class intervals., , SC, ER, , We can similarly make the table for, the number of students with scores, more than or equal to 0 (this, number is same as sum of all the, frequencies), more than above sum, minus the frequency of the first, class interval, more than or equal, to 20 (this number is same as the, sum of all frequencies minus the, sum of the frequencies of the first, two class intervals), and so on., We observe that all 53 students, have scored marks more than or, equal to 0. Since there are 5, students scoring marks in the, interval 0-10, this means that there, , Marks obtained, , Number of students, (Cumulative frequency), , More than or equal to 0, , 53, , More than or equal to 10, , 53 - 5 = 48, , More than or equal to 20, , 48 - 3 = 45, , More than or equal to 30, , 45 - 4 = 41, , More than or equal to 40, , 41 - 3 = 38, , More than or equal to 50, , 38 - 3 = 35, , More than or equal to 60, , 35 - 4 = 31, , More than or equal to 70, , 31 - 7 = 24, , More than or equal to 80, , 24 - 9 = 15, , More than or equal to 90, , 15 - 7 = 8, , Free Distribution by T.S. Government 2021-22
Page 355 :
Statistics, , 345, , are 53-5 = 48 students getting more than or equal to 10 marks. Continuing in the same manner,, we get the number of students scoring 20 or above as 48-3 = 45, 30 or above as 45-4 = 41, and, so on, as shown in the table aside., This table above is called a cumulative frequency distribution of the more than type. Here 0, 10,, , A, , 20, ..., 90 give the lower boundaries of the respective class intervals., Now, to find the median of grouped data, we can make use of any of these cumulative frequency, , G, AN, , distributions., , Now in a grouped data, we may not be able to find the middle observation by looking at the, cumulative frequencies as the middle observation will be some value in a class interval. It is,, halves. But which class should this be?, , AN, , therefore, necessary to find the value inside a class that divides the whole distribution into two, , To find this class, we find the cumulative frequencies of all the classes and, , Marks, 0-10, , n, for the first time. This is called the median class., 2, , T,, TE, L, , class whose cumulative frequency exceeds, , Number of students (f), , Cumulative frequency (cf), , 5, , 5, , 3, , 8, , 4, , 12, , 3, , 15, , 3, , 18, , 50-60, , 4, , 22, , 60-70, , 7, , 29, , 70-80, , 9, , 38, , 80-90, , 7, , 45, , 90-100, , 8, , 53, , 10-20, 20-30, 30-40, , SC, ER, , 40-50, , n, . We now locate the, 2, , n, = 26.5. Now 60-70 is the class whose cumulative, 2, n, frequency 29 is greater than (and nearest to) , i.e., 26.5., 2, , In the distribution above, n = 53. So, , Therefore, 60-70 is the median class., , Free Distribution by T.S. Government 2021-22
Page 356 :
346, , Class-X Mathematics, , After finding the median class, we use the following formula for calculating the median., , A, , æn, ö, çç , cf ÷÷, ÷, ç, ÷÷´ h, Median < l ∗ çç 2, çç f ÷÷÷, ÷ø, çè, where l = lower boundary of median clas,, , G, AN, , n = number of observations,, , cf = cumulative frequency of class preceding the median class,, f = frequency of median class,, , Substituting the values, , n, = 26.5,, 2, , AN, , h = class size (size of the median class)., l = 60,, , in the formula above, we get, , f = 7, h = 10, , T,, TE, L, , é 26.5 , 22 ù, ú ´10, Median < 60 ∗ ê, êë, úû, 7, , cf = 22,, , < 60 ∗, , 45, 7, , < 66.4, , SC, ER, , So, about half the students have scored marks less than 66.4, and the other half have scored, marks more than 66.4., , Example-7. A survey regarding the heights, , Height (in cm), , Number of girls, , (in cm) of 51 girls of Class X of a school was, , Less than 140, , 4, , conducted and data was obtained as shown in, , Less than 145, , 11, , table. Find their median., , Less than 150, , 29, , Less than 155, , 40, , Less than 160, , 46, , Less than 165, , 51, , Free Distribution by T.S. Government 2021-22
Page 357 :
Statistics, , 347, , Solution : To calculate the median, height, we need to find the class, , Class intervals, , Frequency, , intervals and their corresponding, , Cumulative, frequency, , Below 140, , 4, , 4, , being of the less than type, 140,, , 140-145, , 7, , 11, , 145, 150, . . ., 165 give the upper, , 145-150, , 18, , 150-155, , 11, , intervals. So, the classes should be, below 140, 140 - 145, 145 - 150, ., , 155-160, 160-165, , . ., 160 - 165., , 29, , 40, , G, AN, , limits of the corresponding class, , A, , frequencies. The given distribution, , 6, , 46, , 5, , 51, , AN, , Observe that from the given distribution, we find that there are 4 girls with height less than 140,, i.e., the frequency of class interval below 140 is 4 . Now, there are 11 girls with heights less than, 145 and 4 girls with height less than 140. Therefore, the number of girls with height in the interval, , T,, TE, L, , 140 – 145 is 11 – 4 = 7. Similarly, the frequencies can be calculated as shown in table., Number of observations, n = 51, , n 51, th, =, = 25.5 observation, which lies in the class 145 - 150., 2, 2, , \ 145 – 150 is the median class, , SC, ER, , Then, l (the lower boundary) = 145,, , cf (the cumulative frequency of the class preceding 145 – 150) = 11,, f (the frequency of the median class 145 – 150) = 18 and, h (the class size) = 5., , æn, ö, çç , cf ÷÷, ÷ø, ç, Using the formula, Median < l ∗ è 2, ´h, f, < 145 ∗, < 145 ∗, , ∋25.5 ,11(, 18, , ´5, , 72.5, = 149.03., 18, , Free Distribution by T.S. Government 2021-22
Page 358 :
Class-X Mathematics, , 348, , So, the median height of the girls is 149.03 cm. This means that the height of about 50% of the, girls is less than this height, and that of other 50% is greater than this height., Example-8. The median of the following data is 525. Find the values of x and y, if the total, , 2, , 200-, , 300-, , 400-, , 500-, , 200, , 300, , 400, , 500, , 600, , 5, , x, , 12, , 17, , 20, , Class intervals, , Frequency, , 600-, , 700-, , 900-, , 700, , 800, , 900, , 1000, , y, , 9, , 7, , 4, , Cumulative frequency, , 2, , 100-200, , 5, , 200-300, , x, , 300-400, , 12, , 19+x, , 400-500, , 17, , 36+x, , 500-600, , 20, , 56+x, , 600-700, , y, , 56+x+y, , 700-800, , 9, , 65+x+y, , 800-900, , 7, , 72+x+y, , 900-1000, , 4, , 76+x+y, , T,, TE, L, , 0-100, , SC, ER, , 800-, , G, AN, , Fr, , 0-100 100-, , AN, , CI, , A, , frequency is 100. Here, CI stands for class interval and Fr for frequency., , 2, , 7, , 7+x, , Solution :, , It is given that n = 100, , So, 76 + x + y = 100, i.e., x + y = 24 (1), , The median is 525, which lies in the class 500 – 600, So, l = 500, f = 20, cf = 36 + x, h = 100, , Free Distribution by T.S. Government 2021-22
Page 359 :
Statistics, , 349, , Using the formula, , æn, ö, çç , cf ÷÷, çè 2, ø÷, Median < l ∗, ´h, f, 50 , 36 , x, ´100, 20, , i.e.,, , 25 = 70 – 5x, , i.e.,, , 5x = 70 – 25 = 45, x= 9, , Therefore, from (1), we get 9 + y = 24, , Note :, , T,, TE, L, , i.e., y = 15, , AN, , So,, , G, AN, , i.e., 525 – 500 = (14 – x) × 5, , A, , 525 < 500 ∗, , The median of grouped data with unequal class sizes can also be calculated., , 14.5 W HICH, , VALUE OF, , C ENTRAL T ENDENCY, , Which measure would be best suited for a particular requirement., , SC, ER, , The mean is the most frequently used measure of central tendency because it takes into account, all the observations, and lies between the extremes, i.e., the largest and the smallest observations, of the entire data. It also enables us to compare two or more distributions. For example, by, comparing the average (mean) results of students of different schools of a particular examination,, we can conclude which school has a better performance., However, extreme values in the data affect the mean. For example, the mean of classes having, frequencies more or less the same is a good representative of the data. But, if one class has, frequency, say 2, and the five others have frequency 20, 25, 20, 21, 18, then the mean will, certainly not reflect the way the data behaves. So, in such cases, the mean is not a good, representative of the data., In problems where individual observations are not important, especially extreme values, and we, wish to find out a ‘typical’ observation, the median is more appropriate, e.g., finding the typical, productivity rate of workers, average wage in a country, etc. These are situations where extreme, values may exist. So, rather than the mean, we take the median as a better measure of central, tendency., , Free Distribution by T.S. Government 2021-22
Page 360 :
Class-X Mathematics, , 350, , In situations which require establishing the most frequent value or most popular item, the mode is, the best choice, e.g., to find the most popular T.V. programme being watched, the consumer item, in greatest demand, the colour of the vehicle used by most of the people, etc., , Monthly consumption 65-85, Number of consumers, , 2., , 4, , 105-125, , 125-145, , 145-165, , 165-185, , 185-205, , 13, , 20, , 14, , 8, , 4, , 5, , If the median of 60 observations, given below is 28.5, find the values of x and y., , Class interval, , 0-10, , 10-20, , 20-30, , 30-40, , 40-50, , 50-60, , 5, , x, , 20, , 15, , y, , 5, , T,, TE, L, , Frequency, , 3., , 85-105, , G, AN, , The following frequency distribution gives the monthly consumption of electricity of 68, consumers of a locality. Find the median, mean and mode of the data and compare them., , AN, , 1., , A, , EXERCISE - 14.3, , A life insurance agent found the following data about distribution of ages of 100 policy, holders. Calculate the median age. [Policies are given only to persons having age 18, years onwards but less than 60 years.], , Age, , Below Below Below Below Below Below Below Below Below, , (in years), , 25, , 30, , 35, , 40, , 45, , 50, , 55, , 60, , 2, , 6, , 24, , 45, , 78, , 89, , 92, , 98, , 100, , SC, ER, , Number of, , 20, , policy holders, , 4., , The lengths of 40 leaves of a plant are measured correct to the nearest millimetre, and, the data obtained is represented in the following table :, , Length (in mm), , Number of leaves, , 118-126, , 127-135, , 136-144, , 145-153, , 154-162, , 163-171, , 172-180, , 3, , 5, , 9, , 12, , 5, , 4, , 2, , Find the median length of the leaves. (Hint : The data needs to be converted to continuous, classes for finding the median, since the formula assumes continuous classes. The classes then, change to 117.5 - 126.5, 126.5 - 135.5, . . ., 171.5 - 180.5.), , Free Distribution by T.S. Government 2021-22
Page 361 :
Statistics, , The following table gives the distribution of the life-time of 400 neon lamps, Life time, (in hours), , 15002000, , 20002500, , 25003000, , 30003500, , 35004000, , 40004500, , 45005000, , Number of, lamps, , 14, , 56, , 60, , 86, , 74, , 62, , 48, , A, , 5., , 351, , Find the median life time of a lamp., , Number of letters, Number of surnames, , G, AN, , 100 surnames were randomly picked up from a local telephone directory and the frequency, distribution of the number of letters in the English alphabet in the surnames was obtained, as follows, 1-4, , 4-7, , 7-10, , 10-13, , 13-16, , 16-19, , 6, , 30, , 40, , 16, , 4, , 4, , AN, , 6., , Determine the median number of letters in the surnames. Find the mean number of letters in the, surnames? Also, find the modal size of the surnames., The distribution below gives the weights of 30 students of a class. Find the median, weight of the students., , T,, TE, L, , 7., , Weight (in kg), , Number of students, , 40-45, , 45-50, , 50-55, , 55-60, , 60-65, , 65-70, , 70-75, , 2, , 3, , 8, , 6, , 6, , 3, , 2, , OF, , C UMULATIVE FREQUENCY D ISTRIBUTION, , SC, ER, , 14.6 G RAPHICAL R EPRESENTATION, , As we all know, pictures speak better than words. A graphical representation helps us in, understanding given data at a glance. In Class IX, we have represented the data through bar, graphs, histograms and frequency polygons. Let us now represent a cumulative frequency, distribution graphically., , For example, let us consider the cumulative frequency distribution given in example., For drawing ogives, it should be ensured that the class intervals are continuous, because cumulative, frequencies are linked with boundaries, but not with limits., , Free Distribution by T.S. Government 2021-22
Page 362 :
Class-X Mathematics, , Recall that the values 10, 20,, , class intervals. To represent the, data graphically, we mark the, upper boundaries of the class, intervals on the horizontal axis, (X-axis), , and, , 50, 40, , 'Less than' ogive, , 30, 20, 10, , A, , boundaries of the respective, , Less than Cumulative frequency, , 30, ..., 100 are the upper, , 60, , 0, 0, , 80, , 90, , G, AN, , 352, , 100, , Upper limits, , their, , corresponding cumulative frequencies on the vertical axis (Y-axis), choosing a convenient scale., Now plot the points corresponding to the ordered pairs given by (upper boundary, corresponding, , AN, , cumulative frequency), i.e., (10, 5), (20, 8), (30,, 12), (40, 15), (50, 18), (60, 22), (70, 29),, (80, 38), (90, 45), (100, 53) on a graph paper and join them by a free hand smooth curve. The, curve we get is called a cumulative frequency curve, or an ogive (of the less than type)., , T,, TE, L, , The term 'ogive is pronounced as 'ojeev' and is derived from the word ogee. An ogee is, a shape consisting of a concave arc flowing into a convex arc, so forming an S-shaped, curve with vertical ends. In architecture, the ogee shape is one of the characteristics of, th, th, the 14 and 15 century Gothic styles., Again we consider the cumulative frequency distribution and draw its ogive (of the more than, type)., , Cumulative frequency, , SC, ER, , Recall that, here 0, 10, 20, ...., 90, 60, are the lower boundaries of the, 50, respective class intervals 0-10, 10'More than' ogive, 20, ....., 90-100. To represent 'the, 40, more than type' graphically, we plot, 30, the lower boundaries on the X-axis, and the corresponding cumulative, 20, frequencies on the Y-axis. Then we, 10, plot the points (lower boundaries,, 0, corresponding, cumulative, frequency), i.e., (0, 53), (10, 48),, 0 10 20 30 40 50 60 70 80 90, Lower limits, (20, (45), (30, 41), (40, 38), (50,, 35), (60, 31), (70, 24), (80, 15), (90, 8), on a graph paper, and join them by a free hand smooth, curve. The curve we get is a cumulative frequency curve, or an ogive (of the more than type)., , Free Distribution by T.S. Government 2021-22
Page 363 :
Statistics, 14.6.1 O BTAINING M EDIAN, , 353, , FROM A GIVEN CURVE :, , A, , G, AN, , Another way of obtaining the, median :, , Cumulative frequency, , Is it possible to obtain the median from these two cumulative frequency curves . Let us see., n 53, One obvious way is to locate on < < 26.5 on the y-axis. From this point, draw a line, 2, 2, parallel to the X-axis cutting the, 60, 50, curve at a point. From this point,, draw a perpendicular to the X-axis., 40, Foo t of this perpendicular, 30, determines the median of the data., 20, Median (66.4), , 10, 0, 0, , 10, , 20, , 30, , 40, , 50, , 60, , 70, , 80, , 90, , 100, , AN, , Upper limits, Draw both ogives (i.e., of the less, than type and of the more than type), on the same axis. The two ogives will intersect each other at a point. From this point, if we draw, a perpendicular on the x-axis, the point at which it cuts the x-axis gives us the median., 60, , T,, TE, L, , 40, 30, 20, 10, , SC, ER, , Cumulative frequency, , 50, , 0, , 0, , 10, , 20, , 30, , 40, , Limits, , 50, , Limits, , 60, , 70, , 80, , 90, , 100, , Mediam (66.4), , Example-9. The annual profits earned by 30 shops in Sangareddy locality give rise to the, following distribution :, Profit (in lakhs), , Number of shops (frequency), , More than or equal to 5, More than or equal to 10, More than or equal to 15, More than or equal to 20, More than or equal to 25, More than or equal to 30, More than or equal to 35, , 30, 28, 16, 14, 10, 7, 3, , Draw both ogives for the data above. Hence obtain the median profit., , Free Distribution by T.S. Government 2021-22
Page 364 :
Class-X Mathematics, , 354, , Solution : We first draw the coordinate axes, with lower limits of the profit along the horizontal, axis, and the cumulative frequency along the vertical axes. Then, we plot the points (5, 30), (10,, 28), (15, 16), (20, 14), (25, 10), (30, 7) and (35, 3). We join these points with a smooth curve, to get the more than ovive, as shown in the figure below-, , A, G, AN, , 30, 25, 20, 15, 10, , AN, , More than Cumulative frequency, , 35, , 5, , 0, , T,, TE, L, , 0, 5, , 10, 15, 20, 25, Lower limits of profit (in lakhs Rs.), , 30, , 35, , Now, let us obtain the classes, their frequencies and the cumulative frequency from the table, above., , SC, ER, , Classes, , 5-10, , 10-15 15-20 20-25 25-30 30-35 35-40, , Number of shops, , 2, , 12, , 2, , 4, , 3, , 4, , 3, , Cumulative frequency, , 2, , 14, , 16, , 20, , 23, , 27, , 30, , Using these values, we plot the points (10, 2), (15, 14), (20, 16), (25, 20), (30, 23), (35, 27),, (40, 30) on the same axes as in last figure to get the less than ogive, as shown in figure below., The abcissa of their point of intersection is nearly 17.5, which is the median. This can also be, verified by using the formula. Hence, the median profit (in lakhs) is ` 17.5., , Free Distribution by T.S. Government 2021-22
Page 365 :
Statistics, , 355, , 30, 25, 20, 15, 10, , A, , Cumulative frequency, , 35, , 0, 0, , 5, , 10, , 15, , 20, , 25, , 30, , 35, , 40, , Median (17.5), Profit (in lakhs Rs.), , Limits, , E XERCISE - 14.4, , The following distribution gives the daily income of 50 workers of a factory., Daily income (in Rupees) 250-300, 12, , 300-350 350-400 400-450, 14, , T,, TE, L, , Number of workers, , AN, , 1., , G, AN, , 5, , 8, , 6, , 450-500, 10, , Convert the distribution above to a less than type cumulative frequency distribution, and draw its, ogive., During the medical check-up of 35 students of a class, their weights were recorded as, follows :, Weight (in kg), , Number of students, , Less than 38, Less than 40, Less than 42, Less than 44, Less than 46, Less than 48, Less than 50, Less than 52, , 0, 3, 5, 9, 14, 28, 32, 35, , SC, ER, , 2., , Draw a less than type ogive for the given data. Hence obtain the median weight from the graph, and verify the result by using the formula., 3., , The following table gives production yield per hectare of wheat of 100 farms of a village., Production yield, (Qui/Hec), Number of farmers, , 50-55 55-60 60-65 65-70 70-75 75-80, 2, , 8, , 12, , 24, , 38, , Change the distribution to a more than type distribution, and draw its ogive., , Free Distribution by T.S. Government 2021-22, , 16
Page 366 :
356, , Class-X Mathematics, , Suggested Projects, Finding mean - median - mode., Applications of daily life situation., , l, , Collecting information from available sources., , l, , Drawing graphs for mean, median and mode for the above collected data., , A, , l, , G, AN, , WHAT WE H AVE D ISCUSSED, , In this chapter, you have studied the following points :, , 2., , The mean for grouped data is calculated by :, å f i xi, å fi, , The direct method : x <, , (ii), , The assumed mean method : x < a ∗, , (iii), , æ å f u ö÷, i i÷, The step deviation method : x < a ∗ çç, çè å f ø÷÷´ h, i, , AN, , (i), , å fi di, å fi, , T,, TE, L, , 1., , The mode for grouped data can be found by using the formula :, , æ f1 , f 0 ö÷, ÷÷´ h, Mode < l ∗ ççç, è 2 f1 , f0 , f 2 ø÷, , where, symbols have their usual meaning., , The median for grouped data is formed by using the formula :, , SC, ER, , 3., , 4., , æn, ö, çç , cf ÷÷, ÷÷, Median < l ∗ ççç 2, ÷´ h , where symbols have their usual meanings., çç f ÷÷÷, ÷ø, çè, In order to find median, class intervals should be continuous., , 5., , Representing a cumulative frequency distribution graphically as a cumulative frequency, curve, or an ogive of the less than type and of the more than type., , 6., , While drawing ogives, boundaries are taken on X-axis and cumulative frequencies are, taken on Y-axis., , 7., , Scale on both the axes may not be equal., , 8., , The median of grouped data can be obtained graphically as the x-coordinate of the point, of intersection of the two ogives for this data., , Free Distribution by T.S. Government 2021-22
Page 367 :
A, , Mathematical Modelling, , G, AN, , A.I.1 I NTRODUCTION, , On 25th February 2013, the ISRO launcher PSLV C20, placed the satellite SARAL into, orbit. The satellite weighs 407 kg. It is at an altitude of 781 km and its orbit is inclined at an angle, of 98.5º., On reading the above information, we may wonder:, , How did the scientists calculate the altitude as 781km. Did they go to space and measure, it?, , (ii), , How did they conclude that the angle of orbit is 98.5º without actually measuring?, , T,, TE, L, , AN, , (i), , Some more examples are there in our daily life where we wonder how the scientists and, mathematicians could possibly have estimated these results. Observe these examples:, (i), , The temperature at the surface of the sun is about 6,000ºC., , (ii), , The human heart pumps 5 to 6 liters of blood in the body every minute., , (iii), , We know that the distance between the sun and the earth is 149, 600,000 km., , SC, ER, , In the above examples, we know that no one went to the sun to measure the temperature, or the distance from earth. Nor can we take the heart out of the body and measure the blood it, pumps. The way we answer these and other similar questions is through mathematical modelling., , Mathematical modelling is used not only by scientists but also by us. For example, we, might want to know how much money we will get after one year if we invest D100 at 10% simple, interest. Or we might want to know how many litres of paint is needed to whitewash a room., Even these problems are solved by mathematical modelling., , T HINK, , AND, , D ISCUSS, , Discuss with your friends some more examples in real life where we cannot directly, measure and must use mathematical modelling .
Page 368 :
Class-X Mathematics, , 358, , A.I.2 M ATHEMATICAL M ODELS, Do you remember the formula to calculate the area of a triangle?, Area of Triangle =, , 1, ´ base ´ height., 2, , Distance d, =, time, t, , Speed (S) =, , (ii), , æ, r ö÷, ÷, In compound interest sum (A) = P ççç1 ∗, è 100 ø÷, , AN, , (i), , G, AN, , Some more examples for mathematical models., , A, , PTR, . This formula or equation, 100, is a relation between the Interest (I); Principle (P); Time (T); and Rate of Interest (R). These, formulae are examples of mathematical models., , Similarly, simple interest calculation uses the formula I <, , T,, TE, L, , n, , Where, , P = Principle, , r = rate of interest, , n = number of times to be calculated interest., , SC, ER, , So, Mathematical model is nothing but a mathematical description or relation that, describes some real life situation., , D O T HIS, , Write some more mathematical models which you have learnt in previous classes., , A.I.3 M ATHEMATICAL M ODELLING, We often face problems in our day to day life. To solve them, we try to write it as an, , equivalent mathematical problem and find its solution. Next we interpret the solution and check, to what extent the solution is valid. This process of constructing a mathematical model and using, it to find the answer is known as mathematical modelling., , Free Distribution by T.S. Government 2021-22
Page 369 :
Mathematical Modelling, , 359, , Now let us observe some more examples related to mathematical modelling., Example-1. Vani wants to buy a TV that costs D19,000 but she has only D15,000. So she, decides to invest her money at 8% simple interest per year. After how many years will she be, able to buy the TV?, , G, AN, , A, , Step 1 : (Understanding the problem): In this stage, we define the real problem. Here, we are, given the principal, the rate of simple interest and we want to find out the number of years after, which the amount will become Rs. 19000., , Step 2 : (Mathematical description and formulation) In this step, we describe, in mathematical, terms, the different aspects of the problem. We define variables, write equations or inequalities, and gather data if required., , I<, , AN, , Here, we use the formula for simple interest which is, PTR, (Model), 100, , R = rate of interest,, , T,, TE, L, , where P = Principle, T = number of years,, We need to find time = T <, , I = Interest, , 100I, RP, , Step 3: (Solving the mathematical problem) In this step, we solve the problem using the, formula which we have developed in step 2., We know that Vani already has D15,000 which is the principal, P, , SC, ER, , The final amount is D19000 so she needs an extra (19000-15000) = D4000. This will, come from the interest, I ., P = D15,000, Rate = 8%, then I = 4000; T <, T<3, , 100´ 4 0 0 0 40 0, <, 150 0 0 ´8, 12 0, , 4, 1, < 3 years, 12, 3, , or Step4 : (Interpreting the solution): The solution obtained in the previous step is interpreted, here., 1, . This means three and one third of a year or three years and 4 months., 3, So, Vani can buy a TV after 3 year 4 months, , Here T = 3, , Free Distribution by T.S. Government 2021-22
Page 370 :
Class-X Mathematics, , 360, , Step5 : (Validating the model): We can’t always accept a model that gives us an answer that, does not match the reality. The process of checking and modifying the mathematical model, if, necessary, is validation., , G, AN, , A, , In the given example, we are assuming that the rate of interest will not change. If the rate, PTR, changes then our model, will not work. We are also assuming that the price of the washing, 100, machine will remain Rs. 19,000., Let us take another example., , Example-2. In Lokeshwaram High school, 50 children in the 10th class and their Maths teacher, want to go on tour from Lokeshwaram to Hyderabad by vehicles. A jeep can hold six persons, not including the driver. How many jeeps they need to hire?, , AN, , Step 1 : We want to find the number of jeeps needed to carry 51 persons, given that each jeep, can seat 6 persons besides the driver., Step 2 : Number of vehicles = (Number of persons) / (Persons that can be seated in one jeep), , T,, TE, L, , Step 3 : Number of vehicles = 51/6 = 8.5, Step 4 : Interpretation, , We know that it is not possible to have 8.5 vehicles. So, the number of vehicles needed, has to be the nearest whole number which is 9., \ Number of vehicles need is 9., Step 5 : Validation, , SC, ER, , While modelling, we have assumed that lean and fat children occupy same space., , D O T HIS, , 1., , Select any verbal problem from your textbook, make a mathematical model for the, selected problem and solve it., , 2., , Make a mathematical model for the problem given below and solve it., Suppose a car starts from a place A and travels at a speed of 40 Km/h towards, another place B. At the same time another car starts from B and travels towards A at, a speed of 30 Km/h. If the distance between A and B is 100 km; after how much time, will the cars meet?, , Free Distribution by T.S. Government 2021-22
Page 371 :
Mathematical Modelling, , 361, , So far, we have made mathematical models for simple word problems. Let us take a real, life example and model it., , G, AN, , A, , Example-3. In the year 2000, 191 member countries of the U.N.signed a declaration to promote, gender equality. One indicator for deciding whether this goal has been achieved is the ratio of, girls to boys in primary, secondary education. India also signed the declaration. The data for the, percentage of girls in India who are enrolled in primary schools is given in Table A.I.1., Table A.I.1, Enrolment (in %), , 1991 – 92, , 41.9, , 1992 – 93, , 42.6, , 1993 – 94, , 42.7, , 1994 – 95, 1995 – 96, , 42.9, 43.1, 43.2, , T,, TE, L, , 1996 – 97, , AN, , Year, , 43.5, , 1998 – 99, , 43.5, , 1999 – 2000, , 43.6, , 2000 – 01, , 43.7, , 2001 - 02, , 44.1, , SC, ER, , 1997 -98, , Using this data, mathematically describe the rate at which the proportion of girls enrolled, in primary schools grew. Also, estimate the year by which the enrolment of girls will reach 50%., Solution :, , Step 1 : Formulation Let us first convert the problem into a mathematical problem., , Table A.I.1 gives the enrolment for the years 1991 – 92, 1992- 93 etc. Since the students, join at the begining of an academic year, we can take the years as 1991, 1992 etc. Let us assume, that the percentage of girls who join primary schools will continue to grow at the same rate as the, rate in Table A.I.1. So, the number of years is important, not the specific years. (To give a similar, situation, when we find the simple interest for say, ` 15000 at the rate 8% for three years, it does, not matter whether the three – year period is from 1999 to 2002 or from 2001 to 2004. What is, important is the interest rate in the years being considered), , Free Distribution by T.S. Government 2021-22
Page 372 :
Class-X Mathematics, , 362, , Here also, we will see how the enrolment grows after 1991 by comparing the number of, years that has passed after 1991 and the enrolment. Let us take 1991 as the 0th year, and write, 1 for 1992 since 1 year has passed in 1992 after 1991. Similarly we will write 2 for 1993, 3 for, 1994 etc. So, Table A.I.1 will now look like as Table A.I.2, , Enrolment (in%), , 0, , 41.9, , 1, , 42.6, , 2, , 42.7, , 3, , 42.9, , 4, , 43.1, , 5, , 43.2, , 7, , 43.5, 43.5, 43.6, , T,, TE, L, , 8, , AN, , 6, , G, AN, , Year, , A, , Table A.I.2, , 9, , 43.7, , 10, , 44.1, , The increase in enrolment is given in the following table A.I.3., Table A.I.3, , Year, , Enrolment (in%), , Increase, , 41.9, , 0, , 1, , 42.6, , 0.7, , 2, , 42.7, , 0.1, , 3, , 42.9, , 0.2, , 4, , 43.1, , 0.2, , 5, , 43.2, , 0.1, , 6, , 43.5, , 0.3, , 7, , 43.5, , 0, , 8, , 43.6, , 0.1, , 9, , 43.7, , 0.1, , 10, , 44.1, , 0.4, , SC, ER, , 0, , Free Distribution by T.S. Government 2021-22
Page 373 :
Mathematical Modelling, , 363, , At the end of the first year period from 1991 to 1992, the enrolment has increased by, 0.7% from 41.9% to 42.6%. At the end of the second year, this has increased by 0.1% from, 42.6% to 42.7%. From the table above, we cannot find a definite relationship between the, number of years and percentage. But the increase is fairly steady. Only in the first year and in the, , A, , 10th year there is a jump. The mean of these values is, .... (1), , G, AN, , 0.7 ∗ 0.1 ∗ 0.2 ∗ 0.2 ∗ 0.1 ∗ 0.3 ∗ 0 ∗ 0.1 ∗ 0.1 ∗ 0.4, = 0.22, 10, , Let us assume that the enrolment steadily increases at the rate of 0.22 percent., Step 2 : (Mathematical Description), , AN, , We have assumed that the enrolment increases steadily at the rate of 0.22% per year., So, the Enrolment Percentage (EP) in the first year = 41.9 + 0.22, EP in the second year = 41.9 + 0.22 + 0.22 = 41.9 + 2 ´ 0.22, , T,, TE, L, , EP in the third year = 41.9 + 0.22 + 0.22 + 0.22 = 41.9 + 3 ´ 0.22, So, the enrolment percentage in the nth year = 41.9 + 0.22n, for n ³ 1., , .... (2), , Now, we also have to find the number of years by which the enrolment will reach 50%., So, we have to find the value of n from this equation, , 50 = 41.9 + 0.22n, , SC, ER, , Step 3 : Solution : Solving (2) for n, we get, n=, , 50 , 41.9, 8.1, =, = 36.8, 0.22, 0.22, , Step 4 : (Interpretation) : Since the number of years is an integral value, we will take the next, higher integer, 37. So, the enrolment percentage will reach 50% in 1991 + 37 = 2028., Step 5 : (Validation) Since we are dealing with a real life situation, we have to see to what, , extent this value matches the real situation., Let us check Formula (2) is in agreement with the reality. Let us find the values for the, years we already know, using Formula (2), and compare it with the known values by finding the, difference. The values are given in Table A.I.4., , Free Distribution by T.S. Government 2021-22
Page 374 :
364, , Class-X Mathematics, Table A.I.4, , Year, , Enrolment, (in %), , Values given by (2), (in %), , Difference, (in %), , 41.9, , 41.90, , 0, , 1, , 42.6, , 42.12, , 0.48, , 2, , 42.7, , 42.34, , 3, , 42.9, , 42.56, , 4, , 43.1, , 42.78, , 5, , 43.2, , 43.00, , 6, , 43.5, , 43.22, , 7, , 43.5, , 8, , 43.6, , 9, , 43.7, , AN, , G, AN, , 0.36, , 44.1, , 0.34, 0.32, 0.20, 0.28, , 43.44, , 0.06, , 43.66, , -0.06, , 43.88, , -0.18, , 44.10, , 0.00, , T,, TE, L, , 10, , A, , 0, , As you can see, some of the values given by Formula (2) are less than the actual values, by about 0.3% or even by 0.5%. This can give rise to a difference of about 3 to 5 years since the, increase per year is actually 1% to 2%. We may decide that this much of a difference is acceptable, and stop here. In this case, (2) is our mathematical model., , SC, ER, , Suppose we decide that this error is quite large, and we have to improve this model., Then, we have to go back to Step 2, and change the equation. Let us do so., Step 1 : Reformulation : We still assume that the values increase steadily by 0.22%, but we, will now introduce a correction factor to reduce the error, For this, we find the mean of all the, errors. This is, 0 ∗ 0.48 ∗ 0.36 ∗ 0.34 ∗ 0.32 ∗ 0.2 ∗ 0.28 ∗ 0.06 , 0.06 , 0.18 ∗ 0, = 0.18, 10, , We take the mean of the errors, and correct our formula by this value., , Revised Mathematical Description : Let us now add the mean of the errors to our formula, for enrolment percentage given in (2). So, our corrected formula is :, , Free Distribution by T.S. Government 2021-22
Page 375 :
Mathematical Modelling, , 365, , Enrolment percentage in the nth year, = 41.9 + 0.22n + 0.18 = 42.08 + 0.22n, for n ³ 1, , ... (3), , We will also modify Equation (2) appropriately. The new equation for n is :, ... (4), , A, , 50 = 42.08 + 0.22n, , n=, , 50 , 42.08 7.92, =, = 36, 0.22, 0.22, , G, AN, , Altered Solution : Solving Equation (4) for n, we get, , AN, , Interpretation : Since n = 36, the enrolment of girls in primary schools will reach 50% in the, year 1991 + 36 = 2027., , T,, TE, L, , Validation : Once again, let us compare the values got by using Formula (4) with the actual, values. Table A.I.5 gives the comparison., Table A.I.5, , Year Enrolment, (in %), 41.9, 42.6, 42.7, 42.9, 43.1, 43.2, 43.5, 43.5, 43.6, 43.7, 44.1, , SC, ER, , 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, , Values given, by (2), 41.90, 42.12, 42.34, 42.56, 42.78, 43.00, 43.22, 43.44, 43.66, 43.88, 44.10, , Difference, between, Values, 0, 0.48, 0.36, 0.34, 0.32, 0.20, 0.28, 0.06, -0.06, -0.18, 0.00, , Values, given, by (4), 41.9, 42.3, 42.52, 42.74, 42.96, 43.18, 43.4, 43.62, 43.84, 44.06, 44.28, , Difference, between, values, 0, 0.3, 0.18, 0.16, 0.14, 0.02, 0.1, -0.12, -0.24, -0.36, -0.18, , As you can see, many of the values that (4) gives are closer to the actual value than the, values that (2) gives. The mean of the errors is 0 in this case., , Free Distribution by T.S. Government 2021-22
Page 376 :
366, , Class-X Mathematics, , A.I.4 ADVANTAGES, 1., , OF, , M ATHEMATICS M ODELLING, , The aim of mathematical modelling is to get some useful information about a real world, problem by converting it into mathematical problem. This is especially useful when it is, not possible or very expensive to get information by other means such as direct observation, or by conducting experiments., , 2., , G, AN, , A, , For example, suppose we want to study the corrosive effect of the discharge of the, Mathura refinery on the Taj Mahal. We would not like to carry out experiments on the, Taj Mahal directly because that would damage a valuable monument. Here mathematical, modelling can be of great use., , Forecasting is very important in many types of organizations, since predictions of future, events have to be incorporated into the decision – making process., , T,, TE, L, , AN, , For example, (i), In marketing departments, reliable forecasts of demand help in planning of the, sale strategies, (ii), A school board needs to able to forecast the increase in the number of school, going children in various districts so as to decide where and when to start new, schools., 3., Often we need to estimate large values like trees in a forest; fishes in a lake; estimation of, votes polled etc., Some more examples where we use mathematical modelling are:, Estimating future population for certain number of years, , (ii), , Predicting the arrival of Monsoon, , (iii), , Estimating the literacy rate in coming years, , (iv), , Estimating number of leaves in a tree, , (v), , Finding the depth of oceans, , SC, ER, , (i), , A.I.5 L IMITATIONS, , OF, , M ATHEMATICAL, , MODELLING, , Is mathematical modelling the answer to all our problems?, , Certainly not; it has it’s limitations. Thus, we should keep in mind that a model is only a, simplification of a real world problem, and the two are not same. It is some thing like the difference, between a map that gives the physical features of a country, and the country itself. We can find, the height of a place above the sea level from this map, but we cannot find the characteristics of, the people from it. So, we should use a model only for the purpose it is supposed to serve,, remembering all the factors we have neglected while constructing it. We should apply the model, only within the limits where it is applicable., , Free Distribution by T.S. Government 2021-22
Page 377 :
Mathematical Modelling, , 367, , A.I.6 TO WHAT EXTENT W E S HOULD TRY TO IMPROVE OUR M ODEL?, To improve a model we need to take into account several additional factors. When we, do this we add more variables to our mathematical equations. The equations becomes complicated, and the model is difficult to use. A model must be simple enough to use yet accurate; i.e the closer, it is to reality the better the model is., , A, , T RY T HIS, , SC, ER, , T,, TE, L, , AN, , G, AN, , A problem dating back to the early 13th century, posed by Leonardo Fibonacci, asks, how many rabbits you would have in one year if you started with just two and let all of them, reproduce. Assume that a pair of rabbits produces a pair of offspring each month and that, each pair of rabbits produces their first offspring at the age of 2 months. Month by month, the, number of pairs of rabbits is given by the sum of the rabbits in the two preceding months,, except for the 0th and the 1st months. The table below shows how the rabbit population, keeps increasing every month., Month, Pairs of Rabbits, 0, 1, 1, 1, 2, 2, 3, 3, 4, 5, 5, 8, 6, 13, 7, 21, 8, 34, 9, 55, 10, 89, 11, 144, 12, 233, 13, 377, 14, 610, 15, 987, 16, 1597, After one year, we have 233 rabbits. After just 16 months, we have nearly 1600 pairs, of rabbits., Clearly state the problem and the different stages of mathematical modelling in this situation., , Free Distribution by T.S. Government 2021-22
Page 378 :
Class-X Mathematics, , 368, , We will finish this chapter by looking at some interesting examples., Example-4. (Rolling of a pair of dice) : Deekshitha and Ashish are playing with dice. Then, Ashish said that, if she correctly guess the sum of numbers that show up on the dice, he would, give a prize for every answer to her. What numbers would be the best guess for Deekshitha., , A, , Solution :, , G, AN, , Step 1 (Understanding the problem) : You need to know a few numbers which have higher, chances of showing up., Step 2 (Mathematical description) : In mathematical terms, the problem translates to finding, out the probabilities of the various possible sums of numbers that the dice could show., , AN, , We can model the situation very simply by representing a roll of the dice as a random, choice of one of the following thirty six pairs of numbers., (1, 2), , (1, 3), , (1, 4), , (1, 5), , (1, 6), , (2, 1), , (2, 2), , (2, 3), , (2, 4), , (2, 5), , (2, 6), , (3, 1), (4, 1), (5, 1), (6, 1), , T,, TE, L, , (1, 1), , (3, 2), , (3, 3), , (3, 4), , (3, 5), , (3, 6), , (4, 2), , (4, 3), , (4, 4), , (4, 5), , (4, 6), , (5, 2), , (5, 3), , (5, 4), , (5, 5), , (5, 6), , (6, 2), , (6, 3), , (6, 4), , (6, 5), , (6, 6), , SC, ER, , The first number in each pair represents the number showing on the first dice, and the, second number is the number showing on the second dice., , Step 3 (Solving the mathematical problem) : Summing the numbers in each pair above, we, find that possible sums are 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. We have to find the probability, for each of them, assuming all 36 pairs are equally likely., We do this in the following table., , Sum, , 2, , 3, , 4, , 5, , 6, , 7, , 8, , 9, , 10, , 11, , 12, , Probability, , 1, 36, , 2, 36, , 3, 36, , 4, 36, , 5, 36, , 6, 36, , 5, 36, , 4, 36, , 3, 36, , 2, 36, , 1, 36, , Observe that the chance of getting a sum of a seven is, , 1, , which is larger than the, 6, , chances of getting other numbers as sums., , Free Distribution by T.S. Government 2021-22
Page 379 :
Mathematical Modelling, , 369, , Step 4 (Interpreting the solution) : Since the probability of getting the sum 7 is the highest, you, should repeatedly guess the number seven., , A, , Step 5 (Validating the model) : Toss a pair of dice a large number of times and prepare a, relative frequency table. Compare the relative frequencies with the corresponding probabilities., If these are not close, then possibly the dice are biased. Then, we could obtain data to evaluate, the number towards which the bias is., , G, AN, , Before going to the next try this exercise, we need some background information., , AN, , Not having the money you want when you need it, is a common experience for many, people. Whether it is having enough money for buying essentials for daily living, or for buying, comforts, we always require money. To enable the customers with limited funds to purchase, goods like scooters, refrigerators, televisions, cars, etc., a scheme known as an instalment scheme, (or plan) is introduced by traders., , T,, TE, L, , Sometimes a trader introduces an instalment scheme as a marketing strategy to allow, customers to purchase these articles. Under the instalment scheme, the customer is not required, to make full payment of the article at the time of buying it. She/he is allowed to pay a part of it at, the time of purchase and the rest can be paid in instalments, which could be monthly, quarterly,, half-yearly, or even yearly. Of course, the buyer will have to pay more in the instalment plan,, because the seller is going to charge some interest on account of the payment made at a later date, (called deferred payment)., , SC, ER, , There are some frequently used terms related to this concept. You may be familiar with, them. For example, the cash price of an article is the amount which a customer has to pay as full, payment of the article at the time it is purchased. Cash down payment is the amount which a, customer has to pay as part payment of the price of an article at the time of purchase., Now, try to solve the problem given below by using mathematical modelling., , T RY T HIS, , Ravi wants to buy a bicycle. He goes to the market and finds that the bicycle of his, choice costs `2,400. He has only `1,400 with him. To help, the shopkeepr offers to help, him. He says that Ravi can make a down payment of `1400 and pay the rest in monthly, instalments of `550 each. Ravi can either take the shopkeepers offer or go to a bank and, take a loan at 12% per annum simple interest. From these two opportunities which is the best, one to Ravi. Help him., , Free Distribution by T.S. Government 2021-22
Page 380 :
Class-X Mathematics, , 370, , A, , Answers, , 1., , (i), , 90, , G, AN, , E XERCISE - 1.1, (ii) 196, , (iii) 127, , E XERCISE - 1.2, , 6., , (iv), , 5 ≥ 7 ≥ 111 ≥ 13, , (ii) 22 ≥ 3 ≥ 13, (v) 17 ≥ 19 ≥ 23, , (i), , 420, 3, , (ii) 1139, 1, , (iv), , 216, 36, , (v) 22338, 9, , 6, , (iii) 32 ≥ 52 ≥ 17, , AN, , 2., , 22 ≥ 5 ≥ 7, , (i), , T,, TE, L, , 1., , (iii) 1800, 1, , E XERCISE - 1.3, 1., , 0.375, Terminating, , (ii) 0.5725, Terminating, , (iv), , 0.18 , Non-terminating, repeating, , (iii) 4.2, Terminating, (v) 0.064, Terminating, , (i), , Terminating, , (ii) Non-terminating, repeating, , (iii), , Non-terminating, repeating, , (iv) Terminating, , (v), , Non-terminating, , (vi) Terminating, , (vii), , Non-terminating, , (viii) Terminating, , (ix), , Terminating, , (x) Non-terminating, repeating, , 3., , (i), , 0.52, , 4., , (i), , Rational, Prime factors of q will be either 2 or 5 or both only, , (ii), , Not rational, , (iii), , Rational, Prime factors of q will also have a factor other than 2 or 5., , SC, ER, , 2., , (i), , (ii) 0.9375, , (iii) 0.115, , (iv) 32.08, , (v) 1.3, , E XERCISE - 1.5, 1., , (i), , 1, 2, , (vii) -2, , 1, 4, , (iii) -4, , (viii) 3, , (ix) 12, , (ii), , (iv) 0, , (v), , 1, 2, , (vi) 9, , Free Distribution by T.S. Government 2021-22
Page 381 :
Answers, (i) log 10, 1, , (ii) log28, 3, , (iii) log64 64, 1, , æ9ö, (iv) log çç ÷÷÷, çè 8 ø, , (ii) x + y , 1, , (iii) x + y + 2, , ( iv) 3x + 3y + 1, , (v) log 45, 3., , (i) x + y, , 4., , (i) 3, , (iii) 2 log x + 3log y + 4 log z, 3, (iv) 2 log p + 3log q - 4 log r, (v), log x - log y, 2, 7, , 7., , æ 3ö, log ççç ÷÷÷, è 2ø, 8., log 6, , 1, 3, , G, AN, , 6., , (ii) 7log 2 - 4 log 5, , E XERCISE - 2.1, Set, , (ii), , Not set, , (iv), , Set, , (v), , Set, , (i), , Î, , (ii), , Ï, , (v), , Î, , (vi), , 3., , (i), , x ÏA, , (ii), , dÎB, , (iii), , 1ÎN, , (iv) 8 Ï P, , 4., , (i), , False, , (ii), , False, , (iii), , True, , (iv) False, , 5., , (i), , B = {1, 2, 3, 4, 5}, , (ii), , C = {17, 26, 35, 44, 53, 62, 71, 80}, , (iii), , D = {2, 3, 5}, , (iv), , E = {B, E, T, R}, , (i), , A = {x : x is multiple of 3 & less than 13}, , (ii), , B = {x : x = 2a, a Î N, a < 6}, , (iii), , C = {x : x = 5a, a Î N, a < 5}, , (iv), , D = {x : x is square number and x < 10, x Î N}, , (i), , A = {51, 52, 53, .................., 98, 99}, , (ii), , B = {+2, , 2}, , (iii), , D = {L, O, Y, A}, , (iv), , E = {1, 3, 9, 19}, , (iii), , Not set, , Ï, , (iv), , 6., , 7., , Ï, , Î, , SC, ER, , 2., , (iii), , AN, , (i), , T,, TE, L, , 1., , A, , 2., , 371, , Free Distribution by T.S. Government 2021-22
Page 382 :
Class-X Mathematics, , 372, , 8., , (i), , , (c), , (ii), , , (a), , (iii), , (d), , (iv), , (b), , Yes, A Ç B & B Ç B are same, , 2., , AÇ ε=ε, A Ç A= A, , 3., , A , B = {2, 4, 8, 10}, , G, AN, , 1., , A, , E XERCISE - 2.2, , 4., , A È B=B, , 5., , A Ç B = {even natural number}, , AN, , B , A = {3, 9, 12, 15}, , T,, TE, L, , {2, 4, 6, ............}, , A Ç C = {odd natural numbers}, , A Ç D = {2, 3, 5, 7, 11........,97}, B Ç C= f, , B Ç D = {even natural number}, , C Ç D = {3, 5, 7, 11, ..............}, (i), , A , B = {3, 6, 9, 15, 18, 21}, , (ii), , A , C = {3, 9, 15, 18, 21}, , (iii), , A , D = {3, 6, 9, 12, 18, 21}, , (iv), , B , A = {4, 8, 16, 20}, , (v), , C , A = {2, 4, 8, 10, 14, 16}, , SC, ER, , 6., , (vi) D , A = {5, 10, 20}, (vii) B , C = {20}, , (viii) B , D = {4, 8, 12, 16}, (ix) C , B = {2, 6, 10, 14), (x) D , B = {5, 10, 15}, , Free Distribution by T.S. Government 2021-22
Page 383 :
Answers, 7., , (i), , 373, , False, because they have common element '3', , (ii) False, because the two sets have a common element 'a', (iii) True, because no common elements for the sets., (iv) True, because no common elements for the sets., , A, , E XERCISE - 2.3, Yes, equal sets, , 2., , (i) Equal (=), , (ii) Not equal ( ¹ ), , (iii) Equal (=), , (v) Not equal ( ¹ ), , (vi) Not equal ( ¹ ), , (vii) Not equal ( ¹ ), , (i) A = B, , (ii) A ¹ B, , (iii) A ¹ B, , 5., , (iv) A ¹ B, , AN, , 4., , (iv) Not equal ( ¹ ), , (i), , {1, 2, 3, ..... 10} ¹ {2, 3, 4, ..... 9}, , (ii), , x = 2x + 1 means x is odd, , (iii), , x is multiple of 15. So 5 does not exist, , (iv), , x is prime number but 9 is not a prime number, , (i), , {p}, {q}, {p, q}, { ε }, , (ii), , {x}, {y}, {z}, {x, y}, {y, z}, {z, x}, {x, y, z}, ε, , (iii), , {a}, {b}, {c}, {d}, {a, b}, {b, c}, {c, d}, {a, c}, {a, d}, {b, d}, {a, b, c},, , T,, TE, L, , 3., , G, AN, , 1., , SC, ER, , {b, c, d}, {a, b, d}, {a, c, d}, {a, b, c, d}, ε, , (iv), , ε , {1}, {4}, {9}, {16}, {1, 4}, {1, 9}, {1, 16}, {4, 9}, {4, 16}, {9, 16},, , {1, 4, 9}, {1, 9, 16}, {4, 9, 16}, {1, 4, 16}, {1, 4, 9, 16}, , (v), , ε , {10}, {100}, {1000}, {10, 100}, {100, 1000}, {10, 1000},, , {10, 100, 1000}, , E XERCISE - 2.4, 1., , (i), , Not empty, , (ii), , Empty, , (iii), , Empty, , (iv), , Empty, , (v), , Not empty, , 2., , (i), , Finite, , (ii), , Finite, , (iii), , Finite, , 3., , (i), , Finite, , (ii), , Infinite, , (iii), , Infinite, , Free Distribution by T.S. Government 2021-22, , (iv) Infinite
Page 384 :
Class-X Mathematics, , 374, , E XERCISE - 3.1, ,6, , (ii), , 7, , (iii), , ,6, , 1., , (a), , (i), , 2., , (i), , False (, , (ii), , False (Coefficient of x2 is , 4), , (iii), , True (For any constant term, degree is zero), , (iv), , False (It is not a polynomial at all), , (v), , False (Degree of a polynomial is not related with number of terms), , G, AN, , A, , 2, 2 is coefficient of x not a degree), , p(1) = 0, p ( , 1) = , 2, p(0) = , 1, p(2) = 7, p( , 2) = , 9, , 4., , Yes, , 2 and , 2 are zeroes of the polynomial x4-16, , 5., , Yes, 3 and , 2 are zeroes of the polynomial x2 , x , 6, , AN, , 3., , E XERCISE - 3.2, (i), , No zeroes, , (ii), , 1, , (iv), , 2, , (v), , 4, , 2., , (i), , 0, , 3., , (i), (iv), , 4., , (iii), , 3, , (vi), , 3, , T,, TE, L, , 1., , , 2, , 3, , (iii), , , 2, , 3, , 4, , 3, , (ii), , 3, 3, , (iii), , No zeroes, , , 4, 1, , (v), , , 1, 1, , (ii), , (iv) , 2, 2, ° ,4, , æ1ö, p ççç ÷÷÷ = 0 and p ( , 1) = 0, è4ø, , SC, ER, , E XERCISE - 3.3, 1., , 2., , 3., , (i) 4, , 2, , (ii), , (iv) 0, , 2, , (v), , (i) 4x2 , x , 4, , 1 1, ,, 2 2, 15, , 15, , (iii), , 3 ,1, ,, 2 3, , (vi), , ,1,, , 4, 3, , (ii), , 3x2 ,3 2x ∗1, , (iii), , x2 ∗ 5, , (iv) x 2 , x ∗1, , (v), , 4 x2 ∗ x ∗1, , (vi), , x 2 , 4 x ∗1, , (i) x2 , x , 2, , (ii), , x2 , 3, , (iii), , 4 x2 ∗ 3 x ,1, , (iv) 4 x2 , 8 x ∗ 3, 4., , , 1, +1 and 3 are zeros of the given polynomial ., , Free Distribution by T.S. Government 2021-22
Page 385 :
Answers, , 375, , E XERCISE - 3.4, (i), , Quotient = x , 3 and remainder = 7x , 9, , (ii), , Quotient = x2 + x , 3 and remainder = 8, , (iii), , Quotient = , x2 , 2 and remainder = , 5x + 10, , 2., , (i), , Yes, , 3., , , 1, , 1, , 4., , g(x) = x2 , x + 1, , 5., , (i), (iii), , (iii), , p(x) = 2x2 , 2x + 14, g(x) = 2, q(x) = x2 , x + 7, r(x) = 0, , p(x) = x3 + x2 + x + 1, g(x) = x2 , 1, q(x) = x + 1, r(x) = 2x + 2, , p(x) = x3 + 2x2 , x +2, g(x) = x2 , 1, q(x) = x + 2, r(x) = 4, , E XERCISE - 4.1, , 2., , (a), , Intersect at a point, , (b), , Coincident, , (c), , Parallel, , (a), , Consistent, , (b), , Inconsistent, , (c), , Consistent, , (d), , Consistent, , (e), , Consistent, , (f), , Inconsistent, , (g), , Inconsistent, , (h), , Consistent, , (i), , Inconsistent, , T,, TE, L, , 1., , No, , A, , Yes, , G, AN, , (ii), , (ii), , AN, , 1., , Number of pants = 1;, , Number of shirts = 0, , 4., , Number of Girls = 7;, , Number of boys = 3, , 5., , Cost of pencil = ` 3;, , Cost of pen = ` 5, , 6., , Length = 20 m;, , Width = 16 m, , 7., , (i), , SC, ER, , 3., , (ii), , (iii), , 6x , 5y , 10 = 0, 4x + 6y , 10 = 0, 6x + 9y , 24 = 0, , 8., , Length = 40 units;, , Breadth = 30 units, , 9., , Number of students = 16;, , Number of benches = 5, , E XERCISE - 4.2, 1., , Income of Ist person = ` 18000;, , Income of IInd person = ` 14000, , Free Distribution by T.S. Government 2021-22
Page 386 :
Class-X Mathematics, , 42 and 24, , 3., , Angles are 81º and 99º, , 4., , (i) Fixed charge = ` 40;, , 5., , 7, 9, , 6., , 60 km/h;, , 7., , 31º and 59º, , 8., , 659 and 723, , 9., , 40 ml and 60 ml, , 10., , ` 7200 and ` 4800, , G, AN, 1 ö÷, ÷, 4 ø÷, , (iii), , (4, 9), , (4, 5), , (iv), , (1, 2), , (v), , (3, 2), , (vii), , (3, 2), , (viii), , (1, 1), , (i), , Speed of boat = 8 km/h;, , Speed of streem = 3 km/h, , (ii), , Speed of train = 60 km/h;, , Speed of car = 80 km/h, , (iii), , Number of days by man = 18;, , Number of days by woman = 36, , T,, TE, L, , (ii), , æ ,1, çç ,, çè 2, , (i), , SC, ER, , 2., , (ii) ` 490, , 40 km/h., , E XERCISE - 4.3, 1., , Charge per km = ` 18, , A, , 2., , AN, , 376, , (vi), , æ1, çç ,, çè 2, , 1 ö÷, ÷, 3 ø÷, , E XERCISE - 5.1, 1., , 2., , (i), , Yes, , (ii), , Yes, , (iii), , No, , (iv), , Yes, , (v), , Yes, , (vi), , No, , (vii), , No, , (viii), , Yes, , (i), , 2x2 + x , 528 = 0 (x = Breadth), , (ii), , x2 + x , 306 = 0 (x = Smaller integer), , (iii), , x2 + 32x , 273 = 0 (x = Rohan's Age), , (iv), , x2 , 8x , 1280 = 0 (x = Speed of the train), , Free Distribution by T.S. Government 2021-22
Page 387 :
Answers, , 377, , E XERCISE - 5.2, (i), , , 2; 5, , (ii), , , 2;, , (iv), , 1 1, ;, 4 4, , (v), , (vii), , 1,, , (viii), , (iii), , , 2;, , 1, 1, ;, 10 10, , (vi), , , 6; 2, , , 1; 3, , (ix), , 13, 14, , 3., , 17, 18; , 17, , 18, , 4., , 5 cm, 12 cm, , 5., , Number of articles = 6; Cost of each article = 15, , 6., , 4 m; 10 m, , 7., , Base = 12 cm; Altitude = 8 cm, , 8., , 15 km, 20 km, , 9., , 20 or 40, , 10., , 9 kmph, , T,, TE, L, , AN, , 2., , E XERCISE - 5.3, 1., , (i), , SC, ER, , (iii), , ,1 ∗ 33, ,1, 33, ,, 4, 4, ,3, 2,, 5, ,1 ∗ 33, ,1, 33, ,, 4, 4, ,3, 2,, 5, 3 , 13, 3 ∗ 13, ,, 2, 2, , 2., , (i), , (iii), , 3., , (i), , 4., , 7 years, , 5., , Maths = 12, English = 18, , 6., , 120 m; 90 m, , 7., , 18, 12; , 18, , 12, , 8., , 40 kmph, , 9., , 15 hours,, , (or), , (ii), , , 3, ,, 2, , (iv), , , 1,, , (ii), , , 3, ,, 2, , (iv), , , 1,, , (ii), , 1, 2, , Maths = 13,, , 25 hours, , Free Distribution by T.S. Government 2021-22, , 8, 3, , , 3, 2, , ,5, , 3, 2, , ,5, , English = 17, , ,5, 2, , A, , 2, 3, , 3, 2, , 7,, , G, AN, , 1.
Page 388 :
Class-X Mathematics, , 378, , 10., , Speed of the passenger train = 33 kmph, Speed of the express train = 44 kmph, , 11., , 18 m; 12 m, , 12., , 3 seconds, , 13., , 13 sides;, , No, , (i), (ii), , Real roots do not exist, 2, 2, Equal roots;, ,, 3, 3, , (iii), , Distinct roots;, , 2., , (i), , k < °2 6, , 3., , Yes; 40 m; 20 m, , 4., , No, , 5., , Yes; 20 m; 20 m, , G, AN, , 1., , A, , E XERCISE - 5.4, , 3 ∗ 3 3, 3, ,, 2, 2, , k <6, , T,, TE, L, , AN, , (ii), , E XERCISE - 6.1, (i), , AP, , 2., , (i), , 10, 20, 30, 40, , SC, ER, , 1., , 3., , 4., , (ii), , Not AP, , (iii), , AP, , (ii), , , 2, , 2, , 2, , 2, , (iv), , 1, 1, , 1, , , 0,, 2, 2, , (iii), , 4, 1, , 2, , 5, , (v), , , 1.25, , 1.5, , 1.75, , 2, , (i), , a1 = 3; d = , 2, , (ii), , a1 = , 5;, , (iii), , 1, a1 < ;, 3, , (iv), , a1 = 0.6;, , (i), , Not AP, , (ii), , AP, next three terms = 4,, , (iii), , AP, next three terms = , 9.2, , 11.2, , 13.2, , d<, , 4, 3, , (iv), , Not AP, , d=4, d = 1.1, , 9, ,5, 2, , Free Distribution by T.S. Government 2021-22
Page 389 :
Answers, (iv), , AP, next three terms = 6, 10, 14, , (v), , AP, next three terms = 3 + 4, , (vi), , Not AP, , (vii), , AP, next three terms = , 16, , 20, , 24, , (viii), , AP, next three terms =, , (ix), , Not AP, , (x), , AP, next three term = 5a, 6a, 7a, , (xi), , Not AP, , (xii), , AP, next three terms =, , (xiii), , Not AP, , 2,3+6, , 2, , G, AN, , 72 ,, , 98, , AN, , 50 ,, , A, , ,1 ,1 ,1, ,, ,, 2, 2 2, , E XERCISE - 6.2, a8 = 28, , (ii), , d=2, , (iii), , (iv), , n = 10, , (v), , an = 3.5, , 2., , (i), , , 77, , (ii), , 22, , 3., , (i), , a2 = 14, , (ii), , a1 = 18;, , T,, TE, L, , (i), , a = 46, , a3 = 8, , (iii), , a2 =, , 13, ;, 2, , a3 = 8, , (iv), , a2 = , 2;, , a3 = 0;, , a4 = 2;, , a5 = 4, , (v), , a1 = 53;, , a3 = 23;, , a4 = 8;, , a5 = , 7, , SC, ER, , 1., , 2,3+5, , 379, , 4., , 16th term, , 5., , (i), , 6., , No, , 7., , 178, , 8., , 5, , 9., , 1, , 10., , 100, , 11., , 128, , 12., , 60, , 13., , 13, , 14., , AP = 4, 10, 16, ...., , 15., , 158, , 16., , , 13, , 8, , 3, , 17., , 11, , 34, , (ii), , 27, , Free Distribution by T.S. Government 2021-22
Page 390 :
Class-X Mathematics, , 380, , E XERCISE - 6.3, , 180, , 5505, , (iv), , 33, 13, <1, 20, 20, , (ii), , 286, , (iii), , , 8930, , 245, , 2., , (i), , 2093, 1, < 1046, 2, 2, , 3., , (i), , n = 16 , 440, , 4., 5., 6., 7., 8., , (iii), a = 4, S12 = 246, (iv), d = –1, a10 = 8, (v), n = 5; a5 = 34, (vi), n = 7; a = , 8, (vii), a=4, n = 38;, S38 = 6973, 5610, n2, (i), 525, (ii), , 465, S1 = 3;, S2 = 4;, a2 = 1;, a3 = , 1;, an = 5 , 2n, 4920, 10., 160, 140, 120, 100, 80, 60, 40, 234, 12., 143, 13., 16, , 7, d < , S13 < 273, 3, , T,, TE, L, , AN, , G, AN, , (ii), , A, , (i), , 9., 11., , (ii), , (iii), , 1., , a10 = , 15, , 14., , 370, , E XERCISE - 6.4, (i), , No, , (iii), , Yes, , 2., , (i), , 4, 12, 36, ...., , (ii), , 5,, , (iii), , 81, , 27, 9, ...., , (iv), , (i), , Yes; 32, 64, 128, , (iii), , No, , (vi), (viii), , SC, ER, , 1., , 3., , 4., , (ii), , No, , 5 5, ,, ,..., 5 25, , 1 1 1, ,, ,, , ......, 64 32 16, , , 1 1 ,1, ,, ,, 24 48 96, (iv) Yes; -54, -162, -148, (v) No, , (ii), , Yes,, , Yes; , 81, 243, , 729, , (vii), , Yes;, , Yes; , 16, 32 2, ,128, , (ix), , 1 1 1, ,, ,, , ......, x2 x3 x4, Yes; 0.0004, 0.00004, 0.000004, , ,4, , Free Distribution by T.S. Government 2021-22
Page 391 :
Answers, , 381, , (ii), , r = , 3;, , an = 2( , 3)n-1, , (iii), , r = 3;, , an = ( , 1)(3)n-1, , (iv), , 2, r= 5;, , æ 2 ö÷n,1, an < 5çç ÷÷, çè 5 ø, , 2., , a10 = 510;, , an = 5n, , 3., , (i), , 1, 34, , 4., , (i), , 5, , 5., , 3 ´ 210 = 3072, , (ii), , (ii), , ,4, 34, , 12, , (iii), , 6., , 9 3, , , 1, ...., 4 2, , 7, , 7., , T,, TE, L, , E XERCISE - 7.1, , G, AN, , (i), , æ 1 ö÷n,1, an < 3çç ÷÷, çè 2 ø, , AN, , 1., , 1, r= ;, 2, , A, , E XERCISE - 6.5, , 5, , 2 a2 ∗ b2, , 1., 2., , (i), 39, , 3., 5., , Points are not collinear 4. AB = BC = 37 ; AC = 2, AB = BC = CA = 2a (vertices of equilateral triangle), , 6., , AB = CD =, , 7., , AB = BC = CD = DA =, , 8., , (i), , 9., , ( , 7, 0), , 10., , 7 or , 5, , 11., , 3 or , 9, , 12., , 4 5 units, , 13., 14., , AB = 5, BC = 10, AC = 15, AB + BC = AC = 15 (can not form the triangle), x + 13y – 17 = 0, , 15., 16., , AB = BC = CD = DA = 3 2 AC = BD = 6 (vertices of a square), x–y=2, , (ii), , 2 2, , 4 2, , (iii), , 5 2, , SC, ER, , 313 , BC = AD = 104 , AC ¹ BD (vertices of parallogram), , Square, , 9 0 , AC ¹ BD (vertices of a thombus), 72 Sq. units, (ii), Rectangle, (iii), Parallelogram, , E XERCISE - 7.2, 1., , (1, 3), , (iv), , 2., , æ ,5 ÷ö, çç2, ÷, çè 3 ÷ø, , Free Distribution by T.S. Government 2021-22, , and, , æ ,7 ÷ö, çç0, ÷, çè 3 ÷ø
Page 393 :
Answers, , 383, , E XERCISE - 8.3, 1., , 1: 4, , 2 ,1, 1, , 2., , 4., , 96 cm2, , 12., , 1: 2, , 6., , 3.5 cm, , 8., , 6 7 m, , 9., , 13 m, , 2., , (i), , One, , (ii), , Secant of a circle, , (iii), , Infinite, , (iv), , Point of contact, , (v), , Infinite, , (vi), , Two, , 4., , 12 cm, , (v), , c, , PQ = 12 cm, , E XERCISE - 9.2, (i), , d, , 2., , 8 cm, , 5., , 8 cm each, , (ii), , a, , (iii), , b, , (iv), , 4., , AB = 15 cm, AC = 9 cm, , 6., , 2 5 cm, , T,, TE, L, , 1., , AN, , 1., , G, AN, , E XERCISE - 9.1, , A, , E XERCISE - 8.4, , 9., , a, , Two, , E XERCISE - 9.3, (i), , 2., , 28.5 cm2, , (ii), , 285.5 cm2, , 88.368 cm2, , 3., , 1254.96 cm2, , 4., , 57 cm2, , 5., , 10.5 cm2, , 6., , 6.125 cm2, , 7., , 102.67 cm2, , 8., , 57 cm2, , SC, ER, , 1., , E XERCISE - 10.1, 1., , 5500 cm2, , 2. 184800 cm2, , 3. 264 c.c., , 4., , 1:2, , 5. 21, , 7., , 21,175 cm3, , 8. 188.4 m2, , 9. 37 cm, , E XERCISE - 10.2, 1., , 103.62 cm2, , 2., , 1156.57 cm2, , 3., , 219.8 mm2, , 4., , 160 cm2, , 5., , ` 827.20, , 6., , 2:3:1, , Free Distribution by T.S. Government 2021-22
Page 394 :
Class-X Mathematics, , 384, , 7., , æο, ö, x 2 çç ∗ 6÷÷÷ sq. units, çè 4, ø, , 8. 374 cm2, , E XERCISE - 10.3, 693 kg, 89.83 cm3, , 2. Height of the cone(h) = 21 cm; Surface area of the toy = 795.08 cm2, 4. 616 cm3, 5. 309.57 cm3, , 6., , 150, , 7. 523.9 cm3, , G, AN, , A, , 1., 3., , E XERCISE - 10.4, 2.74 cm, , 2., , 12 cm, , 3., , 2.5 m, , 4., , 5m, , 5., , 10, , 6., , 400, , 7., , 100, , 8., , 672, , AN, , 1., , E XERCISE - 11.1, 15, ;, 17, , 8, ;, 17, , tan A =, , 15, 8, , 7, cos π =, ;, 25, , tan π =, , 24, 7, , (iii), , 1, , (iii), , c, , 1., , sin A =, , 2., , 527, 168, , 4., , sin A =, , 5, ;, 13, , tan A =, , 5, 12, , 5., , sin A =, , 4, ;, 5, , cos A =, , 3, 5, , 7., , (i), , 49, 64, , (ii), , 8 ∗ 113, 7, , 8., , (i), , 1, , (ii), , 0, , (ii), , 3, 4 2, , T,, TE, L, , cos A =, , SC, ER, , 3., , E XERCISE - 11.2, 1., , (i), , 2, , (iv), , 2, , (v), , 1, , 2., , (i), , c, , (ii), , d, , 3., , 1, , 4., , Yes, , Free Distribution by T.S. Government 2021-22
Page 395 :
Answers, 5., , QR = 6 3 cm;, , PR = 12 cm, , 6., , Ð YZX = 60º;, , Ð YXZ = 30º, , (i), , 1, , (ii), , 0, , (iv), , 1, , (v), , 1, , 6., , cos 15º + sin 25º, , 3., , A = 36º, , (iii), , E XERCISE - 11.4, (i), , 6., , 1, , 2, , (ii), , 2, , (iii), , 1, , 8., , 1, , 9., , 1, p, , E XERCISE - 12.1, , AN, , 1., , 0, , A, , 1., , Not true, , G, AN, , E XERCISE - 11.3, , 7., , 385, , 15 m, , 2., , 6 3 m, , 3., , 4m, , 4., , 30º, , 5., , 34.64 m, , 6., , 4 3m, , 7., , Length of ladder=8.32m; distance between feet of wall and ladder=4.16m, , 8., , 300 3 m, , T,, TE, L, , 1., , 9., , 15 m, , 10., , 7.5 cm2, , E XERCISE - 12.2, , Height of the tower = 5 3 m;, , Width of the road = 5 m, , 2., , 32.908 m, , 3., , 1.464 m, , 4., , 19.124 m, , 5., , 7.608 m, , 6., , 10 m, , 7., , 51.96 feets;, , 9., , 200 m/sec., , 10., , 1:3, , SC, ER, , 1., , 30 feets, , 8. 6 m, , E XERCISE - 13.1, 1., , (i), , 1, , (ii), , 0, Impossible event, , (iv), , 1, , (v), , 0, 1, , 2., , (i), , Yes, , (ii), , Yes, , (iii), , 3., , 0.95, , 4., , (i), , 0, , 5., , 1 1, , , 1, 0, 13 3, , 6., , 0.008, , 7., , (i), , 1, 2, , Yes, , (ii), , Free Distribution by T.S. Government 2021-22, , (iii), , 1, Sure event, , (iv), , Yes, , (ii), , 1, , 1, 2, , (iii), , 1, 2, , 8., , 1, 26
Page 396 :
Class-X Mathematics, , 386, , E XERCISE - 13.2, (i), , 3, 8, , (ii), , 5, 8, , 2., , (i), , 5, 17, , (ii), , 8, 17, , 3., , (i), , 5, 9, , (ii), , 17, 18, , 4., , 5, 13, , 5., , (i), , 6., , (i), , 3, 26, , (iv), , 1, 52, , 8., , 11, 12, , 10., , (i), , (ii), , 1, 2, , (ii), , 3, 13, , (iii), , 1, 26, , (v), , 1, 4, , (vi), , 11., , 11, 84, , 13., , (i), , 14., , 3, 4, , A, , 1, 8, , 1, 5, , (ii) (a), , 1, 4, , 9, 10, , (ii) (a), 12., , (i), , 1, , 1, 52, , 0, , 1, 5, , (ii), , 15, 19, , 1, 10, , (b), , 1, 5, , (ii), , 5, 36, , (i), , 31, 36, , 1 2, 3 4 5 6 5 4 3 2 1, ,, ,, ,, ,, ,, ,, , ,, ,, ,, 36 36 36 36 36 36 36 36 36 36 36, , 15., , (iv), , AN, , (b), , 9. (i), , 3, 4, , (iii), , T,, TE, L, , (i), , 13, 17, , SC, ER, , 7., , (iii), , G, AN, , 1., , 25, 36, , (ii), , (ii) Yes, , 11, 36, , E XERCISE - 14.1, 1., , 8.1 plants. We have used direct method because numerical values of xi and fi are small., , 2., , ` 313, , 3., , f = 20, , 4., , 75.9, , Free Distribution by T.S. Government 2021-22
Page 397 :
Answers, 5., , 22.31, , 6., , ` 211, , 8., , 49 days, , 9., , 69.43%, , 7., , 387, , 0.099 ppm, , E XERCISE - 14.2, Mode = 36.8 years, Mean = 35.37 years, Maximum number of patients admitted in the, , A, , 1., , admitted to the hospital is 35.37 years., , G, AN, , hospital are of the age 36.8 years (approx.), while on an average the age of a patient, , 65.625 hours, , 3., , Modal monthly expenditure = ` 1847.83, Mean monthly expenditure = ` 2662.5., , 4., , Mode : 30.6, Mean = 29.2. Most states/U.T. have a student teacher ratio of 30.6 and, , T,, TE, L, , on an average, this ratio is 29.2., , AN, , 2., , 5., , Mode = 4608.7 runs., , 6., , Mode = 44.7 cars, , E XERCISE - 14.3, , Median = 137 units, Mean = 137.05 units, Mode = 135.76 units., , SC, ER, , 1., , The three measures are approximately the same in this case., , 2., , x = 8, y = 7, , 3., , Median age = 35.76 years, , 4., , Median length = 146.75 mm, , 5., , Median life = 3406.98 hours, , 6., , Median = 8.05, Mean = 8.32, Modal size = 7.88, , 7., , Median weight = 56.67 kg, , Free Distribution by T.S. Government 2021-22
Page 398 :
388, , Class-X Mathematics, , E XERCISE - 14.4, , 2., , Cumulative frequency, , Less than 300, , 12, , Less than 350, , 26, , Less than 400, , 34, , Less than 450, , 40, , Less than 500, , 50, , Draw ogive by plotting the points :, (300, 12), (350, 26), (400, 34),, (450, 40) and (500, 50), , A, , Daily income (in `), , G, AN, , 1., , Draw the ogive by plotting the points : (38, 0), (40, 3), (42, 5), (44, 9), (46, 14),, n, =17.5. Locate the point on the ogive whose, 2, ordinate is 17.5. The x-coordinate of this point will be the median., , Production yield (kg/ha), , Cumulative frequency, , T,, TE, L, , 3., , AN, , (48, 28), (50, 32) and (52, 35). Here, , 100, , More than or equal to 55, , 98, , More than or equal to 60, , 90, , More than or equal to 65, , 78, , More than or equal to 70, , 54, , More than or equal to 75, , 16, , SC, ER, , More than or equal to 50, , Now, draw the ogive by plotting the points : (50, 100), (55, 98), (60, 90), (65, 78),, (70, 54) and (75, 16)., , Free Distribution by T.S. Government 2021-22
Page 399 :
389, , Note to the Teachers, Dear teachers,, , AN, , G, AN, , A, , The State Government has decided to revise the curriculum of all the subjects based on, State Curriculum Framework (SCF-2011). The framework emphasises that all children must learn, and the mathematics learnt at school must be linked to the life and experience of them. The, NCF-2005, the position paper on Mahtematics of the NCERT and the Govt. emphasise building, understanding and developing the capability, exploration and inclination to mathematize experiences., This would become more possible at the secondary level. We have consolidated the basic framework, of mathematics in class-IX and now we are at level of completion of secondary level of mathematics., In previous classes, we have encouraged the students for greater abstraction and formal mathematical, formulation. We made them to deal with proofs and use mathematical language. It is important to, recognise that as we go forward the language in which mathematical arguments and statements- are, presented would become even more symbolic and terse. It is therefore important in this class to help, children become comfortable and competent in using mathematical ideas. In class-X, we will make, all such idea at level of total abstraction., , SC, ER, , T,, TE, L, , It would be important to consider all the syllabi from class-VI to X while looking at teaching, class X. The nature and extent of abstraction and use of mathematical language is gradually increasing., The program here would also become axiomatic and children must be slowly empowered to deal with, that. One of the major difficulties children have in moving forward and learning secondary mathematics, is their inability to deal with the axiomatic nature and language of symbols. They need to have an, apportunity to learn and develop these perspectives by engaging with, as a team. Peer support in, overcoming the difficulties is critical and it would be important to put them in a group to think, discuss, and solve problems. When children will learn such things in class-X, it will be helpful for them in future, mathematical learning also., The syllabus is based on the structural approach, laying emphasis on the discovery and, understanding of basic mathematical concepts and generalisations. The approach is to encourage, participation and discussion in classroom activities., The syllabus in textbook of class-X Mathematics has been divided broadly into six areas, Number System, Arithmetic, Algebra, Geometry, Trigonometry, Statistics and Coordinate Geometry., Teaching of the topics related to these areas will develop the skills such as problem solving, logical, thinking, mathematical communication, representing data in various forms, using mathematics as, one of the disciplines of study and also in daily life situations., This text book attempts to enhance this endeavor by giving higher priority and space to, opportunities for contemplations. There is a scope for discussion in small groups and activities, required for hands on experience in the form of ‘Do this’ and ‘Try this’. Teacher’s support is needed in, setting the situations in the classroom and also for development of interest in new book., Exercises in ‘Do This’ and ‘Try This’ are given extensively after completion of each concept., The problems which are given under ‘Do This’ are based on the concept taught and ‘Try This’ problems, , Free Distribution by T.S. Government 2021-22
Page 400 :
390, , Class-X Mathematics, , are intended to test the skills of generalization of facts, ensuring correctness and questioning. ‘Think,, Discuss and Write’ has given to understand the new concept between students in their own words., Entire syllabus in class-X Mathematics is divided into 14 chapters with an appendix, so that, a child can go through the content well in bit wise to consolidate the logic and enjoy the learning of, mathematics. Colourful pictures, diagrams, readable font size will certainly help the children to adopt, the contents and care this book as theirs., , G, AN, , A, , Chapter-1 : Real number, we are discussing about the exploration of real numbers in which, the brief account of fundamental theorem of arithmetic, rational numbers their decimal expansion, and non-terminating recurring rational numbers has given. Here we are giving some more about the, irrational numbers. In this chapter, first time we are introducing logarithms in this we are discussing, about basic laws of logarithms and their application., , AN, , Chapter-2 : Sets, this is entirely a new chapter at the level of secondary students. In old, syllabus it was there but here we are introducing it in class X. This chapter is introduced with wide, variety of examples which are dealing about the definition of sets, types of set, Venn diagrams,, operations of sets, differences between sets. In this chapter we dealt about how to develop a common, understanding of sets. How can you make set of any objects?, , T,, TE, L, , Chapter-3 : Polynomials, we are discussing about the fact "what are polynomials?" and, degree and value of polynomials come under it. This time we look at the graphical representation of, linear equations and quadratic equations. Here we are taking care of zeros and coefficients of a, polynomial & their relationship. We also start with cubic polynomials and division algorithm of, polynomials., , SC, ER, , Chapter-4 : Pair of linear equations in two variables, we start the scenario with discussing, about finding of unknown quantities and use of two equations together. Solution of pair of linear, equations in two variables with the help of graphical and algebraic methods has done. Here we have, illustrated so many examples to understand the relation between coefficients and nature of system, of equations. Reduction of equation to two variable linear equation has done here., The problem is framed in such a way to emphasis the correlation between various chapters, within the mathematics and other subjects of daily life of human being. This chapter links the ability, of finding unknown with every day experience., Chapter-5 : Quadratic equations, states the meaning of quadratic equation and solution of, quadratic equation with the factorizations completion of squares. Nature of roots is defined here with, the use of parabola., Chapter-6 : Progressions, we have introduced this chapter first time on secondary level. In, this chapter use are taking about arithmetic progressions and geometric progressions. How the, terms progressing arithmetically and geometrically in progressions discussed. The number of terms,, nth terms, sum of terms are stated in this chapter., Chapter-7 : Coordinate geometry, deals with finding the distance between two points on, cartesion plane, section formula, centroid of a triangle and tsisectional points of a line. In this, we are, also talking about area of the triangle on plane and finding it with the use of 'Heron's formula'. The, slope on straight line is also introduced here., , Free Distribution by T.S. Government 2021-22
Page 401 :
Note to the Teachers, , 391, , A, , We are keeping three chapters (8, 9, 10) in X mathematics book and all of them are having, emphasis on learning geometry using reasoning, intuitive understanding and insightful personal, experience of meanings. If helps in communicating and solving problems and obtaining new relations, among various plane figures. In chapter 9 Tangents and Secants to a circle, we have introduced the, new terms caked tangent and secant with their properties. We also discussed about the segment, and area of that which is formed by secant. Menstruations are presented in combination of solids, and finding of their volume and area., , G, AN, , We are keeping two new chapters (11 & 12) at second level for the first time. The applications, of triangles are used with giving relation with the hypotenuse, perpendicular and base. These chapters, are the introduction of trigonometry which have very big role in high level studies and also in, determination of so many measurements. Applications of trigonometry are also given with brief idea, of using triangle., , AN, , Chapter-13 : Probability, is little higher level chapter than the last chapter which we have, introduced in class IX. Here we are taking about different terms of probability by using some daily life, situations., , T,, TE, L, , Chapter-14 : Statistics, deals with importance of statistics, collection of statistical grouped, data, illustrative examples for finding mean, median and mode of given grouped data with different, methods. The ogives are also illustrated here again. In appendix, mathematical modeling is given, there with an idea about the models and their modeling methods., The success of any course depends not only on the syllabus but also on the teachers and, the teaching methods they employ. It is hoped that all teachers are concerned with the improving of, mathematics education and they will extend their full cooperation in this endeavour., , SC, ER, , The production of good text books does not ensure the quality of education, unless the, teachers transact the curriculum in a way as it is discussed in the text book. The involvement and, participation of learner in doing the activities and problems with an understanding is ensured., Students should be made to digest the concepts given in “What we have discussed”, completely. Teachers may prepare their own problems related to the concepts besides solving the, problems given in the exercises. So therefore it is hoped that the teachers will bring a paradigm shift, in the classroom process from mere solving the problems in the exercises routinely to the conceptual, understanding, solving of problems with ingenity., Teaching learning strategies and the expected learning outcomes, have been developed, class wise and subject-wise based on the syllabus and compiled in the form of a Hand book to guide, the teachers and were supplied to all the schools. With the help of this Hand book the teachers are, expected to conduct effective teaching learning processes and ensure that all the students attain the, expected learning outcomes., “Good luck for happy teaching”, , Free Distribution by T.S. Government 2021-22
Page 402 :
392, , Syllabus, I. NUMBER SYSTEM (23 PERIODS), Real numbers (15 periods), • More about rational and irrational numbers., • Euclid Division algorithm., • Fundamental theorem of Arithmetic - Statements., • Proofs of results - irrationality of 2, 3 etc. and decimal expansions of rational numbers, , •, •, •, •, , in terms of terminating / non-terminating recurring decimals and vice versa., Properties of real numbers (after reviewing lookdone earlier and after illustrating and, motivating through examples), Introduction of logarithms, Conversion of a number in exponential form to a logarithmic form, Properties of logarithms loga a = 1; loga 1 = 0, Laws of logarithms, log xy = log x + log y; log, , (ii), , x, = log x - log y;, y, , log xn = n log x, a log a N = N, , Standard base of logarithm and use of logarithms in daily life situations (not meant for, examination), , T,, TE, L, , •, , AN, , •, , G, AN, , A, , (i), , Sets (8 periods), •, •, •, •, •, •, , Sets and their representations, Empty set, finite and infinite sets, universal set, Equal sets, subsets, subsets of set of real numbers (especially intervals and notations), Venn diagrams and cardinality of sets, Basic set operations - union and intersection of sets, Disjoint sets, difference of sets, , SC, ER, , II. ALGEBRA (46 PERIODS), (i), , (ii), , Polynomials (8 periods), • Zeroes of a polynomial, • Geometrical meaning of zeroes of linear, quadratic and cubic polynomials using graphs., • Relationship between zeroes and coefficients of a polynomial., • Simple problems on division algorithm for polynomials with integral coefficients, Pair of Linear Equations in Two Variables (15 periods), • Forming a linear equation in two variables through illustrated examples., • Graphical representation of a pair of linear equations of different possibilities of solutions, •, •, , (iii), , / in consistency., Algebraic conditions for number of solutions, Solution of pair of linear equations in two variables algebraically - by Substitution, by, elimination., Simple and daily life problems on equations reducible to linear equations., , •, Quadratic Equations (12 periods), • Standard form of a quadratic equation ax2 + bx + c = 0, a ¹ 0., • Solutions of quadratic equations (only real roots) by factorisation, by completing the, square and by using quadratic formula., , Free Distribution by T.S. Government 2021-22
Page 403 :
Syllabus, • Relationship between discriminant and nature of roots., • Problems related to day-to-day activities., Progressions (11 periods), • Definition of Arithmetic Progression (A.P), • Finding nth term and sum of first ‘n’ terms of A.P., • Geometric Progression (G.P.), • Find nth term of G.P., , III. GEOMETRY (33, , PERIODS), , •, •, •, •, •, , •, , SC, ER, , •, , in distinct points, the other two sides are divided in the same ratio., (Motivate) If a line divides two sides of a triangle in the same ratio, then the line is, parallel to the third side., (Motivate) If in two triangles, the corresponding angles are equal, their corresponding, sides are proportional and the triangles are similar (AAA)., (Motivate) If the corresponding sides of two triangles are proportional, their corresponding, angles are equal and the two triangles are similar (SSS)., (Motivate) If one angle of a triangle is equal to one angle of another triangle and the sides, including these angles are proportional, the two triangles are similar (SAS)., (Prove) The ratio of the areas of two similar triangles is equal to the ratio of the squares, on their corresponding sides., (Motivate) If a perpendicular is drawn from the vertex of the right angle to the hypotenuse,, the triangles on each side of the perpendicular are similar to the whole triangle and to, each other., (Prove) In a right triangle, the square on the hypothenuse is equal to the sum of the, squares on the other two sides., (Prove) In a triangle, if the square on one side is equal to sum of the squares on the other, sides, the angles opposite to the first side is a right triangle., (Construction) Division of a line segment using Basic proportionality Theorem., (Construction) A triangle similar to a given triangle as per given scale factor., , AN, , •, , G, AN, , Similar Triangles (18 periods), • Similar figures difference between congruency and similarity., • Properties of similar triangles., • (Prove) If a line is drawn parallel to one side of a triangle to intersect the other two sides, , T,, TE, L, , (i), , A, , (iv), , 393, , (ii), , •, •, Tangents and secants to a circle (15 periods), • Difference between tangent and secant to a circle, • Tangents to a circle motivated by chords drawn from points coming closer and closer to, •, •, •, •, •, •, , the point, (Prove) The tangent at any point on a circle is perpendicular to the radius through the, point contact., (Prove) The lengths of tangents drawn from an external point to a circle are equal., (Construction) A tangent to a circle through a point given on it., (Construction) Pair of tangents to a circle from an external point., Segment of a circle made by the secant., Finding the area of minor/major segment of a circle., , Free Distribution by T.S. Government 2021-22
Page 404 :
Class-X Mathematics, , 394, , COORDINATE GEOMETRY, •, •, •, •, •, , Review the concepts of coordinate geometry by the graphs of linear equations., Distance between two points P(x1, y1) and Q(x2, y2), , PQ = ( x2 - x1 ) 2 + ( y2 - y1 ) 2, Section formula (internal division of a line segment in the ratio m : n)., Area of triangle on coordinate plane., Slope of a line joining two points, , TRIGONOMETRY (23, , (i), , Trigonometry (15 periods), • Trigonometric ratios of an acute angle of a right angled triangle i.e. sine, cosine, tangent,, , VI., (i), , AN, , cosecant, secant and cotangent., Values of trigonometric ratios of 0°, 30°, 45°, 60° and 90°(with proofs)., Relationship between the ratios and trigonometric ratios for complementary angles., Trigonometric Identities., (i) sin2 A + cos2 A = 1, (ii) 1 + tan2 A = sec2 A, (iii) cot2 A + 1 = cosec2 A, , Applications of Trigonometry (8 periods), • Angle of elevation, angle of depression., • Simple and daily life problems on heights and distances, • Problems involving not more than two right triangles and angles of elevation / depression, , T,, TE, L, , (ii), , G, AN, , V., , •, •, •, , PERIODS), , A, , IV., , confined to 30o, 45o and 60o., MENSURATION (10 PERIODS), , Surface Areas and Volumes, • Problems on finding surface area and volumes of combinations of any two of the following, •, , i.e. cubes, cuboids, right circular cylinders, cones spheres and hemispheres., Problems involving converting one type of metallic solid into anothers and finding volumes, and other mixed problems involving not more than two different solids., , VII. DATA HANDLING (25 PERIODS), Statistics, , SC, ER, , (i), , •, •, •, , Revision of mean, median and mode of ungrouped (frequency distribution) data., Understanding the concept of Arithmetic mean, median and mode for grouped (classified), data., Simple problems on finding mean, median and mode for grouped/ungrouped data with, different methods., Usage and different values of central tendencies through ogives., , •, (ii), Probability (10 periods), • Revision of concept and definition of probability., • Simple problems (day to day life situation) on single events using set notation., • Concept of complementary events., APPENDIX, Mathematical Modeling (8 periods), • Concept of Mathematical modelling, • Discussion of broad stages of modelling-real life situations (Simple interest, Fair, installments payments etc. ....), , Free Distribution by T.S. Government 2021-22
Page 405 :
395, , Academic Standards -, , High School, , 1. Problem Solving, , Content, , G, AN, , Areas of Mathematics, , A, , Academic Standards : Academic standards are clear statements about what students, must know and be able to do. The following are categories on the basis of which we lay, down academic standards., , Using concepts and procedures to solve mathematical, problems like following:, a. Kinds of problems :, , SC, ER, , T,, TE, L, , AN, , Problems can take various forms- puzzles, word, problems, pictorial problems, procedural problems,, reading data, tables, graphs etc., • Reads problems., • Identifies all pieces of information/data., • Separates relevant pieces of information., • Understanding what concept is involved., • Recalling of (synthesis of) concerned procedures,, formulae etc., • Selection of procedure., • Solving the problem., • Verification of answers of raiders, problem based, theorems., b. Complexity :, , The complexity of a problem is dependent on• Making connections( as defined in the connections, section)., • Number of steps., • Number of operations., • Context unraveling., • Nature of procedures., , 2. Reasoning Proof, , • Reasoning between various steps (involved invariably, conjuncture)., • Understanding a nd making, generalizations and conjectures, , Free Distribution by T.S. Government 2021-22, , mathematical
Page 406 :
Class-X Mathematics, , 396, , • Understands and justifies procedures, • Examining logical arguments., • Understanding the notion of proof, • Uses inductive and deductive logic, , • Writing and reading, expressing mathematical, notations (verbal and symbolic forms), Example :, , G, AN, , 3. Communication, , A, , • Testing mathematical conjectures, , 3+4=7, n1+n2= n2+n1, Sum of angles in triangle = 180°, , • Connecting concepts within a mathematical domainfor example relating adding to multiplication, parts of, a whole to a ratio, to division. Patterns and symmetry,, measurements and space., , T,, TE, L, , 4. Connections, , AN, , • Creating mathematical expressions, , • Making connections with daily life., • Connecting mathematics to different subjects., • Connecting concepts of different mathematical, domains like data handling and arithmetic or arithmetic, and space., , SC, ER, , • Connecting concepts to multiple procedures., , 5. Visualization &, Representation, , • Interprets and reads data in a table, number line,, pictograph, bar graph, 2-D figures, 3- D figures,, pictures., • Making tables, number line, pictograph, bar graph,, pictures., • Mathematical symbols and figures., , Free Distribution by T.S. Government 2021-22