Page 1 :
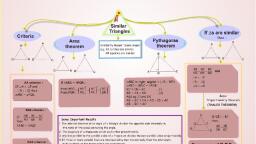
Key Notes, Chapter-06, , Triangles, •, , Similar Triangles: Two triangles are said to be similar if their corresponding angles are, , equal and their corresponding sides are proportional., , •, , All congruent figures are similar but the converse is not true., , •, , Two polygons with same number of sides are similar, if, , •, , •, , (i), , Their corresponding angles are equal and, , (ii), , Their corresponding sides are in the same ration (i.e., proportion)., , Criteria for Similarity: in and ∆ABCand ∆DEF, , (i), , AAA Similarity: ∆ABC ~ ∆DEF When ∠A = ∠D, ∠B = ∠E and ∠C = ∠F, , (ii), , SAS Similarity: ∆ABC ∼ ∆DEF when, , (iii), , SSS Similarity: ∆ABC ~ ∆DEF,, , AB BC, =, and ∠B = ∠E, DE EF, , AB AC BC, =, =, DE DF EF, , The proof of the following theorems can be asked in the examination:, , (i), , Basic Proportionality Theorem: If a line is drawn parallel to one side of a triangle to, , intersect the other sides in distinct points, the other two sides are divided in the same, , ratio., , (ii), , The ratio of the areas of two similar triangles is equal to the square of the ratio of their, , corresponding sides., , (iii), , Pythagoras Theorem: In a right triangle, the square of the hypotenuse is equal to the, , sum of the squares of the other two sides., , (iv), , Converse of Pythagoras Theorem: In a triangle, if the square of one side is equal to, , the sum of the squares of the other two sides then the angle opposite to the first side is, , a right angle., •, , Right Angled Triangle:
Page 2 :
Key Notes, (i), , If a perpendicular is drawn from the vertex of the right angle of a right triangle to the, , hypotenuse, then the triangles on both sides of the perpendicular are similar to the, , Whole triangle and also to each other., , (ii), , In the right triangle, the square of the hypotenuse is equal to the sum of the square of, , the other two sides (Pythagoras Theorem)., , (iii), , If in a triangle, square of one side is equal to the sum of the squares of the other two, , sides, then the angle opposite to the first side is a right angle., , •, , Thales Theorem: If a line is drawn parallel to one side of a triangle to intersect the other two, , sides in distinct points, then the other two sides are divided in the same ratio (Basic, , Proportionally Theorem or Thales Theorem)., , •, , If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the, , third side.