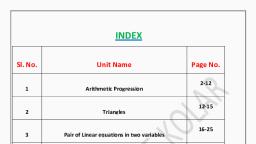
Page 4 :
EXAMINATION PATTERN, Class- X, Session: 2021-22, TERM II, •, •, •, •, •, •, •, , Time Allowed: 2 hours, Maximum Marks: 40, The question paper consists of 14 questions divided into 3 sections A, B, C., All questions are compulsory., Section A comprises of 6 questions of 2 marks each. Internal choice has been, provided in two questions., Section B comprises of 4questions of 3 marks each. Internal choice has been, provided in one question., Section C comprises of 4 questions of 4 marks each. An internal choice has been, provided in one question. It contains two case study-based questions., , COURSE STRUCTURE, CLASS –X (2021-22), SECOND TERM, , UNIT-ALGEBRA, 1. QUADRATIC EQUATIONS, (10) Periods, Standard form of a quadratic equation ax2 + bx + c = 0, (a ≠ 0). Solutions of quadratic, equations (only real roots) by factorization, and by using quadratic formula. Relationship, between discriminant and nature of roots. Situational problems based on quadratic, equations related to day-to-day activities (problems on equations reducible to quadratic, equations are excluded), 2. ARITHMETIC PROGRESSIONS, Motivation for studying Arithmetic Progression Derivation of the nth term and sum of
Page 5 :
the first n terms of A.P. and their application in solving daily life problems. (Applications, based on sum to n terms of an A.P. are excluded), UNIT- GEOMETRY, 3. CIRCLES, Tangent to a circle at, point of contact, 1. (Prove) The tangent at any point of a circle is perpendicular to the radius through the, point of contact., 2. (Prove) The lengths of tangents drawn from an external point to a circle are equal., 4. CONSTRUCTIONS, 1. Division of a line segment in a given ratio (internally)., 2. Tangents to a circle from a point outside it., UNIT-TRIGONOMETRY, 5. SOME APPLICATIONS OF TRIGONOMETRY, HEIGHTS AND DISTANCES-Angle of elevation, Angle of Depression., Simple problems on heights and distances. Problems should not involve more than two, right triangles. Angles of elevation / depression should be only 30°, 45°, 60°., UNIT-MENSURATION, 6. SURFACE AREAS AND VOLUMES, 1. Surface areas and volumes of combinations of any two of the following: cubes, cuboids,, spheres, hemispheres and right circular cylinders/cones., 2. Problems involving converting one type of metallic solid into another and other mixed, problems. (Problems with combination of not more than two different solids be taken)., UNIT-STATISTICS & PROBABILITY, 7. STATISTICS, Mean, median and mode of grouped data (bimodal situation to be avoided). Mean by, Direct Method and Assumed Mean Method only
Page 6 :
STUDY MATERIAL/QUESTION, BANK, QUADRATIC EQUATIONS, ▪, ▪, , General form of quadratic equations ax2 + bx + c = 0 Where a, b, c are real numbers, and a 0 ., A real number is said to be a root of the quadratic equation ax 2 + bx + c = 0 if, a + b + c = 0 ., , Solution of a Quadratic equation by Factorization, To find the solution of quadratic equation by factorization method, we use the following, steps., ▪, ▪, , Write the given quadratic equation as product of two linear factors by splitting the, middle term., Equate each factor to zero to get possible solutions., , Solution of a Quadratic Equation by using Quadratic Formula, ▪, , If and are the roots of a quadratic equations, ax2 + bx + c = 0 then, , −b + b 2 − 4ac, −b − b 2 − 4ac, =, or =, provided b 2 − 4ac 0, 2a, 2a, 𝑏, , 𝑐𝑜𝑓𝑓𝑖𝑐𝑖𝑒𝑛𝑡𝑜𝑓𝑥, , ▪, , Sum of roots 𝛼 + 𝛽 = − 𝑎 = − 𝑐𝑜𝑓𝑓𝑖𝑐𝑖𝑒𝑛𝑡𝑜𝑓𝑥 2, , ▪, , Products of Roots =, , c, cons tan t, =, a cofficient of x 2, , Nature of Roots, ▪, , ▪, ▪, ▪, , , The roots of the quadratic equations ax + bx + c = 0, a 0 is given by, , −b b 2 − 4ac, −b D, x=, or x =, , where D = b2 − 4ac is called discriminant., 2a, 2a, −b + D, −b − D, If D = b2 − 4ac 0 then the two distinct and real roots are, ., and, 2a, 2a, −b −b, If D = b2 − 4ac = 0 then the two real and equal roots are, ,, 2a 2a, If D = b2 − 4ac 0 then the equation has no real roots
Page 7 :
QUESTION BANK, LEVEL-1, 1. If one root of the quadratic equation 2 x2 + kx − 6 = 0 is 2, find the value of k also find, the other root., 2. Solve by factorization., x, x + 1 34, (a), +, = , x 0, x −1, x +1, x, 15, 1, (b) 2 x 2 − x + = 0, 8, (c), , 2 x2 + 7 x + 5 2 = 0, , 3. Determine whether the given quadratic equations have real roots and if so, find the, roots., (a) 2 x2 − 2 2 x + 1 = 0, (b) 3x2 − 5x + 2 = 0, 4. Find the value of k for which given equations has real and equal roots., (a) kx2 − 5x + k = 0, (b) x 2 + k ( 4 x + k − 1) + 2 = 0, 5. The sum of two numbers is 15. If the sum of their reciprocals is, , 3, , find the numbers., 10, , LEVEL-2, 1. If -4 is a root of the quadratic equation x2 + px − 4 = 0 and the quadratic equations, , x2 + px + k = 0 has equal roots, find the value of k., 2. Find the value of k for which given equations has real and equal roots., ( k − 12 ) x 2 + 2 ( k − 12 ) x + 2 = 0, 3. A two-digit number is such that the product of its digits is 18. When 63 is subtracted, from the number, the digits interchange their places, Find the number., 4. A train travels 360 km at a uniform speed. If the speed had been 5km/h more, it would, have taken 1 hour less for the same journey. Find the speed of the train., 5. If -5 is a root of the quadratic equation 2 x2 + px −15 = 0 and the quadratic equation, p ( x 2 + x ) + k = 0 has equal roots, find the value of k., , 6. Find two consecutive odd positive integers, sum of whose squares is 290., LEVEL-1 (Answer), 1., , k=-1, Other root is -3/2., , 3., , (a), , 1 1, ,, 2 2, , (b) 1,, , 2, 3, , 1 1, 3, 5, (b) ,, ,−, 4 4, 2, 2, 5, 2, 4. (a) , (b) , − 1, 2, 3, , 2. (a), , (c) − 2, −, 5. 10, 5, , 5, 2
Page 9 :
3, , What is the common difference of the A.P., 1 (1−𝑝) (1−2𝑝), , 𝑝 , 𝑃 …., 𝑝, , 4, , If k, 2k-1 and 2k+ 1 are three consecutive terms of an A.P., what is the value of k?, , 5, , What is the sum of first 20 odd natural numbers?, , 6, , Find the 9th term from the end (towards the first term) of the A.P. 5, 9, 13, .. 185., , 7, , How many two-digit numbers are divisible by 3, If the first and last terms of an A.P. are 1 and 11 respectively and the sum of its n, 8, terms is 36, then find the number of terms in the A.P., 9 In an A.P., if d = -2, n = 5 and 𝑎𝑛 = 0, then find the value of a., In an A.P, if the common difference is -4 and the seventh term is 4, then find the, 10, first term, Answers, 1, 2, 3, 4, 5, , −69, 9, −1, 3, 400, , 6, 7, 8, 9, 10, , 153, 30, 6, 8, 28, LEVEL-2, , 1, 2, 3, 4, 5, , Find the nth term of the A.P. a, 3a, 5a, ....... ., Determine the 10th term from the end of the AP : 4, 9, 14, ..., 254., Find how many integers between 200 and 500 are divisible by 8., If the common difference of an A.P. is 3, then what is the value of 𝑎20 − 𝑎15 ?, Find the value of the middle term of the A.P. -6, -2, 2,..., 58., If the sum of the first seven terms of an A.P. is 49 and the sum of its first 17 terms, 6, is 289, find the sum of first n terms of the A.P., If the ratio of the first term of two A.P.'s is (7n+1): (4n+27), find the ratio of their, 7, 𝑚𝑡ℎ term, In an A.P, the sum of first ten terms is (-80) and the sum of its next ten terms is, 8, (-280). Find the A.P., Find the sum of first n terms of an A.P., whose nth term is 5n-1. Hence, find the, 9, sum of its first 20 terms., For what value of n are the nth terms of two A.P.'s is 63, 65, 67, .. and 3, 10, 17, .., 10, equal, Answers, 1, 2, 3, 4, 5, , ( 2n-1)a, 209, 37, 15, 26, , 6, 7, 8, 9, 10, , n², ( 14m -6) /(8m+23), 1,-1,-3, -5,..., 1030, 13
Page 10 :
CIRCLES, Circle: A circle is a collection of all points in a plane which are at a constant distance from, a fixed point., Centre: The fixed point is called the center., Radius: The constant distance from the center is called the radius., Chord: A line segment joining any two points on a circle is called a chord., Diameter: A chord passing through the center of the circle is called diameter. It is the, longest chord., Tangent: When a line meets the circle at one point, the line is known as a tangent., , The tangent to a circle is perpendicular to the radius through the point of contact., ⇒ OP ⊥ AB, , The lengths of the two tangents from an external point to a circle are equal., ⇒ AP = PB, Length of Tangent Segment, PB and PA are normally called the lengths of tangents from outside point P., Properties of Tangent to Circle, Theorem 1: Prove that the tangent at any point of a circle is perpendicular to the radius, through the point of contact., Given: XY is a tangent at point P to the circle with center O., To prove: OP ⊥ XY, Construction: Take a point Q on XY other than P and join OQ
Page 11 :
Proof:, If point Q lies inside the circle, then XY will become a secant and not a tangent to the, circle, OQ > OP, This happens with every point on the line XY except the point P. OP is the shortest of all, the distances of the point O to the points of XY, OP ⊥ XY … [Shortest side is the perpendicular], Theorem 2: A line drawn through the end point of a radius and perpendicular to it, is, the tangent to the circle., Given: A circle C (O, r) and a line APB is perpendicular to OP, where OP is the radius., To prove: AB is tangent at P., Construction: Take a point Q on the line AB, different from P and join OQ., , Proof:, Since OP ⊥ AB, OP < OQ ⇒ OQ > OP, The point Q lies outside the circle., Therefore, every point on AB, other than P, lies outside the circle., This shows that AB meets the circle at point P., Hence, AP is a tangent to the circle at P., Theorem 3: Prove that the lengths of tangents drawn from an external point to a circle, are equal, Given: PT and PS are tangents from an external point P to the circle with center O., To prove: PT = PS
Page 12 :
Construction: Join O to P, T and S., , Proof: In ∆OTP and ∆OSP., OT = OS …[radii of the same circle], OP = OP …[common], ∠OTP = ∠OSP …[each 90°], ∆OTP = ∆OSP …[R.H.S.], PT = PS …[c.p.c.t.], Note: If two tangents are drawn to a circle from an external point, then:, •, , They subtend equal angles at the center i.e., ∠1 = ∠2., , •, , They are equally inclined to the segment joining the center to that point i.e.,, ∠3 = ∠4., ∠OAP = ∠OAQ, , QUESTION BANK, LEVEL-1, 1. In the figure, PA is a tangent from an external point P to a circle with center O. If ∠POB, = 115° then find ∠APO., , 2. In the following figure, PA and PB are tangents drawn from a point P to the circle with, center O. If ∠APB = 60°, then what is ∠AOB?
Page 13 :
3. In the figure, CP and CQ are tangents to a circle with center O. ARB is another tangent, touching the circle at R. If QC = 11 cm, BC = 7 cm then find, the length of BR., , 4. In the figure, ΔABC is circumscribing a circle. Find the length of BC., , 5. In the figure, if ∠ATO = 40°, find ∠AOB., , 6. A point P is 13 cm from the center of the circle. The length of the tangent drawn, from P to the circle is 12 cm. Find the radius of the circle., 7. From a point P, the length of the tangent to a circle is 15 cm and distance of P from the, center of the circle is 17 cm, then what is the radius of the circle?, , LEVEL-2, 8. The two tangents from an external point P to a circle with center O are PA and PB. If, ∠APB = 70°, then what is the value of ∠AOB?, 9. Two tangents TP and TQ are drawn to a circle with center O from an external point T., Prove that ∠PTQ = 2 ∠OPQ.
Page 14 :
10. A circle is touching the side BC of a ΔABC at P and touching AB and AC produced at Q, and R. Prove that:, , Answers: 1)250 2)1200 3)4cm 4) 10cm 5)1000 6)5cm 7)8cm 8)1100, , CONSTRUCTIONS, Dividing a given Line Segment, internally in the given Ratio m: n, Let AB be the given line segment of length x cm. We are required to determine a point P, dividing it internally in the ratio m: n., Steps of Construction:, •, , Draw a line segment AB = x cm., , •, , Make an acute ∠BAX at the end A of AB., , •, , Use a compass of any radius and mark off arcs. Take (m + n) points A1, A2, … Am,, Am+1, …, Am+n along AX such that AA1 = A1A2 = … = Am+n-1 , Am+n, , •, , Join Am+nB., , •, , Passing through Am, draw a line AmP || Am+nB to intersect AB at P. The point P so, obtained is the A required point which divides AB internally in the ratio m: n., , Construction of a Tangents from an External Point to a Circle when its Centre is, Known, Steps of Construction:, •, , Draw a circle with center O., , •, , Join the center O to the given external point P.
Page 15 :
•, , Draw a right bisector of OP to intersect OP at Q., , •, , Taking Q as the center and OQ = PQ as radius, draw a circle to intersect the given circle, at T and T’. Join PT and PT’ to get the required tangents as PT and PT’., , QUESTION BANK, LEVEL -1, Q1. Draw a line segment of length 6 cm. Using compasses and ruler, find a point P on it, which divides it in the ratio 3: 4, Q2. Draw two tangents to a circle of radius 3.5 cm, from a point P at a distance of 6.2 cm, from its center, LEVEL -2, Q1. Draw a pair of tangents to a circle of radius 3 cm, which are inclined to each other at, an angle of 60°., Q2. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of, radius 6 cm., Q3. Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on, 𝐴𝑃 3, AB such that 𝐴𝐵 =5, , SOME APPLICATIONS OF TRIGONOMETRY, IMPORTANT FORMULAE, ▪, ▪, , The height or length of an object or the distance between two distant objects, can be determined with the help of trigonometric ratios., In a right triangle, , 𝑝, , (i), , Sin x =ℎ, , (ii), , Cos x =, , (iii), , Tan x =, , 𝑏, ℎ, 𝑝, 𝑏, , 𝑏, , (iv), , Cot x =𝑝, , (v), , Sec x =𝑏, , ℎ, ℎ, , (vi)Cosec x =𝑝
Page 16 :
Values of trigonometric ratios of standard angles:, 00, 300, 450, 1, 1, Sin x, 0, 2, √2, 1, √3, Cos x, 1, √2, 2, 𝟏, Tan x, 0, 1, √𝟑, Cot x, , Not defined, , Sec x, , 1, , Cosec x, , Not defined, , √3, 2, √3, 2, , 1, √2, √2, , 600, √3, 2, 1, 2, , 900, , √𝟑, , Not defined, , 1, √3, 2, 2, √3, , 1, 0, , 0, Not defined, 1, , QUICK REVISION NOTES, One of the important applications of trigonometry is to find the height or length of an, object or the distance between two distinct objects., ▪, , Line of Sight: The line from our eyes to the object we are viewing is known as the line, of sight or line of vision., , ▪, , Angle of elevation: The angle of elevation of an object viewed, is the angle formed by, the line of sight with the horizontal when it is above the horizontal level., , ▪, , Angle of depression: The angle of depression of an object viewed, is the angle formed, by the line of sight with the horizontal level when it is below the horizontal level.
Page 17 :
QUESTION BANK, LEVEL 1, 1. Find the values of x and y in the following figure:, , 2. A circus artist is climbing a 30 m long rope, which is tightly stretched and tied from, the top of a vertical pole to the ground. Find the height of the pole, if the angle made, by the rope with the ground level is 60°., 3. The shadow of a tower standing on a level ground is found to be 30 m longer when the, sun’s altitude is 30° than when it is 60°. Find the height of the tower., LEVEL 2, 1. As observed from the top of a 75 m high lighthouse from the sea-level, the angles of, depression of the two ships are 30° and 45°. If one ship is exactly behind the other on, the same side of the lighthouse, find the distance between the two ships., 2. From the top of a 7 m high building, the angle of elevation of the top of a cable tower, is 60° and the angle of depression of its foot is 30°. Determine the height of the tower., 3. The angles of depression of the top and bottom of a 8 m tall building from the top of a, multi-storied building are 30° and 45°, respectively. Find the height of the multistoried building and the distance between the two buildings., ANSWERS:, LEVEL 1, 1. x = 6m, y = 6√2 m, , 2. 15√3 m, , 3. 15√3 m, , LEVEL 2, 1. 75(√3 – 1) m, , 2. 28 m, , 3. h = 4(3 +√3) m, d = 4(3 +√3) m, , SURFACE AREA AND VOLUMES, Surface Area is the area of the outer part of any 3D figure, Volume is the capacity of the figure i.e., the space inside the solid., To find the surface areas and volumes of the combination of solids, we must know the, surface area and volume of the solids separately., , Some of the formulas of solids
Page 19 :
Hemi Spherical, shell, , 4πR2 (Surface, area of outer), , 4πr2 (Surf, ace area, of inner), , 4/3, π(R3 –, r3) =>, Matter, used in, making, shell, , R = outer, radius, r = inner, radius, , Surface Area of a Combination of Solids, If a solid is mounded by two or more than two solids then we need to divide it in separate, solids to calculate its surface area., Conversion of Solid from One Shape to Another, When we convert a solid of any shape into another shape by melting or remolding then, the volume of the solid remains the same even after the conversion of shape., KEY POINT:, 1cubic meter= 1kilo liters =1000 liter, 1liter= 1000 cm3, 1m=100cm, 1cm=10mm, 1km=1000m, 1 m2=(100cm)2=10000cm2, 1m3= (100cm)3=1000000 cm3, , QUESTION BANK, LEVEL-1, 1. If a solid piece of iron in the form of a cuboid of dimensions 49 cm x 33 cm x 24 cm, is, recast into form a solid sphere. Then find the radius of sphere., 2. Twelve solid spheres of the same size are made by melting a solid metallic cylinder of, base diameter 2 cm and height 16 cm. Find the diameter of each sphere., 3. A solid is in the shape of a cone standing on a hemisphere with both their radii being, equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the, solid in terms of π., 4. If the radii of two spheres are in the ratio 2:3, then find the ratio of their respective, volumes., 5. Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted to form a single, solid sphere. Find the radius of the resulting sphere., LEVEL- 2
Page 20 :
1. A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread, out to form a platform 22 m by 14 m. Find the height of the platform., 2. The rain water from a roof of dimensions 22 m x 20 m drains into a cylindrical vessel, having diameter of base 2 m and height 3.5 m. If the rain water collected from the roof, just fill the cylindrical vessel, then find the rainfall (in cm)., 3. A building is in the form of a cylinder surmounted by a hemispherical dome and, 19, contains 4121 m3 of air. If the internal diameter of dome is equal to its total height, above the floor, find the height of the building?, 4. How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid, rectangular lead piece with dimensions 66 cm, 42 cm and 21 cm?, 5. If the length, breadth and height of a solid cube are in the ratio 4 : 3 : 2 and total surface, area is 832 cm2. Find its volume., ANSWER, LEVEL:1, Q. No., Answer, 1, 21cm, , Q. No., 1, , LEVEL:2, Answer, 2.5 CM, , 2, , 2cm, , 2, , 2.5cm, , 3, , Πcm3, , 3, , 4 cm, , 4, , 8:27, , 4, , 1500, , 5, , 12 cm, , 5, , 1536 cm3, , STATISTICS, MEAN (AVERAGE): Mean [Ungrouped Data] – Mean of n observations, x1, x2, x3 … xn, is, , MEAN [Grouped Data]: The mean for grouped data can be found by the following three, methods:, (i) Direct Mean Method:, , Class Mark = (UCL+LCL)/2, (ii) Assumed Mean Method: In this, an arbitrary mean ‘a’ is chosen which is called,, ‘assumed mean’, somewhere in the middle of all the values of x., , …[where di = (xi – a)], MEDIAN: Median is a measure of central tendency which gives the value of the middlemost observation in the data.
Page 21 :
…where [ l = Lower limit of median class; n = Number of observations; f = Frequency of, median class; c.f. = Cumulative frequency of preceding class; h = Class size], MODE:, (i) Ungrouped Data: The value of the observation having maximum frequency is the, mode., (ii) Grouped Data:, , …where[l = Lower limit of modal class; f1 = Frequency of modal class; f0 = Frequency of, the class preceding the modal class; f2 = Frequency of the class succeeding the modal, class; h = Size of class interval. c.f. = Cumulative frequency of preceding class; h = Class, size], , QUESTION BANK, LEVEL -1, Q1. Consider the following distribution of daily wages of 50 workers of a factory., Daily wages (in Rs.) 100-120 120-140 140-160 160-180 180-200, Number of workers 12, 14, 8, 6, 10, Find the mean daily wages of the workers of the factory by using an appropriate method., Q2. In a hospital, weights of new born babies were recorded, for one month. Data is as, shown:, Weight of new born baby (in kg) 1.4 – 1.8 1.8 – 2.2 2.2 – 2.6 2.6 – 3.0, No of babies, 3, 15, 6, 1, Find the median weight?, Q3. Find the mode of the following frequency distribution:
Page 22 :
LEVEL -2, Q1. A survey regarding the heights (in cm) of 51 girls of Class X of a school was conducted, and the following data were obtained:, Height (in cm) Number of girls, Less than 140 4, Less than 145 11, Less than 150 29, Less than 155 40, Less than 160 46, Less than 165 51, Find the median height., Q2. An aircraft has 120 passenger seats. The number of seats occupied during, 100 flights are given in the following table:, Number of seats, 100-104, 104-108, 108-112, 112-116, Frequency, 15, 20, 32, 18, Determine the mean number of seats occupied over the flights., , 116-120, 15, , Q3. The average score of boys in the examination of a school is 71 and that of the girls is, 73. The average score of the school in the examination is 71.8. Find the ratio of the, number of boys to the number of girls who appeared in the examination., , ANSWER, LEVEL 1 Q1. Rs. 145.20, LEVEL2 Q1. 149.03, , Q2. 2.05 KG Q3. 16.67, , Q2. 109 Q3. 3:2
Page 23 :
CASE STUDY, QUADRATIC EQUATIONS, CASE STUDY 1:, Raj and Ajay are very close friends. Both the families decide to go to Ranikhet by their, own cars. Raj’s car travels at a speed of x km/hr while Ajay’s car travels 5km/hr faster, than Raj’s car. Raj took 4 hours more than Ajay to complete the journey of 400km., , Based on above information answer the following questions:, Q1 write quadratic equation which describe the speed of Raj’s car?, Q2 what is the speed of Ajay’s car?, CASE STUDY 2:, The speed of a motor boat is 20km/hr. For covering the distance of 15 km the boat took, 1 hour more for upstream than downstream., , Based on above information answer the following questions:, Q1 write quadratic equation for the speed of the current?, Q2 How much time boat took in downstream?, CASE STUDY 3:, Swati is a daughter of Varun. Seven years ago, Varun’s age was five times the square of, Swati’s age. Three years hence, Swati’s age will be two-fifth of Varun’s age.
Page 24 :
Based on above information answer the following questions:, Q1 Form a quadratic equation related to the given problem?, Q2 Find the present age of Varun?, CASE STUDY 4:, , John and Jivanti are playing with the marbles. They together have 45 marbles. Both of, them lost 5 marbles each, and the product of the number of marbles they now have is, 124., Based on above information answer the following questions:, Q1write the quadratic equation related to the above problem?, Q2 how many marbles John had?, CASE STUDY 5:, A rectangular park is to be designed whose breadth is 3 m less than its length. Its area is, to be 4 square meters more than the area of a park that has already been made in the, shape of an isosceles triangle with its base as the breadth of the rectangular park and of, altitude 12 m(see the below figure), , Based on above information answer the following questions:, Q1 write a quadratic equation for given situation?, Q2 Find the length of rectangular park?
Page 25 :
ANSWERS of Quadratic equation:, Case Study 1: Q1) x2 + 5x – 500 = 0, , Q2) 25 km/hr, , Case Study 2: Q1) x2 + 30x – 400 = 0, , Q2) 30 minutes, , Case Study 3: Q1) 2x2 - x – 6 = 0, , Q2) 27 years, , Case Study 4: Q1) x2 - 45x + 324 = 0, , Q2) 36 or 9 marbles, , Case Study 5: Q1) x2 - 3x - 4 = 0, , Q2) 7 m, , ARITHMETIC PROGRESSION, CASE STUDY 1:, India is competitive manufacturing location due to the low cost of manpower and strong, technical and engineering capabilities contributing to higher quality production runs. The, production of TV sets in a factory increases uniformly by a fixed number every year. It, produced 16000 sets in 6th year and 22600 in 9th year., , Based on above information answer the following questions:, Q1 Find the production during first year?, Q2 Find the production during first 3 years?, CASE STUDY 2:, Your friend Manohar wants to participate in a 200m race. He can currently run that, distance in 51 seconds and with each day of practice it takes him 2 seconds less. He wants, to do in 31 seconds.
Page 26 :
Based on above information answer the following questions:, Q1 What is the minimum number of days he needs to practice till his goal is achieved?, Q2 The value of x, for which 2x, x + 10, 3x + 2 are three consecutive terms of an AP?, CASE STUDY 3:, Your elder brother wants to buy a car and plans to take loan from a bank for his car. He, repays his total loan of Rs 1,18,000 by paying every month starting with the first, installment of Rs 1,000. If he increases installment by Rs 100 every month., , Based on above information answer the following questions:, Q1 What is the amount paid by him in 30th installment?, Q2 If total installments are 40 then amount paid in the last installment?, CASE STUDY 4:, A mathematics teacher of a school has taken his children to a science center to visit the, science and maths exhibition. When the students were visiting different stalls, one, student Rani observed that some rectangular bars are arranged in ascending order as, shown below. In the meantime, her teacher reached at the stall and asked questions to, Rani and the other students to verify whether the pattern is in AP or not? Just by, observing the pattern shown below Rani and her friends answered., , Based on above information answer the following questions:, Q1 What is the height of 6th bar?, Q2 If there are 30 bars, then what is the height of 7th bar from the end?, CASE STUDY 5:, Aditya is celebrating his birthday. He invited his friends. He bought a packet of, toffees/candies which contains 120 candies. He arranges the candies such that in the
Page 27 :
first row there are 3 candies, in second there are 5 candies, in third there are 7 candies, and so on., , Based on above information answer the following questions:, Q1 Find the total number of rows of candies?, Q2 How many candies are placed in last row?, ANSWERS of Arithmetic Progression:, Case Study 1: Q1) 5000 sets, , Q2) 21600 sets, , Case Study 2: Q1) 11 days, , Q2) 6, , Case Study 3: Q1) 3900, , Q2) 4900, , Case Study 4: Q1) 22, , Q2) 76, , Case Study 5: Q1) 10 rows, , Q2) 21 candies, , CIRCLES, 1. A Ferris wheel (or a big wheel in the United Kingdom) is an amusement ride consisting, of a rotating upright wheel with multiple passenger-carrying components (commonly, referred to as passenger cars, cabins, tubs, capsules, gondolas, or pods) attached to, the rim in such a way that as the wheel turns, they are kept upright, usually by gravity., After taking a ride in Ferris wheel, Aarti came out from the crowd and was observing, her friends who were enjoying the ride. She was curious about the different angles, and measures that the wheel will form. She forms the figure as given below., , (i), , In the given figure find ∠ ROQ, , (ii), , Find ∠ RQP
Page 28 :
2. Varun has been selected by his School to design logo for Sports Day T-shirts for, students and staff. The logo design is as given in the figure and he is working on the, fonts and different colors according to the theme. In given figure, a circle with center, O is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E, , and F respectively. The lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm, respectively., (i) Find the length of AD, (ii) Find the length of CF, 3. In an Online test Ishita come across the statement - if a tangent is drawn to a circle, from an external point, then the square of length of tangent drawn is equal to, difference of square of the distance of the tangent from the center of circle and radius, of the circle., , Help Ishita in answer in the following questions based on the above statement, (i) if AB is a tangent to a circle with Centre O at B such that AB = 10 cm and OB = 5, cm, then find the value of OA., (ii) In the adjoining figure find the radius of the circle.
Page 29 :
4. A backyard is in the shape of triangle with right angle at B, AB=6 m and BC = 8 m. A, pit was dig inside it such that it touches the walls AC, BC and AB at P, Q and R, respectively such that AP= x m, , Based on the above information give answers of the questions:, (i) Find the value of AR., (ii) Find the radius of the pit., ANSWER, CIRCLES, 1(i) ROQ = 1500, 1ii), RQP = 750, 2(i) AD=7 cm, 2(ii) CF=3 cm, 3(i) OA=55, 3ii) PQ=15 cm, OQ=17 cm, 4(i) AR=4CM, 4(ii) Radius=2 cm, , SOME APPLICATION OF TRIGONOMETRY, 1. Two trees of equal heights are standing opposite to each other side of a road in a, garden. Which is 20 m wide. From a point between them on the road the angles of, elevation of their tops are 450 and 600.
Page 30 :
Based on the above information give answers of the questions:, a) Find the distance of the point P from the base of the tree CD., b) Find the height of the two trees, , 2. An observer on the top of 30 m tall light house (including height of the observer), observes a ship at an angle of depression 300 coming towards the base of the light, house along a straight line joining the ship and the base of the light. The angle of, depression of the ship changes to 450 after moving toward the light house 10 m?, , Based on the above information give answers of the questions:, a) Find the distance of the ship from the base of the light house when angle of, depression is 300?, b) Find the distance of the ship from the base of the light house when angle of, depression is 450?, c) Find the distance AC and AD?, 3. The horizontal distance between a towers AB and a building CD is 120 m. The angle of, elevation of the top of the tower AB from the top and bottom of the building CD are 450, and 600 respectively., , Based on the above information give answers of the questions:, a) Find the height of the tower AB?, b) Find the height of the building CD?, c) What is the distance of the straight line joining the top of the tower AB and, bottom of the building?
Page 31 :
4. A boy is standing on the top of light house. He observed that boat P and boat Q are, approaching to light house from opposite directions. He finds that angle of depression, of boat P is 45o and angle of depression of boat Q is 30o. He also knows that height of, the light house is 100 m., , Based on the above information give answers of the questions:, a) Find the distance of Boat P to the light house., b) Find the distance between the two boats P and Q., 5. A clinometer is a tool that is used to measure the angle of elevation. We can use a, clinometer to measure the height of tall things, i.e., flag poles, towers, buildings, tree,, etc., , Study some results after using clinometer., (A) The angle of elevation of the top of a tower from a point on the ground, which is, 30 m away from the foot of the tower is 30°., (B) From a point on the ground, the angles of elevation of the bottom and top of a, transmission tower fixed at the top of a 20 m high building are 45° and 60°, respectively., From (A) Answer the following questions, a) Find the height of the tower., b) In case, the angle of elevation is 60°, then find the height of tower., From (B) Answer the following quest, c) Find the height of the tower., d) Find distance between the observation point and the bottom of building.
Page 32 :
ANSWERS, 1. (a) 10( √3 – 1 ) m, (b) (30 - 10√3) m, 2. (a) 10( √3 + 1 ) m, (b) 30 m, (c) 30√2 m , 60 m, 3. (a) 120√3 m, (b) 120( √3 – 1 ) m, (c) 240 m, 4. (a) 100 m, (b) 100( √3 + 1 ) m, 5. (a) 10√3 m, (b) 30√3 m (c) 20( √3 - 1 ) m, (d) 20 m, , SURFCE AREA AND VOULME, 1. Water is flowing at the rate of 5 km/h through a pipe of diameter 14 cm into a, rectangular tank which is 50 m long and 44 m wide. Determine the time in which the level, of the water in the tank will rise by 7 cm., 2. 500 persons are taking a dip into a cuboidal pond which is 80 m long and 50 m broad., What is the rise of water level in the pond, if the average displacement of the water by a, person is 0.04 m3?, 3. Geeta and Meena have 10 and 6 CD respectively, each of radius 14 cm and thickness 1, cm. They place their CD one above the other to form solid cylinders., Based on the above information, answer the following questions., , (a) Find Curved surface area of the cylinder made by Geeta., (b) What is ratio of curved surface area of the cylinder made by Geeta and Meena., (c) Find the volume of the cylinder made by Meena., 4. On a Sunday, your Parents took you to a fair. You could see lot of toys displayed, and, you wanted them to buy a RUBIK’s cube and strawberry ice-cream for you. Observe the, figures and answer the questions., , (a) Find volume of the solid figure if the length of the edge is 7cm., (b) What is the curved surface area of hemisphere (ice-cream) if the base radius is 7 cm?, (c) Find the slant height and volume of a cone if the radius is 7 cm and the height is 24, cm., ANSWERS, 1. The level of water in the tank will rise by 7 cm in 2 hours., 2.The required rise of water level in the pond is 0.5 cm, 3. (a) 880 cm (b) 5 : 3 (c) 3696 cm3, 4. (a) 343 cm3 (b) 308 cm2 (c) 1232 m3
Page 33 :
STATISTICS, 1. In SBSB test a 100 m race was organized in school to check the physical standard of, children. The data had been recorded as given in the table:, , Time in Seconds, Number of children, , 0-20, 8, , 20-40, 10, , 40-60, 13, , 60-80, 6, , 80-100, 3, , (i) Find the mean time taken by a student to complete the race., (ii) What is the mode of the given distribution of data?, 2. Institutions often want information on how students are doing. How many are, passing and failing, and what is the average achievement in class? Exams can provide, this information. In pre board -1 exam of class 10 students got different marks. The, data is tabulated as follows:, , Marks, Number of children, , 0-20, 8, , 21-40, 10, , 41-60, 13, , 61-80, 6, , 81-100, 3, , (i) How many students are getting more marks than the mean?, (ii) Find the mode of the given data., 3. An electric company conducted a survey about the monthly consumption of some, particular area. The following frequency distribution gives the monthly consumption, of electricity of 68 consumers of a locality.
Page 34 :
Monthly, consumption, (in units), Number of, consumers, , 65 – 85, , 85 – 105, , 105 – 125, , 125 – 145, , 145 – 165, , 165 – 185, , 185 – 205, , 4, , 5, , 13, , 20, , 14, , 8, , 4, , (i) What is the median of the data given in the table?, (ii) Find the mode of the number of consumers in the locality., 4. In a class test the marks of the students are given in the following table:, , Marks, , Below, 10, , Below, 20, , Below, 30, , Below, 40, , Below, 50, , Below, 60, , Number of students, , 3, , 12, , 27, , 57, , 75, , 80, , (i) Find the mean of the given distribution of data., (ii) Find the median of the data., ANSWERS, 1(i), 1ii), , Mean 43, Mode 46, , 2(i), 2(ii), , STATISTICS, Mean 43, 3(i), Mode 46.5, 3ii), , Median 137 4(i), Mode 135.76 4(ii), , Mean 33.15, Median 34.3
Page 35 :
SAMPLE QUESTION PAPERS, (BASIC), BLUE PRINT OF QUESTION PAPER, MATHEMATICS (B -1) (2021-22), Sample paper, CLASS-X, , UNITS, , TYPE OF, QUESTION, , SA-1, 2 marks, , SA-2, 3 marks, , LA, 4 marks, , Total, marks, , TOPIC, MARKS, I, , Algebra, , 2(2), , 3(2), , --, , 10(4), , Geometry, , 2(1), , 3(1), , 4(1), , 9(3), , Trigonometry, , --, , 3(1), , 4(1), , 7(2), , Mensuration, , 2(1), , --, , 4(1), , 6(2), , Statistics and, Probability, Total, , 2(2), , --, , 4(1), , 8(3), , 12(6), , 12(4), , 16(4), , 40(14), , II, III, IV, V
Page 36 :
Sample Question Paper (B1), Mathematics- Basic (241), Class- X, Session: 2021-22, TERM II, , Time Allowed: 2 hours, General Instructions:, , Maximum Marks: 40, , 1. The question paper consists of 14 questions divided into 3 sections A, B, C., 2. All questions are compulsory., 3. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided, in two questions., 4. Section B comprises of 4questions of 3 marks each. Internal choice has been provided, in one question., 5. Section C comprises of 4 questions of 4 marks each. An internal choice has been, provided in one question. It contains two case study-based questions., , SECTION A, S., Marks, No., 1., Find the nature of the roots of the following quadratic equation., 2, 2x2 – 6x + 3 = 0, OR, Find the value of p, for which one root of the quadratic equation px2 – 14x + 8 = 0 is 6, times the other., 2., 3., , 4., 5., , 6., , Three solid metal cubes of edges 6 cm, 8 cm and 10 cm are melted and recasted into a, single solid cube. Find the length of the edge of the cube so obtained., Find the Mode of the given data :, Class Interval 50-55, 55-60, 60-65, 65-70, frequency, 2, 7, 8, 4, How many terms of the AP: 18, 16, 14 ... be taken so that their sum is zero?, Consider the following frequency distribution of heights of 60 students of a class, Height (in 150-155, 155-160, 160-165, 165-170, 170-175, 175-180, cm), No., of, 15, 13, 10, 8, 9, 5, Students, Find the upper limit of Median Class., , 2, 2, , 2, 2, , In the figure, PA is a tangent from an external point P to a circle with centre O. If ∠POB 2, = 115° then find ∠APO.
Page 37 :
7., 8., , 9., , 10., 11., , 12., , OR, The tangent at a point of a circle is perpendicular to the radius through the point of, contact., SECTION B, The sum of the first n terms of an AP is 4n 2 + 2n. Find the n th term of this AP., 3, A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from 3, the top of a vertical pole to the ground. Find the height of the pole, if the angle made, , by the rope with the ground level is 30° (See Figure)., OR, The angle of depression of the top and bottom of a tower as seen from the top of a 60, √3 m high cliff are 45° and 60° respectively. Find the height of the tower. (√3 = 1.73), A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that: AB + 3, CD = AD + BC, , If 2 is a root of the quadratic equation 3x2 + px – 8 = 0 and the quadratic equation, 3, 2, 4x + 2px + k = 0 has equal roots, find the value of k., SECTION C, Draw a line segment of length 7.8 cm and divide it in the ratio 5: 8. Measure the two, 4, parts., OR, Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the, pair of tangents to the circle and measure their lengths., The following data gives the information on the observed life-times (in hours) of 225 4, electrical components., , Determine the mean of the above data.
Page 38 :
13., , A group of students of class X visited India Gate on an educational trip. The teacher 4, and students had interest in history as well. The teacher narrated that India Gate,, official name Delhi Memorial, originally called All-India War Memorial, monumental, sandstone arch in New Delhi, dedicated to the troops of British India who died in wars, fought between 1914, and 1919.The teacher also said that India Gate, which is located at the eastern end of, the Raj path (formerly called the Kingsway), is about 138 feet (42 meters) in height., , (i), , What is the angle of elevation if they are standing at a distance of 42 m away from, the monument?, (ii) They want to see the tower at an angle of 60°. At what distance from the India, Gate they should stand?, 14., , The Great Stupa at Sanchi is one of the oldest stone structures in India, and an 4, important monument of Indian Architecture., It was originally commissioned by the emperor Ashoka in the 3rd century BC. Its, nucleus is a simple hemispherical brick structure built over the relics of the Buddha., It is a perfect example of combination of solid figures. A big hemispherical, dome with a cuboidal structure mounted on it. (Take π = 22/7), , (i) Find the volume of the hemispherical dome if the height of the dome is 21 m., (ii)Find the cloth required to cover the hemispherical dome if the radius of its base is, 14 m
Page 39 :
Marking Scheme, Practice Question Paper (B-1), Mathematics- Basic (241), Class- X, Session: 2021-22(TERM II), Q No, 1., , Hints / Answer, , OR, Let the roots be α and 6α, , Mark, 1, 1, 1, , 1, , 2., , Volume of single cube so obtained, = (63 + 83 + 103) cm3, = 216 + 512 + 1000 = 1728 ⇒ 𝑙 = 12 cm, , 3., 𝑓1−𝑓0, , Mode = 𝑙 + (2𝑓1−𝑓0−𝑓2) ℎ, , 1, 1, 1, , 8−7, , =60 + (2(8)−7−4) 5, , Mode = 61, 4., , 1, , Let the number of terms taken for sum to be zero be n, , 1, , As n ≠ 0, , 1
Page 40 :
5., , Finding Cumulative frequencies, C.I, F, 150-155, 15, 155-160, 13, 160-165, 10, 165-170, 8, 170-175, 9, 175-180, 5, Total, 60, , C.F., 15, 28, 38, 46, 55, 60, , N= 60 ,Hence, N/2 = 30, Therefore Median Class = 160-165, Hence upper limit of median class = 165, 6., , ∠POA = 1800-115 =650, ∠ PAO = 900, Hence by angle sum property in Δ PAO, ∠ APO = 250, OR, , 1, , 1, , 1, 1, 1, 1, , As OP is the shortest line segment and hence Perpendicular to AB., 7., , a = S1 = 4+2=6, S2 = 16+4=20, a+a+d=20, 2a +d=20, 12+d=20, So d=8, Now an = a+(n-1)d, =6+(n-1)x8, = 8n-2, , 1, , 1, , 1
Page 41 :
8., , 1, , 1, , 1, OR, , 1, In ∆ABC, 𝐴𝐵, = tan600, 𝐵𝐶, 60√3, , = √3 , BC = 60m …………….(i), Now in ∆AED, 𝐴𝐸, = tan 450, 𝐸𝐷, 𝐵𝐶, , 1, , 60√3−ℎ, , = 1 [AE=AB-BE and ED = BC], h = 60√3-60 (From i), h= 60(√3-1) = 43.8m, 𝐵𝐶, , 1, , 9., AP=AS………….(i) length of tangents from an external point are equal, BP=BQ…………(ii), CR=CQ ……….(iii), DR=DS …………(iv), ADDING EQUATIONS (i),(ii)(iii)(iv), AP+BP+CR+DR= AS+BQ+CQ+DS, (AP+BP)+ (CR+DR) = (AS+DS) +(BQ+CQ), AB+CD = AD+BC, Hence proved, 10., , 3(2)2 + p(2) – 8 = 0, 12 + 2p – 8 = 0, p = – 2 ...(i), , 1, , 1, 1, 1
Page 42 :
So, equation 4x2+2px+k = 0 becomes, 4x2 - 4x + k = 0 [using (i), For equal roots, D = 0, (-4)2 – 4 × 4 × k = 0, 16 = 16k, k=1, 11., , 1, 1, 3, , 1, STEPS, 1. Draw AB =7.8cm, 2. Draw a ray AX making any suitable angle with AB., 3. Draw ray BY parallel to AX, 4. Cut 5 consecutive equal arc on AX as AA1= A1A2 ……= A4A5, 5. Cut 8 consecutive equal arc on BY as BB1= B1B2=……. B7B8, 6. Join A5 to B8 . Which cut at P on AB, 7. We get AP:PB = 5:8, OR, 1. Draw a circle with centre O and radius = 6cm., 2. Take a point P such that OP=10cm, 3. Draw the perpendicular bisector of OP.Let M be the mid point of OP., 4. With centre M and radius PM = MO ,draw a circle which cuts the given circle at 1, S and T., 5. Join PS and PT., , 3, The lengths of tangents PS = PT = 8cm
Page 43 :
12., , 2, , 1, 1, 13., , (i) tan θ= opp. Side /adj side = 42/42 =1, ⇒ θ = 450, , 1, 1, , (ii) tan θ= opp. Side /adj side, tan 600=42/distance or Required distance = 14√3 m, , 1, 1, , 14., 2, , 2, , 1, 1, , 22, , i) Vol. of hemisphere = 3 𝜋𝑟 3= 3 x 7 x21x21x21, = 19404 cu. m, 22, , ii) Curved surface area of hemisphere = 2π𝑟 2 = 2x 7 x 14x14, = 1232 sq. m, , 1, 1
Page 44 :
Sample Question Paper (B2), Mathematics- Basic (241), Class- X, Session: 2021-22, TERM II, , Time Allowed: 2 hours, General Instructions:, , Maximum Marks: 40, , 1. The question paper consists of 14 questions divided into 3 sections A, B, C., 2. All questions are compulsory., 3. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided, in two questions., 4. Section B comprises of 4questions of 3 marks each. Internal choice has been provided, in one question., 5. Section C comprises of 4 questions of 4 marks each. An internal choice has been, provided in one question. It contains two case study based questions., Q.N, O., , SECTION-A, , MARK, S, , 1, , If the discriminant of the equation 5x2-kx+4=0 is 1, then find the value 2, of k., Or, Solve the quadratic equation 2x2 + x – 300 = 0, , 2, , A cubical block of height 7 cm is surmounted by a hemisphere. What, is the greatest diameter the hemisphere can have ? Find the surface, area of the solid., , 2, , 3, , Find the mode of the following distribution, Marks, 0-10, 10-20, 20-30, 30-40, Number of, 4, 6, 7, 12, students, , 2, , 4, 5, , 50-60, 6, , Find the 12th term from the end of the AP, -2, -4, -6,…., -100, Calculate the mean of the scores of 20 students in mathematical test, Marks, 10-20, 20-30, 30-40 40-50, 50-60, Number of, students, , 6, , 40-50, 5, , 2, , 4, , 7, , 6, , 2, 2, , 1, , Prove that the lengths of tangents drawn from an external point to a, circle are equal, Or, Two concentric circles are of radii 5 cm and 3 cm. Find the length of, chord of larger circle which touches the smaller circle., , 2
Page 45 :
Section-B, 7, 8, , 9, , 10, , 11, , 12, , 13, , 3, Find the sum of first 17 term of an AP whose 4th and 9th term are -15, and -30, respectively., The angle of elevation of top of a building from the foot of the tower is 3, 300 and the angle of elevation of the top of tower from the foot of, building is 600. If the tower is 50m high, then find the height of the, building, Or, A person observed the angle of elevation of the top of a tower as 30°., He walked 50 m towards the foot of the tower along level ground and, found the angle of elevation of the top of the tower as 60°. Find the, height of the tower., 3, From a point P which is at a distance of 13 cm from the centre O of a, circle of radius 5 cm, the pair of tangents PQ and PR to the circle are, drawn. Then find the area of the quadrilateral PQOR., , The diagonal of a rectangular field is 60 m more than the shorter, side .If the longer side is 30 m more than the shorter side, find, the sides of the field., Section-C, Draw a circle of radius 4 cm. Take a point P at distance of 8 cm, from the centre and construct a pair of tangents from the point P, to the circle.Or, Draw a pair of tangents to a circle of radius 6 cm which are, inclined to each other at an angle 600, If the median of a distribution given below is 28.5 then, find the, value of x & y., Class Interval Frequency, 0-10, 5, 10-20, x, 20-30, 20, 30-40, 15, 40-50, y, 50-60, 5, Total, 60, , 3, , 4, , 4, , To make the learning process more interesting, creative and 4, innovative, Vinod’s class teacher brings clay in the classroom, to teach, the topic - Surface Areas and Volumes. With clay, she forms a cylinder, of radius 6 cm and height 8 cm. Then she recast the cylinder into a, sphere and asks some questions to students.
Page 46 :
(i) Find the volume of cylinder, (ii) find the radius of the sphere, 14, , A boy is standing on the top of light house. He observed that boat P and, boat Q are approaching to light house from opposite directions. He, finds that angle of depression of boat P is 45° and angle of depression, of boat Q is 30°. He also knows that height of the light house is 100 m., , Based on the above information, answer the following questions., i., Find ∠APD and ∠AQD, ii., Find the distance between both ships., , 4
Page 47 :
Marking Scheme, Practice Question Paper (B-2), Mathematics- Basic (241), Class- X, Session: 2021-22(TERM II), Q. No., 1, , Solution, 1. 5x2-kx+4=0, a=5 , b=-k, c=4, d=b2-4ac=1, (-k)2-4(5)(4)=1, K2-80=1, K2=81, K=±9, , Marks, ½, ½, ½, ½, , Or, , 2, , 2. 2x2 + x – 300 = 0, 2x2+25x-24x-300=0, X(2x+25)-12(2x+25)=0, (2x+25)(x-12)=0, 25, X=- 2 ,12, , 1, 1, , ½, , Greatest diameter of hemisphere=7 cm, Surface area of the solid= 6a2+2𝜋r2 - 𝜋r2, = 6a2+𝜋r2, 22, =6x7x7+ 7 x3.5x3.5, =294+38.5=332.5 cm2, 3, , ½, 1, , ½, , 12−7, , = 30+(2𝑋12−7−5 )X10, , 1, , 50, , =30+12 = 30+4.166…., =30+4.17=34.17 (approx.), , ½
Page 48 :
4, , −2,−4,−6,..........−100, now 12th term from end is, a12= a+ (n−1) d, , ½, , where a= −100, d= 2, , ½, , a12 = −100 + (12−1) x 2, a12 = −100+22, a12 = − 78, 5., , CI, , 10-20, , fi, 2, Xi 15, fiXi 30, , Mean =, , 1, , 2030, 4, 25, 100, , 30-40, , 40-50, , 50-60, , 7, 35, 245, , 6, 45, 270, , 1, 55, 55, , ∑, fiXi=700, , 1, ½, , ∑ fiXi, ∑ fi, 700, , = 20, = 35, 6, , ∑ fi=20, , Given , Fig, To Prove and Construction, Proof, Or, , ½, , 1, 1, , ½, , In ∆ AOP ,, AP2 = 52-32, = 16 =42, AP= 4cm, AB=2X4=8cm, 7, , Given, the 4th term of AP = -15, The 9th term of AP = -30, We have to find the sum of first 17 terms of an AP., The nth term of the series in AP is given by, an = a + (n - 1)d, When n = 4, a₄ = a + (4 - 1) d, a + 3d = -15 --------------- (i), When n = 9, a₉ = a + (9 - 1)d, a + 8d = -30 ----------------(ii), , 1½, , ½, , ½
Page 49 :
Subtracting (i) from (ii),, a + 8d - (a + 3d) = -30 - (-15), a + 8d - a - 3d = -30 + 15, 8d - 3d = -15, 5d = -15, d=-, , 15, , ½, , 5, , d = -3, Put d = -3 in (1),, a + 3(-3) = -15, a - 9 = -15, a = -15 + 9, a = -6, 𝑛, Sn = 2[2a + (n-1)d], To find the sum of the 17 terms,, S17 =, =, =, =, , ½, , 17, 2, , [2(-6) + (17 - 1)(-3)], , 17, , [-12 + (16)(-3)], , 2, 17, 2, 17, 2, , [-12 - 48], [-60], , = 17(-30), S17 = -510, , 1
Page 52 :
⇒x2 −(90−30)x−2700=0, ⇒x2 – 90x + 30x−2700=0, ⇒x(x−90)+30(x−90)=0, ⇒(x−90)(x+30)=0, If, x+30=0, x=−30(not possible), If, x−90=0, x=90, So, the length of shorter side =x−30=90−30=60m, , 1, , Longer side 90+30=120m, 11., , 4, , Step-by-step explanation:, 1., 2., 3., 4., 5., , 1.Draw a circle with centre 'O' of radius 4cm., 2.Take a point 'P' 8 cm away from its centre., join OP., 3.Draw perpendicular bisector of OP., name the point of intersection as M., , 6. 4.Taking MP as radius and M as centre draw another circle., 7. 5.Name the point A and B where the smaller circle intersects the larger circle, respectively., 8. 6. PA and PB are the required tangents., 9., , Or
Page 53 :
4, , Steps of construction:, Draw a circle of radius 5 cm., 2) Draw horizontal radius OQ., 3) Draw angle 1200 from point O. Let the ray of angle intersect the circle at point R., 4) Now draw 90o at point Q., 5) Draw 90o at point R., 6) Where the two rays intersect, mark it as point P., Therefore, PQ and PR are the tangents at an angle of 60o., 12., , The cumulative frequency for the given data is calculated as follows., , From the table, it can be observed that n = 60, 45 + x + y = 60, x + y = 15 -------------(1), , 1½, , Median of the data is given as 28.5 which lies in interval 20 − 30. Therefore,, median class = 20 − 30, Lower limit (l) of median class = 20, Cumulative frequency (cf) of class preceding the median class = 5 + x, Frequency (f) of median class = 20, Class size (h) = 10, , ½
Page 55 :
Sample Question Paper (B3), Mathematics- Basic (241), Class- X, Session: 2021-22, TERM II, , Time Allowed: 2 hours, General Instructions:, , Maximum Marks: 40, , 1. The question paper consists of 14 questions divided into 3 sections A, B, C., 2. All questions are compulsory., 3. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided, in two questions., 4. Section B comprises of 4questions of 3 marks each. Internal choice has been provided, in one question., 5. Section C comprises of 4 questions of 4 marks each. An internal choice has been, provided in one question. It contains two case study-based questions., , SECTION A, Q.No., 1, Find the difference of the roots of the quadratic equation 𝑥2 − 7𝑥 − 18 = 0., OR, , MARKS, 2, , 1, , 2, 3, , If one root of the quadratic equation 2x2 + 3x + p = 0 is 2 then find the value of, p and the other root of the equation., From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm, is hollowed out. Find the volume of the remaining solid., A survey conducted by a group of students is given below. Find the mean for the, given data., Family, size, , 4, 5, , 1-3, , 3-5, , 5-7 7-9, , 2, , The weight of coffee in 70 packets are shown in the given table. Determine the, modal weight., Weight 200-201 201-202 202-203 203 204 204-205 205-206 206-207, (in g), 26, , 20, , 9, , 2, , 9-11, , Number 7, 8, 2, 2, 1, of, families, which term of the AP: 53, 48, 43, ………. is the first negative term?, , Number 12, of, packets, , 2, , 2, , 1, , 11, , 2
Page 56 :
6, , In the given figure, XP and XQ are tangents from X to the circle with centre O. R, is a point on the circle and AB is tangent at R. Prove that XA + AR = XB + BR, , 2, , OR, In the given figure, a circle is inscribed in a ∆ABC touching BC, CA and AB at P, Q, and R respectively. If AB=10cm, AQ=7cm and CQ=5cm. Find BC., , Section-B, 7, 8, , 9, , 10, , If the sum of the first 14 terms of an AP is 1050 and its first term is 10, then find, the 21st term of the AP., There is a flag staff on a tower of height 20m. At a point on the ground, the, angle of elevation of the foot and top of the flag are 450 and 600, respectively., Find the height of the flag staff., OR, From the top of a 75 m high lighthouse from the sea level the angles of, depression of the two ships are 300 and 450. If the ships are on the opposite, sides of the lighthouse, then find the distance between the two ships., , 3, , Two tangents TP and TQ are drawn to a circle with centre O from an, external point T. Prove that PTQ = 2OPQ., , 3, , Rohan and Rita together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. Find out how, many marbles they had to start with?, , 3, , Section-C, , 3
Page 57 :
11, , 12, , Draw a line segment AB of length 8cm. With A and B as centres, draw circles of, radius 4cm and 3cm respectively. Construct tangents to each circle from the, center of the other circle., OR, Draw a pair of tangents to a circle of radius 5.4cm which are inclined to each, other at an angle of 750. Also find the length of the tangent., The median of the following data is 50. Find the values of p and q, if the sum of, all the frequencies is 90.., Marks, 20-30 30-40 40-50 50-60 60-70 70-80 80-90, Frequencies p, , 13, , i), ii), 14, , 15, , 25, , 20, , q, , 8, , 4, , 4, , 10, , A girl 8m tall spots a parrot sitting on the top of a building of height 58m from, the ground. The angle of elevation of the parrot from the eyes of girl at any, instant is 600. The parrot flies away horizontally in such a way that it remained, at a constant height from the ground. After 8s, the angle of elevation of the, parrot from the same point is 300., , Based on the above information, answer the following questions., Find the distance between the girl and the building., Find the flying distance horizontally covered by parrot in 8s?, On a Sunday, your Parents took you to a fair. You could see lot of toys displayed, and you wanted them to buy a RUBIK’s cube and strawberry ice-cream for you., , Based on the above information answer the following questions:, i), ii), , Find the total surface area of cone with hemispherical ice cream if, radius and slant height are 7cm and 25cm respectively., Find the volume and surface area of solid cube if the length of the edge, is 7cm., , 2, 2
Page 58 :
Marking scheme, Sample paper Basic B3, Mathematics, Term II, Q N., , Hints and solution, , Marks, , SECTION A, 1, , 𝑥2 −, , 7𝑥 − 18 = 0, ⇒ 𝑥2 − 9𝑥 + 2𝑥 − 18 = 0, ⇒ 𝑥(𝑥 − 9) + 2(𝑥 − 9) = 0, ⇒ (𝑥 − 9)(𝑥 + 2) = 0, , 1, , ∵ 𝑥 = 9, −2, Numerical difference of roots = 9-(-2) = 11 or (-2)-9 = -11, OR, Since one root is 1/2 then for value of p, ⇒(1/2)2 + 3 x 1/2 + p = 0 (∵ 𝑎 = 3, 𝑏 = 𝑘, 𝑐 = 3), ⇒ p = -2, ⇒For second roots, 2𝑥2 + 3𝑥 – 2 = 0, ⇒ 2𝑥2 + 4𝑥 – x - 2 = 0, ⇒2x(x + 2) – 1(x + 2) = 0, ⇒ (𝑥 + 2)(2𝑥 - 1) = 0, ⇒ x = -2, ½, Now second root is -2, 2, , Volume of cube = side3, = 73, = 343cm3, , 1/2, 1/2, , 1, , 1, , 1/2, , 1, , Volume of cone =3 r2 h, 1, , =3x, , 22, 7, , 1, , x3x3x7, , = 66cm3, Volume of remaining solid = 343 – 66 = 277cm3, 3, , Class Interval, 1-3, 3-5, 5-7, 7-9, 9-11, TOTAL, , Mean =, =, , 84, 20, , = 4.2, , 𝑓𝑥, 𝑓, , f, 7, 8, 2, 2, 1, 20, , x, 2, 4, 6, 8, 10, , 1/2, fx, 14, 32, 12, 16, 10, 84, , 1, , 1
Page 59 :
4, , 5, , d = 48 - 53= -5, a = 53 ,, an < 0, a + (n - 1)d < 0, 53 + (n - 1)(-5) <0, n > 11.6, n = 12, , 1/2, , The modal class is 201-202., f0 = 12, f1 = 26, f2 = 20, h = 1, , 1/2, , Mode =, , 1/2, , 1, 1/2, , 26−12, , = 201 + 52−12−20 x 1, 1, , = 201 + 0.7, = 201.7, 6, , Tangents drawn from external point are equal in length, XP = XQ (X is an external point)…..(i), AP = AR (A is an external point)……(ii), BQ = BR (B is an external point)……(iii), XP =XQ, XA + AP = XB + BQ, XA + AR = XB + BR (by equation ii and iii), , 1, 1, , OR, , 1, , Tangents drawn from external point are equal in length, AR = AQ = 7cm, CP = CQ = 5cm, Now BR = AB – AR = 10 – 7 = 3cm, , 1
Page 61 :
1, 1=, , 75, 𝑦, , Y = 75 m, Distance between two ships = AB, = x + y = 75√3 + 75, = 75(√3 + 1)m, , 1, , 9, , TP = TQ, TPQ = TQP = x (angles opposite to equal side are equal), In ∆TPQ, PTQ = 1800 – (TPQ + TQP) (angle sum property), = 1800 – (x + x), = 1800 – 2x, OP⊥TP (radius is ⊥ to the tangent at point of contact), OPT = 900, OPQ + TPQ = 900, OPQ + x = 900, OPQ = 900 – x, PTQ = 2OPQ, 10, , Let the Rohan have x marbles and Rita have (45 – x) marbles, According to question, (x - 5)(40 - x) = 124, x2 – 45x + 324 = 0, x2 – 36x – 9x + 324 = 0, x(x – 36) – 9(x - 36) = 0, (x - 36)(x - 9), ⇒ 𝑥 = 36, 9, So Rohan have 36 and Rita have 9 marbles OR Rohan have 9 and Rita, have 36 marbles, , 1, , 1, , 1, 1/2, , 1, 1, 1/2, , SECTION C, 11, , Drawing of line segment and two circles with radii 4cm and 3cm, Construction of tangents neatly and with accurate measurement, OR, 0, Angle between two radii = 180 -750, = 1050, Construction of tangents neatly and with accurate measurement, , 1, 3, 1/2, 3
Page 62 :
Length of tangents, 12, , 1/2, , Construction of cumulative frequency table, Marks, f, cf, 20-30, p, p, 30-40, 15, 15 +p, 40-50, 25, 40 + p, 50-60, 20, 60 + p, 60-70, q, 60 + p + q, 70-80, 8, 68 + p + q, 80-90, 10, 78 + p +q, 𝑁, 90, = 2 = 45, 2, Median class is 50 – 60 , l = 50, f = 20, cf = 40 + p, h = 10, , Median = l +, = 50 +, , 13, , 𝑁, −𝑐𝑓, 2, , 𝑓, , 20, , = 5 - p/2, p=5, 78 + p + q = 90, P + q = 12, Q=7, (i), In ∆ABC, tan600 =, , 1, , xh, , 45−40−𝑝, , 2, , x 10, , 1, , 𝐵𝐶, 𝐴𝐵, , 1, , 50, , √3 = 𝐴𝐵, 50, , (ii), , 50√3, , AB = √3 =, In ∆AED, 𝐵𝐶, tan300 = 𝐴𝐵, 1, , 3, , 1, , m, , 50, , =, √3 𝐴𝐷, AD = 50√3m, Distance between two position of parrot=EC, EC= BD= AD – AB = 50√3 14, , (i), , 50√3, 3, , Total surface area = rl + 2r2, = r(l + 2r), 22, = 7 x 7 x (25 + 14), , =, , 100√3, 3, , m, , 1, , 1, 1
Page 64 :
Sample Question Paper (B4), Mathematics- Basic (241), Class- X, Session: 2021-22, TERM II, , Time Allowed: 2 hours, General Instructions:, , Maximum Marks: 40, , 1. The question paper consists of 14 questions divided into 3 sections A, B, C., 2. All questions are compulsory., 3. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided, in two questions., 4. Section B comprises of 4questions of 3 marks each. Internal choice has been provided, in one question., 5. Section C comprises of 4 questions of 4 marks each. An internal choice has been, provided in one question. It contains two case study-based questions., , SECTION A, Q.NO., 1, Find the roots of the quadratic equation 6 x2 - 7 x – 3 = 0, OR, Find the nature of the roots of 3 x2 - 4√3 x + 4 = 0, 2, The following table gives the daily income of 50 workers of a, factory: Find the mode of the given data., 100 -120 120 -140 140 -160 160 -180 180 -200, Daily, income, in(Rs), Number 12, 14, 8, 6, 10, of, workers:, , MARKS, 2, , 3, , 2, , 4., , 5., 6, , The first term of an A.P. is – 7 and the common difference is 5., Find its 18th term and the general term., Two cubes each of volumes 64 cm3 are joined end to end. Find, the surface area and volume of the resulting cuboid., , The arithmetic mean of the following data is 14. Find the value of, p., xi :, 5, 10, 15, 20, 25, fi :, 7, p, 8, 4, 5, A quadrilateral ABCD is drawn to circumscribe a circle. Prove, that AB + CD = AD + BC, , 2, , 2, , 2, , 2
Page 65 :
R, , C, , D, Q, S, B, P, A, OR, Two concentric circles are radii 5 cm and 3 cm. Find the length of, chord of the larger circle which touches the smaller circle., , SECTION B, 7, 8, , 9, , The first and the last terms of an A.P. are 17 and 350, respectively. If the common difference is 9, how many terms are, there and what is their sum?, The shadow of a tower standing on a level ground is found to be, 40 m longer when the sun, s altitude is 300 than when it was 600 ., Find the height of the tower., OR, A man standing on the deck of a ship, which is 10 m above water, level, observers the angle of elevation of the top of a hill as 600, and the angle of depression of the base of hill as 300 . Find the, distance of the hill from the ship and the height of the hill., PA and PB are tangents to the circle from an external point P, CD, is another touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm,, then find PC + PD, A, , O, , C, Q, , B, , D, , P, , 3, , 3
Page 66 :
10, , The sum of two numbers is 15. If the sum of their reciprocals is, 3, , find the numbers., 10, , 11, , Construct a tangent to a circle of radius 4 cm from a point on the, concentric circle of radius 6 cm and measure its length., OR, Draw a pair of tangents to a circle of radius 5 cm which are, inclined to each other at an angle 600 ., The median of the following data is 525. Find the values of x and, y, if the total frequency is 100., , 3, , SECTION – C, , 12, , 13, , 14, , 4, , 4, , Class interval, Frequency, 0 – 100, 2, 100 - 200, 5, 200 - 300, X, 300 – 400, 12, 400 – 500, 17, 500 – 600, 20, 600 – 700, Y, 700 – 800, 9, 800 - 900, 7, 900 - 1000, 4, Sachin and his sister Suman visited at their uncle place Shimla,, 4, Himachal Pradesh. Sachin, who is standing on the ground spots, a paraglider at distance of 24 m from him at an elevation of 300 ., His sister Suman is also standing on the roof of 6 m high building,, observes the elevation of the same paraglider as 450 . Sachin and, Suman are on the opposite sides of the paraglider., , Answer the following questions., (a) Find the value of PD., (b) Find the distance between the paraglider and the Suman., Pinkis class teacher explained the students about the benefits of, drinking fruits juice in the morning. So , Pinki went to a juice stall, with her friend Ashok. On the stall, they observed that, shopkeeper has three types of glasses of inner diameter 4.6 cm, to serve custumers. The height of each glass is 11 cm., Answer the following questions.
Page 67 :
(a) How much more juice can be filled in type (A) glass than, glass of type (C)?, (b) What is the volume of glass B?, , 2, 2
Page 68 :
Marking SchemeB4, Class - X, Session – 2021 – 2022, TERM – II, Subject - Mathematics (Basic), Q.NO., 1, , HINTS / SOLUTION, - 7x – 3 = 0, 6x2 - 9x + 2 x – 3 = 0, 3x (2x -3) + 1 (2x -3= 0, (2x -3) (3x + 1) = 0, 3, −1, X=2 , x= 3, , 1, 1, , OR, D = b2 - 4 a c, = (−4√3)2 , - 4 × 3 × 4, = 48 – 48, = 0, hence nature of roots are real and equal., 2, , 𝑓1−𝑓0, , Mode = l + 2𝑓1−𝑓0−𝑓2 × h, , Putting the correct values and calculate it, Mode = 135, 3, , 4, , 5, , MARKS, , 6x2, , Given a = - 7, d = 5, A18 = a + (n – 1) d, = - 7 + (18 – 1) 5, = -7 + 85, = 78, General term = – 7 + (n – 1)x5, = 5n - 12, Volume of a cube = 64 cm3, Side of cube = 4 cm, Cuboid , l = 8 cm, b = 4 cm, h = 4 cm, S.A. of cuboid = 2(lb + bh + hl ), = 2 ( 8 × 4 + 4 × 4 + 4 × 8), = 2 (80), = 160 cm2, Volume of cuboid = lbh, =8×4×4, = 128 cm2, xi :, fi :, Fx, ;, , 5, 7, 35, , 10, p, 10 p, , 15, 8, 120, , 20, 4, 80, , 25, 5, 125, , 1, 1, 1/2, 1, 1/2, , 1, 1, , 1, , 1, , 1
Page 69 :
∑f = 24 + p,, ∑𝑓𝑥, Mean = ∑𝑓, 360+10 𝑝, , 14 =, 6, , 7, , ∑fx = 360 + 10 p, 1, , 24+𝑝, , P=6, A quadrilateral ABCD is drawn to circumscribe a circle. Then, AP = AS, BP = BQ, CR = CQ, DR = DS (All are tangents), Adding all, we will get, AB + CD = AD + BC, OR, Using Pythagoras theorem , find the base , base = 4 cm, Length of the chord = 8 cm, a = 17 , l = 350, d = 9, l = a + (n – 1 ) ×d, 350 = 17 + (n – 1) ×9, 350 = 17 + 9n – 9, 350 - 8 = 9n, 342, N = 9 = 38, , 1, 1, 1, 1, 1, , 1, , 𝑛, , Sn = 2 ( a + l), 38, , = 2 ( 17 + 350), = 19 × 367, = 6973, 8, , 1, , A, , 1, , h, , 600, , B, , 𝐴𝐵, , BD =, , 𝐵𝐶, , D, , = tan 600, , 𝐵𝐷, , 𝐴𝐵, , 300, 40 M, , 𝐴𝐵, , C, , 1, , (1), , √3, , = tan 300, , 𝐴𝐵, 𝐵𝐷+40, , =, , 1, √3, , 𝐴𝐵√3 = BD + 40, , (2), , 1
Page 70 :
From equation (1) and (2) AB = 20√3 m, OR, A, h, , D, , 600, 300, , 1, , E, , 10 m, , C, , xm, , 300, , B, , In ∆DBC, 𝐷𝐶, 𝐶𝐵, 10, , = tan 300, =, , 𝑥, , 1, , 1, √3, , x = 10 √3 m, In ∆ADE, 𝐴𝐸, 𝐷𝐸, ℎ, 𝑥, , = tan 600, , = √3, , 1, , h = √3 x, h = 30 m, AB = 30+10 = 40 m, 9., , AP = BP = 12 cm, CQ = QD = 3 cm, PC = AP - AC, = 12 – 3, = 9 cm, Similarly , PD = 9 cm, PC + PD = 18 cm, , 2, , 1
Page 71 :
10., , 11., , 12., , Let one number be x and another number = 15 – x., 1, 1, 3, + 15 − 𝑥 = 10, 𝑥, -x2 + 15x = 50, X2 – 15x + 50 = 0, Then x = 5,10, Draw the circles of given measurment accoding to question, Draw the tangents,measure its lengths., OR, Draw the the circle of radius of 5 cm and draw the angle 1200 at, the centre., Draw the tangents inclined to each other at 600., Class interval, 0 – 100, 100 - 200, 200 - 300, 300 – 400, 400 – 500, 500 – 600, 600 – 700, 700 – 800, 800 - 900, 900 - 1000, Total frequency = 100, 76 + x + y = 100, x + y = 24, Median = l +, 525 = 500 +, , 𝑛, 2, , − 𝑐𝑓, , × h, , 𝑓, 50 −36 − 𝑥, 20, , 25 = (14 – x) × 5, X = 14 – 5 = 9, X=9, Y = 24 – 9 = 15, Y = 15, , 13., , 1, , Frequency, 2, 5, X, 12, 17, 20, Y, 9, 7, 4, , Cf, 2, 7, 7+x, 19 + x, 36 + x, 56 + x, 56 + x + y, 65 + x +y, 72 + x +y, 76 + x+ y, , 1, 1, 2, 2, 2, 2, , 1, , 2, , × 100, 1, , In ∆DQA, 𝐷𝑄, = sin 300, 24, 𝐷𝑄, 24, , =, , 1, 2, , DQ = 12, Pd = 12 – 6, =6m, , 2
Page 73 :
Sample Question Paper (B5), Mathematics- Basic (241), Class- X, Session: 2021-22, TERM II, , Time Allowed: 2 hours, General Instructions:, , Maximum Marks: 40, , 1. The question paper consists of 14 questions divided into 3 sections A, B, C., 2. All questions are compulsory., 3. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided, in two questions., 4. Section B comprises of 4questions of 3 marks each. Internal choice has been provided, in one question., 5. Section C comprises of 4 questions of 4 marks each. An internal choice has been, provided in one question. It contains two case study based questions., , Section – A, Q., No,, 1, Find the nature of the roots of the following quadratic equations. If the real, roots exist, find them 2x2 – 6x + 3 = 0, OR, Find the roots of the following quadratic equation: 2x2 – 7x + 3 = 0, 2, A metallic sphere of radius 4.2 cm is melted and recast into the shape of a, cylinder of radius 6 cm. Find the height of the cylinder., 3, A survey conducted on 20 households in a locality by a group of students, resulted in the following frequency table for the number of family members in, a household:, Find the mode of the given data., Family, 1-3, 3-5, 5-7, 7-9, 9-11, size, Number of 7, 8, 2, 2, 1, families, Find, the sum of the following AP: 2, 7, 12, . . ., to 10 terms, 4, 5, The following frequency distribution gives the monthly consumption of electricity, of 68 consumers of a locality. Find the median of the given data, 65-85, Monthly, consumption, (in units), Number of, 4, consumers, , 6, , 85-105, , 105-125, , 125-145, , 145-165, , 165-185, , 185-205, , 5, , 13, , 20, , 14, , 8, , 4, , Two concentric circles are of radii 10 cm and 6 cm. Find the length of the, , Marks, 2, , 2, 2, , 2, 2, , 2
Page 74 :
chord of the larger circle which touches the smaller circle., OR, If tangents PA and PB from a point P to a circle with centre O are inclined to, each other at angle of 800, then find the value of ∠POA, , Section-B, 7, 8, , 9, , 10, , 11, , 12, , The sum of the 4th and 8th terms of an AP is 24 and the sum of the 6th and, 10th terms is 44. Find the first three terms of the AP., The angles of depression of the top and the bottom of an 8 m tall building from, the top of a multi-storeyed building are 30° and 45°, respectively. Find the, height of the multi-storeyed building and the distance between the two, buildings., OR, From a point on a bridge across a river, the angles of depression of the banks, on opposite sides of the river are 30° and 45°, respectively. If the bridge is at a, height of 3 m from the banks, find the width of the river., In given figure, AB is a chord of the circle and AOC is its diameter such that, ∠ACB = 50°. If AT is the tangent to the circle at the point A, then find the value, of ∠BAT, , 3, , In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had, she got 2 marks more in Mathematics and 3 marks less in English, the product, of their marks would have been 210. Find her marks in the two subjects., Section-C, Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer, circle construct the pair of tangents to the other., OR, Draw a circle of radius 4 cm. Construct a pair of tangents to it, the angle between, which is 60°., Find the missing frequency for the given data if mean of the distribution is 52, Class, 10203040506070Interval 20, 30, 40, 50, 60, 70, 80, Freq., 5, 3, 4, F, 2, 6, 13, , 3, , 3, , 3, , 4, , 4
Page 75 :
13, , In the month of July 2020, it rained heavily throughout the day over the city of, Jaipur. Anil observed the raindrops as they reached him. Each raindrop was in, the shape of a hemisphere surmounted by a cone of the same radius of 1 mm., Volume of one of such drops is 3.14 mm³. Anil collected the rain water in a pot, having a capacity of 1256 mm³. (use 𝜋 = 3.14), , 2+2, , Based on the above situation, answers the following questions., (i), Find the total height of the drop, (ii), How many drops will fill the pot completely., 14, , 2+2, , There is a fire incident in the house. The house door is locked so the Fireman is, trying to enter the house from the window. He places the ladder against the, wall such that its top reaches the window .Based on the above information, answer the following questions:, (i), if window is 6 m above the ground and angle made by the foot of ladder, to the ground is 600 ,find the length of the ladder, (ii), The Fireman placed the another ladder 5 metre away from the wall and, angle of elevation is observed to be 300 then what is length of the other, ladder?
Page 76 :
Marking Scheme, Practice Question Paper (B-5), Mathematics- Basic (241), Class- X, Session: 2021-22(TERM II), Section – A, Q., No,, 1, We have 2x2−6x+3=0, , Marks, 1, , Here, a=2, b=−6, c=3, Therefore, D=b2−4ac = (−6)2−4×2×3 = 36−24=12>0, Hence, given quadratic equation has real and distinct roots, , 2x2−7x+3=0, , Given equation is, Hence, a=2, b=−7, c=3, , 1, , OR, 1, , 1, , 2, , Given:, Radius (r1) of hemisphere = 4.2 cm, Radius (r2) of cylinder = 6 cm, Height (h) = ?, The object formed by recasting the hemisphere will be same in volume., So, Volume of sphere = Volume of cylinder, , 1, , 4/3πr1 3 = πr2 2 h, ⟹4/3π×(4.2)3=π(6)2h, h=2.74 cm, 3, , ⇒ Here, modal class = 3−5, ⇒ l=3,f0=7,f1=8,f2=2 and h=2, , 1, ½
Page 77 :
½, , 1, , =3+0.286, ∴ Mode =3.286, 4, , Clearly, the given sequence is an AP with first term a=2, common, difference d=5 and n=10., Now,, 10, S10= 2 × [2a+(10−1)d], , 1, , =5[2×2+9×5], , 1, , =245, 5, , C.I, 65−85, 85−105, 105−125, 125−145, 145−165, 165−185, 185−205, , xi, 75, 95, 115, 135, 155, 175, 195, , fi, 4, 5, 13, 20, 14, 8, 4, ∑fi, =68, , c.f, 4, 9, 22, 42, 56, 64, 68, , 1, , 1, , 6, , Let the two concentric have the centre O and Let AB be the chord of an outer, circle whose length is D and which will also be tangent to the inner circle at, point D because it is given that the chord touches the inner circle., The radius of inner circle OD = 6cm and the radius of outer circle OB = 10cm, In Δ OAB, ⇒ OA = OB .... radius of outer circle, Hence Δ OAB is isosceles triangle, As radius is perpendicular to tangent OD is perpendicular to AB, OD is altitude from apex and in isosceles triangle the altitude is also the, median
Page 79 :
Section-B, 7, , 8, , We know that,, an = a + (n − 1) d, a4 = a + (4 − 1) d, a4 = a + 3d, Similarly,, a8 = a + 7d, a6 = a + 5d, a10 = a + 9d, Given that, a4 + a8 = 24, a + 3d + a + 7d = 24, 2a + 10d = 24, a + 5d = 12------------ (1), a6 + a10 = 44, a + 5d + a + 9d = 44, 2a + 14d = 44, a + 7d = 22 --------------(2), On subtracting equation (1) from (2), we obtain, 2d = 22 − 12, 2d = 10, d=5, From equation (1), we obtain, a + 5d = 12, a + 5 (5) = 12, a + 25 = 12, a = −13, a2 = a + d = − 13 + 5 = −8, a3 = a2 + d = − 8 + 5 = −3, Therefore, the first three terms of this A.P. are −13, −8, and −3., Consider AB as the height and CD as the building, The angles of depression from A to C and D are 300 and 450, ∠ACE = 300 and ∠ADB = 450, CD = 8 m, Take AB = h and BD = x, From the point C, Construct CE parallel to DB, CE = DB = x, EB = CD = 8 m, AR = AB – EB = h – 8, , 1, , 1, , 1, , 1
Page 80 :
1, , In right triangle ADB, tan θ = AB/DB, Substituting the values, tan 450 = h/x, So we get, 1 = h/x, x=h, In right triangle AEF, tan 300 = AE/FE, Substituting the values, 1/√3 = (h – 8)/ h, By further calculation, h = √3h – 8√3, So we get, √3h – h = 8√3, h (√3 – 1) = 8√3, h = 8√3/(√3 – 1), Multiply and divide by √3 + 1, h = 8√3/ (√3 – 1) × (√3 + 1)/ (√3 + 1), h = 8 (3 + √3)/ (3 – 1), h = 4(3 + √3)m, , 1, , OR, Given:, From a point on a bridge across a river the angles of depression of the banks on, opposite side of the river are 30∘ and 45∘ respectively., The bridge is at the height of 30 m from the banks., To do:, We have to find the width of the river., Solution:, , 1
Page 81 :
9, , 10, , Let AB be the height of the bridge and C,D are the points of depression of the, banks on the opposite side of the river., From the figure,, AB=3m,∠FAD=∠ADB=30∘,∠EAC=∠BCA=45∘, Let the distance between the bridge and point C be BC=x m and the distance, between the bridge and point D be BD=y m., We know that,, tan θ= AB/ BC, ⇒tan45∘=3/x, ⇒1=3/x, ⇒x=3 m.........(i), Similarly,, tan θ = AB /BD, ⇒tan30∘=3/y, ⇒1/√3=3/y, ⇒y=3√3 m..........(ii), ⇒x+y=3+3√3=3(√3+1) m, Therefore, the width of the river is 3(√3+1) m., Given, AB is a chord of the circle., AOC is the diameter of the circle., Also, ∠ACB = 50°, AT is the tangent of the circle., We have to find the measure of the angle BAT., We know that the angle in a semicircle is a right angle., So, ∠CBA = 90°, We know that the sum of all three interior angles of a triangle is always equal to, 180°, In triangle AOB,, ∠CAB + ∠CBA + ∠ACB = 180°, ∠CAB + 90° + 50° = 180°, ∠CAB + 140° = 180°, ∠CAB = 180° - 140°, ∠CAB = 40° ------------------- (1), We know that radius of a circle is perpendicular to the tangent at the point of, contact., From the figure,, OA ⟂ OT, So, ∠CAB + ∠BAT = 90°, Substitute (1) in the above expression,, 40° + ∠BAT = 90°, ∠BAT = 90° - 40°, ∠BAT = 50°, Therefore, the measure of the angle BAT is 50°, Let us say, the marks of Shefali in Maths be x., Then, the marks in English will be 30 – x., As per the given question,, (x + 2)(30 – x – 3) = 210, , 1, , 1, , 1, , 1, , 1, , 1, , 1
Page 82 :
(x + 2)(27 – x) = 210, ⇒ -x2 + 25x + 54 = 210, ⇒ x2 – 25x + 156 = 0, ⇒ x2 – 12x – 13x + 156 = 0, ⇒ x(x – 12) -13(x – 12) = 0, ⇒ (x – 12)(x – 13) = 0, ⇒ x = 12, 13, Therefore, if the marks in Maths are 12, then marks in English will be 30 – 12 =, 18 and the marks in Maths are 13, then marks in English will be 30 – 13 = 17., , 1, , 1, , Section-C, 11, , We have to draw two concentric circles of radii 3 cm and 5 cm. Construct a, tangent to the smaller circle from a point on the larger circle. Also, measure its, length., , 4, , Let P be a point on the outer circle., Steps of construction:, (i) Draw two concentric circles with centre O and radii 3 cm and 5 cm., (ii) Taking a point P on outer circle, join OP., (iii) Bisect OP, let M′ be the mid-point of OP., Taking M′ as centre and OM′ as radius draw a circle dotted which cuts the inner, circle as M and P′., (iv) Join PM and PP′., PM and PP′ are the required tangents., OR, Steps of construction:, 1. Construct a circle with O as centre and 4 cm radius, 2. Construct any diameter AOB, 3. Construct an angle ∠AOP = 60º where OP is the radius which intersect the, circle at the point P, 4. Construct PQ perpendicular to OP and BE perpendicular to OB, PQ and BE intersect at the point R, 5. RP and RB are the required tangents, 6. The measurement of OR is 8 cm
Page 83 :
4, , 12, , C. I., , FREQUENCY (f), , 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80, TOTAL, , 5, 3, f, 7, 2, 6, 13, 36+f, , CLASS MARK, (x), 15, 25, 35, 45, 55, 65, 75, , fx, 75, 75, 35f, 315, 110, 390, 975, 1940+35f, , 2, , 1, Σfx, , Mean = Σf =, , 1940+35𝑓, 36+𝑓, , ….(i), , But mean = 52 …….(ii), From (i) and (ii), 1940+35𝑓, = 52, 36+𝑓, , 1, , 1940+ 35f = 1872 + 52f, 17f = 68, f =4, 13, (i), , Volume of Drop = Volume of cone + Volume of hemisphere, = (1/3)πr²h + (2/3)πr³, h = height of cone, r = 1 mm, Height of drop = h + r = h + 1 mm, (1/3)π(1)²h + (2/3)π(1)³ = 3.14, π = 3.14, = h/3 + 2/3 = 1, = h/3 = 1/3, , 1
Page 84 :
=h=1, 1, , Height of drop = 1 + 1 = 2 mm, Number of drops to fill the pot completely = Volume of pot / volume of one, (ii) drop, = 1256/ (Volume of cone + Volume of hemisphere), = 1256/ [(1/3)πr²h + (2/3)πr³], , 1, , = 1256 / [(1/3) × 3.14 + (2/3) × 3.14] {here h=r=1 mm }, = 1256 / 3.14, , 1, , = 400, 14, (i), , A, , B, , Here AB=6 m , ∠ BCA = 600 , AC = ?, Taking sine in ∆ ABC, 𝐴𝐵, sin C = 𝐴𝐶, sin 600 = 6/x, C, , √3, 2, , =𝑥, , Or x = 4√3 m, (ii), , 1, , 6, , Here BC=5 m , ∠ BCA =, Taking cosine in ∆ ABC, 𝐵𝐶, cos C = 𝐴𝐶, cos 300 = 5/x, √3, 2, , 5, , =𝑥, , Or x =, , 1, , 300, , , AC = ?, 1, , 1, 10√3, 3, , m