Page 1 :
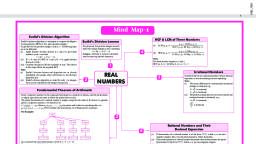
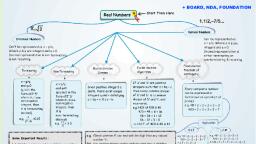
Key Notes, Chapter-03, Pair of Linear Equation in Two Variables, •, , Algebraic Expression: A combination of constants and variables, connected by four, fundamental arithmetical operations of +, −, × and ÷ is called an algebraic expression. For, example, 3 x 2 + 4 xy − 5 y 2 is an algebraic expression., , •, , Equation: An algebraic expression with equal to sign (=) is called the equation. Without an, equal to sign, it is an expression only. For example, 3x + 9 = 0 is an equation, but 3x + 9 is an, expression., , •, , Linear Equation: If the greatest exponent of the variable(s) in a equation is one, then, equation is said to be a linear equation., , •, , The most general form of a pair of linear equations is:, , a1x + b1 y + c1 = 0, a2 x + b2 y + c2 = 0 Where a1 , a2 , b1 , b2 , c1 , c2 are real numbers and, a1, 2 + b1, a12 + b12 ≠ 0, a 22 + b 22 ≠ 0., •, , •, , The graph of a pair of linear equations in two variables is represented by two lines;, (i), , If the lines intersect at a point, the pair of equations is consistent. The point of, intersection gives the unique solution of the equation., , (ii), , If the lines coincide, then there are infinitely many solutions. The pair of equations is, consistent. Each point on the line will be a solution., , (iii), , If the lines are parallel, the pair of the linear equations has no solution. The pair of, linear equations is inconsistent., , If a pair of linear equations is given by a1x + b1Y + c1 = 0, , and a 2 x + b2 y + c2 = 0, , (i), , a1 b1, ≠, ⇒ the pair of linear equations is consistent. (Unique solution)., a 2 b2, , (ii), , a1 b1 c1, =, ≠ ⇒ the pair of linear equations is inconsistent (No solution)., a 2 b2 c2, , (iii), , a1 b1 c1, =, = ⇒ the pair of linear equations is dependent and consistent (infinitely, a 2 b2 c2, , many solutions).