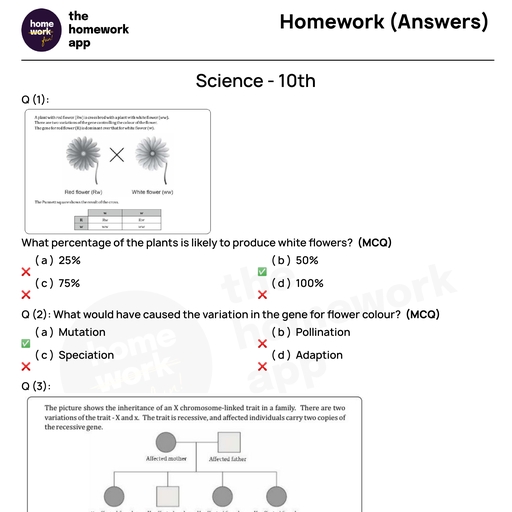
Page 1 :
CONTENT, S, No, , Name of Chapter, , Case Study, questions, , Real Numbers, , Concept, based, questions, 17, , 1, 2, , Polynomials, , 22, , 8, , 3, , Pair of Linear, Equations, Triangle, , 23, , 8, , 25, , 5, , Co – ordinate, Geometry, Introduction to, trigonometry, Area related to, circles, , 17, , 5, , 17, , 5, , 22, , 8, , Probability, , 18, , 8, , 161, , 53, , 4, 5, 6, 7, 8, , Total, , 6

Page 2 :
KENDRIYA VIDYALAYA SANGATHAN, HEDERABAD REGION, CLASS X MCQ QUESTION BANKMATHEMATICS, CHAPTER-1 (REAL NUMBERS), SECTION A, (CONCEPTUAL BASED MCQS), 1., , If m = pq3 and n = p3q,then HCF (m, n) =, a) pq, b) pq3, c) p3q3, , d) p2q3, , 2., , HCF of co-primes a and b is, a) ab, b) 1, , d) b, , 3., , The LCM of smallest composite number and the smallest prime number is, a) 2, b) 1, c) 4, d) 3, , 4., , Which of the following rational numbers have terminating decimal?, 16, 5, 2, 7, i), ii), iii), iv), 125, 18, 21, 250, a) i and ii, b) ii and iii, c) i and iii, d) i and iv, , 5., , After how many places the decimal expansion of 3 2 terminates?, 2 ×5, a) 3, b) 2, c) 4, d) 1, , 6., , The LCM and HCF of two rational numbers are equal, then the numbers must be, a) prime, b) co-prime c) composite d) equal, , 7., , Two positive numbers have their HCF as 12 and their product as 6336.The number of pairs possible, for the numbers, is…., a) 2, b) 3, c) 4, d) 5, , 8., , If the LCM of a and 18 is 36 and the HCF of a and 18 is 2, then a = …, a) 2, b) 3, c) 4, d) 1, , 9., , The least number that is divisible by all the numbers between 1 and 10 (both inclusive) is, a) 2520, b) 2450, c) 2420, d) 2250, , 10., , The smallest number which gives remainders 8 and 12 when divided by 28 and 32 respectively is.., a) 180, b) 240, c) 204, d) 210, , 11., , The smallest 4 digit number divisible by 24,15 and 36 is, a) 1000, b) 1208, c) 1800, d)1080, , 12., , The largest number which exactly divides 280 and 1245 leaving remainders 4 and 3respectively, is…, a) 36, b) 54, c) 138, d) 72, , 13., , The ratio of LCM and HCF of the least composite and the least prime numbers is, a) 1:2, b) 2:1, c) 1:1, d) 1:3, , 14., , If sum of two numbers is 1215 and their HCF is 81, then the possible number of pairsof such, numbers are, , c) a, , 13

Page 3 :
a) 2, , b) 3, , c) 4, , d) 5, , 15., , The sum of the exponents of the prime factors in the prime factorisation of 196,is, a) 1, b) 2, c) 4, d) 6, , 16., , The LCM of two numbers is 1200,Which of the following cannot be their HCF?, a) 600, b) 500, c) 400, d) 200, , 17., , ���� is, 3.27, a) an integer, , b) a rational number c) a natural number, , d) an irrational number, , Answers: 1 (a), 8 (c), 15 (c), , 2 (b), 9 (a), 16 (b), , 3 (c), 10 (c), 17 (b), , 4 (d), 11 (d), , 5 (a), 12 (c), , 6 (d), 13 (b), , 7 (a), 14 (c), , SECTION B, (CASE STUDY BASED QUESTIONS), 1., Three sets of English, Hindi and Mathematics books have to be stacked in such a way that all the, books are stored topic-wise and the height of each stack is same. The number of English books is 96,the, number of Hindi books is 240 and the number of Mathematics books is 336. Assuming that the books are, of the same thickness. Using this data answer the following questions, i. The maximum number of books in each stack is, a) 12, b) 24, c) 48, d) 36, ii. Number of stacks of English books is, a) 2, b) 7, c) 5, , d) 12, , iii. Number of stacks of Mathematics books is, a) 2, b) 7, c) 5, , d) 12, , iv. Number of stacks of Hindi books is, a) 2, b) 7, c) 5, , d) 12, , v. Which Mathematical concept was used in finding the maximum number of books in each stack?, a) LCM b) HCF, c) Neither HCF nor LCM, d) Fundamental theorem of Arithmetic, 2., 105 goats,140 donkeys and 175 cows have to be taken across a river. There is only one boat which, will have to make many trips in order to do so. The lazy boatman has his own conditions for transporting, them. He insists that he will take the same number of animals in every trip and they have to be of same, kind. He will naturally like to take the largest possible number each time., i. How many animals have been taken in each trip?, a) 12, b) 35, c) 70, d) 24, ii. How many trips to be done so that all animals crossed the river?, a) 12, b) 35, c) 70, d) 24, iii. When the animals were doubled,how many animals could be taken in each trip?, a) 12, b) 35, c) 70, d) 24

Page 4 :
iv. The LCM of all animals is, a) 2400, b) 2300, , c) 2100, , d) 2000, , 3., To enhance the reading skills of grade X students, the school nominates you and two of your, friends to set up a class library. There are two sections –Section A and Section B of grade X. There are 32, students in section A and 36 students in section B, i. What is the minimum number of books you will acquire for the class library, so that they can, bedistributed equally among students of Section A or Section B?, a) 144, b) 128, c) 288, d) 272, ii. If the product of two positive integers is equal to the product of their HCF and LCM is true, thenthe, HCF(32,36)is.., a) 2, b) 4, c) 6, d) 8, iii. 36 can be expressed as a product of its primes as, a) 22 x 32, b) 21 x 33, c) 23 x 31, d) 20 x 30, iv. 7 x 11 x 13 x 15 + 15 is a, a) Prime number, b) composite number c) neither prime or composite d) None of the above, v. If p and q are positive integers such that p = ab2 and q = a2b,where a and b are prime, then the LCM (p, q) is…, a) ab, b) a2b2, c) a3b2 d) a3b3, , numbers,, , 4., A seminar is being conducted by an Educational Organisation,where the participants will be, educators of different subjects. The number of participants in Hindi,English and Mathematics are 60, 84, and 108 respectively., i. In each room the same number of participants are to be seated and all of them being in the same, subject, hence maximum number participants that can accommodated in each room are, a) 14, b) 12, c) 16, d) 18, ii. What is the minimum number of rooms required during the event?, a) 11, b) 31, c) 41, d) 21, iii. The LCM of HCF and LCM of 60, 84 and 108 is, a) 3780, b) 3680, c) 4780, d) 4680, iv. The product of HCF and LCM 60,84 and 108 is…, a) 55360, b) 35360, c) 45500, d) 45360, v. 108 can be expressed as a product of its primes as, a) 22 x 32, b) 23 x 33, c) 22 x 32, d) 22 x 33, 5., A mathematical Exhibition is being conducted in your school and one of your friends is making a, model of a factor tree. He has some difficulty and ask for your help in completing a quiz for the audience., Observe the following factor tree and answer the following.

Page 5 :
i. What will be the value of x?, a) 15005, b) 13915, , c) 56920, , d) 17429, , ii. What will be the value of y?, a) 23, b) 22, , c) 11, , d) 19, , iii. What will be the value of z?, a) 22, b) 23, , c) 17, , d) 19, , iv. According to Fundamental Theorem of Arithmetic, 13915 is a., a) Composite number, b) Prime number, c) Neither prime nor composite, d) Even number, v. The prime factorisation of 13915 is, b) 5 x 113 x 232, a) 5 x 113 x 132, , c) 5 x 112 x 23, , d) 5 x 112 x 132, , 6., Klick has a camera that takes film that allows 24 exposures,whereas Snapp has a camera that takes, film that allows 36 exposures.Both of them want to be able to to take the same number of photographs, and complete their rolls of film., i. Minimum number of exposures that should be taken by each, a) 24, b) 36, c) 72, d) 12, ii. Number of rolls Klick should buy, a) 6, b) 3, c) 2, , d) 12, , iii. Number of rolls Snapp should buy, a) 6, b) 3, c) 2, , d) 12, , iv. Which Mathematical concept was used in finding minimum number of exposures taken by each, a) HCF b) LCM, c) Neither HCF nor LCM, d) Fundamental theorem of Arithmetic, Answers: 1 (i) (c), 2 (iii) (c), 4 (i) (b), 5 (iii) (a), , 1 (ii) (a), 2 (iv) (c), 4 (ii) (d), 5 (iv) (d), , 1 (iii) (b), 3 (i) (c), 4 (iii) (a), 5 (v) (d), , 1 (iv) (c), 3 (ii) (b), 4 (iv) (d), 6 (i) (c), , 1 (v) (b), 3 (iii) (a), 4 (v) (d), 6 (ii) (b), , 2 (i) (b), 3 (iv) (b), 5 (i) (b), 6 (iii) (c), , 2 (ii) (a), 3 (v) (b), 5 (ii) (d), 6 (iv) (b)

Page 6 :
CHAPTER-2 (POLYNOMIALS), SECTION A, (CONCEPTUAL BASED MCQS), Choose the correct answer from the given four options in the following questions., 1., The number of zeroes of the given polynomial, (x+1)2(x+2)(x-3)is, (a) 2, (b) 3, (c) 4, d) 1, 2., , The zeroes of the polynomial x2 -3x – m(m+3) are, (a) m, m +3, (b) -m, m+3 (c) m, -(m + 3)(d) -m, -(m + 3), , 3., , If one of the zeroes of the quadratic polynomial (k-1) x2+ k x + 1 is -3, then the Value of k is, 4, −4, 2, −2, (a), (b), (c), (d), , 4., , 3, , 3, , 3, , 3, , 1, , 1, , If α and β are zeroes of the polynomial f(x) = x2- x - 4, then the value of ( )+( )-αβ, (a), , 15, 4, , (b), , −15, 4, , (c) 4, , (d) 15, , α, , β, , 5., , The value of the polynomial x8– x5+ x2- x + 1is, (a) Positive for all the real numbers, (b) Negative for all the real numbers., (c) O, (d) depends on value of x., , 6., , If the zeroes of the quadratic polynomial x2+ (a + 1) x + b are 2 and -3, then, (a) a= -7, b = -1, (b) a = 5, b = -1, (c) a = 2, b = -6, , 7., , Given that one of the zeroes of the cubic polynomial a x3 + b x2 + cx + d is zero, the product of, theother two zeroes is, −c, c, b, (a), (b), (c) 0, (d), a, , a, , (d) a = 0, b = -6, , a, , 8., , The graph of the polynomial ax2+ bx + c is an upward parabola if, (a) a>0, (b) a< 0, (c) a = 0, (d) none, , 9., , If a-b, a and (a + b) are zeroes of the polynomial f(x) = 2x3 – 6x2+ 5x - 7, then the value of a is, (a) 1, (b) 2, (c) -5, (d) 7, , 10., , If one of the zeroes of a quadratic polynomial of the form x2+ ax + b is the negative of the, other,then it, (a) has no linear term and the constant term is negative., (b) has no linear term and the constant term is positive., (c) can have a linear term but the constant term is negative., (d) can have a linear term but the constant term is positive., , 11., , x2 – ax3+ bx2- cx + 8 = 0 divided by (x -1) leaves a remainder of 4, divided by (x + 1) leaves a, remainder 3, then b =, (a) 2.5, (b) -5.5, (c) 3.5, (d) 6.5, , 12., , On dividing x3– 3x2+ x + 2 by a polynomial g(x), the quotient and remainder were(x - 2) and (-2x +, 4) respectively, then g(x) is equal to, (a) x2+ x +1, (b) x2+ 1, (c) x2- x + 1 (d) x2– 1, , 13., , A quadratic polynomial when divided by (x + 2),leaves a remainder of 1 andwhen divided by (x –, 1), leaves a remainder of 4. What will be the remainder if it is divided by (x + 2)(x - 1)?, (a) 1, (b) 4, (c) x +3, (d) x – 3

Page 7 :
14., , The polynomial f(x) = ax3+ bx - c is divisible by the polynomial g(x) = x2+ bx+c, c≠0 if, (a) ab = 2, (b) ab = 1, (c) ac = 2, (d) c = 2b, , 15., , If a cubic polynomial with sum of its zeroes, sum of the product of its zeroes taken two at a time,, and product of its zeroes as 2, -5 and -11 respectively, then the cubic polynomial is, (a) x3-2x2 -5x -11, (b) x3+2x2 -5x -11, (c) x3+2x2 -5x +11, (d) x3-2x2 -5x +11, , 16., , If α and β are the zeroes of the quadratic polynomial f(x) = ax2+ bx + c, then the value ofα4+ β4is, (a), , (b2 −2ac)2 +a2 c2, a4, , (b), , (b2 +2ac)2 +a2 c2, a4, , (c), , (b2 −2ac)2 −2a2 c2, a4, , (d), , (b2 +2ac)2 +2a2 c2, a4, , 17., , If the polynomial x4 – 6x3 + 16x2 – 25x +10 is divided by another polynomialx2 -2x +k,The, remainder comes out to be x +a, then k = _______ a=_______., (a) 5,-5, (b) -5, 5, (c) 0, 5, (d) 5, 0, , 18., , A quadratic of polynomial, whose zeroes are 5 and -8 is, (a) x2 +13x – 40, (b) x2 +4x – 3, (c) x2 -3x +40 (d) x2 +3x – 40, , 19., , The number of polynomials having zeroes as -2 and 5 is, (a) 1, (b) 2, (c) 3, (d) more than 3, , 20., , If 2 and α are zeroes of x2 - 3x +2, then the value of α is, (a) 2, (b) 3, (c) 1, (d) 5, , 21., , If one of the zeroes of the cubic polynomial x3 + px² + qx + r is -1, then the product of the other two, zeroes, is, (a) p + q + 1, (b) p-q- 1, (c) q – p + 1, (d) q – p – 1, , 22. Given that two of the zeroes of the cubic polynomial ax3 + bx2 + cx +d are 0,the value of c is, a) less than 0 b) greater than 0, c) equal to 0, d) can’t say., Answers: 1 (c), 8 (a), 15 (d), 22(c), , 2(b), 9 (a), 16 (c), , 3 (a), 10 (a), 17 (a), , 4 (a), 11 (b), 18(d), , 5 (a), 12 (c), 19(d), , 6 (d), 13(c), 20(c), , 7 (b), 14 (b), 21(c), , SECTION B, (CASE STUDY BASED QUESTIONS), 1., , A child was flying a kite, its string got struck into a tree and touched ground as shown in figure

Page 8 :
i. The string of the kite represents the graph of a, (a) Linear polynomial, (b) Quadratic polynomial, (c) Cubic polynomial, (d) Constant polynomial, ii. The number of zeroes of a quadratic polynomial is, (a) 1, (b) utmost 2, (c) 3, , (d) none of the above., , iii. If the zeroes of polynomial x²-12x+(3k-1) is five times the other then k is, (a) 2, (b) 3, (c) 10, (d) 7, 2., The below pictures are few natural examples of parabolic constructions which are represented by, a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola in structures; their curve, represents an efficient method of load and so can be found in bridges and in architecture in a variety of, forms., , i. In the standard form of quadratic polynomial ax²+bx+c where a,b and c are, (a) All are real, (b) All are rational numbers., (c) a is a non-zero real number and b and c are any real numbers., (d) All are integers, ii. If the roots of the quadratic polynomial are equal then, (a) a²=bc, (b) a=b(c) b=c (d) b2=4ac, iii. If the sum of the roots is –p and product of the roots is -1/p then the quadratic polynomial is, 𝑥𝑥, 𝑥𝑥, 1, 1, (a) k(-px²+ +1) (b) k(-px² - - 1), (c) k(x²+px- )*, (d) k(x²- px+ ), 𝑝𝑝, , 𝑝𝑝, , 𝑝𝑝, , 𝑝𝑝, , 3., Newtonian mechanics demonstrates that the displacement of an object in free fall is given by the, 1, relation s = ut + at², where s is the displacement, u is the initial velocity, a is the acceleration, and t is the, 2, time. This displacement equation is a polynomial expression. Polynomials enable people to describe the, physical world., i. For example, assume that a ball is released from rest at the top of a building measuring 8.52 meters, tall. How long does it take for that ball to reach the ground?, (a) 1.23 seconds, (b) 9.8 seconds, (c) 1.32 seconds, (d) 32 minutes, ii. Which is the true statement, (a) If time increases the displacement increases., (b) If time decreases the displacement increases., (c) Time is not changing, but displacement is happening., (d) None of the above., 4., HONEYCOMB: While playing in the mango garden Sudhir saw honeycomb and asked his father, about that. His father replied that A honeycomb is a mass of hexagonal prismatic wax cells built by honey, bees in their nests to contain their larvae and stores of honey and pollen., Beekeepers may remove the entire honeycomb to harvest honey. Honey bees consume about 8.4 lb (3.8, kg) of honey to secrete 1 lb (450 g) of wax and so beekeepers may return the wax to the hive after

Page 9 :
harvesting the honey to improve honey outputs. The structure of the comb may be left basically intact, when honey is extracted from it by uncapping and spinning in a centrifugal machine, more specifically a, honey extractor. His father told that honeycomb formed is parabolic. The mathematical representation of, the honeycomb structure is shown in the graph., , i. Graph of the quadratic polynomial is ______ in shape., (a) Straight line, (b) Parabola, (c) Circular, , (d) None of the above., , ii. The expression of the polynomial represented by the graph is, (a) x²-49, (b) x²-64, (c) x²-36, (d) x²-81, iii. find the value of the polynomial when x=3, (a) 27, (b) -27, (c) 36, , (d) none of the above., , iv. The product of the zeroes of the polynomial 7x²-3x+4 is, 3, 4, 4, 3, (a) (b), (c) (d), 7, , 7, , 7, , 7, , 5., A metalworker makes an overflow pan by cutting equal squares with sides of length x from the, corners of a 30 cm by 20 cm piece of aluminium, as shown in the figure. The sides are then folded up and, the corners sealed. Drain pans aren’t a requirement for your washer, but they are an inexpensive and, simple way of protecting your home by catching small leaks and reducing the amount of water damage, from broken hoses. If your laundry room is upstairs, a drain pan is recommended to protect against leaks, that can seep into the rooms below., , i. Which of the following polynomial function V (x) gives the volume of the pan?, (a) 4x3-60x2+450x, (b) 4x3-100x2+600x, (c) 4x3-65x2+600x, (d) 4x3-60x2+500x, ii. What is volume of the pan if the height is 6 cm?, (a) 518 cm3, (b) 746 cm3 (c) 648 cm3 (d) 864 cm3, 6., FACOR, VIZIANAGARAM has got an order for making a frame for machine of their client. For, which, they are using a AutoCAD software to create a constructible model that includes the relevant, information such as dimensions of the frame and materials needed The frame will have a solid base and

Page 10 :
will be cut out of a piece of steel. The final area of the frame should be 54 m2. The diagram of frame is, shown below, , AutoCAD is a commercial computer-aided design (CAD) and drafting software application. Developed, andmarketed by Autodesk, AutoCAD was first released in December 1982 as a desktop app running on, microcomputers with internal graphics controllers. Before AutoCAD was introduced, most commercial, CAD programs ran on mainframe computers or minicomputers, with each CAD operator (user) working, at a separate graphics terminal. AutoCAD is also available as mobile and web apps., In order to input the right values in the AutoCAD software, the engineer needs to calculate some basic, values, Answer the questions:, i. What are the dimensions of the outer frame?, (a) 10 + x and 5 + x, (b) 10 - x and 5 – x, , (c) 10 +2x and 5+ 2x, , (d) 10-2x and 5 -2x, , ii. A metal sheet of minimum area is used to make the frame. What should be the minimum area of, metal sheet before cutting?, (c) 5x2 +30 (d) 4x2 +50, (a) 4x2+30x+50 (b) x2+27x+55, 7., In a soccer match, the path of the soccer ball in a kick is recorded as shown in the following, graph., , Based on the above information of the above information, answer the following questions:, i. The shape of path of the soccer ball is a, (a) Circle, (b) Parabola, (c) Line, (d) None of the these, ii. The axis of symmetry of the given parabola is, (a) y-axis, (b) x-axis, (c) Line parallel to y-axis, , (d) Line parallel to y-axis., , iii. The zeroes of the polynomial, represented in the given graph, are, (a) (-1, 7), (b) (5, -2), (c) (-2, 7), (d) (-3, 8), iv. Which of the following polynomial has -2 and -3 as its zeroes, (a) x2 – 5x - 5, (b) x2+ 5x –6, (c) x2+6x - 5, (d) x2+ 5x +6, v. For what value of 'x', the value of the polynomial f(x)=(x−3)2+9 is 9?, (a) 1, (b) 2, (c) 3, (d) 4

Page 11 :
8., While playing badminton in the park Raju seeing the barrier chains hung between two posts at the, edge of the walk way of a street. It is hung in the shape of the parabola. Parabola is the, graphicalrepresentation of a particular type of polynomial., , i., , Which of the following polynomial is graphically represented by a parabola, (a) Linear polynomial, (b) Quadratic polynomial, (c) Cubic polynomial, (d) None of the above., , ii., , If a polynomial, represented by a parabola, intersects the X-axis at -3, 4 and Y-axis at -2 then, itszero(es) is/are, (a) -1,2 and -2, (b) 2 and -2, (c) -1, (d) -3 and 4, , Answers: 1 (i) (a), 3 (ii) (a), 6 (i) (c), 7 (v) (c), , 1 (ii) (b), 4 (i) (b), 6 (ii) (a), 8 (i) (b), , 1 (iii) (d), 4 (ii) (c), 6 (iii) (b), 8 (ii) (d), , 2 (i) (c), 4 (iii) (b), 7 (i) (b), , 2 (ii) (d), 4 (iv) (b), 7 (ii) (c), , 2 (iii) (c), 5 (i) (b), 7 (iii) (c), , 3 (i) (c), 5 (ii) (d), 7 (iv) (d)

Page 12 :
CHAPTER-3 (PAIR OF LINEAR EQUATIONS IN TWO VARIABLES), SECTION A, (CONCEPTUAL BASED MCQS), 1., , If seven books and 5 pens cost Rs 410, whereas five books and seven pens cost Rs.334 then the cost ofthree, books and four pens would be, , a) Rs.135, , b) Rs.145, , c) Rs.255, , d) Rs.198, , 2., , The pair of equations x = 2 and y = 3 graphically represents the lines which are, (a) Coincident (b) intersecting at (2, 3), (c) parallel, (d) intersecting at (3, 2), , 3., , The pair of equations x+3y=12 and 2x +6y-24=0 represents:, a) Consistent system with unique solution, b) Consistent system with infinite solution, c) Inconsistentsystem with unique solution, d) Inconsistent system with no solution, , 4., , The pair of linear equations which has unique solution as x=3 and y= -1 is, a) x – y=4 and 2x –y = 6, b) x+y= 2 and 2x +3y = 3, c) x-2y= 5 and 2x +3y= 9, d) x+2y = 1 and 2x +y =7, , 5., , For what value of k, 2x+3y=4, (k+2) x+6y=3k+2 will have infinitely many solutions., a) 1, b) 4, c) 5, d) 2, , 6., , Two numbers are in the ratio 5:6. If 8 is subtracted from each of the numbers, the ratio becomes, 4:5. Find the numbers, a) 45, 54, b) 40,48, c) 55,66, d) 50,60, , 7., , Given the linear equation 4x +6y − 9 =0, another linear equation in two variables such that the, geometrical representation of the pair(s),so formed will be consistent is:, (i) 2x+3y – 9=0 (ii) 5x -6y – 9=0, (iii) 8x+12y -18=0, (iv) 12x+ 18y -18=0, a) Only (ii) and (iii), b) None of the above, c) All the above, d) Only (i) and (iv), , 8., , The graph of the pair of linear equation𝑠𝑠 𝑎𝑎1 𝑥𝑥 + 𝑏𝑏1 𝑦𝑦 + 𝑐𝑐1 = 0, 𝑎𝑎2 𝑥𝑥 + 𝑏𝑏2 𝑦𝑦 + 𝑐𝑐2 = 0 will be, intersecting if, 𝑎𝑎, 𝑏𝑏, 𝑎𝑎, 𝑏𝑏, 𝑎𝑎, 𝑏𝑏, 𝑐𝑐, 𝑎𝑎, 𝑏𝑏, 𝑐𝑐, a) 1 = 1, b) 1 ≠ 1, c) 1 = 1 ≠ 1 d) 1 = 1 = 1, , 9., , 10., , 𝑎𝑎2, , 𝑏𝑏2, , 𝑎𝑎2, , 𝑏𝑏2, , 𝑎𝑎2, , 𝑏𝑏2, , 𝑐𝑐2, , 𝑎𝑎2, , 𝑏𝑏2, , 𝑐𝑐2, , Solve 2𝑥𝑥 + 3𝑦𝑦 = 11and 2𝑥𝑥 − 4𝑦𝑦 = −24 and hence find the value of ‘m’ for such that 𝑦𝑦 = 𝑚𝑚𝑚𝑚 +, 3., a) -1, b) 1, c) 0, d) -2, , The pair of equations 5𝑥𝑥 − 15𝑦𝑦 = 8 and 3𝑥𝑥 − 9𝑦𝑦 = 24 has, (a) One solution, (b) two solutions, (c) infinitely many solutions, , (d) no solution, , 11., , If2x-3y=7 and (a +b)x - (a+b-3)y=4a+b have infinite solution, then value of(a, b) is, a) (-3,1), b) (-5,-1), c) (5,1) d) (3,-1), , 12., , The sides of a rectangle are 19 units,10 units, 2x - y and - x + 2y units as shown in the figure given below, then the values of x, y and x + y are:

Page 13 :
a) 16,13,29, , b) 13,16,29, , c) 10,19,29, , d) 19,10,29, , 13., , The cost of an article A is 10 % more than the cost of article B if their total cost is ₹441 then cost of, article A and B are, a) ₹210, ₹231, b) ₹231, ₹210, c) ₹ 221, ₹220, d) ₹220, ₹ 221, , 14., , What type of straight lines will be represented by the system of equations 2x + 3y =5 and 4x + 6y =, 7?, a) Always intersecting b) parallel, c) coincident d) coincident or intersecting, , 15., , Difference of the areas of two squares is 144 m2. If the difference of their perimeters is 32 m, then, the sides of the two squares is:, a) 12m and 13 m, b) 13 m and 5 m, c) 13m and 8 m, d) 12 m and 8 m, , 16., , If a pair of linear equations is consistent, then the graph of the lines will be, (a) Parallel, (b) intersecting, (c) intersecting or coincident d) always coincident, , 17., , If the lines given by x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then the value of k is:, −5, −2, 5, a), b), c), d) 5, , 18., , 19., , 4, , 5, , 4, , The solution for the given system 𝑥𝑥 + 𝑦𝑦 = 𝑎𝑎 + 𝑏𝑏, 𝑎𝑎𝑎𝑎 − 𝑏𝑏𝑏𝑏 = 𝑎𝑎2 − 𝑏𝑏 2 is, 1, 1, a) 𝑥𝑥 = 2𝑎𝑎, 𝑦𝑦 = 𝑏𝑏, b) 𝑥𝑥 = 𝑎𝑎, 𝑦𝑦 = 2𝑏𝑏, c) 𝑥𝑥 = 𝑎𝑎, 𝑦𝑦 = 𝑏𝑏, d) 𝑥𝑥 = , 𝑦𝑦 =, 𝑥𝑥, , 𝑦𝑦, , The area of triangle formed by the line + = 1 with the coordinate axes is, a) 2ab, , b) ab, , 1, , c) ab, 4, , 𝑎𝑎, , 𝑏𝑏, , 𝑎𝑎, , 𝑏𝑏, , 1, , d) ab, 2, , 20., , Sharat has ₹2 and ₹5 coins with him.If total number of coins are 16 and the amount of money, is ₹ 50, Then the number of ₹2 and ₹5 coins are, a) 8 and 8, b) 6 and 10 c) 10 and 6, d) 15 and 4, , 21., , The pair of linear equations 𝑦𝑦 = 2 𝑎𝑎𝑎𝑎𝑎𝑎 𝑦𝑦 = −3 has, a) Only one common solution, b) no common solution, c) many common solutions, d) none of the above, , 22., , Which of the following pairs of linear equations are consistent?, a) x – y = 8, 3x – 3y = 16, b) x + y = 5, 2x + 2y = 15, c) 2x + y – 6 = 0, 4x – 2y – 4 = 0, d) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0, , 23., , The solution of the pair of linear equations x + 3y = 6 and 2x – 3y = 12, representedgraphically is, a) (6, 0), b) (0, 0), c) (0, 2), d) (0,-4)

Page 14 :
Answers: 1 (d), 8 (b), 15 (b), 22 (c), , 2 (b), 9 (a), 16 (c), 23(a), , 3 (b), 10 (d), 17 (c), , 4 (b), 11 (b), 18 (c), , 5 (d), 12 (a), 19 (d), , 6 (b), 13 (b), 20 (c), , 7 (a), 14 (b), 21 (b), , SECTION B, (CASE STUDY BASED QUESTIONS), 1., Arav planned a surprise for his grandparents, he and his family consisting of his father,, mother and his sister aged 10 years, planned to take his grandfather and grandmother who were, above 60 years to an amusement park. Arav who is 2 years older than his sister insisted on enjoying, family rides while his sister wanted to go for kids rides in the amusement park.The cost of ticket, and the cost of rides are given in table 1 and 2 respectively:, , Adults, Children, Seniorcitizen(above 60years), , TABLE 1, Cost (onweek days) in₹, 815, 635, 500, , Cost (on weekends) in ₹, 1025, 925, 600, , TABLE 2, Type of ride, Family rides, Kids rides(only for children of age 13 years or less than 13), , Cost of ride for each, member(in ₹), z, P, , i. If x adults and y children went to park on Wednesday and they paid Rs 4985 for the tickets, the linear, equation would be:, a) 1025𝑥𝑥 + 925𝑦𝑦 = 4985, b) 500𝑥𝑥 + 600𝑦𝑦 = 4985, c) 815x + 635y = 4985, d) 635𝑥𝑥 + 925𝑦𝑦 = 4985, , ii. Cost of kids ride is half the cost of family ride then the equation would be, a) z- 2p =0, b) p=2z, c) z+2p=0, d) z=p, , iii. If Arav and his sister took kids ride and remaining 4 members took family rides and they paid, ₹500,the equation representing the situation is:, a) 4p+2z= 500, b) 2z = 4p+500, c) z-2p = 500, d) 4z+2p = 500

Page 15 :
iv. If all 6 of them had taken up family rides then they would have paid ₹600 then what is the cost of a, family ride for each member, a) ₹200, b) ₹100, c) ₹50, d) cannot say, v. If the speed of family ride is 10 more than twice the speed of kids ride, the equation would be:, (taking speed of family ride as 𝑥𝑥 m/sec and kids ride as y m/sec), a) 𝑥𝑥 = 10 + 2𝑦𝑦, b) 𝑦𝑦 = 10 + 2𝑥𝑥, c)𝑥𝑥 + 𝑦𝑦 = 12, d) 4𝑦𝑦 − 4𝑥𝑥 = 12, , 2., Rahul is studying in X Standard. He is making a kite to fly it on a Sunday. Few questions came to, his mind while making the kite. Give answers to his questions by looking at the figure., , The length of the sides are AB = 20 cm, BC = X+Y,CD= 35 CM,AD = X+2Y, i. Based on the information given above which of the following pair of equations are correct:, a) 𝑥𝑥 + 𝑦𝑦 = 20 and 𝑥𝑥 + 2𝑦𝑦 = 35, b) 𝑥𝑥 + 𝑦𝑦 = 35 and 𝑥𝑥 + 2𝑦𝑦 = 20, c) 𝑥𝑥 = 𝑦𝑦 + 20 and 2𝑦𝑦 = 35 + 𝑥𝑥, d) 𝑥𝑥 = 35 + 𝑦𝑦 and 2𝑦𝑦 = 20 + 𝑥𝑥, , ii. On solving the equations the value of y would be, a) 20, b) 15, c) 10, d) 5, , iii. On drawing the graph of equation 𝑥𝑥 + 𝑦𝑦 = 20 which of the points given below will not lie on it, a) (-4,24), b) (0, -20), c) (20,0), d) (10,10), iv. The graph of linear equation 𝑥𝑥 + 𝑦𝑦 = 20 will intercept y axis at, a) ( -4,24) b) (0, -20), c) (20,0), d) (0,20), , v. The area of triangle formed by the line 𝑥𝑥 + 𝑦𝑦 = 20 with x and y axis would be, a) Approximately 200 sq units, b) Exactly 200 square units, c) Less than 200 square units, d) More than 200 sq units, , 3., Ramani and her friend Rita are doing their post-graduation and they have to stay in a hostel, away from their home. At the hostel , part of monthly hostel charges are fixed and the remaining, depends on the mess charge. When Ramani takes food for 22 days from mess, she has to pay ₹ 2000, as hostel charges whereas Rita, who takes food for 30 days, from mess pays ₹ 2400 as hostel, charges., i. Taking fixed monthly hostel charges as x and, mess charge to be y per day the, equationalgebraically representing the amount paid by Ramani would be, a) 𝑥𝑥 + 22𝑦𝑦 = 2000, b) 𝑥𝑥 + 22𝑦𝑦 = 2400 c) 𝑥𝑥 + 30𝑦𝑦 = 2000 d) 𝑥𝑥 + 30𝑦𝑦 = 2400, , ii. Taking fixed monthly hostel charges as x and mess charge to be y per day the equation, algebraically representing the amount paid by Rita would be, a) 𝑥𝑥 + 22𝑦𝑦 = 2000, b)𝑥𝑥 + 22𝑦𝑦 = 2400 c) 𝑥𝑥 + 30𝑦𝑦 = 2000 d) 𝑥𝑥 + 30𝑦𝑦 = 2400, , iii. The amount of fixed monthly hostel charge to be paid is:

Page 16 :
a) ₹800, , b) ₹700, , c) ₹900, , d) ₹65, , iv. The fees one has to pay towards mess charges , if they take food at the hostel for 12 days would, be, a) ₹600, b) ₹1200, c) ₹900, d) ₹1000, v. The equation 2𝑥𝑥 + 𝑦𝑦 = 100 has:, a) infinite solutions, c) (5, 95) is a solution of the equation, , b) only one solution, d) (100, 0) is a solution of the equation, , 4., Places A and B are 56km apart on a highway. One car starts from A and another from B at, the same time. If the cars travel in the same direction at different speeds, they meet in 4 hours. If, they travel towards each other, they meet in one hour., i. Taking the speed of car at A is x km/hr and that of car at B is y km/h. The equation that would, represent the situation algebraically (assume y>x) when the cars are travelling in opposite, direction, a) 𝑥𝑥 + 𝑦𝑦 = 56 b) 𝑥𝑥 − 𝑦𝑦 = 56, c)𝑥𝑥𝑥𝑥 = 56, d) 𝑦𝑦 − 𝑥𝑥 = 56, , ii. Taking the speed of car at A is x km/hr and that of car at B is y km/hr.The equation that would, represent the situation algebraically (assume y>x) when the cars are travelling in samedirection, a) 4𝑥𝑥 + 4𝑦𝑦 = 56, b) 4𝑥𝑥 − 4𝑦𝑦 = 56, c) 𝑥𝑥 + 𝑦𝑦 = 56, d) 4𝑦𝑦 − 4𝑥𝑥 = 56, , iii. The speed of car at A is:, a) 21 km/h, b) 35 km/h, , c) 56 km/h, , d) 15 km/h, , iv. The( speed of car A+ Speed of car B) is:, a) 21 km/h, b) 35 km/h, c) 56 km/h, , d) 25 km/h, , v. The graph of the equations obtained in (i) and (ii) would intersect at, a) (21, 35), b) (35, 21), c) (55, 35), d) (35,55), 5., The members of housing colony of fortune avenue took up the task of planting saplings in the parks, located in their venture it was informed that there are two possibilities, Case 1: 4 men and 6 boys can finish a piece of work in 5 days, Case 2: 3 men and 4 boys can finish it in 7 days., i. Assuming that a man can complete the work alone in x days, his work in four days would be:, 1, 4, a), b) x, c), d) 4x, 𝑥𝑥, , 𝑥𝑥, , ii. If a man alone takes x days to complete the work while a boy takes y days to complete the work. The, equation representing case 1 is given by:, 4, 6, 6, 4, 1, 6, 4, 4, 6, 1, a) + = 5, b) + =, c) + = 5 d) + =, 𝑥𝑥, , 𝑦𝑦, , 𝑥𝑥, , 𝑦𝑦, , 5, , 𝑥𝑥, , 𝑦𝑦, , 𝑥𝑥, , 𝑦𝑦, , 5, , iii. As per the case study, In how many days can a man alone complete the work., a) 35 days, b) 70 days, c) 50 days, d) 100 days, iv. For the equation, a) 4b +3a = 1, , 3, , 𝑥𝑥, , 4, , 1, , + = if, 𝑦𝑦, , 7, , 1, , 𝑥𝑥, , is taken as a and, , b) 3a + 4b = 1, , 1, , 𝑦𝑦, , is taken as b the equation would reduce to, , c) 21a + 28 b =1, , d) 21 b + 28 a = 7, 3, , 4, , v. Identify among the following which is a solution of the equation + =, a) (24,56) b) (42,24), , c) (42,56), , d) (24,24), , 𝑥𝑥, , 𝑦𝑦, , 1, 7

Page 17 :
6., Two students were playing with number cards one of the student observed that the sum of the two-digit, number he picked up and the number obtained by reversing the digits is 66. The digits of the number were found, to differ by 2.He asked his friend to answer the questions given below based on the clues he had given about the, number. His friend took the digit in tens place as x and the digit in ones place to be y, also he was told that 𝑥𝑥 > 𝑦𝑦, , i. The sum digits would be represented by the equation, a) x + y = 6, , b) x+6=y, , c) y +6+ x = 0 d) xy =6, , ii. If 10 x + y is the original number what would be the reversed number, a), , 𝑥𝑥, , 10, , b) 1y + 10 x, , + 𝑦𝑦, , c) x+10y, , d) x+, , 𝑦𝑦, , 10, , iii. The difference between the digits of the two digit number is two , the student wrote the following, equations :, , (I) x – y= 2, , (II) y – x=2, , (III) x=2+y, , (IV) y= 2+x, , Which of the following are true?, , a) All the above equations are correct, , b) None of the equations above are correct, , c) Only equations (I) and (III) are correct, , d) only equations (II) and (IV) are correct, , iv. The original number on the number card picked by the student is, a) 24, , b) 42, , c) 44, , d) 22, , v. The sum of original and twice the reversed number is:, a) 66, , b) 132, , c) 90, , d) 75, , 7., A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km, upstream and 55 km down-stream. Determine the speed of the stream and that of the boat in still water., Assuming the speed of boat to be x km/h and that of stream to be y km/h, Answer the questions below, i. The net speed of boat (in km/h) during upstream would be, 𝑥𝑥, a) x – y, b) x+y c), d) xy, 𝑦𝑦, , ii. The equation representing the first situation would be, 30, 44, 44, 30, 30, a), +, = 13, b), +, = 10 c), +, 𝑥𝑥−𝑦𝑦, , 𝑥𝑥+𝑦𝑦, , 𝑥𝑥−𝑦𝑦, , 𝑥𝑥+𝑦𝑦, , 𝑥𝑥−𝑦𝑦, , 44, , 𝑥𝑥+𝑦𝑦, , = 10, , d), , 40, , 𝑥𝑥−𝑦𝑦, , +, , 55, , 𝑥𝑥+𝑦𝑦, , = 10

Page 18 :
iii. Which of the following statement is true?, a) Speed of boat is 3 km/h, b) Speed of stream is 8 km/h, c) Speed of boat is 8 km/h, d) Speed of boat + stream is 10km/h, iv. The graph of the equation 40u +55v =13 would be, a) Linear, b) parabola, c) line parallel to x axis, , d) line passing through origin, , v. If the system of linear equations kx +2y =5 and 3x +y=1 has a unique solution then, 3, 2, a) 𝑘𝑘 ≠, b) 𝑘𝑘 = 6, c) 𝑘𝑘 ≠ 6, d) 𝑘𝑘 ≠, 2, , 3, , 8., A student was observing Railway tracks at secunderabad railway station, these tracks represent a, pair of linear equations as shown below, based on the observation answer the questions given:, , i. For the pair of linear equations shown in graph, 𝑎𝑎, 𝑏𝑏, 𝑎𝑎, 𝑏𝑏, 𝑎𝑎, 𝑏𝑏, 𝑐𝑐, a) 1 = 1, b) 1 ≠ 1, c) 1 = 1 ≠ 1, 𝑎𝑎2, , 𝑏𝑏2, , 𝑎𝑎2, , 𝑏𝑏2, , 𝑎𝑎2, , 𝑏𝑏2, , ii. The equation 3x+ 2y = 6 intersects x axis at, a) (0,3), b) (3,0), c) (2,0), , d), , 𝑐𝑐2, , 𝑎𝑎1, 𝑎𝑎2, , =, , 𝑏𝑏1, 𝑏𝑏2, , =, , 𝑐𝑐1, 𝑐𝑐2, , d) (0,2), , iii. If (-3,4) is a solution of the system of linear equations 8x+ ay=8, a) 10, b) 8, c) 2, d) 11, iv. The equation of first track is 3x +2y =12, if this is found to intersect another track at certain point, which of the following cannot be the equation of the other track, a) 4y +6x = 24 b) 2x+4y =24 c) 12x+8y=12 d) 9x + 8y = 48, v. The vertices of the triangle formed by the equation 3x+ 2y = 12 with the x and y axis:, a) (0,0) (0,4)(6,0) b) (0,0) (0,6) (4,0), (c) (0,0) (2,0)(0,3), (d) (0,0) (3,0)(0,2), , Answers: 1 (i) (c), 2 (iii) (b), 3 (v) (a), 5 (ii) (d), 6 (iv) (b), 8 (i) (c), , 1 (ii) (a), 2 (iv) (d), 4 (i) (a), 5 (iii) (a), 6 (v) (c), 8 (ii) (c), , 1 (iii) (d), 2 (v) (b), 4 (ii) (d), 5 (iv) (c), 7 (i) (a), 8 (iii) (a), , 1 (iv) (b), 3 (i)(a), 4 (iii)(a), 5 (v) (c), 7 (ii) (c), 8 (iv) (c), , 1 (v) (a), 3 (ii) (d), 4 (iv)(c), 6 (i)(a), 7 (iii) (c), 8 (v) (b), , 2 (i)(a), 3 (iii) (c), 4 (v) (b), 6 (ii) (c), 7 (iv) (a), , 2 (ii) (b), 3 (iv) (a), 5 (i) (c), 6 (iii) (c), 7 (v) (c)

Page 19 :
CHAPTER-6 (TRIANGLES), SECTION A, (CONCEPTUAL BASED MCQS), 1., , In the Fig., ∆ODC ~ ∆OBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠OAB., , (a) 550, 2., , 𝐵𝐵𝐵𝐵, , (b) 6cm, , (c) 4cm, , (d) 2cm, , (b) (√2 – 1):√2, , (c) 1:√2, , (d) 1: (√2 – 1), , In the given fig. DE || BC, ∠ADE =70° and ∠BAC=50°, then angle ∠BCA =, , (a) 500, , 5., , (d) 1100, , In the given figure, P and Q are points on the sides AB and AC respectively of a ∆ABC. PQ‖BC and, divides the ∆ABC into 2 parts, equal in area. The ratio of PA:PB =, , (a) 1:1, 4., , (c) 1250, , DE is drawn parallel to the base BC of a ∆ABC, meeting AB at D and AC at E., 𝐴𝐴𝐴𝐴, If, = 4 and CE = 2cm, find AE., (a) 8cm, , 3., , (b) 700, , (b) 600, , (c) 700, , (d) 800, , In the given figure, AD = 2cm, BD = 3 cm, AE = 3.5 cm and AC = 7 cm. Is DE parallel to BC?

Page 21 :
12., , (𝑎𝑎), , 𝐴𝐴𝐴𝐴, 𝐴𝐴𝐴𝐴, , =, , 𝐴𝐴𝐴𝐴, 𝐴𝐴𝐴𝐴, , (b), , 𝐴𝐴𝐴𝐴, 𝐴𝐴𝐴𝐴, , =, , 𝐴𝐴𝐴𝐴, , (c), , 𝑁𝑁𝑁𝑁, , 𝐴𝐴𝐴𝐴, , 𝐴𝐴𝐴𝐴, , =, , 𝐴𝐴𝐴𝐴, , 𝑁𝑁𝑁𝑁, , (d) None of these., , ∆ABC is an equilateral triangle with each side of length 2p. If AD⊥BC. Then the value of AD is, , (a) √3, , (b) √3p, , (c) 2p, , (d) 4p, , 13., , If ∆ABC ~ ∆APQ and ar(∆APQ) = 4[ar(∆ABC)], then the ratio of BC to PQ is, (a) 2:1, (b) 1:2, (c) 1:4, (d) 4:1, , 14., , The length of the side of a square whose diagonal is 16cm, is, (a) 8√2cm, (b) 2√8cm, (c) 4√2 cm, (d) 2√2 cm., , 15., , Two poles of height 6m and 11m stand vertically upright on a plane ground. If the distance between, their foot is 12m, then distance between their tops is, (a) 12m, (b) 14m, (c) 13m, (d) 11m, , 16., , The areas of two similar triangles are 81cm2 and 49cm2 respectively, then the ratio of their, corresponding medians is, (a) 7:9, (b) 9:81, (c) 9:7, (d) 81:7, , 17., , Sides of two similar triangles are in the ratio 4:9. Ares of these triangles are in the ratio, (a) 2:3, (b) 4:9, (c) 81:16, (d) 16:81, , 18., , A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower, casts a shadow 28 m long. Find the height of the tower., (a) 56m, (b) 24m, (c) 21m, (d) 42m, , 19. O is the point of intersection of two equal chords AB and CD such that OB = OD, then triangles, OAC and ODB are

Page 22 :
(a) Equilateral but not similar (b) Isosceles but not similar, (c) Equilateral and similar, , (d) Isosceles and similar, , 20., , A 5m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4m, high. If the foot of the ladder is moved 1.6m towards the wall, then the distance by which the top of, the ladder would slide upwards on the wall is, (a) 0.6m (b) 0.2m, (c) 0.4m, (d) 0.8m, , 21., , The lengths of the diagonals of a rhombus are 30cm and 40cm. The length of the side of the, rhombus is, (a) 20cm, (b) 25cm, (c) 10cm, (d) 15cm, , 22., , The perimeter of two similar triangles ABC and LMN are 60cm and 48cm respectively. If LM=8cm, then the length of AB is, (a) 20cm, (b) 15cm, (c) 10cm, (d) 25cm, , 23., , In an equilateral triangle PQR if PS ┴ QR then PS2 = ______, (a) 5RS2, (b) 4RS2, (c) RS2, (d) 3RS2, , 24., , The length of the hypotenuse of an isosceles right triangle whose one side is 3√2 is, (a) 6cm, (b) 9cm, (c) 18cm, (d) 27cm, , 25., , A chord of a circle radius 5 cm subtends a right angle at the centre. The length of the chord is, (a) 10cm, , (b) 5√2cm, , (c) 15√2 cm, , (d), , 20cm, , Answers: 1 (a), 8 (d), 15 (c), 22 (c), , 2 (b), 9 (d), 16 (c), 23 (d), , 3 (d), 10 (b), 17 (d), 24 (a), , 4 (b), 11 (a), 18 (d), 25 (b), , 5 (b), 12 (b), 19 (d), , SECTION B, (CASE STUDY BASED QUESTIONS), 1., , Observe the below given figures carefully and answer the questions-, , 6 (c), 13 (b), 20 (d), , 7 (a), 14 (a), 21 (b)

Page 23 :
Figure B, , Figure A, , Figure D, , Figure E, , Figure C, , Figure F, , i. Which among the above shown figures are congruent figures?, (a) A and C, (b) E and F (c) D and F (d) B and F, ii. Tick the correct statement(a) All similar figures are congruent., (b) All congruent figures are similar., (c) The criterion for similarity and congruency is same. (d) Similar figures have same size and shape., iii. If a line divides any two sides of the triangle in the same ratio, then the line is parallel to the third, side. The statement depicts which theorem(a) Pythagoras, (b) Thales Theorem, (c) Converse of Thales theorem, (d) Converse of Pythagoras theorem., iv. Using the concept of similarity, the height of the building is, , a) 20ft, , b) 15ft, , c) 10ft, , d) 7 ft, , v. The height of the tree, when its shadow is 102 ft long and at the same time a man 6ft high standing, in the same straight line casts a shadow 17ft is, , (a) 14ft, , (b) 24ft, , (c) 36ft(d) 12ft

Page 24 :
2., Rahul is studying in X Standard. He is making a kite to fly it on a Sunday. Few questions came to, his mind while making the kite. Give answers to his questions by looking at the figure., , i. Rahul tied the sticks at what angles to each other?, a) 30°, b) 60°, c) 90°, d) 60°, ii. Which is the correct similarity criteria applicable for smaller triangles at the upper part of this kite?, a) RHS, b) SAS, c) SSA, d) AAS, iii. Sides of two similar triangles are in the ratio 4:9. Corresponding medians of these triangles are in the, ratio,, a) 2:3, b) 4:9, c) 81:16, d) 16:81, iv. In a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the, angle opposite the first side is a right angle. This theorem is called as,, a) Pythagoras theorem, b) Thales theorem, c) Converse of Thales theorem, d) Converse of Pythagoras theorem, v. What is the area of the kite, formed by two perpendicular sticks of length 6 cm and 8 cm?, a) 48 cm2, b) 14 cm2, c) 24 cm2, d) 96 cm2, 3., Vijay is trying to find the average height of a tower near his house. He is using the properties of similar, triangles. The height of Vijay’s house if 20m when Vijay’s house casts a shadow 10m long on the ground. At the, same time, the tower casts a shadow 50m long on the ground and the house of Ajay casts 20m shadow on the, ground, , i. What is the height of the tower?, a) 20m, b) 50m, , c) 100m, , d) 200m, , ii. What will be the length of the shadow of the tower when Vijay’s house casts a shadow of 12m?, a) 75m, b) 50m, c) 45m, d) 60m, iii. What is the height of Ajay’s house?, a) 30m, b) 40m, , c) 50m, , d) 20m

Page 25 :
iv. When the tower casts a shadow of 40m, same time what will be the length of the shadow of Ajay’s, house?, a) 16m, b) 32m, c) 20m, d) 8m, v. When the tower casts a shadow of 40m, same time what will be the length of the shadow of Vijay’s, house?, a) 15m, b) 32m c), 16m, d) 8m, 4., Rohan wants to measure the distance of a pond during the visit to his native. He marks points A, and B on the opposite edges of a pond as shown in the figure below. To find the distance between the, points, he makes a right-angled triangle using rope connecting B with another point C are a distance of, 12m, connecting C to point D at a distance of 40m from point C and the connecting D to the point A, which is are a distance of 30m from D such that ∠ADC=900., , i. Which property of geometry will be used to find the distance AC?, a) Similarity of triangles, b) Thales Theorem, c) Pythagoras Theorem, d) Area of similar triangles, ii. What is the distance AC?, a) 50m, b) 12m, , c) 100m, , d) 70m, , iii. Which is the following does not form a Pythagoras triplet?, a) (7,24,25), b) (15,8,17), c) (5,12,13), , d) (21,20,28), , iv. Find the length AB?, a) 12m, b) 38m c) 50m d) 100m, v. Find the length of the rope used., a) 120m, b) 70m c) 82m d) 22m, 5., A scale drawing of an object is the same shape at the object but a different size. The scale of a, drawing is a comparison of the length used on a drawing to the length it represents. The scale is written as, a ratio. The ratio of two corresponding sides in similar figures is called the scale factor Scale factor=, length in image / corresponding length in object If one shape can become another using revising, then the, shapes are similar. Hence, two shapes are similar when one can become the other after a resize, flip, slide, or turn. In the photograph below showing the side view of a train engine. Scale factor is 1:200

Page 26 :
This means that a length of 1 cm on the photograph above corresponds to a length of 200cm or 2 m, of, the actual engine. The scale can also be written as the ratio of two lengths., i. If the length of the model is 11cm, then the overall length of the engine in the photograph above,, including the couplings(mechanism used to connect) is:, a) 22cm, b) 220cm, c) 220m, d) 22m, ii. What will affect the similarity of any two polygons?, a) They are flipped horizontally, b) They are dilated by a scale factor, c) They are translated down, d) They are not the mirror image of one another., iii. What is the actual width of the door if the width of the door in photograph is 0.35cm?, a) 0.7m, b) 0.7cm, c) 0.07cm, d) 0.07m, iv. If two similar triangles have a scale factor 5:3 which statement regarding the two triangles is true?, a) The ratio of their perimeters is 15:1, b) Their altitudes have a ratio 25:15, c) Their medians have a ratio 10:4, d) Their angle bisectors have a ratio 11:5, v. The length of AB in the given figure:, , a) 8cm, , b) 6cm c) 4cm, , d) 10cm, , Answers: 1 (i) (d), 2 (iii) (b), 3 (v) (d), 5 (ii) (d), , 1(ii) (b), 2 (iv) (d), 4 (i) (c), 5 (iii) (a), , 1 (iii) (c), 2 (v) (c), 4 (ii) (a), 5 (iv) (b), , 1(iv) (a), 3 (i) (c), 4 (iii) (d), 5 (v) (c), , 1(v) (c), 3 (ii) (d), 4 (iv) (b), , 2 (i) (c), 3 (iii) (b), 4 (v) (c), , 2 (ii) (b), 3 (iv) (a), 5 (i) (d)

Page 27 :
CHAPTER-7 (COORDINATE GEOMETRY), SECTION A, (CONCEPTUAL BASED MCQS), 1., , The points (- 1, – 2), (1, 0), (- 1, 2), (- 3, 0) forms a quadrilateral of type:, , 2., , If the distance between the points A(2, -2) and B(-1, x) is equal to 5, then the value of x is:, , 3., , The Point (-1,-2) lies on, , 4., , (a) Square, , (a) 2, , (b) Rectangle, , (b) -2, , (a) x-y =1, , (b) 2x =y, , (c) Parallelogram but not rectangle, (c) 1, , (d) -1, , (c) x +y= -3, , (d) All of the above, , The distance of point A(2, 4) from x-axis is, , (a) 2 units, , (b) 4 units, , (c) -2 units, , (d) -4 units, , (c) x=k, , (d) None of the above, , (d) Rhombus but not square, , 5., , Equation of X-axis is is, , 6., , If O( , 4) is the midpoint of the line segment joining the points P(-6, 5) and Q(-2, 3). The value of p, 𝟑𝟑, is:, , (a) x=0, 𝑷𝑷, , (a) 7/2, 7., 8., , (c) 4, , (d) -4, , (b) (-1, -3), , (c) (1, -3), , (d) (1, 3), , The ratio in which the line segment joining the points P(-3, 10) and Q(6, – 8) is divided by O(-1, 6), is:, (b) 3:4, , (c) 2:7, , (d) 2:5, , The coordinates of a point P, where PQ is the diameter of a circle whose centre is (2, – 3) and Q is, (1, 4) is:, (a) (3, -10), , 10., , (b) -12, , The point which divides the line segment of points P(-1, 7) and (4, -3) in the ratio of 2:3 is:, , (a) (-1, 3), , (a) 1:3, 9., , (b) y=k, , (b) (2, -10), , (c) (-3, 10), , (d) (-2, 10), , The area of a rhombus if its vertices are (3, 0), (4, 5), (-1, 4) and (-2,-1) taken in order, is:, , (a) 12 sq.units, , (b) 24 sq.units (c) 30 sq.units (d) 32 sq.units, , 11., , The distance of the point P(–6, 8) from the origin is, (a) 8 units, (b) 2√7 units (c) 10 units, (d) 6 units, , 12., , The distance between the points (0, 5) and (–5, 0) is, (a) 5 units, (b) 5√2 units (c) 2√5 units, (d) 10 units, , 13., , The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is, (a) 5, (b) 12, (c) 11, (d) 7 + √5, , 14., , The point which lies on the perpendicular bisector of the line segment joining the points A(–2, –5) and B(2,, 5) is, (a) (0, 0), (b) (0, 2), (c) (2, 0), (d) (–2, 0), , 15., , If the points A(1, 2), O(0, 0) and C(a, b) are collinear, then, (a) a = b, (b) a = 2b, (c) 2a = b, (d) a = –b

Page 28 :
16., , The line 3x + y – 9 = 0 divides the line joining the points (1, 3) and (2, 7) internally in the ratio, (a) 3 : 4, (b) 3 : 2 (c) 2 : 3, (d) 4 : 3, , 17., , The points (1,1), (-2, 7) and (3, -3) are, (a) vertices of an equilateral triangle, (c) vertices of an isosceles triangle, , (b) collinear, (d) none of these, , Answers: 1 (a), 8 (c), 15 (c), , 2 (a), 9 (a), 16 (a), , 3 (d), 10 (b), 17 (b), , 5 (d), 12 (b), , 4 (b), 11 (c), , 6 (b), 13 (b), , 7 (d), 14 (a), , SECTION B, (CASE STUDY BASED QUESTIONS), 1., One day Ram went to his home town during Dussehra vacation.During his excursion, he noted the four, places Temple, TV tower, Mall and School, then he tried to locate all the places using graph sheet by taking his, position at origin.He marked A,B,C and D for school,TV Tower,Temple and Mall respectively on the graph sheet by, taking, scale, as, I, Unit, =, 1, km, as, shown, below., , i. Find the co-ordinates of C., (a) (0,-1), b) (8,3), , c) (6,7), , d) (-2,3), , ii. Find the distance between School and TV Tower., (a) 4km, b) 4√5 km, c) 2√5 km, , d) 3√5 km, , iii. Find the distance between T.V Tower and Mall., (a) 8km, b) 10km, c) 6km, , d) 9 km, , iv. Find the distance between School and Temple., a) 8km, b) 10km, c) 6km, , d) 9 km, , v. Name the quadrilateral so formed., a) Square, b) Rectangle c) Rhombus, , d) None of these, , 2., To conduct sports day activities, in your rectangular shaped school groundABCD, lines have been drawn, with chalk powder at a distance of 1m each.100 flower pots have been placed at a distance of 1m from each, 1, other along AD,as shown in the below figure. Niharika runs th distance AD on the 2nd line and posts a green, 1, , 4, , flag.Preet runs th distance AD on the 8th line and posts a red flag., 5

Page 29 :
i. At what distance Niharika posted the green flag from the starting point of second line?, (a) 20m, b) 25 m, c) 100m, d) 50m, ii. At what distance Preet posted the red flag from the starting point of 8th line?, (a) 20m, b) 25 m, c) 100m, d) 50m, iii. What is the distance between both the flags?, a) √61 m, b) √101m, c) √51m, , d) √11m, , iv. If Rashmi has to post a blue flag exactly halfway between the line segments joining the twoflags.Where, should she post her flag ?, (a) (5,5), b) (22.5,5), c) (5,22.5), d) None of these, v. If Swetha has to post a blue flag exactly halfway between the line segments joining the point A and green, flag. Where should she post her flag ?, (a) (1,5), b) (12.5,1), c) (1,22.5), d) (1,12.5), 3., (Covid-19 vaccination), Mr. Jaskirat Singh is living in Jalandhar Punjab. As per the government he takes his dose of vaccine in the months, of June 2021 in the Civil Hospital Jalandhar. Now he want to take his second dose. The following map is showing, three vaccination centres near his home. O represents his home. Observe this condition and answer the following, questions. Vaccination centre A, B & C as shown in the figure., , i. The coordinates of nearest vaccination centre., (a) (3, 1), (b) (4, 2), (c) (0, 4), , (d) (7, 4), , ii. According to the figure vaccination centre B is divide the line joining vaccination centre A to C, (a) 2 :3, (b) 3:1, (c) 3: 2, (d) 1 :1, iii. Distance between centre A to C, (a) 4√2, (b) 5√2, , (c) 41√2, , (d) 50

Page 30 :
iv. Assuming he went to centre B and doses are finished. Then what is the closestdistance he has to cover to, reach another Vaccination centre., (a) 4√2, (b) √2, (c) 2√2, (d) 6√2, v. Straight distance between his home to Vaccination centre C is, (a) 11, (b) 12, (c) 13, (d) 10, 4., Kushal is a class X student residing in a village. Oneday, he went to a city Hospital along with his, grandfather for general check-up. From there he visited three places -School, Library and Police station. After, returning to his village, he plotted a graph by taking Hospital as origin and marked three places on the graph as, per his direction of movement and distance. The graph is shown below., , i. What are the coordinates of library?, a) (6,2), b) (2,6), c) (2,-1) d) (2,3), ii. Distance between school and hospital is(in units), a) √11, b) √13, c) √5, , d) √17, , iii. Distance between school and police station is(in units), a) 4, b) 3, c) 2, d) 1, iv. Distance between police station and hospital is(in units), a) 2, b) √5, c) √7, d) 3.5, v. Nearest place to hospital is, a) Police station b) school, , c) hospital, , d) all are at equal distance, , 5., The class X students’ school in Krishnagar have been allotted a rectangular plot of land for their gardening, activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is, triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the, remaining area of the plot.

Page 31 :
i. Taking A as origin, find the coordinates of P, (a) (4, 6), (b) (6, 4), (c) (0, 6), , (d) (4, 0), , ii. What will be the coordinates of mid-point of side QR if A is the origin?, 9 7, 7, 7 9, (a) (8, 6), (b) ( , ), (c) ( , 3), (d) ( , ), 2 2, , 2, , 2 2, , iii. Mid-point of PR, if A is the origin?, 11, (a) (5, ), (b) (-6, 13), (c) (-13, 6), , (d) (13, 6), , iv. Length of side PQ if A is origin is, (a) √24, (b) √17, , (d) 25, , 2, , (c) √62, , v. The length of side QR as A is origin is, (a) 8, (b) 3√2, (c) 2√3, , (d) 4.5, , Answers: 1 (i) (c), 2 (iii) (a), 3 (v) (d), 5 (ii) (b), , 1 (ii) (b), 2 (iv) (c), 4 (i) (a), 5 (iii) (a), , 1 (iii) (b), 2 (v) (d), 4 (ii) (b), 5 (iv) (b), , 1 (iv) (b), 3 (i) (a), 4 (iii) (a), 5 (v) (b), , 1 (v) (b), 3 (ii) (c), 4 (iv) (b), , 2 (i) (b), 3 (iii) (b), 4 (v) (a), , 2 (ii) (a), 3 (iv) (c), 5 (i) (a)

Page 32 :
CHAPTER-8 (INTRODUCTION TO TRIGONOMETRY), SECTION A, (CONCEPTUAL BASED MCQS), 1., , (a), 2., , 3., , 4., , 5., , 3, , (b), , 5, , 4, , 3, , (c) 1, , 5, , (d) none of these, , In ∆OPQ, right-angled at P, OP = 7 cm and OQ – PQ = 1 cm, then the values of sin Q., 7, 24, (a), (b), (c) 1, (d) none of these, 25, , 25, , 13, , 13, , 25, , 25, , In ∆PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm, then the value of sin P is, 5, 12, 3, 4, (a), (b), (c), (d), 5, , 5, , If 4tan θ = 3 then (cos2θ – sin2θ) = ?, 4, 7, 11, (a), (b), (c) 1, (d), 25, , 4sin𝜃𝜃 −3cos𝜃𝜃, , If 3cot θ = 2, then the value of, (a), , 6., , 4, , In triangle ABC, right angled at B, If tan A = , then the value of cosC is, , 3, 2, , (b), , 1, 2, , (c), , 2sin𝜃𝜃 +6cos𝜃𝜃, , 1, , (d) none of these, , 3, , If 7tan θ = 4, then the value of, (a), , 1, 7, , (b), , 5, 7, , (c), , is, , 3, , (d), , 7, , 5, , 14, , 7sin𝜃𝜃 − 3cos𝜃𝜃, , 7sin𝜃𝜃 + 3cos𝜃𝜃, , is, , 7., , The value of 2(sin245°+ cot230°) – 6(cos245°— tan230°) is, (a) 6, (b) 3, (c) 2, (d) 4, , 8., , The value of 2(sin430°+ cos460°) - (tan260°+ cot245°) + 3cosec260° is, (a), , 9., , 10., , 1, 2, , (b), , √3, 2, , (c), , 1, , (d) none of these, , 4, , If tan2450 – cos2300 = x sin450cos450 then x = ?, 1, 1, (a) -2, (b) 2, (c) −, (d), If tan (A – B) =, (a) 45° and 15°, , 1, , √3, , 2, , 2, , and tan (A + B) = √3, then the value of A and B, respectively are, , (b) 30° and 15°, , (c) 45° and 30°, , 11., , (1 + tan θ + sec θ) (1 + cot θ – cosec θ) = ?, (a) 0, (b) 1, (c) 2, , (d) -1, , 12., , (sec A + tan A) (1 – sin A) = ?, (a) sec A, (b) sin A, (c) cosec A, , (d) cos A, , 13., , If A + B = 900, cot B = then tanA is equal to;, (a), , 14., , 3, 4, , (b), 1, , 3, 4, , 4, 3, , 1, , (c), , 1, 4, , If 𝑐𝑐𝑐𝑐𝑐𝑐 𝜃𝜃 = , 𝑠𝑠𝑠𝑠𝑠𝑠 𝜑𝜑 = then value of 𝜃𝜃 + 𝜑𝜑 is, 2, , 2, , (d), , 1, 3, , (d) none of these

Page 33 :
(a) 30°, 15., , 16., , (b) 60°, , The value of 2sin2300 – 3cos2450 + tan2600 + 3sin2900 is, (a) 1, (b) 5, (c) 0, (d) none of these, 𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠−2𝑠𝑠𝑠𝑠𝑠𝑠3 𝜃𝜃, , 2𝑐𝑐𝑐𝑐𝑐𝑐 3 𝜃𝜃−𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐, , = ?, , (a) sin θ, , 17., , (d) 1200., , (c) 90°, , 2𝑡𝑡𝑡𝑡𝑡𝑡300, , 1+𝑡𝑡𝑡𝑡𝑡𝑡2 300, , (b) cos θ, , (c) tan θ, , (d) cot θ, , (b) cos600, , (c) tan600, , (d) sin300, , = ?, , (a) sin600, , Answers: 1 (b), 8 (c), 15 (b), , 2 (a), 9 (d), 16 (c), , 3 (b), 10 (a), 17 (a), , 4 (b), 11 (c), , 5 (c), 12 (d), , 6 (a), 13 (a), , 7 (a), 14 (c), , SECTION B, (CASE STUDY BASED QUESTIONS), 1., Raj is an electrician in a village. One day power was not there in entire village and villagers called, Raj to repair the fault. After thorough inspection he found an electric fault in one of the electric pole of, height 5 m and he has to repair it. He needs to reach a point 1.3m below the top of the pole to undertake, the repair work., , Based on the above situation, answer the following questions:, i. when the ladder is inclined at an angle of α such that √3tanα + 2 = 5 to the horizontal, then find the, angle α?, (a) 45°, (b) 30°, (c) 60°, (d) none of these, ii. How far from the foot of the pole should he place the foot of the ladder? (Use, (a) 2.89 m, (b) 2.14 m, (c) 3 m, (d) none of these, 𝛼𝛼, , 𝛼𝛼, , iii. In the above situation, find the value of sin𝛼𝛼cos – cos𝛼𝛼sin, 2, , 2, , 3 = 1.73)

Page 34 :
(a) 0, , (b) 1, , (c), , 1, 2, , (d) none of these, , iv. In the above situation if BD = 3 cm and BC = 6 cm. Find α, (a) 45°, (b) 30°, (c) 60°, (d) none of these, v. Given 15 cotα=8, find sinα., 17, 17, (a), (b), 15, , 15, , (c), , 17, 8, , (d), , 15, 17, , 2., ‘Skysails’ is that genre of engineering science that uses extensive utilization of wind energy to, move a vessel in the sea water. The ‘Skysails’ technology allows the towing kite to gain a height of, anything between 100 metres – 300 metres. The sailing kite is made in such a way that it can be raised to, its proper elevation and then brought back with the help of a ‘telescopic mast’ that enables the kite to be, raised properly and effectively., Based on the following figure related to sky sailing, answer the questions:, , Based on the above situation, answer the following questions:, i. In the given figure, if √3 tan2θ – 3 = 0, where θ is acute angle, then find the value of θ., (a) 45°, (b) 30°, (c) 60°, (d) none of these, , ii. What should be the length of the rope of the kite sail in order to pull the ship at the angle (calculated, above) and be at a vertical height of 300 m?, (a) 300 m, (b) 400m, (c) 500 m, (d) 600 m, iii. What should be the distance BC in order to pull the ship at the angle (calculated above) and be at a, vertical height of 300 m?, (a) 300√3 m, (b) 400√3 m (c) 500√3 m (d) 600√3 m, iv. If BC = 100 m, θ = 60°, then AB is, (a) 100√3 m, (b) 200√3 m (c) 500√3 m (d) 300√3 m, , v. If the length of the rope, AC = 200m and θ = 30°, then the vertical height, AB is, (a) 300 m, (b) 400m, (c) 100 m, (d) 200 m, , 3., Kings and queens used the Tower in times of trouble to protect their possessions and themselves., Arms and armour were made, tested and stored here until the 1800s. The Tower also controlled the supply, of the nation’s money. All coins of the realm were made at the Tower Mint from the reign of Edward I, until 1810. Kings and queens also locked away their valuables and jewels at the Tower and even today,, the Crown Jewels are protected by a garrison of soldiers. A tower stands vertically on the ground. From a

Page 35 :
point on the ground, which is 15 m away from the foot of the tower, the angle of elevation of the top of, the tower is found to be 60°., , Based on the above situation, answer the following questions:, i. Find the height of the tower in the above situation., (a) 10√3 m, (b) 15√3 m (c) 25√3 m (d) 30√3 m, , ii. If the above tower casts a shadow of length 2√3 m on the ground when the sun's elevation is 60°. The, height of the tower is, (a) 4√3 m, (b) 3 m, (c) 12 m, (d) 6 m, iii. The angle of elevation of the top of a tower from a point on the ground 30 m away from the foot of, the tower is 30°. The height of the tower is, (a) 30 m, (b) 20 m, (c) 10√3 m, (d) 10√2 m, iv. In the above situation if AB = 30 m and AC = 60 m. Find ∠A., (a) 45°, (b) 60°, (c) 30°, (d) none of these, v. If 2cos 3θ = 1 then θ = ?, (a) 10°, (b) 15°, , (c) 30°, , (d) 20°, , 4., The Circus Arts Program is one of the most popular activities at Camp Lohikan. It brings a level of, excitement and enthusiasm to the camp experience that can't be found at home or in school. A circus artist, is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the, ground such that the angle made by the rope with the ground level is 30°, , i. Find the height of the pole in the above situation., (a) 10√3 m, (b) 15√3 m (c) 15 m, (d) 10 m, , ii. In the above situation, if AB = 5 m and ∠ ACB = 30° then find the length of the side BC., (a) 5√3 m, (b) 5 m, (c) 10 m, (d) 6 m

Page 36 :
iii. In the above situation, if the height of pole is 3 m and the length of rope is 6 m then find ∠ACB, (a) 45°, (b) 60°, (c) 30°, (d) none of these, iv. Find the value of 2 tan2 45° + cos2 30° – sin2 60°, (a) 0, (b) 2, (c) 1, (d) none of these, v. If √3 tan 2θ − 3 = 0 then θ = ?, (a) 15°, (b) 30°, , (c) 45°, , (d) 60°, , 5., Kite flying is also a major part of Makar Sankranti, although the states of Gujarat and Rajasthan, indulge in this with a lot more enthusiasm. Makar Sankranti is a major harvest festival celebrated in India, and is dedicated to the Sun God, Surya. It is the first major festival to be celebrated in India and usually, takes place in January, this year the festival will be celebrated on January 14. Aditya flying a kite at a, height of 60 m above the ground. He attached the string to the kite is temporarily tied to a point on the, ground. The inclination of the string with the ground is 60°., , i. In the above situation, find the length of the string, assuming that there is no slack in the string., , (a) 50√3 m, , (b) 40√3 m, , (c) 50√2 m, , (d) 100 m, , ii. The string of a kite is 100 m long and it makes an angle of 60° with the horizontal. If these is no slack, , in the string, the height of the kite from the ground is, (a) 50√3 m, (b) 100√3 m (c) 50√2 m, (d) 100 m, , iii. A kite is flying at a height of 30 m from the ground. The length of string from the kite to the ground, , is 60 m. Assuming that there is no slack in the string, the angle of elevation of the kite at the ground, is, (a) 45°, (b) 60°, (c) 90°, (d) 30°, , iv. The value of (sin230° – sec260° + 4cot245°) = ?, , (a) 4, , (b) 2, , v. If 2sin 2θ = √3 then θ = ?, , (a) 30°, , (b) 45°, , (c) 1/4, , (d) 1, , (c) 60°, , (d) 90°, , Answers: 1 (i) (c), 2 (iii) (a), 3 (v) (d), 5 (ii) (a), , 1(ii) (b), 2 (iv) (a), 4 (i) (d), 5 (iii) (d), , 1 (iii) (c), 2 (v) (c), 4 (ii) (a), 5 (iv) (c), , 1 (iv) (b), 3 (i) (b), 4 (iii) (c), 5 (v) (a), , 1 (v) (d), 3 (ii) (d), 4 (iv) (b), , 2 (i) (b), 3 (iii) (c), 4 (v) (b), , 2 (ii) (d), 3 (iv) (b), 5 (i) (b)

Page 37 :
CHAPTER-12 (AREAL RELATED TO CIRCLES), SECTION A, (CONCEPTUAL BASED MCQS), 1., , The perimeter of a circle is equal to twice that of square, then the ratio of their areas is: a) 22/7, b) 14/11, c) 7/22, d) 56/11, , 2., , The area of the square that can be inscribed in a circle of 10 cm radius is: a) 200 cm2, b) 128cm2, c) 64√2cm2 d) 64cm2, , 3., , Area of a sector to circle of radius 6 cm is 9π cm2. Find the length arc of the corresponding arc of, the circle is: a) 6π cm, b) 3 π cm, c) 5 π cm, d) 8 π cm, , 4., , A wheel has diameter 112 cm. The number of complete revolution it will take to cover 1056 m is: a) 100, b) 150, c) 200, d) 300, , 5., , The length of an arc of a circle with radius 12 cm is 10 π cm. The central angle of this arc is: b) 60, c) 750, d) 1500, a) 1200, , 6., , The area of a circle whose circumference 2π cm is: 𝛑𝛑, 𝛑𝛑, a) π cm2 b) cm2, c) cm2, d) None of these, , 7., , 𝟒𝟒, , In figure ‘o’ is the centre of a circle. The area of sector OAPB is 10/72 of the area of the circle find, x., , a) 30o, 8., , 𝟐𝟐, , b) 40o, , c) 50o, , d) 60o, , If the diameter of a semi-circular protractor is 28 cm, then find its perimeter., , a) 42 cm, , b) 52 cm, , c) 62 cm, , d) 72 cm, , 9., , The diameter of a cycle wheel is 42 cm. How many rotations will it make to travel 1.98km?, a) 900, b) 1200, c) 1500, d) 1800, , 10., , The length of the minute hand of a clock is 15 cm. Find the area swept by the minute hand in 8, minutes., a) 84.285 cm2, b) 94.285 cm2, c) 104.285 cm2, d) 114.285 cm2

Page 38 :
11., , A copper wire when bent in the form of a square encloses an area of 225 cm2. If the same wire is, 22, bent into the form of a circle, find the area of the circle (Use π = )., a), , 900, π, , cm2, , b), , π, , 900, , cm2, , c), , 700, π, , cm2, , d), , π, , 700, , cm2, , 7, , 12., , A wire is looped in the form of a circle of radius 14 cm. It is re-bent into a square form. Determine, 22, the side of the square (Use π = )., 7, a) 12 cm, b) 22 cm, c) 32 cm, d) 42 cm, , 13., , ABC is a quadrant of circle of radius 28 cm and a semi-circle is drawn with BC as diameter. Find, the area of Shaded region., , a) 192 cm2, , b) 292 cm2, , c) 392 cm2, , d) 492 cm2, , 2, , 14., , The length of a minor arc is of the circumference of the circle. Write the measure of the angle, 8, subtended by the arc at the centre of the circle., a) 60o, b) 70o, c) 80o, d) 90o, , 15., , The area of an equilateral triangle is 9√3 cm2. Taking each angular point as centre, circle is drawn, with radius equal to half the length of the side of the triangle. Find the area of triangle not included, in the circles. [Take √3=1.73], , a) 1.43 cm2, , b) 1.33 cm2, , c) 1.23 cm2, , d) 1.13 cm2, , 16., , If the side of a square is 14 cm. find the area of circumscribed circle., a) 68π cm2, b) 78π cm2, c) 88π cm2, d) 98π cm2, , 17., , If the side of a square is 16 cm. find the area of inscribed circle., a) 54π cm2, b) 64π cm2, c) 74π cm2, d) 84π cm2, , 18., , If the radius of a circle is increased by 5%, then its area is increased by, (a) 10%, (b) 10.25% (c) 12.25%, (d) 15.25%

Page 39 :
19., , If the circumference of a circle is reduced by 15%, then its area is decreased by________., (a) 7.75%, (b) 17.75% (c) 27.75%, (d) 37.75%, , 20., , Area of the largest triangle that can be inscribed in a semi-circle of radius 3 units is______., (a) 3 sq units (b) 9 sq units (c) 12 sq units (d) 15 sq units, , 21., , In a circle of radius 21 cm, an arc subtends an angle of 60o at the centre, then the area of the sector, is:, (a) 211 cm2, (b) 221 cm2 (c) 231 cm2 (d) 241 cm2, , 22., , The area of a circular path of uniform width of 3 meter surrounding a circular region of radius 10, meter is, (a) 69π m2, (b) 79π m2, (c) 89π m2, (d) 99π m2, , Answers: 1 (d), 8 (d), 15 (a), 22 (a), , 2 (a), 9 (c), 16 (d), , 3 (b), 10 (b), 17 (b), , 4 (d), 11 (a), 18 (b), , 5 (d), 12 (b), 19 (c), , 6 (a), 13 (c), 20 (b), , 7 (c), 14 (d), 21 (c), , SECTION B, (CASE STUDY BASED QUESTIONS), 1., In a village, there was no playground for children. If a child had to practice for any sports then, thechildhad to go to the city stadium which is 20 km from the village. But village has a circular unused, land and villagers decided to convert this unused land into a football ground, with athletic track around it,, so that children can practice their choice of sports in village itself. Villagers also planned six seating areas, with chairs (brown colour) and six seating area without chairs (grey colour) as shown in the figure., Athletic track (light blue) is between the football ground (light green) and seating area. The distance, between the centre of the ground and the boundary of the stadium is 140 m, width of the athletic track is, 30 m and AB is 20 m., , Based on the above case and figure, answer the following questions: i. What is the area of the football ground?, a) 7100π m2, b) 6100π m2 c) 8100π m2 d) 9100π m2

Page 40 :
ii. What is the length of the athletic track (inner boundary)?, a) 180π m, b) 190π m, c) 170π m, d) 160π m, iii. What is the length of the athletic track (outer boundary)?, a) 210π m, b) 220π m, c) 230π m, d) 240π m, iv. How much area is allocated for six seating corners with chairs?, 2π −3√3, , a) 110600(, , 12, , ), , 2π −3√3, , b) 117600(, , 12, , ), , 2π −3√3, , c) 124600(, , v. What is the total area allocated for athletic track?, b) 5300π m2 c) 4300π m2 d) 3300π m2, a) 6300π m2, , 12, , ), , 2π −3√3, , d) 131600 (, , 12, , ), , vi. What is the total area used to develop this stadium?, a) 16600π, b) 17600π, c) 18600π, d) 19600π, 2., In a school rangoli competition, Tanveer and his friends made a rangoli as shown in the following, figure., During the inspection, judges of the competition asked questions about the dimensions of the rangoli to, his team. As the leader of the team, Raju replied that the rangoli is exactly in a circular shape. The points, A, B, C, D, E, F, G, H, I, J, K, L are the points on the boundary of the rangoli and are at the equal, distance with each other. All these points are directly attached with the centre O and are at a distance of 4, feet from O. To his reply, Judges again asked some specific questions as given in the figure., , Based on the facts provided by Raju and his team, answer the following questions and help the team to, win the competition., i. What is the measurement of ∠LOI?, a) 80o, b) 100o, c) 90o, ii. What is the area of sector ADO?, a) 3π sq ft b) 4π sq ft, c) 5π sq ft, , d) 70o, d) 6π sq ft, , iii. What is the area of segment ABCM?, 176, 176, a), - 1√3 sq ft, b), - 2√3 sq ft, 21, , 21, , iv. What is the area of BOL?, a) 4√3 sq ft, b) 3√3 sq ft, , c) 2√3 sq ft, , c), , 176, 21, , - 3√3 sq ft, , d) 1√3 sq ft, , d), , 176, 21, , - 4√3 sq ft

Page 41 :
v. What is the ratio of area of sector ADO to area of circle with radius OA?, a) 4:1, b) 1:4, c) 1:5, d) 5:1, 3., In a cycling race, the wheel of bicycle of the cyclist take total 304 rotation to complete the circuit., The cycling track is around the Football ground that is of rectangular shape with semi-circular shape on, both side. The perimeter of the inner rectangular ground is 496 m. The inner semi-circular shape on both, side has a length of 154 m each (from A to I to J or from C to L to D). The width of the track is 7 m., , i. What is the area of the Football field?, b) 23246 m2 c) 21246 m2, a) 22246 m2, , d) 22346 m2, , ii. What is the length of the Football ground (From I to L)?, a) 148 m, b) 208 m, c) 348 m, d) 248 m, iii. What is the radius of the wheel of bicycle?, 8, 7, 7, a) m, b) m, c) m, 21, , 22, , 21, , iv. What is the area of Cycling track?, a) 4420 m2, b) 4310 m2, c) 4410 m2, , d), , 9, , 22, , m, , d) 4415 m2, , v. In how many rounds the cyclist will cover 12 km distance?, a) 6000 rounds b) 5000 rounds, c) 4000 rounds, , d) 3000 rounds, , 4., Kritvi invited her best friends on her birthday. Her parents ordered a birthday cake for the, occasion. The diameter of the cake ordered is 18 inch and its 3 kg 600 grams in weight. She wanted to, distribute this cake equally among all the persons present in the party in such a way that cake will be used, up completely., , i. What is the area of the top surface of the cake?, a) 72π, b) 63π, c) 81π, d) 91π

Page 42 :
ii. If each piece cut has an angle of 60o, how many persons are there in the party, if each 60o piece cut is, distributed among three persons., a) 18, b) 20, c) 22, d) 24, iii. What is the weight of each piece distributed to each person, if cake has equal density?, a) 50 gm, b) 100 gm, c) 150 gm, d) 200 gm, iv. What is the top perimeter of each 60o slice?, a) 27.42 inch, b) 17.42 inch c) 37.42 inch d) 07.42 inch, v. If there were 20 persons in party and same size piece to be offered to everyone, then what should be, the weight of the cake ordered., a) 1 kg, b) 3 kg, c) 4 kg, d) 2 kg, 5., A stable owner has four horses. He usually tie these horses with 7 m long rope to pegs at each, corner of a square shaped grass field of 20 m length, to graze in his farm. But tying with rope sometimes, results in injuries to his horses, so he decided to build fence around each horse and let them freely move, and graze separately in their own area. (π = 3.14), , Find: 22, i. The total area of the field in which these horses can graze. (π = ), 7, a) 104 m2, b) 154 m2, c) 134 m2, d) 164 m2, ii. How much the length of the rope of each horse be increased so that they can graze in maximum area, without encroaching in each other’s area (new length of rope after increase)., a) 10 m, b) 5 m, c) 15 m, d) 20 m, iii. What is the area of the field that is left un-grazed after increasing the length of the rope? (π = 3.14), a) 86 m2, b) 76 m2, c) 106 m2, d) 96 m2, iv. If the length of the rope is increased as per part (ii) above, find the cost of fencing around every horse, so that the owner leave these horses untied inside these fenced areas, if the cost per meter length of, the fencing is ₹50., a) ₹3148, b) ₹2140, c) ₹3140, d) ₹2140

Page 43 :
6., An Umbrella frame is made with steel wire. It has 8 spokes which are equally spaced. If these, spokes are expanded fully they are in the form of a circle with diameter of 4 meters. Steel wire is used in, making the ribs and the outer frame of the umbrella to which these ribs are attached., , Find:, i. The total length of the Steel wire used is _____________., a) 08.571 m, b) 11.571 m c) 18.571 m d) 28.571 m, ii. The area between the three consecutive spokes of the umbrella _____________., a) π m2, b) 2π m2, c) 3π m2, d) 4π m2, iii. The angle between any two spoke of the umbrellais _____________., b) 45o, c) 60o, d) 75o, a) 30o, iv. How much water proof cloth was used in making this umbrella., b) 3π m2, c) 4π m2, d) 5π m2, a) 2π m2, 7., In a wall clock (as shown in the figure) the length of the minute hand is 3 cm less than the radius, of the upper semi-circular part of the clock. The circumference of the semi-circular upper part is 6 cm less, than the perimeter of the lower equilateral triangular part. If the circumference of the semi-circular part is, 36 cm. Then find the: -, , i. The Length of the minute hand., a) 4 cm, b) 6 cm, c) 8 cm, , d) 10 cm, , ii. Area of the equilateral lower part. (use√3 = 1.73), a) 74.77 cm2, b) 84.77 cm2 c) 94.77 cm2 d) 104.77 cm2, , iii. Area of the upper semi-circular part., a) 57 cm2 b) 67 cm2, c) 77 cm2, , d) 87 cm2

Page 44 :
iv. Area of the figure., a) 131.77 cm2, b) 141.77 cm2 c) 151.77 cm2 d) 161.77 cm2, 8., Ferris Wheel in an amusement park has cabins attached in the outer ring (Saffron colour), it has, five spokes that are fixed at the centre (circular solid centre) and are attached to the outer ring (carrying, sitting cabins) as shown in the below pictures. Inner circular centre has radius = R1, the central circular, space has width = R2, the width of the outer ring = w and R3 = R1 + R2 + W., , If R1 = 1 meter, R2 = 5 meter and W = 2 meter, then: i. Find the area occupied between any two spokes excluding the area of the width of the spoke(Assume, that the all spokes start from the center O)., a) 13.52 m2, b) 3.52 m2, c) 23.52 m2 d) 33.52 m2, ii. Find the area occupied by the outer ring., b) 78 m2, c) 88 m2, a) 68 m2, , d) 98 m2, , iii. In how many rotations this Ferris Wheel will cover 10 Km?, a) 188.88 rotations, b) 198.88 rotations c) 208.88 rotations, , d) 218.88 rotations, , iv. If in 30 seconds the wheel completes 1 rotation and on a single ticket a person is allowed for only 10, minutes. What is the distance covered by this wheel on single ticket?, a) 1005.6 meters, b) 1015.6 meters, c) 1025.6 meters, d) 1035.6 meters, Answers: 1(i) (c), 2(ii) (b), 3(iv) (c), 5(i) (b), 6(iv) (c), 8(iii) (b), , 1(ii) (a), 2(iii) (d), 3(v) (a), 5(ii) (a), 7(i) (a), 8(iv) (a), , 1(iii) (d), 2(iv) (a), 4(i) (c), 5(iii) (a), 7(ii) (b), , 1(iv) (b), 2(v) (b), 4(ii) (a), 5(iv) (c), 7(iii) (c), , 1(v) (a), 3(i) (a), 4(iii) (d), 6(i) (d), 7(iv) (d), , 1(vi) (d), 3(ii) (d), 4(iv) (a), 6(ii) (a), 8(i) (d), , 2(i) (c), 3(iii) (b), 4(v) (c), 6(iii) (b), 8(ii) (c)

Page 45 :
CHAPTER-15 (PROBABILITY), SECTION A, (CONCEPTUAL BASED MCQS), DIRECTION: In the following questions, each question is followed by 4 options and one of the option is, correct solution of the question. So choose the correct option from the given 4 options., 1., , 2., , A ticket is drawn at random from a bag containing tickets numbered from 1 to 40. The probability, that the selected ticket has a number which is a multiple of 5 is, 3, 1, 1, 4, (a), (b), (c), (d), 5, , 5, , 3, , 5, , Which of the following cannot be the probability of an event?, 7, (a) 1.5, (b), (c) 125%, (d) All the above., 5, , 3., , An event is very unlikely to happen. Its probability is closest to, (a) 0.0001, (b) 0.001, (c) 0.01, (d) 0.1, , 4., , A man is known to speak truth 3 out of 4 times. He throws a die and a number other than six comes, up. Find the probability that he reports it is a six., 3, 1, 1, (a), (b), (c), (d) 1, 4, , 4, , 2, , 5., , The probability of selecting a rotten apple randomly from a heap of 900 apples is 0.18. What is the, number of rotten apples in the heap?, (a) 18, (b) 81, (c) 738, (d) 162, , 6., , The probability of getting exactly one head in tossing a pair of coins is, 1, 1, (a) 0, (b) 1, (c), (d), , 7., , 8., , 3, , 2, , Cards bearing numbers 3 to 20 are placed in a bag and mixed thoroughly. A card is taken out from, the bag at random. What is the probability that the number on the card taken out is an even number?, 3, 20, 1, 4, (a), (b), (c), (d), 20, , 3, , 2, , 5, , 7, , 53, , 53, , 7, , The probability of a non-leap year having 53 Mondays is, 1, 1, 7, 6, (a), (b), (c), (d), , 9., , An experiment whose outcomes has to be among a set of events that are completely known but, whose exact outcomes is unknown is a, (a) sample space, (b) elementary event (c) random experiment, (d) none of these, , 10., , A fair dice is rolled. Probability of getting a number x such that 1 ≤ x ≤ 6, is, (a) 0, (b) > 1, (c) between 0 and 1, (d) 1, , 11., , The probability of getting exactly one tail in tossing a pair of coins is, 1, 1, (a) 0, (b) 1, (c), (d), , 12., , 3, , 2, , A child has a die whose six faces show the letters as given below:, A, , B, , C, , D, , The die is thrown once. The probability of getting a ‘E’ is, , E, , F

Page 46 :
(a), , 1, , (b), , 2, , 1, , (c), , 3, , 1, 4, , (d) None of these, , 13., , A girl calculates that the probability of her winning the first prize in a lottery is 8%. If 6,000 tickets, are sold, how many tickets has she bought?, (a) 400, (b) 750, (c) 480, (d) 240, , 14., , Two different dice are thrown together. What is the probability that the number obtained is a, doublet of odd numbers, 13, 1, 4, 1, (a), (b), (c), (d), , 15., , 16., , 17., , 18., , 18, , 12, , 9, , 4, , 5, , 25, , 5, , 5, , 5, , 36, , 5, , 5, , 18, , 18, , 9, , 12, , A bag contains 25 cards numbered from 1 to 25. A card is drawn at random from the bag. What is, the probability that the number on the drawn card is a perfect square number?, 2, 12, 3, 1, (a), (b), (c), (d), A dice is rolled twice. What is the probability that 5 will not come up either time?, 2, 25, 3, 1, (a), (b), (c), (d), Two different dice are thrown together. What is the probability that the number obtained have a, sum less than 7?, 13, 5, 4, 5, (a), (b), (c), (d), A bag contains 15 white and some black balls. If the probability of drawing a black ball from the, bag is thrice that of drawing a white ball, what is the number of blackballs in the bag?, (a) 40, (b) 45, (c) 50, (d) 55, , Answers: 1 (b), 8 (a), 15 (d), , 2 (d), 9 (c), 16 (b), , 3 (a), 10 (d), 17 (d), , 4 (b), 11 (d), 18 (b), , 5 (d), 12 (d), , 6 (d), 13 (c), , 7 (c), 14 (b), , SECTION B, (CASE STUDY BASED QUESTIONS), 1., , On a weekend Rani was playing cards with her family.The deck has 52 cards.If her brother drew, one card., , i. Find the probability of getting a king of redcolour., 1, 1, 1, 1, a), b), c), d), 26, , 13, , 52, , ii. Find the probability of getting a face card., , 4

Page 47 :
a), , 1, , 26, , b), , 1, , 13, , c), , 2, , 13, , d), , iii. Find the probability of getting a jack of hearts., 1, 1, 3, a), b), c), d), , 3, , 13, 3, , 26, , 52, , 52, , 26, , 26, , 13, , 52, , 4, , 26, , 13, , 52, , iv. Find the probability of getting a red face card., 3, 1, 1, 1, a), b), c), d), v. Find the probability of getting aspade, 1, 1, 1, a), b), c), 2., dice., , d), , 1, 4, , Rahul and Ravi planned to play Business (board game) in which they were supposed to use two, , i. Ravi got first chance to roll the dice. What is the probability that he got the sum of the two numbers, appearing on the top face of the dice is 8?, 1, 5, 1, a), b), c), d) 0, 26, , 36, , 18, , 56, , 18, , 56, , 18, , 36, , 6, , 36, , 18, , ii. Rahul got next chance. What is the probability that he got the sum of the two numbers appearing on, the top face of the dice is13?, 3, 1, a) 1, b), c), d) 0, iii. Now it was Ravi’s turn. He rolled the dice. What is the probability that he got the sum of the two, numbers appearing on the top face of the dice is less than or equal to 12?, 3, 1, a) 1, b), c), d) 0, iv. Rahul got next chance. What is the probability that he got the sum of the twonumbers appearing on, the top face of the dice is equal to 7?, 5, 5, 1, a), b), c), d) 0, 9, , v. Now it was Ravi’s turn. He rolled the dice. What is the probability that he got the sum of the two, numbers appearing on the top face of the dice is greater than 8?, 5, 1, 5, a) 1, b), c), d), 18, , 3., A game of chance consists of spinning an arrow which comes to rest pointing at one of the, numbers 1, 2, 3, 4, 5, 6, 7 and 8 (see the figure) and these are equally likely outcomes.

Page 48 :
i. Find the probability that arrow point line on the number 8, 5, 1, 1, b), c), d) 1, a), 8, , 7, , 8, , 3, , 2, , 4, , 5, , 4, , 4, , ii. What is the probability that arrow point lie on the odd number?, 1, 1, 1, 1, a), b), c), d), iii. What is the probability that arrow point line on the number greater than 2?, 1, 1, 3, a), b) 1, c), d), 2, , iv. Find the probability that, arrow pointer is always on the number greater than 8, 1, 1, a), b) 1, c) 0, d), 2, , 4, , v. If a pointer lies mid of the number 2 and 3, then the probability is, 1, 1, 1, a), b), c), d) None of the above, 2, , 3, , 4, , 4., Rehana and Roseline are best friends.They are staying in the same colony. Both are studying in, the same classand in the same school. During winter vacation Rehana visited Roseline’s house to, playLudo.They decided to play Ludo with 2 dice., , To win a game, Rehana wanted a total of 7., i. What is the probability of winning a game by Rehana?, 1, 7, 5, 1, a), b), c), d), 6, , 12, , 18, , 9, , 12, , 36, , 36, , 4, , 18, , 15, , 18, , 9, , ii. To win a game, Roseline wanted 8 as the sum.What is the probability of winning a game by, Roseline?, 1, 7, 5, 1, a), b), c), d), iii. What is the probability that the sum of the numbers on both the dice is divisible by4 or 6., 7, 7, 5, 2, a), b), c), d)

Page 49 :
iv. The probability of getting a total of at least 10 is, 1, 1, 2, 1, a), b), c), d), 6, , 3, , 3, , 4, , 36, , 36, , 36, , 9, , v. What is the probability that 5 will come up at least in 1 die?, 7, 11, 25, 2, a), b), c), d), 5., In a bridge game, there are four persons play and make a pair of two-two persons apartner. In a, deck of 52 playing cards, distributed around the table clockwise in such a way that each person gets 13, cards., , i. Find the probability that the card drawn is a queen of black colour., 25, 3, 1, 5, a), b), c), d), 26, , 26, , 26, , 26, , 13, , 13, , 13, , 13, , 13, , 13, , 13, , 13, , 13, , 13, , 2, , 3, , 4, , ii. Find the probability that the card drawn is a card with number 5 or 6., 2, 11, 1, 12, a), b), c), d), iii. Find the probability that the card drawn is a card with number less than 8, 6, 5, 7, a), b), c), d) None of these., iv. Find the probability that the card drawn is a card with number between 2 and 9., 7, 5, 6, 3, a), b), c), d), 13, , v. Find the probability that any one person get a queen of spade?, 1, 1, 1, a), b), c), d) 1, 6., One day during games period,four friends namely A,B,C and D planned to play game using, number cards. They prepared 20 numbered cards with labelled 1 to 20 and then they put all the numbered, cards in the empty chalk box available in the class room. In this game every friend was asked pick the, card randomly and after each draw, card was replaced in the chalk box.

Page 50 :
1, 6, 11, 16, , 2, 7, 12, 17, , 3, 8, 13, 18, , 4, 9, 14, 19, , 5, 10, 15, 20, , i. Find the probability, first boy pick the card and he get the card with an even number?, 1, 1, 1, 3, a), b), c), d), 4, , 2, , 6, , 8, , 5, , 25, , 8, , 11, , 11, , 20, , 19, , 19, , ii. If the card drawn in first case is replaced and the second boy draws a card.What is theprobability of, getting a prime number?, 2, 4, 7, 9, a), b), c), d), iii. If the card drawn is not replaced in the second draw,what is the probability that he got amultiple of 3, greater than 4?, 1, 7, 6, 5, a), b), c), d), iv. For a sure event A, P(a) =?, a) 1, b) 100%, , c), , 20, 20, , d) All of the given options., , v. If all cards drawn are replaced then what is the probability of getting a multiple of 3 and 5?, 1, 1, 1, 1, a), b), c), d), 2, , 5, , 20, , 18, , 7., The diagram shows a grid of Squares. A button is placed on one of the squares. A fair dice is, thrown.If 1,2,3or 4 thrown, the button is moved one square to the left. If 5 and 6 is thrown, the button is, moved one square to the right., , i. The button is placed on red coloured square, the dice is thrown once.Then the probability that the, button is moved to the right,is____, 1, 1, 2, 3, a), b), c), d), 2, , 3, , 3, , 4, , 2, , 3, , 9, , 9, , 2, , 3, , 4, , ii. On the other occasion, the button is place on yellow square. The dice is thrown once and the button is, moved.The die is thrown a second time and the button is moved again. The probability that the button, is moved at Violet is, 1, 1, 1, 4, a), b), c), d), iii. In the situation in Q. (ii), The probability that the button is moved at “Pink Sqaure” is, 1, 2, 3, a) 0, b), c), d)

Page 51 :
iv. Inthe situation in Q. (ii), The probability that the button is moved at “YellowSqaure” is, 1, 1, 2, 4, a), b), c), d), 2, , 3, , 9, , 3, , 9, , 9, , v. In the situation in Q. (ii), The probability that the button is moved at Violet, Pink or “Yellowsquare”, is, 1, 1, 1, a), b), c), d) None of the given options., 2, , 8., Tossing of pair of coins., A,B and C are fighting to get a first chance in a game. “A” says let us toss two coins. If both heads appear, “A”will take first chance. If both tail appear, “B” will take first chance and one head and one tail appear, “C” will take first chance., A, B, C, , i. What is the Probability of“A” getting the first chance?, 1, 1, 1, 2, a), b), c), d), 2, , 3, , 4, , 3, , 2, , 3, , 3, , 4, , 2, , 3, , 4, , 3, , ii. What is the Probability of “B” getting the first chance?, 1, 1, 2, 1, a), b), c), d), iii. What is the Probability of “C” getting the first chance?, 1, 1, 1, 2, a), b), c), d), iv. Is “A” s decision is fair?, a) yes, b) no, , c) can’t say, , v. What is the Probability of a sure event?, 1, 2, a) 0, b), c), 3, 3, Answers: 1 (i) (a), 2 (iii) (a), 3 (v) (d), 5 (ii) (a), 6 (iv) (d), 8 (i) (c), , 1 (ii) (d), 2 (iv) (c), 4 (i)(a), 5 (iii) (a), 6 (v) (c), 8 (ii) (d), , 1 (iii) (b), 2 (v) (d), 4 (ii)(c), 5 (iv) (c), 7 (i) (b), 8 (iii) (a), , d) none of the options., d) 1, , 1 (iv) (a), 3 (i) (c), 4 (iii)(a), 5 (v) (c), 7 (i) (c), 8 (iv) (b), , 1 (v) (d), 3 (ii) (b), 4 (iv)(a), 6 (i) (b), 7 (ii) (a), 8 (v) (d), , 2 (i) (b), 3 (iii) (d), 4 (v)(b), 6 (ii) (a), 7 (iii) (d), , 2 (ii) (d), 3 (iv) (c), 5 (i) (c), 6 (iii) (d), 7 (iv) (d)