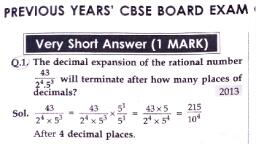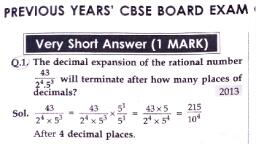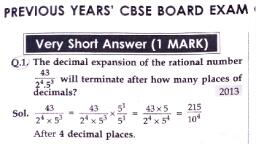Page 1 :
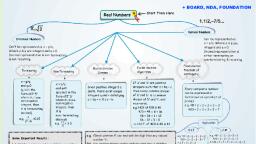
Mathematics (Standard Level) | Class 10 | Term-1 11, Q 28. What will be the least possible number of the planks, if, three pieces of timber 42 m, 49 m and 63 m long have to, be divided into planks of the same length?, Q 20. Given that LCM (91, 26) 182, then HCF (91, 26) is:, (CBSE 2011), a. 13, b. 26, C. 7, Sol. (a) HCF, 91x 26, 13, 182, d. None of these, 021. The values of x and y in the given figure are:, a. x 10: y = 14, b. x 21: y 84, C.X 21; y = 25, d. x = 10 y= 40, Sol. (b) x 21; y 84, Q22. LCM of 2 x 32 and 22 x 3 is:, a. 23, Sol. (c) 23 x33, 0 23. Two alarm clocks ring their alarms at regular intervals of, 50 seconds and 48 seconds. If they first beep together at, 12 noon, at what time will they beep again for the first, (CBSE 2012), Sol. (d) Length of plank HCF of 42. 49 and 63= 7, 42, Number of planks, 69, Vk, E, Q 29. The LCM of 2.5, 0.5 and 0.175 is:, 7., -6+7+9%3D 22, 7., 7., (CBSE 2012), d. 2 x3?, c. 7.5, LCM of numerators, a. 2.5, Sol. (d) LCM of rational number =, GCD of denominators, 25 5 175, Numbers are, 00 wL 00.0, = 17.5, Q 30. What is the smallest number which when increased by 6, becomes divisible by 36, 63 and 108?, time?, a. 12.20 pm, c. 12.11 pm, Sol. (a) LCM of 50 and 48=1200, b. 12.12 pm, d. 756, a. 750, Sol. (a) Number (LCM of 36, 63 and 108)-6, b. 752, c. 754, d. None of these, = 756-6= 750, 1200 sec = 20 min, Hence, at 12.20 pm they will beep again for the first time., Q 31. What is the greatest possible speed at which a man can, walk 52 km and 91 km in an exact number of minutes?, Q 24. On Delhi road, three consecutive traffic lights change after, 36,42 and 72 seconds. If the lights are first switched on at, 9.00 am, at what time will they change simultaneously?, a. 17 m/min, b. 7 m/min, d. 26 m/min, c. 13 m/min, Sol. (c) Speed HCF of 52 and 91 13 m/min, a. 9:08:04, b. 9:08:24, Q 32. LCM of 5, 8, 12, 20 will not be a multiple of:, d. 2, c. 9:08:44, d. None of these, Sol. (b) LCM of 36, 42 and 72 = 504, a. 5, b. 3, Sol. (c) LCM of 5, 8, 12 and 20 = 23 x5 x 3 = 120, which is not a multiple of 9., 504 sec = 8 min 24 sec, Hence, at 9:08:24 they will change simultaneously., Q 25. Two equilateral triangles have the sides of lengths 34 cm, and 85 cm respectively. The greatest length of tape that, Q 33. If A = 2n + 13, B = n + 7, where n is a natural number then, HCF of A and B is:, can measure the sides of both of them exactly is:, a. 2, b. 1, c. 3, d. 4, Sol. (b) Taking different values of n, we find that A and B are, coprime., b. 17 cm, c. 51 cm, d. None of these, Sol (b) Length of tape HCF of 34 and 85 = 17, Hence, length is 17., %3D, Q 34. Three runners running around a circular track, can, complete one revolution in 2, 3 and 4 hrs respectively., They will meet again at the starting point after:, Q 26. The HCF and LCM of two numbers are 33 and 264, respectively. When the first number is completely divided, by 2 the quotient is 33. The other number is:, c. 12 hrs, Sol. (c) They will meet after LCM of 2, 3 and 4 i.e., they will meet, a. 8 hrs, b. 6 hrs, d. 18 hrs, b. 130, c. 132, Sol. (c) First number = 2 x33 =66, after 12 hrs., HCFX LCM, Other number, Q 35. Two natural numbers whose difference is 66 and the least, %3D, 1st number, 33 x 264, common multiple is 360, are:, = 132, a. 120 and 54, b. 90 and 24, d. 130 and 64, 99, Q 27. Find the greatest number of 5 digits, that will give us, remainder of 5, when divided by 8 and 9 respectively., c. 180 and 114, Sol. (b) Difference of 90 and 24 = 66, and, LCM of 90 and 24 360, .Numbers are 90 and 24., Q36. Pairs of natural numbers whose least common multiple is, Sol. (c) The greatest number will be (multiple of LCM of 8 and 9), 78and the greatest common divisor is 13 are:, a. 58 and 13 or 16 and 29, c. 18 and 73 or 56 and 93, Sol. (d) Let numbers are 13x and 13y where x and y are coprime., +5, b.68 and 23 or 36 and 49, d. 78 and 13 or 26 and 39, LCM of 8 and 9 = 72, On verification we find that 99941 when divided by 72 leaves, remainder 5.