Page 1 :
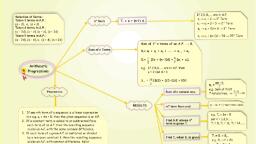
7a, , > — Objective Section MAP, , * Asequence of numbers in which difference between — Wn aieneeiaer iscsi), consecutive terms is constant is called AP., , * Common difference is a difference between two, consecutive numbers in an AP., , , , * When there are an infinite number of, , terms in a sequence. <, * Itcan be positive, negative or zero. £3 69, 2 J, - Common difference is Positive, if AP is increasing. Noten A Fite AP wit nave thelacd Pa le OES, - Common difference is Negative, if AP is decreasing. tarmawherecs an infinite AP won't., , - Common difference is zero, if AP is constant. ». TheniSterma:dfthe Ali wih ilisttermeandithe, General form for an AP: a + d,a + 2d, a + 3d.., , common difference d is given by a, = a + (n - 1)d., Where the first term of an AP is ‘a’ and the common, , diff isd’ “a i z A a, is also called the general term of the AP., ei ea ee iad @. represents the last term which is also denoted by‘., , Eg:, , , , , , , , , , Given APIs 3,5, 7,9, + When there are only a limited number Ee ne ere ee Ee, Here, a=3andd=2 of terms in a sequence. SJ Heese disp esanine?, das tayo ees ae Fg: 22, 24,26 28, 34. :, , , , , , We have a, =a + (n-1)d, So, a,=2+4(7-1)x5$=2+30=32, Note: If, is given,, , First term is a, Second termisa,=a+d=3+2=5, Third termis a, = a+ 2d=3 + 2(2)=7 and soon., , , , , , , , , , , , , , , , , , 7” : then common difference d= :, , * General term: Ifa’ is the first term and ‘d’ is common i Mea, difference in an AP, then n' term is given by a,= a + (n-1)d Tages coe . ave udiered. = a8 tern (General “ai. Ifa, b, eare in AP, then 6 = *** and bis called, Eg: 1.2 3 - arithmetic mean of a and c., , g: 1, 2, 3,, , , , , , , , , , Term: Each of the number in the sequence is called a term., , , , , , ARITHMETIC PROGRESSIONS, , SUM OF n'*TERMS OF ALGEBRA Jaxueal ae) A RS 9, , , , , , Sum of first 1 terms of an AP is givin by: Sequence- It is a collection of number arranged in a difinite order, h according to some different rule., , S=F[2a+ (n-1)d] Eg: 2, 4,68..., , wae uncer Progression- A sequence in which the general term can be, , expressed using a mathematical progression., Series- It is the sum of the element in the corresponding sequences., Eg: 142434445... is the series of natural number., , d= Common difference, n= Total terms