Page 2 :
Production Team, , Anil Kumar Sharma, , Published at Delhi Bureau of Text Books , 25/2 Institutional Area, Pankha, Road, New Delhi-110058 by Prabhjot Singh Secretary, Delhi Bureau, of Text Books and Printed by Supreme Offset Press, New Delhi-110017
Page 3 :
H. RAJESH PRASAD, IAS, , Pr Secretary (Education), , I would like to congratulate the members of Core Academic Unit and the, subject experts of the Directorate of Education, who inspite of dire situation due to, Corona Pandemic, have provided their valuable contributions and support in, preparing the Support Material for classes IX to Xll., The Support Material of different subjects, like previous years, have been, reviewed/ updated in accordance with the latest changes made by CBSE so that the, students of classes IX to Xll can update and equip themselves with these changes. I, feel that the consistent use of the Support Material will definitely help the students, and teachers to enrich their potential and capabilities., Department of Education has taken initiative to impart education to all its, students through online mode, despite the emergency of Corona Pandemic which, has led the world to an unprecedented health crises. This initiative has not only, helped the students to overcome their stress and anxiety but also assisted them to, continue their education in absence of formal education. The support material will, ensure an uninterrupted learning while supplementing the Online Classes., , (H. Rajesh Prasad)
Page 4 : UDIT PRAKASH RAI, IAS, , Directorate of Education, Govt. of NCT of Delhi, Room No. 12, Civil Lines, Near Vidhan Sabha,, Delhi-110054, Ph.: 011-23890172, Mob.: 8700603939, E-mail :
[email protected], , Director, Education & Sports, , The main objective of the Directorate of Education is to provide quality, education to all its students. Focusing on this objective, the Directorate is, continuously in the endeavor to make available the best education material, for, enriching and elevating the educational standard of its students. The expert, faculty of various subjects undertook this responsibility and after deep, discussions and persistent efforts, came up with Support Material to serve the, purpose., Every year the Support Material is revised/ updated to incorporate the, latest changes made by CBSE in the syllabus of classes IX to XII. The contents, of each lesson/chapter are explained in such a way that the students can, easily comprehend the concept and get their doubts solved., I am sure, that the continuous and conscientious use of this Support, Material will lead to enhancement in the educational standard of the students,, which would definitely be reflected in their performance., I would also like to commend the entire team members for their, contributions in the preparation of this incomparable material., I wish all the students a bright future., (UDIT PRAKASH RAI)
Page 5 :
Dr. RITA SHARMA, , Govt. of NCT of Delhi, , Additional Director of Education, (School/Exam), , Directorate of Education, Old Secretariat, Delhi-110054, Ph. : 23890185, D.O. No., Dated:, , (Rita Sharma)
Page 7 :
DIRECTORATE OF EDUCATION, GNCT of Delhi, Delhi Government, , SUPPORT MATERIAL, (2021-2022), , MATHEMATICS, Class: X, , NOT FOR SALE, , PUBLISHED BY : DELHI BUREAU OF TEXTBOOKS
Page 11 :
[L
Page 12 :
(xii)
Page 13 :
(xiii)
Page 14 :
(xiv)
Page 16 :
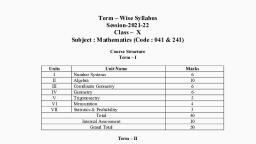
Content, S.No., , Chapter Name, , Page No., , 1., , Real Numbers, , 01–15, , 2., , Polynomials, , 16–26, , 3., , Pair of Linear Equations in Two Variables, , 27–36, , 4., , Quadratic Equations, , 37–55, , 5., , Arithmetic Progression, , 56–73, , 6., , Similar Triangles, , 7., , Co-ordinate Geometry, , 104–116, , 8., , Introduction to Trigonometry, , 117–128, , 9., , Some Applications of Trigonometry, , 129–138, , 74–103, , (Heights and Distances), 10., , Circles, , 139–158, , 11., , Constructions, , 159–166, , 12., , Areas Related to Circles, , 167–188, , 13., , Surface Areas and Volumes, , 189–211, , 14., , Statistics, , 212–228, , 15., , Probability, , 229–247, , , , Case Study Based Questions, , 248–275, , , , Practice Question Paper, , 276–339
Page 17 :
CHAPTER, , 1, , Real Numbers, , KEY POINTS, , PROPERTIES OF REAL NUMBERS, , Mathematics-X, , 1
Page 18 :
VERY SHORT ANSWER TYPE QUESTIONS, , 1., , A number N when divided by 16 gives the remainder 5 ______ is the remainder, when the same number is divided by 8., HCF of 33 × 54 and 34 × 52 is ________ ., If a = xy2 and b = x3y5 where x and y are prime numbers then LCM of (a, b) is, _____ ., In the given factor tree find x and y, , 2., 3., 4., , y, x, , 2, , 7, , 5, , 5., , If n is a natural number, then 252n – 92n is always divisible by :, (i) 16, (ii) 34, (iii), both 16 or 34 (iv), None of these, , 6., , The decimal expansion of the rational number, , 7., , (a) One decimal place, (b) Two decimal place, (c) Three decimal place, (d) More than three decimal place, Which of the following rational numbers have terminating decimal?, (i), , 18, 225, , (ii), , 5, 18, , (iii), , 2, 21, , 327, 23 5, , will terminate after, , (iv), , 7, 250, , (a) (i) and (ii), (b) (ii) and (iii), (c) (i) and (iii), (d) (i) and (iv), Euclid’s division Lemma states that for two positive integers a and b, there, exist unique integers q and r such that a = bq + r, where r must satisfy., (a) 1 < r < b, (b) 0 < r b, (c) 0 r < b, (d) 0 < r < b, n, n, n, p = (a × 5) For p to end with the digit zero a = _____ for natural number n., (a) any natural number, (b) even number, (b) odd number, (d) none of these, , 8., , 9., , 2, , Mathematics-X
Page 19 :
10. HCF is always, (a) multiple of LCM, (b) Factor of LCM, (c) divisible by LCM, (d) (a) and (c) both, 11. All decimal numbers are, (a) rational number, (b) irrational numbers, (c) real numbers, (d) integers, 12. Which of these numbers always end with the digits 6., (a) 4n, (b) 2n, (c) 6n, (d) 8n, 13. Write the prime factof of 2 × 7 × 11 × 13 × 17 + 21, 14. Write the form in which every odd integer can be written taking t as variable., 15. What would be the value of n for which n2–1 is divisible by 8., 16. What can you say about the product of a non-zero rational and irrational number?, 13497, 17. After how many places the decimal expansion of, will terminate?, 1250, 18. Find the least number which is divisible by all numbers from 1 to 10 (both, inclusive)., 19. The numbers 525 and 3000 are divisible by 3, 5, 15, 25 and 75. What is the, HCF of 525 and 3000?, 20. What is x : y in the factor-tree?, x, 2, , 210, 2, , 105, 3, , 35, 5, , y, , SHORT ANSWER TYPE QUESTIONS-I, , 21. If n is an odd integer then show that n2 – 1 is divisible by 8., 22. Use Euclid’s division algorithm to find the HCF of 16 and 28., 23. Show that 12n cannot end with the digit 0 or 5 for any natural number n., (NCERT Exemplar), Mathematics-X, , 3
Page 20 :
395, will have, 10500, terminating or non terminating (repeating decimal expansion.), , 24. Without actually performing the long division, find if, , 25. A rational number in its decimal expansion is 327. 7081. What can you say, about the prime factors of q, when this number is expressed in the form of, Give reasons., , p, ?, q, , 26. What is the smallest number by which 5 – 2 is to be multiplied to make it, a rational number? Also find the number so obtained?, 27. Find one rational and one irrational no between, , 3 and, , 5., , 28. If HCF of 144 and 180 is expressed in the form 13m – 3, find the value of m., (CBSE 2014), 29. Find the value of : (–1)n + (–1)2n + (–1)2n + 1 + (–1)4n+2, where n is any positive, odd integer., (CBSE 2016), 30. Show that any positive odd integer is of the form 4q + 1 or 4q + 3, where q is, some integer., (CBSE 2012), 31. Two tankers contain 850 litres and 680 litres of petrol respectively. Find the, maximum capacity of a container which can measure the petrol of either tanker, in exact number of times., (CBSE 2016), SHORT ANSWER TYPE QUESTIONS-II, , 32. Show that the cube of any positive integer is of the form 4m, 4m + 1 or 4m + 3, for some integer m., 33. If 7560 = 23 × 3p × q × 7, find p and q., 105, is a terminating decimal, what are the least possible values, 2 5 3 p 7q, of p and q., , 34. If, , 3, , 2, , 35. Prove that, , 3 + 5 is irrational, , 36. Prove that 5 –, , 4, , 3, 3 is an irrational number.., 7, , Mathematics-X
Page 21 :
37. Prove that, , 1, is an irrational number.., 2– 5, , 38. Find HCF and LCM of 56 and 112 by prime factorization method., 39. Explain why:, (i) 7 × 11 × 13 × 15 + 15 is a composite number, (ii) 11 × 13 × 17 + 17 is a composite number., (iii) 1 × 2 × 3 × 5 × 7 + 3 × 7 is a composite number., 40. On a morning walk, three persons steps off together and their steps measure 40, cm, 42 cm, and 45 cm respectively. What is the minimum distance each should, walk, so that each can cover the same distance in complete steps?, (NCERT Exemplar), 41. During a sale, colour pencils were being sold in the pack of 24 each and crayons, in the pack of 32 each. If you want full packs of both and the same number of, pencils and crayons, how many packets of each would you need to buy?, (CBSE : 2017), 42. Find the largest number that divides 31 and 99 leaving remainder 5 and 8, respectively., 43. The HCF of 65 and 117 is expressible in the form 65 m – 117. Find the value of, m. Also find the LCM of 65 and 117 using prime factorisation method., 44. Using Euclid’s division algorithm, find the largest number that divides 1251,, 9377 and 15628 leaving remainder 1, 2 and 3 respectively., (NCERT Exemplar), 45. Show that square of any odd integer is of the form 4m + 1, for some integer m., 46. Find the HCF of 180, 252 and 324 by Euclid’s Division algorithm., 47. Find the greatest number of six digits exactly divisible by 18, 24 and 36., 48. Three bells ring at intervals of 9, 12, 15 minutes respectively. If they start, ringing together at a time, after how much time will they next ring together?, 49. Show that either the number n, n + 2 and n + 4 are three consecutive odd, numbers or 3 even numbers., , Mathematics-X, , 5
Page 22 :
50. Find HCF and LCM of 404 and 96 and verify that HCF × LCM = Product of, two given number., (CBSE 2018), LONG ANSWER TYPE QUESTIONS, , 51. Find the HCF of 56, 96, 324 by Euclid’s algorithm., 52. Show that any positive odd integer is of the form 6q + 1, 6q + 3 or 6q + 5,, where q is some integer., 53. Prove that the square of any positive integer is of the form 5q, 5q + 1, 5q + 4 for, some integer, q., 54. Prove that the product of three consecutive positive integers is divisible by 6., 55. For any positive integer n, prove that n3–n is divisible by 6., (NCERT Exemplar), 56. Show that one and only one of n, n + 2, n + 4 is divisible by 3., 57. Aakriti decided to distribute milk in an orphanage on her birthday. The supplier, brought two milk containers which contain 398 l and 436 l of milk. The milk is, to be transferred to another containers so that 7 l and 11 l of milk is left in both, the containers respectively. What will be the maximum capacity of the, drum?, 58. Find the smallest number, which when increased by 17, is exactly divisible by, both 520 and 468., 59. A street shopkeeper prepares 396 Gulab jamuns and 342 ras-gullas. He packs, them, in combination. Each containter consists of either gulab jamuns or rasgullab but have equal number of pieces., Find the number of pieces he should put in each box so that number of boxes, are least. How many boxes will be packed in all., (CBSE 2016), 60. Show that the square of any positive integer cannot be of the form 5q + 2 or, 5q + 3 for integer q., 61. Express the HCF of numbers 72 and 124 as a linear combination of 72 and 124., 62. Show that there is no positive integer n for which, , n 1 +, , n 1 is rational., , 63. Find the number nearest to 110000 but greater than 1 lakh, which is exactly, divisible by 8, 15, 21., 64. In a seminar, the no. of participants in Hindi, English and Mathematics are 60,, 84 and 108 respectively. Find the minimum number of rooms required if in, 6, , Mathematics-X
Page 23 :
each room the some the same number of participants are to be seated and all of, the them being of the the same subject., (HOTS), 65. State fundamental theorem of Arithmetic. Is it possible that HCF and LCM of, two numbers be 24 and 540 respectively. Justify your answer., 66. Find the smallest number which when increased by 20 is exactly divisible by, 90 and 144. If we express the smallest number, the LCM, in the form 144 m +, 90n, then what are the values of m and n? Is LCM, a multiple of 144?, 67. If the HCF of 1032 and 408 is expressible in the form 1032 p – 408×5, find p., 68. The LCM of two numbers is 14 times their HCF. The sum of LCM and HCF is, 600. If one of the number is 280. Find the other number., ANSWERS AND HINTS, , 1. 5, , 2. 33 × 52, , 3. x3 × y5, , 4. x = 35, y = 70, , 5. (iii) 252n – 92n is of the form a2n – b2n which is divisible by both a – b and, a + b so, by both 25 + 9 = 34 and 25 – 9 = 16., 6. (c) three decimal place, , 7. (d) (i) and (iv), , 8. (c) 0 r < b, , 9. (b) even number, , 10. (b) Factor of LCM, , 11. (c) real numbers, , 12. (c) 6n, , 13. 7, , 14. 2t + 1, , 15. An odd integer, , 16. Irrational, , 17. 4, , 18. 2520, , 19. 75, , 20. 60 : 1, 21. Any +ve odd integer is of the form 4q + 1 or 4q + 3 for some integer q so if, n = 4q + 1., n2 – 1 = (4q + 1)2–1 = 16q2 + 8q = 8q(2q + 1) n2 – 1 is divisible by 8., If n = 4q + 3, n2 – 1 = (4q + 3)2 – 1 = 16q2 + 24q + 8 = 8 (2q2 + 3q + 1) n2 – 1 is divisible, by 8., Mathematics-X, , 7
Page 24 :
22. 4, 23. As 12 has factors 2, 2, 3 it doesnot has 5 as its factor so 12 n will never end, with 0 or 5., 24. Non-terminating repeating., 25. Denominator is the multiple of 2’s and 5’s., 26., , 5 2 , 3, , 28. By Euclid’s division lemma, 180 = 144 × 1 + 36, 144 = 36 × 4 + 0, HCF of 180 and 144 is 36., 13m – 3 = 36, 13 m = 39, m= 3, 29. Given that n is a positive odd integer, 2n and 4n + 2 are even positive integers and n and 2n + 1 are odd positive, integers., , , (–1)n = – 1, (–1)2n = + 1, (–1)2n + 1 = – 1, (–1)2n + 2 = + 1, , , , (–1)n + (–1)2n + (–1)2n + 1 + (–1)4n + 2 = – 1 + 1 – 1 + 1 = 0, , 30. By applying Euclid division algorithm to a and b such that a = 4q + r, where, b = 4, Now r = 0, 1, 2, 3., where,, , r = 0,, , a = 4q, , which is even number., , where,, , r = 1,, , a = 4q + 1 an odd number., , where,, , r = 2,, , a = 4q + 2 =2 (2q + 1), an even number., , where,, , r = 3,, , a = 4q + 3, , an odd number., , 31. HCF of 850 and 680 is 2 × 5 × 17 = 170 litres., 32. Let n be any psoitve integer. Then it is of the form 4q, 4q + 1, 4q + 2 and, 4q + 3., When n = 4q, n3 = 64q3 = 4 (16q3) = 4 m, where m = 16q3, When n = 4q + 1, n3 = (4q + 1)3 = 64q3 + 48q2 + 12q + 1, 8, , Mathematics-X
Page 25 :
= 4(16q3 + 12q2 + 3q) + 1 = 4 m + 1., where m = 16q3 + 12q2 + 3q, Similarly discuss for n = 4q + 2 and 4q + 3., 33. p = 3 and q = 5, 34. 0 and 1, 35. Prove that, , 3 and, , 5 is irrational number separately.., , 3, 3 is an irrational number. Difference of a rational, 7, number and irrational number is an irrational number., 38. HCF : 56, LCM : 112, , 36. 5 is rational no. and, , 39. (1) 15 × (7 × 11 × 13 + 1) as it has more than two factors so it is composite no., 40. LCM of 40, 42, 45 = 2520, Minimum distance each should walk 2520 cm., 41. LCM of 24 and 32 is 96, 96 crayons or, , 96, = 3 packs of crayons, 32, , 96 pencils or, , 96, = 4 packs of pencils., 24, , 42. Given number = 31 and 99, 31 – 5 = 26 and 99 – 8 = 91, Prime factors of 26 = 2 × 13, 91 = 7 × 13, HCF of (26, 91) = 13., 13 is the largest number which divides 31 and 99 leaving remainder 5, and 8 respectively., 43. HCF of 117 and 65 by Euclid division algorithm., 117 = 65 × 1 + 52, 65 = 52 × 1 = 52, 52 = 13 × 4 + 0, HCF (117, 52) = 13., Given that 65 m – 117 = 13 65 m = 130 m = 2., LCM (65, 117) = 13 × 32 × 5 = 585, Mathematics-X, , 9
Page 26 :
44. 1251 – 1 =1250, 9377 – 2 = 9375, 15628 – 3 = 15625, HCF of (15625, 9375) = 3125, HCF of (3125, 1250) = 625, HCF of (1250, 9375, 15625) = 625, 45. By Euclid’s division algorithm, we have a = bq + r, where 0 r < 4. On, putting b = 4 we get a = 4q + r where, r = 0, 1, 2, 3., If r = 0,, a = 4q which is even, If r = 1,, a = 4q + 1 not divisible by 2, If r = 2,, a = 4q + 2 = 2(2q + 1) which is even, If r = 3,, a = 4q + 3 not divisible by 2., So, for any +ve integer q, 4q + 1 and 4q + 3 are odd integers., How,, a2 = (4q + 1)2 = 16q2 + 1 + 8q = 4(4q2 + 2q) + 1 = 4m + 1, where m = 4q2 + 2q similarly for 4q + 3., 46. HCF (324, 252, 180) = 36, 47. LCM of (18, 24, 36) = 72., Greatest six digit number = 999999, 72, , 999999, – 72, 279, – 216, 639, – 576, 639, – 576, 639, 576, , 13888, , Require six digit number, 999999, – 63, 999936, , 63, , 48. LCM of (9, 12, 15) = 180 minutes., 49. Let the number divisible by 3 is of the form 3k + r, r = 0, 1, 2, a = 3k, 3k + 1 or 3k + 2, (i) When, a = 3k, n = 3k n is divisible by 3., n + 2 = 3k + 2 n + 2 is not divisible by 3., n + 4 = 3k + 4 = 3k + 3 + 1 = 3(k + 1) + 1 n + 4 is not, divisible by 3., So, only one out of n, n + 2 and n + 4 is divisible by 3., 10, , Mathematics-X
Page 27 :
(ii) When, , 50., , 51., 52., , 54., , a = 3k + 1, n = 3k + 1 n is not divisible by 3., n + 2 = 3k + 1 + 2 = 3k + 3 = 3(k + 1), n + 2 is divisible by 3., n + 4 = 3k + 1 + 4 = 3k + 5 = 3(k + 1) + 2, n + 2 is not divisible by 3., So, only one out of n, n + 2 and n + 4 is divisible by 3., Similarly do for a = 3k + 2., HCF (404, 96) = 4, LCM (404, 96) = 9696, HCF × LCM = 38, 784, Also,, 404 × 96 = 38,784, 4, Let a be +ve odd integer., , a = 6q + r where r = 0, 1, 2, 3, 4, 5, If,, a = 6q + 0 = 2(3q) is an even integer so not possible, If,, a = 6q + 1 is an odd integer, If,, a = 6q + 2 = 2(3q + 1) is an even integer so not possible, If,, a = 6q + 3 is an odd integer, If,, a = 6q + 4 = 2(3q + 2) is an even integer so not possible, If,, a = 6q + 5 is an odd integer., Let the three consecutive integers be a, a+1, a + 2,, Case I : If a is even,, a + 2 is the also even, a(a + 2) is divisible by 2, a(a + 2) (a + 1) is also divisible by 2, Now a, a + 1, a + 2 are three consecutive numbers, a (a + 1) (a + 2) is a multiple by 3, a (a + 1) (a + 2) is divisible by 3, as it is divisible by 2 and 3 hence divisible by 6., Case II : If a is odd, a + 1 is even, , Mathematics-X, , 11
Page 28 :
55., , 57., 58., , 59., , a + 1 is divisible by 2, a(a + 1) (a + 2) is also divisible by 2, Again a, a + 1, a + 2 are three consecutive numbers, a (a + 1) (a + 2) is a multiple by 3, a (a + 1) (a + 2) is divisible by 3, as it is divisible by 2 and 3 hence divisible by 6., n3 – n = n(n2 – 1) = n (n – 1) (n + 1), = (n – 1) (n) (n + 1), = Product of three consecutive +ve integers, Now to show that produce of three consecutive +ve integers is divisible by 6., Any +ve integer a is of the form 3q, 3q + 1 or 3q + 2 for some integer q., Let a, a + 1, a + 2 be any three consecutive integers., Case I : a = 3q, (3q) (3q + 1) (3q + 2) = 3q (2m) [as (3q + 1) and (3q + 2) are consecutive, integers so their product is also even], = 6q m, which is divisible by 6., Case II : If a = 3q + 1, a (a + 1) (a + 2) = (3q + 1) (3q + 2) (3q + 3), = 2m3(q + 1), (as (3q + 1) (3q + 2) = 2m), = 6 m (q + 1), which is divisible by 6., Case III : If a = 3q + 2, a (a + 1) (a + 2) = (3q + 2) (3q + 3) (3q + 4), = (3q + 2) 3(q + 1) (3q + 4), = 6m, which is divisible by 6., 17, 4663, LCM of (468, 520) = 4680, Required no. = 4680 – 17 = 4663, HCF (396, 342) = 18, No. of boxes =, , 12, , 396 342, 738, =, = 41, 18, 18, , Mathematics-X
Page 29 :
61. HCF (124, 72) = 4, 4 = 124 × 7 + 72 × (– 12), x = 7, y = – 12, 62. Let, , n 1 n 1 , , p, (1)q 0, p, q, co-prime., q, , q, =, p, , 1, , n 1 n 1, , q, =, p, , n 1 – n 1, 2, , n 1 n 1 , , 2q, or, p, , n 1 – n 1, n 1 n 1, , n 1 n 1 , , Adding (1) & (2) we get 2 n 1 , , 2q, p, , …(2), , p 2 q p 2 2q 2, , , q, p, pq, , 2, 2, Subtracting (1) & (2) we get 2 n 1 p 2q, pq, , From (3) & (4) we get, But, , , …(3), …(4), , n 1 n 1 are rational numbers., , n 1 n 1 is an irrational number.., These exist no positive integer n, for which, , n 1 n 1 is rational., , 63. 109200, 64. HCF of 60, 84 and 108 is 22 × 3 = 12 = No. of participants in each row., No. of rooms required =, , Total number of participants, 12, , 60 84 108, = 21 rooms, 12, HCF = 24, LCM = 540, , =, , 65., , LCM, 540, =, = 22.5, not an integer., HCF, 24, Hence two numbers cannot have HCF and LCM as 24 and 540 respectively., , Mathematics-X, , 13
Page 30 :
66. [The LCM of (90, 144) – 20] = Required No., Required No. = 700, If 720 = 144m + 90n then m = 5, n = 0, Yes, 67. p = 2, 68. HCF = 40, LCM = 560, Other No. = 80., , 14, , Mathematics-X
Page 31 :
PRACTICE-TEST, Real Number, Time : 1 Hr., , M.M. : 20, SECTION A, , 1., 2., 3., 4., , Check whether 17 × 19 × 21 × 23 + 7 is a composite number., 1, In Euclid’s Division Lemma, when a = bq + r where a, b are positive integers, then what values r can take?, 1, HCF of x4y5 and x8y3 ., 1, LCM of 14 and 122 ., 1, , 5., , Show that 9 can never ends with unit digit zero., , 6., , Without actual division find the type of decimal expansion of, , SECTION B, , 7., , 2, , n, , 805, , if, 10500, terminating, after how many places., 2, Show that the square of any odd integer is of the form 4m + 1, for some integer, m., 2, , SECTION C, 1, is an irrational number.., 3– 2 5, , 8., , Prove that, , 9., , Find the HCF of 36, 96 and 120 by Euclid’s Lemma., , 3, 3, , SECTION D, 10. Once a sports goods retailer organized a campaign “Run to remember” to spread, awareness about benefits of walking. In that Soham and Baani participated., There was a circular path around a sports field. Soham took 12 minutes to, drive one round of the field, while Baani took 18 minutes for the same. Suppose, they started at the same point and at the same time and went in the same direction., After how many minutes have they met again at the starting point?, 4, Mathematics-X, , 15
Page 32 :
CHAPTER, , 2, , Polynomials, , KEY POINTS, , 1., , Polynomial : If x is a variable, n is a natural number and a0, a1, a2, a3, ………. an, are real numbers, then p(x) = an xn + an–1 xn–1 + ......... + a1 x + a0, (an 0) is called, a polynomial in x. The definition of p(x) is n as an 0., , 2., , Polynomials of degree 1, 2 and 3 are called linear, quadratic and cubic polynomials, respectively., , 3., , A quadratic polynomial is an algebraic expression of the form ax2 + bx + c, where a,, b, c are real numbers with a 0., , 4., , Zeros of a polynomial p(x) are precisely the x – coordinates of the points where, the graph of y = p(x) intersects the x–axis, i.e., x = a is a zero of polynomial p(x) if, p(a) = 0 which means (x – a) is a factor of p(x)., , 5., , A polynomial can have at most the same number of zeros as the degree of the, polynomial., , 6., , (i) If one zero of a quadratic polynomial p(x) is negative of the other, then, coefficient of x is 0., (ii) If zeroes of a quadratic polynomial p(x) are reciprocal of each other, then, coefficient of x2 = constant term., , 7., , Relationship between zeros and coefficients of a polynomial, If and are zeros of p(x) = ax2 + bx + c (a 0), then, b, Sum of zeros = + = –, a, c, Product of zeros = =, a, , 16, , Mathematics-X
Page 33 :
8., , If are zeros of a quadratic polynomial p(x), then, p(x) = k[x2 – (sum of zeros) x + product of zeros], p(x) = k [x2 – (+ )x + ]; where k is any non-zero real number., , 9., , Graph of linear polynomial p(x) = ax + b is a straight line., , 10. Division Algorithm states that given any polynomials p(x) and g(x), there exist, polynomial q(x) and r(x) such that:, p(x) = g(x). q(x) + r(x) ; g(x) 0,, [where either r(x) = 0 or degree r(x) < degree g(x)], Graph of different types of polynomials:, •, , Linear Polynomial : The graph of a linear polynomial ax + b is a straight line,, intersecting x-axis at one point., , •, , Quadratic Polynomial:, (i) Graph of a quadratic polynomial p(x) = ax2 + bx + c is a parabola open, upwards like U, if a > 0 and intersect x-axis at maximum two distinct points., y, , x, , 0, , x, , y', , (ii) Graph of a quodratic polynomial p(x) = ax2 + bx + c is a parabola open, downwards like , if a < 0 and intersect x-axis at maximum two distinct, points., y, , x', , Mathematics-X, , 0, , x, , 17
Page 34 :
(iii) Polynomial and its graph : In general a polynomial p(x) of degree n crosses the, x-axis at most n points., y, , x', , 0, , x, , y', , VERY SHORT ANSWER TYPE QUESTIONS, , 1., , If one zero of the polynomial P(x) = 5x2 + 13x + K is reciprocal of the other, then, value of k is, 1, (d) 6, 6, If and are the zeroes of the polynomial p(x) = x2 – p(x + 1) – c such that, ( + 1) ( + 1) = 0, the c = _______ ., If one zero of the quadratic polynomial x2 + 3x + k is 2, then the value of k is, (a) 10, (b) – 10, (c) 5, (d) – 5, 2, If the zeroes of the quadratic polynomial x + (a + 1)x + b are 2 and – 3, then, (a) a = – 7, b = – 1, (b) a = 5, b = – 1, (c) a = 2, b = – 6, (d) a = 0, b = – 6, What should be added to the polynomial x2 – 5x + 4, so that 3 is the zero of the, resulting polynomial:, (a) 1, (b) 2, (c) 4, (d) 5, If and are the zeros of the polynomial, , (a) 0, 2., 3., 4., , 5., , 6., , (b) 5, , f (x) = x2 + x + 1, then, 7., 8., 9., 18, , (c), , 1 1, , , , If a quadratic polynomial f(x) is not factorizable into linear factors, then it has no real, zero. (True/False), If a quadratic polynomial f(x) is a square of a linear polynomial, then its two zeros are, coincident. (True/False)., If p(x) = x3 – 2x2 – x + 2 = (x + 1) (x – 2) (x – d) then what is the value of d?, Mathematics-X
Page 35 :
10. The quadratic polynomial ax2 + bx + c, a 0 is represented by this graph then a is, , (a) Natural no. (b) Whole no. (c) Negative Integer (d) Irrational no., 11. What will be the number of zeros of a linear polynomial p(x) if its graph (i) passes, through the origin. (ii) doesn’t intersect or touch x-axis at any point?, 12. Find the quadratic polynomial whose zeros are, , 5 + 2 3 and 5 – 2 3, , 13. If one zero of p(x) = 4x2 – (8k2 – 40k) x – 9 is negative of the other, find values of, k., 14. What number should be subtracted to the polynomial x2 – 5x + 4, so that 3 is a zero, of polynomial so obtained., 15. How many (i) maximum (ii) minimum number of zeroes can a quadratic polynomial, have?, 16. What will be the number of real zeros of the polynomial x2 + 1?, 17. If and are zeros of polynomial 6x2 – 7x – 3, then form a quadratic polynomial, where zeros are 2 and 2, (CBSE), 1, 18. If and, are zeros of 4x2 – 17x + k – 4, find the value of k., , 19. What will be the number of zeros of the polynomials whose graphs are parallel to (i), y-axis (ii) x-axis?, 20. What will be the number of zeros of the polynomials whose graphs are either touching, or intersecting the axis only at the points:, (i) (–3, 0), (0, 2) & (3, 0) (ii) (0, 4), (0, 0) and (0, –4), SHORT ANSWER TYPE (I) QUESTIONS, , 21. For what value of k, x2 – 4x + k touches x-axis., 22. If the product of zeros of ax2 – 6x – 6 is 4, find the value of a. Hence find the sum of, its zeros., 23. If zeros of x2 – kx + 6 are in the ratio 3 : 2, find k., 24. If one zero of the quadratic polynomial (k2 + k)x2 + 68x + 6k is reciprocal of the, other, find k., Mathematics-X, 19
Page 36 :
25. If and are the zeros of the polynomial x2 – 5x + m such that – = 1, find m., (CBSE), 26. If the sum of squares of zeros of the polynomial x2 – 8x + k is 40, find the value of k., 27. If and are zeros of the polynomial t2 – t – 4, form a quadratic polynomial whose, zeros are, , 1, 1, and ., , , , 28. What should be added to the polynomial x3 – 3x2 + 6x – 15, so that it is completely, divisible by x – 3 ?, (CBSE 2016), m n, 29. If m and n are the zeros of the polynomial 3x2 + 11x – 4, find the value of ., n m, (CBSE, 2012), 30. Find a quadratic polynomial whose zeros are, , 3 5, 3 5, and, ., 5, 5, , (CBSE, 2013), SHORT ANSWER TYPE (II) QUESTIONS, , 31. If (k+ y) is a factor of each of the polynomials y2 + 2y – 15 and y3 + a , find the, values of k and a., 32. Obtain zeros of 4 3 x 2 5 x – 2 3 and verify relation between its zeroes and, coefficients., 33. If x4 + 2x3 + 8x2 + 12x + 18 is divided by (x2 + 5) , remainder comes out to be (px, + q) , find values of p and q., 34. –5 is one of the zeros of 2x2 + px – 15, zeroes of p(x2 + x) + k are equal to each, other. Find the value of k., 35. Find the value of k such that 3x2 + 2kx + x – k– 5 has the sum of zeros as half of, their product., 36. If zeros of the polynomial ax2 + bx – c, a 0 are additive inverse of each other then, what is the value of b?, 37. If and are zeros of x2 – x – 2, find a polynomial whose zeros are (2+ 1) and, (2 + 1), 20, , Mathematics-X
Page 37 :
38. Find values of a and b so that x4 + x3 + 8x2 + ax + b is divisible by x2 + 1., 39. What must be subtracted from 8x4 + 14x3 – 2x2 + 7x – 8 so that the resulting, polynomial is exactly divisible by 4x2 + 3x – 2 ?, 40. What must be added to 4x4 + 2x3 – 2x2 + x – 1 so that the resulting polynomial is, divisible by x2 – 2x – 3 ?, LONG ANSWER TYPE QUESTIONS, , 41. Find all zeros of the polynomial 2x3 + x2 – 6x – 3 if two of its zeroes are, 3 and – 3 ., 42. If, , 3, 2, 2 is a zero of (6 x 2 x – 10 x – 4 2) , find its other zeroes., , 43. If two zeros of x4 – 6x3 – 26x2 + 138 x – 35 are (2 3) , find other zeroes., 44. On dividing the polynomial x3 – 5x2 + 6x – 4 by a polynomial g(x), quotient and, remainder are (x –3) and (– 3x + 5) respectively. Find g(x), 45. Obtain all zeros of the polynomial 2x4 – 2x3 – 7x2 + 3x + 6 if two factors of this, , 3, polynomial are x , ., 2 , , , 46. If the polynomial x4 – 3x3 – 6x2 + kx – 16 is exactly divisible by x2 – 3x + 2, then, find the value of k., (CBSE, 2014), 4, 3, 2, 2, 47. If the polynomial x – 6x + 16x – 25x + 10 is divided by x – 2x + k, the, reaminder is (x + a) then find the value of k and a., (CBSE), 48. If and are zeros of the polynomial x2 + 4x + 3, find the polynomial whose zeros, are 1 , , , , and 1 ., , , , (CBSE), , 49. Find K, so that x2 + 2x + K is a factor of 2x4 + x3 – 14x2 + 5x + 6. Also find all the, zeros of the two polynomials:, (Exempler, HOTS), 50. If x 5 is a factor of the cubic polynomial x3 3 5x2 13x 3 5 , then find, all the zeros of the polynomial., 51. If zeros of x2 – 5kx + 24 are in the ratio 3 : 2, find k., 52. Form a quadratic polynomial one of whose zero is 2 5 and sum of the zeros is 4., Mathematics-X, , 21
Page 38 :
53. Form a polynomial whose zeros are the reciprocal of the zeros of p(x) = ax2 + bx +, c, a 0., 54. If (x + 2) is a factor of x2 + px + 2q and p + q = 4 then what are the values of, p and q?, 55. What should be subtracted from x3 – 3x2 + 6x – 15, so that it is completely divisible, by (x – 3)?, 56. If x2 + 1 is a factor of x4 + x3 + 8x2 + ax + b then what are the values of a and b., 57. If sum of the zeros of 5x2 + (p + q + r)x + pqr is zero, then find p3 + q3 + r3., 58. If the zeros of x2 + px + q are double in value to the zeros of 2x2 – 5x – 3 find p and, q., ANSWERS AND HINTS, , 1. (b) 5, , 2. 1, , 3. (b) –10, , 4. (d) a = 0, b = –6, , 5. (b) 2, , 6. – 1, , 7. True, 9. 1, 11. (i) 1 (ii) 0, , 8. True, 10. (c) Negative Integer, 12. x2 – 10x + 13, , 13. k = 0, 5, , 14. (– 2), , 15. (i) 2 (ii) 0, , 16. 0, , 17. [3x2 – 7x – 6] k, , 18. k = 8, , 19. (i) 1 (ii) 0, , 20. (i) 2 (ii) 1, , 21. 4, , 3, 22. a , sum of zeroes 4, 2, , 23. – 5, 5, , 24. 5, , 25. 6, , 26. 12, , 27. 4t2 + t – 1, 28. On dividing x3 – 3x2 + 6x – 15 by x – 3, remainder is + 3, hence – 3 must be, added to x3 – 3x2 + 6x – 15., , 22, , Mathematics-X
Page 39 :
2, , 11, 4, 2 , 2, , 2, 3, 3 145, m n m n, ( m n) 2mn, , , 29., =, 4, 12, n m, mn, mn, , 3, 6, 4, 30. , , ,, 31. k = –3, 5 and a = –27, 125, 5, 25, 25x2 – 30x + 4, 32. , 34., , 2, ,, 3, , 3, 4, , 33. p = 2, q = 3, , 7, 4, , 35. 1, , 36. b = 0, 38. a = 1, b = 7, , 37. x2 – 4x – 5, 39. 14x – 10, , 40. 61x – 65, , 41., , 42. , , 2 2 2, ,, 2, 3, , 1, 2, , 3, 3, , , 43. – 5, 7, 45. 2, 1, , , 44. x2 – 2x + 3, , 3, 2, , 46. x2 – 3x + 2 = (x – 2) (x – 1), P(1) = 0, K = 24., 47. On dividing x4 – 6x3 + 16x2 – 25x + 10 by x2 – 2x + k we get remainder, (2k – 9)x + (10 – 8k + k2), Given remainder = x + a, 2k – 9 = 1, , , , k5, , 10 – 8k + k2 = a a = 10 – 40 + 25 = – 5, a = – 5, k = 5, 2, 48. x , , 16, 16, 1, x, or (3 x 2 16 x 16), 3, 3, 3, , Mathematics-X, , 23
Page 41 :
PRACTICE-TEST, Polynomials, Time : 1 Hr., , M.M. : 20, SECTION- A, , 1., 2., 3., , If and are zeros of a quadratic polynomial p(x), then factorize p(x)., 1, If and are zeros of x2 – x – 1, find the value of ., , , 1, 1, , If one of the zeros of quadratic polynomial (K –1) x2 + kx + 1 is – 3 then the value, of K is,, (a), , 4., , 4, 3, , 1, (b) , , 4, 3, , (c), , 2, 3, , (d) , , 2, 3, , A quadratic polynomial, whose zeros are – 3 and 4, is, (a) x2 – x + 12, (b) x2 + x + 12, (c), , x2 x, 6, 2 2, , 1, , (d) 2x2 + 2x – 24, , SECTION-B, 1, ., 2, 2, , 5., , If and are zeros of x2 – (k + 6)x + 2(2k –1). find the value of k if + =, , 6., , Find a quadratic polynomial one of whose zeros is (3 2) and the sum, of its zeroes is 6., , 7., , If zeros of the polynomial x2 + 4x + 2a are and, , Mathematics-X, , 2, 2, then find the value of a., , , 2, , 25
Page 42 :
SECTION-C, 8., 9., , Find values of a and b if (x2 + 1) is a factor of the polynomial x4 + x3 + 8x2 + ax, + b., 3, If truth and lie are zeros of the polynomial px2 + qx + r, (p 0) and zeros are, reciprocal to each other, Find the relation between p and r., 3, , SECTION-D, 10. On dividing the polynomial x3 + 2x2 + kx + 7 by (x – 3), remainder comes out to be, 25. Find quotient and the value of k. Also find the sum and product of zeros of the, quotient so obtained., 4, , 26, , Mathematics-X
Page 43 :
CHAPTER, , Pair of Linear Equations, in Two Variables, , 3, KEY POINTS, , Linear equation in, two variables, a1x + b1y + c1 = 0 … (1), a2x + b2y + c2 = 0 … (2), , Equation reducible, to a pair of linear, equation, , Equation of a, straight line, Method to solve, ax + by + c = 0, Solution (x, y) Points, lying on straight line,, , Graphical, method, , 2, x, , +, , 3, y, , = 13,, 1, x, , 5, x, 1, y, , +, , 4, y, , =2, , Put = 0,, =b, 2a + 3b = 13, 5a + 4b = 2, , x', , ax, , +, , by, , +, , c=, , 0, , y, , Algebraic, method, , 0, y', , Substitution Method, a1x + b1y + c1 = 0 …(1), a2x + b2y + c2 = 0 …(2), Substituting the value of, x from eq. (1) in eq. (2), and finding y and, vice versa., , Intersecting lines, , x, Elimination Method, a1x + b1y = c1 …(1), a2x + b2y = c2 …(2), Multiplying eq. (1) by a2, and eq. (2) by a1 making, coefficient of x same and, hence eliminating x and, finding y., , Cross multiplication, method, b1 x c1 y a1 1 b1, b2, x, b1c2 – b2c1, , a1, a2, , b1, b2, , +, , (intersect at 1 point) one solution, a, b, c, Coincident a = b = c, Coincide, Infinite solution, a, b, c, Parallel lines a = b = c, (Not, Non Intersecting) No solution, 1, , 1, , 2, , 2, , 1, 2, , 1, , 1, , 1, , 2, , 2, , 2, , c2, a, b2, y 2, = c a – a c = a 1b – b a, , x=, y=, , 1 2, , 1 2, , 1 2, , 1 2, , b1c2 – b2c1, a1b2 – b1a2, c1a2 – a1c2, a1b2 – b1a2, , VERY SHORT ANSWER TYPE QUESTIONS, , 1., 2., , If the lines given by 3x + 2ky = 2 and 2x + 5y = 1 are parallel, then the value of, k is _______ ., If x = a and y = b is the solution of the equation x – y = 2 and x + y = 4, then, the values of a and b are respectively _______ ., , Mathematics-X, , 27
Page 44 :
3., , 4., 5., 6., , 7., 8., , A pair of linear equations which has a unique solution x = 2 and y = – 3 is, (a) x + y = 1 and 2x – 3y = – 5, (b) 2x + 5y = – 11 and 2x – 3y = – 22, (c) 2x + 5y = – 11 and 4x + 10y = – 22, (d) x – 4y – 14 = 0 and 5x – y – 13 = 0, The area of the triangle formed by the lines x = 3, y = 4 and x = y is _____ ., The value of k for which the system of equations 3x + 5y = 0 and kx + 10y = 0, has a non-zero solutions is ____ ., If a pair of linear equations in two variables is consistent, then the lines, represented by two equations are:, (a) Intersecting, (b) Parallel, (c) always coincident, (d) intersecting or coincident, For 2x + 3y = 4, y can be written in terms of x as _______ ., One of the common solution of ax + by = c and y axis is, c, (a) 0, , b, c, (c) ,, b, , 9., , 10., , 11., 12., 13., 14., 15., , 28, , b, (b) 0, , c, , , 0, , , c, , (d) 0, , b, If ax + by = c and lx + my = n has unique solution then the relation between the, coefficient will be:, (a) am lb, (b) am = lb, (c) ab = lm, (d) ab lm, In ABC, C = 3B, C = 2(A + B) then, A, B, C are respectively., (a) 30°, 60°, 90°, (b) 20°, 40°, 120°, (c) 45°, 45°, 90°, (d) 110°, 40°, 50°, If x = 3m –1 and y = 4 is a solution of the equation x + y = 6, then find the value, of m., What is the point of intersection of the line represented by 3x – 2y = 6 and the, y-axis?, For what value of p, system of equations 2x + py = 8 and x + y = 6 have no, solution., A motor cyclist is moving along the line x – y = 2 and another motor cyclist is, moving along the line x – y = 4 find out their moving direction., Find the value of k for which pair of linear equations 3x + 2y = –5 and x – ky =, 2 has a unique solution., Mathematics-X
Page 45 :
16. Write the solution of y = x and y = –x., 17. If 2x + 5y = 4, write another linear equation, so that lines represented by the, pair are coincident., 18. Check whether the graph of the pair of linear equations x + 2y – 4 = 0 and 2x +, 4y – 12 = 0 is intersecting lines or parallel lines., 19. What is the value of p, for which the pair of linear equations x + y = 3 and, 3x + py = 9 is inconsistent., 20. If we draw lines of x = 2 and y = 3 what kind of lines do we get?, SHORT ANSWER TYPE (I) QUESTIONS (2 MARKS QUESTIONS), , 21. Form a pair of linear equations for: The sum of the numerator and denominator, of the fraction is 3 less than twice the denominator. If the numerator and, denominator both are decreased by 1, the numerator becomes half the, denominator., 22. For what value of p the pair of linear equations (p + 2)x – (2p + 1)y = 3(2p – 1), and 2x – 3y = 7 has a unique solution., 23. ABCDE is a pentagon with BE || CD and BC || DE, BC is perpendicular to CD, If the perimeter of ABCDE is 21 cm, find x and y., A, 3 cm, B, , 3 cm, 5 cm, , E, , x–y, C, , x+y, , D, , 24. Solve for x and y, x–, , y, x 2y 2, 3 and –, , 2, 2 3, 3, , 25. Solve for x and y, 3x + 2y = 11 and 2x + 3y = 4, Also find p if p = 8x + 5y, Mathematics-X, , 29
Page 46 :
26. Solve the pair of linear equations by substitution method x – 7y + 42 = 0 and, x – 3y – 6 = 0, 27. Ram is walking along the line joining (1, 4) and (0, 6), Rahim is walking along the line Joining (3, 4) and (1, 0), Represent on graph and find the point where both of them cross each other, 28. Given the linear equation 2x + 3y – 12 = 0, write another linear equation in, these variables, such that. geometrical representation of the pair so formed is, (i) Parallel Lines (ii) Coincident Lines, 29. The difference of two numbers is 66. If one number is four times the other, find, the numbers., 30. For what value of k, the following system of equations will be inconsistent, kx + 3y = k – 3, 12x + ky = k, SHORT ANSWERS TYPE (II) QUESTIONS, , 31. Solve graphically the pair of linear equations 5x – y = 5 and 3x – 2y = – 4, Also find the co-ordinates of the points where these lines intersect y-axis, 32. Solve for x and y, 5, 1, , =2, x y x – y, 15, 5, –, = –2, x y x – y, 33. Solve by Cross – multiplication method, (CBSE), x y, , =a+b, a b, x, y, 2 =2, 2, a, b, 34. For what values of a and b the following pair of linear equations have infinite, number of solutions?, (CBSE), 2x + 3y = 7, a(x + y) – b(x – y) = 3a + b – 2, 35. Find the value of k for no. solutions, (3k + 1)x + 3y – 2 = 0, 2, (k + 1)x + (k – 2)y – 5 = 0, 36. Solve the pair of linear equations, 152x – 378y = – 74, – 378x + 152y = – 604, 30, , Mathematics-X
Page 47 :
37. Pinky scored 40 marks in a test getting 3 marks for each right answer and, losing 1 mark for each wrong answer. Had 4 marks been awarded for each, correct answer and 2 marks were deducted for each wrong answer, then pinky, again would have scored 40 marks. How many questions were there in the, test?, 38. Father’s age is three times the sum of ages of his two children. After 5 years his, age will be twice the sum of ages of two children. Find the age of the father., 39. On selling a T.V. at 5% gain and a fridge at 10% gain, a shopkeeper gain `, 2000. But if he sells the T.V. at 10% gain and fridge at 5% loss, he gains ` 1500, on the transaction. Find the actual price of the T.V. and the fridge, 40. Sunita has some ` 50 and ` 100 notes amounting to a total of ` 15,500. If the, total number of notes is 200, then find how many notes of ` 50 and ` 100 each,, she has., LONG ANSWER TYPE QUESTIONS, , 41. Solve graphically the pair of linear equations 3x – 4y + 3 = 0 and 3x + 4y – 21, =0, Find the co-ordinates of vertices of triangular region formed by these lines and, x-axis. Also calculate the area of this triangle., 42. Solve for x and y, 1, 12, 1, , =, 2(2 x 3 y ) 7(3x – 2 y ), 2, 7, 4, , =2, (2 x 3 y ) (3x – 2 y, For 2x + 3y 0, 3x – 2y 0., 43. Solve the pair of equations by reducing them to a pair of linear equations, 2x = 8 y – 1, and, 9y = 3x – 6, 44. ABCD is a rectangle. Find the perimeter of the rectangle., , Mathematics-X, , 31
Page 48 :
45. A man travels 600 km to his home partly, by train and partly by bus. He takes, 8 hours, if he travels 120 km by train and rest by bus. Further, it takes 20, minute longer, if he travels 200 km by train and rest by bus. Find the speeds of, the train and the bus., 46. A and B are two points 150 km apart on a highway. Two cars start with different, speeds from A and B at same time. If they move in same direction, they meet in, 15 hours. If they move in opposite direction, they meet in one hour. Find their, speeds, 47. A boat covers 32 km upstream and 36 km downstream, in 7 hours. Also it, Covers 40 km upstream and 48 km downstream in 9 hours. Find the speed of, boat in still water and that of the stream., (CBSE), 48. 8 Women and 12 men can complete a work in 10 days while 6 women and 8, men can complete the same work in 14 days. Find the time taken by one woman, alone and that one man alone to finish the work., 49. The ratio of incomes of two persons A and B is 3 : 4 and the ratio of their, expenditures is 5 : 7. If their savings are ` 15,000 annually find their annual, incomes., 50. Vijay had some bananas and he divided them into two lots A and B. He sold the, first lot at the rate of ` 2 for 3 bananas and the second lot at the rate of ` 1 per, banana and got a total of ` 400. If he had sold the first lot at the rate of ` 1 per, banana and the second lot at the rate of ` 4 for 5 bananas, his total collection, would have been ` 460. Find the total number of bananas he had., (HOTS, Exampler), 51. A railway half ticket cost half the full fare but the reservation charges are the, same on a half ticket as on a full ticket. One reserved first class ticket costs, ` 2530. One reserved first class ticket and one reserved first class half ticket, from stations A to B costs ` 3810. Find the full first class fare from stations A to, B and also the reservation charges for a ticket., (Exemplar), 52. Determine graphically, the vertices of the triangle formed by the times y = x,, 3y = x and x + y = 8., (NCERT Exemplar), 32, , Mathematics-X
Page 49 :
53. Draw the graphs of the equations x = 3, x = 5 and 2x – y – 4 = 0. Also find the, area of the quadrilateral formed by the lines and the x-axis., (NCERT Exemplar, HOTS), 54. A nirudh takes 3 hours more than Nishi to walk 30 km. But if Anirudh doubles, his speed, he is ahead of Nishi by 1½ hours. Find their speed fo walking., 55. In a two digit number, the ten’s place digit is 3 times the unit’s place digit., When the number is decreased by 54, digits get reversed. Find the original, number., 56. A two-digit number is 3 more than 4 times the sum of the digits. If 18 is added, to the number, digits reversed. Find the number., 57. A boat can travel 30 km upstream and 28 km downs stream in 7 hours. It can, travel 21 km upstream and return in 5 hours. Find the speed of the boat in still, water and the speed of the stream., 58. Find the values of a and b for infinite solutions, (i) 2x – (a – 4)y = 2b + 1, 4x – (a – 1)y = 5b – 1, (ii) 2x + 3y = 7, 2ax + ay = 28 – by, ANSWERS AND HINTS, , 1. k , , 15, 4, , 2. a = 3 and b = 1, , 3. (c) 2x + 5y = – 11 and 4x + 10y = – 22, 4., , 1, sq. unit, 2, , 6. (d) intersecting or coincident, c, 8. (a) 0, , b, 10. (b) 20°, 40°, 120°, 12. (0, –3), 14. move parallel, Mathematics-X, , 5. 6, 7. y , , 4 2x, 3, , 9. (a) am lb, 11. m = 1, 13. p = 2, –2, 15. k , 3, 33
Page 50 :
16. (0, 0), , 17. 4x + 10y = 8, , 18. Parallel lines, , 19. p = 3, , 20., 22., 24., 26., 28., , 21., 23., 25., 27., , Intersecting lines, p4, 4, 2, 42, 12, (i) 4x + 6y + 10 = 0, (ii) 4x + 6y – 24 = 0, , x – y = – 3, 2x – y = 1, x = 5, y = 0, x = 5, y = – 2, p = 30, (2, 2), , 29. 88, 22, , 30. k = – 6, , 31. (2, 5) (0, – 5) and (0, 2), , 32. (3, 2), , 33. x = a2, y = b2, , 34. a = 5, b = 1, , 35. k = –1, , 36. 2, 1, , 37. 40 questions, , 38. 45 years, , 39. T.V. = ` 20,000 Fridge = ` 10,000, 40. ` 50 notes = 90, ` 100 notes = 110, 41. Solution (3, 3), Vertices (– 1, 0) (7, 0) and (3, 3), Area = 12 square units, 42. (2, 1), , 43. x = 24, y = 9, , 44. x = 3 and y = 2, , 45. 60 km/hr, 80 km/hr, , 46. 80 km/hr , 70 km/hr, , 47. 10 km/hr, 2 km/hr, , 48. 1 woman in 140 days, 1 man in 280 days, 49. ` 90,000, ` 1,20,000, 50. Let the no. of bananas in lots A be x and in lots B be y, Case I :, , 2, x y = 400, 3, , 2x + 3y = 1200, , 4, y = 460 5x + 4y = 2300, 5, x = 300, y = 200, Total bananas = 500., , Case 2 : x , , 34, , Mathematics-X
Page 51 :
51. Let the cost of full and half ticket be ` x & `, , x, and reservation charge by, 2, , ` y per ticket., Case I : x + y = 2530, , x, y = 3810, 2, x = 2500, y = 3810, Full first class fare is ` 2500 and reservation charge is ` 30., Case 2 : x y , , 52. Vertices of the triangle are (0, 0) (4, 4) (6, 2)., 53. Area of quadrilateral ABCD where,, A(3, 0), B(5, 0), C(5, 6), D(3, 2), , 54., , =, , 1, AB ( AD BC ), 2, , =, , 1, 2 (6 2) = 8 sq. units., 2, , 10, km/hr, 5 km/hr, 3, , 55. 93, 56. 35, 57. 10 km/hr, 4 km/hr, 58. (i) 7, 3, (ii) 4, 8, , Mathematics-X, , 35
Page 52 :
PRACTICE-TEST, Pair of Linear Equations In Two Variables, Time : 1 Hr., , M.M. : 20, SECTION-A, , 1., 2., 3., , 4., , For what value of k system of equations, x + 2y = 3 and 5x + ky + 7 = 0 has a unique solution., 1, Does the point (2, 3) lie on line represented by the graph of 3x – 2y = 5., 1, The pair of equations x = a and y = b graphically representes lines which are:, 1, (a) Parallel, (b) Intersecting at (b, a), (c) Coincident, (d) Intersecting at (a, b), For what value of K, the equations 3x – y + 8 = 0 and 6x – Ky = –16 represent, coincident lines?, 1, (a), , 1, 2, , (b) –, , 1, 2, , (c) 2, , (d) –2, , SECTION-B, 5., , 6., 7., , For what value of a and b the pair of linear equations have infinite number of, solutions, 2x – 3y = 7, ax + 3y = b, 2, Solve for x and y, 0.4x + 0.3y = 1.7, 0.7x – 0.2y = 0.8, 2, If the system of equations 6x + 2y = 3 and kx + y = 2 has a unique solution, find, the value of k., 2, , SECTION-C, 8., , 9., , Solve for x and y by cross multiplication method, x+y =a+b, ax – by = a2 – b2, 3, Sum of the ages of a father and the son is 40 years. If father’s age is three times, that of his son, then find their ages., 3, , SECTION-D, 10. Solve the following pair of equations graphically., 3x + 5y = 12 and 3x – 5y = –18., , 4, , Also shade the region enclosed by these two lines and x-axis., Mathematics-X, 36
Page 53 :
CHAPTER, , 4, , Mathematics-X, , Quadratic Equations, , 37
Page 54 :
NOTES:, 1. Real and distinct roots are, 2. Real and equal roots are, , b b 2 4ac, 2a, , b b, ,, 2a 2a, , 3. There are quadratic equation which donot have any real roots e.g. x2 + 1 = 0, VERY SHORT ANSWER TYPE QUESTIONS, , Multiple Choice Questions:, 1. Which of the following is not a Quadratic Equation?, (a) 2(x – 1)2 = 4x2 – 2x + 1, (b) 3x – x2 = x2 + 6, (c), , , , 2, 3x 2 = 2x – 5x, 2, , (d) (x2 + 2x)2 = x4 + 3 + 4x2, , 2., , Which of the following equation has 2 as a root, (a) x2 + 4 = 0, (b) x2 – 4 = 0, (c) x2 + 3x – 12 = 0, (d) 3x2 – 6x – 2 = 0, , 3., , If, , 1, 5, is a root of x2 + px –, = 0 then value of p is, 2, 4, , (a) 2, (c), 4., , 5., , 6., , 38, , 1, 4, , (b) –2, (d), , 1, 2, , Every Quadratic Equation can have at most, (a) Three roots, (b) One root, (c) Two roots, (d) Any number of roots, 2, Roots of Quadratic equation x – 7x = 0 will be, (a) 7, (b) 0, –7, (c) 0, 5, (d) 0, 7, The value(s) of k for which the quadratic equation 2x2 + kx + 2 = 0 has equal, roots, is, (a) 4, (b) ± 4, (c) – 4, (d) 0, (CBSE 2020), Mathematics-X
Page 55 :
7., , 8., , 9., , Fill in the blanks:, (a) If px2 + qx + r = 0 has equal roots then value of r will be ______ ., (b) The qaudratic equation x2 – 5x – 6 = 0 if expressed as (x + p) (x + q) = 0, then value of p and q respectively are ______ and _______ ., (c) The value of k for which the roots of qaudratic equations x2 + 4x + k = 0 are, real is ______ ., (d) If roots of 4x2 – 2x + c = 0 are reciprocal of each other then the value of c, is ________ ., (e) If in a quadratic equation ax2 + bx + c = 0, value of a is zero then it become, a _____ equation., Write whether the following statements are true or false. Justify your, answers., (a) Every quadratic equation has atleast one real roots., (b) If the coefficient of x2 and the constant term of a quadratic equation have, opposite signs, then the quadratic equation has real roots., (c) 0.3 is a root of x2 – 0.9 = 0., (d) The graph of a quadratic polynomial is a straight line., (e) The discriminant of (x – 2)2 = 0 is positive., Match the following :, (i) Roots of 3x2 – 27 = 0, (a) 169/9, 5, x–2=0, 3, (iii) Sum of roots of 8x2 + 2x – 3 = 0, (iv) A quadratic equation with roots a and b, , (ii) D of 2x2 +, , (v) The product of roots of x2 + 8x = 0, , (b) 0, (c) x2 – (a + b)x + ab = 0, (d) 3, – 3, (e), , 1, 4, , SHORT ANSWER TYPE QUESTIONS-I, , 10. If the Quadratic equation px2 – 2 5 px + 15 = 0 (p 0) has two equal roots then, find the value of p., 11. Solve for x by factorisation, (a) 8x2 – 22x – 21 = 0, (b) 3 5 x 2 25 x 10 5 = 0, (c) 3x2 – 2 6 x + 2 = 0, Mathematics-X, , (CBSE 2010), 39
Page 56 :
(d) 2x2 + ax – a2 = 0, , (CBSE 2014), , (e), , 3 x 2 10 x 7 3 = 0, (f ) 2 x 2 7 x 5 2 = 0, (g) (x – 1)2 – 5(x – 1) – 6 = 0, 12. For what vlaue of ‘a’ quadratic equation 3ax2 – 6x + 1 = 0 has no real roots?, (CBSE 2020), 2, 13. If – 5 is a root of the quadratic equation 2x + px – 15 = 0 and the quadratic, equation p(x2 + x) + k = 0 has equal roots find the value of k., (CBSE 2014, 2016), 2, and x = – 3 are roots of the quadratic equation ax2 + 7x + b = 0. Find, 3, the value of a and b., (CBSE 2016), 15. Find value of p for which the product of roots of the quadratic equation px2 +, 6x + 4p = 0 is equal to the sum of the roots., 16. The sides of two squares are x cm and (x + 4) cm. The sum of their areas is 656, cm2 Find the sides of these two squares., 17. Find K if the difference of roots of the quadratic equation x2 – 5x + (3k – 3) = 0 is 11., , 14. If x =, , SHORT ANSWER TYPE QUESTIONS-II, , 18. Find the positive value of k for which the quadratic equation x2 + kx + 64 = 0, and the quadratic equation x2 – 8x + k = 0 both will have real roots., 19. Solve for x, (a), , (b), , (c), , 1, 1 1 1, = , ab x, a b x, , a + b + x 0,, , 1, 1 1 1, , =, 2a b 2 x, 2a b 2 x, , 2a + b + 2x 0,, , 40, , a, b, x 0, , a, b, x 0, , 2x, 1, 3x 9, 3, , , = 0, x 3,, x 3 2 x 3 ( x 3)(2 x 3), 2, , 1, 1, 6, , , x 1, 5, x 1 x 5 7, (e) 4x2 + 4bx – (a2 – b2) = 0, (f) 4x2 – 2(a2 + b2) x + a2b2 = 0, (d), , (CBSE 2005), , (CBSE 2010), , Mathematics-X
Page 57 :
(g), , 2, 3, 23, , =, , x 0, – 1, 2, x 1 2( x 2), 5x, 2, , 10 x, 2x , 24 = 0, x 5, (h) , , x5, ( x 5), (i) 4x2 – 4a2x + a4 – b4 = 0, (j) 2a2x2 + b(6a2 + 1)x + 3b2 = 0, 3 1, 7 x 1, 5x 3, 4 , = 11, x ,, (k) 3 , 5x 3, 7x 1, 5 7, , (l), , 1, 1, 11, , , x 4, 7, x 4 x 7 30, , (NCERT), , x 4 x 6 10, (m) x 5 x 7 3 , x 5, 7, 1, 2, 4, , , ,, x 1 x 2 x 4, 1, 1, , 1,, (o), 2x 3 x 5, , (n), , (CBSE 2014), x –1, –2, – 4, x, , 3, ,5, 2, , (p) x2 + 5 5x – 70 = 0, 16, 15, 1 , (q), , x 0, – 1, (CBSE 2014), x, x 1, 20. Solve by using quadratic formula abx2 + (b2 – ac) x – bc = 0. (CBSE 2005), 21. If the roots of the quadratic equation (p + 1)x2 – 6(p + 1) x + 3(p + 9) = 0 are, equal find p and then find the roots of this quadratic equation., 22. Find the nature of roots of the quadratic equation 3x2 – 4 3 x + 4 = 0, If the roots are real, find them., (CBSE 2020), 2, 2, 4, 4, 23. Solve 9x – 6a x + a – b = 0 using quadratic formula., (CBSE 2020), LONG ANSWER TYPE QUESTIONS, , 24. A train travels at a certain average speed for a distance of 54 km and then, travels a distance of 63 km at an average speed of 6 km/hr more than the first, speed. If it takes 3 hours to complete the total journey, what is its first speed?, 25. A natural number, when increased by 12, equals 160 times its reciprocal. Find, the number., Mathematics-X, , 41
Page 58 :
26. A thief runs with a uniform speed of 100 m/minute. After one minute a policeman, runs after the thief to catch him. He goes with a speed of 100 m/minute in the, first minute and increases his speed by 10 m/minute every succeeding minute., After how many minutes the policemen will catch the thief?, 27. Two water taps together can fill a tank in 6 hours. The tap of larger diameter, takes 9 hours less than the smaller one to fill the tank separately. Find the time, in which each tap can separately fill the tank., (CBSE 2020), 28. In the centre of a rectangular lawn of dimensions 50 m × 40 m, a rectangular, pond has to be constructed, so that the area of the grass surrounding the pond, would be 1184 m2. Find the lenght and breadth of the pond., 29. A farmer wishes to grow a 100 m2 recangular garden. Since he has only 30 m, barbed wire, he fences three sides of the rectangular garden letting compound, wall of this house act as the fourth side fence. Find the dimensions of his garden., 30. A peacock is sitting on the top of a pillar, which is 9 m high. From a point 27 m, away from the bottom fo a pilar, a snake is coming to its hole at the base of the, pillar. Seeing the snake the peacock pounces on it. If their speeds are equa, at, what distance from the hole is the snake caught?, 31. If the price of a book is reduced by ` 5, a person can buy 5 more books for, ` 300. Find the original list price of the book., 32. ` 6500 were divided equally among a certain number of persons. If there been, 15 more persons, each would have got ` 30 less. Find the original number of, persons., 33. In a flight of 600 km, an aircraft was slowed down due to bad weather. Its, average speed was reduced by 200 km/hr and the time of flight increased by 30, minutes. Find the duration of flight., (CBSE 2020, Outside Delhi), 34. A fast train takes 3 hours less than a slow train for a journey of 600 km. If the, speed of the slow train is 10 km/hr less than the fast train, find the speed of the, two trains., (CBSE 2020, Outside Delhi), 35. The speed of a boat in still water is 15 km/hr. It can go 30 km upstream and, return downstream to the orignal point in 4 hrs 30 minutes. Find the speed of, the stream., 42, , Mathematics-X
Page 59 :
36. Sum of areas of two squares is 400 cm2. If the difference of their perimeter is, 16 cm. Find the side of each square., 37. The area of an isosceles triangle is 60 cm2. The length of equal sides is 13 cm, find length of its base., 38. The denominator of a fraction is one more than twice the numerator. If the sum, 16, of the fraction and its reciprocal is 2 . Find the fraction., 21, 39. A girl is twice as old as her sister. Four years hence, the product of their ages, (in years) will be 160. Find their present ages., 40. A two digit number is such that the product of its digits is 18. When 63 is, subtracted from the number, the digits interchange their places. Find the number., (CBSE 2006), 41. Three consecutive positive integers are such that the sum of the square of the, first and the product of other two is 46, find the integers., (CBSE 2010), 42. A piece of cloth costs ` 200. If the piece was 5 m longer and each metre of, cloth costs ` 2 less, then the cost of the piece would have remained unchanged., How long is the piece and what is the original rate per metre?, 43. A motor boat whose speed is 24 km/hr in still water takes 1 hour more to go 32, km upstream than to return downstream to the same spot. Find the speed of the, stream, (CBSE 2016), 44. If the roots of the quadratic equation (b –, prove 2b = a + c., , c)x2, , + (c – a)x + (a – b) = 0 are equal,, , 45. If the equation (1 + m2)n2x2 + 2mncx + (c2 – a2) = 0 has equal roots, prove that, c2 = a2 (1 + m2)., 46. A train covers a distance of 480 km at a uniform speed. If the speed had been, 8 km/hr less, then it would have taken 3 hours more to cover the same distance., Find the original speed of the train., (CBSE 2020), 47. A rectangular park is to be designed whose breadth is 3 m less than its length., Its area is to be 4 square metres more than the area of a park that has already, been made in the shape of an isosceles triangle with its base as the breadth of, the rectangular park and of altitude 12 m. Find the length and breadth of the, park., (CBSE 2020), , Mathematics-X, , 43
Page 60 :
ANSWERS AND HINTS, , 1., , (d) [x4 + 4x2 + 4x3 = x4 + 3 + 4x2 4x3 = 3 degree = 3], , 2., , (b) [Check by substituting x = 2 in the equation.], , 3., , (a) [Substitute x =, , 4., , (c) [ A quadratic polynomial is of degree 2 and it has atmost two zeroes.], , 5., , (d) [x(x – 7) = 0 x = 0, x = 7.], , 6., , (b) ± 4 (D = 0, k2 – 16 = 0), , 7., , q2, (a) [r =, (D = 0 q2 – 4pr = 0)], 4p, , 1, 5, in x2 + px –, = 0.], 2, 4, , (b) p = – 6, q = 1 [x2 – 5x – 6 = 0 (x – 6) (x + 1) = 0], (c) K 4 [D 0 16 – 4 K 0 16 4K 4 K], (d) c = 4 ( product = 1 , , c, c, =1, =1), a, 4, , (e) Linear equation (x = 0 ax2 + bx + c = 0 reduces to bx + c = 0), 8., , (a) False (A quadratic equation has atmost two real root)., (b) True (Coefficient of x2 = a, Constant = – c, D = b2 – 4ac = b2 – 4(a) (– c) =, b2 + 4ac > 0), (c) False ((0.3)2 – 0.9 = 0.09 – 0.9 0), (d) False (Degree of quadratic polynomial is 2 not 1 Not a straight line), , 9., , (i) d, (ii) a, (iii) e, (iv) c, (v) b, , 10. D = 0, , 20p2 – 60p = 0, p 0, 20p (p – 3) = 0, p= 3, , 11. (a) x =, 44, , 7, 3, ,x= , 2, 4, , (b) x = – 5 , x =, , 2 5, 3, , Mathematics-X
Page 61 :
2, ,x=, 3, , (c) x =, , 2, 3, , (d) x =, , 7 3, 3, (g) Take (x – 1) = y, , (e) x = 3 , x =, , a, ,x=–a, 2, , (f) x = 2 , x =, , 5 2, 2, , y2 – 5y – 6 = 0 (y + 1) (y – 6) = 0, y = –1, y = 6, x – 1 = – 1, x – 1 = 6, x = 0, x = 7, 12. D < 0, (– 6)2 – 4(3a) (1) < 0, 12a > 36 a > 3, 13. 2(– 5)2 + p(– 5) – 15 = 0 p = 7, 7x2 + 7x + k = 0,, k=, , D = 49 – 28 k = 0, , 49, 7, =, 28, 4, , 14. Substituting, x =, , 2, we get, 3, , Substituting, x = – 3 we get, , 4a + 9b = – 42, , ...(1), , 9a + b = 21, , ...(2), , Solve (1) and (2) to get a = 3, b = – 6., 15. Product =, , ATQ =, , 4p, c, =, = 4,, p, a, , 6, =4, p, , p=, , sum =, , 6, b, =, p, a, , 6, 3, =, 4, 2, , 16. x2 + (x + 4)2 = 656, x2 + 4x – 320 = 0, D = 1296, x=, , x=, , 4 36 4 36, 4 1296, =, ,, 2, 2, 2, , 32, = 16, (rejecting –ve value), 2, , Sides are 16 cm, 20 cm, Mathematics-X, , 45
Page 62 :
17. ATQ – = 11, Solve to get = 8, = – 3, Sum of roots + =, , b, =5, a, , = 8, = – 3, Product of roots =, , c, a, , – 24 = 3k – 3, – 21 = 3k k = –7, , Ans., , 18. x2 + kx + 64 = 0 D1 = k2 – 256 0,, k 16, , k2 256, , ...(1), , k – 16, x2 – 8x + k = 0 D2 = 64 – 4k 0, 64 4k, k 16, , ...(2), , (1) and (2) gives k = 16, 19. (a), , 1, 1, 1 1, = , ab x x, a b, , xab x, ab, =, (a b x) x, ab, – (a + b) ab = (a + b) (a + b + x) x, x2 + xa + bx + ab = 0, (x + a) (x + b) = 0, x = – a, x = – b, (b), , 1 1, 1, 1, , , =, 2a b, 2a b 2 x 2 x, , 2 x 2a b 2 x, 2a b, =, (2a b 2 x)2 x, 2ab, – (2a + b)2ab = (2a + b) (2a + b + 2x)2x, 2x2 + 2xa + bx + ab = 0, (x + a) (2x + b) = 0, x = – a, x = –, 46, , b, 2, , Mathematics-X
Page 64 :
(j) Find D = b2 (6a2 – 1)2, B D, to get answer, 2A, , Use x =, , Ans. x =, (k) Let, , b, , – 3b, 2a 2, , 7x 1, =y, 5x 3, , 3y –, , 4, = 11 3y2 – 111y – 4 = 0. Solve to get, y, , 1, y= ,y=4, 3, Substitute y and get x = 0, 1, , (l) Take LCM to get x2 – 3x + 2 = 0, Solve to get x = 1, x = 2, (m) Take LCM to get 2x2 – 27x + 88 = 0, x = 8,, , 11, 2, , (n) Take LCM to get x2 – 4x – 8 = 0 (Use quadratic formula), Ans. x = 2 2 3, (o) Take LCM to get 2x2 – 16x + 23 = 0, Solve using Quadratic formula, Ans. x =, , 8 3 2, 2, , (p) x 2 7 5 x 2 5 x 70 = 0, , x 7 5 x 2 5 , , =0, , x = 2 5, 7 5, (q), , 16 x, 15, =, x, x 1, 2, x – 16 = 0, , x=±4, 48, , Mathematics-X
Page 65 :
20. abx2 + b2x – acx – bc = 0, (bx – c) (ax + b) = 0, b c, x= ,, a b, 21. D = 0, p2 – 2p – 3 = 0 ; p = –1, 3, rejecting p = –1,, Ans. p = 3., , , , , , 2, , 22. Find D, D = 4 3 – 4(3)(4) = 0, Roots are equal and real, 2 2, b b, ,, ,, =, 3 3, 2a 2a, 23. D = (–6a2)2 – 4(9) (a4 – b4), = 36b4, Roots are, , x=, , a 2 b2, (6a 2 ) 36b 4, =, 3, 29, , 54, 63, , = 3, x speed of train at first, x + 6 Increased speed., x x6, Ans. x = 36, x – 3., , 24. Equation, , 25. Let the natural number be x., ATQ, x + 12 =, , 160, to get, x, , x2 + 12x – 160 = 0, (x + 20) (x – 8) = 0, x = 8,, , x – 20 (rejected), , 26. Let time taken by thief be n minutes., Policeman will catch the thief in (n – 1) minutes., Total distance covered by thief = (100 n) metres, , ...(1), , (as distance covered in 1 min = 100 min), Distance covered by policemen, 100 + 110 + 120 + .... + to (n – 1) 10, Mathematics-X, , ...(2), 49
Page 66 :
(1) and (2) 100 n =, Solve and get, , (n 1), [2 × 100 + (n – 2) 10], 2, , n2 – 3n – 18 = 0, n = 6,, , n–3, , Policeman will catch the thief in 5 minutes., 27. Time taken by top of smaller diameter = x hrs, Time taken by larger tap = (x – 9) hrs, ATQ, , 1, 1, 1, , =, and get x 2 – 21x + 54 = 0, x x9, 6, , Ans. x = 3, x = 18, x = 3 rejeced as x – 9 = – 6 < 0, x = 18 hrs x – 9 = 18 – 9 = 9 hrs, 28., , Pond, , x, , 40, , x, 50, , Length of rectangular lawn = 50 m, Breadth of rectangular lawn = 40 m, Length of pond = 50 – 2x, Breadth of pond = 40 – 2x, Area of lawn – Area of pond = area of grass, 50 × 40 – (50 – 2x) (40 – 2x) = 1184, get x2 – 45x + 296 = 0, x = 37, x = 8, x = 37 rejected 40 – 2x = 40 – 2(37) < 0, Ans. Length of pond = 34 m, Breadth of pond = 24 m, , 50, , Mathematics-X
Page 67 :
House, , 29. x + y + x = 30, xy = 100, Solve x = 5m, 10 m,, , x, , y = 20 m, 10 m, dim. are 5 m × 20 m or 10 m × 10 m, , x, y, , 30., , 27, , –, , x, , A, , x, , 27 – x, C, , D, , B, , In ABD, pythagoras theorem 92 + x2 = (27 – x)2. Solve it to get x = 12 m., 31. Let original list price = ` x, ATQ, , 300 300, , =5, x5, x, , Solve and get x = 20, x = – 15 rejected, Ans. ` 20, 32. Let original number of persons be x, ATQ, , 6500 6500, , = 30, x, x 15, , Solve and get x = 50, x = – 65 (rejected)., 33. ATQ, , 600, 600, 1, , =, x 200, x, 2, , [Speed of aircraft = x km/hr], , Solve to get x = 600, x – 400, Duration of flight, , Mathematics-X, , 600, = 1hr.., 600, , 51
Page 68 :
34. ATQ, , 600 600, , = 3 (Speed of slow train x km/hr), x, x 10, , Solve to get x = 40, x – 50 (rejected)., Ans. 40 km/hr, 50 km/hr., 30, 30, 9, , , 35. ATQ, (Speed of stream x km/hr), 15 x 15 x 2, Solve to get x = 5, x –5 (rejected), Ans. 5 km/hr, 36. x2 + y2 = 400, ...(1), 4x – 4y = 16 x – y = 4, ...(2), y–x=4, ...(3), Solve (1) and (2) to get x = 16, x –12 (rejected), Solve (1) and (3) to get x = 12, x –16 (rejected), Ans. x = 16 m, y = 12 m from (1) and (2), x = 12 m, y = 16 m from (1) and (3), 37. BC = 2x, BD = x (Draw a from A on BC), Use pythagoreas to get, AD = 169 x 2 60, 1, 2 x 169 x 2 60, 2, Solve to get x2 = 144, x2 = 25, x = 12 or x = 5, x –12, –5 (rejected), base 2x = 24 cm or 10 cm, , A=, , 38. Fraction is, ATQ, , x, 2x 1, , x, 2x 1, 16, 58, , =2, =, 2x 1, x, 21 21, , Solve to get x = 3, x , Ans. Fraction =, 52, , 7, (rejected), 11, , 3, ., 7, , Mathematics-X
Page 69 :
39. Age of sister = x years, Age of girl = 2x, ATQ (x + 4) (2x + 4) = 160, Solve to get x2 + 6x – 72 = 0, Ans. x = 6 years, x – 12 (rejected), 2x = 12 years, 40. Let tens place digit = x, then units digits =, No, 10x +, , 18, ., x, , 18, x, , 18 10 18, , , x = 63, ATQ 10 x , x x, , , Solve to get x = 9, x – 2 (rejected)., Ans. Number is 92, 41. Let no. be x, x + 1, x + 2 (rejected)., ATQ (x)2 + (x + 1) (x + 2) = 46, To get 2x2 + 3x – 44 = 0, Use quadratic formula to get x = 4, x –, , 11, (rejected), 2, , Numbers are 4, 5, 6., 42. Let length of piece be x metre., ATQ, , 200 200, , =2, x, x5, , Solve to get x2 + 5x – 500 = 0, Solve to get x = 20, x –25 (rejected), Rate per meter =, , 200, 200, =, = ` 10, x, 20, , 43. Let speed of boat = x, ATQ, , 32, 32, , =1, 24 x 24 x, , Mathematics-X, , 53
Page 70 :
x2 + 64x – 576 = 0, (x + 72) (x – 8) = 0, x 8 km/hr, x = –72 km/hr (rejected), 44. Find D and let D = 0, (c – a)2 – 4(b – c) (a – b) = 0, Solve to get (a + c – 2b)2 = 0, a + c = 2b, 45. D = 0, (2 mnc)2 – 4 (1 + m2) n2 (c2 – a2) = 0, to get 4n2c2 = 4n2a2 (1 + m2), c2 = a2 (1 + m2), 46. Let the speed of the train = x km/hr, ATQ,, , 480 480, –, =3, x 8, x, , x2 – 8x – 1280 = 0, x = 40, –32 (rejected), x = 40 km/hr, 47. Let Lm be the length of the rectangular park, Breadth = (L – 3) m, Altitude of the isosceles triangle = 12 m, ATQ L(L – 3) =, , 1, (12) (L – 3) + 4, 2, , L2 – 9L + 14 = 0, (L – 7) (L – 2) = 0, L = 7, 2, So, L = 7m (L = 2 rejected L – 3 = –1), Length = 7 m, Breadth = 4 m, , 54, , Mathematics-X
Page 71 :
Practice Test, Quadratic Equations, Time: 1 Hour, , M.M : 20, SECTION-A, , 1., , The value of k is .................. if x = 3 is one root of x2 – 2kx – 6 = 0., , 2., , If the discriminant of 3x + 2x + = 0 is double the discriminant of x – 4x + 2, = 0 then value of is ............... ., 1, , 3., , If discriminant of 6x2 – bx + 2 = 0 is 1 then value of b is ............... ., , 4., , (x – 1)3 = x3 + 1 is quadratic equation. (T/F), , 2, , 1, 2, , 1, 1, , SECTION-B, 5., , If roots of x2 + kx + 12 = 0 are in the ratio 1 : 3 find k., , 6., , Solve for x : 21x2 – 2x +, , 7., , Find k if the quadratic equation has equal roots : kx (x – 2) + 6 = 0., , 2, , 1, =0, 21, , 2, 2, , SECTION-C, 8., , Solve using quadratic formula, , 3, , 4 3x 2 5 x 2 3 0, 9., , For what value of k, (4 – k)x2 + (2k + 4)x + (8k + 1) = 0 is a perfect square. 3, SECTION-C, 7, hours. The tap with longer diameter, 8, takes 2 hours less than the tap with smaller one to fill the tank separately. Find, the time in which each tap can fill the tank separately., (CBSE 2018), , 10. Two water taps together can fill a tank in 1, , 4, , Mathematics-X, , 55
Page 72 :
CHAPTER, , 5, , 56, , Arithmetic Progression, , Mathematics-X
Page 73 :
VERY SHORT ANSWER TYPE QUESTIONS, , 1., 2., 3., 4., 5., 6., , Find 5th term of an A.P. whose nth term is 3n – 5, Find the sum of first 10 even numbers., Write the nth term of odd numbers., Write the sum of first n natural numbers., Write the sum of first n even numbers., Find the nth term of the A.P. – 10, – 15, – 20, – 25, ..........., , 7., , 1 2 1, Find the common difference of A.P. 4 , 4 , 4 , ............., 9 9 3, , Write the common difference of an A.P. whose nth term is an = 3n + 7, What will be the value of a8 – a4 for the following A.P., 4, 9, 14, ............., 254, 10. What is value of a16 for the A.P. – 10, – 12, – 14, – 16, ......., 11. 3, k – 2, 5 are in A.P. find k., 12. For what value of p, the following terms are three consecutive terms of an A.P., 8., 9., , 4, 5, p, 2., 13. In the following A.Ps, find the missing terms in the boxes :, (a) 2,, , 26, (b), , 13,, ,3, , (c) 5,, , ,, , ,9, , 1, 2, , (d) – 4,, , ,, , ,, , ,, , ,, (NCERT), , ,6, , (e), , 38,, ,, ,, , – 22, 14. Multiple Choice Questions:, (a) 30th term of the A.P. 10, 7, 4 .... is, (A) 97, (B) 77, (C) –77, (D) –87, 1, (b) 11th term of an A.P. – 3, , , ... is, 2, (A) 28, (B) 22, , (C) –38, Mathematics-X, , (D) 48, , 1, 2, 57
Page 74 :
(c) In an A.P. if d = – 4, n = 7, an = 4, then a is, (A) 6, (d), , (e), , (f), , (g), , (h), , (B) 7, , (C) 120, (D) 28, The first three terms of an A.P. respectively are 3y – 1, 3y + 5 and 5y + 1, then y equals:, (CBSE 2014), (A) –3, (B) 4, (C) 5, (D) 2, The list of numbers – 10, – 6, – 2, 2, ... is, (A) An A.P. with d = – 16, (B) An A.P. with d = 4, (C) An A.P. with d = – 4, (D) Not an A.P., th, The 11 term from the last term of an A.P. 10, 7, 4, ...., – 62 is (NCERT), (A) 25, (B) –32, (C) 16, (D) 0, The famous mathematician associated with finding the sum of the first, 100 natural numbers is, (A) Pythagoras, (B) Newton, (C) Gauss, (D) Euclid, What is the common difference of an A.P. in which a18 – a14 = 32 ?, (A) 8, (B) – 8, (C) – 4, (D) 4, , , , , , , , , , (i) The nth term of the A.P. 1 3 , 1 2 3 , 1 3 3 , .... is, (A) 1 + n 3, (C), , , , n 1 3, , (B) n +, , , , (D) n 3, , (j) The common difference of the A.P., (A), , 2, , 3, , 2 , 2 2 , 3 2 , 4 2 ...... is, , (B) 1, , (C) 2 2, (D) – 2, (k) The first term of an A.P. is p and the common difference is q, then its 10th, term is, (A) a + 9p, (B) p – 9q, (C) p + 9q, (D) 2p + 9q, 58, , Mathematics-X
Page 75 :
15. Match the following :, Column A, (a) a = – 18, n = 10, d = 2 then an of A.P., , Column B, (a), , ac, 2, 0, – 41, 8, A.P., , (b) a, b and c are in A.P. then their Arithmetic mean is, (b), (c) If 2, 4, 6, are in A.P. then 4, 8, 12 will also be an, (c), (d) If an = 9 – 5 n of an A.P. then a10 will be, (d), (e) If d = – 2, n = 5 and an = 0 in A.P. then a is, (e), 16. State True/False and justify, (a) 301 is a term of an A.P. 5, 11, 17, 23 ...., (NCERT), th, th, (b) Difference of m and n term of an A.P. = (m – n) d., (c) 2, 5, 9, 14, .... is an A.P., (d) Sum of first 20 natural numbers is 410., (e) nth term of an A.P. 5, 10, 15, 20 .... n terms and nth term of A.P. 15, 30, 45,, 60, ... n terms are same., SHORT ANSWER TYPE QUESTIONS-I, , 17., 18., 19., 20., 21., 22., , 23., 24., 25., 26., , Is 144 a term of the A.P. 3, 7, 11, ......... ? Justify your answer., Show that (a – b)2, (a2 + b2) and (a + b2) are in A.P., Which term of the A.P. 5, 15, 25, ....... will be 130 more than its 31 st term?, The first term, common difference and last term of an A.P. are 12, 6 and 252, respectively, Find the sum of all terms of this A.P., Find the sum of first 15 multiples of 8., Is the sequence formed in the following situations an A.P., (i) Number of students left in the school auditorium from the total strength of, 1000 students when they leave the auditorium in batches of 25., (ii) The amount of money in the account every year when Rs. 100 are deposit, annually to accumulate at compound interest at 4% per annum., Find the sum of even positive integers between 1 and 200., If 4m + 8, 2m2 + 3m + 6, 3m2 + 4m + 4 are three consecutive terms of an A.P., find m., How many terms of the A.P. 22, 20, 18, ....... should be taken so that their sum, is zero., If 10 times of 10th term is equal to 20 times of 20th term of an A.P. Find its 30th, term., , Mathematics-X, , 59
Page 76 :
27. Solve 1 + 4 + 7 + 10 + ... + x = 287, 28. Find whether (– 150) is a term of A.P. 11, 8, 5, 2, ..... ?, 29. Find how many two digit numbers are divisible by 6?, 30. If, , (CBSE 2020), (NCERT), (CBSE 2011), , 1, 1, 1, ,, and, are in A.P. find x., x2 x3, x5, , (CBSE 2011), , 31. Find the middle term of an A.P. – 6, – 2, 2, .... 58., , (CBSE 2011), , 32. In an A.P. find Sn, where an = 5n – 1. Hence find the sum of the first 20 terms., (CBSE 2011), 33. Which term of A.P. 3, 7, 11, 15 .... is 79? Also find the sum 3 + 7 + 11 + ... + 79., (CBSE 2011C), 34. Which term of the A.P. : 121, 117, 113 ... is the first negative terms ?, (NCERT), 35. Find the 20th term from the last term of the A.P. 3, 8, 13, ... 253., , (NCERT), , SHORT ANSWER TYPE QUESTIONS-II, , 36. Find the middle terms of the A.P. 7, 13, 19, ......., 241., 37. Find the sum of integers between 10 and 500 which are divisible by 7., 38. The sum of 5th and 9th terms of an A.P. is 72 and the sum of 7th and 12th term is, 97. Find the A.P., 39. If the mth term of an A.P. be, , 1, 1, and nth term be, , show that its (mn)th is 1., n, m, , 40. If the pth term A.P. is q and the qth term is p, prove that its nth term is (p + q – n)., 41. Find the number of natural numbers between 101 and 999 which are divisible, by both 2 and 5., 42. The sum of 5th and 9th terms of an A.P. is 30. If its 25th term is three times its 8th, term, find the A.P., 43. If Sn, the sum of first n terms of an A.P. is given by Sn = 5n2 + 3n, then find its, nth term and common difference., 44. Which term of the A.P. 3, 15, 27, 39 .... will be 120 more than its 21 st term?, (CBSE 2018), , 60, , Mathematics-X
Page 77 :
45. If Sn, the sum of first n terms of an A.P. is given by Sn = 3n2 – 4n, find the nth, term., (CBSE 2018), 46. In a flower bed, there are 23 rose plants in the first row, 21 in the second, 19 in, the third and so on. There are 5 rose plants in the last row. How many rows are, there in the flower bed?, (NCERT), 47. For what value of n, are the nth term of two A.P’s 63, 65, 67 ......... and 3, 10, 17, ..... are equal ?, (NCERT), th, th, th, 48. The 17 term of an A.P. is 5 more than twice its 8 term. If the 11 term of the, A.P. is 43, then find the nth term of the A.P., (CBSE 2020), (NCERT), 49. If the sum of the first 14 terms of an A.P. is 1050 and its fourth term is 40, find, its 20th term., (CBSE 2020), 50. Find the sum of odd numbers between 0 and 50., (NCERT), 2, 51. If Sn = 4n – n in an A.P. find the A.P., (NCERT), 52. How many terms of the A.P. 9, 17, 25, ..... must be taken to give a sum of 636?, (NCERT), LONG ANSWER TYPE QUESTIONS, , 53. The sum of third and seventh terms of an A.P. is 6 and their product is 8. Find, the sum of first 16 terms of the A.P., 54. Determine the A.P. whose 4th term is 18 and the difference of 9th term from the, 15th term is 30., 55. The sum of first 9 terms of an A.P. is 162. The ratio of its 6 th term to its 13th, term is 1:2. Find the first and fifteenth terms of the A.P., 56. The sum of the first 9 terms of an A.P. is 171 and the sum of its first 24 terms is, 996. Find the first term and common difference of the A.P., (CBSE 2020), 57. The sum of first 7 terms of an A.P. is 63 and the sum of its next 7 term is 161., Find the 28th term of this A.P., 58. The sum of first 20 terms of an A.P. is one third of the sum of next 20 term. If, first term is 1, find the sum of first 30 terms of this A.P., 59. If the sum of the first four terms of an AP is 40 and the sum of the first fourteen, terms of an AP is 280. Find the sum of first n terms of the A.P. (CBSE 2018), Mathematics-X, , 61
Page 78 :
60. Ramkali required 2500 after 12 weeks to send her daughter to school. She, saved 100 in the first week and increased her weekly savings by 20 every, week. Find wheather she will be able to send her daughter to school after 12, weeks., (CBSE 2015), 61. In an AP of 50 terms, the sum of first 10 terms is 210 and the sum of last 15, terms is 2565. Find the A.P., (CBSE 2014), 62. The sum of first n terms of an A.P. is 5n2 + 3n. If the mth term is 168, find the, value of m. Also find the 20th term of the A.P., (CBSE 2013), 63. If the sum of the first seven terms of an A.P. is 49 and the sum of its first 17, terms is 289. Find the sum of first n terms of an A.P., (CBSE 2016), 64. If the 4th term of an A.P. is zero, prove that the 25th term of the A.P. is three, times its 11th term., (CBSE 2016), 65. In an A.P. if S5 + S7 = 167 and S10 = 235. Find the A.P., where Sn denotes the, sum of its first n terms., (CBSE 2015), 66. In an AP prove S12 = 3 (S8 – S4) where Sn represent the sum of first n terms of an, A.P., (CBSE 2015), 67. The sum of four consecutive numbers in A.P. is 32 and the ratio of the product, of the first and last term to the product of two middle terms is 7 : 15. Find the, numbers., 68. Find the sum of first 16 terms of an Arithmetic Progression whose 4 th and 9th, terms are –15 and –30 respectively., (CBSE 2020), ANSWERS AND HINTS, VERY SHORT ANSWER TYPE QUESTIONS-I, , 1., , an = 3n – 5, , 2., , Sn =, , 3., , 4., 62, , a5 = 10, , 10, [2 × 2 + 9 × 2] = 110, 2, 1, 3, 5, ......, an = 1 + (n – 1)2 = 2n – 1., , 1 + 2 + ........ + n =, , n, [1 + n], 2, , Mathematics-X
Page 79 :
5., 6., , n, [2 + 2n] = n(n + 1), 2, an = a + (n – 1)d = – 5(n + 1), , 2 + 4 + 6 + ... + 2n =, , 1, 9, 8. a1 = 3 + 7 = 10, a2 = 6 + 7 = 13, d = 3, 9. (a + 7d) – (a + 3d) = 4d = 20, 10. a16 = a + 15d = – 40, 11. 3, k – 2, 5 are in A.P., , 7., , d = a2 – a1 =, , k–2=, 12. p =, , 35, =4, 2, , k=6, , 7, (same as Q.11), 5, , 13. (a) 14, 1, (c) 6 , 8, 2, , (b) 18 , 8, (d) 2 , 0 , 2 , 4, , (e) 53 , 23 , 8 , 7, 14. (a), (c), (e), (g), (i), (k), 15. (a), (c), (e), 16. (a), , C, (b) B, D, (d) C, B, (f) B, C, (h) A, A, (j) A, C, (b), (b) (a), (e), (d) (c), (d), False, 301 = 5 + (n – 1) 6, 151, Solving we get n =, which is not a natural number.., 3, 301 is not a term of this A.P., (b) True [a + (m – 1) d] – [a + (n – 1) d] = (m – n) d, , Mathematics-X, , 63
Page 80 :
(c) False a2 – a1 = 5 – 2 = 3, a3 – a2 = 9 – 5 = 4, (d) False Sn =, , n( n 1), 20 21, =, = 210, 2, 2, , (e) False (If a, b, c, d ... are in AP then ka, kb, kc, kd ..... are in AP), k 0, nth term = k times nth term of original A.P. of new A.P., 17. 144 = 3 + (n – 1) 4, 141, 1 = n which is not possible, 4, , 18. a1 = (a – b)2 a2 = a2 + b2 a3 = (a + b)2, a2 – a1 = a2 + b2 – (a – b)2, = 2ab, a3 – a2 = (a + b)2 – (a2 + b2), = 2ab, a2 – a1 = a3 – a2, in A.P., 19. Let an = 130 + a31, Solve to get n = 44, Ans. 44th term, 20. a = 12, d = 6, an = 252 n = 41, Find S41 = 5412, use Sn =, 21. S15 =, , n, [2a + (n – 1) d], 2, , 15, [2a + 14d], 2, , where a = 8, d = 8, Ans. 960, 22. (i) Yes (1000, 975, 950, 925 .....), (ii) No (104, 108.16, 112.48 .....), 23. 2 + 4 + 6 + .... + 198, a = 2, d = 2, an = 198 n = 99, Sn =, , 64, , n, [ a l ] = 9900, 2, , Mathematics-X
Page 81 :
24. b =, , ac, 2, , 4m 8 3m 2 4m 4, 2, Solve to get m2 – 2m = 0, m = 0, 2, 2m2 + 3m + 6 =, , n, [44 + (n – 1) (– 2)] = 0., 2, Solve n = 23, , 25. Sn = 0 , , 26. ATQ 10 a10 = 20 a20, a10 = 2a20, a + 9d = 2a + 38d, a = – 29d ...(1), a30 = a + 29d, Substitute a from (1), Ans. a30 = 0, 27. a = 1, d = 3, an = x, Sn = 287, n, 2 1 (n 1)3, 2, 3n2 – n – 574 = 0, , 287 =, , –41, (rejected), 3, n = 14, , n = 14,, , x = a14 = 40, 28. Let an = –150, 11 + (n – 1) (– 3) = – 150, 164 , , Solve and get n is not a natural number. n , , 3 , , Ans. No., , Mathematics-X, , 65
Page 82 :
29. Two digit numbers divisible by 6 are 12, 18, 24, .... 96., a2 – a1 = a3 – a2 = 6, A.P., an = 96 n = 15, 30., , 2, 1, 1, , =, (2b = a + c), x3, x2 x5, , Solve to get x = 1., 31. an = a + (n – 1) d, 58 = – 6 + (n – 1) 4, find n = 17, Find Middle term using concept of median, n 1, = , , 2 , , th, , term = 9th term, , a9 = – 6 + 8(4) = 26, 32. an = 5n – 1, Find A.P. a1 = 4, a2 = 9, a3 = 14, 4, 9, 14, ...., a2 – a1 = 5 = a3 – a2, Sn =, , n, n, [2a + (n – 1)d] = [8 + (n – 1) 5], 2, 2, , n, [5n + 3], 2, 20, S20 =, [100 + 3] = 10 × 103 = 1030, 2, 33. 79 = 3 + (n – 1) 4, n = 20, , =, , 20, [3 + 79] = 10[82], 2, S20 = 820, 34. Let an < 0, 121 + (n – 1) (– 4) < 0, 121 – 4n + 4 < 0, 125 < 4n, , S20 =, , 66, , Mathematics-X
Page 83 :
125, 4, n = 32, 32nd term will be first negative term., 35. 20th term from end using [l – (n – 1) d], = 253 – 19 × 5, = 253 – 95 = 158, , n>, , SHORT ANSWER TYPE QUESTIONS-II, , 36. Same as Q.27, n = 40 Middle terms are a20, a21, Ans. 121, 127, 37. Numbers between 10 and 500 which are divisible by 7, 14, 21, 28 ..., 497, Find n, using an = a + (n – 1) d , then use Sn =, , n, [2a + (n – 1) d], 2, , Ans. Sn = 17885. (n = 70), 38. a5 + a9 = 72, a7 + a12 = 97, Solve these equations to get a and d, a = 6, d = 5, A.P., 6, 11, 16, 21, 26, ......., 1, n, 1, an =, m, , 39. am =, , 1, n, 1, a + (n – 1)d =, m, – –, –, ––––––––––––––, , a + (m – 1)d =, , (m – n) d =, , 1 1, mn, =, n m, mn, , 1, 1, , find a =, mn, mn, = a + (mn – 1) d, , d=, amn, , 1, 1, (mn 1), mn, mn, amn = 1., , =, , Mathematics-X, , 67
Page 84 :
40. ap = q,, , aq = p, , Solve to get a and d, a = q + p – 1, d = – 1, an = p + q – n, 41. Numbers divisible by both 2 and 5, Numbers divisible by 10., Numbers between 101 and 999 divisible by 2 and 5 both 110, 120, 130, 140, ...,, 990., Use an = 990 to get n = 89., 42. ATQ a5 + a9 = 30, a25 = 3 a8, Solve to get a = 3, d = 2, A.P. 3, 5, 7, 9, ..., 43. Sn = 5n2 + 3n, Find an = Sn – Sn – 1 = 10 n – 2, Use it to get d = 10, 44. Let an = 120 + a21, 3 + (n – 1)d = 120 + [3 + 20d], 3 + (n – 1)12 = 120 + [3 + 20 × 12], = 120 + 243, (n – 1)12 = 363 – 3 = 360, n = 31, 45. Sn = 3n2 – 4n, an = Sn – Sn–1, = (3n2 – 4n) – [3(n – 1)2 – 4(n – 1)], = (3n2 – 4n) – [3n2 + 3 – 6n – 4n + 4], = – [7 – 6n], an = 6n – 7, 46. 23, 21, 19, ... 5, an = a + (n – 1) d, 5 = 23 + (n – 1) (– 2), n = 10, 68, , Mathematics-X
Page 85 :
47. 63, 65, 67, ....., an = 63 + (n – 1) 2 = 61 + 2n, 3, 10, 17, ...., an = 3 + (n – 1) 7, = 7n – 4, 61 + 2n = 7n – 4, 65 = 5n, n = 13, 48. ATQ,, a17 = 5 + 2 × a8, a + 16d = 5 + 2a + 14 d, a – 2d = – 5, ...(1), a11 = a + 10d = 43, ....(2), Solving (1) & (2), we get, a = 3, d = 4, an = 4n – 1, 49. S14 = 1050, a4 = 40, S14 =, , 14, [2 × a + 13d], 2, , 1050, = 2a + 13d, 7, Solve 2a + 13d = 150 and a + 3d = 40 to get a = 10, d = 10, a20 = a + 19d = 10 + 190 = 200, 50. Odd numbers between 0 to 50, 1, 3, 5, 7, ..., 49, an = 49, a + (n – 1)d = 49, 1 + (n – 1)2 = 49, n = 25, n, [a + l], 2, 25, S25 =, [1 + 49] = 25 × 25 = 625, 2, , Sn =, , Mathematics-X, , 69
Page 89 :
Practice Test, Arithmetic Progression, Time: 1 Hr., , M.M. : 20, Section-A, , 1., , Find the sum of first 10 natural numbers., , 1, , 2., , 1 2 3, What is the common difference of an A.P. 8 ,8 ,8 ,..........., 8 8 8, , 1, , 3., , If k, 2k – 1 and 2k + 1 are in A.P. them value of k is ..................., , 1, , 4., , The 10th term from the end of the AP 8, 10, 12, ...., 126 is ..................., , 1, , Section-B, 5., , How many 2 digit number are there in between 6 and 102 which are divisible, by 6., 2, , 6., , The sum of n terms of an A.P. is n2 + 3n. Find its 20th term., , 2, , 7., , Find the sum (–5) + (–8) + (–11) + ...+(–230), , 2, , Section-C, 8., , Find the five terms of an A.P. whose sum is 12, is 2 : 3., , 9., , 1, and first and last term ratio, 2, 3, , Find the middle term of an A.P. 20,16,12,.......,– 176., , 3, , Section-D, 10. The sum of three numbers in A.P. is 24 and their product is 440. Find the, numbers., 4, , Mathematics-X, , 73
Page 90 :
CHAPTER, , 6, , Triangles, , s, , A., A., A., , S.S.S., S.A, .S., , Tr, , gl e, ian, , Cr, i, Sim terio, n, Tri ila, an g r, les, , s, lem, b, o, Pr, THE, , Areas of, Triangles, Converse of BPT, , TH, , EO, RE, M, , S, , MS, ORE, , BPT, , Pythagoras, Theorem, , 74, , Converse, of Pythagoras, Theorem, , Mathematics-X
Page 91 :
Key Points:, 1., , Similar Triangles: Two triangles are said to be similar if their corresponding, angles are equal and their corresponding sides ar proportional., , 2., , Criteria for Similarity:, In ABC and DEF, (i) AAA Similarity: ABC ~ DEF when A =D, B = E and C = F, (ii) SAS Similarity :, ABC ~ DEF when, , AB, BC, =, and B = E, DE, EF, , (iii) SSS Similarity : ABC ~ DEF,, 3., , AB, AC, BC, =, =, DE, DF, EF, , The proof of the following theorems can be asked in the examination :, (i) Basic Proportionality Theorem : If a line is drawn parallel to one side of, a triangle to intersect the other sides in distinct points, the other two sides, are divided in the same ratio., (ii) The ratio of areas of two similar triangles is equal to the square of the ratio, of their corresponding sides., (iii) Pythagoras Theorem: In a right triangle, the square of the hypotenuse is, equal to the sum of the squares of the other two sides., (iv) Converse of pythagoras theorem : In a triangle, if the square of one side, is equal to the sum of squares of other sides then the angle opposite to the, first side is a right angle., , (Theorems without Proof), (i) Converse of BPT Theorem : If a line divides any two sides of a triangle, in the same ratio, then the line is parallel to the third side. (without proof)., (ii) If a perpendicular is drawn from the vertex of the right triangle to the, hypotenuse then triangles on both sides of the perpendicular are similar to, the whole triangle and to each other., , Mathematics-X, , 75
Page 92 :
VERY SHORT ANSWER TYPE QUESTIONS, , 1., , Fill in the blanks :, (i), , All equilateral triangles are __________ ., , (ii) If ABC ~ FED, then, , AB, , =, , ED, , ., , (iii) Circles with equal radii are _________ ., (iv) If a line is drawn parallel to one side of a triangle to intersect the other, two sides in distinct points, the other two sides are divided in the, _________ ratio., (v), , In __________ triangle, the square of the hypotenuse is equal to the sum, of the squares of the other two sides., , (vi) If two triangles are similar, their corresponding sides are __________., (CBSE 2020), (vii) In ABC, AB = 6 3 , AC = 12 cm and BC = 6 cm, then B = _______ ., (viii) Let ABC ~ DEF and their areas be respectively 81 cm2 and 144 cm2. If, EF = 24 cm, then length of side BC is _________ cm., 2., , State True or False :, (i) All the similar figures are always congruent., (ii) The Basic Proportionality Theorem was given by Pythagoras., (iii) The mid-point theorem can be proved by Basic Proprotionality Theorem., (iv) Pythagoras Theorem is valid for right angled triangle., (v) If the sides of two similar triangles are in the ratio 4 : 9, then the areas of, these triangles are in the ratio 16 : 81., , 76, , Mathematics-X
Page 93 :
3., , Match the following :, Column I, , Column II, , (a) If corresponding angles are equal in two, , (i) SAS similarity criterion, , triangles, then the two triangles are similar., (b) If sides of one triangle are proportional to (ii) ASA similarity criterion, the sides of the other triangle, then the two, triangles are similar., (c) If one angle of a triangle is equal to one, , (iii) AAA similarity criterion, , angle of the other triangle and the sides, including these angles are proportional,, then the two triangles are similar., 4., , In the following figure, XY || QR and, , (iv) SSS similarity criterion, , PX, PY, 1, =, = , then, XQ, YR, 2, , P, , X, , Y, , Q, , R, , 1, QR, 3, 1, (c) XY2 = QR2, (d) XY = QR, 2, In the following figure, QA AB and PB AB, then AQ is, , (a) XY = QR, , 5., , (b) XY =, , P, A, , 10 units, , 9 units, , O, 6 units, , B, , Q, , (a) 15 units, (c) 5 units, Mathematics-X, , (b) 8 units, (d) 9 units, 77
Page 94 :
6., , 7., , 8., , The ratio of areas of two similar triangles is equal to the, (a) ratio of their corresponding sides., (b) ratio of their corresponding altitudes., (c) ratio of the square of their corresponding sides., (d) ratio of their perimeter., The areas of two similar triangles are 144 cm2 and 81 cm2. If one median of the, first triangle is 16 cm, length of corresponding median of the second triangle is, (a) 9 cm, (b) 27 cm, (c) 12 cm, (d) 16 cm, In a right triangle ABC, in which C = 90° amd CD AB. If BC = a, CA = b,, AB = c and CD = p, then, A, (a), (c), , 1, 1, 1, 2 2, 2, p, a, b, , (b), , 1, 1, 1, 2 2, 2, p, a, b, , (d), , 1, 1, 1, 2 2, 2, p, a, b, 1, 1, 1, 2 2, 2, p, a, b, , b, , C, , 9., , D, , c, , p, , a, , B, , AB, 1, = , then ar(ABC) is, DE, 2, 2, (b) 25 cm, (d) 200 cm2, , If ABC ~ DEF, ar(DEF) = 100 cm2 and, (a) 50 cm2, (c) 4 cm2, , 10. If the three sides of a triangle are a,, , 3a and, , 2a , then the measure of hte, , angle opposite to longest side is, (a) 45°, (b) 30°, (c) 60°, (d) 90°, 11. A vertical pole of length 3 m casts a shadow of 7 m and a tower casts a shadow, of 28 m at a time. The height of tower is, (a) 10 m, (b) 12 m, (c) 14 m, (d) 16 m, 12. The length of the diagonals of a rhombus are 16 cm and 12 cm. Then, the, length of the side of the rhombus is, (NCERT Exempler), (a) 9 cm, (b) 10 cm, (c) 8 cm, (d) 20 cm, 78, , Mathematics-X
Page 95 :
13. If ABC ~ EDF and ABC is not similar to DEF, then which of the following, is not true?, (NCERT Exempler), (a) BC.EF = AC.FD, , (b) AB.EF = AC.DE, , (c) BC.DE = AB.EF, , (d) BC.DE = AB.FD, , 14. Write the statement of pythagoras theorem., 15. Write the statement of Basic Proportionality Theorem., 16. Is the triangle with sides 12 cm, 16 cm and 18 cm a right triangle?, 17. If ABC ~ QRP,, , Area ( ABC), 9, = , AB = 18 cm, BC = 15 cm, then find, Area ( PQR), 4, , the length of PR., , (CBSE 2018), , 18. In the given Fig., M = N = 46°, Express x in terms of a, b and c., L, , P, , a, x, 46°, M, , 46°, , b, , c, , K, , 19. In the given Fig. AHK ~ ABC. If AK = 10 cm, BC = 3.5 cm and HK = 7 cm,, find AC., (CBSE 2010), H, , C, , A, , K, , B, , 20. It is given that DEF ~ RPQ. Is it true to say that D = R and F = P?, 21. If the corresponding Medians of two similar triangles are in the ratio 5 : 7., Then find the ratio of their sides., 22. An aeroplane leaves an airport and flies due west at a speed of 2100 km/hr. At, the same time, another aeroplane leaves the same place at airport and flies due, Mathematics-X, , 79
Page 96 :
south at a speed of 2000 km/hr. How far apart will be the two planes after 1, hour?, 23. The areas of two similar triangles ABC and DEF are 225 cm2 and 81 cm2, respectively. If the longest side of the larger triangle ABC be 30 cm, find the, longest side of the smaller triangle DEF., 24. In the given figure, if ABC ~ PQR, find the value of x?, A, R, 6 cm, , B, , 5 cm, , 3.75 cm, , x, , Q, 4.5 cm, , C, , 4 cm, , P, , 25. In the given figure, XY || QR and, , PX PY 1, =, = , find XY : QR., XQ YR 2, P, , X, , Y, , Q, , R, , 26. In the given figure, find the value of x which will make DE || AB ?, (NCERT Exempler), A, , B, , 3x + 19, , 3x + 4, D, , E, x+3, , x, C, , 27. If ABC ~ DEF, BC = 3EF and ar (ABC) = 117cm2 find area (DEF)., , 80, , Mathematics-X
Page 97 :
28. If ABC and DEF are similar triangles such that A = 45° and F = 56°,, then find the value of C., 29. If the ratio of the corresponding sides of two similar triangles is 2 : 3, then find, the ratio of their corresponding attitudes., 30. It is given that ABC ~ PQR with, , BC 1, ar( PRQ), = , then find the value of, ., QR 3, ar( ACB), , SHORT ANSWER TYPE QUESTIONS-I, , 31. In the given Fig. PQ = 24 cm, QR = 26 cm, PAR = 90°, PA = 6 cm and AR =, 8 cm, find QPR., Q, , P, A, R, , 32. In the given Fig., DE || AC and DC || AP Prove that, , BE BC, =, (CBSE 2020), EC CP, , 33. In ABC, AD BC such that AD2 = BD × CD. Prove that ABC is right, angled triangle., 34. In the given Fig., D and E are points on sides AB and CA of ABC such that, B = AED. Show that ABC ~ AED., A, D, E, B, , Mathematics-X, , C, , 81
Page 98 :
35. In the given fig., AB || DC and diagonals AC and BD intersects at O. If OA =, 3x – 1 and OB = 2x + 1, OC = 5x – 3 and OD = 6x – 5, find the value of x., D, 6x –, , 3x –, , 1, , C, 3, 5 5x –, 2x +, O, , 1, , A, , B, , 36. In the given Fig. PQR is a triangle, right angled at Q. If XY || QR, PQ = 6 cm,, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR., P, , X, , Y, R, , Q, , 37. In the given figure, AB || DE. Find the length of CD., B, 6 cm, 5 cm, A, , C, E, 3 cm, D, , 38. In the given figure, ABCD is a parallelogram. AE divides the line segment BD, in the ratio 1 : 2. If BE = 1.5 cm find BC., D, , C, O, , A, , 82, , E, B, , Mathematics-X
Page 99 :
39. In the given figure, ODC ~ OBA, BOC = 115° and CDO = 70°. Find,, (i) DOC, (ii) DCO, (iii) OAB, (iv) OBA., D, , C, , 70°, , O 115°, B, , A, , 40. Perimeter of two equilateral triangles ABC and PQR are 144 m and 96 m,, Find ar (ABC) : ar (PQR)., SHORT ANSWER TYPE QUESTIONS-II, , 41. In the given figure,, , QR QT, =, and 1 = 2 then prove that PQS ~ TQR., QS PR, (NCERT), T, P, , Q, , 1, , 2, S, , R, , 42. In equilateral ABC, AD BC. Prove that 3BC2 = 4AD2., 43. In ABC, ACB = 90° and CD AB. Prove that, , BC 2 BD, ., =, AC 2 AD, , (HOTS), , 44. In the adjoining figure ABC and DBC are on the same base BC. AD and BC, intersect at O. Prove that, , area ( ABC), AO, =, ., area ( DBC), DO, A, , (CBSE 2020), , C, O, , Mathematics-X, , B, , D, , 83
Page 100 :
45. If AD and PS are medians of ABC and PQR respectively where ABC ~, PQR, Prove that, , AB AD, ., =, PQ PS, , 46. In the given figure, DE || AC. Which of the following is correct?, x, , ab, ay, , or, , x, , B, , ay, ab, , a, E, , D, , x, , b, C, , A, , y, , 47. Prove that the sum of the squares of the sides of a rhombus is equal to the sum, of the squares of its diagonals., (NCERT, CBSE 2019, 2020), 48. A street light bulb is fixed on a pole 6 m above the level of the street. If a, woman of height 1.5 m casts a shadow of 3 m, find how far she is away from, the base of the pole., (NCERT Exempler), 49. Two poles of height a metrs and b metres are p metres apart. Prove that the, height of the point of intersection of the lines joining the top of each pole to the, foot of the opposite pole is given by, , ab, metres., ab, , 50. In the given figure AB || PQ || CD, AB = x, CD = y and PQ = z. Prove that, 1 1 1, ., x y z, A, , C, x, , P, z, , B, , 84, , Q, , y, D, , Mathematics-X
Page 101 :
51. In the given figure D = E and, triangle., , AD, AE, =, . Prove that BAC is an isoscles, DB, EC, (CBSE 2020), , 52. In the figure, a point O inside ABC is joined to its vertices. From a point D on, AO, DE is drawn parallel to AB and from a point E on BO, EF is drawn parallel, to BC. Prove that DF || AC., A, D, O, E, B, , F, C, , 53. Two triangles BAC and BDC, right angled at A and D respectively are drawn, on the same base BC and on the same side of BC. If AC and DB intersect at P., PRove that AP × PC = DP × PB., (CBSE 2019), , 54. Hypotenuse of a right triangle is 25 cm and out of the remaining two sides, one, is larger than the other by 5 cm, find the length of the other two sides., (NCERT Exempler), , Mathematics-X, , 85
Page 102 :
55. In the given figure DE || AC and, , BE BC, . Prove that DC || AP.., =, EC CP, A, , D, , B, , E, , C, , P, , 56. In a quadrilateral ABCD, B = 90°, AD2 = AB2 + BC2 + CD2. Prove that, ACD = 90°., , 57. In the given figure, DE || BC, DE = 3 cm, BC = 9 cm and ar (ADE) = 30 cm2., Find ar (BCED)., A, , D, , B, , 86, , 3cm, , 9 cm, , E, , C, , Mathematics-X
Page 103 :
58. In an equilateral ABC, D is a point on side BC such that BD =, that 9A D 2 = 7AB2., , 1, BC. Prove, 3, , (NCERT, CBSE 2018, 2020), , 59. In PQR, PD QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR =, d and a, b, c, d are positive units. Prove that (a + b) (a – b) = (c + d) (c – d)., (NCERT Exempler), 60. Prove that the ratio of the areas of two similar triangles is equal to the ratio of, the squars of their corresponding sides., (CBSE 2010, 2018, 2019), 61. In the given figure, the line segment XY is Parallel to AC of ABC and it, divides the triangle into two parts of equal areas. Prove that, , AX, =, AB, , 2 1, ., 2, , A, X, , B, , Y, , C, , 62. Through the vertex D of a parallelogram ABCD, a line is drawn to intersect the, sides BA and BC produced at E and F respectively. Prove that, , DA FB FC, =, =, ., AE BE CD, , 63. Prove that if in a triangle, the square on one side is equal to the sum of the, squares on the other two sides, then the angle opposite to the first side is a right, angle., (CBSE 2019, 2020), 64. Prove that in a right angle triangle, the square of the hypotenuse is equal the, sum of the squares of other two sides., (CBSE 2018, 2019, 2020), Mathematics-X, , 87
Page 104 :
65. If a line is drawn parallel to one side of a triangle to intersect the other two, sides in distinct points, then prove that the other two sides are divided in the, same ratio., (CBSE 2019, 2020), 66. In an Obtuse ABC (B is obtuse), AD is perpendicular to CB produced., Then prove that A C2 = AB2 + BC2 + 2BC × BD., 67. In figure BN and CM are medians of a ABC right angled at A. Prove that, 4(BN2 + CM2) = 5 BC2, (CBSE (C) 2020), C, , N, , A, , B, , M, , 68. Sides AB and AC and median AD of ABC are respectively proportional to, sides PQ and PR and median PM of PQR. Show that ABC ~ PQR., (CBSE 2020), 69. In figure if ABC ~ DEF and their sides of lengths (in cm) are marked along, them, then find the lengths of sides of each triangle., (CBSE 2020), A, 2x – 1, B, , D, 3x, , 2x + 2, , 6x, , 18, C, , E, , 3x + 9, , F, , 70. The Perimeters of two similar triangles are 30 cm and 20 cm repsectively. If, one side of the first triangle is 9 cm long. Find the length of the corresponding, side of the second triangle., (CBSE 2020), 71. In figure PQR is right-angled at P.M is a point on QR such that PM is, perpendicular to QR. Show that PQ2 = QM × QR., (CBSE 2020), 88, , Mathematics-X
Page 105 :
R, M, Q, , P, , ANSWERS AND HINTS, VERY SHORT ANSWER TYPE QUESTIONS-I, , 1., , (ii), , (iv) Same, , (v) Right, , (vii)90°, 2., 3., , AB BC, =, FE E D, , (i) Similar, , (iii) Congruent, (vi) Proportional, , (viii) 18 cm, , (i) False, , (ii) False, , (iv) True, , (v) True, , (iii) True, , (a) (iii) AAA similarity criterion., (b) (iv) SSS similarity criterion., (c) (i) SAS similarity criterion., 1, QR, 3, , 4., , (B) XY =, , 5., , (A) 15 units, , 6., , (C) Ratio of the square of their corresponding sides., , 7., , (C) 12 cm, , 8., , (A), , 9., , (B) 25 cm2, , 1, 1, 1, 2 2, 2, p, a, b, , 10. (D) 90°, 11. (B) 12 m, 12. (B) 10 cm, Mathematics-X, , 89
Page 106 :
13. (C) BC.DE = AB.EF, 14. See point 3(iii) of Key Points, 15. See point 3(i) of Key Points., 16. No, because (12)2 + (16)2 (18)2, 17. 10 cm, 18. KPN ~ KLM, x, c, , a bc, , x=, 19., , ac, bc, , AK HK, =, AC BC, , 10, 7, =, AC 3.5, , , , AC = 5 cm, , 20. D = R (True), F = P (False), 21. 5 : 7, N, , 2100 Km, , 22., , W, , E, , 0, , A, , B, , AB =, , (2100) 2 (2000) 2 = 2900 km, , 2000 Km, , 5, B, , 23. Let longest side of the DEF be x cm., 225 30 , = , 81, x, , 2, , x = 18 cm, 90, , Mathematics-X
Page 107 :
24., , AB, BC, =, PQ, QR, , , , 6, 4, =, 4.5, x, , x = 3cm, , 25. PXY ~ PQR, PX, XY, 1, =, =, PQ, QR, 3, XY : QR = 1 : 3, 26., , x3, x, =, 3 x 19, 3x 4, , (By B.P.T.), , x=2, 27., , ar (ABC) BC 2 3EF 2 3 2, = , = , = , ar (DEF), EF , EF , 1, 117, =9, ar(DEF), , ar(DEF) = 13 cm2, , 28. F = C = 56°, 29. 2 : 3, 30. 1/9, 31. PR =, , (6) 2 (8) 2 = 10 cm., , As QR2 = PQ2 + PR2 , therefore QPR = 90°., (By Converse of Pythagoras theorem), 32. DE || AC,, , AD, EC, =, DB, BE, , ...(1) [ BPT], , DC || AP,, , AD, CP, =, DB, BC, , ...(2) [ BPT], , From (1) and (2), we get, BE, BC, =, EC, CP, , Mathematics-X, , 91
Page 109 :
36., , PX, PY, =, XQ, YR, , , , 1, 4, =, 2, YR, , YR = 8 cm, , PR = 8 + 4 = 12 cm, QR =, , (12) 2 (6) 2 = 6 3 cm, , 37. ABC ~ EDC, , (AA Similarity criterion), , 6, 5, =, 3, CD, , CD = 2.5 cm, 38. BOE ~ DOA, , (AA Similarity criterion), , BO, BE, =, DO, DA, 1, 1.5, =, 2, DA, , DA = 3 cm, BC = DA = 3 cm, , (Opposite sides of a parallelogram), , 39. (i) 65°, (ii) 45°, (iii) 45°, (iv) 70°, ar ( ABC) 144 2 9, 40., =, =, ar ( PQR) 96 , 4, ar (ABC) : ar (PQR) = 9 : 4, 41. In PQR, 1 = , PR = PQ, , , QR, QT, =, and 1 = 1, QS, PQ, , PQS ~ TQR, Mathematics-X, , [Opposite sides of equal angles], (Common), (SAS Similarity criterion), 93
Page 113 :
1 , BC, 1, EF , , =, , AB CD , BC, 1 1 , EF = 1, a b, EF =, , ab, ab, , 50. Same as Q. 48., 51., , AD AE, , DB EC, , By converse of BPT, DE || BC, D = B and, , E = C, , (Corresponding Angles), , But D = E, So, B = C, AB = AC, So, ABC is an isosceles triangle., 52. In OAB,, , OD, OE, =, .... (1), DA, EB, , ( BPT), , In OBC,, , OE, OF, =, .... (2), EB, FC, , ( BPT), , From (1) and (2), we get, OD, OF, =, DA, FC, , By converse of BPT, DF || AC., 53. APB ~ DPC, AP, PB, =, DP, PC, , (AA Similarity criterion), ( C.P.S.T.), , AP.PC = DP.PB, Mathematics-X, , 97
Page 119 :
PRACTICE-TEST, Triangles, Time : 1 Hrs., , M.M. : 20, SECTION - A, , 1., , If sides of two similar triangles are in the ratio of 8:10, then areas of these, triangles are in the ratio __________ ., 1, , 2., , If in two triangles ABC and PQR,, , 3., , 4., , CA, BC, AB, =, =, , then, PQ, RP, QR, , 1, , (A) PQR ~ CAB, (B) PQR ~ ABC, (C) CBA ~ PQR, (D) BCA ~ PQR, ABC is an isosceles right triangle, right angled at C, then AB2 = .........., (A) AC2, (B) 2 AC2, (CBSE 2020), 2, 2, (C) 4 AC, (D) 3 AC, 1, A line DE is drawn parallel to base BC of ABC, meeting AB in D and AC at, E, ., If, , AB, = 4 and CE = 2 cm, find the length of AE., BD, , SECTION B, 5., 6., 7., , The lengths of diagonals of a rhombus field are 32 m and 24 m. Find the length, of the side of the field., 2, A man goes 24 m towards West and then 10 m towards North. How far is he, from the starting point?, 2, Using converse of Basic Proportionality Theorem, prove that the line joining, the mid-points of any two sides of a triangle is parallel to the third side., 2, , SECTION C, 8., 9., , E is a point on the side AD produced of a parallelogram ABCD and BE intersect, CD at F. Show that ABE ~ DCB., 3, In an equilateral triangle, prove that three times the square of one side is equal, to four times the square of one of its altitude., 3, , SECTION D, 10. State and prove Basic Proportionality Theorem., Mathematics-X, , 4, 103
Page 120 :
CHAPTER, , 7, , Co-ordinate Geometry, , Key Points, 1. Coordinate Geometry, Coordinate Geometry, A system of geometry where the position of points, on the plane is described using an ordered pair P(x, y), , The distance of a point from y-axis, is called x-coordinate or abscissa, , The distance of a point from x-axis, is called y-coordinate or ordinate, , The coordinate of point on x-axis is (x, 0). The coordinate of point, on y-axis is (0, y). The coordinate of point on 2-Dimensional, plane i.e., cartesian plane is (x, y), , Cartesian Plane, , 104, , Mathematics-X
Page 121 :
2., , Distance Formula, Finding distance between two given points :, , A(x1, y1), , B(x2, y2), , AB (Distance between A and B) =, 3., , ( x2 x1 )2 ( y2 y1 ) 2, , Distance of a point from origin :, , (0, 0), 0, A (x, y), , Using distance formula, OA =, 4., , 5., , ( x 0)2 ( y 0) 2 =, , x2 y2, , Midpoint formula :, Coordinates of mid points of AB where A(x 1 , y 1 ) and B(x 2 , y 2 ) are :, x1 x2 y1 y2 , ,, , , 2, 2 , Section formula:, The coordinates of a point P(x, y) which divides the line segment joining, A(x1, y1) and B(x2, y2) internally in the ratio m : n are given by, mx nx1, my2 ny1 , , P x 2, ,y, , , mn, mn , P (x, y), A, (x1,y1), , Mathematics-X, , m, , :, , n, , B, (x2,y2), , 105
Page 122 :
6., , Centroid of a triangle is given by :, , x x x y y y3 , O 1 2 3 , 1 2, , , 3, 3, , 7., , The area of ABC, where A(x1, y1), B(x2, y2), (x3, y3) are its vertices, 1, ar () =, [x (y – y ) + x2 (y3 – y1) + x3 (y1 – y2)] sq. units, 2 1 2 3, A (x1, y1), , B (x2, y2), , 8., , C (x3, y3), , If area of a triangle is zero then points are collinear and vice versa., VERY SHORT ANSWER TYPE QUESTIONS, , Fill in the blanks :, 1., , The distance of a point from the y-axis is called its x-coordinate or ______ ., , 2., , The distance of a point from the x-axis is called its __________ or ordinate., , 3., , The point (5, 0) lies on ____ axis., , 4., , A point which lies on y-axis are of the form _______ ., , 5., , A linear equation of the form ax + by + c = 0 when represented graphically, gives a _______ ., , 6., , The distance of a point P(x, y) from the origin is ________, , Multiple Choice Question :, 7., 106, , P is a point on x-axis at a distance of 3 unit from y-axis to its left. The coordinates of P are :, Mathematics-X
Page 123 :
8., , 9., , (a) (3, 0), , (b) (0, 3), , (c) (– 3, 0), , (d) (0, – 3), , The distance of P(3, – 2) from y-axis is, (a) 3 units, , (b) 2 units, , (c) – 2 units, , (d), , 13 units, , The co-ordinates of two ponts are (6, 0) and (0, – 8). The co-ordinates of the, mid points are, (a) (3, 4), , (b) (3, – 4), , (c) (0, 0), , (d) (– 4, 3), , 10. If the distance between P(4, 0) and Q(0, x) is 5 units, the value of x will be, (a) 2, , (b) 3, , (c) 4, , (d) 5, , 11. The co-ordinates of the point where line, , x y, 7 intersects y-axis are, a b, , (a) (a, 0), , (b) (0, b), , (c) (0, 7b), , (d) (2a, 0), , 12. The area of triangle OAB, the co-ordinates of whose vertices are A(4, 0),, B(0, – 7) and O origin, is :, (a) 11 sq. units, , (b) 18 sq. units, , (c) 28 sq. units, , (d) 14 sq. units, , 11 , 2 , 13. The distance between the points P , 5 and Q , 5 is, 3, 3, (a) 6 units, , (b) 4 units, , (c) 3 units, , (d) 2 units, , 14. The distance between the points (5 cos 35°, 0) and (0, 5 cos 55°) is, (a) 10 units, , (b) 5 units, , (c) 1 unit, , (d) 2 units, , Mathematics-X, , 107
Page 124 :
15. The co-ordinates of vertex A of ABC are (– 4, 2) and a point D which is mid, point of BC are (2, 5). The coordinates of centroid of ABC are, (a) (0, 4), , 7, , (b) 1, , 2, , 7, , (c) 2, , 3, , (d) (0, 2), , 16. The distance between the line 2x + 4 = 0 and x – 5 = 0 is, (a) 9 units, , (b) 1 unit, , (c) 5 units, , (d) 7 units, , 17. The perimeter of triangle formed by the points (0, 0), (2, 0) and (0, 2) is, (a) 4 units, , (b) 6 units, , (c) 6 2 units, , (d) 4 2 2 units, , 18. If the centroid of the triangle formed by (9, a), (b, – 4) and (7, 8) is (6, 8), then, the value a and b are :, (a) a = 4, b = 5, , (b) a = 5, b = 4, , (c) a = 5, b = 2, , (d) a = 20, b = 2, , VERY SHORT ANSWER TYPE QUESTIONS, , 19. The centre of circle having end points of its diameter as (–4, 2) and (4, –3) is, (a) (2, –1), (c) (0, –, , 1, ), 2, , (b) (0, –1), (d) (4, –, , 5, ), 2, , (CBSE 2020 Basic), , 20. The distance between the points (0, 0) and (a – b, a + b) is, (a) 2 ab, , (b), , 2a 2 ab, , (c) 2 a 2 b 2, , (d), , 2a 2 2b 2, , (CBSE 2020 Standard), , SHORT ANSWER TYPE QUESTIONS-I, , 21. For what value of P, the points (2, 1), (p, – 1) and (– 1, 3) are collinear., 108, , Mathematics-X
Page 125 :
22. Find the area of triangle formed by A(0, 0), B(4, 0) and C(0, 9), (CBSE 2020 Basic), 23. Find the point of trisection of the line segment joining the points (1, – 2) and, (– 3, 4)., 24. The midpoints of the sides of a triangle are (3, 4), (4, 1) and (2, 0). Find the, vertices of the triangle., 25. A circle has its centre at (4, 4). If one end of a diameter is (4, 0) then find the, coordinates of the other end., (CBSE 2020 Standard), 26. Find the ratio in which P(4, m) divides the line segment joining the points, A(2, 3) and B(6, –3). Hence find m., (CBSE 2018), 27. Show that the points (– 2, 3), (8, 3) and (6, 7) are the vertices of a right angle, triangle., 28. Find the point on y-axis which is equidistant from the points (5, –2) and, (–3, 2)., (CBSE 2019), 29. Find the ratio in which y-axis divides the line segment joining the points, A(5, – 6) and B(– 1, – 4)., 30. Find the co-ordinates of a centroid of a triangle whose vertices are (3, – 5),, (– 7, 4) and (10, – 2)., 31. Find the relation between x and y such that the points (x, y) is equidistant from, the points (7, 1) and (3, 5)., 32. Find the ratio in which the segment joining the points (1, –3) and (4, 5) is, divided by x-axis. Also find the coordinates of the point on x-axis., (CBSE 2019), 33. What is the value of a if the points (3, 5) and (7, 1) are equidistant from the, point (a, 0) ?, 34. Find a relation between x and y if the points A(x, y), B(– 4, 6) and C(– 2, 3) are, collinear., 35. If the points A(2, 0), B(6, 1) and C(p, q) from a triangle of area 12 sq units, (positive only) and 2p + q = 10, then find the values of p and q., (CBSE 2020 Standard), Mathematics-X, , 109
Page 126 :
36. Name the type of triangle formed by the points A(– 5, 6), B(– 4, – 2) and, C(7, 5)., (NCERT Exempler), 37. Find the points on the x-axis which are at a distance of 2 5 from the point, (7, – 4). How many such points are there?, (NCERT Exempler), 38. A line intersects the y-axis and x-axis at the point P and Q. If (2, –5) is the, midpoint of PQ then find the co-ordinates of P and Q., (CBSE 2017), 39. If A(–2, 1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram, ABCD, find the values of a and b. Hence find the lengths of its sides., (CBSE 2018), 40. Let P and Q be the points of trisection of the line segment joining the points, A(2, – 2) and B(– 7, 4) such that P is nearer to A. Find the co-ordinates of, P and Q., SHORT ANSWER TYPE QUESTIONS-II, , 41. The line segment joining the points A(2, 1) and B(5, – 8) is trisected at the point P, and Q such that P is nearer to A. If P also lies on the line given by 2x – y + k = 0,, find the value of k., (CBSE 2019), 42. Find the ratio in which the line x – 3y = 0 divides the line segment joining the, points (– 2, – 5) and (6, 3). Find the co-ordinates of the point of intersection., (HOTS), 43. Point A lies on the line segment XY joining X(6, – 6) and Y(– 4, – 1) in such a, XA, 2, = . If point A also lies on the line 3x + k(y + 1) = 0, find the, XY, 5, value of k., , way that, , (HOTS), 44. Find the area of the triangle formed by joining the mid points of the sides of the, triangle ABC, whose vertices are A(0, – 1), B(2, 1) and C(0, 3)., 45. Find the value of k so that the area of triangle ABC with A(k + 1, 1), B(4, – 3), and C(7, – k) is 6 square units., 46. Point P divides the line segment joining the points A(2, 1) and B(5, – 8) such, that, 110, , AP, 1, = . If P lies on the line 2x – y + k = 0. Find the value of k., PB, 3, , Mathematics-X
Page 127 :
47. If the distances of P(x, y) from A(5, 1) and B(–1, 5) are equal then prove that, 3x = 2y., (CBSE 2017), 24 , 48. In what ratio does the point , y divides the line segment joining the points, 11 , P(2, –2) and Q(3, 7) ?, (CBSE 2017), 49. If A(– 3, 2), B(x, y) and C(1, 4) are the vertices of an isosceles triangle with AB, = BC. Find the value of (2x + y)., 50. If the point P(3, 4) is equidistant from the points A(a + b, b – a) and, B(a – b, a + b) then prove that 3b – 4a = 0., LONG ANSWER TYPE QUESTIONS-III, , 51. Find the area of the quadrilateral ABCD whose vertices are A(–4, –3),, B(3, – 1), C(0, 5) and D(–4, 2)., (CBSE 2020 Standard), 52. If P(x, y) is any point on the line joining A(a, 0) and B(0, b) then show that, x y, = 1., a b, , 53. If the points (x, y), (– 5, – 2) and (3, – 5) are collinear, prove that, 3x + 8y + 31 = 0., 54. Find the relation between x and y if A(x, y), B(– 2, 3) and C(2, 1) form an, isosceles triangle with AB = AC., , , , , , 55. Prove that the point x, 1 x 2 is at a distance of 1 unit from the origin., 56. If the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear then find, the value of k., (CBSE 2017), 57. If the points (a, b), (c, d) and (a – c, b – d) are collinear show that bc = ad., 58. Find the co-ordinates of the circumcenter of the triangle whose vertices are, (3, 7), (0, 6) and (– 1, 5). Find the circumradius., (HOTS), 59. In a triangle PQR, the co-ordinates of points P, Q and R are (3, 2), (6, 4) and, (9, 3) respectively. Find the co-ordinates of centroid G. Also find the areas of, PQG and PRG., 60. If the points (5, 4) and (x, y) are equidistant from the point (4, 5), prove that, x2 + y2 – 8x – 10y + 39 = 0., Mathematics-X, , 111
Page 128 :
ANSWERS AND HINTS, VERY SHORT ANSWER TYPE QUESTIONS-I, , 1., 3., , abscissa, x-axis, , 2. y-coordinate, 4. (0, y), , 5., , straight line, , 6., , 7., 9., 11., 13., 15., , (iii) (– 3, 0), (ii) (3, – 4), (iii) (0, 7b), (c) 3 units, (a) (0, 4), , 8., 10., 12., 14., 16., , 17. (d), , 4 2 2 , , units, , 19. (c), 21. P = 3, , x2 y2, (i) 3 units, (ii) 3, (iv) 14 sq. units, (b) 5 units, (d) 7 units, , 18. (d) a = 20, b = 2, 20. (d), 22. 18 sq. units, , 23., AP : PB = 1 : 2, AQ : QB = 2 : 1, 1 , P = , 0, 3, 5 , Q = , 2, 3, 24. Let A(x1, y1), B(x2, y2), C(x3, y3) are vertices of given triangle, Let, Midpoints of AB = D(3, 4), Midpoints of BC = E(4, 1), Midpoints of AC = F(2, 0), 112, , Mathematics-X
Page 129 :
Apply Midpoint formula on AB, BC, AC, We get, x1 + x2 = 6,, , y1 + y2 = 8, , x2 + x3 = 8,, , y2 + y3 = 2, , x1 + x3 = 4,, , y1 + y3 = 0, , Solving we get, x1 = 1, , y1 = 3, , x2 = 5, , y2 = 5, , x3 = 3, , y3 = –3, , A(1, 3), B(5, 5), C(3, –3), 25. (4, 8), 26. Ratio 1 : 1, m = 0, 27. Show using pythagoras theorem and distance formula., 28. (0, –2), 29. 5 : 1, 30. (2, – 1), 31. x – y = 2, 32. 3 : 5 ;, , 17 , , 0, 8, , 33. a = 2, 34. 3x = – 2y, 35. p = 2, q = 6, 36. Using distance formula, scalene triangle., 37. x = 1, x = – 15, Two such points are there., 38. (4, –10), 39. a = 1, b = 1, AB = CD = 10 , AD = BC = 10, 40. P(– 1, 0), Q (– 4, 2), Mathematics-X, , 113
Page 130 :
41. P(3, – 2), Put value of x = 3, y = – 2 is equation, then k = – 8., 42. Let P(x, y) be the point and m : n is the ratio, then x =, , 6n 2m, ,, mn, , y=, , 3n 5m, mn, , From equation of line x = 3y , By putting x = 3y or, , ...(1), , x, =3, y, , x, = 3 is (1), y, , m : n = 3 : 13, 9 3, Then P(x, y) = , , 2 2, XA, 2, = ., AY, 3, Let A(x , y) is the point., x = 2, y = – 4, A (2, – 4), Put x = 2 and y = – 4 in equation., K=2, 44. 1 sq. unit, 45. K = 3, , 43. Find, , 17, 4, PA = PB, Use distance formula, 2:9, 2x + y = 1, 3b – 4a = 0 proved by using distance formula., Area of quadrilateral = 34 sq units., Prove by section formula., Prove by area of = 0 if points are collinear., Prove by distance formula., , 46. K =, 47., 48., 49., 50., 51., 52., 53., 54., 114, , Mathematics-X
Page 131 :
55. Prove by distance formula., 1, , k = –2, 2, 58. Find co-ordinates of mid points of AB, BC, CA, then DO = OE = OF, , 56. k =, , A, , 13 , then (circumcentre) O(x, y) = 1, , 2, circumradius AO =, , 17, ., 2, , F, , D, O, B, , E, , C, , 59. G(x, y) = (6, 3), ar PQG =, , 3, sq. units, 2, , 3, sq. units, 2, 60. Use distance formula, , ar PRG =, , Mathematics-X, , 115
Page 132 :
PRACTICE-TEST, Coordinate Geometry, Time : 1 Hr., , M.M. : 20, SECTION - A, , 1., , 1 15 , Find the value of m for which the points (3, 5), (m, 6) and , are collinear.., 2 2, , 2., 3., 4., , 1, What is the distance between the points A(c, 0) and B(0, –c), 1, The distance of point P(– 6, 8) from the origin is _______ ., 1, Find the value of ‘a’ so that the point (3, a) lies on the line segment 2x – 3y = 5., 1, , SECTION B, 5., 6., 7., , For what value of p, the points (– 3, 9), (2, p) and (4, – 5) are collinear., 2, If the points A(8, 6) and B(x, 10) lie on the circle whose centre is (4, 6) then, find the value of x., 2, Find the perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0)., 2, , SECTION C, 8., 9., , Show that the points A(–3, 2), B(– 5, –5), C(2, –3) and D(4, 4) are the vertices, of a rhombus., 3, Find the ratio in which the point (2, y) divides the line segment joining the, points A(–2, 2) and B(3, 7). Also find the value of y., 3, , SECTION D, 10. If the point P divides the line segment joining the points A(–2, –2) and B(2, –, 4) such that, , 116, , AP, 3, = , then find the coordinate of P.., AB, 7, , 4, , Mathematics-X
Page 133 :
CHAPTER, , Introduction to, Trigonometry, , 8, KEY POINTS, , A, , A branch of mathematics which deals, with the problems related to right, H (hypotenuse), angled triangles. It is the study of rela- (Perpendicular) P, tionship between the sides and angles, of a right angled triangle., C, B, B, Note : For A, Perpendicular is BC and, (base), base is AB., For C, Perpendicualr is AB and Base is BC., Trigonometric Ratios of an acute angle in a right angled triangle express the, relationship between the angle and the length of its sides., , Mind Trick: To learn the relationship of sine, cosine and tangent follow this, sentence., Some People Have Curly Brown Hair Through Proper Brushing, sin A , , P, H, , Mathematics-X, , cos A , , B, H, , tan A , , P, B, 117
Page 135 :
5., , Trigonometric ratios of some specific angles, A, , 0°, , 30°, , 45°, , 60°, , 90°, , sin A, , 0, , 1, 2, , 1, 2, , 3, 2, , 1, , cos A, , 1, , 3, 2, , 1, 2, , 1, 2, , 0, , tan A, , 0, , 1, 3, , 1, , 3, , Not defined, , cot A, , Not defined, , 3, , 1, , 1, 3, , 0, , sec A, , 1, , 2, 3, , 2, , 2, , Not defined, , Not defined, , 2, , 2, , 2, 3, , 1, , cosec A, 6., , Trigonometric ratios of complimentary angles, sin (90° – ), =, cos , cos (90° – ), =, sin , tan (90° – ), =, cot , cot (90° – ), =, tan , sec (90° – ), =, cosec , cosec (90° – ) =, sec , VERY SHORT ANSWER TYPE QUESTIONS, , 1., 2., 3., , If sin = cos , find the value of , If tan = cot (30° + ), find the value of , If sin = cos (– 6°), find the value of , , 4., , If tan =, , 5., , If 3x = cosec and, , 4, sin +cos , then find the value of, 3, sin – cos , , Mathematics-X, , 3, = cot then find, x, 119
Page 136 :
6., , If x = a sin and y = a cos then find the value of x2 + y2, , 7., 8., , Find the value of cosec 70° – sec 20°, Find the value of 9 sec2 A – 9 tan2 A, , 9., , Express sec in terms of cot , , 10. Find the value of cos cos (90° – ) – sin sin (90° – ), 11. If sin (20° + ) = cos 30° then find the value of ., 12. Find the value of, , 1 tan 2 , 1 cot 2 , , cosec2 sec 2 , 1, 13. Given tan =, , find the value of, ., 3, cosec2 sec 2 , , (CBSE, 2010), , 14. Express cosec 48° + tan 88° in terms of trigonometric ratios of angle between, 0° and 45°., 15. If 5 tan – 4 = 0, then value of, , 5 sin 4 cos , is, 5 sin 4 cos , , 5, 5, (b), (c) 0, 3, 6, 16. If A and B are complementary angles, then, , (a), , (a) sin A = sin B, , (b) cos A = cos B, , (c) tan A = tan B, , (d) sec A = cosec B, , (d), , 1, 6, , 17. In Fig. if AD = 4 cm, BD = 3 cm and CB = 12 cm. then cot =, (a), , 12, 5, , (b), , 13, (c), 12, , A, , 5, 12, , 12, (d), 13, , D, , , C, , B, , 18. The value of tan 1° x tan 2° x tan 3° x ... x tan 89° is., (a) 1, (b) – 1, (c) 0, (d) None of these, 19. If and 2 – 45° are acute angles such that sin = cos (2 – 45°) then tan is, (a) 1, 120, , (b) – 1, , (c), , 3, , (d), , 1, 3, Mathematics-X
Page 137 :
SHORT ANSWER TYPE QUESTIONS (1), , Prove that :, 20. sec4 – sec2 = tan4 + tan2 , 21., , 1 + sin , = tan + Sec , 1 – sin , , 22. If x = p sec + q tan & y = p tan + q sec then prove that x2 – y2 = p2 – q2, 23. If 7 sin2 + 3 cos2 = 4 then show that tan =, 24. If sin (A – B) =, , 1, 3, , 1, 1, , cos (A + B) =, then find the value of A and B., 2, 2, , cos 2 20° + cos 2 70°, 25. Find the value of, ., sin 2 59° + sin 2 31°, , 26. If 3 cot A = 4, find the value of, , cosec 2 A + 1, ., cosec 2 A – 1, , 27. If tan (3x – 15°) = 1 then find the value of x., 28. If A, B, C are interior angles of ABC, the prove that, A B, C, cos ec , sec ., 2 , 2, (CBSE 2011), 29. In ABC, right angled at B, AB = 5 cm and ACB = 30°. Find BC and AC., 30. Show that :, , 1 sin 60, = 2 3., cos 60, , 31. Find the value of , if, , Mathematics-X, , cos , cos , , 4 , 90°., 1 sin 1 sin , , (CBSE, 2014), (CBSE, 2014), , 121
Page 138 :
SHORT ANSWER TYPE QUESTIONS, , Prove that :, tan A + Sec A – 1 1+Sin A, 32. tan A – Sec A+1 = Cos A, 1, 1, 1, 1, –, , –, 33., sec x – tan x, cos x cos x sec x tan x, 34., , tan , cot , +, =1+ tan + cot = sec cosec +1, 1– cot 1 – tan , , (CBSE 2019), , 35. (sin + cosec )2 + (cos + sec )2 = 7 + tan2 + cot2 , 36. sec A (1 – sin A) (sec A + tan A) = 1, 37. If sec = x +, , 1, 1, , prove that sec + tan = 2x or, 4x, 2x, , 38. If sin + sin2 = 1, prove that cos2 + cos4 = 1, 39. Without using trigonometric table, the value of, cot tan (90° – ) – sec (90° – ) cosec + sin2 65° + sin2 25° +, tan 85°., cot (90° – ) cosec(90° – ) sin , 40. Prove that :, +, = sec2 , tan , tan (90° – ), 41. Find the value of :, , 3 tan 5°, , cos 2 20° + cos 2 70°, + 2 Cosec2 58° – 2 Cot 58° tan 32° – 4 tan 13° tan 37°, sec 2 50° – cot 2 40, tan 77° tan 45° tan 53°., 42. If A, B, C are the angles of ABC then prove that cosec2, 43. Find the value of sec2 10° – cot2 80° +, 44. If cos + sin =, 45. Evaulate :, , sin 15°cos 75° +cos 15° sin 75°, ., cos sin (90° – ) + sin cos (90° – ), , 2 cos , then show that cos – sin =, , tan 2 60 4cos 2 45 3sec2 30 5cos 2 90, cosec 30° sec 60 cot 2 30, , 46. If a cos + b sin = m and a sin – b cos = n, Prove that : a2 + b2 = m2 + n2, 122, , 2 sin ., , (CBSE, 2001 C), Mathematics-X
Page 139 :
LONG ANSWER TYPE QUESTIONS, , Prove That:, 1, , 1 , 1 , 47. 1 +, 1 +, = sin 2 – sin 4 , 2, 2, tan , cot , , , 48., 49., 50., 51., , 2 (sin6 + cos6 ) – 3 (sin4 + cos4 ) + 1 = 0, (1 + cot A + tan A) (sin A – cos A) = sin A tan A – cot A cos A, If sin + cos = m and sec + cosec = n then show that n(m2 – 1) = 2m, find the value of :, cot (90° – ) tan – cosec (90° – ) sec , sin 2 (50° + ) + sin 2 (40° – ), +, sin 12° Cos 15° sec 78° cosec75°, tan 15° tan 37° tan 53° tan 75°, , 52. Prove that :, 1, 1, 1, 1, –, =, –, cosec + cot sin sin cosec – cot , , 53. If, , cos , cos , = m and, = n , then prove that (m2 + n2) Cos2 = n2, cos , sin , , 54. Prove that :, sin 2 – 2sin 4 , sec –, =1, 2cos 4 – cos 2 , 2, , 55. cot tan (90° – ) – sec (90° – ) cosec +, , 3 tan 12° tan 60° tan 78° find its, , value., 56. Find the value of —, sec (90° – ) cosec – tan (90° – ) cot + cos 2 25° + cos 2 65°, 3 tan 27° tan 63°, 57. If sin + cos =, 58. Prove, , 3 , then prove that tan + cot = 1, , cotA – cosA, = sec2A + tan2A – 2secA tanA, cotA+ cosA, , Mathematics-X, , (CBSE 2020), (CBSE 2020 Basic), 123
Page 140 :
sin 2sin 3 , 59. Prove, = tan , 2 cos3 cos , 60. If cos(A + B) = sin(A – B) =, of A and B., , (CBSE 2020 Basic), , 1, , 0 < A + B < 90° and A > B then find the value, 2, (CBSE 2020 Basic), , 61. If tan + sin = m, tan – sin = n, then prove that m2 – n2 = 4 mn ., (CBSE 2020 Standard), sec 2 (90 – ) cot 2 2 cos 2 60 tan 2 28 tan 2 62, , 62. Find, 2(sin 2 25 sin 2 65), 3(sec 2 43 cot 2 47), (CBSE 2020 Standard), 63. Prove, , 1 sec tan 1 sin , =, 1 sec tan , cos , , (CBSE 2020 Standard), , 2, , cos 37 cosec 53, 3sin 43 , 64. Evaluate , –, tan 5 tan 25 tan 45 tan 65 tan 85, cos 47 , , (CBSE 2019), 65. Prove that, , sin , sin , = 2, cot cosec , cot cosec , , 66. If 4 tan = 3 then find the value of, , 4 sin cos 1, 4 sin cos 1, , sinA – 2sin 3A, 67. Prove, = tan A, 2 cos3A – cosA, , (CBSE 2019), (CBSE 2018), , (CBSE 2018), , ANSWERS AND HINTS, , 1., 3., 5., 7., 124, , 45°, 48°, 1, 3, 0, , 2. 30°, 4. 7, 6. a2, 8. 9, Mathematics-X
Page 141 :
9., 11., 13., 15., 17., 19., 20., , 21., 22., 23., 24., 25., , 1 cot 2 , cot , 40°, , 10. 0°, 12. tan2 , , 1, 14. sec 42° + cot 2°, 2, (c), 16. (d), (a), 18. (a), (a), LHS = sec2 (sec2 – 1), RHS = tan2 (tan2 + 1), Use 1 + tan2 = sec2 , Relationalise and proceed in LHS, Squaring both sides of x and y and subtracting., Divide both sides by cos2, A = 45°, B = 15°, 1, , 26., , 17, 8, , 27., 28., , 20°, Use (A + B + C = 180°), , 29., , AC = 10, BC = 5 3 , use Pythagoras theorem, , 30. Substitute values of sin 60° and cos 60° and solve, 31. 60°, Note : 32 to 38 use trigonometric identities and prove (based on Ex. 8.4 of, NCERT), 39., 40., 41., 42., 43., , 3, Use cot (90 – ) = tan , cosec (90 – ) = sec , tan (90 – ) = cot , –1, Use A + B + C = 180°, 2, , Mathematics-X, , 125
Page 142 :
cos + sin = 2 cos , Square both sides and get 1 + 2 cos sin = 2 cos2 , 2 cos sin = 2 cos2 – 1, Now square (cos – sin )2 and get, (cos – sin )2 = 1 – 2 cos sin , Substitute (1) in (2), 45. 9., 46. Find m2 and n2 and add, Note : Q47 to Q50 Use identities to prove, 51. 0, 44., , 52., , 53., 54., 55., , ...(1), ...(2), , Rationalise, , 1, 1, in LHS and proceed, use, = cosec ., cosec cot , sin , , Rationalise, , 1, 1, on RHS and proceed, use, = cosec ., cosec – cot , sin , , Find m2 and n2 and substitute in LHS., Take common sin2 in Numerator and cos2 in Denominator of 2nd term, on LHS and replace 1 by sin2 + cos2 ., 0, , 56., , 2, 3, , 57., , (sin + cos ) =, , 3, , square both sides and get value of, , 1, sin cos , , Change tan + cot into sin and cos proceed., 58., , cos A, Change cot A = sin A , take cos A common from Numerator and, , Denominator, Rationalise remaining term and change into sec A and tan, A., , 126, , Mathematics-X
Page 143 :
sin (1 2sin 2 ), 59. LHS =, , write 1 = sin2 + cos2 and proceed., cos (2 cos 2 1), 60., , cos (A + B) =, , 1, = cos 60°, 2, , 1, = sin 30°, 2, A = 45°, B = 15°, , , , A B 60, Solve these equations, A – B 30 , , sin (A – B) =, , 61., , Find m2 and n2 substitute in m2 – n2 and substitute m and n in 4 mn, , 62., , 2, 3, , 63., 64., 65., , Refer NCERT, (Use complementary form), 8, Convert cot and cosec into sin and cos , and use sin2 = 1 – cos2, , 66., , Divide Numerator and Denominator by cos , and use sec = 1 tan 2 , or use pythagoras theorem and trigonometeric ratios,, Ans., , 67., , 13, 11, , Same as Q 59., , Mathematics-X, , 127
Page 144 :
PRACTICE-TEST, Introduction to Trigonometry, Time : 1 Hrs., , M.M.: 20, SECTION-A, 4, what is the value of cos , 5, , 1., , If sin =, , , , 2., 3., , Write the value of sin (45° + ) – cos (45° – )., If cos 9 = sin and 9 < 90°, then the value of tan 5 is, , 1, 1, , 1, (b) 3, (c) 1, (d) 0, 3, If sin A + sin2 A = 1, then the value of (cos2 A + cos4 A) is, , 1, , (a), 4., , (a) 1, , (b), , 1, 2, , (c) 2, , (d) 3, , SECTION-B, 5 sin – 3cos , 5 sin + 2cos , , 5., , If 5 tan = 4 then find the value of, , 6., , Find the value of tan 35° tan 40° tan 45° tan 50° tan 55°, , 2, , 7., , Prove that (sin + cos ) (tan + cot ) = sec + cosec , , 2, , 2, , SECTION-C, 8., , Prove that, , sin , 1 + cos , +, = 2 cosec , 1 + cos , sin , , 3, , 9., , Prove that, , cos A, sin 2 A, –, = sin A+ cos A, 1 – tan A cos A – sin A, , 3, , SECTION-D, 10. Prove that, 128, , cos , tan + sec – 1, =, ., tan – sec + 1 1 – sin , , 4, Mathematics-X
Page 145 :
CHAPTER, , Some Applications, of Trigonometry, , 9, KEY POINTS, , Angle of Elevation: Let AB, be height of object. C is the, observer looking upto to A (the, top of AB). AC is called the, line of sight and ACB is, angle of elevation., Angle of Depression : Let A, is the observer looking at C (the object) from a height BC. AC is line of sight, and BAC is angle of depression., A (Observer), , B, t, igh, of s, e, Lin, , C, , If the observer moves towards the object the angle of elevation increases and if, the observer moves away from the object, the angle of elevation decreases., Numerically, angle of elevation is equal to angle of depression (both are, measured with the same horizontal parallel planes)., VERY SHORT ANSWER TYPE QUESTIONS, , 1., , The length of the shadow of a tower on the plane ground is, height of the tower. The angle of elevation of sun is :, (a) 45°, , Mathematics-X, , (b) 30°, , (c) 60°, , 3 times the, , (d) 90°, 129
Page 146 :
2., , The tops of the poles of height 16 m and 10 m are connected by a wire of length, l metres. If the wire makes an angle of 30° with the horizontal, then l =, (a) 26 m, , 3., , 4., , 5., , 6., , 7., 8., , (b) 16 m, , (c) 12 m, , (d) 10 m, , A pole of height 6 m casts a shadow 2 3 m long on the ground. the angle of, elevation of the sun is, (CBSE 2017), (a) 30°, (b) 60°, (c) 45°, (d) 90°, A ladder leaning aginast a wall makes an angle of 60° with the horizontal. If, the foot of the ladder is 2.5 m away from the wall, then the length of the ladder, is —, (CBSE 2016), (a) 3 m, (b) 4 m, (c) 5 m, (d) 6 m, If a tower is 30 m high, casts a shadow 10 3 m long on the ground, then the, angle of elevation of the sun is:, (CBSE, 2017), (a) 30°, (b) 45°, (c) 60°, (d) 90°, A tower is 50 m high. When the sun’s altitude is 45° then what will be the, length of its shadow?, 50, m. find the sun’s altitude., 3, Find the angle of elevation of a point which is at a distance of 30 m from the, The length of shadow of a pole 50 m high is, base of a tower 10 3 m high., , 9., , A kite is flying at a height of 50 3 m from the horizontal. It is attached with a, string and makes an angle 60° with the horizontal. Find the length of the string., , 10. In the given figure find the perimeter of rectangle ABCD., D, , C, , 10 m, 30°, A, , 130, , B, , Mathematics-X
Page 147 :
SHORT ANSWER TYPE QUESTIONS, , 11. In the figure, find the value of BC., A, , D, 100 m, 80 m, 45°, , 60°, , B, , C, , E, , 12. In the figure, two persons are standing at the opposite direction P & Q of the, tower. If the height of the tower is 60 m then find the distance between the two, persons., A, , 60 m, 30°, , 45°, , P, , 13. In the figure, find the value of AB., , Q, , B, , A, , B, 60°, 45°, , D, , 14. In the figure, find the value of CF., , 1000 m, , C, , C, , B, , 45°, , D, , 5m, A, , Mathematics-X, , 20 m, , F, , 131
Page 148 :
15. If the horizontal distance of the boat from the bridge is 25 m and the height of, the bridge is 25 m, then find the angle of depression of the boat from the bridge., 16. If the length of the shadow of a tower is increasing, then the angle of elevation, of the sun is also increasing., (True / False), 17. If a man standing on the deck of a ship 3 m above the surface of sea observes a, cloud and its reflection in the sea, then the angle of elevation of the cloud is, equal to the angle of depression of its reflection., (True / False), 18. The string of a kite is 150 m long and it makes an angle 60° with the horizontal., Find the height of the kite above the ground. (Assume string to be tight), 19. The shadow of a vertical tower on level ground increases by 10 m when the, altitude of the sun changes from 45° to 30°. Find the height of the tower., (Use, , 3 = 1.73), , 20. An aeroplane at an altitude of 200 m observes angles of depression of opposite, points on the two banks of the river to be 45° and 60°, find the width of the, river., , (Use, , 3 = 1.732), , 21. The angle of elevation of a tower at a point is 45°. After going 40 m towards, the foot of the tower, the angle of elevation of the tower becomes 60°. Find the, height of the tower., , (Use, , 3 = 1.732), , 22. The upper part of a tree broken over by the wind makes an angle of 30° with, the ground and the distance of the foot of the tree from the point where the top, touches the ground is 25 m. What was the total height of the tree?, 23. A vertical flagstaff stands on a horizontal plane. From a point 100 m from its, foot, the angle of elevation of its top is found to be 45°. Find the height of the, flagstaff., 24. The length of a string between kite and a point on the ground is 90 m. If the, 3, string makes an angle with the level ground and sin . . Find the height, 5, of the kite. There is no slack in the string., 25. An aeroplane, when 3000 m high, passes vertically above another plane at an, instant when the angle of elevation of two aeroplanes from the same point on, the ground are 60° and 45° respectively. Find the vertical distance between the, two planes., 132, , (Use, , 3 = 1.732), , Mathematics-X
Page 149 :
26. A 7 m long flagstaff is fixed on the top of a tower on the horizontal plane. From, a point on the ground, the angle of elevation of the top and the bottom of the, flagstaff are 45° and 30° respectively. Find the height of the tower., (Use, , 3 = 1.732), , 27. From the top of a 7 m high building, the angle of elevation of the top of the, tower is 60° and the angle of depression of the foot of the tower is 45°. Find the, height of the tower., (CBSE 2020), 28. Anand is watching a circus artist climbing a 20m long rope which is tightly, stretched and tied from the top of vertical pole to the ground. Find the height of, the pole if the angle made by the rope with the ground level is 30°., LONG ANSWER TYPE QUESTIONS, , 29. A statue 1.6 m tall, stands on the top of a pedestal. From a point on the ground,, the angle of elevation of the top of the statue is 60° and from the same point the, angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal., (Use, , 3 = 1.73) (CBSE 2020), , 30. A man standing on the deck of a ship, 10 m above the water level observes the, angle of elevation of the top of a hill as 60° and angle of depression of the, bottom of the hill as 30°. Find the distance of the hill from the ship and height, of the hill., 31. From a window 60 m high above the ground of a house in a street, the angle of, elevation and depression of the top and the foot of another house on the opposite, side of the street are 60° and 45° respectively. Show that the height of opposite, house is 60(1 3) metres., 32. The angle of elevation of an aeroplane from a point A on the ground is 60°., After a flight of 30 seconds, the angle of elevation changes to 30°. If the plane, is flying at a constant height of 3600 3 m, find the speed in km/hour of the, plane., 33. A bird is sitting on the top of a tree, which is 80 m high. The angle of elevation, of the bird, from a point on the ground is 45°. The bird flies away from the, point of observation horizontally and remains at a constant height. After 2, seconds, the angle of elevation of the bird from the point of observation becomes, 30°. Find the speed of flying of the bird., Mathematics-X, , (Use, , 3 = 1.732), 133
Page 150 :
34. The angles of elevation of the top of a tower from two points on the ground at, distances 9 m and 4 m from the base of the tower are in the same straight line, with it are complementary. Find the height of the tower., 35. The angle of elevation of the top of a building from the foot of a tower is 30°., The angle of elevation of the top of the tower from the foot of the building is, 60°. If the tower is 60 m high, find the height of the building. (CBSE 2020), 36. An observer from the top of a light house, 100 m high above sea level, observes, the angle of depression of a ship, sailing directly towards him, changes from, 30° to 60°. Determine the distance travelled by the ship during the period of, observation., , (Use, , 3 = 1.732), , 37. The angles of elevation and depression of the top and bottom of a light house, from the top of a building 60 m high are 30° and 60° respectively. Find, (i) The difference between the height of the light house and the building., (ii) distance between the light house and the building., 38. A fire in a building ‘B’ is reported on telephone in two fire stations P an Q, 20, km apart from each other on a straight road. P observes that the fire is at an, angle of 60° to the road, and Q observes, that it is at an angle of 45° to the road., Which station should send its team to start the work at the earliest and how, much distance will this team has to travel?, 39. A 1.2m tall girl spots a balloon on the eve of Independence Day, moving with, the wind in a horizontal line at a height of 88.2 m from the ground. The angle, of elevation of the balloon from the girl at an instant is 60°. After some time,, the angle of elevation reduces to 30°. Find the distance travelled by the balloon., 40. The angle of elevation of the cloud from a point 10 m above a lake is 30° and, the angle of depression of the reflection of the cloud in the lake is 60°. Find the, height of the cloud from the surface of lake., (CBSE 2020), 41. Two pillars of equal heights stand on either side of a roadway 150 m wide., From a point on the roadway between the pillars, the angles of elevation of the, top of the pillars are 60° and 30°. Find the height of pillars and the position of, the point., (CBSE, 2011), 42. The angle of elevation of the top of tower from certain point is 30°. If the, observer moves 20 m towards the tower the angle of elevation of the top, increases by 15°. Find the height of the tower., 134, , Mathematics-X
Page 151 :
43. A moving boat is observed from the top of a 150 m high cliff moving away, form the cliff. The angle of depression of the boat changes form 60° to 45° in 2, minutes. Find the speed of the boat in m/h., , (Take, , 3 = 1.732), , 44. From the top of a 120 m high tower a man observes two cars on the opposite, sides of the tower and in straight line with the base of tower with angles of, depression as 60° and 45°. Find the distance between the cars., (Use, , 3 = 1.732), , 45. A vertical tower of height 20 m stands on a horizontal plane and is surmounted, by a vertical flag-staff of height h. At a point on the plane, the angle of elevation, of the bottom and top of the flag staff are 45° and 60° respectively. Find the, value of h., (CBSE 2020), 46. The rod AC of a TV disc antenna is fixed at right angles to the wall AB and a, rod CD is supporting the disc as shown in the figure. If AC = 1.5 m long and, CD = 3 m, find (i) tan (ii) sec + cosec ., , (CBSE 2020), , C, , A, , , D, B, , ANSWERS AND HINTS, , 1. (b), , 2. (c), , 3. (b), , 4. (c), , 5. (c), , 6. 50 m, , 7. 60°, , 8. 30°, , 9. 100 m, , 10. 20, , , , 3 1 m, , 11. 130 m, , 12. 60, , , , 3 1 m, , Mathematics-X, , , , , , 135
Page 152 :
13. 1000, , , , , , 3 –1 m, , 14. 25 m, , 15. 45°, , 16. False, , 17. False, , 18. 75 3 m, , 19. 13.65 m, , 20. 315.46 m, , 21. 94.64 m, , 22. 25 3 m, , 23. 100 m, , 24. 54 m, , 25. 1268 m, , 26. 9.562 m, , 27. 7( 3 1) m, , 28. 10 m, , 29. 2.184 m, , 30. 10 3 m, 40 m, , 32. 864 km/hr, , 33. 29.28 m, , 34. 6 m, , 35. 20 m, , 36. 115.46 m, , 37. 20 m, 20 3 m, , 38. Station P, 7.4 km (approx), , 39. 58 3m, , 40. 20 m, 41. height = 64.95 m, distance (Position) = 112.5 m from the pillar having angle, of elevation 60°, 42. 10( 3 1) m, , 43. 1902 m/h (approx.), , 44. 189.28 m, , 45. h = 20( 3 1) m, , 46. (i) tan =, , 1, 3, , (ii) sec + cosec =, , 136, , 2, 2, 3, , Mathematics-X
Page 153 :
PRACTICE-TEST, Some Applications of Trigonometry, , Time : 1 Hr., , M.M.: 20, SECTION-A, , 1., , A pole which is 6 m high cast a shadow 2 3 on the ground. What is the sun’ss, angle of elevation., , 1, , 2., , The height of a tower is 100 m. When the angle of elevation of sun is 30°, then, what is the shadow of the tower?, 1, , 3., , The angle of elevation of the sun, when the shadow of a pole h meters high is, 3 h is., , (a) 30°, 4., , (b) 45°, , (c) 60°, , (d) 90°, , 1, , An observer 1.5 metre tall is 20.5 metre away from a tower 22 metres high. The, angle of elevation of the top of the tower from the eye of the observer is,, (a) 30°, , (b) 45°, , (c) 60°, , (d) 0°, , 1, , SECTION-B, 5., , From a point on the ground 20 m away from the foot of a tower the angle of, elevation is 60°. What is the height of tower?, 2, , 6., , The ratio of height and shadow of a tower is 1:, of the sun?, , 7., , 137, , 1, .What is the angle of elevation, 3, 2, , The angle of elevation of the top of a tower is 30°. If the height of the tower is, tripled, then prove that the angle of elevation would be doubled., 2, , Mathematics-X
Page 154 :
SECTION-C, 8., , The tops of the two towers of height x and y standing on level ground, subtend, angles of 30° and 60° respectively at the centre of the line joining their feet,, then find x : y., 3, , 9., , The angle of elevation of the top of a rock from the top and foot of a 100 m high, tower are 30° and 45° respectively. Find the height of the rock., 3, SECTION-D, , 10, , 138, , A man standing on the deck of a ship, 10 m above the water level observes the, angle of elevation of the top of a hill as 60° and angle of depression of the base, of the hill as 30°. Find the distance of the hill from the ship and height of the, hill., 4, , Mathematics-X
Page 155 :
CHAPTER, , 10, , Circles, , KEY POINTS, , 1., , A circle is a collection of all those points in a plane which are at a constant, distance from a fixed point. The fixed point is called the centre and fixed, distance is called the radius., , 2., , Secant: A line which intesects a circle in two distinct points is called a secant, of the circle., , P, , 3., , Q, , Tangent: It is a line that intersects the circle at only one point. The point where, tangent touches the circle is called the point of contact., Here A is the point of contact., , Mathematics-X, , 139
Page 156 :
P, , A, , B, , 4., , Number of Tangent: Infinitely many tangents can be drawn on a circle., , 5., , Number of Secant: There are infinitely many secants which can be drawn to a, circle., , 6., , The proofs of the following theorems can be asked in the examination:–, (i) The tangent at any point of a circle is perpendicular to the radius through, the point of contact., (ii) The lengths of tangents drawn from an external point to a circle are equal., , 7., , The tangent to a circle is a special case of the secant., , 8., , There is no tangent to a circle passing through a point lying inside the circle., , 9., , There is one and only one tangent to a circle passing through a point lying on, the circle., , 10. There are exactly two tangents to a circle through a point lying outside the, circles., VERY SHORT ANSWER TYPE QUESTIONS, , 1., , In fig., ABC is circumscribing a circle. Find the length of BC., A, , 9 cm, , 3 cm, , M, , N, , 6 cm, , 4 cm, B, , 140, , L, , C, , Mathematics-X
Page 157 :
2., , The length of the tangent to a circle from a point P, which is 25 cm away from, the centre, is 24 cm. What is the radius of the circle., , 3., , In fig., ABCD is a cyclic quadrilatreral. If BAC = 50° and DBC = 60°,, then find BCD., , C, , D, , 60 °, 50°, , A, , 4., , B, , In figure, O is the centre of a circle, PQ is a chord and the tangent PR at P, makes an angles of 50° with PQ. Find POQ., P, , R, 50°, , O, Q, , 5., , If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm,, then find the length of each tangent., , 6., , If radii of two concentric circles are 4 cm and 5 cm, then find the length of the, chord of that circle which is tangent to the other circle., , 7., , In the given figure, PQ is tangent to outer circle and PR is tangent to inner, circle. If PQ = 4cm, OQ = 3 cm and OR = 2 cm then find the length of PR., Q, , P, , O, R, , Mathematics-X, , 141
Page 158 :
8., , In the given figure, O is the centre of the circle, PA and PB are tangents to the, circle then find AQB., (CBSE 2016), , 9., , In the given figure, If AOB = 125° then find COD., B, , A, 125°, O, , D, , C, , 10. If two tangent TP and TQ are drawn from an external point T such that, TQP = 60° then find OPQ., P, , T, , O, 60°, Q, , 11. How many tangents can a circle have?, 12. A tangent to a circle intersects it in _________ point., 13., , If PQ is a tangent then find the value of POQ + QPO ., 142, , Mathematics-X
Page 159 :
14. Choose the correct Answer., A tangent PQ at a point P of a circle of radius 5 cm meets a line through the, centre O at a point Q so that OQ = 12 cm. Length PQ is :, (a) 12 cm, , (b) 13 cm, , (c) 8.5 cm, , (d), , 119 cm, , 15. A circle can have _______ parallel tangents at the most., 16., , The common point of a tangent to a circle and radius of the circle is called, ________., SHORT ANSWER TYPE QUESTIONS, , 17. If diameters of two concentric circles are d1 and d2 (d2 > d1) and c is the, length of chord of bigger circle which is tangent to the smaller circle. Show, that d22 = c2 + d12., 18. The length of tangent to a circle of radius 2.5 cm from an external point P is 6, cm. Find the distance of P from the nearest point of the circle., 19. TP and TQ are the tangents from the external point T of a circle with centre O., If OPQ = 30° then find the measure of TQP., 20. In the given fig. AP = 4 cm, BQ = 6 cm and AC = 9 cm. Find the semi perimeter, of ABC., A, m, 4c, , R, , C, , P, , Q, , 6 cm, , B, , 21. A circle is drawn inside a right angled triangle whose sides are a, b, c where c, is the hypotenuse, which touches all the sides of the triangle. Prove, r=, , a+b–c, where r is the radius of the circle., 2, , Mathematics-X, , 143
Page 160 :
22. Prove that the tangent at any point of a circle is perpendicular to the radius, through the point of contact., 23. Prove that in two concentric circles the chord of the larger circle which is, tangent to the smaller circle is bisected at the point of contact., 24. In the given Fig., AC is diameter of the circle with centre O and A is the point, of contact, then find x., C, x, B, , O, 40°, , P, , A, , Q, , 25. In the given fig. KN, PA and PB are tangents to the circle. Prove that:, KN = AK + BN., , 26. In the given fig. PQ is a chord of length 6 cm and the radius of the circle is 6, cm. TP and TQ are two tangents drawn from an external point T. Find PTQ., P, , T, , O, , Q, , 144, , Mathematics-X
Page 161 :
LONG ANSWER TYPE QUESTIONS, , 27. In the given figure find AD, BE, CF where AB = 12 cm, BC = 8 cm and, AC = 10 cm., C, , E, , F, , A, , B, , D, , 28. Two tangents PA and PB are drawn to a circle with centre O from an external, point P. Prove that APB = 2 OAB, (NCERT, Exemplar), A, , O, , P, , B, , 29. In the given fig. OP is equal to the diameter of the circle with centre O. Prove, that ABP is an equilateral triangle., A, , o, , P, , B, , Mathematics-X, , 145
Page 162 :
30. In the given fig., find PC. If AB = 13 cm, BC = 7 cm and AD = 15 cm., A, , R, B, O, , S, C, , 4 cm, Q, , D, , P, , 31. In the given figure, find the radius of the circle., A, , cm, 23, , R, B, 29 cm, , 5 cm, , O, , S, , C, , r, , Q, , D, , P, , 32. In the given fig. PQ is tangent and PB is diameter. Find the values of angles x, and y., P, y, A, , o, , x, , y, , Q, , 35°, B, , 146, , Mathematics-X
Page 163 :
33. In given figure, two circles touch each other at the point C. Prove that the, common tangent to the circles at C, bisects the common tangent at P and Q., , P, T, , A, , Q, , C, B, , 34. In the given figure, a circle touches all the four sides of a quadrilateral ABCD., If AB = 6 cm, BC = 9 cm and CD = 8 cm, then find the length of AD., C, , D, , B, , A, , 35. In figure, PA is a tangent from an external point P to a circle with centre O, If, POB = 115°. Find APO., A, O, , P, 115°, , B, , 36. Prove that the angle between the two tangents drawn from an external point to, a circle is supplementary to the angle subtended by the line segment joining, the points of contact at the centre., , Mathematics-X, , 147
Page 164 :
37. In figure, XP and XQ are tangents from X to the circle with centre O, R is a, point on the circle and AB is tangent at R. Prove that :, XA + AR = XB + BR, , 38. In the given figure, find the perimeter of ABC, if AP = 12 cm., , A, , B, P, , D, , C, Q, , 39. In the given figure, a quardrilateral ABCD is drawn to circumscribe a circle., Prove that AB + CD = BC + AD, A, , D, , B, , C, , 40. Prove that the tangents drawn at the ends of a diameter of a circle are parallel., , 148, , Mathematics-X
Page 165 :
ANSWERS AND HINTS, , 1. Since length of both the tangents from a point outside the circle is equal, So, BN = BL, CM = CL, BL + CL = BC = 10 cm, , 2., , By Pythagoras Theorem, QR = 7 cm., 3. Angle in the same segment are euqal., DC is the chord so DAC = DBC = 60°., The sum of the opposite angles of a cyclic quadrilateral is 180°., So BCD = 70°, 4. The tangent at any point of a circle is perpendicular to the radius through the, point of contact., RPO = 90°, OPQ = OQP = 40°, POQ = 100°, , So,, Q, 3 cm, , 60°, , O, 3 cm, , 5., , R, , , In QPO,, , P, , QPO RPO, 60, 30, 2, OQP = 90°(Tangent is perpendicular at the point of contact)., , QPO = RPO , , tan 30° =, , Mathematics-X, , OQ, QP, , QP = 3 3 cm, , 149
Page 166 :
6., , In AOP, right angled at P., OA2 = AP2 + OP2, , , AP = 3, , , , AB = 6 cm, (4)2 + (3)2 = (OP)2, , 7. In PQO, , (5)2 = AP2 + 42, , AP2 = 9, , ( OP AB so OP bisects AB), , 5 = OP, (5)2 = (2)2 + (PR)2, , In PRO,, , PR =, , 21 cm, , A, 4, , 8., , Q, , 5, , O, , 3, , 40°, , 1, , P, , 2, B, , In Quadrilateral OAPB, 1 + 2 + 3 + 4 =, 1 + 3 =, 3 =, 3 =, Now,, 5 =, , 9., , 360°, 180°, 140°, 2 5, 70° or AQB = 70°, , 1 2 , 3 4 , 5 6 (CPCT) of their corresponding triangles., , 7 8, , °, , 2 ( 2 3 6 7) =360°, , or AOB + COD = 180°, , 6, , or COD = 55°, 150, , Mathematics-X
Page 167 :
OQT = 90° (Angle between tangent & radius), PQO = 30°, PQO = OPQ = 30°, 11. Infinitely many, , 10., , 12. One, 13. 90°, 14. d( 119 cm), 15. Two, 16. Point of Contact, 17., , AB = c, AO2 = OP2 + AP2, 2, , 2, d2 , d , = 1 AP 2, 2, 2, 2, , 2, , d2 , d1 , = AP2, 2, 2, , 1, 2, 2, (d 2 ) (d1) , 4, 2, , = AP, , 1, 2, 2, (d 2 ) (d1 ) = AB, 4, , (d 2 )2 (d1 )2 = c, 2, (d 2 )2 (d1 )2 = c, d 2 2 = c2 + d 2, 1, , 18., , Mathematics-X, , 151
Page 168 :
(OP)2 = (OT)2 + (PT)2, (OP)2 = (2.5)2 + (6)2, = 42.25, (OP)2 = (6.5)2, , OP = 6.5 cm, , QP = 4 cm, 19., , OQP = OPQ = 30°, OQT = 90° (Angle between radius and tangent), TQP = OQT – OQP, = 90° – 30° = 60°, 20., , AP = AR = 4 cm, CR = CQ = (9 – 4) cm = 5 cm, Semi perimeter =, =, , 1, [AC + AB + BC], 2, , 1, 9 10 11 = 15 cm, 2, A, , 21., c, b, , F, o, , B, , 152, , a, , D, , r, , E, , C, , Mathematics-X
Page 169 :
b – r = AF, a – r = BF, AB = c = AF + BF = b – r + a – r, , or,, This gives,, , r=, , a+b–c, 2, , 23. Join OP, AB is tangent to circle C1 at P and OP is radius, , C1, , OP AB, , C2, , O, , AB is chord of circle C2 and OP AB., Therefore OP is the bisector of the chord AB as the, perpendicular from the centre bisects the chord i.e,, , A, , P, , B, , AP = BP, OAB = 50°, , 24., , x + B + OAB = 180°, x + 90° + 50° = 180°, x = 40°, 25., , AK = KC, BN = NC, , , 26., , KN = KC + NC =AK + BN, POQ + PTQ = 180°, 60° + PTQ = 180°, PTQ = 120°, , 27., , AC = AF + FC = 10 cm …(1), AB = AD + DB = 12 cm …(2), BC = BE + CE = 8 cm, , …(3), , BD = BE , AD = AF , CF = CE , , , , …(4), , AC = AD + FC = 10 cm …(5), AB = AD + DB = 12 cm …(6), BC = BD + CF = 8 cm …(7), Mathematics-X, , 153
Page 170 :
Add (5, 6, 7), 2(AD + FC + DB) = 30, AD + FC + DB = 15, Substitute values from (1), (2) & (3), and find. AD = 7 cm, BE = 5 cm, CF = 3 cm., A, 28., PA = PB, 2, 1, O, 4, So,, 2 = 3 = (180 1), 3, 2, 1, P, 1, B, 2 = 3 = 90 1, 2, 4 = 90° (Angle between tangent & Radius), OAB = 4 – 2, 1 , , = 90 90 1, 2, 1, , OAB = APB, 2, OAB = APB, 29., OP = 2r, , OQ = QP = r, A, , O, , Q, , P, , B, , Consider AOP in which OA AP and OP is the hypotenuse., OQ = AQ = OA, (Mid point of hypotenuse is equidistance from the vertices)., OAQ is an equilitateral triangle., , , AOQ = 60°, , Consider right angled triangle OAP, AOQ = 60°, OAP = 90°, , APO = 30°, , APB = APO = 2 × 30° = 60°, PA = PB (tangents), 154, , Mathematics-X
Page 171 :
, , PAB = PBA, APB = 60°, PAB = PBA =, , 180 60, 60, 2, , ABP is an equilateral triangle., 30. PC = 5 cm, 31. 11 cm, 32., , In ABP,, 1 =, 1 + 35° + y =, 90° + 35° + y =, y =, OPQ,, 2 =, 2 + x + y =, 90° + x + =, x =, 34. AD = 5 cm, 35. 25°, 38. 24 cm, , Mathematics-X, , 90°, 180°, 180°, 55°, 90°, 180°, 180°, 35°, , (Angle in semi-circle), , (Angle between tangent and radius), , 155
Page 172 :
PRACTICE-TEST, CIRCLES, , Time : 1 Hr., , M.M.: 20, SECTION-A, , 1., , In the given figure find x, where ST is the tangent., , 1, , T, x-40°, , x, , S, , O, , 2., , In the given figure if AC = 9 cm, find BD., B, , A, , 1, , C, , D, , 3., , In the given figure, ABC is circumscribing a circle, then find the length of, BC., 1, , 3c, m, , A, , M, , N, 4c, m, , 8 cm, , B, , 4., , 156, , L, , C, , From the external point P, tangents PA and PB are drawn to a circle with centre, O. If PAB = 50°, then find AOB., 1, , Mathematics-X
Page 173 :
SECTION-B, 5., , If the angle between two tangents drawn from an external point P to a circle of, radius a and centre O is 60° then find the length of OP. (All India 2017) 2, , 6., , In the following figure find x., , 7., , Two concentric circle with centre O are of radii 6 cm and 3 cm. From an external, point P, tangents PA and PB are drawn to these circle as shown in the figure. If, AP = 10 cm. Find BP, 2, , 2, , A, , o, , P, , SECTION-C, 8., , In the given figure, AB is a tangent to a circle with centre O. Prove, BPQ = PRQ., 3, R, , O, , Mathematics-X, , A, , Q, , P, , B, , 157
Page 174 :
9., , In the given figure ABC is drawn to circumscribe a circle of radius 3 cm,, such that the segment BD and DC into which BC is divided by the point of, contact D are of length 6 cm and 8 cm respectively, find side AB if the ar(ABC), = 63 cm², 3, A, , E, , F, , B, 6 cm, , D, , 8 cm, , C, , SECTION-D, 10. AB is a diameter of a circle with centre O and AT is a tangent. If AOQ = 58°, find ATQ., 4, , 158, , Mathematics-X
Page 175 :
CHAPTER, , 11, , Constructions, , TOPICS, , Division of a line segment., Construction of a Triangle., Construction of Tangents of a Circle., MIND MAPING, , KEY POINTS, , 1., , Construction should be neat and clean and there should be no doubling., , 2., , Construction should be as per a given scale factor which may be less than 1 or, greater than 1 for a triangle similar to a given triangle., , 3., , Steps of construction should be provided only when it is mentioned in the, question., , Mathematics-X, , 159
Page 176 :
4., , We make use of compass and ruler only for angles which are multiple of 15°, but in case of non-standard angles, protractor can be used., , 5., , Divide a line segment in the given ratio means to determine a point on the, given line segment which divides it in the the given ratio., , 6., , A tangent to a circle is a straight line which touches the circle at exactly one, point. This point is called the point of contact and the radius through the point, of contact is perpendicular to the tangent., , 7., , Tangents drawn from an external point to a circle are equal., VERY SHORT ANSWER TYPE QUESTIONS, , 5, of the, 3, corresponding sides of ABC, a ray BX is drawn such that CBX is an acute, angle and X is on the opposite side of A with respect to BC. What is the minimum, no. of points to be located at equal distances on ray BX., , 1., , Construct a triangle similar to a given ABC with its sides, , 2., , Draw a pair of tangents to a circle which are inclined to each other at an angle, of 30°. What should be the angle between two radii?, , 3., , Construct a triangle similar to a given ABC with its sides, , 4., , Divide a line segment AB in the ratio 3:7. What is the minimum number of, points marked on a ray AX at equal distances?, , 5., , How many tangents can be drawn from a point lying inside a circle?, , 6., , Divide a line segment AB in the ratio 4:5, a ray AX is drawn first such that, BAX is an acute angle and then points A1, A2, A3, ........ are located at equal, distances on the ray AX which should be joined to B?, , 7., , Divide a line segment AB in the ratio 4:5, the points A1, A2, A3,....and B1, B2,, B3,.... are located at equal distances on the ray AX and BY respectively. Which, two points should be joined to divide a line segment?, , 160, , 2, of the, 5, corresponding sides of ABC , firstly a ray BX is drawn such that CBX is an, acute angle and X lies on the opposite side of A with respect to BC then points, B1, B2, B3, B4, B5 are located on BX at equal distances Which two points will, be joined in the next step., , Mathematics-X
Page 177 :
8., 9., , Draw a line segment of length 6 cm. Find a point P on it which divides it in the, ratio 3 : 4., (Delhi-2011), Draw a line segment AB = 8 cm and divide it internally in the ratio 3 : 2., , 10. Draw a line segment AB of length 6.5 cm. Find a point P on it such that, , AP 3, , AB 5, , 11. Geometrically divide a line segment of length 8.4 cm in the ratio 5 : 2., (Foreign–2011), 12. Draw a line segment of length 7.6 cm and divide it in the ratio 3 : 2., (Foreign – 2011), 13. Write True or False., By geometrical construction, it is possible to divide a line segment in the ratio, 3:, , 14., , 1, ., 3, , (NCERT Exampler), , Is it possible to construct a pair of tangents from point P to circle of radius 5, cm situated at a distance of 4.9 cm from the centre?, , 15. Is it possible to construct a pair of tangents from point A lying on the circle of, radius 4 cm and centre O., 16. Compare the length of the tangents drawn from the external point to circle., LONG ANSWER TYPE QUESTIONS, , 17. AB is a line segment of length 8 cm. Locate a point C on AB such that AC =, , 1, CB., 3, , 18. Construct a ABC in which AB = 6.5 cm, B = 60° and BC = 5.5 cm. Also, 3, construct a triangle ABC similar to ABC, whose each side is, times the, 2, corresponding sides of ABC., 19. Construct a ABC in which BC = 5 cm, CA = 6 cm and AB = 7. Construct a, ABC similar to ABC, each of whose side are times, , 7, the corresponding, 5, , sides of ABC., , Mathematics-X, , 161
Page 178 :
20. Construct a triangle with side 4 cm, 5 cm, 6 cm. Then construct a triangle, 2, similar to it whose sides are of the corresponding sides of the given triangle., 3, (NCERT), 21. Construct a ABC in which BC = 8 cm, B = 45° cm and C = 30°. Construct, another triangle similar to ABC such that each side are, , 3, of the corresponding, 4, , sides of ABC, 22. A triangle ABC is given such that AB = 4 cm, BC = 7 cm and BAC = 50°., Draw another triangle ABC similar to ABC with sides BA and BC equal to, 6 cm and 10.5 cm respectively. Find the scale factor., 23. Construct an isosceles ABC in which AB = 8 cm and attitude CD = 4 cm., Construct another triangle similar to ABC where sides are 1.5 times that of, the corresponding sides of isosceles ABC., 24. Draw an isosceles ABC with AB=AC and base BC=7cm, vertical angle is, 1, 120°. Construct AB´C´ ~ABC with its sides 1 times of the corresponding, 3, , sides of ABC., 25. Draw a circle of radius 3 cm. From a point 5 cm from the centre of the circle,, draw two tangents to the circle. Measure the length of each tangent., 26. Draw a circle of radius 4 cm with centre O. Draw a diameter POQ. Through P, or Q draw a tangent to the circle., 27. Draw two circle of radius 5 cm and 3 cm with their centres 9 cm apart. From, the centre of each circle, draw tangents to other circles., 28. Draw two concentric circles of radii 6 cm and 4 cm. From a point on the outer, circle, draw a tangent to the inner circle and measure its length., 29. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended, diameter each at a distance of 7 cm from its centre. Draw tangents to the circle, from these two points., , 162, , Mathematics-X
Page 179 :
30. Draw a line segment PQ = 10 cm. Take a points A on PQ such that, , PA, 2, =, PQ, 5, , Measure the length of PA and AQ, 31. Draw an equilateral triangle PQR with side 5cm. Now construct PQ´R´ ~, PQ, 1, PQR such that, = ., PQ ' 2, 32. Draw a line segment AB of length 7 cm. Taking A as centre draw a circle of, radius 3 cm and taking B as centre draw another circle of radius 2 cm. Construct, tangents to each circle from the centre of other circle., (CBSE 2020), 33. Draw a ABC with BC = 6 cm, AB = 5 cm and ABC = 60°. Then construct, 3, of the corresponding sides of ABC., 4, (CBSE 2018), 34. Draw a ABC with side BC = 7 cm, B = 45°, A = 105°. Then construct, , a triangle whose sides are, , 3, times the corresponding sides of ABC., 4, (CBSE 2017), 35. Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at angle, of 60° to each other., (CBSE 2016), 36. Construct a ABC in which AB = 6 cm, A = 30° and B = 60°. Construct, another ABC similar to ABC with base AB = 8 cm., (CBSE 2015), 37. Write the steps of construction of ABC in which BC = 6.5 cm, B = 60° and, C = 45°. Again write the steps of construction of another triangle whose, , another triangle whose sides are, , 4, of the corresponding sides of ABC. (CBSE 2020, Standard), 5, 38. Draw an equilateral triangle of side length 7 cm. Then construct a triangle, , sides are, , 2, of the corresponding sides of ABC., 3, (CBSE 2020, Standard and Basic), 39. Draw a circle of radius 2.5 cm. Take a point P outside the circle at a distance of, 7 cm from the centre. Then construct a pair of tangents to the circle from point, P., (CBSE 2020, Standard), , whose sides are, , Mathematics-X, , 163
Page 181 :
B, , P, , 8. A, A1, , A2, , A3, , R, , 9. P, P1, , P2, , P3, , A4, , A5, , A6, , X, A7, , Q, , P4, , P5, X, , 10. Similar to Example 1 (NCERT), 11. As above Question-9., 12. As above question No. 9., 13. True as 3 :, , 1, can be simplified as 3 : 1., 3, , 14. No, 15. No, 16. Equal., Questions No. 17 to 39., Questions are similar to examples given in NCERT. Please refer NCERT, example., , Mathematics-X, , 165
Page 182 :
PRACTICE-TEST, CONSTRUCTIONS, , Time : 1 Hrs., , M.M.: 20, SECTION-A, , 1., , Draw a perpendicular bisector of line segment AB = 8cm., , 1, , 2., , Draw a line parallel to a given line., , 1, , 3., , Draw the tangent to a circle of diameter 4 cm at a point P on it., , 1, , 4., , Draw two tangents to a circle of radius 4 cm from a point T at a distance of 6, cm from its centre., 1, SECTION-B, , 5., , Draw a pair of tangents to a circle of radius 5 cm, which are inclined to each, other at an angle of 60°., (Foreign - 2014) 2, , 6., , Draw an angle bisector of 75°., , 2, , 7., , Draw a line segment of 5.6cm. Divide it in the ratio 2:3., , 2, , SECTION-C, 8., , Draw two tangents to a circle of radius 3.5cm from a point P at a distance of, 5.5cm from its centre. Measure its length., 3, , 9., , Draw a circle of radius 3.5cm. Draw two tangents to the circle such that they, include an angle of 120°., 3, SECTION-D, , 10. Construct a ABC of sides AB = 4cm, BC = 5cm and AC = 7 cm. Construct, another triangle similar to ABC such that each of its sides is, corresponding sides of ABC., , Mathematics-X, , 5, of the, 7, , 4, , 166
Page 183 :
CHAPTER, , 12, , Areas Related to Circles, , TOPICS, , Perimeter and Area of a circle., Area of sector and segment of a circle., MIND MAPING, , KEY POINTS, , Circle: A circle is the locus of a point which moves in a plane in such a way, that its distance from a fixed point always remains the same. The fixed point is, called the centre and the constant distance is known as the radius of the circle., Mathematics-X, 167
Page 184 :
If r is radius of a circle, then, (i), , Circumference = 2r or d where d = 2r is the diameter of the circle, , (ii), , Area = r2 or, , d 2, 4, , (iii) Area of semi circle =, , r2, 2, , (iv) Area of quadrant of a circle =, , r2, , 4, Area enclosed by two concentric circles: If R and r are radii of two concentric, circles, then area enclosed by the two circles =R2 – r2, , = (R2 – r2), r, R, , = (R + r) (R – r), , (i) If two circles touch internally, then the distance between their centres is, equal to the difference of their radii., (ii) If two circles touch externally, then distance between their centres is equal, to the sum of their radii., (iii) Distance covered by rotating wheel in one revolution is equal to the, circumference of the wheel., (iv) The number of revolutions completed by a rotating wheel in, one minute =, , Distance moved in one minute, Circumference of the wheel, , Segment of a Circle: The portion (or part) of a circular, region enclosed between a chord and the corresponding arc, is called a segment of the circle. In adjacent fig. APB is, minor segment and AQB is major segment., , Q, Major, segment, O, , B, or nt, in e, M egm, P, s, , A, , 168, , Mathematics-X
Page 185 :
Area of segment APB = Area of the sector OAPB – Area of OAB, Q, , O, , , A, , B, , P, , Sector of a circle: The portion (or part) of the circular region enclosed by the, two radii and the corresponding arc is called a sector of the circle., In adjacent figure OAPB is minor sector and OAQB is the major sector., Q, Major, sector, O, , A, , Area of the sector of angle =, =, , Minor, scetor, , P, , B, , , × r2, 360°, 1, 1, × length of arc × radius = lr, 2, 2, , Length of an arc of a sector of angle =, , , × 2r, 360, , (i) The sum of the arcs of major and minor sectors of a circle is equal to the, circumference of the circle., (ii) The sum of the areas of major and minor sectors of a circle is equal to the, area of the circle., (iii)Angle described by minute hand in 60 minutes = 360°, Angle described by minute hand in one minute =, , 360°, = 6°, 60, , Thus minute hand rotates through an angle of 6° in one minute, Mathematics-X, , 169
Page 186 :
(iv)Angle described by hour hand in 12 hours = 360°, Angle described by hour hand in one hour =, , 360°, = 30°, 12, , Angle described by hour hand in one minute =, , 30° 1 , = , 60, 2, , 1 , Thus, hour hand rotates through an angle of in one minute., 2, VERY SHORT ANSWER QUESTIONS, , 1., , If the diameter of a semi circular protactor is 14 cm, then find its perimeter., , 2., , If circumference and the area of a circle are numerically equal, find the diameter, of the circle., , 3., , Find the area of the circle ‘inscribed’ in a square of side a cm., , 4., , Find the area of a sector of a circle whose radius is r and length of the arc is l., , 5., , The radius of a wheel is 0.25 m. Find the number of revolutions it will make to, travel a distance of 11 kms., , 6., , If the area of a circle is 616 cm², then what is its circumference?, , 7., , What is the area of the circle that can be inscribe in a square of side 6 cm?, , 8., , What is the diameter of a circle whose area is equal to the sum of the areas of, two circles of radii 24 cm and 7 cm?, , 9., , A wire can be bent in the form of a circle of radius 35 cm. If it is bent in the, form of a square, then what will be its area?, , 10. What is the angle subtended at the centre of a circle of radius 6 cm by an arc of, length 3 cm?, 11. Write the formula for the area of a sector of angle (in degrees) of a circle of, radius r., 12. If the circumference of two circles are in the ratio 2:3, what is the ratio of their, areas?, 13. If the difference between the circumference and radius of a circle is 37 cm,, 22, then find the circumference of the circle. ( Use =, ), 7, Mathematics-X, 170
Page 187 :
14. If diameter of a circle is increased by 40%, find by how much percentage its, area increases?, 15. The minute hand of a clock is 6 cm long. Find the area swept by it between, 11:20 am and 11:55 am., 16. The perimeter of a sector of a circle of radius 14 cm is 68 cm. Find the area of, the sector., (CBSE 2020), 17. The circumference of a circle is 39.6 cm. Find its area., 22, ) (CBSE 2020), 7, 18. The length of the minute hand of a clock is 14 cm. Find the area swept by the, , (Use =, , minute hand in one minute., , (Use =, , 22, ), 7, , 19. Area of a sector having length of corresponding arc ‘l’ and radius ‘r’ is ______., 20. Circumference of a circle of radius s is ___________ ., 21. Area of a circle of radius is _______ ,, 22. Length of an arc of a sector of a circle with radius r and angle is _______ ., 23. Area of a sector with radius r and angle with degrees measure is _______ ., 24. Area of segment of a circle = Area of the corresponding sector ________ ., SHORT ANSWER TYPE QUESTIONS (1), , 25. Find the area of a quadrant of a circle whose circumference is 22 cm., 22, ), 7, 26. What is the angle subtended at the centre of a circle of radius 10 cm by an arc, of length 5 cm?, , (Use =, , 27. If a square is inscribed in a circle, what is the ratio of the area of the circle and, the square?, 28. Find the area of a circle whose circumference is 44 cm., , (CBSE 2020), , 29. If the perimeter of a circle is equal to that of square, then find the ratio of their, areas., , Mathematics-X, , 171
Page 188 :
30. What is the ratio of the areas of a circle and an equilateral triangle whose, diameter and a side are respectively equal?, 5, 31. In fig., O is the centre of a circle. The area of sector OAPB is, of the area of, 18, the circle. Find x., , O, x, A, , B, P, , 32. Find the perimeter of the given fig, where AED is a semicircle and ABCD is a, rectangle., (CBSE 2015), 20 cm, , 14 cm, , B, , A, , E, , C, , D, , 20 cm, , 33. In fig. OAPBO is a sector of a circle of radius 10.5 cm. Find the perimeter of, the sector., P, B, , A, , 60°, O, , 34. In the given fig, APB and CQD are semi circles of diameter 7 cm each, while, ARC and BSD are semicircles of diameter 14 cm each. Find the perimeter of, 22, the shaded region. (Use =, ), (Delhi, 2011), 7, , 172, , Mathematics-X
Page 189 :
R, , P, 7 cm, , A, , 7 cm, , 7 cm, D, , C, , B, , Q, , S, , SHORT ANSWER TYPE II QUESTIONS, , 35. Area of a sector of a circle of radius 36 cm is 54cm2 . Find the length of the, corresponding arc of the sector., 36. The length of the minute hand of a clock is 5 cm. Find the area swept by the, minute hand during the time period 6:05 am to 6:40 am., 37. In figure ABDC is a quadrant of a circle of a radius 28 cm and a semi circle, BEC is drawn with BC as diameter find the area of shaded region:, 22 , , Use , 7 , , B, , D, , A, , E, , C, , 38. In fig, OAPB is a sector of a circle of radius 3.5 cm with the centre at O and, AOB = 120°. Find the length of OAPBO., P, , O, 120°, A, , B, , 39. Circular footpath of width 2 m is constructed at the rate of ` 20 per square, meter, around a circular park of radius 1500 m. Find the total cost of construction, of the foot path. (Take = 3.14 ), Mathematics-X, , 173
Page 190 :
40. A boy is cycling such that the wheels of the cycle are making 140 revolutions, per minute. If the diameter of the wheel is 60 cm. Calculate the speed of cycle., 41. In a circle with centre O and radius 4 cm, and of angle 30°. Find the area of, minor sector and major sector AOB., (Use = 3.14), 42. Find the area of the largest triangle that can be inscribed in a semi circle of, radius r unit., (NCERT Exemplar), 43. Figure ABCD is a trapezium of area 24.5 cm, In it AD||BC, DAB = 90°, AD, = 10 cm, BC= 4cm. If ABE is a quadrant of a circle. Find the area of the shaded, 22 , , Use , 7 , , , region., E, , D, , B, , C, , 44., , A, , From each of the two opposite corners of a square of side 8 cm, a quadrant of a, circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from, the centre as shown in fig. Find the area of the shaded portion. (Use =, , 22, )., 7, , 45. A sector of 100° cut off from a circle contains area 70.65 cm². Find the radius, of the circle., (Use = 3.14 ), 46. In fig. ABCD is a rectangle with AB= 14 cm and BC= 7 cm. Taking DC, BC, and AD as diameter, three semicircles are drawn. Find the area of the shaded, portion., D, , C, 7 cm, , 174, , A, , 14 cm, , B, , Mathematics-X
Page 191 :
47. A square water tank has its each side equal to 40 m. There are four semi circular, grassy plots all around it. Find the cost of turfing the plot at Rs 1.25 per sq. m., (Use = 3.14 ), 48. Find the area of the shaded region shown in the fig., , (NCERT – Exemplar), , 8m, 4m, , 6m, , 49. Find the area of the minor segment of a circle of radius 21 cm, when the angle, of the corresponding sector is 120°., 50. A piece of wire 11 cm long is bent into the form of an arc of a circle subtending, an angle of 45° at its centre. Find the radius of the circle., 51. Find the area of the shaded region., , 16 cm, 44 cm, , 52. In fig. from a rectangular region ABCD with AB= 20 cm, a right triangle AED, with AE= 9 cm and DE= 12 cm, is cut off. On the other end, taking BC as, diameter, a semi circle is added on outside the region. Find the area of the, shaded region., 22 , , Use , 7 , , B, , A, 9 cm, 90°, , E, , 15 cm, , 12 cm, D, , C, , 53. The circumference of a circle exceeds the diameter by 16.8 cm. Find the radius, of the circle., Mathematics-X, , 175
Page 192 :
54. Find the area of the shaded region., , (NCERT Exemplar), 4m, 3m, , 3m, , 12 m, , 4m, 26 m, , LONG ANSWER TYPE QUESTIONS, , 55. Two circles touch externally. The sum of their areas is 130 sq. cm and the, distance between their centres is 14 cm. Find the radii of the circles., 56. Three circles each of radius 7 cm are drawn in such a way that each of them, touches the other two. Find the area enclosed between the circles., 57. Find the number of revolutions made by a circular wheel of area 6.16 m² in, rolling a distance of 572 m., 58. All the vertices of a rhombus lie on a circle. Find the area of the rhombus, if, area of the circle is 2464 cm²., 59. With vertices A, B and C of a triangle ABC as centres, arcs are drawn with, radius 6 cm each in fig. If AB= 20 cm, BC= 48 cm and CA= 52 cm, then find, 22 , , Use , , 7 , , , the area of the shaded region., A, 52 cm, 20 cm, , B, , 48 cm, , C, , 60. ABCDEF is a regular hexagon. With vertices A, B, C, D, E and F as the centres,, circles of same radius ‘r’ are drawn. Find the area of the shaded portion as, shown in the given figure., , 176, , Mathematics-X
Page 193 :
A, , B, , C, , F, , E, , D, , 61. ABCD is a diameter of a circle of radius 6 cm. The lengths AB, BC and, CD are equal. Semicircles are drawn on AB and BD as diameter as shown, in the fig. Find the perimeter and area of the shaded region., 22 , , Use , 7 , , A, , B, , C, , D, , 62. A poor artist on the street makes funny cartoons for children and earns, his living. Once he made a comic face by drawing a circle within a circle,, the radius of the bigger circle being 30 cm and that of smaller being, 20 cm as shown in the figure. What is the area of the cap given in this, figure?, , Cap, , 63. In the given figure ABCD is a trapzium with, AB || DC, AB = 18 cm, DC = 32 cm and, distance between AB and DC is 14 cm. If arc, of equal radii 7 cm with centres A B, C and D, have been drawn, then find the area of shaded, 22 , , region. Use , 7 , , Mathematics-X, , 177
Page 194 :
64. Find the area of the shaded region as shown in the given figure., 22 , , Use , 7 , , , 20 cm, 7 cm, , ANSWERS AND HINTS, , 22, 7 14 = 36 cm, 7, , 1., , r + d =, , 2., , 2r = r2 diameter = 4 units, , 3., , Side of the square is equal to diameter of the circle,, 2, , r = , , a, a2, (side = a, radius = ), 2, 4, , lr, , , l r 2, 2 r , Area =, r 2 =, =, sq. units, 2, 360, 360, 2 r, , 4., , l=, , 5., , distance, 11 1000 7 100, , = 7000, circumference, 2 22 25, , 6., , r2 = 616, , 7., , Side of the square is equal to the diameter of the circle, , r = 14 cm, , or 2r = 88 cm, , r = 3 cm or r2 = (3)2 = 9 cm2 ., 8., , R 2 r12 r22 R = 25 and diameter = 50 cm., , 9., , 2r = 2 , , 178, , 22, 220, 35 = 220 cm , Side of square, = 55 cm, 7, 4, Area of square = 55 × 55 = 3025 cm2, , Mathematics-X
Page 195 :
10. l =, , 11., , , 2r, 360, , , , 3 , , , 2 6, 360, , = 90°, , , r 2, 360, 2, , 2 , 2, r2 , 12. 2r1 2 r1 2 r2 or r1 3 4 : 9, 2r2 3, 3, r22, r22, 13. (2r – r) = 37, , or, , r = 7,, , 2r = 2 , , 22, 7 = 44 cm, 7, , 14. 96%, 210 22 6 6, = 66 cm2 ( = 210°) (11: 20 to 11: 55 = 35 minutes), 360 7, 16. 280 cm2, , 15., , 17. 124.74 cm2, 18. 10.27 cm2, 19. A =, , 1, lr, 2, , 20. 2r, 21. s2, 22., , , 2r, 360, , 23., , , r 2, 360, , 24. Area of the corresponding triangle, 25. 2r = 22, r =, , 7, 2, , r 2, 22 7 7, , Area of quadrant =, = 9.625 cm2, 4, 74 22, , Mathematics-X, , 179
Page 196 :
26. l =, , , , 2r 5 , 2 10 90, 360, 360, , 27., , If side of square is 1 unit, by Pythagoras Theorem, Diameter, , 2 unit., Area of square = 1 × 1 = 1 sq units., 2, Area of Circle = r , , 2, 2 11, , =, 2, 2, 2 7, , Required ratio = 11 : 7, 28. 154 cm2, 29. 2r = 4 unit, , or, , 2r, Perimeter of circle, , (Let side of square = 1 unit), 4 unit Perimeter of square, r=, , 7, unit, 11, , r 2 22 7 7, 14, , , , 1, 7 11 11, 11, , or 14 : 11, , 30. Area of equilateral triangle =, , 3 2, a, 4, , a, Area of circle = , 2, , Required ratio =, , 2, , 3:, , 5, , r 2 = r 2 , 18, 360, = 100°, 32. 20 cm + 14 cm + 20 cm + r, , 31., , 20 cm + 14 cm + 20 cm +, 180, , 22, × = 76 cm, 7, , Mathematics-X
Page 197 :
33., , , 60 2 22 105, 2r , 11 cm, 360, 360 7 10, , Perimeter = 10.5 + 10.5 + 11 cm = 32 cm, 34. Perimeter of shaded region = Perimeters of semi circles,, = ARC + APB + BSD + CQD, = (r1 + r2 + r3 + r4), =, , 22 , 7, 7 22, 7 7 , 21 = 66 cm, , 7 , 2, 2 7, , 36 36, 360, = 15°, , 54 =, , 35., , l=, 36. Area =, , , 15 2 36, 2r =, = 3 cm, 360, 360, , , 210 22 5 5 1650, 5, r 2 , , 45 cm 2, 360, 360 7, 36, 6, , ( = 210° in 35 minutes), 37. AC = 28 cm, BC = 28 2 cm (by Pythagoras Theorem)., radius = 14 2 cm =, , BC, 2, , Shaded region = Area of semicircle – Area of segment BCD, =, , 1, 90, 1, (14 2)2 , (28) 28 28, 2, 360, 2, , = 392 cm2, 38., , l=, , 240 2 22 35, 360 7 10, , = 14.67, Length of OAPBO = 14.6 + 3.5 + 3.5, = 21.67 cm, Mathematics-X, , 181
Page 198 :
39., , (r22 r12 ) = [(1502) 2 – (1500) 2 ] 20, = 3.14 [(1502)2 – (1500)2] × 20, = ` 377051.2, , 40., , Circumference of cycle = 2r, 22, 30 cm, 7, = 188.57 cm, , = 2, , Speed of cycle =, , 18857 140 60, 100 1000, , = 15.84 km/h, 41., , Area of Minor sector =, , , r 2, 360, , 30, 3.14 4 4 cm 2, 360, = 4.19 cm2 (approx.), , =, , Area of major sector =, , , r 2, 360, , 330, 3.14 4 4, 360, = 46.1 cm2 (approx), , =, , Area of =, , 42., , =, =, , 1, base × height, 2, , C, r, , 1, AB OC, 2, 1, 2r r = r2 square unit, 2, , A, , r, O, , B, , 43. Let AB = h cm, Area of trapezium =, 24.5 =, 182, , 1, ( AD BC ) AB, 2, 1, (10 4) h, 2, , (AB = h), Mathematics-X
Page 199 :
h = 3.5 cm, 90, (3.5) 2 sq.cm, 360, = 9.625 sq.cm, , Area of quadrant ABE =, , Area of shaded region = 24.5 – 9.625, = 14.875 sq.cm, 44. Area of shaded portion =, Area of square – Area of circle – (Area of 2 quadrants), 22 42 42 22 14 14 1, , 7 10 10, 7 10 10 2, = 64 – 55.44 – 3.08, , = 64 , , = 5.48 cm2, 100 314 r 2, 7065, =, 360 100, 100, , 45., , 7065 360, = r2, 100 314, 9= r, r = 9 cm., , , 2 , Area of shaded portion = r AB BC , , , 2, DC , , , , 2, , 46., 2, , 22, 22 7 7 , , (3.5) 2 98 , =, 7, 7 2 , , = 38.5 + [98 – 77], = 38.5 + 21, = 59.5 cm2, 47. Four semicircluar means 2 circles ,, , Area of 2 circles = 2r 2, = 2 × 3.14 × 20 × 20, = 2512 sq.m, Total cost = 2512 × 1.25, = ` 3140, Mathematics-X, , 183
Page 200 :
r 2, Area of shaded region = l b , 2, , 48., , 2 2, 2, 2, = (32 + 2) cm, Area of the segment = Area of sector – Area of , , = 8 4 , , 49., , Area of sector =, Area of =, , 120 22, , 21 21 = 462 cm2, 360 7, , 441, 3 cm 2, 4, , 441 , , 3 cm2, Area of segment = 462 , , 4, =, 50., , l=, 11 =, , , , , , 21, 88 21 3 cm 2, 4, , 2r, 360, 45 2 22 r, , 360, 7, r, 14 cm, l × b + r2, (44 × 16 + × 8 × 8), (704 + 64) cm2, , 51., , 14 =, r=, Shaded Area =, =, =, , 52., , Shaded Area = 20 × 15 + 28.12 –, , 1, 12 9, 2, , = 334.39 cm2, 53., , 2r = 2r + 16.8, 2, , or,, 184, , 22, 168, r 2r =, 7, 10, 168, 15 , 2r =, 7, 10, , or, , 22 168, 2r 1 , 7, 10, , or r =, , 168 7, 1176, =, = 3.92 cm, 10 2 15, 300, , Mathematics-X
Page 201 :
54. Area of shaded region = Area of rectangle – [Area of 2 semicircles + Area of, rectangle], r 2, , l b, = L B 2, 2, , = 26 12 [ 2 2 16 4], = 312 – 4 – 64 = (248 – 4) m2, 2, 2, r12 r22 = 130 r1 r2 130, , 55., , , r1 + r2 = 14, , ...(1), , …(2), , Substitute the value of r1 from (2) in (1) and solve., 2r22 – 28 r2 + 66 = 0, , r22 – 14r2 + 33 = 0, , (Neglecting – ve), , r2 = 11 cm and r1 = 3 cm, 56., , Area of shaded region = Area of – Area of 3 sectors., area =, , 3, 3, 14 14 =, 196 = 49 3, 4, 4, , Area of 3 Sectors = 3 , , 60 22, 7 7 = 77 sq. cm, 360 7, , required Area = (49 3 77) cm2, r2 =, , 57., , 616, 100, , 2r = 2 , , Number of revolutions =, 58., Mathematics-X, , or, , r 2 1.96, , or, , r = 1.4 m, , 22 14 616, , =, = 8.8 m, 7 10 100, , 572, = 65, 8.8, , r2 = 2464 cm2, 185
Page 202 :
r = 28 cm, , or, , d = 28 + 28 = 56 cm, , 1, 1, d1d 2 or d 22 (d1 d 2 ), 2, 2, , Area of rhombus =, , 1, 56 56 = 1568 cm2, 2, , =, , 59. By converse of Pythagoras theorem ABC is right ., Area of shaded region = Area of – Area of 3 sectors., 1, r 2, , 48, , 20, , (1 2 3 ), =, 2, 360, 22 6 6, (180), 7 360, = 480 – 56.57, , = 480 , , = 423.43 cm2, 60. 2r2 (Area is equal to 2 circles.), 61., , Perimeter =, =, =, Area =, =, , 2r1 2r2 2r3, , , 2, 2, 2, 22 6, 22 4, 22 2 , , 2 7 2 2 7 2 2 7 2 , 22, 2 3 2 1 = 37.71 cm, 7, r12, r22, r32 , , 2, 2, 2, 2, 31.71 cm, , 62. Radius of bigger circle O = 30 cm, Radius of Smaller circle O = 20 cm, Difference of their radii = (30 – 20) = 10 cm, AB is tangent to small circle, Radius = OC i.e. OD AB, , OCA = 90° = OCB, , In OCA by Phythagoras Theorem, 186, , O, , Mathematics-X
Page 203 :
AC = 20 2 cm, , , AB = 2 × 20 2 cm, = 40 2 cm, CD = Radius of bigger circle-OC, , O, , = 30–10 = 20 cm, Area of cap =, , 1, AB × CD, 2, , =, , 1, 40 2 20 cm 2, 2, , = 400 2 cm 2, 63., , Area of trapezium =, =, , 1, h (a b), 2, 1, 14 (18 32) = 350 cm2, 2, , r 2, (A B C D ), Area of four sectors =, 360, 77, 360 = 154 cm2, 360, area of shaded region = 350 – 154 = 196 cm2, , =, , 64., , r 2 r 2 r 2 , Area of shaded region = 1 2 3 , 2, 2, 2, 17 17 10 10 7 7 , , , = , , 2, 2, 2 , = 688.28 cm2, , Mathematics-X, , 187
Page 204 :
PRACTICE-TEST, AREAS RELATED TO CIRCLES, , Time : 1 Hr., , M.M.: 20, SECTION-A, , 1., , If the circumference of two circles are equal, then what is the ratio between, their areas?, 1, , 2., , If the diameter of a protractor is 21 cm, then find its perimeter., , 1, , 3., , Area of a circle of radius P is ___________ ., , 1, , 4., , Choose the correct answer., If the perimeter and the area of a circle are numerically equal then the radius of, the circle is, 1, (a) 2 units, , (b) units, , (c) 4 units, , (d) 7 units, , SECTION-B, 5., 6., , The length of minute hand of a clock is 14 cm. Find the area swept by the, minute hand in 8 minutes., 2, Find the area of a circle whose circumference is 22 cm., 2, , 7., , Find the area of a quadrant of a circle whose circumference is 44 cm., , 2, , SECTION-C, 8., , A horse is tied to a pole with 28 cm long string. Find the, area where the horse can graze., 3, , 9., , In fig. two concentric circles with centre O, have radii, 21 cm and 42 cm. If AOB = 60° find the area of the, shaded region. (Use =, , 22, ), 7, , 3, , O, 60°, A, , B, , SECTION-D, 10. A chord AB of a circle of radius 10 cm makes a right angle at the centre of the, circle. Find the area of the minor and major segments. (Use = 3.14), 4, 188, , Mathematics-X
Page 205 :
CHAPTER, , 13, , Mathematics-X, , Surface Areas and Volumes, , 189
Page 206 :
KEY POINTS, , 1., , Cuboid: 3-D shapes like a book, a match box, an almirah, a room etc. are, called Cuboid., , For cuboid length = l, breadth = b, height = h, Volume = l × b × h, Lateral surface area of solid cuboid = 2h( l + b), Total surface area of solid cuboid = 2(lb + bh + hl), 2., , Cube: 3-D shapes like ice-cubes, dice etc. are called cube., , a, a, a, , In cube, length = breadth = height = a, Volume = a³, Lateral surface area of solid cube = 4a², Total surface area of solid cube = 6a², 3., , 190, , Cylinder: 3-D shapes like jars, circular pillars, circular pipes, rood rollers etc., are called cylinder., , Mathematics-X
Page 207 :
(a) For right circular cylinder solid, base radius = r, height = h, Volume = r2h, Curved surface area of solid cylinder = 2rh, Total surface area of solid cylinder = 2r (r + h), (b) For right circular cylinder (Hollow), external radius = R, internal radius = r, height = h, Volume = (R² – r²)h, Curved surface area = 2(R + r)h, Total surface area = 2(R + r) h + 2(R² – r²), 4., , Cone: 3-D shapes like conical tents, ice-cream cone etc. are called Cone., , For right circular cone,, base radius = r, height = h, slant height = l, l=, , h2 r 2, , Volume =, , 1, r2h, 3, , Curved surface area of solid cone = rl, Total surface area of solid cone = r (r + l), It may be noted that if radius and height of a cone and cylinder are same then, 3 × volume of a cone = volume of right circular cylinder, Mathematics-X, , 191
Page 208 :
5., , Sphere: 3-D shapes like cricket balls, footballs etc. are called sphere., , r, , (a) For sphere : Radius = r, 4 3, r, 3, , Volume =, , surface area = 4r2, (b) For Hemisphere (solid): Radius = r, Volume =, , 2 3, r, 3, , r, , Curved surface area = 2r2, Total surface area = 3r2, 6., , Frustum: When a cone is cut by a plane parallel to the base of the cone, then, the portion between the plane and the base is called the frustum of the cone., Example: Turkish Cap, For a frustum of cone:, Base radius = R, Top radius = r, Height = h, slant height = l, l=, Volume =, , h 2 + (R – r ) 2, 1, h(r2 + R2 + Rr), 3, , Curved surface area (solid frustum) = l(R + r), Total surface area (solid frustum) = l(R + r) + (R² + r²), , 192, , Mathematics-X
Page 209 :
VERY SHORT ANSWER TYPE QUESTIONS, , 1., , Match the following:, Column I, , 2., , Column II, , (a) Surface area of a sphere, , (i) 2rh, , (b) Total surface area of a cone, , (ii), , (c) Volume of a cuboid, , (iii) 2r(r + h), , (d) Volume of hemisphere, , (iv), , (e) Curved surface area of a cone, , (v) r (r + l ), , (f) Total surface area of hemisphere, , (vi) l × b × h, , (g) Curved surface area of a cylinder, , (vii), , (h) Volume of a cone, , (viii) rl, , 1 2, r h, 3, , 1, h( r 2 R 2 rR ), 3, , 2 3, r, 3, , (i) Total surface area of a cylinder, , (ix) 3 r2, , (j) Volume of a frustum of a cone, , (x) 4r2, , Fill in the Blanks:, (i) The total surface area of cuboid of dimension a × a × b is __________., (ii) The volume of right circular cylinder of base radius r and height 2r is, ______________., (iii) The total surface area of a cylinder of base radius r and height h, is_____________., (iv) The curved surface area of a cone of base radius r and height h, is_______________., (v) If the height of a cone is equal to diameter of its base, the volume of cone, is_________________ ., (vi) The total surface area of a solid hemisphere of radius r is____________., (vii) The curved surface area of a hollow cylinder of outer radius R, inner, radius r and height h is __________ ., , Mathematics-X, , 193
Page 210 :
(viii) If the radius of a sphere is doubled, its volume becomes__________times, the volume of original sphere., (ix) If the radius of a sphere is halved, its volume becomes__________times, the volume of original sphere., (NCERT Exemplar), 3., , Write ‘True’ or ‘False’ in the following:, (i) Two identical solid hemispheres of equal base radius r are stuck together, along their bases. The total surface area of the combination is 6r2., (ii) A solid cylinder of radius r and height h is placed over other cylinder of, same height and radius. The total surface area of the shape so formed is, (4rh + 4r2)., (iii) A solid cone of radius r and height h is placed over a solid cylinder having, same base radius and height as that of a cone. The total surface area of, the combined solid is r ( r 2 h 2 3r 2h ) ., , 4., , (iv) A solid ball is exactly fitted inside the cubical box of side ‘a’. The volume, 4 2, of the ball is a ., 3, 1, 2, 2, (v) The volume of the frustum of a cone is h( r1 r2 r 1r2 ), where h is, 3, vertical height of the frustum and r1; r2 are the radii of the ends., The total surface area of a solid hemisphere of radius r is, , 5., , (a) r2, (b) 2r2, (c) 3r2, (d) 4r2, The volume and the surface area of a sphere are numerically equal, then the, radius of sphere is, , 6., , (a) 0 units, (b) 1 unit, (c) 2 units, (d) 3 units, A cylinder, a cone and a hemisphere are of the same base and of the same, height. The ratio of their volumes is, , 7., , (a) 1:2:3, (b) 2:1:3, (c) 3:1:2, (d) 3:2:1, A solid sphere of radius ‘r’ is melted and recast into the shape of a solid cone of, height ‘r’. Then the radius of the base of cone is, , 8., , (a) 2r, (b) r, (c) 4r, (d) 3r, Three solid spheres of diameters 6 cm, 8 cm and 10 cm are melted to form a, single solid sphere. The diameter of the new sphere is, (a) 6 cm, , 194, , (b) 4.5 cm, , (c) 3 cm, , (d) 12 cm, Mathematics-X
Page 211 :
9., , The radii of the ends of a frustum of a cone 40 cm high are 38 cm and 8 cm. The, slant height of the frustum of cone is, (a) 50 cm, , (b) 10 7 cm, , (c) 60.96 cm, , (d) 4 2 cm, 10. A metallic spherical shell of internal and external diameters 4 cm and 8 cm,, respectively is melted and recast into the form of a cone of base diameter 8 cm., The height of the cone is:, (a) 12 cm, (b) 14 cm, (c) 15 cm, (d) 18 cm, 11. A solid piece of iron in the form of a cuboid of dimensions 49 cm × 33 cm, × 24 cm, is moulded to form a solid sphere. The radius of the sphere is, (a) 21 cm, (b) 23 cm, (c) 25 cm, (d) 19 cm, 12. A shuttle cock used for playing badminton has the shape of the combination of, (NCERT Exemplar), (a) A cylinder and a sphere, (b) a cylinder and a hemisphere, (c) a sphere and a cone, (d) frustum of a cone and hemsphere, 13. The radii of the top and bottom of a bucket of slant height 45 cm are 28 cm and, 7 cm respectively. The curved surface area of the bucket is, (NCERT Exemplar), (a) 4950 cm2, (b) 4951 cm2, (c) 4952 cm2, (d) 4953 cm2, 14. A solid shape is converted from one form to another. What is the change in its, volume?, 15. What cross-section is made by a cone when it is cut parallel to its base?, 16. Find total surface area of a solid hemi-sphere of radius 7cm., 17. Volume of two spheres is in the ratio 64 : 125. Find the ratio of their surface, areas., 18. A cylinder and a cone are of same base radius and of same height. Find the, ratio of the volumes of cylinder to that of the cone., 19. If the volume of a cube is 1331 cm³, then find the length of its edge., 20. Two cones have their heights in the ratio 1 : 3 and radii in the ratio 3 : 1. What, is the ratio of their volumes?, (CBSE 2020), Mathematics-X, , 195
Page 212 :
SHORT ANSWER TYPE QUESTION (TYPE-I), , 21. How many cubes of side 2 cm can be cut from a cuboid measuring, (16cm × 12cm × 10cm)?, 22. Find the height of largest right circular cone that can be cut out of a cube whose, volume is 729 cm³., 23. Two identical cubes each of volume 216 cm³ are joined together end to end., What is the surface area of the resulting cuboid?, 24. Twelve solid spheres of the same sizes are made by melting a solid metallic, cylinder of base diameter 2 cm and height 16cm. Find the radius of each sphere., 25. The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The, height of the bucket is 35cm. Find the volume of the bucket., 26. The volume of a right circular cylinder with its height equal to the radius is, 22 , , Use , , 7 , , , 1, 25 cm3. Find the height of the cylinder.., 7, , (CBSE 2020), SHORT ANSWER TYPE QUESTION (TYPE-II), , 27. A bucket is in the form of a frustum of a cone and hold 28.490 litres of water., The radii of the top and bottom are 28 cm and 21 cm respectively. Find the, height of the bucket., 28. Three cubes of a metal whose edge are in the ratio 3:4:5 are melted and converted, into a single cube whose diagonal is 12 3 cm. Find the edge of three cubes., 29. Find the depth of a cylindrical tank of radius 10.5 cm, if its capacity is equal to, that of a rectangular tank of size 15 cm × 11 cm × 10.5 cm., 30. A cone of radius 8 cm and height 12 cm is divided into two parts by a plane, through the mid-point of its axis parallel to its base. Find the ratio of the volumes, of the two parts., 31. A petrol tank is a cylinder of base diameter 28 cm and length 24 cm filted with, conical ends each of axis length 9 cm. Determine the capacity of the tank., 32. Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/, hour. How much area will it irrigate in 30 minutes; if 8 cm standing water is, needed?, (NCERT, CBSE 2019), 196, , Mathematics-X
Page 213 :
33. A solid is in the form of a cylinder with hemispherical ends. The total height of, the solid is 20 cm and the diameter of the cylinder is 7 cm. Find the total, 22 , , volume of the solid. Use , 7 , , , (CBSE 2019), , 34. Two spheres of same metal weight 1 kg and 7 kg. The radius of the smaller, sphere is 3 cm. The two spheres are melted to form a single big sphere. Find, the diameter of the new sphere., (CBSE 2019), 35. A cone of height 24 cm and radius of base 6 cm is made up of modeling clay, A, child reshapes it in the form of a sphere. Find the radius of the sphere and, hence find the surface area of this sphere., (NCERT, CBSE 2019), 36. A farmer connects a pipe of internal diameter 20 cm from a canal into a, cylindrical tank in his field which is 10 m in diameter and 2 m deep. If water, flows through pipe at the rate of 3 km/hr, how much time will the tank be, filled?, (NCERT, CBSE 2019), 37. A juice seller was serving his customers using glasses as shown in figure. The, inner diameter of the cylindrical glass was 5 cm but bottom of the glass had a, hemispherical raised portion which reduced the capacity of the glass. If the, height of a glass was 10 cm, find the apparent and actual capacity of the glass., [Use = 3.14], (NCERT, CBSE 2019, 2009), , 38. A girl empties a cylindrical bucket full of sand, of base radius 18 cm and height, 32 cm on the floor to form a conical heap of sand. If the height of this conical, heap is 24 cm, then find its slant height correct to one place of decimal., (CBSE 2019), , Mathematics-X, , 197
Page 214 :
39. Water is flowing at the rate of 5 km/hour through a pipe of diameter 14 cm into, a tank with rectangular base which is 50 m long and 44 m wide. Find the time, 22 , , in which the level of water tank rises by 7 cm. Use , 7 , , (CBSE 2019), 40. A field is in the form of rectangle of length 20 m and width 14 m. A 10 m deep, well of diameter 7 m is dug in one corner of the field and the earth taken out of, the well is spread evenly over the remaining part of the field. Find the rise in, 22 , , the level of the field. Use , (CBSE 2019), 7 , , 41. A solid metallic cuboid of dimension 24 cm × 11 cm × 7 cm is melted and, recast into solid cones of base radius 3.5 cm and height 6 cm. Find the number, of cones so formed., (CBSE 2020), 42. A cone of base radius 4 cm is divided into two parts by drawing a plane through, the mid-point of its height and parallel to its base. Compare the volume of the, two parts., (CBSE 2020), LONG ANSWER TYPE QUESTIONS, , 43. A bucket open at the top is in the form of a frustum of a cone with a capacity of, 12308.8 cm2. The radii of the top and bottom of the circular ends of the bucket, are 20 cm and 12 cm respectively. Find the height of the bucket and also the, area of the metal sheet used in making it. ( Use = 3.14 ), (CBSE 2019), 44. A solid iron pole consists of a cylinder of height 220 cm and base diameter, 24 cm, which is surmounted by another cylinder of height 60 cm and radius, 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8, gm mass. (Use = 3.14), (NCERT, CBSE 2019), 45. A right cylindrical container of radius 6 cm and height 15 cm is full of icecream, which has to be distributed to 10 children in equal cones having, hemispherical shape on the top. If the height of the conical portion is four, times its base radius, find the radius of the ice-cream cone., (CBSE 2019), 46. A container opened at the top and made up of a metal sheet, is in the form of a, frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm, and 20 cm respectively. Find the cost of milk which can completely fill the, container, at the rate of `50 per litre. Also find the cost of metal sheet used to, make the container, if it costs ` 10 per 100 cm2., (Take = 3.14)., (NCERT, CBSE 2019), 198, , Mathematics-X
Page 215 :
47. An open metallic bucket is in the shape of a frustum of a cone, If the diameters, of the two circular ends of the bucket are 45 cm and 25 cm and the vertical, height of the bucket is 24 cm, find the area of the metallic sheet used to make, 22 , , the bucket. Also find the volume of the water it can hold., Use , , 7 , , 48. In the given figure, from the top of a solid cone of height 12 cm and base radius, 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total, 22, surface area of the remaining solid.(Use =, and 5 = 2.236 ) (CBSE 2015), 7, , 49. A solid wooden toy is in the form of a hemi-sphere surmounted by a cone of, same radius. The radius of hemi-sphere is 3.5 cm and the total wood used in the, 5, making of toy is 166 cm3. Find the height of the toy. Also, find the cost of, 6, painting the hemi-spherical part of the toy at the rate of ` 10 per cm²., 22 , , (CBSE, 2015), Use , , 7 , , 50. In the given figure, from a cuboidal solid metalic block of dimensions 15 cm ×, 10 cm × 5 cm a cylindrical hole of diameter 7 cm is drilled out. Find the surface, 22 , , area of the remaining block. Use , (CBSE – 2015), 7 , , 7 cm, , 5 cm, 10 cm, 15 cm, , Mathematics-X, , 199
Page 216 :
51. A solid toy is the form of a right circular cylinder with a hemispherical shape at, one end and a cone at the other end. Their diameter is 4.2 cm and the heights of, the cylindrical and conical portions are 12 cm and 7 cm respectively. Find the, volume of the toy., 52. A tent is in the shape of a right circular cylinder upto a height of 3 m and, conical above it. The total height of the tent is 13.5 m and radius of base is 14, m. Find the cost of cloth required to make the tent at the rate of 80 per m2., 53. The rain water from a roof 22 m × 20 m drains into a cylindrical vessel having, diameter of base 2 m and height 3.5 m. If the vessel is just full, find the rainfall in, cm., 54. The difference between outer and inner curved surface areas of a hollow right, circular cylinder, 14 cm long is 88 cm2. If the volume of the metal used in, making the cylinder is 176 cm3. Find the outer and inner diameters of the, cylinder., (HOTS), 55. An open metal bucket is in the shape of a frustum of cone of height 21 cm with, radii of its lower and upper ends 10 cm and 20 cm respectively. Find the cost of, milk which can completely fill the bucket at the rate of `40 per litre., (CBSE 2020), 56. A solid is in the shape of a cone surmounted on a hemisphere. The radius of, each of them being 3.5 cm and the total height of the solid is 9.5 cm. Find the, volume of the solid., (CBSE 2020), 57. A hemispherical depression is cut out from one face of a cubical wooden block, of edge 21 cm, such that the diameter of the hemisphere is equal to edge of the, cube. Determine the volume of the remaining block., (CBSE 2020), 58. A solid metallic cylinder of diameter 12 cm and height 15 cm is melted and, recast into 12 toys in the shape of a right circular cone mounted on a hemisphere, of same radius. Find the radius of the hemisphere and total height of the toy, if, the height of the cone is 3 times the radius., (CBSE 2020), ANSWERS AND HINTS, , 1. (a) (x) 4r2, (c) (vi) l × b × h, (e) (viii) rl, 200, , (b) (v) r (r + l), 2 3, r, 3, (f) (ix) 3r2, , (d) (vii), , Mathematics-X
Page 217 :
(g) (i) 2rh, , (h) (ii), , 1 2, r h, 3, , (i) (iii) 2r(r + h), , (j) (iv), , 1, h(r 2 R 2 rR), 3, , 2. (i) 2a2 + 4ab, , (ii) 2r3, (iv) r r 2 h 2, , (iii) 2r(r + h), (v), , 2 3, r, 3, , (vi) 3r2, , (vii) 2h(R + r), (ix), , (viii) 8, , 1, 8, , 3. (i) False, , (ii) False, , (iii) False, , (iv) False, , (v) True, 4. (c) 3r2, , 5. (d) 3 units, , 6. (c) 3 : 1 : 2, , 7. (a) 2r, , 8. (d) 12 cm, , 9. (a) 50 cm, , 10.(b) 14 cm, , 11. (a) 21 cm, , 12.(d) Frustem of a cone and a hemisphere13. (a) 4950 cm2, 14., , Remains unchanged, , 15. Circle, , 16., , 462 cm2, , 17. 16 : 25, , 18., , 3:1, , 19. 11 cm, , 20., , 3:1, , 21., , No. of cubes =, , 16 12 10, = 240, 222, , 22., , Side of cube =, , 3, , 729 9cm, , Height of largest cone = Side of cube = 9 cm, Mathematics-X, , 201
Page 218 :
23., , Side of cube =, , 24., , Length, breadth and height of new cuboid is 12 cm, 6 cm and 6 cm respectively., Surface area of cuboid = 2[12 × 6 + 6 × 6 + 6 × 12] = 360 cm 2, Volume of 12 solid sphere = Volume of solid cylinder, , 3, , 216 = 6 cm, , 4 3, r = (1)2 × 16, 3, r3 = 1, r = 1 cm, 12 , , 25., , Volume of bucket =, , 1 22, 35 [(22)2 + (12)2 + 22 × 12], 3 7, , 2, cm3, 3, Let the height and radius of cylinder be x cm and x cm respectively., , = 32706, 26., , Volume of cylinder =, , 176, cm3, 7, , 22, 176, × (x)2 × x =, 7, 7, 3, x =8, , x=, 27., , 28., , 3, , 8 = 2 cm, Volume of bucket = 28490 cm3, 1 22, , h [(28)2 + (21)2 + 28 × 21] = 28490, 3 7, h = 15 cm, Let the edges of three cubes be 3x cm, 4x cm and 5x cm., Volume of single cube = Sum of volume of three cubes, (Side)3 = (3x)3 + (4x)3 + (5x)3, Side = 6x cm, , Diagonal of single cube = 12 3 cm, 3 (6 x ) 12 3, x=2, Hence edges of three cubes are 6 cm, 8 cm and 10 cm, 202, , Mathematics-X
Page 219 :
29. Capacity of cylindrical tank = Capacity of rectangular tank, 22, (10.5) 2 × h = 15 × 11 × 10.5, 7, h = 5 cm, 30. OAB ~ OCD, AB OA, , CD OC, AB = 4 cm, , 1, (4)2 6, 3, , 1, Volume of conical part, , =, 1, Volume of frustum part, 6[(8)2 (4) 2 8 4] 7, 3, required ratio is 1 : 7 or 7 : 1, 31. Capacity of tank = Volume of cylindrical part + 2 × Volume of conical part, = 18480 cm2, , 32. Length of canal covered in 30 mins = 5000 m, Volume of water flown in 30 mins, = 6 × 1.5 × 5000 m3, 6 1.5 5000, = 562500 m2, 0.08, 33. Height of cylinder = 20 – 3.5 – 3.5 = 13 cm, Volume of solid =Volume of cylindrical part + 2, × Volume of hemispherical part, , Area irrigated =, , =, , 22, 2 22, (3.5)2 13 2 (3.5)3, 7, 3 7, , = 680, Mathematics-X, , 1, cm3, 6, 203
Page 220 :
34. Radius of first sphere = 3 cm, Let density of metal be d kg/cm3, , , 4, (3)3 d = 1, 3, , ...(1), , Let radius of second sphere be r cm., , , 4, (r)3 d = 7, 3, , ...(2), , From (1) and (2), we have, r3 = 7(3)3, Let the radius of new sphere by R cm., A.T.Q, 4, 4, 4, R 3 = (3)3 r 3, 3, 3, 3, 3, 3, 3, R = (3) + 7(3), R = 6 cm, Diameter of new sphere = 2 × 6 = 12 cm., 35. Volume of sphere = Volume of cone, 4 3, 1, r = (6) 2 24, 3, 3, r = 6 cm, Surface area of sphere = 4 × × (6)2 = 144 cm2, , 36., , Time to fill tank =, =, , Volume of cylindrical tank, Volume of water flown in 1 hour, (5) 2 2, 2, , 1, 3000, 10 , , = 100 minutes or 1 hour 40 minutes., , 2, , 5, 37. Apparent capacity = 3.14 × 10 = 196.25 cm3., 2, Actual capacity = Volume of cylindrical part – Volume of hemispherical, part, 2, 5, = 196.25 3.14 , 2, 3, 3, = 163.54 cm approx, 204, , 3, , Mathematics-X
Page 221 :
38. Volume of conical heap = Volume of cylindrical bucket, 1 2, r 24 = (18)2 × 32, 3, r = 36 cm, , Slant height,, , l=, , (36) 2 (24) 2 = 43.27 cm aprox., , 39. Volume of raised water in tank = 50 × 44 ×, , 7, = 154 m3, 100, 2, , Volume of water flown in 1 hr =, , 22 7 , , 5000 = 77 m3, , 7, 100, , 154, = 2 hours, 77, Earth taken out, Rise in level =, Area of the remaining part of field, , Time taken =, , 40., , 2, , 22 7 , , 10, 7 2, =, = 1.5 m approx., 22 7 7 , , 20, , 14, , , , , 7 2 2 , Volume of Cuboid, 41. Number of cones = Volume of one cone, , 24 11 7, = 1 22 (3.5) 2 6, 3 7, = 24, , 42. 1 : 7 or 7 : 1, 43. Volume of bucket = 12308.8 cm3, 1, 3.14 h [(20)2 + (12)2 + 20 × 12] = 12308.8, 3, h = 15 cm, , l=, , (15)2 (20 12) 2 = 17 cm, , Surface area of metal sheet used, = 3.14 × 17 × (20 + 12) + 3.14 × (12)2, = 2160.32 cm2, Mathematics-X, , 205
Page 222 :
44., , Volume of solid = 3.14 × (12)2 × 220 + 3.14 × (8)2 × 60, = 111532.8 cm3, 8, kg, 1000, = 892.2624 kg, 45. Let radius of conical section be r cm., Height of conical section be 4r cm., According to the question, 10 × Volume of ice-cream in 1 cone = Volume of cylindrical container, , Mass of the pole = 111532.8 ×, , 2, 1, , 10 r 2 4r r 3 = (6)2 × 15, 3, 3, , r = 3 cm, 3.14 16, [(20)2 + (8)2 + 20 × 8], 3, = 10450 cm3 approx., = 10.45 litres, Cost of milk = 10.45 × 50 = ` 522.50, , 46. Volume of the container =, , Slant height =, , (16) 2 (20 8)2 = 20 cm, , Surface area of container, = 3.14 × 20 (20 + 8) + 3.14 × (8)2, = 1959.36 cm2, Cost of metal sheet =, 206, , 10, 1959.36 = ` 195.94, 100, , Mathematics-X
Page 223 :
47. Slant height =, , 45 25 , (24) , 2, 2, 2, , 2, , = 26 cm, , 22, 45 25 22 25 25, 26 , , 2, 7, 2 7, 2, 2, , Surface area of bucket =, , = 3351.07 cm2 approx., , 45 2 25 2 45 25 , 1 22, Volume = 24 , 3 7, 2, 2, 2 2 , = 23728.57 cm3 approx., 48. Radii of frustum are 6 cm and 2 cm., Height of frustum = 12 – 4 = 8 cm, Slant height =, , (8) 2 (6 – 2)2 = 4 5 cm, , Total surface area of frustum, 22, 22, 22, 4 2.236 [6 2] , (6) 2 , (2) 2, 7, 7, 7, 2, = 350.592 cm approx., , =, , 49. Volume of toy =, , 1001, cm3, 6, , 3, , 2, , 1001, 2 22 7 , 1 22 7 , , , h =, , , , , 6, 3 7, 2, 3 7, 2, , h = 6 cm, Area of hemispherical part of toy, 2, , 22 7 , = 2 = 77 cm2, 7 2, Cost of painting =, 77 × 10 = ` 770, 50. Surface of the remaining block = TSA of cuboidal block + CSA of cylinder –, Area of two circular bases, 22, 7, 22 7 , = 2(15 × 10 + 10 × 5 + 15 × 5) + 2 ×, ×, ×5–2×, × , 2, 7, 2, 7, , 2, , = 583 cm2, Mathematics-X, , 207
Page 224 :
51. Volume of toy = Volume of cylindrical part + Volume of hemispherical part, + Volume of conical part, 22, 1 22, 2 22, (2.1) 2 12 , (2.1) 2 7 , (2.1)3, 7, 3 7, 3 7, = 218.064 cm3, , =, , 52. Slant height =, , (14)2 (10.5)2 = 17.5 m, , 22, 22, 3 14 , 14 17.5, 7, 7, = 1034 m2, Cost of cloth = 1034 × 80 = ` 82720, , Surface area of tent = 2 , , 53., , Rainfall =, , Volume of cylindrical vessel, Area of roof, , 22, (1)2 3.5, 1, 7, =, =, m, 22 20, 40, 1, × 100 cm = 2.5 cm, 40, 54. Let inner and outer radius of hallow cylinder be r cm and R cm respectively., Difference between Outer and Inner CSA = 88 cm2, , =, , 22, 14 [R r] = 88, 7, R–r= 1, Volume of hollow cylinder = 176 cm3, 2, , ...(1), , 22, 14 [R 2 r 2 ] = 176, 7, R2 – r2 = 4, (R – r) (R + r) = 4, R+r= 4, ...(2) [, From (1) and (2), we get, R = 2.5 cm and r = 1.5 cm, Outer and inner diameter are 5 cm and 3 cm respectively., 208, , from (1)], , Mathematics-X
Page 225 :
55., , Volume of bucket =, , 1 22, 21 (10) 2 (20) 2 10 20 , , , 3 7, , = 15400 cm3, = 15.4 litre, Cost of milk @ ` 40 per litre = 15.4 × 40 = `616, 56., Height of cone = 9.5 – 3.5 = 6 cm, Volume of solid =, , 2 22, 1 22, (3.5)3 (3.5) 2 6, 3 7, 3 7, , = 166.83 cm3 approx, 57. Radius of hemisphere =, , 21, = 10.5 cm, 2, , Volume of remaining block = (21)3 –, , 2 22, , × (10.5)3, 3 7, , = 6835.5 cm3, 58. Let radius of cone = x cm, and height of cone = 3x cm, 12 × volume of 1 toy = Volume of solid cylinder, 1, 2, , 12 x3 ( x )2 3 x = (6) 2 15, 3, 3, , , x3 = 27, x3 = 3, Radius of hemisphere = 3 cm, and Total height of toy = 3 + (3 × 3), = 3 + 9 = 12 cm, , Mathematics-X, , 209
Page 226 :
PRACTICE-TEST, SURFACE AREAS AND VOLUMES, , Time : 1 Hr., , M.M.: 20, SECTION-A, , 1., , The total surface area of a hemisphere of radius r is .............., , 2., , Which two geometrical shapes are obtained by cutting a cone parallel to its, base?, 1, , 3., , 4., , 1, , (a) a cylinder and a cone, , (b) a cone and a hemisphere, , (c) a sphere and a cone, , (d) frustum of a cone and a cone, , The radius (in cm) of the largest right circular cone that can be cut out from a, cube of edge 4.2 cm is, 1, (a) 4.2, , (b) 2.1, , (c) 8.4, , (d) 1.05, , The volume of a cube is 1000 cm3. Find the length of the side of the cube. 1, SECTION-B, , 5., , The radii of the ends of a frustum of a cone 45 cm high are 28 cm and 7 cm., Find its volume., 2, , 6., , A solid sphere of radius 10.5 cm is melted and recast into smaller solid cones,, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed., 2, , 7., , A cube and a sphere have equal total surface area. Find the ratio of the volume, of sphere and cube., 2, SECTION-C, , 8., , A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its, top, which is open, is 5 cm. It is filled with water up to brim. When lead shots,, each of which is a sphere of radius 0.5 cm are dropped in to the vessel, onefourth of the water flows out. Find the number of lead shots dropped in the vessel., 3, , 210, , Mathematics-X
Page 227 :
9., , A large right circular cone is made out of a solid cube edge 9 cm. Find the, volume of the remaining solid., 3, SECTION-D, , 10. In a hospital, used water is collected in a cylindrical tank of diameter 2 m and, height 5 m. After recycling, this water is used to irrigate a park of hospital, whose length is 25 m and breadth is 20 m. If tank is filled completely then what, will be the height of standing water used for irrigating the park?, 4, , Mathematics-X, , 211
Page 228 :
CHAPTER, , 14, , 212, , Statistics, , Mathematics-X
Page 229 :
KEY POINTS:, , 1., , Mean x , (a) For raw data, x =, , i.e. x =, , x1 x2 ... xn, xi, =, n, n, , sum of observations, no of observations, , (b) For Grouped data, (i) For small calculation, we apply Direct method, , x =, , f i xi, fi, , (ii) If calculations are tedius or observations are large, then we apply short cut/, Assumed Mean method or step Deviation method, Short cut/Assumed Mean Method, fi di, x = a + f i , a assumed mean, , di = xi – a, Step Deviation Method, f i ui, di, , h class size, x = a + f h , ui =, h, i, , 2., , Median, (a) For ungrouped data, we first arrange data in ascending or descending order., th, , n 1, Count number of times say ‘n’. If n is odd, then Median = , observation, 2 , th, , n, n, , 1, 2, , If n is even, then Median = 2 , 2, Mathematics-X, , th, , obsevation, 213
Page 230 :
(b) For grouped data, , n, – cf, 2, Median = l + , f, , , , h, , f1 – fo , (3) Mode = l + 2 f – f – f h (For grouped data), 1 o 2, For ungrouped data mode is the most frequent observation., NOTES:, , 1., , Empirical relationship between three measures of central tendency:, mode = 3 median – 2 mean., , 2., , If class interval is discontinuous, then make it continuous by subtracting 0.5, from Lower Limit and adding 0.5 to upper limit., , 3., , xi = class mark =, , 4., , h = class size = Upper Limit – Lower limit, , 5., , Modal class A class interval having maximum frequency., , 6., , Median class A class interval is which cumulative frequency is greater than, and nearest to, , 7., , n, 2, , Upper Limit Lower Limit, 2, , n f i , , The median of a group data can be obtained graphically as the x coordinate of, the point of intersection of ‘more than’ and ‘less than’ ogive., (Graphical Method), Y, , More than, ogive, Less than ogive, , X, Median, , 214, , Mathematics-X
Page 231 :
8., , If mean of x1, x2, ...., xn is x then, (a) Mean of kx1, kx2, ...., kxn is k x, x1 x2, x, x, ,, , ...., n is, k k, k, k, (c) Mean of x1 + k, x2 + k, ....., xn + k is x + k, , (b) Mean of, , (d) Mean of x1 – k, x2 – k, ....., xn – k is x – k, 9., , If mean of n1 observation is x 1 and mean of n2 observation is x 2 then their, combined, n1 x1 n2 x2, Mean =, n n, 1, , 2, , 10. xi = n x, 11. Range = Highest observation – Lowest observation, 12. Graphical Representation of Mode is a Histogram., VERY SHORT ANSWER TYPE(I) QUESTIONS, , 1., 2., , What is the mean of first 12 prime numbers?, The mean of 20 numbers is 18. If 2 is added to each number, what is the new, mean?, 3. The mean of 5 observations 3, 5, 7, x and 11 is 7, find the value of x., 4. What is the median of first 5 natural numbers?, 5. What is the value of x, if the median of the following data is 27.5?, 24, 25, 26, x + 2, x + 3, 30, 33, 37, 6. What is the mode of the observations 5, 7, 8, 5, 7, 6, 9, 5, 10, 6?, 7. The mean and mode of a data are 24 and 12 respectively. Find the median., 8. Write the class mark of the class 19.5 – 29.5., 9. Multiple Choice Question, (i) If the class intervals of a frequency distribution are 1 – 10, 11 – 20, 21 – 30,, ....., 51 – 60, then the size of each class is:, (a) 9, (b) 10, (c) 11, (d) 5.5, (ii) If the class intervals of a frequency distribution are 1 – 10, 11 – 20, 21 – 30 ....,, 61 – 70, Then the upper limit of 21 – 30 is:, (a) 21, (b) 30, (c) 30.5, (d) 20.5, Mathematics-X, , 215
Page 232 :
(iii) Consider the frequency distribution., Class, Frequency, , 0–5, , 6 – 11, , 12 – 17, , 18 – 23, , 24 – 29, , 13, , 10, , 15, , 8, , 11, , The upper limit of median class is :, (a) 17, (b) 17.5, (c) 18, (iv) Daily wages of a factory workers are recorded as:, , (d) 18.5, , Daily wages (in `) 121 – 126 127 – 132 133– 138 139 – 144 145 – 150, No. of workers, , 5, , 27, , 20, , 18, , 12, , The lower limit of Modal class is:, (a) ` 127, (b) ` 126, (v) For the following distribution, Class, Frequency, , (c) ` 126.50, , (d) ` 133, , 0–5, , 5 – 10, , 10 – 15, , 15 – 20, , 20 – 25, , 10, , 15, , 12, , 20, , 9, , The sum of Lower limits of the median class and modal class is (CBSE 2020), (a) 15, (b) 25, (c) 30, (d) 35, (vi) The median and mode respectively of a frequency distribution are 26 and 29., Then, its mean is, (CBSE 2020), (a) 27.5, (b) 24.5, (c) 28.4, (d) 25.8, 10. Find the class-marks of the classes 10-25 and 35-55., (CBSE 2020), 11. Fill in the blank, (a) Mode = 3_________ – 2 _________, (b) An ogive curve is used to determine _________ ., (c) If the point of intersection of ‘more than’ and ‘less than’ ogive is (20. 5, 30.7),, then the value of median is _________ ., (d) The mode of a frequency distribution is determined graphically by _________, ., (e) If the mode is 8 and mean is also 8, then median will be _________ ., (f) The measure of central tendency which cannot be determined graphically is, _________ ., (g) If the class marks of a continuous frequency distribution are 22, 30, 38, 46, 54,, 62 then the class corresponding to class mark 46 is _________ ., Mathematics-X, 216
Page 233 :
(h) Construction of cumulative frequency distribution table is useful in determining, _________ ., (i), (j), (k), (l), , The step deviation formula for finding mean is _________ ., The formula to find median of grouped data is _________ ., The formula to find mode of grouped data is _________ ., The Range of the observations 255, 125, 130, 160, 185, 170, 103 is _______ ., 1, (m) Class mark =, (________ + ________) ., 2, (n) The median of Ist ten prime numbers is ________ ., (o) The assumed mean method to find mean is ________ ., SHORT ANSWER TYPE QUESTIONS (I), 12. The mean of 11 observation is 50. If the mean of first Six observations is 49 and, that of last six observation is 52, then find sixth observation., 13. Find the mean of following distribution:, x, f, , 12, 5, , 16, 7, , 20, 8, , 24, 5, , 28, 3, , 32, 2, , 18, 4, , 20, 3, , 14. Find the median of the following distribution:, x, f, , 10, 3, , 12, 5, , 14, 6, , 16, 4, , 15. Find the mode of the following frequency distribution:, Class, Frequency, , 0–5 5–10 10 –15 15–20 20–25, 2, 7, 18, 10, 8, , 25–30, 5, , 16. Draw a ‘less than’ ogive of the following data:, Less, Less, Less, Less, Less, Less, Less, Less, Less, , Marks, than 20, than 30, than 40, than 50, than 60, than 70, than 80, than 90, than 100, , Mathematics-X, , No. of students, 0, 4, 16, 30, 46, 66, 82, 92, 100, 217
Page 234 :
17. Write the following data into less than cummulative frequency distribution table :, Marks, No. of students, , 0–10, 7, , 10–20, 9, , 20–30 30–40, 6, 8, , 40–50, 10, , 18. Find mode of the following frequency distribution :, Class Interval, , 25 – 30, , Frequency, , 30 – 35 35 – 40, , 25, , 34, , 40 – 45 45 – 50, , 50, , 42, , 50 – 55, , 38, , 14, , (CBSE 2018 - 19), 19. What is the median of the following data?, , (CBSE 2011), , x, , 10, , 20, , 30, , 40, , 50, , f, , 2, , 3, , 2, , 3, , 1, , 20. Mean of a frequency distribution ( x ) is 45. If f i = 20 find f i x i, (CBSE 2011), 21. Find the mean of the following distribution :, Class, , 3–5, , 5–7, , 7–9, , 5, , 10, , 10, , Frequency, , (CBSE 2020), 9 – 11 11 – 13, 7, , 8, , 22. Find the mode of the following data :, Class, , 0 – 20 20 – 40, , Frequency, , 6, , 8, , 40 – 60, , (CBSE 2020), 60 – 80 80 – 100 100 – 120 120-140, , 10, , 12, , 6, , 5, , 23. Compute the mode for the following frequency distribution:, Size of items 0 – 4, (in cm), Frequency, , 4–8, , 8 – 12, , 7, , 9, , 5, , 12 – 16 16 – 20, 17, , 3, , (CBSE 2020), , 20 – 24, , 24 – 28, , 10, , 6, , 12, , SHORT ANSWER TYPE QUESTIONS (II), , 24. If the mean of the following distribution is 54, find the value of P., Class, , 0–20, , 20–40, , 40–60, , 60–80, , 80–100, , 7, , P, , 10, , 9, , 13, , Frequency, , 25. Find the median of the following frequency distribution :, , 218, , C.I., , 0–10, , 10–20, , 20–30, , 30–40, , 40–50, , f, , 5, , 3, , 10, , 6, , 4, , 50–60, 2, Mathematics-X
Page 235 :
26. The median of following frequency distribution is 24 years. Find the missing, frequency x., Age (In years), No. of persons, , 0–10, 5, , 10–20, 25, , 20–30, x, , 30–40, 18, , 40–50, 7, , 27. Find the median of the following data:, Marks, , Below 10, , Below 20, , Below 30, , Below 40, , below 50, , Below 60, , No. of student, , 0, , 12, , 20, , 28, , 33, , 40, , 28. Draw a ‘more than type’ ogive of the following data :, Weight (In kg.), No. of Students, , 30–35, 2, , 35–40, 4, , 40–45, 10, , 45–50, 15, , 50–55, 6, , 55–60, 3, , 29. Find the mode of the following data:, Height (In cm) Above 30 Above 40 Above 50 Above 60 Above 70 Above 80, No. of plants, 34, 30, 27, 19, 8, 2, 30. The following table represent marks obtained by 100 students in a test:, Marks obtained, No. of students, , 30 – 35 35 – 40, 14, , 16, , 40 – 45, , 45 – 50, , 28, , 23, , 50 – 55 55 – 60 60 – 65, 18, , Find mean marks of the students., , 8, , 3, , (CBSE 2018 -19), , 31. The following table represent pocket allowance of children of a colony. The, mean pocket allowance is ` 18. Find the missing frequency., Daily pocket, 11 – 13 13 – 15 15 – 17 17 – 19, allowance (in `), No. of children, , 3, , 6, , 9, , 19 – 21 21 – 23 23 – 25, , 13, , k, , 5, , 4, , (CBSE – 2018), 32. Find mode of the following frequency distribution:, Class Interval, No. of Students, , 0–20, 15, , 20–40, 18, , 40–60, 21, , 60–80, 29, , 80–100, 17, , The mean of above distribution is 53. Use Empirical formula to find approximate, value of median., , Mathematics-X, , 219
Page 236 :
LONG ANSWER TYPE QUESTIONS, , 33. The mean of the following data is 53, Find the values of f1 and f2., C.I, f, , 0–20, 15, , 20–40, f1, , 40–60, 21, , 60–80, f2, , 80–100, 17, , Total, 100, , 34. If the median of the distribution given below is 28.5, find the values of x and y., C.I, f, , 0–10, 5, , 10–20, 8, , 20–30, x, , 30–40, 15, , 40–50, y, , 50–60, 5, , Total, 60, , 35. The median of the following distribution is 35, find the values of a and b., C.I, f, , 0–10 10–20, 10, 20, , 20–30, a, , 30–40, 40, , 40–50, b, , 50–60, 25, , 60–70, 15, , Total, 170, , 36. Find the mean, median and mode of the following data:, C.I, f, , 11–15, 2, , 16–20, 3, , 21–25, 6, , 26–30, 7, , 31–35, 14, , 36–40 41–45 46–50, 12, 4, 2, , 37. The rainfall recorded in a city for 60 days is given in the following table:, Raifall (In cm), No. of Days, , 0–10, 16, , 10–20, 10, , 20–30, 8, , 30–40, 15, , 40–50, 5, , 50–60, 6, , Calulate the median rainfall using a more than type ogive., 38. Find the mean of the following distribution by step- deviation method:, Daily Expenditure 100–150, (in `), , 150–200, , 4, , No. of Households, , 5, , 200–250 250–300 300–350, 12, , 2, , 2, , 39. The distribution given below show the marks of 100 students of a class:, Marks, No. of, Students, , 0–5, , 5–10, , 10–15, , 15–20, , 20–25, , 25–30, , 30–35, , 35–40, , 4, , 6, , 10, , 10, , 25, , 22, , 18, , 5, , Draw a ‘less than’ type and a ‘more than’ type ogive from the given data. Hence, obtain the median marks from the graph., , 220, , Mathematics-X
Page 237 :
40. The annual profit earned by 30 factories in an industrial area is given below:, Profit (` in lakh), No. of Factories, More than or equal to 5, 30, More than or equal to 10, 28, More than or equal to 15, 16, More than or equal to 20, 14, More than or equal to 25, 10, More than or equal to 30, 7, More than or equal to 35, 3, More than or equal to 40, 0, Draw both ogives for the data and hence find the median., 41. Convert the following distribution into ‘Less than’ and then draw its ogive, (CBSE 2018 -19), Class Interval 30 – 40, Frequency, , 40 – 50, , 50 – 60, , 5, , 8, , 7, , 60 – 70 70 – 80, 10, , 6, , 80 – 90 90 – 100, 6, , 8, , 42. If mean of the given distribution is 65.6 find the missing frequency., (CBSE 2017), Class Interval, Frequency, , 10 – 30, , 30 – 50, , 50 – 70, , 70 – 90, , 5, , 8, , f1, , 20, , 90 – 110 110 – 130, f2, , 2, , Total, 50, , 43. The mode of the frequency distribution is 36. Find the missing frequency (f)., (CBSE 2020), Class, Frequency, , 0 – 10, , 10 – 20, , 20 – 30, , 30 – 40, , 8, , 10, , f, , 16, , 40 – 50 50 – 60, 12, , 6, , 60 – 70, 7, , 44. The mean of the following frequency distribution is 18. The frequency f in the, class interval 19-21 is missing. Determine f., (CBSE 2020), Class Interval 11– 13, Frequency, , 13 – 15, , 15 – 17, , 17 – 19, , 6, , 9, , 13, , 3, , 19 – 21 21 – 23 23 – 25, f, , 5, , 4, , 45. The following table gives production yield per hectare of wheat of 100 farms, of a village :, (CBSE 2020), Production Yield 40 – 45, Frequency, 4, , 45 – 50, 6, , 50 – 55, 16, , 55 – 60, 20, , 60 – 55, 30, , 65 – 70, 24, , Change the distribution to a ‘more than’ type distribution and draw its ogive., Mathematics-X, 221
Page 238 :
ANSWERS AND HINTS, , 1. 16.4 approx., , 2. 20, , 3. 9, , 4. 3, , 5. x = 25, , 6. 5, , 7. Median = 20, , 8. 24.5, , 9. (i) B (First make intervals continuous, Then find class size), (ii) C, (iii) B, (iv) C, Modal class 15 – 20 , (v) B , , Median class 10 –15 , (vi) B, 10., , 17.5 and 45, , 11. (a) 3 Median – 2 mean, , (b) Median, , (c) 20.5, , (d) Histogram, , (e) 8, , (f) Mean, , (g) 42 – 50 (as difference b/w 2 consecutive observation is 8, Subtract, , 8, 8, form 46 for Lower Limit and Add, to 46 for upper Limit), 2, 2, f i ui, (i) x = a + f h, i, , (h) Median, , n, 2 – cf, (j) Median = l + , f, , , 222, , , , h, , , , (k) Mode = l +, , ( f1 fo ), h, (2 f1 fo f 2 ), , 1, (upper limit + Lower limit), 2, , (l) Range = 255 – 103 = 152, , (m), , (n) 12.9, , fi d i, (o) x = a + f, i, , Mathematics-X
Page 239 :
12. 56, , 13. 20, , 14. 14, , 15. 12.89 approx., , 17., , 18., , Marks, , No. of students, , less than 10, , 7, , less than 20, , 16, , less than 30, , 22, , less than 40, , 30, , less than 50, , 40, , Class Interval, , Frequency, , 25 – 30, , 25, , 30 – 35, , 34 = f0, , 35 – 40, , 50 = f1, , 40 – 45, , 42 = f2, , 45 – 50, , 38, , 50 – 55, , 14, , Mode = l +, , f1 – f 0 , , 50 – 34 5, 16 5, h = 35 +, =, 35, +, 2 f1 – f0 – f 2 , 100 – 34 – 42 , 24, , = 35 + 3.33 = 38.33 approx., 19., , xi, , fi, , cf, , 10, , 2, , 2, , 20, , 3, , 5, , 30, , 2, , 7, , 40, , 3, , 10, , 50, , 1, , 11, , Total, , 11, , N = 11 (odd), N 1, Median = , , 2 , , Mathematics-X, , th, , observation = 6th observation = 30, , 223
Page 240 :
fi xi, fi xi, 20. x = f 45 20 fi xi 900, i, , 21. 8.15, , 22. 62.5, , 23. 14.46 cm, , 24. 11, , 25. 27, , 26. 25, , 27. 30, , 29. 63.75 cm, , 30., , Mark, , xi, , di, , ui, , fi, , fiui, , 30 – 35, , 32.5, , – 15, , –3, , 14, , – 42, , 35 – 40, , 37.5, , – 10, , –2, , 16, , – 32, , 40 – 45, , 42.5, , –5, , –1, , 28, , – 28, , 45 – 50, , 47.5 = a, , 0, , 0, , 23, , 0, , 50 – 55, , 52.5, , 5, , 1, , 18, , 18, , 55 – 60, , 57.5, , 10, , 2, , 8, , 16, , 60 – 65, , 62.5, , 15, , 3, , 3, , 9, , 110, , –59, , x =a+, , fi ui, 59, h = 47.5 –, 5 = 47.5 – 2.68 = 44.82, f i, 110, , 31. (Make Table just like Q. 30), x =a+, , 18 = 18 +, , fi ui, h, f i, , k – 8 2, 40 k, , 2k – 16 = 0, k=8, 32., , f1 – f0 , Mode = l + 2 f – f – f h, 1 0 2, 29 – 21, = 60 + 2 29 – 21 – 17 20 = 68, , , , 224, , Mathematics-X
Page 241 :
Mode = 3 Median – 2 mean, 68 = 3 Median – 2 × 53, 68 106, = Median, 3, Median = 58, , 33. f1 = 18, f2 = 29, , 34. x = 20, y = 7, , 35. a = 35, b = 25, 36. Mean = 32, median = 33, mode = 34.39 approx., 37. Median = 25 cm, , 38. Mean = ` 211, , 39. Median = 24, , 40. Median = ` 17.5 lakhs., , 41. Less than, Less than 40, Less than 50, Less than 60, Less than 70, Less than 80, Less than 90, Less than 100, , f, , cf, , 7, 5, 8, 10, 6, 6, 8, , 7, 12, 20, 30, 36, 42, 50, , Plot (40,7), (50, 12), (60, 20), (70, 30) (80, 36), (90, 42), (100, 50), Join free hand to get ogive., 42., , C.I, , fi, , xi, , fixi, , 10 – 30, , 5, , 20, , 100, , 30 – 50, , 8, , 40, , 320, , 50 – 70, , f1, , 60, , 60f1, , 70 – 90, , 20, , 80, , 1600, , 90 – 110, , f2, , 100, , 100f2, , 110 – 130, , 2, , 120, , 240, , 35 + f1 + f2, Mathematics-X, , 2260 + 60 f1 + 100 f2, 225
Page 243 :
PRACTICE-TEST, Statistics, Time : 1 Hr., 1., 2., 3., , SECTION-A, Find the class mark of a class a – b, Find the mean of all the even numbers between 11 and 21., An ogive curve is used to detemine, (a) Range, , 4., , M.M. : 20, , (b) Mean, , (c) Mode, , 1, 1, 1, , (d) Median, , State True/False :, , 1, , “Mean can be determined graphically.”, 5., 6., 7., , SECTION-B, The mean of 50 observations is 20. If each observation is multiplied by 3, then, find the new mean., 2, The mean of 10 observations is 15.3. If two observations 6 and 9 are replaced, by 8 and 14 respectively. Find the new mean., 2, Write the modal class for the following frequency distribution, 2, Classes, frequency, , 1–4, , 5–8, , 9 – 12, , 13 – 16, , 17 – 20, , 21 – 24, , 8, , 9, , 1, , 12, , 8, , 9, , SECTION-C, 8., , Find the mean:, , 3, , Marks, less than 20 less than 40 less than 60 less than 80 less than 100, No. of Students, 4, 10, 28, 36, 50, 9., , Find the value of x if the mode is given to be 58 years., Age (in years) 20–30, No. of patients, 5, , 30–40, 13, , 40–50, x, , 50–60, 20, , 60–70, 18, , 3, 70–80, 19, , SECTION-D, 10. The mean of the following frequency distribution is 57.6 and the number of, observations is 50. Find the value of f1 & f2., 4, Mathematics-X, , 227
Page 244 :
Class Interval 0–20, frequency, , 20–40, 7, , 40–60, f1, , 60–80, 12, , 80–100, f2, , 100–120, 8 5, , OR, Following is the age distribution of cardiac patients admitted during a month, in a hospital:, Age (in years), No. of patients, , 20–30, 2, , 30–40, 8, , 40–50, 15, , 50–60, 12, , 60–70, 10, , 70–80, 5, , Draw a ‘less than type’ and ‘more than type’ ogives and from the curves, find, the median., , 228, , Mathematics-X
Page 245 :
CHAPTER, , 15, , Probability, Probabilty, , Experiment, , Experimental, probability, , Random, experiment, , Event, , Outcomes, , Equally likely, , Sample, space, , Complementary, event, Sure event, , Favourable, outcomes, , Impossible, event, , Theoritical, or classical, probabilty, , KEY POINTS:, , 1., , Probability is a quantitative measure of likelihood of occurrence of an event., , 2., , Probability of an event, , 3., , 0 P (E) 1, , 4., , If P(E) = 0, then it is an impossible event., , 5., , If P(E) = 1, then it is sure event., , 6., , If E is an event, then not E( E ) is called complementary event., , 7., , P( E ) = 1 – P(E) P(E) + P( E ) = 1, , 8., , Probability of an event is never negative., , 9., , Sample space (S) : The collection of all possible outcomes of an event., , Mathematics-X, , E=, , Number of outcomes favourable to E, Total number of outcomes, , 229
Page 246 :
Examples of Sample space, 1., , When one coin is tossed, then S = H, T, , 2., , When two coins are tossed, then S = HH, TT, HT, TH, , 3., , When three coins are tossed, then S = HHH, TTT, HTT, THT, TTH, THH,, HTH, HHT, , 4., , When four coins are tossed, then S = HHHH, TTTT, HTTT, THTT, TTHT, TTTH,, HHHT, HHTH, HTHH, THHH, HTHT, THTH, TTHH, HHTT, THHT, HTTH., , , , , , , , , 1 coin, , 2coins, , 3 coins, , 2 outcomes, , 2 × 2 outcomes, , 2×2×2=8, outcomes, , , , , , , , 4 coins, , , 2 × 2 × 2 × 2 = 16, outcomes, , 1., 2., , When a die is thrown once, then S = 1, 2, 3, 4, 5, 6, n(S) = 6, When two dice are thrown together or A die is thrown twice, then, S = (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6), n(S) = 6 × 6 = 36, 3. When 3 dice are thrown or a die is thrown thrice then, n(S) = 6 × 6 × 6 = 216,, n(S) no. of outcomes in sample space, Playing cards n(s) = 52, Red Cards (26), Heart (13), , Diamond (13), , Black Cards (26), Spade (13), , Class (13), , Each suit contains 1 ace, 1 king, 1 Queen, 1 jack and nine, number cards 2, 3, 4, 5, 6, 7, 8, 9, 10, Face card 12, 4 king, 4 Queen & 4 Jack, 230, , Non face card 40, 36 number cards + 4 aces, Mathematics-X
Page 247 :
VERY SHORT ANSWER TYPE QUESTIONS, , 1., , Fill in the Blanks, (a) The probability of an event is greater than or equal to ............... and is less, than or equal to ..............., [NCERT], (b) The probability of an impossible event is ..............., (c) The probability of an event that is certain to happen is ............... and such, an event is called ..............., [NCERT], (d) The sum of probabilities of all the elementary events of an experiment is, ..............., [NCERT], (e) Probability of an event E + probability of the event not E is equal to ..............., [NCERT], (f) If probability of winning a game is, ..............., , 4, , then the probability of its losing is, 9, , (g) If coin is tossed twice, then the number of possible outcomes is ..............., (h) If a die is thrown twice, then the number of possible outcomes is ..............., 2., , State True/False, (a) The probability of an event can be negative., (b) The probability of an event is greater than 1., , 3., , Multiple Choice Questions, (i) Which of the following cannot be the probability of an event?, (A) 0.7, , (B), , 2, 3, , (C) – 1.5, , [NCERT], , (D) 15%, , (ii) Which of the following can be the probability of an event?, [NCERT Exemplar], 18, 8, (D), 23, 7, (iii) An event is very unlikely to happen, its probability is closest to, , (A) – 0.04 (B) 1.004, , (C), , [NCERT Exemplar], (A) 0.0001 (B) 0.001, Mathematics-X, , (C) 0.01, , (D) 0.1, 231
Page 248 :
(iv) Out of one digit prime numbers, one number is selected at random. The, probability of selecting an even number is:, 1, 1, 4, 2, (B), (C), (D), 2, 4, 9, 5, (v) When a die is thrown, the probability of getting an odd number less than 3, is:, , (A), , 1, 1, 1, (B), (C), (D) 0, 6, 3, 2, (vi) Rashmi has a die whose six faces show the letters as given below:, , (A), , A, , B, , C, , D, , A, , C, , If she throws the die once, then the probability of getting C is:, (A), , 1, 3, , (B), , 1, 4, , (C), , 1, 5, , (D), , 1, 6, , (vii) A card is drawn from a well shuffled pack of 52 playing cards. The event E, is that the card drawn is not a face card. The number of outcomes favourable, to the event E is:, (A) 51, (B) 40, (C) 36, (D) 12, Choose the correct answer from the given four options, , 4., , (i) If the probability of an even is ‘p’ then probability of its complementary, event will be:, (A) p – 1, , (B) p, , (C) 1 – p, , (D) 1 , , 1, p, , (ii) In a family of 3 children, the probability of having atleast one boy is:, [CBSE 2014], 7, 1, 5, 3, (B), (C), (D), 8, 8, 8, 4, (iii) The probability of a number selected at random from the numbers 1, 2, 3,, .... 15 is a multiple of 4 is:, (CBSE 2020), , (A), , (A), , 232, , 4, 15, , (B), , 2, 15, , (C), , 1, 15, , (D), , 1, 5, , Mathematics-X
Page 249 :
(iv) The probability that a non-leap year selected at random will contains 53, Mondays is:, 1, 2, 3, 5, (A), (B), (C), (D), 7, 7, 7, 7, (v) A bag contains 6 red and 5 blue balls. One ball is drawn at random. The, probability that the ball is blue is:, 5, 5, 6, 2, (A), (B), (C), (D), 6, 11, 11, 11, (vi) One alphabet is chosen from the word MATHEMATICS. The probability, of getting a vowel is:, 6, 5, 3, 4, (B), (C), (D), 11, 11, 11, 11, (vii) Two coins are tossed simultaneously. The probability of getting at most, one head is, , (A), , 1, 1, 2, 3, (B), (C), (D), 4, 2, 3, 4, A card is drawn at random from a pack of 52 playing cards. Find the probability, that the card drawn is neither an ace nor a king., , (A), , 5., 6., , Out of 250 bulbs in a box, 35 bulbs are defective. One bulb is taken out at, random from the box. Find the probability that the drawn bulb is not defective., , 7., , Non Occurance of any event is 3:4. What is the probability of Occurance of, this event?, , 8., , If 29 is removed from (1, 4, 9, 16, 25, 29), then find the probability of getting a, prime number., , 9., , A card is drawn at random from a deck of playing cards. Find the probability of, getting a face card., , 10. In 1000 lottery tickets, there are 5 prize winning tickets. Find the probability of, winning a prize if a person buys one ticket., 11. One card is drawn at random from a pack of cards. Find the probability that it, is a black king., (CBSE 2020), 12. A die is thrown once. Find the probability of getting a perfect square., 13. Two dice are rolled simultaneously. Find the probability that the sum of the, two numbers appearing on the top is more than and equal to 10., Mathematics-X, , 233
Page 250 :
14. Find the probability of multiples of 7 in 1, 2, 3, .......,33, 34, 35., 15. If a pair of dice is thrown once, then what is the probability of getting a sum of, 8?, (CBSE 2020), 16. A letter of English alphabet is chosen at random. Determine the probability, that chosen letter is a consonant., (CBSE 2020), 17. If the probability of winning a game is 0.07, what is the probability of losing, it?, (CBSE 2020), SHORT ANSWER TYPE QUESTIONS-I, 18. A card is drawn at random from a well shuffled pack of 52 playing cards. Find, probability of getting neither a red card nor a queen., [CBSE 2016], 19. Two different dice are rolled together. Find the probability, (a) of getting a doublet,, (b) of getting a sum of 10, of the numbers on the two dice., [CBSE 2018], 20. A box contains 12 balls of which some are red in colour. If 6 more red balls are, put in the box and a ball is drawn at random, the probability of drawing a red, ball doubles than what it was before. Find the number of red balls in the box., [CBSE 2018], 21. An integer is chosen random between 1 and 100. Find the probability that (i) it, is divisible by 8, (ii) Not divisible by 8., [CBSE 2018], 22. Three different coins are tossed together. Find the probability of getting (i), exactly two heads, (ii) at least two heads., 23. Cards marked with number 3, 4, 5, .... 50 are placed in a box and mixed, thoroughly. A card is drawn at random from the box. Find the probability that, the selected cards bears a perfect square number., [CBSE 2016], 24. A bag contains 5 red balls and some blue balls. If the probability of drawing a, blue ball at random from the bag is three times that of a red ball, find the, number of blue balls in the bag., (CBSE 2020), 25. Two different dice are thrown together, find the probability that the sum of the, numbers appeared is less than 5., (CBSE 2020), 26. Find the probability that 5 sundays occurs in the month of November of a, randomly selected year., (CBSE 2020), , 234, , Mathematics-X
Page 251 :
27. In a family of three children. Find the probability of having at least two boys., (CBSE 2020), 28. Two dice are thrown at the same time. Find the probability of getting different, numbers on the two dice., (CBSE 2020), 29. If a number x is chosen at random from the numbers –3, –2, –1, 0, 1, 2, 3. What, is probability that x2 4 ?, (CBSE 2020), SHORT ANSWER TYPE QUESTIONS-II, 30. A number x is selected at random from the numbers 1, 2, 3 and 4. Another, number y is selected at random from the numbers 1, 4, 9 and 16. Find the, probability that the product of x and y is less than 16., [CBSE 2016], 31. In a single throw of a pair of different dice, what is the probability of getting, (a) a prime number on each dice,, (b) a total of 9 or 11?, [CBSE 2016], 32. A bag contains 15 white and some black balls. If the probability of drawing a, black ball from the bag is thrice that of drawing a white ball, find the number of, black balls in the bag., [CBSE 2017], 33. Two dice are rolled once. Find the probability of getting such numbers on the, two dice,, (a) whose product is 12., (b) Sum of numbers on the two dice is atmost 5., 34. There are hundred cards in a bag on which numbers from 1 to 100 are written., A card is taken out from the bag at random. Find the probability that the number, on the selected card., [CBSE 2016], (a) is divisible by 9 and is a perfect square., (b) is a prime number greater than 80., 35. In a lottery, there are 10 prizes and 25 are empty. Find the probability of getting, a prize. Also verify P(E) + P( E ) = 1 for this event., 36. P(winning) =, , Mathematics-X, , [CBSE 2020], , x, 1, , P(Losing) = . Find x., 12, 3, , 235
Page 252 :
LONG ANSWER TYPE QUESTIONS, , 37. Cards marked with numbers 3, 4, 5, .........,50 are placed in a box and mixed, thoroughly. One card is drawn at random from the box, find the probability that, the number on the drawn card is, (i) divisible by 7 (ii) a two digit number., 38. A bag contains 5 white balls, 7 red balls, 4 black balls and 2 blue balls. One ball, is drawn at random from the bag. Find the probability that the balls drawn is, (i) White or blue, , (ii) red or black, , (iii) not white, , (iv) neither white nor black, , 39. The king, queen and jack of diamonds are removed from a pack of 52 playing, cards and the pack is well shuffled. A card is drawn from the remaining cards., Find the probability of getting a card of, (i) diamond, , (ii) a jack, , 40. The probability of a defective egg in a lot of 400 eggs is 0.035. Calculate the, number of defective eggs in the lot. Also calculate the probability of taking out, a non defective egg from the lot., 41. Slips marked with numbers 3,3,5,7,7,7,9,9,9,11 are placed in a box at a game, stall in a fair. A person wins if the mean of numbers are written on the slip., What is the probabilty of his losing the game?, 42. A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn, at random from the box, find the probability that it bears, (i) a two digit number, , (ii) a perfect square number, , (iii) a number divisible by 5., 43. A card is drawn at random from a well shuffled deck of playing cards. Find the, probability that the card drawn is, (i) a card of spade or an ace, , (ii) a red king, , (iii) neither a king nor a queen, , (iv) either a king or a queen, , 44. A card is drawn from a well shuffled deck of playing cards. Find the probability, that the card drawn is, (i) a face card, , (ii) red colour face card, , (iii) black colour face card, 236, , Mathematics-X
Page 253 :
45. Ramesh got ` 24000 as Bonus. He donated ` 5000 to temple. He gave ` 12000, to his wife, ` 2000 to his servant and gave rest of the amount to his daughter., Calculate the probability of, (i) wife’s share, , (ii) Servant’s Share, , (iii) daughter’s share., 46. 240 students reside in a hostel. Out of which 50% go for the yoga classes early, in the morning, 25% go for the Gym club and 15% of them go for the morning, walk. Rest of the students have joined the laughing club. What is the probability, of students who have joined laughing club?, 47. A box contains cards numbered from 11 to 123. A card is drawn at random, from the box. Find the probability that the number on the drawn card is:, [CBSE 2018], (i) A square number, , (ii) a multiple of 7., , 48. A die is thrown twice. Find the probability that:, (i) 5 will come up at least once, (ii) 5 will not come up either time, , [CBSE 2019], , 49. Cards marked 1, 3, 5 .... 49 are placed in a box and mixed thoroughly. One card, is drawn from the box. Find the probability that the number on the card is :, [CBSE 2017], (i) divisible by 3, , (ii) a composite number, , (iii)not a perfect square, , (iv) multiple of 3 and 5, , 50. Red queens and black jacks are removed from a pack of 52 playing cards. Find, the probability that the card drawn from the remaining cards is:, [CBSE 2015], (i) a card of clubs or an ace, , (ii) a black king, , (iii) neither a jack nor a king, , (iv) either a king or a queen, , 51. A box contain 100 red cards, 200 yellow cards and 50 blue cards. If a card is, drawn at random from the box, find the probability that it will be:, [CBSE 2012], (a) a blue card, (b) not a yellow card, (c) neither yellow nor a blue card, Mathematics-X, , 237
Page 254 :
ANSWERS AND HINTS, , 1., , 2., , (a) 0 and 1, , (b) 0, , (e) 1, , (f), , 5, 9, , (c) 1 and sure event(d) 1, (g) 4, , (h) 36, , (a) False, because 0 P(A) 1, (b) False, because 0 P(A) 1, , 3., , (i) (C), (iii) (A) (as unlikely to happen), (v) (A), , (ii) (C), (iv) (B) (prime no. 2, 3, 5, 7), (vi) (A), , (vii) (B) (Face card = 12, Remaining cards = 40), 4., , (i) (C), (ii) (A) (Sample space = bbb, bbg, bgb, gbb, ggg, ggb, gbg, ggb), 1, ), 15, (iv) (A) (Total weeks 52, Remaining day 1, sample space = {S, M, Tu, W, Th,, F, Sat}), , (iii) (D) (Probability, , (v) (C), (vi) (D) (vowels A, A, E, I), (vii) (D), 5., , Total = 52, No. of Aces = 4, No. of kings = 4, P (neither ace nor king) =, , 6., , P(not defective) = 1 , , 7., , Total case = 3 + 4 = 7, P(occurrence) =, , 238, , 44 11, , 52 13, , 35 43, , 250 50, , 4, 7, , Mathematics-X
Page 255 :
8., 9., , P(prime no.) = 0, No. of face card = 12, P(face card) =, , 12 3, , 52 13, , 10. Probability of winning =, , 5, 0.005, 1000, , 11. Total black king = 2, 2, 1, =, 52, 26, 12. Sample space : 1, 2, 3, 4, 5, 6, Perfect square : 1, 4, , P(Black King) =, , P(perfect square) =, , 2 1, , 6 3, , 13. Total cases = 36, Favourable cases (4, 6), (5, 5), (6, 4), (5, 6), (6, 5), (6, 6), 6 1, , 36 6, 14. Multiples of 7 are 7, 14, 21, 28, 35, , P(sum of two numbers is 10) =, , Probability (multiple of 7) =, 15. P(sum of 8) =, , 5 1, , 35 7, , 5, 36, , 21, 26, 17. P (losing) = 1 – 0.07 = 0.93, 18. No. of red cards = 26, No. of Queens = 04 – 2 = 02 (as 2 red queens are included already), No. of cards that are neither red nor queen = 56 – (26 + 2) = 24, , 16. P (consonant) =, , Required probability =, , Mathematics-X, , 24 6, , 52 13, , 239
Page 256 :
19. (i) Doublets are (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), 6 1, , 36 6, (ii) Sum 10 cases : (4, 6), (5, 5), (6, 4), , Required probability =, , Required probability =, 20., , 3, 1, , 36 12, , x6, x, 2 x = 3, 12 , 18, , 21. Total outcomes between 1 and 100 = 98, (i) Nos. divisible by 8 : 8, 16, 24, ...., 96, favourable cases = 12, Required probability =, , 12 6, , 98 49, , 6 43, , 49 49, 22. Sample space : HHH, TTT, HTT, THT, TTH, THH, HTH, HHT, , (ii) Probability (integer is not divisible by 8) = 1 , , (i) P(exactly 2 heads) =, , 3, 8, , 4 1, , 8 2, 23. Total cards = 50 – 3 + 1 = 48, perfect squares are 4, 9, 16, 25, 36, 49, , (ii) P(atleast 2 heads) =, , 6 1, , 48 8, 24. Let the number of blue balls = x, Total balls = (5 + x), P (Blue ball) = 3 × P (Red ball), , Required probability =, , x, 5 , = 3 , , 5 x, 5 x , , x = 15, 240, , Mathematics-X
Page 257 :
25. Favourable outcomes : (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (3, 1), 6, 1, =, 36, 6, 26. Number of total days in the month of November = 30, i.e. 4 complete weeks and 2 days., , P (sum less than 5) =, , P (5 Sundays) =, , 2, 7, , 27. P (atleast two boys) =, , 4, 1, =, 8, 2, , 30, 5, =, 36, 6, 29. Favourable outcomes : –2, –1, 0, 1, 2, , 28. P (Different numbers) =, , 5, 7, 30. Sample space, , P (x2 4) =, , (1, 1), (1, 4), (1, 9), (1, 16), (2, 1), (2, 4), (2, 9), (2, 16), (3, 1), (3, 4), (3, 9), (3, 16), (4, 1), (4, 4), (4, 9), (4, 16), , Favourable cases xy < 16, (1, 1), (1, 4), (1, 9), (2, 1), (2, 4), (3, 1), (3, 4), (4, 1), Required probability =, , 8 1, , 16 2, , 31. Total outcomes = 36, (a) Favourable outcomes, (2, 2), (2, 3), (2, 5), (3, 2), (3, 3), (3, 5), (5, 2), (5, 3), (5, 5), Required probability, , 9 1, , 36 4, , (b) Favourable outcomes, (3, 6), (4, 5), (5, 4), (6, 3), (5, 6), (6, 5), Required probability =, Mathematics-X, , 6 1, , 36 6, 241
Page 258 :
32., , x, 15, , 3, 15 x, 15 x, No. of black balls = 45, , x = 45, , 33. (a) S = (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) , (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) , , , (3,, 1), (3,, 2), (3,, 3), (3,, 4), (3,, 5), (3,, 6), , , (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) , , , (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) , Favourable outcomes: (2, 6), (3, 4), (4, 3), (6, 2), 4 1, , 36 9, (b) Favourable outcomes (sum 5), = (1, 1), (1, 2), (1, 3) (1, 4) (2, 1) (2, 2) (2, 3) (3, 1) (3, 2) (4, 1), , Required probability =, , Required probability =, , 10 5, , 36 18, , 34. (i) Total number = 100, Number divisible by 9 and a perfect square are 9, 36, 81, 3, = 0.03, 100, (ii) Prime no. > 80 are 83, 89, 97, , Required probability, , Required probability, , 3, = 0.03, 100, , 35. Total tickets = 35, P(E) = P(getting a prize) =, , 10 2, , 35 7, , P (E) = P(not getting a prize) =, , 25, 5, =, 35, 7, , 2 5 7, 1, 7 7 7, 36. P(winning) + P(losing) = 1, , P(E) + P (E) =, , x 1, 1 x = 8, 12 3, 242, , Mathematics-X
Page 259 :
37. Total cards = 50 – 3 + 1 = 48, (i) No. divisible by 7 are 7, 14, 21, 28, 35, 42, 49, 7, 48, (ii) Two digit no. are 10, 11, 12, .... 50, No. of favourable outcomes = 50 – 10 + 1 = 41, , Required probability =, , Required probability =, 38. (i), , 5 2 7, , 18, 18, , (ii), , 41, 48, , 7 4 11, , 18, 18, , 7 4 2 13, 72 9 1, , , , (iv), 18, 18, 18, 18 2, 39. (i) Remaining cards = 52 – 3 = 49, Remaining diamonds = 13 – 3 = 10, , (iii), , Required probability =, , 10, 49, , 3, (as 1 jack has been removed), 49, 40. Total eggs = 400, P(defective eggs) = 0.035, Let defective eggs = x, , (ii) P(jack) =, , x, = 0.035, 400, x = 400 × 0.035, x = 14, P(non defective eggs) = 1 – 0.035 = 0.965, , 41. Mean =, , 3 3 5 7 7 7 9 9 9 11 70, 7, =, 10, 10, , P(he loses) = 1 , , 3, 7, , 10 10, , 42. Total no. = 90, (i) Two digit no.s 10, 11, 12, ...., 90, No. of favourable cases = 90 – 10 + 1 = 81, Required probability =, Mathematics-X, , 81 9, , 90 10, 243
Page 260 :
(ii) Perfect square no. : 1, 4, 9, 16, 25, 36, 49, 64, 81, Required probability =, , 9, 1, , 90 10, , (iv)No.s divisible by 5 :, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, Required probability =, , 18 1, , 90 5, , 13 3 16 4, , , 52, 52 13, , 43. (i) P(a card of spade or an ace) =, (ii) P(red king) =, , 2, 1, , 52 26, , (iii)P(neither a king nor a queen) = 1 –, (iv)P(either a king or a queen) =, 44. (i), , 12 3, , 52 13, , 45. (i) P(wife’s share) =, , 8, 2, , 52 13, , 6, 3, , 52 26, , (ii), , 8, 2 11, 1 , 52, 13 13, , (iii), , 6, 3, , 52 26, , 12000 1, , 24000 2, , (ii) P(servant’s share) =, , 2000, 1, , 24000 12, , 5000, 5, , 24000 24, 46. 10% students joined laughing club, , (iii)P(Daughter’s share) =, , P(students who have joined laughing clubs) =, , 10, 1, , 100 10, , 47. Total cards = 123 – 11 + 1 = 113, (i) Square numbers : 16, 25, 36, 49, 64, 81, 100, 121, 8, 113, (ii) Multiple of 7 are 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105,, 112, 119., , Required probability =, , Required Probality =, 244, , 16, 113, , Mathematics-X
Page 261 :
48. Total outcomes = 36, 11, 36, Favourable cases (1, 5), (2, 5), (3, 5), (4, 5), (5, 5), (6, 5), (5, 1), (5, 2), (5,, 3), (5, 4), (5, 6), , (i) P(5 will come up at least once) =, , (ii) P(5 will not come up either time) = 1 , , 11 25, , 36 36, , 49. S = 1, 3, 5, ...., 49. Total outcome = 25, (i) No. divisible by 3 are 3, 9, 15, 21, 27, 33, 39, 45, 8, 25, (ii) Composite Nos : 9, 15, 21, 25, 27, 33, 35, 39, 45, 49, , Required probability =, , 10 2, , 25 5, (iii)P(not a perfect square) = 1 – P(perfect square) {Perfect square no. : 1, 9,, 25, 49}, , Required probability =, , = 1, , 4, 21, =, 25, 25, , (iv)Multiple of 3 and 5, Multiple of 15 = 15, 45, Required probability =, 50. (i), (iii), , 2, 25, , 16 1, , 48 3, 1, , (ii), 6, 1 7, 1 , 48, 8 8, , 51. (a) P(blue card) =, , Mathematics-X, , (iv), , 50 1, , 350 7, , (c) P(neither yellow nor blue) =, , 2, 1, , 48 24, 6 1, , 48 8, , (b) P(not yellow card) =, , 150 3, , 350 7, , 100 2, , 350 7, , 245
Page 262 :
PRACTICE-TEST, Probabiltiy, Time : 1 Hr., , M.M. : 20, SECTION-A, , 1., , A die is thrown once. find the probability of getting an odd number., , 1, , 2., , A bag contains 4 red and 6 black balls. one ball is drawn from the bag at random., Find the probability of getting a black ball., 1, , 3., , A single letter is selected from the word PROBABILITY. The probability it is, a vowel = ..............., 1, , 4., , The probability of selecting a rotten apple randomly from a heap of 900 apples, is 0.18. The number of rotten apples are ..............., (CBSE 2017)1, SECTION-B, , 5., , Find the probability of having 53 friday in a year., , 2, , 6., , One card is drawn at random from the well shuffled pack of 52 cards. Find the, probability of getting a black face card or a red face card., 2, , 7., , A coin is tossed twice. Find the probability of getting atleast one tail., , 2, , (CBSE 2014), SECTION-C, 8., , A box contains 5 Red, 4 green and 7 white marbles. One marbles is drawn at, random from the box. What is the probability that marble is, (i) not white, , 8., , (ii) neither red nor white, , A die is thrown once. Find the probability that the number., (i) is an even prime number, , 246, , 3, , (ii) is a perfect square, , 3, , Mathematics-X
Page 263 :
SECTION-D, 10. A box contains cards numbered 1,3,5,........,35. Find the probability that the, card drawn is, (i) a prime number less than 15, , (ii) divisible by both 3 and 15, , 4, , OR, From a deck of 52 playing cards, king, queen and jack of a club are removed, and a card is drawn from the remaining cards. Find the probability that the card, drawn is, (i) A spade, (ii) A queen, (iii) A club, , Mathematics-X, , 247
Page 264 :
CASE STUDY BASED QUESTIONS, , 1., , During a health checkup camp three types of patients registered themselves., 60 were suffering from joint problem , 84 were suffering from some type of, fever and 108 were diabetic. The organisers wants to call doctors for this camp., (i) What is the maximum number of doctors required if each doctor treat same, number of patients of each type of problem., (a) 64, , (b) 14, , (c) 16, , (d) 12, , (c) 21, , (d) 9, , (ii) How many patients each doctor will treat., (a) 7, , (b) 12, , (iii)At the end of the day when the total count was done the number of patients, with joint problems were 48, suffering from fever were 60 and diabetic, patients were 72 only. How many patients each doctor treated., (a) 21, , (b) 15, , (c) 14, , (d) 12, , (iv) If HCF (48, 60, 72) = 7m – 2, what is the value of m, (a) 2, , (b) 1, , (c) 3, , (d) 12, , (v) If HCF (60, 108) = 60 a + 108 b what are the values of a & b., (a) 2, 1, 248, , (b) –2, 1, , (c) –2, –1, , (d) 2, –1, Mathematics-X
Page 265 :
2., , On children's day the supplier of mid day meal supplied packets of biscuits and, chocolates to the students of two schools . One packet of biscuit contains 20, small packets and a packet of chocolate contains 12 pieces of chocolates . He, supplied p packets of biscuit and q packets of chocolate in school A and 2p, packets of biscuits together with some packets of chocolate in the school B., (i) How many students are there in school A., (a) 60, , (b) 240, , (c) 840, , (d) 1200, , (ii) How many large packets of biscuits were supplied in school A., (a) 42, , (b) 20, , (c) 14, , (d) 28, , (iii)How many packets of chocolate were supplied in school A., (a) 42, , (b) 35, , (c) 70, , (d) 40, , (iv) The number of large packets of biscuits distributed in school B., (a) 42, , (b) 84, , (c) 28, , (d) 24, , (v) What is the total number of students in school B., (a) 2520, , Mathematics-X, , (b) 840, , (c) 1680, , (d) 420, , 249
Page 266 :
3., , For a family of three members a cuboidal tank has been made . The volume of, the tank is expressed in the form of a polynomial p(x) = x 3 + 10x2 + 27x + 18, cubic units., (i) What are the possible dimensions of the tank ,if the largest is the length,, the smallest is the height and the third is the breadth., (a) (x + 9)(x + 2)(x + 1), , (b) (x + 6)(x + 3)(x + 1), , (c) (x – 6)(x + 3)(x – 1), , (d) (x – 9)(x – 2)(x + 1), , (ii) If x = 2, what is the quantity of water each member will require., (a) 120, , (b) 40, , (c) 30, , (d) 56, , (iii)Two more members joined the family, how much is the total requirement, of water now., (a) 180, , (b) 200, , (c) 80, , (d) 50, , (iv) If these members are to stay now then how much height of the tank be, increased to fulfill the total requirement without changing length and, breadth., (a) 5, , (b) 2, , (c) 3, , (d) x, , (v) If x remains the same what could be the possible polynomial for the volume, of tank required for these five persons now., , 250, , (a) (x + 3)(x + 9)(x + 1), , (b) (x + 3)(x + 3)(x + 6), , (c) (x – 6)(x + 3)(x + 3), , (d) (x + 6)(x + 3)(x – 3), Mathematics-X
Page 267 :
4., , Three NCC Cadets, of a college planted some plants. The polynomial p(x) = x3, – 12x2 + 47x – 60 shows the number of plants planted by them. If Akool, one of, cadets planted 5 plants, then, (i) How many plants are planted by the remaining two cadets, (a) 12, , (b) 47, , (c) 9, , (d) 7, , (ii) How many plants each of them planted, (a) 3, 4, (iii), , (b) 5, 4, , (c) 5, 3, , (d) 12, 5, , Factorise the given polynomial, (a) (x – 5) (x + 4) (x – 3), , (b) (x – 5) (x – 4) (x + 3), , (c) (x – 12) (x – 5) (x – 1), , (d) (x – 5) (x – 4) (x – 3), , (iv)Instead of 5, if Akool planted 4 plants only what will be the polynomial, (a) x3 – 5x2 + 40x – 48, , (b) x3 – 8x2 + 8x – 48, , (c) x3 – 11x2 + 40x – 48, , (d) x3 – 5x2 + 8x – 48, , (v) What is the polynomial corresponding to the total plants planted by the, remaining two cadets., (a) x2 – x – 12, Mathematics-X, , (b) x2 – x + 12, , (c) x2 – 7x + 12, , (d) x2 + 7x + 12, 251
Page 268 :
5., , The consumption of water in a family is divided into two parts one is fixed, consumption used for various activities like cleaning, washing etc. and the, other is individual consumption. For a family of 6 persons the water required is, 445 cubic units and for a family of 8 members the total requirement of the, water is 575 cubic units . full form of pair of linear equations for the above, situation, (i) What type of lines are these, (a) parallel, , (b) intersecting, , (c) coincident, , (d) inconsistent., , (ii) What is the individual and fixed consumption., (a) 55,65, , (b) 65, 55, , (c) 55, 55, , (d) 65, 65, , (iii)If we draw the graph of the pair of equations then what is the distance of, the point of intersection from y axis, (a) 55, , (b) 65, , (c) 45, , (d) 50, , (iv)How much water is required for a family of 4 members,, (a) 260, (v), , 252, , (b) 315, , (c) 265, , (d) 245, , Form a linear equation for the total consumption of a family of four members., (a) x + 4y = 265, , (b) y + 4x = 315, , (c) x + 4y = 315, , (d) y + 4x = 265, Mathematics-X
Page 269 :
6., , On Diwali occasion two rocket cracers were launched at the same time from, two different places opposite to each other and the path followed by them are, along the lines 3x – 2y = 6 and x + y =12., (i) What type of set of lines they are representing, (a) Intersecting, , (b) Parallel, , (c) Coincident, , (d) cannot say., , (ii) What is the point of start i.e. the point of intersection of the first line with x, -axis., (a) (0, 2), , (b) (2, 0), , (c) (3, 0), , (d) (0,3), , (iii)At what point the second line intersect y-axis., (a) (0, 12), , (b) (12, 0), , (c) (6, 0), , (d) (0,6), , (iv) What is the point of intersection of the two rockets,, (a) (6,0), , (b) (6,6), , (c) (0,6), , (d) (–6, –6), , (v) If both are launched from x-axis,at what height they cross each other,, (a) 6, , Mathematics-X, , (b) 12, , (c) 4, , (d) 24, , 253
Page 270 :
7., , In junior forms, we learnt that numbers which can be arranged in a compact, triangular pattern are called triangular numbers, , 1, , 3, , 6, , 10, , A triangular number p can be expressed as p =, , n(n 1), where n is a positive, 2, , integer., It can be rewritten as n2 + n – 2p = 0, which is called a quadratic equation in n, (i) Consider the quadratic equation x2 + 5x – 6 = 0. Try to substitute the, following values of x into the equation and find which one satisfies it., (a) x = – 6, , (b) x = –3, , (c) x = 0, , (d) x = 1, , (c) 3, 0, , (d) 0,, , (ii) What will be the roots of 2x2 – 3x = 0, (a) 0, 2, , (b) 2, 3, , 3, 2, , (iii)What is the condition for a quadratic equation to have equal roots?, (a) D < 0, , (b) D = 0, , (c) D 0, , (d) D > 0, , (iv) What will be the sum of roots of the equation 3x 2 + 4x – 5 = 0, (a), , 2, 3, , (b), , –2, 3, , (c), , –5, 3, , (d), , –4, 3, , (v) If ax2 + bx + c = 0 is a quadratic equation what is the must have condition?, (a) a = 0, , 254, , (b) b 0, , (c) a 0, , (d) c = 0, , Mathematics-X
Page 271 :
8., , A farmer wants to make a rectangular pen for his sheep in the garden near his, house. To make the pen the farmer planned to make it with wooden fencing to, cover the three sides. He has 60m fencing material to cover three sides and the, other side being a brick wall., (i) If the width be x, then the length of the pen, (a) 60 – 2x, , (b) 2x + 6, , (c) 6x + 20, , (d) 20 – 6x, , (ii) According to the given conditions area of the pen is (Hint: use length as, calculated in (i)), , (iii), , (a) 60x2 – 2x, , (b) 60x + 2x2, , (c) 6x – 20x2, , (d) 60x – 2x2, , If the area of the pen is 250 then the quadratic equation will be, (a) x2 – 30x + 250 = 0, , (b) 2x2 – 30x + 250 = 0, , (c) x2 – 30x + 125 = 0, Mathematics-X, , (d) 2x2 – 60x + 125 = 0, 255
Page 272 :
(iv)Now let’s sketch a graph for the quadratic equation obtained in question(iii)., Which is as follows:, , The area is maximum when, (a) the width = 20m, , (b) the width = 15m, , (c) the width = 25m, , (d) the width = 35m, , (v) If the area of pen is 400, then its width is, (a) 10 or 20, 9., , 256, , (b) 40 or20, , (c) 20 or 20, (d) 40 or 40, As we know a tree or a plant needs both soil and water along with sunlight to, grow. It will have the necessary nourishment in both water and sun to make its, leaves green and fruit to grow. A rural Indian school Gardner planted some, trees on his school at certain distances from the water body following a sequence., There are 25 trees at equal distances of 5 meters in a line with a well, the, distance of the well from the nearest tree being 10 meters. A gardener waters, all the trees separately starting from the well and he returns to the well after, watering each tree to get water for the next., , Mathematics-X
Page 273 :
(i) Distance travelled to water nearest tree and back to the well is:, (a) 10m, , (b) 15m, , (c) 20m, , (d) 25m, , (ii) Progression so formed in the above condition is, , (iii), , (a) 20, 30, 40, 50, ..., , (b) 15, 30, 45, 60,..., , (c) 10, 15, 20, 25,..., , (d) 25, 35, 45, 55, , To find the total distance we have to use the formula, (a) an = a + (n + 1), (c) Sn =, , n, (2a + (n + 1) d), 2, , (b) an = a + (n –1), (d) Sn =, , n, (20 + (n – 1)d), 2, , (iv)Distance travelled to water 25th tree, (a) 250 m, , (b) 260 m, , (c) 270 m, , (d) 280 m, , (v) The total distance the gardener will cover in order to water all the trees., (a) 3000 m, (b) 3500 m, (c) 3800 m, (d) 4000 m, 10. A construction company will be penalized each day of delay in the construction, of the bridge. The penalty will be ` 4000 for the first day and will increase by, ` 1000 for each following day. Based on its budget, the company can afford to, pay a maximum of ` 165000 toward penalty., , Mathematics-X, , 257
Page 274 :
(i) The penalty amount paid by the construction company from the first day as, a sequence, (a) 4000, 8000, 12000,..., , (b) 4000,5000,6000,..., , (c) 5000, 6000, 7000,..., , (d) 1000,5000,9000, , (ii) First-term and difference respectively of the above series is, , (iii), , (a) 4000 and 4000., , (b) 5000 and 1000, , (c) 4000 and 1000, , (d) 1000 and 4000, , Find the maximum number of days by which the completion of work, can be delayed (take Sn = 165000), (a) 10 days, , (b) 20 days, , (c) 15 days, , (d) 25 days, , (iv)The penalty will be charged on the tenth day, (a) ` 16000, , (b) ` 15000, , (c) ` 14000, , (d) ` 13000, , (v) If (x + 1), 3x, and (4x + 2) are the first three terms of an AP, then its 5th, term is:, (a) 14, (b) 19, (c) 24, (d) 28, 11. Rahul is studying in X Standard. He is making a kite to fly it on a Sunday. Few, questions came to his mind while making the kite. Give answers to his questions, by looking at the figure., , (i) Rahul tied the sticks at what angles to each other?, (a) 30°, (b) 60°, (c) 90°, 258, , (d) 60°, Mathematics-X
Page 275 :
(ii) Which is the correct similarity criteria applicable for smaller triangles at, the upper part of this kite?, (a) RHS, (b) SAS, (c) SSA, (d) AAS, (iii) Sides of two similar triangles are in the ratio 4:9. Corresponding medians, of these triangles are in the ratio:, (a) 2 : 3, (b) 4 : 9, (c) 81 : 16, (d) 16 : 81, (iv)In a triangle, if the square of one side is equal to the sum of the squares of, the other two sides, then the angle opposite the first side is a right angle., This theorem is called:, (a) Pythagoras theorem, (b) Thales theorem, (c) The converse of Thales theorem, (d) The converse of Pythagoras theorem, (v) What is the area of the kite, formed by two perpendicular sticks of length 6, cm and 8 cm?, (a) 48 cm2, (b) 14 cm2, (c) 24 cm2, (d) 96 cm2, 12. There exist a tower near the house of Shankar. The top of the tower AB is tied, with steel wire and on the ground, it is tied with string support., One day Shankar tried to measure the longest of the wire AC using Pythagoras, theorem., , (i) In the figure, the length of wire AC is: (take BC = 60 ft), (a) 75 ft, (b) 100 ft, (c) 120 ft, (d) 90 ft, (ii) What is the area of ABC?, (a) 2400 ft2, (b) 4800 ft2, (c) 6000 ft2, (d) 3000 ft2, Mathematics-X, 259
Page 276 :
(iii), , What is the length of the wire PC?, (a) 20 ft, (b) 30 ft, (c) 25 ft, (d) 40 ft, (iv)What is the length of the hypotenuse in ABC?, (a) 100 ft, (b) 80 ft, (c) 60 ft, (d) 120 ft, (v) What is the area of a POC?, (a) 100 ft2, (b) 150 ft2, (c) 200 ft2, (d) 250 ft2, 13. The ECO Club of a senior secondary school in Rohini have to make a Herbal, Garden in a rectangular plot of a land (See figure). Saplings of Tulsi are planted, on the boundary at a distance of 1 m from each other. There is a square land, inside the plot as shown in the figure for planting ‘ALOEVERA’. The students, are to sow seeds of other herbal pants on the remaining area of the plot., Answer the questions given below the diagram:, , (i) Considering A as the origin, what are coordinates of M?, (a) (4, 0), (b) (4, 2), (c) (4, 1), (d) (0, 4), (ii) What are the coordinates of D?, (a) (0, 23), (b) (22, 0), (c) (23, 0), (d) (23, 1), (iii)What is the distance MO?, (a), , (b) 3 3 units, 2 units, (iv) The mid point of PN is, (a) (7, 5), (b) (14, 10), 260, , (c) 5 2 units, , (d) 6 2 units, , (c) (4, 8), , (d) (10, 2), Mathematics-X
Page 277 :
(v) If we join diagonals of square MNOP, in what ratio Q divides diagonals PN, and MO?, (a) 2 : 1, (b) 1 : 1, (c) K : 1, (d) m : n, 14. RPVV, Suraj Mal organised Sports Day in which one of the event is 100 m, race. Participants have to run in the rows which are marked at a distance of 1, metre as shown in the figure. At one time the participants are at position A, B,, 1, th distance PQ, C, 4, has covered the distance PQ, D has covered half the distance PQ., Considering P as origin, answer the questions given below the diagram., , C, D. A has covered half the distance PQ, B has covered, , Q, , P, , (i) On joing A, B, C, D which figure you will get, (a) Square, (b) Rectangle, (c) Rhombus, (d) Quadrilateral, Mathematics-X, , 261
Page 278 :
(ii) What area is enclosed by ABCD ?, (a) 250 sq units (b) 275 sq units, (c) 225 sq units, (d) 300 sq units, (iii)If another participant at E could not run due to some shoe problem, what, are the co-odinates of E, (a) (0, 5), (b) (5, 10), (c) (5, 0), (d) (5, 5), (iv) What is the distance CE?, (a) 10 units, (b) 100 units, (c) 50 units, (d) 70 units, (v) In what ratio B divides AE?, (a) 2 : 1, (b) 1 : 2, (c) 3 : 2, (d) 1 : 1, 15. An electrician has to repair an electric fault on a pole of height 5 m. He needs, to reach a point 1.3 m below the top of the pole to undertake the repair work., The ladder is inclined at an angle of 45° to the horizontal., (you may use, , 2 = 1.41), , (i) What is the length of RB?, (a) 3.7 m, (b) 1.3 m, (c) 7.4 m, (d) 2.6 m, (ii) What is the distance between the foot of the pole and the foot of the ladder?, (a) 1.3 m, , (b) 3.7 m, , (iii)What is the length of the ladder ?, (a) 3.7 m, (b) 7.4 m, 262, , (c) 7.4 m, , (d) 3.7 2 m, , (c) 5.217 m, , (d) 7.05 m, Mathematics-X
Page 279 :
(iv) What is the measure of LRB?, (a) 90°, (b) 30°, (c) 60°, (d) 45°, (v) What type of LRB is ?, (a) Scalene triangle, (b) Obtuse angled triangle, (c) Equilateral triangle, (d) Isosceles triangle, 16. Suresh was going to his school on his bicycle. Suddenly his bicycle chain got, stuck on the chians wheel. He decided to take it to the nearest cycle repairer., There he carefully observed the chain wheels of the cycle. He found that both, chain wheel were almost of the shape of circles., , (i) If both chain wheels are considered as circles then the total number of, tangents are, (a) 1, (b) 2, (c) 3, (d) 4, (ii) If both chain wheels are kept side by touching each other and their diameters, are 42 cm and 14 cm, the distance between their centres is, (a) 7 cm, (b) 14 cm, (c) 28 cm, (d) 56 cm, (iii)The common point of tangent and the circle is called, (a) point of tangent, (b) point of circle, (c) point of radius, (d) point of contact, (iv) Distance between two parallel tangents of a circle is always equal to its, (a) radius, (b) chord, (c) diameter, (d) secant, (v) In a circle of radius 14 cm, length of tangent PT = 48 cm, drawn from a, point P to the circle of centre O. Then length of OP is, (a) 62 cm, (b) 50 cm, (c) 25 cm, (d) 34 cm, 17. A horse is tied to a peg at one corner of a square shaped grass field of sides 15, m by means of a 5 m long rope. Use = 3.14 to answer the following questions., , Mathematics-X, , 263
Page 280 :
(i) What is the area of the grass field?, (a) 225 m, , (b) 225 m2, , (c) 225 m2, , (d), , 225, m2, 4, , (ii) The area of that part of the field in which the horse can graze is :, (a) 19.625 m2, (b) 78.5 m2, (c) 196.25 m2, (d) 19.265 m2, (iii)If the length of rope is 10 m, the grazing area is :, (a) 7.85 m2, (b) 78.5 m2, (c) 225 m2, (d) 785 m2, (iv) The increase in the grazing area if the rope were 10 m long instead of 5 m, is:, (a) 58.875 m2, (b) 58 m2, (c) 58.758 m2, (d) 78.5 m2, (v) The angle made by the horse in grazing the grass field is is :, (a) 45°, (b) 90°, (c) 60°, (d) 360°, 18. On a square handkerchief, nine circular designs each of radius 7 cm are made, as shown in the figure., , (i) What is the side of the square?, (a) 7 cm, (b) 21 cm, (ii) What is the area of square?, (a) 1764 cm2, (b) 441 cm2, (iii)What is the area of one circle ?, (a) 49 cm2, (b) 7 cm2, 264, , (c) 42 cm, , (d) 84 cm, , (c) 49 cm2, , (d) 7056 cm2, , (c) 9 cm2, , (d) 14 cm2, Mathematics-X
Page 281 :
(iv) What is the area of nine circles ?, (a) 154 cm2, (b) 1386 cm2, , (c) 1836 cm2, , (d) 451 cm2, , (v) What is the area of the remaining portion of square handkerchief?, (a) 378 cm2, , (b) 783 cm2, , (c) 738 cm2, , (d) 387 cm2, , 19. Uttar Bantra Sarbojanin Durgotsav Committee had started planning for their, Durga puja a year in advance with a mega budget in mind., Bholeram Tents is given a contract by municipal corporation of Budaun (Uttar, Pradesh), India to setup a mega function pandal (tent). The architect has designed, a tent of height 7.7 m in the form of a right circular cylinder of diameter 36 m, and height 4.4 m surmounted by a right circular cone. This tent is setup in a, rectangular park of dimensions 70 m × 60 m as shown below. The tent is made, up of canvas., (Take = 3.14), , On the basis of the above information, answer any four of the following, questions:, (i) For the workers to finalise the purchase of material, the height of the conical, part is :, (a) 2.3 m, (b) 6.3 m, (c) 3.3 m, (d) 12.1 m, (ii) The slant height of the conical part is :, (a) 18.3 m, (b) 18.7 m, (c) 19.1 m, (d) 19.4 m, Mathematics-X, , 265
Page 282 :
(iii)To purchase the canvas, the area of the canvas to be used approximate in, making the tent, is :, (a) 1353 m2, (b) 1386 m2, (c) 1406 m2, (d) 1533 m2, (iv) The cost of canvas at ` 4.50 per m2 is:, (a) ` 6327, (b) ` 6237, (c) ` 6898.50, (d) ` 6088.50, (v) The area of the rectangular park outside the tent is :, (a) 1883 m2, (b) 2864.64 m2, (c) 3182.64 m2, (d) 4200 m2, 20. In a toys manufacturing company, wooden parts are assembled and painted to, prepare a toy. One specific toy is in the shape of a cone mounted on a cylinder., For the wood processing activity center, the wood is taken out of storage to be, saved, after which it undergoes rought polishing, then is cut, drilled and has, holes punched in it. It is then fine polished using sand paper., , For the retail packaging and delivery activity center, the polished wood subparts are assembled together, then decorated using paint., The total height of the toy is 26 cm and the height of its conical part is 6 cm., The diameters of the base of the conical part is 5 cm and that of the cylinderical, part is 4 cm., On the basis of the above information, answer any four the following questions:, (i) If its cylinderical part is to be painted yellow, the surface area need to be, painted is :, (a) 80 cm2, (b) 82 cm2, (c) 84 cm2, (d) 88 cm2, (ii) If its conical part is to be painted green, the surface area need to be painted, is :, (a) 26.5 cm2, 266, , (b) 22.5 cm2, , (c) 20.5 cm2, , (d) 18.5 cm2, Mathematics-X
Page 283 :
(iii)The volume of the wood used in making this toy, is, (a) 92.5 cm3 (b) 89.5 cm3, (c) 85.5 cm3, (d) 72.5 cm3, (iv) If the cost of painting the toy is 3 paise per cm2, then the cost of painting, the toy is :, (Use = 3.14), (a) r` 10, (b) r` 9.65, (c) r` 9.84, (d) r` 10.25, (v) The paint company gives a discount of 5% if the number of toys to be, painted is 100 or more. The cost of painting of 200 toys will be :, (a) ` 1900.50, (b) ` 1869.50, (c) ` 1833.50, (d) ` 1805.50, 21. As part of the ‘Swachh Bharat Abhiyan’, some houses of a locality in Delhi, decided to clean up and beautify a school of their locality by planting a number, of plants. They involved the school kids and the local community in doing so., , Here is the data indicating the number of plants contributed by different houses:, Number of Plants, 1–3 4–6 7–9, 10 – 12 13 – 15 16 – 18, contributed, Number of houses, , 10, , 8, , x, , 7, , 12, , 4, , On the basis of the above information, answer any four of the following, questions:, (i) If the mean number of plants contributed be 8.9, then how many houses, contributed 7 to 9 plants?, (a) 6 houses, (b) 7 houses, (c) 8 houses, (d) 9 houses, , Mathematics-X, , 267
Page 284 :
(ii) How many houses of the locality came forward to beautify the school?, (a) 50 houses, (b) 49 houses, (c) 48 houses, (d) 47 houses, (iii)The mode of the frequency distribution is :, (a) 11.5, (b) 12.65, (c) 13.25, (d) 13.65, (iv) Calculate the median of the frequency distribution, using empirical relation, among mean, median and mode., (a) 9.77, (b) 10.48, (c) 10.35, (d) 10.15, (v) The median class of the frequency distribution is :, (a) 3.5 – 6.5, (b) 6.5 – 9.5, (c) 9.5 – 12.5, (d) 12.5 – 15.5, 22. 100 surnames were randomly picked up from a local telephone directory and, the frequency distribution of the number of letters in the English alphabets in, the surnames was obtained as follows :, , Number of letters, Number of Surnames, , 1–4, 6, , 4 – 7 7 – 10, 30, , 10 – 13, , 13 – 16, , 16 – 19, , 16, , 4, , 4, , 40, , On the basis of the above information, answer any four of the following, questions:, (i) What is the upper limit of median class?, (a) 10, , (b) 13, , (c) 16, , (d) 19, , (ii) Determine the median number of letters in the sur names., (a) 8.5, , (b) 8, , (c) 7.88, , (d) 8.32, , (iii)What is the upper limit of modal class?, (a) 13, 268, , (b) 19, , (c) 10, , (d) 16, Mathematics-X
Page 285 :
(iv) Sum of lower limits of median and modal class is, (a) 10, , (b) 12, , (c) 20, , (d) 14, , (v) Cumulative frequency of median class is, (a) 36, , (b) 76, , (c) 92, , (d) 96, , 23. In a club, men are playing the card game. A man named Ramesh draw a card, from a well-shuffled deck of cards., , On the basis of the above information, answer any four of the following, questions:, (i) Find the probability of getting a king of red colour., (a), , 1, 26, , (b), , 3, 13, , (c), , 3, 26, , (d), , 1, 52, , 3, 26, , (d), , 1, 52, , (d), , 1, 4, , (d), , 1, 4, , (ii) Find the probability of getting a face card., (a), , 1, 26, , (b), , 3, 13, , (c), , (iii)Find the probability of getting a jack of hearts., (a), , 1, 26, , (b), , 3, 13, , (c), , 1, 52, , (iv) Find the probability of getting a spade card., (a), , 1, 26, , Mathematics-X, , (b), , 3, 13, , (c), , 1, 52, , 269
Page 286 :
(v) Find the probability of getting a queen of diamonds., (a), , 1, 26, , (b), , 3, 13, , (c), , 1, 52, , (d), , 1, 4, , 24. A game of chance consists of spinning an arrow which comes of rest pointing, at one of the numbers 1, 2, 3, 4 5, 6, 7, 8 (see figure) and these are equally, likely outcomes, , :, , On the basis of the above information, answer any four of the following, questions:, (i) What are the total number of possible outcomes?, (a) 8, (b) 1, (c) 36, (d) 4, (ii) What is the probability that spinning arrow will point at 8?, (a), , 1, 8, , (b), , 1, 2, , (c), , 3, 4, , (d) 1, , (iii)What is the probability that spinning arrow will point at a number greater, than 2?, (a), , 1, 8, , (b), , 1, 2, , (c), , 3, 4, , (d) 1, , (iv) What is the probability that spinning arrow will point at an odd number ?, (a), , 1, 8, , (b), , 1, 2, , (c), , 3, 4, , (d) 1, , (v) What is the probability that spinning arrow will point at a number less, than 9 ?, (a), 270, , 1, 8, , (b), , 1, 2, , (c), , 3, 4, , (d) 1, Mathematics-X
Page 287 :
ANSWERS AND HINTS, , 1., , (i) (d) No. of doctors = 12, (ii) (c) 21, (iii) (b) 15, (iv) (a) m = 2, (v) (d) 2, – 1, , 2., , (i) (c) 840, (ii) (a) 42, (iii) (c) 70, (iv) (b) 84, (v) (c) 1680, , 3., (i) (b) (x + 6), (x + 3), (x + 1), (ii) (b) 40 cubic units, (iii) (b) 200, (iv) (b) 2, (v) (b) (x + 3) (x + 3) (x + 6), 4., (i) (d) 7, (ii) (a) 3, 4, (iii) (d) (x – 5) (x – 4) (x – 3), (iv) (c) x3 – 11x2 + 40x – 48, (v) (c) x2 – 7x + 12, 5., , (i) (b) Intersecting, (ii) (b) 65, 55, (iii) (a) 55, (iv) (b) 315, (v) (c) x + 4y = 315, , Mathematics-X, , 271
Page 288 :
6., (i) (a) Intersecting, (ii) (b) (2, 0), (iii) (d) (0, 6), (iv) (b) (6, 6), (v) (a) 6, 7., , (i) (d) x = 1, (ii) (d) x = 0,, , 3, 2, , (iii) (b) D = 0, (iv) (d) –, , 4, 3, , (v) (c) a 0, 8., , (i) (a) 60 – 2x, (ii) (d) 60x – 2x2, (iii) (c) x2 – 30x + 125 = 0, (iv) (b) the width = 15 m, (v) (a) 10 or 20, , 9., , (i) (c) 20 m, (ii) (a) 20, 30, 40, 50 ....., (iii) (d) Sn =, , n, (2a + (n – 1)d), 2, , (iv) (b) 260 m, (v) (b) 3500 m, 10. (i) (b) 4000, 5000, 6000, (ii) (c) 4000 and 1000, (iii) (c) 15 days, (iv) (d) 13000, (v) (d) 28, , 272, , Mathematics-X
Page 289 :
11. (i) (c) 90°, (ii) (b) SAS, (iii) (b) 4 : 9, (iv) (d) Converse of Pythagoras theorem, (v) (a) 48 cm 2, 12. (i) (b) 100 ft, (ii) (a) 2400 ft2, (iii) (c) 25 ft, (iv) (a) 100 ft, (v) (b) 150 ft2, 13. (i) (b) M (4, 2), (ii) (c) (23, 0), (iii) (d) 6 2, (iv) (a) (7, 5), (v) (b) 1 : 1, 14. (i) (d), (ii) (c), (iii) (c), (iv) (b), (v) (d), 15. (i) (a), (ii) (b), (iii) (c), (iv) (d), (v) (d), 16. (i) (b), (ii) (c), Mathematics-X, , 273
Page 290 :
(iii) (d), (iv) (c), (v) (b), 17. (i) (b), (ii) (a), (iii) (b), (iv) (a), (v) (b), 18. (i) (c), (ii) (a), (iii) (a), (iv) (b), (v) (a), 19. (i) (c) 3.3 m, (ii) (a) 18.3 m, (iii) (d) 1533 m2, (iv) (c) r` 6898.50, (v) (c) 3182.64 m2, 20. (i) (c) 84 cm2, (ii) (d) 18.5 cm2, (iii) (a) 92.5 cm3, (iv) (b) ` 9.65, (v) (c) ` 1833.50, 21. (i) (d) 9 houses, (ii) (a) 50 houses, (iii) (c) 13.65, (iv) (b) 10.48, (v) (b) 6.5 – 9.5, 274, , Mathematics-X
Page 291 :
22. (i) (a) 10, (ii) (a) 8.5, (iii) (c) 10, (iv) (d) 14, (v) (b) 76, 23. (i) (a), , 1, 26, , (ii) (b), , 3, 13, , (iii) (c), , 1, 52, , (iv) (d), , 1, 4, , (v) (c), , 1, 52, , 24. (i) (a) 8, (ii) (a), , 1, 8, , (iii) (c), , 3, 4, , (iv) (b), , 1, 2, , (v) (d) 1, , Mathematics-X, , 275
Page 292 :
Practice Question Paper – 1, Time : 3 Hours, , Max. Marks : 80, , General Instructions:, 1., , This question paper contains two parts A and B., , 2., , Both Part A and Part B have internal choices., , Part – A:, 1., , It consists of two sections I and II., , 2., , Section I has 16 questions of 1 mark each. Internal choice is provided in 5, questions., , 3., , Section II has 4 questions on case study. Each case study has 5 case-based subparts. An examinee is to attempt any 4 out of 5 sub-parts., , Part – B:, 1., , Question No 21 to 26 are Very Short Answer Type questions of 2 marks each., , 2., , Question No 27 to 33 are Short Answer Type questions of 3 marks each., , 3., , Question No 34 to 36 are Long Answer Type questions of 5 marks each., , 4., , Internal choice is provided in 2 quesitons of 2 marks. 2 questions of 3 marks, and 1 question of 5 marks., PART A, Section-I, , 1., , If two positive integers p and q can be expressed as p = a3b2 and q = ab3c2, a, b, c being, prime numbers, then what is L.C.M. of p and q?, OR, Given that HCF (306, 657) = 9, find LCM (306, 657)., , 2., , If x = 1 is a zero of the polynomial f(x) = x3 – 2x2 + 4x + k, find the value of k., , 3., , Find value of cos in the given figure., , 276, , Mathematics-X
Page 293 :
4., , If ad bc, then find whether the pair of linear equations ax + by = p and cx + dy = q, has no solution, unique solution or infinitely many., , 5., , For what value of k, equation kx(x – 2) + 6 = 0 have equal root., , 6., , Find the quadratic equation whose roots are 3 and –3., OR, Solve by factorization, , 7., , 3x 2 10x 7 3 0, , Find the sum of the A.P., 1 + 2 + 3 + 4 + 5 + 6 + ............. + 10., OR, Find the 10th term of the AP in 2, 7, 12, ..........., , 8., , In the given figure, DE||BC. Then find the value of x., , 9., , Find the coordinates of a point A, where AB is the diameters of a circle whose centre, is (2, –3) and B is (1,4)., , 10. Find the value of the expression (cos2 23° – sin2 67°), , Mathematics-X, , 277
Page 294 :
OR, In ABC, right angled at B, AB = 24 cm, BC = 7 cm. Determine sin A., 11. A line m is tangent to the circle with radius 5 cm. Find the distance between the centre, and the line m., 12. A tangent PQ at a point P to a circle of radius 5 cm meets a line through the centre O, at a point Q, so that OQ = 13cm, then what will be length of PQ?, OR, If tangents PA and PB from a point P to a circle with centre O are inclined to each, other at angle of 80°, then, what is the measure of POA?, 13. To divide the line segment AB in the ratio 2 : 3, a ray AX is drawn such that BAX is, acute, AX is then marked at equal intervals. Find a minimum number of these marks., 14. Calculate the perimeter of a semicircular protractor whose radius is 7cm., 15. A metallic solid cone is converted into a solid cylinder of equal radius. If the height of, the cylinder is 5 cm, then find the height of the cone., 16. Find the lengths of the medians AD of ABC whose vertices are A(7, –3), B(5,3) and, C(3, –1)., , Section-II, CASE STUDY BASED QUESTIONS, Read the case study based questions given below and answer any four out of five sub parts, in the following:, 17. The below quadratic function can model the natural shape of a banana. Now, we, know that a parabolic shape must have a quadratic function, therefore an equation in, the standard form of f(x) = ax2 + bx + c. To find an equation for the parabolic shape of, the banana, we need to find the values of a, b, and c., , +, , (i) If one zero of the quadratic polynomial x2 + 3x + k is 2, then the value of k is, , (a) 10, 278, , (b) – 10, , (c) 5, , (d) –5, Mathematics-X
Page 295 :
(ii) Find the number of zeroes of the polynomial for the shape of the banana given in, the figure., , (a) 3, , (b) 2, , (c) 1, , (d) 0, , (iii) If the curve of banana is represented by f(x) = x + x – 12. Find its zeroes., 2, , (a) 2,6, , (b) 4, –3, , (c) –4, 3, , (d) – 2, 6, , (iv) The representation of curves whose one zero is 4 and the sum of the zeroes is 0, then the quadratic polynomial is, , (a) x2 – 4, , (b) x2 – 8, , (c) x2 + 16, , (d) x2 –16, , (v) From the banana picture above, we can see that a quadratic function is able to, model the banana quite accurately, if a = 1, b = 0, and c = 0. Then the polynomial, is, , (a) p(x) = 0.1 × 2, (c) p(x) = x2, , (b) p(x) = x2 + 1, (d) p(x) = x2 – x, , 18. There is some fire incident in the house. The fireman is trying to enter the house from, the window as the main door is locked. The window is 6 m above the ground. He, places a ladder against the wall such that its foot is at a distance of 2.5 m from the wall, and its top reaches the window., , (i) Here, _______ be the ladder and___________be the wall with the window., , (a) CA, AB, , (b) AB, AC, , (c) AC,BC, , (d) AB, BC, , (ii) We will apply Pythagoras Theorem to find length of the ladder. It is:, , (a) AB2 = BC2 – CA2, (c) BC2 = AB2 + CA2, (iii) The length of the ladder is, , (a) 4.5 m, Mathematics-X, , (b) 2.5 m, , (b) CA2 = BC2 + AB2, (d) AB2 = BC2 + CA2, ., , (c) 6.5 m, , (d) 42.25 m, 279
Page 296 :
(iv) What would be the length of the ladder if it is placed 6 m away from the wall and, the window is 8 m above the ground?, , (a) 12 m, , (b) 10 m, , (c) 14 m, , (d) 8 m, , (v) How far should the ladder be placed if the fireman gets a 9 m long ladder?, , (a) 6.7 m (approx.), (c) 3.7 m (approx.), , (b)7.7 m (approx.), (d)4.7 m (approx.), , 19. The Class X students of a secondary school in Krishinagar have been allotted a, rectangular plot of land for their gardening activity. Sapling of Gulmohar is planted, on the boundary of the plot at a distance of 1 m from each other. There is a triangular, grassy lawn inside the plot as shown in Fig. The students have to sow seeds of flowering, plants on the remaining area of the plot., , (i) Considering A as the origin, what are the coordinates of A?, , (a) (0, 1), , (b) (1, 0), , (c) (0, 0), , (d) (–1, –1), , (c) (4, 5), , (d) (5, 4), , (c) (6, 0), , (d) (7, 4), , (c) (0, 16), , (d) (16, 1), , (ii) What are the coordinates of P?, , (a) (4, 6), , (b) (6, 4), , (iii) What are the coordinates of R?, , (a) (6, 5), , (b) (5, 6), , (iv) What are the coordinates of D?, , (a) (16, 0), , (b) (0, 0), , (v) What are the coordinates of P if D is taken as the origin?, , (a) (12, 2), , (b) (–12, 6), , (c) (12, 3), , (d) (6, 10), , 20. The agewise participation of students of a school in the International Yoga day, Celebration that was held in Central City Ground Patna is shown in the following, distribution. By Analysing the data given below answer the questions that follow:, 280, , Mathematics-X
Page 297 :
Age (in, years), Number, of students, , 5–7, , 7–9, , 9 – 11, , 11 – 13, , 13 – 15, , 15 – 17, , 17 – 19, , X, , 15, , 18, , 30, , 50, , 48, , X, , Find the following when the sum of frequencies is 181., (i) The mode of the data is:, , (a) 17.81, , (b) 11.81, , (c) 18.41, , (d) 14.81, , (ii) The value of missing frequency(x) is:, , (a) 12, , (b) 10, , (c) 13, , (d) 14, , (c) 15 – 17, , (d) 17 – 19, , (iii) The modal class is:, , (a) 13-15, , (b) 11 – 13, , (iv) The upper limit of the modal class is:, , (a) 17, , (b) 19, , (c) 15, , (d) 13, , (v) The construction of the cumulative frequency table is useful in determining, , the:, , (a) Mean, , Mathematics-X, , (b) Median, , (c) Mode, , (d) All of the above, , 281
Page 298 :
PART-B, , All questions are compulsory. In case of internal choices, attempt any one., Section-III, , 21. Show that, number., , (2 3 2), is not a rational number, given that, 7, , 2 is an irrational, , 22. If sin (36 + ) ° = cos (16 + ) °, then find , where (36 + )° and (16 + ) ° are, both acute angles., 23. In the given figure, ABC is a triangle in which B = 90°, BC = 48 cm and AB, = 14 cm. A circle is inscribed in the triangle, whose centre is O. Find radius r of, in-circle. (In cm), , OR, Prove that the tangents drawn at the ends of a diameter of a circle are parallel., 24. Draw a right angled ABC in which BC = 12 cm, AB = 5 cm, and B = 90°., Construct a triangle similar to it and of scale factor 2/3. Is the new triangle also, a right triangle?, OR, Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct, the pair of tangents to the circle and measure their lengths., 25. The arithmetic mean of the following frequency distribution is 25. Determine, the value of p., Class, Frequency, 282, , 0 – 10, , 10 – 20, , 20 – 30, , 30 – 40, , 40 – 50, , 5, , 18, , 15, , P, , 6, Mathematics-X
Page 299 :
26. The age of two friends Ani and Biju differ by 3 years. Ani's father Dharam is, twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of, Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju., Section-IV, , 27. Find the values of a and b if the HCF of the polynomials., f(x) = (x + 3) (2x2 – 3x + a), and g(x) = (x – 2)(3x2 + 10x – b) is (x + 3)(x – 2), 28. Find the value of k for which the roots are real and equal of equation:, (k + l)x2 + 2(k + 3)x + (k + 8) = 0, 29. How many terms are there in the A.P. – 1,, , 5 2 1, 10, , , ,...,, 6 3 2, 3, , 30. BL and CM are medians of ABC right angled at A. Prove that, 4(BL2 + CM2) = 5BC2, OR, In the given figure the line segment XY||AC and XY divides triangular region, ABC into two parts equal in area, Determine AX/AB., , 31. A person observed the angle of elevation of the top of a tower is 30°. He walked, 50 m towards the foot of the tower along level ground and found the angle of, elevation of the top of the tower as 60°. Find the height of the tower., OR, 1 tan 2 A 1 – tan A 2, Prove the identity , tan 2 A , where the angle A is, , , 2, 1, –, cot, A, , 1 cot A , acute angle., , Mathematics-X, , 283
Page 300 :
32. Calculate the area of the designed region in figure common between the two, quadrants of circles of radius 8 cm each., , 33. Formulate the problem as a pair of equations, and hence find its solutions: 2, women and 5 men can together finish an embroidery work in 4 days, while 3, women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone, to finish the work, and also that taken by 1 man alone., Section-V, , 34. From the top of a building 15 m high, the angle of elevation of the top of a, tower is found to be 30°. Form the bottom of the same building, the angle of, elevation of the top of the tower is found to be 45°. Determine the height of the, tower and the distance between the tower and the building., OR, The angle of elevation of a bird observed by a hunter who is 12 m above a lake, is 30° and the angle of depression of bird's reflection in the lake is 60°. Find the, distance between the bird and the hunter., 35. A solid is in the form of a right circular cone mounted on a hemisphere. The, radius of the hemisphere is 3.5 cm and the height of the cone is 4 cm. The solid, is placed in a cylindrical tub, full of water, in such a way that the whole solid is, submerged in water. If the radius of the cylinder is 5 cm and its height is 10.5, cm, find the volume of water left in the cylindrical tub. (Use = 227), 36. Two different dice are thrown together. Find the probability that the numbers, obtained have, (i) even sum, 284, , (ii) even product., Mathematics-X
Page 301 :
SOLUTION PRACTICE PAPER, Section-I, , 1., , Given numbers are, p = a3b2 and q = ab3c2, Now, , LCM(p, q) = a3b3c2, OR, L.C.M = 22,338, , 2., , f(x) = x – 2x + 4x + k, 3, , 2, , f(x) = x3 – 2x2 + 4x+k, f(1) = 13 – 2(1)2 + 4 × 1 + k, 0=1–2+4+k, –3 = k, Hence, the value of k is = –3., 3., , 4, 5, , 4., , Pair of linear equations ax + by = p and cx + dy = q, ad bc or, a b, , c d, , Hence, the pair of given linear equations has unique solution, 5., , k=6, , 6., , X2 – 9 = 0, OR, x = 3, 7 7 3, 3, 3, , 7., , 55, , 8., , 3, , 9., , (3, – 10), , 10. 0, , OR, , OR, , Mathematics-X, , 47, , 7, 25, 285
Page 302 :
11. A line m is tangent to the circle with radius 5 cm., , , Distance between the centre and the line m = Radius of the circle = 5 cm., , 12. 12 cm, OR, 50°, 13. The line segment AB in the ratio 2 : 3., So, minimum number of marks = 2 + 3 = 5, 14. 36 cm., 15. Let height of cone = h, cm., Given, height of cylinder (h) = 5 cm., Hence, the volume of a cylinder = r2h, , .... (i), , And , the volume of cone = 1/3r2h1, , .... (ii), , According to the question,, r2h = 1/3r2h1 (given radius of both are same), h1 = 3h, , , h1 = 3 × 5 = 15 cm., , Ans., , 16. Vertices of ABC are A(7, – 3), B(5, 3) and C(3 – 1), Coordinates of, , D = [(3 + 5)/2, (–1 + 3)/2, = (4, 1), AD2 = (x2 – x1)2 + (y2 – y1)2, = (7 – 4)2 + (3 + 1)2, = 32 + 42, = 9 + 16 = 25, AD = 5 units., , Section-II, 17. (i) (b) – 10, (ii) (c) 1, (iii) (c) (4, – 3), (iv) (d) x2 – 16, (v) (c) p(x) = x2, 286, , Mathematics-X
Page 303 :
18. (i) (b) AB, AC, (ii) (d) AB2 = BC2 + CA2, (iii) (c) 6.5 m, (iv) (b) 10 m, (v) (a) 6.7 m (approx), 19. It can be observed that the coordinates of point P, Q and R are (4, 6), (3, 2), and (6, 5), respectively., (i) (c) (0, 0), , (ii) (a) (4, 6), , (iii) (a) (6, 5), , (iv) (a) (16, 0), , (v) (b) (–12, 6), 20. Sum of the frequencies = 181, x + 15 + 18 + 30 + 50 + 48 + x = 181, , , , 2x + 161 = 181, x = 10, , Thus, the missing frequencies are 10 and 10., Clearly, the modal class is 13 – 15, as it has the maximum frequency., 1 = 13, h = 2, f1 = 50, f0 = 30, f2 = 48, , (f1 f 0 ) , = 13 + 1.81 = 14.81, (2f1 f 0 f 2 ) , , Mode,, , M0 = l + {h ×, , (i) (d) 14.81, , (ii) (b) 10, , (iv) (c) 15, , (v) (b) Median, , (iii) (a) 13 – 15, , Section-III, 21. Let us assume that (2 3 2) / 7 is a rational no., so (2 3 2) / 7 = p/q, q 0, HCF(p, q) = 1, , , 3 2 / 7 = p/q – 2, , , , 2 / 7 = (p – 2q)/3q, , , , 2 = 7(p – 2q)/3q, , Clearly R.H.S is rational and L.H.S is irrational, which is impossible., Hence our assumption is false., So, (2 3 2) / 7 is an irrational number.., , Mathematics-X, , 287
Page 304 :
22. sin(36 + )° = cos(16 + )°, sin = cos (90° + ), or,, or,, , cos (90° – (36 + ) = cos (16 + )°, 90° – 36° – = 16° + , 2 = 90° – 36° – 16° = 38°, , , , = 19°, , 23. AC2 = AB2 + BC2, = 142 + 482 = 2500, AC = 50 cm, , OQB = 90°, OPBQ is a square, , , BQ = r, QA = 14 – r = AR (tangents from an external point are equal in length), Again PB = r,, PC = 48 – r, RC = 48 – r (tangents from an external point are equal in length), AR + RC = AC, , , , 14 – r + 48 – r = 50, , , , r = 6 cm., OR, , To prove: PQ || RS, 288, , Mathematics-X
Page 305 :
Given: A circle with centre O and diameter AB. Let PQ be the tangent at point A & RS, at the point B., Proof: Since PQ is a tangent at point A., OA PQ(Tangent at any point of circle is perpendicular to the radius through point of, contact)., OAP = 90°, , ...(1), , OBS = 90°, , ...(2), , OB RS, From (1) & (2), OAP = OBS, BAP = ABS, , i.e.,, , for lines PQ & RS and transversal AB, BAP = ABS i.e., both alternate angles are equal. So, lines are parallel., 24. Here, scale factor or ratio factor is 2/3 < 1, so triangle to be constructed will be smaller, than given ABC., ABC is the required triangle of scale factor 2/3. This triangle is also a right triangle., OR, Correct Construciton, 25. Explanation:, Class Interval, , Frequency(f1), , Class Mark xi, , (fi × xi), , 0 – 10, , 5, , 5, , 25, , 10 – 20, , 18, , 15, , 270, , 20 – 30, , 15, , 25, , 375, , 30 – 40, , p, , 35, , 35p, , 40 – 50, , 6, , 45, , 270, , fixi = (44 + p), , Mathematics-X, , (fi × xi) = (+940 + 35p), 289
Page 306 :
let unknown frequencey is p,, give mean = 25, , , mean = (fi × xi)/fi, , , , (940 + 35p)(44 + p) = 25, , , , (35p – 25p) = (1100 – 940), , , , 10p = 160, , , , p = 16, , 26. Let the present age of Ani and Biju be x years and y years respectively., Age of Dharam = 2x years and Age of Cathy =, Case I, , y, years According to question,, 2, , x–y=3, , 2x , , ...(1), , y, = 30, 2, , 4x – y = 60, , ...(2), , Subtracting (1) from (2), we obtain:, 3x = 60 – 3 = 57, , , x = Age of Ani = 19 years, , Age of Biju = 19 – 3 = 16 years, Case II, y–x=3, , 2x , , , ...(3), , y, = 30, 2, , 4x – y = 60, , ...(4), , Adding (3) and (4), we obtain:, 3x = 63, , , x = 21, , Age of Ani = 21 years, Age of Biju = 21 + 3 = 24 years, , 290, , Mathematics-X
Page 307 :
Section-IV, 27. f(x) = (x + 3)(2x2 – 3x + a), g(x) = (x – 2)(3x2 + 10x – b), since (x + 3)(x – 2) is the HCF of f(x) and g(x), , , x – 2 is a factor of 2x2 – 3x + a, , ...(i), , and x + 3 is a factor of 3x2 + 10x – b, , ...(ii), , From (i) follow that 2 is a zero of 2x – 3x + a, 2, , , , a=–2, , From (ii), it follows that, – 3 is a zero of 3x2 + 10x – b, , , b=–3, , The values of a and b are – 2 and – 3 respectively., 28. The given quadratic equation is:, (k + l)x2 + 2(k + 3)x + (k + 8) = 0, Here, a = k + 1, b = 2(k + 3) and c = k + 8, We know that D = b2 – 4ac, Therefore,, D = [2(k + 3)]2 – 4 × (k + 1) × (k + 8), = 4[k + 3]2 – 4[k2 + 8k + k + 8], = 4[k2 + 9 + 6k] – 4[k2 + 9k + 8], = 4k2 + 36 + 24k – 4k2 – 36k – 32, = – 12k + 4, Hence, D = – 12k + 4, It is given that the given equation has real and equal roots, therefore Discriminant is, equal to zero i.e.,, D=0, , , – 12k + 4 = 0, , , , 12k = 4, , , , Mathematics-X, , k = 1/3, , 291
Page 308 :
29. Here, A.P is –1, –5/6, –2/3 – 1/2,..., 10/3, The first term (a) = –1, The last term (an) = 10/3, Now, common difference (d) = a2 – a, = –5/6 –(–1) = 1/6, Thus, using the formula for nth term, viz. an = a + (n – 1) b, we get, 10/3 = –1 + (n – 1)1/6, , 13 1 1, n, 3 6 6, Thus, n = 27, 30., , BL and CM are medians of a ABC in which A = 90°, From ABC, BC2 = AB2 + AC2, , ....(i), , From right angled ABL,, BL2 = AL2 + AB2, i.e.,, , , BL2 = (AC/2)2 + AB2, 4BL2 = AC2 + 4AB2, , ...(ii), , similarly, In right-angled CMA,, 4CM2 = 4AC2 + AB2, , ...(iii), , Adding (ii) and (iii), we get, i.e., , 4(BL2 + CM2) = 5(AC2 + AB2) = 5BC2 [From (i)], OR, , 292, , Mathematics-X
Page 310 :
Let height of the tower be DC = h m and BC = x m, AC = x m, AC = (50 + x)m, In, , DBC, h/x = tan60° =, , , , h=, , 3, , 3x, , ...(i), , In DAC, h/(x + 50) = tan 30° = 1 3, , , 3 h = 50 + x, , ...(ii), , Substituting the value of h from (i) in (ii), we get, 3x = x + 50, , , x = 25 m, h = 25 3 = 25 × 1.732 m, = 43.3 m, , Hence, Height of tower = 43.3 m., OR, , 1 tan 2 A , sec2 A, , , L.H.S. , [ 1 + tan2 = sec2, 1 + cot2 = cos ec2 ], 2, 2, 1 cot A cos ec A, , 1, sin 2 A, , tan 2 A R.H.S., =, 2, 1, cos A, Now, Middle side, , 2, 2, 1 tan A , 1 tan A 1 tan A , , =, = tan A 1 , , , , 1 cot A 1 1 , , , tan A , tan A , , 2, , 2, , 1 tan A , ( tan A)2 tan 2 A R.H.S., = (1 tan A) , , , tan A, , , 32. In right triangle ADC,, AC2 = AD2 + CD2 ..... [By Pythagoras theorem], , , AC = 82 + 82 = 64 + 64 = 128, , , , AC =, , 128 = AC = 8 2, , Draw BM AC, 294, , Mathematics-X
Page 311 :
Then,, , AM = MC =, , 1, AC, 2, , AM = 1/2( 8 2 ) = 4 2 cm, In right triangle AMB, AB2 = AM2 + BM2 ...... [By Pythagoras theorem], (8)2 = (4 2) 2 + BM2, , , , , 64 = 32 + BM2, , , , BM2 = 64 – 32, , , , BM2 = 32, , , , BM = 4 2, , , , Area of, , ABC = 1/2AC × BM, = 1/2 × 8 2 4 2 = 32 cm2, , Shaded Area, , =, , 1, (8) 2 – 32, 4, , = 16 – 32, = 16 × 22/7 – 32 = 128/7cm2, Area of the designed region, = 2 × 128/7 = 256/7cm2, , Mathematics-X, , 295
Page 312 :
33. Let the time taken by 1 woman alone to finish an embroidery be x days and the time, taken by 1 man alone to finish an embroidery be y days. Then 1 woman's 1 day's work, = 1/x, and 1 man’s 1 day’s work = 1/y, 2 women’s 1 day’s work = 2/x, and 5 man’s 1 day’s work = 5/y, 2 women and 5 men can together finish a piece of embroidery in 4 days., 4(2/x + 5/y) = 1, , , , 2/x+5/y = l/4, , ...(1), , Again, 3 women and 6 men can together finish a piece of embroidery in 3 day, 3(3/x + 6/y) = 1 3/x + 6/y = 1 /3, , ...(2), , Put 1/x = u and 1/y = v, Solve to get, , , , x = 18 and y = 36, , Hence, the time taken by 1 women alone to finish the embroidery is 18 days and the, time taken by 1 man alone to finish the embroidery is 36 days., , SECTION V, 34. According to question it is given that a building AB of height 15 m and tower CD of, h meter respectively., , Angle of elevation DAE = 30°, Angle of elevation DBC = 45°, 296, , Mathematics-X
Page 313 :
To find: BC and CD, Proof: In right DEA,, DE/x = tan30°, , , , , (h – 15)/x = 1 3, , AE = BC = x), ...(i), , In right DCB, h/x = tan45°, , , h=x, , ....(ii), , x = 35.49, Thus h = 35.49 m, OR, Let, , DE = h m, AB = 12 m, , In ADF,, tan 60° = DF/AD, , 3 =, AD =, , Mathematics-X, , h 12 12, AD, , h 24, 3, , ...(1), 297
Page 314 :
In AED,, , tan 30° =, , h, AD, , AD = h 3, , ...(2), , Solving (1) and (2), , h = 12 m, sin 30° = h/AE, AE = 24 m, 35. We have, radius of the hemisphere = 3.5 cm, In ADE,, , Height of the cone = 4 cm, Radius of the cylinder = 5 cm, Height of the cylinder = 10.5 cm, We have to find out the volume of water left in the cylindrical tub, , Volume of the solid = Volume of its conical part + Volume of its hemispherical part, =, , 1 2, 2, r h r 3, 3, 3, , Clearly, when the solid is submerged in the cylindrical tub the volume of water that, flows out of the cylinder is equal to the volume of the solid., = 1/3 × 22/7 × (7/2)2 × 11, Hence, Volume of water left in the cylinder = Volume of cylinder – Volume of the, solid = r2h – vol. of solid = 683.83 cm3, 36. (i) Let A be the event that sum of digits is even., Total possible outcomes = 36, n(A) = (1, 3) (1, 5) (1, 1) (2, 2) (2, 4) (2, 6) (3, 1) (3, 3) (3, 5) (4, 2) (4, 4) (4, 6) (5, 1), (5,3) (5, 5)(6, 2) (6, 4) (6, 6) =18, P(A) = 18/36 =, , 1, 2, , P(A) = 0.5, 298, , Mathematics-X
Page 315 :
(ii) Let A be the event that product of digits is even., Total possible outcomes =36, n(A) = (1, 2) (1, 4) (1, 6) (2, 1) (2, 2) (2, 3) (2, 4) (2, 5), (2, 6) (3, 2) (3, 4) (3, 6) (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) (5, 2) (5, 4) (5, 6), (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6), n(A) = 27, P(A) =, , 27 3 0.75, =, 36 4, , Mathematics-X, , 299
Page 316 :
Practice Question Paper – 2, Time : 3 Hours, , Max. Marks : 80, , General Instructions:, 1., , This question paper contains two parts A and B., , 2., , Both Part A and Part B have internal choices., , Part – A:, 1., , It consists of two sections I and II., , 2., , Section I has 16 questions of 1 mark each. Internal choice is provided in 5, questions., , 3., , Section II has 4 questions on case study. Each case study has 5 case-based subparts. An examinee is to attempt any 4 out of 5 sub-parts., , Part – B:, 1., , Question No 21 to 26 are Very Short Answer Type questions of 2 marks each., , 2., , Question No 27 to 33 are Short Answer Type questions of 3 marks each., , 3., , Question No 34 to 36 are Long Answer Type questions of 5 marks each., , 4., , Internal choice is provided in 2 quesitons of 2 marks. 2 questions of 3 marks, and 1 question of 5 marks., PART A, Section-I, , 1., , Express 429 as a product of its prime factors., OR, If p is a prime number, then find LCM of p, p2 p3., , 2., , How many polynomials can be formed with –2 and 5 as zeroes?, , 3., , For whoat avalue of k, the pair of linear equations 3x + y = 3 and 6x + ky = 8, does not have a solution?, , 4., , Two lines are given to be parallel. The equaiton of one of the lines is, 4x + 3y = 14, then find the equaiton of the second line., , 300, , Mathematics-X
Page 317 :
5., , If the nth term of an A.P. –1, 4, 9, 14, ... is 129, find the value of n., OR, In the A.P., if d = –4, n = 7, an = 4, then find a., , 6., , For what value of k, the roots of the equation x 2 + 4x + k = 0 are real?, , 7., , For what value of k, the roots of the equation 3x 2 – 10x + k = 0 are reciprocal of, each other?, OR, Find the roots of the equaiton x 2 + 7x + 10 = 0, , 8., , In the given figure, ‘O’ is the centre of the circle, PQ is a chord and the tangent, PR at P makes an angles of 50° with PQ, then find POQ., , 9., , PQ is a tangent to a circle with centre O at point P. If OPQ is an isosceles, triangle, then find OQP., OR, In the given figure. If PR = 12 cm, OP = 5cm, OQ = 4cm, find RQ., , 10. In ABC, AB = 6 3 cm, AB = 12 cm, BC = 6 cm, find measure of B., 11. Given ABC ~ PQR, if, 12. Find the value of, , Mathematics-X, , AB 1, ar(ABC), then find, PQ 3, ar(PQR), , 1, 1, , 2, cos ec 1 tan 2 , , 301
Page 318 :
2, , sin35 cos 43 , 13. Find the value of , , 2 cos 60, cos 55 sin 47 , 14. In the figure OAB is a sector of circle of radius 10.5 cm. Find the perimeter of, 22 , , the sector take , 7 , , , 15. The volume and the surface area of a sphere are numerically equal, find the, radius of the sphere., 16. A card is drawn at random from a deck of 52 playing cards. Find the probability, of getting a face card., OR, A die is thrown once. What is the probability of getting an even prime number?, Section-II, , 17. Case Study Based-1, The diagram shows the map where the library is location at point A, city hall, building at B and the school at C., , 302, , Mathematics-X
Page 319 :
(i) What are the coordinates of city hall building?, (a) (3, –1), , (b) (2, –2), , (c) (1, –2), , (d) (–2, 1), , (ii) W hat is the distance between library and city hall builidng?, (a) 15 units, , (b) 1 unit, , (c) 5 unit, , (d) 7.5 unit, , (iii) W hat are the coordinaties of the mid-point of the segment joining school, and library?, , 5 1 , , 2 2 , , 1 5, (b) , , 2 2, , (a) ,, , 1 5 , (c) , , 2 2, , (d) (0, 0), , (iv) Which shape is formed by connecting the three locations?, (a) Quadrilateral, , (b) Right anged trignle, , (c) Acute angled triangle, , (d) Obtuse angled triangle, , (v) What is the area of ABC?, (a) 3.5 sq. units, , (b) 7.5 sq. units, , (c) 10 sq. units, , (d) 15 sq. units, , 18. Case Study Based-2, The folloiwng table shows the ages of the patiends coming to a hospital for, OPD treatment during a week., Age (in years), , 5–15, , 15–25, , 25–35, , 35–45, , 45–55, , 55–65, , No. of patients, , 10, , 12, , 25, , 14, , 5, , 4, , Mathematics-X, , 303
Page 320 :
(i) What is the width of the class?, (a) 10, , (b) 25, , (c) 5, , (d) 65, , (ii)What is the class mark of class 15–25?, (a) 15, , (b) 25, , (c) 20, , (d) 40, , (iii) What is the modal class of the given data?, (a) 15–25, , (b) 25–35, , (c) 35–45, , (d) 55–65, , (iv) What is the median class of the given data?, (a) 15–25, , (b) 35–45, , (c) 25–35, , (d) 45–55, , (v) What is the difference of lower limit of modal class and upper limit of median, class?, (a) 40, , (b) 5, , (c) 10, , (d) 25, , 19. Case Study Based-3, , In the given figure, CD = a, AD = b, CE = c, BE = d, (i) Choose the correct option from the folloiwng., (a) a = b, (b) a > b, (c) a < b, (ii)Which of the following statement is correct?, , (d) c = d, , 1, AB, (b) DE||AB, 2, (c) ABED is a trapezium, (d) both (b) and (c), (iii), The relation between ADE and BED is, , (a) DE , , (a) ar (ADE) ~ 2 ar (BED), (c) ar (ADE) =, 304, , 1, ar (BED), 2, , (b) ar (ADE) = ar (BED), (d) None of these, Mathematics-X
Page 321 :
(iv) The first figure is changed by moving points D & E and a new figure as, shown here, is obtained. Now which of following is correct?, , (a) D & E are the mid points of AC & BC respectively., (b) a = C, (c) b = d, (d) a + b = c + d, (v) “If a line divides any two sides of a triangle in the same ratio, then the line, is parallel to the third side.”, This statement is of which theorem?, (a) Basic proportionality theorem, (b) Mid-point theorem, (c) Converse of Pythagoras theorem, (d) Converse of Basic Proportionality theorem, , Mathematics-X, , 305
Page 322 :
20. Case Study Based-4, Ramesh wanted to make a circle from a copper wire. He tried it by bending the, wire but he got the shape as shown in the figure., (i) Name the shape in which the wire is bent., (a) Sphere, , (b) Ellipse, , (c) Parabola, , (d) Triangle, , (ii) If the shape of wire so bent is plotted on graph, then how many zeroes are, there? (as shown in the figure), (a) 0, , (b) 1, , (c) 2, , (d) 3, , (c) 1, –4, , (d) –1, –4, , (iii) Zeroes of the polynomial are, (a) –1, 1, , (b) –1, 4, , (iv) The expression for this polynomial is, (a) x 2 + 3x + 4, , (b) x2 – 3x + 4, , (c) x2 + 3x – 4, , (d) x2 – 3x – 4, , (v) Value of this quadratic polynomial at x = 0 is, (a) 4, , (b) –4, , (c) 3, , (d) –3, , PART B, Section-III, , 21. Three bells ring at intervals of 9, 12, 15 minutes respectively. If they start, ringing together at a time, after what time will they next ring together?, Mathematics-X, 306
Page 323 :
22. Find a relation between x and y is the points A(x, y), B(–4, 6) and C(–2, 3) are, collinear., OR, Find the value of k so that the area of triangle ABC with A(k +1, 1), B(4, –3), and C(7, –k) is 6 square units., OR, 23. If –3 is one of the zeroes of the polynomial (k – 1) x 2 + kx + 1, find the value of, k., 24. Construct a triangle with sides 4 cm, 5 cm and 7 cm. Then construct of triangle, 2, similar to it whose sides are of the corresponding sides of the given triangle., 3, 3 sin – cos = 0 and 0° < < 90° find the value of ., OR, Prove that :, (sin + coses )2 + (cos + sec )2 = 7 + tan2 + cot2 , , 25. If, , 26. Prove that the tangents drawn at the ends of a diameter of a circle are parallel., SECTION IV, , 27. Prove that 5 , , 3, 3 is an irrational number, given that, 7, , 3 is irrational., , 28. The numerator of a fraction is 3 less than its denominator. If 2 is added to both, the numerator and the denominator, then the sum of the new fraction and the, 29, original fraction is, . Find the original fraction., 20, OR, If the roots of the quadratic equation (a – b)x 2 + (b – c)x + (c – a) = are equal,, prove that 2a = b + c., 29. In the given figure, from a rectangular region ABCD, with AB = 20 cm, a right triangle AED with AE = 9, cm, DE = 12 cm is cut off. On the other end taking, BC as diameter, a semi-circle is drawn on outside, of the region. Find the area of the shaded region., 22 , , use , , 7 , , Mathematics-X, , 307
Page 324 :
30. Prove Pythagoras Theorem, OR, In the given figure AB||PQ||CD, AB = x, CD = y and PQ = z. Pove that, 1 1 1, , x y z, , 31. The mode of the following data is 67. Find the missing frequency x., Class, Freqeueny, , 40~50, , 50–60, , 60–70, , 70–80, , 80–90, , 5, , x, , 15, , 12, , 7, , 32. A 7m long flag staff is fixed on the top of a tower on the horizontal plane. From, a point on the ground, the angle of elevation of the top and bottom of the, flagstaff are 45° and 30° respectively. Find the height of the tower., 33. The different coins are tossed together. Find the probability of getting, (i) exactly two heads, (ii) atleast two heads, (iii) atleast two tails, Section-V, , 34. A 1.2 m tall girl spots a balloon on the eve of Independence Day, moving with, the wind in a horizontal line at a height of 88.2m from the ground. The angle of, elevation of the balloon from the eye of the girl at an instant is 60°. After some, time, the angle of elevation reduces to 30°. Find the distance travelled by the, balloon., OR, Two pillars of equal heights stand on either side of a roadway 150 m wide., From a point on the roadway between the pillars the angles of elevation of the, top of the pillars are 60° and 30°. Find the height of pillars and the position of, the point., 308, , Mathematics-X
Page 325 :
35. A solid is in the shape of a hemisphere surmounted by a cone. If the radius of, hemisphere and base radius of cone is 7 cm and height of cone is 3.5 cm, find, 22 , , the volume of the solid. take , 7 , , 36. A boat goes 30 km upstream and 44 km down stream is 10 hours. In 13 hours,, it can go 40 km upstream and 55 km down stream. Determine the spead of the, stream and the of the boat in still water., , Answers, 1., , 429 = 3 × 11 × 13, , OR, , LCM = p3, , 2., , Infinite, , 3., , k=2, , OR, , k not equal to, , 4., , One of several possible lines is 8x + 6y = 10, , 5., , n = 27, , 6., , k4, , 7., , k=3, , 8., , 100°, , 9., , 45°, , 8, 3, , OR, , a = 28, , OR, , –5, –2, , OR, , RQ 153 cm, , 10. < B = 90°, 11., , 1, 9, , 12. 1, , 13. 1, , 14. 32 cm, , 15. 3 units, , 16., , 17., , 3, 13, , OR, , 1, 6, , (i) (d), , 18. (i) (a), , 19. (i) (b), , 20. (i) (c), , (ii) (c), , (ii) (c), , (ii) (d), , (ii) (c), , (iii) (a), , (iii) (b), , (iii) (b), , (iii) (b), , (iv) (c), , (iv) (c), , (iv) (a), , (iv) (d), , (v) (c), , (v) (d), , (v) (b), , (v) (b), Mathematics-X, , 309
Page 326 :
21. 180 minutes, 22. 3x + 2y = 0, 23., , OR, , 4, 3, , 29. 334.39 cm2, 33. (i), , 3, 8, , (ii), , 1, 2, , (iii), , k=3, 7, 10, , 25. = 30°, , 28., , 31. x = 8, , 32. 9.6 m, , 1, 2, , 34. 58 3m, OR, height = 64.95 m, distance = 112.5 m from the pillar having angle of elevation, 60°, 35. 898.33 cm3, 36. speed of stream = 4 km/hour, speed of boat in still water = 7 km/hour, , 310, , Mathematics-X
Page 327 :
Practice Question Paper – 3, Time : 3 Hours, , Max. Marks : 80, , General Instructions:, 1., , This question paper contains two parts A and B., , 2., , Both Part A and Part B have internal choices., , Part – A:, 1., , It consists of two sections I and II., , 2., , Section I has 16 questions of 1 mark each. Internal choice is provided in 5, questions., , 3., , Section II has 4 questions on case study. Each case study has 5 case-based subparts. An examinee is to attempt any 4 out of 5 sub-parts., , Part – B:, 1., , Question No 21 to 26 are Very Short Answer Type questions of 2 marks each., , 2., , Question No 27 to 33 are Short Answer Type questions of 3 marks each., , 3., , Question No 34 to 36 are Long Answer Type questions of 5 marks each., , 4., , Internal choice is provided in 2 quesitons of 2 marks. 2 questions of 3 marks, and 1 question of 5 marks., PART A, Section-I, , 27, ., 2 53, , 1., , After how many places the decimal will terminate in, , 2., , If the zeroes of the polynomial x2 – px + 1 are negative of each other, then what, is the value of p?, , 3., , What is the greatest number which when divided by 245 and 1029 leaves, remainder 5 always?, , 2, , OR, Which of the following is a decimal expansion of an irrational number, (i) 3.205, Mathematics-X, , (ii) 2.33, , (iii) 4.07007000..., , (iv) 4.03, 311
Page 328 :
4., , What type of lines are represented by the graph of x = b and y = a, (i) parallel to y-axis and x-axis respectively, (ii) intersecting, (iii) consistent, (iv)passing through (0,0), , 5., , Write 1260 as a product of prime numbers., , 6., , If area of a circle is 38.5 square cm find the diameter., OR, The chord of a circle of radius 10 cm subtends an angie of 90°at the centre then, what is the length of the chord., , 7., , The corresponding sides of two similar triangles are in the ratio 3 : 4 then what, is the ratio between their areas, OR, S and T are respectively the points on the sides PQ and PR of a PQR such that, ST, QR . If PT = 2 cm, TR = 4cm then what is the ratio of the areas of the PST, and PQR., , 8., , R and r are the radii of two concentric circles what is the area of the region, between the bigger and smaller circles. (R > r), , 9., , AB and CD are two equal towers. Distance between their foot is 20 metres . If, the angle of elevation from the foot of one tower to the top of the other is 60 °, what is the the angle of depression from the top of the second tower to the foot, of the first tower., , 10. The perimeter of the sector of a circle of radius 14 cm is 68 cm, what is the area, of this sector., 11. The median and the mode of a frequency distribution are 26 and 29 respectively, then what is the mean of the data., 12. If the length of the tangent is 4 cm and the distance of the point from the centre, is 5 cm then what will be the radius of the circle we draw to construct a pair of, tangents., 13. If a pair of linear equations is consistent then its representation on the the graph, is, , 312, , (i) parallel lines, , (ii) intersecting & coincident lines, , (iii) always coincident lines, , (iv) always intersecting lines, Mathematics-X
Page 330 :
18. When we go to the fair we saw girls walking on the tightrope .She balances, herself due to the centre of gravity and laws of forces A girl walking on the, tightrope is at the position A as in the adjoining figure. She has to walk from A, to B ,B to C and C to A., (i) What are the coordinates of the midpoint D of the side BC., (a) (3, 4), , (b) (4, 3), , (c) (8, 6), , (d) (4, 6), , (ii) If she walks along the median to the side BC how much distance will she, cover (in units)?, (a) 10, , (b), , 50, , (c), , 34, , (d), , 26, , (iii)How much total distance (in units) will she walk from A to B then B to D?, (a), , 2 10, , (b) 2 10, , (c) 10, , (d), , 20, , (iv)Which of the following coordinates are collinear with points B and C?, (a) (1,2), , (b) (4,4), , (c) (2, 4), , (d) (2, 3), , (c) D, , (d) B and D, , (v) Which point is nearer to A?, (a) B, , 314, , (b) C, , Mathematics-X
Page 331 :
19., , Geometry is an important branch of mathematics. Here is the figure of a very, large triangular field ABC in a village. A Small road DE is made for convienence, of old people such that DE//BC, (i) Which of the following is not correct, (a) AD/DB = AE/EC, , (b) AD/DB = AE/AC, , (c) AD/AB = AE/AC, , (d) DB/AB = EC/AC, , (ii) Which of the following theorems of Geometry we are using here, (a) Pythagoras theorem, (b) Converse of Pythagoras theorem, (c) Thales theorem, (d) Converse of Thales theorem, (iii)If AD = 4cm, DB = 6cm, DE = 5cm then what is the length of side BC, (a) 7 cm, , (b) 7.5 cm, , (c) 10cm, , (d) 12.5cm, , (iv)If D and E are the midpoints of AB and AC respectively then which of the, following is correct, (a) AD = AE, , (b) 2DE = BC, , (c) AD = 2DB, , (d) DE = 2BC, , (v) Which of the following is a correct criterion for ADE – ABC, (a) SSS, , Mathematics-X, , (b) ASA, , (c) AA, , (d) RHS, , 315
Page 332 :
20., , A toy manufacturer who wants to give a hit me toy as return gift to each of the, children, on the first birthday of his son. The width of the roll of plastic sheet, used for making the toy is 50cm. The radius of the hemisphere is 5 cm and the, height of the cone is 2 cm more than twice the radius. In making of one toy 0.9, cm of plastic sheet is used in stitching., (i) What is the height of the cone (In cm)?, (a) 10, , (b) 5, , (c) 12, , (d) 20, , (ii) What is the slant height of the conical part. (In cm)?, (a) 12, , (b) 5, , (c) 7, , (d) 13, , (iii)If he invited 250 children on the birthday then what is the length of the, plastic sheet required to make 250 toys?, (a) 77 m, , (b) 770 m, , (c) 7.7 m, , (d) 15.4 m, , (iv)If he doubles the radius and height, how much plastic sheet is required for, this toy?, (a) 29.16 cm, , (b) 28.26 cm, , (c) 1413 cm, , (d) 450 cm, , (v) He wants to fill this bigger toy with glitters how much glitter is required to, fill this toy if 1 cm cube of glitter weighs 1 gram?, (a) 440 g, , 316, , (b) 4.605 kg, , (c) 460 g, , (d) 465 g, , Mathematics-X
Page 333 :
PART B, SECTION-III, , 21. If a point P(x, y ) is equidistant from the points A (5, 1) and B(–1, 5 ), show that, 3x=2y, OR, The endpoints of a diameter of a circle are(–4, 2 )and (4, –3) find the coordinates, of the centre and length of the radius., 22. In a rectangle ABCD, P is a point in the interior. Prove that PA2 + PC2 = PB2 + PD2, 23. The radius of two concentric circles is 25 cm and 7cm . Find the length of the, chord of larger circle that touches the smaller circle., 24. From a point 6cm away from the centre of the circle of radius 4 cm, draw two, tangents to the circle. What is the length of the tangent., 25. If tan =, , 3 then what is the value of, , sin cos , sin cos , , OR, If x =3 sin + 4 cos and y =3 cos – 4 sin , prove that x2 + y2 = 25., 26. How many two digit numbers are divisible by 6?, SECTION-IV, , 27. Prove that 2 – 3 is irrational number when, , 3 is given irrational number, , 28. Prove that the perimeter (PAB) = 2 × length of the tangent., , Mathematics-X, , 317
Page 334 :
In the figure two circles touch each other at point C. PQ is common tangent to, the circles. Prove that CR bisects PQ., , 29. Find a and b for which the following pair of linear equations has infinitely, many solutions, 2x – 3y = 7, (a + b) x – (a + b – 3) y = 4a + b, 30. A two digit number is chosen from all the two digit whole numbers What is the, probability that, (i) both the digits are same., (ii) a multiple of 10., OR, Two dice are thrown together. What is the probability of the following :, (i) An even number on both the dice, (ii) The sum of both the numbers on the dice is greater than 9., 31. The total surface area of a solid hemisphere is 462 square cm .Find its volume., 32. Prove that (tan + sec – 1) / (tan – sec + 1) = (1 + sin )/cos ., 33. Three consecutive positive integers are such that the square of the first number, when added to the product of the other two numbers gives 46, find the integers., OR, The sum of the reciprocals of the ages of Mona 3 years ago and 5 years hence, from now is 1 /3, find her present age., 34. The angles of depression of the top and bottom of a building 50 metres high as, observed from the top of a tower are 30° and 60° respectively , find the height, of the tower., 35. The 10th term of an A.P. is 25 and the sum of its first 20 terms is 610 .Find the, sum of its first 30 terms., 318, , Mathematics-X
Page 335 :
36. Find the values of x and y if the median for the following data is 31., Class Interval, , Frequency, , 0-10, , 5, , 10-20, , X, , 20-30, , 6, , 30-40, , Y, , 40-50, , 6, , 50-60, , 5, , Total, , 40, , Answers, 1., , Three places of decimal., , 2., , +=0p=0, , 3., , 245 – 5 = 240, 1029 – 5 = 1024, HCF (240, 1024) = 16, OR, (iii) 4.07007000 ..., , 4., , Parallel to y-axis and x-axis., , 5., , 1260 = 2 × 2 × 3 × 3 × 5 × 7 = 22 × 32 × 5 × 7, , 6., , Area of circle = 38.5 sq. cm., r2 = 38.5 r2 =, , 7 7, 7, r = cm, 2 2, 2, , OR, r = 10 m OB2 + OA2 = AB2 10 2 cm, , Mathematics-X, , 319
Page 336 :
7., , ArI (Side I)2 32, , , 9 :16, ArII (Side II) 2 42, OR, PST ~ PQR (AA similarity rule), ar(PST) PT 2, , 1: 4, ar(PQR) TR 2, , 8., , Area = R2 – r2 = (R2 – r2), , 9., , Angle of depression = 60°, , 10. Perimeter of sector = 2r + l, 68 = 28 +, , r, 180, , =, , 40 180, 14, , r 2, So area of sector =, = 280 sq. cm, 360, 11. Mode + 2 Mean = 2 Median, , 29 + 2 × 26 = 3 median, Median =, , 81, = 27, 3, , 12. r = 3 cm, 13. (ii) Interesting lines or coincident lines., 320, , Mathematics-X
Page 337 :
14. (ii) –0.3, 15. tan 45° =, , 16. P(E) =, , OR, BC, AB, , P(not E) = 1 – 0.60 = 0.40, AB = BC = 10 m, , 6, 3, , 52 26, , 17. (i) (c) (x – 4), (x – 5), (ii) (d) (4, 5), (iii) (c) (4, 0), (iv) (c) 2, (v) (a) x2 – 18x + 80, 18. (i) (b) (4, 3), (ii) (a) AD = 10, (iii) (b) AB + BD = 2 +, , 10, , (iv) (a) (1, 2), (v) (d) B and D, 19. (i) (b), , AD AE, , DB EC, , (ii) (c) Thales Theorem, (iii) (d) 12.5 cm, (iv) (b) 2DE = BC, (v) (c) AA, 20. (i) (c) 12 cm, (ii) (d) 13 cm, (iii) (d) 15.4 cm, (iv) (a) 29.16 cm, (v) (b) 4.605 kg, Mathematics-X, , 321
Page 338 :
21. PA = PB PA2 = PB2, (x – 5)2 + (y – 1)2 = (x + 1)2 + (y – 5)2, –10x – 2y + 25 + 1 = 2x – 10y + 1 + 25, 3x = 2y, OR, 1, 4 4 2 3 , ,, 0, , Coordination of O = , 2, 2 , 2, 2, , OA =, , 25, 1, , (O 4) 2 2 16 , 2, , 4, , 89, units, 2, 22. BD = AC I (Diagonals of a rectangle), , , , OA =, , Here AP = PC II and BP = PD III, from I, II, III AP = PC = BP = DP, Hence PA2 + PC2 = PB2 +PD2, 23. OPA = 90° (tangent), AP = PB, So by pythagoras Theorem, AP =, , OA 2 OP 2 = 24 cm, , 24. Construction of circle of radius 4 cm and centre O and construction of P such, OP = 6cm. Construction of pair of tangents., 25. Dividing each term by cos , tan 1, 3 1 4 2 3, , , 2 3, tan 1, 2, 3 1, OR, LHS = x2 + y2 = (3 sin + 4 cos )2 + (3 cos – 4 sin )2, = 25 = RHS, , 322, , Mathematics-X
Page 339 :
26. AP : – 12,18, ..., 96, a = 12, d = 6, an = 96, a + (n – 1)d = 96, 12 + (n – 1)6 = 96, , 27. Let, , n = 14 + 1 = 15, p, 2 3 , q 0, HCF(p, q) =1, q, , 3 2, , , p, q, , , , 2q p, 3 =, q, irrational rational, , Our assumption is false. 2 3 is an irrational number.., , 28. Perimeter of PAB = PA + PB + AB, AS = AQ, BS = BR and PQ = PR (Length of tangents from external points), Perimetre PAB = PA + PB + AB, = PA + PB + AQ + BR, = PQ + PR, = 2PQ, = 2 × length of the tangent, OR, RP = RC (I), RQ = RC (II) from, (Length of tangents from external point), from I and II PR = RC = RQ RC bisects PQ, 29. Finding a1 = 2, b1 = –3, c1 = 7, a2 = (a + b), b2 = –(a + b – 3), c2 = 4a + b, For infinite solutions, 2, 3, 7, a1 b1 c1, , , , , , a b (a b 3) 4a b, a 2 b 2 c2, 2(a + b – 3) = 3(a + b) and 2(4a + b) = 7(a + b), a+b=6, and, a = 5b, a = 5 and b = 1, Mathematics-X, , 323
Page 340 :
30. Total -digit numbers = 90, (i) Numbers having both same digits = 9, 9, 1, , 90 10, 9, 1, , (ii) P(multiple of 10) =, 10 10, , P(E) =, , OR, , Total outcomes = 36, (i) Favourable out comes = 9, P(E) =, , 9 1, , 36 4, , (ii) Favourable out comes = 3, P(E) =, , 3, 1, , 36 12, , 31. T.S.A. of Hemisphere = 3r2, 462 = 3 ×, , , 22, × r2 , 7, , r = 7 cm, , Volume of Hemisphere =, , 2 3 2156, r =, cm3, 3, 3, , tan sec 1 tan sec (sec 2 tan 2 ), =, 32. LHS, tan sec 1, tan sec 1, , =, , (tan sec )(tan 1 sec ), (tan sec 1), , = tan + sec =, , 1 sin , = RHS, cos , , 33. I2 + II × III = 46, Let the nos be x, x + 1, x + 2, then x2 + (x + 1)(x + 2) = 46, 2x2 + 3x – 44 = 0, 11, x = 4, –, (not possible), 2, x, x + 1, x + 2 = 4, 5, 6, 324, , Mathematics-X
Page 341 :
OR, Let the present age of Mona be = x yrs, then 3 years ago of Mona = (x – 3) yrs, and 5 years hence of Mona = (x + 5) yrs, Now, , 1, 1, 1, , , x 3 x 5 3, , x2 – 4x – 21 = 0, x = 7 or x = –3 (Not possible), Mona’s present age = 7 years., 34. In ADE, h, = tan 30° 3 h = x, x, , In BCE,, , h 50, h 50, tan 60 , =x, 3, x, , h = 25, and Height of tower = 75 m, 35. a10 = 25, s20 = 610, S30 = ?, a + 9d = 25 (I) and, , 20, [2a + 19d] = 610, 2, , 2a + 19d = 61 (II), From (I) and (II) d = 11, a = –74, , 36., , S30 =, C.I., 0–10, 10–20, 20–30, 30–40, 40–50, 50–60, , Mathematics-X, , 30, [2 × (–74) + 29 × 11] = 15 × 171 = 2565, 2, Frequency, CF, , 5, x, 6, y, 6, 5, 40, , 5, 5+x, 11+x, 11+x+y, 17+x+y, 22+x+y, , 325
Page 342 :
x + y = 18, , (I), , N, = 20. So median lies in30–40 as median is 31 given., 2, , l = 30, f=y, cf = 11 + x, h = 10, , N, , cf , h, Median = 1 2, f, , 20 11 x , 31 = 30 + , × 10, y, , , 10x + 5y = 90, (II), From I and II x = 8 and y = 10, , 326, , Mathematics-X
Page 343 :
Practice Solution Pape – 4, Time : 3 Hours, , Max. Marks : 80, , General Instructions:, 1., , This question paper contains two parts A and B., , 2., , Both Part A and Part B have internal choices., , Part – A:, 1., , It consists of two sections I and II., , 2., , Section I has 16 questions of 1 mark each. Internal choice is provided in 5, questions., , 3., , Section II has 4 questions on case study. Each case study has 5 case-based subparts. An examinee is to attempt any 4 out of 5 sub-parts., , Part – B:, 1., , Question No 21 to 26 are Very Short Answer Type questions of 2 marks each., , 2., , Question No 27 to 33 are Short Answer Type questions of 3 marks each., , 3., , Question No 34 to 36 are Long Answer Type questions of 5 marks each., , 4., , Internal choice is provided in 2 quesitons of 2 marks. 2 questions of 3 marks, and 1 question of 5 marks., PART A, Section-I, , Directions (Q. No. 1-16) Section 1 has 16 questions of 1 mark each. Internal, choice is provided in 5 questions., 1., , What is LCM of P and q were P = a2b3 and q = ab4, a & b are prime numbers., OR, 987, will have terminating, 10500, or non-terminating repeating decimal expansion. Give reason., , Without actually performing long division, find if, , Mathematics-X, , 327
Page 344 :
2., , If , are zeroes of a polynomial f(x) = px 2 – 2x + 3p and + = , then find, the value of p., , 3., , If the lines given by 3x + 2ky = 2 and 2x + 5y = –1 are parallel, then find value, of k., , 4., , What is the condition for pair of linear equations to have infinite solutions?, , 5., , Find 9th term from the end of the AP 5, 9, 13, .... 185., OR, If in an A.P, a18 – a14 = 32, find the common difference., , 1, sin 2 , , 6., , Write the value of cot 2 , , 7., , One card is drawn from a pack of 52 cards. Find the probability that the card, drawn is either red or queen., OR, In a simultaneous throw of a pair of dice, find the probability of getting a sum, of numbers on both dice as 4., 3 n, , find its 8th term., 4, , 8., , If 9th term of an AP is, , 9., , For what value of k, –2 is a root of the equation 3x 2 + 4x + 2k = 0 ?, OR, Find the discriminant of the quadratic equation 4 2x 2 8x 2 2 0 ., , 10. If the ratio of the perimeter of two similar triangles is 9 : 16, then find ratio of, the areas of these triangles., 11. AB and CD are common tangents to two circles which intersect each other at C, as shown in the figure, If AB = 6 cm find CD., , 328, , Mathematics-X
Page 345 :
OR, In the given figure, AP and AQ are pair of tangents drawn, from and external point A to a circle with centre O. AP, and AQ are perpendicular to each other and, AP = AQ = 5 cm. Find the radius of the circle., 12. What is the acute angle satisfying 3 sin = Cos ?, 13. Write the area of a sector of a circle whose radius is r and length of the are is l, in terms of r and l., 14. State Basic Proportionality Theorem., 15. If two cubes of edge 5 cm each are joined end to end, what is the volume of the, resulting cuboid., 16. What is value of x in the given figure:, , SECTION-II, Directions (Question Numbers 17-20) Case study based questions are, compulsory. Attempt any four sub parts of each question. Each sub part carries, 1 mark., 17. Given picture is of Golden Gate Bridge of San Francisco. Which is parabolic, in shape. A parabola is the graph of the quadratic polynomial, f(x) = ax2 + bx + c, , Answer any four sub parts :, (a) If the golden gate bridge is represented by x 2 – 5x + 6, then its zeroes are, (i) x = –3, x = –2, (ii) x = 3, x = –2, (iii) x = 3, x = 2, (iv) x = –3, x = 2, Mathematics-X, , 329
Page 346 :
(b) Graph of a quadratic polynomial is a, (i) straight line, (ii) Parabola, (iii) Circle, (iv) None of these., (c) If the Golden Gate Bridge is represented by a quadratic polynomial whose, one zero is 4 and sum of zeroes is 0, then the quadratic polynomial is, (i) x2 – 16, (ii) (x2 – 8x + 16), (iii) x2 – 4, (iv) x2 – 6, (d) The Golden Gate Bridge is represented graphically. Zeroes of a quadratic, polynomial can be expressed graphically. Number of zeroes of this, polynomial is equal to number of points where the graph of polynomial, (i) Intersects x- axis, (ii) Intersects y - axis, (iii) Intersects y axis and x axis(iv) None of the above, (e) The number of zeroes of the polynomial f(x) = (x – 3)2 – 9 are, (i) 1, (ii) 2, (iii) 0, (iv) 3, 18. Students of Senior Secondary school are standing in rows and columns in their, playground for a drill practice. P, Q, R and S are the positions of four students, as shown in figure, , 330, , Mathematics-X
Page 347 :
Taking A as origin, answer the following (any four subparts), (a) Find mid point of QS, , (b), , (c), , (d), , (e), , (i) (5, 5), (ii) (3, 5), (iii) (5, 7), (iv) (–3, –5), Find distance between P and Q, (i) 32, (ii) 22, (iii) 25, (iv) 5, If the point M divides PR in 1 : 3 then coordinate of M is, (i) (5, 4), (ii) (4, 5), (iii) (6, 5), (iv) (5, 6), The position of Aman is (x, y) and is equidistant from. P and Q then relation, between x and y will be, (i) –4x – 8y + 48 = 0, (ii) 4x – 8y – 72 = 0, (iii) x + 2y = 36, (iv) None of these, Find the area of region formed by joining the points P, Q, R and S, (i) 32 sq. units, (ii) 18 sq. units, (iii) 12 sq. units, (iv) 16 sq. units, , 19. In a periodic test 1, the English teacher maintain a record of marks out of 100, of 50 students. On the basis of recorded data she made the following Histogram :, , Mathematics-X, , 331
Page 348 :
Read the Histogram and answer the following, (a) What will be the lower limit of the modal class?, (i) 60, (iii) 40, , (ii) 20, (iv) 80, , (b) What will be the sum of upper limit of median class and modal class?, (i) 120, (iii) 140, , (ii) 100, (iv) 130, , (c) How many students got marks more than 60?, (i) 50, (iii) 60, , (ii) 45, (iv) 42, , (d) What will be the mean marks?, (i) 53, (iii) 54.4, , (ii) 52.2, (iv) 50, , (e) The construction of cumulative frequency table is useful in determining, the, (i) mean, (iii) mode, , (ii) median, (iv) all of these, , 20. Pankaj has a triangular plot for gardening. He divided the plot by headges MN, and OP which are parallel to boundary YZ as shown in the figure-, , (a) What is length of hedge MN?, (i) 6 m, (iii) 8 m, 332, , (ii) 4 m, (iv) 2 m, Mathematics-X
Page 349 :
(b) How many pair of triangular plots are similar?, (i) 2 pairs, (iii) 1 pairs, , (ii) 3 pairs, (iv) 4 pairs, , (c) What is length OP?, (i) 11.5 m, (iii) 12 m, , (ii) 11 m, (iv) 12.5 m, , (d) What is area MN?, (i) 25 m2, (iii) 23.5 m2, , (ii) 22 m2, (iv) 6.4 m2, , (e) Choose the theorems used in these questions, (i) Pythagoras and its converse, (ii) Converse of BPT, (iii) BPT and theorem related to area of similar triangles, (iv) Converse of pythagoras theorem., PART B, SECTION-III, , Sections (Question Number 21-26) very short answer type questions., 21. Find the values of y for which the distance between the points P(2, –3) and, Q(10, y) is 10 units, OR, Find the coordinates of the points of trisection of the line segment joining, (4, –1) and (–2, –3), 22. Find the zeroes of the quadratic polynomials t2 – 15 and verify the relation, between the zeroes and the coefficients., 23. Show that any positive odd integer is of the form 4q + 1 or 4q+3, where q is, some integer., 24. In the given figure KN, PA and PB are tangents to the circle. Prove that, KN = AK + BN, , Mathematics-X, , 333
Page 350 :
., , 25. If 7sin2 + 3cos2 = 4 then show that tan =, , 1, 3, , OR, , cos 20 cos 70, Find the value of, sin 2 59 sin 2 31, 2, , , , 2, , 26. Construct an equilateral triangle of side 4.8 cm and then another triangle similar, 7, to given triangle whose sides are, of the first triangle., 4, SECTION-IV, , Directions (Question Number 27-33) These are short answer type questions of, 3 marks each., 27. Prove that 5 – 3 2 is an irrational number, given that 2 is irrational., 28. State and prove Pythagoras Theorem., OR, PS PT, In the given figure, and PST = PRQ, Prove that PQR is an, , SQ TR, isosceles triangles., , 334, , Mathematics-X
Page 351 :
29. In the given figure, OACB is a quadrant of a circle with centre o and radius 3.5, cm, If OD = 2 cm, find the area of the (i) Quadrant OACD (ii) Shaded region., , 30. Solve for x:, , 1, 1, 11, –, , , x –4, 7, x 4 x – 7 30, , OR, Find the values of K for which the quadratic equation kx(x – 2) + 6 = 0 have, two equal roots., 31. Out of a pack of 52 playing cards, two black kings and 4 red cards (not king), are removed. A card is drawn at random. Find the probability that the card, drawn is, (i) a black jack (ii) a red card, , (iii) a king, , 32. An aeroplane when 3000m high, passes vertically above another plane at an, instant when the angle of elevation of two aeroplanes from the same point on, the ground are 60º and 45º respectively. Find the vertical distance between the, two planes., 33. The distribution below gives the marks of 100 students of a class:, Marks, No. of students, , 0 – 5 5 – 10 10 – 15 15 – 20 20 – 25 25 – 30 30 – 35 35 – 40, 4, , 6, , 10, , 10, , 25, , 22, , 18, , 5, , Draw a less than type and a more than type ogive from the given data., SECTION-V, , 34. A container, opened from the top and made up of a cone of height 16 cm with, radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost, of the milk which can completely fill the container at the rate of `20 per litre., Also, find the cost of metal sheet used to make the container, if it costs `8 per, 100 cm2. (Take = 3.14), Mathematics-X, , 335
Page 352 :
35. Points A and B are 70 km apart on a highway. A car starts from A and another, car starts from B simultaneously. If they travel in the same direction, they meet, in 7 hours, but if they travel towards each other, they meet in one hour. Find the, speed of the two cars., 36. A 1.5 m tall boy is standing at some distance from a 30 m tall building. The, angle of elevation from his eyes to the top of the building increases from 30º to, 60º as he walks towards the building. Find the distance he walked towards the, building, OR, Two poles of equal heights are standing opposite each other either side of the, road which is 80 m wide. From a point between them on the road, the angles of, elevation of the top opf the poles are 60º and 30º respectively. Find the height, of poles and the distance of the point from the poles., , Answers, PART A, Section-I, , 1., , LCM = a2b4, OR, Terminating decimal Denominator is of the form 2m × 5n, , 2., , p=, , 2, 3, , 3., , k=, , 15, , k –5, 4, , 4., , a1 b1 c1, , , a 2 b 2 c1, , 5., , 153 OR d = 8, , 6., , 1, , 7., , 7, 1, or, 13, 12, , 336, , Mathematics-X
Page 353 :
8., , 11, 4, , 9., , K = –2 or D = 0, , 10., , 81, 256, , 11. 3 cm or r = 5 cm, 12. = 30º, 13., , 1, lr, 2, , 14. Correct statement, 15. 250 cm2, 16. 90º, SECTION-II, , 17. (a) (i) x = 3, x = 2, , (b) (ii) Parabola, , (c) (i) x2 – 16, , (d) (i) Intersects x axis (e) (ii) 2, 18. (a) (i) (5, 5), , (b) (iii) (2 5), , (d) (iii) x + 2y = 36, 19., , C.I., , (c) (ii) (4, 5), , (e) (iv) 16 sq. units., , 0-20, , 20-40, , 40-60, , 60-80, , 80-100, , 16, , 17, , 25, , 24, , 18, , Marks, (a) (iii) 40, , (b) (i) 120, , (d) (ii) 52.2, , (e) (ii) median, , 20. (a) (ii) 4m,, , (b) (iii) 3 pairs,, , (c) (iv) 42, (c) (i) 11.5 m, , (d) (iv) 6.4 m2, (e) (iii) Pt and theorem related to area of similar triangles., , Mathematics-X, , 337
Page 354 :
PART B, SECTION-III, , 21. y = 3, y = –9, 22. Zeroes 15 , –15, sum of zeroes = 0 = –b 0, a, 1, product of zeroes = –15 =, , c 15, , a, 1, , 23. Using Euclids division lemma, prove, 24. Use tangents drawn from external points are equal, 25. Divide both sides by cos2 & use 1 + tan2 = sec2, , cos 2 20º cos 2 70º, or, = 1, use complementary angle, sin 2 59º sin 2 31º, 26. Correct construction of equilatial traingle having each side 4.8 cm and similar, triangle., SECTION-IV, , 27. Prove by method of contradiction., 28. Statement, given to prove construction and proof., OR, PS PT, , = (given), SQ TR, Apply BPT converse, ST || QR, PST = PQR = PRQ, PR = PQ, PQR is an isoscles , 338, , Mathematics-X
Page 355 :
29. (i) ar (Qualrant OACB) = 9.625 cm2, (ii) ar (shaded region) = 6.125 cm2, 30. x = 1, 2 OR k = 6, k 0, 31. (i), , 2, 1, or, 46 23, , (ii), , 22 11, or, 46 23, , (iii), , 2, 1, or, 46 23, , 32. 1268 m, 33. Convert given distribution into less than type and more than or equals to type, cumulative frequency distribution. Then draw ogive, SECTION-V, , 34. Cost of milk = Rs 209 (approx), Cost of metal sheet = Rs 156.75, 35. Speed of car at A = 40 km/hr, Speed of car at B = 30 km/hr, 36. Distance he walked towards the building = 193 m., OR, h = 20 3m, point is 20m and 60m away from these poles., , Mathematics-X, , 339
Page 356 :
340, , Mathematics-X
Page 357 :
Mathematics-X, , 341
Page 358 :
342, , Mathematics-X
Page 359 :
Mathematics-X, , 343
Page 360 :
344, , Mathematics-X