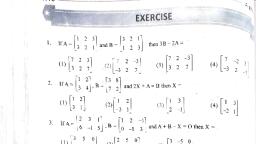Page 1 :
Properties of Matrix Multiplication, (¢) Matrix multiplication is associative: If three matri, echeiiiiaan : ces A, B and C, multiplication in the order A B C, then (AB) C=A(BC)= <e Cc Righerceneen ih, (ii) Matrix multiplication is distributive with respect to addition of matrices: The distributiy, property, A(B+C)=A B+AC, , holds good for the matrices A, B and C, provided that they are conformable for the product, and the sum., , (iii) Matrix multiplication in general is non-commutative: A B + B A, although both A B and, B A may be defined., , (iv) If AB is a null matrix, that is, AB = O, it does not necessarily mean that either A or B, should be null matrix., For example, if, 3 1 1 -1 1x1+1x(-1) 1x(-1)+1x1 -|' 0), A=\ 4 48> | ten a icin oes" 0 0,, , L, , Here AB is a null matrix but A and B are not null matrices.
Page 2 :
(v) Powers of matrices: If A = la, ] is a square matrix, the product AA can be defined by A?., Similarly, AAA can be denoted rey A? because using the associative law, one can write, , = (A?) A=A (A?), In general, AAA............ n times = A”, , (vi) If I is a unit matrix of order 7, it has the property that it can commute with every square, matrix of order 7, i.e., if A is a square matrix of order n, then, , A= IA=AI
Page 3 :
@1 . cos 26 sin 26 Fink, = 4 -sin 28 cos20|° "°°, , 2. Compute AB and BA and show that AB # BA, , Be 4, (i) A= and B=, (ii) A=, , [2 -1, (iii) A= and B=, 2, 4, 3, 2, , 3, (iv) A=] 1 2 and B, |, , , , 123, (vy) A=/4 5 6] and B=, 7 8
Page 4 :
5.5. Transpose of a Matrix, , Let A = [a,] be an m x n matrix. Then the transpose of A denoted by A’ or A’, is ann» m, matnix obtained by interchanging the rows and coloumns of A, i.é.,, , A! = la,’ = dy, for all i and /., For example,, , ee |, tame > se Ol en 4 6, 1 = ‘=, (76 9p, 32 7, Properties of Transpose, Let A and B be two matrices, then, @(AY=A, , (ii) (A + B)' = A’ + B’, A and B being of the same order., (iii) (KA)' = kA’, k be any scalar (real or complex)., (iv) (AB)' = B'A', A and B being conformable for the product AB.
Page 5 :
NX oFN Z, , Symmetric and Skew symmetric Matrix, , A square matrix A is said to be symmetric if its transpose coincides with itself, ie., A’ = A., , In other words, a square matrix A = [a,] is said to be symmetric if a,, = a,, for all integral, values of i and /, e.g., if Rd, , ah g ah g, A=|h b flthnA'=|h 5b fF, efie gfe, , ie., A’ = A and hence A is the symmetric matrix., Again, a square matrix A such that A‘ = — A is said to be skew-symmetric. In other words, a, , square matrix A is skew-symmetric if a, = — a;, for all integral values of i and j. It follows that a,, =—a, for i=j, so that 2 a,,= 0,12, a, whieh shows that all the diagonal elements of a skew, symmetric matrix are zero., 0 ab, , The matrix A= |—a@ 0 c| is askew symmetric matrix., -b -c 0