Page 1 :
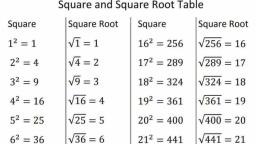
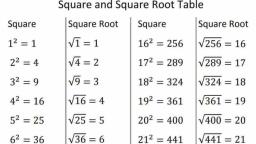
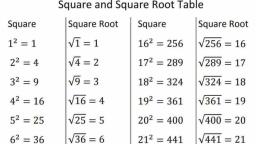
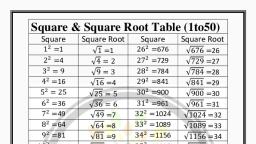
07, SQUARE-SQUARE ROOT, AND CUBE-CUBE ROOT, , Square : Square and Square Root of, , Some Standard Numbers, When a number is multiplied by itself, the, , , , , , , , , , , , number thus obtained is called square of Square | Square Root Square | Square Root, given number. , P= Vizt 1 ata] Vai =11, = onan areas es 2? = V4=2 12? =144]" J744 =12, cere Bead P= = 13?'=169/ Vi69 =, The numbers 4, 9 and 16 are the squares of 2, s=9 V9 =3 : 169 169 =13, Sand 4 and 4, 9, 16 are called perfect squares. =16 Vib =4 “14° =196] Vi96=14, 5’ =25/ V25=5 15° =225| 225 = 15, Properties.of Square ; :, ¢ Anumber ending in 2, 3, 7 or 8 is never a . =36| V36=6 e =256| V256=16, perfect square. 7 7 =49| V49=7 17° =289] 289 =17, = The feanbae oF ope {oe oe @a64} Ve=e 18° 304] Vana 4g, perfect square is never odd. 2 : 5, * Squares of even numbers are always even. ? 81 vBi=9 19° = 3611 V361=19, © Squares of odd numbers are always odd. 10" = 100] V100 = 10 20? = 400| ¥400 = 20, or, Square Root Methods of Finding Square Root, The square root of a number is ft ee a Factoris ation Method, the number which, when multiplied by itself, Following steps are to bi, will give that number. ber is indicated by fctorization metheg® °° followed fing the square root b;, The square root of a num! Y Step I Write the given Y, the sign J. pants wedliteeyns SR 3 factors, eg. a 48 product of prime, eg. The square root of 25 1s : “ep It Make pairs of . ., Thus, /25 = {5x 5=5 by choosing oa and take the product, Eq. VI44 = V2xD seq each paird, mS ABMAXE = 2x 2x30 19
Page 2 :
52, , Example 1. The value of V1764 is equal to, (1) 40 (2) 32 (3) 52, Sol. (4)1764 =2 x2x3x3 x7x7, V1764 =2X3x7=42, , (4) 42, , Example 2. The value of V8 is equal to, , (1) 6.289 (2)6.829 (3) 6.928, Sol. (3) 48 =2x2x2x2x3, , ee, V48 =2 x2 x V3 = 4V3 [We know that, V3 =1732], = 41732, eM ABET Io, Division Method, The steps of this method can be easily understood, with the help of following example. ., Example 3. Find the square root of 18769., (1) 133 (2) 137 (3) 135, Sol. (2), , Step | In the given number, mark off the digits in pairs, starting from the unit digit. Each pair and the, remaining one digit (if any) is called a period., , (4) 7.729, , , , (4) 134, , “reves, ‘Step Il Choose a number whose square is less than or, equal to 1, Here, 1? =1, on subtracting, we get O, (zero) as remainder., _tt, 1]18769, 1, , , , , , , , Step Ill Bring down the next period, i.e. 87. Now, the, trial divisor is 1x 2 =2 and trial dividend is 87., So, we take 23 as divisor and put 3 as quotient., The remainder is 18 now., at, 1/187 69, —|1, 23] 87, 69, 18, Bring down the next period, which is 69. Now,, trial divisor is 13 x 2 = 26 and trial dividend is, 1869. So, we take 267 as dividend and 7 as, quotient. The remainder is 0., , 137, Theres, a, 23). 87, 69, 1369, [169, x, , , , , , Step IV, , , , , , , , 267, , , , Navodaya Vidyalaya (Class VI) Entrance Exam, , Step V The process (processes like III and IV) goes on till, all the periods (pairs) come to an end and We get, remainder as 0 (zero) now., , Hence, the required square root = 137, , Square Root of a Decimal Number, , To make periods in decimal number, make pair near, decimal point, number before decimal point will be, paired starting from left of decimal and number, after decimal will be paired starting from right of, decimal., , Example 4. Find the square root of 232.5625., (1) 10.50 (2) 15.25 (3) 14.50 (4) 17.25, Sol. (2) 15.25, 1) 232.5625, 1, 25 | 132, §|125, 302 756, 2 604, 3045 15225, 5 15225, < « Me, , V232.5625 = 1525, Square Root of Fractions, , If denominator of the fraction is perfect square, then, find the square root of numerator and denominator, separately. If denominator of the fraction is not a, , perfect square, then make it a perfect square by, multiply a number. ‘, , , , , , , , , , Example 5. Find the square root of 7/5:, *(1)11832 (2) 1.2437 ° (3) 1.1932, Sol. (1) Since, 5 is not a perfect square. ., 75 — 35_ /35, 5x5 25 V25, , V25=5, , (4) 1.2071, , , , Now,, , ‘4 Nowwe will calculate the square root of 35., , 5.916, 5) 35 . 00 00 00, 25, , 109 | 1000, , 9| 981, , 1181] 1900, , 1|__ 1181, 11826 | 71900, 6| 70956, 944, , «. Square root of 35 at three places of decimal, = 5.916 .
Page 3 :
gquare-Square Root and Cube-Cube Root, , 7 _ 5.916, fe 28s vans, , square root of fraction can be fing, decimal number., , i 0.081x 0.4, 6. Find the value of [008txoa8, panel 0.0068 6.35, (1) 7.64 (2) 1.84 (3) 0.99 (4) 2.48, @) 0.081 x 0.484 = [81x 484, Sol.) 190064 x6.25 ~ \eaxeas, _ PROX22%27 _ 9x22 198. 99, ~Y¥BX8xX25x25 ~ 8X25 > 200 709 = 999, , Cube, , Ifanumber is multiplied two times with itself, then, the result of this multiplication is called the cube of, that number, e.g., cube of 6 = 6 x 6 x 6 = 216, , Cube Root, , The cube root of a number is that number in which, we multiply thricely, it gives the given number., , Now,, , after convert it into, , 53, , The cube root is denoted by the symbol ‘3’., eg, 18 =Y2x2x2=2 ., , Method of Finding Cube Root, , Prime Factorisation Method, This method has following steps, Step 1 Express the given number as the product of, prime factors., Step II Keep these factors in a group of three., Step III Take the product of these prime factors, picking one out of every group (group of, three) of the same primes. This product, gives us the cube root of given number., , , , , , ‘ 3/9261, , Example 7. Find the cube root of 9261. 373087, (1) 22 (2) 21 311029, , (3) 23 (4) 24 “7343, , Sol. (2) Prime factors of 9261 “7 49, =(3x3x3)x(7x7x7) a4, , 49261 =43x3x3x7X7X7, , "Now, taking one number from each group of three,, _we get 79261 =3x7=21, , Entrance Corner, , 1. The product of two numbers is 18.75. If, one number is thrice of another. Find, the larger number. UNV 2018], ()25 (2) 9.5 (3) 4.5 (4) 7.5, , Aschool collected = 2304 as fees from its, Students. If each student paid as many, Paise as there were students in the, School, how many students were there, , ~, , In the school? UNV 20171, (1)240 (ay4so. (3) 480. (4) 440, ®. Square root of 4096 is UNV 2016], (74 yea = gypes (A) 68, 1 :, 4 What is the square root of a “[JNV 2012],, 1 . 4) 0, (1) ie @, (ey @, 5 Simplify 256)9/*, [INV 2012], (1) 52 (2) 62 (3) 84 (4) 64, 8 4 man plants his orchard with 729 trees, , ond arranges them 50 that there are as, , many rows as there are trees in a row., , , , How many rows are there? UNV 2000], (1).25 (2) 26 (3) 27 (4) 28, 7. Square root of 25 is ~ [JINV 2000], (12 (2)3 (3) 4 (4)5, 8. Simplify J169 + V144 - V196. yy 1999), (1) 14 (2) 12 (3) 13 (4) 14, 9. ¥72: is equal to UNV 1999], (1)6V2 (2) 4V6 (3) VE) GS, V28 x J24.,, 10. ———— is equal to, V42 x V8 UNV 1998], 1) 2 (2) 21 3) V2 4), (1) (3) (4) Be, 11. Square root of 289 is UNV 1998], (1) 15 (2) 16 (3) 17 (4) 18, 12. Simplify, : INV, (1)49 «(264 ~—s (3) 81 iy 1998]
Page 4 :
54, , 13. By what, , least number, 720 be, multiplied so that the resulting number, , , , Navodaya Vidyalaya (Class VI) Entrance Bran, , 18. A general wishing to draw up his, soldiers in the form of a solid g, , 16169, , , , , , , , , , , , , , , , , , , , , , , , , , , , “Larger number = 3x =3x25=75, 2. Total money collected =% 2304 = 230400 paise, , , , As number of students = Money paid by studonts — el, “.Number of students in school = ¥230400 = 480 a rae, Se oa 47/329, 6| 4096 _ 7/329, , gy —— Be, :, , 124 | 496 “.Thore are 27 rows in the orchard., —41496, , x 7. __|5, , .. Square root of 4096 = 64 2 e, , x, , i . ree, in the orchard is equal to the number of Y, each row. Therefore, number of rows, equal to the square root of 729., , . ‘quar, Idiers na, i NV 1997] found that he had 31 so over, F, ab Pe Oe 5 we the number of men in the front line,, UNV, 14, Find the least number which must be (1) 127 (2) 138 (3) 160 ma, subtracted to make 175 a perfect ;, square. UNV 1997] 19. A gardener plants 3600 trees in garden,, (1) 2 (2)3 (3) 6 (4)7 he arranges them so that there are, : many rows as there are trees in a to,, 15. Square root of 0.09 is [NV 1997] how many rows are there? UNV 55, wy bas (2) 018 (45 (285) (3)57 (A), (3) 0.3 (4) 0.5 aaa « ‘i, 16. Simplify ¥8464 + J? = 102. UNV 1997] 20. The square root of 555 is equal to, (1) 100 (2) 225 (3) 400 «° (4) 625 UNV 1995, 1694 6 oF e@F @f wt, 17. Simplify a +14=25. [NV 1996] 17 7, (1) 14 (2) 12 21. 27 x 243 is equal to INV 1555, (3) 14 (4) 22 (1) 38 (2) 3 (33? ay", 1.(44 | 2.0) | 3) | 4.2 | 5.4 | 6.3) 7. (4) 8.) | 9.) | 10@, 11. (3)_| 12. (1) | 13. (3) | 14. (3) | 15. (3) | 16.1) | 17.(3) | 18. (1) | 19. (4) | 20.2, 21. (1), Hints and Solutions, 1. Let smaller number = x a Ee a1, Larger number =3x 4. Square root of s =Va 732, According to the question Sal GNi= ax? wees, x XBx = 1875 3x" = 18.75 5, (asap =a =i a oroftt, x? =6,.25 =x = 6.25 =25 6. According to the given condition num sv, , 5 2
Page 5 :
care Square Root and Cube-Cube Root, , , , , , , , , , , , , , , , , , , , , , 55, 9 2|72, , 2136 17. Let? =x, then,|2649 414=25, = 218.8, :, can koe > set =25-14=11, V72 =2 x2 x2x3x3 =65 2084 121 x= 1884-14, x, ) We6xNe4_ V7 x ave 18. 16160 -31=16129, ee i. =, Tnexi8 V2 xJ3xJ7 xaos 127, _4xV7 x V3 x J2 5 1 /161.29, aa AVG KN?, 4axJ3xV7 2 1/4, ne ale, 1 |289 so, 1 247| 1729, "27 |189 7} 1729, 7 |189 *, x «. Number of men in the front line = 127, «Square root of 289 is 17. 19. “Fare:, 2. tet? =x fo 8, 6 6 er _ yy — 6136, x Tox 7 120] 00, => Vx=7 >x=49 ol oo, 13. Prime factors of 720 are x, , 2x2x2x2x3x3x5, , , , , , “-Required number =5 20. Now,, 14, 13, 14175, in, 23] 75, 9, 4 e and, , , , Extracting the square root we get a remainder 6., Hence, 6 is the least number which ought to be, Subtracted to make it a perfect square., , 1. 009-9, 100, Now, ¥g =3, 100 =10, 9 _ 3 _o3, , «Required rows = 60, , 17, 2 89, Ht, 27 |189, , , , —1189, , x, , 5, 1/225, 1H, , 25 [125, 51125, , x, , [289 _17, 225. 15, , , , 21. 27 X243 = X3 x3] x[3x3 X3X3x3], , =3° x 3% =38