Page 1 :
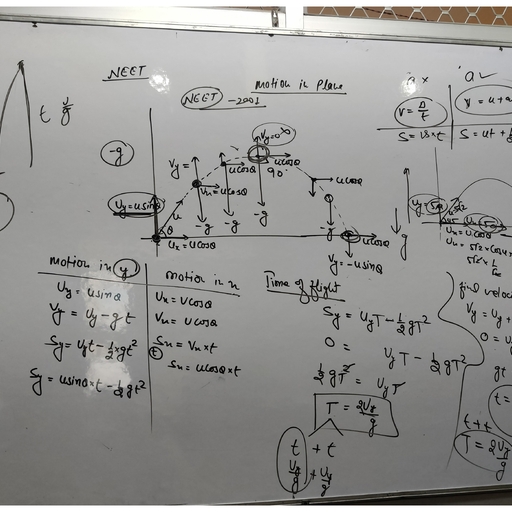
xample [} A stone is thrown by a student Haare va, the bottom of a hill with a velocity 30 ms“! Shae 2ne5, from tne angle of 60° with the horizontal. If the ~ 0, Oy = 308, g =, , an 10 ms-2, wat the hill is 30° with the horizontal, find er, , 2, R= 2x30 £08 60° sin (60°, , from the student to a point at which 1 7 = 30"), we gone falls on ill use g = 10 ms, Oxcos? 30°, Solution. Refer to a 2(d).9, the distance = 2X 900% (1/2) (1/2, 2u* cos @sin(8—8,) 10x (3/22, lope is R =————— ae, covered on slope g cos? 8% = 60m, , TEST YOUR GRIP, , , , , , , , MULTIPLE CHOICE QUESTIONS }, , 1. A particle has initial velocity (3? +4) and has acceleration (0-4 + 0-3) .Its speed after , a, z 10 seconds is It, (&) 7-V2 units (c) 85 units (d) 10 units +—, , certain height and at the same time another stone is thrown, e sam height. Which one will reach the ground earlier ?, __ (b) Second stone (c) Simultaneously (d) Not sure a=, , , , , , , , , , , , , , , (d) none of the above, y with a velocity of 5 ms“ from the top of a building 19-6 m, ball take to hit the ground ?, (2s (© Bs @3s +, at its maximum height is half of its initial speed. The angle of 7, (c) 30° (4 ai + el, horizontal range and maximum height of projectile are i, : . = tan! (025) ;, (c) @= tan! 4 05 arf, reaches the other in 2 seconds. The maximum height attained by Eo, ion will be (g = 10 m/s*) : wo, (c) 75m @ 10m anche, s of 45° and 60° with the horizontal with same | oe, ontal range is |}, @2: B Lo, per second is r, @isn |, , adi, neds ohse, , el (6) 200 me cm/s? \ |

Page 2 :
Solution, Here, 2 r= 40 cm Taking motion of projectile from O to P along, , re p= 20cm = 0-20 m; x-axis we have Xo = 0, x =x, uy =u, a,=0, t= 7,, 120 Using th i = 1, ency v= 20 2dipes'* sing the relation, x = x9 + u.t+ 5%: 2,, , we get x=ut or t=x/u, , Angular velocity, 0 = 2 mv = 2m x 2=4 m rad/s afi) f, , , , , , , , , |, |, Linear velocity, » =r = 0:2 x4 = 08 1 ti save on ao ae paeties along Y-axis, we, f =0,y=y, u,=0,a,=9,t=, Centripetal acceleration = reo? = 0-2 x (4 0)? y see cn, = 3-2 12 ms Using the relation, y = yp + Wy tt ; a, 2,, exampehl Calculate the magnitude of h Sg Ce :, , linear acceleration of a particle moving in a circle wehave y= 040+ 3, of radius 0-5 m at — instant when its angular 1 32, velocity is 2°5 rad s~ and its angular acceleration == gt? =—2— ’, eee =~ yep oma, , Solution. Here, r= 0-5 m ; @ = 2:5 rads“, gx, , 6 rad 52 Here, y = x tan 8, so a + = xtang, . we, Tangential acceleration, : nat, ap=re=05 x 6 = 3.0 ms? Peer, , _ Centripetal acceleration, 8, , ; p? = 0-5 x (2:5)? = 3-125 ms 2u? tan? 0, , , " Bs and y=xtan@=—————, eisai, &, , Distance OP = Je +y, , = 2u? tan. Fate 2 2u? tan@ sec?, 8 c, , Example P¥] A football is kicked at a speed, of 20 m/s at a projection angle of 45°. A receiver, on the goal line 25 metres away in the direction, of the kick runs the same instant to meet the ball., What must be his speed, if he is to catch the ball, , , , , , , , , , , , before it hits the ground ?, Solution. Here ; « = 20 m/s, 6=45° d=35m., Horizontal range ;, 2 “, Rat sin2@ =20-sin2x45* = 4082 m, g 9s, Qwsin® 207. ace, a =—xsin45, Time of flight, T= : os, = 2886s, , Since the man is already 25 m away in, Aho dana the bal 20 to cach he bal Bes ©, cover a distance = 40:82 - 25 = 15-82 m, in ime, 3.886 s, Therefore, the velocity of goa! man to catch, , iets” = Sere, , , , = 5481 ms*

Page 4 :
2/182, The distance through which the monkey falls, , 1, vertically in time f= ae =AB,, , It means the bullet and monkey will pass, through the point B simultaneously. Therefore, the, bullet will hit the monkey., , Exampte[0) The maximum height, attained by a projectile is increased by 10% by, increasing its speed of projection, without, changing the angle of projection. What will the, percentage increase in the horizontal range., , Solution. As max. height,, , ee eg :, =—sin26 s, saan (i), , Let A H be the increase in H when u changes, by A u. Differentiating (i), we get, , 2uAusin? 6, , , , , , , , , , , , , , , , , , , , , , , , , , , AH =, , , , Gass FUNDAMENTAL PHYSICS (XI) ma, , FIGURE 2(d).26, , , , , , , ucos0 |, 1, , D, , B c x, , Component of velocity along OY, =u sin 0 = 39-2 sin 30° = 19-6 ms!, , Let t be the total time of flight (i.e. time in, going from O to D). Consider the vertical downward, direction OB as the positive direction of Y-axis., Taking motion of a projectile from O to D along, Y-axis, we have, , Yo = 0, y = 156-8 m,, u, =— u sin 30° = — 19-6 m/s,, , a, ay=98 m/s?, t= 1, , Bs, AS ir Yorn thy age, , 1 >, 156-8 =0 + (19-6) t+ 5 x98xP, 156-8 =— 19-61+4.9 2, , or, , or 4.9 7 - 19-6 1- 156-8 =0, , Or is 43 Oo, , or ?-81+4t-32=0, , or t(t-8)+4(¢-8)=0, , or (t+4)(t-8)=0 or t=—4or8., , As t= —4s is not possible, therefore ¢ = 8 s, , Distance from the foot of tower where it strikes, the ground is, , BD = ucos 30° x t = 33-947 x 8 = 271-57 m, , Example [J] A machine gun is mounted, on the top of a tower 60 m high. At what angle, should the gun be inclined to cover a maximum, range of firing on the ground below ? The muzzle, speed of the bullet is 90 ms~!, take g = 10 ms~., , Solution. Let the machine gun be mounted at, O and fired with a speed of 90 ms~! at an angle ©, with the horizontal. Fig. 2(d).27., , Total range of firing on ground, , a, Bb laa mean ROME) ont b

Page 5 :
i : 2, + 20 sin @) t+ 3 x (— 10) ¢, , We, , , , , , 6 2, os 8, , 6, i ——-5x, of j= (20sin 0) Scos® (, , 5x36, , eset, of 12 = 24100 0 55 cos? 0, , 36 1.3, J 4tand— “= 8° 8, , 36 2, _ 22 (1+ tan* 8), é 22 24tan® 3 ¢, , = jp0 tan 0 — 36 - 36 tan” @, ot Oe 29 120 tan 0 +96=0, , 6 tan’, © Jot9—101an 0+ 8=0, nd 2) Gn O-4) =0, or ten = 2004/3, , a O= 63° 26’ or 53° 4V, example fy] A body is projected with a, m of 40 ms 1 After 2 s it crosses a vertical, ‘height 20-4 m. Find the angle of projection, + ontal range of projectile. (g = 9°8 ms~)., e0mss), =204m, , , , , , , , , , , , , , , , , , , Solution. Let the monk aren, fi ey stati, fired with a gun from O with a More at A, be, 8 with the horizontal direction OX ba angle, perpendicular to OX. Let the bi . Draw AC,, , , i ullet cross i, line AC at B after time ¢ and ribs iene Eb, ; =, , (iy) wnt. otigin O. Fig. 2(4).25,, FIGURE 2(@).28, , , , , , , , ba OC organ i, ucos® ucos® ~@, (where OC = x), In A OAC, AC= OC tan8=<xtan@ _...(ii), Clearly CB = y = the vertical distance, travelled by the bullet in time ft., Taking motion of the bullet from O to B along, Y-axis we have, Yo = 0, Y=, Uy =u sin 8, a,=—g.t=t, , we Lee, As, yay ture e*, , y=O4usinores Ce)?, , 1 2, =usinOr— 3 gi? ...(ii), , «. AB = AC - BC =x tan8-y, , 1, - stan0-(wsinor—5 2", , , , , , = tan {sins, uc, , [from (@], , ; gobprty, =xtanO—xtanOt+ st mine, , Il pass through the point, , 1, a vertical distance 3, , It means the bullet wil, , 2, gt, B on vertical line AC at, , below point.A.