Page 1 :
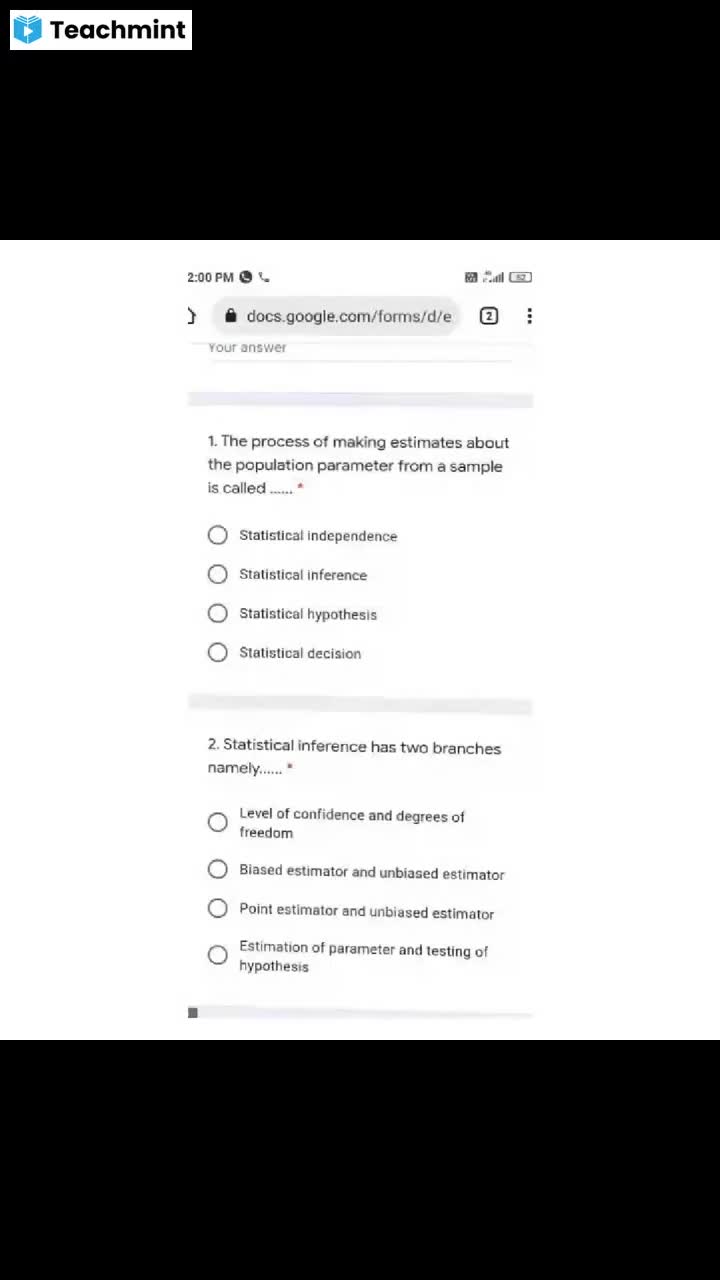
Chapter 12, , Nonparametric Statistical, , Methods, , , , SECTION-A, Short Essay Type Questions, , Q1. Give a brief account of the need of nonparametric statistical methods., , ‘Ans. Parametric statistical methods are based on, stringent assumptions about the population from, which the sample has teen drawn. Particularly the, assumptions like form of the probability distribution,, accuracy of observations, etc., are more common., ‘Also, the parametric methods are applicable primarily, to the data which are measured in interval or ratio, scale. In practice, however, stringent assumptions, are seldom fully valid. Moreover, the measurements, are often made on nominal or ordinal scale., , If the assumption do not hold good or the data, do not meet the requirement of parametric statistical, methods, nonparametric methods come to the, rescue of the worker. Nonparametric methods, entail very mild assumptions like continuity and, symmetry of the distribution. Also most of the, nonparametric methods are applicable for, ordered statistics., , Q.2._ Distinguish between nonparametric methods, and distribution free methods., , ‘Ans. Those statistical methods, which are not concerned with the estimation or testing of hypothesis, , for one or more parameters of probability distribution functions are termed as nonparametric methods. Those inferences whose validity do not rest on, the form of specific probability distribution of the, population from which the sample has been drawn, are termed as distribution free methods. These two, terms are not synonyms. But the statistical methods, applied in the two cases are almost same and they, are interchangeably used., , Q3_ When should the nonparametric methods be, preferably used?, , ‘Ans. Non ic methods be used when one, ‘or more of the following situations ¢», , , , i) ‘The hypothesis does not involve a parameter, of the probability function of the population,, (Gi) The observations are not as accurate as reQuired for a parametric inference. Also when, the measurements are on the nominal or orinal scale., (iii) The assumptions necessary for a validity of a, ‘parametric method are suspected to hold good., For example, the assumption of normal population is doubtful.

Page 2 :
NONPARAMETRIC STATISTICAL METHODS:, , (iv) One wants to avoid complicated analysis of, data,, (v) One is interested in quick results., , Q4 What are the advantages of nonparametric, methods?, , Ans. ‘There are many advantages of nonparametric, methods over parametric ones. The advantages can, precisely be delineated as under:, , (i) Any inference based on the parametric analysis which does not uphold the underlying, assumptions necessitated for it will be exroneous. In such a situation nonparametric, methods can safely be applied., , If the measurement scale of data is nominal, of ordinal, nonparametric methods ¢an be, used., , In case the measurements are not so accurate, as to apply parametric methods, nonparametric methods perform better., , With so-called dirty data (contaminated observations, outliers, etc.), many nonparametric, methods are appropriate., , There is no restriction for minimum size of, sample for nonparametric methods for valid, and reliable results., , Nonparametric methods require minimum, assumption like continuity of the sampled, population,, , ‘The analysis of data is simple and involves, little computation work., , Nonparametric test may be quite powerful, even if the sample size is small., Nonparametric test are inherently robust, against certain violation of assumptions., QS What are the disadvantages of non-para‘metric procedures?, , ‘Ans. Nonparametric procedures are also not free, from demerits. Some of the main disadvantages are, a follows:, , (i) Because of the simplicity of nonparametric, procedures, they are often used even if appropriate parametric methods are available., , (i) All nonparametric methods are not as simple, as they are claimed to be., , (iii) It is not possible to determine the actual power, , , , Gi), , ii), , (iv), , Ww), , wi), , wii), (viii), , (ix), , 293, , of a nonparametric test due to the want of, actual situation., Q6 How can one judge the relative performance, of two tests?, ‘Ans. In many situations there can be more than, ‘one tests which appear appropriate for the test of a, hypothesis. Then there is a need to fix some criteria, to choose one out of many alternative tests. The, asymptotic relative efficiency (ARE) is a single, ‘measure which provides satisfactory results for comparing the performance of two tests based on large, samples. The concept of ARE was given by S.J.G., Pitman in 1961, and hence ARE is often named as, Pitman efficiency. The calculation of ARE is based, ‘on the classical distribution and assumption of the, nonparametric tests that have parametric analogues,, ‘The asymptotic relative efficiency of test A relative toa test Bean be defined as the limiting value of, n/n, where n, and n, are the sample sizes required, for the tests A and B to have the same power., Q.7 What is power efficiency?, ‘Ans. The power efficiency of test A relative to a, test B is the ratio of sample sizes ng/n, where both, the tests are for the same H, and Hand having same, power of the tests A and B. Since it is difficult to, calculate power efficiency, ARE is more frequently, used., Q.8 What is meant by tied observations?, ‘Ans. Under the assumption of continuous distribution, no two observations can be equal. But due to, the rounding of figures, precision of measuring instruments, inaccuracy of measurements, etc., some, observations seldom occur which are exactly equal, in magnitude, Such observations are called tied ob, servations. Due to tie among observations, one faces, the problem in awarding ranks to them., 9 How to surmount the problem of tied obser=, vations?, ‘Ans. There are different approaches to overcome, the problem of tied observations. Five important, approaches are discussed over here., () Midranks approach. Under this approach, each, ‘group of tied observations is ranked as if they are all, distinguishable and then take the average of the

Page 3 :
294, ranks of tied values and assign the same average, rank ¢o the tied observations of that group. This is, the most frequently used methods of breaking the, ties, When the mid rank method is used, a correction, of ties is often applied in most of the tests and, ‘measures of associations., , (i) Average statistics approach. If there are K, groups of different observations ina set and # group, , ., is of size 7, there are in all 117! possible arange, ments of values. Now calculate the test statistic for, each arrangement and take their average. Use this, average value for taking the decision. Under this, approach, the test statistic will have the same mean, but smaller variance. This method is generally not, used because it usually involves too much computation,, (ii) Least favourable statistic approach. Instead, of averaging the test statistics for all possible, arrangements under tied observations, one might, choose that statistics value out of all which minimises, the probability of rejection. Under this approach,, there is least chance of committing type I error., (iv) Range of probability approach. In this method one chooses two values of test statistics, the, least and most favourable values. But a decision is, possible only if both the values fall either inside or, Outside the region of rejection. If not so, the method, fails., (v) Omitting the tied observations. This is the, simplest but nsky approach. In this method one, discards all tied values and reduce the sample by, that number. If the number of tied observations is, small as compared to the sample size, the test is not, affected much otherwise, there is a loss of information and the prodecure introduces bias towards rejection of the null hypothesis., Q. 10 What assumptions are generally made for a, nonparametric test?, ‘Ans. Following assumptions are most commonly, ‘made about any nonparametric test:, , (i) The sample at hand is a random sample, , drawn from a population whose median is, unknown., , , , , , PROGRAMMED STATISTICS, Gi) All the observations in the sample are inde, pendent., (iii) The variable of interest is continuous., {iv) The sampled population is symmetric., (¥) The observations are measured at least on, ‘ordinal scale., Q. 11 What are the basic steps involved in any, nonparametric test of hypothesis?, , ‘Ans. Various basic steps involved in a test are:, , (@) First of all one should look for the assump, tions necessary for the validity of a test procedure,, , ii) The sample data required should be collected,, , , , (iv) The test statistic or procedure should be decided,, , (v) The decision criteria should be fixed to decide about the rejection or acceptance of Hy, vis-a-vis H,., , (vi) The interpretation to the conclusions drawn, should be given., , Q.12 What do you understand by ordered statis, tics?, Ans. LetX,,X», continuous population with probability of any X's, being equal to zero. If x,, is the smallest X value in, Xj Xp oon Xp ay the next larger valve and x,y. the, highest, then the set of values 44, +) + om Xj iS, called the ordered statistics. This is an ascending, , order. If one wants he can put the observations in, descending order a8 4) + Lys) +o Xyy If qq, denotes the * ordered value for r= 1, 2, .... m, the, ‘ordered statistics deals with the propertics of x,, Ordered statistics is extremely useful in nonparametric methods., , ‘The ordered statistics do not possess the same, probability distribution as the original variable X., ‘Also the values in the ordered statistics are not independent even if original variate values are independ, ‘ent as is always true in case of random samples., Q.13 Give the names of various nonparametric tests, and statistics., , ‘Ans. The names of the nonparametric tests and, Slatistics are as follows:

Page 4 :
NONPARAMETRIC STATISTICAL METHODS, , ‘One sample nonparametric tests:, (i) Kolmogorov-Smirmnov test, , Gi) Ordinary sign test, , ii) Wilcoxon signed-rank test, , (iv) Runs test, , Two or more samples nonparametric tests and, statistics:, , (i) Kolmogorov-Smimov two-sample test, Sign test for paired samples, Wilcoxon paired sample signed-rank test, Median test, Wald-Wolfowitz runs test, , Mann-Whitney U-test, i). Menemar's test, Cochran's Qutest, Mood's test for dispersion, ‘Moses test for dispersion, Kruskal-Wallis one way analysis, Friedman's method of two way analysis, Jonckheere Terpstra test, Page's test, ‘Spearman's rank correlation, Kendall's correlation coefficient t, Coefficient of concordance, Brown and Mood’s test, Moods test,, Theil’ test, Confidence interval, (xxii) Confidence band, Q. 14 Describe briefly Kolmogorov-Smimov test, of goodness of fit in case of one sample., Ans. Let Xj Xy oy X, be a random sample from, an unknown continuous population having the curmulative distribution function F(x). Also let the, ordered statistics be Xp Xp oe Xyy The K-S testis, based on Glivenko-Cantel theorem which states, that the step function S, (x) with jumps occurring at, the values Sy Koyo» Ky) of the ordered statistics, {for the sample approaches the trae distribution for, all X. Kolmogorov-Smimov used this theorem and, compared the empirical distribution function S, (x), ‘of the sample for any value of x with the population, calf, under Hy ie. Fy (2)., ‘The hypothesis under testis,, , , , , , Gx), w, (xi), (xii), (xiii), (xiv), (xy), (xvi), (xvii), (xviii), (xix), (xx), (xxi), , 295, , Ho: F(x) = Fo(x) vs. Hy: F(x) # Fa (2), , where F, (x) is a completely specified continuous, distribution., To test Hy, the numerical difference |s, (x) ~ Fo(3)|, is used in K-S test. Since the difference depends on, x, the K-S statistic D, is taken to be the supremum of, such differences, i.e., , Dy= Sup s(x) Fala}, , Under Hy the statistic D, has a distribution which is, independent of the e.d.f- F (x) that defines Hy, The, statistic D, is distribution free., , To take a decision about Ho, the test criteria are,, reject Hy if D, 2 D,,q (tabulated value), otherwise, accept Hy., , Q.15 Compare the Chi-square test of goodness of, fit with Kolmogorov-Smirnov test., , ‘Ans. The Chi-square test is also one of the very, popular test of goodness of fit. If we compare the, two, we find that:, , (D 2-testis specially meant for categorical data, ‘whereas K-S statistics are for random samples from continuous populations. However,, when the data are categorical, the two tests, can interchangeably be used., , Chi-square requires categorical data, whereas, the K-S statistic utilises each of the n observations. Hence, the K-5 makes better use of, available information :han Chi-square statis., tic., , ‘The Kolmogorov-Smirnov statistic is more, flexible than Chi-square statistic as it can be, used to determine minimum sample size and, confidence band., , (iv) In K-S test, we can use one side test also, which is not possible in Chi-square test., , (¥) ‘The K-S testis easier to apply., , (vi) The Chi-square test also comes in the categroy, of parametric tests whereas K-S testis only a, ‘nonparametric test., , Q.16 How can you perform ordinary sign test?, Ams. Let typ Sizy + Xp be the ordered sample, values from a population F (x) and M be its median., , , , wi), , , , Git)

Page 5 :
Also P(X = M) = 0. Here we test, Hy: M = Mg ¥5., Hy: M # My where My is the given value of the, median and hence P(X > My) = P(X <Mg)=05., So we can test Hy:P(X > Mg) = P(X <Mo), Hy:P(X> Mo) # P(X < Mo), , To perform the sign test, find the differences, (Xyy~ Mo) for i= 1, 2, «.. 0 and consider their signs., Suppose the number of +ve signs is r and negative, signs, (n = 7). For the purpose of test we consider, ‘only positive signs. So r follows binomial distribution. Also the null hypothesis Hy changes to, p=05., , So the hypothesis under test amounts to testing,, Ho:p=05 vs. Hy:p205, , reject My if F2 faa where far, , is the critical value at significance level «. fa is, , the smallest integer which satisfies the conditions,, , LOOC", ‘or FS fda is the smallest integer such that, , & (QV GY =, , , , vs., , , , , , ‘The test criterion is, , , , For one-sided test use r, instead of fa2 . Rest of the, test procedure remains the same., , Large sample case: If n 2 25, normal deviate test, is applied to decide about Hy. Z is given by the, statistic,, , , , ga ltt05)—nP, Po do, , where r <p, , (O30 where r> nPo, Ino dn, Sand qg= 1-05 =05, ‘The decision about Hy is taken in a usual manner as, described with parametric tests., , , , PROGRAMMED STATISTICS, , Q.17 How to resolve the problem of zero differ‘ences in sign test?, ‘Ans. In practice zero differences seldom occur. To, resolve this problem, the best way is to discard zero, differences and reduce the sample size by that, number. Another way is to count half zeros as positive and half zeros as negative., Q. 18 Following are the yields of maize in q/ha, recorded from an experiment and arranged in ascending order with median M = 20., 15.4, 16.4, 17.3, 18.2, 19.2, 20.9, 22.7, 23.6, 24.5., “Test Hy: M = 20 vs, Hy: M # 20 at a = 0.05, [Given: P (x < 4) = 0.50), ‘Ans. To test Hy, we find the difference (X ~ 20), and write their signs., , , , , , Here n= 9,, , P (xs 4)=05 is greater than «= 0.05. Hence Hy, , is not rejected at 5 per cent level of significance., Q. 19 How Wilcoxon's signed-rank test differ from, sign test and how to perform it?, ‘Ans. Ordinary sign test was based only on the, direction of differences ignoring their magnitudes., But Wilcoxon's signed rank test takes into consi, ‘eration, the both. This test is more sensitive and, powerful than ordinary sign test., , To perform the test for Hy:M = My vs. Hy:, ‘M- Mo, find the differences d, = Xy- My for, 1 = 1, 2, ony md, will be distributed symmetrically, about the median zero so that +ve and ~ve differences, of equal absolute magnitude have equal probabilities, of occurrences. The steps of the test are as follows:, , Step-1. Arrange the differences in ascending order ignoring the sign and rank them from, lion., , ‘Now assign the signs to the ranks which, the original differences, , Suppose the sum of ranks of +ve ds is, T° and that of ranks of ~ve d's is T. For, a symmetric distribution, it is expected, that T* and 7 will approxiamtely be, ‘equal., , , , Suep-2., , Step-3.