Page 2 :
© Government of Andhra Pradesh, Hyderabad., New Edition, First Published 2014, , All rights reserved., No part of this publication may be reproduced, stored, in a retrieval system, or transmitted, in any form or by, any means without the prior permission in writing of the, publisher, nor be otherwise circulated in any form of, binding or cover other than that in which it is published, and without a similar condition including this condition, being imposed on the subsequent purchaser., The copy right holder of this book is the Director, of School Education, Hyderabad, Andhra Pradesh., We have used some photographs which are under, creative common licence. They are acknowledged, at the end of the book., This Book has been printed on 70 G.S.M. S.S. Maplitho,, Title Page 200 G.S.M. White Art Card, , Free Distribution by Government of Andhra Pradesh, , Printed in India, at the Andhra Pradesh Govt. Text Book Press,, Mint Compound, Hyderabad,, Andhra Pradesh., , ii
Page 4 :
Intro ..., We believe that class-10 education is a key aspect of school education and a, turning point in student’s life. The present tenth class Science textbook in your, hands is developed in accordance with the National and State Curriculum Framework, and the Right to Education Act. This book helps the student to review various, concepts that were learned through the learning experiences provided in the school, and to get comprehensive knowledge about these conecepts. The lessons in the, textbooks are presented in such way that they help in preparing the student for, competitive examinations and also to prepare him/her for intermediate education., The new science textbooks are specially designed with suitable pedagogy in, tune with Continuous Comprehensive Evaluation (CCE) which we are right now, implementing in school education. These textbooks help the teacher to assess, students learning during teaching learning processes. They facilitate effective learning, of various concepts of science in scientific method apart from getting knowledge, about concepts. It is essential to complete the syllabus in the stipulated time as, students have to write the Board Examination in class-10. But don’t forget that, completion of syllabus means making the students understand the concepts and, trying to achieve the learning competencies. It is mandatory on the part of teacher, to implement teaching strategies like, making the student to read the content of, the textbook, discussion, analysis, lab activity, field trips, preparing reports, etc., Teacher must take special care to avoid the practice of rote memorisation of, scientific information from guides and question banks., The classroom teaching of science must be in such a way that it encourages, children to think and work scientifically. Also, it must enhance love towards nature., Even it should enable to comprehend and appreciate the laws governing the nature, in constructing so much diversity all around. Scientific learning is not just disclosing, new things. It is also necessary to step forward without interrupting the, interrelationship and interdependency along with understanding of the nature’s, intrinsic principles.High School children possess cognitive capacity of comprehending, the nature and characteristics of the transforming world surrounding them. And, they are able to analyze abstract concepts., At this level, we cannot quench their sharp thinking capability with the dryteaching, of mere equations and theoretic principles. For that, we should create a learning, environment in the classroom which provides an opportunity for them to apply the, scientific knowledge, explore multiple alternatives in solving problems and establish, new relations., Scientific learning is not just confined to the four walls of classroom. It has a, definite connection to lab and field as well. Therefore, there is a lot of importance, to field experience/ experiments in science teaching., , iv
Page 5 :
There is a great need for compulsory implementation of instructions of the, National Curriculum Framework- 2005 which emphasizes linking of the science teaching, with local environment. The Right to Education Act- 2009 also suggested that, priority should be given to the achievement of learning competencies among children., Likewise, science teaching should be in such a way that it would help cultivate a, new generation with scientific thinking., The key aspect of science teaching is to make the children understand the, thinking process of scientists and their efforts behind each discovery. The State, Curriculum Framework- 2011 stated thatchildren should be able to express their, own ideas and opinions on various aspects. These Science Text Books are prepared, to meet the set standards of the SCF and thus assist children in becoming selfreliant researchers capable of thinking intensely in scientific terms., The new textbooks are developed to achieve desired academic standards. So, teachers should develop various teaching learning strategies to make their students, to achieve class specific academic standards. We should avoid rote learning methods, for the successful implementation of Continuous Comprehensive Evaluation (CCE)., It is very impart to know more about different methods to assess students’, progress by summative and formative evaluation. The new textbooks reflect, Continuous Comprehensive Evaluation and teaching method with respect to discussed, concepts. This is very useful to teachers and students., In the new textbooks, the design of concepts and activities help in achieving, the specified academic standards. Teachers need to plan appropriate teaching, strategies to improve the academic standards among the students by the end of, teaching the lesson. For effective implementation of continuous comprehensive, evaluation the teaching must move away from the methods of rote memorisation, of concepts. There is a need for teachers to have a good understanding of the, methods of evaluation which help them in assessing the progress of children in a, constructive and comprehensive way. The new textbooks are not confined to, simply provide necessary informations about concepts. Instead they focus on the, new teaching strategies and evaluation techniques which are very important for, both teachers and students., We thank the VidyaBhavan Society, Rajasthan for their cooperation in designing, these new text books,the writers for preparing the lessons, the editors for checking, the textual matters and the DTP group for cutely composing the textbook. We, invite suggestions from educationists, teachers, parents, students and others to, make this book more meaningful., Teachers play a pivotal role in children’s comprehensive use of the text book., We hope, teachers will make their best efforts for proper utilization of the text book, so as to inculcate scientific thinking among children and inspire them to be great, scientists., Director,, SCERT, AP, Hyderabad, Free distribution by A.P. Government, , v
Page 6 :
Dear teachers..., New Science Text Books are prepared in such a way that they develop children’s observation, power and research enthusiasm. The official documents of National and State Curriculum Frame, Works and the Right to Education Act are aspairing to bring grossroute changes in science, teaching. These textbooks are adopted in accordance with such an aspiration. Hence, science, teachers need to adapt to the new approach in their teaching., In view of this, let us observe certain Dos and Don’ts:, • There is an immediate need to discard the practices adopted in the schools on a false belief, that teaching of 10th class means preparing the children for public examination. In 10th, class the teaching learning process should focus on achieving the academic standards rather, winning race of scoring marks., • Avoid practices like using guides and question banks, asking the children to read only, important questions, focussing on lessons which help in scoring more marks., • Read the lesson thoroughly before you start teaching and ask the children to read the text., Then initiate a discussion to make the children understand the concepts in the lessons., • Encourage children to express their own views and ideas while writing the answers. Give, weightage to such type of writing in examination., • Some instructions are given in the textbook regarding the collection of certain information, by the teacher. Collect such information and make it available to students., • In public examination, the weightage will be given to all aspects of the syllabus. Except, foreword of the textbook everything else must be treated as a part of the curriculum., • Textual concepts are presented in two ways: one as the classroom teaching and the other, as the laboratory performance., • Lab activities are part and parcel of a lesson. So, teachers must make the children conduct, all such activities during the lesson itself, but not separately., • Teachers are advised to follow the following teaching steps while transacting lessons-mind, mapping, reading lesson and identifyng new words by children, performing activities,, demonstration and discussion, conclusion and evaluation., • In the text, some special activities are presented as box items: ‘think and discuss, let us do,, conduct interview, prepare report, display in wall magazine, participate in Theatre Day, do, field observation, organize special days’. To perform all of them is compulsory., • The abbreviation (A.S.) given at the end of each question in the section “Improve your, learning” indicates academic standard., • Collect information of relevant website addresses and pass on to students so that they can, utilize internet services for learning science on their own., • Plan and execute activities like science club, elocution, drawing, writing poetry on science,, making models etc.to develop positive attitude among children about environment,, biodiversity, ecological balance etc., , vi
Page 7 :
•, , As a part of continuous comprehensive evaluation, observe and record children’s, learning abilities during various activities conducted in classroom, laboratory and field., We believe, you must have realized that the learning of science and scientific thinking are, not mere drilling of the lessons but, in fact, a valuable exercise in motivating the children to, explore for solutions to the problems systematically and preparing them to meet life’s challenges, properly., , Dear Students..., Learning science does not mean scoring good marks in the subject. Competencies like, thinking logically and working systematically, learned through it,have to be practiced in daily, life. To achieve this, instead of memorizing the scientific theories by rote, one must be able to, study them analytically. That means, in order to understand the concepts of science, you need, to proceed by discussing, describing, conducting experiments to verify, making observations,, confirming with your own ideas and drawing conclusions. This textbook helps you to learn in, that way., What you need to do to achieve such things:, • In 10th class the range of concepts is wide. So go through each lesson thoroughly, before the teacher actually deals with it., • Note down the points you came across so that you can grasp the lesson better., • Think of the principles in the lesson. Identify the concepts you need to know further,, to understand the lesson in depth., • Do not hesitate to discuss analytically about the questions given under the sub-heading, ‘Think and Discuss’ with your friends or teachers., • You may get some doubts while conducting an experiment or discussing about a lesson., Express them freely and clearly., • Plan to implement experiment/lab periods together with teachers, to understand the, concepts clearly. While learning through the experiments you may come to know, many more things., • Observe how each lesson is helpful to conserve nature. Put what you learnt into practice., • Analyse how each teaching point has relation with daily life and discuss the things you, learned in your science class with farmers, artisans etc., • Work as a group during interviews and field trips. Preparing reports and displaying, them is a must. Discuss on the report prepared., • List out the observations regarding each lesson to be carried through internet, school, library and laboratory., • Whether in note book or exams, write analytically, expressing your own opinions., • Read books related to your text book, as many as you can., • You organize yourself the Science Club programs in your school., • Observe problems faced by the people in your locality and find out what solutions you, can suggest through your science classroom., , Free distribution by A.P. Government, , vii
Page 8 :
ACADEMIC STANDARDS, S.No., , Academic Standard, , Explanation, , 1., , Conceptual understanding Children are able to explain, cite examples, give reasons,, and give comparison and differences, explain the process, of given concepts in the textbook. Children are able to, develop their own brain mappings., , 2., , Asking questions and, making hypothesis, , Children are able to ask questions to understand, to, clarify the concepts and to participate in discussions., They are able to make hypothesis on given issues., , 3., , Experimentation and field, investigation., , To understand given concepts in the textbook children, are able to do experiments on their own. They are able, to participate in field investigation and making reports, on them., , 4., , Information skills and, Projects, , Children are able to collect information (by using, interviews, internet etc.) and analyses systematically., They are able to conduct their own project works., , 5., , Communication through, drawing, model making, , Children are able to explain their conceptual, understanding by drawing figures and making models., Able to ploting graphs by using given information or, collected data., , 6., , Appreciation and, aesthetic sense, values, , Children are able to appreciate man power and nature,, and have aesthetic sense towards nature. They are also, able to follow constitutional values., , 7., , Application to daily life,, concern to bio diversity., , Children are able to utilize scientific concept to face, their daily life situations. They are able to show concern, towards bio diversity., , viii
Page 9 :
INDEX, Periods Month Page No., , 1, , Heat, , 8, , June, , 1-19, , 2, , Chemical Reactions and Equations, , 8, , July, , 20-44, , 3, , Reflection of light by different surfaces, , 8, , July, , 45-68, , 4, , Acids, Bases and Salts, , 8, , Aug, , 69-92, , 5, , Refraction of Light at Plane Surfaces, , 9, , Aug, , 93-111, , 6, , Refraction of Light at Curved Surfaces, , 10, , Sept, , 112-134, , 7, , Human Eye and Colourful world, , 8, , Sept-Oct, , 135-159, , 8, , Structure of Atom, , 5, , Oct, , 160-175, , 9, , Classification of Elements- The Periodic Table, , 10, , Nov, , 176-201, , 10, , Nov-Dec, , 202-227, , 9, , Dec, , 228-257, , 12 Electromagnetism, , 10, , Dec-Jan, , 258-285, , 13 Principles of Metallurgy, , 5, , Jan, , 286-301, , 14 Carbon and its Compounds, , 12, , Feb, , 302-341, , 10 Chemical Bonding, 11, , Electric Current, , Reference Books, , Free distribution by A.P. Government, , 342, , ix
Page 11 :
Chapter, , 1, Heat, Recall the experiments you did in Class 7 with the glass tumblers, containing of cold water, lukewarm water and hot water. We understood, that ‘hot’ and ‘cold’ are relative terms and that heat was a form of energy., We use the terms “Temperature and Heat” to describe these observations., These words, technically, have special meanings. In order to understand, their meanings let us do some activities, , Activity 1, Take a piece of wood and a piece of metal and keep them in a fridge or, ice box. After 15 minutes, take them out and ask your friend to touch them., • Which is colder? Why?, When we keep materials in a fridge, they become cold i.e., they lose, heat energy. The iron and wooden pieces were kept in the fridge for the, same period of time but we feel that the metal piece is colder than the, wooden piece., • What could be the reason for this difference in coldness?, • Does it have any relation to the transfer of heat energy from our body, to the object?, When you touch the metal or wooden piece, you feel that they are, cold. This means that heat energy is being transferred from your finger to, the pieces. When you remove your finger, you don’t get a feeling of, ‘coldness’. This means that when heat energy flows out of your body you, get the feeling of ‘coldness’ and when heat energy enters your body you, get a feeling of ‘hotness’. You can test this by bringing your finger near the, flame of a matchstick!, Free distribution by A.P. Government, , 1
Page 12 :
So, if you feel that the metal piece is ‘colder’ than the wooden piece,, it must mean that more heat energy flows out of your body when you touch, the metal piece as compared to the wooden piece. In other words, the, ‘degree of coldness’ of the metal piece is greater than that of the wooden, piece., The conventional definition of temperature is “the degree of hotness, or coldness”., We say that the metal piece is at a lower ‘temperature’ as compared to, the wooden piece, when they are taken out of the fridge., • Why does transfer of heat energy take place between objects ?, • Does transfer of heat take place in all situations?, • What are the conditions for transfer of heat energy?, Let us find out, , Thermal equilibrium-heat and temperature, When two bodies are placed in thermal contact, heat energy will be, transferred from the ‘hotter’ body to the ‘colder’ body. This transfer of, heat energy continues till both bodies attain the same degree of hotness, (or) coldness. At this stage, we say that the bodies have achieved ‘thermal, equilibrium’. Thus, the state of thermal equilibrium denotes a state of a, body where it neither receives nor gives out heat energy., If you are not feeling either hot or cold in your surroundings, then, your body is said to be in thermal equilibrium with the surrounding, atmosphere. Similarly, the furniture in the room is in thermal equilibrium, with air in the room. So we can say that the furniture and the air in the, room are at the same temperature., , Heat, •, •, , What is temperature?, How can you differentiate it from heat?, Let us find out, , Activity 2, Take two cups and fill one of them with hot water and another with, cold water. Now take a laboratory thermometer, observe the mercury level, in it and note it in your book. Keep it in hot water. Observe changes in the, mercury level. Note the reading., • What change did you notice in the reading of the thermometer?, (mercury level)?, 2, , X Class, , Heat
Page 13 :
•, , Did the mercury level increase or decrease?, Now place the thermometer in cold water and observe changes in the, mercury level. Did the level decrease or increase?, We know that bodies in contact achieve thermal equilibrium due to, transfer of heat energy. When you kept the thermometer in hot water you, observe that there is a rise in mercury level. This happens because heat got, transferred from the hotter body (hot water) to the colder body (mercury, in thermometer). Similarly in the second case you will observe that the, mercury level comes down from its initial level because of the transfer of, heat from mercury (hotter body) to water (colder body). Thus we define, heat as follows:, “Heat is a form of energy in transit, that flows from a body at higher, temperature to a body at lower temperature.”, The steadiness of the mercury column of the thermometer indicates, that flow of heat between the thermometer liquid (mercury) and water, has, stopped. Thermal equilibrium has been attained between the water and, thermometer liquid (mercury). The thermometer reading at thermal, equilibrium gives the “temperature”. Thus ‘temperature’ is a measure of, thermal equilibrium., If two different systems, A and B in thermal contact, are in thermal, equilibrium individually with another system C(thermal contact with A and, B), will the systems A and B be in thermal equilibrium with each other?, We know that if A is in thermal equilibrium with C, they both have the, same temperature. Similarly, B and C have the same temperature. Thus A, and B will have the same temperature and would therefore be in thermal, equilibrium with each other. (A,B and C are in thermal contact)., The SI unit of heat is Joule (J) and CGS unit is calorie (cal).The amount, of heat required to raise the temperature of 1gram of water by 10C is called, calorie., 1cal = 4.186 Joules, The SI unit of temperature is Kelvin (K). It can also be expressed as, degree Celsius (0C)., 00C = 273K, • How would you convert degree Celsius to Kelvin?, Temperature in Kelvin = 273+Temperature in degree Celsius, Add 273 to the value of temperature in degree Celsius to get the, temperature on the Kelvin scale., Free distribution by A.P. Government, , 3
Page 14 :
Note: Temperature measured on Kelvin scale is called absolute, temperature., , Temperature and Kinetic energy, , Activity 3, Take two bowls one with hot water and second with cold water. Gently, sprinkle food colour on the surface of the water in both bowls .Observe, the motion of the small grains of food colour., • How do they move?, • Why do they move randomly?, • Why do the grains in hot water move more rapidly than the grains in, cold water?, You will notice that the grains of food colour jiggle (move randomly)., This happens because the molecules of water in both bowls are in random, motion. We observe that the jiggling of the grains of food colour in hot, water is more when compared to the jiggling in cold water., We know that bodies possess kinetic energy when they are in, motion., As the speed of motion of particles (grain of food colour) in the bowls, of water is different, we can say that they have different kinetic, energies.Thus we conclude that the average kinetic energy of molecules /, particles of a hotter body is greater than that of a colder body. So we can, say that the temperature of a body is an indicator of the average kinetic, energy of molecules of that body., “The average kinetic energy of the molecules is directly proportional, to the absolute temperature”, Thermometer, , Take water in a container and heat it to 60°C. Take a, cylindrical transparent glass jar and fill half of it with this, hot water. Very gently pour coconut oil over the surface of, the water. (Take care that the water and oil do not mix). Put a, lid with two holes on the top of the glass jar. Take two, thermometers and insert them through the holes of the lid in, such a way that bulb of the one thermometer lies only inside, the water and other lies only inside the coconut oil as shown, in figure 1., , Lid, , Coconut, oil, , fig-1, 4, , Activity 4, , X Class, , Hot water, , Heat
Page 15 :
Now observe the readings of the two thermometers. The reading of, the thermometer kept in water decreases, while, at the same time, the, reading of the thermometer kept in oil increases., • Why does this happen?, Because the average kinetic energy of the molecules of oil increases,, while the average kinetic energy of the molecules of water decreases. In, other words, the temperature of oil increases while the temperature of, water decreases., • Can you say that the water loses energy?, From the above discussion it is clear that, water loses energy while oil, gains energy; because of the temperature difference between the water, and oil. Thus some heat energy flows from water to oil. This means, the, kinetic energy of the molecules of the water decreases while the kinetic, energy of the molecules of oil increases., • Can you now differentiate between heat and temperature based on the, discussion we made of the above activities?, With activities 2, 3 and 4 we can differentiate heat and temperature as, follows:, Heat is the energy that flows from a hotter to a colder body. Temperature, is a quantity that denotes which body is hotter and which is colder. So, temperature determines direction of heat (energy) flow, whereas heat is, the energy that flows., , Specific Heat, , Activity 5, Take a large jar with water and heat it up to 80oC.Take two identical, boiling test tubes with single-holed corks. One of them is filled with 50g, of water and the other with 50g of oil, both at room temperature. Insert, two thermometers through holes of the, corks, one each into two test tubes. Now, clamp them to a retort stand and place them, in a jar of hot water as shown in figure 2., Oil at, Observe the readings of thermometers room, temperature, every three minutes .Note the readings in, your notebook., • In which test tube does the temperature, rise quickly?, , Water at, room, temperature, Hot water, at 80 oC, , fig-2, , Free distribution by A.P. Government, , 5
Page 16 :
•, , Are the amounts of heat given to the water and oil same? How can you, assume this?, We believe that the same amount of heat is supplied to water and oil, because they are kept in the jar of hot water for the same interval of, time., We observe that the rate of rise in temperature of the oil is higher than, that of the rise in temperature of the water., • Why does this happen?, We conclude that the rate of rise in temperature depends on the nature, of the substance., , Activity 6, Take 250 ml of water in one beaker (a small beaker) and 1 litre of, water in another beaker (a larger beaker), and note down their initial, temperature using a thermometer (initial temperatures should be the same)., Now heat both beakers till the temperature of water in the two beakers, rises to 60 0C. Note down the heating times required to raise the, temperature of water to 60 0C in each beaker., • Which beaker needed more time?, You will notice that you need more time to raise the temperature of, water in the larger beaker when compared to water in the small beaker., That means you need to supply more heat energy to water in a larger beaker, (greater quantity of water) than water in a small beaker for same change in, temperature., For same change in temperature the amount of heat (Q) absorbed by a, substance is directly proportional to its mass (m), @ Q ∝ m ( when ΔT is constant ), ……………..(1), Now take 1 litre of water in a beaker and heat it over a constant flame., Note the temperature changes (ΔT ) for every two minutes., • What do you notice?, You will notice that the change in temperature rise with time is constant,, that means, for the same mass (m) of water the change in temperature is, proportional to amount of heat (Q) absorbed by it., @ Q ∝ΔT ( when ‘m’ is constant ), …………….(2), From equation (1) and (2), we get, Q ∝mΔT @ Q = mSΔT, Where ‘s’ is a constant for a given substance. This constant is called, “specific heat” of the substance., 6, , X Class, , Heat
Page 17 :
Q, S = ––––, mΔT, The specific heat of a substance is the, amount of heat required to raise the, temperature of unit mass of the substance, by one unit., • How much heat energy is required to, raise the temperature of unit mass of, substance by 1°C ?, CGS unit of specific heat is cal/g-oC, and SI unit of it is J / kg - K, 1 cal/g- oC = 1 kcal /kg-K, = 4.2 x 103J/kg-K, , Substance, Lead, Mercury, Brass, Zinc, Copper, Iron, Glass(flint), Aluminum, Kerosene oil, Ice, Water, Sea water, , Specific heat, In cal/g-oC, In J/kg-K, 0.031, 130, 0.033, 139, 0.092, 380, 0.093, 391, 0.095, 399, 0.115, 483, 0.12, 504, 0.21, 882, 0.50, 2100, 0.50, 2100, 1, 4180, 0.95, 3900, , We have seen that the rise in temperature depends on the nature of the, substance; hence the specific heat of a substance depends on its nature. If, the specific heat is high, the rate of rise (or fall) in temperature is low for, same quantity of heat supplied. It gives us an idea of the degree of, ‘reluctance’ of a substance to change its temperature., • Why is the specific heat different for different substances?, Let us find out., We know that the temperature of a body is directly proportional to the, average kinetic energy of particles of the body.The molecules of the system, (body or substance) have different forms of energies such as linear kinetic, energy, rotational kinetic energy, vibrational energy and potential energy, between molecules. The total energy of the system is called internal, energy of the system. When we supply heat energy to the system the heat, energy given to it will be shared by the molecules among the various forms, of energy., This sharing will vary from substance to substance. The rise in, temperature is high for a substance, if the maximum share of heat energy, is utilised for increasing its linear kinetic energy. This sharing of heat, energy of the system also varies with temperature .That is why the specific, heat is different for different substances., If we know the specific heat of a substance, we can determine how, much heat (Q) is needed to raise the temperature of a certain mass of the, substance through certain degrees by using the equation Q = mSΔT, Free distribution by A.P. Government, , 7
Page 18 :
Applications of Specific heat capacity, 1. The sun delivers a large amount of energy to the Earth daily. The, water sources on Earth, particularly the oceans, absorb this energy for, maintaining a relatively constant temperature. The oceans behave like heat, “store houses” for the earth. They can absorb large amounts of heat at the, equator without appreciable rise in temperature due to high specific heat, of water.. Therefore, oceans moderate the surrounding temperature near, the equator. Ocean water transports the heat away from the equator to areas, closer to the north and south poles. This transported heat helps moderate, the climates in parts of the Earth that are far from the equator., 2. Water melon brought out from the refrigerator retains its coolness, for a longer time than any other fruit because it contains a large percentage, of water. (water has greater specific heat)., 3. A samosa appears to be cool outside but it is hot when we eat it, because the curry inside the samosa contains ingredients with higher, specific heats., , Method of mixtures, , Activity - 7, Situation – 1: Take two beakers of the same size and pour 200 ml of, water in each of them. Now heat the water in both beakers till they attain, the same temperature. If you pour this water from these two beakers into, a larger beaker, what temperature could you expect the mixture to be?, Measure the temperature of the mixture., • What do you observe?, • What could be the reason for the fact you observed?, Situation – 2: Now heat the water in one beaker to 90oC and the other, to 60oC . Mix the water from these beakers in a larger beaker., • What will the temperature of the mixture be?, • Measure temperature of the mixture. What did you notice?, • Can you give reasons for the change in temperature?, Situation – 3: Now take 100 ml of water at 90oC and 200 ml of water, at 60oC and mix the two., • What is the temperature of the mixture?, • What difference do you notice in the change of temperature?, Let us find out., Let the initial temperatures of the samples of masses m1 and m2 be T1, and T2 (the higher of the two temperatures is called T1, the lower is called, T2). Let T be the final temperature of the mixture., 8, , X Class, , Heat
Page 19 :
The temperature of the mixture is lower than the temperature of the, hotter sample but higher than the temperature of the colder sample. This, means that the hot sample has lost heat, and the cold sample has gained, heat., The amount of heat lost by the hotter sample Q1 is m1S(T1- T)., The amount of heat gained by the cooler sample Q2 is m2S(T - T2)., Since heat lost by the hotter sample is equal to the heat gained by the, cooler sample (assuming no loss of heat) i.e Q1 = Q2, which can be written as, m1S(T1 - T) = m2S(T - T2), which can be simplified to, T = (m1T1 + m2T2)/(m1 + m2), You will notice the temperatures of mixtures in situation – 2 and, situation – 3 are not equal., • Can you guess the reason for this?, • Can we find temperature of the mixture using a thermometer?, , Principle of method of mixtures, When two or more bodies at different temperatures are brought into, thermal contact, then net heat lost by the hot bodies is equal to net heat, gained by the cold bodies until they attain thermal equilibrium. (If heat is, not lost by any other process), Net heat lost= Net heat gain, This is known as principle of method of mixtures., , Determination of Specific heat of a solid, , Lab Activity 1, Aim: To find the specific heat of given solid., Material required: calorimeter, thermometer, stirrer, water, steam, heater, wooden box and lead shots., Procedure: Measure the mass of the calorimeter along with stirrer., Mass of the calorimeter, m1 = ........................, Now fill one third of the volume of calorimeter with water. Measure, its mass and its temperature., Mass of the calorimeter plus water, m2 = ................., Mass of the water, m2–m1 =, Temperature of water in calorimeter, T1 = ..........., Note: Calorimeter and water are at same temperature., Free distribution by A.P. Government, , 9
Page 20 :
Take a few lead shots and place them in hot water or steam heater., Heat them upto a temperature 100oC. Let this temperature be T2., Transfer the hot lead shots quickly into the calorimeter (with minimum, loss of heat). You will notice that the mixture settles to a certain temperature, after some time., Measure this temperature T3 and mass of the calorimeter along with, contents (water and lead shots)., Mass of the calorimeter along with contents, m3 = ........., Mass of the lead shots, m3 – m2 = ............, Since there is no loss of heat to surroundings, we can assume that the, entire heat lost by the solid (lead shots) is transferred to the calorimeter, and water to reach the final temperature., Let the specific heats of the calorimeter, lead shots and water be Sc, Sl, and Sw respectively. According to the method of mixtures, we know;, Heat lost by the solid = Heat gain by the calorimeter + Heat gain by the water, (m3- m2 ) Sl(T2-T3) = m1 Sc(T3-T1)+(m2-m1) Sw(T3-T1), [m1Sc+(m2-m1)Sw] (T3-T1), Sl = ––––––––––––––––––––––––, (m3-m2)(T2-T3), Knowing the specific heats of calorimeter and water, we can calculate, the specific heat of the solid (lead shots)., , Evaporation, When wet clothes dry, you will notice that water in the clothes, disappears., • Where does the water go?, Similarly, when the floor of a room is washed with water, the water on, the floor disappears within minutes and the floor becomes dry., • Why does water on the floor disappear after some time?, Let us see., , Activity 8, Take a few drops of spirit on your palm using a droper., • Why does your skin become colder?, Take a few drops of spirit (say 1 ml) in two petri dishes (a shallow, glass or plastic cylindrical lidded dish used in the laboratory) separately., Keep one of the dishes containing spirit under a ceiling fan and switch on, the fan . Keep another dish with its lid closed. Observe the quantity of, spirit in both dishes after 5 minutes., 10, , X Class, , Heat
Page 21 :
•, , What do you notice?, You will notice that spirit in the dish that is kept under the ceiling fan, disappears, where as you will find some spirit left in the dish that is kept in, the lidded dish., • What could be the reason for this change?, To answer the above questions, you need to understand the process of, evaporation. The molecules of spirit that is kept in petri dish, continuously, move with random speeds in various directions. As a result these molecules, collide with other molecules., During the collision they transfer energy to other molecules. When, the molecules inside the liquid collide with molecules at the surface, the, molecules at the surface acquire energy and may fly off from the surface., Some of these escaping molecules may be directed back into liquid, when they collide with the particles of air. If the number of escaping, molecules is greater than the number returned, then the number of, molecules in the liquid decreases. Thus when a liquid is exposed to air, the, molecules at the surface keep on escaping from the surface till the entire, liquid disappears into air. This process is called evaporation., During the process of evaporation, the energy of the molecules inside, the liquid decreases and they slow down. They transfer this energy to, escaping molecules during the collisions., “The process of escaping of molecules from the surface of a liquid at, any temperature is called evaporation”, Let us determine the reason for faster evaporation of spirit kept under, the fan. If air is blown over the liquid surface in an open pan or perti dish,, the number of molecules returned is reduced to a large extent. This is, because any molecule escaping from the surface is blown away from the, vicinity of the liquid. This increases the rate of evaporation. This is the, reason why the spirit in petri dish, that is kept under ceiling fan evaporates, quickly when compared to that kept closed. You will notice that clothes, dry faster when a wind is blowing., It means that the temperature of a system falls during evaporation., Evaporation is a surface phenomenon., We can also define evaporation as “the change of phase from liquid to, gas that occurs at the surface of the liquid”. It is a cooling process, because, the particles of liquid continuously give up their energy to the particles, that are escaping from the surface., Free distribution by A.P. Government, , 11
Page 22 :
Let us look at the following example., • Why do we sweat while doing work?, When we do work, we spend our energy mostly in the form of heat, energy from the body. As a result the temperature of the skin becomes, higher and the water in the sweat glands starts evaporating. This evaporation, cools the body., Rate of evaporation of a liquid depends on its surface area, temperature, and amount of vapour already present in the surrounding air., • Does the reverse process of evaporation take place?, • When and how does it take place?, Let us find out., , Condensation, , Activity 9, Place a glass tumbler on the table. Pour cold water up to half its height., • What do you observe on the outer surface of the tumbler?, • Why do water droplets form on the outer side of the glass?, We know that the temperature of surrounding air is higher than the, temperature of the cold water., Air contains water molecules in the form of vapour., When the molecules of water in air, during their motion, strike the, surface of the glass tumbler which is cool; they lose their kinetic energy, which lowers their temperature and they get converted into droplets., The energy lost by the water molecules in air is gained by the molecules, of the glass tumbler. Hence the average kinetic energy of the glass, molecules increases. In turn the energy is transferred from glass molecules, to the water molecules in the glass., In this way, the average kinetic energy of water molecules in the, tumbler rises. Hence we can conclude that the temperature of the water in, glass increases. This process is called ‘condensation’. It is a warming, process., Condensation can also be defined as “the phase change from gas to, liquid”., Let us examine a situation:, You feel warm after you finish your bath under the shower on a hot, day. In the bathroom, the number of vapour molecules per unit volume is, , 12, , X Class, , Heat
Page 23 :
greater than the number of vapour molecules per unit volume outside the, bathroom. When you try to dry yourself with a towel, the vapour molecules, surrounding you condense on your skin and this condensation makes you, feel warm., , Humidity, Some vapour is always present in air. This vapour may come from, evaporation of water from the surfaces of rivers, lakes, ponds and from, the drying of wet clothes, sweat and so on. The presence of vapour, molecules in air is said to make the atmosphere humid. The amount of, water vapour present in air is called humidity., , Dew and Fog, In early morning, during winter, you might have noticed that water, droplets form on window panes, flowers, grass etc., • How are these water droplets formed?, Let us find out., During winter nights, the atmospheric temperature goes down. The, surfaces of window-panes, flower, grass etc, become still colder. The air, near them becomes saturated with vapour and condensation begins. The, water droplets condensed on such surfaces are known as dew., If the temperature falls further, the whole atmosphere in that region, contains a large amount of vapour. So the water molecules present in vapour, condense on the dust particles in air and form small droplets of water., These droplets keep floating in the air and form a thick mist which restricts, visibility. This thick mist is called fog., • Does the temperature of the water rise continuously if heat is supplied, to it continuously?, , Boiling, , Activity 10, Take a beaker of water, keep it on the burner .Note the readings of, thermometer for every 2 minutes., • Did you see any rise or fall in the level of the surface of the water, in, the beaker? Why?, • Does the temperature rise continuously?, • When does the rise in temperature of water stop?, You will notice that, the temperature of the water rises continuously,, till it reaches 100°C. Beyond 100°C no further rise of temperature of, Free distribution by A.P. Government, , 13
Page 24 :
water is seen. At 100 0C, though supply of heat continues, the temperature, does not increase further. We also observe a lot of bubbling at the surface, of water at 1000C. This is what we call boiling of water, • Why does this happen?, Water is a solution, there are many impurities dissolved in it including, some gases. When water or any liquid is heated, the solubility of gases it, contains reduces. As a result, bubbles of gas are formed in the liquid (at, the bottom and on walls of the vessel). Evaporation of water molecules, from the surrounding causes these bubbles, to become filled with saturated, vapour, whose pressure increases as we increase the temperature of the, liquid by heating. At a certain temperature, the pressure of the saturated, vapour inside the bubbles becomes equal to the pressure exerted on the, bubbles from the outside (this pressure is equal to the atmospheric, pressure plus the pressure of the layer of water above the bubble). As a, result, these bubbles rise rapidly to the surface and collapse at the surface, releasing vapour present in bubbles into air at the surface. This process of, converting the liquid into vapour (gas) continues as long as you supply, heat. This appears as boiling of water for us., “Boiling is a process in which the liquid phase changes to gaseous, phase at a constant temperature at a given pressure.” This temperature is, called boiling point of the liquid., • Are the processes of evaporation and boiling the same?, As you have seen in activity – 8 and 10, the boiling of a liquid differs, essentially from evaporation. Note that evaporation takes place at any, temperature, while boiling occurs at a definite temperature called the, boiling point. Let us recall your observation in activity – 10 that, when, boiling process starts, the temperature of the liquid cannot be raised further,, no matter how long we continue to heat it. The temperature remains constant, at the boiling point until all of the liquid has boiled away., In activity – 10, you have noticed that, while heating the water in the, beaker, the temperature of water rises continuously till it reaches 100 0C., But once boiling got started, no further rise of temperature is seen though, supply of heat continues., • Where does the heat energy supplied go?, This heat energy is used to change the state of water from liquid to, vapour (gas). This is called latent heat of vapourization., The heat energy required to change 1gm of liquid to gas at constant, temperature is called latent heat of vapourization., 14, , X Class, , Heat
Page 25 :
Consider a liquid of mass ‘m’ that requires heat energy of ‘Q’ calories, to change from its state from liquid phase to gas phase. Then Latent heat, of vaporization is Q/m. Latent heat of vaporization is denoted by ‘L’., CGS unit of latent heat of vaporization is cal/gm and SI unit is J/kg., The boiling point of water at constant atmospheric pressure (1atm) is, 100°C or 373K and Latent heat of vaporization of water is 540 cal/gm., Let us now consider the transformation of ice into water., • Why does an ice cube get converted into water?, , Melting, , Activity 11, Take small ice cubes in a beaker. Insert the thermometer into ice cubes, in the beaker. Observe the reading of the thermometer. Now start heating, the beaker keeping it on a burner. Observe changes in the thermometer, reading every 1 minute till the ice completely melts and gets converted, into water., • What changes do you notice in the reading of thermometer as time, passes by?, • Does the temperature of the ice change during the process of melting?, You will observe that the temperature of ice at the beginning is equal, to or below 0oC. If the temperature of ice is below 0oC, it goes on changing, till it reaches 00C. When ice starts melting, you will notice no change in, temperature though you are supplying heat continuously., • Why does this happen?, The heat energy supplied to the ice increases the internal energy of, the molecules of the ice. This increase in internal energy of molecules, weakens the bonds as well as breaks the bonds between the molecules, (H2O) in the ice. That is why the ice (in solid phase) becomes water (in, liquid phase).This process takes place at a constant temperature 0°C or, 273K. This temperature is called melting point. This process of converting, solid into a liquid is called “Melting”., The temperature of the ice does not change during melting because, the heat energy given to the ice is totally utilized in breaking the bonds, between the water molecules., The process in which solid phase changes to liquid phase at a constant, temperature is called melting. This constant temperature is called melting, point., Free distribution by A.P. Government, , 15
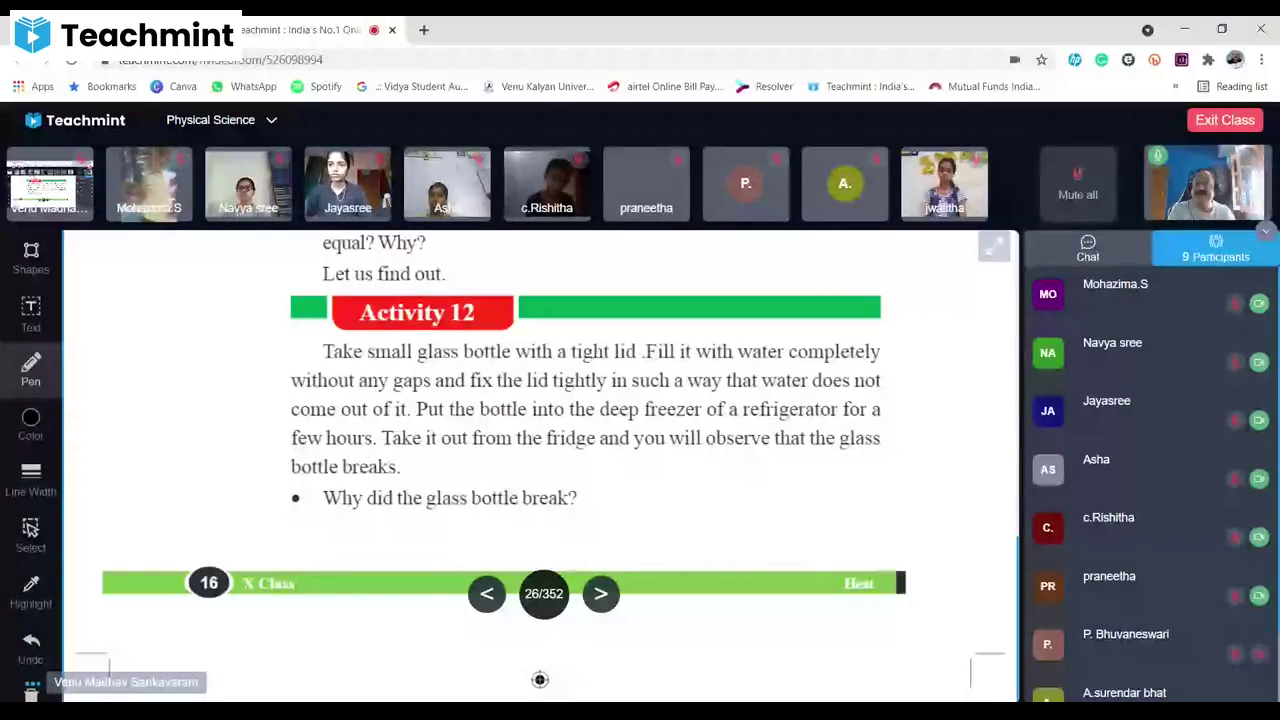
Page 26 :
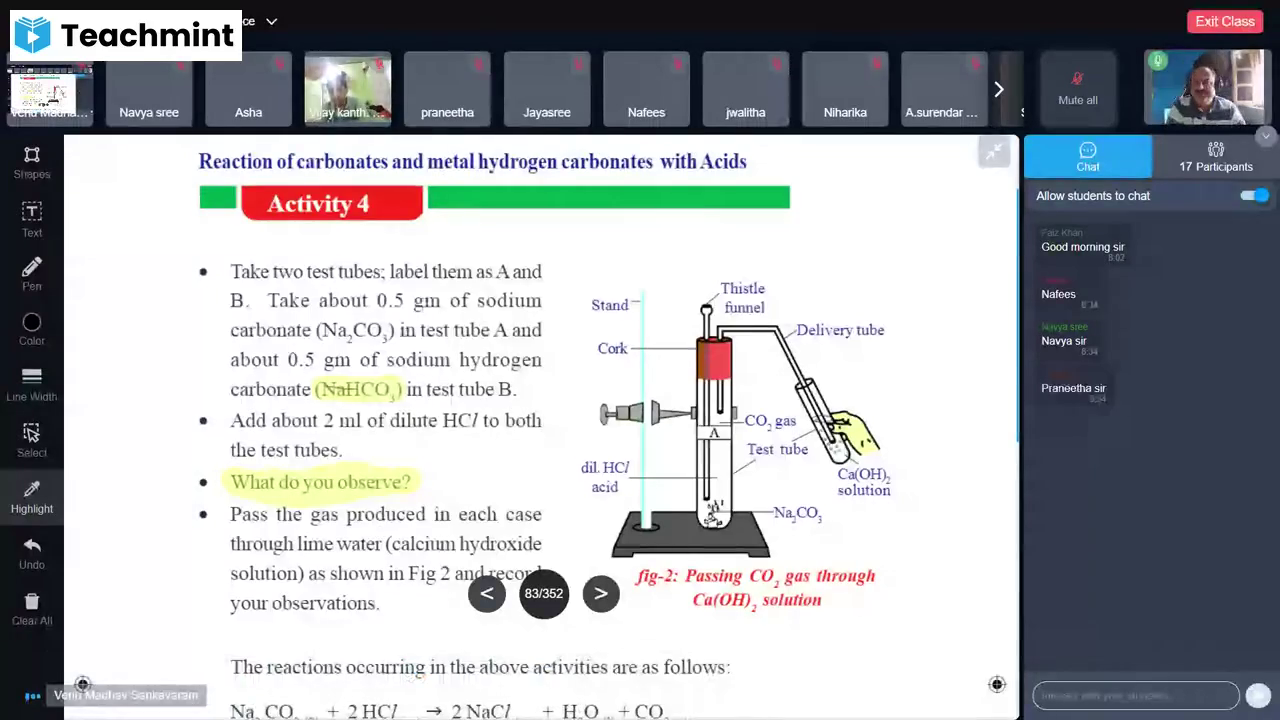
•, , How much heat energy is required to convert 1gm of ice to liquid?, The Heat energy required to convert 1gm of solid completely into, liquid at a constant temperature is called Latent heat of fusion., Consider a solid of mass m. Let heat energy Q be required to change it, from the solid phase to liquid phase. The heat required to change 1gm of, solid into liquid is Q/m., Latent heat of fusion L = Q/m. The value of Latent heat of fusion of, ice is 80cal/gm, , Freezing, You might have observed coconut oil and ghee getting converted from, liquid state to solid state during winter season., • What could be the reason for this change?, • What happens to water kept in a refrigerator?, • How does it get converted from liquid phase to solid phase?, We know that the water that is kept in a refrigerator converts to solid, ice. You know that initial temperature of water is more compared to the, temperature of ice. It means that during the process of conversion from, liquid to solid, the internal energy of the water decreases so that it becomes, a solid ice. This process is called freezing., “The process in which the a substance in liquid phase changes to solid, phase by losing some of its energy is called freezing.”, Freezing of water takes place at 0°C temperature and at one, atmospheric pressure., • Are the volumes of water and ice formed with same amount of water, equal? Why?, Let us find out., , Activity 12, Take small glass bottle with a tight lid .Fill it with water completely, without any gaps and fix the lid tightly in such a way that water does not, come out of it. Put the bottle into the deep freezer of a refrigerator for a, few hours. Take it out from the fridge and you will observe that the glass, bottle breaks., • Why did the glass bottle break?, , 16, , X Class, , Heat
Page 27 :
We know that the volume of the water poured into the glass bottle is, equal to the volume of the bottle. When the water freezes to ice, the bottle, is broken .This means that the volume of the ice should be greater than the, volume of the water filled in the bottle., In short, we say that water ‘expands’ (increases in volume) on freezing!, Thus the density of ice is less than that of water and this explains why, ice floats on water., , Key words, Temperature, Heat, Thermal equilibrium, Specific heat, Evaporation,, Condensation, Humidity, Dew, Fog, Boiling, Latent heat of vaporization,, Melting, Freezing., , What we have learnt, •, , If two different systems, A and B, (thermal contact) are in thermal equilibrium individually with, another system C, then the systems A and B are in thermal equilibrium with each other., , •, •, , The average kinetic energy of the molecules is directly proportional to the absolute temperature., The specific heat of a substance is the amount of heat required to raise the temperature of unit, mass of the substance by one unit., S=Q/mΔt, , •, , The process of escaping of molecules from the surface of a liquid at any temperature is called, evaporation and it is a cooling process., , •, •, , Condensation is the reverse process of evaporation., Boiling is the process in which the liquid phase changes to gaseous phase at a constant temperature, and constant pressure., , Improve your learning, 1. What would be the final temperature of a mixture of 50g of water at 20oC temperature and 50g, of water at 40oC temperature? (AS1), 2. Explain why dogs pant during hot summer days using the concept of evaporation? (AS1), 3. Why do we get dew on the surface of a cold soft drink bottle kept in open air? (AS1), 4. Write the differences between evaporation and boiling? (AS1), Free distribution by A.P. Government, , 17
Page 28 :
5. Does the surrounding air become warm or cool when vapour phase of H2O condenses? Explain., 6. Answer these. (AS1), a) How much energy is transferred when 1gm of boiling water at 100oC condenses to water at, 100oC?, b) How much energy is transferred when 1gm of boiling water at 100oC cools to water at 0oC?, c) How much energy is released or obsorbed when 1gm of water at 0oC freezes to ice at 0oC?, d) How much energy is released or obsorbed when 1gm of steam at 100oC turns to ice at 0oC?, 7. Explain the procedure of finding specific heat of solid experimentally. (AS1), 8. Covert 20oC into Kelvin scale.(AS1), 9. Your friend is asked to differentiate between evaporation and boiling. What questions could, you ask to make him to know the differences between evaporation and boiling? (AS2), 10. What happens to the water when wet clothes dry? (AS3), 11. Equal amounts of water are kept in a cap and in a dish. Which will evaporate faster? Why?, (AS3), 12. Suggest an experiment to prove that the rate of evaporation of a liquid depends on its surface, area and vapour already present in surrounding air. (AS3), 13. Place a Pyrex funnel with its mouth-down in a sauce pan full of water, in such a way that the, stem tube of the funnel is above the water or pointing upward into air. Rest the edge of the, bottom portion of the funnel on a nail or on a coin so that water can get under it. Place the pan, on a stove and heat it till it begins to boil. Where do the bubbles form first? Why? Can you, explain how a geyser works using this experience. (AS4), 14. Collect information about working of geyser and prepare a report. (AS4), 15. Assume that heat is being supplied continuously to 2kg of ice at -5oC. You know that ice melts, at 0oC and boils at 100oC. Continue the heating till it starts boiling. Note the temperature every, minute. Draw a graph between temperature and time using the values you get. What do you, understand from the graph. Write the conclusions. (AS5), 16. How do you appreciate the role of the higher specific heat of water in stabilising atmospheric, temperature during winter and summer seasons? (AS6), 17. Suppose that 1l of water is heated for a certain time to rise and its temperature by 2oC. If 2l of, water is heated for the same time, by how much will its temperature rise? (AS7), 18. What role does specific heat play in keeping a watermelon cool for a long time after removing, it from a fridge on a hot day? (AS7), 19. If you are chilly outside the shower stall, why do you feel warm after the bath if you stay in the, bathroom? (AS7), , 18, , X Class, , Heat
Page 29 :
ks, Fill in the blan, 1. The SI unit of specific heat is_____________, 2. _____________ flows from a body at higher temperature to a body at lower temperature., 3. _____________ is a cooling process., 4. An object ‘A’ at 10 0C and another object ‘B’ at 10K are kept in contact, then heat will flow, from _________ to ___________., 5. The latent heat of fusion of ice is _____________., 6. Temperature of a body is directly proportional to _____________., 7. According to the principle of method of mixtures, the net heat lost by the hot bodies is equal to, _____________ by the cold bodies., 8. The sultryness in summer days is due to _____________., 9. ____________ is used as a coolant., 10. Ice floats on water because _____________., , s, Multiple choice question, 1. Which of the following is a warming process, a) Evaporation, , b) condensation, , c) boiling, , [, , ], , [, , ], , d) all the above, , 2. Melting is a process in which solid phase changes to, a) liquid phase, , b) liquid phase at constant temperature, , c) gaseous phase, , d) any phase, , 3. Three bodies A, B and C are in thermal equilibrium. The temperature of B is 45oC. then the, temperature of C is ___________, [ ], a) 45oC, , b) 50oC, , c) 40oC, , d) any temperature, , 4. The temperature of a steel rod is 330K. Its temperature in oC is ________, a) 55 C, o, , b) 57 C, o, , c) 59 C, o, , d) 53 C, , 5. Specific heat S =, a) Q/Δt, , [ ], b) QΔt, , c) Q/mΔt, , d) mΔt/Q, , 6. Boiling point of water at normal atmospheric pressure is _________, a) 0oC, , [ ], , o, , b) 100oC, , c) 110oC, , 7. When ice melts, its temperature, , d) -5oC, [ ], , a) remains constant, , b) increases, , c) decreases, , d) cannot say, , Free distribution by A.P. Government, , [ ], , 19
Page 30 :
Chapter, , 2, Chemical Reactions, and Equations, In lower class you studied about temporary, permanent , natural, man, made changes etc. They may be categorized into two types known as, physical changes and chemical changes. In this chapter we discuss about, the chemical changes and express them in the form of chemical equations., Consider the following processes and think about the reactions taking, place during the occurance of these processes., - coal is burnt., - food gets digested in our body., - iron nail is exposed to humid atmosphere for a longtime., - we respire., - milk is converted into curd., - water is added to quicklime., - crackers are burnt., • What changes do you notice?, • Are they physical changes or chemical changes?, • Are they temporary changes or permanent changes?, In all the above processes, the nature of original substance would be, changed. If new substances are formed with properties completely unlike, those of the original substances, we say a chemical change has taken place., • How do we know a chemical reaction has taken place?, Let us perform some activities to know this., 20, , X Class, , Chemical reactions and Equations
Page 31 :
Activity 1, Take about 1 g of quick lime (calcium oxide) in a beaker. Add 10 ml of, water to this. Touch the beaker with your finger., • What do you notice?, Do you notice that the beaker is hot when you touch it. The reason is, that the calcium oxide (quick lime) reacts with water and in that process, heat energy is released. Calcium oxide dissolves in water producing, colourless solution. Test the nature of solution with litmus paper., • What is the nature of the solution?, A red litmus paper turns blue when dipped in the above solution. This, solution is a basic solution., , Activity 2, Take about 100 ml of water in a beaker and dissolve, a small quantity of sodium sulphate (Na2SO4)., Take about 100ml of water in another beaker and, dissolve a small quantity of barium chloride (BaCl2),, observe the colours of the solutions obtained., • What are the colours of the above solutions?, • Can you name the solutions obtained?, Add Na2SO4 solution to BaCl2 solution and observe., • Do you observe any change on mixing these, solutions?, , Activity 3, , Na2SO4, , BaCl2, , fig-1:Formation of barium, sulphate precipitate, , Take a few zinc granules in a conical flask., Add about 5 ml of dilute hydrochloric acid to, the conical flask., Observe the changes in the conical flask., • What changes do you notice?, Now keep a burning match stick near the, Glass tube, mouth of the conical flask., H2 gas, • What happens to burning match stick?, Conical plask, • Touch the bottom of the conical flask with, your fingers. What do you notice?, Dil. HCl, • Is there any change in temperature?, Zinc granules, From the above activities you can conclude fig-2:Formation of hydrogen gas by action, of dilute HCl on zinc and testing of H2 gas, that during a chemical change:, Free distribution by A.P. Government, , 21
Page 32 :
1. The original substances lose their characteristic properties. Hence, these may be products with different physical states and colours., 2. Chemical changes may be exothermic or endothermic i.e, they may, involve heat energy liberation or heat energy absorption., 3. They may form an insoluble substance known as precipitate., 4. There may be gas liberation in a chemical change., In our daily life we observe variety of changes taking place around us., In this chapter we study various types of chemical reactions and their, symbolic representation., , Chemical Equations, In activity 1, when calcium oxide reacts with water a new substance is, formed which is unlike either calcium oxide or water. The description of, chemical reactions in a sentence in activity-1 is quite long. It can be written, in shorter form as a word equation., The word equation of the above reaction is,, calcium oxide + water, calcium hydroxide ......................... (1), (Reactants), , (Product), , The substances which undergo chemical change in the reaction are, called reactants and the new substances formed are called products., A chemical reaction written in the form of word equation shows the, change of reactants to products by an arrow placed between them. The, reactants, are written on the left side of arrow and the final substances, or, products are written on the right side of the arrow. The arrow head point, towards the product shows the direction of the reaction., If there is more than one reactant or product involved in the reaction,, they are indicated with a plus (+) sign between them., , Writing a Chemical Equation, •, , Can you write a chemical reaction in any other shorter way other than, the way we discussed above?, Chemical equations can be made more precise and useful if we use, chemical formulae instead of words., Generally, a compound is written by giving its chemical formula,, which lists the symbols of the constituent elements and uses the subscript, to indicate the number of atoms of each element present in the compound., If no subscript is written the number 1 is understood. Thus we can write, 22, , X Class, , Chemical reactions and Equations
Page 33 :
calcium oxide as CaO, water as H2O and the compound formed by the, reaction of these two compounds is calcium hydroxide Ca (OH) 2., Now the reaction of calcium oxide with water can be written as:, CaO, , +, , H2O, , Ca (OH)2 ............................ (2), , In the above chemical equation, count the number of atoms of each, element on left side and right side of arrow., • Is the number of atoms of each element on both sides equal?, Observe the following reactions and their chemical equations. Zinc, metal reacts with dilute HCl to yield ZnCl2 and liberates Hydrogen gas., Zn +, , HCl, , ZnCl2 +, , H2 ............................ (3), , Sodium sulphate reacts with barium chloride to give white precipitate,, barium sulphate., Na2SO4, •, , + BaCl2, , BaSO4 + NaCl ............................. (4), , Do the atoms of each element on left side equal to the atoms of the, element on the right side of the equation?, , Balancing Chemical Equations, According to the law of conservation of mass, the total mass of the, products formed in chemical reaction must be equal to the mass of reactants, consumed. You know an atom is the smallest particle of an element that, takes part in a chemical reaction. It is the atom which accounts for the, mass of any substance. The number of atoms of each element before and, after reaction must be the same., All the chemical equations must balance, because atoms are neither, created nor destroyed in chemical reactions. A chemical equation in which, the numbers of atoms of different elements on the reactants side (left, side) are same as those on product side (right side) is called a balanced, reaction., Balancing a chemical equation involves finding out how many formula, units of each substance take part in the reaction. A formula unit, as the, name implies, is one unit – whether atom, ion, or molecule – corresponding, to a given formula. One formula unit of NaCl for example is one Na+ ion, and one Cl– ion; one formula unit of MgBr2 is one Mg2+ ion and two Br –, ions and one formula unit of water is one H2O molecule., Now let us balance the chemical equation using a systematic method., Free distribution by A.P. Government, , 23
Page 34 :
For this take the example of hydrogen reacting with oxygen to form water., Step 1: Write the equation with the correct chemical formulae for, each reactant and product., Eg: In the reaction of hydrogen, with oxygen to yield water, you can, Element, No of atoms, write chemical equations as follow:, LHS, RHS, H2 + O2, H 2O, ……(5), H, 2, 2, Step 2: After writing the molecular, O, 2, 1, formulae of the substances the equation, is to be balanced. For this we should not touch the ratio of atoms in the, molecules of the susbtances but we may put suitable numbers as the, coefficients before the formulae., In the above equation put ‘2’ before the molecular formula of hydrogen, and also ‘2’ before the molecular formula of water. Observe whether atoms, of both the elements hydrogen and oxyen are same (or) different on both, the sides. They are in the same number on both sides. Therefore, the equation, is balanced., 2H2, +, O2, 2H2O …………..(6), Step 3: Sometimes there is a possibility that the coefficients of all the, substances getting divided with a suitable number. Since we require the, lowest ratio of coefficient for reactants and products the above operation, is to be done. If no common factor is there, there is no need to divide the, equation. The above equation needs no division of the coefficients of the, substances., Step 4: Verify the equation for the balancing of atoms on both sides of, the equations. The above equation (6) is a balanced equation., Let us work out some more examples to see how equations are balanced., , Eg-1: Combustion of propane (C3H8), Propane, C 3 H8 is a colourless, odourless gas often used as a heating, and cooking fuel. Write the chemical equation for the combustion reaction, of propane. The reactants are propane and oxygen and the products are, carbon dioxide and water., Write the reaction in terms of symbols and formulae of the substances, involved and follow the four steps described in previous discussion., Step 1: Write the unbalanced equation using correct chemical formulae, for all substances., C3H8 + O2, CO2 + H2O ............(7), (Skeleton equation), 24, , X Class, , Chemical reactions and Equations
Page 35 :
Note: Unbalanced chemical equation, No of atoms, Element, containing molecular formulae of the, LHS, RHS, substances is known as skeleton equation., 3(inC3H8) 1 (inCO2), Step 2: Compare number of atoms of C, each element on both sides., H, 8 (inC3H8) 2(inH2O), Find the coefficients to balance the O, 2 (inO2), 3 (inCO2H2O), equation. It is better to start with the most, complex substance – in this case C3H8. Look at the skeleton equation, and, note that there are 3 carbon atoms on the left side of the equation but only, 1 on the right side. If we add a coefficient of 3 to CO2 on the right side the, carbon atoms balance., C3H8, +, O2, 3CO2 + H2O ................... (8), Now, look at the number of hydrogen atoms. There are 8 hydrogens, on the left but only 2 on the right side. By adding a coefficient of 4 to the, H2O on the right, the hydrogen atoms get balanced., C3H8, +, O2, 3CO2 + 4H2O .................(9), Finally, look at the number of oxygen atoms. There are 2 on the left, side but 10 on the right side, by adding a coefficient of 5 to the O2 on the, left, the oxygen atoms get balanced., C3H8, +, 5O2, 3CO2 + 4H2O .....................(10), Step 3: Make sure the coefficients are reduced to their smallest wholenumber values. In fact, the equation (10) is already with the coefficients, in smallest whole number. There is no need to reduce its coefficients, but, this might not be achieved in each chemical reaction., Let us assume that you have got chemical equation as shown below:, 2C3H8, +, 10O2, 6CO2 + 8H2O ................... (11), • Is it a balanced equation as per rules?, • How do you say?, Though the equation (11) is balanced, the coefficients are not the, smallest whole numbers. It would be necessary to divide all coefficients, of equation (11) by 2 to reach the final equation., C3H8, +, 5O2, 3CO2 + 4H2O ................... (12), Step 4: Check the answer. Count the numbers and kinds of atoms on, both sides of the equation to make sure they are the same., , Eg-2:, Iron oxide reacts with aluminum to form iron and aluminum trioxide., Write the chemical equation to show the reaction and balance it., Free distribution by A.P. Government, , 25
Page 36 :
Step 1: Write the equation using the correct chemical symbols and, formulae for all the reactants and products., Fe2O3, +, Al, Fe, + Al2O3 ................. (13), Step 2: Find the suitable coefficient for the reactants and products, to, equate the number of atoms of each element on both sides., i. Examine the number of atoms of each element present in, equation (13) on both sides., No. of atoms in reactants, , Elements, , No. of atoms in products, , Fe, , 2 (in Fe2O3), , 1 (in Fe), , O, , 3 (in Fe2O3), , 3 (in Al2O3), , Al, , 1 (in Al), , 2 (in Al2O3), , In the above equation (13), Number of oxygen atoms is equal on both, sides. We have to balance the remaining atoms., ii. There are 2 Fe atoms on left side(on reactant side). There is one Fe, atom on right side(on products side). To equate number of Fe atoms,, multiply Fe by 2 on product side., Now the partially balanced equation is:, +, Al, 2Fe +, Al2O3 .................. (14), Fe2O3, iii. In the above equation(14) number of aluminum atoms still, unbalanced., There is one ‘Al’ atom on left side and 2 ‘Al’ atoms on the right side, (in Al2O3), to balance ‘Al’ atoms on both sides multiply ‘Al’ by 2 on left, side of arrow mark., Now the partially balanced equation:, Fe2O3, +, 2Al, 2Fe + Al2O3 ................ (15), The above equation(15), the number of atoms of each element is same, on both sides of arrow mark. This is a balanced chemical equation., Step 3: The above equation(15) is balanced and coefficients are also, smallest whole numbers., Step4: Finally to check the correctness of balanced equation, count, the number of atoms of each element on both sides of equation., Fe2O3, +, 2Al, 2Fe + Al2O3 ................. (16), Elements, , No of Atoms of Reactants, , Fe, , 2 (in Fe2O3), , 2(in Fe), , O, , 3 (in Fe2O3), , 3(in Al2O3 ), , Al, , 2 (in 2 Al), , 2(in Al2O3 ), , 26, , X Class, , No. of Atoms in products, , Chemical reactions and Equations
Page 37 :
(Note: The above method of balancing is called trial and error method, only. Sometimes you may have to take more care to balance the equation.), , Making Chemical Equations more informative:, Chemical equations can be made more informative by expressing, following characteristics of the reactants and products., i. Physical state, ii. Heat changes (exothermic or endothermic change), iii. Gas evolved (if any), iv. Precipitate formed (if any), i. Expressing the physical state: To make the chemical equation, more informative, the physical states of the substances may be mentioned, along with their chemical formulae. The different states ie., gaseous, liquid,, and solid states are represented by the notations (g), (l) and (s) respectively., If the substance is present as a solution in water, the word ‘aqueous’ is, written. In the short form it is written as (aq)., The balanced equation(16) is written along with the physical states as:, Fe2O3(s) + 2Al(s), , Δ, , 2Fe(s) + Al2O3 (s) ...... (17) ; Δ represents heating., , fig-3(a): Aluminium in solid state, , fig-3(b): Iron in solid state, , ii. Expressing the heat changes: Heat is liberated in exothermic, reactions and heat is absorbed in endothermic reactions. See the following, examples., CO2 (g) + Q (exothermic reaction), 1. C(s) + O2 (g), 2. N2 (g) + O2 (g), 2NO (g) - Q (endothermic reaction), Free distribution by A.P. Government, , 27
Page 38 :
‘Q’ is heat energy which is shown with plus ‘+’ sign on product side, for exothermic reactions and minus ‘–’ sign on product side for endothermic, reactions., iii. Expressing the gas evolved: If a gas is evolved in a reaction, it is, denoted by an upward arrow ‘ ’or (g), Eg: Zn (s) + H2SO4 (aq), ZnSO4 (aq) + H2 (g), iv. Expressing precipitate formed: If a precipitate is formed in the, reactions it is denoted by a downward arrow., Eg: AgNO3 (aq) + NaCl (aq) AgCl(s) + NaNO3 (aq), Sometimes the reaction conditions such as temperature, pressure,, catalyst, etc are indicated above and/or below the arrow in the equation., For example,, sunlight, , 2AgCl(s), , –––––, , 6CO2 (g), , + 6 H2O (l), , 2 Ag (s) + Cl2(g), Sunlight, , –––––, , Chlorophyll, , C6H12O6 (s) + 6O2 (g), glucose, , Interpreting a balanced chemical equation, i. A chemical equation gives information about the reactants and, products through their symbols and formulae., ii. It gives the ratio of molecules of reactants and products., iii. As molecular masses are expressed in ‘Unified Masses’ (U), the, relative masses of reactants and products are known from the equation., iv. If the masses are expressed in grams then the equation also gives, the molar ratios of reactants and products., v. If gases are involved, we can equate their masses to their volumes, and calculate the volumes or those gases liberated at given condition of, temperature and pressure using molar mass and molar volume relationship., vi. Using molar mass and Avagadro’s number we can calculate the, number of molecules and atoms of different substances from the equation., It gives information about relative masses of reactants and products., from the equation we get,, a) mass - mass relationship, b) mass - volume relationship, c) volume - volume relationship, d) mass - volume - number of molecules relationship etc.,, 28, , X Class, , Chemical reactions and Equations
Page 39 :
Eg-1: Al (s) + Fe2O3 (s), Al2O3 (s) + Fe (s), (atomic masses of Al = 27U, Fe = 56U, and O = 16U), 2Al (s), + Fe2O3 (s), Al2O3 (s), + 2Fe (s) , is a balanced equation., (2x27)U + (2x56+3x16)U, (2x27+3x16)U + (2x56)U, 54 U, + 160 U, 102 U, + 112 U, or 2 mol + 1 mol, 1 mol, + 2 mol, 54 g, + 160 g, 102 g, + 112 g, Suppose that your are asked to calculate the amount of aluminium,, required to get 1120 kg of iron by the above reaction., Solution: As per the balanced equation, Aluminium, Iron, 54 g, 112 g, x?, (1120 x 1000)g, (1120x1000)g x 54 g, ∴ x g = ––––––––––––––––––, 112 g, = 10000 x 54 g, = 540000 g or 540 kg, ∴ to get 1120 kg of iron we have to use 540 kg of aluminium., Eg-2: Calculate the volume, mass and number of molecules of hydrogen, liberated when 230 g of sodium reacts with excess of water at STP.(atomic, masses of Na = 23U, O = 16U, and H = 1U), The balanced equation for the above reaction is,, 2Na (s) + 2H2O (l), 2NaOH (aq), + H2 (g), (2x23)U + 2(2x1+1x16)U, 2(23+16+1)U + (2x1)U, 46 U, + 36 U, 80 U, + 2U, or 46 g, + 36 g, 80 g, + 2g, Solution: As per the balanced equation:, 46 g of Na gives 2g of hydrogen, 230g of Na gives ______? g of hydrogen., 230 g x 2g, ––––––––––– = 10g of hydrogen, 46 g, 1 gram molar mass of any gas at STP i.e, standard temperature 273K, and standard pressure 1 bar, occupies 22.4 litres known as gram molar, volume., ∴ 2.0g of hydrogen occupies 22.4 litres at STP., 10.0g of hydrogen occupies ........? litres at STP., Free distribution by A.P. Government, , 29
Page 40 :
10.0g x 22.4 litres, ––––––––––––––––– = 112 litres, 2.0g, 2 g of hydrogen i.e, 1 mole of H2 contains 6.02x1023 (NO) molecules, 10 g of hydrogen contain ....................?, 10.0g x 6.02x1023 molecules, –––––––––––––––––––––––––, 2.0g, 23, = 30.10 x 10 molecules, = 3.01 x 1024 molecules, , Types of chemical reactions, In chemical reactions atoms are neither created nor destroyed. A, chemical reaction is a process that is usually characterized by a chemical, change in which the starting materials (reactants) are different from the, products. Chemical reactions occur with the formation and breaking, of chemical bonds. (you will learn about chemical bonding in chapter …), Some common reaction types are discussed below., , Chemical Combination, , Activity 4, , •, , (This activity needs Teacher’s assistance), - Take a small piece (about 3 cm long) of magnesium ribbon., - Rub the magnesium ribbon with sand paper., - Hold it with a pair of tongs., - Burn it with a spirit lamp or burner., What you observe?, You will notice that,, Magnesium burns in oxygen by producing dazzling, white flame and changes into white powder. The white, powder is magnesium oxide., 2Mg(s), , Magnesium, , fig-4: Burning of magnesium, ribbon, 30, , X Class, , +, , O2 (g), , Oxygen, , 2MgO (s) ......... (18), , Magnesium oxide, , In this reaction magnesium and oxygen combine to, form a new substance magnesium oxide. A reaction in, which single product is formed from two or more, reactants is known as chemical combination reaction., You will also notice release of enormous amount, of heat energy when magnesium is burnt in air., Chemical reactions and Equations
Page 41 :
Let us discuss some more examples of combination reactions., i. Burning of Coal: When coal is burnt in oxygen, carbon dioxide is, produced., C (s), + O2 (g), CO2 (g) + Q (heat energy) .............(19), ii. Slaked lime is prepared by adding water to quick lime., Ca O (s) + H20 (l), Ca (OH) 2 (aq) + Q (heat energy).....(20), Large amount of heat energy is released on, reaction of water with CaO(s). If you touch the walls, of the container you will feel the hotness. Such, Beaker, reactions are called exothermic reactions., A solution of slaked lime produced in the, reaction equation(20) is used to white wash the, walls. Calcium hydroxide reacts slowly with the, Water, carbon dioxide in air to form a thin layer of calcium, carbonate on the walls. It gives a shiny finish to the, walls., CaO, Ca (OH)2(aq) + CO2(g), CaCO3(s) + H2O(l), fig-5: Formation of slaked, lime, by the reaction of CaO, The chemical formula of marble is CaCO3, with water, , Decompostion Reaction, , Activity 5, - Take a pinch of calcium carbonate (lime stone) in a boiling tube., - Heat the boiling tube over the flame of spirit lamp or burner., - Now bring a burning match stick near the evolved gas as shown in, the figure., - What do you observe?, You will notice that match stick would be put off., Delivery tube, Clamp, , Boiling tube, , Stand, , Calcium carbonate, Putoff match stick, Bunsen, burner, , Burning match stick, , fig-6: Heating of calcium carbonate and testing, the gas evolved with burning match stick, Free distribution by A.P. Government, , 31
Page 42 :
In the above activity, on heating calcium carbonate decomposes to, calcium oxide and carbon dioxide., Heat, , CaCO3 (s) –––––, Lime stone, , CaO(s) + CO2 (g) .................. (21), quick lime, , It is a thermal decomposition reaction. When a decomposition reaction, is carried out by heating, it is called thermal decomposition reaction., , Activity 6, - Take about 0.5g of lead nitrate powder in a, Clamp, boiling test tube., - Hold the boiling tube with a test tube holder., Delivery tube, - Heat the boiling tube over a flame. (see, Stand, figure), - Note down the change., Bunsen, burner, Gas, - What do you observe?, collecting, jar, Heating of lead nitrate and emission of, NO2, nitrogen dioxide, fig-7:Heating of lead nitrate and, On heating lead nitrate decomposes to, emission of nitrogen dioxide, lead oxide, oxygen and nitrogen dioxide. You, observe the brown fumes liberating in the boiling tube. These brown fumes, are of nitrogen dioxide (NO2)., Lead nitrate, , Boiling, tube, , Heat, , 2Pb (NO3)2(s) –––––, , 2PbO(s) + 4NO2 (g), , Lead Nitrate, , lead oxide, , + O2 (g) ........ (22), , Nitrogen dioxide, , Oxygen, , This is also a thermal decomposition reaction., Let us perform some more decomposition reactions, , Activity 7, •, 32, , X Class, , Take a plastic mug. Drill two holes at its base., Fit two ‘one holed rubber stoppers’ in these holes., Insert two carbon electrodes in these rubber stoppers., Connect the electrodes to 9V battery as shown in fig., Fill the mug with water, so that the electrodes are immersed., Add few drops of dilute sulphuric acid to water., Take two test tubes filled with water and invert them over the two carbon, electrodes., Switch on the current and leave the apparatus undisturbed for some time., What do you observe in the test tubes?, Chemical reactions and Equations
Page 43 :
You will notice the liberation of gas, bubbles at both the electrodes. These, bubbles displace the water in the test, tubes., Is the volume of gas collected in, both the test tubes same?, Once the test tubes are filled with, gases take them out carefully. Test both, the gases separately by bringing a, burning candle near the mouth of each, test tube., , Plastic mug, O2, , H2, , Test tubes, Graphite rods, , Acidified, water, Anode, , +, , – Cathode, , Switch, , 9V, battery, , fig-8: Electrolysis of water, , •, , What do you observe in each case?, Can you predict the gas present in each test tube?, In the above activity on passing the electricity, water dissociates to, hydrogen and oxygen., 2H2O (l), , Electrolysis, , –––––, , 2 H2 (g) + O2 (g) ...................... (23), , Activity 8, , •, •, , - Take some quantity of silver bromide on a watch glass., - Observe the colour of silver bromide., - Place the watch glass in sunlight for some time., - Now observe the colour of silver bromide., What changes do you notice?, Did the colour of the silver bromide change?, , fig-9(a): Silver bromide, (light yellow colour), , fig-9(b) when exposed to sunlight, (gray colour) silver metal, , Silver bromide decomposes to silver and bromine in sunlight. Light, yellow coloured silver bromide turns to gray due to sunlight., Free distribution by A.P. Government, , 33
Page 44 :
sunlight, , 2AgBr(s) ––––– 2 Ag (s) + Br2 (g), , ............................ (24), , This decomposition reaction occurs in presence of sunlight and such, reactions are called photochemical reactions., All the above decomposition reactions require energy in the form of, heat, light or electricity for converting the reactants to products. All these, reactions are endothermic., Carry out the following Activities:, i) Take a pinch of AgCl2 in a watch glass. Keep it in sunlight for some, time and observe the change., ii) Take some ferrous sulphate crystals in a boiling tube. Heat it over, spirit lamp., iii) Take about 2 gm of barium hydroxide in a test tube. Add about 1 gm of, ammonium chloride and mix with glass rod. Touch the test tube with, your palm., What do you observe?, , Displacement reaction., In displacement reaction one element displaces another element from, its compound and takes its place there in., Displacement of hydrogen from acids by metals:, Generally metals which are more active than hydrogen displace it from, an acid., Let us observe the reaction in following activity., , Activity 9, - Take a small quantity of zinc dust in a conical flask., - Add dilute hydrochloric acid slowly., - Now take a balloon and tie it to the mouth of the conical flask., - Closely observe the changes in the conical flask and balloon., - What do you notice?, You can see the gas bubbles coming out from the solution and the, balloon bulges out (figure 10b). Zinc pieces react with dilute hydrochloric, acid and liberate hydrogen gas as shown below., Zn (s), + 2HCl (aq), ZnCl2(aq ) + H2 (g) ..........................(25), In reaction (25) the element zinc has displaced hydrogen from, hydrochloric acid. This is displacement reaction., 34, , X Class, , Chemical reactions and Equations
Page 45 :
Balloon, with H2, gas, Dil. HCl, Conical flask, , Conical flask, , Zinc dust, , Dil. HCl, , Zinc dust, , fig-10(a), , fig-10(b), , Activity 10, -, , Take two iron nails and clean them by rubbing with sand paper., Take two test tubes and mark them as A and B., Take about 10ml of copper sulphate solution in each test tube. Dip, one iron nail in copper sulphate solution of test tube A and keep it, undisturbed for 20 minutes., - Keep the other iron nail aside., - Now take out the iron nail from copper sulphate solution and, compare with the other iron nail that has been kept aside., (see fig11-a), - Compare the colours of the solutions in the test tubes., (see fig11-b), - What changes do you observe?, You will find the iron nail dipped in copper sulphate solution becoming, brown. The blue colour of copper sulphate solution in test tube ‘A’ fades., , A, , B, fig-11(a):Iron nail dipped in, copper sulphate solution, Free distribution by A.P. Government, , fig-11(b): Iron nail and copper, sulphate solutions compared before, and after the experiment, 35
Page 46 :
The chemical reaction in this activity is:, Fe (s) +, , CuSO4 (aq), , FeSO4 (aq) + Cu (s), , ...............(26), , Iron is more reactive than copper, so it displaces copper from copper, sulphate. This is another example of displacement reaction., Other examples of displacement reaction are:, i) Zn(s) + 2AgNO3 (aq), , Zn (NO3)2 (aq) + 2 Ag (s) ............ (27), , ii) Pb (s) + CuCl2 (aq), , PbCl2 (aq) + Cu (s), , .................. (28), , Double displacement reaction, , Activity 11, - Take a pinch of lead nitrate and, dissolve in 5.0ml of distilled water, in a test tube., - Take a pinch of potassium iodide, in a test tube and dissolve in, distilled water., - Mix lead nitrate solution with, potassium iodide solution., - What do you observe?, A yellow coloured substance, which is insoluble in water, is, formed as precipitate. The, precipitate is lead iodide., , Pb(NO3)2, KNO3, , KI, Lead Iodide, , fig-12: formation of lead iodide, and potassium nitrate, , Pb (NO3) 2(aq) + 2KI (aq), lead nitrate, , PbI2 (s) + 2KNO3 (aq) ..................(29), , potassium Iodide, , lead iodide, , potassium nitrate, , This reaction is double displacement reaction. If two reactants exchange, their constituents chemically and form two products, then the reaction is, called as double displacement reaction., Other examples of double displacement reactions are:, 1) Sodium sulphate solution on mixing with barium chloride solution, forms a white prepitate of barium sulphate and soluble sodium chloride., Na2SO4 (aq) + BaCl2 (aq), 36, , X Class, , BaSO4(s) + 2 NaCl (aq) ...........................(30), Chemical reactions and Equations
Page 47 :
2) Sodium hydroxide reacts with hydrochloric acid to form sodium, chloride and water., NaOH (aq) + HCl(aq), , NaCl(aq) + H2O(l), , ............................(31), , 3) Sodium chloride spontaneously combines with silver nitrate in, solution giving silver chloride precipitate., NaCl (aq) + AgNO3(aq), , AgCl(s) + NaNO3(aq) ............................(32), , Oxidation and Reduction, ‘Oxidation’ is a reaction that involves the addition of oxygen or removal, of hydrogen., ‘Reduction’ is a reaction that involves the addition of hydrogen or, removal of oxygen., Let us try to understand more clearly doing this experiment., , Activity 12, - Take about 1.0g of copper powder in a china dish., - Keep the china dish on a tripod stand containing wire gauge., - Heat it with a bunsen burner or with a spirit lamp., - Do you find any change in colour of copper?, You will notice that the surface layer of copper becomes black., • Why does the colour of copper change?, • What is the black colour product formed on the surface of copper?, In the activity on heating copper it reacts with, oxygen present in the atmosphere to form copper, Chind dish, oxide., containing, The reaction is shown below., Copper, , Wire gauze, , powder, , Cu(s), , Heat, , + O2(g) –––––, , 2 CuO(S) ........(33), Tripod, stand, , fig-13(a): Black, copper oxide, , Bunsen, burner, , fig-13(b), China dish, , fig-13(c): Oxidation of copper to copper oxide, Free distribution by A.P. Government, , 37
Page 48 :
Here copper combines with oxygen to form copper oxide. Here oxygen, is gained and the process is called oxidation., Now pass hydrogen gas over hot copper oxide obtained in above activity, and observe the change., • What do you notice?, • Is there any change in black colour of copper oxide?, You will notice that the black coating on copper turns brown because, copper oxide loses oxygen to form copper. In this process oxygen is lost, and the process is called Reduction., Heat, , CuO(s) + H2(g), , –––––, , Cu(s) + H2O (g), Black copper oxide, , H2 gas, , Cork, H2O(g), , Glass tube, Bunsen, burner, , Stand, , fig-14: Reduction of copper oxide to copper, , In the above reaction hydrogen is gained; such reaction is called, reduction reaction., Generally oxidation and reduction occur in the same reaction. If one, reactant gets oxidized, the other gets reduced. Such reactions are called, oxidation-reduction reactions or redox reactions., In the CuO, H2 reaction CuO is reduced and H2 is oxidized., Some other examples of redox reactions are:, i) 2 Fe2O3(s) + 3C(s), , 4 Fe (s) + 3CO2 (g), , .............. (34), , ii) 2 PbO (3) + C(s), , 2Pb(s) + CO2 (g), , .............. (35), , Have you observe the effects of oxidation reactions in daily life, Corrosion:, You must have observed that a freshly cut apple turns brown after some, time. The shining iron articles gradually become reddish brown when left, for some time. Burning of crackers produce dazzling light with white, fumes., 38, , X Class, , Chemical reactions and Equations
Page 49 :
•, , How do these changes occur?, They are all the examples of the process called oxidation., Let us know how?, , Oxidation is the reaction of oxygen, molecules with different substances, starting from metal to living tissue which, may come in contact with it., Apples pears, bananas, potatoes etc.,, contain enzyme called polyphenol, oxidase or tyrosinase, which reacts with, oxygen and changes the colour on the cut, surface of the fruit., The browning of iron, when left for, sometime in moist air, is a process, fig-15: Rusting of iron, commonly known as rusting of iron. This, process is basically oxidation reaction which requires both oxygen and, water. Rusting does not occur in oxygen free water or dry air., Burning of crackers is also oxidation process of variety of chemicals., •, , Did you notice the colour coating on silver and copper articles?, , When some metals are exposed to moisture, acids etc., they tarnish, due to the formation of respective metal oxide on their surface. This process, is called corrosion., Look at the following examples:, i. The black coatings on silver(see fig-16), , fig-16: Tarnishing, of silverware, (before & after), , 4Ag + 2H2S, , + O2, , 2Ag2S + 2H2O, , .............. (37), , black, Free distribution by A.P. Government, , 39
Page 50 :
ii. Green coating on copper (see fig-17), , fig-17: Corrosion of copper, , 2Cu + O2, , 2CuO, , .............. (38), , Corrosion is the oxidative deterioration of a metal., Corrosion causes damage to car bodies, bridges, iron railings, ships, etc., and to all other objects that are made of metals. Especially corrosion, of iron is a serious problem., Corrosion can be prevented or at least minimized by shielding the, metal surface from oxygen and moisture. It can be prevented by painting,, oiling, greasing, galvanizing, chrome plating or making alloys. Galvanizing, is a method of protecting iron from rusting by coating them a thin layer of, Zinc., Alloying is also a very good method of improving properties of metal., Generally pure form of iron is very soft and stretches easily when hot., Iron is mixed with carbon, nickel and chromium to get an alloy stainless, steel. The stainless steel is hard and does not rust., A metallic substance made by mixing and fusing two or more metals,, or a metal and a nonmetal, to obtain desirable qualities such as hardness,, lightness, and strength is known as alloy., For example: Brass, bronze, and steel., , Do you know?, Gold one of the most valuable of elements has been prized since antiquity for, its beauty and resistance to corrosion., 40, , X Class, , Chemical reactions and Equations
Page 51 :
Some more effects of oxidation on everyday life, •, , Combustion is the most common example for oxidation reactions., For example: burning of wood involves release of carbon dioxide, water, vapour along with huge amount of energy., • Rising of dough with yeast depends on oxidation of sugars to carbon, dioxide and water., • Bleaching of coloured objects using moist chlorine, Cl2 + H2O, , HOCl + HCl, , .............. (39), , HOCl, HCl + (O), .............. (40), Coloured object + (O), Colourless object., Some times during rainy season the power supply to our home from, the electric pole will be interrupted due to formation of the metal oxide, layer on the electric wire. This metal oxide is an electrical insulator. On, removing the metal oxide layer formed on the wire with a sand paper, supply, of electricity can be restored., , Rancidity, •, , Have you ever tasted or smelt the fat/oil containing food materials, left for a long time?, • When fats and oils are oxidized they become rancid. Their smell and, taste change., Thus we can say that oxidation reactions in food material that were, left for a long period are responsible for spoiling of food., Rancidity is an oxidation reaction., • How can we prevent the spoiling of food?, The spoilage of food can be prevented by adding preservatives like, Vitamin C and Vitamin E., Usually substances which prevent oxidation (Antioxidants) are added, to food containing fats and oil. Keeping food in air tight containers helps, to slow down oxidation process., Do you know that manufacturers of potato chips flush bags of chips, with nitrogen gas to prevent the chips from getting oxidized., , Key words, Reactants, products, exothermic reaction, endothermic reaction, chemical, combination, chemical decomposition, displacement reaction, double, displacement reaction, oxidation, reduction, corrosion, rancidity, antioxidants., Free distribution by A.P. Government, , 41
Page 52 :
What we have learnt, •, •, •, •, •, •, •, •, •, •, •, •, •, •, •, •, , Chemical change is permanent change., A Chemical equation represents a chemical reaction., Complete chemical equation represents the reactants, products and their physical state., A Chemical equation is said to be balanced, when the number of atoms of each element is same, on both reactants side and products side., A chemical equation must always be balanced., In a combination reaction two or more substances combine to form a new single substance., In a decomposition reaction a single substance decomposes to give two or more substances., Reactions in which heat energy is absorbed by the reactants are endothermic reactions., In exothermic reaction heat energy is released by the reactants., A displacement reaction occurs, when an element displaces another element from its compound., Two different atoms or ions are exchanged in double displacement reactions., Oxidation is the gain of Oxygen or loss of Hydrogen., Loss of oxygen or gain of Hydrogen is Reduction., Corrosion causes damage to iron appliances., When fats and oils are oxidized, they become rancid., Precipitate is an insoluble substance., , Improve your learning, 1. What is a balanced chemical equation? Why should chemical equations be balanced? (AS1), 2. Balance the following chemical equations. (AS1), a) NaOH + H2SO4, Na2SO4 + H2O, b) Hg (NO3)2 + KI, Hg I2 + KNO3, c) H2 + O2, H2O, d) KClO3, KCl + O2, e) C3H8 + O2, CO2 + H2O, 3. Write the balanced chemical equations for the following reactions. (AS1), a) Zinc + Silver nitrate, Zinc nitrate + Silver., b) Aluminum + copper chloride, Aluminum chloride + Copper., c) Hydrogen + Chlorine., Hydrogen chloride., d) Ammonium nitrate, Nitrogen + Carbon dioxide + water., 4. Write the balanced chemical equation for the following and indentify the type of reaction in each, case. (AS1), a) Calcium hydroxide (aq) + Nitric acid (aq), Water (l) + Calcium nitrate (aq), 42, , X Class, , Chemical reactions and Equations
Page 53 :
b) Magnesium (s) + Iodine (g), , Magnesium Iodide. (s), , c) Magnesium(s) + Hydrochloric acid(aq), d) Zinc(s) + Calcium chloride (aq), , Magnesium chloride(aq) + Hydrogen(g), , Zinc Chloride (aq) + Ca(s), , 5. Write an equation for decomposition reaction where energy is supplied in the form of, Heat / light / electricity. (AS1), 6. What do you mean by precipitation reaction? (AS1), 7. How chemical displacement reactions differ from chemical decomposition reaction? Explain, with an example for each. (AS1), 8. Name the reactions taking place in the presence of sunlight? (AS1), 9. Why does respiration considered as an exothermic reaction? Explain. (AS1), 10. What is the difference between displacement and double displacement reactions? Write equations, for these reactions? (AS1), 11. MnO2 + 4HCl, , MnCl2 + 2H2O + Cl2, , In the above equation, name the compound which is oxidized and which is reduced? (AS1), 12. Give two examples for oxidation-reduction reaction. (AS1), 13. In the refining of silver, the recovery of silver from silver nitrate solution involved displacement, by copper metal. Write the reaction involved. (AS1), 14. What do you mean by corrosion? How can you prevent it? (AS1), 15. Explain rancidity. (AS1), 16. Balance the following chemical equations including the physical states. (AS1), a) C6H12O6, b) Fe, , + O2, , c) NH3, , + Cl2, , d) Na, , +, , H2O, , –––––, –––––, –––––, –––––, , C2H5OH + CO2, Fe2O3, N2H4+NH4Cl, NaOH +H2, , 17. Balance the chemical equation by including the physical states of the substances for the following, reactions. (AS1), a) Barium chloride and sodium sulphate aqueous solutions react to give insoluble Barium, sulphate and aqueous solution of sodium chloride., b) Sodium hydroxide reacts with hydrochloric acid to produce sodium chloride and water., c) Zinc pieces react with dilute hydrochloric acid to liberate hydrogen gas and forms zinc, chloride, 18. A shiny brown coloured element ‘X’ o n heating in air becomes black in colour. Can you, predict the element ‘X’ and the black coloured substance formed? How do you support your, predictions? (AS2), 19. Why do we apply paint on iron articles? (AS7), 20. What is the use of keeping food in air tight containers? (AS7), Free distribution by A.P. Government, , 43
Page 54 :
ks, Fill in the blan, 1., 2., 3., 4., 5., 6., , The decomposition of vegetable into compost is an example of ____________ reaction., The chemical reactions in which energy is absorbed to form a new compound is called ________, The reaction 2N2O 2N2 + O2 is an example for ________ reaction., The reaction Ca + 2H2O Ca(OH)2 + H2 is an example for _______ reaction., The substances that are present on left side of a chemical equation are called _____., The arrow mark between the products and reactants of a chemical equation shows ______ of, the reaction., 7. Match the following:, 1) 2AgNO3 + Na2CrO4, Ag2CrO4+ 2NaNO3 ( ) a) combination reactions, 2) 2 NH3, N2+ 3H2, ( ) b) decomposition reactions, 3) C2H4 + H2O C2H6O, ( ) c) displacement reactions, ( ) d) double displacement Reactions, 4) Fe2O3 + 3CO 2 F2+ 3CO2, , s, Multiple choice question, 1. Fe2O3 + 2Al Al2O3 + 2 Fe., [, ], The above reaction is an example of:, a) Combination reaction, b) Decomposition reaction, c) Displacement reaction, d) Double decomposition reaction, 2. What happens when dil. hydrochloric acid is added to iron filings? Choose the correct answer., a) Hydrogen gas and iron chloride are produced., [, ], b) Chlorine gas and iron hydroxide are produced., c) No reaction takes place., d) Iron salt and water are produced., 3. 2 PbO(s) + C (s), 2Pb(s) + CO2 (g), [, ], Which of the following statements are correct for the above chemical reaction?, a) Lead is reduced, b) Carbon dioxide is oxidized, c) Carbon is oxidized, d) Lead oxide is reduced., i) (a) and (b), ii) (a) and (c), iii) (a), (b) and (c), iv) all., 4. The chemical equation BaCl2 + Na2SO4 BaSO4 + 2NaCl represents following type of, chemical reaction., [, ], i) displacement, ii) combination, iii) decomposition, iv) double-displacement, 5. The reaction of formation hydrogen chloride from hydrogen and chloride represents following, type of chemical reaction, [, ], i) decomposition, ii) displacement, iii) combination, iv) double-displacement, 44, , X Class, , Chemical reactions and Equations
Page 55 :
Chapter, , 3, Reflection of light by, different surfaces, In class 6, we have learnt about shadows and we carried out many, experiments with light rays and also discussed the rectilinear propagation, of light i.e., light travels in a straight line. In class 7 we learnt the laws of, reflection., Let us recall some of them., − A source of light, an opaque object and a screen are needed to form a, shadow., − Light travels in a straight line., − When light gets reflected from a surface, the angle of reflection is, equal to the angle of incidence., − The incident ray, the normal at the point of incidence and the reflected, ray all lie in the same plane., You must have observed shadows and images in your daily life. Sme, questions might have come to your mind while observing these shadows, or images., • Why does our image appear thin or bulged out in some mirrors?, • Why is there right-left inversion (lateral inversion) when we look into, a mirror?, • Can we focus sunlight at a point using a mirror instead of a magnifying, glass?, • Why is the angle of reflection equal to the angle of incidence when a, light ray gets reflected from a surface?, • Are the angle of reflection and angle of incidence also equal for, reflection by curved surfaces?, Free distribution by A.P. Government, , 45
Page 56 :
In this lesson we are going to learn about reflection of light in detail, so that we can answer the above questions. Let’s start with some activities, based on your previous knowledge., , Activity 1, Formation of image by a pinhole camera, Recall how an image forms in a pinhole camera that you have learnt in, class 6. Draw a ray diagram of the formation of an image in a pinhole, camera., What whould happen if we increase the size of, the hole of the pinhole camera. Observe the flame of, a candle with a pinhole camera making a big hole. Try, to draw a ray diagram of the formation of an image in, a pinhole camera with a big hole. Look at figure 1., fig-1, By observing the figure we can understand that the, light rays coming from the top of the candle flame fall at different points, on the screen. Similarly the rays coming from bottom of the candle flame, also fall at different points on the screen. Thus we get blurred image on, the screen due to the big hole of the camera as shown figure 1., , Think and discuss, •, •, •, , Does the explanation match your observation?, What happens if the hole is much bigger i.e. equal to the size of the flame?, If so, can we get an image of a flame on the screen of the pinhole camera?, Why?, • What happens if we observe the same flame with the same pinhole camera, from a long distance?, Think and answer. Do the experiment and check your answer., Now think about reflection of light, and solve the task given below., , Activity 2, A smart crow is on a tree at point ‘A’ as shown in figure-2. Some grains, are on the ground. If the crow wants to take a grain and reach the point ‘B’, on the other tree as early as possible(in least time), from where should, the crow pick up the grain?, 46, , X Class, , Reflection of Light by Different Surfaces
Page 57 :
A, , With the mathematical knowledge you have, about angles and triangles can you guess the path, that the crow selects? If you can’t, read the, fig-2, following., The crow can pick the grain from any point on the ground but the, condition is; selecting a point on the ground to reach point ‘B’ from point, ‘A’ in least possible time. If we assume that the speed of the crow is constant, the path that the crow selects should be the shortest. Let us find the shortest, path., Observe some of the paths in figure-3., A, Which among the paths ACB, ADB, AEB and, AFB is the shortest path?, To compare the lengths of these paths, we, C, D, E, fig-3, make duplicates of them as shown in, figure-4., A, In the figure, CB = CG. The length of path, ACB = AC+CB = AC+CG = ACG. Thus the, length of the path ACG is equal to the length of, D, E, C, the path ACB. similarly ,, fig-4, length of the path ADB = length of the path ADG, length of the path AEB = length of the path AEG, EI, A, length of the path AFB = length of the path AFG, If you observe Fig-4 carefully, you will, 2, 1, notice that, among the paths ACG, ADG, AEG, fig-5 E, and AFG, the shortest path is AEG, because it, is the straight line distance between points A, and G. You can measure and check this using a scale. As AEG=AEB, path, AEB is the shortest path to reach point B from point A. It would take the, least time. So the smart crow will pick the grain from point E., Observe the path AEB once again in figure-5., If we draw a normal EEI at point E, we can easily find that angle AEEI, (angle 1) is equal to angle EIEB (angle 2)., Like the crow in the above situation, light also selects the path which, takes the least time to travel. This principle was first given by Pierre de, Fermat, a French lawyer and an amateur mathematician., It is also applicable to reflection of light. When light gets reflected, from a surface, it selects the path that takes the least time. That is why the, Free distribution by A.P. Government, , B, , B, , F, , B, , F, G, , B, , 47
Page 58 :
angle of incidence is equal to the angle of reflection as shown in figure-5., Now, before a detailed discussion on reflection, perform a fun activity, and refresh your previous knowledge., , Activity 3, Check your understanding of reflection, Look at figures 6a and 6b. Let us suppose that you have been given a, plane mirror strip., • What will you do to obtain figures that are shown in figure 6(b) using, mirror strip and figure 6(a)?, Place the plane mirror strip on the figure shown in 6(a) in such a manner, that you see one of the figures shown in figure-6b. The procedure is shown, in figure-6c., , Mirror, , fig-6a, fig-6c, fig-6b, , • Are you able to obtain all figures shown in 6(b)?, Take the help of your friends to complete the task., Let us begin the detailed discussion on reflection of light by plane, surfaces., , Reflection of light by plane mirrors, , Lab Activity 1, Aim: Verification of laws of reflection, Required material: mirror strip, drawing board, white paper, pins,, clamps, scale and pencil, Procedure: Take a drawing board and fix a white paper on it with the, help of clamps. Draw a straight line AB at the centre of the paper and also, 48, , X Class, , Reflection of Light by Different Surfaces
Page 59 :
a normal (ON) to AB at the point ‘O’. Draw a straight, line PQ making certain angle (angle i) with ON as, P1, shown in figure 7. Fix two pins at the points P and Q, on the paper vertically. Observe the image PI of the, Q1, pin P and QI of the pin Q, in the mirror kept along, O, the line AB. Fix two more pins R and S such that A, Q i, they are in the same line as that of PI and QI. Join R,, r, P, S and O as shown in figure-7., Measure the angle between RS and ON, N, (angle of reflection). You will find that angle, fig-7, of incidence = angle of reflection. Repeat the, experiment for different angles of incidence and measure the corresponding, angles of reflection (r)., • Is the angle of reflection equal to the angle of incidence in all cases ?, In which plane does the incident ray, reflected ray and the normal lie, nd, (2 law of reflection of light) ? Let us discuss this., , B, R, S, , Plane of reflection, In the above activity, the incident ray is the ray which passes through, the points P and Q touching the paper. The reflected ray is the ray which, passes through the points R and S touching the same paper, and ON is the, normal to the mirror at point O., • Do the two rays and the normal lie in the same plane? If yes, which is, that plane?, If the incident ray, reflected ray and normal are in the plane parallel to, the plane of the paper, where will that plane be?, Assume that the heads of all pins pierced at points P,Q,R and S in the, above activity are at the same height. The incident ray is the ray which, passes through the heads of pins which are located at points P and Q, and, reflected ray is the ray which passes through the heads of pins which are, located at points R and S., • Where will the normal be?, • In which plane will the incident ray, reflected ray and the normal lie?, The plane in which the incident ray, reflected ray and normal lie is the, plane of reflection., Assume that the heads of the pins which are located at the points P and, Q are not of the same height., • How will the incident ray be?, • How will the reflected ray be?, Free distribution by A.P. Government, , 49
Page 60 :
•, •, , How will the normal be?, How will the plane of reflection be?, Arrange two pins with different heights. Arrange the incident ray,, reflected ray and the normal with the help of spokes of a cycle. Then think, of the plane of reflection., • How does a mirror form the image of a pin or any object?, Let us discuss., , Formation of an image by a plane mirror, O, , I, , Observe figure 8., O is a point object. Some rays from O reach, the mirror and get reflected. When we look into, the mirror, the reflected rays seem to be coming, from the point I. So point I is the image of point, object O., , fig-8, , I, , II, , Observe the distances of object O and image I, from the surface of the mirror and try to compare, these distances by approximate estimation in figure, 8. We find that these distances are equal., , Let us assume that an object (OOI) is kept in, front of a mirror as shown in figure 9. Draw a few, O, incident rays from the object to the mirror and, reflected rays from the mirror using laws of, reflection. Your drawing may look like that shown, I, O, in figure 9., In the figure, the rays coming from the point O, fig-9, get reflected from the mirror and seem to be coming, from the point I. So we say I is the image of O., The rays coming from the point OI get reflected from the mirror and, seem to be coming from the point II. So we say II is the image of OI., The rays coming from the middle part of the O and OI will form their, own images between I and II., Thus, III is the image of the object OOI., • What is the size of the image compared to the size of the object?, Let us discuss some of the characteristics like size, distance and rightleft inversion of an image formed by a plane mirror., , 50, , X Class, , Reflection of Light by Different Surfaces
Page 61 :
Characteristics of an image formed by a plane mirror, Take an object, say pen or pencil. Put it in front of a plane mirror,, touching the surface of the mirror., • What do you say about the size of the image compared to the size of, the object?, Move the object towards your eye. What do you observe?, • Is the size of the image decreasing or increasing?, Figure 9 shows the formation of an image by a plane mirror. In that, figure, you might have noticed that the size of the image is equal to the size, of the object. Why does the size of the image seem to be decreased when, you move the object towards your eye?, To understand this see figure 10, which, shows how our eyes judge the size of an object., 1, Observers 1 and 2 are looking at the object, which is at point O. It looks smaller to observer, fig-10, O, 2 than to observer 1, because the light rays, coming from the object make a smaller angle at the eye of observer 2 who, is at a larger distance compared to observer 1. The angle plays a role in, judging the size of the object., In the same way when we move the object from the mirror to our eye,, the image in the mirror seems to move back in the mirror. Then the distance, from the image to our eye increases. The angle made by image at our eye, is smaller than the angle made by the object. That is why the image looks, smaller than the object., When you stand in front of a mirror you might have observed that the, distance of your image in a plane mirror seems to be equal to the distance, between the mirror and yourself. What you observe is generally true. You, can verify this by observing figure-9., You also might have observed the right-left inversion of your image in, a plane mirror., • Why does an image suffer lateral (right-left) inversion?, See figure-11., • What do you understand from the figure 11?, The light rays which come from our right ear get reflected from, the plane mirror and reach our eye. Our brain feels that the ray, (reflected ray) is coming from the inside of the mirror (shown by, dotted line in the figure-11). That is why our right ear looks like left, ear in the image., , 2, , fig-11, Free distribution by A.P. Government, , 51
Page 62 :
Now observe the lateral inversion of a letter, with a ray diagram in figure-12., Think of the process of image formation by, a plane mirror and explain lateral inversion by, observing figure-12., fig-12, We now know how light reflects from plane, surfaces. In class 7, we learnt about spherical, mirrors and why they were called spherical mirrors., We already did a simple activity to get an image with a concave mirror, in class 7. Now we shall study the reflection of light by curved surfaces in, detail., , Reflection of light by spherical mirrors, The first law of reflection tells us;, A light ray incident at an angle with the normal at the point of incidence, will get reflected making equal angle with the normal., This law is true for all surfaces, be it a plane surface or a curved one., The important words here are ‘the angle made with normal at the point of, incidence’. If for any surface one can decide the normal and find the incident, angle, it is possible to deduce the angle made by the reflected ray. It is very, easy to find a normal at any point on the plane surface but for a curved or, uneven surface it is not straightforward., , Activity 4, Finding the normal to a curved surface, Take a small piece of thin foam or rubber (like the sole of a slipper)., Put some pins along a straight line on the foam as shown in the figure -13a., , fig-13(a), , fig-13(b), , fig-13(c), , All these pins are perpendicular to the plane of foam. If the foam is, considered as a mirror, each pin would represent the normal at that point., Any ray incident at the point where the pin makes contact with the surface, will reflect with the same angle as the incident ray made with the pinnormal., 52, , X Class, , Reflection of Light by Different Surfaces
Page 63 :
Now bend the foam piece inwards as shown in figure-13b, what happens, to the pins?, They still represent the normal at various points, but you will notice, that all the pins tend to converge at a point (or intersect at a point)., If we bend the foam piece outwards, we will see that the pins seem to, move away from each other or in other words they diverge as shown in, figure-13c., This gives us an idea of what is likely to happen with a spherical mirror., A concave mirror will be like the rubber sole bent inwards (fig-13b) and, the convex mirror will be like the rubber sole bent out wards (fig-13c)., For a concave mirror, like these pins in figure-13b, all normals will, converge towards a point. This point is called centre of curvature(C) of, the mirror., Recall a little bit of geometry: while learning about circles, and tangents, you may have learnt that a radius is always, perpendicular to the tangent to the circle drawn at the point., This gives us a clue about how we can find normal to any point on a, spherical mirror. All that we have to do is to draw a line from the point on, the mirror to centre of the sphere., It is much easier to imagine this in a two dimensional figure as shown, in figure-14a. The concave mirror is actually a part of a big sphere. In, order to find this centre point (centre of curvature) we have to think of the, centre of the sphere to which the concave mirror, belongs. The line drawn from C to any point on the, Normal, mirror gives the normal at that point., principal axis, For the ray R, the incident angle is the angle it, P (pole), C, makes with the normal shown as i and the reflected, fig-14(a), angle is shown as r in figure-14b. We know by first, law of reflection i = r., The mid point (Geometrical centre) of the mirror, R, is called pole (P) of the mirror. The horizontal line, i, r, shown in the figures which passes through the centre, P, C, of curvature and pole is called principal axis of the, mirror. The distance between P and C is radius of, fig-14(b), curvature (R) of the mirror., Free distribution by A.P. Government, , 53
Page 64 :
Using the construction method described above, try to construct, different reflected rays for any array of rays that are parallel to the principal, axis. What is your conclusion?, , Verifying your drawing with experiments, To verify this we must first find out some way of obtaining a beam of, parallel rays. How do we do that?, First we need to create a situation in which one gets parallel rays of, light., In the figure-15 we have stuck two pins on a, thermocole block. The pins are parallel to each other., As we see in the figure, when a source of light is, kept very near, we see the shadows diverging (from, the base of the pins). As we move the source away, fig-15, from the pins, the angle of divergence gets reduced., If we move the source far away we will get parallel, shadows. But as we move the candle away, the light intensity becomes low., That means to get a beam of parallel rays the source should be at a long, distance and it must be of sufficient intensity., Where do we find one such source?, Yes, we have one easily available source, you probably have guessed, it: The Sun., Let us do an experiment with sun rays and a concave mirror., , Activity 5, , P, , 54, , Hold a concave mirror such that sunlight falls on, it. Take a small paper and slowly move it in front of, the mirror and find out the point where you get the, smallest and brightest spot, which will be the image, F, C, of the sun. (See to it that your paper is small so that it, does not obstruct the incoming sun rays.), fig-16, The rays coming from the sun parallel to the, principal axis of concave mirror converge to a point (see figure-16). This, point is called Focus or focal point (F) of the concave mirror. Measure, the distance of this spot from the pole of the mirror. This distance is the, focal length (f) of the mirror. The radius of curvature will be twice this, distance (R=2f)., Does this help you to verify the conclusions you arrived at, with your, drawing?, , X Class, , Reflection of Light by Different Surfaces
Page 65 :
•, , What happens if you hold the paper at a distance shorter than the focal, length from the mirror and move it away?, • Does the image of the sun become smaller or bigger?, You will notice that the image of the sun first keeps on becoming small,, beyond the focal point it keeps on becoming enlarged., Note: while drawing a ray diagram sometimes it is not clear which is, the reflecting side of the mirror. Hence we follow a convention of showing, lines on the non-reflecting side(coated side)., Can you draw the same diagram for a convex, mirror?, See figure-17. The parallel rays appear to diverge, after reflection. If we extend the reflected rays, backwards they meet at ‘F’ i.e. focus of the convex, mirror., , C, , F, , P, , fig-17, , Think and discuss, •, •, , See figure-17. A set of parallel rays are falling on a convex mirror. What, conclusions can you draw from this?, Will you get a point image if you place a paper at the focal point?, , When parallel rays are incident on a concave mirror, on reflection they, meet at the focus., • Do we get an image with a concave mirror at the focus every time? Let, us find out., , Lab Activity 2, Aim: Observing the types of images and measuring the object distance, and image distance from the mirror., Material required: A candle, paper, concave mirror (known focal, length), V-stand, measuring tape or meter scale., Procedure: Place the concave mirror on V-stand, a candle and meter, scale as shown in figure-18., Keep the candle at different distances from the mirror (10cm to 80cm), along the axis and by moving the paper (screen) find the position where, Free distribution by A.P. Government, , 55
Page 66 :
you get the sharp image on paper. (Take care that flame is above the axis of, mirror, paper is below the axis)., , fig-18, , Note down your observations in table-1., Table-1, Observation, no., , Distance of candle Distance of paper, from mirror, from mirror, (object distance-u) (image distance-v), , Enlarged/, diminished, , Inverted or, erect, , 1, 2, 3, 4, Group your observations based on the type of image you see (e.g. Image, is bigger and inverted). It is possible you may not get any image at some, positions, note down that too!, Since we know the focal point and centre of curvature, we can reclassify, our above observations as shown in table-2. What do you infer from this, table?., At this point we suggest that you make one more observation. You, have been trying to get the image on a paper when the object is at different, positions. At the same time also look into the mirror and note your, observations about how the image appears., • Is it inverted or erect, enlarged or diminished?, Table - 2, Position of the, candle (object), , Position of, the image, , Enlarged/, diminished, , Inverted or, erect, , Real or, virtual, , Between mirror & F, At focal point, Between F and C, At centre of curvature, Beyond C, 56, , X Class, , Reflection of Light by Different Surfaces
Page 67 :
What do you infer from the table-2?, Let us try to draw ray diagrams with concave mirrors and compare, them with your inferences., , Ray diagrams for concave mirror, In activity-5 we saw the ray diagram of sunrays parallel to the concave, mirror and the image of the sun was very small at the focal point (See, figure-16). Now we shall develop a technique to draw ray diagrams when, an object is placed anywhere on the axis of the mirror and validate the, above observations., Here we will take at least two rays originating from the same point on, the object but with different direction, see how they get reflected from the, mirror and find out the point where they meet to form the image., Let us take an example., As shown in the figure-19, assume a concave mirror, and a candle placed at some distance along the axis of the, mirror., The diagram shows two rays coming from the tip of, the flame (object). The reflected rays are constructed, A, based on the laws of reflection.They meet at point A. The, tip of the flame of the reflected image will be at the point, of intersection, A., • Why only at point A?, If we hold the screen at any point before or beyond point A (for example, at point B), we see that the rays will meet the screen at different points., Therefore, the image of the tip of the flame will be formed at different, points due to these rays. If we draw more rays emanating from the same tip, we will see that at point A they will meet but at point B they won’t. So, the, image of the tip of the flame will be sharp if we hold the screen at point A, and will become blurred (due to overlaping of multiple images) when we, move the paper slightly in any direction (forward or backward). Is this not, something that you observed during the previous experiment with sun rays?, However, it is not going to be easy to evaluate the angle of reflection, for any arbitrary ray, every time we will have to find the normal, measure, the incident angle and construct a ray with equal angle on the other side., This would be a tedious task, can we find any other simpler method?, Yes, there are a few. Based on our discussion so far, we can identify, some appropriate rays which we can take as representative rays to find the, point ‘A’., Free distribution by A.P. Government, , B, , fig-19, , 57
Page 68 :
We have seen that all rays that are parallel to the, axis get reflected such that they pass through the focal, point of the mirror. So, for drawing any diagram the, most suitable ray to draw will be the one that comes, P F, C, from the object and goes parallel to the axis of the, fig-20, mirror. The reflected ray will be the line drawn from, the point of incidence on the mirror and passes, through the focal point of the mirror. To make it more convenient we will, always take rays that come from the tip of the object. See the ray R1 in, figure-20., The converse situation of previous one is also true; that is, a ray that, passes through the focal point of the mirror will travel, parallel to the axis after reflection., R2, This gives us our second ray. This will be the ray, coming from the tip of the flame and going through, C, F, the focal point and falling on the mirror. After, reflection, this ray travels parallel to the axis. So we, draw the reflected ray as a line parallel to the axis, fig-21, coming from the point where the incident ray meets, the mirror. See R2 in figure-21., Using the rays R1, R2 and finding the point where they intersect we, know the point where the image of the tip is formed., There is one more ray which is convenient to draw., We have seen earlier that any ray that is normal to the surface, on, reflection, will travel along the same path but in the opposite direction., Which ray can such a one be for a spherical mirror?, We know that a line drawn from the centre of, R3, curvature to the mirror is perpendicular to the tangent, at the point where the line meets the curve. So if we, F, C, draw a ray coming from the tip of the object going, through the centre of curvature to meet the mirror, it, fig-22, will get reflected along the same line. This ray is shown, as R3 in the figure-22. In general, a ray travelling along normal retraces its, path., Along with these three rays ‘the ray which comes from the object and, reaches the pole of the mirror’ is also useful in drawing ray diagrams. For, this ray, the principal axis is the normal., R1, , P, , P, , 58, , X Class, , Reflection of Light by Different Surfaces
Page 69 :
If we have our object (candle) placed as shown, in figure-23, we can draw the ray diagram to get the, R1, point of intersection A, of any two rays coming from, R2, B, the top of the object and point of intersection B, of, P, F, C, any two rays coming from the botom of the object., A, We notice that point B is exactly at the same distance, fig-23, from mirror as point A. Hence the image is vertical, and inverted., • Where is the base of the candle expected to be in the image when the, candle is placed on the axis of the mirror?, Since any ray coming from any point on the axis and travelling along, the axis will get reflected on the axis itself, we can conclude that the base, of the image is going to be on the axis. Using the knowledge, that if the, object is placed vertically on the axis, the image is going to be vertical, all, that we do is to draw a perpendicular from point A, to the axis. The intersection point is the point where, R1, the base of the image of the candle is likely to be, R2, P, formed. See figure-24. Hence, as shown in the, F, C, diagram the image will be inverted and diminished., A, Figure-24 is drawn for the case where the object, fig-24, is placed beyond the centre of curvature., Does this conclusion match with your, observations? (Lab Activity 2), Draw similar diagrams for other cases and verify that they match with, your observations., • During the experiment, did you get any positions where you could not, get an image on the screen?, Consider the case shown in the figure-25. The, R1, candle object (O) is placed at a distance less than the, focal length of the mirror., P O F, C, The first ray (R1) will start from tip of the object, and run parallel to axis to get reflected so as to pass, through the focal point. This one is easy to draw. The, fig-25, second ray that we chose for earlier ray diagrams is, the ray coming from the tip of the object and going through the focal point, but it is not possible as such a ray will not meet the mirror. So we must use, the third ray, a ray coming from the tip of the object and going through the, centre of curvature., Free distribution by A.P. Government, , 59
Page 70 :
I, , P, , R1, P, , But that too does not seem to be possible. So we make a small change., Instead of drawing a ray from the candle tip to centre of curvature, we, consider a ray that comes from the tip and goes in such a direction that it, would go through the centre of curvature if extended backwards. This ray, is normal to the surface and so will be reflected along the same line in, opposite direction and will go through centre of curvature., We notice that the two reflected rays (figure-25) diverge and will not, meet. While doing the experiments for a case such as this we were unable, to find any place where we got a sharp image on the screen. This ray diagram, tells us that since the reflected rays are diverging we will not get an image, anywhere. So even if we had moved the screen much away from the mirror,, we would not have found an image., In such situations, however, we do see an image when we look in the, mirror. Is it possible to explain this image with a ray diagram?, Remember what we did to find the image in a plane mirror. To decide, the position of image we extended the reflected rays backwards till they, met. We will do the same here. When we look in the mirror we are looking, at these diverging reflected rays. They appear to be coming from one point., We can get this point by extending the rays, R1, backwards as shown in figure-26. The image does, R3, not really exist the way we saw in other cases, but it, is visible to us., O F, C, As seen in the figure-26, the image will be erect, and enlarged. Does this match with your, fig-26, observations?, This image that we got by extending the rays backwards is called a, virtual image. We cannot get this on a screen like, a real image., The case in which the object is at the centre of, curvature is another interesting situation. See, R2, figure-27., C, F, From the ray diagram (figure-27) we conclude, that the image of the object will be formed at the, same distance as the object and it will be inverted, fig-27, and be of the same size. What is your observation?, , Think and discuss, •, , 60, , X Class, , How can one see an image formed on the object itself? Draw a, ray diagram. Do the experiment., Reflection of Light by Different Surfaces
Page 71 :
From the ray diagrams and the observations you may have noticed some, peculiar properties of concave mirrors. They enlarge the image when the, object is held close to the mirror (less than the focal length). Also, the, image is erect. This property is used at many places and most commonly, in shaving mirrors and mirrors used by dentists., Another property is the way that it can converge the rays to its focal, point. This is extensively used in many places. Look at the shape of TV, dish antennas., If you look around you will see many curved surfaces but all surfaces, are not concave, many of these are convex., Have you observed the rare view mirrors of a car?, What type of surface do they have?, Have you observed images formed on the rear and, window glasses of a car? What type of surfaces are these?, See figure -28., Can we draw ray diagrams for convex surfaces?, fig-28, , Ray diagrams for convex mirrors, , One can draw ray diagrams for a convex mirror too. The ‘easy’ rays, that we identified earlier can be used in this case with small modification., Here there are three rules which describe these rays. The procedure for, drawing the diagram is similar and is not repeated here., , R1, C, , F, , P, , Rule 1: A ray parallel to the axis, on, meeting the convex mirror will get reflected, so as to appear as if it is coming from the, focal point. See figure-29., , fig-29, , Rule 2: This is, converse of Rule 1. A ray travelling in the direction of the, focal point, after reflection, will become parallel to the, axis. See figure-30., R3, , C, , F, , P, , fig-31, Free distribution by A.P. Government, , R2, , C, , F, , P, , fig-30, , Rule 3: A ray travelling in the direction, of the centre of curvature will, on, reflection, travel in the opposite direction, and appears to be coming from the centre, of curvature. See figure-31., 61
Page 72 :
Using these rules, draw ray diagrams to show formation of images, when an object is placed at different positions and note down your, conclusions. Verify your results experimentally., If necessary use another ray which comes from the object and reaches, the pole of the mirror., You may get the image at a particular distance when you place the object, at a certain distance. Do you find any relation between the object distance(u), and the image distance(v)?, , Derivation of formula for curved mirrors, , P, , A, h, PI, , 62, , Observe figure 32., A ray coming from the point O which is, A, on the principal axis of the mirror falls on the, θ, mirror at point A which is at height ‘h’ from, h, θ, the axis and after reflection, passes through, γ, β, α, P, I, P, F I, C, O, point I which is also on the axis., Here AC is the normal. The angle of, fig-32, incidence (angle OAC) and the angle of, reflection (angle CAI) are equal and they are, denoted by θ in the figure. Line segment API is the perpendicular drawn to, the axis from the point A. Now we can observe three right angled triangles, namely, Triangle AOPI, ACPI and AIPI., Let the angles at the vertices O, C and I of three triangles be α, β and γ, respectively as shown in figure 32., In a triangle, sum of the interior angles is equal to the exterior angle., From the triangle AOC; β = α + θ, θ=β–α, From the triangle ACI; γ = β + θ, By substituting θ = β – α in the above, When h is very small, then, I, P coincides with P, equation, we get, θ, α, γ=β+β–α, C, I, O, 2β = α + γ ..........(1), γ F θ β, • What happens when ‘h’ becomes very, small?, fig-33, Observe figure 33., When ‘h’ becomes very small,, 1. PI may coincide with point P, which is pole of the mirror., Then we can say PIO = PO, PIC = PC and PII = PI., X Class, , Reflection of Light by Different Surfaces
Page 73 :
2. The angles α, β and γ become very small as shown in figure 33., Let us calculate “Tan” values of the angles α, β andγ., (In a right angled triangle, Tan value of acute angle is the ratio of the, length of the opposite side to the length of the adjacent side of that acute, angle), Here PI is assumed to coincide with P, then we have, Tan α = PIA/ PIO = h / PIO = h/PO, Tan β = PIA/ PIC = h / PIC = h/PC, Tan γ = PIA/ PII = h / PII = h/PI, When an angle θ becomes very small i.e. close to zero, the value of, numerator (length of the opposite side of the θ) becomes very small. You, can observe this in figure 33. Then the value of Tan θ becomes very small, i.e. close to zero. So the value of Tan θ is taken as θ. That is Tan θ ≈ θ., Similarly here,, Tan α = α = h/PO, Tan β = β = h/PC, Tan γ = γ = h/PI, By substituting the values of α, β and γ in the equation- 1, we get:, 2 h/PC = h/PO + h/PI, 2/PC = 1/PO + 1/PI, .................. (2), To take the values with correct sign (direction), follow the sign, conventions given below., , Sign convention for the parameters related to the mirror equation, 1. All distances should be measured from the pole., 2. The distances measured in the direction of incident light, to be, taken positive and those measured in the direction opposite to, incident light to be taken negative., 3. Height of object (Ho) and height of image (Hi) are positive if, measured upwards from the axis and negative if measured, downwards., Substitute the values of PC, PO and PI in equation 2 according to the, sign convenction., Radius of curvature PC = –R, Object distance PO = –u, Image distance PI = –v, 2/–R = 1/–u + 1/–v, 2/R = 1/u + 1/v, Free distribution by A.P. Government, , 63
Page 74 :
We know that, radius of curvature(R) = 2 (focal length) = 2f, So,, 2/2f = 1/u + 1/v, 1/f = 1/u + 1/v, This mirror formula should be used according to the sign convention, in every situation., Now let us understand magnification, i.e. the relation between the size, of the object and the size of the image., , Magnification (m), , P, , F, , The image formed by a spherical mirror varies in size, here we discuss, the variation in height only., Observe figure 34., A ray coming from OI is incident at pole with an angle of incidence θ,, and get reflected with same angle θ., From the triangle POOI , Tan θ = OOI/PO .....(1), From the triangle PIII, Tan θ = III/PI ............(2), OI, From 1 & 2 OOI/PO = III/PI, I, C, O, B, III/OOI = PI/PO, ................(3), I, I, according to sign convention, PO = –u; PI = –v; OOI = h0; III = –hi, fig-34, Substuting the above values in equation (3)., –hi / h0 = – v/–u, B hi / h0 = – v/u, ∴ Magnification m = hi / h0 = – v/u, We define the magnification,, m = height of image(hi) /height of object (h0), In all cases it can be shown that, m = – image distance (v)/ object distance (u), Calculate the magnifications with the information you have in table-2,, for all the five cases., , Example, An object 4cm in size, is placed at 25cm infront of a concave mirror, of focal length 15cm. At what distance from the mirror whould a screen be, placed in order to obtain a sharp image?Find the nature and the size of the, image., 64, , X Class, , Reflection of Light by Different Surfaces
Page 75 :
Solution, Accordint to sign convention:, OI, focal length, (f) = –15cm, F O C, P, object distance (u) = –25cm, object height (ho) = +4cm, fig-E, image distance (v) = ?, image height (hi) = ?, Substitute teh above values in the equation, 1/f = 1/u + 1/v, 1/–15 = 1/v + 1/–25, 1/v = 1/25 – 1/15, 1/v = – 2/75, B, v = –37.5cm, So the screen should be placed at 37.5cm from the pole of the mirror., The image is real., magnification m = hi / ho= – v/u, by substituting the above values, hi/4 = –(–37.5) / (–25), hi = –(37.5 x 4)/25, hi = –6cm, So, the image is inverted and enlarged., ––––––––––––––––, We have learnt the phenomenon of reflection of light by curved mirrors., Let us make use of it in our daily life., , Making of solar cooker, You might have heard the story of Archimedes that, he burned ships using mirrors., Can we at least heat up a vessel using a mirror?, F, P, Let us try:, We already learnt that a concave mirror focuses, parallel sun rays at the focal point of the mirror. So, with a small concave mirror we can heat up and burn, paper as shown in the figure-35. (Try this with convex, mirror also. What do you observe?), In the same way make a big concave mirror to heat up a vessel., You might have observed the TV dish antenna. Make a wooden/ iron, frame in in the shape of TV dish. Cut acrylic mirror sheets in to 8 or 12, Free distribution by A.P. Government, , C, , fig-35, , 65
Page 76 :
pieces in the shape of isosceles triangles with a height equal to, the radius of your dish antenna. The bases of 8 or 12 triangles, together make the circumference of the dish. Stick the triangle, mirrors to the dish as shown in figure-36., Your solar heater/cooker is ready., Arrange it so that concave part faces sun. Find its focal point, and place a vessel at that point. It will get heated. You can even, cook rice in that vessel!, In practical applications (like in car-headlights), concave, mirrors are of parabolic shape (see figure 37), , fig-36, , P F, , fig-37, , Key words, angle of incidence, angle of reflection, normal, plane of reflection, lateral inversion,, centre of curvature, radius of curvature, principal axis, pole, focus/focal point, focal, length, object distance, image distance, virtual image, real image, magnification, , What we have learnt, •, •, •, , Fermat principle: Light chooses the path which takes the least time to travel. It is also applicable, to reflection of light., Mirror formula: 1/f = 1/u + 1/v, Magnification, m = size of the image/ size of the object (or), m = – object distance/ image distance, , Position of the, candle (object), , Position of, the image, , Enlarged?/, diminished?, , Inverted or, erect, , Between mirror & F, , Behind the mirror Enlarged, , On focal point, , At infinity, , -, , -, , Between F and C, , Beyond C, , Enlarged, , Inverted, , Real, , On centre of curvature On C, , Same size, , Inverted, , Real, , Beyond C, , Diminished, , Inverted, , Real, , 66, , X Class, , Between F and C, , Erect, , Real or, virtual, Virtual, -, , Reflection of Light by Different Surfaces
Page 77 :
Improve your learning, 1. State the laws of reflection of light. (AS1), 2. How do you find the focal length of a concave mirror? (AS1), 3. Where will the image form when we place an object, on the principal axis of a concave mirror, at a point between focus and centre of curvature? (AS1), 4. Find the distance of the image when an object is placed on the principal axis at a distance of, 10cm in front of a concave mirror whose radius of curvature is 8 cm. (AS1), 5. State the differences between convex and concave mirrors. (AS1), 6. Distinguish between real and virtual images. (AS1), 7. How do you get a virtual image using a concave mirror? (AS1), 8. What do you know about the terms given below related to spherical mirrors? (AS1), a) Pole, b) Centre of curvature c) Focus, d) Radius of curvature, e) Focal length, f) Principal axis, g) Object distance, h) Image distance, i) Magnification, 9. Write the rules for sign convention. (AS1), 10. The magnifaction produced by a plane mirror is +1. What does this mean? (AS1), 11. Imagine that spherical mirrors were not known to human beings. Guess the consequences., (AS2), 12. By observing steel vessels and different images in them; Surya, a third class student, asked his, elder sister Vidya some questions. What may be those questions? (AS2), 13. How do you verify the 1st law of reflection of light with an experiment? (AS3), 14. How do you verify the 2nd law of reflection of light with an experiment? (AS3), 15. What do you infer from the experiment which you did with concave mirrors and measured the, distance of object and distance of image? (AS3), 16. Find the plane of the reflection experimentally for the incident ray which passes through the, heads of the pins pierced in front of the mirror. (AS3), 17. Collect information about the history of spherical mirrors in human civilization. Display it in your, class room. (AS4), 18. Think about the objects which act as a concave or convex mirrors in your surroundings. Make, a table and display it in your class room. (AS4), 19. How will our image be in concave and convex mirrors? Collect photographs and display in, your class room. (AS4), 20. Draw and explain the process of formation of image with a pinhole camera? (AS5), 21. Draw suitable rays by which we can guess the position of the image formed by a concave, mirror. (AS5), 22. Show the formation of image with a ray diagram when an object is placed on the principal axis, of a concave mirror away from the centre of curvature. (AS5), 23. Make a solar heater/cooker and explain the process of making. (AS5), 24. To form the image on the object itself, how should we place the object in front of a concave, mirror? Explain with a ray diagram. (AS5), 25. How do you appreaciate the role of spherical mirrors in daily life? (AS6), Free distribution by A.P. Government, , 67
Page 78 :
26. How do you appreciate the use of reflection of light by a concave mirror in making of TV, antenna dishes? (AS6), 27. Have you ever observed the image of the sky in rain water pools on earth? Explain the reflection, of light in this context. (AS6), 28. Discuss the merits and demerits of using mirrors in building elevation. (AS7), 29. Why do we prefer a convex mirror as a rear-view mirror in the vehicles? (AS7), 30. A convex mirror with a radius of curvature of 3m is used as rear view in an automobile. If a bus, is located at 5m from this mirror, find the position, nature and size of the imaze. (AS7), 31. An object is placed at a distance of 10cm from a convex mirror of focal length 15cm. Find the, position and nature of the image. (AS7), , ks, Fill in the blan, 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., , The centre of sphere to which a sperical mirror belongs, is called .............................., The geometric centre of the mirror is ..........................., The line which passes through the centre of curvature and pole is .........................., The rays which are parallel to the principal axis of a concave mirror on reflection, meet at, ............................, The distance between pole and centre of curvature is ............................., The distance between pole and focus is ............................., The relation between focal length and radius of curvature is given by .............................., The relation between the angle of incidence and angle of reflection is given by ......................., Light selects the least time path to travel between two points. This principle was stated by, ........................., The equation of mirror formula is ...................., , s, Multiple choice question, 1. If an object is placed at C on the principal axis in front of a concave mirror, the position of the, image is ........................, [, ], a) at infinity, b) between F and C, c) at C, d) beyond C, 2. We get a diminished image with a concave mirror when the object is placed .......... [, ], a) at F, b) between the pole and F, c) at C, d) beyond C, 3. We get a virtual image in a concave mirror when the object is placed .............., [, ], a) at F, b) between the pole and F, c) at C, d) beyond C, 4. Magnification m = ......................, [, ], a) v/u, b) u/v, c) ho / hi, d) hi / ho, 5. A ray which seems to be travelling through the focus of a convex mirror passes ........................, after reflection, [, ], a) parallel to the axis, b) along the same path in opposite direction, c) through F, d) through C, 68, , X Class, , Reflection of Light by Different Surfaces
Page 79 :
Chapter, , 4, Acids, Bases and Salts, In class VII you learnt about acids, bases and salts., You know that acids are sour to taste and turn blue litmus to red, bases, are soapy to touch and turn red litmus to blue., If someone in the family is suffering from a problem of acidity, which, of the following would you suggest as a remedy?, lemon juice, vinegar or baking soda solution., • Which property do you think of while suggesting the remedy?, There are many natural materials like litmus, extract of red cabbage,, turmeric solution and extracts of coloured petals of some flowers contain, dye molecules which are weak acids or bases. These can be used as acidbase indicators to detect the nature of the solution for acidity or basicity., In adition to the above natural acid-base indicators, there are some synthetic, indicators such as methyl orange and phenolphthalein that can be used to, test for acids and bases., In this chapter you study the reactions of acids and bases. How do, acids neutralize bases? Many more interesting activities that we use and, see in our day-to-day life are also studied., , Do you know?, Litmus solution is a dye extracted from lichen, a plant belonging to the division, of Thallophyta and is used as indicator. In neutral solution litmus colour is purple., Coloured petals of some flowers such as Hydrangea, Petunia and Geranium are also, used as indicators., Free distribution by A.P. Government, , 69
Page 80 :
Chemical properties of Acids and Bases, Response of various laboratory substances with indicators., , Activity 1, Collect the following samples from the science laboratory;, hydrochloric acid (HCl), sulphuric acid (H2SO4), nitric acid (HNO3),, acetic acid (CH3COOH), sodium hydroxide (NaOH), calcium hydroxide, [Ca(OH)2], magnesium hydroxide [Mg(OH)2],ammonium hydroxide, (NH4OH) and potassium hydroxide (KOH), prepare dilute solutions of, the respective substances., Take four watch glasses and put one drop of the first solution in each, one of them and test the solution as follows., i. dip the blue litmus paper in the first watch glass., ii. dip the red litmus paper in the second watch glass., iii. add a drop of methyle organge to the third watch glass, and, iv. add a drop of phenolphthalein to the fourth watch glass., Observe the respective colour changes and note down in the chart, below., Table-1, S.No., 1, 2, 3, 4, 5, 6, 7, 8, 9, , Sample, solution, , Red litmus, paper, , Blue litmus, paper, , Phenolphthalein, solution, , Methyl, orange, solution, , HCl, H2SO4, HNO3, CH3COOH, NaOH, KOH, Mg(OH)2, NH4OH, Ca(OH)2, •, •, , What do you conclude from the observations noted in table-1?, Identify the sample as acidic or basic solution., There are some substances whose odour changes in acidic or basic, media. These are called olfactory indicators., Let us work with some of such indicators., 70, , X Class, , Acids, Bases and Salts
Page 81 :
Activity 2, -, , Put some finely chopped onions in a plastic bag along with some, clean cloth. Tie up the bag tightly and keep it overnight in the fridge., The cloth strips can now be used to test for acid or base., - Check the odour of the cloth strips., - Keep two strips on a clean surface and put a few drops of dilute, HCl on one strip and a few drops of dilute NaOH on the other., - Rinse both the strips separately with distilled water and again check, their odour and note the observation., - Take some clove oil and vanilla essence., - Take some dilute HCl in one test tube and dilute NaOH in another, test tube. Add a drop of dilute vanilla essence to both test tubes, and shake well. Check the odour and record your observations., - Test the change of odour with clove oil using dilute HCl and dilute, NaOH and record your observations., Suggest which of these- onion, vanilla essence and clove oil, can be, used as olfactory indicators on the basis of your observations., • What do you conclude from above activity?, • Can you give example for use of olfactory indicators in daily life?, Discuss with your teacher., Why pickles and sour substances are not stored in brass and copper, vessels?, , Reaction of Acids and bases with Metals, , Lab Activity, Delivery tube, Stand, Testing of hydrogen gas, HCl, , Test tube, , H2, , Zinc granules, , Soap water, Free distribution by A.P. Government, , fig-1:Reaction of zinc, granules with dil. HCl, and testing hydrogen gas, by a burning match stick, 71
Page 82 :
Materials required: test tube, delivery tube, glass trough, candle,, soap water, dil. HCl, and zinc granules., Procedure: Set the apparatus as shown in fig. 1., -, , Take about 10ml of dilute HCl in a test tube and add a few zinc, granules to it., , -, , What do you observe on the surface of the zinc granules?, , -, , Pass the gas being evolved through the soap water., , -, , Why are bubbles formed in the soap solution?, , -, , Bring a burning candle near the gas filled bubble., , -, , What do you observe?, , You will notice the gas evolved burns with a pop sound indicating H2 ., The chemical reaction of the above activity is:, Acid, , + Metal, , 2 HCl (aq) + Zn(s), , Salt, , +, , Zn Cl2 (aq) +, , Hydrogen, H2 (g), , Repeat the above experiment with some other acids like H2SO4 and, HNO3., • What do you observe in all these cases?, From the above activities you can conclude that when acid reacts with, metal H2 gas is evolved., Caution: This activity needs the teacher’s assistance., , Activity 3, Place a few granules of zinc metal in one of the test tubes and add, 10 ml of sodium hydroxide (NaOH) solution and warm the contents of the, test tube., Repeat the rest of the steps as in activity-2 and record your, observations., In this activity also you will notice that evolved gas is hydrogen (H2), and salt formed is sodium zincate., The reaction is written as follows., 2 NaOH + Zn, , Na2 ZnO2 + H2, (Sodium zincate), , However, such reactions are not possible with all metals., 72, , X Class, , Acids, Bases and Salts
Page 83 :
Reaction of carbonates and metal hydrogen carbonates with Acids, , Activity 4, •, , •, , Take two test tubes; label them as A and, B. Take about 0.5 gm of sodium, carbonate (Na2CO3) in test tube A and, about 0.5 gm of sodium hydrogen, carbonate (NaHCO3) in test tube B., Add about 2 ml of dilute HCl to both, the test tubes., , •, , What do you observe?, , •, , Pass the gas produced in each case, through lime water (calcium hydroxide, solution) as shown in Fig 2 and record, your observations., , Thistle, funnel, , Stand, , Delivery tube, Cork, , CO2 gas, Test tube, dil. HCl, acid, , Ca(OH)2, solution, Na2CO3, , fig-2: Passing CO2 gas through, Ca(OH)2 solution, , The reactions occurring in the above activities are as follows:, Na2 CO3 (S) + 2 HCl (aq), , 2 NaCl (aq) + H2O (l) + CO2 (g), , NaHCO3 (S) + HCl (aq), , NaCl (aq) + H2O (l) + CO2 (g), , Pass the gas evolved through lime water., Ca (OH)2 (aq) + CO2 (g), , CaCO3, , +, , H2O (l), , (White precipitate), , On passing excess carbon dioxide the following reaction takes places:, CaCO3 (S) + H2O (l) + CO2 (g), , Ca (HCO3)2 (aq), (Soluble in water), , Thus from above activities you can conclude that the reaction of metal, carbonates and hydrogen carbonates with acids give a corresponding salt,, carbon dioxide and water. We can write generalized form of these chemical, reactions as shown below:, metal carbonate + acid, , salt + carbon dioxide + water, , metal hydrogen carbonate + acid, Free distribution by A.P. Government, , salt + carbon dioxide + water, 73
Page 84 :
Neutralization reaction, , Activity 5, Acid – base (Neutralization) reaction, Take about 2 ml of dilute NaOH solution in a test tube and add one, drop of phenolphthalein indicator. Observe the colour of the solution., - Add dilute HCl solution to the above solution drop by drop. Is, there any change of colour of the solution?, • Why did the colour of the solution change after adding the HCl, solution?, - Now add one or two drops of NaOH to the above mixture., • Does the Pink colour reappear?, • Do you guess the reason for reappearance of pink colour?, In the above activity you observe that the pink colour disappears on, adding HCl because NaOH is completely reacted with HCl. The effect of, base is nullified by an acid. Pink colour reappears on adding a drop of, NaOH because the solution becomes basic once again. The reaction, occuring between acid and base in the above activity can be written as:, NaOH (aq) +, , HCl (aq), , NaCl (aq) + H2O (l), , The reaction of an acid with a base to give a salt and water is known as, a neutralization reaction. In general, a neutralization reaction can be written, as:, Base + Acid, Salt + Water, , Think and discuss, • Is the substance present in antacid tablet acidic or basic?, • What type of reaction takes place in stomach when an antacid tablet is consumed?, , Reaction of metal oxides with acids, , Acivity 6, •, •, 74, , X Class, , Take a small amount of copper oxide in a beaker and slowly add dilute, hydrochloric acid while stirring. Observe the changes in the solution., Note the colour of the solution., Acids, Bases and Salts
Page 85 :
•, , What do you observe in the above reaction?, You will notice that the copper oxide present in the beaker dissolves, in dilute HCl and the colour of the solution becomes blueish-green. The, reason for this change is the formation of copper (II) chloride in the, reaction. The general reaction between a metal oxide and an acid can be, written as:, Metal oxide + Acid, Salt + Water, Write the chemical equation for the reaction between copper oxide, and HCl and balance it., In above reaction metal oxide reacts with acid to give salt and water., This reaction is similar to the reaction of a base with an acid that we have, observed in activity - 5., • What do you conclude from the Activity-5 and 6?, In both the reactions salt and water are the products. Both metallic, oxides and metal hydrides give salt and water when they react with an acid., Thus we can conclude that metal oxides are basic in nature like the metal, hydroxides., , Reaction of a non-metal oxide with a base, You saw the reaction between carbon dioxide and calcium hydroxide, (lime water) in activity-4. Calcium hydroxide, which is a base, reacts with, carbon dioxide to produce a salt and water. This reaction is similar to the, reaction between a base and an acid. Thus we can conclude that carbon, dioxide which is a non metal oxide is acidic in nature. In general all nonmetal oxides are acidic in nature., , Think and discuss, • You are provided with three test tubes containing distilled water, an acid and a, base solution respectively. If you are given only blue litmus paper, how do you, identify the contents of each test tube?, • Which gas is usually liberated when an acid reacts with a metal? How will you, test for the presence of this gas?, • A compound of a calcium reacts with dilute hydrochloric acid to produce, effervescence. The gas evolved extinguishes a burning candle; turns lime water, milky. Write a balanced chemical equation for the reaction if one of the, compounds formed is calcium chloride., What do acids have in common?, In previous sections you have seen that acids have similar chemical, properties. In lab activity you have observed that acids generate hydrogen, gas on reacting with metals, so hydrogen seems to be common element to, Free distribution by A.P. Government, , 75
Page 86 :
all acids. Let us perform an activity to investigate whether all compounds, containing hydrogen are acids or not., , Activity 7, Prepare solutions of glucose, alcohol, hydrochloric acid and sulphuric, acid etc.,, Connect two different coloured electrical wires to graphite rods, separately in a 100 ml beaker as shown in figure., Connect free ends of the wire to 230 volts AC plug and complete the, circuit as shown in the fig-3 by connecting a bulb to one of the wires., Now pour some dilute HCl in the beaker and switch on the current., • What do you notice?, Repeat activity with dilute sulphuric acid and glucose and alcohol, solutions separately., AC plug, •, What do you observe?, 230 volt, Bulb, •, Does the bulb glow in all cases?, You will notice that the bulb glows only, in acid solutions but not in glucose and, alcohol solutions. Glowing of bulb indicates, that there is flow of electric current through, Beaker, the solution. Acid solutions have ions and the, moment of these ions in solution helps for, flow of electric current through the solution., dil. HCl solution, The positive ion (cation) present in HCl, Graphite rods, solution is H+. This suggests that acids, produce hydrogen ions H+ in solution, which, fig-3: Acid solution in water, conducts electricity, are responsible for their acidic properties. In, glucose and alcohol solution the bulb did not, glow indicating the absence of H+ ions in these solutions. The acidity of, acids is attributed to the H+ ions produced by them in solutions., , Properties of Bases, What do Bases have in common?, Repeat the Activity-7 using alkalis such as sodium hydroxide, calcium, hydroxide solutions etc., instead of acid solutions., • Does the bulb glow?, • What do you conclude from the results of this activity?, , 76, , X Class, , Acids, Bases and Salts
Page 87 :
Do acids produce ions only in aqueous solution? Let us test this., , Activity 8, , •, , - Take about 1.0g of solid NaCl in a clean and dry test tube., - Add some concentrated sulphuric acid to the test tube., What do you observe? Is there a gas coming out of the delivery tube?, Let us write chemical equation for the above reaction., 2NaCl(s) + H2SO4(l), , 2HCl(g), , + Na2SO4(s), , Test the gas evolved successively with dry and wet blue litmus paper., In which case does the litmus paper change colour?, • What do you infer from the above observation?, You can conclude that dry HCl gas (Hydrogen chloride) is not an acid, because you have noticed that there is no change in colour of dry litmus, paper but HCl aqueous solution is an acid because wet blue litmus paper, turned into red., Note to teachers: If the climate is very humid, pass the gas produced, through a guard tube (drying tube) containing calcium chloride to dry the, gas., • Can you write the chemical equation for the reaction taking place at, the mouth of delivery tube?, , Moist litmus paper, , Conical flask, containing, conc H2SO4, , Test tube, , Delivery tube, Cork, Test tube, , NaCl, , fig-4: Preparation of HCl gas, , The HCl gas evolved at delivery tube dissociates in presence of water, to produce hydrogen ions. In the absence of water dissociation of HCl, molecules do not occur., Free distribution by A.P. Government, , 77
Page 88 :
The dissociation of HCl in water is shown below., HCl + H2O, , H3O+ + Cl-(aq), , Hydrogen ions cannot exist as bare ions. They associate with water, molecules and exist as as hydrated ions with each H+ attached by 4 to 6, water molecules. For this we represent H+ as hydronium ion, H3O+., H+ + H2O, , H3O+, , You have learnt that acids give H3O+ or H+ (aq) ion in water., Let us see what happens when a base is dissolved in water., H2O, , NaOH (s), , –––––, , KOH (s), , –––––, , H2O, , H2O, , Mg (OH) 2(s) –––––, , Na + (aq) + OH – (aq), K + (aq) + OH – (aq), Mg2 (aq) + 2OH – (aq), , On dissolving bases in water produces hydroxide (OH-) ions. Bases, which are soluble in water are called alkalis. All bases donot dissolve in, water. Be(OH)2 is slightly soluble in water., , What do you observe when water is mixed with acid or base?, , Activity 9, - Take 10 ml water in a test tube., - Add a few drops of concentrated H2SO4 to it and swirl the test tube slowly., - Touch the bottom of the test tube., • What do you feel?, • Is it an exothermic or endothermic process?, Carry out the above activity with sodium hydroxide, pellets instead of H2SO4 and record your observation., The process of dissolving an acid or a base in water is, an exothermic process. Care must be taken while mixing, concentrated nitric acid or sulphuric acid with water. The, acid must always be added slowly to water with constant, stirring. If water is added to a concentrated acid, the heat, generated may cause the mixture to splash out and cause, fig-5: Warning sign, displayed on containers, burns. The glass container may also break due to excessive, containing concentrated, local heating. Look out for the warning sign (shown in, Acids and Bases, 78, , X Class, , Acids, Bases and Salts
Page 89 :
Fig.5) on the can of concentrated sulphuric acid and on the bottle of sodium, hydroxide pellets., Mixing an acid or base with water result in decrease in the concentration, of ions (H3O +/OH– ) per unit volume. Such a process is called dilution, and the acid or the base is said to be diluted., , Think and discuss, •, •, , Why do HCl, HNO3 etc., show acidic characters in aqueous solutions while, solutions of compounds like alcohol and glucose do not show acidic character?, While diluting an acid, why is it recommended that the acid should be added to, water and not water to the acid?, , Can you decide the strength of an acid or base solutions?, Let us find., , Strength of acid or base:, , Activity 10, A test to know whether the Acid is strong or weak., - Take two beakers A and B., - Fill the beaker A with dil. CH3 COOH (acetic acid) and beaker B, with dil. HCl (Hydrochloric Acid), - Arrange the apparatus as used in activity-7, and pass electric current, through the solutions in separate beakers., • What do you observe?, • Can you guess the reason for the changes you observed?, You notice that the bulb glows brightly in HCl solution while the, intensity of the bulb is low in acetic acid solution. This indicates that there, are more ions in HCl solution and fewer ions are present in acetic acid, solution. More ions in HCl solution mean more H3O+ions.Therfore it is a, strong acid. Whereas acetic acid has fewer H3O+ions and hence it is weak, acid., Carry out the above experiment by taking bases like dil. NaOH (sodium, hydroxide) and dil. NH4OH (ammonium hydroxide) instead of acids., • What do you observe? Explain your observations., The universal indicator can also be used to know the strength of acid, or base. Universal indicator is a mixture of several indicators. The universal, indicator shows different colours at different concentrations of hydrogen, ions in a solution., Free distribution by A.P. Government, , 79
Page 90 :
pH scale, A scale for measuring hydrogen ion concentration in a solution is called, pH scale. (The ‘p’ in pH stands for ‘Potenz’ German ‘Potenz’ is power)., pH value of a solution is simply a number which indicates the acidic or, basic nature of a solution., The pH of neutral solutions is 7. Values less than 7 on the pH scale, represent an acidic solution. As the pH value increases from 7 to 14, it, represents a decrease in H3O+ ion concentration or an increase in OH– ion, concentration in the solution. pH value of a solution above ‘7’ represents, a basic solution., Observe the following figure., , Activity 11, •, 80, , X Class, , Test the pH value of solutions given in table using pH paper., Record your observations in column three of Table – 2., Write approximate pH values in column 4 using Universal Indicator, solution., What is the nature of each substance on the basis of your observations?, Acids, Bases and Salts
Page 91 :
Table-2, S.No., , Solution, , Colour pH, paper, , 1, , HCl, , 2, , CH3COOH, , 3, , NH4Cl, , 4, , CH3COONa, , 5, , NaHCO3, , 6, , Na2CO3, , 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, , NaOH, Distilled water, Lemon juice, Carrot juice, Coffee, Tomato juice, Tap water, Banana juice, Colourless aerated drink, Saliva (before meal), Saliva (after meal), , ACID, strong, , NEUTRAL, weak, , weak, , Approximate, pH value, , Nature of, substances, , ALKALI, strong, , fig -7: pH value as shown by different colour in universal indicator, , The strength of acid or base depends on the concentraction of H3O+, ions or OH– produced in solution. If we take hydrochloric acid and acetic, acid of the same concentration then they produce different concentration, of hydrogen ions. Acids that give more H3O+ ions are said to be strong, acids that give fewer H3O+ ions are said to be weak acid. Can you now, predict what weak and strong bases are?, Free distribution by A.P. Government, , 81
Page 92 :
Do you know?, To avoid the negative powers, of H+ concentration in dilute acid, and base solutions Sorensen, introduced the concept of pH. Due, to this pH concept may be, restricted for solutions of [H+], less than 1 molar., The pH scale is from 0-14., The pH is an indication of, concentration of H+. For example,, at a pH of zero the hydronium ion, concentration is one molar., Typically the concentrations of H+, in water in most solutions fall, between a range of 1 M (pH=0), and 10-14 M (pH=14). Figure 8, depicts the pH scale with common, solutions., , battery acid, , lemon juice, , pure rain (H2O in, equilibrium with, atmospheric CO2, freshly, distilled water, , gastric fluid, carbonated, beverages, vinger, orange juice, beer, coffee, egg yolks, milk, blood, , seawater, baking soda, (NaHCO3 solution), household, ammonia (NH3), household bleach, (NaClO solution), household lye, (NaOH solution), , milk of, magnesia, [Mg(OH)2], solution, , fig -8: Solutions and the, placement of them on pH, scale, , Importance of pH in everyday life, 1. Are plants and animals pH sensitive?, Living organisms can survive only in a narrow range of pH change., When pH of rain water is less than 5.6, it is called acid rain. When acid, rain flows in to the rivers, it lowers the pH of the river water, the survival, of aquatic life in such rivers becomes difficult., , Think and discuss, •, •, 82, , What will happen if the pH value in our body increases?, Why do living organism have narrow pH range?, X Class, , Acids, Bases and Salts
Page 93 :
2. Is pH change cause of tooth decay?, Tooth decay starts when the pH of the mouth is lower than 5.5. Tooth, enamel, made of calcium phosphate is the hardest substance in the body., It does not dissolve in water, but is corroded when the pH in the mouth is, below 5.5. Bacteria present in the mouth produce acids by degradation of, sugar and food particles remaining in the mouth. The best way to prevent, this is to clean the mouth after eating food. Using tooth pastes, which are, generally basic neutralize the excess acid and prevent tooth decay., , 3. pH in our digestive system:, It is very interesting to note that our stomach produces hydrochloric, acid. It helps in the digestion of food without harming the stomach. During, indigestion the stomach produces too much acid and this causes pain and, irritation. To get rid of this pain, people use bases called antacids. These, antacids neutralize the excess acid in the stomach. Magnesium hydroxide, (milk of magnesia), a mild base, is often used for this purpose., , Activity 12, -, , •, •, , Take dil. HCl in a beaker and add two to three drops methyl orange, indicator. Note the colour of the solution, - Mix antacid tablet powder to the above solution in the beaker. Now, observe the change in colour of solution., What is the reason for the change in colour of solution?, Can you write the chemical equation for this reaction?, , 4. pH of the soil, Plants require a specific pH range for their healthy growth. To find, out the pH required for the healthy growth of a plant, you can collect the, soil samples from various places and check the pH in the manner described, below in the following activity. Also you can note down what type of, plants are growing in the region from which you have collected the soil., , Activity 13, Put about 2g soil in a test tube and add 5ml water to it. Shake the, contents of the test tube. Filter the contents and collect the filtrate in a, test tube., Check the pH of this filtrate with the help of universal indicator paper., • What can you conclude about the ideal soil pH for the growth of plants, in your region?, • Under what soil conditions a farmer would treat the soil of his fields, with quicklime (calcium hydroxide) or calcium carbonate?, Free distribution by A.P. Government, , 83
Page 94 :
Self defense by animals and plants through chemical war fare?, Have you ever been stung by a honey-bee? Bee sting leaves an acid, which causes pain and irritation. Use of a mild base like baking soda on, the stung area gives relief. Stinging hair of leaves of nettle plant, inject, methanoic acid causing burning pain., • A traditional remedy is rubbing the area with the leaf of the dock plant,, which often grows besides the nettle in the wild., , More about salts, In the previous sections you have studied the formation of salts by the, neutralization reaction of base with an acid. Let us understand more about, the preparation, properties and uses of salts., , Family of salts, , Activity 14, -, , •, , Write the formulae of the following salts., Potassium sulphate, sodium sulphate, calcium sulphate, magnesium, sulphate, copper sulphate, sodium chloride, sodium nitrate, sodium, corbonate and ammonium chloride., - Identify the acids and bases from which the above salts are obtained., - Salts having the same positive or negative radicals belong to a, family. For example, NaCl and Na2SO4 belong to the family of, sodium salts. Similarly, NaCl, and KCl belong to the family of, chloride salts., How many families can you identify among the salts given above?, , pH of Salts, , Activity 15, -, , 84, , X Class, , Collect the salt samples like, sodium chloride, aluminum chloride,, copper sulphate, sodium acetate, ammonium chloride, sodium, hydrogen carbonate and sodium carbonate., Dissolve them in distilled water., Check the action of these solutions with litmus papers., Find the pH using pH paper (universal indicator)., Classify them into acidic, basic or neutral salts?, Identify the acid and base used to form the above salts., Record your observations in Table - given below., Acids, Bases and Salts
Page 95 :
Salt, , pH, , Acidic, , Basic, , Neutral, , Salt of a strong acid and a strong base are neutral and the pH value is 7., The salts of a strong acid and weak base are acidic and the pH value is less, than 7. The salts of a strong base and weak acid are basic in nature and the, pH value is more than 7., • What do you say about salts of both weak acid and weak base?, In such cases the pH depends on the relative strengths of acid and, base., , Chemicals from common salt, Salts are the ionic compounds which are produced by the neutralization, of acid with base. Salts are electrically neutral. There are number of salts, but sodium chloride is the most common among them. Sodium chloride, is also known as table salt or common salt. Sodium chloride is used to, enhance the taste of food., Sea water contains many salts dissolved in it. Sodium chloride is the, predominant component and it is separated from these salts. Deposits of, solid salt are also found in several parts of the world. These deposits of, large crystals are often brown due to impurities. This is called rock salt., Beds of rock salt were formed when seas of bygone ages dried up. Rock, salt is mined like coal., , Common salt – A raw material for chemicals, The common salt is an important raw material for various materials of, daily use, such as sodium hydroxide, baking soda, washing soda, bleaching, powder and many more. Let us see how one substance is used for making, all these different substances., , Sodium hydroxide from common salt, When electricity is passed through an aqueous solution of sodium, chloride (called brine), it decomposes to form sodium hydroxide. The, process is called the chlor-alkali process – because of the products formed, chlor for chlorine and alkali for sodium hydroxide., Free distribution by A.P. Government, , 85
Page 96 :
Do you know?, Salt – a symbol of freedom struggle: You, know common salt as a substance which enhances, the taste of food; it also has played a remarkable, role in motivating the people towards freedom, struggle. The tax levied by the British government, on common food substance (salt), for both the, poor and the rich, made them to become unite in, the freedom struggle., You must have heard about Mahatma Gandhi’s, Dandi March and about ‘salt satyagraha’ in the, struggle for freedom of India., , at Anode, , at Cathode, , H2, , Fuels, margarine,, ammonia for fertilisers, , Cl2, , NaOH, , Water treatment, swimming pools, PVC,, disinfectants, CFC’s, pesticides, , HYDROCHLORIC ACID, For: cleaning steel, ammonium chloride, medicines, cosmetics, , De-greasing metals, soaps and detergents,, paper making, artificial fibres, , BLEACH (CaOCl2), For: household bleahes, bleaching fabric, , fig-9: Important product from chlor-alkali process, , 2 NaCl ( aq) + 2H2O (l), 2 NaOH (aq) + Cl2 (g) + H2 (g), Chlorine gas is given off at the anode and hydrogen gas at the cathode,, sodium hydroxide solution is formed near the cathode the three products, produced in this process are all useful Fig. shows the different uses of, these products., , Bleaching Powder, You know that chlorine is produced during the electrolysis of aqueous, sodium chloride (brine). This chlorine gas is used for the manufacture of, 86, , X Class, , Acids, Bases and Salts
Page 97 :
bleaching powder. Bleaching power is produced by the action of chlorine, on dry slaked lime [Ca(OH)2]. Bleaching powder is represented by formula, CaOCl2, though the actual composition is quite complex., Ca (OH)2 + Cl2, 1., , 2., 3., 4., , CaOCl2 + H2O, , Uses of Bleaching Powder:, It is used for bleaching cotton and linen in the textile industry for, bleaching wood pulp in paper industry and for bleaching washed clothes, in laundry., Used as an oxidizing agent in many chemical industries., Used for disinfecting drinking water to make it free of germs., Used as a reagent in the preparation of chloroform., , Baking soda, Baking soda is sometimes added for faster cooking. The chemical, name of the compound is sodium hydrogen carbonate (NaHCO3). It is, prepared as follows:, NaCl + H2O + CO2 + NH3, , NH4 Cl + NaHCO3, , Can you find the pH of sodium hydrogen carbonate as you have done, in activity-14? Can you predict the reason for using NaHCO3 to neutralize, an acid?, Baking soda is a mild non-corrosive base., The following reaction takes place when it is heated during cooking., Heat, , 2NaHCO3 –––––, , Na2CO3 + H2O+CO2, , Uses of sodium hydrogen carbonate, i) Baking powder is a mixture of baking soda and a mild edible acid such, as tartaric acid. When baking powder is heated or mixed in water, the, following reaction takes place., NaHCO3 + H+, , CO2 + H2O + sodium salt of acid., , Carbon dioxide produced during the reaction causes bread or cake to, rise making them soft and spongy., ii) Sodium hydrogen carbonate is also an ingredient in antacids. Being, alkaline, it neutralizes excess acid in the stomach and provides relief., iii) It is also used in soda-acid fire extinguishers, iv) It acts as mild antiseptic., Free distribution by A.P. Government, , 87
Page 98 :
Washing soda (sodium carbonate), Another chemical that can be obtained from sodium chloride is, Na2CO3. 10 H2O(washing soda). You have seen above that sodium, carbonate can be obtained by heating baking soda. Recrystallisation of, sodium carbonate gives washing soda. It is also a basic salt., Na2 CO3 + 10 H2O, , Na2 CO3 .10 H2O, , Sodium carbonate and sodium hydrogen carbonate are useful, chemicals for many industrial processes., , Uses of Washing soda, i) Sodium carbonate (washing soda) is used in glass, soap and paper, industries., ii) It is used in the manufacture of sodium compounds such as borax., iii) Sodium carbonate can be used as a cleaning agent for domestic, purposes., iv) It is used for removing permanent hardness of water., • What does 10 H2O signify?, • Does it make Na2CO3 wet?, • Are the crystals of salts really dry?, Let us find, Removing water of crystallisation, , Activity 16, - Take a few crystals of copper sulphate in a dry test tube and heat, the test tube., - What change did you, notice in the colour of the copper, sulphate after heating?, Test tube holder, Boiling, Water droplets, tube, • Did you notice water droplets, Copper sulphate, on sides of the test tube?, crystals, Where did they come from?, Burner, Add 2-3 drops of water on the, sample of copper sulphate obtained, after heating., • What do you observe? Is the, blue colour of copper sulphate, fig-10: Removing water of, restored?, crystallisation, , 88, , X Class, , Acids, Bases and Salts
Page 99 :
In the above activity copper sulphate crystals which seem to be dry, contain the water of crystallization, when these crystals are heated, water, present in crystals is evaporated and the salt turns white., When the crystals are moistened with water, the blue colour reappears., Water of crystallization is the fixed number of water molecules present, in one formula unit of a salt. Five water molecules are present in one, formula unit of copper sulphate. Chemical formula for hydrated copper, sulphate is CuSO4.5 H2O., Now you would be able to answer the question whether the molecule, of Na2 CO3. 10 H2O is wet or not., Another salt which possesses water of crystallisation is gypsum. It has, two water molecules in its crystals and the formula is CaSO4. 2H2O., Let us see the use of this salt., , Plaster of paris (CaSO4 ½ H2O), On careful heating of gypsum (CaSO4 2 H2O) at 373 K it loses water, molecules partially to become calcium sulphate hemihydrate, (CaSO4.½ H2O). This is called plaster of paris, the substance which, doctors use as plaster for supporting fractured bones in the right position., Plaster of paris is a white powder and on mixing with water, it sets into, hard solid mass due to the formation of gypsum., CaSO4. ½ H2O +, (Plaster of Paris), , 1½ H2O, , CaSO4. 2H2O, (Gypsum), , Note: You might have noticed that only half a water molecule is shown, to be attached as water of crystalisation., •, , How can you get half a water molecule?, , It is written in this form because two formula units of CaSO4 share, one molecule of water., Plaster of paris is used for making toys, materials for decoration and, for making surfaces smooth., •, , Try to collect the information for calling calcium sulphate hemihydrates, as Plaster of Paris., , Free distribution by A.P. Government, , 89
Page 100 :
Key words, Indicator, Acid, Base, Red litmus, Blue litmus, Phenolphthalein,, Methyl orange, Salts, Neutralization, Guard tube, Hydronium ion,, Alkali, Strong acid, Strong base, Universal indicator, pH scale,, Potenz, Antacids, tooth decay, Family of Salts, Common salt, Bleaching, powder, Baking soda, Washing soda,Hydrated salt, Water of, crystallization, Plaster of Paris., , What we have learnt, •, •, •, •, •, •, •, •, •, •, •, •, , Acid – base indicators are dyes or mixtures of dyes which are used to indicate the presence of, acids and bases., Acidic nature of a substance is due to the formation of H+ (aq) ions in solution. Formation of, OH- (aq) ions in solution is responsible for the basic nature of a substance., When a base reacts with a metal with the evolution of hydrogen gas, a salt is formed., When an acid reacts with a metal carbonate or metal hydrogen carbonate gives the corresponding, salt, carbon dioxide gas and water., Acidic and basic solutions in water conduct electricity because they produce hydrogen ions and, hydroxide ions respectively., The strength of an acid or an alkali can be tested by using a scale called the pH scale (0-14), which gives the measure of hydrogen ion concentration in a solution., A neutral solution has a pH of 7, while an acidic solution has a pH less than 7 and a basic, solution has a pH more than 7., Living beings carry out their metabolic activities within an optimal pH range., Mixing concentrated acids or bases with water is a highly exothermic process., Acids and bases neutralize each other to form corresponding salts and water., Water of crystallization is the fixed number of water molecules chemically attached to each, formula unit of a salt in its crystalline form., Salts have various uses in everyday life and in industries., , Improve your learning, 1. Five solutions A, B, C, D and E when tested with universal indicator showed pH as 4, 1, 11, 7, and 9, respectively, which solution is (AS1), (a) neutral (b) strongly alkaline (c) strongly acidic (d) weakly acidic (e) weakly alkaline, Arrange the pH in increasing order of hydrogen ion concentration., 90, , X Class, , Acids, Bases and Salts
Page 101 :
2. What is a neutralization reaction? Give two examples. (AS1), 3., 4., 5., 6., , What happens when an acid or base is mixed with water? (AS1), Why does tooth decay start when the pH of mouth is lower than 5.5? (AS1), Why does not distilled water conduct electricity? (AS2), Dry hydrogen chloride gas does not turn blue litmus to red whereas hydrochloric acid does., Why? (AS1), 7. Why pure acetic acid does not turn blue litmus to red? (AS2), 8. A milkman adds a very small amount of baking soda to fresh milk. (AS2), a) Why does he shift the pH of the fresh milk from 6 to slightly alkaline?, b) Why does this milk take a long time to set as curd?, 9. Plaster of Paris should be stored in moisture – proof container. Explain why? (AS2), 10. Fresh milk has a pH of 6. Explain why the pH changes as it turns into curd? (AS3), 11. Compounds such as alcohols and glucose contain hydrogen but are not categorized as acids., Describe an activity to prove it. (AS3), 12. What is meant by “water of crystallization” of a substance? Describe an activity to show the, water of crystallisation. (AS3), 13. Equal lengths of magnesium ribbons are taken in test tubes A and B. Hydrochloric acid is, added to test tube A, while acetic acid is added to test tube B. Amount and concentration of, both the acids is same. In which test tube will the fizzing occur more vigorously and why?, (AS4), 14. Draw a neat diagram showing acid solution in water conducts electricity. (AS5), 15. How do you prepare your own indicator using beetroot? Explain. (AS5), 16. How does the flow of acid rain into a river make the survival of aquatic life in a river difficult?, (AS7), 17. What is baking powder? How does it make the cake soft and spongy? (AS7), 18. Give two important uses of washing soda and baking soda. (AS7), , ks, Fill in the blan, 1. i., , ____________ taste is a characteristic property of all acids in aqueous solution., , ii. Acids react with some metals to produce _____________ gas., iii. Because aqueous acid solutions conduct electricity, they are identified as ________, iv. Acids react with bases to produce a ________ and water., v. Acids turn ____________ different colours., 2. i. Bases tend to taste _____________ and feel ____________, ii. Like acids, aqueous basic solutions conduct _____, and are identified as______., iii. Bases react with ______________ to produce a salt and ______________., iv. Bases turn _________________ different colours., Free distribution by A.P. Government, , 91
Page 102 :
3. Match the following:, a) Plaster of Paris, b) Gypsum, c) Bleaching powder, d) Baking soda, e) Washing soda, , (, (, (, (, (, , ), ), ), ), ), , 1), 2), 3), 4), 5), , CaO Cl2, NaHCO3, Na2 CO3, CaSO4 . ½ H2O, CaSO4 . 2 H2O, , s, Multiple choice question, 1. The colour of methyl orange indicator in acidic medium is …………, , [, , ], , a) yellow, b) green, c) orange, d) red, 2. The colour of phenolphthalein indicator in basic solution is …………, [, ], a) yellow, b) green, c) pink, d) orange, 3. Colour of methyl orange in alkali conditions?, [, ], a) orange, b) yellow, c) red, d) blue, 4. A solution turns red litmus blue, its pH is likely to be …………, [, ], a) 1, b) 4, c) 5, d) 10, 5. A solution reacts with crushed egg-shells to give a gas that turns lime-water milky the solution, contains ………………, [, ], a) NaCl, b) HCl, c) LiCl, d) KCl, 7. If a base dissolves in water by what name is it better known?, [, ], a) neutralization b) basic, c) acid, d) alkali, 8. Which of the following substances when mixed together will produce table salt?, [, ], a) Sodium thiosulphate and sulphur dioxide, b) Hydrochloric acid and sodium hydroxide, c) Chlorine and oxygen, d) Nitric acid and sodium hydrogen carbonate, 9. What colour would hydrochloric acid (pH=1) turn universal indicator?, [, ], a) orange, b) purple, c) yellow, d) red, 10. Which one of the following types of medicines is used for treating indigestion?, [, ], a) antibiotic, b) analgesic, c) antacid, d) antiseptic, 11. What gas is produced when magnesium is made to react with hydrochloric acid? [, ], a) hydrogen, b) oxygen, c) carbon dioxide, d) no gas is produced, 12. Which of the following is the most accurate way of showing neutralization?, [, ], a) Acid + base, acid-base solution, b) Acid + base, salt + water, c) Acid + base, sodium chloride + hydrogen, d) Acid + base, neutral solution, 92, , X Class, , Acids, Bases and Salts
Page 103 :
Chapter, , 5, Refraction of Light at, Plane Surfaces, We have learnt about the reflection of light in an earlier chapter. Beauty, of the nature is made apparent with light. Light exhibits many interesting, phenomena., Let us try to explore a few of them., You might have observed that a coin kept at the bottom of a vessel, filled with water appears to be raised. Similarly, a lemon kept in a glass of, water appears to be bigger than its size. When a thick glass slab is placed, over some printed letters, the letters appear raised when viewed through, the glass slab., • What could be the reasons for the above observations?, , Activity 1, Take some water in a glass tumbler. Keep a pencil in it. Look at the, pencil from one side of the glass and also from the top of the glass., • How does it look?, • Do you find any difference between the two views?, , Activity 2, Go to a long wall (of length about 30 feet) facing the Sun. Go to one, end of a wall and ask your friend to bring a bright metal object near the, other end of the wall. When the object is a few inches from the wall it, appears distorted and you will see a reflected image in the wall as though, the wall were a mirror., • Why is there an image of the object on the wall?, To answer the above questions and to give reasons for the situations, mentioned we need to understand the phenomenon of refraction of light., Free distribution by A.P. Government, , 93
Page 104 :
Refraction, , Activity 3, , Eye, , Eye, , Eye, , 94, , Take a shallow vessel with opaque walls such as a mug. (A tin or a pan, is suitable). Place a coin at the bottom of the vessel. Move away from the, vessel until you cannot see the coin. See figure 1(b). Stand there. Ask your, friend to fill the vessel with water. When the vessel is filled with water the, coin comes back into view. See figure 1(c)., • Why are you able to see the coin when the, vessel is filled with water?, Light ray, You know that the ray of light originating, from the coin, doesn’t reach your eye when the, Opaque, vessel is empty (see figure1b). Hence you, walls, couldn’t see the coin. But the coin becomes, Coin, visible to you after the vessel is filled with, fig-1(a), water., • How is it possible?, • Do you think that the ray reaches your eye, Light ray, when the vessel is filled with water?, If yes, draw a ray diagram from the coin to, the eye. Keep in mind that the light ray travelling, Opaque, in a medium takes a straight line path., walls, Coin, •What happens to the light ray at the interface, fig-1(b), between water and air?, •What could be the reason for this bending of, the light ray in the second instance?, Light ray, The above questions can be answered by, Fermat’s principle, which states that the light, ray always travels between two points in a path, Water, Opaque which needs the shortest possible time to cover., walls, Let us apply this principle to our activity., Coin, By observing the path of the ray, it is clear, fig-1(c), that the light ray changes its direction at the, interface separating the two media i.e, water and air. This path is chosen by, the light ray so as to minimize time of travel between coin and eye. This is, possible only if the speed of the light changes at interface of two media., Thus we can conclude that the speed of the light changes when light, propagates from one medium to another medium., X Class, , Refraction at Plane Surfaces
Page 105 :
“The process of changing speed at an interface when light travels from, one medium to another resulting in a change in direction is refraction of, light. The process of refraction involves bending of light ray except when, it is incident normally”., N, Consider that light travels from medium 1with, NN-normal, V1, speed v1 to medium 2 with speed v2 as shown in, figures 2(a) and (b)., Rarer, • What difference do you notice in fig 2(a) and, Interface, Fig 2(b) with the respect to refracted rays?, • Is there any relation between behaviour of, V2, refracted rays and speeds of the light?, Denser, Experiments have showed that refraction, N, occurs due to change in the speed of the light in, fig-2(a), the medium., N, If v2 is less than v1 then medium 2 is said to be, V1, denser with respect to medium 1., Denser, If v2 is greater than v1 then medium 2 is said to, be rarer with respect to medium 1., If light ray enters from rarer medium to denser, medium then refracted ray moves towards the, normal drawn at the interface of separation of two, Rarer, V2, media. When it travels from denser medium to, fig-2(b), rarer medium it bends away from normal. We have, N, seen that the ray of light deviates from its path at, the interface. Draw a normal at the point of, incidence as shown in figure (3)., N, Let ‘i’ be the angle made by incident ray with, normal and r be the angle made by refracted ray with, the normal. These angles are called angle of, i, incidence and angle of refraction respectively., To explain the process of refraction we need to, know about a constant called refractive index which, r, is the property of a transparent medium. Let us learn, about it., fig-3, Free distribution by A.P. Government, , N, 95
Page 106 :
The extent of the change in direction that takes place when a light ray, propagates through one medium to another medium is expressed in terms, of refractive index., , Refractive index, Light travels in vacuum with a speed nearly equal to 3x108 m/s (denoted, by letter ‘c’). The speed of light is smaller than ‘c’ in other transparent, media., Let ‘v’ be the speed of light in a certain medium. Then the ratio of, speed of light in vacuum to the speed of light in that medium is defined as, refractive index ‘n’. It is called absolute refractive index., Absolute refractive index = Speed of light in vacuum/ Speed of light, in medium., n = c/v, ...............(1), It is a dimensionless quantity because it is a ratio of the same physical, quantities. Refractive index gives us an idea of how fast or how slow light, travels in a medium. The speed of light in a medium is low when refractive, index of the medium is high and vice versa. The refractive index ‘n’ means, that the speed of light in that medium is nth part of speed of light in vacuum., For example the refractive index of glass is 3/2 .Then the speed of, light in glass is (2/3) of 3 x108 m/s equal to 2 x108 m/s., Table:1 Refractive indices of some material media., Material medium Refractive index Material medium Refractive index, Air, 1.0003, Canada balsam, 1.53, Ice, 1.31, Rock salt, 1.54, Water, 1.33, Carbon Diasulphide, 1.63, Kerosene, 1.44, Dense flint glass, 1.65, Fused quartz, 1.46, Ruby, 1.71, Turpentine oil, 1.47, Sapphire, 1.77, Crown glass, 1.52, Diamond, 2.42, Benzene, 1.50, Note : From table 1, you know that an optically denser medium may, not possess greater mass density. For example, kerosene with high, refractive index is optically denser than water although its mass density is, less than water., • Why do different material media possess different values of refractive, Indices?, 96, , X Class, , Refraction at Plane Surfaces
Page 107 :
•, , On what factors does the refractive index of a medium depend?, Refractive index depends on the following factors., (1) nature of material (2) wavelength of light used. (You will learn, about this in the chapter Human-eye-and Colourful world), , Relative refractive index, The refractive index of a medium with respect to another medium is, defined as the ratio of speed of light in the first medium to the speed of, light in the second medium. Let v1 and v2 be the speeds of light in the first, and second media respectively. Then,, Refractive index of second medium with respect to first medium is, given by, n21 = speed of light in medium -1 / speed of light in medium – 2, n21 = v1/v2, Dividing both numerator and denominator by c we get, n21 = ( v1/c) / ( v2/c) = (1/ n1 ) /(1/ n2 ), D n21 = n2 / n1, ....................(2), This is called relative refractive Index. We define relative Refractive, index as follow, Refractive index of second medium ( n2 ), Relative refractive index, ( n21 ) =, Refractive index of first medium ( n1 ), , Lab Activity 1, Aim: Obtaining a relation between angle of incidence and angle of, refraction., Materials required: A plank, white chart, protractor, scale, small black, painted plank, a semi circular glass disc of thickness nearly 2cm, pencil, and laser light., Procedure, Take a wooden plank which is covered with white, chart. Draw two perpendicular lines, passing through, the middle of the paper as shown in the figure 4(a)., Let the point of intersection be O. Mark one line as, NN which is normal to the another line marked as, MM. Here MM represents the line drawn along the, interface of two media and NN represents the normal, drawn to this line at ‘O’., Free distribution by A.P. Government, , fig-4(a), 97
Page 108 :
Take a protractor and place it along NN in such, way that its centre coincides with O as shown in, figure 4(a). Then mark the angles from 00 to 900 on, both sides of the line NN as shown in figure 4(a)., Repeat the same on the other side of the line NN., The angles should be indicated on the curved line., Now place a semi-circular glass disc so that its, diameter coincides with the interface line (MM) and, fig-4(b), its center coincides with the point O. Point a laser, light along NN in such a way that the light propagates from air to glass, through the interface at point O and observe the path of laser light coming, from other side of disc as shown in figure 4 (b). (If you cannot observe the, path of laser light put a black-coloured plank against the curved line and, observe the light point and imagine the light path)., • Is there any deviation?, Send Laser light along a line which makes150 (angle of incidence), with NN and see that it passes through point O. Measure its corresponding, angle of refraction, by observing laser light coming from the other side, (Circular side) of the glass slab. Note these values in table (2). Do the, same for the angles of incidence such as 200,300,400,500 and 600 and note, the corresponding angles of refraction., Table 2, i, , r, , Sin i, , Sin r, , Sin i / Sin r, , Find sin i, sin r for every ‘i’ and ‘r’ and evaluate sin i/ sin r for every, incident angle ‘i’., Note : Take the help of your teacher to find the values of sin i and, sin r for each case., Finally, we will get the ratio sin i / sin r as a constant., • Is this ratio equal to refractive index of glass? Why?, This ratio gives the value of refractive index of glass. In the above, experiment you might have noticed that ‘r’ is less than ‘i’ in all cases and, the refracted ray bends towards normal in each case., • What do you conclude from these observations?, 98, , X Class, , Refraction at Plane Surfaces
Page 109 :
From the above experiment we can conclude that when light ray travels, from a rarer medium (air) to a denser medium (glass) the value of r is less, than the value of ‘i’ and the refracted ray bends towards the normal., • Can you guess what happen when light ray travels from a denser medium, to a rarer medium?, Let us take up another activity to find this., , Actitivy 4, Take a metal disk. Use a protractor and mark, angles along its edge as shown in the figure 5(a)., Arrange two straws at the centre of the disk in such, a way that they can be rotated freely about the, centre of the disc., Adjust one of the straws to make an angle 100., Immerse half of the disc vertically into the water,, filled in a transparent vessel. While dipping, verify, that the straw at 100 is inside the water. From the, top of the vessel try to view the straw which is inside, the water as shown in figure 5(b). Then adjust the, other straw which is outside the water until both, straws appear to be in a single straight line., Then take the disc out of the water and observe, the two straws on it. You will find that they are not, in a single straight line., •, , fig-5(a), , Straw, , Straw, , fig5(b), , Why do the straws appear to be in a straight, line when we view them from the top?, , Measure the angle between the normal and second straw. Draw table, (2) again in your notebook and note the value. Do the same for various, angles. Find the corresponding angles of refraction and note them in the, table drawn. Use the data in the table and find refractive index of water. Do, not take up this activity for angles of incidence greater than 48 degrees., You will learn the reasons for this in the following sections., You will observe that in the above activity, ‘r’ is greater than ‘i’ in all, cases that means when light travels from water (denser) to air (rarer). It, behaves in an opposite way to that we observed in lab activity 1., Free distribution by A.P. Government, , 99
Page 110 :
time t, , From this activity we can generalize that when the light ray travels, from denser to rarer, it bends away from the normal and r > i., • Can we derive the relation between the angle of incidence and the, angles of refraction theoretically?, Consider the following analogy to derive it., Let us imagine that a person has fallen out of boat and is screaming, for help in the water at point B as shown in figure 6(a)., The line marked through point ‘X’ is the shore, A, line. Let us assume that we are at a point ‘A’ on the, the shore and we saw the accident. In order to save, X, the person we need to travel a certain distance on, land and a certain distance in water. We know that,, B, we can run faster on land than we can swim in water., • What do we do to save the person?, fig-6(a), • Which path enables us to save the person in the, shortest possible time?, • Do we go in a straight line?, By careful thought we would realize that it, would be advantageous to travel a greater distance, on the land in order to decrease the distance in water, because we go much slower in water. For whatever, D C, speeds on land and in water, the final path that one, Z, has to follow to reach the person is ACB, and that, fig-6(b), this path takes the shortest time of all the possible, paths (see figure 6c). If we, A, N A, take any other route, it will be, i, i, E, longer. If we plot a graph for, C, X, D, the time taken to reach the girl, r, F r, At D and C angle of refraction is, r, against the position of any, N, taken as r because the points, B, point when we cross the shore, C and D are assumed to be close, line, we would get a curve, fig-6(c), something like that shown in, figure 6(b)., Where ‘C’, the point on shore line, corresponds to the shortest of all, possible times. Let us consider a point ‘D’ on shore line which is very, close to point ‘C’ such that there is essentially no change in time between, path ACB and ADB., , 100, , X Class, , Refraction at Plane Surfaces
Page 111 :
Let us try to calculate how long it would take to go from A to B by the, two paths one through point D and another through point C (see figure 6c)., First look at the paths on the land as shown in figure 6(c). If we draw a, perpendicular DE; between two paths at D, we see that the path (AD) on, land is shortened by the amount EC. On the other hand, in the water, by, drawing a corresponding perpendicular CF we find that we have to go the, extra distance DF in water. In other words, we gain a time that is equal to, go through distance EC on land but we lose the time that is equal to go, extra distance DF in water. These times must be equal since we assumed, there no change in time between the two paths., Let the time taken to travel from E to C and D to F be Δt and v1 and v2, be the speeds of running and swimming. From figure 6(c) we get,, EC = v1 Δt and DF = v2 Δt, D EC / DF = v1/v2, ——————(3), Let i and r be the angles measured between the path ACB and normal, NN, perpendicular to shore line X., • Can you find sin i and sin r from figure 6(c)?, (Note: Take the help of your teacher), From figure 6(c), we get;, sin i = EC / DC and sin r = DF / DC, Therefore,, sin i / sin r = EC / DF, ——————(4), from equations (3) and (4), we have, sin i / sin r = v1 / v2, ––—————(5), Thus to save the person, one should take such a path to satisfy the, above equation. We used the principle of least time to derive the above, result. Hence we can apply the same for the light ray also. From (5) we, get,, sin i / sin r = v1 / v2 = n2 / n1,, (since v1 / v2 = n2 / n1), D n1 sin i = n2 sin r., This is called Snell’s law., From the above discussion we can conclude that when light travels, from one medium to another, the ratio of speeds v1/v2 is equal to n2 / n1., The light should enter at such an angle that the ratio of sine of the angles ‘i’, and ‘r’ is equal to ratio of speeds v1/v2 in the two media., Above experiments and activities show that refraction of light occurs, according to certain laws., Free distribution by A.P. Government, , 101
Page 112 :
•, , Following are the laws of refraction., 1. The incident ray, the refracted ray and the normal to interface of, two transparent media at the point of incidence all lie in the same, plane., 2. During refraction, light follows Snell’s law, n1 sin i = n2 sin r (or) sin i / sin r = constant., Is there any chance that angle of refraction is equal to 900? When does, this happen?, Let us find out, , Total Internal Reflection, , Activity 5, Use the same materials as used in lab activity 1. Place the semi circular, glass disc in such a way that its diameter coincides with interface line, MM and its centre coincides with point ‘O’ as we have done in lab activity., Now send light from the curved side of the semicircular glass disc. This, means that we are making the light travel from denser medium to rarer, medium. Start with angle of incidence (i) equal to 00 i.e., along the normal, and look for the refracted ray on the other side of the disc., • Where do you find the refracted ray?, • Does it deviate from its path when it enters the rarer medium?, You might have noticed that it doesn’t deviate., Send laser light along angles of incidence 50, 100, 150 etc.., and measure, the angle of refraction. Tabulate the results in table (3) as shown below, and note the values ‘i’ and ‘r’ in the table., Table 3, i, , r, , •, , At what angle of incidence do you notice that the refracted ray grazes, the interface separating the two media (air and glass)?, You will observe that at a certain angle of incidence the refracted ray, does not come out but grazes the interface separating air and glass. Measure, the angle of incidence for to this situation. This angle of incidence is known, as critical angle., 102, , X Class, , Refraction at Plane Surfaces
Page 113 :
The above results can be explained using Fermat’s principle., Let us consider the light ray that travels from medium 1 with refractive, index n1 to medium 2 with refractive index n2.See figure (7). It is already, found that the angle of refraction is more than angle of incidence when a, light ray travels from denser(n1) to rarer medium (n2)., For the angle of incidence i, let r be the angle of refraction., From Snell’s law, N, n1 sin i = n2 sin r B n1/n2 = sin r/ sin i, Rarer, we know that, n1/n2 is greater than 1, so that sin, r/ sin i is greater than 1.So we conclude that the, angle of refraction is greater than the angle of, C, incidence, i.e, r is greater than i., The angle of incidence at which the light ray, Denser, N, travelling from denser to rarer medium, grazes the, fig-7, interface is called critical angle for denser medium., It is shown in figure7., Let C be the critical angle. Then r becomes 900, we get, n1/n2 = sin 900/ sin c B n1/n2 = 1/sin c ., We get sin c = n2/ n1 .We know that n1/n2 i.e., n12 is called refractive, index of denser medium with respect to rarer medium, sin c = 1/n12, • Can you find the critical angle of water using the above equation?, Discuss it in your class., • What happens to light when the angle of incidence is greater than, critical angle?, When the angle of the incidence is greater than critical angle, the light, ray gets reflected into the denser medium at the interface i.e., light never, enters the rarer medium. This phenomenon is called total internal, reflection. It is shown in figure 7., Discuss these ideas in your class and find out the critical angle of, water., Let us see an example on total internal reflection., , Example, A rectangular glass wedge (prism) is immersed in water, as shown in figure E-a. For what value of angle α, will the, beam of light, which is normally incident on AB, reach AC, entirely as shown in figure E-b. Take the refractive index of, water as 4/3 and the refractive index of glass as 3/2., Free distribution by A.P. Government, , A, , α, , B, , C, , fig E-a, 103
Page 114 :
A, , C, , Solution: From the geometry of figure E-b it is clear that, the angle, of incidence on the side BC is equal to α (dotted line is a normal drawn at, the point of incidence). The ray should undergo total internal reflection to, reach AC. For occurence of total internal reflection, the value of α must, be greater than the critical angle at interface of water and glass., Let ‘C’ be the critical angle for the interface of glass and water., From the given condition, α > C ———(1), α, We know, sin C = 1/n12, ———(2), B, n12 = n1/n2 = (3/2) /(4/3) = 9/8., α, From equation 2, we get, sin C = 8/9 B C = 620301, Hence α is greater than C = 62030 |, Let us see few activities of total internal reflection., fig E-b, , Activity 6, Take a transparent glass tumbler and coin. Place the coin on a table, and place glass tumbler on the coin. Observe the coin from the side of the, glass., • Can you see the coin?, Now fill the glass tumbler with water and observe the coin from the, side of the glass tumbler., • Can you see the coin?, • Explain why the coin disappears from view., , Activity 7, Image of, the coin, on the, water, surface, , Coin at, bottom, , fig-8, , 104, , Take a cylindrical transparent vessel (you may use, 1 L beaker). Place a coin at the bottom of the vessel., Now pour water until you get the image of the coin, on the water surface (look at the surface of water, from a side). See figure 8., • Can you explain why the image of the coin is, formed?, There are many interesting situations around us, which involve the phenomenon of total internal, reflection. One of that is a mirage which we witness while driving or while, walking on a road during a hot summer day., , X Class, , Refraction at Plane Surfaces
Page 115 :
Mirages, Mirage is an optical illusion where, it appears that water has collected on the, road at a distant place but when we get, there, we don’t find any water., • Do you know the reason why it, appears so?, The formation of a mirage is the best, example where refractive index of a, medium varies throughout the medium., During a hot summer day, air just, above the road surface is very hot and, the air at higher altitudes is cool. It, means that the temperature decreases, with height. As a result density of air, increases with height. We know that, refractive index of air increases with, density. Thus the refractive index of air, increases with height. So, the cooler air, at the top has greater refractive index, than hotter air just above the road. Light, travels faster through the thinner hot air, than through the denser cool air, , fig-9(a), , fig-9(b): The paths of light rays when there, is no change in density of air, , Refractive index, decreases with depth, , fig-9(c), , above it., When the light from a tall object such as tree or from the sky passes, through a medium just above the road, whose refractive index decreases, towards ground, it suffers, refraction and takes a curved path because of, total internal reflection. See figure 9(c)., This refracted light reaches the observer in a direction shown in Figure9c. This appears to the observer as if the ray is reflected from the ground., Hence we feel the illusion of water being present on road (shown in figure, 9a) which is the virtual image of the sky (mirage) and an inverted image of, tree on the road (shown in figure 9c)., , Think and discuss, • Why should you see a mirage as a flowing water?, • Can you take a photo of a mirage?, Free distribution by A.P. Government, , 105
Page 116 :
Applications of total internal reflection, i) Brilliance of diamonds: Total internal reflection is the main reason, for brilliance of diamonds. The critical angle of a diamond is very, low(24.4o). So if a light ray enters a diamond it is, very likely to undergo total internal reflection which, makes the diamond shine., ii), Optical fibres: Total internal reflection is, the basic principle behind working of optical fibre., fig-10(a), An optical fibre is very thin fibre made of glass (or), plastic having radius about a micrometer (10-6 m). A, bunch of such thin fibres form a light pipe., Figure 10(a) shows the principle of light, transmission by an optical fibre. Figure 10(b), sketches a optical fibre cable. Because of the small, fig-10(b), radius of the fibre, light going into it makes a nearly, glancing incidence on the wall. The angle of incidence is greater than the, critical angle and hence total internal reflection takes place. The light is, thus transmitted along the fibre., All organs of the human body are not accessible to the naked eye of, the doctor, for example intestines. The doctor inserts an optical fiber pipe, into the stomach through the mouth. Light is sent down through one set of, fibres in the pipe. This illuminates the inside of the stomach. The light, from the inside travels back through another set of fibres in the pipe and, the viewer gets the image at the outer end (generally fed to the computer, screen)., The other important application of fibre optics is to transmit, communication signals through light pipes. For example, about 2000, telephone signals, appropriately mixed with light waves, may be, simultaneously transmitted through a typical optical fibre. The clarity of, the signals transmitted in this way is much better than other conventional, methods., • How does light behave when a glass slab is introduced in its path?, Let us see, , Refraction Through a Glass Slab, A thin glass slab is formed when a medium is isolated from its, surroundings by two plane surfaces parallel to each other. Let us determine, position and nature of the image formed when the slab is placed in front of, 106, , X Class, , Refraction at Plane Surfaces
Page 117 :
Lab Activity 2, an object. Let us do an activity., Aim: Determination of position and nature of image formed by a glass, slab., Material required: plank, chart paper, clamps, scale, pencil, thin glass, slab and pins., Procedure:, Place a piece of chart (paper) on a plank. Clamp it. Place a glass slab in, the middle of the paper. Draw border line along the edges of the slab by, using a pencil. Remove it. You will get a figure of a rectangle. Name the, vertices of the rectangle as A, B, C and D., Draw a perpendicular at a point on the longer side (AB) of the rectangle., Again keep the slab on paper such that it coincides with the sides of the, rectangle ABCD. Take two pins. Stick them on the perpendicular line to, AB. Take two more pins and stick them on the other side of the slab in, such a way that all pins come to view along a straight line. Remove the slab, from its place. Take out the pins. Draw a straight line by using the dots, formed by the pins such that it reaches first edge (AB) of the rectangle., You will get a long straight line., • What does it mean?, The light ray that falls perpendicular to one side of the slab surface, comes out with out any deviation., Now take another piece of white chart on the plank. Clamp it. Place a, glass slab in the middle of the paper. Again draw a border line along the, edges of the slab by using a pencil. Remove the slab and name the vertices, of the rectangle formed as A,B,C and D. Draw a perpendicular at a point on, the longer side AB. Now draw a line, from the point of, intersection where side AB of rectangle and perpendicular, i, 0, meet, in such a way that it makes 30 angle with normal. This D, line represents the incident ray falling on the slab and the angle, it makes with normal represents the angle of incidence., Now place the slab on the paper in such way that it fits in, the rectangle drawn. Fix two identical pins on the line making A, 300 angle with normal such that they stand vertically with equal, • pins, height. By looking at the two pins from the other side of the, slab, fix two pins in such a way that all pins appear to be along, , C, , r, , r, , B, i, , fig-11, , Free distribution by A.P. Government, , 107
Page 118 :
a straight line. Remove slab and take out pins. Draw a straight line by joining, the dots formed by the pins up to the edge CD of the rectangle. This line, represents emergent ray of the light., Draw a perpendicular ON to the line CD where our last line drawn, meets the line CD. Measure the angle between emergent ray and normal., This is called angle of emergence. (Check your drawing with the figure, 11)., • Is the line formed a straight line?, • Are the angles of incidence and emergence equal?, • Are the incident and emergent rays parallel?, You will notice an important result that the incident and emergent rays, are parallel., • Can you find the distance between the parallel rays?, The distance between the parallel rays is called lateral shift. Measure, this shift. Repeat the experiment for different angles of incidence and, tabulate the values of angle of incidence and shift corresponding to each, angle of incidence in table (4)., • Can you find any relation, Table 4, between the angle of incidence, Agle of Inciddene, Shift, and shift?, • Can you find the refractive, index of the slab?, Let us find the refractive, index of the slab., , Activity 8, , Glass, slab, , A, D, , 108, , Measure the thickness of the slab. Note it in your notebook. Take a, white chart and fix it on the table. Take the slab and place it in the middle, of the chart. Draw its boundary. Remove the slab from its, P, place. The lines form a rectangle. Name the vertices as A,B,C, and D. Draw a perpendicular to the longer line AB of the, Q, rectangle at any point on it. Place slab again in the rectangle, ABCD. Take a pin. Place at a point P in such a way that its, length is parallel to the AB on the perpendicular line at a, distance of 15cm from the slab. Now take another pin and by, B, looking at the first pin from the other side of the slab try to, C, place the pin so that it forms a straight line with the first pin., fig-12, Remove the slab and observe the positions of the pins., , X Class, , Refraction at Plane Surfaces
Page 119 :
•, , Are they in the same line?, Draw a perpendicular line from the second pin to the line on which, first pin is placed. Call the intersection point Q. Find the distance between, P and Q. We may call it vertical shift., • Is this shift independent of distance of first pin from slab?, To find this, do the same activity for another distance of the pin from, the slab. You will get the same vertical shift. We could use a formula to, find out refractive index of the glass., R.I = Thickness of the slab / (thickness of slab – vertical shift), , Key words, Refraction, Incident ray, Refracted ray, Angle of incidence, Angle of, Refraction, Absolute refractive index, Relative refractive index, Snell’s law,, Critical angle, Total internal Reflection, Mirage, Shift, Optical fibre., , What we have learnt, •, •, •, •, •, •, , •, , When light travels from one medium to another, its direction changes at the interface. The, phenomenon of changing direction at the interface of the two media is known as refraction., Refraction is a result of change in speed of light at the interface., Absolute refractive index = Speed of light in vacuum/ Speed of light in medium B n=c/v., Relative refractive index , n21 = v1/v2 = n2/n1 ., Snell’s law is given by, n1 sin i = n2 sin r ., The angle of incidence, at which the light ray travelling from denser to rarer medium grazes the, interface, is called the critical angle for those media. sin C = n2/ n1 , where n1 is the refractive, index of denser medium and n2 is the refractive index of rarer medium. (n1>n2), When the angle of incidence is greater than the critical angle, the light ray is reflected into denser, medium at interface. This phenomenon is called total internal reflection., , Improve your learning, 1. Why is it difficult to shoot a fish swimming in water? (AS1), 2. The speed of the light in a diamond is 1, 24, 000 km/s. Find the refractive index of diamond if, the speed of light in air is 3,00,000 km/s. (AS1), (Ans: 2.42), 3. Refractive index of glass relative to water is 9/8. What is the refractive index of water relative, to glass? (AS1), (Ans: 8/9), 4. The absolute refractive index of water is 4/3. What is the critical angle? (AS1) (Ans: 48.50), 5. Determine the refractive index of benzene if the critical angle is 420.(AS1) (Ans: 1.51), 6. Explain the formation of mirage? (AS1), Free distribution by A.P. Government, , 109
Page 120 :
7. How do you verify experimentally that sin i /sin r is a constant? (AS1), 8. Explain the phenomenon of total internal reflection with one or two activities. (AS1), 9. How do you verify experimentally that the angle of refraction is more than angle of incidence, when light rays travel from denser to rarer medium. (AS1), 10. Take a bright metal ball and make it black with soot in a candle flame. Immerse it in water. How, does it appear and why? (Make hypothesis and do the above experiment). (AS2), 11. Take a glass vessel and pour some glycerine into it and then pour water up to the brim. Take a, quartz glass rod. Keep it in the vessel. Observe the glass rod from the sides of the glass vessel., , • What changes do you notice?, , • What could be the reasons for these changes?(AS2), , 12. Do activity-7 again. How can you find critical angle of water? Explain your steps briefly. (AS3), 13. Collect the values of refractive index of the following media. (AS4), Water, coconut oil, flint glass, crown glass, diamond, benzene and hydrogen gas., 14. Collect information on working of optical fibres. Prepare a report about various uses of optical, fibres in our daily life. (AS4), 15. Take a thin thermocol sheet. Cut it in circular discs of different, radii like 2cm, 3cm, 4cm, 4.5cm, 5cm etc and mark centers, with sketch pen. Now take needles of length nearly 6cm. Pin, a needle to each disc at its centre vertically. Take water in a, large opaque tray and place the disc with 2cm radius in such a, fig-Q15, way that the needle is inside the water as shown in fig-Q15., Now try to view the free end (head) of the needle from surface of the water., , • Are you able to see the head of the needle?, Now do the same with other discs of different radii. Try to see the head of the needle, each, time., Note: the position of your eye and the position of the disc on water surface should not be, changed while repeating the activity with other discs., , •, •, •, •, , At what maximum radius of disc, were you not able to see the free end of the needle?, Why were you not able to view the head of the nail for certain radii of the discs?, Does this activity help you to find the critical angle of the medium (water)?, Draw a diagram to show the passage of light ray from the head of the nail in different, situations. (AS4), , 16. Explain the refraction of light through a glass slab with a neat ray diagram. (AS5), 17. Place an object on the table. Look at the object through the transparent glass slab. You will, observe that it will appear closer to you. Draw a ray diagram to show the passage of light ray, in this situation. (AS5), 18. What is the reason behind the shining of diamonds and how do you appreciate it? (AS6), 19. How do you appreciate the role of Fermat principle in drawing ray diagrams. (AS6), 110, , X Class, , Refraction at Plane Surfaces
Page 121 :
20. A light ray is incident on air-liquid interface at 450and is refracted at 300. What is the refractive, index of the liquid? For what angle of incidence will the angle between reflected ray and refracted, ray be 900? (AS7), (Ans: 1.414, 54.70), 21. Explain why a test tube immersed at a certain angle in a tumbler of water appears to have a, mirror surface for a certain viewing position? (AS7), 22. What is the angle of deviation produced by a glass slab? Explain with ray diagram. (AS7), 23. In what cases does a light ray not deviate at the interface of two media?(AS7), 24. A ray of light travels from an optically denser to rarer medium. The critical angle of the two, media is ‘c’. What is the maximum possible deviation of the ray? (AS7), (Ans:π-2c), 25. When we sit at a camp fire, objects beyond the fire are seen swaying. Give the reason for it., (AS7), 26. Why do stars appear twinkling? (AS7), 27. Why does a diamond shine more than a glass piece cut to the same shape? (AS7), , ks, Fill in the blan, 1. At critical angle of incidence, the angle of refraction is ................, 2. n1 sin i = n2 sin r, is called.................., 3. Speed of light in vaccum is ......................, 4. Total internal reflection takes place when a light ray propagates from .......... to ............. medium., 5. The refractive index of a transparent material is 3/2. The speed of the light in that medium is, .............., 6. Mirage is an example of ....................., , s, Multiple choice question, 1. Which of the following is Shell’s law., [, ], b) n1/n2 = sin r / sin i, a) n1 sin i = sin r/ n2, c) n2 / n1 = sin r / sin i, d) n2 sin i = constant, 2. The refractive index of glass with respect to air is 2. Then the critical angle of glass-air interface, is .................., [, ], o, o, o, o, a) 0, b) 45, c) 30, d) 60, 3. Total internal reflection takes place when the light ray travels from..............., [, ], a) rarer to denser medium, b) rarer to rarer medium, c) denser to rarer medium, d) denser to denser medium, 4. The angle of deviation produced by the glass slab is ..................., [, ], a) 0o, b) 20o, c) 90o, d) depends on the angle formed by the light ray and normal to the slab, Free distribution by A.P. Government, , 111
Page 122 :
Chapter, , 6, Refraction of Light at, Curved Surfaces, It is a common observation that some people use spectacles for, reading. The watch repairer uses a small magnifying glass to see tiny parts, of a watch., • Have you ever touched a magnifying glass with your hand?, • Have you touched the glass in the spectacles used for reading with, your hand?, • Is it a plane or curved surface?, • Is it thicker in the middle or at the edge?, We have learnt about refraction of light at a plane surface in the previous, chapter. Now let us understand refraction of light at curved surfaces., Let us do an activity to understand refraction of light at curved surfaces., , Refraction of light at a curved surface, , Activity 1, Draw an arrow of length 4 cm using a black sketch pen on a thick sheet, of paper. Take an empty cylindrical-shaped transparent vessel such as glass, tumbler. Keep it on the table. Ask your friend to bring the sheet of paper, on which arrow was drawn behind the vessel while you look at it from the, other side (The arrow mark should be in horizontal position)., • What do you see?, You will see a diminished (small-sized) image of the arrow, • Why do you see a diminished image?, • Is the image real or virtual?, • Can you draw a ray diagram showing how it is formed?, 112, , X Class, , Refraction of Light at Curved Surfaces
Page 123 :
Ask your friend to fill the vessel with water. Look at the figure of, arrow from the same position as before., • What do you see now?, • Do you get an inverted image?, • How could this happen?, In the first case, when the vessel is empty, light from the arrow refracts, at the curved interface, moves through the glass and enters into air then it, again undergoes refraction on the opposite curved surface of the vessel, (at the other end from where we are looking) and comes out into the air. In, this way light travels through two media and comes out of the vessel and, forms a diminished image., In the second case, light enters the curved surface,, Air, Water, moves through water, comes out of the glass and forms, an inverted image., When the vessel is filled with water, there is a, curved interface between two different media (air and, Curved, surface, water). Assume that the refractive indices of both water, and glass are the same (they really are not equal). This, fig-1, setup of air and water separated by a curved surface is, shown in figure 1., • What happens to a ray that is incident on a curved surface separating, the two media?, • Are the laws of refraction still valid?, Let us find out., Consider a curved surface seperating two different, Normal, media as shown in figure 2. The centre of the sphere, Light, rays, of which curved surface is a part, is called as centre of, C, curvature. It is denoted by letter ‘C’., Principal, P, axis, Any line drawn from the centre of curvature to a, point on the curved surface becomes normal to the, curved surface at that point. The direction of the normal, fig-2, changes from one point to another point on the curved, surface. The centre of the curved surface is called the pole (P) of the, curved surface. The line that joins the centre of curvature and the pole, is called ‘principal axis’., •, , How do rays bend when they are incident on a curved surface?, , Free distribution by A.P. Government, , 113
Page 124 :
P, , Rarer, , Denser, , As in the case of plane surfaces, a ray will bend towards the normal if, it travels from a rarer to denser medium and it bends away from the normal, if it travels from a denser to a rarer medium ., Let us see how we can draw ray diagrams for certain useful cases., • What happens to a ray that travels along the principal axis? Similarly, a, ray that travels through the centre of curvature?, According to Snell’s law the ray which travels along, the normal drawn to the surface does not deviate from, Ray passing, thorugh C, its path. Hence both rays mentioned above, travel, C, along the normal (see figure 3), so they do not deviate., Ray passing, • What happens to a ray travelling parallel to the, thorugh, pole, principal axis?, Observe the following figures 4a, 4b, 4c, and 4d., fig-3, In all the cases as represented by the diagrams, the, incident ray is parallel to the principal axis., Case1: A ray travelling parallel to the principal axis, strikes a convex surface and passes from a rarer, medium to denser medium. (see figure 4a), Case2: A ray travelling parallel to the principal axis, Normal, strikes a convex surface and passes from a denser, C, medium to rarer medium. (see figure 4b), Denser, Case3: A ray travelling parallel to the principal axis, strikes a concave surface and passes from a denser, fig-4(a), medium to rarer medium. (see figure 4c), Case4: A ray travelling parallel to the principal axis, Normal, strikes a concave surface and passes from a rarer, medium to denser medium. (see figure 4d), C, • What difference do you notice in the refracted rays, Rarer, in 4a and 4b?, fig-4(b), Normal, Normal, C, Denser, , Rarer, , fig-4(c), 114, , X Class, , C, Denser, , Rarer, , fig-4(d), Refraction of Light at Curved Surfaces
Page 125 :
•, •, •, , What could be the reason for that difference?, What difference do you notice in refracted rays in figure 4c and 4d?, What could be the reasons for that difference?, You might have noticed that in figures 4(a) and 4 (c) the refracted ray, reaches a particular point on the principal axis. In figures 4(b) and 4(d) the, refracted ray moves away from the principal axis. When you extend the, refracted ray backwards along the ray as shown in 4b and 4d, the extended, ray intersects the principal axis at some point. The point where refracted, ray intersects the axis in all the above cases is called the focal point., You might have observed that a lemon in a glass of water appears bigger, than its actual size, when viewed from the sides of tumbler., • How can you explain this change in the size of lemon?, • Is the lemon that appears bigger in size an image of lemon or is it the, real lemon?, • Can you draw a ray diagram to explain this phenomenon?, Let us find out., , Image formation, Consider a curved surface separating two media of refractive indices, n1 and n2 ( figure 5) . A point object is placed on the principal axis at point, O. The ray, which travels along the principal axis passes through the pole, undeviated. The second ray, which forms an angle α with principal axis,, meets the interface (surface) at A. The angle of incidence is θ1. The ray, bends and passes through the second medium along the line AI. The angle, of refraction is θ2. The two refracted rays, meet at I and the image is formed there., A, Let the angle made by the second, θ, θ, refracted ray with principal axis be γ and, α, β, N, the angle between the normal and, P, O, C, principal axis be β. (see figure 5), n, n, In figure 5,, PO is the object distance which we, denote as ‘u’, fig-5, PI is image distance which we denote, as ‘v’, PC is radius of curvature which we denote as ‘R’, n1, n2 are refractive indices of two media., Can you establish any relation between the above mentioned quantities?, 1, , 2, , γ, I, , 1, , 2, , Free distribution by A.P. Government, , 115
Page 127 :
–, , The heights measured vertically down from points on axis are taken, as negative., Here PO is called the object distance (u), PI is called the image distance (v), PC is called radius of curvature (R), According to sign convention mentioned above, we have, PO = -u ; PI = v ; PC = R, Substituting these values in equation (4) we get,, n2/v - n1/u = (n2-n1 ) /R, ....................... (5), This formula can also be used for plane surfaces. In the case of a plane, surface, radius of curvature (R) approaches infinity. Hence 1/R becomes, zero. Substituting this in equation 5, we get formula for the plane surfaces, n2/v - n1/u = 0 B n2/v = n1/u, NOTE: The distances u and v are measured from the plane interface., Let us consider the following examples., , Example 1, A bird is flying down vertically towards the surface of water in a pond, with constant speed. There is a fish inside the water. If that fish is exactly, vertically below the bird, then the bird will appear to the fish to be:, a. farther away than its actual distance., b. closer than its actual distance., c. moving faster than its actual speed., I, d. moving slower than its actual speed., Which of the four options are true? How can you prove it?, Solution: For refraction at a plane surface,, O, we use n2/v = n1/u, ..................(1), Let x be the height of the bird above the water surface at an, y, x, instant and n be the refractive index of water., n1= refractive index of air,, Then n1 =1, n2 = n, u= -x and let v = -y, (see figure E-1), Substituting these values in equation (1), n/(-y) = 1/(-x) B y = nx, In the above equation, we know that n is greater than 1. Hence, fig-E1, y is greater than x. Thus the bird appears to the fish to be farther, away than its actual distance. We have assumed that bird is flying vertically, , Free distribution by A.P. Government, , 117
Page 128 :
down with constant speed. For the observer on the ground, bird appears, that it has covered ‘x’ distance for certain time. But for fish, it appears that, bird has covered a distance ‘y’ in the same time. As y is greater than x , we, can conclude that the speed of the bird, observed by the fish, is greater, than its actual speed., So, options (a) and (c) are correct., , Example 2, A transparent sphere of radius R and refractive index n is kept in air. At, what distance from the surface of the sphere should a point object be, placed on the principal axis so as to form a real, image at the same distance from the second, surface of the sphere?, O, , x, , x, , R, , I, , fig-E2, , Solution: From the symmetry of figure E2,, the rays must pass through the sphere parallel, to the principal axis., From the figure,, , u = -x, v= ∞ (refracted ray is parallel to the optical axis after refraction, at first surface), n1 =1 and n2 = n, (where n1 is refractive index of air), Using n2/v –n1/u = (n2-n1)/R, n/ ∞ - 1/ (-x) = (n-1)/R B 1/x = (n-1)/R, B x = R/(n – 1), Object distance from the first surface of the sphere is x= R/(n-1), , Example 3, A transparent (glass) sphere has a small, opaque dot at its centre. Does, the apparent position of the dot appear to be the same as its actual position, when observed from outside?, Solution: Let refractive index of glass n1= n, refractive index of air n2 = 1, Then u = –R (radius of sphere) ; Radius of curvature R = –R, Using n2/v –n1/u = (n2-n1)/R, 1/v – n/(-R) = (1-n)/(-R) B 1/v + n/R = (n–1)/R, After solving this equation, we get, Image distance v = –R, 118, , X Class, , Refraction of Light at Curved Surfaces
Page 129 :
Thus we can say that the image distance and object distance are equal, and that the apparent position of dot is the same as its actual position., It is independent of the refractive index of the material of the sphere., _______________, Till now we have discussed refraction of light at a single curved surface, either convex or concave. Let us suppose that a transparent material has, two curved surfaces., • What happens to the light ray when a transparent material with two, curved surfaces is placed in its path?, • Have you heard about lenses?, • How does a light ray behave when it is passed through a lens?, Let us learn about refraction of light through lenses., , Lenses, A lens is formed when a transparent material is bounded by two surfaces, of which one (or) both surfaces are spherical. That is a lens is bounded by, atleast one curved surface. Lenses can be of various types. Some typical, lenses along with their names are shown in figure 6., , fig-6(a):, , fig-6(b):, , fig-6(c):, , fig-6(d):, , fig-6(e):, , Biconvex, , Biconcave, , Plano-convex, , Plano-concave, , Concavo-convex, , figure 6 : Different types of lenses, , A lens may have two spherical surfaces bulging outwards. Such a lens, is called double convex lens (Biconvex lens, see figure 6(a) ). It is thick at, the middle as compared to edges., Similarly, a double concave lens is bounded by two spherical surfaces, curved inwards. (Biconcave lens, see figure 6(b) ). It is thin at the middle, and thicker at the edges., Observe the 6(c), 6(d) and 6(e) to understand structure of PlanoConvex lens, Plano-Concave lens; Concavo-Convex lens., Free distribution by A.P. Government, , 119
Page 130 :
Here we are concerned only with thin lenses i.e. the thickness of the, lens is negligible., Let us learn the terminology used in the case of lenses., Each curved surface of a lens is part of a sphere. The, centre of the sphere which contains the part of the curved, R, surface is called centre of curvature. It is denoted by a, letter ‘C’. If a lens contains two curved surfaces then their, C, centres of curvature are denoted as C1 and C2.The distance, between the centre of curvature and curved surface is, fig-7, called radius of curvature (R). Radii of curvature are, represented by R1 and R2 respectively. Let us consider a, double convex lens as shown in figure 7., The line joining the points C1 and C2 is called principal axis. The, midpoint of a thin lens is called optic centre of lens (P)., 1, , R2, P, , C2, , 1, , Focal length of the lens, A parallel beam of light incident on a lens converges to a point as, shown in figure 8(a) or seems to emanate from a point on the principal, axis as shown in figure 8(b). The point of convergence (or) the point from, which rays seem to emanate is called focal point or focus (F). Every lens, has two focal points. The distance between the focal point and optic centre, is called the focal length of lens denoted by ‘f’., , C2, , F2, , C1, , F1, , C1, , F1, , fig-8(a), , F2, , C2, , fig-8(b), >—<, , For drawing ray diagrams related to lenses we represent convex lens, with a symbol R and concave lens with . See figures 8(c) and 8(d)., , C2, , F2, , F1, , fig-8(c), 120, , X Class, , C1, , C1, , F1, , F2, , C2, , fig-8(d), Refraction of Light at Curved Surfaces
Page 131 :
•, , How does the lens form an image?, To know the formation of image by lenses, we need to know the, behavior of light rays when they meet a lens., Though we know that the lens has two surfaces; while drawing ray, diagrams, we can consider the lens as a single surface element because we, assume that the thickness of the lens is very small and show the net, refraction at only one of the surfaces, as shown in the figure 8(c) and 8(d)., Behaviour of certain light rays when they are incident on a lens, The behaviour of a light ray when it passes through a lens can be, understood by observing its behaviour in the following situations:, Situation I: Ray passing along the principal axis, Any ray passing along the principal axis is undeviated., (see Figures 9a and 9b), C, F, Situation II: Ray passing through the optic centre., fig-9(a), Any ray passing through the optic centre is also, undeviated. (see Figure 10a and 10b), , C2, , F2, , F1, , C1, , C1, , F1, , F2, , 2, , 2, , F1, , C1, , C1, , F1, , F2, , C2, , fig-9(b), , C2, , fig-10(b), , fig-10(a), , Situation III: Rays travelling parallel to the principal axis., We know that the rays passing parallel to the principal axis converge, at the focus or appear to diverge from the focus as shown in figure 8(c), and 8(d)., • If we allow a light ray to pass through the focus, which path does it, take?, Situation IV: Ray passing through focus., Light rays obey the principle of least time. Hence the ray passing, through the focus will take a path parallel to principal axis after refraction., (see Figure 11(a) and 11(b) ), , C2, , F2, , F1, , fig-11(a), Free distribution by A.P. Government, , C1, , C1, , F1, , F2, , C2, , fig-11(b), 121
Page 132 :
•, , C2, , What happens when parallel rays of light fall on a lens making some, angle with the principal axis?, Let us observe the following figures, , F2, , F1, , fig-12(a), , C1, , C1, , F2, , F1, , C2, , fig-12(b), , When parallel rays, making an angle with principal axis, fall on a lens,, as shown in figures 12(a) and 12(b), the rays converge at a point or appear, to diverge from a point lying on the focal plane. Focal plane is the plane, perpendicular to the principal axis at the focus., Rules to draw ray diagrams for image formation by lenses, Let us learn a few basic rules to draw ray diagrams to locate the position, of images., For drawing a ray diagram to find position and size of the image formed, by lens for any position of object on the principal axis you need to follow, the rules mentioned below:, For locating position and to find the size of image, we need two rays, out of four rays that were mentioned in the situations I to IV., - Select a point on the object placed at a point on the principal axis., - Draw two rays that were chosen by you from rays mentioned in, situations I to IV., - Extend both rays to intersect at a point. This point gives position, of the image., - Draw a normal from point of intersection to the principal axis., - Length of this normal represents the size of the image., Observe the following diagrams. They represent image formation by a, convex lens for various positions of the object., 1. Object at infinity, • What do you mean by an object at infinity?, • What type of rays fall on the lens?, You know that the rays falling on the lens from an object at infinity are, parallel to the principal axis., 122, , X Class, , Refraction of Light at Curved Surfaces
Page 133 :
They converge to the focal point. So a point sized image is formed at, the focal point. This can be seen in figures 8(a)., , Object, , 2. Object placed beyond the centre of curvature on the principal axis, In figure (13) you notice that when, object is placed beyond the centre of, F, curvature (C 2 ), a real, inverted and, F, C, diminished image is formed on the, principal axis between the points F1 and C1., fig-13, In figure (13) we have chosen two rays,, one ray passing parallel to the principal axis and another ray passing through, the optic centre to locate the position of the image., Try to draw ray diagram using the pair of rays, one passing parallel to, the axis another passing through the focus., 3. Object placed at the centre of curvature, When an object is placed at the centre, of curvature (C2) on the principal axis, you, Object, will get an image at C1 which is real,, F, C, inverted and of the same size as that of, fig-14, object. See figure 14., , F1, , Image, , 4. Object placed between the centre of curvature and focal point, When an object is placed between, centre of curvature (C2) and focus (F2), you Object, F, will get an image which is real, inverted, F, C, and magnified. See figure 15. The image, fig-15, will form beyond C1., 1, , Free distribution by A.P. Government, , C1, , 2, , Object, C2, , C1, , 2, , 2, , 2, , Image, , 2, , 2, , 5. Object located at the focal point, When an object is placed at focus (F2),, the image will be at infinity. See figure 16., When the image is formed at an infinite, distance away we can not discuss the size, and nature of the image., , C1, , 1, , Image, , F1, , C1, , F2, , fig-16, , Image at, infinity, , 123
Page 134 :
Object, , 6. Object placed between focal point and optic centre, If we place an object between focus and optic, Image, centre, we will get an image which is virtual, erect, C, F, and magnified., C, F, From the ray diagram shown in figure 17, you, will notice that the image formed is a virtual, erect, fig-17, and is formed on the same side of the lens where, the object is placed. The size of the image is larger than that of the object., It is a magnified image., In the above situation of image formation, we understand two things:, 1. As the image formed is virtual, we can see it with our eyes. In all other, cases the image is real which we can’t see with our eyes but can be, viewed if the image is captured on a screen., 2. A magnified virtual image is formed on the same side of the lens where, the object is placed. Thus the image you are seeing through a lens is, not real, it is a virtual image of the object., This particular behaviour of convex lens helps to construct a, microscope, which gives a magnified image. You might remember that the, magnification of the virtual image is possible only when the object is at, the distance less than the focal length of the lens., Till now we have drawn ray diagrams for various positions of object, placed on principal axis using convex lens. Draw ray diagram for an object, placed between C1 and F1 for a concave lens., • What do you notice?, Verify your ray diagram with the ray diagram, we have drawn for a convex lens. See figure 18., Object, C, F, Try to draw ray diagrams for other positions of, Image, C, F, an object. You will notice that irrespective of the, fig-18, position of object, on the principal axis, you will, get an erect, virtual image, diminished in size in between the focal point, and optic centre for concave lens., Let us see a few examples of ray diagrams, 2, , 1, , 1, , 1, , 2, , 2, , 2, , 1, , Example 4, Draw a ray diagram to locate the position of image when a point source, (S) is placed on optical axis MN of a convex lens, in such a way that it is, beyond focal point (F). See figure E(4)., Solution, - Draw a perpendicular line to principal axis passing through the, focus (FI)., 124, , X Class, , Refraction of Light at Curved Surfaces
Page 135 :
-, , -, , Draw a ray from point source (S) in any, P/, I, direction to meet lens at point (P )., Now draw another line parallel to the ray M S, P, F, drawn from the point source (S) such, fig-E(4), that it passes through the optic centre, (P); This line intersects the normal at point FO., Now draw a line passing from point PI to pass through the point FO, such that it meets principal axis at a point say (I)., ‘I’ is the image point for the point source (S)., , F0, F/, , I, , N, , Example 5, Complete the ray diagram to, F/, F, show the paths of the rays after, F/, F, M S, refraction through the lenses shown, F, fig-E5(a), fig-E5(b), in the figures E5(a) and E5(b)?, Solution, Follow the steps mentioned in Example (4) to complete the ray, diagrams., You will notice that the paths of the rays are shown in figures E5(c), and 5(d)., F/, , F, F/, , F, , fig-E5(c), , •, , fig-E5(d), _______________, Can we realise in practice the results obtained in the ray diagrams, when we perform experiments with a lens?, Let us see, , Activity 2, Take a v-stand and place it on a long (nearly 2m) table at the middle., Place a convex lens on the v-stand. Imagine the principal axis of the lens., Light a candle and ask your friend to take the candle far away from the lens, along the principal axis. Adjust a screen (a sheet of white paper placed, perpendicular to the axis) which is on other side of the lens until you get, an image on it., • Why are we using a screen to view this image? Why don’t we see it, directly with our eye?, Free distribution by A.P. Government, , 125
Page 136 :
Measure the distance of the image from the v-stand of lens and also, measure the distance between the candle and stand of lens., Record the values in a table 1., Now place the candle at a distance, Table 1, of 60 cm from the lens, such that the, Image, Focal, Object, flame of the candle lies on the principal, length (f), distance (u) distance (v), axis of the lens. Try to get an image of, the candle flame on the other side on a, screen. Adjust the screen till you get a, clear image. Measure the image, distance (v) from lens and record the values of ‘u’ and ‘v’ in table 1. Repeat, this for various object distances like 50 cm, 40 cm, 30 cm, etc. Measure, image distances in all the cases and note them in table 1., • Could you get an image on the screen for every object distance?, • Why don’t you get an image for certain object distances?, • Can you find the minimum limiting object distance for obtaining a, real image?, • What do you call this minimum limiting object distance for real images?, When you do not get an image on the screen, try to see the image with, your eye directly from the place of the screen., • Could you see the image?, • What type of image do you see?, You will see a magnified image on the same side where we kept the, object. This is a virtual image of the object which we cannot capture on, the screen., • Can you find the image distance of this virtual image?, In table-1, you got different values of ‘v’ for various position of candle, (u)., • Could you find focal length of the lens from the values recorded in, table-1?, • Can we establish a relation between ‘u’, ‘v’ and ‘f’?, Let us find out., Consider an object OOI placed on the principal axis in front of a convex, lens as shown in figure(19). Let III be the real image formed by the lens on, the other side of it. Observe the figure(19)., • How is the image formed?, 126, , X Class, , Refraction of Light at Curved Surfaces
Page 137 :
Lens formula, The ray, starting at OI and moving parallel to the principal axis and, which falls on the lens, should pass through the focal point F1 as shown in, figure (19). To locate the point of image (II) for the object point (OI),, consider another ray that passes through the optic centre P. We know that, any ray passing through the optic centre P will not deviate., The ray starting from OI and passing through optic centre P, will meet, the refracted ray (first ray) at the point II. This point is the image of the, point OI of the object. Similarly, the image of the point O on the principal, axis is formed at point I on the principal axis (see Figure 19). We get the, inverted image III of object OOI., PO, PI and PF1 are the object distance, image distance and focal length, respectively. From figure 19, triangle PPIF1 and triangle F1III are similar, triangles,, .................(1), B PPI/III = PF1/F1I, But from the figure 19,, F1I = PI – PF1, substituting F1I in equation (1) above, we get, PPI/III = PF1/(PI – PF1) .................(2), We have another set of similar triangles OOIP and PIII., From these triangles we get, OOI/III = PO/PI, but from figure (19), OOI = PPI, hence, we have, P/, O/, PPI/III = PO/PI, .................(3), O, F, P, From (2) and (3), we get, PO/PI = PF1/(PI-PF1), fig-19, PI/PO = (PI-PF1)/PF1, PI/PO = PI/PF1 – 1, On dividing the equation by PI, we get, 1/PO = 1/PF1 -1/PI, 1/PO + 1/PI = 1/PF1, .................(4), The above equation is derived for a particular case of the object while, using a convex lens. To convert this into a general equation, we need to, use the sign convention., According to the sign convention, PO = -u ; PI = v ; PF1 = f, Substituting these values in equation 4, we get, 1/v – 1/u = 1/f, 2, , Free distribution by A.P. Government, , F1, , I, I/, , 127
Page 138 :
This equation is called lens formula. It can be used for any lens. But, remember to use the sign convention while using this equation., We have ‘u’ and ‘v’ values in table – 1 that were measured during activity, – 2. Find focal length of the lens from the values of the table for each set, of values of ‘u’ and ‘v’., • Is the focal length same for each set of values?, You might have noticed that irrespective of object distance and image, distance, you will get same focal length. If you do not get the same value, of focal length, there may be some experimental error while doing the, experiment. In such a case, find the average of all the values. This will be, equal to the focal length of the lens., Let us see an example, , Example 6, An electric lamp and a screen are placed on the table, in a line at a, distance of 1m. In what positions of convex lens of focal length of f = 21, cm will the image of lamp be sharp?, Solution, Let ‘d’ be distance between the lamp and screen and ‘x’ be the distance, between lamp and lens. From figure E-6, we have u = -x and v = d-x, By substituting these in lens formula,, We get, Screen, 1/f = 1/(d-x) + 1/x, Lamp, After solving this equation, we, x, d-x, d, get, fig-E(6), x2 – dx + fd = 0, It is a quadratic equation. Hence we get two solutions. The solutions, of the above equation are, _______, x = [d + √(d2-4fd)] / 2, .................(1), Given that f = 21cm and d= 1m =100cm., Substituting these values in equation 1, we get, x1 =70 cm and x2 = 30cm., NOTE: Image of the lamp can be sharp only when f is less than or, equal to 25cm., Discuss the reason for this using equation (1). Take the help of your, teacher., _______________, 128, , X Class, , Refraction of Light at Curved Surfaces
Page 139 :
•, , On what factors does the focal length of the lens depend?, Let us find out., , Activity 3, Take the same lens that was used in activity 2. Note the average, focal length of the lens that was calculated in the activity. Take a, cylindrical vessel such as glass tumbler. Its height must be much, greater than the focal length of the lens. (We require the vessel, which has a length (depth) nearly equal to four times of the focal, Lens, Circular, lens, length of lens). Keep a black stone inside the vessel at its bottom., holder, Stone, Now pour water into the vessel up to a height such that the height, fig-20, of the water level from the top of the stone is greater than focal, length of lens. Now dip the lens horizontally using a circular lens holder, as shown in the figure (20) above the stone. Set the distance between stone, and lens that is equal to or less than focal length of lens measured in activity, 2. Now look at the stone through the lens. (Do this in open ground), • Can you see the image of the stone?, • If Yes / Not, why? Give your reasons., You can see the image of the stone if the distance between lens and, stone is less than the focal length of the lens (in air). Now increase the, distance between lens and stone until you cannot see the image of the, stone., • What do you conclude from this activity?, • Does the focal length of the lens depend on surrounding medium?, You have dipped the lens to a certain height which is greater than the, focal length of lens in air. But you can see the image (when lens is raised, further, you could not see the image). This shows that the focal length of, lens has increased in water. Thus we conclude that the focal length of lens, depends upon the surrounding medium in which it is kept., , Lens maker’s formula, Imagine a point object ‘O’ placed on the principal axis of the thin lens, as shown in figure 21. Let this lens be placed in a medium of refractive, index na and let refractive index of, n, n, A, B, lens medium be nb., n, Consider a ray, from ‘O’ which is O, R P R, I, v, incident on the convex surface of the, u, x, lens with radius of curvature R1 at A, fig-21, as shown in figure 21., a, , a, , b, , 1, , Free distribution by A.P. Government, , 2, , Q, , 129
Page 140 :
The incident ray refracts at A., Let us assume that, it forms image at Q, if there were no concave, surface., From the figure(21), Object distance, PO = –u;, Image distance, v = PQ = x, Radius of curvature R = R1, n1 = na and n2 = nb, Substitute the above values in the equation, n2 / v - n1 / u = (n2-n1) / R, B nb / x + na / u = (nb-na) / R1, ...................(1), But the ray that has refracted at A suffers another refraction at B on the, concave surface with radius of curvature (R2). At B the ray is refracted and, reaches I on the principal axis., The image Q of the object due to the convex surface is taken as object, for the concave surface. So, we can say that I is the image of Q for concave, surface. See figure 21., Object distance, u = PQ = + x, Image distance, PI = v, Radius of curvature R = –R2, For refraction, the concave surface of the lens is considered as, medium-1 and surrounding medium is considered as medium2. Hence the, suffixes of refractive indices interchange. Then we get,, n1 = nb and n2 = na, Substituting the above values in equation n2 / v - n1 / u = (n2-n1) / R, na / v - nb / x = (na-nb) / (-R2), ...................(2), By adding (1) and (2) we get,, B na / v + na / u = (nb-na)( 1 / R1 + 1 / R2), Dividing both sides by na, We get, B 1 / v + 1 / u = (nb/ na – 1)(1 / R1 + 1 / R2), We know nb / na = nba called refractive index of lens with respect to, surrounding medium., 1 / v +1 / u = (nba– 1)(1 / R1 + 1 / R2), This is derived for specific case for the convex lens so we need to, generalize this relation. For this we use sign convention. Applying sign, convention to this specific case we get,, 1/v - 1/u = (nba– 1)(1/R1 - 1/R2), 130, , X Class, , Refraction of Light at Curved Surfaces
Page 141 :
We know that, 1/v -1/u = 1/f, So, we get, 1/f = (nba– 1)(1/R1 - 1/R2), ...................(3), If the surrounding medium is air, then the relative refractive index, could be absolute refractive index of the lens., ...................(4), 1/f = (n– 1)(1/R1 - 1/R2), This can be used only when the lens is kept in air., Where n is absolute refractive index and this equation is called lens, maker’s formula., NOTE: Always use sign convention while using any formula derived, in this chapter and the above formula can be used for any thin lens., The convex lens behaves as a converging lens, if it is kept in a medium, with refractive index less than the refractive index of the lens. It behaves, like a diverging lens when it is kept in a transparent medium with greater, refractive index than that of the lens., For example an air bubble in water behaves like a diverging lens., Let us see an example for lens maker formula., , Example 7, What is the focal length of double concave lens kept in air with two, spherical surfaces of radii R1 = 30cm and R2 =60cm. Take refractive index, of lens as n = 1.5., Solution:, From the figure E-7 using sign convention we get, R1 = -30cm, R2 = 60cm and also given that n = 1.5, using 1/f = (n-1)(1/R1 – 1/R2), 1/f = (1.5 - 1)[1/(-30)-1/60], Solving this, we get, C, Light rays, f = -120cm, fig-E(7), Here minus indicates that the lens is, divergent., 1, , C2, , Key words, Lens, Focal length, Focus, Optic centre, Principal axis,, Radius of curvature, Centre of curvature., Free distribution by A.P. Government, , 131
Page 142 :
What we have learnt, •, , •, •, •, , The formula used when a light ray enters a medium with refractive index n2 from a medium with, refractive index n1 at curved interface with a radius of curvature R is, n2/v –n1/u = (n2- n1)/R, A lens is formed when one medium is separated from another medium by two surfaces, one of, which is curved., Lens formula is 1/f =1/v – 1/u, where f is the focal length of lens, u is the object distance and v is the image distance., Lens maker’s formula is, 1/f = (n-1)(1/R1-1/R2), where R1 and R2 are radii of curvature , n is the refractive index and f is the focal length., , Improve your learning, 1. A man wants to get a picture of a zebra. He photographed a white donkey after fitting a glass,, with black stripes on to the lens of his camera. What photo will he get? Explain. (AS1), 2. Two converging lenses are to be placed in the path of parallel rays so that the rays remain, parallel after passing through both lenses. How should the lenses be arranged? Explain with a, neat ray diagram. (AS1), 3. The focal length of a converging lens is 20cm. An object is 60cm from the lens. Where will the, image be formed and what kind of image is it? (AS1), (Ans: A real, diminished, inverted image formed at 30cm from the lens), 4. A double convex lens has two surfaces of equal radii ‘R’ and refractive index n = 15. Find the, focal length ‘f’. (AS1), 5. Write the lens maker’s formula and explain the terms in it. (AS1), 6. How do you verify experimentally that the focal length of a convex lens is increased when it is, kept in water? (AS1), 7. How do you find the focal length of a lens experimentally? (AS1), 8. Harsha tells Siddhu that the double convex lens behaves like a convergent lens. But Siddhu, knows that Harsha’s assertion is wrong and corrected Harsha by asking some questions. What, are the questions asked by Siddhu? (AS2), 9. Assertion (A): A person standing on the land appears taller than his actual height to a fish, inside a pond. (AS2), Reason (R): Light bends away from the normal as it enters air from water., Which of the following is correct? Explain., a) Both A and R are true and R is the correct explanation of A., b) Both A and R are true and R is not the correct explanation of A., c) A is true but R is false., d) Both A and R are false., e) A is false but R is true., 132, , X Class, , Refraction of Light at Curved Surfaces
Page 143 :
10. A convex lens is made up of three different materials as shown in the figure, Q-10. How many of images does it form? (AS2), 11. Can a virtual image be photographed by a camera?(AS2), 12. You have a lens. Suggest an experiment to find out the focal length of the lens., (AS3), 13. Let us assume a system that consists of two lenses with focal length f1 and f2, respectively. How do you find the focal length of the system experimentally, when fig-Q(10), i) two lenses are touching each other, ii) they are separated by a distance ‘d’ with common principal axis. (AS3), 14. Collect the information about the lenses available in an optical shop. Find out how the focal, length of a lens may be determined by the given ‘power’ of the lens. (AS4), 15. Collect the information about lenses used by Galileo in his telescope. (AS4), 16. Use the data obtained by activity-2 in table-1 of this lesson and draw the graphs of u vs v and, 1/u vs 1/v. (AS5), A, , B, F/, , S, , N2, , N1, , N2, , N1, , F, , S/, , fig-Q(17), , fig- Q(18), , fig-Q(19), , 17. Figure Q-17 shows ray AB that has passed through a divergent lens. Construct the path of the, ray up to the lens if the position of its foci is known. (AS5), 18. Figure Q-18 shows a point light source and its image produced by a lens with an optical axis, N1N2. Find the position of the lens and its foci using a ray diagram. (AS5), 19. Find the focus by drawing a ray diagram using the position of source S and the image S/ given, in the figure Q-19. (AS5), 20. A parallel beam of rays is incident on a convergent lens with a focal length of 40cm. Where, should a divergent lens with a focal length of 15 cm be placed for the beam of rays to remain, parallel after passing through the two lenses? Draw a ray diagram. (AS5), 21. Draw ray diagrams for the following positions and explain the nature and position of image., i. Object is placed at C2, ii. Object is placed between F2 and optic centre P., (AS5), 22. How do you appreciate the coincidence of the experimental facts with the results obtained by, a ray diagram in terms of behaviour of images formed by lenses? (AS6), 23. Find the refractive index of the glass which is a symmetrical convergent lens if its focal length is, equal to the radius of curvature of its surface., (AS7) (Ans:1.5), 24. Find the radii of curvature of a convexo –concave convergent lens made of glass with refractive, index n=1.5 having focal length of 24cm. One of the radii of curvature is double the other., (Ans:R1=6cm,R2=12cm) (AS7), Free distribution by A.P. Government, , 133
Page 144 :
25. The distance between two point sources of light is 24cm .Where should a convergent lens with, a focal length of f=9cm be placed between them to obtain the images of both sources at the, same point? (AS7), 26. Suppose you are inside the water in a swimming pool near an edge. A friend is standing on the, edge. Do you find your friend taller or shorter than his usual height? Why?(AS7), , ks, Fill in the blan, 1., 2., 3., 4., , The rays from the distant object, falling on the convex lens pass through ......................, The ray passing through the ........................... of the lens is not deviated., Lens formula is given by .........................., The focal length of the plano convex lens is 2R where R is the radius of curvature of the surface., Then the refractive index of the material of the lens is....................., 5. The lens which can form real and virtual images is ........................., , s, Multiple choice question, 1. Which one of the following materials cannot be used to make a lens?, a) water, , b) glass, , c) plastic, , d) clay, , 2. Which of the following is true?, , [, , ], , [, , ], , a) the distance of virtual image is always greater than the object distance for convex lens, b) the distance of virtual image is not greater than the object distance for convex lens, c) convex lens always forms a real image, d) convex lens always forms a virtual image, 3. Focal length of the plano-convex lens is ............. when its radius of curvature of the surface is, R and n is the refractive index of the lens., [, ], a) f = R, , b) f = R/2, , c) f = R/(n–1), , d) f = (n–1)/R, , 4. The value of the focal length of the lens is equal to the value of the image distance when the rays, are, [, ], a) passing through the optic centre, , b) parallel to the principal axis, , c) passing throught he focus, , d) in all the cases, , 5. Which of the following is the lens maker’s formula, , [, , a) 1/f = (n-1)(1/R1+1/R2), , b) 1/f = (n+1)(1/R1-1/R2), , c) 1/f = (n-1)(1/R1-1/R2), , d) 1/f = (n+1)(1/R1+1/R2), , 134, , X Class, , ], , Refraction of Light at Curved Surfaces
Page 145 :
Chapter, , 7, Human Eye and, Colourful world, You have studied refraction of light through lenses in the previous, chapter. You have learnt about nature, position and relative size of image, formed by lenses for various distances of objects. In class IX, chapter VI, on sense organs in Biological science text book, explained the structure, of the human eye. The human eye functions on the principle of sensation, of vision. We see objects because the light scattered from them falls on, the eye. The eye has a lens in its structure., In the previous chapter, you learned that the focal length of lens and, object distance determine the nature, position and size of image., • What is the function of lens in human eye?, • How does it help to see objects at long distances and short distances?, • How is it possible to get the image at the same distance on the retina?, • Are we able to see all objects in front of our eye clearly?, • How do the lenses used in spectacles correct defects of vision?, To answer these questions, you need to understand the structure and, functioning of the human eye., Let us do the following activities to know about some interesting facts, about our vision., , Least distance of distinct vision, , Activity 1, Take a text book and hold it with your hands in front of you at a, certain distance. Now try to read the contents on the page. Slowly move, the book towards your eye till it is very close to your eyes., • What changes do you notice?, Free distribution by A.P. Government, , 135
Page 146 :
You may see that printed letters on the page of the text book appear, blurred or you feel strain in the eye., Now slowly move the book backwards to a position where you can see, clear printed letters without straining your eye. Ask your friend to measure, the distance between your eye and text book at this position. Note down, its value. Repeat the activity with other friends and note down the distances, for distinct vision in each case., Find the average of all these distances of clear vision., • What value do you get for average distance?, From this activity you will come to know that to see an object, comfortably and distinctly, you must hold it at a distance about 25 cm, from your eyes. This distance is called least distance of distinct vision., This varies from person to person and with age. At a young age (say below, 10 years) the muscles around the eye are strong and flexible and can bear, more strain. Therefore the least distance of distinct vision at this age is as, close as 7 to 8 cm. In old age the muscles cannot sustain more strain, hence the least distance of distinct vision shifts to a larger value, say, about, 1 to 2 m or even more., • Are you able to see the top and bottom of an object placed at a distance, of about 25 cm from your eye irrespective of its shape?, Let us find out., , Activity 2, Collect a few wooden sticks used in cloth roller in, clothes store (or) collect waste PVC pipes that are used, for electric wiring. Prepare sticks or pipes of 20 cm, 30, cm, 35 cm, 40 cm, 50 cm from them. Place a retort stand, on a table and stand near the table such that your head is, beside the vertical stand (see fig 1). Adjust the clamp on, the horizontal rod and fix it at a distance of 25 cm from, your eyes. Ask one of your friends to fix a wooden stick, fig-1, of 30 cm height to the clamp in a vertical position as shown, in fig1., Now keeping your vision parallel to horizontal rod of, the stand, try to see the top and bottom of wooden stick kept in vertical, position., • Are you able to see both ends of the stick simultaneously without any, movement (shaking) in your eyes?, 136, , X Class, , Human Eye and Colourful World
Page 147 :
In activity-1, you learned that least distance for distinct vision is about, 25 cm. It varies from person to person. If you are not able to see both end, of the stick at this distance (25 cm), adjust the vertical stick on the, horizontal rod till you are able to see both ends of the stick at the smallest, possible distance from your eye. Fix the vertical stick at this position with, the help of the clamp., Without changing the position of the clamp on the horizontal rod,, replace this stick of 30 cm length with other sticks of various lengths one, by one and try to see the top and bottom of the stick simultaneously without, any change in the position of eye either upwards downwards or side ways., • Are you able to see both ends of the sticks in all these cases? If not, why?, Let us know., Observe the following figure-2. You can see the whole object AB which, is at a distance of 25 cm (least distance of distinct vision) because the, rays coming from the ends A and B of the object AB will enter the eye., Similarly you can also see whole object CD with eye as explained above., Let us assume that AB moves closer to the eye to a position AI BI as shown, in figure2., • Will you be able to see the whole object now?, From the figure 2, you notice that you will be able, to see only the part (EF) of the object AI BI because the, A, rays coming from E and F enter your eye. The rays, E, coming from AI and BI cannot enter your eye., F, The rays coming from the extreme ends of an object, 0, form an angle at the eye. If this angle is below 60 , we, B, can see the whole object. If this angle is above 600, then, fig-2, we can see only the part of the object., This maximum angle, at which we are able to see the whole object is, called angle of vision. The angle of vision for a healthy human being is, about 600. It varies from person to person and with age., You have learnt that the value of least distance of distinct vision is, about 25 cm and the value of angle of vision of human beings is about 600., You also learnt that these values change from person to person and with, age of person., • Why do the values of least distance of distinct vision and angle of, vision change with person and age?, To answer the above question, we need to understand the structure of, eye and its functioning., Free distribution by A.P. Government, , I, , A, , I, , B, , C, , D, , 137
Page 148 :
ciliary, muscles, iris, pupil, aqueous, humour, cornea, , 138, , Structure of human eye, The human eye is one of the most important, sense organs. It enables us to see the object and, retina, colours around us., lens, Figure 3 shows schematically the basic, components of human eye. The eye ball is nearly, spherical in shape. The front portion is more, sharply curved and is covered by a transparent, fig-3, optic nerve, protective membrane called the ‘cornea’. It is this, portion which is visible from outside. Behind the cornea, there is place, filled with a liquid called aqueous humour and behind this a crystalline, lens which is responsible for the image formation. Between the aqueous, humour and the lens, we have a muscular diaphragm called ‘iris’ which has, a small hole in it called pupil. Iris is the coloured part that we see in an, eye., The pupil appears black because any light falling on it goes into the, eye and there is almost no chance of light coming back to the outside. Iris, helps in controlling the amount of light entering the eye through ‘pupil’., In low light condition, the iris makes the pupil to expand so that more light, is allowed to go in and in the case of bright (or) excess light condition, it, makes the pupil contract and there by prevent the excess light not to go, into eye. Thus ‘iris’ enables pupil to act as a “variable aperture” for entry, of light into the eye., The lens is hard in the middle and gradually becomes soft towards the, outer edge. The light that enters the eye forms an image on the retina. (It, covers the rear part of eyeball). The distance between the lens and retina, is about 2.5 cm i.e., for any position of object in front of the eye the, image distance is fixed and about 2.5 cm., • How can we get this same image distance for various positions of, objects?, • Can you answer this question using concepts of refraction through, lenses?, In the previous chapter, you have learnt that for different positions of, object, the image distance remains constant only when there is a change in, focal length of lens. Further, the focal length of a lens depends on the, material by which it has been made and radii of curvature of lens. We need, to change focal length of eye lens to get same image distance for various, positions of object in front of the eye. This is only possible when the, eyelens is able to change its shape., , X Class, , Human Eye and Colourful World
Page 149 :
•, •, , How does eye lens change its focal length?, How does this change take place in the eye ball?, Let us know, The ciliary muscle to which eye lens is attached (see fig-3) helps the, eye lens to change its focal length by changing the radii of curvature of the, eye lens., When the eye is focussed on a distant object, the ciliary muscles are, relaxed so that the focal length of eye lens has its maximum value which is, equal to its distance from the retina. The parallel rays coming into the eye, are then focussed on to the retina and we see the object clearly., When the eye is focussed on a closer object, the ciliary muscles are, strained and focal length of eye-lens decreases. The ciliary muscles adjust, the focal length in such a way that the image is formed on retina and we, see the object clearly. This process of adjusting focal length is called, “accommodation”. However these muscles cannot strain beyond a limit, and hence if the object is brought too close to eyes, the focal length cannot, be adjusted to form an image on the retina. Thus there is a minimum distance, for distinct vision of an object which is roughly equal to 25 cm as we have, learned in activity-1., • Does eye lens form a real image or virtual image?, • How does the image formed on retina help us to perceive the object, without change in its shape, size and colour?, Let us know, The eye-lens forms a real and inverted image of an object on the retina., The retina is a delicate membrane, which contains about 125 million, receptors called ‘rods’ and ‘cones’ which receive the light signal (rodsidentify the colour: cones-identify the intensity of light). These signals, are transmitted to the brain through about 1 million optic-nerve fibres., The brain interprets these signals and finally processes the information so, that we perceive the object in terms of its shape, size and colour., In our previous discussion, you have learnt that eye-lens itself changes, its focal length in accordance with distance of the object with the help of, ciliary muscles., • Is there any limit to the change of focal length of the eye-lens?, • What are the maximum and minimum focal lengths of the eye lens?, How can we find them?, Let us find, Free distribution by A.P. Government, , 139
Page 150 :
When the object is at infinity, the parallel rays from, the object falling on the eye lens are refracted and, they form a point sized image on retina (see fig-4a)., In this situation, eye-lens has a maximum focal, length., fig-4(a), When the object is at infinity,, u= - ∞; v = 2.5 cm (image distance which is equal, to distance between eye-lens and retina), using the formula, 1/f = 1/v – 1/u, 1/f max = 1/ 2.5 + 1/ ∞, 1/f max=1/2.5+0, fmax = 2.5 cm, we get,, fmax = 2.5 cm, consider that an object is placed at distance of 25 cm from our eye. In, this situation eye has minimum focal length., Here u = - 25 cm; v = 2.5 cm, Using the formula 1/f = 1/v – 1/u, 1/fmin = 1/ 2.5 + 1/ 25, fig-4(b), 1/fmin=11/ 25, fmin = 25 /11 = 2.27 cm, If the position of an object is between infinity and the point of least, distance of distinct vision, then the eye lens adjusts it’s focal length in, between 2.5 cm to 2.27 cm to form a clear image on the retina., The ability of eye-lens to change its focal length is called, “accommodation of lens”., • What happens if the eye lens is not able to adjust its focal length?, • What happens if the focal length of eye lens is beyond the range of 2.5, cm to 2.27 cm?, Let us find out., Sometimes the eye may gradually lose its ability for accommodation., In such conditions the person cannot see an object clearly and comfortably., The vision becomes blurred due to defects of the eye lens. There are mainly, three common defects of vision., They are:, i. Myopia, ii. Hypermetropia, iii. Presbyopia., , L, , 140, , X Class, , Human Eye and Colourful World
Page 151 :
Myopia, Some people cannot see objects at long distances but can see nearby, objects clearly. This type of defect in vision is called ‘Myopia’. It is also, called ‘near sightedness’. For these people the maximum focal length is, less than 2.5 cm. In such cases the rays coming from distant objects, after, refraction through the eye, lens, form an image before the, retina as shown in figures 5(a), M, L, and (b)., fig-5(a), A healthy person can see, objects at all distances more, than 25 cm clearly but a, M, L, person with myopia can see, fig-5(b), objects clearly up to a certain, distance. Let the extreme, point from where an object, L, appears clearly to a person, M, fig-5(c), with myopia be ‘M’ (shown in, figure 5(c))., If the object is at M or in, L, O, between M and point of least, M, fig-5(d), distance of distinct vision, (L),the eye lens can form an, image on the retina (see, figure 5(c) and 5(d)). This point M is called ‘far point’., The point of maximum distance at which the eye lens can form an, image on the retina is called ‘far point’., The defect, in which people cannot see objects beyond far point is, called ‘Myopia’., • What can we do to correct myopia?, The eye lens can form clear image on the retina, when an object is, placed between far point and point of least distance of distinct vision. If, we are able to bring the image of the object kept beyond far point , between, the far point and the point, of least distance of distinct, L, vision using a lens, this, M, image acts as an object for, fig-5(e), the eye lens., Free distribution by A.P. Government, , 141
Page 152 :
This can be made possible only when a concave lens is used (recollect, image formation by refraction through a concave lens)., • How can you decide the focal length of the lens to be used to correct, myopia?, To correct one’s Myopia, we need to select a lens which forms an, image at the far point for an object at infinity. We need to select bi-concave, lens to achieve this., This image acts like an object for the eye lens. Hence the final image, is formed on the retina., Let us find the focal length of this bi-concave lens., Here object distance (u) is infinity and image distance (v) is equal to, distance of far point., u = - ∞ ; v = distance of far point = -D, let ‘f’ be the focal length of bi-concave lens., Using lens formula, 1/f = 1/v – 1/u, 1/f = 1/ -D B f = -D, Here ‘f’ is negative showing that it is a concave lens., • What happens when the eye has a minimum focal length greater than, 2.27 cm?, Let us find out., , Hypermetropia, L, , H, , fig-6(a), , L, , H, , fig-6(b), H, , L, , fig-6(c), , 142, , X Class, , Hypermetropia is also, known as “far sightedness”. A, person with hypermetropia, can see distant objects clearly, but cannot see objects at near, distances, because the, minimum focal length of eye, lens for the person of, hypermetropia is greater than, 2.27 cm. In such cases, the, rays coming from a nearby, object, after refraction at eye, lens, forms an image beyond, the retina as shown in figure, 6 (a)., Human Eye and Colourful World
Page 153 :
Let the point of least distance at which the eye lens forms a clear, image on the retina for a person with hypermetropia be ‘H’. See figure, 6(b)., If an object is at H or beyond H, the eye can form its image on retina, (see figures 6(b) and 6(c)). If the object is between H and point of least, distance of distinct vision (L) then it cannot form an image. See figure, 6(a)., The point of minimum distance at which the eye lens can form an image, on the retina is called near point (d). The people with defect of, hypermetropia cannot see objects placed between near point (H) and point, of least distance of distinct vision (L)., • How can you correct this defect?, Eye lens can form a clear image on the retina when any object is placed, beyond near point. To correct the defect of hypermetropia, we need to use, a lens which forms an image of an object beyond near point, when the, object is between near point (H) and least distance of distinct vision (L)., This is possible only when a double convex lens is used., • How can you decide the focal length of the convex lens to be used?, To find the focal length of, lens, let us consider that the, L, object is at point of least, H, distance of distinct vision (L)., fig-6(d), Then the defect of vision,, hypermetropia, is corrected when the image of the object at L is formed at, the near point (H) by using a bi-convex lens as shown in figure 6(d)., This image acts like an object for the eye lens. Hence final image due, to eye is formed at retina (see figure 6(d)), Here object distance (u) = -25 cm, Image distance (v) = distance of near point = -d, Let ‘f’ be the focal length of bi-convex lens., Using lens formula, 1/f = 1/v – 1/u, 1/f = 1/ -d – 1/(-25), 1/ f = -1/d +1/25, 1/ f = (d – 25)/25d, f= 25d / (d – 25) (f is measured in centimeters), we know that if d > 25cm, then ‘f’ becomes +ve i.e., we need to use, biconvex lens to correct defect of hypermetropia., Free distribution by A.P. Government, , 143
Page 154 :
Presbyopia, Presbyopia is vision defect when the ability of accommodation of the, eye usually decreases with ageing. For most people the near point gradually, recedes away. They find it difficult to see nearby objects clearly and, distinctly., This happens due to gradual weakening of ciliary muscles and, diminishing flexibility of the eye lens. This effect can be seen in aged, people. Sometimes a person may suffer from both myopia and, hypermetropia with ageing ., To correct this type of defect of vision we need bi-focal lenses which, are formed using both concave and convex lenses. Its upper portion consists, of the concave lens and lower portion consists of the convex lens., If you go to an eye hospital to get tested for vision defects, the doctor, gives you a prescription that contains some information regarding type of, lens to be used to correct vision., • Have you ever observed details in the prescription?, You might have heard people saying “my sight is increased or, decreased”., • What does it mean?, Usually doctors, after testing for defects of vision, prescribe corrective, lenses indicating their power which determines the type of lens to be used, and its focal length., • What do you mean by power of lens?, Power of lens:, The degree of convergence or divergence of light rays that can be, achieved by a lens is expressed in terms of its power., The reciprocal of focal length is called power of lens., Let ‘f’ be the focal length of lens., Power of lens P = 1 / f(in m); P = 100 / f (in cm), The unit of power is dioptre., It is denoted by the letter ‘D’., , Example1, Doctor advised to use 2D lens. What is its focal length?, Solution: Given that power of lens P = 2D, Using, P = 100 / f (in cm); 2 = 100 / f, Therefore, f = 100/2 = 50 cm., The lens has focal length, f = 50 cm., 144, , X Class, , Human Eye and Colourful World
Page 155 :
Dispersion and Scattering of Light, You might have seen a rainbow form in the sky just after a rain shower., It must have fascinated you with spectacular colours appearing as a semicircular band of colours., • How could the white light of the sun give us various colours of the, rainbow?, In previous chapters, you have studied the behaviour of light when it, refracts through plane surface and curved surfaces, such as a lens. You, also studied the nature, position and relative size of image formed by lenses., • What happens to a light ray when it passes through a transparent, medium bounded by plane surfaces which are inclined to each other?, • What is a prism?, , Prism, A prism is a transparent medium separated, P, from the surrounding medium by at least two plane, surfaces which are inclined at a certain angle in, Normal, such a way that, light incident on one of the plane, surfaces emerges from the other plane surface., i, M, To understand the behaviour of light when it is, ray, t, n, de, Inci, incident on the plane of a prism and passes into, the prism, we need to define certain terms, associated with prisms., Q, Consider a triangular glass prism. It contains, fig-7, two triangular bases and three rectangular plane, lateral surfaces. These lateral surfaces are inclined to each other., Let us consider that triangle PQR represents outline of the prism where, it rests on its triangular base. Let us assume that a light ray is incident on, the plane surface PQ of a prism at M as shown in figure 7. Draw a, perpendicular to the surface at M. It becomes a normal to that surface. The, angle between the incident ray and normal is called angle of incidence, (i1). The ray is refracted at M. It moves through prism and meets the other, plane surface at N and finally comes out of the prism. The ray which comes, out of the surface PR at N is called emergent ray. Draw a perpendicular to, PR at point N. The angle between the emergent ray and normal is called, angle of emergence (i2 ).The angle between the plane surfaces PQ and PR, is called the angle of the prism or refracting angle of prism A and the, angle between the incident ray and emergent ray is called angle of, deviation(d)., , Normal, , 1, , Free distribution by A.P. Government, , N, , i2, Em, , er, , ge, , nt, , ra, , R, , 145, , y
Page 156 :
Let us now take up an activity to study the refraction of light through a, triangular prism., , Lab Activity, Aim: Finding the refractive index of a prism., Material required: Prism, piece of white chart of size 20x20 cm,, pencil, pins, scale and protractor., Procedure: Take a prism and place it on the white chart in such a way, that the triangular base of the prism is on the chart. Draw a line around the, prism (boundry) using a pencil. Remove the prism., • What is the shape of the outline drawn?, It is a triangle. Name its vertices as P,Q, and R.[for many prisms the, triangle formed is equilateral]. The refracting surfaces could be rectangular, in shape. Find the angle between PQ and PR . This is the angle of the prism, (A)., Mark M on the side of triangle PQ and also draw a perpendicular to, PQ at M. Place the centre of the protractor at M and along the normal., Mark an angle of 300 and then draw a line up to M. This line denotes the, incident ray. This angle is called angle of incidence. Note it in a table (1)., Draw a small arrow on it as shown in figure 8., Place the prism in its position, (triangle) again. Now fix two pins, vertically on the line at points A and, B as shown in figure 8. Look for, the images of pins through the, prism from the other side (PR) and, fix another two pins at points C and, D in such a way that all the four pins, appear to lie along the same straight line. Do, it carefully. Now remove the prism and take, out pins. Draw a line joining the two pin-holes, formed by the pins to meet surface ‘PR’, this, is the emergent ray which ‘emerges from’ the, surface PR at a point ‘N’. The angle between, the normal at N and the emergent ray is the, angle of emergence. Measure this angle and, note its value in the table (1)., , Table 1, Angle of, Angle of, Angle of, incidence (i1) emergence (i2) deviation (d), , P, A, , Normal, i1, B, , O, M, , d, N, , A, , Normal, i2, C, D, , Q, , fig-8, , Pin, , 146, , X Class, , R, , Human Eye and Colourful World
Page 157 :
Angle of deviation d, , Now join the points M and N by a straight line. The line passing through, the points A,B, M,N,C and D represents the path of light when it suffers, refraction through the prism., • How do you find the angle of deviation?, Extend both incident and emergent rays till they meet at a point ‘O’., Measure the angle between these two rays. This is the angle of deviation., It is denoted by a letter ‘d’. Note it in table (1). Repeat this procedure for, various angles of incidence such as 400,500 etc. Find the corresponding, angles of deviation and angles of emergence and note them in table (1)., • What do you notice from the angles of deviation?, You will notice that the angle of deviation decreases first and then, increases with increase in the angle of incidence., • Can you draw a graph between angle of incidence and angle of, deviation?, Take angle of incidence along X- axis and the angle of deviation along, Y- axis. Using a suitable scale, mark points on a graph paper for every pair, of angles. Finally join the points to obtain a graph (smooth curve). Check, your graph with graph shown in figure 9., Y, • From the graph, can you find the minimum of the, angles of deviation?, Yes we can. Draw a tangent line to the curve,, D, parallel to X- axis, at the lowest point of the graph., The point where this line cuts the Y- axis gives the, i =i, X, angle of minimum deviation. It is denoted by D., Angle of incidence i, Draw a parallel line to y-axis through the point, where the tangent touches the graph. This line meets, fig-9, x-axis at a point showing the angle of incidence, corresponding to the minimum deviation. If you do the experiment with, this angle of incidence you will get an angle of emergence equal to the, angle of incidence. Look at your table (1)., • Is there any relation between the angle of incidence and angle of, emergence and angle of deviation?, • Can you find refractive index of a prism? If yes, how?, Let us find out., 1, , 2, , 1, , Derivation of formula for refractive index of a prism, Observe the ray diagram in the figure 10(a)., From triangle OMN, we get, d = i1- r1 + i2 – r2, Free distribution by A.P. Government, , 147
Page 158 :
d = (i1+i2) – (r1+r2) ––—— (1), From triangle PMN, we have, A, O, A + (900-r1) + (900-r2) = 1800, d, By simplification, we get, i, M, N, r, r1 + r 2 = A, ———(2), r, From (1) and (2), we have, d = (i1+i2) – A, R, A+d = i1+i2, ––——(3), fig-10(a), This is the relation between angle of, incidence, angle of emergence, angle of deviation and angle of prism., From Snell’s law, we know that n1 sin i = n2 sin r, Let n be the refractive index of the prism., Using Snell’s law at M, with refractive index of air, n1 =1; i = i1 ; n2 = n ; r = r1 , gives, sin i1 = n sin r1, ———(4), similarly, at N with n1 = n ; i = r2 ; n2 = 1 ; r = i2 , gives, n Sin r2 = Sin i2, ———(5), We know that at the angle of minimum deviation (D), the angle of, incidence is equal to the angle of emergence i.e., i1 = i2. Observe figure, 10(b). You will note that MN is parallel to the side QR, actually ray MN is, parallel to the base of the prism. (See figure 10(b))., When i1 = i2, angle of deviation (d) becomes angle of minimum, deviation (D)., Then equation (3) becomes, P, A+D = 2i1, A, or i1 = (A+D)/2, D, O, When i1 = i2 then, it is clear that r1 = r2, i, N, So from equation (2) we get,, M, r, r, 2r1 = A, or r1 = A/2, Substituting i1 and r1 in (4) we get, R, Sin{(A+D)/2)} = n. Sin(A/2), fig-10(b), Therefore, n = Sin(A+D/2)/Sin(A/2) —(6), This is the formula for the refractive index of the prism., Now use the results of lab activity (1) and find refractive index of the, prism using equation (6), P, , i1, , 2, , 1, , Q, , i1, , 1, , 1, , Q, , 148, , X Class, , 2, , 1, , Human Eye and Colourful World
Page 159 :
Let us see an example., , Example 2, A prism with an angle A = 600 produces an angle of minimum deviation, of 300. Find the refractive index of material of the prism., Solution: Given that A = 600 and D = 300., Using n = Sin[(A+D)/2]/Sin(A/2) = Sin(900/2)/Sin(300), = Sin 450/ Sin300 = (1/√2)/(1/2) = √2, B n = √2, thus, the refractive index of the given prism = √2, ––––––––––––, Let us take up a simple activity with prism., , Activity 3, Do this experiment in the dark room. Take a prism and place it on the, table near a vertical white wall. Take a thin wooden plank. Make a small, hole in it and fix it vertically on the table. Place the prism between the, wooden plank and wall. Place a white light source behind the hole of the, wooden plank. Switch on the light. The rays coming out of the hole of, plank become a narrow beam of light. Adjust the height of the prism such, that the light falls on one of the lateral surfaces. Observe the changes in, emerged rays of the prism. Adjust the prism by slightly rotating it till you, get an image on the wall., • What do you observe on the wall?, • Could you get a coloured image on the wall?, • Why does white light split into colours?, • What colours do you see?, • Can you notice any change in the angle of deviation of each colour?, • Which colour has the minimum deviation?, Let us do another experiment., , Activity 4, Take a metal tray and fill it with water. Place a, mirror in the water such that it makes an angle to the, water surface. Now focus white light on the mirror, through the water as shown in figure 11. Try to obtain, colour on a white card board sheet kept above the water, surface. Note the names of the colours you could see, in your book., Free distribution by A.P. Government, , Dispersed light, , White, light, , Water, Metal, tray, , Mirror, , fig-11, 149
Page 160 :
In activity (3) and (4), we observe that white light is splitting into, certain different colours., •, , Is this splitting of white light into colours explained by using ray, theory?, , It is not possible to explain the splitting of white light into different, colours using ray theory., •, , Why is this so?, Let us see, , Dispersion of Light, In activity 3, we observe that the angle of deviation is minimum for, red as compared to the angles of deviation of other colours and maximum, for violet., The splitting of white light into different colours (VIBGYOR) is called, dispersion., In our previous discussion, we learnt that for a particular refractive, index of prism there must be only one angle of minimum deviation and, according to Fermat’s principle, light ray always chooses the path of least, time. But in activity-3,we noticed that light has chosen different paths., •, , Does this mean that the refractive index of the prism varies from colour, to colour?, , •, , Is the speed of light of each colour different?, , The situation we witnessed in activities (3) and (4) rule out ray theory, of light. We can consider that white light is a collection of waves with, different wavelengths. Violet colour is known to have the shortest, wavelength while red is of the longest wavelength., According to wave theory, light can be thought of a wave propagating, in all directions. Light is an electromagnetic wave. Here no particle, physically oscillates back and forth. Instead, the magnitude of electric and, magnetic fields, associated with the electromagnetic wave, vary, periodically at every point. These oscillating electric and magnetic fields, propagate in all directions with the speed of light., •, , 150, , X Class, , Can you guess now, why light splits into different colours when it, passes through a prism?, , Human Eye and Colourful World
Page 161 :
The reason lies in the fact that, while the speed of light is constant in, vacuum for all colours, it depends on the wavelength of light when it passes, through a medium. We know that refractive index is the ratio of speeds in, vacuum and in the medium. Consequently, the refractive index of a medium, depends on wavelength of light. When white light passes through a medium,, each colour selects its least time path and we have refraction of different, colours to different extents. This results in separation of colours, producing, a spectrum on the wall and in the mirror as we saw in activities (3) and (4)., It has been experimentally found that refractive index decreases with an, increase in wavelength. If we compare the wave lengths of seven colours, in VIBGYOR, red colour has longest wavelength and violet colour has, shortest wavelength. The refractive index of red is low hence it suffers, low deviation., We noticed that when white light passes through a prism, it splits into, seven colours. Let us assume that you have sent a single colour ray through, the prism., • Does it split into more colours? Why?, We know that the frequency of light is the property of the source and, it is equal to number of waves leaving the source per second. This cannot, be changed by any medium. Hence frequency doesn’t change due to, refraction. Thus coloured light passing through any transparent medium, retains its colour., While refraction occurs at the interface, the number of waves that are, incident on the interface in a second must be equal to the number of waves, passing through any point taken in another medium. This means that the, frequency of the light wave remains unaltered while its wavelength changes, depending on the medium through which it passes. We know that the relation, between the speed of wave (v), wavelength ( λ) and frequency (f) is., v=fλ, (frequency (f) may be denoted by υ), For refraction at any interface, v is proportional to λ. Speed of the, wave increases with increase in wavelength of light and vice versa., • Can you give an example in nature, where you observe colours as seen, in activity 3?, Your answer certainly is a rainbow. That is a good example of dispersion, of light., • When do you see a rainbow in the sky?, • Can we create a rainbow artificially?, Let us see how., Free distribution by A.P. Government, , 151
Page 162 :
Activity 5, Select a white coloured wall on which the sun rays fall. Stand in front, of a wall in such a way that the sun rays fall on your back. Hold a tube, through which water is flowing. Place your finger in the tube to obstruct, the flow of water. Water comes out through the small gaps between the, tube and your finger like a fountain. Observe the changes on the wall, while the water shower is maintained; you can see colours on the wall., • How is that you are able to see colours on, Sun l, ight, the wall?, Water drop, • Are the sun rays coming back to your eyes, from the wall or from water drops?, Let us find out., 40, The beautiful colours of the rainbow are due, 42, to dispersion of the sunlight by millions of tiny, water droplets. Let us consider the case of an, t, le, individual water drop., Vio, d, e, R, Observe figure 12. The rays of sunlight enter, fig-12, the drop near its top surface. At this first refraction,, the white light is dispersed into its spectrum of colours, violet being, deviated the most and red the least. Reaching the opposite side of the, drop, each colour is reflected back into the drop because of total internal, reflection. Arriving at the surface of the drop, each colour is again refracted, into air. At the second refraction the angle between red and violet rays, further increases when compared to the angle between those at first, refraction., The angle between the incoming and outgoing rays can be anything, between 00 and about 420. We observe bright rainbow when the angle, between incoming and outgoing rays is near the maximum angle of 420., Diagrammatically it is shown in figure 12.Although each drop disperses a, full spectrum of colours, an observer is in a position to see only a single, colour from any one drop depending upon its position., If violet light from a single drop reaches the eye of an observer, red, light from the same drop can’t reach his eye. It goes elsewhere possibly, downwards of the eye of the observer (see in figure 13). To see red light,, one must look at the drop higher in the sky. The colour red will be seen, when the angle between a beam of sunlight and light sent back by a drop is, 420. The colour violet is seen when the angle between a sunbeam and light, sent back by a drop is 400. If you look at an angle between 400 and 420, you, o, , o, , 152, , X Class, , Human Eye and Colourful World
Page 163 :
will observe the remaining, Sun l, colours of VIBGYOR, ight, 40, • Why does the light dispersed, by the raindrops appear as a, 42, bow?, let, To find answer this, Vio, let, Vio, question, we need a little, d, Re, geometric reasoning. First of, d, Re, all, a rainbow is not the flat two, fig-13, dimensional arc as it appears to, us. The rainbow you see is actually a three dimensional cone with the tip at, your eye as shown in figure 14. All the drops that disperse the light towards, you lie in the shape of the cone, – a cone of different layers. The, Sun light, drops that disperse red colour, to your eye are on the outer, 40, Sun, 42, most layer of the cone, similarly, the drops that disperse orange, colour to your eye are on the, fig-14, layer of the cone beneath the red, colour cone. In this way the cone responsible for yellow lies beneath orange, and so on it till the violet colour cone becomes the innermost cone.(see, in figure 14)., o, , Water, drops, , o, , o, , o, , Think and discuss, • Can you imagine the shape of rainbow when observed during travel in an airplane?, Discuss with your friends and collect information., It is our common experience that the sky appears blue in colour on a, bright dry day., • Why is the sky blue?, To answer this question, you need to understand another phenomenon, of light called scattering., • What is scattering?, Let us see, Free distribution by A.P. Government, , 153
Page 164 :
Scattering of Light, , Sun light, , fig-15, , 154, , Scattering of light is a complex phenomenon. Let us try to understand, the idea of scattering., • Do you know what happens to the free atom or molecule when it is, exposed to certain frequency of light?, Atoms or molecules which are exposed to light absorb light energy, and emit some part of the light energy in different directions. This is the, basic process happens in scattering of light., The effect of light on a molecule or an atom depends on the size of, atom or molecule. If the size of the particle (atom or molecule) is small,, it will be affected by higher frequency (lower wave length) light and vice, versa., Let us consider that a certain frequency of light, Scattered light, is incident on an atom. Then the atom comes into, vibration due to this light. This in turn releases or reemits light in all directions with different intensity., Atom, The intensity of light is the energy of light passing, through unit area of plane, taken normal to the, direction of propagation of light, in one second., Let us consider that the free atom or free, molecule is somewhere in space as shown in figure, 15., Light of certain frequency falls on that atom or molecule. This atom, or molecule responds to the light whenever the size of the atom or molecule, is comparable to the wave length of light. If this condition is satisfied, the, atom absorbs light and vibrates. Due to these vibrations, the atom re-emits, a certain fraction of absorbed energy in all directions with different, intensities. The re-emitted light is called scattered light and the process, of re-emission of light in all directions with different intensity is called, scattering of light. The atoms or molecules are called scattering centre., Let us take the angle ‘θ’ between the incident light and a direction in which, the intensity of scattered light is observed, we call this angle as angle of, scattering. It is experimentally observed that the intensity of scattered, light varies with angle of scattering. The intensity is maximum at 900 angle, of scattering., This is the reason for the appearance of clear blue colour when look at, the sky in a direction perpendicular to the direction of the sun rays. If our, angle of view is changed, the intensity of blue colour also changes., , X Class, , Human Eye and Colourful World
Page 165 :
Now you might have got a doubt why scattering of light gives blue, colour only. Why can’t it give other colours?, Let us find out whether the scattering centres are responsible for the, blue of the sky?, We know that our atmosphere contains different types of molecules, and atoms. The reason for blue sky is due to the molecules N2 and O2. The, sizes of these molecules are comparable to the wavelength of blue light., These molecules act as scattering centres for scattering of blue light., • Why is that the sky appears white sometimes when you view it in certain, direction on hot days?, Our atmosphere contains atoms and molecules of different sizes., According to their sizes, they are able to scatter different wavelengths of, light. For example, the size of the water molecule is greater than the size, of the N2 or O2. It acts as a scattering centre for other frequencies which, are lower than the frequency of blue light., On a hot day, due to rise in the temperature water vapour enters into, atmosphere which leads to abundant presence of water molecules in the, atmosphere. These water molecules scatter the colours of other frequencies, (other than blue). All such colours of other frequencies reach your eye, and the sky appears white., • Can we demonstrate scattering of light by an experiment?, Let us try, , Activity 6, Take a solution of sodium-thio-sulphate (hypo) and sulphuric acid in a, glass beaker. Place the beaker in an open place where abundant sun light is, available. Watch the formation of grains of sulphur and observe changes in, the beaker., You will notice that sulphur precipitates as the reaction is in progress., At the beginning, the grains of sulphur are smaller in size and as the reaction, progresses, their size increases due to precipitation., Sulphur grains appear blue in colour at the beginning and slowly their, colour becomes white as their size increases. The reason for this is, scattering of light. At the beginning, the size of grains is small and almost, comparable to the wave length of blue light. Hence they appear blue in the, beginning. As the size of grains increases, their size becomes comparable, to wave lengths of other colours. As a result of this, they act as scattering, centres for other colours. The combination of all these colours appears as, white., Free distribution by A.P. Government, , 155
Page 166 :
•, , Do you know the reasons for appearance the red colour of sun during, sunrise and at sunset?, The atmosphere contains free molecules and atoms with different sizes., These molecules and atoms scatter light of different wavelengths which, are comparable to their size. Molecules having a size that is comparable, to the wavelength of red light are less in the atmosphere. Hence scattering, of red light is less when compared to the other colours of light. The light, from the sun needs to travel more distance in atmosphere during sunrise, and sunset to reach your eye. In morning and evening times, during sunrise, and sunset, except red light all colours scatter more and vanish before, they reach you. Since scattering of redlight is very small, it reaches you., As a result sun appears red in colour during sunrise and sunset., • Can you guess the reason why sun doesnot appear red during noon, hours?, During noon hours, the distance to be travelled by the sun rays in the, atmosphere is less than that compared to morning and evening hours., Therefore all colours reach your eye without much scattering. Hence the, sun appears white during noon hours., , Do you know?, Our beloved scientist and Noble prize winner, Sir C.V., Raman explained the phenomenon of light scattering in gases, and liquids. He found experimentally that the frequency of, scattered light by the liquids is greater than the frequency of, incident light. This is called Raman Effect. By using this effect, scientists determine the shapes of the molecules., , Sir CV Raman, , So far, we have learned some ideas of the light such as refraction,, dispersion and scattering. These are wonderful phenomena occuring in, our surroundings. When you observe any phenomena, try to resolve the, problem and appreciate the wonderful world based on the behaviour of, light., , Key words, Least distance of distinct vision, Angle of vision, Accommodation of eye lens,, Myopia, Hypermetropia, Presbyopia, Power of lens, Prism, Angle of prism or, refracting angle of prism, Angle of minimum deviation, Dispersion, Scattering., 156, , X Class, , Human Eye and Colourful World
Page 167 :
What we have learnt, •, •, •, •, •, •, •, , •, •, , The least distance of distinct vision is about 25cm and the angle of vision is about 600., The ability of eye lens to change its focal length is called accommodation of lens., The defect in which people cannot see objects beyond far point is called Myopia., The defect in which people cannot see objects situated before near point is called, Hypermetropia., Presbyopia is a vision defect indicating that the power of accommodation of the eye usually, decreases with ageing., The reciprocal of focal length is called power of the lens., The refractive index of prism is given by, n = Sin[(A+D)/2]/Sin(A/2), where A is angle of prism and D is angle of minimum deviation., The splitting of white light into colours (VIBGYOR) is called dispersion., The process of re-emission of absorbed light in all directions with different intensities by atoms, or molecules, is called scattering of light., , Improve your learning, 1. How do you correct the eye defect Myopia? (AS1), 2. Explain the correction of the eye defect Hypermetropia. (AS1), 3. How do you find experimentally the refractive index of material of a prism. (AS1), 4. Explain the formation of rainbow. (AS1), 5. Explain briefly the reason for the blue of the sky. (AS1), 6. Explain two activities for the formation of artificial rainbow. (AS1), 7. Derive an expression for the refractive index of the material of a prism. (AS1), 8. Light of wavelength λ1 enters a medium with refractive index n2 from a medium with refractive, index n1. What is the wavelength of light in second medium?, (Ans: λ2 = n1λ1/n2), , (AS1), , NOTE: For questions 9 and 10 the following options are given. Choose the correct option by, making hypothesis based on given assertion and reason. Give an explanation., a. Both A and R are true and R is the correct explanation of A., b. Both A and R are true and R is not the correct explanation of A., c. A is true but R is false., d. Both A and R are false., e. A is false but R is true., Free distribution by A.P. Government, , 157
Page 168 :
Mirror, , 9. Assertion (A): The refractive index of a prism depends only on the kind of glass of which it is, made of and the colour of light. (AS 2), Reason (R): The refractive index of a prism depends on the refracting angle of the prism and, the angle of minimum deviation., 10. Assertion (A): Blue colour of sky appears due to scattering of light., Reason (R): Blue colour has shortest wavelength among all colours, of white light. (AS 2), B, 11. Suggest an experiment to produce a rainbow in your classroom, and explain the procedure. (AS 3), 12. Prisms are used in binoculars. Collect information why prisms are, used in binoculars. (AS 4), C, 13. Incident ray on one of the face (AB) of a prism and emergent ray A, from the face AC are given in figure Q-13. Complete the ray diagram., fig-Q-13, (AS 5), 14. How do you appreciate the role of molecules in the atmosphere for the blue colour of the sky?, (AS 6), 15. Eye is the only organ to visualise the colourful world around us. This is possible due to, accommodation of eye lens. Prepare a six line stanza expressing your wonderful feelings., (AS 6), 16. How do you appreciate the working of Ciliary muscles in the eye? (AS 6), 17. Why does the sky sometimes appear white? (AS 7), 18. Glass is known to be a transparent material. But ground glass is opaque and white in colour., Why? (AS 7), 19. If a white sheet of paper is stained with oil, the paper turns transparent. Why? (AS 7), 20. A light ray falls on one of the faces of a prism at an angle 40o so that it suffers angle of minimum, deviation of 30o. Find the angle of prism and angle of refraction at the given surface., (Ans:50o, 25o) (AS 7), 21. The focal length of a lens suggested to a person with Hypermetropia is 100cm. Find the distance, of near point and power of the lens. (Ans: 33.33cm, 1D ) (AS 7), 22. A person is viewing an extended object. If a converging lens is placed in front of his eye, will he, feel that the size of object has increased? Why? (AS7), , ks, Fill in the blan, 1. The value of least distance of distinct vision is about ....................., 2. The distance between the eye lens and retina is about ........................, 3. The maximum focal length of the eye lens is about ............................, 4. The eye lens can change its focal length due to working of .................... muscles., 158, , X Class, , Human Eye and Colourful World
Page 169 :
5. The power of lens is 1D then focal length is ..................., 6. Myopia can be corrected by using ............................... lens., 7. Hypermetropia can be corrected by using ............................... lens., 8. In minimum deviation position of prism, the angle of incidence is equal to angle of .............., 9. The splitting of white light into different colours (VIBGYOR) is called ....................., 10. During refraction of light, the character of light which does not change is ........................, , s, Multiple choice question, 1. The size of an object as perceived by an eye depends primarily on, , [, , a) actual size of the object, , b) distance of the object from the eye, , c) aperture of the pupil, , d) size if the image formed on the retina, , ], , 2. When objects at different distances are seen by the eye which of the following remain constant?, a) focal length of eye-lens, , b) object distance from eye-lens, , c) the radii of curvature of eye-lens, , d) image distance from eye-lens, , 3. During refraction, ________ will not change., a) wavelength, , b) frequency, , c) speed of light, , d) all the above, , [, , ], , [, , ], , 4. A ray of light falls on one of the lateral surface of an equilateral glass prism placed on the, horizontal surface of a table as shown in fig. MCQ-4. For minimum deviation of ray, which of, the following is true?, [, ], a) PQ is horizontal, , Q, , b) QR is horizontal, , R, , P, , c) RS is horizontal, d) either PQ or RS is horizontal, , S, , fig-MCQ-4, , 5. Far point of a person is 5m. In order that he has normal vision what kind of spectcles should he, use, [, ], a) concave lense with focal length 5m, , b) concave lense with focal length 10m, , c) convex lense with focal length 5m, , d) convex lense with focal length 2.5m, , 6. The process of re-emission of absorbed light in all directions with different intensities by the, atom or molecule is called ..............., [, ], a) scattering of light, , b) dispersion of light, , c) reflection of light, , d) refraction of light, , Free distribution by A.P. Government, , 159
Page 170 :
Chapter, , 8, Structure of Atom, You have studied in the previous class about sub-atomic particles like, negatively charged electrons, positively charged protons and electrically, neutral neutrons., • How do these sub-atomic particles coexist in an electrically neutral, atom?, You have acquired some fundamental ideas about atomic models, suggested by J J Thomson, Ernest Rutherford and Niels Bohr which have, been presented in Class 9., , Activity 1, On the basis of your previous knowledge can you prepare a model of, an atom?, • Can you arrange the sub-atomic particles in any other way in an atom?, (Take the help of your friends, your teacher and the Internet). Observe, your atomic model and the models of your friends carefully and try to, answer the questions., • Do all atoms have the same sub-atomic particles?, • Why is an atom of one element different from the atoms of other, elements?, • How are the electrons distributed in the space of an atom?, To answer the above questions, we need to understand the nature of, light, coloured flames and their characteristics., 160, , X Class, , Structure of Atom
Page 171 :
Spectrum, You must have observed the formation of a rainbow., • How many colours are there in a rainbow?, There are seven colours namely violet, indigo, blue, green, yellow,, orange and red (VIBGYOR) in a rainbow., You can find the colours spreading continuously and the intensity of, each colour varies from one point to the other., Wave nature of light, • When you throw a stone into a still pond, you observe ripples, which, are transmitting the disturbance in the form of waves on the surface of, water., • You know that sound waves are produced when something vibrates;, like a drum., • In the same way electromagnetic waves are produced when an electric, charge vibrates (moves back and forth)., • How do the vibrating electric and magnetic fields around the charge, become a wave that travel through space?, A vibrating electric charge creates a change in the electric field. The, changing electric field creates a changing magnetic field., This process continues, with both the created fields being perpendicular, to each other and at right angles to the direction of propagation of the, wave., Visible light is an electromagnetic wave and the speed of light (c) is, 3 × 108 m s–1., • What are the characteristics of electromagnetic waves?, Wave, length, , Electric field, , Direction, , fig-1: An electromagnetic wave, , Magnetic field, , Electromagnetic energy travelling through a vacuum behaves in, some way like ocean waves travelling through water. Like ocean waves,, electromagnetic energy is characterized by wavelength (λ), and frequency, (υ)., Free distribution by A.P. Government, , 161
Page 172 :
The wavelength (λ) of the wave is the distance from one wave peak to, the next. The frequency (υ) of a wave is simply the number of wave peaks, that pass by a given point per unit time, expressed in units of reciprocal, seconds (1/s or s–1). The relation between these quantities is given by, λα 1/υ or c = υλ, • Can we apply this equation to a sound wave?, Yes. It is a universal relationship and applies to all waves. As the, frequency increases, the wavelength becomes smaller., Electromagnetic waves can have a wide variety of frequencies. The, entire range of electromagnetic wave frequencies is known as the, electromagnetic spectrum., The familiar example of the visible spectrum in nature is the formation, of a rainbow., Each colour in a rainbow is characterized by a specified wavelength, from red (higher wavelength) to violet (shorter wavelength). These colours, (wavelengths), that the human naked eye is sensitive to, are called visible, light. The range of wavelengths covering red colour to violet colour is, called the visible spectrum., • Are there any other wavelengths of light other than visible spectrum?, , Electromagnetic spectrum, Electromagnetic waves can have a wide variety of wavelengths. The, entire range of wavelengths is known as the electromagnetic spectrum., The electromagnetic spectrum consists of a continuous range of, wavelengths of gamma rays at the shorter wavelength to radio waves at the, longer wavelength. But our eyes are sensitive only to visible light., , 10-12 m, , 10 -9 m, , 10 -6 m, , 1 nm, , 1000 nm, , Cosmic, rays, , x-rays, γ−rays, , 10 -3 m 10 0 m, 1 mm, , Micro, waves, UV, , IR, , 1 km, , Radio, , Broadcast, band, , Radar, , Short wavelength, , Ultraviolet (UV), rays, 400 nm, , 10 3 m, , 1m, , Long wavelength, , Infrared (IR) rays, , Visible light, 500 nm, , 600 nm, , 700 nm, , fig-2: Electromagnetic Spectrum, , 162, , X Class, , Structure of Atom
Page 173 :
•, •, , What happens when you heat an iron rod on a flame?, Do you find any change in colour on heating an iron rod?, When you heat an iron rod, some of the heat energy is emitted as, light. First it turns red (lower energy corresponding to higher wavelength), and as the temperature rises it glows orange, yellow, blue(higher energy, and of lower wavelength) or even white (all visible wavelengths) if the, temperature is high enough., • Do you observe any other colour at the same time when one colour is, emitted?, When the temperature is high enough, other colours will also be, emitted, but due to higher intensity of one particular emitted colour, (e.g., red), others cannot be observed., Max Planck broke with the ‘continuous energy’ tradition of, electromagnetic energy by assuming that the energy is always emitted in, multiples of hυ;, For example: hυ, 2 hυ, 3 hυ... nhυ, That is, the energy for a certain frequency E can be represented by the, equation E = hυ, where ‘h’ is Planck’s constant which has the value, 6.626 X 10-34Js and ‘υ’ is the frequency of the radiation absorbed or, emitted., The energy (E) for the red colour (higher wavelength or lower, frequency) is lower compared to the energy of blue colour (lower, wavelength or higher frequency). The energy emitted from a material body, increases with increase in heat energy., The significance of Planck’s proposal is that, electromagnetic energy, can be gained or lost in discrete values and not in a continuous manner., Hence, emission or absorption of light spectrum is a collection of a, group of wavelengths., • Do you enjoy Deepavali fireworks?, Variety of colours is seen from fireworks., • How do these colours come from fireworks?, , Activity 2, Take a pinch of cupric chloride in a watch glass and make a paste with, concentrated hydrochloric acid. Take this paste on a platinum loop and, introduce it into a non-luminous flame., • What colour do you observe?, Carry out similar activity with strontium chloride., Free distribution by A.P. Government, , 163
Page 174 :
Niels Henrik David, Bohr was a Danish physicist, who made foundational, contributions to, understanding atomic, structure and quantum theory,, for which he received, the Nobel Prize in Physics in, 1922. Bohr was also, a philosopher and a promoter., , Cupric chloride produces a green colour, flame while strontium chloride produces a, crimson red flame., • Do you observe yellow light in street lamps?, Sodium vapours produce yellow light in street, lamps., • Why do different elements emit different flame, colours when heated by the same non-luminous, flame?, Scientists found that each element emits its, own characteristic colour. These colours, correspond to certain discrete wavelengths of, light and are called line spectra., The lines in atomic spectra can be used to, identify unknown atoms, just like fingerprints are, used to identify people., , Bohr’s model of hydrogen atom and its, limitations, , Let us examine the spectrum of hydrogen, atom., • What does a line spectrum tell, us about the structure of an atom?, Niels Bohr proposed that, electrons in an atom occupy, ‘stationary’ orbits (states) of fixed, energy at different distances from, the nucleus., fig-3: Hydrogen Spectrum, When an electron ‘jumps’ from, a lower energy state (ground state) to higher energy states (excited state), it absorbs energy or emits energy when such a jump occurs from a higher, energy state to a lower energy state., The energies of an electron in an atom can have only certain values, E1, E2, E3 ……; that is, the energy is quantized. The states corresponding, to these energies are called stationary states and the possible values of, the energy are called energy levels., • The lowest energy state of the electron is known as ground state., • What happens when an electron gains energy?, The electron moves to a higher energy level, the excited state., , 164, , X Class, , Structure of Atom
Page 175 :
•, , Does the electron retain the energy forever?, The electron loses the energy and comes back to its ground state. The, energy emitted by the electron is seen in the form of electromagnetic, energy and when the wavelength is in the visible region it is visible as an, emission line., Bohr’s model explains all the line spectra observed in the case of, hydrogen atom. It is a successful model as far as line spectra of hydrogen, atom is concerned., But the line spectrum of hydrogen atom when observed through a high, resolution spectroscope appears as groups of finer lines., • Did Bohr’s model account for the splitting of line spectra of a hydrogen, atom into finer lines?, Bohr’s model failed to account for splitting of line spectra., , Bohr-Sommerfeld model of an atom, , l=0, , l=0, , l=0, , l=0, l=1, , l=1, , l=1, , l=2, , l=2, l=3, , n=1, , n=2, , n=3, , n=4, , fig-4: The allowed electronic orbits for the main Quantum numbers by Bohr - Sommerfeld model, , In an attempt to account for the structure (splitting) of line spectra, known as fine spectra, Sommerfeld modified Bohr’s atomic model by, adding elliptical orbits. While retaining the first of Bohr’s circular orbit, as such, he added one elliptical orbit to Bohr’s second orbit, two elliptical, orbits to Bohr’s third orbit, etc., such that the nucleus of the atom is one, of the principal foci of these elliptical orbits. He was guided by the fact, that, in general, periodic motion under the influence of a central force, will lead to elliptical orbits with the force situated at one of the foci., Bohr-Sommerfeld model, though successful in accounting for the fine, line structure of hydrogen atomic spectra, does not provide a satisfactory, picture of the structure of atom in general., This model failed to account for the atomic spectra of atoms of more, than one electron., • Why is the electron in an atom restricted to revolve around the nucleus, at certain fixed distances?, Free distribution by A.P. Government, , 165
Page 176 :
Max, , Karl, , Ernst, , Ludwig, , Planck, , was, a German theoretical physicist who originated quantum, theory, which won him the Nobel Prize in Physics in 1918., Planck made many contributions to theoretical physics, but, his fame rests primarily on his role as originator of the, quantum theory. This theory revolutionized human, understanding of atomic and subatomic processes., , Quantum mechanical model of an atom, •, , Do the electrons follow defined paths around the nucleus?, If the electron revolves around the nucleus in defined paths or orbits,, the exact position of the electron at various times will be known. For that, we have to answer two questions:, • What is the velocity of the electron?, • Is it possible to find the exact position of the electron?, Electrons are invisible to naked eye. Then, how do you find the position, and velocity of an electron?, To find articles during dark nights we take the help of torchlight., Similarly, we can take the help of suitable light to find the position and, velocity of electron. As the electrons are very small, light of very short, wavelength is required for this task., This short wavelength light interacts with the electron and disturbs the, motion of the electron. Hence, simultaneously the position and velocity, of electron cannot be measured accurately., From the above discussion, it is clear that electrons do not follow, definite paths in an atom., Do atoms have a definite boundary, as suggested by Bohr’s model?, If the electrons are not distributed in orbits around the nucleus this, means that an atom does not have a definite boundary., As a result, it is not possible to pinpoint an electron in an atom., Under these circumstances in order to understand the properties of, electrons in an atom, a quantum mechanical model of atom was developed, by Erwin Schrodinger., According to this model of an atom, instead of orbits of Bohr’s model,, the electrons are thought to exist in a particular region of space around the, nucleus at a given instant of time, • What do we call the region of space where the electron might be, at a, given time?, The region of space around the nucleus where the probability of finding, the electron is maximum is called an orbital., 166, , X Class, , Structure of Atom
Page 177 :
In a given space around the nucleus, only certain orbitals can exist., Each orbital of a stable energy state for the electron is described by a, particular set of quantum numbers., , Quantum numbers, Each electron in an atom is described by a set of three numbers n, l,, and ml .These numbers are called quantum numbers. These numbers, indicate the probability of finding the electron in the space around the, nucleus., • What information do the quantum numbers provide?, The quantum numbers describe the space around the nucleus where, the electrons are found and also their energies. These are called atomic, orbitals., • What does each quantum number signify?, , 1. Principal Quantum Number (n), The principal quantum number is related to the size and energy of the, main shell., ‘n’ has positive integer values of 1, 2, 3,…, As ‘n’ increases, the shells become larger and the electrons in those, shells are farther from the nucleus., An increase in ‘n’ also means higher energy. n = 1, 2, 3, ... are often, represented by the letters K, L, M… For each ‘n’ value there is one main, shell., Shell, n, , K, 1, , L, 2, , M, 3, , N, 4, , 2. The angular - momention quantum number (l), ‘l’ has integer values from 0 to n-1 for each value of ‘n’. Each ‘l’ value, represents one sub-shell., Each value of ‘l’ is related to the shape of a particular sub-shell in the, space around the nucleus., The value of ‘l’ for a particular sub-shell is generally designated by the, letters s, p, d . . . as follows:, l, Name of the sub-shell, , 0, s, , 1, p, , 2, d, , 3, f, , When n = 1, there is only one sub-shell with l = 0. This is designated, as ‘1s’ orbital., When n = 2, there are two sub-shells, with l = 0, the ‘2s’ sub-shell and, with l = 1, the ‘2p’ sub-shell., Free distribution by A.P. Government, , 167
Page 178 :
•, •, , What is the maximum value of ‘l’ for n=4?, How many values can ‘l’ have for n = 4?, , 3. The magnetic quantum number (ml), , l, 0, 1, 2, 3, , The magnetic quantum number (ml) has integer values between -l and, l, including zero. Thus for a certain value of l, there are (2l +1) integer, values of ml as follows:, -l, (-l+1) . . ., –1, 0, 1, . . . (+l - 1), +l, These values describe the orientation of the orbital in space relative to, the other orbitals in the atom., When l = 0, (2l+ 1) = 1 and there is only one value of ml, thus we have, only one orbital i.e., 1s., When l= 1, (2l+ 1) = 3, that means ml has three values, namely, -1, 0,, and 1 or three p orbitals, with different orientations along x, y, z axes., These are labelled as px, py, and pz., • Do these three p-orbitals have the same, Table-1, energy?, Sub-shell Number of, The number of ‘ml’ values indicates the, orbitals, number of orbitals in a sub-shell with a particular, s, l value. Orbitals in the sub-shell belonging to, p, the same shell possess same energy., d, Fill the table-1 with the number of orbitals, f, per sub-shell using (2l+1) rule., s-orbital is spherical in shape, p-orbital is, dumbell-shaped and d-orbital are double dumbell-shaped as shown below., , fig-5: Shapes of orbitals in s, p and d subshells, 168, , X Class, , Structure of Atom
Page 179 :
The following table-2 represents the shells, sub-shells and the number, of orbitals in the sub-shells., Table-2, n, , l, , ml, , sub-shell notation, , No of orbitals, in the subshell, , 1, , 0, , 0, , 1s, , 1, , 0, , 0, , 2s, , 1, , 1, , -1,0,+1, , 2p, , 3, , 0, , 0, , 3s, , 1, , 1, , -1,0,+1, , 3p, , 3, , 2, , -2,-1,0,+1,+2, , 3d, , 5, , 0, , 0, , 4s, , 1, , 1, , -1,0,+1, , 4p, , 3, , 2, , -2,-1,0,+1,+2, , 4d, , 5, , 3, , -3,-2,-1,0,+1,+2,+3, , 4f, , 7, , 2, , 3, , 4, , Each sub-shell holds a, maximum of twice as many, electrons as the number of, orbitals in the sub-shell., The maximum number of, electrons that can occupy, various sub-shells is given in the, following table., , Sub shells, s (1=0), p (1=1), d (1=2), f (l=3), , Table-3, Number of, orbitals (2l+1), 1, 3, 5, 7, , Maximum, number of, electrons, 2, 6, 10, 14, , 4. Spin Quantum Number (ms), The three quantum numbers n, l, and ml describe the size (energy),, shape, and orientation, respectively, of an atomic orbital in space., As you have observed in the case of street lights (sodium vapour lamp),, yellow light is emitted. This yellow light is comprised of a very closely, spaced doublet when analyzed using high resolution spectroscope., Alkali and alkaline earth metals show such type of lines., To account for such a behavior of electron an additional quantum, number is introduced. This is spin quantum number. This represents the, property of the electron. It is denoted by ‘ms’., Free distribution by A.P. Government, , 169
Page 180 :
This quantum number refers to the two possible orientations of the, spin of an electron, one clockwise and the other anticlockwise spin. These, are represented by +1/2 and -1/2. If both are positive values, then the spins, are parallel otherwise the spins are anti-parallel., The importance of the spin quantum number is seen when electrons, occupy specific orbitals in multi-electron atoms., • How do electrons in an atom occupy shells, sub-shells and orbitals?, The distribution of electrons in shells, sub-shells and orbital in an, atom is known as electronic configuration., , Electronic Configuration, Let us first consider the hydrogen atom for understanding the, arrangement of electrons, as it contains only one electron., The shorthand notation consists of the principal energy level (n value),, the letter representing sub-level (l value), and the number of electrons (x), in the sub-shell is written as a superscript as shown below:, , nl x, For the hydrogen (H) atom having atomic number (Z) = 1, the number, of electrons is one, then the electronic configuration is 1s1., Denotes the number of, electrons in orbital, Denotes the principle, quantum number, , 1s1, Denotes the angular momentum, quantum number, , The electron configuration can also be represented by showing the, spin of the electron., For the electron in H, as you have seen, the set of quantum numbers is:, n = 1, l = 0, ml = 0, ms = ½ or – ½., , �, , For many-electron atoms, we must know the electron configuration, of the atom. The distribution of electrons in various atomic orbitals, provides an understanding of the electronic behavior of the atom and, in, turn, its reactivity. Let us consider the helium (He) atom., • Helium (Z=2) atom has two electrons., • How are these two electrons arranged?, To describe the electronic configuration for more than one electron, in the atom, we need to know three principles:, Those are the Pauli Exclusion Principle, Aufbau principle and Hund’s Rule., Let us discuss them briefly., 170, , X Class, , Structure of Atom
Page 181 :
The Pauli Exclusion Principle, Helium atom has two electrons. The first electron occupies ‘1s’ orbital., The second electron joins the first in the 1s-orbital, so the electron, configuration of the ground state of ‘He’ is 1s2., • Then the question is: What are the spins of these two electrons?, According to Pauli Exclusion Principle no two electrons of the same, atom can have all four quantum numbers the same., If n, l, and ml are same for two electrons then ms must be different. In, the helium atom the spins must be paired., Electrons with paired spins are denoted by ‘��’. One electron has, ms= +1/2, the other has ms= –1/2. They have anti-parallel spins., • How many electrons can occupy an orbital?, The major consequence of the exclusion principle involves orbital, occupancy. Since only two values of ms are allowed, an orbital can hold, only two electrons and they must have opposite spins., Hence, the electronic configuration of helium atom is:, , �, , �, , 1s2, , Aufbau Principle, As we pass from one element to another one of next higher atomic, number, one electron is added every time to the atom., The maximum number of electrons in any shell is ‘2n2’, where ‘n’ is, the principal quantum number., The maximum number of electrons in a sub-shell (s, p, d or f) is equal, to 2(2l+1) where l = 0, 1, 2, 3… Thus these sub-shells can have a maximum, of 2, 6, 10, and 14 electrons respectively., In the ground state the electronic configuration can be built up by, placing electrons in the lowest available orbitals until the total number of, electrons added is equal to the atomic number. This is called the Aufbau, principle (The German word “Aufbau” means “building up.”).Thus orbitals, are filled in the order of increasing energy., Two general rules help us to predict electronic configurations., 1. Electrons are assigned to orbitals in order of increasing value of (n+l)., 2. For sub-shells with the same value of (n+l), electrons are assigned, first to the sub-shell with lower ‘n’., Free distribution by A.P. Government, , 171
Page 182 :
The following diagram shows the increasing, value of (n+l). Ascending order of energies of, various atomic orbitals is given below., 1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s <, 4d < 5p < 6s < 4f < 5d < 6p < 7s < 5f < 6d < 7p <, 8s …, The electronic configuration of some elements, in the increasing atomic number (Z) value is given, below., , He(Z=2) 1s2, , �, , �, , Li(Z=3) 1s22s1, , �, , �, , �, , Be(Z=4), , 1s22s2, , �, , �, , �, , B(Z=5), , 1s22s22p1, , �, , �, , fig-6: The filling order of, atomic orbitals, (Moeller Chart), , �, , •, •, , �, , �, , �, , 1s1, , H(Z=1), , �, , For carbon (C) atom (Z=6), where does the 6th electron go?, Whether the electron pairs up in the same p-orbital or will it go to the, next p-orbital?, , Hund’s Rule, According to this rule electron pairing in orbitals starts only when all, available empty orbitals of the same energy (degenerate orbitals) are singly, occupied., The configuration of Carbon (C) atom (Z=6) is 1s22s22p2. The first four, electrons go into the 1s and 2s orbitals. The next two electrons go into separate, 2p orbitals, with both electrons having the same spin, , �, , �, , �, , �, , �, , �, , Note that the unpaired electrons in the 2p orbitals are shown with parallel, spins., , 172, , X Class, , Structure of Atom
Page 183 :
Activity 3, Complete the electronic configuration of the following elements., Table.4, Element, , Atomic number (Z), , C, N, O, F, Ne, Na, Mg, Al, Si, P, S, Cl, Ar, K, Ca, , 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, , Electronic configuration of elements, , Key words, Wave, spectrum, intensity, discrete energy, line spectrum, orbital, quantum numbers,, shell, sub-shell, shapes of orbitals electron spin, electronic configuration, the Pauli’s, exclusion principle, Aufbau principle, Hund’s rule., , What we have learnt, •, •, •, •, , Light can be characterized by its wavelength (λ) and frequency (υ), and these quantities are, related to the speed of light (c) as: c = υλ., Spectrum is a group of wavelengths., Electromagnetic energy (Light) can have only certain discrete energy values which is given by, the equation E=hυ, Electrons in an atom can gain energy by absorbing a particular frequency of light and can lose, energy by emitting a particular frequency., , Free distribution by A.P. Government, , 173
Page 184 :
•, , •, •, •, •, •, •, •, •, •, , Bohr’s model of atom: Electrons are present in stationary states. The electron moves to higher, energy level if it absorbs energy in the form of electromagnetic energy or moves to a lower, energy state by emitting energy in the form of electromagnetic energy of appropriate frequency., Atomic line spectra arise because of absorption /emission of certain frequencies of light energy., It is not possible to measure accurately the position and velocity of an electron simultaneously., The space around the nucleus where the probability of finding the electron is maximum is called, orbital., The three quantum numbers n, l, ml describe the energy, shape and orientation respectively, of, an atomic orbital., Spin is an intrinsic property of an electron., The arrangement of electrons in shells, sub-shells and orbitals in an atom is called the electron, configuration., According to Pauli Exclusion Principle no two electrons of the same atom can have all the four, quantum numbers same., Aufbau principle: The lowest-energy orbitals are filled first., Hund’s rule: The orbitals of equal energy (degenerate) are occupied with one electron each, before pairing of electrons starts., , Improve your learning, 1. What information does the electronic configuration of an atom provide? (AS1), 2. a. How many maximum number of electrons that can be accommodated in a principal energy, shell?, b. How many maximum number of electrons that can be accommodated in a sub shell?, c. How many maximum number of electrons can be accommodated in an orbital?, d. How many sub shells present in a principal energy shell?, e. How many spin orientations are possible for an electron in an orbital?, 3. In an atom the number electrons in M-shell is equal to the number of electrons in the K and L, shell. Answer the following questions. (AS1), a. Which is the outer most shell?, b. How many electrons are there in its outermost shell?, c. What is the atomic number of element?, d. Write the electronic configuration of the element., 4. Rainbow is an example for continuous spectrum – explain.(AS1), 5. How many elliptical orbits are added by Sommerfeld in third Bohr’s orbit? What was the, purpose of adding these elliptical orbits?(AS1), 6. What is absorption spectrum?, 7. What is an orbital? How is it different from Bohr’s orbit?(AS1), 8. Explain the significance of three Quantum numbers in predicting the positions of an electron in, an atom.(AS1), 9. What is nl x method? How it is useful? (AS1), 174, , X Class, , Structure of Atom
Page 185 :
10. Following orbital diagram shows the electron configuration of nitrogen atom. Which rule does, not support this? (AS1), N (Z = 7), , �, , �, , 11., 12., 13., 14., , �, , �, , �, , �, , �, , 1s, 2s, 2p3, Which rule is violated in the electronic configuration 1s0 2s2 2p4 ?, Writ e the four quantum numbers for the differentiating electron of sodium (Na) atom? (AS1), What is emisssion spectrum?, i. An electron in an atom has the following set of four quantum numbers to which orbital it belong, to: (AS2), n, 2, , 2, , l, 0, , ml, 0, , 2, , ms, +½, , ii. Write the four quantum numbers for 1s1 electron.(AS1), 15. Which electronic shell is at a higher energy level K or L? (AS2), 16. Collect the information regarding wave lengths and corresponding frequencies of three primary, colours red, blue and green. (AS4), 17. The wave length of a radio wave is 1.0m. Find its frequency.(AS7), , ks, Fill in the blan, 1., 2., 3., 4., 5., 6., 7., , If n = 1 then angular momentum quantum number (l) = ...................., If a sub-shell is denoted as 2p then its magnetic quantum number values are ......., ......, ........, Maximum number of electrons that an M-shell contain is/are ....................., For ‘n’, the minimum value is …………… and the maximum value is …………….., For ‘l’, the minimum value is …………..and the maximum value is …………., For ‘ml’ the minimum value is ………… and the maximum value is …………., The value of ‘ms’ for an electron spinning in clock-wise direction is ……………… and for, anti-clockwise direction is ………., , s, Multiple choice question, 1. An emission spectrum consists of bright spectral lines on a dark back ground. Which one of the, following does not correspond to the bright spectral lines?, [, ], a) Frequency of emitted radiation, b) Wave length of emitted radiation, c) Energy of emitted radiations, d) Velocity of light, 2. The maximum number of electrons that can be accommodated in the L – shell of an atom is :, a) 2, b) 4, c) 8, d) 16, [, ], 3. If l = 1 for an atom then the number of orbitals in its sub-shell is, [, ], a) 1, b) 2, c) 3, d) 0, 4. The quantum number which explains about size and energy of the orbit or shell is: [, ], d) ms, a) n, b) l, c) ml, Free distribution by A.P. Government, , 175
Page 186 :
Chapter, , 9, Classification of ElementsThe Periodic Table, A medical shop contains a vast number of medicines. The shop keeper, finds difficult or impossible to remember all the names of medicines that, he has. When you go to a medical shop and ask the shopkeeper for a, particular medicine, he hands over it to you without any difficulty. How is, it possible?, Think of a super bazaar. When you step inside you see a particular, arrangement of goods inside it. When you look for grocery that you need,, you go to it and select what you want. In what way it makes your selection, easy?, From the above observations you understand that for any system, involving several things, a particular order of arrangement of those things, is essential., Even in chemistry, from the earliest times, scientists have been trying, to classify the available elements on the basis of their properties., , Need for the arrangement of elements in an organised manner, Robert Boyle (1661) defined an element as any substance that cannot, be decomposed into a further simple substance by a physical or chemical, change., At his time, about thirteen elements were known., Towards the end of the eighteenth century, by the time of Lavoisier, another eleven elements were discovered. By 1865 about sixty three, elements were known and by 1940, a total of ninety one elements from, natural sources and another seventeen elements synthetically were, obtained., 176, , X Class, , Classification of Elements - The Periodic Table
Page 187 :
By now, including synthetic elements, there are more than 115, elements. As the number of elements increased, it became difficult to, keep in memory the chemistries of individual elements and their, compounds., In previous classes we learnt that elements were classified into metals, and non-metals. But this classification had so many limitations. So, there, was a need to classify them in other ways. Hence, chemists started to, frame ways to group these elements and compounds on the basis of their, physical and chemical properties., In the beginning of the 18th century Joseph Louis Proust stated that, hydrogen atom is the building material and atoms of all other elements, are simply due to the combination of number of hydrogen atoms. (It is to, be noted that at his time the atomic weights of all elements were given as, whole numbers and the atomic weight of hydrogen was taken as one.), , Dobereiner’s law of Triads, A German chemist Johann Wolfgang Döbereiner (1829) noted that, there were groups of elements with three elements known as triads in, each group with similar chemical properties. He tried to give a relationship, between the properties of elments and their atomic weights., Döbereiner stated that when elements with similar properties are taken, three at a time and arranged in the ascending order of their atomic weights,, the atomic weight of the middle element is the average of the atomic, weights of the first and third elements. This statement is called the, Dobereiner’s law of triads., , Activity 1, Observe the following table., Elements in each row represent a triad., Group Elements and their Atomic weight, A, B, C, D, E, , Lithium (Li), , Sodium (Na), , Potassium (K), , 7.0, , 23.0, , 39.0, , Calcium (Ca), , Strontium(Sr), , Barium (Ba), , 40.0, , 87.5, , 137.0, , Chlorine (Cl), , Bromine (Br), , Iodine (I), , 35.5, , 80.0, , 127.0, , Sulphur (S), , Selenium (Se), , Tellurium (Te), , 32.0, , 78.0, , 125.0, , Manganese(Mn) Chromium(Cr), , Iron (Fe), , 55.0, , 56.0, , 52.0, , Free distribution by A.P. Government, , Arithmetic mean of Atomic weight, 7.0 + 39.0, ––––––––– = 23.0, 2, , 177
Page 188 :
In the first row you will find that atomic weight of sodium (Na) is, equal to the average of relative atomic weight of Li and K., • Can you establish the same relationship with the set of elements given, in the remaining rows?, • Find average atomic weights of the first and thired elements in each, row and compare it with the atomic weight of the middle element., • What do you observe?, Döbereiner’s attempts gave a clue that atomic weights could be, correlated with properties of elements. It made chemists look, at elements in terms of groups of elements with similar chemical and, physical properties. This eventually led to rigorous classification, of elements and the modern periodic table of elements., , Limitations, i. All the known elements at that time could not be arranged in the form of triads., ii. The law failed for very low mass or for very high mass elements., In case of F, Cl, Br, the atomic weight of Cl is not an arithmetic mean, of atomic weights of F and Br., iii. As the techniques improved for measuring atomic masses accurately,, the law was unable to remain strictly valid., , Think and discuss, •, •, , What relation about elements did Döbereiner want to establish?, The densities of calcium (Ca) and barium (Ba) are 1.55 and 3.51 gcm-3, respectively. Based on Dobereiner’s law of triads can you give the, approximate density of strontium (Sr)?, , Newlands’ law of Octaves, John Newlands was a British chemist. Newlands (1865) found that, when elements were arranged in the ascending order of their atomic weights, they appeared to fall into seven groups. Each group contained elements, with similar chemical properties. Based on these observations, Newlands, proposed the law of octaves., The law of octaves states that when elements are arranged in the, ascending order of their atomic weights they fall into a pattern in which, their properties repeat at regular intervals. Every eighth element starting, from a given element resembles in its properties to that of the starting, element., 178, , X Class, , Classification of Elements - The Periodic Table
Page 189 :
Table 1: Newlands’ table of elements., Element No. Element No. Element No. Element No. Element No. Element No. Element No., , Element No., , H, , 1 F, , 8 Cl, , 15 Co&Ni 22 Br, , 29 Pd, , 36 I, , 42 Pt&Ir, , 50, , Li, , 2 Na, , 9 K, , 16 Cu, , 23 Rb, , 30 Ag, , 37 Cs, , 44 Os, , 51, , G, , 3 Mg, , 10 Ca, , 17 Zn, , 24 Sr, , 31 Cd, , 38 Ba&V 45 Hg, , 52, , Bo, , 4 Al, , 11 Cr, , 19 Y, , 25 Ce&La 33 U, , 40 Ta, , 46 Tl, , 53, , C, , 5 Si, , 12 Ti, , 18 In, , 26 Zr, , 32 Sn, , 39 W, , 47 Pb, , 54, , N, , 6 P, , 13 Mn, , 20 As, , 27 Di&Mo34 Sb, , 41 Nb, , 48 Bi, , 55, , O, , 7 S, , 14 Fe, , 21 Se, , 28 Ro&Ru 35 Te, , 43 Au, , 49 Th, , 56, , Elements with similar chemical properties are to be present along a, horizantal row., Newlands was the first to assign atomic numbers to the elements., Unfortunately his work was neither accepted by his seniors nor by the, journal of the Chemical society, which rejected its publication., In Newlands’ table of elements, if we start with hydrogen and move, down and then start at the top the eighth element is fluorine and next eighth, element is chlorine and so on. The properties hydrogen, fluorine and, chlorine are similar., Similarly, if you start at lithium, then eighth element is sodium and, next coming eighth is potassium and so on. These elements show similar, physical and chemical properties., , Think and discuss, •, •, , •, •, , Do you know why Newlands proposed the law of octaves? Explain your, answer in terms of the modern structure of the atom., Do you think that Newlands’ law of octaves is correct? Justify, , Newlands’ table is not without problems., There are instances of two elements fitted into the same slot, e.g., cobalt and nickel., Certain elements, totally dissimilar in their properties, were fitted into, the same group,, , Free distribution by A.P. Government, , 179
Page 190 :
For example he arranged Co, Ni, Pd, Pt and Ir which have different, properties compared with halogens in the same row (F, Cl, Br, I). (see, Newlands’ first horizontal row), It was found that the law of octaves holds good only for the elements, up to calcium. The law was not valid for elements that had atomic masses, higher than calcium., Newlands periodic table was restricted to only 56 elements and did, not leave any room for new elements. Elements that were discovered later, could not be fitted into Newlands table in accordance with their properties., Newlands attempted to link the periodicity of the chemical properties, of elements with the periodicity found in the music. In musical scale any, note in a key is separated from its octave by an interval of seven notes., This must have made him to force all the elements into this active pattern, sometimes without caring the similarities., , Do you know?, Are you familiar with musical notes?, In the Indian system of music, there are seven musical notes in a scale – sa, re, ga, ma, pa, da, ni. In the west, they use the notations - do, re, mi, fa, so, la, ti., Naturally, there must be some repetition of notes. Every eighth note is similar to, the first one and it is the first note of the next scale., , Mendeleeff’s Periodic Table, Mendeleeff arranged the elements known at that time in a chart in a, systematic order in the increasing order of their atomic weights. He divided, the chart into 8 vertical columns known as groups. Each group is divided, into A, B sub groups. Each column contained elements of similar chemical, properties., The elements in the first column, for example, react with oxygen to, form compounds with the general formula R2O. For example, Li, Na and K, when react with oxygen and form compounds Li2O, Na2O and K2O, respectively., Elements of the second column react with oxygen to form compounds, with the general formula RO. For example, Be, Mg and Ca when react with, oxygen form BeO, MgO and CaO., Mendeleeff tried to explain the similarities of elements in the same, group in terms of their common valency., 180, , X Class, , Classification of Elements - The Periodic Table
Page 191 :
The Periodic Law, , Reihen, , Based on Mendeleeff’s observations regarding the properties of, elements in the periodic table, a law known as the periodic law of the, properties of elements was proposed as follows., The law states that the physical and chemical properties of the elements, are a periodic function of their atomic weights., Table-2 : Mendeleeff’s Periodic Table (1871 version), Gruppe I., –, R 2O, , 1, 2, , Gruppe IV., RH4, RO2, , Gruppe V., RH3, R2O5, , Gruppe VI., RH2, RO3, , Gruppe VII., RH, R2H7, , Gruppe VIII., –––, RO4, , H=1, Li=7, , 3, 4, , Gruppe II. Gruppe III., –, –, RO, R 2O 3, , Be=9.4, , Na=23, K=39, , B=11, , Mg=24, Ca=40, , C=12, , Al=27.3, –=44, , N=14, Si=28, , Ti=48, , O=16, , P=31, V=51, , F=19, , S=32, Cr=52, , Cl=35.5, Mn=55, , Fo=56, Co=59, Ni=59, Cu=63, , 5, 6, , (Cu=63), Rb=85, , Zn=65, Sr=87, , –=68, ?Yt=88, , –=72, Zr=90, , As=75, Nb=94, , So=78, Mo=96, , Br=80, –=100, , Ru=104, Rh=104, Pd=106, Ag=108, , 7, 8, , (Ag=108), Cs=133, , 9, 10, , Cd=112, Ba=137, , (–), –, , In=113, ?Di=138, , –, –, , Sn=118, ?Ce=140, , –, ?Ek=178, , Sb=122, –, , –, ?La=180, , Te=125, –, , –, Ta=182, , J=127, –, , –, , – – – –, –, , W=184, , –, , Os=195, Ir=197,, Pt=198, Au=199, , 11, 12, , (Au=198), –, , Hg=200, –, , Tl=204, –, , Pb=207, Th=231, , Bi=208, –, , –, U=240, , –, –, , – – – –, , Salient features and achievements of the Mendeleeff’s periodic, table, 1. Groups and sub-groups: There are eight vertical columns in, Mendeleeff’s periodic table called as groups. They are represented, by Roman numerals I to VIII. Elements present in a given vertical, column (group) have similar properties. Each group is divided into, two sub-groups ‘A’ and ‘B’. The elements within any sub-group, resemble one another to great a extent. For example, sub-group IA, elements called ‘alkali metals’ (Li, Na, K, Rb, Cs, Fr) resemble each, other very much in their properties., 2. Periods: The horizontal rows in Mendeleeff’s periodic table are called, periods. There are seven periods in the table, which are denoted by, Arabic numerals 1 to 7. Elements in a period differ in their properties, from one another. A period comprises the entire range of elements, after which properties repeat themselves., Free distribution by A.P. Government, , 181
Page 192 :
3. Predicting the properties of missing elements: Based on the, arrangement of the elements in the table he predicted that some, elements were missing and left blank spaces at the appropriate places, in the table., Mendeleeff believed that some new elements would be discovered, definitely. He predicted the properties of these new additional elements, in advance purely depending on his table. His predicted properties were, almost the same as the observed properties of those elements after their, discovery., He named those elements tentatively by adding the prefix ‘eka’ (eka, is a Sanskrit word for numeral one) to the name of the element, immediately above each empty space. The predicted properties of elements, namely eka-boron, eka-aluminium and eka-silicon were close to the, observed properties of scandium, gallium and germanium respectively, which were discovered later., S., No., , Property, , Predicted property by, Mendeleeff, Eka-Aluminium (Ea), , 1, 2, 3, 4, , Atomic weight, Density, Formula of oxide, Formula of chloride, , 68, 5.9, Ea2O3, EaCl3, , Eka-Silicon (Es), , 72, 5..5, EsO2, EsCl4, , Observed property, Gallium (1875), , 69.72, 5.94, Ga2O3, GaCl3, , Germanium (1886), , 72.59, 5.47, GeO2, GeCl4, , Do you know?, Do you know what Mendeleeff said about the melting point of eka Al?, ‘If I hold it in my hand, it will melt’. The melting point of Ga is 30.2oC and our, body temprature 37oC., 4. Correction of atomic weights: The placement of elements in, Mendeleeff’s periodic table helped in correcting the atomic masses, of some elements like, beryllium, indium and gold., For example, At the time of Mendeleeff, beryllium (Be) was given, atomic weight 13.5., Atomic weight = equivalent weight × valency, The equivalent weight of Be was found experimentally as 4.5 and its, valency was thought as 3. Therefore, the atomic weight of beryllium, was given as 4.5 × 3 = 13.5. With this atomic weight it had to be placed, in a wrong group in the table. He said that its valency should be only 2., Then its atomic weight would be 4.5 × 2 = 9. If atomic weight of ‘Be’, 182, , X Class, , Classification of Elements - The Periodic Table
Page 193 :
is 9 it would be fit in the second group and its properties practically, are similar to Mg, Ca etc., of the second group elements. He also, helped in the calculation of the correct atomic weights of ‘Indium’, and ‘Gold’ in this manner., 5. Anomalous series: Some anomalous series of elements like ‘Te’ and, ‘I’ were observed in the table. The anomalous series contained elements, with more atomic weights like ‘Te’ (127.6 U) placed before the, elements with less atomic weights like ‘I’ (126.9 U). Mendeleeff, accepted minor inversions in the order of increasing atomic weights, as these inversions resulted in elements being placed in the correct, groups., It was the extraordinary thinking of Mendeleeff that made the chemists, to accept the periodic table and recognise Mendeleeff more than anyone, else as the originator of the periodic law., , Do you know?, At the time when Mendeleeff introduced his periodic table even electrons were, not discovered. Even then the periodic table was able to provide a scientific base, for the study of chemistry of elements. In his honour the 101th element was named, Mendelevium., , Limitations of Mendeleeff’s periodic table, 1. Anomalous pair of elements: Certain elements of highest atomic, weights precede those with lower atomic weights., For example, tellurium (atomic weight 127.6) precedes iodine (atomic, weight 126.9)., 2. Dissimilar elements placed together: elements with dissimilar, properties were placed in same group as sub-group A and sub-group B., For example, alkali metal like Li, Na, K etc., of IA group have little, resemblance with coinage metals like Cu, Ag, Au of IB group.Cl is of, VII a group and ‘Mn’ is of VII B, but chlorine is a non metal, where as, manganese is a metal., , Think and discuss, •, •, , Why Mendeleeff had to leave certain blank spaces in his periodic table?, What is your explanation for this?, What is your understanding about Ea2O3, EsO2?, , Free distribution by A.P. Government, , 183
Page 194 :
Think and discuss, •, , All alkali metals are solids but hydrogen is a gas with diatomic, molecules. Do you justify the inclusion of hydrogen in first group with, alkali metals?, , Modern Periodic Table, H.J. Moseley (1913) found that each element emits a characteristic, pattern of X-rays when subjected to bombardment by high energy, electrons. By analyzing the X-ray patterns, Moseley was able to calculate, the number of positive charges in the atoms of respective elements. The, number of positive charges (protons) in the atom of an element is called, the atomic number of the element. With this analysis Moseley realised, that the atomic number is more fundamental characteristic of an element, than its atomic weight., After knowing the atomic numbers of elements, it was recognized that, a better way of arranging the elements in the periodic table is according to, the increasing atomic number. This arrangement eliminated the problem, of anomalous series. For example, though tellurium (Te) has more atomic, weight than iodine (I), it has atomic number less by one unit compared to, iodine. This atomic number concept forced the periodic law to be changed., The periodic law is changed from atomic weight concept to atomic, number concept and now it is called the modern periodic law., We know that Mendeleeff’s periodic law is stated as “The properties, of elements are the periodic functions of their atomic weights”. Now, let, us try to understand modern periodic law., The modern periodic law may stated as “the properties of the elements, are periodic function of their atomic numbers.”, Based on the modern periodic law, the modern periodic table which is, given here (page 186) is proposed. It is the extension of the original, Mendeleeff’s periodic table known as short form of the table and this, modern table is called the long form of the periodic table. It is given in, fig (2). Atomic number of an element (Z) indicates not only the positive, charges i.e., the protons in the nucleus of the atom of the element but also, the number of electrons in the neutral atom of that element., , 184, , X Class, , Classification of Elements - The Periodic Table
Page 195 :
The physical and chemical properties of atoms of the elements depend, not on the number of protons but on the number of electrons and their, arrangements (electronic configurations) in atoms. Therefore, the modern, periodic law may be stated as “The physical and chemical properties of, elements are the periodic function of the electronic configurations of, their atoms.”, , Positions of elements in the Modern Periodic Table, The modern periodic table has eighteen vertical columns known as, groups and seven horizontal rows known as periods., Let us see what decides the position of an element in modern periodic, table., We can explain the classification of the elements in the modern, periodic table in terms of certain electron arrangements which are, periodically repeated. The elements with similar outer shell (valence shell), electronic configurations in their atoms are in the same column called, group. Elements listed in a group down to it are in the order of their, increasing principal quantum numbers., In the chapter ‘Structure of atom’ you have learnt that ‘s’ sub-shell, with one orbital contains a maximum of two electrons. Each ‘p’ sub-shell, contains 3 orbitals and accommodates a maximum of six electrons. The‘d’, sub-shell contains 5 orbitals and accommodates a maximum of 10 electrons, and ‘f’ sub-shell contains 7 orbitals with 14 electrons maximum. Depending, upon to which sub-shell the differentiating electron. i.e., the last coming, electron enters in the atom of the given element, the elements are classified, as ‘s’ ‘p’, ‘d’ and ‘f’ block elements., For example, sodium (Na) gets its new coming electron (differentiating, electron) into 3s level. Therefore ‘Na’ is an s-block element., Aluminium (Al) gets its differentiating electron into ‘p’ subshell and it is, a p-block element. Scandium (Sc) gets its differentiating electron into, ‘d’ subshell. Therefore it is a d-block element. Cerium (Ce) gets its new, coming electron into ‘f’ subshell, hence,it is an f-block element., Let us observe the electronic configurations of the following elements., The last coming electron is underlined., 11, , Na 1s2 2s2 2p6 3s1, Al 1s2 2s2 2p6 3s2 3p1, , 13, 21, , Sc 1s2 2s2 2p6 3s2 3p6 4s2 3d1, Ce 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 5s2 5p6 6s2 4f1, , 58, , Free distribution by A.P. Government, , 185
Page 196 :
186, , X Class, , Classification of Elements - The Periodic Table
Page 197 :
Z Elements n, , 1, , 2, , 3, , 4, , 5, , 6, , l, , 0, , 0, , 1, , 0, , 1, , 2, , 0, , 1, , 2, , 3, , 0, , 1, , 2, , 3, , 0, , Sub, Shell, , 1s, , 2s, , 2p, , 3s, , 3p, , 3d, , 4s, , 4p, , 4d, , 4f, , 5s, , 5p, , 5d, , 5f, , 6s, , 6, , 10, , 1, , 2, , 6, , 1, , 11, , Na, , 2, , 2, , 6, , 1, , 13, , Al, , 2, , 2, , 6, , 2, , 1, , 21, , Sc, , 2, , 2, , 6, , 2, , 6, , 1, , 2, , 58, , Ce, , 2, , 2, , 6, , 2, , 6, , 10, , 2, , 2, , Groups, The vertical columns in the periodic table are known as groups. There, are eighteen groups in long form of periodic table. They are represented, by using Roman numeral I through VIII with letters A and B in traditional, notation., According to latest recommendation of the IUPAC, these groups are, represented by Arabic numerals 1 through 18 with no A and B designations., We use the latest system with the traditional heading following in, parenthesis., Eg: Group 2 (II A); Group 16 (VI A), Group of elements is also called element family or chemical family., For example Group 1 (IA) has from Li to Fr with outer shell electronic, configuration ns1 and is called Alkali metal family., , Activity 2, Some main group elements of s-block and p-block have family names, as given in the following table., Observe the long form of the periodic table and complete the table, with proper information., Group, No., , Name of the, element family, , 1 (IA), 2 (IIA), 13 (IIIA), 14 (IVA), 15 (VA), 16 (VIA), , Valence Valence Valency, shell, electrons, configuration, From To, Elements, , Alkali metal family, Li, Alkali earth metal family, Boron family, Carbon family, Nitrogen family, Oxygen family or, (Chalcogen family), 17 (VIIA) Halogen family, 18 (VIIIA) Noble gas family, Free distribution by A.P. Government, , Fr, , ns1, , 1, , 1, , 187
Page 198 :
Periods, The horizontal rows in the periodic table are called periods. There are, seven periods in the modern periodic table. These periods are represented, by Arabic numerals 1 through 7., 1. The number of main shells present in the atom of particular element, decides to which period it belongs. For example, hydrogen (H) and, helium (He) atoms contain only one main shell (K). Therefore they, belongs to period-1. Similarly, the elements Li, Be, B, C, N, O, F and, Ne contain two main shells (K and L) in their atoms. Therefore they, belong to period-2., , Do you know?, •, , Do you know how are the names of certain families of periodic table derived?, Alkali metal family: aliquili = plantashes, Na, K etc.... were obtained from, plant ash, group IA elements are called alkali metals family., Chalcogen family: chalcogenous = ore product, as the elements in group, 16(VIA) form ores with metals. They are called as chalcogenous family., Halogen family: halos = sea salt, genus = produced. As most of the elemetns in, group 17(VIIA) are obtained from nature as sea salt. They are called as halogen, family., Noble gases: as the elements of group 18(VIIIA) are chemically least active., They are called as noble gases. There outer shell electronic configurations are, basis for octet rule., 2. The number of elements in period depend on how electrons are filled, into various shells. Each period starts with a new main shell ‘s’ subshell, and ends when the main shell is filled with respect to the ‘s’ and ‘p’, subshells (except the first period)., The first period starts with K-shell. The first main shell (K) contains, only one sub-shell, the (1s). For this subshell only two types of, electronic configurations are possible and they are 1s1 (H) and 1s2, (He). Therefore, the first period contains only two elements., 3. Second period starts with the 2nd main shell (L). L-shell has two subshells, namely, 2s and 2p. Eight types of configurations are possible in, this shell (L) like 2s1 and 2s2 and 2p1 to 2p6. Hence the second period, contains 8 elements Li, Be, B, C, N O, F and Ne in the order given., Thus, the 2nd period consists two s-block elements (Li, Be) and six pblock elements (B to Ne)., 188, , X Class, , Classification of Elements - The Periodic Table
Page 199 :
4. Third period starts with third main shell (M). This shell (M) has 3 subshells, namely, 3s, 3p and 3d, but while electrons are being filled into, the shell ‘3d’ gets electrons only after ‘4s’ is filled. Therefore, the 3rd, period contains again 8 elements, which includes two s-block elements, (Na, Mg) and six p-block elements (Al to Ar)., 5. Fourth main shell (N). This shell (N) has four sub-shells namely 4s,, 4p, 4d and 4f, but while electrons are being filled into the shell ,, electrons enter the atoms in the order 4s, 3d and 4p. Due to this, the, fourth period contains 18 elements which includes two s-block (K,, Ca), 10 elements from d block (Sc to Zn) and six elements from pblock (31Ga to 36 Kr). There are altogether eighteen elements in the, fourth period., On the same lines, we can explain why there are 18 elements in the, fifth period (37Rb to 54Xe)., There are thirty two elements in the Sixth period from 55Cs to 86 Rn, which includes 2 elements from s-block (6s) and 14 elements from, f-block (4f). 10 elements from d-block (5d) and 6 elements from p-block, (6p)., ‘4f’ elements are called Lanthanoids or lanthanides. Elements from, Ce to 71Lu possess almost the same properties as 57 La. So, the name, 58, lanthanoids is the most appropriate one for these elements., 7th period is incomplete and contains 2 elements from s-block (7s), and 14 elements from f-block (5f), 10 elements from d-block (6d) and, some elements from p-block (7p). The 5f elements are called Actinoids, or as Actinides. They are from 90Th to 103Lr ., The f-block elements known as lanthanoids and actinoids are shown, separately at the bottom of the periodic table., , Do you know?, ‘Ide’ means ‘heir’ and it is used generally for a change like Cl to Cl-. ‘Cl’ is, chlorine atom and Cl- is chloride ion. ‘Oid’ means ‘the same’., Some scientists suggest lanthanoids as 57La to 70Yb, some suggest them as, Ce to 71Lu and some take 57La to 71Lu (15 elements). There is another argument, 58, that even 21Sc and 39Y should be included in lanthanoids. All these suggestions have, substance because 21Sc, 39Y and 57La to 71Lu all have the similar outer shells, configurations., Also in the case of actinoids. There are different arguments like actinoids are, from 90Th to 103Lr or 89Ac to 102No or 89Ac to 103Lr., Free distribution by A.P. Government, , 189
Page 200 :
Think and discuss, •, •, , Why lanthanoids and actinoids placed separately at the bottom of the, periodic table?, If they are inserted within the table imagine how the table would be?, , Metals and Non metals, You have learnt about the properties of metals in the chapter Metals, and Non Metals in class VIII. Let us study the metallic properties elements, in periodic table., The elements with three or less electrons in the outer shell are, considered to be metals and those with five or more electrons in the outer, shell are considered to be non metals. We may find some exceptions to, this. ‘d’ block elements (3rd group to 12th group) are metals and they are, also known as transition metals and the metallic character of d-block, elements decreases gradually from left to right in periodic table., Lanthanoids and actinoids actually belong to 3rd group (III B) which is within, the transition elements: hence they are called the inner transition elements., Metalloids or semi-metals are elements which have properties that, are intermediate between the properties of metals and non metals. They, possess properties like metals but brittle like non metals. They are generally, semi conductors. Eg: B, Si, Ge., All elements in s-block are metals, whereas in p-block (except 18th, group) there are metals, non metals and metalloids. In periodic table you, will notice a staircase like demarcation. The elements to the left of this, demarcation are metals and to the right are non-metals. The elements on, staircase (or) very near to it like B, Si, As, Ge etc., are metalloids., , Periodic properties of the elements in the modern table, The modern periodic table is organized on the basis of the electronic, configuration of the atoms of elements. Physical and chemical properties, of elements are related to their electronic configurations particularly the, outer shell configurations. The atoms of the elements in a group possess, similar electronic configurations. Therefore, we expect all the elements, in a group should have similar chemical properties and there should be a, regular gradation in their physical properties from top to bottom., Similarly, across the table, i.e., from left to right in any period elements, get an increase in the atomic number by one unit between any two successive, 190, , X Class, , Classification of Elements - The Periodic Table
Page 201 :
elements. Therefore, the electronic configuration of valence shell of any, two elements in a given period is not same. Due to this reason elements, along a period possess different chemical properties with regular gradation, in their physical properties from left to right. To understand this we will, take some properties of elements and discuss how they vary in groups and, in periods., , Properties of elements and their trends in Groups and in Periods, 1. Valence: Valence (or) valency of an element was defined as the, combining power of an element with respect to hydrogen, oxygen or, indirectly any other element through hydrogen and oxygen., Valence of an element with respect to hydrogen is the number of, hydrogen atoms with which one atom of that element chemically combines., Valence of an element with respect to oxygen is twice the number of, oxygen atoms with which one atom of that element combines., For example one atom of ‘Na’ chemically combines with one atom of, ‘H’ to give NaH. Therefore, the valence of Na is 1. One atom of ‘Ca’, combines with one atom of ‘O’ to give CaO. So the valency of Ca is 2., In general, the valence of an element with respect to hydrogen is its, traditional group number. If the element is in the group V or above, its, valence is 8– group number. For example, chlorine valence is 8-7 = 1., In general, each period starts with valency 1 for 1st group elements,, increases upto 4 with respect to the group number and then decreases, from 4 to 3 to 2 to 1 to zero in the following groups (this is applicable, only for main group elements i.e., ‘s’ and ‘p’ block elements., Now a days the valence of an elment is generally taken as the number, of valence shell (outer most shell) electrons in its atom. Oxidation number, concept almost is the latest subsititute to the valence concept in the modern, literatura., , Activity 3, •, •, •, , Find out the valencies of first 20 elements., How does the valency vary in a period on going from left to right?, How does the valency vary on going down a group?, , Atomic radius, Atomic radius of an element may be difined as the distance from the, centre of the nucleus of the atom to its outermost shell., Free distribution by A.P. Government, , 191
Page 202 :
Atomic radius of an element is not possible to measure in its isolated, state. This is because it is not possible to determine the location of the, electron that surrounds the nucleus. However, we can measure the distance, between the nuclei of adjacent atoms in a solid. From this we can estimate, the size of the atom by assigning half of this distance to the radius of each, atom. This method is best suited to elements such as the metals that exist, in the solid state. More than 75 percent of the elements are metals and, atomic radii of metals are called metallic radii. Another way of estimating, the size of an atom is to measure the distance between the two atoms in, covalent molecules. The size of a chlorine atom is estimated by measuring, the length of the covalent bond between two chlorine atoms in a Cl2, molecule. Half of this distance is taken as atomic radius which is called, as the covalent radius of chlorine atom., Atomic radius is measured in ‘pm’ (pico meter) units., 1 pm = 10-12m, , Variation of atomic radii in group, Atomic radii increase from top to bottom in a group (column) of the, periodic table. As we go down in a group, the atomic number of the element, increases. Therefore to accommodate more number of electrons, more, shells are required. As a result the distance between the nucleus and the, outer shell of the atom increases as we go down the group in spite of, increase in nuclear change., Element (atomic radius in pm), , Group, Group1:, , Li (152), Na (186), K (231), Rb (244) and Cs (262), , Group 17:, , F (64), Cl (99), Br (114), I (133) and At (140), , Variation of atomic radii in period, Atomic radii of elements decrease across a period from left to right., As we go to right, electrons enter into the same main shell or even inner, shell in case of ‘d’ block and ‘f’ block elements. Therefore, there should, be no change in distance between nucleus and outer shell but nuclear charge, increases because of the increase in the atomic number of elements in, period. Hence, the nuclear attraction on the outer shell electrons increases., As a result the size of the atom decreases., 192, , X Class, , Classification of Elements - The Periodic Table
Page 203 :
Element (atomic radius in pm), , Period, 2nd period, , Li (152), Be (111), B (88), C (77), N (74), O (66), F (64), , 3rd period, , Na (186), Mg (160), Al (143), Si (117), P(110), S(104), Cl(99), , •, , Do the atom of an element and its ion have same size?, Let us consider the following situation., , Assume that sodium (Na) atom has lost an electron and formed a cation, of sodium (Na+)., Which one between Na and Na+ would have more size? Why?, Atomic number of sodium (Na) is 11. Therefore sodium (Na) atom, contains 11 protons and 11 electrons with outer electron as 3s1. On the, other hand Na+ ion has 11 protons but only 10 electrons. The 3s shell of, Na+ level has no electron in it. Hence its outer shell configuration is, 2s2 2p6. As proton number is more than electrons in it, the nucleus of Na+, ion attracts outer shell electrons with strong nuclear force. As a result the, Na+ ion shrinks in size. Therefore, the size of Na+ ion is less than ‘Na’, atom. In general the positive ion (cation) of an element has less size than, its neutral atom., Consider another example: Assume that chlorine (Cl) atom has, gained an electron to form anion of chlorine (Cl –) i.e. chloride ion., • Which one, between Cl and Cl – would have more size? Why?, Electronic configuration of chlorine (Cl) atom is 1s2 2s2 2p6 3s2 3p5, and the electronic configuration of chloride (Cl –) ion is 1s2 2s2 2p6, 3s2 3p6. Both chlorine and chloride ion have 17 protons each but there are, 17 electrons in chlorine atom, where as 18 electrons in chloride ion., Therefore, the nuclear attraction is less in Cl – ion when compared with, chlorine atom. Therefore the size of the chlorine (Cl) atom is less size, than Cl- ion. In general negative ion (anion) of an element has bigger size, than its neutral atom., • Which one in each of the following pairs is larger in size?, (a) Na, Al (b) Na, Mg+2 (c) S2-, Cl – (d) Fe2+, Fe3+ (e) C4-, F –, , Ionization Energy, The energy required to remove an electron from the outer most orbit, or shell of a neutral gaseous atom is called ionization energy. The energy, required to remove the first electron from the outer most orbit or shell of, Free distribution by A.P. Government, , 193
Page 204 :
a neutral gaseous atom of the element is called its first ionization energy., The energy required to remove the an electron from uni- positive ion of, the element is called the 2nd ionization energy of that element and so on., M(g) + IE1, M+(g) + IE2, , M+(g) + eM+2(g) + e-, , (IE1= first ionization energy), (IE2= second ionization energy), , Think and discuss, •, , Second ionization energy of an element is higher than its first ionization, energy. why?, Ionization energy of an element depends on its, 1. Nuclear charge: more the nuclear charge more is the ionization, energy.eg:Between 11Na and 17Cl, Chlorine atom has more ionization energy., 2. Screening effect or sheilding effect: more the shells with, electrons between the nucleus and the valence shell, they act as screens, and decrease nuclear attraction over valence electron. This is called the, screening effect. More the screening effect, less is the ionization energy., Between 3Li and 55Cs, the element 55Cs with more inner shells has less, ionization energy., 3. Penetration power of the orbitals: orbitals belonging to the same, main shell have diffrent piercing power towards the nucleus, for examle, 4s>4p>4d>4f> in the penetration. There fore, it is easier to remove 4f, electron than 4s. Between 4Be 1s2 2s2 and B 1s2 2s2 2p1, the element B has, less ionization energy due to less penetration power of ‘2p’ compared to, ‘2s’, 4. Stable configuration: it is easier to remove one electron from 8O, (1s22s22p4) than 7N (1s22s22p3). This is because, 7N has stable half filled, configuration., 5. Atomic radius: more the atomic radius, less is the ionization energy., Therefore, ionization energy of ‘F’ is greater than that of ‘I’ and the, ionization energy of ‘Na’ is more than that of ‘Cs’., Ionization energy decreases as we go down in a group and generally, increases from left to right in a period., Ionization energy is expressed in kJ mol-1, , 194, , X Class, , Classification of Elements - The Periodic Table
Page 205 :
Ionization energy is also called the ionization potential but when we use, the term the ionization potential, it is better to write the unit eV atom–1., , Electron affinity, Atoms of some elements gain electrons while forming ionic, compounds. An atom is able to gain an electron only when the electron, outside the atom is attracted by its nucleus. Attraction involves the, liberation of energy., The electron affinity of an element is defined as the energy liberated, when an electron is added to its neutral gaseous atom. Electron affinity of, an element is also called electron gain enthalpy of that element., M(g) + e-, , M-(g) + EA, , (EA = Electron affinity), , The energy liberated when an electron is added to a uni-negative ion, of the element is called the 2nd electron affinity of that element. However,, practically no element shows liberation of energy when the 2nd electron is, added to its uni-negative ion. It does not mean that di-negative or trinegative ions do not form. They do form, but for adding 2nd electron, energy, in another way like bond formation must be given., Electron affinity values of halogens are (in kJ mol-1); F(-328); Cl(-349);, Br (-325); I(-295) kJ mol-1 . Similarly for group 16 elements, the electron gain, enthalpies are O(-141); S(-200); Ge(-195) and Te(-190) kJ mol-1., Electron gain enthalpy values decrease as we go down in a group, but, increase along a period from left to right. Metals have very low electron, gain enthalpy values and alkaline earth metals have even positive values., Note that the negative sign for energy value in table indicates that energy, is liberated or lost, and the positive sign tells that the energy is gained or, absorbed. All the factors which influence the ionization energy would also, influence the electron gain enthalpy., , Think and discuss, •, •, , The calculated electron gain enthalpy values for alkaline earth metals and, noble gases are positive. How can you explain this?, The second period element for example ‘F’ has less electron gain enthalpy, than the third period element of the same group for example ‘Cl’. Why?, , Free distribution by A.P. Government, , 195
Page 206 :
Electronegativity, The ionization energy and the electron gain enthalpy are properties of, isolated atoms of elements. There has been a need to have a comparative, scale relating the abilities of elements to attract electrons when their atoms, are combined. For this purpose, the concept of electronegativity is, introduced., The electronegativity of an element is defined as the relative tendency, of its atom to attract electrons towards it self when it is bonded to the, atom of another element., All the factors that influence the ionization energy and the electron, affinity of elements influence the electronegativity values of those, elements. Because of this, Milliken proposed that the electronegativity of, an element is the average value of its ionization energy and electron affinity., Electronegativity = ionization energy + electron affinity, 2, Pauling assigned the electronegativity values for elements on the basis, of bond energies. He assumed that the electronegativity of hydrogen is, 2.20 and calculated the values of other elements with respect to hydrogen., Observe the values in the following example, Period, , Element (electronegativity with respect hydrogen), , Halogens:, 2nd period:, , F(4.0), Cl(3.0), Br(2.8), I(2.5), Li(1.0), Be(1.47), B(2.0), C(2.5), N(3.0), O(3.5), F(4.0), Ne(-), Electronegativity values of elements decrease as we go down in a group, and increase along a period from left to right. The most electronegative, element is ‘F’ and the least electronegative stable element is ‘Cs’., , Metallic and Non-Metallic Properties, Metals generally show less electronegative character. In compounds,, they generally show a tendency to remain as positive ions. This property is, often termed as electropositive character. Metals are electropositive, elements., Non metals are generally more electronegative due to their smaller, atomic radii., Let us examine the elements of 3rd period., 3rd period:, 196, , X Class, , Na, , Mg, , Al, , Si, , P, , S, , Cl, , Classification of Elements - The Periodic Table
Page 207 :
We know that Na and Mg are metals, Al and Si are semi metals, (metalloids), P, S and Cl are non metals. So we find metals on left side and, non metals on right side of the periodic table. This means metallic character, decreases while non metallic character increases as we move along a period, (from left to right)., Let us take group 14 (IVA) elements., IVA group:, C, Si, Ge, Sn, Pb, Here also we know that carbon is nonmetal. Si and Ge are metalloids., Sn and Pb are metals., So we find nonmetals particularly at the right hand side top and metals, at the left and right hand side bottom of the periodic table. This means, metallic character increases while non metallic character decreases in a, group as we move from top to bottom., , Key words, Triad, Octave, Periodic Law, Periodic table, period, group, Lanthanides,, Actinides, Element family, Metalloids, Periodicity, Atomic radius, Ionization, energy, Electron affinity, Electronegativity, Electropositivity, , What we have learnt, •, •, •, •, •, •, , •, •, •, •, , Elements are classified on the basis of similarities in their Properties., Dobereiner grouped the elements into Triads and Newlands gave the law of Octaves., Mendeleeff’s Periodic law: The physical and chemical Properties of the elements are the periodic, functions of their Atomic Masses., Moseley’s Periodic law : The physical and chemical properties of the elements are the periodic, functions of their Atomic numbers., Modern Periodic Law: The Physical and chemical Properties of the elements are the periodic, functions of their Electronic Configurations., Anomalies in arrangement of elements based on increasing atomic mass could be removed, when the elements were arranged in order of increasing atomic number, a fundamental property, of the element discovered by Moseley., Elements in the Modern Periodic table are arranged in 18 groups and 7 periods., Elements are classified into s, p, d, f blocks, depending upon to which sub shell the differentiating, electron enters in the atom of the given element., All the d- block elements (except Zn group) are known as transition elements and all the, f-block elements (both Lanthanides, Actinides) are known as inner transition elements., Periodic properties of elements and their trends in groups and in periods, , Free distribution by A.P. Government, , 197
Page 208 :
Periodic property, , Trend in, groups, , periods, , From top to bottom, , From left to right, , Atomic radius, , Increasing, , Decreasing, , Ionisation energy, , Decreasing, , Increasing, , Electron affinity, , Decreasing, , Increasing, , Electronegativity, , Decreasing, , Increasing, , Electropositivity, , Increasing, , Decreasing, , Metallic nature, , Increasing, , Decreasing, , Non-Metallic nature, , Decreasing, , Increasing, , Valency, , Improve your learning, 1. Newlands proposed the law of octaves. Mendeleeff suggested eight groups for elements in his, table. How do you explain these observations in terms of modern periodic classification?(AS1), 2. What are the limitations of Mendeleeff’s periodic table? How could the modern periodic table, overcome the limitations of Mendeleeff’s table? (AS1), 3. Define the modern periodic Law. Discuss the construction of the long form of the periodic table., (AS1), 4. Explain how the elements are classified into s, p, d and f- block elements in the periodic table, and give the advantage of this kind of classification. (AS1), 5. Given below is the electronic configuration of elements A, B, C, D., (AS1), 2, 2, A.1s 2s, 1. Which are the elements coming with in the same period, B.1s2 2s2 2p6 3s2, 2. Which are the ones coming with in the same group?, 2, 2, 6, 2, 3, C.1s 2s 2p 3s 3p, 3. Which are the noble gas elements?, D.1s2 2s2 2p6, 4. To which group and period does the elements ‘C ‘belong, 6. Write down the characteristics of the elements having atomic number 17. (AS1), Electronic configuration, ____________________________________, Period number, ____________________________________, Group number, ____________________________________, Element family, ____________________________________, No. of valence electrons ____________________________________, Valency, ____________________________________, Metal or non-metal, ____________________________________, 7. a. State the number of valence electrons, the group number and the period number of each, element given in the following table: (AS1), 198, , X Class, , Classification of Elements - The Periodic Table
Page 209 :
Element, , Valence electrons, , Group number, , Period number, , Sulphur, Oxygen, Magnesium, Hydrogen, Fluorine, Aluminum, b. State whether the following elements belong to a Group (G), Period (P) or Neither Group nor, Period (N). (AS1), , Elements, , G/P/N, , Li,C,O, Mg, Ca, Ba, Br, Cl, F, C,S, Br, Al, Si, Cl, Li, Na, k, C,N,O, K, Ca, Br., 8. Elements in a group generally possess similar properties, but elements along a period have, different properties. How do you explain this statement? (AS1), 9. s - block and p - block elements except 18th group elements are sometimes called as, ‘Representative elements’ based on their abundant availability in the nature. Is it justified? Why?, (AS1), 10. Complete the following table using the periodic table. (AS1), , Period, number, 1, 2, 3, 4, 5, 6, 7, , Filling up orbital’s, (sub shells), , Maximum number of, electrons, filled in all, the sub shells, , Total no. of, elements in the, period, , 4s, 3d, 4p, , 18, , 18, , 7s, 5f, 6d, 7p, , 32, , incomplete, , Free distribution by A.P. Government, , 199
Page 210 :
11. Complete the following table using the periodic table. (AS1), , Period, number, , Total no. of, elements, , Elements, From, , To, , Total no. of elements in, s-block p-block d-block, , f-block, , 1, 2, 3, 4, 5, 6, 7, 12. The electronic configuration of the elements X, Y and Z are given below?, a) X = 2 b) Y = 2, 6, c) Z = 2, 8, 2, i) Which element belongs to second period?, ii) Which element belongs to second group?, iii) Which element belongs to 18th group?, 13. Identify the element that has the larger atomic radius in each pair of the following and mark it, with a symbol (3). (AS1), (i) Mg or Ca, (ii) Li or Cs, (iii) N or P, (iv) B or Al, 14. Identify the element that has the lower Ionization energy in each pair of the following and mark, it with a symbol (3). (AS1), (i) Mg or Na, (ii) Li or O, (iii) Br or F, (iv) K or Br, 15. In period 2, element X is to the right of element Y. Then, find which of the elements have:, (i) Low nuclear charge, (ii) Low atomic size, (iii) High ionization energy, (iv)High electronegativity (v) More metallic character, (AS1), 16. How does metallic character change when we move, i. Down a group, ii. Across a period?, 17. Why was the basis of classification of elements changed from the atomic mass to the atomic, number? (AS1), 18. What is a periodic property? How do the following properties change in a group and period?, Explain. (AS1), (a) Atomic radius (b) Ionization energy (c) Electron affinity (d) Electronegativity., (b) Explain the ionization energy order in the following sets of elements:, a) Na, Al, Cl b) Li, Be, B c) C, N, O d) F, Ne, Na e) Be, Mg, Ca. (AS1), 19. Name two elements that you would expect to have chemical properties similar to Mg. What is, the basis for your choice? (AS2), 20. On the basis of atomic numbers predict to which block the elements with atomic number 9,, 37, 46 and 64 belongs to? (AS2), 21. Using the periodic table, predict the formula of compound formed between and element X of, group 13 and another element Y of group 16. (AS2), 200, , X Class, , Classification of Elements - The Periodic Table
Page 211 :
22. An element X belongs to 3rd period and group 2 of the periodic table. State, (a) The no. of valence electrons (b) The valency (c) Whether it is metal or a nonmetal. (AS2), 23. An element has atomic number 19. Where would you expect this element in the periodic table, and why? (AS2), 24. Aluminium does not react with water at room temperature but reacts with both dil. HCl and, NaOH solutions. Verify these statements experimentally. Write your observations with chemical, equations. From these observations, can we conclude that Al is a metalloid? (AS3), 25. Collect the information about reactivity of VIII A group elements (noble gases) from internet or, from your school library and prepare a report on their special character when compared to, other elements of periodic table. (AS4), 26. Collect information regarding metallic character of elements of IA group and prepare report to, support the idea of metallic character increases in a group as we move from top to bottom., (AS4), 27. How do you appreciate the role of electronic configuration of the atoms of elements in periodic, classification? (AS6), 28. Without knowing the electronic configurations of the atoms of elements Mendeleev still could, arrange the elements nearly close to the arrangements in the Modern periodic table. How can, you appreciate this? (AS 6), 29. Comment on the position of hydrogen in periodic table. (AS7), 30. How the positions of elements in the periodic table help you to predict its chemical properties?, Explain with an example. (AS7), , ks, Fill in the blan, 1., 2., 3., 4., 5., , Lithium, _____________ and potassium constitute a Dobereiner’s triad., _______ was the basis of the classifications proposed by Dobereiner, Newlands and Mendeleeff., Noble gases belongs to _______________ group of periodic table., The incomplete period of the periodic table is _____________ ., The element at the bottom of a group would be expected to show __________ metallic character, than the element at the top., , s, Multiple choice question, 1. Number of elements present in period – 2 of the long form of periodic table, [, ], a) 2, b) 8, c) 18, d) 32, 2. Nitrogen (Z = 7) is the element of group V of the periodic table. Which of the following is the, atomic number of the next element in the group?, [, ], a) 9, b) 14, c) 15, d) 17, 3. Electron configuration of an atom is 2, 8, 7 to which of the following elements would it be, chemically similar?, [, ], a) nitrogen(Z=7) b) fluorine(Z=9), c) phosphorous(Z=15) d) argon(Z=18), 4. Which of the following is the most active metal?, [, ], a) lithium, b) sodium, c) potassium, d) rubidium, Free distribution by A.P. Government, , 201
Page 212 :
Chapter, , 10, Chemical Bonding, You have learnt about electron configuration of elements and periodic, table in previous lessons. It was learnt that there are over 115 elements., • How do they usually exist?, • Do they exist as a single atom or as a group of atoms?, In Class IX, we saw that several elements like oxygen, nitrogen and, hydrogen exist as diatomic molecules. What is the force that is holding, these constituent atoms together in molecules?, • Are there elements which exist as atoms?, • Why do some elements exist as molecules and some as atoms?, In lower classes you have also learnt about the different laws of, chemical combinations. Since the formation of chemical compounds takes, place as a result of combination of atoms of various elements in different, ways, it raises many questions., • Why do some elements and compounds react vigorously while others, are inert?, • Why is the chemical formula for water H2O and for sodium chloride, NaCl, why not HO2 and NaCl2?, • Why do some atoms combine while others do not?, We will try to answer such questions in this chapter., • Are elements and compounds simply made up of separate atoms, individually arranged?, • Is there any attraction between atoms?, Let us take the example of common salt, NaCl. When you shake salt, from a shaker does it separate into sodium and chlorine? No! This shows, that the sodium and chlorine atoms are being held together., • What is that holding them together?, 202, , X Class, , Chemical Bonding
Page 213 :
By the late 19th century and early twentieth century, scientists knew, about three types of forces – gravitational, magnetic and electrostatic., They also knew about the existence of electrons and protons. So it was, believed that electrostatic forces were the cause of attraction between, atoms in a molecule. When two atoms come sufficiently close together,, the electrons of each atom experience the attractive force of the nucleus, of the other atom. But the electrons which are negatively charged and repel, each other, and the positively charged nuclei also repel each other. The, strength of attraction or repulsion will decide bond formation. If attraction, is more than the repulsion then atoms combine. If repulsion is more than, attraction then the atoms do not combine. The nucleus and the electrons, in the inner shell remain unaffected when atoms come close together. But, the electrons in the outermost shell (valence shell) of atoms get affected., , Do you know?, , Davy’s experiment –, Humphry Davy (1778-1819),, a professor of chemistry at the, Royal Institution in London,, constructed a battery of over 250, metallic plates. In 1807, using, electricity from this battery, he, was able to extract highly reactive, metals like potassium and sodium, by electrolysis of fused salts., , A Votaic pile, , It was seen that the metal part of the compound, migrated towards the negative electrode and the, non-metal part towards the positive electrode. So, it was proposed that metals are responsible for, positively charged particles and non-metals are, responsible for negatively charged particles. The Experimental set up by Davy, oppositely charged particles are held together by, electrostatic forces in a compound. Do you agree with this explanation? Why?, While this explanation could explain bonding in NaCl, KCl etc. it could not explain, bonding in carbon compounds or diatomic molecules of elements., Free distribution by A.P. Government, , 203
Page 214 :
Electrons in valence shell (valence electrons) are responsible for the, formation of bonds between atoms., In previous lessons you studied about exothermic and endothermic, reactions. You also studied about reactivity of elements in periodic table., Some elements are more reactive and some are less reactive;, • Why there is absorption of energy in certain chemical reactions and, release of energy in other reactions?, • Where the absorbed energy goes?, • Is there any relation to energy and bond formation between atoms?, • What could be the reason for the change in reactivity of elements?, Lewis symbols (or) Lewis dot structures:, Periodic Classification and arrangement of elements in the periodic, table according to the electron configuration gave a new thought about, chemical bond., The discovery of noble gases and the understanding of their electronic, configurations helped us in explaining the formation of chemical bonds, among the atoms of the elements. Noble gases which belong to zero group, (18th group or VIII A) are typical gases with almost negligible chemical, activity when compared to other elements. They undergo few or no chemical, changes. They are more stable and do not form molecules by allowing, their atoms to combine among themselves or with the atoms of other, elements., • What could be the reason for this?, Let us investigate., Consult the periodic table given in the previous chapter and fill the, following table:, Table-1, Element, , Z, , Helium (He), Neon (Ne), Argon(Ar), Krypton(Kr), , 2, 10, 18, 36, , Electronic configuration, K, L, M, N, 2, 2, 8, 2, 8, 8, 2, 8, 18, 8, , Valence elctrons, 2, 8, 8, 8, , Look at the second column and third column. It is clear that all the, noble gases have eight electrons in the outermost shell, except, Helium (He)., 204, , X Class, , Chemical Bonding
Page 215 :
: :, , The arrangement of electrons in different shells of atoms (electronic, configuration) of 18th group elements is shown in the table-1. The valence, electrons in the atom of an element is depicted in a short form by Lewis, symbol or electron dot structure. We represent the nucleus and inner shell, electrons of the atom by the symbol of the element and electrons in the, outer shell by dots or cross marks., Let us see how? Lewis dot structure of argon and sodium atoms are, written., Let us start with argon. Its atom has eight valence electrons., First write the symbol of element argon. Ar, Place the valence electrons around the symbol. Put two dots at a time, on each of the four sides of the symbol of the element till all are used up., So, we get,, , : Ar :, , Similarly, for sodium, the number of valence electrons in sodium is, one and the symbol is Na. We can also use cross mark for the electrons., The Lewis structure for sodium atom is therefore:, , Na x, , : : : :, , : Kr : : Ne :, , : :, , He, , : : : :, , :, , The Lewis dot structures of the atoms of noble gases are shown below:, , : Xe : : Ar : : Rn :, Activity 1, Write the Lewis structures of the given elements in the table. Also, consult the periodic table and fill in the group number of the element., Table – 2:, Element Hydrogen, , Helium Beryllium Boron Carbon Nitrogen oxygen, , Group, 1, number, Valence 1, electron, Lewis dot H, structure, , ., , Free distribution by A.P. Government, , 205
Page 216 :
Look at the periodic table. Do you see any relation between the number, of valence electrons and group numbers? We find that for groups 1-2 and, 13 –18, we can use the periodic table to find the number of valence, electrons. Group1 has one outer electron, group 2 has two, and group 13, has three and so on., • What did you notice in Lewis dot structure of noble gases and, electronic configurations of the atoms of these elements shown in, table - 1., It was found that the elements which participate in chemical reactions, get octet or ns2 np6 configuration similar to that of noble gas elements. It, is to be noted that octet rule is still a rule not the law, because there are, considerable exceptions for this rule., , Electronic theory of valence by Lewis and Kossel, There were number of attempts to explain the chemical bond formation, between atoms in terms of electrons but a satisfactory explanation for, this concept was given by Kossel and Lewis in 1916. They gave this concept, independently. The basis for their theory was valence in terms of electrons., They provided logical explanation of valence on the basis of the lack of, chemical activity of noble gases which led to the proposal of octet rule., Observe the practical behaviour of atoms of main group elements, (Group IA, IIA, IIIA, IVA, VA, VIA, VIIA and zero or VIIIA group elements)., When they are allowed to undergo chemical changes, they try to get octet, electronic configuration in the outer shells., Let us understand this with the following illustrations., Group IA elements (Li to Cs) try to lose one valence shell electron, from their atoms to form corresponding uni-positive ions which get octet, in their outer shells., Example: 11Na 2, 8, 1 ; 11Na+ 2, 8, Group IIA elements (Mg to Ba) try to lose two valence electrons from, their atoms during chemical changes and form di– positive ions with the, octet in the outer shells., Example: 12Mg 2, 8, 2 ; 12Mg2+ 2, 8, Group IIIA elements try to lose three valence electrons from their, atoms and form corresponding tri positive ions with octates in the outer, shells., 206, , X Class, , Chemical Bonding
Page 217 :
Example: 13Al 2, 8, 3 ; 13Al3+ 2, 8, Group VIA elements try to gain two electrons into the valence shells, of their atoms during the chemical changes and form corresponding di, negative anions which get octet in their outer shells., Example: 8O 2, 6 ; 8O2– 2, 8, Group VIIA elements try to gain one electron into the valence shells, of their atoms during the chemical changes and form corresponding, uni– anions which get octet in their outer shells., Example: 9F 2, 7 ; 9F– 2, 8, Group VIIIA elements, the noble gases do not try to lose or gain, electrons. Generally, helium and neon do not participate in chemical, changes. Even other elements of VIIIA do not gain or lose electrons from, their atoms when they participate in a very few chemical changes., Example: 10Ne 2, 8 ; No electron gain or loss from the neon, atom., Gain Electrons, , Lose Electrons, Magic, octet, , +1, , +2, , VII, , VIII, , I, , II, , O, , F, , Ne, , Na, , Mg Al, , P, , S, , Cl, , Ar, , K, , Ca, , Ga, , As, , Se, , Br, , Kr, , Rb, , Sr, , In, , Sb, , Te, , I, , Xe, , Cs, , Ba, , Tl, , Bi, , Po, , At, , Ra, , Fr, , Ra, , Net charge on } –3, the species, V, , –2, , –1, , VI, , N, , Non metals, , Noble gases, , +3, III, , Metals, , •, , What have you observed from the above conclusions about the main, groups?, • Why do atoms of elements try to combine and form molecules?, Noble gases of VIII A possess eight electrons in the valence shells of, their atoms. Helium is an exception. Its atom has only two electrons, but, its only shell is completely filled. Noble gases with eight electrons in the, valence shell in their atoms are highly stable and rarely participate in, chemical changes. Therefore it is concluded that any species (atom or, ion) with eight electrons in the valence shell is stable., Free distribution by A.P. Government, , 207
Page 218 :
•, , Is it accidental that IA to VIIA main group elements during chemical, reactions get eight electrons in the outermost shells of their ions,, similar to noble gas atoms?, No. It cannot be simply accidental. Eight electrons in the outermost, shell definitely gives stability to the ion or atom. Based on the above, observations a statement known as “ The Octet Rule” is framed., , Octet rule:, It may be stated as “The atoms of elements tend to undergo chemical, changes that help to leave their atoms with eight outer-shell electrons.”, Lewis depicted the atom in terms of a positively charged kernel (Kernel, is the nucleus and all other electrons in the atom except the outer most, shell electrons) and the outershell that could accommodate a maximum, of eight electrons., Chemically active elements do not have an octet of electrons in the, valence shell of their atoms. Their reactivity arises from their tendency to, achieve the octet, by forming bonds either with atoms of their own type or, with atoms of other elements., The force of attraction between any two atoms or a group of atoms, that results a stable entity is called a ‘chemical bond’. There are many, types of chemical bonds, but here we discuss only about ionic bond and, covalent bond., , Ionic and Covalent bonds with Lewis dot formulae, A. Ionic bond, Kossel proposed the ionic bond (electrostatic bond) based on the, following facts., i. Ionic bond is formed between atoms of two dissimilar elements due, to transfer of electrons from the atom of one element to the other., ii. There are highly reactive metals like alkali metals (IA) and highly, reactive non-metals like halogens (VIIA) on the left side and right side, of the periodic table respectively., iii. Noble gases except helium have eight electrons in the valence shells, of their atoms. They are chemically inactive and stable., iv. To attain eight electrons in the outermost shell similar to noble gases, metal atoms that have one two or three electrons in the valence shells, generally lose those electrons and form stable positive ions called, cations., , 208, , X Class, , Chemical Bonding
Page 219 :
Example:, , 11, , Na 2, 8, 1 ; Na+ 2, 8, , 12, , Mg 2, 8, 2 ; Mg2+ 2, 8, , 13, , Al 2, 8, 3 ; Al3+ 2, 8, , Do you know?, The number of electrons lost from a metal atom is the valence of its element, which is equal to its group number., Ex. Na and Mg have valence 1 and 2 respectively., v. To attain eight electrons in the outermost shell, non-metal atoms that, have 5,6 or 7 valence electrons gain 3,2 or 1 electron respectively and, form negative ions known as anions., Example:, , 15, , P 2, 8, 5 ; P3- 2, 8, 8, , 16, , S 2, 8, 6 ; S2-, , 2, 8, 8, , 17, , Cl 2, 8, 7 ; Cl-, , 2, 8, 8, , Do you know?, The number of electrons gained by a non-metal element for its atom is its valency,, which is equal to (8 - its group number)., Ex. The valency of chlorine is (8 – 7) = 1., , vi. Formation of ionic bond, The positive ions (cations) and negative ions (anions) that are formed, due to the transfer of electrons from the metal atoms to the non-metal, atoms experience the electrostatic forces and get attracted to form, chemical bond. As this bond is between charged particles known as, ions, it is called ionic bond. Sometimes based on the forces being, electrostatic, the bond is also called the electrostatic bond. As the, valence concept has been explained in terms of electrons, it is also, called the electrovalent bond., Thus, we can define ionic bond as follows:, The electrostatic attractive force that keeps cation and anion (which, are formed from metal atoms and non-metal atoms due to transfer of, electrons) together to form a new electrically neutral compounds is called, ‘ionic bond’., • Explain the formation of ionic compounds NaCl, MgCl2, Na2O and, AlF3 through Lewis electron dot symbols (formulae), Free distribution by A.P. Government, , 209
Page 220 :
Eg-1. Formation of sodium chloride (NaCl):, Sodium chloride is formed from the elements sodium and chlorine. It, can be explained as follows:, Na(s) + 1/2 Cl2(g), NaCl(s), , Cation formation, , When sodium (Na) atom loses one electron to get octet electron, configuration it forms a cation (Na+) and gets electron configuration that, of Neon (Ne) atom., Na (g), Na+ (g) + e11, 11, E.C. 2, 8, 1, 2, 8, or [Ne] 3s1 [Ne], , Anion formation, Chlorine has shortage of one electron to get octet in its valence shell., So it gains the electron from Na atom to form anion and gets electron, configuration as that of argon (Ar)., Cl (g), + eCl– (g), 17, Electronic configuration 2, 8, 7, 2, 8, 8, or [Ne] 3s2 3p5, [Ne] 3s2 3p6 or [Ar], Formation of the compound NaCl from its ions:, Transfer of electrons between ‘Na’ and ‘Cl’ atoms, results in the, formation of ‘Na+’ and ‘Cl–’ ions. These oppositely charged ions get, attracted towards each other due to electrostatic forces and form the, compound sodium chloride (NaCl)., Na+Cl– (s) or NaCl, Na+(g) + Cl–(g), Eg-2. Formation of magnesium chloride (MgCl2):, Magnesium chloride is formed from the elements magnesium and, chlorine. The bond formation MgCl2 in brief using chemical equation is as, follows:, Mg(s) + Cl2(g), Mg Cl2(s), , Cation formation, , Mg (g), Electronic configuration 2, 8, 2, or, [Ne] 3s2, 11, , 11, , Mg2+ (g) + 2e–, 2, 8, [Ne], , Anion formation, 2Cl (g) + 2e–, Electronic configuration 2, 8, 7, or [Ne] 3s2 3p5, 210, , X Class, , 2Cl– (g), 2, 8, 8, [Ne] 3s2 3p6 or [Ar], Chemical Bonding
Page 221 :
The compound MgCl2 formation from its ions:, Mg2+ gets ‘Ne’ configuration and, Each Cl– gets ‘Ar’ configuration, Mg2+ (g) + 2Cl–(g), MgCl2 (s), One ‘Mg’ atom transfers two electrons one each to two ‘Cl’ atoms and, so formed Mg2+ and 2Cl– attract to form MgCl2., Eg-3. Formation of di sodium monoxide(Na2O):, Di sodium monoxide formation can be explained as follows:, Cation formation (Na+ formation):, 2Na (g), 2Na+ (g) + 2eElectronic configuration 2, 8, 1, 2, 8, or, [Ne] 3s1, [Ne], Anion formation (O2–, the oxide formation):, O (g) + 2eO2- (g), Electronic configuration 2, 6, 2, 8, or [Ne] 2s2 2p4, [He] 2s2 2p6 or [Ne], The compound Na2O formation from its ions is as shown., 2Na+ (g) + O2-(g), Na2O(s), Two ‘Na’ atoms transfer one electron each to one oxygen atom to, form 2Na+ and O2Each Na+ gets ‘Ne’ configuration and O2- gets ‘Ne’ configuration., These ions (2Na+ and O2-) attract to form Na2O., Eg-4. Formation of aluminium chloride (AlCl3):, Aluminium chloride formation can be explained as follows:, Formation of aluminium ion (Al3+), the cation:, Al(g), Al3+ (g) + 3e13, Electronic configuration 2, 8, 3, 2, 8, 2, 1, or, [Ne] 3s 3p, [Ne], Formation of chloride ion (Cl-), the anion:, 3Cl(g) + 3e3Cl–(g), Electronic configuration 2, 8, 7, 2, 8,8, or [Ne] 3s2 3p5, [Ne] 3s2 3p6 or [Ar], Each aluminium atom loses three electrons and three chlorine atoms, gain them, one electron each., Free distribution by A.P. Government, , 211
Page 222 :
The compound AlCl3 is formed from its component ions by the, electrostatic forces of attractions., Al3+ (g) + 3Cl–(g), AlCl3 (s), , The arrangement of ions in ionic comounds, •, , Na+, Cl –, , 212, , How do cations and anions of an ionic compound exist in its solid, state?, • Let us explain this with sodium chloride as our example:, • Do you think that pairs of Na+ Cl- as units would be present in the solid, crystal?, If you think so, it is not correct. Remember that electrostatic forces, are non directional. Therefore, it is not possible for one Na+ to be attracted, by one Cl– and vice-versa. Depending upon the size and charge of a particular, ion, number of oppositely charged ions get attracted by it, but, in a definite, number. In sodium chloride crystal each Na+ is surrounded by 6 Cl- and, each Cl– by six Na+ ions. Ionic compounds in the crystalline state consist, of orderly arranged cations and anions held together by electrostatic forces, of attractions in three dimensions. The crystal structure of sodium chloride, is given below:, NaCl is said to possess face centred cubic lattice crystal, structure (see figure-1)., The number of ions of opposite change that surround a, given ion of given charge is known as the coordination, number of that given ion., For example, in sodium chloride crystal, the, coordination number of Na+ is 6 and that of Cl- is also 6., Factors affecting the formation of cation and anion:, In previous lesson you have learnt about variation of, fig-1, metallic and non metallic character of elements in a group, or period of the periodic table. Recall the facts about metallic and non, metallic character of elements., Generally elements of metals have tendency of losing electron to attain, the octet in their valence shell. This property is called as the metallic, character or electropositivity. Elements with more electropositive, character form cations. Similarly non metals like oxygen (8O), fluorine, (9F) and chlorine (17Cl) acquire electron configuration of elements of inert, gases by gaining electrons this property is called the non-metallic, character or electronegativity of the element. Elements with more, electronegative character form anions., X Class, , Chemical Bonding
Page 223 :
•, , Can you explain the reasons for all these?, Ionic bond is formed between atoms of elements with electronegativity, difference equal to or greater than 1.9., In ionic bond formation, you have noticed that atoms either lose, electrons or gain electrons to attain octet in valence shell. i.e., in an ionic, bond, transfer of electrons takes place between combining atoms., The tendency of losing electrons to form cations (or) gaining electron, to form anions depends on the following factors:, i. Atomic size, ii. Ionisation potential, iii. Electron affinity, iv. Electronegativity, The atoms of elements with low ionisation energy, low electron affinity, high atomic size and low electronegativity form cations., The atoms of elements with high ionisation potential, high electron, affinity, small atomic size and hight electronegativity form anions., , B. Covalent bond, G.N. Lewis (1916) proposed that atoms of some elements could, achieve an octet in their valence shells without transfer of electrons, between them. They can attain octet configuration in their valence shells, by sharing the valence electrons with one or more atoms., The electrons shared between two atoms belong to both the atoms and, the sharing of electrons between them leads to the formation of a chemical, bond known as covalent bond., For example, take two fluorine atoms which form a stable molecule., Each fluorine atom contributes one electron for bonding and the electron, pair that is formed in this way is mutually shared by both the fluorine, atoms. Each atom in the F2 molecule has an octet of valence electrons., , Free distribution by A.P. Government, , 213
Page 224 :
The dots around fluorine atom shows the valence electrons of, respective atoms., The chemical bond formed between two atoms by mutual sharing of a, pair of valence shell electrons so that both of them can attain octet or, duplet in their valence shell is called the covalent bond., The prefix co – is used to indicate when things are equal or joined., (for example, co exist, cooperate etc). Here each atom contributes one, electron from the valence shell for the bonding. Therefore, the name, covalent is given (equal valence electrons contribution) for this bond., , Formation of O2 molecule, The electronic configuration of 8O is 2, 6. Oxygen atom has six, electrons in its valence shell. It requires two more electrons to get octet, in its valence shell. Therefore oxygen atoms come close and each oxygen, atom contributes two electrons for bonding. Thus, there exist two covalent, bonds between two oxygen atoms in O2 molecule as there are two pairs of, electrons shared between them., We can say that a double bond is formed between two oxygen atoms in, O2 molecule. Observe the following figures. Both the oxygen atoms have, octet in the valence shell., , •, , Can you say what type of bond exists between atoms of nitrogen, molecule?, Let us see, , Nitrogen (N2) molecule, The electronic configuration of ‘N’ atom is 2,5 and to have octet in the, valence shell it requires three more electrons. When two nitrogen atoms, approach each other, each atom contributes 3 electrons for bonding. There, are six electrons shared between two nitrogen atoms in the form of three, pairs. Therefore, there is a triple bond between two nitrogen atoms in N2, molecule., , 214, , X Class, , Chemical Bonding
Page 225 :
Methane (CH4) molecule, In the formation of methane, CH4 molecule, carbon contributes 4, electrons, (one electron to each hydrogen atom) and 4 hydrogen atoms, contribute one electron each. Thus in CH4 molecule, there are four C – H, covalent bonds as shown below:, , Ammonia (NH3) molecule, In ammonia molecule, three N – H single covalent bonds are present., Electron configuration of 7N is 2, 5 and 1H is 1., Nirogen atom contributes three electrons for bonding. Three hydrogen, atoms at the same time contribute one electron each for bonding. Six, electrons form three pairs and each pair is shared between nitrogen and, one hydrogen atom as shown below:, , Free distribution by A.P. Government, , 215
Page 226 :
Water (H2O) molecule, In water molecule (H2O), there are two O – H single covalents bonds., Electron configuration of 8O is 2,6 and 1H is 1., Oxygen atom needs ‘2’ electrons to attain octet in its valence shell., Therefore it shares ‘2’ electron with two hydrogen atoms to form water, (H2O) molecule., , The total number of covalent bonds that an atom of an element forms, is called its ‘covalency’., , The Bond lengths and Bond energies of covalent bonds, Bond length or bond distance is the equilibrium distance between the, nuclei of two atoms which form a covalent bond., It is generally given in nm (nanometer) or Å (Angstrom unit)., Bond energy or Bond dissociation energy is the energy needed to break, a covalent bond between two atoms of a diatomic covalent compound in, its gaseous state., , Do you know?, •, •, , An angstrom (Å) is a unit of length equal to 10-10 metre, or 0.1 nanometre, or, 100 picometre., 1 nanometre = 10-9 metre, , Draw backs of electronic theory of valence, 1) When a covalent bond is formed between any two atoms, irrespective, of the nature of the atoms, the bond lengths and bond energies are expected, to be the same. This is because any covalent bond between any two atoms, is a result of mere sharing of two identical electrons. But, practically it, was observed that bond lengths and bond energies are not same when the, atoms that form the bond are different. (See table - 3), • What do you understand from bond lengths and bond energies?, 216, , X Class, , Chemical Bonding
Page 227 :
•, , Are the values not different for the bonds between different types of atoms?, ∧, ∧, 2) The theory could not explain why ClB eCl in BeCl2 is 1800, FBF in, ∧, BF3 is 120o, HCH in CH4 is, ∧, Table – 3, 109 028 /, HNH in NH 3 is, ∧, Bond, Bond, Bond (dissociation), 107018/ and HOH in H2O is, length (Å) energy (KJmol-1), 104o31/ etc., H –H, 0.74, 436, i.e., it fails to explain the, F–F, 1.44, 159, shapes of the molecules., Cl – Cl, 1.95, 243, Valence shell electron, Br – Br, 2.28, 193, pair repulsion theory, I–I, 2.68, 151, To explain the bond, H–F, 0.918, 570, angles in the molecules with, H – Cl, 1.27, 432, three or more than three, H – Br, 1.42, 366, atoms with all atoms, attached to a central atom, H–I, 1.61, 298, through covalent bonds a, H – O (of H2O), 0.96, 460, theory called the valence –, H – N (of NH3), 1.01, 390, shell – electron – pair, H – C (of CH4), 1.10, 410, repulsion, –, theory, (VSEPRT) was proposed by Sidgwick and Powell (1940). It was further, improved by Gillespie and Nyholm (1957)., This theory suggests the following points., 1. VSEPRT considers electrons in the valence shells which are in covalent, bonds and in lone pairs as charge clouds that repel one another and, stay as far apart as possible. This is the reason why molecules get, specific shapes., 2. If we know the total number of electron pairs in the valence shell as, covalent bonds and lone pairs in the central atom, it will help us to, predict the arrangement of those pairs around the nucleus of the central, atom and from that the shape of the molecule., 3. Lone pairs occupy more space around the central atom than bond pairs., Lone pair means unshared electron pair or non-bonding electron pair., These are attracted to only one nucleus where as the bond pair is shared, by two nuclei. Thus, the presence of lone pairs on the central atom, causes slight distortion of the bond angles from the expected regular, shape. If the angle between lone pair and bond pair increases at the, central atom due to more repulsion, the actual bond angles between, atoms must be decreased., Free distribution by A.P. Government, , 217
Page 228 :
4.i) If two bond pairs are present in two covalent bonds around the, nucleus of the central atom without any lone pairs in the valence shell,, they must be separated by 1800 to have minimum repulsion between them., Thus, the molecule would be linear., Example:, , 4.ii) If three bond pairs are there in three covalent bonds around the, nucleus of the central atom, without any lone pairs they get separated by, 1200 along three corners of a triangle. Therefore, the shape of the molecule, is trigonal-planar., Example:, , NOTE: Did you notice that in BeCl2 and BF3 the central atoms Be and, B did not possess 8 electrons around them in the valence shell. They have, only 4 and 6 electrons respectively. These molecules are known as electron, deficient molecules., 4.iii) If there are four bond pairs in the valence shell of the central, atom, the four bond pairs will orient along the four corners of a tetrahedron, (three dimensional arrangement) and the bond angle expected is 109028/, .Example: Methane., ∧, * In methane molecule (CH4), HCH is 109028/ because of four electron, pairs (bonding) around carbon, as shown below:, 218, , X Class, , Chemical Bonding
Page 229 :
4.iv) If there are three bond pairs and one lone pair i.e., unshared, electron pair, then the lone pair occupies more space around the nucleus, of the central atom. The remaining three bond pairs come relatively closer, as in NH3 molecule., Example: Ammonia, In ammonia (NH3) molecule, there are three bond pairs in, covalent bonds (3 N – H) around the nucleus of the nitrogen atom, and one lone pair. Lone pair – bond pair repulsion is greater than, bond pair – bond pair repulsion. Therefore, NH3 which is expected, to be tetrahedral with four electron pairs in the valence shell and, ∧, ∧, HNH = 109028/, it has HNH = 107048/ due to the more repulsion by lone, pair on the bond pairs., The shape of the NH3 molecule is triagonal pyramidal with N at the, apex of the pyramid., 4.v) If there are two bond pairs and two lone pairs of electrons around, the nucleus of the central atom in its valence shell, lone pair – lone pair, repulsion is greater than lone pair – bond pair repulsion. Therefore, the, angle between bond pairs further decreases., Example: Water, In water molecule, (H2O) there are four electron pairs around the, nucleus of oxygen atom, but, two of them are lone pairs and two bond, pairs. Therefore, H2O molecule gets ‘V’ shape or bent shape or angular, instead of tetrahedral shape as that of CH4 due to lone pair – lone pair, ∧, and lone pair – bond pair repulsions. HOH is 104031/., • What is the bond angle in a molecule?, It is the angle subtended by two imaginary lines that pass from, the nuclei of two atoms which form the covalent bonds with the, central atom through the nucleus of the central atom at the central, atom. (see figure ‘α’ is the bond angle)., Valence Shell Electron Pair Repulsion Theory (VSEPRT) mainly fails, in explaining the strengths of the bonds. This is because; the theory still, depends on the Lewis concept of covalent bond formation. It could not, say anything extra about the electronic nature of covalent bonds., Free distribution by A.P. Government, , 107 0 48 /, , α, , 219
Page 230 :
To describe covalent bonding, a quantum mechanical model called, valence bond theory has been suggested by Linus Pauling (1954)., , Valence bond theory, To describe covalent bonding, a quantum mechanical model called, valence bond theory has been suggested by Linus Pauling (1954). It is, explained as follows:, 1. A covalent bond between two atoms is formed when the two atoms, approach each other closely and one atom overlaps its valence orbital, containing unpaired electron, the valence orbital of the other atom that, contains the unpaired electron of opposite spin. The so formed paired, electrons in the overlapping orbitals are attracted to the nuclei of both the, atoms. This bonds the two atoms together., Eg: In the formation of H2 molecule, the 1s orbital of one ‘H’ atom, containing an unpaired electron overlaps the ‘1s’ orbital of the other ‘H’, atom containing unpaired electron of opposite spin giving H-H bond and, H2 molecule., , H atom, , H atom, , H2 molecule, , 2. The greater the overlapping of the orbitals that form the bond, the, stronger will be the bond. This gives a directional character to the bond, when other than ‘s’ orbitals are involved., 3. Each bonded atom maintains its own atomic orbitals but the electron, pair in the overlapping orbitals is shared by both the atoms involved in the, overlapping., 4. If two atoms form multiple bonds between them the first bond is, due to the overlap of orbitals along the inter-nuclear axis giving a stronger, sigma(σ) bond. After formation of (σ) bond the other bonds are formed, due to the overlap of orbitals side wise or laterally giving weaker π bonds., The ‘σ’ bond is stronger because the electron pair shared is concentrated, more between the two nuclei due to end-end or head on overlap and, attracted to both the nuclei. The π bond overlap gives a weaker bond due to, the lateral overlap of ‘p’ orbitals which is not to greater extent., , Consider Cl-Cl molecule, Cl - 1s2 2s2 2p6 3s2 3px2 3py2 3pz1, In the formation of Cl2 molecule, the 3pz orbital of one chlorine, atom containing an unpaired electron overlaps the 3pz orbital of other, chlorine atom that contains unpaired electron of opposite spin., 17, , 220, , X Class, , Chemical Bonding
Page 232 :
If Be forms two covalent bonds with two chlorine atoms, one bond, should be σ2s-3p due to the overlap of ‘2s’ orbital of Be, the ‘3pz’ orbital, of one chlorine atom and the other bond should be σ2p-3p due to the overlap, of ‘2px’ orbital of Be atom the 3p orbital of the other chlorine atom. As the, orbitals overlapping are different, the bond strengths of two Be-Cl must, ∧, be different. But, both bonds are of same strength and ClBeCl is 1800. To, explain the discrepancies like this a phenomenon called ‘hybridisation of, atomic orbitals’ was proposed by Linus Pauling (1931)., Hybridisation is a phenomenon of intermixing of atomic orbitals of, almost equal energy which are present in the outer shells of the atom and, their reshuffling or redistribution into the same number of orbitals but, with equal properties like energy and shape., Be atom in its excited state allows its 2s orbital and 2px orbital which, contain unpaired electrons to intermix and redistribute to two identical, orbitals. As per Hund’s rule each orbital gets one electron. The new orbitals, based on the types of orbitals that have undergone hybridisation are called, sp orbitals. The two sp orbitals of Be get separated by 1800. Now, each, chlorine atom comes with its 3pz1 orbital and overlaps it the sp orbitals of, ∧, Be forming two identical Be-Cl bonds (σsp-p bonds) . ClBeCl = 1800., Both the bonds are of same strength., , Boron triflouride, , Formation of BF3 molecule, , B has electronic configuration 1s2 2s2 2px1., As it has one unpaired electron (2px1) it should form only one covalent, bond to give B-F molecule. But we get practically BF3 molecule., To explain this, it is suggested that,, i. Boron (B) first undergoes excitation to get electronic configuration, 2, 1s 2s1 2px1 2py1., ii. As it forms three identical B-F bonds in BF3, it is suggested that, excited ‘B’ atom undergoes hybridisation. There is an intermixing of 2s,, 2px, 2py orbitals and their redistribution into three identical orbitals called, sp2 hybrid orbitals. For three sp2 orbitals to get separated to have minimum, 5, , 222, , X Class, , Chemical Bonding
Page 233 :
repulsion the angle between any two orbitals is 1200, at the central atom and each sp2 orbital gets one, electron. Now three fluorine atoms overlap their, 2pz orbitals containing unpaired electrons (F9 1s2, 2s2 2px2 2py2 2pz1) the three sp2 orbitals of ‘B’ that, contain unpaired electrons to form three σsp2-p, bonds., , Ammonia, , Formation of NH3 molecule, One nitrogen atom and three hydrogen atoms are present in one, ammonia molecule. All the three N-H bonds are of same strength and, ∧, HNH = 107048/, N has electronic configuration 1s2 2s2 2px1 2py1 2pz1., 7, If three hydrogen atoms overlap their 1s orbitals on the three ‘p’, orbitals, of nitrogen atom, they give identical σ p-s bonds but, then the, ∧, HNH should be equal to 900 where as 107048/ . To explain the discrepancy, in the bond angle ‘N’ atom is said to undergo sp3 hybridisation., In this process ‘2s’ and 2px, 2py, 2pz orbitals of nitrogen, intermix and redistribute into four identical sp3 orbitals. One, of the four sp3 orbitals get a pair of electrons and the other, three sp3 orbitals get one electron each. Now hydrogen atoms, overlap their 1s orbitals containing unpaired electrons the sp3, orbitals of ‘N’ atom, containing unpaired electrons to give three, ∧, 3, σs-sp bonds. HNH should be 1090 28/ for sp3 hybridisation. As there is, a lone pair in one of the sp3 orbitals, there is a greater lone pair – bond pair, ∧, repulsion which decreases the bond angle HNH to 107048/., , 107 0 48 /, , Shape of water molecule, ∧, , It is found that HOH is 104031/ ., The electronic configuration of 8O is 1s2 2s2 2px2 2py1 2pz1 and, H is 1s1., 1, Therefore, there should be two σ s-p bonds due to the overlap of ‘s’, orbitals of two hydrogen atoms, the ‘p’ orbitals of oxygen atom which, ∧, contain unpaired electrons. HOH should be 900., ∧, But HOH observed is 104031/ . To explain this, sp 3, hybridisation is suggested for the valence orbitals of ‘O’ atom., One s-orbital (2s) and three ‘p’ orbitals (2px, 2py, 2pz) intermix, and redistribute into four identical sp3 orbitals. As there are six, electrons and two sp3 orbitals get pairs and two sp3 orbitals get, one electron each. Now, the two sp3 orbitals of ‘O’ atom overlap, Free distribution by A.P. Government, , 223
Page 234 :
the ‘s’ orbitals of two hydrogen atoms to give σsp3-s bonds. Due to the, ∧, lone pair – lone pair repulsions and lone pair – bond pair repulsions HOH, decreases from 109028/ (expected for sp3 – tetrahedral hybridisation) to, 104031/., CH4, C2H4 and C2H2 molecules and their structures will be explained, in carbon and its compounds chapter later in this class., , Properties of ionic and covalent compounds, Table -4, S.No Property, , NaCl (ionic), , HCl (polar covalent) C2H6 (covalent), , 1., 2., 3., 4., 5., 6., , Formula mass, Physical appearance, Type of bond, Melting point, Boiling point, Solubility, , 58.5, White crystalline solid, Ionic, 801 0C, 1413 0C, Soluble in polar, solvents like water, and insoluble in non, -polar solvents, , 36.5, Colourless gas, Polar covalent, -115 0C, -84.9 0C, Soluble in polar solvents, like water and to some, extent in non-polar, solvents, , 7., , Chemical activity, , Highly reactive in polar Moderately, solvents and reactions reactive, are instantaneous, , 30.0, Colourless gas, Covalent, -183 0C, -88.63 0C, Soluble in non-polar, solvents but insoluble, in polar solvents like, water, Slow or very slow at, room temperature, , From the above table we understand that ionic compounds like NaCl, are solids at room temperature., Polar compounds like HCl possess properties like melting point,, boiling point, reactivity, solubility etc, between those of ionic compounds, and covalent compounds. If the covalent bond is between atoms of two, different elements, the shared electron pair shift more towards the atom, of more electronegative element. Thus within the molecule the more, electronegative atom bears a partial negative charge and the less, electronegative atom bears a partial positive charge. A molecule of this, type which is neutral but possesses partial charges on the atoms within the, molecule is called a polar molecule and the bond is called a polar covalent, bond or partial ionic and partial covalent bond., +δ, -δ, Eg:, H+Cl, H - Cl, , In ionic compounds there exist stronger electrostatic forces of, attractions between the oppositely charged ions of these compounds., Therefore, they are solids with high melting points and boiling points. Based, 224, , X Class, , Chemical Bonding
Page 235 :
on the principle “like dissolves in like”, they being highly polar, soluble in, polar solvents. In chemical reaction of solution of ionic compounds simply, rearrangement of ions take place in the solutions, the reactions are, instantaneous or very fast., The forces of attractions among covalent molecules are weak., Therefore, the covalent compounds are gases or liquid at room temperature., They have low melting points and low boiling points. Based on the principle, that “like dissolve in like” these covalent compounds are soluble in nonpolar solvents because of non-polar nature of solvent molecules. In, chemical reactions of covalent compounds there exist bond breaking and, bond forming to get products. There fore, these reactions are moderate or, very slow., ‘Like dissolves in like’ means what type of chemical bonds are there, in the solute particles that solute could be soluble in that solvent which, has the similar type of chemical bonds in its molecules., , Key words, Electrons, noble gases, Lewis dot structures, Octet rule, chemical bond, Ionic, bond, covalent bond, cation, anion, electrostatic force, electrovalent, polar solvent,, non-polar solvent, formation of molecules, ionic compounds, covalent compounds,, electro positive character, electro negative character, polar bonds, bonded pair, of electrons, lone pairs, bond length, bond energy, shape of the molecule, linear,, tetrahedral, properties of ionic and covalent compounds., , What we have learnt, •, •, •, •, •, •, •, •, •, •, , Location of elements in the periodic table helps in predicting the type of bonding that will take, place between the elements., Ions are positively or negatively charged partiCles formed by the loss or gain of electrons., The force between any two atoms or a group of atoms that results in the formation of a stable, entity is called chemical bond., The outer most shell is called valence shell and electrons in this are called valence electrons., The gases belongs to ‘O’ group are called noble gases because they reluctant to combine other, atoms. Except helium all other noble gases have an octet of electron configuration in their, valence shell., The reason why atoms bond can be explained on the basis of the octet rule, Chemically active elements have an incomplete octet in their valence shell of the atoms., The number of valence electrons available in the atoms decides the type of bond, Elements which have tendency to gain electrons for attaining octet in their valence shell called, electro negative character elements. They form anions., In the formation of ionic bond the atoms of electro positive elements lose their valence electrons, to atoms of electro negative elements so that both of them can attain octet in their valence shell., , Free distribution by A.P. Government, , 225
Page 236 :
•, •, •, •, •, •, •, •, •, •, •, , The electrostatic attractive force that keeps cation and anion together to form a new electrically, neutral entity is called an ionic bond., Ionic compounds are often crystalline solids with high melting points., A chemical bond that formed by sharing of valence-shell electrons between the atoms so that, both of them can attain octet or duplet in their valence shell is called covalent bond., A single covalent bond is formed when two atoms share a pair of electrons, Each shared pair of electron is equivalent to a covalent bond., Electrons are not always shared equally between the atoms in a covalent bond. This leads to, bond polarity., Formation of various molecules., Factors affecting the formation of cation and anion:, To explain the bond angles in the molecules through covalent bonds the valence – shell –, electron – pair repulsion theory (VSEPRT), Bond lengths and bond energies in covalent compounds, Properties of ionic and covalent compounds., , Improve your learning, 1. List the factors that determine the type of bond that will be formed between two atoms? (AS1), 2. Explain the difference between the valence electrons and the covalency of an element. (AS1), 3 A chemical compound has the following Lewis notation: (AS1), a) How many valence electrons does element Y have?, b) What is the valency of element Y?, c) What is the valency of element X?, d) How many covalent bonds are there in the molecule?, Fig-Q3, e) Suggest a name for the elements X and Y. (AS2), 4. Why do only valence electrons involve in bond formation? Why not electron of inner shells?, Explain. (AS1), 5. Explain the formation of sodium chloride and calcium oxide on the basis of the concept of, electron transfer from one atom to another atom. (AS1), 6. A, B, and C are three elements with atomic number 6, 11 and 17 respectively., i. Which of these cannot form ionic bond? Why? (AS1), ii. Which of these cannot form covalent bond? Why? (AS1), iii. Which of these can form ionic as well as covalent bonds? (AS1), 7. How bond energies and bond lengths of molecule helps us in predicting their chemical properties?, Explain with examples. (AS1), 8. Predict the reasons for low melting point for covalent compounds when compared with ionic, compound. (AS2), 9. Collect the information about properties and uses of covalent compounds and prepare a report? (AS4), 10. Draw simple diagrams to show how electrons are arranged in the following covalent molecules:, (AS5), a) Calcium oxide (CaO), (b) Water (H2O), (c) Chlorine (Cl2), 226, , X Class, , Chemical Bonding
Page 237 :
11. Represent the molecule H2O using Lewis notation. (AS5), 12. Represent each of the following atoms using Lewis notation: (AS5), (a) beryllium (b) calcium (c) lithium, 13. Represent each of the following molecules using Lewis notation: (AS5), (a) bromine gas (Br2), , (b) calcium chloride (CaCl2), , (c) carbon dioxide (CO2), , (d) Which of the three molecules listed above contains a double bond?, 14. Two chemical reactions are described below. (AS5), • Nitrogen and hydrogen react to form ammonia (NH3), • Carbon and hydrogen bond to form a molecule of methane (CH4)., For each reaction, give:, (a) The valency of each of the atoms involved in the reaction. (AS1), (b) The Lewis structure of the product that is formed. (AS5), 15. How Lewis dot structure helps in understanding bond formation between atoms? (AS6), 16. What is octet rule? How do you appreciate role of the ‘octet rule’ in explaining the chemical, properties of elements? (AS6), 17. Explain the formation of the following molecules using valence bond theory, a) N2 molecule, , b) O2 molecule, , 18. What is hybridisation? Explain the formation of the following molecules using hybridisation, a) Be Cl2, , b) BF3, , ks, Fill in the blan, 1., 2., 3., 4., 5., , Electrons in ............ shell are called valence electrons., Except ............. gas all other noble gases have octet in their valence shell., Covalency of elements explains about member of ................ formed by the atom., Valence bond theory was proposed by ........................., In …………………bonding the valence electrons are shared among all the atoms of the metallic, elements., , s, Multiple choice question, 1) Which of the following elements is electronegative?, [, ], a) Sodium, b) Oxygen, c) Magnesium, d) Calcium, 23, 2) An element 11X forms an ionic compound with another element ‘Y’. Then the charge on the, ion formed by X is, [, ], a) +1, b) +2, c) -1, d) -2, 3) An element ‘A’ forms a chloride ACl4. The number electrons in the valence shell of ‘A’, a) 1, b) 2, c) 3, d) 4, [, ], Free distribution by A.P. Government, , 227
Page 238 :
Chapter, , 11, Electric Current, In previous classes, you had learnt about electric current, battery,, electric circuit and its components., • What do you mean by electric current?, • Which type of charge (positive or negative) flows through an electric, wire when it is connected in an electric circuit?, • Is there any evidence for the motion of charge in daily life situations?, In class VIII you learned about lightning. Lightning is an electric, discharge between two clouds or between cloud and earth. This electric, discharge through air appears to us as an electric spark or lightning., Lightning is a live example which provides evidence for the motion of, charge in the atmosphere., • Does motion of charge always lead to electric current?, Let us see., , Activity 1, Situation 1: Take a bulb, a battery, a switch and few insulated copper, wires. Connect the ends of the copper wires to the terminals of the battery, through the bulb and switch. Now switch on the circuit and observe the, bulb., • What do you notice?, Situation 2: Remove the battery from the circuit and connect the, remaining components to make a complete circuit. Again switch on the, circuit and observe the bulb. Does the bulb glow?, 228, , X Class, , Electric Current
Page 239 :
Situation 3: Replace the copper wires with nylon wires and connect, the nylon wires to the terminals of the battery through a bulb and switch., Now switch on the circuit and observe the bulb. Does the bulb glow?, After doing these activities you will notice that the bulb glows only in, situation 1., • Can you predict the reason for the bulb not glowing in situations 2 and, 3?, In class VII, you have learnt that the battery stores chemical energy, and this energy converts into electric energy and makes the bulb to glow, as you observed in situation 1 i.e. the battery supplies the required energy, to make the bulb glow. But in situation 3, though there is a battery in the, circuit, the bulb does not glow because the connecting wires (nylon wires), are not able to carry the energy from source (battery) to bulb., Hence, the nature of the substance plays an important role in the transfer, of energy from battery to bulb. The material which transfers energy from, battery (source) to the bulb is called a conductor and the material which, cannot transfer energy from battery (source) to the bulb is called a non, conductor., • Why do all materials not act as conductors?, • How does a conductor transfer energy from source to bulb?, Let us see., , Electric current, Drude and Lorentz, scientists of the 19th century, proposed that, conductors like metals contain a large number of free electrons while the, positive ions are fixed in their locations. The arrangement of the positive, ions is called lattice., Let us understand the behaviour of electrons in lattice space. Assume, that a conductor is an open circuit. The electrons move randomly in lattice, space of a conductor as shown in figure 1. When the electrons are in random, motion, they can move in any direction. Hence, if you imagine any cross, section as shown in figure 1, the number of electrons, crossing the cross, section of a conductor from left to right in one second is equal to that of, electrons passing the cross section from right to left in one second. It, means that net charge moving along a conductor, through any cross section is zero when the conductor, is in open circuit., fig-1: Random motion of, • What happens to the motion of electrons when, electrons, the ends of the conductor are connected to the, (in open circuit), battery?, Free distribution by A.P. Government, , 229
Page 240 :
When the ends of the conductor are connected, to the battery through a bulb, the bulb glows because, energy transfer takes place from battery to the bulb., fig-2: Ordered motion, The electrons are responsible for this transfer of, of electrons, energy. If the electrons are responsible for transfer, of energy from battery to bulb, they must have an ordered motion. When, the electrons are in ordered motion, there will be a net charge crossing, through any cross section of the conductor. See figure 2. This ordered, motion of electrons is called electric current., Thus we can say that electric current is ordered motion of charges., Let us define electric current quantitatively,, Electric current is defined as the amount of charge crossing any cross, section of the conductor in one second., Let Q be the charge crossing through any cross section of the conductor, in a time interval t. Then the amount of charge crossing through that cross, section in one second is Q/t. Therefore,, Electric current = electric charge/time interval, I = Q/t, The SI unit of electric current is ampere denoted by A., 1 Ampere = 1 Coloumb/1 Second, 1 A = 1 C/s, • Why do electrons move in specified direction?, When the conductor is not connected to the circuit through a battery,, the electrons inside the conductor are in random motion but when the, conductor is connected to a battery, the electrons move in a specified, direction. This shows that something causes the electron to move it in a, specified direction. When the ends of the conductor are connected to the, terminals of a battery a uniform electric field is set up throughout the, conductor. This field makes the electrons move in a specified direction., • In which direction do the electrons move?, • Do the electrons accelerate continuously?, • Do they move with a constant speed?, The free electrons in the conductor are accelerated by the electric, field and move in a direction opposite to the direction of the field. When, electrons are in motion under the influence of the field, they collide with, lattice ions, lose energy and may even come to a halt at every collision., They are again accelerated by the electric field and make collisions with, other lattice ions. In this way they continue to move along the conductor., 230, , X Class, , Electric Current
Page 241 :
The motion of electron is shown in figure 3., Potential difference, Hence, we assume that electrons in the, B, A, conductor move with a constant average speed. We, Direction of electric field, call this speed as drift speed or drift velocity., fig-3: Motion of electron, Let us calculate the drift speed of free charges, quantitatively., Consider a conductor with cross sectional area A. Assume that the, ends of the conductor are connected to a battery to make the current flow, through it. Let vd be the drift speed of the charges as shown in figure 4 and, n be the number of charges present in the conductor, D, in an unit volume (charge density). The distance, vd, covered by each charge in one second is vd. Then, vd, the volume of the conductor for this distance is equal, A (cross section area), to Av d (see figure 4). The number of charges, fig-4: Drift of positive charges, contained in that volume is equal to nAvd. Let q be, the charge of each carrier. Then the total charge crossing the cross sectional, area at position D in one second is nqAvd. This is equal to electric current., Hence,, Electric current I = nqAvd, ………………. (1), Therefore, vd = I/nqA, ………………. (2), We know that the charge carriers in a conductor are electrons. The, magnitude of electric charge ‘e’ is 1.602 x 10-19C., Let us calculate the drift speed of electron in a copper wire carrying a, current of 1A and cross sectional area A = 10-6 m2. The electron density of, copper that was found experimentally is n = 8.5x1028m–3. Substituting these, values in equation (2) with q = e, we get,, vd = 1/(8.5x1028x10-6x1.6x10-19), vd = 7x10-5m/s = 0.07mm/s, This shows that the electrons are moving very slowly., • Why does a bulb glow immediately when we switch on?, When we switch on any electric circuit, irrespective of length of the, connecting wire (conductor) an electric field is set up throughout the, conductor instantaneously due to the potential difference of the source, (battery) connected to the circuit. This electric field makes all the electrons, to move in a specified direction simultaneously., • How can we decide the direction of electric current?, The equation I = nqAvd Indicates that the values of n and A are positive., The direction of electric current is determined by the signs of the charge, Free distribution by A.P. Government, , 231
Page 242 :
q and drift speed vd. For electrons (negative charges), q is negative and vd, is positive. Then the product of q and vd is negative. This negative sign, shows that the direction of electric current is opposite to the flow of, negative charge. For positive charges the product of q and vd is positive., Hence, the direction of electric current can be taken as the direction of, flow of positive charges., • How can we measure electric current?, Usually an ammeter is used to measure electric current. It is always, connected in series to the circuit., • Where do the electrons get energy for their motion from?, , Potential Difference, When the ends of a conducting wire are connected to the terminals of, a battery, an electric field is setup throughout the conductor. This field, exerts a force on the charge (electron). Let Fe be the force exerted by the, electric field on a free charge q. The free charges accelerate in the direction, of the electric field (If the free charges are electrons, then the direction, of electric force on them is opposite to the direction of electric field). It, means the electric field does some work to move free charges in a specified, direction., • Can you find the work done by the electric force?, Let the electric force made the charges move, through a distance ‘l’ from A to B as shown in, B, figure 5. We know that, the work is the product of, l, force and distance along the direction of force., fig-5, Hence, work done by the electric force on a, free charge q is given by, W = Fe l, What is the work done by the electric force on unit charge?, Work done by the electric force on unit charge = W/q = Fe l/q, Work done by the electric force on unit positive charge to move it, through a distance ‘l’ from A to B is called potential difference between, those points. Potential difference is denoted by a symbol V. The potential, difference between two points separated by a distance l in a conducting, wire is given by,, V = W/q = Fe l/q, , Direction of electric field, A, , 232, , Fe, , X Class, , Electric Current
Page 243 :
This potential difference is also called voltage. The SI unit of potential, difference is “Volt” and it is denoted by V., 1 Volt = 1 Joule/1 Coulomb, 1V = 1J/C, • What is the direction of electric current in terms of potential, difference?, • Do positive charges move in a conductor? Can you give an example of, this?, Let us recall your experience of electrolysis and electroplating and, conductivity of fluids that you had learned in earlier classes. When electric, current is allowed to pass through fluids, the positive ions (cations) and, negative ions (anions) move in opposite directions. The direction of the, motion of positive charges in an electrolyte is always in the direction of, the electric field while negative charges move in a direction opposite to, that of positive charges. Thus for conduction in fluids there exists motion, of both positive and negative charges. Whereas in case of metal conductors, there will be only motion of electrons. (The positive charges are fixed in, the lattice), If positive charges move from point A to B in a conductor, the electric, field does positive work so W/q is positive for free positive charges. You, can say that the direction of the electric field is from A to B and the point, A is at high potential and point B is at low potential. As negative charges, always move in a direction opposite to the electric field we consider that, electrons move from low potential to high potential., We know that in a battery or cell a constant potential difference is, maintained till the battery is completely discharged., • How does a battery maintain a constant potential difference between, its terminals?, • Why does the battery discharge when its positive and negative terminals, are connected through a conductor?, To answer this, we need to know about how a battery or a cell works., A battery consists of two metal plates (electrodes) and a chemical, (electrolyte). The electrolyte (chemical) between the two metal plates, consists of positive and negative ions which move in opposite directions, (see figure 6). The electrolyte exerts a certain force on these ions and, makes them move in a specified direction. Let us call this force as a, chemical force (Fc). Depending upon the nature of the chemical, positive, ions move towards one of the plates and accumulate on that plate. As a, Free distribution by A.P. Government, , 233
Page 244 :
result of this accumulation of charges on this plate it becomes positively, charged (called anode). Negative ions move in a direction opposite to the, motion of positive ions and accumulate on the other plate. As a result of, this the plate becomes negatively charged (called cathode). This, accumulation of different charges on respective plates continues till both, plates are sufficiently charged., But the ions in motion experience another force when sufficient, number of charges are accumulated on the plates. Let us call this force as, electric force (Fe). The direction of this force is opposite to the direction, of chemical force Fc and the magnitude of this force depends on the amount, of charge accumulated on the plates., , fig-6, , Fc, , Fe, Fe, , Fc, , fig-7, , Fc, , Fe, Fe, , Fc, , fig-8, , fig-9, , 234, , X Class, , The motion of ions continue towards their, respective plates if the chemical force Fc is, stronger than electric force Fe. See figure 7., The accumulation of charges on plates is, continuous till the electric force Fe becomes, equal to chemical force Fc. At this situation, there will not be any motion in ions due to, balance of forces Fe and Fc. It is shown in, figure 8. The new battery that we buy from, the shop is at a stage where the ions in the, electrolyte are under the influence of, balanced forces. See figure 9. This is the, reason for the constant potential difference, between the terminals of a battery., The amount of charge accumulated on the, plates depends on nature of the chemical used, in the battery., • What happens when the battery is, connected in a circuit?, When a conducting wire is connected to, the terminals of the battery, a potential, difference is created between the ends of the, conductor. This potential difference sets up, an electric field throughout the conductor, (the direction of electric field is from, positive terminal to negative terminal in the, conductor)., Electric Current
Page 245 :
We know that the conductor contains large number of electrons. The, electrons near the positive terminal of the battery are attracted by it and, start to move towards positive terminal. As a result, the amount of positive, charge on this plate decreases. So the electric force Fe becomes weaker, than chemical force Fc and chemical force pulls negative ions from the, positive plate (anode) and makes them move towards the negative plate, (cathode). The negative terminal pushes one electron into the conductor, because of stronger repulsion between negative terminal and negative ion., Hence, the total number of electrons in the conductor remains constant, during the current flow. The above said process continuous till equilibrium, is attained between the forces Fe and Fc., , Electromotive force (emf), When the ends of the conductor are connected to the terminals of a, battery, the electrons in the conductor move with a drift speed from negative, terminal to positive terminal because of the electric force acting on them., At the same time negative ions of equal amount of charge move from, positive terminal to negative terminal against the electric force (Fe) because, of the chemical force acting on them within battery. Thus, some chemical, energy is spent to move ions in the battery. It means that an amount of, work is done by the chemical force (Fc)., Let us assume that work done by the chemical force to move a negative, charge q from positive terminal to negative terminal against the electric, force Fe be ‘W’ and also assume that the magnitude of chemical force Fc is, equal to magnitude of electric force (Fe)., The work done on negative charge q by the chemical force, W = Fcd, where ‘d’ is the distance between the terminals. Then work done by the, chemical force to move 1 Columb charge from positive terminal to negative, terminal is given by, W/q = Fcd/q. We know that Fc = Fe, then we get, W/q = Fed/q., This W/q is the work done by the chemical force on unit negative, charge to move it from positive terminal to negative terminal. This is called, emf (ε)., ε = W/q = Fed/q, Generally, emf is defined as the work done by the chemical force to, move unit positive charge from negative terminal to positive terminal of, the battery., • How can we measure potential difference or emf?, Free distribution by A.P. Government, , 235
Page 246 :
Generally a volt meter is used to measure potential difference or emf, across an electric device like battery. It must be connected in parallel to, the electric device to measure the potential difference across the ends of, the electric device., When a battery in a torch is used for several weeks, the light from its, bulb becomes dim. We say that the battery or cell in the torch is discharged., What does it mean?, • Is there any relation between emf of battery and drift speed of electrons, in the conductor connected to a battery?, , Ohm’s law, , Lab Activity, Aim: To show that the ratio V/I is a constant for a conductor., Materials required: 5 dry cells of 1.5V each, conducting wires, an, ammeter, a volt meter, thin iron spoke of length 10cm, LED and key., V, Iron spoke, I, A, Battery, , key, , fig-10, , Procedure: Connect a circuit as shown in figure, 10. Solder the conducting wires to the ends of the, iron spoke. Close the key. Note the readings of, current from ammeter and potential difference from, volt meter in table 1., Table:1, , Potential difference (V), , SI.No., , Current (I), , V/I, , Now connect two cells (in series) instead of one cell in the circuit., Note the respective readings of the ammeter and volt meter and record the, values in table 1. Repeat the same for three cells, four cells and five cells, respectively. Record the values of potential difference (V) and current (I), corresponding to each case in the table 1. Find V/I for each set of values., What do you notice? The ratio V/I is a constant. We can write this, mathematically as, 236, , X Class, , Electric Current
Page 247 :
I, (in ampere), , V∝I, From this experiment we can conclude that the potential, difference between the ends of the iron spoke (conductor) is, directly proportional to the current passing through it (assuming, the temperature of the iron spoke is constant during the flow, of current through it)., Draw a graph between V and I taking the current (I) along, y-axis and potential difference (V) along x-axis with appropriate, fig-11, scale. You will get a straight line graph passing through the, origin as shown in figure 11., Repeat the process by using a LED instead of iron spoke., The long terminal of the LED is connected to the positive, terminal of the battery and short terminal of the LED is, connected to negative terminal of the battery. Note the values, of current ‘I’ and potential difference ‘V’ in each case and record, the values in table 1 (draw this table in your notebook). Find, V/I for each set of values I and V. You will notice that the ratio, fig-12, V/I is not a constant. Draw a graph between V and I for LED., You will get a curved graph as shown in figure 12., From the above lab activity we can conclude that the ratio between V, and I is constant for some materials at constant temperature. This fact was, established by German Physicist, George Simon Ohm and it is popularly, known as Ohm’s law., We can define Ohm’s law as follow., The potential difference between the ends of a conductor is directly, proportional to the electric current passing through it at constant, temperature., Let V be the potential difference between the ends of the conductor, and I be the current passing through it., V ∝ I (temperature is constant), V/I = Constant, This constant is called resistance of the conductor. It is denoted by, ‘R’. Then we get V/I = R., V = IR, The SI unit of resistance is ohm. The symbol of ohm is Ω., 1 Ohm = 1 Volt/1 Ampere, 1 Ω = 1V/A, I, (in ampere), , V, (in volt), , Free distribution by A.P. Government, , V, (in volt), , 237
Page 248 :
•, , Can you guess the reason why the ratio of V and I in case of LED is not, constant?, • Do all materials obey Ohm’s law?, • Can we classify the materials based on Ohm’s law?, Based on Ohm’s law materials are classified into two categories. Those, which obey Ohm’s law are called ohmic materials. For example, metals, are ohmic materials. Those which do not obey Ohm’s law are called non, ohmic materials. For example, LEDs are non ohmic materials., , Limitations of Ohm’s Law, Ohm’s law is valid for metal conductors provided the temperature and, other physical conditions remain constant. The resistance of the material, changes with temperature. Hence for changing temperature the V-I graph, for a conductor will be non-linear. Ohm’s law is not applicable to gaseous, conductors. It is also not applicable to semiconductors such as germanium, and silicon., • What is resistance?, • Is the value of resistance the same for all materials?, When a conductor is connected to a battery the free electrons start, moving with a drift speed in a specified direction. During the motion, the, electrons collide with positive ions (fixed) of the lattice and come to halt., This means that they lose mechanical energy in the form of heat. Due to, the electric field that was set up by the battery throughout the conductor,, these electrons regain the energy from the field and proceed to move. The, motion of electrons is obstructed by the lattice ions. The obstruction, offered to the flow of electrons in a conductor by lattice ions depends, upon the nature of the material., Therefore, the resistance of a conductor is defined as the obstruction, to the motion of the electrons in a conductor. The material which offers, resistance to the motion of electrons is called resistor., • Is there any application of Ohm’s law in daily life?, • What causes electric shock in the human body – current or voltage?, Let us see., , Electric shock, Let us assume that human body is a resistor. The resistance of the, human body generally varies from 100 Ω (if body is wet with salt water), to 5,00,000 Ω (if the skin is very dry). Let us calculate the amount of, current that flows through the human body. Let us assume you have touched, the two electrodes of a battery of 24V with dry fingers in such a way that, the circuit is complete. Let your body resistance be 1,00,000Ω. Then the, 238, , X Class, , Electric Current
Page 249 :
current flowing through your body is given by I = 24/100000 = 0.00024A., This current is very small. When such small current passes through the, human body, it does not affect the functioning of various organs inside the, body., • Do you know the voltage of mains that we use in our household, circuits?, • What happens to our body if we touch live wire of 240V?, The current passing through our body when we touch a live wire of, 240V is given by I = 240/100000 = 0.0024A. When this quantify of current, flows through the body the functioning of organs inside the body gets, disturbed. This disturbance inside the body is felt as electric shock. If the, current flow continues further, it damages the tissues of the body which, leads to decrease in resistance of the body. When this current flows for a, longer time, damage to the tissues increases and thereby the resistance of, human body decreases further. Hence, the current through the human body, will increase. If this current reaches 0.07A, it effects the functioning of, the heart and if this much current passes through the heart for more than, one second it could be fatal. If this current flows for a longer time, the, person in electric shock is being killed. See the table 2 that describes the, effects of electric current on human body., Table-2, Current in Effect, ampere, 0.001, Can be felt, 0.005, Is painful, 0.010, Causes involuntary muscle contractions (spasms), 0.015, Causes loss of muscle control, 0.070, If through the heart, causes serious disruption ; probably fatal if current, lasts for more than 1 s, From the above discussions, we can conclude that an electric shock, can be experienced when there is a potential difference exists between, one part of the body and another part. When current flows through human, body, it chooses the path which offers low resistance. The resistance of a, body is not uniform throughout it. For example, skin offers more resistance, than the organs inside the body. As long as current flow continues inside, the body the current and resistance of human body goes on changing, inversely. Hence, the electric shock is a combined effect of potential, difference, electric current and resistance of the human body., Free distribution by A.P. Government, , 239
Page 250 :
•, , Why doesn’t a bird get a shock when it stands on a high voltage wire?, There are two parallel transmission lines on electric poles. The potential, difference between these two lines is 240V throughout their lengths. If, you connect any conducting device across these two wires, it causes current, to flow between the wires. When the bird stands on a high voltage wire,, there is no potential difference between the legs of the bird because it, stands on a single wire. So no current passes through the bird. Hence, it, doesn’t feel any electric shock., , Do you know?, A multi meter is an electronic measuring instrument that combines several, measurement functions in one unit., Digital multi meter displays the measured value in, numerals., A multi meter has three parts, Display: The display usually has four digits and the ability, to display a negative sign., Selection knob: The selection knob allows the user to, set the multi meter to read different functions such as, milliamps (mA) of current, voltage (V) and resistance (Ω)., Ports: Multi meters generally have two ports. One is, usually labelled as ‘COM’ (common or ground port). This is, where black test lead is connected. The other is labelled as, mAVΩ port where the red lead is conventionally plugged in., WARNING: Most multi meters can measure AC quantities also, but AC circuits, can be dangerous. So measure DC quantities only., , Factors affecting the resistance of a material, Temperature and resistance, , Activity 2, Measure the resistance of the bulb when it is in open circuit using a, multi meter. To measure the resistance of a bulb set the multi meter as, ohm meter and place the multi meter knob at 20K Ω. Now place the leads, of the multi meter on the terminals of the bulb. The meter will show one, of the following readings., 0.00 or 1 or the actual resistance of the bulb., 240, , X Class, , Electric Current
Page 251 :
− Ιf the multi meter reads 1, or displays OL, it’s overloaded. You will, need to try a higher mode such as 200K Ω or 2M Ω etc., − If the multi meter reads 0.00 or nearly 0, then you need to lower the, mode to 2K Ω or 200 Ω., Note the value of resistance in your note book. Connect a circuit with, components as shown in figure 13. Switch on the circuit. After few minutes,, measure the resistance of the bulb again as explained, above. Note this value in your note book. What, difference do you notice between these two, readings? The value of resistance of the bulb in, I, second instance is more than the resistance of the, key, Battery, bulb in open circuit., fig-13, • What could be the reason for increase in the, resistance of the bulb when current flows, through it?, You will notice that the bulb gets heated. The increase in temperature, of the filament in the bulb is responsible for increase in resistance of the, bulb. Hence we can conclude that there is a relation between resistance of, the bulb and its temperature., Thus the value of resistance of a conductor depends on temperature, for constant potential difference between the ends of the conductor., , Nature of material and resistance, , Activity 3, Collect different metal rods of the same length and same cross, sectional area like copper, aluminum, iron etc. Make, different metal rods are connected, a circuit as shown in figure 14. P and Q are the free, between P and Q, P, Q, ends of the conducting wires. Connect one of the, metal rods between the ends P and Q. Switch on the, I, circuit. Measure the electric current using the, A, ammeter connected to the circuit and note it in your, key, Battery, notebook. Repeat this with other metal rods and, fig-14, measure electric currents in each case. What do you, notice? The values of current are different for different metal rods for a, constant potential difference., From this activity, we conclude that the resistance of a conductor, depends on the material of the conductor., • What happens to the resistance of a conductor if we increase its length?, Free distribution by A.P. Government, , 241
Page 252 :
Let us find out., , Length of the conductor and resistance, , Activity 4, Collect iron spokes of different lengths with the same cross sectional, areas. Make a circuit as shown in figure 14. Connect one of the iron spokes,, say 10cm length, between P and Q. Measure the value of the current using, the ammeter connected to the circuit and note the value in your note book., Repeat this for other lengths of the iron spokes. Note corresponding values, of currents in your note book. What do you notice? The current decreases, with increase in the length of the spoke. Thus the resistance of each spoke, increases with increase in the length for a constant potential difference., From this activity, we can conclude that the resistance (R) of a, conductor is directly proportional to its length (l) for a constant potential, difference., i.e., R ∝ l (at constant temperature and cross sectional area), .................. (1), • Does the thickness of a conductor influence its resistance?, Let us find out., , Crosssection area and resistance, , Activity 5, Collect iron rods of equal lengths but different cross section areas., Make a circuit as shown in figure 14. Connect one of the rods between, points P and Q. Note the value of the current using the ammeter connected, to the circuit and note it in your note book. Repeat this with other rods., Note the corresponding values of currents in each case and note them in, your note book. You will notice that the current flowing through the rod, increases with increase in its cross sectional area. Hence, the resistance, of a rod decreases with increase in the cross section area of the rod., From this activity, we conclude that the resistance of a conductor is, inversely proportional to its cross section area., i.e., R ∝ 1/A (at constant temperature and length of the conductor), .................. (2), From the equations (1) and (2), we get, R ∝l/A (at constant temperature), 242, , X Class, , Electric Current
Page 253 :
R = ρl/A, Where, ρ is a proportionality constant and it, A, is called specific resistance or resistivity. See, figure 15 to get clear picture of this equation., l, Specific resistance depends on the I, temperature and nature of the material where as, Po, diffe tential, the resistance of the conductor depends on nature, renc, I, e (V, ), of material, temperature and geometrical factors, fig-15, like length and cross section area of the, conductor., The SI unit of resistivity is Ω - m., The reciprocal of resistivity is called conductivity (σ)., The values of resistivity of material determine their conductivity., Metals with low resistivity behave as good conductors. Metals such as, copper are therefore used for making electric, Table 3, wires. The filament of an electric bulb is, Resistivity of various materials, usually made of tungsten, because of its higher, resistivity values and melting point (34220C)., The values of resistivity of insulators are, very high of the order of 1014 to 1016 Ω-m., Alloys like Nichrome (Nickel, chromium and, iron) and Manganese (86% copper, 12%, manganese, 2% nickel) have 30-100 times, larger values of resistivity than those of metals., This makes them suitable for use in the heating, elements of electric irons, toasters etc. These, alloys also have the advantage that their, resistance varies very little with temperature, and they do not oxidise easily. The resistivity, of materials such as silicon and germanium, are 105 to 1010 times more than that of metals,, but 10 15 to 10 16 times less than that of, insulators. Such materials are called, semiconductors. Semiconductors are used to, make diodes, transistors and integrated, Circuits (ICs). ICs are used in all sorts of, electronic devices, including computer, TV,, mobile phones etc., Free distribution by A.P. Government, , Material, Silver, Copper, Gold, Aluminium, Calcium, Tungsten, Zinc, Nickel, Iron, Lead, Nichrome, Carbon (Graphite), Germanium, Drinking water, Silicon, Wet wood, Glass, Rubber, Air, , ρ(ΩΩ-m) at 20 °C, 1.59 × 10-8, 1.68 × 10-8, 2.44 × 10-8, 2.82 × 10-8, 3.36 × 10-8, 5.60 × 10-8, 5.90 × 10-8, 6.99 × 10-8, 1.00 × 10-7, 2.20 × 10-7, 1.10 × 10-6, 2.50 × 10-6, 4.60 × 10-1, 2.00 × 10-1, 6.40 × 102, 1.00 × 103, 10.0 × 1010, 1.00 × 1013, 1.30 × 1016, 243
Page 254 :
•, , How are electric devices connected in circuits?, , Electric Circuits, A closed path created by the connecting wires through a battery along, which electrons can flow is called a circuit. For a continuous flow of, electrons in the circuit it must be a complete circuit with no gaps left in, between. Usually a gap is provided in the circuit by an electric switch that, can be opened or closed to either cut off or allow current flow through the, circuit. Circuits may have more than one device (called as component), that receives electric energy from the source. These devices are commonly, connected in the circuit either in series or in parallel., When the components of the circuit are connected in series, there, will be a single path for flow of electrons between the terminals of the, battery, generator or wall socket (which is simply and extension of these, terminals). When these components are connected in parallel, they form, branches and each branch provides a separate path for the flow of electrons., Both the series and parallel connections have their own distinctive, characteristics. We shall briefly study circuits, using these two types of, connections., , Series connection of resistors, , Activity 6, Take different bulbs. Measure their resistances with a multi meter., Note their values in your book as R1, R2, R3., Connect them as shown in figure 16., , V1, , I, Battery, , 244, , Measure the potential difference between, terminals of the battery connected to the circuit., V3, V2, Measure the potential differences between the, ends of each bulb and note them as V1, V2 and V3, from voltmeters in your note book. Compare, the potential difference of the battery and, A, resistors., key, • What do you notice?, fig-16, The sum of the potential differences of the, bulbs is equal to potential difference across the combination of the, resistors. Then we get,, ......................... (1), V = V1 + V2 + V3, , X Class, , Electric Current
Page 255 :
Measure the value of the current flowing in the circuit with help of the, ammeter. Note its values in your book as I., • What do you notice?, , Equivalent resistance of a series, connection:, , V, V1, , V2, , V3, , I, Observe figure 17. In this figure the bulbs, R1, R2, R3, fig-17, are shown as resistors with symbols., In series connection of resistors there is, V, only one path for the flow of current in the, circuit. Hence, the current in the circuit is, I, fig-18, Req, equal to I., According to Ohm’s law,, Potential difference across R1 is , V1 = IR1, Potential difference across R2 is , V2 = IR2, Potential difference across R3 is , V3 = IR3, Let Req is the equivalent resistance of the combination of resistors in, series., • What do you mean by equivalent resistance?, If the current drawn by a resistor is equal to the current drawn by the, combination of resistors then the resistor is called as equivalent resistor, (provided the source in the circuit is constant)., So, we have V = I Req, Substituting the values of V1, V2, V3 and V in the equation (1), we get, IReq = IR1 + IR2 + IR3, Req = R1 + R2 + R3, From the above equation you can conclude that the sum of individual, resistances is equal to their equivalent resistance when the resistors are, connected in series., • What happens when one of the resistors in series breaks down?, When one of the resistors in series breaks down, the circuit becomes, open and flow of current cannot take place in the circuit. This is the reason, why household electrical appliances are not connected in series., • Can you guess in what way household wiring has been done?, Let us see, , Free distribution by A.P. Government, , I, , I, , 245
Page 256 :
Parallel Connection of resistors, , Activity 7, , P, , I, , Use the bulbs used in activity 6 and connect, these bulbs as shown in figure 19., A, Measure the potential difference across each, I1, bulb using a voltmeter or multi meter. Note these, values in your note book. What do you notice? The, A, Q, potential difference at the ends of each bulb is the, I2, same. These bulbs are said to be in parallel conne, I3, ction. Measure electric currents flowing through, A, each bulb using ammeters. Note these values., ammeter 1, Let I1,I2 and I3 be the currents flowing through, A, R1, R2 and R3 resistors respectively., Battery key, fig-19, • How much current is drawn from the battery?, • Is it equal to individual currents drawn by the resistors?, Measure the current (I) drawn from the battery using the ammeter 1., You will notice that the current drawn from the battery is equal to the sum, of individual currents drawn by the bulbs., Hence we can write, I = I1 + I2 + I3, .................. (1), , Equivalent resistance of a parallel connection, The schematic circuit of figure 19 is shown in, R1, figure 20., I2, I, A, According to the Ohm’s law,, R2, I3, Current through R1 is, I1 = V/R1, A, R3, Current through R2 is, I2 = V/R2, fig-20, Current through R3, is, I3 = V/R3, Req, Let Req be the equivalent resistance of the, I, A, resistors is parallel. It is shown in figure 21., fig-21, Then we get; I = V/Req, Substituting the values I, I1, I2 and I3 in equation (1), we get, V/Req = V/R1 +V/R2 + V/R3, 1/Req = 1/R1 + 1/R2 + 1/R3, Let two resistors R1 and R2 are connected in parallel,, 1/Req = 1/R1 + 1/R2, Req = R1R2/(R1+R2), I1, I, , I, , 246, , X Class, , A, , Electric Current
Page 257 :
The equivalent resistance of a parallel combination is less than the, resistance of each of the resistors., You can use this result to explain why the resistance of a metal wire is, inversely proportional to its area of cross section. Let us imagine a thick, wire as a parallel combination of several thin wires. Then the resistance of, the combination is less than that of each thin wire. In other words, the, resistance of a thick wire is less than that of a thin wire., Though the methods discussed in the previous section for replacing, series and parallel combination of resistors by their equivalent resistances, are very useful for simplifying many combinations of resistors, they are, not sufficient for the analysis of many simple circuits particularly those, containing more than one battery., Let us see., , Kirchhoff’s laws, Two simple rules called Kirchhoff’s rules are applicable to any DC, circuit containing batteries and resistors connected in any way., , Junction Law, See figure 19., We have seen that the current divides at P. The current drawn from the, battery is equal to the sum of the currents through the resistors. P is called, junction. The junction is a point where three or more conducting wires, meet., At any junction point in a circuit where the current can divide,, the sum of the currents into the junction must equal the sum of, the currents leaving the junction. This means that there is no, I6, accumulation of electric charges at any junction in a circuit., From figure 22, we have, I5, I1 + I4 + I6 = I5 + I2 + I3, This law is based on the conservation of charge., , Loop Law, , I1, I2, I3, I4, , fig-22, , The algebraic sum of the increases and decreases in potential difference, across various components of the circuit in a closed circuit loop must be, zero. This law is based on the conservation of energy., Let us imagine in a circuit loop the potential difference between the, two points at the beginning of the loop has a certain value. As we move, around the circuit loop and measure the potential difference across each, Free distribution by A.P. Government, , 247
Page 258 :
component in the loop, the potential difference may decrease or increase, depending upon the nature of the element like a resistor or a battery. But, when we have completely traversed the circuit loop and arrive back at our, starting point, the net change in the potential difference must be zero., Thus, the algebraic sum of changes in potential differences is equal to, zero., Let us apply Loop law to the circuit shown in, V1, R1, B figure 23., For the loop ACDBA,, -V2 + I2R2 – I1R1+V1 = 0, V2, R2, D, For the loop EFDCE, -(I1+I2) R3 – I2R2 + V2 = 0, R3, F, For the loop EFBAE, fig-23, -(I1+I2) R3 – I1R1+V1 = 0, , A I1, C I2, E I1+I2, , Example, E, , D, , I2, , C, , I1+I2, , I1, , Find electric current drawn(fig-E)from the battery of emf 12V., , Solution:, , Let I = I1+I2 be the current drawn from emf 12V., From the figure E. Using the loop law,, 2Ω, 4Ω, For the loop DABCD,, 12V, 5V, -3 (I1+I2) + 12 – 2I1-5 = 0 ……….. (a), I1+I2, For the loop DAFED,, -3 (I1+I2) + 12 – 4I2 = 0, ………. (b), I2 A, I1, B, Solving the equation (a) & (b), fig-E, We get I1 = 0.5 A and I2 = 1.5 A, Total current drawn is then I = 0.5 + 1.5 = 2A, –––––––––––––, • You might have heard the sentences like “this month we have consumed, 100 units of current”. What does ‘unit’ mean?, • A bulb is marked 60W and 120V. What do these values indicate?, Let us see., 3Ω, , F, , Electric power, The electric appliances that we use in our daily life like heater, cooker,, fan, and refrigerator etc. consume electric energy. Let us consider a, conductor of resistance ‘R’ through which an electric current ‘I’ passes., 248, , X Class, , Electric Current
Page 259 :
We know that when current passes through conductor, heat energy is, generated., Consider that a charge Q Coulomb passes through a, Potential difference V, point A, moves to point B in the time interval ‘t’ seconds, A Q Fe, as shown in figure 24. Let V be the potential difference t=0, between the points A and B. The work done by electric, l, Direction of electric field, field in time ‘t’ is given by, fig-24, W = QV, .........................(1), This work is equal to the energy lost by the charge while passing, through the conductor., • What is the energy lost by the charge in 1 see?, It is equal to W/t., From equation (1), we get, W/t = QV/t, .........................(2), In above equation Q/t represents the current (I) flowing through the, conductor and W/t represents the work done per second., In lower classes you had studied that power is nothing but the rate of, doing work. Hence, W/t represents electric power (P)., Electric power P = VI, .........................(3), This equation can be used to calculate power consumption by any, electric device that is connected in a circuit., According to the ohm’s law,, V = IR, We can write equation (3) as, P = I2 R = V2/R, The equation P = VI can also be used to know the power that can be, extracted from a battery or any source. In such case we modify the equation, P = VI as P = ε I., Where ε is the emf of the battery., Le us consider an example to understand power consumption., A bulb is marked 60W and 120V. This means that if this bulb is, connected to 120V source, it will able to convert 60J of electrical energy, into heat or light in one second., From the marking of bulb we can measure the resistance of the bulb., From the relation P = V2/R R = V2/P, Substituting the values V and P in above equation, we get, R = 120 x 120/ 60 = 240 Ω, Free distribution by A.P. Government, , B, t, , 249
Page 260 :
Thus, the bulbs marked as 60W and 120V will offer a resistance of, 240 Ω to the flow current through it in normal condition., If this bulb is connected to the 12V a battery, the consumption by the, bulb is given by, P = V2/R = 12 x 12/ 240 = 3/5 = 0.6 W, Since watt is a small unit of power, a bigger unit Kilowatt is generally, used to express power consumption., 1 KW = 1000 W = 1000 J/S, You might have seen the current bill that comes to your home every, month. In that bill, consumption of electricity is marked in units. What, does the unit represent?, The unit of electric power consumption is equal to 1 KWH (one Kilo, Watt Hour)., 1 KWH = (1000 J/S) (60 x 60 S), = 3600 x 1000 J, = 3.6 x 105 J, • What do you mean by overload?, • Why does it cause damage to electric appliances?, We frequently hear news about overload of current and damages caused, by this overload., Electricity enters our homes through two wires called lines. These, line wires have low resistance and the potential difference between the, wires is usually about 240V. These two line wires run throughout the, household circuit, to which we connect various appliances such as fan, TV,, refrigerator etc., All the electric devices of our home are connected at different points, between these two wires. This means all the electric appliances are in, parallel connection. Hence, potential drop across each device is 240V. If, we know the value of resistance of the electric device, we can calculate, the current passing through it using the equation I = V/R. For example, the, current passing through a bulb with resistance 240 Ω is 1 A., Based on the resistance of each electric device, it draws some current, from the supply. Total current drawn from the mains is equal to the sum of, the currents passing through each device (Junction law)., If we add more devices to the household circuit the current drawn, from the mains also increases., • What happens when this current increases greatly?, 250, , X Class, , Electric Current
Page 261 :
To answer this, observe the values noted on digital meters fixed at, your home. You will notice the following values on the meter., Potential difference: 240 V, Current: 5 – 20A, Heater, This means the line wires that are entering the meter have a, potential difference of 240V. The minimum and maximum limit, 4A, Fan, of current that can be drawn from the mains is 5 – 20A. Thus, the, maximum current that we can draw from the mains is 20A. When, 2A Bulb, the current drawn from the mains is more than 20A. Overheating, occurs and may cause a fire. This is called over loading. See figure, 8A Fridge, 25. If we switch on devices, such as heater shown in figure 25, the, current drawn from the mains exceeds the max limit 20A., TV, 6A, • How can we prevent damage due to overloading?, To prevent damages due to overloading we connect an electric, Fuse, 20A, fuse to the household circuit as shown in figure 25. In this, arrangement, the entire current from the mains must pass through, the fuse. The fuse consists of a thin wire of low melting point., 240V, When the current in the fuse exceeds 20A, the wire will heat up, fig-25, and melt. The circuit then becomes open and prevents the flow of, current into the household circuit. So all the electric devices are, saved from damage that could be caused by overload., Thus we can save the house holding wiring and devices by using fuses., Note: The value of overload current varies from the household currents, to factories., , Think and discuss, •, •, , What do you mean by short circuit?, Why does a short circuit damage electric wiring and devices connected to, it?, , Key words, Charge, Potential difference, Electric current, Multi-meter, Ohm’s law,, Resistance, Resistivity, Kirchhoff’s laws, Electric power, Electric energy., Free distribution by A.P. Government, , 251
Page 262 :
What we have learnt, •, , Electric potential difference between points in an electric circuit is the work done to move a unit, positive charge from one point to another., , •, , Electric current is expressed as the amount of charge flowing through a particular cross section, 0area in unit time., , •, , A multi-meter is an electronic measuring instrument that combines several measuring functions, (electric potential difference, electric current and electric resistance) in one unit., , •, , Ohms law: The current through a conductor element is proportional to the potential difference, applied between its ends, provided the temperature remains constant. Mathematically V=IR., , •, , Ohm’s law is valid for metal conductors at constant temperature. It is not applicable for gaseous, conductors and semiconductors., , •, , Resistance is the opposition that a substance offers to the motion of electrons., , •, , Resistance of a wire depends on the material of the wire, its length and its area of cross section, Rα l/A., , •, , The resistivity of a material is the resistance per unit length of a unit cross section of the material., , •, , Two or more resistors are said to be connected in series if the same current flows through them., , •, , Two or more resistors are said to be connected in parallel if the same potential difference exist, across them., , •, , The junction law: At any junction point in a circuit where the current can divide, the sum of the, currents into the junction must equal the sum of the currents leaving the junction., , •, , The loop law: The algebraic sum of the increases and decreases in potential difference across, various components of a closed circuit loop must be zero., , •, , Electric power is the product of potential difference and the current. SI unit of power is watt, (W)., , •, , Electrical energy is the product of power and time. Units of electrical energy W-s and KWH., , Improve your learning, 1. Explain how electronflow causes electric current with Lorentz – Drude theory of electrons.(AS1), 2. How does a battery work? Explain. (AS1), 3. Write the difference between potential difference and emf. (AS1), 4. How can you verify that the resistance of a conductor is temperature dependent? (AS1), 252, , X Class, , Electric Current
Page 263 :
5. What do you mean by electric shock? Explain how it takes place. (AS1), 6. Derive R = ρl/A. (AS1), 7. How do you verify that resistance of a conductor is proportional to the length of the conductor, for constant cross section area and temperature? (AS1), 8. Explain Kirchhoff’s laws with examples. (AS1), 9. What is a value of 1 KWH in Joules? (AS1), 10. Explain overloading of household circuit. (AS1), 11. Why do we use fuses in household circuits? (AS1), 12. Deduce the expression for the equivalent resistance of three resistors connected in series., (AS1), 13. Deduce the expression for the equivalent resistance of three resistors connected in parallel., (AS1), 14. Silver is a better conductor of electricity than copper. Why do we use copper wire for conduction, of electricity? (AS1), 15. Two bulbs have ratings 100 W, 220V and 60 W, 220 V. Which one has the greater resistance?, (AS1), 16. Why don’t we use series arrangement of electrical appliances like bulb, Television, fan and, others in domestic circuits? (AS1), 17. A wire of length 1m and radius 0.1 mm has a resistance of 100 Ω. Find the resistivity of the, material. (AS1), 18. Why do we consider tungsten as a suitable material for making the filament of a bulb? (AS2), 19. Are the head lights of a car connected in series or parallel? Why? (AS2), 20. Why should we connect electric appliances in parallel in a household circuit? What happens if, they are connected in series?, 21. Suppose that you have three resistors each of value 30 Ω. How many resistors can you obtain, by various combinations of these three resistors? Draw diagrams in support of your predictions., (AS2), 22. State Ohm’s law. Suggest an experiment to verify it and explain the procedure. (AS3), 23. a. Take a battery and measure the potential difference. Make a circuit and measure the, potential difference when the battery is connected in the circuit. Is there any difference in, potential difference of battery? (AS4), b. Measure the resistance of a bulb (filament) in open circuit with a multi-meter. Make a, circuit with elements such as bulb, battery of 12V and key in series. Close the key. Then, again measure the resistance of the same bulb (filament) for every 30 seconds. Record the, observations in a proper table. What can you conclude from the above results? (AS4), , Free distribution by A.P. Government, , 253
Page 264 :
24. Draw a circuit diagram for a circuit in which two resistors A and B are connected in series with, a battery and a voltmeter is connected to measure the potential difference across the resistor A., (AS5), 25. How can you appreciate the role of a small fuse in house wiring circuit in preventing damage to, various electrical appliances connected in the circuit?, (AS7), 26. In the figure Q-26 the potential at A is —————, —— when the potential at B is zero. (AS7), , 1A, A, , V= 0, , 5Ω, , 2V, , B, , fig-Q26, , 27. Observe the circuit and answer the questions given, below. (AS7), i., , Are resistors 3 and 4 in series?, , ii., , Are resistors 1 and 2 in series?, , +, , 1 V1, –, VB, , –, , v., , What is the total emf in the circuit if the potential, drop across resistor 1 is 6V?, , +, , 3, , iii. Is the battery in series with any resistor?, iv. What is the potential drop across the resistor 3?, , V3, , +, , 2, G, , –, , +, , 4, , V2=14V, , –, , V4=8V, , fig-Q27, , 28. If the resistance of your body is 100000Ω what would, be the current that flows in your body when you touch, the terminals of a 12V battery? (AS7), 29. A uniform wire of resistance 100Ω is melted and recast into wire of length double that of the, original. What would be the resistance of the new wire formed?(AS7), 30. A house has 3 tube lights, two fans and a Television. Each tube light draws 40W. The fan draws, 80W and the Television draws 60W. On the average, all the tube lights are kept on for five, hours, two fans for 12 hours and the television for five hours every day. Find the cost of electric, energy used in 30 days at the rate of Rs. 3.oo per Kwh. (AS7), , ks, Fill in the blan, 1. The kilowatt hour is the unit of..........................., 2. A thick wire has a ........................... resistance than a thin wire., 3. An unknown circuit draws a current of 2A from a 12V battery its equivalent resistance, is...................., 4. The SI unit of potential difference is ......................, 254, , X Class, , Electric Current
Page 265 :
5. The SI unit of current is .........................., 6. Three resistors of values 2Ω, 4Ω, 6Ω are connected in series. The equivalent resistance of, combination of resistors is ....................., 7. Three resistors of values 2Ω, 4Ω, 6Ω are connected in parallel. The equivalent resistance of, combination of resistors is ....................., 8. The power delivered by a battery of emf, 10V is 10W. Then the current delivered by the, battery is ......................, , s, Multiple choice question, 1., , A uniform wire of resistance 50 Ω is cut into five equal parts. These parts are now connected, in parallel. Then the equivalent resistance of the combination is, a) 2 Ω, , b) 12 Ω, , c) 250 Ω, , d) 6250 Ω, , [, , ], , 2. A charge is moved from a point A to a point B. The work done to move unit charge during this, process is called., a) potential at A, , b) potential at B, , c) potential difference between A and B, , d) current from A to B, , 3. Joule/ coulomb is the same as, a) 1 - watt, , b) 1 - volt, , c) 1- ampere, , d) 1 - ohm, , 4. The current in the wire depends, , [, , ], , [, , ], , [, , ], , [, , ], , a) only on the potential difference applied b) only on the resistance of the wire, c) on both of them, , d) none of them, , 5. Consider the following statements., A. In series connection, the same current flows through each element., , B. In parallel connection, the same potential difference gets applied across each element., a) both A and B are correct, , b) A is correct but B is wrong, , c) A is wrong but B is correct, , d) both A and B are wrong, , Free distribution by A.P. Government, , 255
Page 266 :
Annexure, Can we apply Newton law’s to the motion of electrons?, Note: In this explanation, the random motion of electrons is neglected., Let us consider a conductor of length l and cross sectional area A. Let, n be the density of electrons of a conductor., The current passing through the conductor when the ends of the, conductor is maintained at a constant potential difference V is given by, I = nAevd, , ....................... (a), , Where e is the charge of electron and vd is the drift velocity of, electrons., Work done by the source to move electron between the ends (along, the conductor) is given by,, W = Ve, , ....................... (b), , We know that the work done by the electric force,, W =Fl, , ....................... (c), , Where F is the force applied by the electric field., From equations (b) and (c), We get, Fl = Ve, , F = Ve/l, , From Newton’s second law, we know that F = ma is applicable to any, particle. Hence we have,, ma = Ve/l, , a = Ve/lm, , ......................(d), , Assuming that the initial velocity (u) of electron is zero. Let v velocity, acquired by the electron in a time interval τ (interval between successive, collisions). Then u = 0 and t = τ, From equation, , v = u+at, v = aτ = Veτ/lm, , (from equation d), , Due to collisions with lattice ions, the motion of electrons is restricted., Hence the average velocity of electron in time τ becomes its drift velocity., Average velocity of electron vd = (v+u)/2 = v/2, Substituting the value of v in above equation, we get, , 256, , X Class, , Electric Current
Page 267 :
Average velocity = Drift velocity, vd = Veτ/2lm, Substituting the value of vd in equation (a) we get,, I = nAe(Veτ/2lm), I = V(ne2τ/2m)(A/l), I (2m/ne2τ)(l/A) = V, , ......................(e), , In the above equation, mass of the electron (m) and charge of the, electron (e) are constants because these values are characteristics of, the electron., The electron density (n) of a metal conductor depends on its nature, so it is also constant for a particular conductor., For a given conductor, the length (l) and cross section area (A) are, also constants. The value of τ depends on temperature of the conductor., When the temperature increases the random motion of electrons, increases hence the value of τ decreases., For a constant temperature of a conductor the value of τ becomes, constant., Hence (2m/ne2τ) (l/A) becomes a constant for a particular, conductor at constant temperature. Let this value be R (called resistance, of a conductor). The we get, IR = V, , (from equation e), , ...................(f), , This is what we call Ohm’s law., Where R = (2m/ne2τ) (l/A), , ..................(g), , In the above equation 2m/ne2τ is the characteristic value of a, conductor. The value of resistance R is different for different, geomentrical values for a particular conductor (material). Hence 2m/, ne2τ is taken as a constant independent of geomentrical values. Let it, be ρ. It is called specific resistance., ρ = 2m/ne2τ, From equation (g) we get, R = ρl/A, , Free distribution by A.P. Government, , ..................(h), , 257
Page 268 :
Chapter, , 12, Electromagnetism, In the previous chapter on ‘Electricity’ you have learnt about the heating, effects of electric current. We use many electric appliances in our daily, life such as electric motor, electric generators, electric calling bells,, electric cranes etc.,, • How do they work?, • How do electromagnets work?, • Is there any relation between electricity and magnetism?, • Can we produce magnetism from electricity?, In this chapter we will study electromagnetic effects. We also study, electric motors which involve magnetic effects of electric current and, electric generator which involves electric effects of moving magnets., , Hans Christian Oersted (1777 - 1851) was, one of the leading scientists of the 19th century, played a, crucial role in understanding electromagnetism. He gave, lectures which were quite popular among the public and, also learnt a lot during the tours. During one such lecture, in April 1820, Oersted carried out an experiment that, was never performed before. He placed a compass needle, underneath a wire and then turned on electric current., The needle of compass showed deflection., Oersted recognized the significance of what he had, just done. Earlier, it was believed that electricity and magnetism were two different, 258, , X Class, , Electromagnetism
Page 269 :
unconnected sciences. Oersted had demonstrated that they were interconnected., Through this observation he showed that electricity and magnetism were related, phenomena. Some scientists, influenced by this experiment, continued to work in, the modern field of “electromagnetism”. Their research resulted in several new, scientific theories and various vital inventions like the dynamo and the electric, motor, with this a new technology prospered, leading to inventions such as radio,, television and fiber optics., The unit of magnetic field strength is named Oersted in his honour., Oersted was made a foreign member of the Royal Swedish Academy of Sciences, in 1822., , Activity 1, Oersted experiment, Take a thermocole sheet and fix two thin wooden sticks of height 1cm, which have small slit at the top of their ends. Arrange a copper wire of 24, gauge so that it passes through these slits and make a circuit. The circuit, consists of a 3 (or 9) volt battery, key and copper wire which are connected, in series as shown in figure 1. Now, keep a magnetic compass below the, wire. Bring a bar magnet close to the compass., • Does the needle get deflected by the bar magnet?, • Why does the needle get deflected by the, magnet?, Take the bar magnet far away from the circuit, and switch on the circuit. Look for changes in, the position of the needle., fig-1, • What do you notice?, • Is there any change in the position of the compass needle?, • Which force is responsible for the deflection of the compass needle?, • Does the current-carrying wire apply a force on the needle?, • What do we call this force? (Recall the idea of field forces in class 8,, chapter “Force”)., In order to understand the reasons for the deflection of the compass, needle with no bar magnet near it we need to understand the idea of, ‘magnetic field’ and the influence of electric field on magnetic field., Let us learn about it., Free distribution by A.P. Government, , 259
Page 270 :
Magnetic Field, We use the term field when a force gets applied on an object by another, object without there being any physical contact between them. You have, observed this already in activity 1. Let us call this field which is responsible, for deflection of the compass needle as ‘magnetic field’., • How was this field produced?, • Can we observe the field of a bar magnet?, Let us try., , Activity 2, Take a sheet of white paper and place it on the horizontal table. Place a, bar magnet in the middle of the sheet. Place a magnetic compass near the, magnet. It settles to a certain direction. Use a pencil and put dots on the, sheet on either side of the needle. Remove the compass. Draw a small line, segment connecting the two dots. Draw an arrow on it from South Pole of, the needle to North Pole of the needle. Repeat the same by placing the, compass needle at various positions on the paper. The compass needle, settles in different directions at different positions., • Why does this happen?, Remove the bar magnet and place the magnetic compass on the paper., It comes to rest along the north-south direction. Now place the bar magnet, in its previous place., • Is there any change in the direction of the needle of the magnetic, compass? Why?, The needle of the magnetic compass is affected by the bar magnet, without any physical contact. A force causes the needle to deflect and makes, it to come to rest in a certain direction., • What is the nature of force that acts on the needle?, The force which acts on the needle from a distance is due to the, magnetic field of the bar magnet., In activity 2, you have already seen that the orientation of needle is, different at different places on paper. This gives us an idea that the magnetic, field has direction and it varies from one point to another., When you changes the place of the compass near the bar magnet you, can observe that its orientation changes from point to point. Now take the, needle too places far away on the sheet and observe the orientation of the, compass needle in each case., • What do you observe?, 260, , X Class, , Electromagnetism
Page 271 :
The compass needle shows almost the same direction along north and, south at places far from the magnet., • What does it mean?, From these observations we conclude that the strength of the field, varies with distance from the bar magnet. Now hold the compass a little, above the table and at the top of the bar magnet. You can observe that field, exists in all directions around the bar magnet. Hence we can say that the, magnetic field is three dimensional i.e., magnetic field surrounds its source, such as bar magnet. From the above discussion we can generalize that:, A magnetic field exists in the region surrounding a bar magnet and is, characterized by strength and direction., • How can we find the strength of the field and direction of the field?, You know that the direction of the field can be determined by using a, compass. Let us find out how to determine the strength of the field., , Activity 3, Place a white sheet of paper on a horizontal table. Place a compass in, the middle of it. Put two dots on either side of the compass needle. Take it, out. Draw a line connecting the dots which shows the North and South of, the earth. Now place the bar magnet on the line drawn in such a way that its, north pole points towards geographic north. Now place the compass at the, north pole of the bar magnet. Put a dot at the north pole of the compass, needle. Now remove the compass and place it at the dot. It will point in, other direction. Again put a dot at the north pole of the compass needle., Repeat the process till you reach the south pole of the bar magnet. Connect, the dots from ‘N’ of the bar magnet to ‘S’ of the bar magnet. You will get a, curved line. Now select another point from the north pole of the bar, magnet. Repeat the process for many, points taken near the north pole. You will, get different curves as shown in figure, 2., • What are these curves?, Technically those curves are called, “magnetic field lines”. Field lines are, imaginary lines. These lines help us to, understand the nature of the field. So, fig-2: Magnetic field lines, these curved lines represent the field, Free distribution by A.P. Government, , 261
Page 272 :
lines. If you place a compass at any point on the line, the needle comes to, rest along the tangent to the line. So we conclude that the tangent drawn to, the field line at a point gives the direction of the field., • Are these field lines closed or open loops?, The field lines appear to be closed loops, but you can’t conclude that, lines are closed or open loops by looking at the picture of field lines because, we do not know about the alignment of lines that are passing through the, bar magnet. We will come to know about this point later in this chapter., Observe the spacing between lines. In some places the field lines are, crowded (near the poles of a bar magnet) and in some places the field, lines are spread apart (at long distances from the bar magnet). From this, picture we can conclude that the field is strong when lines are crowded, and field is weak when lines are spaced apart., Thus, the field drawn is non uniform because the strength and direction, both change from point to point., We may define the nature of the field with its characteristics such as, its strength and direction. The field is said to be non uniform when any one, of the characterstics of field i.e., strength or direction changes from point, to point, similarly the field is said to be uniform if both strength and, direction are constant throughout the field. Let us define the strength of a, uniform magnetic field., • Can we give certain values to magnitude of the field at every point in, the magnetic field?, Consider a uniform magnetic field in space. Imagine a plane of certain, area ‘A’ placed perpendicular to the field at a certain point in the magnetic, field as shown in figure 3(a). You notice that a few field, lines pass through this plane. This number gives an, estimation of strength of the field at that point., The number of lines passing through the plane of, area ‘A’ perpendicular to the field is called magnetic, Area A, flux. It is denoted by ‘Φ’., fig-3(a), Magnetic flux represents the number of lines, passing through the imagined plane in the field. Of course, flux depends, on the orientation of the plane in the field. But here we are concerned only, with the perpendicular case. The S.I unit of magnetic flux is Weber. Now, strength of the field is easily defined using the idea of flux. If the imagined, plane is perpendicular to the field and has unit area, then the flux through, this plane of unit area gives the strength of the field. This strength of the, , B, , 262, , X Class, , Electromagnetism
Page 273 :
field is technically called magnetic flux density (B). So, magnetic flux, density is defined as the magnetic flux passing through unit area taken, perpendicular to the field. B is also known as magnetic field induction., Let the flux through the area ‘A’ be Φ., • What is the flux through unit area perpendicular to the field?, It is equal to Φ/A. The ratio of magnetic flux passing through a plane, perpendicular to the field and the area of the plane is called the magnetic, flux density., So magnetic flux density = magnetic flux/ area., B = Φ/A., Φ = BA, Units of magnetic flux density is Weber/(meter)2. It is also called, Tesla., • Can we generalize the formula of flux for any, θ, orientation of the plane taken in the field?, Let ‘θ’ be the angle between magnetic field (B), Area A, Area A cosθ, and normal to the plane with area (A) as shown in, figure 3(b). The effective area of the plane, perpendicular to the field is A cosθ. Then magnetic B, fig-3(b), flux density is given by,, B = magnetic flux /effective area, (this formula is used when plane makes an angle with the field)., Then B = Φ/A cosθ, The flux through the plane, is given by, Φ = BA cosθ., • What is the flux through the plane taken parallel to the field?, • What is the use of introducing the ideas of magnetic flux and magnetic, flux density?, Later in this chapter, you will see how these ideas are used., • Are there any sources of magnetic field other than magnets?, • Do you know how old electric calling bells work?, Let us see, , Magnetic field due to currents, In activity 1 we observed that the compass needle is deflected when, current flows through the circuit. This observation helps us to conclude, that, “Current carrying wire produces magnetic field.”, Let us discuss about the magnetic fields produced by a current carrying, wire., Free distribution by A.P. Government, , 263
Page 274 :
(i) Magnetic field due to straight wire carrying current, , Activity 4, Stand, , Compass, needle, , Table, Battery, , Wooden, plank, , Switch, , Conducting, wire, , fig-4(a), , Current out of the page, , fig-4(b), , Current into the page, , fig-4(c), , I, B, , Take a wooden plank and make a hole as, shown in figure 4(a). Place this plank on the, table. Now place a retort stand on the plank as, shown in figure 4(a). Pass 24 gauge copper wire, through hole of the plank and rubber knob of, the retort stand in such a way that the wire be, arranged in a vertical position and not touch the, stand. Connect the two ends of the wire to a, battery via switch. Place 6 to 10 compass, needles in a circular path around the hole so that, its centre coincides with the hole. Use 3 (or 9), volt battery in the circuit. Switch on. Current, flows through the wire., , • How do the directions of the compass needles change?, You may notice that they are directed as tangents to the, circle., • What is the shape of the magnetic field line around wire?, It must be a circular line. So we conclude that magnetic, field lines are closed lines. The magnetic field lines due to, straight wire carrying the current is shown in figures 4(b) and, 4(c). This can be verified by sprinkling iron filings around the, wire when current flows in the wire., • What is the direction of magnetic field induction at any point, on the field line?, If the current flow is vertically upwards (out of the page),, the field lines are in anticlockwise direction, as shown in figure, 4(b). If current flows into the page, in downward direction, the, field lines are in clockwise direction as shown in figure 4(c)., How do we determine the direction of field lines? It can be, easily determined with right hand thumb rule. If you grab the, current carrying wire with your right hand in such way that thumb, is in the direction of current, then the curled fingers show the, direction of the magnetic field as shown in figure 4(d)., , fig-4(d), 264, , X Class, , Electromagnetism
Page 275 :
(ii) Magnetic field due to circular coil, , Activity 5, Take a thin wooden plank covered with white paper, and make two holes on its surface as shown in figure, 5(a). Pass insulated copper wire (24 gauge) through the, To current, holes and wind the wire 4 to 5 times through holes such, supply, that it looks like a coil (figure 5(a)). The ends of the, circuit, wire are connected to terminals of the battery through a, fig-5(a), switch. Now switch on the circuit. Place a compass, needle on the plank at the centre of the coil. Put dots on either side of the, compass. Again place compass at one of the dots, put other dot further. Do, the same till you reach the edge of the plank. Now repeat this for the other, side of the coil from the centre. Then draw a line joining the dots, you will, get a field line of the circular coil. Do the same for the other points taken, in between the holes. Draw corresponding lines. You will get field lines of, the circular coil., • Can you tell the direction of the magnetic field of the coil?, This could be answered from the orientation of the compass needle., You can observe this when the compass needle is kept at the centre of the, coil. The direction in which the compass needle comes to rest indicates, the direction of the field due to the coil. Thus the direction of the field is, perpendicular to the plane of the coil., • Why does the compass needle point in the direction of field?, Place the compass in front of one of the faces of the coil and observe, the orientation of the compass needle. Note the pole of the needle that, faces the coil. We know that south pole is attracted to the north pole. The, needle is oriented in such a way that its south pole points, B, B, towards the north pole of the coil. So we can say that the, r, I, I, direction of magnetic field, due to coil, points towards I, N, r, you when the current in the coil is in anticlockwise, direction. Verify this in your experiment (do not touch, S, the wires of the coil). When the current in the coil is in, fig-5(b), clock-wise direction, the direction of magnetic field due, to the coil points away from you. The direction of the field due to coil or, solenoid is determined by using right hand rule, which states that,, “When you curl your right hand fingers in the direction of current,, thumb gives the direction of magnetic field.”, Observe the direction of magnetic field in figure 5(b)., Free distribution by A.P. Government, , 265
Page 276 :
(iii) Magnetic field due to solenoid, , Activity 6, Take a wooden plank covered with white paper., Make equidistant holes on its surface as shown in, figure 6(a). Pass copper wire through the holes as, shown in figure 6(a). This forms a coil. Join the ends, To current, of the coil to a battery through a switch. Switch on, supply circuit, the circuit. Current passes through the coil. Now, fig-6(a), sprinkle iron filings on the surface of the plank around, the coil. Give a small jerk to it. An orderly pattern of, iron filings is seen on the paper., • How do they adjust in such an orderly pattern?, I, I, This long coil is called solenoid. A solenoid is a, N, S, long wire wound in a close packed helix. The field, of solenoid is shown in the figure 6(b). The magnetic, field lines set up by solenoid resemble those of a, fig-6(b), bar magnet indicating that a solenoid behaves like a, bar magnet. The direction of the field due to solenoid, is determined by using right hand rule. One end of the solenoid behaves, like a north pole and other behaves like a south pole. The field lines outside, the solenoid are continuous with those inside. Outside the solenoid the, direction of the field lines is from north to south while inside the direction, is from south to north. Thus the magnetic field lines are closed loops., This is so for the bar magnet too!, We have seen that current carrying wires produce magnetic field. So,, electric charges in motion produce magnetic fields., • What happens when a current carrying wire is kept in a magnetic field?, Let us see., , Magnetic Force On Moving Charge And Current Carrying Wire, , Activity 7, •, •, , •, 266, , X Class, , Stand near the TV screen. Switch on the TV. (The old CRT type TV), Do you feel any sensation on your skin?, What could be the reason for that?, Take a bar magnet and bring it near the TV screen. What do you observe?, You can observe that the picture on the screen is distorted., Why does the picture get distorted?, Electromagnetism
Page 277 :
•, , Is the motion of electrons reaching the screen affected by the magnetic, field of the bar magnet?, Move the bar magnet away from the screen. Now you will get a clear, picture. Repeat this to confirm that the motion of electrons is affected by, the field produced by the bar magnet. This must be due to the fact that the, magnetic field exerts a force on the moving charges. This force is called, magnetic force., X indicates the direction of B, • Can we calculate the force experienced by a charge, and it is into the page, moving in a magnetic field?, Let a charge ‘q’ move with a velocity ‘v’ perpendicular, q v, to the magnetic field ‘B’ as shown in figure 7. The value of, magnetic force on the moving charge can be found, experimentally and it is given by,, F=qvB, fig-7, Magnetic force on the charge is the product of three, quantities charge, speed and magnetic flux density. The equation for, magnetic force acting on a charge ‘q’ is F = q v B and holds well only when, the direction of velocity of charged particle ‘v’ is perpendicular to the, direction of the magnetic field ‘B’., • Can we generalize the equation for magnetic force on charge when, there is an angle ‘θ’ between the directions of field B and velocity v?, It is experimentally proved that when there is an angle between direction of, field and velocity, the magnetic force experienced by the charge is given by,, F = q v B sinθ., • What is the magnetic force on the charge moving parallel to a magnetic, field?, When charge moves parallel to the magnetic field (along the magnetic, field or against the field) the value of θ becomes zero. In the above, equations θ is 00 so that sinθ = 0., Thus the charge experiences no force when it is moving parallel to the, magnetic field (along field direction or against field direction)., • What is the direction of magnetic force acting on a moving charge?, We have an easy method to find out the direction of magnetic force, acting on a charge moving in a magnetic field. Keep your right hand fingers, along the direction of velocity of moving charge and next curl your fingers, towards the direction of magnetic field then the thumb gives the direction, of magnetic force as shown in figure 8(a). This rule is applied for any case, Free distribution by A.P. Government, , 267
Page 278 :
F, , B, , V, , fig-8(a), , F, v or I, , B out of, paper, , fig-8(b):Right hand, rule for positive, charge, , of angle between directions of velocity and field. The direction, of magnetic force is always perpendicular to the direction of, both velocity and magnetic field., Generally right hand rule is used when velocity and field, are perpendicular to each other. This law states that, “If the, fore-finger points towards the direction of velocity of charge, or current, middle finger points to the direction of field (B), then thumb gives direction of force when the three fingers, are stretched in such a way that they are perpendicular to each, other as shown in figure 8(b).”, This rule is applicable to positive charge., • What is the direction of force acting on a negative charge, moving in a field?, First find the direction of force acting on a positive charge., Next reverse its direction. This new direction is the direction, of force acting on the negative charge., Let us see an example of force acting on a charged particle., , Example 1, , A charged particle ‘q’ is moving with a speed ‘v’, perpendicular to the magnetic field of induction B. Find the radius of the, path and time period of the particle., Solution: Let us assume that the field is directed into the page as shown, in figure E-1. Then the force experienced by the particle is F = q v B. We, know that this force is always directed perpendicular to velocity. Hence, the particle moves along a circular path and the magnetic force on a charged, particle acts like a centripetal force., v, Let r be the radius of the circular path., v, v, We know that centripetal force = mv2 / r, F, F R, q v B = mv2 / r, v, F, F, Solving this equation, we get; r = mv / Bq, F, Time period of the particle; T = 2πr / v, F, v, Substituting r in above equation, we get, v, v, T = 2πm / Bq, fig-E-1, –––––––––––––––––, • What happens when a current carrying wire is, placed in a magnetic field?, , 268, , X Class, , Electromagnetism, , B, , v
Page 279 :
Electric current is charges in motion. We know that each charge, experiences a magnetic force. Thus the current carrying wire (constituting, collection of charges in motion) experiences magnetic force when it is, kept in a magnetic field., • Can you determine the magnetic force on a current carrying wire which, is placed along a magnetic field?, We know that each charge experiences no magnetic force because, they are moving parallel to the direction of field along the field. So the, force acting on wire is zero when it is kept along a magnetic field., Let us find the magnetic force on a straight wire carrying current which, is kept perpendicular to a uniform magnetic field ‘B’. This ‘B’ is directed, into the page. It is represented by ‘x’ as shown in the figure 9. Let the field, be confined to the length L. So only the part of the wire of the length ‘L’ is, inside the magnetic field. Remaining wire is outside the magnetic field., We know that the electric current means charges in motion hence they, move with a certain velocity called drift velocity ‘v’., The magnetic force on a single charge is given by,, F0 = q v B, Let total charge inside the magnetic field be Q. So magnetic force on, the current carrying wire is given by, Assume that the ends of, F=QvB, ..................(1), the wire is connected to, the terminals of the battery, The time taken by the charge (Q) to cross the field be, t =L/v, v = L/t, ..................(2), substituting this in equation 1, we get,, F = Q (L/t) B, F = (Q / t) LB, ..................(3), We know that Q / t is equal to the electric current in, B, B, the wire,, L, I=Q/t, Substituting ‘I’ in the equation 3, we get, I=0, I, F = ILB, .................(4), fig-9, , Note: This equation holds well only when direction of, electric current is perpendicular to magnetic field., In figure 9, you can observe the bending in the wire due to the force, applied on it., • What is the force on the wire if its length makes an angle ‘θ’ with the, magnetic field?, Free distribution by A.P. Government, , 269
Page 280 :
Let ‘θ’ be the angle between direction of current and magnetic field,, then the force acting on the current carrying wire is given by, F = ILB sinθ (at any angle), ...................(5), • How could you find its direction?, You can use right hand rule to find out the direction of force on the, current carrying wire., Let us see the result of force applied on a current carrying wire by an, experiment., , Activity 8, Take a wooden plank. Fix two long wooden sticks on it. These wooden, sticks are split at their top ends., A copper wire is passed through these splits and the ends of the wire, are connected to battery of 3 volt, through a switch. Close the switch to, make the circuit. Current passes through the wire. Now bring a horseshoe, magnet near the copper wire as shown in figure 10., • What happens to the wire?, • In which way does it deflect?, Use the right thumb rule to find the, direction of force., I S N, • Is the direction of deflection observed, F, experimentally same as that of the, theoretically expected one?, Change polarities of the horse shoe, magnet. Again observe the deflection., fig-10, Repeat this by changing the direction of, current in the circuit., • Does the right hand rule give the explanation for the direction of, magnetic force exerted by magnetic field on the wire?, Right hand rule helps you to find the direction of magnetic force exerted, by the magnetic field on current carrying wire. It does not help you explain, the reason for deflection of wire., • Can you give a reason for it?, Imagine a situation where there is no current in the wire. Then there, exists only magnetic field due to external source (horse shoe magnet)., When there is a current in the wire, it also produces a magnetic field., These fields overlap and give non- uniform field. Let us see this clearly, with diagrams., 270, , X Class, , Electromagnetism
Page 281 :
B, , fig-11(a): Field lines due to, horseshoe magnet between its poles, , fig-11(b): Current, into the page, , fig-11(c), , The field in between north and south pole of horse shoe magnet is, shown in the figure 11 (a). Let us imagine a wire passing perpendicular to, the paper. Let the current pass through it (into the page). It produces a, magnetic field as shown in figure 11(b). Now let us try to sketch the resultant, field by observing the field lines. We can see that the direction of the field, lines due to the wire in upper part (of circular lines) coincides with the, direction of the field lines of horse shoe magnet. The direction of field, lines by wire in lower part (of circular lines) is opposite to the direction, of the field lines of horse shoe magnet. So that the net field in upper part, is strong and in lower part it is weak. Hence a non-uniform field is created, around the wire. This non uniform field is shown in figure 11 (c). Therefore, the wire tries to move to the weaker field region., • Does this deflection fit with the direction of magnetic force found by, right hand rule?, • What happens when a current carrying coil is placed in a uniform, magnetic field?, • Can we use this knowledge to construct an electric motor?, Let us try to answer., , Electric Motor, To understand the working of an electric motor we need, to understand the behaviour of a current carrying coil kept in a, uniform magnetic field., Consider a rectangular coil kept in a uniform magnetic, field as shown in figure 12(a). Switch on the circuit so that the, current flows through the rectangular coil. The direction of, current in the coil is shown in figure 12(a)., • What is the angle made by AB and CD with magnetic field?, You will notice that they are always at right angles to the, magnetic field., Free distribution by A.P. Government, , B, C, A, D, Magnetic field (B), , fig-12(a), 271
Page 282 :
•, , Can you draw the direction of magnetic force on sides AB and CD?, Apply right hand rule to get the direction of magnetic force. At AB, the, magnetic force acts inward perpendicular to field of the magnet and on, CD, it acts outward., See the figure 12(b). This figure is drawn showing top, F(on AB), view. The force on the sides BC and DA varies because they, make different angles at different positions of the coil in, B, the field., B, • What are the directions of forces on BC and DA?, C, At BC, magnetic force pulls the coil up and at DA, F(on CD) magnetic force pulls it down., fig-12(b), • What is the net force on the rectangular coil?, The force on AB is equal and opposite to the force on CD due to external, magnetic field because they carry equal currents in the opposite direction., Sum of these forces is zero; similarly the sum of the forces on sides BC, and DA is also zero for the same reason. So, net force on the coil is zero., But there is rotation of the coil. How is it possible?, F, • Why does the coil rotate?, Let us consider opening a cap of the bottle as an example, where two equal and opposite forces act on the cap. Two forces, equal in magnitude but opposite in direction must act on the, either side of cap of the bottle as shown in figure 12 (c). These, forces bring the cap into rotation. Similarly the rectangular coil, F, comes into rotation in clockwise direction because of equal, fig-12(c), and opposite pair of forces acting on the two sides of the coil., • What happens to the rotation of the coil if the direction of current in, the coil remains unchanged?, If the direction of current in the coil is unchanged, it rotates up to a, vertical position then due to its inertia it rotates further in clockwise, direction. But now the sides of the coil experience forces which are in the, opposite direction to the previous case. Hence these forces try to rotate it, in anti clockwise direction. As a result, this coil comes to halt and rotates, in anti clock wise direction, this will go on if the direction of current, remains unchanged., • How could you make the coil rotate continuously?, If the direction of current in the coil, after the first half rotation, is, reversed, the coil will continue to rotate in the same direction. Thus if the, direction of current through the coil is reversed every half rotation, the, coil will rotate continuously in one and the same direction., 272, , X Class, , Electromagnetism
Page 283 :
•, , How can we achieve this?, Anticlockwise, rotation, To achieve this, brushes B1 and B2 are used,, N, as shown in figure 12 (d). These brushes are, connected to the battery. The ends of the coil, B, C, S, are connected to slip rings C1 and C2, which, rotate along with the coil. Initially C1 is in, contact with B1 and C2 is in contact with B2., A, D, After half rotation, the brushes come into, C, 1, Split-ring, C2, contact with the other slip rings in such a way Communicator, that the direction of current through the coil is, Current, reversed. This happens every half rotation. Thus, (reverses at, B1, B2 half turn), the direction of rotation of the coil remains the Brushes, same. This is the principle used in “electric, +, fig-12(d), motor.”, In electric motors, electrical energy is converted into mechanical, energy., We have learned that a current carrying coil rotates when it is kept in, a uniform magnetic field., • What happens when a coil without current is made to rotate in magnetic, field?, • How is current produced?, , Electromagnetic induction - Faraday’s law, , Activity 9, Take a wooden base as shown in figure 13(a). Fix a soft iron cylinder, on the wooden base vertically. Wind copper wire around the soft iron as, shown in figure 13(a). Now take a metal ring which is slightly greater in, radius than the radius of the soft iron cylinder and insert it through the, soft iron cylinder on the wooden base. Connect the ends of the coil, to an AC source and switch on the current., • What do you notice?, You notice that the metal ring is levitated on the coil., Switch off the current, the ring will jump into the air very, dramatically. Remove the AC supply and connect a DC supply. Observe, what happens., • Why is there a difference in behaviour in these two cases?, • What force supports the ring against gravity when it is being, fig-13(a), levitated?, Free distribution by A.P. Government, , 273
Page 284 :
• Could the ring be levitated if DC is used?, The metal ring levitates when AC is used, therefore the net, force on it should be zero according to Newton’s second law. The, free body diagram of metal ring is shown in figure 13 (b). Weight, (w) acts down. To balance it, a force (F) equal in magnitude and, opposite in direction should act as shown in figure 13 (b)., W, fig-13(b), •, What is this unknown force acting on the metal ring?, In this activity AC is used. AC changes both its magnitude and, direction in regular time intervals. We know that the current through the, coil, produces a magnetic field so that one end of the coil behaves like, north pole and other end behaves like south pole for a certain time interval., For the next interval, coil changes its polarities., Hence we can say that coil undergoes changes in, its poles in the same intervals of time. The, Falling ring, levitation of metal ring is possible only when the, metal ring behaves like a magnet and should change, Direction of, induced emf, its polarities in the same time intervals but in a, sense opposite to that of the solenoid (coil) as, shown in figure 13(c). Assume that the current, flows in an clockwise direction in the solenoid as, viewed from the top. Then the upper end becomes, fig-13(c), a south pole. An upward force is applied on the, ring only when the upper side of the ring becomes a north pole (i.e. south, pole of the ring faces towards the south pole of solenoid). It is only possible, when there exists a anticlockwise current (viewed from the top) in the, ring. After certain intervals, solenoid changes its polarities, so that the, ring should also change its polarities in the same intervals. This is the, reason why the metal ring is levitated., • What is responsible for the current in the metal ring?, AC is not a constant current. So that, the magnetic induction changes, in both magnitude and direction in the solenoid and in the ring., Here the area of the metal ring is constant. But the field through the, metal ring changes so that flux linked with the metal ring changes., • If DC is used, the metal ring lifts up and falls down immediately. Why?, The flux linked with metal ring is zero when no current flows through, the solenoid. When the current is allowed to flow through the solenoid, it, behaves like bar magnet. So the flux is linked to the metal ring when the, F, , 274, , X Class, , Electromagnetism
Page 285 :
switch is on. At that instant there is a change in flux linked with ring. Hence, the ring rises up. There after, there is no change in flux linked with coil,, hence it falls down. If the switch is off, the metal ring again lifts up and, falls down. In this case also, there is a change in flux linked with ring when, the switch is off., • What could you conclude from the above analysis?, Let us understand the results of activity 9 by the, N, following hypothetical activity., Connect the terminals of a coil to a sensitive, N, ammeter or a galvanometer as shown in the figure-14., fig-14, Normally, we would not expect any deflections of needle, in the galvanometer because there is to be no, electromotive force in this circuit. Now if we push a bar, G, magnet towards the coil, with its north pole facing the, coil, a remarkable thing happens. While the magnet is moving towards the, coil, the needle in galvanometer deflects, showing that a current has been, set up in the coil, the galvanometer does not deflect if the magnet is at, rest. If the magnet is moved away from the coil, the needle in the, galvanometer again deflects, but in the opposite direction, which means, that a current is set up in the coil in the opposite direction., If we use the end of south pole of a magnet instead of north pole in the, above activity, the experiment works just as described but the deflections, are exactly reversed., Further experimentation enables us to understand that the relative, motion of the magnet and coil set up a current in the coil. It makes no, difference whether the magnet is moved towards the coil or the coil towards, the magnet., “Whenever there is a continuous change of magnetic flux linked with, a closed coil, a current is generated in the coil.”, This is one form of Faraday’s law., The current generated is called induced current and is set up by an, induced electromotive force (induced EMF). This phenomenon of getting, induced current is called electromagnetic induction., Faraday observed that the changes in the magnetic flux through the, coil are responsible for the generation of current in the coil. He also, observed that the rapid changes in flux through coil generate greater induced, current or induced EMF. After observing this important factor, he proposed, a law of electromagnetic induction, which is as follow,, “The induced EMF generated in a closed loop is equal to the rate of, change of magnetic flux passing through it.”, Free distribution by A.P. Government, , S, , 275
Page 286 :
S, , N, , S, , N, , S, , N, , S, S, , N, N, , 276, , In mathematical form, we can write this as, Induced EMF = change in flux/ time, ε = ΔΦ/Δt, .....................(6), The equation is called Faraday’s law of induction where Φ (phi) is the, flux linked with coil. Let Φ0 be the flux linked with single turn. If there are, N turns in the coil, the flux linked with the coil is N Φ0., Φ = N Φ0, ......................(7), So far we have not specified the direction of the induced EMF or, induced current. In the previous example, we have observed that an induced, current is set up in the loop., • What is its direction?, • Can you apply conservation of energy for electromagnetic induction?, When we push the bar magnet towards the coils, current is generated,, in other word electromagnetic induction takes place and mechanical energy, is converted into electrical energy., Let us discuss it in detail., We know that when a bar magnet is pushed towards a coil with its north, pole facing the coil an induced current is set up in the coil. Let the direction, of current in the coil be in clockwise direction with respect to north pole, of the bar magnet. Then this current carrying loop behaves like a magnet,, with its south pole facing the north pole of bar magnet. In such a case, the, bar magnet attracts the coil. Then it gains kinetic energy. This is, contradictory to conservation of energy. So our assumed clockwise, direction of induced current is wrong. Hence the, correct direction of induced current has to be in, anticlockwise direction with respect to north pole, of the bar magnet. In such a case, the north pole of, S, N, the coil faces the north pole of the bar magnet as, shown in figure 15. Then north pole of bar magnet, fig-15, is repelled by the north pole of the coil. Hence we, need to do work to overcome this force. This work, done on the magnet is converted into electrical energy in the coil. In this, way conservation of energy takes place in electromagnetic induction., Let us see a case where the bar magnet is pulled away from the coil,, with north pole facing the coil. In such case, the coil opposes the motion, of bar magnet to balance the conversion of mechanical energy into electric, energy. This happens only when the north pole of the magnet faces the, south pole of the coil., , X Class, , Electromagnetism
Page 287 :
•, , Can you guess what could be the direction of induced current in the, coil in such case?, Invariably the direction of induced current in the coil must be in anti, clock wise direction. In simple terms, when flux increases through coil,, the coil opposes the increase in the flux and when flux decreases through, coil, it opposes the decrease in the flux., This is Lenz’s law., Lenz’s law states that “the induced current will appear in such a direction, that it opposes the changes in the flux in the coil.”, • Could we get Faraday’s law of induction from conservation of energy?, Let us see., Let us arrange an apparatus as shown in figure 16. It consists of a pair, of parallel bare conductors which are spaced l meters apart in uniform, magnetic field of ‘B’. We can hold another bare conductor in such a way, that it is in contact with the two parallel wires(see figure-16). A galvano, meter is connected to the ends, of parallel conductors to, Distance s, complete an electric circuit. Flow of induced N, current, Now if the cross wire (cross, conductor) placed across, parallel conductors is moved to, S, the left, galvanometer needle will, deflect in one direction., If this cross wire is moved Galvanometer, Cross, to the right, its needle deflects, wire, in a direction opposite to the, previous deflection. Suppose, fig-16, that the crosswire is moved to, the left to a distance of ‘s’ meters in a time of ‘Δ t’. Then the reading of, galvanometer gives us the amount of current that flows in the circuit. A, current will be set up in the circuit only when there is an EMF in the circuit., Let this EMF be ‘ε’. The principle of conservation of energy tells us that, this electric energy (associated with flow of current) must come from the, work that we have done in moving the crosswire. If we ignore friction, everywhere, in the arrangement, the work done by this applied force = Fs., It is evident that there is a current of ‘I’ amperes flowing through the length, of l meters of the cross wire, and the cross wire is in a magnetic field., With this information,, Free distribution by A.P. Government, , Flux, density B, l, , Parallel, conductors, , 277
Page 288 :
•, , Can you derive an expression for the force applied on crosswire by, the field B?, We know that it is equal to BIl, from equation-4 of previous discussion, (see page 269), i.e., F = BIl, .............................(8), This force must oppose the applied force. The direction of applied, force determines the direction of current through the cross wire. Here we, are doing positive work. The work done by us in moving the cross wire, converts into electric energy. So the work done is given by,, W = Fs =BIls, .............................(9) (using equation-8), When we put the cross wire across parallel conductors it makes a, complete electrical circuit which encloses a certain amount of magnetic, flux. Now as we move the cross wire to the left, the area of the loop (formed, by the parallel conductors and cross wire) decreases and the flux through, the loop also decreases. The decrease in flux is given by,, ΔΦ = Bls, .............................(10), Here B is perpendicular to the area, (ls). From equations 9 and 10, l, W = (ΔΦ) Ι, Let us divide both sides of this equation by Δt, W/Δ t = I (ΔΦ/ Δt), .............................(11), Electric power, P = IΔΦ/ Δt, We know that electric power is the product of current and emf or, voltage. ε=ΔΦ/Δt is obviously equal to induced EMF., Electric power, P = εΙ .............................(12), Thus the electric power generated in the circuit is equal to product of, induced EMF and the current. Thus the mechanical energy utilised to move, the cross wire in one second is converted into electric power (ΔΦ/Δt) I., This is nothing but conservation of energy., Dividing equation (9) by Δt, we have, W/Δt = Fs/Δt =BIls/Δt, ..................(13), Here s/Δt gives the speed of the cross wire, let it be taken as v. Then, we get, Electric power P = W/Δ t = Fv = BIlv ......(14), Power is also given as force times velocity. From equations (12) and, (14), we get, W/Δ t = εI, εI = BIlv, 278, , X Class, , Electromagnetism
Page 289 :
We get,, ε = Blv, This is called motional EMF. The above equation is not Faraday’s law, of induction because it is not related to the loop. It is useful when a, conductor moves in a uniform magnetic field., Let us see a few examples on induced emf., , Example 2, The magnetic flux inside a coil of 400 turns, changes for each single turn with time as shown in, figure, fig-E-2, Determine the maximum induced emf generated, in the coil. Is there any change in induced EMF from t = 0.1 second to 0.3, second?, Solution: From the given graph, the increase in magnetic flux through, one turn of coil in 0.1 second is 0.001 Wb. According to Faraday’s law,, the maximum induced emf generated in the coil is given by,, ε = N Δ Φ /Δt, Substituting the values, we get, ε = 400(0.001/0.1) = 4V, From graph, there is no change in magnetic flux through coil from t =, 0.1s to 0.3s hence no emf is generated., , Example 3, Find the length of the conductor which is moving with a speed of 10, m/s in the direction perpendicular to the direction of magnetic field of, induction0.8T, if it induces an emf of 8V between the ends of the conductor., Solution: Given that B = 0.8T, v = 10 m/s and ε = 8V., Using ε = Blv, 8 = 0.8(l)(10), l (length of the conductor) = 1m, –––––––––––––––––, Let us see some applications of Faraday’s law of electromagnetic, induction., Electromagnetic induction is all around us., • You might have seen that, during security check, people are made to, walk through a large upright coil of wire which produces a weak AC, (alternating) magnetic field. If we are carrying any significant quantities, of iron, the magnetic flux linked with the large coil changes and the, induced current generated in coil triggers an alarm., Free distribution by A.P. Government, , 279
Page 290 :
•, , The tape recorder which we use to listen to songs (or) record voices, works on the principle of electromagnetic induction. It consists of a, piece of plastic tape coated with iron oxide and is magnetised more in, some parts than in others. When the tape is moved past as a small coil, of wire (head of the tape recorder), the magnetic field produced by the, tape changes, which leads to generation of current in the small coil of, wire., How could we use the principle of electromagnetic induction in the, case of using ATM card when its magnetic strip is swiped through a, scanner? Discuss with your friends and your teacher., An induction stove works on the principle of electromagnetic, induction. A metal coil is kept just beneath the cooling surface. It carries, alternating current (AC) so that AC produces an alternating magnetic, field. When you keep a metal pan with water on it, the varying magnetic, field beneath it crosses the bottom surface of the pan and an EMF is, induced in it. Because the pan is metal the induced EMF generates an, induced current in it. Since the pan has a finite resistance, the flow, induced current in it produces heat in it and this heat is conducted to, the water. That’s why we call this stove as induction stove., Have you ever thought, from where do we get electrical energy?, Let us learn about it., , •, , •, , Electric Generator and Alternating - Direct Currents, , Rotation, , A, , S, B, , N, Slip rings, , fig-17(a):, Brushes, 280, , X Class, , • What happens when a coil is, continuously rotated in a uniform, magnetic field?, • Does it help us to generate electric, current?, Let us see:, Consider a rectangular coil. Let it be, held between the poles of Curve- shaped, permanent magnet as shown in figure, 17(a). As the coil rotates, the magnetic, flux passing through the coil changes., According to the law of electro magnetic, induction an induced current is generated, in the coil., • Is the direction of current induced in, the coil constant? Does it change?, Electromagnetism
Page 291 :
emf generated in the coil, , 1. Consider initially the coil, positioned in such a way that magnetic, flux passes through it. When the coil is at rest in vertical position, with, side (A) of coil at top position and side (B) at bottom position, no current, will be induced in it. Thus current in the coil is zero at this position., 2. When the coil is rotated in clockwise direction, current will be, induced in it and it flows from A to B. During the first quarter of rotation,, the current increases from zero to a maximum and reaches peak value, when the coil is in, One complete cycle, horizontal position., 3. If we continue the, No. of, rotation of coil, current, revolutions, decreases during the, 1/2, 1, 3/4, 0, 1/4, second quarter of the, rotation and once again, becomes zero when coil, Position of, coil with, comes to vertical position, respect to, with side B at top (A) at, direction of, bottom position. During, magnetic flux, the second part of the, Zero emf Maximum Zero, Maximum, Zero, rotation, current genercoil, reversed, emf, coil, emf, emf, vertical horizontal, emf, ated follows the same, pattern as that in the first, fig-17(b), half except that the, direction of current is reversed. (see figure-17(b) ), • Can you guess the reason for variation of current from zero to maximum, and vice-versa during the rotation of coil?, • Can we make use of this current? If so, how?, Let us find out., As shown in figure17(a) the ends of the coil are connected to two slip, rings. Two carbon brushes arranged in such a way that they press the slip, rings to obtain current from the coil. When these brushes are connected, to external devices like TV, radio, we can make them work with current, supplied from ends of carbon brushes., The current obtained by this process changes its direction alternatively, for each half cycle as shown in figure 17(b)., This current is called alternating current (AC) in which, the direction, of charge flow reverses periodically. So AC possesses certain frequency., The generator that we discussed here is called AC generator., Free distribution by A.P. Government, , 281
Page 292 :
Rotation, , A, S, , B, , Commutator, , N, Brush, , emf generated coil, , fig-17(c), , 0, , R, , These AC - EMF and AC are expressed in terms, of rms values., Let I0 and V0 be the peak values of AC and, AC - EMF., Irms = I0/ and Vrms = V0/, • How can we get DC current using a generator?, • What changes do we need to make in an AC, generator to be converted into a DC generator?, Let us find out., If two half slip rings are connected to ends, of the coil as shown in figure 17(c), the AC, generator works as DC generator to produce, DC current., Let us see how it works., , When the coil is in the vertical position the induced current generated, during the first half rotation, rises from zero to maximum and then falls to, zero again. As the coil moves, further from this position,, the ends of the coil go to, No. of, other slip rings. Hence, revolutions, during the second half, 1, 1/4, 1/2, 3/4, 1/, rotation, the current is, Position of, reversed in the coil itself, the, coil and, commutator current generated in the, with, second half rotation of the, respect to, direction, coil is identical with that, of, during the first half of direct, Zero, Maximum, magnetic, Maximum Zero, emf, current (DC) as shown in, emf, flux, emf, emf, figure, 17(d)for, one, fig-17(d), revolution., 1, , 4, , Zero emf, , In generators, mechanical energy is converted into the electrical, energy., ., 282, , X Class, , Electromagnetism
Page 293 :
Key words, Magnetic flux, Magnetic flux density, Electric motor, Slip rings,, Induced current, Induced EMF, Electric generator, DC and, AC currents, rms values, , What we have learnt, •, , Magnetic flux density (B) is defined as the ratio of flux passing through a plane perpendicular to, field and the area of the plane., , •, •, •, •, , Current carrying wire produces magnetic field., F = qvB sin θ and F = ILB sin θ, In electric motor, electrical energy is converted into mechanical energy., Faraday’s law: The induced EMF generated in a closed loop is equal to the rate of change of, magnetic flux passing through it., , •, , Lenz’s law: the induced current set up in the coil is in such a direction that it opposes the, changes in the flux., , •, , When a conductor of length ‘l’ moves perpendicular to field B with a speed v then potential, difference (voltage) developed between the ends of conductor is Blv. This EMF is called motional, EMF., , •, , In generators, mechanical energy is converted into electrical energy., , Improve your learning, 1. Are the magnetic field lines closed? Explain. (AS1), 2. See fig. Q-2, magnetic lines are shown. What is the direction of the current flowing through the, wire?(AS1), 3. A bar magnet with North Pole facing towards a coil moves as shown in fig.Q-3. What happens, to the magnetic flux passing through the coil? (AS1), 4. A coil is kept perpendicular to the page. At P, current flows into the page and at Q it comes out, of the page as shown in figure Q-4. What is the direction of magnetic field due to the coil?, (AS1), Q, , N, , fig- Q2, Free distribution by A.P. Government, , fig- Q3, , P, , x, , fig- Q4, 283
Page 294 :
5. The direction of current flowing in a coil is shown in fig.Q-5. What type of, magnetic pole is formed at the face that has flow of current as shown in, fig.Q-5? (AS1), 6. Why does the picture appear distorted when a bar magnet is brought close, fig- Q5, to the screen of a television? Explain (AS1), i, 7. Symbol ‘X’ indicates the direction of a magnetic field into the page. A straight, long wire carrying current along its length is kept perpendicular to the magnetic, B, field. What is the magnitude of force experienced by the wire? In what direction, L, does it act? (AS1), 8. Explain the working of electric motor with a neat diagram. (AS1), 9. Derive Faraday’s law of induction from law of conservation of energy. (AS1), fig- Q7, 10. The value of magnetic field induction which is uniform is 2T. What is the flux, passing through a surface of area 1.5m2 perpendicular to the field? (AS1), 11. An 8N force acts on a rectangular conductor 20cm long placed perpendicular to a magnetic, field. Determine the magnetic field induction if the current in the conductor is 40A. (Ans: 1tesla), (AS1), 12. Explain with the help of two activities that current carrying wire produces magnetic field. (AS1), 13. How do you verify experimentally that the current carrying conductor experiences a force, when it is kept in magneticfield? (AS1), 14. Explain Faraday’s law of induction with the help of activity. (AS1), 15. Explain the working of AC electric generator with a neat diagram. (AS1), 16. Explain the working of DC generator with a neat diagram. (AS1), 17. Rajkumar said to you that the magnetic field lines are open and they start at north pole of bar, magnet and end at south pole. What questions do you ask Rajkumar to correct him by saying, “field lines are closed”? (AS2), 18. As shown in figure Q-18 both coil and bar magnet moves in the, same direction. Your friend is arguing that there is no change in, V, flux. Do you agree with his statement? If not what doubts do you, N, have? Frame questions about the doubts you have regarding, change in flux. (AS2), fig- Q18, 19. What experiment do you suggest to understand Faraday’s law?, What items are required? What suggestions do you give to get, good results of the experiment? Give precautions also. (AS3), C, 20. How can you verify that a current carrying wire produces a magnetic field with the help of an, experiment? (AS3), 21. Collect information about generation of current by using Faraday’s law. (AS4), 22. Collect information about material required and procedure of making a simple electric motor, from internet and make a simple motor on your own. (AS4), 284, , X Class, , Electromagnetism
Page 295 :
23., 24., 25., 26., , Collect information of experiments done by Faraday. (AS4), Draw a neat diagram of electric motor. Name the parts. (AS5), Draw a neat diagram of an AC generator. (AS5), How do you appreciate Faraday’s law, which is the consequence of conservation of energy?, (AS6), 27. How do you appreciate the relation between magnetic field and electricity that changed the life, style of mankind? (AS6), 28. Give a few applications of Faraday’s law of induction in daily life. (AS7), 29. Which of the various methods of current generation protects nature well? Give examples to, support your answer. (AS7), , ks, Fill in the blan, 1. The SI unit of magnetic field induction is ........................, 2. Magnetic flux is the product of magnetic field induction and ................., 3. The charge is moving along the direction of magnetic field. Then force acting on it is ..............., 4. A current carrying wire of length L is placed perpendicular to a uniform magnetic field B. Then, the force acting on the wire with current I is ....................., 5. Faraday’s law of induction is the consequence of ....................., , s, Multiple choice question, 1. Which converts electrical energy into mechanical energy, a) motor, , b) battery, , c) generator, , d) switch, , 2. Which converts mechanical energy into electrical energy, a) motor, , b) battery, , c) generator, , d) switch, , [, , ], , [, , ], , 3. The magnetic force on a current carrying wire placed in uniform magnetic field if the wire is, oriented perpendicular to magnetic field, is ................., [, ], a) 0, , b) ILB, , c) 2ILB, , d) ILB/2, , Free distribution by A.P. Government, , 285
Page 296 :
Chapter, , 13, Principles of Metallurgy, In class 8 you have studied about certain properties of metals like,, malleability, ductility, sonarity etc. Metals play an important role in our, daily life. We use various metals for various purposes like gold and silver, as jewellary, copper, iron, alluminium for making conducting wires and, for making utensils etc. We use many house hold articles made up of metals, and their alloys at our home., • Can you mention some articles that are made up of metals?, • Do metals exist in nature in the form same as that we use in our daily, life?, • Have you ever heard the words like ore, mineral and metallurgy?, • Do you know how these metals are obtained?, To understand these questions you need to know about metallurgy. In, this chapter we discuss various concepts related to metallurgy and the, process by which we are able to obtain the pure form of metal that we use, in our daily life., “Metallurgy is the process of extraction of metals from their ores”., Human history in terms of materials had the Bronze Age and Iron Age, pertaining to the metals they started to use the bronze (an alloy of copper, and tin) and iron. Now we have more than 75% metals among the elements, available., , Occurrence of the metals in nature, •, , How the metals are present in nature?, The earth’s crust is the major source of metals. Sea water also contains, some soluble salts such as sodium chloride and magnesium chloride etc., 286, , X Class, , Principles of Metallurgy
Page 297 :
Some metals like gold (Au), silver (Ag) and copper (Cu) are available in, nature in free state (native) as they are least reactive. Other metals mostly, are found in nature in the combined form due to their more reactivity. The, elements or compounds of the metals which occur in nature in the earth, crust are called minerals. At some places, minerals contain a very high, percentage of a particular metal and the metal can be profitably extracted, from it. The minerals from which the metals are extracted without, economical loss are called ores., Aluminium, for example, is the most common metal in the Earth’s, crust, occurring in most of minerals. However, it isn’t economically, feasible to extract it from most of these minerals. Instead, the usual ore, from which it is profitable to extract it is bauxite – which contains from, 50 – 70 % of aluminium oxide ., , Think and discuss, •, , Do you agree with the statement “All ores are minerals but all, minerals need not be ores?” Why?, , Activity 1, Look at the following ores., Identify the metal present in each ore., Table - 1, ORE, , Formula, , metal, , ORE, , Formula, , metal, , Bauxite, , (Al2O3 2H2O) Al, , Zincite, , (ZnO), , Zn, , Copper Iron Pyrites, , (CuFeS2), , Cu, , Rock salt, , (NaCl), , Na, , Zinc Blende, , (ZnS), , Zn, , Cinnabar, , (HgS), , Hg, , Magnesite, , (MgCO3), , Mg, , Magnetite, , (Fe3O4), , Fe, , Epsom salt, , (MgSO4 7H2O) Mg, , Galena, , (PbS), , Pb, , Horn Silver, , (AgCl), , Ag, , Gypsum, , Pyrolusite, , (MnO2), , Mn, , Lime stone, , Haematite, , (Fe2O3), , Fe, , Carnallite, , Free distribution by A.P. Government, , (CaSO4 2H2O), , Ca, , (CaCO3), , Ca, , (KCl MgCl2 6H2O), , Mg, , 287
Page 298 :
Now try to classify them as shown in the table., Table - 2, I, Oxides, , Sulphides, , Chlorides, , Carbonates, , Sulphates, , •, •, •, , What metals can we get from the ores mentioned in the Table – 1?, Can you arrange these metals in the order of their reactivity?, What do you notice in Table – 2?, You will notice that the ores of many metals are oxides and sulphides., This is why oxygen - sulphur (16th group) group is called chalcogen family, (chalco = ore; genus = produce), The metals like K, Na, Ca, Mg and Al are so reactive that they are, never found in nature in free state., The metals like Zn, Fe, Pb etc., are moderately reactive. They are found, in the earth crust mainly as oxides, sulphides and carbonates., Metals like Au, Ag are least reactive and they are found even in free, state in nature., Based on reactivity we can arrange metal in descending order of their, reactivity as shown below:, K, Na, Ca, Mg, Al, Zn, Fe, Pb, Cu, Ag, Au, –––––––––––––––, –––––––––––––––, –––––––––––––, High reactivity, , •, •, , •, •, , Moderate reactivity, , Low reactivity, , Can you think how do we get these metals from their ores?, Does the reactivity of a metal and form of its ore (oxides, sulphides,, chlorides, carbonates sulphates) has any relation with process of, extraction?, How are metals extracted from mineral ores?, What methods are to be used?, Let us find., , Extraction of metals from the ores:, The extraction of a metal from its ore involves mainly three stages., They are:, I) Concentration or Dressing, II) Extraction of crude metal, III)Refining or purification of the metal., 288, , X Class, , Principles of Metallurgy
Page 299 :
Ore, Concentration of ore, , Hand picking, by, , Froth flotation, Magnetic Separation, , Extraction of crude, metal from the ore, Metals of high, reactivity, , Washing, , Metals of medium, reactivity, , Metals of low, reactivity, Sulphide ore, , Halides, , Oxides, Electrolysis of, molten ore, , Metal, (eg: Na, Mg, Al, etc.,), Chemical Reduction, Auto Reduction, Displacement method, Electrolytic reduction, , Carbonate, ore, , Sulphide, ore, , Calcination, , Roasting, , Roasting, Oxides, Reduction, , Oxide ofmetal, , Metal, , Reduction of metal, , Refining, (eg:Ag), , Refining of metal, (eg. Cu, Zn, etc.,), , Distillation, Poling, Liquation, Electrolytic refining, , I. Concentration or Dressing of the ore, Ores that are mined from the earth are usually contaminated with large, amount of impurities such as soil and sand etc., Concentration or Dressing means, simply getting rid of as much of, the unwanted rocky material as possible from the ore. The impurities like, clay are called gangue. Here, we should get as for as possible pure or, more concentrated ore., Enrichment (concentration) of the ore: Various physical methods are, used to enrich the ore. In many cases, it is possible to separate the metal, compound from unwanted rocky material by physical means. An example, for this is froth flotation., The physical methods adopted in dressing of the ore (or) enriching of, the ore depends upon difference between physical properties of ore and, gangue., Free distribution by A.P. Government, , 289
Page 300 :
Table-3, Process, , Name of the, method, Hand picking, , If the ore particles and the impurities are different in, one of the properties like colour, size etc., Using that, property the ore particles are handpicked separating, them from other impurities., , Washing, , Ore particles are crushed and kept on a slopy surface., They are washed with controlled flow of water. Less, densive impurities are carried away by water flow,, leaving the more densive ore particles behind., , Froth floatation, , This method is mainly useful for sulphide ores which, have no wetting property whereas the impurities get, wetted. The ore with impurities is finely powdered and, kept in water taken in a flotation cell. Air under pressure, is blown to produce froth in water. Froth so produced,, takes the ore particles to the surface whereas impurities, settle at the bottom. Froth is separated and washed to, get ore particles.(see fig.1), , Magnetic separation, , If the ore or impurity, one of them is magnetic substance, and the other non-magnetic substance they are separated, using electromagnets. (see Fig.2), , Froth bubbles, carrying sulphide, ore particles, , Powdered ore, , Compressed, Air, Sulphide ore, particles, , Magnetic, wheel, Non, Magnetic, wheel, , Moving belt, , Water, containing, pine oil, Gangue, , fig-1: Froth floatation process for the, concentration of sulphide ores, , Non Magnetic ore, , Magnetic ore, , fig-2: Magnetic separation, , There are some other methods also for dressing which you will learn at higher classes., 290, , X Class, , Principles of Metallurgy
Page 301 :
Free distribution by A.P. Government, , 291, , Au, , Pt, , Ag, , Hg, , Cu, , Pb, , Fe, , Zn, , Al, , Mg, , Ca, , Na, , K, , Metals, , Don’t burn or, oxidise even on, the surface, , Don’t burn, but, only form a surface, layer of oxide, PbO, CuO, HgO, , Burn with, decreasing vigour, to form oxides, CaO, MgO,, Al2O3, ZnO,, Fe2O3, , Form Na2O, K2O, in limited supply of, O2 but form, peroxides in excess, of O2, , Action of, Oxygen, , From Al to Au do, not displace H2, from cold water, , K to Mg displace, H2 from cold, water with, decreasing, reactivity, {K violently but, Mg very slowly}, , Reaction with, cold water, , From Pb to Au, donot displace H2, from steam, , K to Fe displace, H2 with steam, without decreasing, reactivity., {K very violently, but Fe very, slowly}, , Reaction with, steam, , Reactivity of Metals, , Cu to Au do not, displace H2 from, dilute strong acids, , K to Pb displace H2, from dilute strong, acids with decreasing, reactivity., {K-explosively,, Mg-very vigorously,, Fe-steadily,, Pb-very slowly}, , Reaction with dilute, strong Acids, , Table-4, , and AuCl3 are formed, , FeCl3, PbCl2, CuCl2,, HgCl2, AgCl, PtCl3, , MgCl2, Al2Cl3, ZnCl2,, , KCl, NaCl, CaCl2,, , All metals react with, Chlorine on heating toform, their respective Chlorides, but with decreasing, reactivity from top to, bottom. This is understood, from the heat evolved, when the metal reacts with, one mole of Chlorine gas, to form Chloride., , Reaction with, chlorine on heating
Page 302 :
II Extraction of crude metal from the ore, Extraction of the metal from its ores depends on the reactivity of the, metal. To understand the order of reactivity of metals that are very familiar,, we study their chemical reactions with cold water, steam, dilute strong, acids and Cl2 and based on their vigorous activity order in these reactions, we frame out activity series. Arrangement of the metals in decreasing order, of their reactivity is known as activity series. (See table - 4), , Reduction of purified ore to the metal, The method used for a particular metal for the reduction of its ore to, the metal depends mainly on the position of the metal in the activity series., , A) Extraction of Metals at the top of the activity series, (K, Na, Ca, Mg and Al). Simple chemical reduction methods like, heating with C, CO etc to reduce the ores of these metals are not feasible., The temperature required for the reduction is too high and more expensive., To make the process economical, electrolysis methods are to be adopted., Again the electrolysis of their aqueous solutions also is not feasible, because water in the solution would be discharged at the cathode in, preference to the metal ions., The only method viable is to extract these metals by electrolysis of, their fused compounds. For example to extract Na from NaCl, fused NaCl, is electrolysed with steel cathode (-) and graphite anode (+). The metal, (Na) will be deposited at cathode and chloride liberated at the anode., At Cathode 2Na+ + 2e–, At Anode 2Cl –, , 2Na, , Cl2 + 2e–, , For the above electrolysis, a large quantity of electricity is required, to keep the ore in molten state. Suitable impurities are added to the ore to, decrease its melting point., , B) Extraction of metals in the middle of the activity series, (Zinc, iron, tin, lead and copper): The ores of these metals are generally, present as sulphides or carbonates in nature. Therefore prior to reduction, of ores of these metals, they must be converted into metal oxides., Sulphide ores are converted into oxides by heating them strongly in, excess of air. This process is known as roasting. Generally the sulphide, 292, , X Class, , Principles of Metallurgy
Page 303 :
ores are roasted to convert them into oxides before reducing them to, metal., Eg: 2PbS + 3O2, , 2PbO + 2SO2, , The metal oxides are then reduced to the corresponding metal by using, suitable reducing agent such as carbon, i) Reduction of metal oxides with carbon: The oxides are reduced, by coke in a closed furnace which gives the metal and carbon monoxide, (CO)., Eg: PbO + C, , at 1400 oC, , ––––––––––>, , Pb + CO, , ii) Reduction of oxide ores with CO., in blast furnace, , Eg: Fe2O3 + 3CO ––––––––––––> 2Fe + 3CO2, iii) Auto (self) reduction of sulphide ores: In the extraction of Cu, from its sulphide ore, the ore is subjected partial roasting in air to give its, oxide., 2Cu2S + 3O2, , 2Cu2O + 2SO2, , When the supply of air is stopped and the temperature is raised. The, rest of the sulphide reacts with oxide and forms the metal and SO2., 2Cu2O + Cu2S, , 6Cu + 2SO2, , iv)Reduction of ores (compounds) by more reactive metals., Thermite process involves the reaction of metal oxides with, aluminium. When highly reactive metals such as sodium, calcium,, aluminium etc., are used as reducing agents, they displace metals of lower, reactivity from the compound. These displacement reactions are highly, exothermic. The amount of heat evolved is so large that the metals, produced are in molten state., 850 oC, , Eg: TiCl4 + 2Mg ––––––––––––>Ti + 2MgCl2, 850 oC, , TiCl4 + 4Na ––––––––––––> Ti + 4NaCl, , Free distribution by A.P. Government, , 293
Page 304 :
The reaction of Iron (III) oxide (Fe2O3), with aluminium is used to, join railings of railway tracks or cracked machine parts. This reaction is, known as the thermite reaction., 2Al + Fe2O3, Al2O3 + 2Fe + Heat, 2Al + Cr2O3, Al2O3 + 2Cr + Heat, , fig-3(a), , fig-3(b), , fig-3(c), , C) Extraction of metals at the bottom of the activity series, (Ag, Hg etc), Metals at the bottom of the activity series are often found in free, state. Their reactivity with other atoms is very low. The oxides of these, metals can be reduced to metals by heat alone and sometimes by, displacement from their aqueous solutions., i) When cinnabar (HgS) whch is an ore of mercury, heated in air, it is, first converted into (HgO) then reduced to mercury on further heating., Eg: 2HgS + 3O2 ––––> 2HgO + 2SO2 ––––> 2HgO –––> 2Hg + O2, Heat, , Heat, , Heat, , ii) Displacement from aqueous solutions:, Eg: Ag2S + 4CN- 2[Ag(CN)2]- + S22[Ag(CN)2]- (aq) + Zn(s), [Zn(CN)4]2- (aq) + 2Ag (s), Here Ag2S is dissolved in say KCN solution to get dicyanoargentate, (I) ions. From these ions Ag is precipitated by treating with Zn dust powder., , III. Purification of the crude metal, The metal obtained by the reduction of the ore is usually contaminated, with impurities like unchanged ore, other metals present in the ore and, non metals from the anions in the ore., For example, the (blister) copper obtained from its sulphide ore, a, compound of copper iron pyrites (CuFeS2), contains some copper sulphide,, iron and sulphur. It is purified by suitable methods including electrolysis., The process of obtaining the pure metal from the impure metal is called, refining of the metal. Refining of the metal involves several types of, processes. Some refining methods are given below:, 294, , X Class, , Principles of Metallurgy
Page 305 :
a) Distillation (b) Poling (c) Liquation (d) Electrolysis etc., The process that has to be adopted for purification of a given metal, depends on the nature of the metal and its impurities?, a) Distillation: This method is very useful for purification of low, boiling metals like zinc and mercury containing high boiling metals as, impurities. The extracted metal in the molten state is distilled to obtain, the pure metal as distillate., b) Poling: The molten metal is stirred with logs (poles) of green wood., The impurities are removed either as gases or they get oxidized and form, scum (slag) over the surface of the molten metal. Blister copper is purified, by this method. The reducing gases, evolved from the wood, prevent the, oxidation of copper., c) Liquation: In this method a low melting metal like tin can be made, to flow on a slopy surface to separate it from high melting impurities., d) Electrolytic refining: In this method, the impure metal is made, to act as anode. A strip of the same metal in pure form is used as cathode., They are put in a suitable electrolytic bath containing soluble salt of the, same metal. The required metal gets deposited on the cathode in the pure, form. The metal, constituting the impurity, goes as the anode mud. The, reactions are:, Anode: M, Mn+ + neCathode: Mn+ + neM, (M = pure metal ), Where n = 1,2,3, ..., We use this electrolytic method, to refine copper., For this an impure copper is, fig-4: Experimental setup for the electrolytic, taken as anode and pure copper strips, refining of copper, are taken as cathode. The electrolyte, is an acidified solution of copper sulphate. As a result of electrolysis, copper in pure form is transferred from the anode to the cathode., Anode: Cu, Cu2+ + 2eCathode: Cu2+ + 2eCu, The soluble impurities go into the solution, where as insoluble, impurities from the blister copper get deposited at the bottom of anode as, anode mud which contains antimony selenium, tellurium, silver, gold and, platinum; recovery of these elements may meet the cost of refining., Zinc may also be refined this way., Free distribution by A.P. Government, , 295
Page 306 :
Corrosion, The rusting of iron (iron oxide), tarnishing of silver (silver sulphide),, development of green coating on copper (copper carbonate) and bronze, are some of the examples of corrosion., • Do you know why corrosion occurs?, Let us find, , Activity 2, •, , Take three test tubes and place clean iron nails in each of them., , •, , Label these test tubes A,B and C. pour some water in test tube A and, cork it., , •, , Pour boiled distilled water in test tube B, add about 1 ml of oil and, cork it. The oil will float on water and prevent the air from dissolving, in the water., , Air, , Air, , Dry, air, , Layer, of oil, Rusty, iron, nails, Water, Boiled, distilled water, , Anhydrous, calcium chloride, , fig-5: Investigating the conditions, under which iron rusts, , • Put some anhydrous calcium chloride in test, tube C and cork it. Anhydrous calcium chloride, will absorb the moisture, if any, from the air., Leave these test tubes for a few days and then, observe (see figure)., You will observe that iron nails rust in test, tube A, but they do not rust in test tubes B and C., In the test tube A. The nails are exposed to both, air and water. In the test tube B, the nails are, exposed to only water, and the nails in test tube, C are exposed to dry air., , • What does this tell us about the conditions, under which iron articles rust?, In metallic corrosion, a metal is oxidised by loss of electrons generally, to oxygen and results in the formation of oxides. Corrosion of iron, (commonly known as rusting) occurs in presence of water and air., The chemistry of corrosion is quite complex but it may be considered, essentially as an electrochemical phenomenon. During corrosion at a, particular spot on the surface of an object made of iron, oxidation takes, place and that spot behaves as anode. We can write the reaction as., Anode: 2Fe(s), 296, , X Class, , 2Fe2+ + 4e–, Principles of Metallurgy
Page 307 :
Electrons released at this anodic spot move through the metal and go, to another spot on the metal and reduce oxygen at that spot in presence of, H+ (which is believed to be available from H2CO3 formed due to dissolution, of carbon dioxide from air into water in moist air condition of atmosphere., Hydrogen ion in water may also be available due to dissolution of other, acidic oxides from the atmosphere). This spot behaves as cathode with the, reaction is., 2H2 O(l), Cathode: O2(g) + 4H+ (aq) + 4e+, The overall reaction is: 2Fe(s)+O2(g)+4H (aq) 2Fe2+(aq)+2H2O(l), The ferrous ions are further oxidised by atmospheric oxygen to ferric, ions which come out as rust in the form of hydrated ferric oxide, (Fe2O3.XH2O) and with further production of hydrogen ions., , Prevention of corrosion, Prevention of corrosion is of prime importance. It not only saves money, but also helps in preventing accidents such as a bridge collapse or failure, of a key component due to corrosion., One of the simplest methods of preventing corrosion is to prevent the, surface of the metallic object to come in contact with atmosphere. This, can be done by covering the surface with paint or by some chemicals, (eg: bisphenol)., Another simple method is to cover the surface by other metals, (Sn, Zn etc) that are inert or react themselves with atmosphere to save the, object. This is generally done by electroplating., An electrochemical method is to provide a sacrificial electrode of, another metal (like Mg, Zn etc) which corrodes itself but saves the object., , Do you know?, Alloying is a method of improving the properties of a metal. We can get desired, properties by this method. For example, iron is the most widely used metal. But it, is never used in its pure state. This is because pure iron is very soft and stretches, easily when hot. But, if it is mixed with a small amount of carbon, it becomes hard, and strong. When iron is mixed with nickel and chromium we get stainless steel, which will not rust. Pure gold, known as 24 carat gold, is very soft. It is, therefore,, not suitable for making jewellery. It is alloyed with either silver or copper to, make it hard. Generally in India 22carat gold is used for making ornaments. It, means that 22 parts of pure gold is alloyed with 2 parts of either silver or copper., Free distribution by A.P. Government, , 297
Page 308 :
A few important processes used in metallurgy, Smelting: Smelting is a pyrochemical (pyre = heat) process, in which, the ore is mixed with flux and fuel and strongly heated. The heat is so strong, that the ore is reduced to even metal as in the case of iron (Fe), and the metal, is obtained in molten state. During smelting the impurities (gangue) in the, ore react with flux to form slag which is removed. For haematite (Fe2O3)ore,, coke is used as fuel and lime stone (CaCO3) is used as flux. The smelting is, carried out in a specially built furnace known as blast furnace., The reactions inside the furnace are:, 2C(s) + O2 (g) ––––> 2CO(g), , Fuel, , Skip, car, , Fe2O3(s) + 3CO(g) ––––> 2Fe(l) + 3CO2(g), Charge, hoppers, , haematite, , ––––> CaO(s) + CO2 (g), , CaCO3(s), Limestone(flux), , lime, , ∼200 oC, ∼700 oC, Reduction, , Waste, gases, Alternating, layers of iron, ore and coke, , Heat, absorption, zone, , ∼1200 C, o, , Fusion, zone, , ∼2000 oC, , Hot air, , Combustion, zone, , Molten, slag, , Molten iron, , CaO(s) + SiO2(s) ––––> CaSiO3(l), Lime, , silica(gangue), , calcium silicate(slag), , Roasting: Roasting is a pyrochemical process, in which the ore is heated in the presence of, oxygen or air below its melting point. The products, (like metal oxide from sulphide ore) obtained in, the process also are in solid state. Generally, reverberatory furnace is used for roasting., 2ZnS(s) + 3O2(g) ––––> 2ZnO(s) + 2SO2(g), zinc blende, , fig-6: Blast furance, , Ore, Hearth, , fig-7: Reverberatory, furnace, 298, , X Class, , Fire, box, , Principles of Metallurgy
Page 309 :
Calcination: Calcination is a pyrochemical process in which the, ore is heated in the absence of air. The ore gets generally decomposed in, the process., Eg: MgCO3(s), MgO(s) + CO2(g), CaCO3(s), CaO(s) + CO2(g), Flux: Flux is a substance added to the ore to remove the gangue from, it by reacting with the gangue. If the impurity (gangue) is acidic substance, like SiO2, basic substance like CaO is used as flux and if the impurity is of, basic nature like FeO acidic flux like SiO2 is added to the gangue., CaO(s) + SiO2(s), ––––> CaSiO3(l), flux, , silica(gangue), , FeO(s) + SiO2(s), gangue, , calcium silicate(slag), , ––––> FeSiO3(l), , flux, , calcium silicate(slag), , •, •, •, , What is the role of furnace in metallurgy?, How they bear large amounts of heat?, Do all furnaces have same structure?, Let us see:, Furnace: Furnace is the one which is used to carry out pyrochemical, processes in metallurgy. We have mainly three parts in a furnace known, as Hearth, Chimney and fire box., Hearth is the place inside the furnace where the ore is kept for heating, purpose., Chimney is the outlet through which flue (waste) gases go out of the, furnace., Fire box is the part of the furnace where the fuel is kept for burning., In Blast furnace both fire box and hearth are combined in big chamber, which accommodates both ore and fuel. Reverberatory furnace has both, fire box and hearth separated, but the vapours (flame) obtained due to the, burning of the fuel touch the ore in the hearth and heat it., In furnaces like retort furnaces there is no direct contact between the, hearth or fire box and even the flames do not touch the ore., , Key words, Minerals, ores, froth flotation, Thermite process, distillation,, poling, liquation, electrolytic refining, smelting, roasting,, calcinations, blast furnace, reverberatory furnace., Free distribution by A.P. Government, , 299
Page 310 :
What we have learnt, •, •, •, •, •, •, •, •, •, •, •, •, •, •, , A metallic compound occurring in the earth crust along with impurities is called mineral., A mineral from which a metal can be extracted economically and conveniently is called ore., The impurity present in the ore is called gangue.., The substance added to the ore to remove gangue from it is called flux., The extraction of metal from its ore involves mainly three stages: Concentration, Extraction of, crude metal, Refining of the metal., Physical methods adopted in dressing the ore are : hand picking, washing, froth flotation, Magnetic, separation etc., Activity series., The methods used for Extracting of Crude metal are Calcination, Roasting, Chemical reduction,, Auto reduction, Displacement method, Electrolytic reduction ., Calcination is a process of heating the ore strongly in the absence of air or oxygen., During calcinations, carbonate is converted to its oxide., Roasting is a process of heating the ore strongly in a free supply of air or oxygen., Calcination and Roasting are carried out in a reverberatory furnace, Purification methods, Corrosion and prevention of corrosion., , Improve your learning, 1., 2., 3., 4., 5., 6., 7., 8., , List three metals that are found in nature as Oxide ores.(AS1), List three metals that are found in nature in uncombined form. (AS1), Write a note on dressing of ore in metallurgy? (AS1), What is an ore? On what basis a mineral is chosen as an ore? (AS1), Write the names of any two ores of iron? (AS1), How do metals occur in nature? Give examples to any two types of minerals. (AS1), Write short notes on froth floatation process? (AS1), When do we use magnetic separation method for concentration of an ore? Explain with an, example? (AS1), 9. Write short notes on each of the following : (AS1), i)Roasting ii) Calcination iii) Smelting., 10. What is the difference between roasting and calcinations? Give one example for each? (AS1), 11. Define the terms i) gauge ii) slag. (AS1), 12. Magnesium is an active metal if it occurs as a chloride in nature, which method of reduction is, suitable for its extraction? (AS2), 13. Mention two methods which produce very pure metals? (AS2), 14. Which method do you suggest for extraction of high reactivity metals? Why? (AS2), 15. Suggest an experiment to prove that the presence of air and water are essential for corrosion., Explain the procedure. (AS3), 300, , X Class, , Principles of Metallurgy
Page 311 :
16. Collect information about extraction of metals of low reactivity silver, platinum and gold and, prepare a report. (AS4), 17. Draw the diagram showing i) Froth floatation ii) Magnetic separation. (AS5), 18. Draw a neat diagram of Reverboratory furnace and label it neatly? (AS5), 19. What is activity series? How it helps in extraction of metals? (AS6), 20. What is thermite process? Mention its applications in daily life? (AS7), 21. Where do we use handpicking and washing methods in our daily life? Give examples. How do, you correlate these examples with enrichment of ore? (AS7), , ks, Fill in the blan, 1., 2., 3., 4., 5., , The method suitable to enrich the sulphide ores is………………………, Arranging metals in the decreasing order of their reactivity is called ………………, The method suitable for purification of low boiling metals is ……………………, Corrosion of iron occurs in the presence of ………….. and …………….., The chemical process in which the ore is heated in the absence of air is called …, , s, Multiple choice question, 1. The impurity present in the ore is called as _________, a) Gangue, b) flux, c) Slag, 2. Which of the following is a carbonate ore?, a) Magnesite, b) Bauxite, c) Gypsum, 3. Which of the following is the correct formula of Gypsum, a) CuSO4. 2H2O, b) CaSO4. ½ H2O, c) CuSO4. 5H2O, 4. The oil used in the froth floatation process is __________, a) kerosene oil, b) pine oil, c) coconut oil, 5. Froth floatation is method used for the purification of ______ore., a) sulphide, b) oxide, c) carbonate, 6. Galena is an ore of ————————, a) Zn, b) Pb, c) Hg, 7. The metal that occurs in the native form is __________, a) Pb, b) Au, c) Fe, 8. The most abundant metal in the earth’s crust is ——————, a) Silver, b)Aluminium, c) zinc, 9. The reducing agent in thermite process is ___________, a) Al, b) Mg, c) Fe, 10. The purpose of smelting an ore is to __________ it., a) Oxidise, b) Reduce, c) Neutralise, Free distribution by A.P. Government, , [, ], d) Mineral, [, ], d) Galena, [, ], d) CaSO4. 2H2O, [, ], d) olive oil., [, ], d) nitrate, [, ], d) Al, [, ], d) Hg, [, ], d) iron, [, ], d) Si, [, ], d) none of these, 301
Page 312 :
Chapter, , 14, Carbon and its, Compounds, The food you eat, the clothes you wear, the cosmetics you use, the, fuels you use to run automobiles are all the compounds of carbon., Carbon was discovered in prehistory and it was known to the ancients., They used to manufacture charcoal by burning organic material., Carbon is a non-metal. It belongs to the fourteenth group or IV A, group in the modern periodical table. The elements of this group have four, electrons in the valence shell., Let us write the electronic configuration of Carbon (6C)., Atomic number of carbon is 6., Electronic configuration of carbon (ground state) 6C: 1s2 2s2 2p2. To, get the octet in its outer shell it has to gain four more electrons to form, C4-. The electronegativity of carbon is only 2.5 and its nucleus has only, six protons. Therefore it would be difficult for a nucleus with six protons, to hold ten electrons. Hence, carbon cannot form C4- ions so easily., • Can carbon get helium configuration by losing four electrons from, the outer shell?, If carbon loses four electrons from the outer shell, it has to form C4+, ions. This requires huge amount of energy which is not available normally., Therefore C4+ formation also is a remote possibility. Carbon has to satisfy, its tetravalency by sharing electrons with other atoms. It has to form four, covalent bonds either with its own atoms or atoms of other elements., 302, , X Class, , Carbon and its Compounds
Page 313 :
The possibility of bonds formation by a carbon atom is as:, a) i. Four single covalent bonds, with atoms of same element like, hydrogen, Chlorine, Eg: CH4, CCl4, , H, |, H–C–H, |, H, , or, , Cl, |, Cl – C – Cl, |, Cl, , ,, , ii. Four single covalent bonds with atoms of different elements ;, , Eg:, , H, |, H – C – Cl, |, Br, , b) Carbon atoms may form one double bond and two single bonds, H, , Eg:, , H, C, , C, , H, , ;, , H, , H, , H, , O, , C, , C, , H, , H, , c) Carbon atom may form one single bond and a triple bond, Eg: H–C C–H or CH3 –C N or carbon atoms may also, form two double bonds as in CH2 = C = CH2., • How do carbon atoms form bonds in so many different ways as, mentioned above?, • Explain the four unpaired electrons in carbon atom through excited, state., As per valence bond theory (see chapter, chemical bonding), the four, unpaired electrons in a carbon atom are shown by suggesting excited state, to carbon atom., Electronic configuration of carbon (ground state):, 1s2 2s2 2p2 (or) 1s2 2s2 2px1 2py12pz0, , 1s, , 2s, , 2p, , Carbon (ground state), , Electronic configuration of carbon (excited state):, 1s2 2s1 2px1 2py1 2pz1, 1s, , 2s, , 2p, , Carbon (excited state), Free distribution by A.P. Government, , 303
Page 314 :
Linus Pauling - The world’s, one of the greatest scientists, and a great humanist. He was, acknowledged as the most, influential chemist., He is the only person ever, to receive two unshared Nobel, Prizes — for Chemistry, (1954) and for Peace (1962)., , •, , In excited state carbon atom gets its, one of the ‘2s’ electrons to say 2pz., Each carbon atom has four unpaired, electrons when excited and tends to form, four covalent bonds., • Where this energy to excite electron, comes from?, We have to understand that free, carbon atom would not be in excited state, under normal conditions. When the, carbon atom is ready to form bonds with, other atoms, the energy required for, excitation is taken up from bond, energies, which are the liberated energies, when bonds are formed between carbon, atom and other atoms., • In methane (CH4) molecule all four, carbon – hydrogen bonds are, ∧, identical and bond angle HC H is, 109o28/. How can we explain this?, In the above discussion, we have, found that in excited state, carbon atom, has three unpaired electrons in p-orbitals, and one electron in s-orbital. These four, valence electrons are with different, energies., , How these energetically unequal valence electrons form four equivalent, covalent bonds in methane molecule?, Let us see how?, , Promotion of an electron, When bonds are formed, energy is released and the system becomes more, stable. If carbon forms four bonds rather than two, still more energy is, released and so the resulting molecule becomes even more stable., , 304, , X Class, , Carbon and its Compounds
Page 315 :
Energy, , Energy, , The energy difference between the 2s, Promotion, and 2p orbitals is very small. When carbon, atom is ready to form bonds it gets a small, amount of energy from bond energies and, gets excited to promote an electron from, 2px, 2py, 2pz, the 2s to the empty 2p to give four unpaired, 2s, electrons., We have got four unpaired electrons, From ground state to, excited state, ready for bonding, but these electrons are, in two different kinds of orbitals and their, energies are different. We are not going to, 2px, 2py, 2pz, get four identical bonds unless these, 2s, unpaired electrons are in four identical, orbitals., How to explain the four orbitals of, carbon containing unpaired electrons as energetically equal?, We can explain it by the phenomenon called hybridisation., , Do you know?, The concept of hybridisation was introduced by Linus Pauling (1931). The, redistribution of orbitals of almost equal energy in individual atoms to give equal, number of new orbitals with identical properties like energy and shape is called, “hybridisation”. The newly formed orbitals are called as ‘hybrid orbitals.’, , Hybridisation, , Energy, , In the excited carbon atom its one s-orbital (2s) and three p-orbitals, (2px, 2py, 2pz) intermix and reshuffle into four identical orbitals known as, sp3 orbitals. Thus, carbon atom undergoes sp3 hybridisation., The four electrons enter into the new four identical hybrid orbitals, known as sp3 hybrid orbitals one each as per Hund’s rule. (because they, are made from one ‘s-orbital’ and three ‘p-orbitals’ they are called sp3, orbitals)., NOTE: Read “ sp3 “ as “ s p three”. or “yes pee three”, , 2s, , 2px, , 2py, , Free distribution by A.P. Government, , 2pz, , sp3 hybrids, 305
Page 316 :
The hybridisation enables the carbon to have four identical sp3 hybrid, orbitals and these have one electron each. Since carbon has four unpaired, electrons, it is capable of forming bonds with four other atoms may be, carbon or atoms of some other monovalent element. When carbon reacts, with hydrogen, four hydrogen atoms allow their ‘s’ orbitals containing one, electron each to overlap the four sp3orbitals of carbon atom which are, orieted at an angle of 109o28/ . (Four orbitals of an atom in the outer shell, orient along the four corners of a tetrahedron to have minimum repulsion, between their electrons). The nucleus of the atom is at the centre of the, tetrahedron. See figures below:, , overlap, , overlap, This leads to form four sp3 – s sigma bonds between carbon atom and, four hydrogen atoms. All these bonds are of equal energy., , sp2 hybridisation, , Energy, , How do you explain the ability of C – atom to form two single covalent, bonds and one double bond?, Consider ethene (ethylene, CH2 = CH2) molecule as the example., , 2px, , 2s, , 2py, , 2pz, , sp2 hybrids, , 2pz, , In the formation of CH2=CH2 each carbon atom in its excited state, undergoes sp2 hybridisation by intermixing one s-orbital (2s) and two, p-orbitals (say 2px, 2py) and reshuffling to form three sp2 orbitals. Now, each carbon atom is left with one ‘p’ orbital (say pz) unhybridised. The, three sp2 orbitals having one electron each get separated around the nucleus, of carbon atoms at an angle of 120o. When carbon is ready to form bonds, one sp2 orbital of one carbon atom overlaps the sp2 orbital of the other, 306, , X Class, , Carbon and its Compounds
Page 317 :
carbon atom to form sp2 – sp2 sigma (σ) bond. The remaining two sp2, orbitals of each carbon atom get overlapped by‘s’ orbitals of two hydrogen, atoms containing unpaired electrons. The unhybridised pz orbitals on the, two carbon atoms overlap laterally as shown in figure to form a π bond., That means there exists a sigma (σ) bond and a pi (π) bond between two, carbon atoms in ethene molecule. Hence, the molecule ethene (C2H4) is, H, , H, C, , C, H, , H, , σsp2-s, , σsp2-s, , σsp2-sp2, , figure of, C 2H 4, πp z-p z, σsp2-s, , σsp2-s, , The common name for Ethene is Ethylene., , sp hybridisation, Each carbon is only joining to two other atoms rather than four (as in, methane or ethane) or three (as in ethene). Here the carbon atoms hybridise, their outer orbitals before forming bonds, this time they only hybridise, two of the orbitals., They use the ‘s’ orbital (2s) and one of the 2p orbitals, but leave the, other 2p orbitals unchanged. The new hybrid orbitals formed are called sp, hybrid orbitals, because they are made by an s-orbital and a p-orbital, reorganizing themselves., How do you explain the ability of carbon atom to form one single, bond and one triple bond?, To know the ability of ‘C’ to form one single bond and one triple bond,, let us consider ethyne (acetylene, C2H2) molecule as our example., In acetylene molecule there exists a triple bond between two carbon, atoms and the fourth valency of each carbon atom is satisfied by hydrogen, atoms (H–C C–H )., Free distribution by A.P. Government, , 307
Page 318 :
πp y-p y, σsp-sp, , Η, , Η, σs-sp, , πp z-p z, , σs-sp, , figure of C2H2, , Energy, , In C2H2 molecule there are two carbon atoms and two hydrogen atoms., In excited state each carbon atom undergoes sp- hybridisation by mixing, its one ‘s’ orbital (2s) and one ‘p’ orbital (2px) and reshuffling to form two, identical orbitals known as sp-orbitals. Each carbon atom has two, unhybridised p-orbitals (say 2py, 2pz)., , 2px, , 2s, , 2py, , 2pz, , 2py, , sp hybrids, , 2pz, , One sp-orbital of a carbon overlaps the sp-orbital of other carbon to, give sp-sp sigma bond. The other sp-orbital of each carbon atom overlaps, ‘ s ’ orbital of a hydrogen atom to form a s-sp sigma bond. The unhybridised, ‘p’ orbitals of one carbon atom laterally overlap the unhybridised ‘p’ orbitals, of other carbon atom to give two π bonds between two carbon atoms, (say πpy-py, πpz-pz , see figure). Thus ethyne molecule H–C C–H and, there exists three σ-bonds and two π-bonds in the molecule., • Predict the bond distance between the nuclei of carbon atoms that, form bonds and bond energies order of H–C =_ C–H ,, H, , •, , H, , H, , C, , C, , H, , H, , H, H, , H, , H, C, , C, , and, , H, , Explain it., ∧, , What are bond angles HCH in CH4, C2H4 and C2H2 molecules?, , Allotropes of Carbon, The property of an element to exist in two or more physical forms, having more or less similar chemical properties but different physical, properties is called allotropy. The different forms of the element are called, allotropes. Allotropes form due to the difference in the arrangement of, atoms in the molecules., 308, , X Class, , Carbon and its Compounds
Page 319 :
The allotropes of carbon are classified into two types. They are, • Amorphous forms, • Crystalline forms, , Amorphous forms, Different amorphous allotropes of carbon are: Coal; Coke; Wood, Charcoal; Animal charcoal; Lamp black; Gas carbon; Petroleum coke; Sugar, charcoal., , Crystalline forms, Carbon atoms can arrange themselves into different hybridised, chemical bonds. Therefore they exhibit different physical and chemical, structures such as diamond and graphite. Carbon in solid phase can exist, in three crystalline allotropic forms: diamond, graphite and, buckminsterfullerene., Diamond and graphite form covalent network structures whereas, buckminster fullerene has a molecular solid structure with discrete C60, molecules. As these crystalline allotropes differ in their structures, they, possess different physical properties., , Diamond, In diamond each carbon atom undergoes in its excited state sp3, hybridisation. Hence, each carbon atom has a tetrahedral environment. The, three dimensional structure of diamond is as shown:, , Lattice structure of diamond, , Diamond structure, , As C-C bonds are very strong any attempt to distort the diamond, structure requires large amount of energy. Hence diamond is one of the, hardest materials known., , Graphite, Graphite forms a two dimensional layer structure with C-C bonds within, the layers. There are relatively weak interactions between the layers., Free distribution by A.P. Government, , 309
Page 320 :
The arrangement of carbon atoms in graphite layers, , In the layer structure, the carbon atoms are in a trigonalplanar, environment. This is consistent with each carbon atom in sp2 hybridisation., Interactions between the sp2 orbitals (overlaps) lead to the formation of, C-C bonds. Each carbon atom is with one unhybridised ‘p’ orbital. The, unhybridised ‘p’ orbitals interact to form a π system which is delocalised, over the whole layer. The interactions known as London dispersion forces, o, between the layers which are separated by a distance of 3.35 A are weakened, by the presence of water molecules so that it is easy to cleave graphite., For this reason graphite is used as lubricant and as the ‘lead’ in pencils., • How do you understand the markings (writings) of a pencil on a paper?, When we write with a pencil, the interlayer attractions breakdown and, leave graphite layers on the paper. Pencil marks are easy to remove from, paper with an eraser because, the layers do not bind strongly to the paper., Graphite is a good conductor of electricity because of the delocalised, π electron system., , Buckminsterfullerene (60C), Buckminsterfullerenes are molecules of varying sizes that are, composed entirely of carbon. The arrangement of these molecules leads, to the form of a hollow sphere, ellipsoid, or tube depending upon their, orientations. Fullerenes are formed when vaporized carbon condenses in, an atmosphere of an inert gas., , Do you know?, The buckminsterfullerene, or usually just fullerene for short, was discovered, in 1985 by a team of scientists, Robert F. Curl, Harold W. Kroto and Richard E., Smalley from Rice University and the University of Sussex, three of whom were, awarded the 1996 Nobel Prize in Chemistry. They are named so for the resemblance, of their structure to the geodesic structures devised by the scientist and architect, Richard Buckminster “Bucky” Fuller., 310, , X Class, , Carbon and its Compounds
Page 321 :
Buckyballs: Spherical fullerenes are also called buckyballs., Buckminsterfullerene (60C) contains nearly spherical 60C molecules, with the shape of a soccer ball., , Buckminsterfullerene (60C), , 3D structure of Buckminsterfullerene (60C), , Fullerene, 60C molecule contains 12 pentagonal and 20 hexagonal, faces on its soccer ball shape, and each carbon atom has sp2 hybridized, orbitals., Fullerenes are under study for potential medicinal use - such as specific, antibiotics to target resistant bacteria and even target certain cancer cells, such as melanoma., , Nanotubes, Nanotubes are another allotropic, form of carbon discovered in 1991by, Sumio li jima. Nano tubes consist of, hexagonal arrays of covalently bonded, carbon atoms, similar to the sheets in, graphite. Unlike the flat graphite sheets,, in nanotubes the sheets are rolled into, cylinders. Due to this reason they are, called nanotubes. Nanotubes like, graphite, are electrical conductors and can, be used as molecular wires. In integrated, circuits nanotubes are used instead of, copper to connect the components, together., Scientists, inserted, biomolecules into nanotubes to inject, them into a single cell., Free distribution by A.P. Government, , Single-walled carbon, nanotube or Buckytube, 311
Page 322 :
Do you know?, Graphene - The new wonder material:, , 3D illustration showing a sheet of, graphene, , A piece of graphene aerogel - weighing, only 0.16 milligrams per cubic, centimeter - is placed on a flower., , As its name indicates, graphene is extracted from graphite, the material used, in pencils. Like graphite, graphene is entirely composed of carbon atoms. For a, thickness of 1mm graphite contains some 3 million layers of graphene. The, carbons are perfectly distributed in a hexagonal honeycomb formation only in, 0.3 nanometers thickness., Graphene conducts electricity better than copper. It is 200 times stronger, than steel but six times lighter. It is almost perfectly transparent to light., , Versatile nature of carbon, By the eighteenth century scientists tried to explain the difference, between the compounds in a broader way., J. J. Berzelius (1807) named the compounds that derived from living, organism as organic compounds and those from non-living materials as, inorganic compounds. He thought that organic compounds would be, prepared in the living bodies through vital force, the essence of life. As, this force is absent outside the living bodies, it was thought that the so, called organic compounds could not be synthesized in the laboratories., Surprisingly F. Wohler (1828) produced an organic compound Urea, in the laboratory by heating an inorganic salt ammonium cyanate., , O, NH4CNO, Ammonium, cyanate, 312, , X Class, , H, heat, , H, , C, N, , N, Urea, , H, H, , Carbon and its Compounds
Page 323 :
Wöhler Friedrich (1800 – 1882), German chemist who was a student of Berzelius. In, attempting to prepare ammonium cyanate from silver cyanide, and ammonium chloride, he accidentally synthesized urea in, 1828. This was the first organic synthesis, and shattered, the vitalism theory., Wöhler pursued the matter further and discovered that urea, and ammonium cyanate had the same chemical formula, but, very different chemical properties. This was an early discovery of isomerism, since, urea has the formula CO(NH2)2 and ammonium cyanate has the formula NH4CNO., It inspired many other chemists and they were successful to prepare, the so called organic compounds, methane, acetic acid etc., in the, laboratory. This gave a death blow to the idea that organic compounds are, derived from living organism. Chemists thought about a new definition, for organic compounds. After observing the structures and elements of, organic compounds, they defined organic compounds as compounds of, carbon. Therefore, organic chemistry is totally allotted to carbon, compounds., • Allotting completely one special branch in chemistry to compounds, of only one element. Is it justified when there are so many elements, and their compounds but not with any special branches?, We understand that all molecules that make life possible –, carbohydrates, proteins, nucleic acids, lipids, hormones, and vitamins, contain carbon. The chemical reactions that take place in living systems, are of carbon compounds. Food that we get from nature, various medicines,, cotton, silk and fuels like natural gas and petroleum almost all of them are, carbon compounds. Synthetic fabrics, plastics, synthetic rubber are also, compounds of carbon. Hence, carbon is a special element with the largest, number of compounds., , Catenation, Another peculiar behaviour of carbon is its ability to form longest, chains with its own atoms. If any element forms bonds between its own, atoms to give big molecules we call that property as catenation property., Carbon has the ability to form longest chains containing millions of carbon, atoms in molecules like some proteins. Sulphur, phosphorus and some, other non metals have this property but to a very less extent., Free distribution by A.P. Government, , 313
Page 324 :
You have understood that carbon can form:, , H, a) Four single covalent bonds ,, , H, , C, , H, , H, b) A double bond and two single covalent bond s ( C C ), c) A single covalent bond and a triple bond (–C C), or two double, bonds (C = C = C) with its own atoms or atoms of other elements – to, satisfy its tetravalency., This ability of carbon to form bonds in so many ways made it as, versatile element in nature. Hence, carbon’s ability 1) to form largest, number of compounds 2) to show catenation 3) to form various types of, bonds made it the versatile element., , Hydrocarbons, •, , What are hydrocarbons?, The compounds containing only carbon and hydrogen in their molecules, are called hydrocarbons., Hydrocarbons are classified into two categories known as open chain, hydrocarbons and closed chain hydrocarbons. Open chain hydrocarbons, are also called aliphatic hydrocarbons or acyclic hydrocarbons., , Open and closed chain hydrocarbons, Let us observe the following structural formulae of different, hydrocarbons., 1) CH3–CH2–CH2–CH2–CH3 n-pentane, a straight chain compound, 2) CH3–CH–CH2–CH3. Iso pentane, a branched chain compound, |, CH3, 3) CH2 – CH2 cyclo pentane, a cyclic compound or a ring compound, |, |, CH2 CH2, \, /, CH2, • Do all the above compounds have equal number of C and H atoms?, In the first example you will notice that all carbons are linked to one, another resulting a linear structure, where as in the second example four, carbons are linked in linear way and the fifth carbon is linked to the parent, chain resulting a branch. In the third example we find that carbon chain is, closed to form a ring. So, it is a closed chain hydrocarbon or ring, hydrocarbon., 314, , X Class, , Carbon and its Compounds
Page 326 :
Binding of carbon with other elements, We have understood that the compounds of carbon and hydrogen are, called hydrocarbons., • Can carbon form bonds with the atoms of other elements?, Practical observations reveal that carbon forms compounds not only, with atoms of hydrogen but also with atoms of other elements like oxygen,, nitrogen, sulphur, phosphorus, halogens etc., Let us see the compounds of carbon with other elements., , Carbon compounds with C, H, X., •, , Compounds containing C, H, X where ‘X’ represents halogens (Cl, Br,, I atoms)., Eg: CH3Cl, CH3– CH2–Br, CH2Cl – CH2I, CH3 – CHCl2, These are known as halogen derivatives of hydrocarbons or halo, hydrocarbons., , Carbon compounds with C, H, O., •, , Compounds containing C, H, O are of different types:, , Alcohols, If a hydrogen atom of H2O molecule is replaced by ‘R’ we get alcohols, R-OH., The hydrocarbons that contain –OH group are called alcohols. Observe, the following examples:, CH3OH, CH3CH2OH, CH3-CHOH-CH3 etc., General formula of alcohols is R – OH where ‘R’ is alkyl group, CnH2n+1., , Aldehydes, , The hydrocarbons with functional group –CHO are called aldehydes., Observe the following examples:, H – C = O, CH3 – C = O, CH3 – CH2 - C = O etc., |, |, |, H, H, H, Formaldehyde, , Acetaldehyde, , Propionaldehyde, , General formula of aldehydes is R – CHO, where R = alkyl group or, hydrogen and -CHO is functional group., , Ketones, , The hydrocarbons with C C O functional group are called ketones., C, O, O, ||, ||, CH3 – C – CH3, CH3 – CH2 – C – CH3 etc., Di methyl ketone, , C, C, 316, , X Class, , ethyl methyl ketone, , C O group is known as Ketone group(common system), Carbon and its Compounds
Page 327 :
General formula of Ketones is R/ C O, R, R and R1 are alkyl groups which may be same or different., , Carboxylic acids, The general molecular formula of carboxylic acid is R – COOH,, where R is an alkyl group or H atom., H – C = O,, CH3 – C = O, CH3 – CH2– C = O,, |, |, |, OH, OH, OH, Formic acid, , Acetic acid, , Propionic acid, , – C = O group is called the carboxyl group., |, OH, , Ethers, Ethers are carbon compounds related to H2O in such a way that both, hydrogen atoms are replaced by two alkyl groups which may be same or, different., Eg: CH3 – O – CH3 , CH3 – CH2 – O – CH3, CH2 = CH – O – CH3 etc., Di methyl ether, , ethyl methyl ether, , methyl vinyl ether, , Esters, These compounds are derivatives of carboxylic acids. If the hydrogen, atom of - COOH gets replaced by ‘R’, the alkyl group esters are obtained., O, O, O, ||, ||, ||, CH3 - C - OCH3, CH3 - CH2 – C - OCH3 , CH3 - CH2 – C – OCH2CH3 etc., Di methyl ester, , ethyl methyl ester, , Di ethyl ester, , Compounds containing C, H, N, Amines, , NH2, , |, Eg: CH3–NH2, CH3–CH–NH2, CH3CH2NH2, CH3–CH2–C–CH3 etc., |, |, CH3, CH3, - NH2 group is called amine group. We may compare amines to NH3, as we have done ROH and R – O – R/ to H2O., If one hydrogen atom is replaced from NH3 by an alkyl group we get, the so called primary amines. If two hydrogen atoms of NH3 are replaced, by two alkyl groups (same or different) we get secondary amines and if, all the three hydrogen atoms are replaced by the same or different alkyl, groups we get tertiary amines., Free distribution by A.P. Government, , 317
Page 328 :
Eg:, , CH3 NH, , CH3 N, , H3C, , H3C, , (secondary amine), N-methyl methanamine, , CH3, , (Tertiary amine), N,N-di methyl methanamine, , Functional groups in carbon compounds, The characteristic properties of an organic compound depend mainly, on an atom or group of atoms in its molecule known as the functional, group., Organic compounds are classified by the type of functional group they, contain. Functional groups are responsible for the behavior of the organic, compounds. Compounds containing the same functional group undergo, similar types of reactions., , Isomerism, Observe the following two structures:, (a) CH3–CH2–CH2–CH3, (b) CH3–CH–CH3, |, CH3, • How about their structures? Are they same?, • How many carbon and hydrogen atoms are there in (a) and (b) structures?, • Write the condensed molecular formulae for (a) and (b).Do they have, same molecular formulae?, (Take the help of your teacher and name the compounds mentioned in, the above examples)., The first one is called butane (or) in the common system it is known, as n-butane., The second one is called 2-methyl propane or iso-butane in the, common system., We find both of these compounds in nature. They have different, properties due to the difference in their structures. Compounds of this, type which have the same molecular formula but different properties are, called isomers., The phenomenon of possessing same molecular formula but different, properties by the compounds is known as isomerism. The compounds that, exhibit isomerism are called isomers., (iso = same; meros = part, i.e., they have same molecular formula), In the above example isomerism is due to the difference in the, structures. Therefore, it is called the structural isomerism., Try to draw different structures for the following carbon compounds, and name the isomers of each (Take the help of your teacher), (a) C5H12 (b) C6H14, 318, , X Class, , Carbon and its Compounds
Page 329 :
Homologous series, Till now we have classified Organic compounds on the basis of carbon, chains and functional groups. There is another classification based on, Homologous series., The series of carbon compounds in which two successive compounds, differ by –CH2 unit is called homologous series., Eg:, 1) CH4, C2H6, C3H8 …, 2) CH3OH, C2H5OH, C3H7OH …, If you observe above series of compounds, you will notice that each, compound in the series differs by –CH2 unit by its successive compound., Homologous series of organic compounds have following, characteristic features., 1) They have one general formula., Eg: alkanes (CnH2n+2); alkynes(CnH2n-2); alcohols (CnH2n+1)OH etc., 2) Successive compounds in the series possess a difference of (-CH2), unit., 3) They possess similar chemical properties due to the same functional, group, Eg: alcohols, aldehydes and carboxylic acids have functional groups, C–OH, C–CHO and C-COOH respectively., 4) They show a regular gradation in their physical properties (see the, table-1)., For example: we may take alkanes, alkenes, alkynes, alcohols,, aldehydes, and carboxylic acids etc. as homologous series. The individual, members of a homologous series are called homologs., Observe the following tables 1, 2 and 3. They represent three different, homologous series., Table-1: Homologous series of Alkanes, Alkane Molecular Structure, formula, Methane, Ethane, Propane, Butane, Pentane, , CH4, C2H6, C3H8, C4H10, C5H12, , H-CH2-H, H-(CH2)2-H, H-(CH2)3-H, H-(CH2)4-H, H-(CH2)5-H, , No. of, Boiling Melting, carbons Point ( C) Point ( C), o, , 1, 2, 3, 4, 5, , –164, –89, –42, 0, 36, , o, , –183, –183, –189, –138, –136, , Density, (gml, , -1, , at20 o C), , 0.55, 0.51, 0.50, 0.58, 0.63, , The general formula of this homologous series Alkanes is CnH2n+2, where, n = 1,2,3..., Free distribution by A.P. Government, , 319
Page 330 :
Table-2:Homologous series of Alkenes, Alkane, , No. of Carbons, , Ethene, Propene, Butene, Pentene, , 2, 3, 4, 5, , Structure, , Formula, , CH2 =CH2, CH3-CH=CH2, CH3-CH2-CH=CH2, CH3-CH2-CH2-CH=CH2, , C2H4, C3H6, C4H8, C5H10, , Alkenes have general molecular formula CnH2n, where ‘n’ is 2, 3, 4, …, Table-3: Homologous series of Alkynes, Alkane, , No. of Carbons, , Ethyne, Propyne, Butyne, Pentyne, , 2, 3, 4, 5, , Structure, , Formula, , _ CH, HC =, _ CH, CH3- C =, _ CH, CH3-H2C-C =, _CH, CH3-CH2-CH2-C =, , C2H2, C3H4, C4H6, C5H8, , Alkynes have general molecular formula CnH2n-2, where ‘n’ is 2, 3, 4, …, , Nomenclature of organic compounds, , We have millions of organic compounds. As number of organic, compound is very big it is difficult to remember their names individually., To overcome this problem they have to be properly named. For this, the, International Union of Pure and Applied Chemistry (IUPAC) had been, formed, and one of its responsibilities is to name the organic and inorganic, compounds in a systematic order. The basic idea behind the systematic, nomenclature is that there should be only one name for the given structure, throughout the world and also there should be only one structure for the, given name., The IUPAC name of an organic compound gives information about:, a) The number of carbon atoms present in the molecules we call this part, of the name as word root., C3 - prop;, C4 - but ; C5-pent; C6 - hex;, C1 - Meth; C2 - eth;, C8-oct;, C9-non;, C10 - dec and so on., C7 - hept;, b) The substituents in the molecule ; which are shown as the prefix, c) The functional group in the molecule; which is shown as the suffix., Prefix: Prefix again has several parts known as primary prefix, secondary prefix, numerical prefix and number prefix etc., Primary prefix is ‘cyclo’ and it is useful only for cyclic compounds, which have properties similar to aliphatic compounds. If the compounds, are not cyclic, this part of the name is absent., 320, , X Class, , Carbon and its Compounds
Page 331 :
Secondary prefix tells about the second grade functional groups known, as substituents. They are ‘halogens’ which are written as halo; alkyl, groups(R), alkoxy groups(-OR) etc. which are written as alkyl, alkoxy., Suffix: It also contains several parts known as primary suffix,, secondary suffix, numerical suffix and number suffix etc., Primary suffix tells about the saturation of the compound. For, saturated (C-C) it is ‘an’ and carbon atoms are attached to one another, only through single bonds in the compounds., For unsaturated (C=C) double bonded compounds it is ‘en’ and for, unsaturated triple bonded (C C ) compounds it is ‘yn’., There is a Secondary suffix that tells about the functional groups with, the particular term., For example:, For hydrocarbons it is ‘e’, for Alcohols it is ‘ –ol ’, Aldehydes it is ‘ –al ‘, Ketones it is ‘ –one ‘ and, Carboxylic acid it is ‘ –oic acid’, Numerical prefixes like di, tri are written before the secondary, prefixes, primary suffixes and secondary suffixes, when the same, substituent, multiple bond or functional group is repeated twice, thrice, etc., as di, tri etc respectively., Numbers are written to tell about to which carbon atoms of the, compound the substituent(s), multiple bond(s) or functional group(s) are, attached., The following order is to be followed while naming carbon compound., The order is as follows:, Numbers - Numerical Prefixes – Secondary Prefix – Primary Prefix - Word Root – Numbers, 1, 2, 3, 4, 5, 6, -Numerical Prefix, Primary Suffix, numbers, numerical Prefixes and Secondary Suffixes., 7, 8, 9, 10, 11, , What differences among (1), (2), (3); (6), (7), (8) and (9), (10) and, (11) do you find?, (1), (2) are numbers and numerical designations to be written for, secondary prefixes(3) which tell about the position and repetitions of, second grade functional groups known as substituents respectively., 1, , 2, , 3, , 4, , Eg: CH3–CH–CH–CH3, |, |, Cl Cl, Free distribution by A.P. Government, , 2, 3 – di chloro but, (1), , (2), , (3), , (5), , an, , e, , (8), , (11), , 321
Page 332 :
(6) and (7) tell about the positions and repetitions of the multiple, bonds in the structures of the molecule of the compound. These are related, to the primary suffix (8) that tells about the unsaturation., 5, , 4, , 3, , 2, , 1, , Eg: CH3-C=CH-CH CH, , but – 3 – ene – 1 – yn –, (5), , (6), , (8), , (9), , (8), , e, (11), , (9) and (10) tell about the positions and repetitions of the functional, group or principal functional group (11) in a poly functional compound. It, gives the information which carbon represents it or to which carbon that, functional group is attached and how many times it is repeated. If it comes, only once we need not write mono i.e., if no numerical prefix is present it, is understood that the functional group is not repeated. Similarly, in the, names of aliphatic compounds word root (5), primary suffix (8) and, secondary suffix (11) are definitely present and all others may or may, not be present., but ane – 1,2 – di ol, CH3-CH2-CH-CH2-OH, |, (5), (8), (9), (10) (11), OH, Punctuation: Numbers are separated by comma (,) and numbers &, designations by hyphen(-), If you find more than one substituent in the structure you have to follow, alphabetical order while naming them. For this numerical prefixes should, not be considered. Substituents: X (halo), R (alkyl), -OR (alkoxy),, -NO2 (nitro), NO (nitroso) etc., If you find more than one functional group in the structure you select, the principal functional group and write it as secondary suffix. All other, functional groups become substituents., A decreasing order of priority for choosing and naming a principal, characteristic group. This should be written as secondary suffix., Eg:, , -COOH > (CH3CO)2O > -COOR > -COX > - CONH2 > -CN > -CHO >, Acid, , anhydride, , ester, , acid halide, , amide, , nitrile, , aldehydes, , >C=O >, ketones, , R-OH > -NH2, alcohols, , amines, , Activity 1, Observe the names of the following compounds. Give reasons in the, space provided., Divide the given name as per the notations given above and identify the, parts in the name through the numbers given above from (1) to (11) and, write them in your note book., (Take the help of your teacher), 322, , X Class, , Carbon and its Compounds
Page 336 :
Cl, 8, , 7, , 6, , 5, , |, , 4, , 3, , 2, , 1, , Example-5: CH2 = C = CH – CH –CH2 – CH2 – CH – CH2, |, |, |, Cl, OH OH, 5,6 – di chloro – octa – 6,7 – di en – 1,2 – di ol, –––, ––, –––––, ––––, –––, ––, ––, –––, –––, –––, (1), (2), (3), (5), (6), (7), (8), (9), (10), (11), Example-6:, OH, CH3, , 1, 6, 5, , 2, , 2,3 – di methyl – cyclo, –––, –– –––––, ––––, (1), (2), (3), (4), , hex an – 1 – ol, –––, ––, ––, –––, (5), (8), (9), (11), , 3, 4, , CH3, , •, , Can we write the structure of a compound if the name of the compound, is given?, Yes, we can write the structures from the name of the compound as, follows:, 1) From the word root in the name write the carbon atoms in the main, chain, 2) Select counting of carbon atoms in the appropriate manner from left, to right or right to left as for the name given., 3) Attach the substituent at respective numbers of carbon atoms as per, their numbers and numerical designations., 4) Write the functional groups formulae as per the name at the respective, carbon atom., 5) Keeping in view that the tetravalency of each carbon atom has to be, satisfied use hydrogen atoms in the required number., Examples:, 1) 2–methyl pentan–3–ol, 2) 2–bromo–3–ethyl penta–1,4–diene, 3) 3–bromo–2–chloro–5–oxohexanoic acid, 4) 3–amino–2–bromo hexan–1–ol, 5) 3, 4–dichloro but–1–ene, OH, CH, |, |, 1, 5, 3, 4, 2, Solution : 1. CH3 - CH2 - CH2 - CH2 - CH3 ; CH3 - CH2 - CH2 - CH2 - CH3, H, 2. H2C = C - C - C = CH2, 3, , Br CH2 H, CH3, 326, , X Class, , Carbon and its Compounds
Page 337 :
Chemical properties of carbon compounds, Though we have millions of organic compounds, the reactions they, undergo are limited. Some important reactions among them are discussed, here., They are:, 1) Combustion, 2) Oxidation reactions, 3) Addition reactions, 4) Substitution reactions, , 1. Combustion reactions, Carbon, and its compounds burn in presence of oxygen or air to give, CO2, heat and light., The process of burning of carbon or carbon compound in excess of, oxygen to give heat and light is called the combustion reaction. In the, reactions carbon is in its maximum oxidation state of 4+ in the product., Eg: 1) C + O2 CO2 + Energy, 2) 2C2H6 + 7O2, 4CO2 + 6H2O + Energy, 3) CH3CH2OH + 3O2, CO2 + 3H2O + Energy, Generally, saturated hydrocarbons burn with a clear light blue flame,, whereas unsaturated hydrocarbons burn with yellow flame with soot, (carbon). If air is not sufficiently available during combustion, even, saturated hydrocarbons give sooty flame. When Coal, Petroleum etc., burn, in air they give oxides of sulphur and nitrogen in addition to CO2 and H2O, which pollute the environment. When Coal or Charcoal is burnt sometimes, they just glow red without flame. This is because to get a flame gaseous, fuels should burn., Most of the aromatic compounds burn with sooty flame., • Why do sometimes cooking vessels get blackened on a gas or kerosene, stove?, Because of the inlets of air getting closed, the fuel gases donot, completely undergo combustion. Hence, it forms a sooty carbon form, which gets coated over the vessels., A combustion reaction is generally defined as any reaction that sustains, a flame. It usually involves burning with oxygen, though some exceptions, are there, combustion reaction is always exothermic, that is energy is, liberated during combustion reaction., , 2. Oxidation reactions, Though combustion is generally oxidation reaction, all oxidation, reactions are not combustion reactions. Oxidation reactions may be carried, out using oxidizing agents. Oxidizing agents or Oxidants are substances, that oxidize other substances. They themselves undergo reduction., Free distribution by A.P. Government, , 327
Page 338 :
Eg: Alkaline Potassium permanganate or Acidified Potassium, dichromate in solutions act as oxidizing agents and supplies oxygen to, convert alcohols into carboxylic acids., Ethyl alcohol undergoes oxidation to form the product Acetaldehyde, and finally Acetic acid.(see following equation), , CH3CH2OH, Ethanol, (Ethyl alcohol), , alkaline KMnO4+Heat, acidified K2Cr2O7+Heat, , CH3CHO, , CH3COOH, , Ethanal, (Acetadehyde), , Ethanoic acid, (Acetic Acid), , 3. Addition reactions, Unsaturated organic compounds that contain multiple bonds, (=, bonds) like alkenes and alkynes undergo addition reactions to become, saturated. During the reactions addition of the reagent takes place at the, double bonded or triple bonded carbon atoms., , CH3C =_ C–CH3, But–2-yne, , Ni catalyst, H2, , CH3CH=CH–CH3, But–2-ene, , Ni catalyst, H2, , CH3–CH2–CH2–CH3, Butane, , In the above reactions ‘Ni’ acts as ‘catalyst.’, • Do you know what is a ’catalyst’?, A catalyst is a substance which regulates (increase/decrease) the rate, of a given reaction without itself finally undergoing any chemical change., These reactions are commonly used in the hydrogenation of vegetable, oils using nickel as catalyst. Vegetable oils generally have long unsaturated, carbon chains, while animal fats have saturated carbon chains., , Think and discuss, •, •, , Why we are advised not to use animal fats for cooking?, Which oil is recommended for cooking? Why?, , Fats and oils are both of fatty acids. Oils are generally liquids at room, temperature due to unsaturated fatty acids but fats are solids due to saturated, fatty acids., , 4. Substitution reactions, A reaction in which an atom or a group of atoms in a given compound, is replaced by other atom or group of atoms is called a substitution reaction., Alkanes, the saturated hydrocarbons are chemically least reactive., Therefore they are also called paraffins (parum = little; affins = affinity,, 328, , X Class, , Carbon and its Compounds
Page 339 :
i.e., no affinity towards chemical changes). However they undergo some, chemical changes under suitable conditions which are substitution, reactions., For example, methane (CH4) reacts with chlorine in the presence of, sunlight. Hydrogen atoms of CH4 are replaced by chlorine atoms., CH4, + Cl2 sunlight, CH3Cl, + HCl, Methane, , CH3Cl, , Methyl Chloride, , + Cl2, , sunlight, , Methyl Chloride, , CH2Cl2, , +, , HCl, , Methylene Chloride, , + Cl2, , sunlight, , Methylene Chloride, , CHCl3, , CH2Cl2, , Hydrogen Chloride, , CHCl3, , Hydrogen Chloride, , + HCl, , Chloroform, , sunlight, , + Cl2, , Chloroform, , CCl4, , Hydrogen Chloride, , + HCl, , Carbon, Tetrachloride, , Hydrogen Chloride, , Some important carbon compounds, Many carbon compounds are invaluable to us. But here we study, the, properties of Ethanol (Ethyl alcohol) and Ethanoic acid (Acetic acid), which are two very important carbon compounds., , Ethanol (Ethyl alcohol), Preparation: Ethanol is prepared on large scale from ethene by the, addition of water vapour to it in the presence of catalysts like P2O5 ,, Tungsten oxide at high pressure and temperature., CH2 = CH2 + H2O, ethene, , catalyst, 100-300 atm, At 300 oC, , CH3CH2OH, ethyl alcohol, , Grains such as corn, wheat, barley are common sources for ethanol., Therefore, it is also called grain alcohol., Cooking grain + sprouted barley, glucose yeast ethanol + CO2, (starch), , (called Malt), , enzymes, , The process of conversion of starches and sugars to C2H5OH is called, fermentation process., , Properties, Ethanol is a colourless liquid with characteristic sweet odour. Pure, ethanol boils at 78.3 oC. Pure ethanol is called absolute (100 %) alcohol., Denatured alcohol is ethanol that contains impurities that make it, undrinkable. The impurities are methanol, methyl isobutyl ketone, aviation, gasoline etc. It is toxic and 200 ml of it is a fatal dose to an adult. Solution, of about 10% ethanol in gasoline (gasohol) is a good motor fuel., Free distribution by A.P. Government, , 329
Page 340 :
Ethanol is commonly called alcohol and is active ingredient of all, alcoholic drinks. Consumption of small quantity of dilute ethanol causes, drunkenness. In addition, as it is a good solvent it is also used in medicines, such as tincture iodine, cough syrups and many tonics, • Do you know how the police detect whether suspected drivers have, consumed alcohol or not?, , The police officer asks the suspect to blow air into a plastic, bag through a mouth piece of the detecting instrument which, contains crystals of potassium-di-chromate (K2Cr2O 7). As, K2Cr2O7 is a good oxidizing agent, it oxidizes any ethanol in the, driver’s breath to ethanal and ethanoic acid., Orange Cr2O72- changes to bluish green Cr3+ during the process, of the oxidation of alcohol. The length of the tube that turned into, green is the measure of the quantity of alcohol that had been drunk., Now a days police are using even an electronic instrument, containing small fuel cell that measures the electrical signal, produced when ethanol in the breath is oxidized., The police even use the IR Spectra to detect the bonds, C – OH and C – H of CH3 – CH2OH., As ethanol is similar to water molecule (H2O) with C2H5 group in place, of hydrogen, it reacts with metallic sodium to liberate hydrogen and form, sodium ethoxide., 2C2H5OH + 2Na, 2C2H5ONa + H2, Ethanol, , sodium ethoxide, , Action of conc. H2SO4: Ethanol reacts with conc. H2SO4 at about, 170 C (443 K) to give ethene. It is a dehydration reaction. H2SO4 is a, dehydrating agent and removes H2O., at 170 C, CH3CH2OH, CH2 = CH2 + H2O, o, , o, , Conc.H2SO4, , Ethanoic acid (Acetic acid, CH3COOH), , Ethanoic acid is a colourless liquid with characteristic unpleasant odour., It is soluble in water and more acidic than H2O or ethanol, but less acidic, than mineral acids., Ethanoic acid is commonly called as acetic acid. 5-8% solution of, acetic acid in water is called vinegar and is used widely as a preservative in, pickles., , 330, , X Class, , Carbon and its Compounds
Page 341 :
Chemical properties, Acidity: (Reaction with metals and alkalies), 1) Ethanoic acid reacts with active metals like Na to liberate hydrogen., This reaction is similar to that of ethanol., 2CH3COOH + 2Na, 2CH3COONa + H2, acetic acid, , sodium, , sodium acetate, , 2) Ethanoic acid reacts with NaOH to form salt and water., CH3COOH + NaOH, 2CH3COONa + H2O, sodium hydroxide, , 3) Ethanoic acid reacts with sodium carbonate and sodium hydrogen, carbonate which are weaker bases and liberates CO2., 2CH3COONa + Na2CO3, 2CH3COONa + H2O + CO2, Sodium carbonate, , CH3COOH + NaHCO3, , CH3COONa + H2O + CO2, , sodium bi carbonate, , The strength of acids may be expressed in terms of their pKa values., These values are related to their dissociation in aqueous solutions., What is pKa?, pKa is the negative value of logarithm of dissociation constant of an acid., pKa is a measure of how much an acid dissociates in a solution., pKa = -log10Ka, The lower the pKa value, the stronger is the acid., Note that pKa of 1.0M HCl is zero but pKa of CH3COOH is 4.76., pKa values are useful to tell about acid strength. Strong acids have pKa <, 1, acids with pKa between 1 and 5 are moderately strong and weak acids, have pKa between 5 and 15. The weakest acids have pKa > 15., Note that pKa values less than zero are not generally given as they are, of no use to give in terms of pKa. They may be directly given in terms of, Ka., , 4) Esterification Reactions, •, , What are esters?, Esters contain the functional group, , O, C, , C, , O–C, , and the general formula is R – COO - R/ . R and R/ are alkyl groups, or phenyl groups., Free distribution by A.P. Government, , 331
Page 342 :
Activity2-2, Activity, , Test, tube, containing, reaction, mixture, , Take 1 ml of ethanol (absolute alcohol) and 1ml of, glacial acetic acid along with a few drops of concentrated, Beaker, Water, sulphuric acid in a test tube., Wire, gauze, Warm it in a water-bath or a beaker containing water, Tripod for at least five minutes as shown in Fig., stand, Burner, Pour the warm contents into a beaker containing, 20-50 ml of water and observe the odour of the resulting, mixture., Formation of ester, •, What do you notice?, You will notice that the resulting mixture is a sweet, odoured substance. This substance is nothing but ethyl acetate, an ester., The reaction in activity – 2 is called esterification reaction., , Esterification, The reaction between carboxylic acid and an alcohol in the presence, of conc. H2SO4 to form a sweet odoured substance, ester with the functional, O, , group, C, , C, , is called esterification., O–C, , The esterification reaction is slow and reversible., The equation for the reaction between an acid RCOOH and an alcohol, /, R OH, (where R and R/ can be the same or different) is:, O, R–C, , O, /, , O–H, , + R OH, , R–C, , /, , O–R, , + H2 O, , So, for example, if you want to prepare ethyl ethanoate or ethyl acitate, from ethanoic acid and ethanol, the equation would be:, , O, CH3–C, Ethanoic acid, (acetic acid), , 332, , X Class, , + CH3CH2OH, O–H, Ethanol, (ethyl alcohol), , conc.H2SO4, , O, CH3–C, , + H2 O, O–CH2CH3, ethyl acetate, , Carbon and its Compounds
Page 343 :
Soaps – Saponification and Micelles, Do you know what ‘soap’ is?, Soap is a sodium or potassium salt of a higher fatty acid like palmitic, acid (C 15 H 31 COOH), stearic acid (C 17 H 35 COOH), oleic acid, (C17H33COOH) etc. The formula of a soap in general is RCOONa or, RCOOK, where R = C15H31 ; C17H35 etc., Fats are esters of higher fatty acids and the trihydroxy alcohol known, as glycerol., CH2OH, |, Glycerol is, CHOH , propane – 1, 2, 3 – triol., |, CH2OH, When fats are treated with sodium hydroxide, sodium salts the fatty, acids and glycerol is formed. The sodium salts of these higher fatty acids, being soaps the reaction is the soap formation reaction which is generally, called as ‘saponification reaction’., O, ||, CH2 – OH, CH2 – O – C – C17H35, |, |, CH – OH, + 3 C17H35COONa, CH – O – C – C17H35 + 3NaOH, ||, |, O, CH2 – OH, CH2 – O – C – C17H35, ||, O, Tristearin, , glycerol, , sodium stearate (soap), , Saponification reaction, Alkaline hydrolysis of tristers of higher fatty acids producing soaps, is called saponification., Soaps are good cleansing agents. Do you know how they do this?, For understanding this you should know about a ‘true solution’ and a, colloidal solution., • What is a true solution?, A true solution is that in which the solute particles dispersed in the solvent, are less than 1nm in diameter. A colloidal solution contains the solute known, as ‘dispersed phase’ with its particles with diameters greater than 1nm but, lesser than 1000 nm in the solvent known as ‘dispersion medium’., Free distribution by A.P. Government, , 333
Page 344 :
Soap is an electrolyte. When soap is put in water in very small amount, it gives low concentrated solutions. It gives true solution but, above a, particular concentration known as critical micelle concentration (CMC),, the soap particles get aggregated and these aggregated particles are of, colloidal size known as micelles or associated colloids., , Micelle, A spherical aggregate of soap molecules in water is called micelle., When soap is dissolved in water, it forms a colloidal suspension in which, the soap molecules cluster together to form spherical micelles., , Formation of micelle, , Activity 3, , Micelle, , 3D structure of a micelle, , Take about 10 ml of water each in two test tubes., Add a drop of oil (cooking oil) to both the test tubes and label them as, A and B., Add a few drops of soap solution to test tube B., Now shake both the test tubes vigorously for the same period of time., What is that you find in them?, Can you see the oil and water layers separately in both the test tubes, immediately after, • You stop shaking them?, • Leave the test tubes undisturbed for sometime and observe. Does the, oil layer separate out?, • In which test tube does this happen first? Give your observations., , Cleansing action of soap, Suppose that we put dirty cloth in the soap solution. Dirt is mainly, greasy matter. The soap molecules are arranged radially with hydrocarbon, ends directed inwards into the greasy matter and ionic part directed outwards, into water., 334, , X Class, , Carbon and its Compounds
Page 345 :
When a dirty cloth is inserted in the solution, then the hydrocarbon part sticks to the dirt or, oil. With a little agitation the dirt particles get, entrapped by the soap micelles and get, Hydrophobic, dispersed in water due to which the soap water, end, A soap molecule, gets dirty and the cloth gets cleaned., • What is the action of soap particles on the greasy cloth?, We know that soaps and detergents make oil and dirt present on the, cloth come out into water, thereby making the cloth clean., , Hydrophilic, end, , O, , Soap has one polar end (the end with C O carboxy) and one nonpolar end (the end with hydrocarbon chain) as shown in the figure., The polar end is hydrophilic in nature and this end is attracted towards, water., The non-polar end is hydrophobic, in nature, Soap, and it is attracted towards grease or oil on the, molecules, Soap, cloth, but not attracted towards water., solution, When soap is dissolved in water, its cloth, Dirt, hydrophobic ends attach themselves to dirt and, remove it from the cloth, as shown sequentially, in the figure that follows., •, , The hydrophobic end of the soap molecules, move towards the dirt or grease particle., • The hydrophobic ends attached to the dirt, particle and try to pull out., dirt with micelle, • The molecules of soap surround the dirt, clean cloth, particle at the centre of the cluster and form, Representing the, cleansing action of, a spherical structure called micelle., soap, These micelles remain suspended in water, like particles in a colloidal solution., The various micelles present in water do not come together to form a, precipitate as each micelle repels the other because of the ion-ion, repulsion., Thus, the dust particles remain trapped in micelles (which remain, suspended) and are easily rinsed away with water. Hence, soap micelles, remove dirt by dissolving it in water., Free distribution by A.P. Government, , 335
Page 346 :
Key words, Hybridisation, allotropy, diamond, graphite, buckminsterfullerene,, nanotubes, catenation, tetravalency, hydrocarbons, alkanes, alkenes,, alkynes, saturated hydrocarbons, unsaturated hydrocarbons, functional, group, isomerism, homologous series, nomenclature, combustion,, oxidation, addition reaction, substitution reaction, ethanol, ethanoic, acid, ester, esterification, saponification, micelle., , What we have learnt, •, , Carbon forms a large variety of compounds. Its tetravalency and the property of catenation and, ability to form four single bonds, a double bond and two single bonds, a triple bond and a single, bond or two double bonds makes carbon versatile and brings one special branch in chemistry, for carbon compunds., , •, •, , Hydrocarbons are the compounds of carbon and hydrogen., , •, , Carbon forms covalent bonds with its own atoms and atoms of other elements such as hydrogen,, oxygen, sulphur, nitrogen and chlorine., , •, , The functional groups such as alcohols, aldehydes, ketones and carboxylic acids bestow, characteristic properties to the carbon compounds that contain them. Even C = C,C C , give, characteristic properties., , •, , A group / series of hydrocarbons having same general formula, with two successive compounds, possessing difference of - CH2 and with similar structures and similar properties (i.e., same, functional group) are called a homologous series., , •, •, , Carbon chains may be in the form of straight chains, branched chains or rings., , •, , Saturated hydrocarbons on combustion give carbon dioxide and water with the liberation of, heat., , •, , Unsaturated hydrocarbons undergo addition reactions while saturated hydrocarbons undergo, substitution reactions., , •, , Ethanol and Ethanoic acid (glacial acetic acid) are carbon compounds of importance in our, daily life., , Hydrocarbons are of two types – saturated hydrocarbons (alkanes) and unsaturated, hydrocarbons (alkenes and alkynes)., , Carbon compounds with identical molecular formula but different structures are called structural, isomers., , 336, , X Class, , Carbon and its Compounds
Page 347 :
•, •, •, , The molecules of soap are sodium or potassium salts of long chain carboxylic acids., Detergents are ammonium or sulphonate salts of long chain carboxylic acids., The action of soaps and detergents is based on the presence of both hydrophobic and hydrophilic, groups in the molecule and this helps to emulsify the oily dirt and hence its removal., , Improve your learning, 1. Name the simplest hydrocarbon. (AS1), 2. What are the general molecular formulae of alkanes, alkenes and alkynes. (AS1), 3. Name the carboxylic acid used as a preservative. (AS1), 4. Name the product other than water formed on burning of ethanol in air. (AS1), 5. Give the IUPAC name of the following compounds. If more than one compound is possible, name all of them. (AS1), i. An aldehyde derived from ethane., ii. A ketone derived from butane., iii.A chloride derived from propane., iv. An alcohol derived from pentane., 6. A mixture of oxygen and ethyne is burnt for welding; can you tell why a mixture of ethyne and air, is not used? (AS1), 7. Explain with the help of a chemical equation, how an addition reaction is used in vegetable ghee, industry. (AS1), 8. a. What are the various possible structural formulae of a compound having molecular formula, C3H6O? (AS1), b. Give the IUPAC names of the above possible compounds and represent them in structures. (AS1), c. What is the similarity in these compounds? (AS1), 9. Name the simplest ketone and write its molecular formula. (AS1), 10. What do we call the Self linking property of carbon? (AS1), 11. Name the compound formed by heating ethanol at 443 K with excess of conc. H2SO4. (AS1), 12. Give an example for esterification reaction. (AS1), 13. Name the product obtained when ethanol is oxidized by either chromic anhydride or alkaline, potassium permanganate. (AS1), 14. Write the chemical equation representing the reaction of preparation of ethanol from ethane.(AS1), 15. Write the IUPAC name of the next homologous of CH3OHCH2CH3. (AS1), 16. Define homologous series of carbon compounds; Mention any two characteristics of homologous, series. (AS1), Free distribution by A.P. Government, , 337
Page 348 :
17. Give the names of functional groups, , (i) -CHO, , (ii) -C=0. (AS1), , 18. Why does carbon form compounds mainly by covalent bonding? (AS1), 19. Allotropy is a property shown by which class substance: elements, compounds or mixtures?, Explain allotropy with suitable examples. (AS1), 20. Explain how sodium ethoxide is obtained from ethanol? Give chemical equations. (AS1), 21. Describe with chemical equation how ethanoic acid may be obtained from ethanol. (AS1), 22. Explain the cleansing action of soap. (AS1), 23. Distinguish between esterification and saponification reactions of organic compounds. (AS1), 24. Explain the structure of graphite in term of bonding and give one property based on this structure. (AS1), 25. Name the acid present in vinegar. (AS1), 26. What happens when a small piece of sodium is dropped into ethanol? (AS2), 27. Two carbon compounds A and B have molecular formula C3H8 and C3H6 respectively. Which, one of the two is most likely to show addition? Justify your answer. (AS2), 28. Suggest a test to find the hardness of water and explain the procedure. (AS3), 29. Suggest a chemical test to distinguish between ethanol and ethanoic acid and explain the, procedure.(AS3), 30. An organic compound ‘X’ with a molecular formula C2H6O undergoes oxidation with alkaline, KMnO4 and forms the compound ‘Y’, that has molecular formula C2H4O2. (AS3), a. Identify ‘X’ and ‘Y’, b. Write your observation regarding the product when the compound ‘X’ is made to react, with compound ‘Y’ which is used as a preservative for pickles., 31. Prepare models of methane, ethane, ethene and ethyne molecules using clay balls and, match sticks. (AS4), 32. Collect information about artificial ripening of fruits by ethylene. (AS4), 33. Draw the electronic dot structure of ethane molecule (C2H6). (AS5), 34. How do you appreciate the role of esters in everyday life. (AS6), 35. How do you condemn the use of alcohol as a social practice. (AS7), 36. An organic compound with molecular formula C2H4O2 produces brisk effervescence on addition, of sodium carbonate / bicarbonate. Answer the following:, a. Identify the organic compound. (AS1), b. Write the chemical equation for the above reaction. (AS1), c. Name the gas evolved. (AS2), d. How will you test the gas evolved? (AS3), e. List two important uses of the above compound. (AS1), 338, , X Class, , Carbon and its Compounds
Page 349 :
37. 1ml glacial acetic acid and 1ml of ethanol are mixed together in a test tube. Few drops of, concentrate sulphuric acid is added in the mixture are warmed in a water bath for 5 min., Answer the following:, a. Name the resultant compound formed. (AS2), b. Represent the above change by a chemical equation. (AS1), c. What term is given to such a reactions. (AS1), d. What are the special characteristics of the compound formed? (AS1), , ks, Fill in the blan, 1. Carbon compounds containing double and triple bonds are called ________., 2. A compound which is basic constituent of many cough syrups __________ ., 3. Very dilute solution of ethanoic acid ____________., 4. A sweet odour substance formed by the reaction of an alcohol and a carboxylic acid is ___., 5. When sodium metal is dropped in ethanol _________ gas will be released., 6. The functional group present in methanol is _____________., 7. IUPAC name of alkene containing 3 carbon atoms is _______________., 8. The first member of homologous series among alkynes is ___________., 9.The product that is formed by dehydration of ethanol in conc. sulphuric acid is ______., 10. Number of single covalent bonds in ammonia are __________., 11. Type of reactions shown by alkanes is ______________., , s, Multiple choice question, 1. Which of the four test tubes containing the following chemicals shows the brisk effervescence, when dilute acetic acid was added to them?, [, ], i) KOH, , ii) NaHCO3, , iii) K2CO3, , iv) NaCl, , a) i & ii, , b) ii & iii, , c) i & iv, , d) ii & iii, , 2. Which of the following solution of acetic acid in water can be used as preservative? [, a) 5-10%, , b) 10-15%, , c) 15-20%, , d) 100%, , 3. The suffix used for naming an aldehyde is, a) -ol, , b) -al, , Free distribution by A.P. Government, , ], , [, c) -one, , ], , d) -ene, 339
Page 350 :
4. Acetic acid, when dissolved in water, it dissociates into ions reversibly because it is a:[, a) Weak acid, , b) strong acid, , c) weak base, , d) strong base, , 5. Which one of the following hydrocarbon can show isomerism?, a) C2H4, , b) C2H6, , c) C3H8, , [, , ], , ], , d. C4H10, , 6. Combustion of hydrocarbon is generally accompanied by the evolution of, a) Heat, , b) Light, , c) both heat and light, , d) Electric current., , 7. 2ml of ethanoic acid was taken in each of the three test tubes A, B and C and 2ml, 4ml and 8ml, water was added to them, respectively. A clear solution is obtained in:, , [, , ], , 8. If 2 ml of acetic acid was added slowly in drops to 5ml of water then we will notice[, , ], , a) Test tube A only, , b) Test tubes A & B only., , c) Test tubes B and C only, , d) All the test tubes., , a) The acid forms a separate layer on the top of water., b) Water forms a separate layer on the top of the acid., c) Formation of a clear and homogenous solution., d) Formation of a pink and clear solution., 9. A few drops of ethanoic acid were added to solid sodium carbonate. The possible results of the, reactions are:, , [, , a) A hissing sound was evolved, , b) Brown fumes evolved., , c) Brisk effervescence occurred., , d) A pungent smelling gas evolved., , ], , 10. When acetic acid reacts with ethyl alcohol, we add conc. H2SO4, it acts as……….and the, process is called………………….., , [, , ], , a) Oxidizing agent, saponification, b) Dehydrating agent, esterification, c) Reducing agent, Esterification, d) Acid & esterification, , 340, , X Class, , Carbon and its Compounds
Page 351 :
Homi Jehangir Bhabha, Homi J. Bhabha, (30 October 1909 – 24 January 1966) was a nuclear Physicist,, founding Director and Professor of Physics at TIFR, Mumbai. He is known as, the father of the Indian Nuclear Programme. Bhabha was the founding director, of two well-known research institutions, namely the Tata Institute of Fundamental, Research(TIFR) and the Bhabha Atomic Research Centre both institutions, were the cornerstone of Indian development of nuclear reactors and nuclear, energy which Bhabha also supervised as its director., In January 1933, Bhabha received his doctorate in nuclear physics after, publishing his first scientific paper, “The Absorption of Cosmic radiation”. The, paper helped him win the Isaac Newton Studentship in 1934., Starting his scientific career from Great Britain, Bhabha returned to India and accepted a post of reader in, physics at theIndian Institute of Science(IISC),Bangalore, headed by Nobel Laurate Sir C.V.Raman. During, this time, Bhabha played a key role in convincing Jawaharlal Nehru who later became India’s first Prime, Minister, to start the ambitious nuclear programme. In 1945, he established the Tata Institute of Fundamental, Research(TIFR),Bombay and set up the Atomic Energy Commission in 1948, serving its first chairman. In the, 1950s, Bhabha represented India in IAEA conferences, and served as President of the UN Conference on the, Peaceful Uses of Atomic Energy in Geneva in 1955., Bhabha gained international prominence after deriving a correct expression for the probability of scattering, positrons by electrons, a process now known as Bhabha scattering . His major contribution included his work, on Compton scattering, R-process and furthemore the advancement of nuclear physics. He was awarded, Padma Bhushan by Government of India in 1954. In January 1966, Bhabha died in a plane crash near Mont, Blanc, while heading to Vienna, Austria to attend a meeting of theIAEA’s Scientific Advisory Committee., , Chintamani Nagesa Ramachandra Rao, C.N.R. Rao was born in Bangalore in a Kannada family to Hanumantha, Nagesa Rao and Nagamma Nagesa Rao. He completed secondary school, leaving certificate in first class in 1947. He studied BSc at Central College,, Bangalore. He obtained his bachelor’s degree from Mysore University in, 1951, in first class, and only at the age of seventeen. He obtained a master’s, in chemistry from BHU two years later. In 1953 he was granted a scholarship, for PhD in IIT Kharagpur. His first research paper was published in the Agra, University Journal of Research in 1954. He completed PhD in 1958, only, after two years and nine months, at age twenty-four., Rao is an eminent scientist and a well recognised international authority, on solid state and materials chemistry., He is currently the Head of the Scientific Advisory Council to the Prime Minister of India., He has published over 1,400 research papers and 45 books., Rao was awarded Hughes Medal by the Royal Society in 2000, and he was first recipient of the India, Science Award in 2004., Some of the major areas of his research are transition metal oxide systems, (new synthesis and novel, structures, metal-insulator transitions, CMR materials, superconductivity, multiferroics etc), hybrid materials, and nanomaterials including nanotubes and graphene., Rao’s current passion is graphene, the new wonder material, and artificial photosynthesis., He was awarded ‘Bharat Ratna’ by the Government of India in the year 2013., Free distribution by A.P. Government, , 341
Page 352 :
REFERENCE BOOKS, S.No., , Name of the Book, , Author(s), , Synopsis, , 1, , Conceptual Physics, , Paul G Hewitt, , Explain the principles of Physics with, examples., , 2., , Feynman Lectures on, Physics, , Feynman, , Discussions and analysis on concepts, of Physics., , 3., , Flying circus of, Physics, , Jearl Walker, , Contains applications and, daily life experiences., , 4., , Concise Inorganic, Chemistry, , J.D. Lee, , Explains concepts in chemistry, , 5., , Problems and, Questions in School, Physics, , Tarasova &, Tarasov, , Explains principles of Physics in a, dialogue form. It is useful for seminors, and symposiams, , 6., , Physics, , Cutnell & Johnson, , Useful for teaching school Physics and, preparing for competition exams., , 7., , The elements of, Physical Chemistry, , Atkins, , Explain the concepts of Physicsl, Chemistry in detail, , 8., , Chemistry, , Mc Murray &, Fay, , Explains concepts of Chemistry, in a simple way, , 9., , Thinking Physics, , C Epstein, , Contains questions and reason behind, every scientific phenomena., , 10., , University Physics, , Harris Benson, , Contains good problems, , 11., , Physics can be fun, , Y Perel man, , Contains good applications with, experiments, , 12., , Vogali text book of Quantitative, ChemicalAnalysis, , Jefery & Others, , An experimental book, , 13., , Organic Chemistry, , Wade Jr. & Singh, , Explain the concepts of Organic, Chemistry in detail, , 14., , Vogali text book of Practical, OrganicChemistry, , Jefery & Others, , An experimental book, , WEBSITES AND e-RESOURCES, http://unesdoc.unesco.org/images/0010/001023/102321eb.pdf Provides ideason how to make school science equipment, using inexpensive materials., http://unesdoc.unesco.org/images/0007/000728/072808eb.pdf Provides ideas on how to make school science equipment, using inexpensive materials., http://www.freeindia.org/biogrphies/greatscientists/has biographies of Indian scientists., http://www.calcuttaweb.com/people/snbose.shtml has some more biographies of Indian scientists., http://www.bbc.co.uk/schools/gcsebitesize/chemistry/classifyingmaterials/contains exercises for assessing classification of, matter, atomic structure, bonding and formulae/equations for class VIII and above, http://www.bbc.co.uk/schools/gcsebitesize/physics/electricity/has some thinking-type questions for class VIII and above, http://www.bbc.co.uk/schools/gcsebitesize/physics/forces/has excellent questions for classes VII, VIII and above, http://www.fordham.edu/Halshall/science/sciencebook.html is an internet sourcebook for the History of Science, http://www.learner.org/resources/series90.html has a set of videos on the science of teaching science, http://edugreen.teri.res.in/index.asp is a website for children that makes environmental learning fun, http://www.nuffieldcurriculumcentre.org/go/Default.htaml provides links to websites of various science projects that, undertake to enliven science teaching, , 342, , X Class, , Reference Books