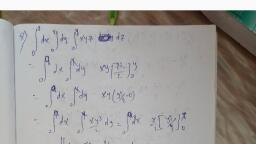Page 1 :
6. Spectroscopic Terms and their Notations, The quantised energy states (simply called as quantum states) of an atomic electron, are described in terms of the quantum numbers n, l, s and j. The electrons having orbital, quantum number l = 0, 1, 2, 3, 4 ., atomic states in the atom are specified by writing the corresponding principal quantum, number alongwith these letters. Thus, an electron for whichn = 2 and 7= 0 is in a 2s, are named as s*, p, d, f, g, electrons. The, 3 and l = 1 is in a 3 p atomic state, and so on., atomic state, and one for which n =, The energy levels of electrons of an atom are called 'terms' of the atom. The, corresponding energies, expressed in wave numbers, are called 'term values'. For a, one-electron atom, the energy levels corresponding to l=0, 1, 2, 3, 4,, S, P, D, F, G . . terms respectively., By spin-orbit interaction, each energy level of a given l is splitted into two sub-levels, corresponding to, are called, 1, j = l + s = 1 +, 1, j = 1 – s = |, %3D, and, *This s should not be confused with the spin quantum number s.

Page 2 :
80, Atomic and Molecular Spectra: Laser, IshoM motA, with the exception of S term (1 = 0) for whichj, only. (j, which determines the, total angular momentum of the electron, cannot be negative). The number of different, possible orientations of L' and S and hence the number of different possible values of j, is known as the 'multiplicity' of the term. It is equal to (2 s+ 1). Thus, the multiplicity of, the terms of a one-electron atom is (2 s + 1), 2. It is added as a left superscript to the, term symbol, thus : S, P, 'D, and so forth. These are called "doublet terms"*. In, addition, the j value is added as a right subscript. Thus, Term, 1., Full Notation, 0., 1/2, 1, 3/2, 1/2, ?P3/2, P1/2, 5/2, 3/2, 2D5/2. D3/2, Sometimes the principal quantum number is also added to the term symbol, such as, 2*P3/2. Here n = 2,1 = '1 , s =, j = 3/2., 2, %3D, atom containing several electrons, the orbital angular momenta, Li= 1, 2, 3 .. of the individual electrons couple among themselves to give a, In, an, resultant electronic orbital angular momentum L' for the atom whose magnitude is, VIL (L + 1) h/2 Tt, where L is the orbital quantum number for the atom. Similarly,, S,i = 1,2,3, ., add, up to give a resultant spin angular momentum S'of magnitude, ......, VS (S + 1), 2 Tt, h, where S is spin quantum number for the atom. Finally, L and s, couple to give the total electronic angular momentum J' for the atom, with magnitude, h, VJ (J+1), J is the inner quantum number for the atom. The terms of the atom may, 2 Tt, now be singlets, doublets, triplets and so forth. They are denoted in the same way as the, terms of a one-electron atom. We shall return to this point in a subsequent chapter, Starn