Page 2 :
_ where (¢ + d) is the grating element., , , , , , , , , , , , , , , , , , , , 304, , id to be resolved. If, however, the patterns overlap to such, alge seouliant intensity shows no drop in the a (Fig. 2b), thee ew, impossible to judge whether the pattern corresponds to a single ling op - iy, close lines. In this case the lines are not resolved. ; Wo, , Rayleigh’s Criterion of Resolution : Lord Rayleigh proposed the follows. |, criterion for resolution which has been universally adopted :, , Two spectral lines of equal intensities are just resolved by an, instrument when the principal maximum of the diffraction pattern deg, falls on the first minimum of the diffraction pattern of the other, One, , In Fig. 3 are shown the intensity curves of two, patterns such thatthe principal maximum of one, coincides with the first minimum of the other. The eye, will see the combined effect of the two which is, shown by the resultant dotted curve. This curve shows, a distinct ‘dip’ in the middle, indicating the presence, of two different spectral lines. The lines are said to be, ‘just’ resolved., , If an optical instrument ‘just’ resolves two ‘Fig. 3), spectral lines of wavelengths A and A + di, then :, , X/dh is taken as a measure of the ‘resolving power’ or ‘chromatic Tesolving, power’ of the instrument., , Rayleigh’s criterion provides us a simple method of calculating the resolvi, power of optical instruments. This is because when two spectral line are just, resolved by the instrument then, by Rayleigh’s criterion the principal maximum, of one coincides with the first minimum of the other. This means that the an;, separation between the principal maxima of the two lines ‘is equal to half the ©, angular width of either maximum., , Q. 2. (a) What is meant by resolving power of a plane transmission, grating ? Derive an expression for it. Show that the maximum resolving, power is proportional to the width of the grating. (Allahabad 2001, 00,, , Lucknow 02, Agra 01, 00, Kanpur 02, Purvanchal 00, Ajmer 00), , (b) Give a method for the experimental determination of the resolving, power of a grating. M, , (c) Distinguish between dispersive power and resolving power of 2,, grating., , Grating A has a length double than grating B but both have the same, number of rulings. Compare their resolving and dispersive powers. oe, , Ans, (a) Resolving Power of a Grating : The resolving power of a grating, Tepresents its ability to form separate spectral lines for wavelengths very ClO%, together. It is measured by 1/dA, where dA is the smallest wavelength differen, that can be ‘just’ resolved at wavelength A. ne, , Let a parallel beam of light of two wavelengths 4 and (A + dA) be incidst |, aoe Be an poe ane If the n th principal maximum of A is formed it,, , ny 4, , (e+ d) sin 8, =n,, , , , ee

Page 3 :
yon Power of Optical Instruments 305, et the first minimum adjacent to, , nth maximum be obtained in the d@n, ion (0, + d0,). The grating I, ica for the minima is — <-1'n, , N(e + d)sin® = m), (ii) __,, N is the total number of Tulings, , ing, and m takes all integral ——>, , ale or eat 0, Ny 2N....,..., nN, —_», secause these values of m give 0 th,, , nth ~OF A+dd, AND Fine? MIN. OF A, , dé, nth MAX.OF A, j¢, 2. nd....nth principal maximum ——>, |, spectively. Clearly, the first minimum ——» “—<16n, jacent to the n th principal Maximum A AND |, in the direction of @ increasing will, te obtained §=for om = (nn + 1). (Fig. 4), , Therefore, if this minimum is obtained, inthe direction (8, + d®,), we have from eq. (ii), , N(e+ 4) sin (8, + 0,) = (nN + 1)%, 3 (e + d)sin(®, + d0,) = wet i” wliii), By Rayleigh’s criterion, the wavelengths 4 and (A + dh) are just resolved by, , the grating when the nth maximum of (A + dh) is also obtained in the, direction 8, + d®,. Then, we have from eq. (i), , (e + d)sin (6, + d8,) = n(X + da). wiv), Comparing eq. (iii) and (iv), we get, wat A= n(d + dh), , or nN + = Nuk + Nn dh, or X= Nndr, or X = Nn., , a 3, But 4/dh, is the resolving power R of the grating. Therefore ae, , R = Nn. Pi ae, , ‘total number, ‘the resolving,, , Thus, the resotvi ce, , , , 0), all, deat epi, Rie

Page 4 :
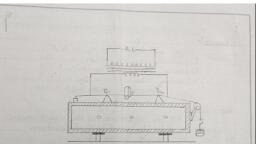
306, , (b) Experimental Determination t ie, resolving power Of a grating may Pes, experimentally determined by finding ©, minimum width of the grating for jus, resolution of two close lines, Say, D, and Dz lines of sodium. 5, , The grating is mount on ,, , Mees ishie of Sadie spectrometer. An ORATING, adjustable slit is placed between the, telescope and the grating with its edges, , parallel to the rulings of the grating (Fig. 5)., , The slit of the spectrometer is illuminated by, , sodium light, and the D, and Dy lines in Noiterte \3\\, the first order are observed through the SLIT, , telescope. The adjustable slit is now closed, gradually until the D, and D» lines ‘just’, merge together. The slit-width is then, measured by a travelling microscope. Let it, be w. Then w is the minimum width of the, grating for resolving D, and Do lines. @, , Now, wavelengths of D, and Dy lines (Fig. 5) solving |, , are 5896 and 5890 A, Thus, there is a wavelength-difference of 6 A at a mean, , wavelength 5893 A. Hence the resolving power necessary to resolve the Dd,, Dy lines is, , , , , , A. _ 5893 _ 94 es, he = 982., , Clearly, the grating-width w measured above corresponds to a resolving power of —, , 982. Since the resolving power of the grating js i its width, i, grating is proportional t, R for the whole grating will be given by (see Fig) vel id, , R = 982 x Micoe By ;, w, , where W is the width of th t i, angle of diffraction of dD, aad oe ay pean te i ae, , (c) Difference betw j ; ‘, dispersive power Shea nee Dispersive Power and Resolving Power : Tie, , bee on grating gives us an idea of the angular separation, , lines of, 48/dX., where d@ Chee Produced by the grating, It is measured by, , angul i i‘ e, wavelengths differ by di. le valooiy gives tae two spectral lines whose, i), , emer foe n, , = aa rel, Thus, higher is De 4) cos @, , 18 the order py, Srating (that is, smaller the ie aE pa Fenris toe Felis a, , Tesolving power of the prarn, 1” Eicaler is the dispersive power, rati : ve pow, the spectra} Hines can Hae other hand, expresses the, , and yet be distinguished, , , , , , , of closeness which

Page 5 :
ove, , ving Power of Optical Instruments, wes, , ured by A/dA, where dA is the smallest wavelength-difference that can, , st wxolVed at wavelength A. Its value is give by, A, , — = Nn,, , dh, , nere WV is the total number of rulings on the grating. Thus, greater is the width, whe ruled sufrace, higher is the resolving power. The higher resolving power, ou :, results in sharp maxima,, , <—dd—», , ~— dO—», RR L\\, (a) ib), , (Fig. 6), , The difference between dispersive power and resolving power is illustrated, in Fig. 6 in which the diffraction maxima of two wavelengths formed by two, diffraction gratings of same grating clement but different widths of the ruled, surface are shown. The angular dispersion d@ is the same in the two cases but the, resolving power in case (a), where the maxima are shaper, is greater than that in, case (b)., , Ifa grating A is longer than a grating B (both having the same number of, rulings), then A has a higher resolving power, but a lower dispersive power, because its(e + d) is larger., , Q. 3. (a) Derive an expression for the chromatic resolving power of a, prism placed in the position of minimum deviation., , (Allahabad 2000, Garhwal 02, Purvanchal 02, 00), , (b) Show that the chromatic resolving power of a Spectroscopic, instrument is given by, , resolving power = dispersive power x width of the dispersed beam,, , Ans, (a) Chromatic Resolving Power of Prism : The chromatic resolving, power of a prism represents its ability to form separate spectral lines for, wavelengths very close together. It is measured by A/dA, where dA is the, smallest wavelength difference that can be just resolved by the prism at the, wavelength A,, , , , Aa-s5{6-d6, , PL. Arar, , , , , , , , , , (Fig. 7)