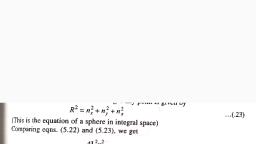Page 1 :
Sey ae crepes Se aa ae et a reas, , , , , , , , , , , , , , , 5. RECIPROCAL LATTICE, , X-ray diffraction is equivalent to reflection by the sets of parallel lattice planes in the crystal. But the, icture of X-ray diffraction as given by nA = 2d sin @ (Bragg’s law) is very much over simplified. There exist, ay sets of planes, with varying slopes and spacings, which can diffract a given beam of X-rays. It is, ifficult to visualize several slopes of two dimensional surfaces, such as planes. We know that the slope of a, 8c is determined by its normal which is a line, so it has one dimension. Hence if we are concerned with a, ide of planes, we can think in terms of their normals (A normal represents the slope of a set of parallel, )., If the length assigned to each normal is proportional to the reciprocal of the interplaner spacing of, plane, then the points at the end of their normal drawn from a common origin is called reciprocal, , This concept of normals is used in the construction of reciprocal lattice, which was proposed to tabulate, wo important properties of crystal planes, their slopes and their interplanar spacings. Let us see how we, onstruct the reciprocal lattice following the treatment given by M.J. Buerger., ____We take a point in the direct lattice as origin and then, , _ (a) From this origin draw normal to every set of planes in the direct lattice., (b) Set the length of each normal equal to (or 27 time) the reciprocal of the interplanar spacing for its, lar set of planes., (c) Place a point at the end of each normal., Thus an assembly of points is obtained. This assembly represents :, , Scanned with CamSc

Page 2 :
: a8, , (i) the normals to all the direct lattice planes, and (ii) their interplanar spacings. —=_ "y, This collection of points represents a lattice array which is known as ‘reciproéal lattice.’, Graphical Construction of Reciprocal lattice, The reciprocal lattice can be constructed by using the above rules. We shall have graphical TEPTeseniag, , of two dimensional reciprocal lattice. Fig 2.6 shows, , the unit cell of monoclinic crystal along its unique axis, , which is designated by b. The cell edges seen in, , , , , , , \, , e----*, 2. Place a point on the normal to each plane (Aki), ata distance from the origin equal to W/dy,)., , The collection of such points form a periodic, array and is called the reciprocal lattice. Each of the, point preserves all the important characteristics of thé Fig. 2.6. Reciprocal lattice, stack of planes it represents. t, , ', , ' we t, fig 2.6 are a and c. The figure also shows four planes, ong Ac ne om, namely (100), (101), (102) and (001). Since all these oe NOD to tT, planes are parallel to 6, their normal lies in the plane 003 *~ Le “hq,, of paper. The rules for finding these points:are as ' oe tice a i, follows : 1208 Ain, , 1, From a common origin erect a normal to each + an {, plane. 1200 ', I ', , t t, , ' ', , , , te, , 2.7. RECIPROCAL LATTICE VECTOR ,, ., , : 1 |, , A vector whose magnitude is equal to the reciprocal of interplanar spacing i.e. a and directis, . aan : kL, , is parallel to the normal to (hkl) plane is called reciprocal lattice vector. :, , 3 > : : ee ‘, The primitive translation vectors a*,b* and ct, of reciprocal lattice and the primitive translation vecta, , 2 ina, , a, B and © beara simple relationship ie., , G* isnormalto 5 and @, , b**is normal toe and ‘a, , c* isnormalto q and F ., Hence we can write i ; : ae ‘ ', , a*-B=0;at-¢ =0 i, , 5+. 2 =0;5%-a =0, , e.g =0;c%. 5 =0, , 2 agteB beat chen, , , , o> . 6 ide > d >, Since a* is perpendicular to the plane containing 6 and c ,, Hence we can write ’, at=A(bxe), , where A is scalar multiplier., , 2, , , , ae., , Scanned with CamSc

Page 3 :
Ri lee - —— ail, , , , , , gnYSTAL DIFFRACTION AND RECIPROCAL LATTICE |, , , , , , , , 31, Putting Eq, (2.11) in (2.10), we get, >, aA @ x e) =2n, A= 2n, or “2 . (2.12), a-(B x 2) “ 7, So Eq. (2.11) becomes ‘ :, 5 i, a*=2n Ane, a-bxe, > >, at cxa, Similarly, sii ar., a-bxe, > >, >, axb, and eS, a-bxe, The dimensions of reciprocal lattice vectors se 5* and c* has the dimensions of (length)!, The points R of the crystals lattice are given by ‘, Rena +mb+pe, (m, n, p= integers) ~@13), , Similarly, we define the reciprocal lattice points or reciprocal lattice vectors G@ in Fourier space as, , ahah + e+ ee, PROPERTIES OF THE RECIPROCAL LATTICE 7, 1. The reciprocal of the reciprocal lattice is the direct lattice. i.e., , @ared eR |, @h*=8, , , , 2. Every reciprocal lattice Vector is normal to the lntice plane of the: ee lattice. |, , 3. The volume of the unit cell of the reciprocal lattice is inversely proportional to the volume of a unit, 1] of direct lattice., , 4. Every point in a reciprocal lattice corresponds to particular set of. parallel planes of the direct lattice., , le, 5. The spacing d,,, of the plane crystal lattice is equal ta aah =, , .8. RECIPROCAL LATTICE TO'SC LATTICE, The primitive translation vectors of a simple cubic lattice are, , Ge =al,b Bebfe= 7¢, , Where 7, } and & are orthogonal vectors of unit length., , a ie Teter Rha ro seerpne nr, , OLdIINICU WILT bai Hoc

Page 4 :
The volume of unit cell, = ap x 2), , zal (b} x ch), , [ve a= b =], , V=a, (214, , Hence, the primitive lattice vectors of the reciprocal lattice to the sc lattice are, , , , Similarly, b*= (2.15), oe, , ; . ' . : 2n, , Hence we find that the reciprocal lattice to sc lattice is itselfasc lattice with lattice constant 7:, , 2.9. RECIPROCAL LATTICE TO BCC LATTICE, , Let 2: B. 2+ be the translational vectors of a primitive unit cell of bec lattice (Fig. 2.7): Then,, ~, , [7, , , , , , , lf, £, , »,, , U, ‘\, , , , , , , , , , penny cle, AG Seto yidlie, , , , , , , , 3, , , , \., Fig. 2.7. Primitive basis vectors of bcc lattice., , OUdINeU WILT Udall

Page 5 :
wal Rb, 2, 1a a A, b =z Ctafeky, eS PHF 4k, , , , , where a is the side of the conventional unit cell and - } and & are orthogonal vectors of unit length., , 2, Since Bx d=£ 2742}),, 2, Fuck, Bix c= (hf), , So volume of primitive cell, V = |a'.B" x Cy, - 2, , a,A A “A a na, = > +j-k)-—(-7, a7 GtI-D TED, 4, 2, eo : 2, , The primitive translation vector of the reciprocal lattice to bcc lattice are, ? a, a Qn b'xc, [a Bix, 2, a nan a, 2, Se et Oe., oe 2R P49), } a, oe :, Similarly Bra fsh) ; ATE), eee], a, , But these are the primitive translation vectors of a fcc lattice|_, Thus fee lattice is the reciprocal lattice of the bcc lattice., , 0. RECIPROCAL LATTICE TO FCC LATTICE, , Let a’ 1B, C' be the translational vectors ofa Primitive uni, Cc lattice Fig. 2.8) then, , , , a'=S (+7), Dads, Bat ek), ~2 ;, 2 “a ( he fy Fig. 2.8. Primitive basis vectors of the fc, 2 lattice, , Scanned with CamSc