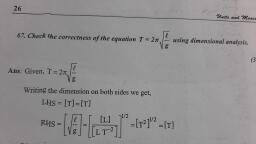Page 1 :
HSPTA MALAPPURAM, PHYSOL-The Solution for Learning Physics, , Question Bank, Physical World, Units and Measurement, Each question scores One, 1 ----------------is the area of physics concerned with the motions of physical objects, more, specifically the relationships among force, matter, and motion., Ans:Mechanics, 2 -----------------is a branch of physics that deals with the study of mechanical waves in gases, liquids,, and solids ( including topics such as vibration, sound, ..etc), Ans:Acoustics., 3 -----------------is a branch of physics that deals with heat, work, and temperature, and their relation, to energy, radiation, and physical properties of matter., Ans:, Thermodynamics., 4 -----------------is the branch of physics which deals with rapidly changing electric and magnetic, fields., Ans: Electrodynamics., 5 -----------------is the branch of physics that studies the behaviour and properties of light, including, its interactions with matter and the construction of instruments that use or detect it., Ans:Optics, 6 Relativistic mechanics and Quantum mechanics includes in -------------(Classical Physics/Modern, Physics)., Ans:Modern Physics., 7 -------------refers to mechanics compatible with special relativity (SR) and general relativity (GR)., Ans:Relativistic Mechanics., 8 -------------deals with physical properties of atomic and Sub atomic particles., Ans:Quantum mechanics., 9 List the fundamental forces in nature., 10 Which is the strongest force among fundamental forces?, a), 11 The weakest force in nature, (i)Strong nuclear force (ii) weak nuclear force, (iii)Gravitation force, (iv) electromagnetic force, 12 The dimensional formula of force is ................, 13 Give two dimensionless quantities., 14 Define one radian., 15 “All constants are dimensionless”. Do you agree the statement?, 16, b), 17, c), , Pick out the odd one, (a)Kilogram (b) second, Find the odd one:, Ans:Charge., , (c) ampere, , (d)candela, , (e) impulse, , (mass, luminous intensity, charge, temperature), , Prepared by Higher Secondary Physics Teachers Association Malappuram

Page 2 :
d), 18, e), , 1 fermi (femto meter) (fm) = --------------m., Ans:10-15m, , 19, g), , Find the odd one:, Ans:newton., , h), 20, , 1 angstrom (A0) = ------------m., Ans:10-10 m, , (Kilogram, second, ampere, candela, newton.), , 21 Which is the largest practical unit of length (distance used in astronomy)?, Ans:Parallactic second or Par second (Par sec)., 22 1 Astronomical Unit (AU) = -----------m, Ans:1 Astronomical Unit (AU) = 1.496x1011 m, 23 1 light year (ly) = -------------m, Ans:1 light year (ly) = 9.46x1015 m, 24 1 par second (parallactic second) or par sec = ------m, Ans:1 par second (parallactic second) or par sec = 3.08x1016 m, 25 The powers to which the fundamental quantity must be raised to get a Physical quantity are called, ---------of that quantity., Ans:Dimensions., 26 State true or false: “ A quantity have dimensions but still has no units”, Ans:False., 27 “If an equation is correct all the terms will have the same dimension”. This is the ---(a) Principle of moments., (b) Principle of homogeneity of dimensions., k), (c) Principle of continuity., (d) Principle of Bernaulli, Ans:(b) Principle of homogeneity of dimensions., 28 1 micron = ----------m, Ans:1 micron = 10-6 m, 29 hertz is the unit of --------------Ans:Frequency, 30 1 amu (atomic mass unit) = -----kg, Ans:1 amu = 1.66 x 10 -27 kg, 31 Which of the following equations can’t be obtained by the dimensional method?, (a), , T =k, (d), , Ans: (b), , √, , l, g, , (b), , N =N 0 e(− λ t ), , (c), , E=kmv 2, , P=h ρ g, , (− λ t ), , N =N 0 e, , 32 a)Pick out the odd one in the given pairs., i) Angular velocity and frequency., ii) Work and energy., iii) Angle and strain., iv) Impulse and momentum., Ans: Angle and Strain, , Prepared by Higher Secondary Physics Teachers Association Malappuram

Page 3 :
33 Light year is the unit of ........…, i) time, ii)length, iii) year, Ans: Length., , iv)velocity, , 34 kilowatt-hour is the unit of......…, i) energy, ii)power, iii)time, Ans: Energy., , iv)mass, , 35 Pick out the fundamental unit from the following:, (Second, m/s, Newton, Joule), Ans: second., 36 Select a true statement from the following:, a) Year and light year have the same dimensions., b) Intensity of gravitational field has same dimensions as that of acceleration., c) One angstrom is the mean distance between sun and earth., d) parsec is a unit of time., Ans: b) Intensity of gravitational field has same dimensions as that of acceleration., Each question scores Two, 1 Explain briefly the two domains of Physics., Ans: In Physics, there are two domains of interest macroscopic and microscopic. Macroscopic, domain: It includes phenomena at the laboratory, terrestrial and astronomical scales. Microscopic, domain: It includes atomic, molecular and nuclear phenomena., 2, , a) What do you mean by dimensions of a physical quantity?, b) Give the dimensions of the following quantities., i) Momentum, ii) Force, Ans: (a)The dimensions of a physical quantity are the powers to which the fundamental, must be raised to get that quantity., (b) i) Momentum, -->, [M1L1T-1], ii) Force, -->, [ M1L1T-2], , quantity, , 3 Give four pairs of physical quantities having the same dimensions., Ans:, 1), Momentum and Impulse., 2), Work, energy , Torque, 3), Angular momentum and Planck’s constant, 4), Pressure and Stress, 4 Give four examples for dimensionless physical quantities., Ans: ., 1. Angle (Plane angle), 2. Solid angle., 3. Strain, 4. Relative density., 5 Give two examples for dimensionless unit less physical quantities., Ans: 1. Relative density., 2. Coefficient of friction, 6 Give four examples for the Physical constants having dimensions., Ans:, 1. Gravitational constant (G), [M-1L3T-2], 2. Planck’s Constant (h), , [ML2T-1], , Prepared by Higher Secondary Physics Teachers Association Malappuram

Page 4 :
3. Universal gas constant (R), 4. Force Constant (k), , [ML2T-2K-1mol-1], [MT-2], , 7 Give two examples for dimensionless physical constants., Ans:, 1) Relative permittivity (or Dielectric constants)., 2) Relative permeability., 3) Refractive index., 8 Can a quantity have units but still be dimensionless? Justify your answer., Ans: Yes. A quantity having units may be dimensionless. For example , the quantity ‘angle’ has no, dimension but it has the unit ‘radian’., 9 What are the uses of dimensional analysis (method) ?, Ans:, a) To check the correctness of an equation., b) To derive a relation for a physical quantity., c) To convert a unit from one system into another., 10 A student was asked to write the equation for displacement at any instant in a simple harmonic, motion of amplitude ‘a’. He wrote the equation as, , y=a sin, , 2π v, t, k, , Where ‘v’ is the velocity at instant’t’. For the equation to be dimensionally correct, what should, be the dimensions of k?, Ans: Dimension of [k] = Dimension of [vt], = [L1T-1 T1], = [L1], 11 All physical quantities can be expressed in terms of dimension.Write the physical quantities of the, following dimensions, 1 1 -1, 1 2 -2, i) M L T, ii) M L T, Ans:, i) momentum or impulse., ii) work or energy or torque., 12, , Fv 2, A physical quantity is given by h=, where ‘F’ is the force, ‘v’ is the velocity and ‘L’ is the, L, angular momentum. Find the dimension of ‘h’., Ans: Dimension of h,, =, =, , [ F][ v2 ], [h]=, [ L], −2, MLT ( LT −1 )2, ML2 T −1, MLT −2 L2 T −2, ML2 T −1, , 0 1 -3, There fore dimension of h = [M L T ], 13 Using the principle of homogeneity of equations, check whether the equation is correct., , T =2 π, , √, , g, l, , Ttime, gacceleration due to gravity l is the length of the pendulum, Prepared by Higher Secondary Physics Teachers Association Malappuram

Page 5 :
1, Ans: Dimension of [T] = [T ], Dimension of, , 1, , −2, , g, L T, =, 1, l, L, , √ √, , =[T, , -1, , ], , Dimension of LHS not equal to Dimension of RHS. Thus the equation is wrong., 14 Check whether the equation mv2 = mgh is dimensionally consistent. Based on the above equation, justify the following statement. “A dimensionally correct equation need not be actually an exact, equation”, Ans:The equation mv2 = mgh is dimensionally consistent., 1, m v 2 = mgh., But the exact equation is, 2, Thus the given statement is correct. A dimensionally correct equation need not be physically, true., 15 Mention any four limitations of dimensional analysis., Ans:, 1. The method does not give any information about the dimensionless constant K., 2. It fails when a physical quantity depends on more than three physical quantities., 3. It fails when a physical quantity is the sum or difference of two or more quantities., 4. It fails to derive the equations involving trignometric, logarithmic and exponential functions., 16 Differentiate between plane angle and solid angle., 17 Which are the fundamental forces in nature?, 18 List any two physical quantities having same dimension., 19 Write two limitations of dimensional analysis., 20 Give the dimensional formula of the following quantities, a) energy, b) momentum, 21 Differentiate between macroscopic domain and microscopic domain in physics., 22 Write the full form of MKS and FPS systems., Each question scores Three, 1 Match the following, Coefficient of viscosity, Gravitational constant, Modulus of elasticity, Ans:, Coefficient of viscosity, Gravitational constant, Modulus of elasticity, , 2, , Force/area x number, [ML-1T-2], Force/area x velocity gradient [ML-1T-1], Force x (distance)2/(mass)2 [M-1L3T-2], Force/area x velocity gradient [ML-1T-1], Force x (distance)2/(mass)2, [M-1L3T-2], Force/area x number, [ML-1T-2], , Mechanical power is represented by, P = Fv + Av3ρ., Where F is the force , v is the velocity, A is the area and ρ is the density., a) The dimensional formula of power is -------., b) Check the dimensional validity of the above equation., , Prepared by Higher Secondary Physics Teachers Association Malappuram

Page 6 :
Ans: a) The dimensional formula for power is [ML2T-3], b)[P] = [ML2T-3], [Fv] = MLT-2 x LT-1 =[ML2T-3], [Av3ρ] =[L2 (LT-1)3]=[ML-3]= [L2 L3T-3ML-3]= [ML2T-3], All the terms have the same dimension. Therefore the equation is correct., 3, , Give examples for following:, a) A dimensionless unit less physical quantity., b) A dimensionless physical quantity but having unit in SI system., c) Two physical quantities which have the same dimensions., Ans: a) Strain., b) Angle., c) Work and Energy., , 4, , Check whether the equation, , T =2 π, Where, , Ans: Given, , √, , m, g, , is dimensionally correct., , T is the time period, m is the mass of the bob, g is the acceleration due to gravity., , T =2 π, , √, , m, g, , Dimension of LHS ,, Dimension of [RHS],, , There fore, , T 2=4 π 2 (, , m, ), g, , 0 0 2, [T2] = M L T, , m, M1, =, g L1 T −2, , 1 -1 2, = [M L T ], Dimension of LHS and RHS are not equal. Thus according to principle of homogeneity the, equation is wrong., 5, , The correctness of equations can be checked using the principle of homogeneity., a) State the principle of homogeneity., b) Using this principle, check whether the following equation is dimensionally correct., 1, m v 2 = mgh, 2, Where m is the mass of the body, v is its velocity, g is the acceleration due to gravity and h is, the height., Ans; a) It states that “ If an equation is correct all the terms will have the same dimension”., 2, 1 1 -1 2, b) Dimension of [mv ] = M (L T ), 1 2 -2, = [M L T ], 1 1 -2 1, Dimension of [mgh] = [M L T L ], 1 2 -2, = [M L T ], Both the terms have the same dimension. There fore by the principle of homogeneity the equation, is correct., , 6, , The centripetal force on a body depends on mass of the body , velocity and radius of circular path., Prepared by Higher Secondary Physics Teachers Association Malappuram

Page 7 :
Find the expression for centripetal force acting on the body by using principle of dimensional, analysis. (Take constant k = 1), Ans: Centripetal force F α ma vb rc, ie., F = k ma vb rc --------(1), Taking dimensions M1L1T-2 = (M1)a (L1T-1)b (L1)c, M1L1T-2 =Ma LbT-b Lc, M1L1T-2 = Ma Lb+c T-b, Equating dimensions on both sides, a=1 b =2 c = -1 also given k=1, Thus equation (1) becomes, , mv 2, F=, r, , 7, , “ Velocity can not be added to temperature”, a), This is in accordance with which law of physics?, b), Check the dimensional correctness of the equation PV =Fx where P is the pressure ,V is, the volume, F is the force and x is the displacement., Ans: a) Principle of homogeneity of dimensions., -1 -2 3, b) Dimension of LHS [PV] = ML T L, 2 -2, = ML T, 1 -2 1, Dimens ion of RHS [Fx] = ML T L, 2 -2, = ML T, ie., Dimension of LHS = Dimension of RHS, Thus the equation is correct., , 8, , Pair the physical quantities according to their dimensions, a. Energy b. Pressure c. Momentum d. Work e. Energy density f. impulse, , 9, , Check the correctness of given equation using the method of dimensions, a) F=ma where F is force, m-mass, a -acceleration, b) v=u+at where v-final velocity, u- initial velocity a-acceleration, t-time, , 10, , One student doubts the expression for kinetic energy as K . E=mv 3 or, , 1, K . E= m v 2 how can, 2, , you help him with the method of dimension., 11 A company manufacturing PVC pipes claims in an advertisement that the volume of water flowing out, 2, through the pipe in a given time as per the equation V =KA ut where A is the area of cross section of, the pipe, u is the speed of flow, t is the time and K is a dimensionless constant., a) Name and State the principle that can be used to check the dimensional correctness of this, equation., b) Check the equation and state whether the claim can be correct., Ans: a)The principle of homogeneity of dimensions., It states that “ If an equation is correct all the terms will have the same dimension”, 3, (b) [V] = L, 2, 22, -1 1, 4 -1 1 5, [A ut] = (L ) LT T = L LT T =L, , Prepared by Higher Secondary Physics Teachers Association Malappuram

Page 8 :
2, Dimension of [V] is not equal to the dimension of [A ut]., The equation is not correct . That is the claim cannot be correct., 12 If dimension of young modulus is [ML-1T-2], test by method of dimensions the correctness of the, equation, Mg l 3, where δ is the depression at middle of a beam of length l, breadth b, and thickness d., δ=, 4 b d3Y, and M is the mass It is placed over two knife edge symmetrically and loaded at the middle by a, weight W., Ans:, Applying the principle of homogeneity, [M ][ g][l]3, [δ ]=, and [Y] is given [ML-1T-2], 3, 4 [b ][d ] [Y ], δ is depression so its dimension is [L], , [ M ][L T ][ L]3, by solving we get the result [L] which is the dimension of δ, 4 [L][ L]3 [ M L−1 T −2 ], −2, , [δ ]=, , 13 The correctness of an equation is checked using the principle of homogeneity for an equation, X= a + bt +ct2 , where ‘X’ is in meter and t in second. What will be the dimension of a,b and c?, a. Ans:, According to the principle of homogeneity, b., [X]= [a] + [bt] +[ct2], c., [X]= [a]=[L], [X ] [ L], d., [X] =[bt] which means [b]=, =, =L T −1 [b]=[LT-1], [t] [T ], e., [ X ] [ L], [X] =[ct2] which means [c]= 2 = 2 =LT −2 [c]=[LT-2], [t ] [ T ], 14, , State the Principle of homogeneity of dimensions., Find the dimensions of each terms in the equations given below and check whether the, equations obeys the above principle., i) S= ut + 1/2 at2, ii) v2 = u2 + 2as, Where u--> initial velocity. v--> final velocity, a--> acceleration S--> displacement, t--> time, Ans: (a)It states that “ If an equation is correct all the terms will have the same dimension”, 2, (b) (i), S= ut + 1/2 at, 1, Dimension of [s] = L, 1 -1 1, 1, Dimension of [ut] = L T T = L, 2, 1 -2 2, 1, Dimension of [ at ] = L T T = L, All the terms have the same dimensions. Thus the equation obeys the principle of, homogeneity of dimensions., (ii) V2 = u2 + 2as, Dimension of [V2] = (L1T-1)2 = L2T-2, Dimension of [u2] = (L1T-1)2 = L2T-2, , Prepared by Higher Secondary Physics Teachers Association Malappuram

Page 9 :
Dimension of [as] = L1T-2 L1 = L2T-2, All the terms have the same dimensions. Thus the equation obeys the principle of, homogeneity of dimensions., 15, , The correctness of equation can be checked using the principle of homogeneity in dimensions., (a) State the principle of homogeneity,, (b) Using this principle, check whether the equation is dimensionally correct, f =2 π, , √, , l, g, , where f-frequency, l - length and g-acceleration due to gravity., 2, (c) The velocity V of a particle depends on time 't' as V = At + Bt., Find the dimensions and units of A and B, Ans: a) It states that “ If an equation is correct all the terms will have the same dimension”, b) Dimension of f = T-1, Dimension of, , 1, , l, L, = 1 −2, g, L T, , √ √, , 2, , √, , = T, = T1, Dimension of LHS not equal to RHS. There fore the equation is wrong., c) Dimension of A = L1T-3 unit of A = ms-3, m), Dimension of B = L1T-2 unit of B = ms-2, 16, , A physical quantity can be expressed in term of dimension, a) Write the physical quantities of the following dimensions?, i)[M1L1T-2.], ii)[M1L2T-2], b) Check whether the equation, , T=2 π, , √, , m, g, , is dimensionally correct?, , Ttime period of simple pendulum, mmass of the bob, gacceleration due to gravity, 17 A boy recalls the relativistic Equation for mass almost correctly but forgets to put the constant, m0, ‘c’.velocity of light . m=, Guess where to put the missing c using dimensional formula, √(1−v 2), analysis., Ans:, m0, By applying the principle of homogeneity, m=, √(1−v 2), [m]=, , [m 0 ], 2, , √(1−[v ]), , √(1−v 2), , since m and m0 having the same dimension the denominator term the equation, , must be dimensionless so in order to make it dimensionless, , c2 must be put as follows, , √, , (1−, , v2, ) so, c2, , √, , (1−, , [v ]2, ), [c] 2, , [v]=[LT-1] and [c]=[LT-1] so cancel and become dimensionless, Prepared by Higher Secondary Physics Teachers Association Malappuram

Page 10 :
so the equation to be corrected as follows, , [m0 ], , [m]=, , √, , 2, , [v ], (1− 2 ), [c ], , Prepared by Higher Secondary Physics Teachers Association Malappuram