Page 1 :
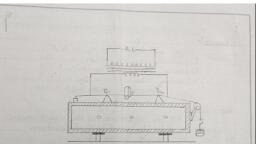
CHAPTER - IV, , LATTICE VIBRATIONS, , inTRODUCTION, , A lattice may be regarded as a regular arrangement of atoms which, are joined together by elas, tic springs as shown in Fig., , 4.1 for a two-dimensional, , case. The motion of any, , single atom is, therefore,, , shared by all the atoms,, , i.e., the motion of the atom, , is coupled. The lattice may, , vibrate freely in its nor, mal modes due to its inter, nal energy or may experi, ence forced vibrations, , under the effect of dynam, ical external forces which, , may be mechanical or, , electromagnetic in nature., , Fig. 4.1. Two-dimensional model of @ lattice compris- The yibrations of the, , | ig atoms attached to one another by elastic springs: ¢ mer type yield infor, mation about the thermal roperties of solids, such as specific heat and, aa al we The latter type of, , thermal conductivity and are described in this chapter., vibrations are associated with aco’, } ‘lids and are beyond the scope of thi, | ‘ibtational motion of a crystal bee, tring a one-dimensiona’ lattice, L€- 4, ls of atoms, and the results are a for two and, , without titative deta, Ses AL MONOATOMIC

Page 2 :
ya, , , , my pos, Veley ipitie® ida, , 104, ies a non-homogencous medium wh, cous medium wherein the line of th iy, . © OF Alon, between, Consider the equilibrium Me na, , lly spaced sites represented by, |, , ent of atoms consul, n a homogen, breaks in, , jtuated atequa, , atoms are placed on the x-axis yar ea, wi ‘, , " din, , x coordinates of the corresponding atoms are 9;, In the state of vibratory motion along the om sp, the atoms will execute periodic motion about their equilibrium positon, become sources of elastic waves which propagate through the Negi, at any instant of time, the displacements of nth, (n-l)th, (n-2)th,., ae, , « alomy, , from their mean positions be Ups Mpaty Mad respectively, Assuming 4h,, springs to be ideally elastic, the force between any two atoms will be {ie :, ; ae w ire 1 no, ic., the force required to produce an atomic displacement 1s propel, 1Onal, , to the displacement itself. Let the force experienced by an atom be m, due to the nearest neighbours. If wis the displacement of a spring with aa since, constant fi, the force exerted by a spring on an atom is given by eo, F= fu, or, — |)th and (n + I)th atoms by two springs,, , arrangem, distinguished from, ntinuous without any, , n these are 5, vig. 4.2, If the, , Ol, the atoms whe!, n, n+l). as shown 10 I, interatomic spacing 4, the, by...(n-1)a, nae (n+ Va,, , Since the nth atom is attached to (n, it experiences two opposite forces ea h one ich is i, net displacement of the eegansing oe oh mcs is proportional sae eT, a g spring. The net force on the nth atom, Fe Blunt Uy) - BU, a Uy), he ce Bling + Mn t ~ 2u,) (4.1), n= n n+ n+2 or, i, a | State off equilibriunt, ! | Ifc, 1 ' 1 x the, ' ' 1, , 1 1, 1 G Q g, pray | ‘ —b 4, a <r +>, Un-2 Un i ‘u ; ; ch at ;, = n Une ¢, Fig. 4.2, paaueaiticat oes i, monoatomic lattice in equilibrium and disturbed states, , Using the Ni ', iz lewton's second law, the equation of motion is written as, , 2, , aes, Sas BCU pg + Mpg — 2p) (42), , , , where ay represents, ae nts the acceleration of the nth atom. We seek the periodi®, , solution to this wave equation as