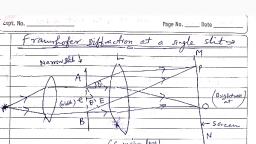
Page 1 :
sea, R RA ATIO : :,, rere rodced by fant mohng charged particles passing through dsl,, , tan ate ti ic, , Since it was first detected by Cherenkov, a Russian pe atmaina ee eo radi :, The fast moving charged particle passing Ce Cherenkov radiation in cete ote :, medium. These excited electrons as a result give out Che between Che hg erative fap, while returning to their normal state. The see name al Ov radia :, bremsstrahlung is that while the former 1s emitted by the m Ch e latter ig Cmittey td, ke the target (cf. production of X-rays). Cherenkoy Tadiation <4 by, , electrons themselves which stri r ein ; Ne, produced by particles of larger mass while bremsstrahlung ceases in case of heavier Particles, , wn that the uniformly moving charge in vacuum does not radiate, Howey..., , we aa the aera of a uniformly fast moving charge through a me medium fo, wet, the dielectric constant is greater than unity, the radiant energy Is Set out. Of course, the vel ich, of the particle v <c. If an electron with a velocity approaching the velocity of light enters a dicen., medium, where the velocity of the particle in the medium is greater than the velocity of light in thet, medium, an intense conical beam of radiation is observed at a’ definite angle. t, , The free space inhomogeneous wave equation in terms of vector potential A is Written ag, , , , , , tion, , , , 1 2A, DA=WA- 59 =~ Hod ', | But for a medium of refractive index n, the sauatian becomes, | 2, nm OA _, | DA=WA- a 52 = Hod oa, , where Dis the D’ Alembertian operator. In the solution of this equation, the time of signal emission, , ) at source ¢’ is related to the time of reception at the field point ¢ through the relation, , | t=(r-(r/o)], ;, , . where r is the distance between the source and the field point, t.e., [t — (r/c)] represents the source, , i time at which the signal received at field point at time ¢ would have started. In the present case,, since medium is dielectric therefore above relation is written as, , , , , , , , | t= [t-(rn/c)]., | The solution of equation (a) is written as, i _Ho fda’, 4nd fr)’, , , , where [r] is the retarded distance given by, {r] a(tstg mel ta case ):, ce ¢c, However, the value of [r] for a dielectic medium is given by, i=r(2-22ee82),, c, , Specifically if this retarded distance {r] in the solution of equation (a) for retarded potential [Al, is zero, the value of potential and hence field is very intense for that particular direction. That, direction is given by, | 1-vuncos 6@/c=0, or cos 8=c/nu wo (b), , Theoretically field intensity is infinite for this condition. It may be noted that though equation, (a) is written for current density J, but since it is constituted by uniformly moving charges, hence, , , , , , Scanned with CamScanner

Page 2 :
ecTROME ae . a ers, , ag Ss, ation is also valid for a moving charge. In oth i, such & 7 Lienard-Wiechert potential due to a moving aoe | The peered pavential 4) ST, , ese ern ‘., rep The quantitative estimate of Cherenkov radiation can be made by making use of Fourier, , lysis: iati, ani Relation (b) shows that the radiation of definite frequency emitted forward is confined in a, , of gemi-vertical angle 8 and the distribution is fre d i, ene of Cherenkov ra dintlonis deyelaiedaagiven et ependent. However the classical, , Maxwell’s field equations are, , V.D=p, V.B=0, VxE=-B, Taras} ), Homogeneous pair of relations given in (1) leads to following relation :, B=VxA, : /, and 2%. | ve (2), , If n be the refractive index of a dielectric medium, then we know that, , “Va, nant =, £, where € and €p are the respective electric permittivities of the medium and vacuum., In the present case if we consider a charge e moving with velocity v, then the corresponding, yolume and current density of charges are expressed as, p =e8(r - vt), . (3), and J=evé(r-vi), If Lorentz condition, , 2, n” ob _ 1 (4D), V.A+ at. 0, is satisfied, then the inhomogeneous pair of relation (1) is written as, OA=- Hod, and Oo=-p/e +), 32, where o=v?- =, Ho & a2, , and it has been assumed legitimately that permeability of dielectric 1 = Ho. In light of relation (3),, relations (5) are written as, 2A, , 2, Vea Oa = Hoev ev), , 2, ow |e, , -. (6), , 5, ry}, I, w, , and Vo , to, we, , e, =— &r-ve, c* att E om, , Taking electrodynamic potential A and 9 in the form of Fourier space integral, i.e.,, , a-| A, el®¥ dk, -= (D, and o= | melt dk, , The Laplacian of relations (7) are, , Scanned with CamScanner