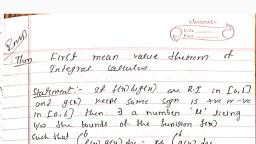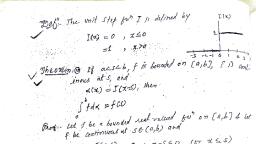Page 3 :
(Co Der te — te) = (Gr — to) +(e — t+ Gn - tnt) = th — fo =D -), , Note (1): Let S and T be non-empty bounded subsets of R .If S © T, Then InfT < InfS < Sup S < Sup T, , Note (2): Let f be bounded function [a,b]. If P and Q are partition, of [a,b] and Pc Q. Then (i) L(f, P) < LC, Q), (ii) Uf, P) 2 UF, Q), , Note (3): Let f be bounded function [a,b]. If P and Q are partition, of [a,b] and PcQ., Then L(f,P) < L(f,Q) < UG,Q) < UG, P), , Note (4): Let f be bounded function [a,b]. If P and Q are partition, of [a,b]. Then Lf, P) < L(f,Q)

Page 4 :
Upper Darboux Integral: Let f be bounded function [a, b].The, , upper Darboux Integral of f over [a, b].is written as U(f) or er, , and is defined as U(f) = inf {U(f,P);P is a partition of [a,b], , Lower Darboux Integral: Let f be bounded function [a, b].The, , upper Darboux Integral of f over [a, b].is written as L(f) or ior, , and is defined as L(f) = sup {L(f, P);P is a partition of [a, b|, , Note: (l) U(f) < U(Gf,P), (ll) LG, P) S$ Lf), , Darboux (Riemann) Integral or Integral: Let f be bounded, function [a,b]. If L(f) = UCf) then we say that f is integrable or, Darboux integrable on [a,b] and common value is called integral of, , f on [a, b] .It is denoted by If = fo f@)dx =L(f) = U(f)

Page 5 :
Theorem: Let f be bounded function [a, b].Then L(f) < U(f), Proof: Let P and Q be any two partition of [a,b]. Then we have, , LG,P) s UGF,Q), , Fix a partition Q of [a,b] .Then, , U(f,Q) is an upper bound for the set {L(f, P); P is a partition of, , [a,b], , Hence sup {L(f, P);P is apartition of [a,b]} < U(f,Q), , => L(f) < UC, Q) which is true for every Q, , { L(f) = sup {L(f, P); P is partition of [a,b], We get L(f) is an Lower bound for the set {U(f,Q);Q isa, Partition of [a, b], , => L(f) < inf {UG, Q); Qis partition of [a, b]}, =L(f) < Uf), { U(f) = inf{UCf, Q); Q is partition of [a,b], , That is, every lower Darboux integral < upper Darboux integral