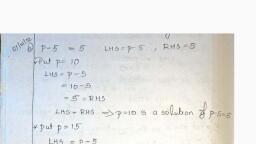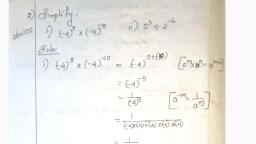Page 1 :
Chapter, , 2 3 2, Tf | * * * | +3=0, then the value of xis:, 1, [CBSE 2020], (a) 3 (b) 0, () -1 (dy) 1, 120 200 50 aa 50 40 Kenlttpl §, LetA=!1) | and B=), |, then is, equal to: [CBSE 2020], (a) 460 (b) 2000, (©) 3000 (d) -7000, a 0 0, . IFA=|0 a 0], then det (adj A) equals:, 0 0 a, [CBSE 2020], (a) a?” (b) a?, (c) a& (d) a2, , . If Ais a square matrix of order 3, such that A (adj, , A)=101, then |adj Al is equal to: [CBSE 2020], (a) 1 (b) 10, (c) 100 (d) 101, , . If Ais a3 x3 matrix such that | A! = 8, then I3AI, equals: [CBSE 2020], (a) 8 (b) 24, (c) 72 (d) 216, , . If Ais askew symmetric matrix of order 3, then the, , , , , , value of |AI is: [CBSE 2020], (a) 3 (b) 0, () 9 (a) 27, x 2 |6, he x he d then the value of x is:, (a) +2 (b), (c) +3 (d) +6, x sin® cos®, . The determinant |-sin@ -—x 1 | is:, cos @ 1 &, (a) Independent of 0 only, (b) Independent of x only, (c) Independent of both 9 and x, , (a) None of the above, , 10., , 11., , 13., , 14., , Determinants, , |. The area of triangle with vertices (x1, 4), (x, Yo), , and (x3, 43) is:, , ya wt 2 * }, (a) A=5)% Y2 1 (b) Aaah v2 it, % Ys 1 % Ys 1, yoy tf, () A=[x, y 1) @) None of these, X% Y3 1, , The arca of the triangle formed by 3 collinear, points is :, (a) one (by, (c) zero (d), Minor of an element of a determinant of order, n(1 2 2) is a determinant of order :, , two, four, , (a) 1” (b) 2-1, , (Q n-2 (d) nt1, 1 a be, , . IfA=|1 b cal, then the minor My, is:, , 1c ab, , (a) —c(a?- b) (b) ¢(b? - 2), , (c) ca? +B) (d) e(a2- 0?), ah g, , WfA=|h bf], then the cofactor Ay is:, gs fie, , (a) ~ (he +fg) (b) fg—he, , (c) fe+he (d) he-fg, , Tf My, = - 40, My = - 10 and M,; = 35 of the, , 1 3 -2, determinant A= |4 -5 6), then the value, 3 5 2, of Ais:, (a) -80 (b) 60 () 70 (d) 100, % %2 M13, - HEA = fa, a2 3] and Aj is cofactor of a,,, M31 43233, then value of A is given by:, , (a) ay, Ag] + Aygo + 443A93, (DB) ay Aga + aypAgy + Ay3Aqy, (©) ayy Aq, + @9Aq9 + a3A)3, , (ay An + Aon ANAT

Page 2 :
2 3, 16. If A= [_ a, A then which of the following is, , true?, (a) Aladj A) 4 AIT, (b) Aladj A) # (Adj AVA, , 0 0, (c) Aladj A) = (adj A)A = |AIT= [° a, , (a) None of the above, , 17. If A and B are invertible matrices, then which of, the following is not correct ?, , (a) adj A= |AL-Ac}, , (b) det (A)! =[det (A)P!, (oc) (AB) 1=B-1a-1, , (d) (A+By1=Bl+act, , 0 x-a x-b, 18. If fix)=|x+a 0 x—-c|, then:, x+b x+e 0, [NCERT Exemplar], (a) fla)=0 (b) fib)=0, (c) fQ)=0 (da) fa)=0, 22 -3, 19. IfA=]0 2 5 |, then A-! exist if:, 11 3, [NCERT Exemplar], (a) 4=2 (b) 242, (c) A=-2 (d) None of these, 20. Let A be a square matrix of order 3 3, then IkA| is, equal to:, (a) KIAl (b) RIAL, () IAI (d) 3kIAl, , 21. Which of the following is correct ?, (a) Determinant is a square matrix, (b) Determinant is a number associated to a matrix, , (c) Determinant is a number associated to a square, matrix, , (d) None of these, 22. If area of a triangle is 35 sq. units with vertices, (2, - 6), (5, 4) and (k, 4), then k is :, (a) 12 (b) -2, (c) -12,2 (d) 12,-2, , 3.5, 23. If A= [ 2 ak then which of the following is, , true ?, (a) A (adj: A)=(A)I, (b) A (adj- A) # (adj A) A, , o 0, () A(adj-A)=(@d) A) A=IAIT= 9 0|, , (d) None of the above, , 26., , 27., , 28., , 29., , 31., , 32., , is equal to:, (a) det (A), , (1, , 1 2, . Find the adjoint of the matrix A = [; | al, , 4 2, @ [5 4], , , , . If Ais an invertible matrix of order 2, then det (A~), , 1, () et (A), , , , (d) 0, , 4, , , , , , £ 2 Le, Mls 4 @) |3 4, 1 2 x, Findx,if}1 1 1] is singular:, 21 a], (a) 1 (b) 2, (©) 3 (d) 4, 0 11 A231, IfA=/1 0 1], then ——— =, 1 10, (@) At (b) 2A, 3, (©) 2a} @) 3A", cos15° sin 15°| |, Value of sin15° cosi5°| 19!, i, 1 =, (a) (b) 3, (c) al (d) None of these, a €, The value of |b a\ is:, c b, , (a) abc(a+b +c), , (c) -8-B-343abe (d), , a+ib, , . Find the value of, (a) +P @, , () @+P+e2+a, , c+ id, , , , (b) @&+b3+0-3abe, None of these, c+id, a-ib, , , , (b) @-b +2 de, (d) None of these, , If A is square matrix x, such that A? =I, then A7lis, , equal to:, (a) 2A, (co) A, , (b) 0, (d) A+1, , If AG, 4), B(—7, 2), C(x, y) are collinear, then :, , (a) x+5y+17=0, (c) x—5y+17=0, , (b) x+5y+13=0

Page 3 :
33., , 34., , If the point A(3, — 2), B(k, 2) and C(8, 8) are collinear,, then the value of k is:, , (a) 2 b) -3, , () 5 (d) -4, , Find the minor of the element of second row and, third column in the following determinant :, , 2-3 8, 6 o 4, 1 5 -7, , (a) 13 (b) 4 () 5 (d) 0, , , , , , Choose the correct option :, , (a) Both (A) and (B) are true and Ris the correct, explanation A., , Both (A) and (RR) are true but R is not correct, explanation of A., , (b), , , , , , 35., , 36., , 37., , 38., , 2, , 39., , (Ais true but R is false., (@)_ Ais false but R is true., Assertion (A):, a? +x? ab-cx ac +bx ze © “EF, ab+cx b? 4x2 be-ax| =|-c x a, ac-bx bet+ax c2 +x? bo -aox, Reason (R) : Ao = A®! where n is order of, determinant, and A° is the determinant of, , cofactors of A., Assertion (A) :, , cos(8+a) cos(@+f) cas (0+y)], , sin(O+a) sin(O+B) — sin(+y), , sin(B-y) sin(y-@) — sin(a—B)}, is independent of 9., , Reason (R) : If f (8) = ¢, then f (9) is independent, of 0., , , , Ai@) — falx), Assertion (A) : If A (x) = gi) g(x), , AD fy), 8i(x) (x), , , , , , then A’ (x) #, , d d..d, Reason (R) : a {fod g @}s Fe fe) ze (x)., , F(x) glx), , Assertion (A) :IfA (x)= | 9 b, , , then, , , , , , , , [A(x) dx = [irene Jat) dx, , Reason (R): Ja f(x) dx = Af f(x) dx, , Assertion : If a, 5, c are even natural numbers then, , a-1l a atl, A=|b-1 6 b+1) isan even natural number., e-l ¢€ etl, , 42., , 43., , 46., , Reason : Sum and product of two even natural, number is also an even natural number., , 2 8 1/72, . Assertion : The matrix A = |7 3 2) is, 301 1, singular., , Reason : The value of determinant of matrix A is zero., , . Assertion : For a matrix A = [jjjls, if det (adj A) = 49,, , then det (A) =+7., Reason : For a square matrix A of order #.ladj Al =, tAIPr, , Assertion : Value of x for which the matrix, 2 1 0), , 0 1 2| is singular is -5., , 1-2 x, , Reason : A matrix A is singular if |A| #0., , Assertion : Minor of the element 6 in the matrix, o 2 6, 1 2 -1) is3., , 2 1 3, , Reason : Minor of an element a, of a matix is the, , determinant obtained by deleting it i" row., , . Assertion : For two matrices A & B of order 3, |A! =, , 3, |B| =—4, then |2AB| is — 96., , Reason : For a matrix A of order m & a scalar k, |kKA|, = IAL, , 5 0, . Assertion : For a matrix A = A (adj A) = | | ., , 0 5, , Reason : For a square matrix A, A (adj A) = (adj AJA, =IAIL, , Assertion : Values of k for which area of the triangle, with vertices (1, 1), (0, 2), (k, 0) is 3 sq. units are 4, and 8., , Reason : Area of the triangle with vertices (xj, )),, , 1 4 om 1, (a Yo), (Xa Ya) 18 I]t. Ya TY, Xs Ys 1, , . Manjit wants to donate a rectangular plot of land, , for a school in his village. When he was asked, to give dimensions of the plot, he told that if its, length is decreased by 50 mand breadth is increased, by 50 m, then its area will remain same but if, length is decreased by 10 mand breadth is decreased, by 20 m, then its area will decrease by 5300 m2., , , , , , , , , , , , , , ©, , Based on the information given above, answer the, following questiorss

Page 4 :
(i) The equations in terms of x and y are :, (a) x-y=50, 2x-y=550, (b) x—y=50, 2x+y, (c), (d) x+y =50, 2x+y=550, , (ii) Which of the following matrix equation, represents the given information :, , abd, mf fells, © [als blss|, © all Fes], , (iii) The value of x (length of rectangular field) is :, , , , , , x+y=50,2x+y, , (a), , (a) 150m (b) 400m, (c) 200m (d) 320m, (iv) The value of y (breadth of rectangular field) is :, (a) 150m (b) 200m, (c) 430m (d) 350m, , (v) How much is the area of rectangular field ?, (a) 60000 sq.m. (b) 30000 sq. m., (c) 30000 m. (a) 3000 m., The sum of three numbers x, y, z is 6. If we multiply, third number by 3 and add second number to it,, we get 11. By adding first and third numbers, we, get double fo the second number., On the basis of above information, answer the, following questions :, (i) If we represent the above information in matrix, form, we can write it as:, , 48., , 1 1 1]fx, (@) }O 1 3i/yl=}i1, 1 2 -I]/z, 1 1 17x] fo, () jo 1 3fyj=}u, 1 -2 1fz] [0, 1 1 17x] [6, ( Jo -1 3iyj=}, 1 -2 1fz 0, 1 1. 17x] [6, (@) |O 1 -3\y|=|11, 1-2 1ffz] [o, , (ii) In inverse of matrix, , 49., , 7-3 2, @ J 3 9 -3, -i @ F, , aw, w, , (, , a, |, , 7 3 a, m4) 0 3, , -3 2, 0-3, -3 ;, or, 3, 1, , Hw NT, , 7 B, a3 0, 1 3 =, , (d), , sole, , (iii) The value of xis :, , (a) 1 (b) 2, , () 3 (d) 4, (iv) The value of y is :, , (a) 1 (b) 2, , (©) 3 (d) 4, (v) The value of z is :, , (a) 1 (b) 2, , () 3 (d) 4, , Aschool wants to award their students for the values, of honesty, regularity and hardwork with a total cash, award of % 6000. Three times the award money for, hardwork added to that given for Honesty amounts, to = 11,000. The ward money given for honestry, and hardwork together is double for regularity., The amount of award for honesty, regularity and, hardwork be % x, @ y, ® z respectively., On the basis of above information, answer the, following questions :, , () If we represent the above situation in matric, , form as AX = X, then A =, , 6000 1 1, (a) | 11000 ) {1 0 3, 0 1 -2, x, © ly (d) None of these, Zz, 1 1 173, @i1 0 3) =, 1 - 1, fe 3 3, @ 72 0 2, 2 3 4, fo 2 2], ) 73 0 3, 3 2 -1

Page 5 :
6 3 3 (a) 3500 (6) 2000, ©) a > 0 2 (©) 1000 (d) 500, 2 3 4 (iv) The value of y is :, (a) 3500 (b) 2000, 6 2 2 (c) 1000 (d) 500, (d) mi «(OC (v) The value of z is :, 3 92 0°21 (a) 3500 (b) 2000, (iii) The value of x is : (@) 1000 (d) 500, Solutions, kd ; = x2 36 = 36-36, Explanation : = sS_ see Gases, ; a 8. (a) Independent of 0 only, Given: |x x x/+3=0 Explanation, P., 49 | © sin® cos, => 2 (x — 9x) —3 (x —4x) +2 Gx —4x)43-=0 LetA=|-sin0 -x 1, > 16x + 9x + 10x +3 =0 cosO aL x, = Stans =x(-x2—1) —sin 0 (x sin 6 — cos 0), => x=-1 + cos 0 (— sin 0 +x cos 8), 2. (d) -7000 =-29-x+x sin? 0 +sin 0 cos 0 -sin 0 cos 0, Explanation : +x cos? 8, !ABI = | AI IBI = (400-500) (150 - 80) =-x3—x + x(sin? 6 + cos? 6) =- x3 —x +x, = (100) (70) = - 7000. [-- sin? 0 + cos? 0=1], 3. (c) a® ~—x3 which is independent of 0., Explanation: | Al =a? 9. (a) By formula of area of triangle., ue ladj Al = |A|2= (a3)? = 08, 10. (c) Zero, 4. (c) 100 Explanation : The area of triangle formed by, Explanation : Given : A (adj A) = 101 three collinear points is zero., We know, A.adj A =1AI.L 11. (b) n-1, . |AL =10 Explanation : By definition of minor., ladj Al = 1AIe-1 12: (Ge 0), é jadj Al = |AIS-1=102=100. Baplanaten?, 2 a be, “A — : Mil g| “Ee, Given: IAI=8 13. () fe-he, We know, IkA|=/31A1, where k is constant Explanation :, ‘ ISA =3°|A| =27x 8=216, E, 6. (b) 0 An = (1)? +1 Mp, =- Mp) = — |, Explanation : Since, A is a skew symmetric J, matrix. =— (he —fg) = fe —he., ih ATs-A 14. (@) -80, > 1AT| = 1-Al Explanation :, > IAI =1-1171Al Az ay Ay tapAy + aA, - = Oy My, — 42M jp + 4 3M)3, > = 1+ (-40)-3¢ 10) + 2) (35), = =-40+30-70=-80., % (a) 28 . 18. (A) ay Aqy | ay Any | A317Aq1, Explanation : Explanation :, , , , , , A = Sum of product of elements of any row (or, , column) with their corresnadine cofactors. _