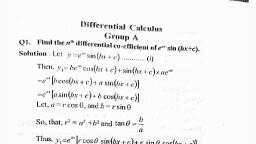Page 1 :
| SEMESTER B.SC. (BNU) MATHEMATICS — PAPER - |, , ob Xe,, , , , , , | SEMESTER B.SC. (BNU), MATHEMATICS — PAPER - |, , , , CALCULUS — | DIFFERENTIAL CALCULUS, , “6, , Dr.SHIVASHARANAPPA SIGARKANTI, HOD DEPARTMENT OF MATHEMATICS, GFGC K.R.PURAM,, BANGALORE - 560036
Page 2 :
GFGC K.R.PURAM | SEM B.Sc. PAPER —1 CALCULUS — | DIFFERENTIAL CALCULUS, , | SEMESTER B.Sc. MATHEMATICS (BNU), CALCULUS - I, DIFFERENTIAL CALCULUS, , Successive differentiation: Let y =f(x) be a function of x. Then, , d:, First derivative is = and denote this by y,, , 2., , d, Second derivative is = and denote this by yz, , d3, Third derivative is = and denote this by y3, , d”, In general the n'" derivative is = and denote this by y,, , Ex.1. Find then" derivative of y = e*, , Soln: y = e*, , dif ferentiating w.r.t.x we get y,; = e*, again dif f erentiating w.r.t.x we get y, = e*, again dif ferentiating w.r.t.x we get y3 = e*, , again dif ferentiating w.r.t.x we get y, = e*, , In general y, = e*, , ax+b, , Ex.2. Find the n™ derivative ofy=e ,»where aand bare constants, , ax+b, , Soln:y=e, , dif ferentiating w.r.t.x we get y, = ae%**?, , again dif ferentiating w.r.t.x we get yz = a?e%*?, , again dif ferentiating w.r.t.x we get y3 = a2ev*?, , again dif ferentiating w.r.t.x we get y, =ate™*?, , In general y, = a"e%**, Ex.3.Find the n derivative of y = x™, Soln:y =x™, , dif ferentiating w.r.t.x we get y, =mx™1, , Dr. SHIVASHARANAPPA SIGARKANTI HOD OF MATHEMATICS Page 1 of 40
Page 3 :
GFGC K.R.PURAM | SEM B.Sc. PAPER —1 CALCULUS — | DIFFERENTIAL CALCULUS, , again dif ferentiating w.r.t.x we get yz =m(m—1)x™?, , again dif ferentiating w.r.t.x we get y3 = m(m — 1)(m— 2)x™-3, again dif ferentiating w.r.t.x we get y, = m(m—1)(m — 2)(m— 3)x™*, in general y, = m(m — 1)(m — 2)(m — 3)...(m— (n—-1))x™™, , Yn = m(m— 1)(m — 2)(m— 3)...(m—n4+1)x™™, , _ m(m-— 1)(m-2)(m— 3)...(m—n+ 1)(m—n)...3.2.1.x"™, nn (m—n)(m—n-—1)...3.2.1., , , , m!, , Yn x" if0O0<n<m, , ~ Ga=n)!, ifm=n,y, =n! =m!, , ifn>m,theny, =0, , Ex.4. Find the n"" derivative of y = (ax +b)™,where aand bare constants, Soln: y = (ax +b)™, , dif ferentiating w.r.t.x we get y, = m(ax+b)™ 1a, , again differentiating w.r.t.x we get y. =m(m — 1)(ax + b)™?a?, , again dif ferentiating w.r.t.x we get y3 =m(m— 1)(m — 2)(ax + b)™ 4a, , again differentiating w.r.t.x we get y, = m(m— 1)(m — 2)(m-— 3)(ax + b)™*a*, in general y, = m(m — 1)(m — 2)(m — 3) ...(m— (n— 1))(ax + b)™ "a", , Yn = m(m— 1)(m — 2)(m — 3)...(m—n+ 1)(ax + b)™™"a", , _mi™m-1)(m- 2)(m — 3)...(m—n+ I) (m—n)...3.2.1. (ax + b)™ "a", a= (m—n)(m—n— 1)...3.2.1., , , , m!, Yn = Gomi r+ bm an ifO<n<m, , ifm=n,y, =n!a"=n!a", , ifn>m,theny, =0, , , , Ex.5. Find the n™ derivative of y= , Where aand bare constants, , ax+b, , Solniy = = (ax+b)1, , ax +b, dif ferentiating w.r.t.x we get y, = (-1)(ax + b)~7a, again differentiating w.r.t.x we get yz = (—1)(—2)(ax + b)~3.a?, , again dif ferentiating w.r.t.x we get y3 = (—1)(—2)(—3)(ax + b)~*a?, , Dr. SHIVASHARANAPPA SIGARKANTI HOD OF MATHEMATICS Page 2 of 40
Page 4 :
GFGC K.R.PURAM | SEM B.Sc. PAPER —1 CALCULUS — | DIFFERENTIAL CALCULUS, , again differentiating w.r.t.x we get y, = (—1)(—2)(—3)(—4) (ax + b)~a*, in general yp, = (—1)(—2)(—3)(—4) ... (-n) (ax + ba", , _ (-1)"n! a", , Ja = (ax + b)ntt, Ex.6.Find then" derivative of y = log (ax + b) ,where aand b are constants, , Soln : y = log (ax + b), , dif ferentiating w.r.t.x we get y; = =a.(ax+b)*, , 7, ax+b, again differentiating w.r.t.x we get y, = (—1)(ax + b)~?a?, , again dif ferentiating w.r.t.x we get y3 = (—1)(—2)(ax + b)-3.a®, again dif ferentiating w.r.t.x we get y, = (—1)(—2)(—3)(ax + b)~*a*, in general y, = (—1)(—2)(—3) (A) ... (-(m — 1)) (ax + b)“a", , _ ©1)""4*(- 1)! a", yn ~“Cax+ by", , Ex.7.Find then" derivative of y = sin (ax + b) ,where a and bare constants, Soln : y = sin (ax + b), , dif ferentiating w.r.t.x we get, 1, y, = cos(ax + b)a =a.sin G +axt b), 1, similarily y, = a? sin (2 ztaxt b), 1, ee cf, y3 =a sin (35+ ax +b), 1, ms pHed oe, Y4 =a sin (45 +ax+b), 1, — Aaa ue, ys =a sin (55+ ax +b), 1, in general y, = a" sin (n5+ ax + b), Ex.8.Find the n" derivative of y = cos(ax + b) ,where aand b are constants, , Soln : y = cos (ax + b), , dif ferentiating w.r.t.x we get, , 1, y, = —sin(ax + b)a=a.cos 5 +axt+ b), , Dr. SHIVASHARANAPPA SIGARKANTI HOD OF MATHEMATICS Page 3 of 40
Page 5 : GFGC K.R.PURAM | SEM B.Sc. PAPER —1 CALCULUS — | DIFFERENTIAL CALCULUS, , 1, similarily y, = a? cos (2 staxt b), 2, 1, — 73 ee,, y3=a cos (35+ ax +b), 1, — 74 i, y4=a cos (45+ax +b), a, —= 25 ‘, ys =a cos (55 +ax +b), 1, in general y, = a" cos (n5 +ax+ b), Ex.9.Find the n"" derivative of y = e™sin(bx + c),where a,b,c are constants, Soln: y = e™sin(bx + c) dif ferentiating w.r.t.x we get, yy, = e“bcos(bx +c) + sin(bx + c)ae™*, =e (b.cos(bx +c) +a. sin(bx + c)), , put b = rsin@ and a = rcos@, , b_ rsin@, , a _rcos@, , = tan0 or 6 = tan“, , , , b, , — and, , a, , a? +b? =r? sin? 6 +r? cos? 6 = r?(sin? 6 + cos? 6) =r?, 1, , orr = ya? + b? = (a? + b?)2, , yy = e™(b.cos(bx + c) +. a.sin(bx + c)), , y, = e™ (rsinO.cos(bx + c) +
[email protected](bx + c)), , y, = re™ sin(6 + bx +c) (y =e™sin(bx + c)), yz = r7e™ sin(26 + bx +c), , y3 = ree™ sin(36 + bx +c), , y4 = rte™ sin(40 + bx +c), , Yn = r"e™ sin(né + bx +c), , Ex.10. Find the n“ derivative of y = e™cos(bx + c),where a,b,c are constants, Soln: y = e™cos(bx + c) differentiating w.r.t.x we get, , yy = e(—bsin(bx + c) + cos(bx + c) ae™, , = (ae™ cos(bx + c) — b. sin(bx + c)e™), , = e™(acos(bx + c) — b. sin(bx + c), , put b = rsin@ and a = rcos@, , Dr. SHIVASHARANAPPA SIGARKANTI HOD OF MATHEMATICS Page 4 of 40