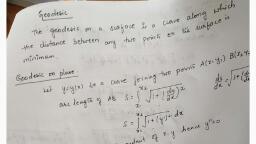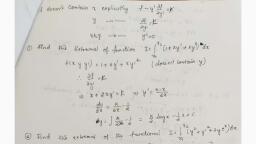Page 1 :
MATHEMATICS, DIFFERENTIAL CALCULUS, SESSION 12, , ASYMPTOTES

Page 2 :
ASYMPTOTES, , A straight line is said to be an asymptote of an infinite branch of the, curve if as the point P recedes to infinity along the branch, the, perpendicular distance of P from the straight line tends to zero., , Asymptote parallel to y axis, , The asymptotes parallel to Y axis are obtained by equating the, coefficient of the highest power of y in the equation of the curve to, zero., , Asymptote parallel to x axis, , The asymptotes parallel to X axis are obtained by equating the, coefficient of the highest power of y in the equation of the curve to, zero., , 1.Find the asymptotes parallel to the coordinate axes for the following, , curve:x*y? — a*x? = a*y?, , Solution : The given equation is x*y? — a?x? = a? y* i.e x?(y*-a?) =, 24,2, , a’y, , Coefficient of the highest power of x is y? — a”, equating this to zero,, , we get y? — a? = 0 >y = +aare the asymptotes parallel to x -axis., , Again re-writing the given equation in the form x” y? — a? y? = a?x?, , y? (x? _ a’) = a2x2, Equating to zero, the coefficient of highest power of y, we get x? —, , a? = 0 > x = taare the asymptotes parallel to y -axis. Thus the, asymptotes parallel to the coordinate axes are x = +a andy = +a, , 2)Find the asymptotes parallel to the coordinate axes for the, following curves: y? —x*y=x?+1, , The given equation is y> — x?y = x? +1, y?—x*y—x?-1=0, , Equating to zero the coefficient of highest power of x, we get

Page 3 :
-(y+1) =0y,+1=0> y= -1is an asymptote parallel to x -axis., The coefficient of highest power of y i.e of y? is 1, a constant., Therefore there is no asymptote parallel to y -axis., , 3) Find the aapmpintes parallel to the coordinate axes for the, following curves © ae a >S=1, , The given equation may be rewritten as y?a” + b?x? — x?y? =0, y*a + (b* _ y?) x? =0, equating coefficient of highest power of x to zero, , b? -y?=05y*=b? sy = +bare the asymtotes parallel to x axis, the equation may be put in the form (a?— x”)y” + b?x? = 0 the, coefficient of highest, , power of y i.e (a? — x7) = 05 x? =a? > x = +aare the asymptotes, parallel to y axis, , EXERCISES:, , Find the asymptotes parallel to the coordinate axes for the following, curves:, , da?r? — (x —y)?(y* +07) =0, , 2)x*y?-y*=2

Page 4 :
To determine Asymptotes of general algebraic equation., , Working rule, , Let f(x,y) = 0 bean n™ degree equation representing the given, curve,, , Step 1: Arrange the terms in LHS of the polynomial equation to the, curve into groups of homogeneous expressions of the same degree in, the form H, + Hy_; + Hp_2 + ++... = 0 where H, consists of terms of, degree nana, , 2: Put x = 1,y = m in the left side of the equation written in step (1)., Step Then the equation takes the form ¢,(m) + dy-1(m) +, , $n_2(m) + =0, , 3: Solve the equation ¢, (m) = 0 to get the slopes of the asymptotes., Ste, , Let, 1m, ... be non repeated values of m., , p4: Use the formula c = — a for non repeated values of m, which, gives int Step ., C4, C2, ... Then the asymptotes corresponding to them are y = m,x +, C1, Y = M2x + cz etc., , If f4(m) = 0 and ¢,_;(m) ¥ 0 then there exists no asymptotes for, this valy:, , of m., , Step 5: If¢,(m) = 0 has a repeated root twice then use the formula,, 2g" n(m) + cf’n— 1(m) + ¢,_2(m) = 0 to find the corresponding, values of c, , In this case we get two parallel asymptotes., , 1.Find the asymtotes of the curve, , 2x3 — x2y — 2xy? + y? — 4x? + Bxy— 4x +1=0, , solution: coefficients of highest powers of x and y are constants., Hence there are no asymtotes parallel to the coordinate axes, The, given equation is rewritten in the form, , Put y=m,x=1, , Le (y? — 2xy? — x?y + 2x3) — 4x? + 8xy—4x+1=0, , in the equation, we get (m3 — 2m?—m+2)-4+8m-—4+1=0

Page 5 :
3 (m) = m? — 2m? — m + 2,$,(m) = —(4 — 8m), p; (mM) = —4, bp (m), =1, , asymptotes are given by $;(m) = 0 i.em? — 2m?-m+2=0, , m?(m—2)-—1(m—2)=0 => (m?-1)(m—- 2) =0, , (m—1)(m+1)(m—-2) =0>m=1,-1,2, —2(m) 3 -( —44+8m ), , , , we use ¢ = '3(m) 3 m2-4m-1, a (<tt8) teas, me OSN\3 = 41) 2, Lee (2-8) oy, mee \344-1)- 6, , coset “2,, meoc=~\W7-=8-1/)- 3, , the asymptotes are y = x +2,y = —x +2 andy = 2x-—4, 2: Find all the asymptotes of the curve, x3 + 2x*y+ xy?-x*-xy+2=0, , Solution : There are no asymptotes parallel to x -axis since the, coefficient of the highest power in sisaconstant., , The coefficient of the highest powerin y i.e., of y” is x and hence, asymptote parallel to y -axisis x = Oi.e., the y -axis., , the given equation is written in the form H3 + H; +H; +H») =0, ie (x? + 2x*y + xy?) —x? —xy+2=0, , Atx = 1,y =m, we get (1+ 2m+m?)—1—m+2=043(m) =, m*+2m-+1, ¢,(m) = —1—m,¢,(m) = 0 and ¢o( m) = 2, , The slopes of the asymptotes are given by, , ¢3(m) = 0iem?+2m+1=0+ >(m+1)?=0>m=-1,-1, Since the root is repeated, to find c, we use the formula, , Therefore the asymptotes corresponding to m = —1 are y = —x and, y = —x + 1. Thusthe asymptotes of the given curve are x = 0.x +y =, Ox+y—-1=0.