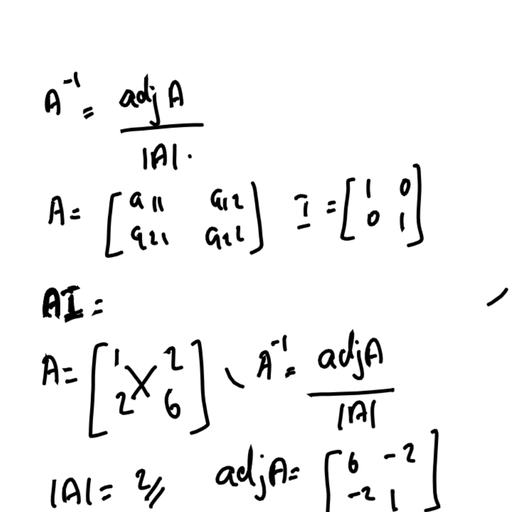Page 1 :
File Ref.No.59902/GA - IV - J3/2019/Admn, , UNIVERSITY OF CALICUT, Abstract, , General & Academic - CBCSS UG Regulations 2019 - Scheme and Syllabus of B.Sc Mathematics Programme, w.e.f 2020, Admission onwards -Incorporating Outcome Based Education - Implemented - Subject to ratification of Academic Council Orders Issued., G & A - IV - J, , U.O.No. 5657/2021/Admn, , Dated, Calicut University.P.O, 27.05.2021, , Read:-1) U.O.No. 9389/2020/Admn Dated,13.10.2020., 2) Item no.3 in the minutes of the meeting of Board of Studies in Mathematics, Dated, 31.03.2021., 3) Remarks of the Dean, Faculty of Science, Dated 16.04.2021., 4) Orders of the Vice Chancellor in the file of even no, Dated 17.04.2021., ORDER, , 1. The scheme and syllabus of B.Sc Mathematics Programme under CBCSS UG Regulations 2019 of, the University, w.e.f 2020 admission onwards has been implemented, vide paper read (1) above., , 2. The Board of Studies in Mathematics UG has resolved to incorpate Outcome Based Education (OBE), , in the scheme and syllabus of B.Sc Mathematics Programme, in tune with the new CBCSS UG, Regulations 2019 with effect from 2020 Admission onwards, vide paper read (2) above., , 3. The Dean, Faculty of Science, vide paper read (3) above, has approved to implement the scheme, and syllabus of B.Sc Mathematics Programme (CBCSS-UG-2019) incorporating Outcome Based, Education (OBE), in the existing syllabus forwarded by the Chairperson, Board of Studies in, Mathematics, in tune with the new CBCSS UG Regulations 2019 with effect from 2020 Admission, onwards., , 4. Considering the urgency, the Vice Chancellor has accorded sanction to implement the scheme and, , syllabus of B.Sc Mathematics Programme incorporating Outcome Based Education (OBE), in the, existing syllabus forwarded by the Chairperson, Board of Studies in Mathematics UG in tune with the, new CBCSS UG Regulations 2019 of the University with effect from 2020 Admission onwards, subject, to ratification by the Academic Council., , 5. Scheme and syllabus of B.Sc Mathematics (CBCSS) programme incorporating Outcome Based, Education (OBE) in the existing syllabus, in tune with CBCSS UG Regulations 2019, is therefore, implemented with effect from 2020 Admission onwards, subject to ratification by the Academic, Council., , 6. Orders are issued accordingly., 7. U.O.No. 9389/2020/Admn, Dated13.10.2020 is modified to this extend.( syllabus appended)., Ajitha P.P, Joint Registrar, To, , Principals of all affiliated colleges, Copy to: PS to VC/PA to PVC/ PA to Registrar/PA to CE/DR, DOA/JCE I/JCE IV/DoA/EX and EG, Sections/GA I F/CHMK Library/Information Centres/SF/DF/FC, Forwarded / By Order, Section Officer, , Page 1 of 115
Page 2 :
B.Sc. DEGREE PROGRAMME, CHOICE BASED CREDIT, SEMESTER SYSTEM, , (CBCSS-UG Regulations 2019), B.Sc. MATHEMATICS, (CORE, OPEN & COMPLEMENTARY COURSES), OBE implemented SYLLABUS, (Effective from 2020 admission onwards), , UNIVERSITY OF CALICUT, , Page 2 of 115
Page 3 :
1, , Preface, The LOCF (Learning Outcomes based Curriculum Framework) committee constituted by, University Grants Commission (UGC) has submitted its report concerning the syllabi for B.Sc., Mathematics and B.A./B.Sc. with Mathematics as a subject. The BoS Mathematics(UG),, keeping this report in mind, took steps for implementing the Outcome Based Education (OBE), in the existing syllabus, without changing the content of the existing syllabus., , Aims of Bachelor’s degree programme in Mathematics, The overall aim of B.Sc. Mathematics and B.A./B.Sc. with Mathematics as a Complementary, course is to, 1. create deep interest in learning mathematics;, 2. develop broad and balanced knowledge and understanding of definitions, concepts,, principles and theorems;, 3. familiarize the students with suitable tools of mathematical analysis to handle issues and, problems in mathematics and related sciences;, 4. enhance the ability of learners to apply the knowledge and skills acquired by them during, the programme to solve specific theoretical and applied problems in mathematics;, 5. provide students/learners sufficient knowledge and skills enabling them to undertake, further studies in mathematics and its allied areas on multiple disciplines concerned with, mathematics;, 6. encourage the students to develop a range of generic skills helpful in employment,, internships and social activities., , Page 3 of 115
Page 4 :
2, , Programme Outcomes, The programme outcome of the B.Sc Mathematics undergraduate course are the summation of, the expected course learning outcomes given below., PO1 Disciplinary knowledge :, Capability of demonstrating comprehensive knowledge of mathematics and understanding, of one or more disciplines which form a part of an undergraduate programme of study., PO2 Communications skills :, (i) Ability to communicate various concepts of mathematics effectively using examples, and their geometrical visualizations., (ii) Ability to use mathematics as a precise language of communication in other branches, of human knowledge., (iii) Ability to show the importance of mathematics as precursor to various scientific, developments since the beginning of the civilization., PO3 Critical thinking :, Ability to employ critical thinking in understanding the concepts in every area of mathematics., PO4 Analytical reasoning :, Ability to analyze the results and apply them in various problems appearing in different, branches of mathematics., PO5 Problem solving :, (i) Capability to solve problems using concepts of linear algebra., (ii) Capability to solve various models such as growth and decay models, radioactive, decay model, LCR circuits and population models using techniques of differential, equations., (iii) Ability to solve linear system of equations, linear programming problems and network flow problems., (iv) Ability to provide new solutions using the domain knowledge of mathematics acquired during this programme., PO6 Research-related skills :, (i) Capability for inquiring about appropriate questions relating to the concepts in, various fields of mathematics., (ii) To know about the advances in various branches of mathematics., , Page 4 of 115
Page 5 :
3, , PO7 Information/digital literacy : Capability to use appropriate software to solve system, of equations and differential equations., PO8 Self-directed learning :, Ability to work independently and do in-depth study of various notions of mathematics., PO9 Lifelong learning :, Ability to think, acquire knowledge and skills through logical reasoning and to inculcate, the habit of self-learning., PO10 Application skills :, Ability to apply the acquired knowledge in all aspects., PO11 Experimental skills :, PO12 Moral and ethical awareness/reasoning :, Ability to identify unethical behaviour such as fabrication, falsification ormisrepresentation of data and adopting objective, unbiased and truthful actions in all aspects, , Page 5 of 115
Page 6 :
4, , Course learning outcomes, Course learning outcomes of each course in B.Sc. Mathematics and B.A./B.Sc. Programme, with Mathematics as a complementary course have been enshrined in the beginning of course, contents of each course., , Basic Analysis, , Numerical Analysis, , Linear Programming, , Introduction to Geometry, , Real Analysis, , Complex Analysis, , Calculus of Multi variable, , Differential Equations, , X, , X, , X, , X, , X, , Communication skills, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , Critical thinking, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , Analytical thinking, , X, , X, , X, , X, , X, , X, , Problem solving, , X, , X, , X, , X, , X, , X, , X, , X, , Research related skills, , X, , X, , X, , X, , X, , X, , Information/ Digital, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , Self-directed learning, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , Lifelong learning, , X, , Applicational skills, , X, , X, , X, , X, , X, , X, , Experimental learning, , X, , X, , X, , Employability options, , X, , Ethics, , X, , and Theory of Equations, , Abstract Algebra, , X, , Single Variable – 2, , X, , Calculus of, , X, , Single Variable – 1, , X, , Calculus of, , X, , Number Theory, , X, , Disciplinary, , Basic Logic and, , X, , outcomes, , X, , Programme, , Linear Algebra, , CORE COURSES, , knowledge, , X, X, , X, , X, , X, , X, , X, X, , Literacy, X, X, , X, X, , X, , X, X, , X, , X, , X, , X, , X, X, , X, , X, , X, , X, , X, , X, , X, , X, , X, , X, X, , X, , X, , X, , X, , X, , X, , Page 6 of 115
Page 7 :
5, , ELECTIVE COURSES, Programme outcomes, , Graph, , Topology of Metric, , Mathematical, , Theory, , spaces, , with Python and LATEX, , Disciplinary knowledge, , X, , X, , X, , Communication skills, , X, , X, , X, , Critical thinking, , X, , X, , Analytical thinking, , X, , X, , Problem solving, , X, , X, , X, , Research related skills, , X, , X, , X, , Information/Digital Literacy, , X, , X, , X, , Self-directed learning, , X, , X, , X, , Lifelong learning, , X, , X, , X, , Applicational skills, , X, , X, , X, , Experimental learning, , X, , Employability options, , X, , X, , X, , Ethics, , X, , X, , X, , Programming, , X, , OPEN COURSES, Programme outcomes, , Applied, , Discrete Mathematics, , Linear, , Mathematics for, , Calculus, , for Basic and Applied, , Mathematical, , Decision Making, , Sciences, , Models, , Disciplinary knowledge, , X, , X, , X, , X, , Communication skills, , X, , X, , X, , X, , Critical thinking, , X, , X, , X, , X, , Analytical thinking, , X, , X, , X, , Problem solving, , X, , X, , X, , X, , Research related skills, , X, , X, , X, , X, , Information/ Digital, , X, , X, , X, , X, , Self-directed learning, , X, , X, , X, , X, , Lifelong learning, , X, , X, , X, , X, , Applicational skills, , X, , X, , X, , X, , Experimental learning, , X, , X, , X, , X, , Employability options, , X, , X, , X, , X, , Ethics, , X, , X, , X, , X, , Literacy, , Page 7 of 115
Page 8 :
6, , COMPLEMENTARY COURSES, Programme, , Mathematics, , Mathematical, , outcomes, MTS1 C01, , MTS2 C02, , MTS3 C03, , MTS4 C04, , MEC1 C01, , MEC2 C02, , MEC3 C03, , MEC4 C04, , Economics, , Disciplinary knowledge, , X, , X, , X, , X, , X, , X, , X, , X, , Communication skills, , X, , X, , X, , X, , X, , X, , X, , X, , Critical thinking, , X, , X, , X, , X, , X, , X, , X, , X, , Analytical thinking, , X, , X, , X, , Problem solving, , X, , X, , X, , Research related skills, , X, X, , X, , X, , X, , X, X, , X, , X, , Information/ Digital Literacy, , X, , X, , X, , X, , X, , X, , X, , X, , Self-directed learning, , X, , X, , X, , X, , X, , X, , X, , X, , Lifelong learning, , X, , Applicational skills, , X, , X, X, , Experimental learning, Employability options, , X, , Ethics, , X, , X, , X, , X, , X, , X, X, , X, , X, , X, , X, , X, X, , X, X, , X, , X, X, , X, , X, , X, , Page 8 of 115
Page 9 :
7, , Core Courses, The following courses are compulsory for BSc Mathematics programme., , Code, , Name of the course, , Semester, , No of contact, , Internal, , External, , Total, , Exam dur.(Hrs), , 1, , MTS1B01, , Basic Logic and Number Theory, , 1, , 4, , 4, , 20, , 80, , 100, , 2.5, , 2, , MTS2B02, , Calculus of Single Variable-1, , 2, , 4, , 4, , 20, , 80, , 100, , 2.5, , 3, , MTS3B03, , Calculus of Single Variable-2, , 3, , 5, , 4, , 20, , 80, , 100, , 2.5, , 4, , MTS4B04, , Linear Algebra, , 4, , 5, , 4, , 20, , 80, , 100, , 2.5, , 5, , MTS5B05, , Abstract Algebra, , 5, , 5, , 4, , 20, , 80, , 100, , 2.5, , 6, , MTS5B06, , Basic Analysis, , 5, , 5, , 4, , 20, , 80, , 100, , 2.5, , 7, , MTS5B07, , Numerical Analysis, , 5, , 4, , 3, , 15, , 60, , 75, , 2, , 8, , MTS5B08, , Linear Programming, , 5, , 3, , 3, , 15, , 60, , 75, , 2, , 9, , MTS5B09, , Introduction to Geometry and, , 5, , 3, , 3, , 15, , 60, , 75, , 2, , 5, , 2, , 5, , 3, , 3, , 15, , 60, , 75, , 2, , hours/Week, Credits, , Sl. No, , Max. Marks, , Theory of Equations, Project OR, Research Methodology, 10, , Open Course (Offered by Other, Departments), , 11 MTS6B10, , Real Analysis, , 6, , 5, , 5, , 20, , 80, , 100, , 2.5, , 12 MTS6B11, , Complex Analysis, , 6, , 5, , 5, , 20, , 80, , 100, , 2.5, , 13 MTS6B12, , Calculus of Multi variable, , 6, , 5, , 4, , 20, , 80, , 100, , 2.5, , 14 MTS6B13, , Differential Equations, , 6, , 5, , 4, , 20, , 80, , 100, , 2.5, , 15 MTS6B14, , Elective, , 6, , 3, , 2, , 15, , 60, , 75, , 2, , 6, , 2, , 2, , 15, , 60, , 75, , 16 MTS6P15(PR) Project Viva OR, MTS6P15, , Research Methodology, , 2, 34, , 58, , 1450, , Page 9 of 115
Page 10 :
8, , Elective Courses, One of the following three courses (Code MTS6B14(E01), MTS6B14(E02) and MTS6B14(E03)) can, be offered in the sixth semester as an elective course., , Code, , Name of the course, , Semester, , No of contact, , Credits, , Internal, , External, , Total, , Exam dur.(Hrs), , 1, , MTS6B14(E01), , Graph Theory, , 6, , 3, , 2, , 15, , 60, , 75, , 2, , 2, , MTS6B14(E02), , Topology of Metric Spaces, , 6, , 3, , 2, , 15, , 60, , 75, , 2, , 3, , MTS6B14(E03), , Mathematical, , 6, , 3, , 2, , 15, , 60, , 75, , 2, , Programming, , hours/Week, , Sl. No, , Max. Marks, , with Python and LATEX, , Open Courses, One of the following four courses (MTS5D01, MTS5D02, MTS5D03 and MTS5D04) can be offered, in the fifth semester as an open course for the students not having Mathematics as Core Course and, Mathematics and Physics dual Core programme., , Name of the course, , Semester, , No of contact, , Credits, , Internal, , External, , Total, , Unty. exam, , 1, , MTS5D01, , Applied Calculus, , 5, , 3, , 3, , 15, , 60, , 75, , 2, , 2, , MTS5D02, , Discrete Mathematics for Basic and, , 5, , 3, , 3, , 15, , 60, , 75, , 2, , Dur. (Hrs), , Code, , hours/Week, , Sl. No, , Max. Marks, , Applied Sciences, 3, , MTS5D03, , Linear Mathematical Models, , 5, , 3, , 3, , 15, , 60, , 75, , 2, , 4, , MTS5D04, , Mathematics for Decision Making, , 5, , 3, , 3, , 15, , 60, , 75, , 2, , Page 10 of 115
Page 11 :
9, , Complementary Courses, , Name of the course, , Semester, , No of contact, , Credits, , Internal, , External, , Total, , Unty. exam, , 1, , MTS1C01, , Mathematics – 1, , 1, , 4, , 3, , 15, , 60, , 75, , 2, , 2, , MTS2C02, , Mathematics – 2, , 2, , 4, , 3, , 15, , 60, , 75, , 2, , 3, , MTS3C03, , Mathematics – 3, , 3, , 5, , 3, , 15, , 60, , 75, , 2, , 4, , MTS4C04, , Mathematics – 4, , 4, , 5, , 3, , 15, , 60, , 75, , 2, , Dur. (Hrs), , Code, , hours/Week, , Sl. No, , Max. Marks, , Mathematical Economics, 1, , MEC1C01, , Mathematical Economics, , 1, , 4, , 3, , 15, , 60, , 75, , 2, , 2, , MEC2C02, , Mathematical Economics, , 2, , 4, , 3, , 15, , 60, , 75, , 2, , 3, , MEC3C03, , Mathematical Economics, , 3, , 5, , 3, , 15, , 60, , 75, , 2, , 4, , MEC4C04, , Mathematical Economics, , 4, , 5, , 3, , 15, , 60, , 75, , 2, , Credit Distribution of BSc Mathematics Programme, Sl., , Course, , Credits, , 1, , English, , 22, , 2, , Additional Language, , 16, , No, , 3, , Core Course, , 13 Courses, , 51, , 1 Elective, , 2, , Project OR Research Methodology, , 2, , 55, , 4, , Complementary course - I, , 12, , 5, , Complementary course - II, , 12, , 6, , Open Course, , 3, , Total, , 120, , Page 11 of 115
Page 12 :
10, , Scheme of Evaluation, The evaluation scheme for each course shall contain two parts: internal evaluation and external, evaluation., , Internal Evaluation, 20% of the total marks in each course are for internal evaluation. The colleges shall send only, the marks obtained for internal examination to the university., , Components of Internal Evaluation, Sl, No, 1, 2, 3, 4, , Components, Class Room Participation, (Attendance), Assignment, Seminar, Test paper, Total, , Marks (for Courses with, Max. Marks 75), 3, , Marks (for Courses with, Max. Marks 100), 4, , 3, 3, 6, 15, , 4, 4, 8, 20, , a) Percentage of Class Room Participation (Attendance) in a Semester and, Eligible Internal Marks, % of Class Room Participation (At-, , Out of 3 (Maximum, , Out of 4 (Maximum, , tendance), , internal marks is 15), , internal marks is 20), , 50% ≤ CRP < 75%, , 1, , 1, , 75% ≤ CRP < 85%, , 2, , 2, , 85% and above, , 3, , 4, , CRP means % of class room participation (Attendance), b) Percentage of Marks in a Test Paper and Eligible Internal Marks, Range of Marks in test paper (TP), Less than 35%, 35% ≤ T P < 45%, 45% ≤ T P < 55%, 55% ≤ T P < 65%, 65% ≤ T P < 85%, 85% ≤ T P ≤ 100%, , Out of 6 (Maximum internal marks is 15), 1, 2, 3, 4, 5, 6, , Out of 8 (Maximum internal marks is 20), 1, 2, 3, 4, 6, 8, , Page 12 of 115
Page 13 :
11, , Evaluation of Project, 1. Evaluation of the Project Report shall be done under Mark System., 2. The evaluation of the project will be done at two stages:, • Internal Assessment (supervising teachers will assess the project and award internal Marks), • External evaluation (external examiner appointed by the University), 3. Grade for the project will be awarded to candidates, combining the internal and external marks., 4. The internal to external components is to be taken in the ratio 1 : 4., Assessment of different components may be taken as below., , Internal assessment of Project (15 Marks), (Supervising Teacher will assess the Project and award internal Marks), Sl. No., , Components, , Internal Marks, , 1, , Originality, , 3, , 2, , Methodology, , 3, , 3, , Scheme / Organization of Report, , 4.5, , 4, , Viva Voce, , 4.5, Total, , 15, , External Evaluation of Project (60 Marks), (To be done by the External Examiner appointed by the University), Sl. No., , Components, , External Marks, , 1, , Relevance of the Topic, Statement of Objectives, , 12, , 2, , Reference/ Bibliography, Presentation, quality of Analysis/ Use of, , 12, , Statistical Tools., 3, , Findings and recommendations, , 18, , 4, , Viva-Voce, , 18, Total, , 60, , Page 13 of 115
Page 14 :
12, , Pattern of Question Paper for University Examinations, , Section A, , Section B, , Section C, , For Courses with Maximum Ex-, , For Courses with Maximum Ex-, , ternal Marks 80 (2.5 Hrs), , ternal Marks 60 (2 Hrs), , Short answer type carries 2, , Short answer type carries 2, , Ceiling - 25, , marks each -, , marks each -, , 15 questions, , 12 questions, , Paragraph/Problem, , type, , Ceiling - 35, , carries 5 marks each -, , carries 5 marks each -, , 8 questions, , 7 questions, , Essay, , type, , carries, , 10, , 2 × 10 = 20, , marks (2 out of 4), Total, , Paragraph/Problem, , Essay, , type, , carries, , Ceiling - 20, , type, , Ceiling - 30, , 10, , 1 × 10 = 10, , marks (1 out of 2), 80, , 60, , * Questions are to be evenly distributed over the entire syllabus. At least 20% of questions from, each module must be included in each section of the question paper for courses having four modules, in the syllabus and 30% for courses having three modules in the syllabus., , Page 14 of 115
Page 15 :
., , SYLLABUS, , Page 15 of 115
Page 16 :
15, , SEMESTER – I, MTS1B01 : BASIC LOGIC AND NUMBER THEORY, 4 Hours/Week, , 4 Credits 100 Marks[Int: 20 + Ext : 80], , Aims, Objectives and Outcomes, Logic, the study of principles of techniques and reasoning, is fundamental to every branch of, learning. Besides, being the basis of all mathematical reasoning, it is required in the field of computer, science for developing programming languages and also to check the correctness of the programmes., Electronic engineers apply logic in the design of computer chips. The first module discusses the, fundamentals of logic, its symbols and rules. This enables one to think systematically, to express ideas, in precise and concise mathematical terms and also to make valid arguments. How to use logic to arrive, at the correct conclusion in the midst of confusing and contradictory statements is also illustrated., The classical number theory is introduced and some of the very fundamental results are discussed, in other modules. It is hoped that the method of writing a formal proof, using proof methods discussed, in the first module, is best taught in a concrete setting, rather than as an abstract exercise in logic., Number theory, unlike other topics such as geometry and analysis, doesn’t suffer from too much, abstraction and the consequent difficulty in conceptual understanding. Hence, it is an ideal topic for, a beginner to illustrate how mathematicians do their normal business. By the end of the course, the, students will be able to enjoy and master several techniques of problem solving such as recursion,, induction etc., the importance of pattern recognition in mathematics, the art of conjecturing and a, few applications of number theory. Enthusiastic students will have acquired knowledge to read and, enjoy on their own a few applications of number theory in the field of art, geometry and coding theory., Successful completion of the course enables students to, • Prove results involving divisibility, greatest common divisor, least common multiple and a few, applications., • Understand the theory and method of solutions of LDE., • Solve linear congruent equations., • Learn three classical theorems viz. Wilson’s theorem, Fermat’s little theorem and Euler’s theorem and a few important consequences., , Page 16 of 115
Page 17 :
16, , Syllabus, Text (1), , Discrete Mathematics with Applications :, , Thomas Koshy, Elsever Academic, , Press(2004) ISBN:0-12-421180-1, Text (2), , Elementary Number Theory with Applications (2/e) : Thomas Koshy, Elsever Academic Press(2007) ISBN:978-0-12-372487-8, , Module – I, , Text (1), , (15 hrs), , 1.1: Propositions- definition, Boolean (logic) variables, Truth Value, Conjunction, Boolean expression,, Disjunction (inclusive and exclusive), Negation, Implication, Converse, Inverse and Contra positive,, Biconditional statement, Order of Precedence, Tautology Contradiction and Contingency [‘Switching, Networks’ omitted], 1.2 : Logical equivalences- laws of logic [‘Equivalent Switching Networks’ ‘Fuzzy logic’ & ‘Fuzzy, decisions’omitted], 1.3 : Quantifiers- universal & existential, predicate logic, 1.4 : Arguments- valid and invalid arguments, inference rules, 1.5: Proof Methods – vacuous proof, trivial proof, direct proof, indirect proof-contrapositive & contradiction, proof by cases, Existence proof- constructive & non constructive, counter example, , Module – II, , Text (2), , (12 hrs), , 1.3 : Mathematical induction- well ordering principle, simple applications, weak version of principle of, mathematical induction, illustrations, strong version of induction (second principle of MI), illustration, 1.4 : Recursion- recursive definition of a function, illustrations., 2.1: The division algorithm – statement and proof, div & mod operator, card dealing, The two, queens puzzle (simple applications), pigeonhole principle and division algorithm, divisibility relation,, illustration, divisibility properties, union intersection and complement-inclusion exclusion principle &, applications, even and odd integers., 2.5: Prime and Composite Numbers- definitions, infinitude of primes, [‘algorithm 2.4‘ omitted] The, sieve of Eratosthenes, a number theoretic function, prime number theorem (statement only), distribution of primes (upto and including Example 2.25). [rest of the section omitted], , Page 17 of 115
Page 18 :
17, , Module – III, , Text (2), , (17 hrs), , 3.1 : Greatest Common Divisor- gcd, symbolic definition, relatively prime integers, Duncan’s identity,, Polya’s theorem, infinitude of primes, properties of gcd, linear combination, gcd as linear combination,, an alternate definition of gcd, gcd of n positive integers, a linear combination of n positive integers,, pairwise relatively prime integers, alternate proof for infinitude of prime., 3.2: The Euclidean Algorithm- The Euclidean algorithm [algorithm 3.1 omitted], A jigsaw puzzle,, Lame’s theorem (statement only; proof omitted), 3.3: The Fundamental Theorem of Arithmetic- Euclid’s lemma on division of product by a prime,, fundamental theorem of arithmetic, Canonical Decomposition, number of trailing zeros, highest power, of a prime dividing!, [only statement of Theorem 3.14 required; proof omitted] Distribution of Primes, Revisited, Dirichlet’s Theorem (statement only), 3.4 : Least Common Multiple- definition, canonical decomposition to find lcm, relationship between, gcd and lcm, relatively prime numbers and their lcm, 3.5: Linear Diophantine Equations – LDE in two variables, conditions to have a solution, Aryabhatta’s, method, number of solutions, general solution, Mahavira’s puzzle, hundred fowls puzzle, Monkey and, Coconuts Puzzle, [‘Euler’s method for solving LDE’s omitted] Fibonacci numbers and LDE, LDE in, more number of variables and their solutions- Theorem 3.20, , Module – IV, , Text (2), , (20 hrs), , 4.1: Congruences - congruence modulo m, properties of congruence, characterization of congruence,, least residue, [‘Friday-the-Thirteenth’ omitted], congruence classes, A Complete Set of Residues Modulo m, properties of congruence, use of congruence to find the remainder on division, [‘Modular, Exponentiation’ method omitted], Towers of Powers Modulo m, further properties of congruence and, their application to find remainder [‘Monkey and Coconut Puzzle revisited’(example 4.17) omitted], congruences of two numbers with different moduli, 4.2: Linear Congruence- solvability, uniqueness of solution, incongruent solutions, Modular Inverses,, applications, 5.1: Divisibility Tests-Divisibility Test for 10, Divisibility Test for 5, Divisibility Test for 2i , Divisibility, Tests for 3 and 9, Divisibility Test for 11 [ rest of the section from Theorem 5.1 onwards omitted], 7.1: Wilson’s Theorem- self invertible modulo prime, Wilson’s theorem and its converse [‘Factorial,, Multifactorial and Primorial Primes’ omitted], 7.2: Fermat’s Little Theorem(FLT)- FLT and its applications, [Lagrange’s alternate proof of Wilson’s, theorem omitted], inverse of a modulo p using FLT, application-solution of linear congruences [ ‘Factors, of 2n +1‘ omitted], extension of FLT in various directions [‘The Pollard p−1 factoring method’ omitted], 7.4 : Euler’s Theorem- motivation, Euler’s Phi Function φ, Euler’s Theorem, applications, generalisation of Euler’s theorem (koshy), , Page 18 of 115
Page 19 :
18, , References:, 1. Susanna S Epp: Discrete Mathematics with Applications(4/e) Brooks/ Cole Cengage Learning(2011) ISBN: 978-0-495-39132-6, 2. Kenneth H. Rosen: Discrete Mathematics and Its Applications(7/e) McGraw-Hill, NY (2007), ISBN: 978-0-07-338309-5, 3. David M. Burton : Elementary Number Theory(7/e) McGraw-Hill (2011) ISBN: 978-0- 07338314-9, 4. Gareth A. Jones and J. Mary Jones: Elementary Number Theory, Springer Undergraduate, Mathematics Series(1998) ISBN: 978-3-540-76197-6, 5. Underwood Dudley : Elementary Number Theory(2/e), Dover Publications (2008) ISBN : 9780-486-46931-7, 6. James K Strayer : Elementary Number Theory, Waveland Press, inc. (1994), ISBN : 978-157766-224-2, 7. Kenneth H. Rosen: Elementary Number Theory(6/e), Pearson Education (2018), ISBN: 978-013-43100-531-1, , Page 19 of 115
Page 20 :
19, , SEMESTER – II, MTS2B02 : CALCULUS OF SINGLE VARIABLE – 1, 4 Hours/Week, , 4 Credits 100 Marks[Int: 20 + Ext : 80], , Aims, Objectives and Outcomes, The mathematics required for viewing and analyzing the physical world around us is contained, in calculus. While Algebra and Geometry provide us very useful tools for expressing the relationship, between static quantities, the concepts necessary to explore the relationship between moving/changing, objects are provided in calculus. The objective of the course is to introduce students to the fundamental, ideas of limit, continuity and differentiability and also to some basic theorems of differential calculus., It is also shown how these ideas can be applied in the problem of sketching of curves and in the, solution of some optimization problems of interest in real life. This is done in the first two modules., The next two modules deal with the other branch of calculus viz. integral calculus. Historically,, it is motivated by the geometric problem of finding out the area of a planar region. The idea of, definite integral is defined with the notion of limit. A major result is the Fundamental Theorem of, Calculus, which not only gives a practical way of evaluating the definite integral but establishes the, close connection between the two branches of Calculus. The notion of definite integral not only solves, the area problem but is useful in finding out the arc length of a plane curve, volume and surface, areas of solids and so on. The integral turns out to be a powerful tool in solving problems in physics,, chemistry, biology, engineering, economics and other fields. Some of the applications are included in, the syllabus., , Page 20 of 115
Page 21 :
20, , Syllabus, Text, , Calculus: Soo T Tan Brooks/Cole, Cengage Learning(2010) ISBN: 978-0-534-46579-7, , Module – I, , (20 hrs), , (Functions and Limits), 0.2 : Functions and their Graphs - Definition of a Function, Describing Functions, Evaluating Functions, Finding the Domain of a Function, The Vertical Line Test, Piecewise Defined Functions, Even, and Odd Functions (quick review), 0.4 : Combining functions - Arithmetic Operations on Functions, Composition of Functions, Graphs of, Transformed, , Functions,, , Vertical, , Translations,, , Horizontal, , Translations,, , Vertical, , Stretching and Compressing, Horizontal Stretching and Compressing, Reflecting, 1.1 : Intuitive introduction to Limits - A Real Life Example, Intuitive Definition of a Limit, One-Sided, Limits, Using Graphing Utilities to Evaluate Limits, 1.2 : Techniques for finding Limits - Computing Limits Using the Laws of Limits, Limits of Polynomial, and Rational Functions, Limits of Trigonometric Functions, The Squeeze Theorem., 1.3 : Precise Definition of a Limit - � − δ definition. A Geometric Interpretation, Some illustrative, examples., 1.4 : Continuous Functions - Continuity at a Number, Continuity at an Endpoint, Continuity on an, Interval, Continuity of Composite Functions, Intermediate Value Theorem., 1.5 : Tangent Lines and Rate of change - An Intuitive Look, Estimating the Rate of Change of, a Function from its Graph, More Examples Involving Rates of Change, Defining a Tangent Line,, Tangent Lines, Secant Lines, and Rates of Change, 2.1 : The Derivatives - Definition, Using the Derivative to Describe the Motion of the Maglev, Differentiation, Using the Graph of f to Sketch the Graph of f 0 Differentiability, Differentiability and, Continuity., 2.4 : The role of derivative in the real world - Motion Along a Line, Marginal Functions in Economics, 2.9 : Differentials and Linear Approximations - increments, Differentials, Error Estimates, Linear, Approximations, Error in Approximating ∆y by dy., , Page 21 of 115
Page 22 :
21, , Module – II, , (17 hrs), , (Applications of the Derivative), 3.1 : Extrema of Functions - Absolute Extrema of Functions, Relative Extrema of Functions, Fermat’s, Theorem, Finding the Extreme Values of a Continuous Function on a Closed Interval, An Optimization, Problem, 3.2 : The Mean Value Theorem - Rolle’s Theorem, The Mean Value Theorem, Some Consequences of, the Mean Value Theorem, Determining the number of zeros of a function., 3.3 : Increasing and Decreasing Functions - definition, inferring the behaviour of function from sign, of derivative, Finding the relative extrema of a Function, first derivative test, 3.4 : Concavity and Inflection points - Concavity, Inflection Points, The Second Derivative Test, The, Roles of f 0 and f 00 in Determining the Shape of a Graph, 3.5 : Limits involving Infinity; Asymptotes - Infinite Limits, Vertical Asymptotes, Limits at Infinity,, Horizontal Asymptotes, Infinite Limits at Infinity, Precise Definitions, 3.6 : Curve Sketching - The Graph of a Function, Guide to Curve Sketching, Slant Asymptotes,, Finding Relative Extrema Using a Graphing Utility, 3.7 : Optimization Problems - guidelines for finding absolute extrema, Formulating Optimization, Problems- application involving several real life problems, , Module – III, , (14 hrs), , (Integration), 4.1 : Anti derivatives, Indefinite integrals, Basic Rules of Integration, a few basic integration formulas, and rules of integration, Differential Equations, Initial Value Problems, 4.3 : Area - An Intuitive Look, The Area Problem, Defining the Area of the Region Under the Graph, of a Function-technique of approximation [‘Sigma Notation’ and ‘Summation Formulas’ Omitted] An, Intuitive Look at Area (Continued), Defining the Area of the Region Under the Graph of a Functionprecise definition, Area and Distance, 4.4 : The Definite Integral - Definition of the Definite Integral, Geometric Interpretation of the Definite, Integral, The Definite Integral and Displacement, Properties of the Definite Integral, More General, Definition of the Definite Integral, 4.5 :, , The Fundamental Theorem of Calculus - How Are Differentiation and Integration, , Related?, The Mean Value Theorem for Definite Integrals, The Fundamental Theorem of, Calculus: Part I, inverse relationship between differentiation and integration, Fundamental Theorem of Calculus: Part 2, Evaluating Definite Integrals Using Substitution, Definite Integrals of Odd, and Even Functions, The Definite Integral as a Measure of Net Change., , Page 22 of 115
Page 23 :
22, , Module – IV, , (13 hrs), , (Applications of Definite Integral), 5.1 : Areas between Curves - A Real Life Interpretation, The Area Between Two Curves, Integrating, with Respect to y-adapting to the shape of the region, What happens when the Curves Intertwine?, 5.2 : Volume - Solids of revolution, Volume by Disk Method, Region revolved about the x-axis, Region, revolved about the y-axis, Volume by the Method of Cross Sections [‘Washer Method’omitted], 5.4 : Arc Length and Areas of surfaces of revolution- Definition of Arc Length, Length of a Smooth, Curve, arc length formula, The Arc Length Function, arc length differentials, Surfaces of Revolution,, surface area as surface of revolution,, 5.5 : Work-Work Done by a Constant Force, Work Done by a Variable Force, Hook’s Law, Moving, non rigid matter, Work done by an expanding gas, 5.7: Moments and Center of Mass - Measures of Mass, Center of Mass of a System on a Line, Center, of Mass of a System in the Plane, Center of Mass of Laminas [upto and including Example 3; rest of, the section omitted], , References:, 1. Joel Hass, Christopher Heil & Maurice D. Weir : Thomas’ Calculus (14/e), Pearson (2018), ISBN: 0134438981, 2. Robert A Adams & Christopher Essex : Calculus Single Variable (8/e) Pearson Education, Canada (2013) ISBN: 0321877403, 3. Jon Rogawski & Colin Adams : Calculus Early Transcendentals (3/e) W. H. Freeman and, Company(2015) ISBN: 1319116450, 4. Anton, Bivens & Davis : Calculus Early Transcendentals (11/e) John Wiley & Sons, Inc.(2016), ISBN: 1118883764, 5. James Stewart : Calculus (8/e) Brooks/Cole Cengage Learning(2016) ISBN: 978-1-285-74062-1, 6. Jerrold Marsden & Alan Weinstein : Calculus I and II (2/e) Springer Verlag NY (1985) ISBN:0387-90974-5, ISBN: 0-387-90975-3, , Page 23 of 115
Page 24 :
23, , SEMESTER – III, MTS3B03 : CALCULUS OF SINGLE VARIABLE–2, 5 Hours/Week, , 4 Credits 100 Marks[Int: 20 + Ext : 80], , Aims, Objectives and Outcomes, Using the idea of definite integral developed in previous semester, the natural logarithm function, is defined and its properties are examined. This allows us to define its inverse function namely, the natural exponential function and also the general exponential function. Exponential functions, model a wide variety of phenomenon of interest in science, engineering, mathematics and economics., They arise naturally when we model the growth of a biological population, the spread of a disease, the, radioactive decay of atoms, and the study of heat transfer problems and so on. We also consider certain, combinations of exponential functions namely hyperbolic functions that also arise very frequently in, applications such as the study of shapes of cables hanging under their own weight., After this, the students are introduced to the idea of improper integrals, their convergence and, evaluation. This enables to study a related notion of convergence of a series, which is practically done, by applying several different tests such as integral test, comparison test and so on. As a special case,, a study on power series-their region of convergence, differentiation and integration etc.,-is also done., A detailed study of plane and space curves is then taken up. The students get the idea of, parametrization of curves, they learn how to calculate the arc length, curvature etc. using parametrization and also the area of surface of revolution of a parametrized plane curve. Students are introduced, into other coordinate systems which often simplify the equation of curves and surfaces and the relationship between various coordinate systems are also taught. This enables them to directly calculate, the arc length and surface areas of revolution of a curve whose equation is in polar form. At the, end of the course, the students will be able to handle vectors in dealing with the problems involving, geometry of lines, curves, planes and surfaces in space and have acquired the ability to sketch curves, in plane and space given in vector valued form., , Page 24 of 115
Page 25 :
24, , Syllabus, Text, , Calculus: Soo T Tan Brooks/Cole, Cengage Learning(2010) ISBN: 978-0-534-46579-7, , Module – I, , (20 hrs), , (The Transcendental Functions), 6.1 : The Natural logarithmic function - definition, The Derivative of ln x, Laws of Logarithms, The, Graph of the Natural Logarithmic Function, The Derivatives of Logarithmic Functions, Logarithmic, Differentiation, Integration Involving Logarithmic Functions, 6.2 : Inverse Functions - The Inverse of a Function, The Graphs of Inverse Functions, Which Functions, have Inverses?, Finding the Inverse of a Function, Continuity and Differentiability of Inverse Functions., 6.3 : Exponential Functions - The number e, Defining the Natural Exponential Function, properties, The Laws of Exponents, The Derivatives of Exponential Functions, Integration of the Natural, Exponential Function, 6.4 : General Exponential and Logarithmic Functions - Exponential Functions with Base a, laws of, exponents, The Derivatives of ax , au , Graphs of y = ax , integrating ax , Logarithmic Functions with, Base a, change of base formula, The Power Rule (General Form), The Derivatives of Logarithmic, Functions with Base a, The Definition of the Number e as a Limit[ ‘Compound Interest’ omitted], 6.5 : Inverse trigonometric functions - definition, graph, inverse properties, Derivative of inverse, trigonometric functions, Integration Involving Inverse Trigonometric Functions, 6.6 : Hyperbolic functions - The Graphs of the Hyperbolic Functions, Hyperbolic Identities, Derivatives and Integrals of Hyperbolic Functions, Inverse Hyperbolic Functions, representation in terms of, logarithmic function, Derivatives of Inverse Hyperbolic Functions, An Application, 6.7 : Indeterminate forms and L Hospital’s rule-motivation, The Indeterminate forms, Indeterminate forms ∞ − ∞ and 0 · ∞. The Indeterminate forms 00 , ∞0 and 1∞, , Module – II, , ∞, 0, and, , The, 0, ∞, , (20 hrs), , (Infinite Sequences and Series), 7.6 : Improper integrals - definition, Infinite Intervals of Integration, Improper Integrals with Infinite, Discontinuities, A Comparison Test for Improper Integrals, 9.1 :, , Sequences - definition, recursive definition, Limit of a Sequence, limit laws, squeeze, , theorem, Bounded Monotonic Sequences, definition, monotone convergence theorem (only statement;, its proof omitted), , Page 25 of 115
Page 26 :
25, , 9.2 : Series - defining the sum, convergence and divergence, Geometric Series, The Harmonic Series,, The Divergence Test, Properties of Convergent Series, 9.3 : The Integral Test - investigation of convergence, integral test, The p - series, its convergence and, divergence, 9.4 : The Comparison Test - test series, The Comparison Test, The Limit Comparison Test, 9.5 : Alternating Series - definition, the alternating series test, its proof, examples, Approximating, the Sum of an Alternating Series by Sn, 9.6 : Absolute Convergence - definition, conditionally convergent, The Ratio Test, The Root Test,, Summary of Tests for Convergence and Divergence of Series, Rearrangement of Series, , Module – III, , (20 hrs), , 9.7 : Power Series - definition, Interval of Convergence, radius of convergence, Differentiation and, Integration of Power Series, 9.8 :, , Taylor and Maclaurin Series - definition, Taylor and Maclaurin series of functions,, , Techniques for Finding Taylor Series, 10.2 : Plane Curves and Parametric Equations - Why we use Parametric Equations, Sketching Curves, Defined by Parametric Equations, 10.3 : The Calculus of parametric equations - Tangent Lines to Curves Defined by Parametric Equad2 y, from Parametric Equations, The Length of a, tions, Horizontal and Vertical Tangents, Finding, dx2, Smooth Curve, The Area of a Surface of Revolution, 10.4 :, , Polar coordinate - The Polar Coordinate System, Relationship Between Polar and, , Rectangular Coordinates, Graphs of Polar Equations, Symmetry, Tangent Lines to Graphs of Polar Equations, 10.5 : Areas and Arc Lengths in polar coordinates - Areas in Polar Coordinates, area bounded by, polar curves, Area Bounded by Two Graphs, Arc Length in Polar Coordinates, Area of a Surface of, Revolution, Points of Intersection of Graphs in Polar Coordinates, , Module – IV, , (20 hrs), , 11.5 : Lines and Planes in Space - Equations of Lines in Space, parametric equation, symmetric, equation of a line, Equations of Planes in Space, standard equation, Parallel and Orthogonal Planes,, The Angle Between Two Planes, The Distance Between a Point and a Plane, 11.6 : Surfaces in Space - Traces, Cylinders, Quadric Surfaces, Ellipsoids, Hyperboloids of One Sheet,, Hyperboloids of Two Sheets, Cones, Paraboloids, Hyperbolic Paraboloids, , Page 26 of 115
Page 27 :
26, , 11.7 : Cylindrical and Spherical Coordinates - The Cylindrical Coordinate System, converting cylindrical to rectangular and vice verse, The Spherical Coordinate System, converting spherical to rectangular, and vice verse,, 12.1 : Vector Valued functions and Space Curves - definition of vector function, Curves Defined by, Vector Functions, [‘Example 7’ omitted] Limits and Continuity, 12.2 : Differentiation and Integration of Vector Valued Function - The Derivative of a Vector Function,, Higher Order Derivatives, Rules of Differentiation, Integration of Vector Functions, 12.3 : Arc length and Curvature - Arc Length of a space curve, Smooth Curves, Arc Length Parameter,, arc length function, Curvature, formula for finding curvature, Radius of Curvature., 12.4 : Velocity and Acceleration - Velocity, Acceleration, and Speed; Motion of a Projectile, 12.5 : Tangential and Normal Components of Acceleration - The Unit Normal, principal unit normal vector, Tangential and Normal Components of Acceleration [The subsections Kepler’s Laws of, Planetary Motion, and Derivation of Kepler’s First Law omitted], , References:, 1. Joel Hass, Christopher Heil & Maurice D. Weir : Thomas’ Calculus (14/e), Pearson (2018), ISBN: 0134438981, 2. Robert A Adams & Christopher Essex : Calculus Single Variable (8/e) Pearson Education, Canada (2013) ISBN: 0321877403, 3. Jon Rogawski & Colin Adams : Calculus Early Transcendentals (3/e) W. H. Freeman and, Company(2015) ISBN: 1319116450, 4. Anton, Bivens & Davis : Calculus Early Transcendentals (11/e) John Wiley & Sons, Inc.(2016), ISBN: 1118883764, 5. James Stewart : Calculus (8/e) Brooks/Cole Cengage Learning(2016) ISBN: 978-1-285-74062-1, 6. Jerrold Marsden & Alan Weinstein : Calculus I and II (2/e) Springer Verlag NY (1985) ISBN:0387-90974-5, ISBN: 0-387-90975-3, , Page 27 of 115
Page 28 :
27, , SEMESTER – IV, MTS4B04 : LINEAR ALGEBRA, 5 Hours/Week, , 4 Credits 100 Marks[Int: 20 + Ext : 80], , Aims, Objectives and Outcomes, An introductory treatment of linear algebra with an aim to present the fundamentals in the clearest, possible way is intended here. Linear algebra is the study of linear systems of equations, vector spaces,, and linear transformations. Virtually every area of mathematics relies on or extends the tools of linear, algebra. Solving systems of linear equations is a basic tool of many mathematical procedures used, for solving problems in science and engineering. A number of methods for solving a system of linear, equations are discussed. In this process, the student will become competent to perform matrix algebra, and also to calculate the inverse and determinant of a matrix. Another advantage is that the student, will come to understand the modern view of a matrix as a linear transformation. The discussion, necessitates the introduction of central topic of linear algebra namely the concept of a vector space., The familiarity of the students with planar vectors and their algebraic properties under vector addition, and scalar multiplication will make them realize that the idea of a general vector space is in fact an, abstraction of what they already know. Several examples and general properties of vector spaces are, studied. The idea of a subspace, spanning vectors, basis and dimension are discussed and fundamental, results in these areas are explored. This enables the student to understand the relationship among, the solutions of a given system of linear equations and some important subspaces associated with the, coefficient matrix of the system., After this, some basic matrix transformations in the vector spaces R2 and R3 , having interest in, the field of computer graphics, engineering and physics are studied by specially pinpointing to their, geometric effect., Just like choosing an appropriate coordinate system greatly simplifies a problem at our hand, as we usually see in analytic geometry and calculus, a right choice of the basis of the vector space, Rn greatly simplifies the analysis of a matrix operator on it. With this aim in mind, a study on, eigenvalues and eigenvectors of a given matrix (equivalently, that of the corresponding matrix operator), is taken up. Practical method of finding out the eigenvalues from the characteristic equation and the, corresponding eigenvectors are also discussed. A bonus point achieved during this process is a test for, the invertibility of a square matrix. As diagonal matrices are the matrices with simplest structure, the, idea of diagonalization of a matrix (and hence the diagonalization of a matrix operator) is introduced, and students learn a few fundamental results involving diagonalization and eigenvalues which enable, them to check whether diagonalization is possible. They realise that there are matrices that cannot be, diagonalized and even learn to check it. Also they are taught a well defined procedure for diagonalizing, , Page 28 of 115
Page 29 :
28, , a given matrix, if this is actually the case. The topic is progressed further to obtain the ultimate goal of, spectral decomposition of a symmetric matrix. In this process, students realise that every symmetric, matrix is diagonalizable and that this diagonalization can be done in a special way ie., by choosing, an orthogonal matrix to perform the diagonalization. This is known as orthogonal diagonalization., Students also learn that only symmetric matrices with real entries can be orthogonally diagonalized, and using Gram-Schmidt process a well defined procedure for writing such a diagonalization is also, taught. In short, the course gives the students an opportunity to learn the fundamentals of linear, algebra by capturing the ideas geometrically, by justifying them algebraically and by preparing them, to apply it in several different fields such as data communication, computer graphics, modelling etc., , Syllabus, Text, , Elementary Linear Algebra: Application Version (11/e) : Howard Anton & Chris Rorres,, Wiley (2014), ISBN : 978-1-118-43441-3, , Module – I, , (17 hrs), , Systems of Linear Equations & Matrices, 1.1 : Introduction to Systems of Linear Equations linear equation in n variables, linear system of m, equations in n variables, solution, Linear Systems in Two and Three Unknowns, solution by geometric, analysis, consistent and inconsistent systems, linear system with no, one, and infinite number of, solutions, augmented matrix and elementary row operations, 1.2 : Gaussian elimination Considerations in Solving Linear Systems, Echelon Forms, reduced row echelon, , form,, , Elimination, , Methods,, , Gauss, , –, , Jordan, , elimination,, , Gaussian, , elimination,, , Homogeneous Linear Systems, Free Variables, Free Variable Theorem for Homogeneous Systems,, Gaussian Elimination and Back Substitution, Some Facts about Echelon Forms, 1.3 : Matrices and Matrix operations Matrix Notation and Terminology, row vector, column vector,, square matrix of order n, Operations on Matrices, Partitioned Matrices, Matrix Multiplication by, Columns and by Rows, Matrix Products as Linear Combinations, linear combination of column vectors,, Column Row Expansion, Matrix Form of a Linear System, Transpose of a Matrix, Trace of a Matrix, 1.4 : Inverses and algebraic properties of matrices Properties of Matrix Addition and Scalar Multiplication, Properties of Matrix Multiplication, Zero Matrices and Properties, Identity Matrices, Inverse, , Page 29 of 115
Page 30 :
29, , of a Matrix, Properties of Inverses, Solution of a Linear System by Matrix Inversion, Powers of a, Matrix, Matrix Polynomials, Properties of the Transpose, 1.5 : Elementary matrices and a method for finding A−1 row equivalence, elementary matrix, Row, Operations by Matrix Multiplication, invertibility of elementary matrices, invertibility and equivalent, statements, A Method for Inverting Matrices, Inversion Algorithm, illustrations., 1.6 : More on linear systems and invertible matrices Number of Solutions of a Linear System, Solving, Linear Systems by Matrix Inversion, Linear Systems with a Common Coefficient Matrix, Properties, of Invertible Matrices, equivalent statements for unique solution of Ax = b, determining consistency, 1.7 : Diagonal, Triangular and Symmetric matrices Diagonal Matrices, Inverses and Powers of Diagonal, Matrices, Triangular Matrices. Properties of Triangular Matrices, Symmetric Matrices, algebraic, properties of symmetric matrices, Invertibility of Symmetric Matrices, 1.8 : Matrix transformation definition, Properties of Matrix Transformations, standard matrix, A, Procedure for Finding Standard Matrices, 2.1 : Determinants by cofactor expansion minors, cofactors, cofactor expansion, Definition of a General, Determinant, A Useful Technique for Evaluating 2 × 2 and 3 × 3 Determinants, 2.2 : Evaluating determinants by row reduction a few basic theorems, elementary row operations and, determinant, determinant of elementary matrices, determinant by row reduction, , Module – II, , (18 hrs), , General Vector Spaces, 4.1 : Real vector space - Vector Space Axioms, examples, Some Properties of Vectors, 4.2 : Subspaces - definition, criteria for a subset to be a subspace, examples, Building Subspaces,, linear combination, spanning, Solution Spaces of Homogeneous Systems as subspace, The Linear, Transformation View point, kernel, different set of vectors spanning the subspace., 4.3 : Linear Independence - Linear Independence and Dependence, illustrations, A Geometric Interpretation of Linear Independence, Wronskian, linear independence using wronskian, 4.4 : Coordinates and basis - Coordinate Systems in Linear Algebra, Basis for a Vector Space, finite, and infinite dimensional vector spaces, illustrations, Coordinates Relative to a Basis, Uniqueness of, Basis Representation, 4.5 : Dimension - Number of Vectors in a Basis, dimension, Some Fundamental Theorems, dimension, of subspaces, , Page 30 of 115
Page 31 :
30, , Module – III, , (22 hrs), , 4.6 : Change of basis - Coordinate Maps, Change of Basis, Transition Matrices, Invertibility of Transition Matrices, An Efficient Method for Computing Transition Matrices for Rn , Transition to the, Standard Basis for Rn, 4.7 : Row space, Column space and Null space - vector spaces associated with matrices, consistency of, linear system, Bases for Row Spaces, Column Spaces, and Null Spaces, basis from row echelon form,, Basis for the Column Space of a Matrix, row equivalent matrices and relationship between basis for, column space, Bases Formed from Row and Column Vectors of a Matrix, 4.8 : Rank Nullity and Fundamental matrix spaces - equality of dimensions of row and column spaces,, Rank and Nullity, Dimension Theorem for Matrices, The Fundamental Spaces of a Matrix, rank of a, matrix and its transpose, A Geometric Link Between the Fundamental Spaces, orthogonal complement,, invertibility and equivalent statements, Applications of Rank, Over determined and Under determined, Systems, 4.9 : Basic matrix transformations in R2 and R3 - Reflection Operators, Projection Operators, Rotation Operators, Rotations in R3 , Dilations and Contractions, Expansions and Compressions, Shears,, Orthogonal Projections onto Lines Through the Origin, Reflections About Lines Through the Origin, 4.10 : Properties of matrix transformation- Compositions of Matrix Transformations, One - to - One, Matrix Transformations, Kernel and Range, fundamental relationship between invertibility of a matrix, and its matrix transformation, Inverse of a One-to-One Matrix Operator, , Module – IV, , (23 hrs), , 4.11 : Geometry of matrix operators- Transformations of Regions, Images of Lines Under Matrix Operators, Geometry of Invertible Matrix Operators, Elementary matrix and its matrix transformation,, consequence, 5.1 : Eigen values and Eigen Vectors - definition, Computing Eigenvalues and Eigenvectors, characteristic equation, alternative ways of describing eigen values, Finding Eigenvectors and Bases for, Eigenspaces, Eigenvalues and Invertibility, Eigenvalues of General Linear Transformations,, 5.2 : Diagonalization - The Matrix Diagonalization Problem, linear independence of eigen vectors and, diagonalizability, Procedure for Diagonalizing a Matrix, Eigenvalues of Powers of a Matrix, Computing, Powers of a Matrix, Geometric and Algebraic Multiplicity, 6.1 : Inner Product - definition of General inner product, Euclidean inner product (or the standard, inner product) on Rn , norm of a vector, properties (upto and including theorem 6.1.1), a few examples, , Page 31 of 115
Page 32 :
31, , (only example 7 and example 10) [rest of the section omitted], 6.2 : Angle and orthogonality in Inner product spaces - only the definition of orthogonality in a real, inner product space (to be motivated by the relation in the definition (3) of section 3.2) and examples, (2),(3) and (4), 6.3 : Gram–Schmidt Process - definition of Orthogonal and Orthonormal Sets, examples, linear independence of orthogonal set, orthonormal basis, Coordinates Relative to Orthonormal Bases [Orthogonal Projections omitted] The Gram–Schmidt Process [only statement of Theorem 6.3.5 and the, step by step construction technique are required; derivation omitted], illustrations - examples 8 and, 9, Extending Orthonormal Sets to Orthonormal Bases [rest of the section omitted], 7.1 : Orthogonal Matrices - definition, characterisation of orthogonal matrices, properties of orthogonal, matrices, Orthogonal Matrices as Linear Operators, a geometric interpretation [rest of the section, omitted], 7.2 : Orthogonal Diagonalization - The Orthogonal Diagonalization Problem, Conditions for Orthogonal Diagonalizability, Properties of Symmetric Matrices, Procedure for Orthogonally Diagonalizing an, n × n Symmetric Matrix, Spectral Decomposition (upto and including example 2) [rest of the section, omitted], , References:, 1. Jim DeFranza, Daniel Gagliardi : Introduction to Linear Algebra with Applications Waveland, Press, Inc (2015), ISBN: 1-4786-2777-8, 2. Otto Bretscher: Linear Algebra with Applications (5/e) Pearson Education, Inc (2013), ISBN:, 0-321-79697-7, 3. Ron Larson, Edwards, David C Falvo : Elementary Linear Algebra (6/e), Houghton Mifflin, Harcourt Publishing Company (2009) ISBN: 0-618-78376-8, 4. David C. Lay, Steven R. Lay, Judi J. McDonald: Linear Algebra and its Application (5/e), Pearson Education, Inc(2016) ISBN: 0-321-98238-X, 5. Martin Anthony, Michele Harvey: Linear Algebra: Concepts and Methods Cambridge University, Press (2012) ISBN: 978-0-521-27948-2, 5. Jeffrey Holt: Linear Algebra with Applications W. H. Freeman and Company (2013), ISBN:, 0-7167-8667-2, , Page 32 of 115
Page 33 :
32, , SEMESTER – V, MTS5B05 : ABSTRACT ALGEBRA, 5 Hours/Week, , 4 Credits 100 Marks[Int: 20 + Ext : 80], , Aims, Objectives and Outcomes, The brilliant mathematician Evariste Galois developed an entire theory that connected the solvability by radicals of a polynomial equation with the permutation group of its roots. The theory now, known as Galois theory solves the famous problem of insolvability of quintic. A study on symmetric, functions now becomes inevitable. One can now observe the connection emerging between classical, algebra and modern algebra. The last three modules are therefore devoted to the discussion on basic, ideas and results of abstract algebra. Students understand the abstract notion of a group, learn several, examples, are taught to check whether an algebraic system forms a group or not and are introduced to, some fundamental results of group theory. The idea of structural similarity, the notion of cyclic group,, permutation group, various examples and very fundamental results in the areas are also explored., , Syllabus, Text :, , Abstract Algebra (3/e): John A Beachy and William D Blair Waveland Press, Inc.(2006),, ISBN: 1-57766-443-4, , Module – I, , (15 hrs), , (The Transcendental Functions), 1.4 : Integers modulo n - congruence class modulo n, addition and multiplication, divisor of zero,, multiplicative inverse, 2.2 : Equivalence relations - basic idea, definition, equivalence class, factor set, partition and equivalence relation, examples and illustrations, 2.3 : Permutations - definition, cycles, product of cycles, permutation as product of disjoint cycles,, order of cycles, transposition, even and odd transpositions, , Module – II, , (25 hrs), , 3.1 : Definition of Group - binary operation, uniqueness of identity and inverse, definition and examples, of groups, properties, Abelian group, finite and infinite groups, general linear groups, , Page 33 of 115
Page 34 :
33, , 3.2 : Subgroups - the notion of subgroup, examples, conditions for a subgroup, cyclic subgroups, order, of an element, Lagrange theorem, Euler’s theorem, 3.3 : Constructing examples - groups with order upto 6, multiplication table, product of subgroups,, direct products, Klein four group as direct product, subgroup generated by a subset, 3.4 : Isomorphism – definition, consequences, structural properties, method of showing that groups, are not isomorphic, isomorphic and non isomorphic groups., , Module – III, , (25 hrs), , 3.5 : Cyclic groups - subgroups of cyclic groups, characterisation, generators of a finite cyclic group,, structure theorem for finite cyclic group, exponent of a group, characterisation of cyclic groups among, finite abelian groups., 3.6 : Permutation groups - definition, Cayley’s theorem, rigid motions of n-gons, dihedral group,, alternating group, 3.7 : Homomorphism - basic idea, examples, definition, properties, kernel, normal subgroups, subgroups related via homomorphism, 3.8 : Cosets - left and right cosets, normal subgroups and factor groups, fundamental homomorphism, theorem, simple groups, examples and illustrations of concepts, , Module – IV, , (15 hrs), , 7.1 : (Structure of Groups) Isomorphism theorems; Automorphism - first isomorphism theorem, second, isomorphism theorem, inner automorphism, 5.1 : Commutative Rings; Integral Domains - definition, examples, subring, criteria to be a subring,, divisor of zero, integral domain, finite integral domain., , References:, 1. Joseph A. Gallian : Contemporary Abstract Algebra (9/e), Cengage Learning, Boston (2017),, ISBN: 978-1-305-65796-0, 2. John B Fraleigh : A First Course in Abstract Algebra (7/e) Pearson Education LPE (2003), ISBN 978-81-7758-900-9, 3. David Steven Dummit, Richard M. Foote: Abstract Algebra (3/e), Wiley, (2004), ISBN :, 8126532289, , Page 34 of 115
Page 35 :
34, , 4. Linda Gilbert and Jimmie Gilbert: Elements of Modern Algebra (8/e), Cengage Learning,, Stamford (2015), ISBN: 1-285-46323-4, 5. John R. Durbin :, , Modern Algebra :, , An Introduction (6/e), Wiley (2015), ISBN :, , 1118117611, 6. Jeffrey Bergen: A Concrete Approach to Abstract Algebra - From the integers to Insolvability, of Quintic, Academic Pres [Elsever](2010), ISBN: 978-0-12-374941-3, , Page 35 of 115
Page 36 :
35, , SEMESTER – V, MTS5B06 : BASIC ANALYSIS, 5 Hours/Week, , 4 Credits 100 Marks[Int: 20 + Ext : 80], , Aims, Objectives and Outcomes, In this course, basic ideas and methods of real analysis are taught. Real analysis is a theoretical, version of single variable calculus. So many familiar concepts of calculus are reintroduced but at a, much deeper and more rigorous level than in a calculus course. At the same time there are concepts, and results that are new and not studied in the calculus course but very much needed in more advanced, courses. The aim is to provide students with a level of mathematical sophistication that will prepare, them for further work in mathematical analysis and other fields of knowledge, and also to develop, their ability to analyse and prove statements of mathematics using logical arguments. The course will, enable the students, • to learn and deduce rigorously many properties of real number system by assuming a few, fundamental facts about it as axioms. In particular they will learn to prove Archimedean, property, density theorem, existence of a positive square root for positive numbers and so on, and the learning will help them to appreciate the beauty of logical arguments and embolden, them to apply it in similar and unknown problems., • to know about sequences, their limits, several basic and important theorems involving sequences, and their applications. For example, they will learn how monotone convergence theorem can, be used in establishing the divergence of the harmonic series, how it helps in the calculation, of square root of positive numbers and how it establishes the existence of the transcendental, number e (Euler constant)., • to understand some basic topological properties of real number system such as the concept of, open and closed sets, their properties, their characterization and so on., • to understand some basic topological properties of real number system such as the concept of, open and closed sets, their properties, their characterization and so on., • to get a rigorous introduction to algebraic, geometric and topological structures of complex, number system, functions of complex variable, their limit and continuity and so on. Rich use, of geometry, comparison between real and complex calculus-areas where they agree and where, they differ, the study of mapping properties of a few important complex functions exploring, , Page 36 of 115
Page 37 :
36, , the underlying geometry etc. will demystify student’s belief that complex variable theory is, incomprehensible., , Syllabus, Text(1), , Introduction to Real Analysis(4/e) : Robert G Bartle, Donald R Sherbert, John Wiley, & Sons (2011) ISBN : 978-0-471-43331-6, , Text(2), , Complex Analysis A First Course with Applications (3/e) : Dennis Zill & Patric, Shanahan Jones and Bartlett Learning(2015) ISBN:1-4496-9461-6, , Module – I, , Text (1), , (20 hrs), , 1.3 : Finite and Infinite Sets - definition, countable sets, denumerability of Q, union of countable sets,, Cantor’s theorem, 2.1 : The Algebraic and Order Properties of R - algebraic properties, basic results, rational and, √, irrational numbers, irrationality of 2, Order properties, arithmetic-geometric inequality, Bernoulli’s, Inequality, 2.2 : Absolute Value and the Real Line - definition, basic results, Triangle Inequality, The real line,, �-neighborhood, 2.3 : The Completeness Property of R - Suprema and Infima, alternate formulations for the supremum,, The Completeness Property, , Module – II, , Text (1), , (21 hrs), , 2.4 : Applications of the Supremum Property - The Archimedean Property, various consequences,, √, Existence of 2, Density of Rational Numbers in R - The Density Theorem, density of irrationals, 2.5 : Intervals - definition, Characterization of Intervals, Nested Intervals, Nested Intervals Property,, The Uncountability of R [binary, decimal and periodic representations omitted] Cantor’s Second Proof., 3.1 : Sequences and Their Limits - definitions, convergent and divergent sequences, Tails of Sequences,, Examples, 3.2 : Limit Theorems - sum, difference, product and quotients of sequences, Squeeze Theorem, ratio, test for convergence, 3.3 : Monotone Sequences - definition, monotone convergence theorem, divergence of harmonic series,, calculation of square root, Euler’s number, , Page 37 of 115
Page 38 :
37, , Module – III, , Text (1), , (18 hrs), , 3.4 : Subsequences and the Bolzano - Weierstrass Theorem - definition, limit of subsequences, divergence criteria using subsequence, The Existence of Monotone Subsequences, monotone subsequence, theorem, The Bolzano-Weierstrass Theorem, Limit Superior and Limit Inferior, 3.5 : The Cauchy Criterion - Cauchy sequence, Cauchy Convergence Criterion, applications, contractive sequence, 3.6 : Properly divergent sequences - definition, examples, properly divergent monotone sequences,, “comparison theorem”, “limit comparison theorem”, 11.1: Open and Closed sets in R, neighborhood, open sets, closed sets, open set properties, closed set, properties, Characterization of Closed Sets, cluster point, Characterization of Open Sets, The Cantor, Set, properties, , Module – IV, , Text (2), , (21 hrs), , 1.1 : Complex numbers and their properties - definition, arithmetic operations, conjugate, inverses,, reciprocal, 1.2 : Complex Plane - vector representation, modulus, properties, triangle inequality, 1.3 : Polar form of complex numbers - polar representation, principal argument, multiplication and, division, argument of product and quotient, integer powers, de Moivre’s formula., 1.4 : Powers and roots - roots, principal nth root, 1.5 : Sets of points in the complex plane - circles, disks and neighbourhoods, open sets, annulus,, domains, regions, bounded sets, 2.1 : Complex Functions - definition, real and imaginary parts of complex function, complex exponential function, exponential form of a complex number, Polar Coordinates, 2.2 : Complex Functions as mappings - complex mapping, illustrations, Parametric curves in complex planes, common parametric curves, image of parametric curves under complex mapping [The, subsection ‘Use of Computers’ omitted], 2.3 : Linear Mappings - Translations, Rotations, Magnifications, general linear mapping, image of, geometric shapes under linear map., 1, , 2.4 : Special Power functions - The power function z n , The power function z n , principal square root, function, Inverse Functions, multiple valued functions, , Page 38 of 115
Page 39 :
38, , References:, 1. Charles G. Denlinger: Elements of Real Analysis Jones and Bartlett Publishers Sudbury, Massachusetts (2011), ISBN:0-7637-7947-4 [Indian edition: ISBN- 9380853157], 2. David Alexander Brannan:, , A First Course in Mathematical Analysis Cambridge, , University Press, US (2006) ISBN: 9780521684248, 3. John M. Howie:, , Real Analysis Springer Science & Business Media (2012) [Springer, , Undergraduate Mathematics Series] ISBN: 1447103416, 4. James S. Howland:, , Basic Real Analysis Jones and Bartlett Publishers Sudbury,, , Massachusetts (2010) ISBN:0-7637-7318-2, 5. James Ward Brown, Ruel Vance Churchill: Complex variables and applications (8/e), McGrawHill Higher Education, (2009) ISBN: 0073051942, 6. Alan Jeffrey : Complex Analysis and Applications (2/e), Chapman and Hall/CRC Taylor Francis, Group (2006), ISBN:978-1-58488-553-5, 7. Saminathan Ponnusamy, Herb Silverman: Complex Variables with Applications Birkhauser, Boston(2006) ISBN:0-8176-4457-4, 8. Terence Tao: Analysis I & II (3/e) TRIM 37 & 38 Springer Science+Business Media Singapore, 2016; Hindustan book agency(2015) ISBN 978-981-10-1789-6 (eBook) & ISBN 978-981-10-1804-6, (eBook), 9. Ajith Kumar & S Kumaresan : A Basic Course in Real Analysis CRC Press, Taylor & Francis, Group(2014) ISBN: 978-1-4822-1638-7 (eBook – PDF), 10. Hugo D Junghenn : A Course in Real Analysis CRC Press, Taylor & Francis Group (2015), ISBN: 978-1-4822-1928-9 (eBook - PDF), , Page 39 of 115
Page 40 :
39, , SEMESTER – V, MTS5B07 : NUMERICAL ANALYSIS, 4 Hours/Week, , 3 Credits, , 75 Marks[Int: 15 + Ext : 60], , Aims, Objectives and Outcomes, The goal of numerical analysis is to provide techniques and algorithms to find approximate numerical solution to problems in several areas of mathematics where it is impossible or hard to find, the actual/closed form solution by analytical methods and also to make an error analysis to ascertain, the accuracy of the approximate solution. The subject addresses a variety of questions ranging from, the approximation of functions and integrals to the approximate solution of algebraic, transcendental,, differential and integral equations, with particular emphasis on the stability, accuracy, efficiency and, reliability of numerical algorithms. The course enables the students to, • Understand several methods such as bisection method, fixed point iteration method, regula falsi, method etc. to find out the approximate numerical solutions of algebraic and transcendental, equations with desired accuracy., • Understand the concept of interpolation and also learn some well known interpolation techniques., • Understand a few techniques for numerical differentiation and integration and also realize their, merits and demerits., • Find out numerical approximations to solutions of initial value problems and also to understand, the efficiency of various methods., , Page 40 of 115
Page 41 :
40, , Syllabus, , Text, , Numerical Analysis (10/e): Richard L. Burden, J Douglas Faires, Annette M. Burden,, Brooks Cole Cengage Learning (2016) ISBN:978-1-305-25366-7, , Module – I, , (28 hrs), , Solutions of Equations in One Variable, Note : Students should be familiar with concepts and definitions such as ‘round off error’, ‘rate of, convergence’etc. discussed in sections 1.2 and 1.3, Introduction, 2.1 : The Bisection Method, 2.2 : Fixed - Point Iteration, 2.3 : Newton’s Method and its Extensions - Newton’s Method (Newton - Raphson method), Convergence using Newton’s Method, The Secant Method, The Method of False Position, 2.4 : Error Analysis for Iterative Methods - Order of Convergence, linear and quadratic convergence,, Multiple Roots, Modified Newton’s method for faster convergence, [Algorithms are omitted], Interpolation and Polynomial Approximation, Introduction, 3.1 : Interpolation and the Lagrange Polynomial - motivation, Lagrange Interpolating Polynomials,, error bound, 3.2 : Data Approximation and Neville’s Method - motivation, Neville’s Method, recursive method to, generate Lagrange polynomial approximations., 3.3 : Divided Differences - k th divided difference, Newton’s divided difference formula, Forward Differences, Newton Forward–Difference Formula, Backward Differences, Newton Backward–Difference, Formula, Centered Differences, Stirling’s formula., [Algorithms are omitted], , Page 41 of 115
Page 42 :
41, , Module – II, , (18 hrs), , Numerical Differentiation and Integration, Introduction, 4.1 : Numerical Differentiation - approximation of first derivative by forward difference formula,, backward difference formula, Three Point Formulas, Three Point Endpoint Formula, Three Point, Midpoint Formula, [Five Point Formulas, Five Point Endpoint Formula, Five Point Midpoint Formula omitted], Second Derivative Midpoint Formula to approximate second derivative, Round Off Error Instability, 4.3 : Elements of Numerical Integration - numerical quadrature, The Trapezoidal Rule, Simpson’s, Rule, Measuring Precision, Closed Newton - Cotes Formulas, Simpson’s Three - Eighth’s rule, Open, Newton-Cotes Formulas, 4.4 : Composite Numerical Integration - composite Simpson’s rule, composite trapezoidal rule, composite midpoint rule, round off error stability, 4.7 : Gaussian Quadrature - motivation, Legendre Polynomial, Gaussian Quadrature on Arbitrary, Intervals, [Algorithms are omitted], , Module – III, , (18 hrs), , Initial–Value Problems for Ordinary Differential Equations, Introduction, 5.1 : The Elementary Theory of Initial - Value Problems, 5.2 : Euler’s Method - derivation using Taylor formula, Error bounds for Euler Method, 5.3 : Higher Order Taylor Methods - local truncation error, Taylor method of order n and order of, local truncation error, 5.4 : Runge – Kutta Methods - only Mid Point Method, Modified Euler’s Method and Runge–Kutta, Method of Order Four are required., [derivation of formula omitted in each case], 5.6 : Multistep Methods - basic idea, definition, Adams-Bashforth Two-Step Explicit Method, AdamsBashforth Three-Step Explicit Method, Adams - Bashforth Four-Step Explicit Method, AdamsMoulton Two-Step Implicit Method, Adams-Moulton Three-Step Implicit Method, Adams-Moulton, Four-Step Implicit Method, Predictor-Corrector Methods [derivation of formula omitted in each case], [Algorithms are omitted], , Page 42 of 115
Page 43 :
42, , References:, 1. Kendall E. Atkinson, Weimin Han: Elementary Numerical Analysis (3/e), John Wiley &, Sons(2004) ISBN:0-471-43337-3[Indian Edition by Wiley India, ISBN: 978-81-265-0802-0], 2. James F. Epperson: An Introduction to Numerical Methods and Analysis (2/e) John Wiley &, Sons (2013), ISBN: 978-1-118-36759-9, 3. Timothy Sauer : Numerical Analysis (2/e), Pearson (2012), ISBN: 0-321-78367-0, 4. S S Sastri : Introductory Methods of Numerical Analysis (5/e), PHI Learning Pvt. Ltd. (2012),, ISBN:978-81-203-4592-8, 5. Ward Cheney, David Kincaid : Numerical Mathematics and Computing (6/e), Thomson Brooks/, Cole (2008), ISBN: 495-11475-8, , Page 43 of 115
Page 44 :
43, , SEMESTER – V, MTS5B08 : LINEAR PROGRAMMING, 3 Hours/Week, , 3 Credits, , 75 Marks[Int: 15 + Ext : 60], , Aims, Objectives and Outcomes, Linear programming problems are having wide applications in mathematics, statistics, computer, science, economics, and in many social and managerial sciences. For mathematicians it is a sort of, mathematical modelling process, for statisticians and economists it is useful for planning many economic activities such as transport of raw materials and finished products from one place to another, with minimum cost and for military heads it is useful for scheduling the training activities and deployment of army personnel. The emphasis of this course is on nurturing the linear programming skills of, students via. the algorithmic solution of small-scale problems, both in the general sense and in the, specific applications where these problems naturally occur. On successful completion of this course,, the students will be able to, • solve linear programming problems geometrically, • understand the drawbacks of geometric methods, • solve LP problems more effectively using Simplex algorithm via. the use of condensed tableau, of A.W. Tucker, • convert certain related problems, not directly solvable by simplex method, into a form that can, be attacked by simplex method., • understand duality theory, a theory that establishes relationships between linear programming, problems of maximization and minimization, • understand game theory, • solve transportation and assignment problems by algorithms that take advantage of the simpler, nature of these problems, , Page 44 of 115
Page 45 :
44, , Syllabus, Text, , Linear Programming and Its Applications : James K. Strayer Undergraduate Texts in, Mathematics Springer (1989), ISBN: 978-1-4612-6982-3, , Module – I, , (16 hrs), , Chapter 1 Geometric Linear Programming :, Profit Maximization and Cost Minimization, typical motivating examples, mathematical formulation, Canonical Forms for Linear Programming Problems, objective functions, constraint set, feasible, solution, optimal solution, Polyhedral Convex Sets, convex set, extreme point, theorems asserting, existence of optimal solutions, The Two Examples Revisited, graphical solutions to the problems, A, Geometric Method for Linear Programming, the difficulty in the method, Concluding Remarks, Chapter 2 The Simplex Algorithm : Canonical Slack Forms for Linear Programming Problems; Tucker Tableaus, slack variables, Tucker, tableaus, independent variables or non basic variables, dependent variables or basic variables. An Example: Profit Maximization, method of solving a typical canonical maximization problem, The Pivot, Transformation, The Pivot Transformation for Maximum and Minimum Tableaus, An Example : Cost, Minimization, method of solving a typical canonical minimization problem, The Simplex Algorithm for, Maximum Basic Feasible Tableaus, The Simplex Algorithm for Maximum Tableaus, Negative Transposition; The Simplex Algorithm for Minimum Tableaus, Cycling, Simplex Algorithm Anti cycling, Rules, Concluding Remarks, , Module – II, , (14 hrs), , Chapter 3 Noncanonical Linear Programming Problems : Unconstrained Variables, Equations of Constraint, Concluding Remarks, Chapter 4 : Duality Theory : Duality in Canonical Tableaus, The Dual Simplex Algorithm, The Dual Simplex Algorithm for, Minimum Tableaus, The Dual Simplex Algorithm for Maximum Tableaus, Matrix Formulation of, Canonical Tableaus,The Duality Equation, Duality in Noncanonical Tableaus, Concluding Remarks, , Module – III, , (18 hrs), , Chapter 5 Matrix Games:-, , Page 45 of 115
Page 46 :
45, , An Example; Two-Person Zero-Sum Matrix Games, Domination in a Matrix Game, Linear Programming Formulation of Matrix Games, The Von Neumann Minimax Theorem, The Example Revisited, Two More Examples, Concluding Remarks, Chapter 6 Transportation and Assignment Problems :The Balanced Transportation Problem, The Vogel Advanced-Start Method (VAM), The Transportation Algorithm, Another Example, Unbalanced Transportation Problems, The Assignment Problem, The Hungarian Algorithm, Concluding Remarks, The Minimum-Entry Method, The NorthwestCorner Method, , References:, 1. Robert J. Vanderbei : Linear Programming : Foundations and Extensions (2/e), Springer, Science+Business Media LLC (2001), ISBN : 978-1-4757-5664-7, 2. Frederick S Hiller, Gerald J Lieberman : Introduction to Operation Research (10/e), McGrawHill Education, 2 Penn Plaza, New York (2015), ISBN : 978-0-07-352345-3, 3. Paul R. Thie, G. E. Keough : An Introduction to Linear Programming and Game Theory (3/e),, John Wiley and Sons, Ins. (2008), ISBN : 978-0-470-23286-6, 4. Louis Brickman : Mathematical Introduction to Linear Programming and Game Theory UTM,, Springer Verlag, NY (1989), ISBN :0-387-96931-4, 5. Jiri Matoušek, Bernd Gartner : Understanding and Using Linear Programming Universitext,, Springer-Verlag Berlin Heidelberg (2007), ISBN : 978-3-540-30697-9, , Page 46 of 115
Page 47 :
46, , SEMESTER – VI, MTS5B09 : INTRODUCTION TO GEOMETRY AND, THEORY OF EQUATIONS, 3 Hours/Week, , 3 Credits, , 75 Marks[Int: 15 + Ext : 60], , Aims, Objectives and Outcomes, Geometry, Geometry is, basically, the study concerned with questions of shape, size, and relative position of, planar and spatial objects. The classical Greek geometry, also known as Euclidean geometry after the, work of Euclid, was once regarded as one of the highest points of rational thought, contributing to, the thinking skills of logic, deductive reasoning and skills in problem solving., In the early 17 th century, the works of Rene Descartes and Pierre de Fermat put the foundation, stones for the creation of analytic geometry where the idea of a coordinate system was introduced to, simplify the treatment of geometry and to solve a wide variety of geometric problems., Desargues, a contemporary of Descartes was fascinated towards the efforts of artists/painters to, give a realistic view of their art works/paintings usually done on a flat surface such as canvas or, paper. To get a realistic view of a three dimensional object/scene depicted on a flat surface, a right, impression of height, width, depth and position in relation to each other of the objects in the scene is, required. This idea is called perspective in art. If two artists make perspective drawings of the same, object, their drawings shall not be identical but there shall be certain properties of these drawings, that remain the same or that remain invariant. The study of such invariant things crystallised into, what is now called projective geometry. Now days, it plays a major role in computer graphics and in, the design of camera models., Another development is the evolution of affine geometry. In simple terms, if we look at the, shadows of a rectangular window on the floor under sunlight, we could see the shadows not in perfect, rectangular form but often in the shape of a parallelogram. The size of shadows also changes with, respect to the position of the sun. Hence, neither length nor angle is invariant in the transformation, process. However, the opposite sides of the images are always parallel. So this transformation keeps, parallelism intact. The investigation of invariants of all shadows is the basic problem of affine geometry., Towards the end of nineteenth century, there were several different geometries: Euclidean, affine,, projective, inversive, spherical, hyperbolic, and elliptic to name a few. It was the idea of Felix Klein, to bring the study of all these different geometries into a single platform. He viewed each geometry, as a space together with a group of transformations of that space and regarded those properties of, figures left unaltered by the group as geometrical properties. In this course, it is intended to take up, a study of a few geometries based on the philosophy of Klein., , Page 47 of 115
Page 48 :
47, , Theory of equations, Theory of equations is an important part of traditional algebra course and it mainly deals with, polynomial equations and methods of finding their algebraic solution or solution by radicals. This, means we seek a formula for solutions of polynomial equations in terms of coefficients of polynomials, that involves only the operations of addition, subtraction, multiplication, division and taking roots., A well knitted formula for the solution of a quadratic polynomial equation is known to us from high, school classes and is not difficult to derive. However, there is an increasing difficulty to derive such, a formula for polynomial equations of third and fourth degree. One of our tasks in this learning, process is to derive formulae for the solutions of third and fourth degree polynomial equations given, by Carden and Ferrari respectively. In the mean time, we shall find out the relationship between the, roots and coefficients of an n th degree polynomial and an upper and lower limit for the roots of such, a polynomial. This often help us to locate the region of solutions for a general polynomial equation., Methods to find out integral and rational roots of a general n th degree polynomial with rational, coefficients are also devised., Upon successful completion of the course, students will be able to, 1. Understand several basic facts about parabola, hyperbola and ellipse (conics) such as their, equation in standard form, focal length properties, and reflection properties, their tangents and, normal., 2. Recognise and classify conics., 3. Understand Kleinian view of Euclidean geometry., 4. Understand affine transformations, the inherent group structure, the idea of parallel projections, and the basic properties of parallel projections., 5. Understand the fundamental theorem of affine geometry, its use in the proof of Median theorem,, Ceva’s theorem, Menelaus’ theorem etc., 6. Learn to solve polynomial equations upto degree four., , Page 48 of 115
Page 49 :
48, , Syllabus, Text (1), , Geometry (2/e) : David A Brannan, Mathew F Espen, Jeremy J Gray, Cambridge, University Press (2012), ISBN : 978-1-107-64783-1, , Text (2), , Theory of Equations : J V Uspensky McGraw Hill Book Company, Inc., , (1948),, , ISBN:07-066735-7, , Module – I, , Text (1), , (20 hrs), , Conics, 1.1.1 : Conic Sections, 1.1.3 : Focus - Directrix Definition of the Non-Degenerate Conics - definition, parabola in standard, form, ellipse in standard form, hyperbola in standard form, Rectangular Hyperbola, Polar Equation, of a Conic, 1.1.4 : Focal Distance Properties of Ellipse and Hyperbola - Sum of Focal Distances of Ellipse, Difference of Focal Distances of Hyperbola,, 1.2 : Properties of Conics - Tangents, equation of tangents to ellipse, hyperbola, and parabola, polar of, a point w.r.t. unit circle, normal, Reflections, The Reflection Law, Reflection Property of the Ellipse,, Reflection Property of the Hyperbola, Reflection Property of the Parabola, Conics as envelopes of, tangent families, 1.3 : Recognizing Conics - equation of conic in general form, identifying a conic, Affine Geometry, 2.1 : Geometry and Transformations - What is Euclidean Geometry? Isometry, Euclidean properties,, Euclidean transformation, Euclidean-Congruence, 2.2 : Affine Transformations and Parallel Projections- Affine Transformations, Basic Properties of, Affine Transformations, Parallel Projections, Basic Properties of Parallel Projections, Affine Geometry,, Midpoint Theorem, Conjugate Diameters Theorem, Affine Transformations and Parallel Projections,, affine transformations as composite of two parallel projections, 2.3 : Properties of Affine Transformations-Images of Sets Under Affine Transformations, The Fundamental Theorem of Affine Geometry(without proof), Proofs of the Basic Properties of Affine Transformations, , Page 49 of 115
Page 50 :
49, , Module – II, , Text (2), , (14 hrs), , Theory of Equations, Chapter II, II.3 Division of polynomials, quotient and remainder, method of detached coefficients, II.4 The remainder theorem, II.5 Synthetic Division, II.7 Taylor formula, expansion of a polynomial in powers of x − c, Chapter III, III.1 Algebraic equations, roots, maximum number of roots, III.2 Identity theorem, III.3 The Fundamental theorem of Algebra (statement only), factorisation to linear factors, multiplicity of roots, III.4 Imaginary roots of equations with real coefficients, III.5 Relations between roots and coefficients, Chapter IV, IV.1 Limits of roots, IV.2 Method to find upper limit of positive roots, IV.3 Limit for moduli of roots [only the method to find out upper limit from the auxiliary equation is, required; derivation omitted], IV.4 Integral roots, IV.5 Rational roots, , Module – III, , Text (2), , (14 hrs), , Chapter V, V.1 What is the solution of an equation?, V.2 Cardan’s formulas, V.3 Discussion of solution, V.4 Irreducible case, V.6 Solutions of biquadratic equations, Ferrari method [example2 omitted], Chapter VI, VI.1 Object of the Chapter, VI.2 The sign of a polynomial for small and large values of variables- locating roots of polynomial, between two numbers having values of opposite sign-geometric illustration only-[rigorous reasoning in, , Page 50 of 115
Page 51 :
50, , the starred section omitted], VI.4 Corollaries- roots of odd and even degree polynomial, number of roots in an interval counted, according to their multiplicity, VI.5 Examples, VI.6 An important identity and lemma [derivation not needed], VI.7 Rolle’ s Theorem [proof omitted], use in separating roots, VI.10 Descarte’s rule of signs-only statement and illustrations are required, , References:, 1. George A Jennings: Modern Geometry with Applications University text, Springer (1994),, ISBN:0-387-94222-X, 2. Walter Meyer: Geometry and its Application(2/e) Elsever, Academic Press (2006)ISBN : 0-12369427-0, 3. Judith N Cederberg : A Course in Modern Geometries(2/e) UTM, Springer (2001) ISBN :, 978-1-4419-3193-1, 4. Patric J Ryan: Euclidean and Non Euclidean Geometry-An Analytic Approach Cambridge, University Press, International Student Edition (2009) ISBN : 978-0-521-12707-3, 5. David C Kay: College Geometry: A Unified Approach CRC Press Tayloe and Francic Group, (2011) ISBN : 978-1-4398-1912-8 (Ebook-PDF), 6. James R Smart: Modern Geometries (5/e) Brooks/Cole Publishing Co., (1998) ISBN : 0-53435188-3, 7. Michele Audin : Geometry University text, Springer (2003) ISBN : 3-540-43498-48, 8. Dickson L.E : Elementary Theory of Equations John Wiley and Sons,Inc. NY (1914), 9. Turnbull H.W : Theory of Equations (4/e) Oliver and Boyd Ltd. Edinburg (1947), 10. Todhunter I : An Elementary Treatise on the Theory of Equations (3/e) Macmillan and Co., London (1875), 11. William Snow Burnside and Arthur William Panton : The Theory of Equations with an, Introduction to Binary Algebraic Forms Dublin University Press Series(1881), , Page 51 of 115
Page 52 :
51, , SEMESTER – VI, MTS6B10 : REAL ANALYSIS, 5 Hours/Week, , 5 Credits 100 Marks[Int: 20 + Ext : 80], , Aims, Objectives and Outcomes, The course is built upon the foundation laid in Basic Analysis course of fifth semester. The course, thoroughly exposes one to the rigour and methods of an analysis course. One has to understand, definitions and theorems of text and study examples well to acquire skills in various problem solving, techniques. The course will teach one how to combine different definitions, theorems and techniques, to solve problems one has never seen before. One shall acquire ability to realise when and how to, apply a particular theorem and how to avoid common errors and pitfalls. The course will prepare, students to formulate and present the ideas of mathematics and to communicate them elegantly., On successful completion of the course, students will be able to, • State the definition of continuous functions, formulate sequential criteria for continuity and, prove or disprove continuity of functions using this criteria., • Understand several deep and fundamental results of continuous functions on intervals such as, boundedness theorem, maximum-minimum theorem, intermediate value theorem, preservation, of interval theorem and so on., • Realise the difference between continuity and uniform continuity and equivalence of these ideas, for functions on closed and bounded interval., • Understand the significance of uniform continuity in continuous extension theorem., • Develop the notion of Riemann integrability of a function using the idea of tagged partitions, and calculate the integral value of some simple functions using the definition., • Understand a few basic and fundamental results of integration theory., • Formulate Cauchy criteria for integrability and a few applications of it. In particular they learn, to use Cauchy criteria in proving the non integrability of certain functions., • Understand classes of functions that are always integrable, • Understand two forms of fundamental theorem of calculus and their significance in the practical, problem of evaluation of an integral., • Find a justification for ‘change of variable formula’ used in the practical problem of evaluation, of an integral., • Prove convergence and divergence of sequences of functions and series, , Page 52 of 115
Page 53 :
52, , • Understand the difference between pointwise and uniform convergence of sequences and series, of functions, • Answer a few questions related to interchange of limits., • Learn and find out examples/counter examples to prove or disprove the validity of several, mathematical statements that arise naturally in the process/context of learning., • Understand the notion of improper integrals, their convergence, principal value and evaluation., • Learn the properties of and relationship among two important improper integrals namely beta, and gamma functions that frequently appear in mathematics, statistics, science and engineering., , Syllabus, Text (1), , Introduction to Real Analysis(4/e) : Robert G Bartle, Donald R Sherbert, John Wiley, & Sons (2011), ISBN : 978-0-471-43331-6, , Text (2), , Improper Riemann Integrals: Ioannis M. Roussos CRC Press by Taylor & Francis, Group, LLC(2014), ISBN : 9781466588080 (eBook PDF), , Module – I, , Text (1), , (18 hrs), , 5.1 : Continuous Functions definition, sequential criteria for continuity, discontinuity criteria, examples of continuous and discontinuous functions, Dirichlet and Thomae function, 5.3 : Continuous Functions on Intervals Boundedness Theorem, The Maximum Minimum Theorem,, Location of Roots Theorem, Bolzano’s Intermediate Value Theorem, Preservation of Intervals Theorem, 5.4 : Uniform Continuity definition, illustration, Nonuniform Continuity Criteria, Uniform Continuity, Theorem, Lipschitz Functions, Uniform Continuity of Lipschitz Functions, converse, The Continuous Extension Theorem, Approximation by step functions & piecewise linear functions, Weierstrass, Approximation Theorem (only statement), , Page 53 of 115
Page 54 :
53, , Module – II, , Text (1), , (22 hrs), , 7.1 : Riemann Integral – Partitions and Tagged Partitions, Riemann sum, Riemann integrability,, examples, Some Properties of the Integral, Boundedness Theorem, 7.2 : Riemann Integrable Functions Cauchy Criterion, illustrations, The Squeeze Theorem, Classes, of Riemann Integrable Functions, integrability of continuous and monotone functions, The Additivity, Theorem, 7.3 : The Fundamental Theorem - The Fundamental Theorem (First Form), The Fundamental Theorem (Second Form), Substitution Theorem, Lebesgue’s integrability Criterion, Composition Theorem,, The Product Theorem, Integration by Parts, Taylor’s Theorem with the Remainder, , Module – III, , Text (1), , (17 hrs), , 8.1 : Pointwise and Uniform Convergence definition, illustrations, The Uniform Norm, Cauchy Criterion for Uniform Convergence, 8.2 : Interchange of Limits - examples leading to the idea, Interchange of Limit and Continuity, Interchange of Limit and Derivative [only statement of theorem 8.2.3 required; proof omitted] Interchange, of Limit and Integral, Bounded convergence theorem(statement only) [8.2.6 Dini’s theorem omitted], 9.4 : Series of Functions – (A quick review of series of real numbers of section 3.7 without proof), definition, sequence of partial sum, convergence, absolute and uniform convergence, Tests for Uniform, Convergence, Weierstrass M Test (only upto and including 9.4.6), , Module – IV, , Text (2), , (23 hrs), , Improper Riemann Integrals, 1.1 : Definitions and Examples, 1.2 : Cauchy Principal Value, 1.3 : Some Criteria of Existence, 2.1 : Calculus Techniques [‘2.1.1 Applications’ Omitted], 2.2 : Integrals Dependent on Parameters upto and including example 2.2.4, 2.6 : The Real Gamma and Beta Functions upto and including Example 2.6.18, , References :, 1. Charles G. Denlinger : Elements of Real Analysis Jones and Bartlett Publishers Sudbury, Massachusetts (2011), ISBN : 0-7637-7947-4 [Indian edition: ISBN- 9380853157], , Page 54 of 115
Page 55 :
54, , 2. David Alexander Brannan :, , A First Course in Mathematical Analysis Cambridge, , University Press, US (2006) ISBN : 9780521684248, 3. John M. Howie :, , Real Analysis Springer Science & Business Media (2012) [Springer, , Undergraduate Mathematics Series] ISBN: 1447103416, 4. James S. Howland :, , Basic Real Analysis Jones and Bartlett Publishers Sudbury,, , Massachusetts (2010) ISBN : 0-7637-7318-2, 5. Terence Tao: Analysis I & II (3/e), TRIM 37 & 38, Springer Science+ Business Media Singapore 2016; Hindustan book agency(2015), ISBN : 9789811017896 (eBook) & ISBN : 978981101804(eBook), 6. Richard R Goldberg : Methods of Real Analysis Oxford and IBH Publishing Co.Pvt.Ltd. New, Delhi (1970), 7. Saminathan Ponnusamy : Foundations of Mathematical Analysis Birkhauser (2012), ISBN :, 9780817682910, 8. William F Trench : Introduction to Real Analysis, ISBN : 0130457868, 9. Ajith Kumar & S Kumaresan : A Basic Course in Real Analysis CRC Press, Taylor & Francis, Group (2014), ISBN : 978148221638(eBook PDF), 10. Hugo D Junghenn : A Course in Real Analysis CRC Press, Taylor & Francis Group(2015),, ISBN : 978148221928(eBook PDF), , Page 55 of 115
Page 56 :
55, , SEMESTER – VI, , MTS6B11 : COMPLEX ANALYSIS, 5 Hours/Week, , 5 Credits 100 Marks[Int: 20 + Ext : 80], , Aims, Objectives and Outcomes, The course is aimed to provide a thorough understanding of complex function theory. It is intended to develop the topics in a fashion analogous to the calculus of real functions. At the same time, differences in both theories are clearly emphasised. When real numbers are replaced by complex numbers in the definition of derivative of a function, the resulting complex differentiable functions (more, precisely analytic functions) turn out to have many remarkable properties not possessed by their real, analogues. These functions have numerous applications in several areas of mathematics such as differential equations, number theory etc. and also in science and engineering. The focus of the course is on, the study of analytic functions and their basic behaviour with respect to the theory of complex calculus., The course enables students, • to understand the difference between differentiability and analyticity of a complex function and, construct examples., • to understand necessary and sufficient condition for checking analyticity., • to know of harmonic functions and their connection with analytic functions, • to know a few elementary analytic functions of complex analysis and their properties., • to understand definition of complex integral, its properties and evaluation., • to know a few fundamental results on contour integration theory such as Cauchy’s theorem,, Cauchy-Goursat theorem and their applications., • to understand and apply Cauchy’s integral formula and a few consequences of it such as Liouville’s theorem, Morera’s theorem and so forth in various situations., • to see the application of Cauchy’s integral formula in the derivation of power series expansion, of an analytic function., • to know a more general type of series expansion analogous to power series expansion viz. Laurent’s series expansion for functions having singularity., , Page 56 of 115
Page 57 :
56, , • to understand how Laurent’s series expansion lead to the concept of residue, which in turn, provide another fruitful way to evaluate complex integrals and, in some cases, even real integrals., • to see another application of residue theory in locating the region of zeros of an analytic function., , Syllabus, Text, , Complex Analysis A First Course with Applications (3/e): Dennis Zill & Patric Shanahan,, Jones and Bartlett Learning (2015), ISBN : 1-4496-9461-6, , Module – I, , (25 hrs), , Analytic Functions, 3.1 : Limit and Continuity - Limit of a complex function, condition for non existence of limit, real and, imaginary parts of limit, properties of complex limits, continuity, discontinuity of principal square root, function, properties of continuous functions, continuity of polynomial and rational functions, Bounded, Functions, Branches, Branch Cuts and Points, 3.2 : Differentiability and Analyticity – Derivative of a complex Function, rules of differentiation,, function that is nowhere differentiable, Analytic functions, entire functions, singular points, Analyticity, of sum product and quotient, L’Hospital rule, 3.3 : Cauchy Riemann Equations - Necessary condition for analyticity, Criterion for non analyticity,, sufficient condition for analyticity, sufficient condition for differentiability, Cauchy Riemann equations, in polar coordinates, 3.4 : Harmonic Functions - definition, analyticity and harmonic nature, harmonic conjugate functions,, finding harmonic conjugate, , Elementary Functions, 4.1 : Exponential and logarithmic functions-Complex Exponential Function, its derivative, analyticity,, modulus argument and conjugate, algebraic properties, periodicity, exponential mapping and its properties, Complex Logarithmic Function, logarithmic identities, principal value of a complex logarithm,, Ln z as inverse function, derivative, logarithmic mapping, properties, other branches, 4.3 : Trigonometric and Hyperbolic functions - Complex Trigonometric Functions, identities, periodicity of sine and cosine, Trigonometric equations and their solution, Modulus, zeroes analyticity,, , Page 57 of 115
Page 58 :
57, , [subsection ‘Trigonometric Mapping’ omitted], Complex Hyperbolic Functions, relation to sine and, cosine, , Module – II, , (20 hrs), , Integration in the Complex plane, 5.1 : Real Integrals - Definite Integral, simple, smooth, closed curves, Line integrals in the plane,, Method of Evaluation-curves defined parametrically and curves given as functions, Orientation of a, Curve, 5.2 : Complex Integral - contours, definition of complex integral, complex valued function of a real, variable, evaluation of contour integral, properties of contour integral, ML-inequality, 5.3 : Cauchy–Goursat Theorem - simply and multiply connected regions, Cauchy theorem, Cauchy–, Goursat theorem for simply connected domain (without proof), Multiply Connected Domains, principe, of deformation of contours, Cauchy–Goursat theorem for multiply connected domains, illustrations, 5.4 : Independence of Path - definition, analyticity and path independence, anti derivative, Fundamental theorem for contour integrals, Some Conclusions, Existence of anti derivative, 5.5 : Cauchy’s Integral Formulas & their Consequences - Cauchy’s Two Integral Formulas, illustration, of their use, Some Consequences of the Integral Formulas cauchy’s inequality, Liouville theorem,, Morera’s theorem, Maximum modulus theorem, , Module – III, , (15 hrs), , Series, 6.1 : Sequences and Series - definition, criteria for convergence, Geometric series, necessary condition, for convergence, test for divergence, absolute and conditional convergence, Ratio test, root test, Power, Series, circle of convergence, radius of convergence, Arithmetic of Power Series, 6.2 : Taylor Series - differentiation and integration of power series, term by term differentiation and, integration, Taylor Series, Maclaurian series, illustrations, 6.3 : Laurent’s Series - isolated singularities, Laurent’s Theorem [proof omitted], illustrations, , Module – IV, , (20 hrs), , Residues, 6.4 : Zeros and Poles- classification of isolated singular points, removable singularity, pole, essential, , Page 58 of 115
Page 59 :
58, , singularity, order of zeros and poles, 6.5 : Residues and Residue Theorem - residue, method of evaluation of residue at poles, (Cauchy’s), Residue Theorem, illustrations, 6.6 : Some Consequences of Residue theorem 6.6.1 : Evaluation of Real Trigonometric Integrals, , References:, 1. James Ward Brown, Ruel Vance Churchill: Complex variables and applications (8/e), McGrawHill Higher Education, (2009) ISBN: 0073051942, 2. Alan Jeffrey : Complex Analysis and Applications (2/e), Chapman and Hall/CRC Taylor Francis, Group (2006), ISBN:978-1-58488-553-5, 3. Saminathan Ponnusamy, Herb Silverman: Complex Variables with Applications Birkhauser, Boston(2006) ISBN:0-8176-4457-4, 4. John H. Mathews & Russell W. Howell : Complex Analysis for Mathematics and Engineering, (6/e), 5. H A Priestly : Introduction to Complex Analysis (2/e), Oxford University Press, (2003), ISBN:, 0-19-852562-1, 6. Jerrold E Marsden, Michael J Hoffman: Basic Complex Analysis (3/e) W.H Freeman, N.Y., (1999) ISBN:0-7167-2877-X, , Page 59 of 115
Page 60 :
59, , SEMESTER – VI, MTS6B12 : CALCULUS OF MULTI VARIABLE, 5 Hours/Week, , 4 Credits 100 Marks[Int: 20 + Ext : 80], , Aims, Objectives and Outcomes, The intention of the course is to extend the immensely useful ideas and notions such as limit,, continuity, derivative and integral seen in the context of function of single variable to function of, several variables. The corresponding results will be the higher dimensional analogues of what we, learned in the case of single variable functions. The results we develop in the course of calculus of, multivariable is extremely useful in several areas of science and technology as many functions that, arise in real life situations are functions of multivariable., The successful completion of the course will enable the student to, • Understand several contexts of appearance of multivariable functions and their representation, using graph and contour diagrams., • Formulate and work on the idea of limit and continuity for functions of several variables., • Understand the notion of partial derivative, their computation and interpretation., • Understand chain rule for calculating partial derivatives, • Get the idea of directional derivative, its evaluation, interpretation, and relationship with partial, derivatives., • Understand the concept of gradient, a few of its properties, application and interpretation., • Understand the use of partial derivatives in getting information of tangent plane and normal, line., • Calculate the maximum and minimum values of a multivariable function using second derivative, test and Lagrange multiplier method., • Find a few real life applications of Lagrange multiplier method in optimization problems., • Extend the notion of integral of a function of single variable to integral of functions of two and, three variables., • Address the practical problem of evaluation of double and triple integral using Fubini’s theorem, and change of variable formula., , Page 60 of 115
Page 61 :
60, , • Realise the advantage of choosing other coordinate systems such as polar, spherical, cylindrical, etc. in the evaluation of double and triple integrals., • See a few applications of double and triple integral in the problem of finding out surface area,, mass of lamina, volume, centre of mass and soon., • Understand the notion of a vector field, the idea of curl and divergence of a vector field, their, evaluation and interpretation., • Understand the idea of line integral and surface integral and their evaluations., • Learn three major results viz. Green’s theorem, Gauss’s theorem and Stokes’ theorem of multivariable calculus and their use in several areas and directions., , Syllabus, Text, , Calculus: Soo T Tan Brooks/Cole, Cengage Learning (2010) ISBN: 978-0-534-46579-7, , Module – I, , (18 hrs), , 13.1 : Functions of two or more variables - Functions of Two Variables, Graphs of Functions of Two, Variables, Level Curves, Functions of Three Variables and Level Surfaces, 13.2 : Limits and continuity - An Intuitive Definition of a Limit, existence and non existence of limit,, Continuity of a Function of Two Variables, Continuity on a Set, continuity of polynomial and rational, functions, continuity of composite functions, Functions of Three or More Variables, The �−δ Definition, of a Limit, 13.3 : Partial Derivatives - Partial Derivatives of Functions of Two Variables, geometric interpretation,, Computing Partial Derivatives, Implicit Differentiation, Partial Derivatives of Functions of More Than, Two Variables, Higher Order Derivatives, clairaut theorem, harmonic functions, 13.4 : Differentials - Increments, The Total Differential, interpretation, Error in Approximating ∆z, by dz [only statement of theorem1 required; proof omitted] Differentiability of a Function of Two, Variables, criteria, Differentiability and Continuity, Functions of Three or More Variables, 13.5 : The Chain rule - The Chain Rule for Functions Involving One Independent Variable, The, Chain Rule for Functions Involving Two Independent Variables, The General Chain Rule, Implicit, Differentiation, , Page 61 of 115
Page 62 :
61, , Module – II, , (16 hrs), , 13.6 : Directional Derivatives and Gradient vectors - The Directional Derivative, The Gradient of a, Function of Two Variables, Properties of the Gradient, Functions of Three Variables, 13.7 : Tangent Planes and Normal Lines - Geometric Interpretation of the Gradient, Tangent Planes, and Normal Lines, Using the Tangent Plane of f to approximate the Surface z = f (x, y), 13.8 : Extrema of Functions of two variables - Relative and Absolute Extrema, Critical Points Candidates for Relative Extrema, The Second Derivative Test for Relative Extrema, Finding the, Absolute Extremum Values of a Continuous Function on a Closed Set, 13.9 : Lagrange Multipliers - Constrained Maxima and Minima, The Method of Lagrange Multipliers,, Lagrange theorem, Optimizing a Function Subject to Two Constraints, , Module – III, , (21 hrs), , 14.1 :Double integrals - An Introductory Example, Volume of a Solid Between a Surface and a Rectangle, The Double Integral Over a Rectangular Region, Double Integrals Over General Regions, Properties of Double Integrals, 14.2 : Iterated Integrals - Iterated Integrals Over Rectangular Regions, Fubini’s Theorem for Rectangular Regions, Iterated Integrals Over Non rectangular Regions, y–simple and x– simple regions,, advantage of changing the order of integration, 14.3 : Double integrals in polar coordinates - Polar Rectangles, Double Integrals Over Polar Rectangles,, Double Integrals Over General Regions, r– simple region, method of evaluation, 14.4 : Applications of Double integral - Mass of a Lamina, Moments and Center of Mass of a Lamina,, Moments of Inertia, Radius of Gyration of a Lamina, 14.5 : Surface Area- Area of a Surface z = f (x, y), Area of Surfaces with Equations y = g(x, z) and, x = h(y, z), 14.6 : Triple integrals - Triple Integrals Over a Rectangular Box, definition, method of evaluation as, iterated integrals, Triple Integrals Over General Bounded Regions in Space, Evaluating Triple Integrals, Over General Regions, evaluation technique, Volume, Mass, Center of Mass, and Moments of Inertia, 14.7 : Triple Integrals in cylindrical and spherical coordinates - evaluation of integrals in Cylindrical, Coordinates, Spherical Coordinates, 14.8 : Change of variables in multiple integrals - Transformations, Change of Variables in Double, Integrals [only the method is required; derivation omitted], illustrations, Change of Variables in Triple, Integrals, , Page 62 of 115
Page 63 :
62, , Module – IV, , (25 hrs), , 15.1 : Vector Fields - V.F. in two and three dimensional space, Conservative Vector Fields, 15.2 : Divergence and Curl- Divergence- idea and definition, Curl - idea and definition, 15.3 : Line Integrals - Line integral w.r.t. arc length-motivation, basic idea and definition, Line, Integrals with Respect to Coordinate Variables, orientation of curve Line Integrals in Space, Line, Integrals of Vector Fields, 15.4 : Independence of Path and Conservative Vector Fields - path independence through example,, definition, fundamental theorem for line integral, Line Integrals Along Closed Paths, work done by, conservative vector field, Independence of Path and Conservative Vector Fields, Determining Whether, a Vector Field is Conservative, test for conservative vector field Finding a Potential Function, Conservation of Energy, 15.5 : Green’s Theorem - Green’s Theorem for Simple Regions, proof of theorem for simple regions,, finding area using line integral, Green’s Theorem for More General Regions, Vector Form of Green’s, Theorem, 15.6 : Parametric Surfaces - Why We Use Parametric Surfaces, Finding Parametric Representations of, Surfaces, Tangent Planes to Parametric Surfaces, Area of a Parametric Surface [derivation of formula, omitted], 15.7 : Surface Integrals - Surface Integrals of Scalar Fields, evaluation of surface integral for surfaces, that are graphs, [derivation of formula omitted; only method required] Parametric Surfaces, evaluation, of surface integral for parametric surface, Oriented Surfaces, Surface Integrals of Vector Fields definition, flux integral, evaluation of surface integral for graph[method only], Parametric Surfaces,, evaluation of surface integral of a vector field for parametric surface [method only], 15.8 : The Divergence Theorem - divergence theorem for simple solid regions (statement only), illustrations, Interpretation of Divergence, 15.9 : Stokes Theorem - generalization of Green’s theorem –Stokes Theorem, illustrations, Interpretation of Curl, , References:, 1. Joel Hass, Christopher Heil & Maurice D. Weir : Thomas’ Calculus (14/e), Pearson (2018),, ISBN: 0134438981, 2. Robert A Adams & Christopher Essex : Calculus Single Variable (8/e), Pearson Education, Canada (2013) ISBN: 0321877403, , Page 63 of 115
Page 64 :
63, , 3. Jon Rogawski & Colin Adams : Calculus Early Transcendentals (3/e), W. H. Freeman and, Company (2015), ISBN: 1319116450, 4. Anton, Bivens & Davis : Calculus Early Transcendentals (11/e), John Wiley & Sons, Inc., (2016), ISBN: 1118883764, 5. James Stewart : Calculus (8/e) Brooks/ Cole Cengage Learning(2016) ISBN: 978-1-285-74062-1, 6. Jerrold Marsden & Alan Weinstein : Calculus I and II (2/e), Springer Verlag NY (1985),, ISBN:0-387-90974-5, ISBN: 0-387-90975-3, 7. Arnold Ostebee & Paul Zorn: Multivariable Calculus (2/e), W. H. Freeman Custom Publishing,, N.Y.(2008)ISBN: 978-1-4292-3033-9, , Page 64 of 115
Page 65 :
64, , SEMESTER – VI, MTS6B13 : DIFFERENTIAL EQUATIONS, 5 Hours/Week, , 4 Credits 100 Marks[Int: 20 + Ext : 80], , Aims, Objectives and Outcomes, Differential equations model the physical world around us. Many of the laws or principles governing natural phenomenon are statements or relations involving rate at which one quantity changes, with respect to another. The mathematical formulation of such relations (modelling) often results, in an equation involving derivative (differential equations). The course is intended to find out ways, and means for solving differential equations and the topic has wide range of applications in physics,, chemistry, biology, medicine, economics and engineering., On successful completion of the course, the students shall acquire the following skills/ knowledge., • Students could identify a number of areas where the modelling process results in a differential, equation., • They will learn what an ODE is, what it means by its solution, how to classify DEs, what it, means by an IVP and so on., • They will learn to solve DEs that are in linear, separable and in exact forms and also to analyse, the solution., • They will realise the basic differences between linear and non linear DEs and also basic results, that guarantees a solution in each case., • They will learn a method to approximate the solution successively of a first order IVP., • They will become familiar with the theory and method of solving a second order linear homogeneous and nonhomogeneous equation with constant coefficients., • They will learn to find out a series solution for homogeneous equations with variable coefficients, near ordinary points., • Students acquire the knowledge of solving a differential equation using Laplace method which, is especially suitable to deal with problems arising in engineering field., • Students learn the technique of solving partial differential equations using the method of separation of variables, , Page 65 of 115
Page 66 :
65, , Syllabus, Text :, , Elementary Differential Equations and Boundary Value Problems (11/e): William E, Boyce, Richard C Diprima and Douglas B Meade John Wiley & Sons (2017), ISBN :, 1119169879, , Module – I, , (22 hrs), , 1.1 : Some Basic Mathematical Models; Direction Fields, 1.2 : Solutions of some Differential equations, 1.3 : Classification of Differential Equations, 2.1 : Linear Differential Equations; Method of Integrating Factors, 2.2 : Separable Differential Equations, 2.3 : Modelling with First Order Differential Equations, 2.4 : Differences Between Linear and Nonlinear Differential Equations, 2.6 : Exact Differential Equations and Integrating Factors, 2.8 : The Existence and Uniqueness Theorem (proof omitted ), , Module – II, , (23 hrs), , 3.1 : Homogeneous Differential Equations with Constant Coefficients, 3.2 : Solutions of Linear Homogeneous Equations; the Wronskian, 3.3 : Complex Roots of the Characteristic Equation, 3.4 : Repeated Roots; Reduction of Order, 3.5 : Nonhomogeneous Equations; Method of Undetermined Coefficients, 3.6 : Variation of Parameters, 5.2 : Series solution near an ordinary point, part1, 5.3 : Series solution near an ordinary point, part2, , Module – III, , (15 hrs), , 6.1 : Definition of the Laplace Transform, 6.2 : Solution of Initial Value Problems, 6.3 : Step Functions, 6.5 : Impulse Functions, 6.6 : The Convolution Integral, , Page 66 of 115
Page 67 :
66, , Module – IV, , (20 hrs), , 10.1 : Two Point Boundary Value Problems, 10.2 : Fourier Series, 10.3 : The Fourier Convergence Theorem, 10.4 : Even and Odd Functions, 10.5 : Separation of Variables; Heat Conduction in a Rod, 10.7 : The Wave Equation: Vibrations of an Elastic String, , References:, 1. Dennis G Zill & Michael R Cullen: Differential Equations with Boundary Value Problems (7/e):, Brooks/ Cole Cengage Learning (2009), ISBN: 0495108367, 2. R Kent Nagle, Edward B. Saff & Arthur David Snider: Fundamentals of Differential Equations, (8/e) Addison Wesley (2012) ISBN: 0321747739, 3. C. Henry Edwards & David E. Penney: Elementary Differential Equations (6/e) Pearson Education, Inc. New Jersey (2008), ISBN 0132397307, 4. John Polking, Albert Boggess & David Arnold : Differential Equations with Boundary Value, Problems (2/e) Pearson Education, Inc New Jersey(2006) ISBN 0131862367, 5. Henry J. Ricardo: A Modern Introduction to Differential Equations (2/e) Elsevier Academic, Press. (2009). ISBN: 9780123747464, 6. James C Robinson: An Introduction to Ordinary Differential Equations Cambridge University, Press (2004). ISBN: 0521533910, , Page 67 of 115
Page 68 :
., , ELECTIVE COURSES, , Page 68 of 115
Page 69 :
68, , SEMESTER – VI (Elective), MTS6B14(E01) : GRAPH THEORY, 3 Hours/Week, , 2 Credits, , 75 Marks[Int: 15 + Ext : 60], , Aims, Objectives and Outcomes, Graph theory has been applied to several areas of physics, chemistry, communication science,, biology, electrical engineering, operations research, psychology, linguistics, among others fields, to, solve problems that can be modelled as discrete objects called graphs., The successful completion of the course will enable the student to, • understand and apply the fundamental concepts in graph theory, • apply graph theory based tools in solving practical problems, • improve the proof writing skills., • analyze properties of graphs, • understand trees and their properties, • distinguish between Eulerian and Hamiltonian graphs, • analyze planar graphs, , Syllabus, Text (1), , A First Look at Graph Theory: John Clark & Derek Allan Holton, Allied Publishers,, First Indian Reprint 1995, , Module – I, , (16 hrs), , 1.1 Definition of a graph, 1.2 Graphs as models, 1.3 More definitions, 1.4 Vertex degrees, 1.5 Sub graphs, , Page 69 of 115
Page 70 :
69, , 1.6 Paths and Cycles, 1.7 Matrix representation of a graph [up to Theorem 1.6 ; proof of Theorem 1.5 is omitted], , Module –II, , (16 hrs), , 2.1 Definitions and Simple Properties, 2.2 Bridges [Proof of Theorem 2.6 and Theorem 2.9 are omitted], 2.3 Spanning Trees, 2.6 Cut Vertices and Connectivity [Proof of Theorem 2.21 omitted], , Module – III, , (16 hrs), , 3.1 Euler Tour [up to Theorem 3.2, proof of Theorem 3.2 omitted], 3.3 Hamiltonian Graphs [Proof of Theorem 3.6 omitted], 5.1 Plane and Planar graphs [Proof of Theorem 5.1 omitted], 5.2 Euler’s Formula [Proofs of Theorems 5.3 and Theorem 5.6 omitted], , References:, 1. R.J. Wilson: Introduction to Graph Theory, 4th ed., LPE, Pearson Education, 2. J.A. Bondy & U.S.R. Murty : Graph Theory with Applications, 3. J. Clark & D.A. Holton: A First Look at Graph Theory, Allied Publishers, 4. N. Deo : Graph Theory with Application to Engineering and Computer Science, PHI., , Page 70 of 115
Page 71 :
70, , SEMESTER – VI (Elective), MTS6B14(E02) : TOPOLOGY OF METRIC SPACES, 3 Hours/Week, , 2 Credits, , 75 Marks[Int: 15 + Ext : 60], , Aims, Objectives and Outcomes, The aim of this course is to give theoretical foundation for key concepts appearing in Analysis:, open sets, closed sets, connected sets, continuous maps. This will be done in the context of metric, and topological spaces. After this course student will be able to perform simple theoretical analysis, involving sets in metric and topological spaces and maps between these spaces. Be able to apply these, concepts to other areas of mathematics., , Syllabus, Text, , Metric Spaces : Mı́cheál Ó Searcóid Undergraduate Mathematics Series Springer Verlag, London Limited (2007) ISBN: 1846283698, , Module – I, , (19 hrs), , Chapter – 1 : Metrics, 1.1 : Metric Spaces, 1.3 : Metric Subspaces and Metric Superspaces, 1.4 : Isometries, 1.6 : Metrics on Products, 1.7 : Metrics and Norms on Linear Spaces[example1.7.8 omitted], Chapter – 2 : Distance, 2.1: Diameter, 2.2 : Distances from Points to Sets, 2.3 : Inequalities for Distances, 2.4 : Distances to Unions and Intersections, 2.5 : Isolated Points, 2.6 : Accumulation Points, 2.7 : Distances from Sets to Sets, , Page 71 of 115
Page 72 :
71, , Chapter – 3 : Boundary, 3.1 : Boundary Points, 3.2 : Sets with Empty Boundary, 3.3 : Boundary Inclusion, 3.6 : Closure and Interior, 3.7 : Inclusion of Closures and Interiors, , Module – II, , (17 hrs), , Chapter – 4 : Open, Closed and Dense Subsets, 4.1 : Open and Closed Subsets, 4.2 : Dense Subsets, 4.3 : Topologies, 4.4 : Topologies on Subspaces and Superspaces, 4.5 : Topologies on Product Spaces, Chapter – 5 : Balls, 5.1 : Open and Closed Balls, 5.2 : Using Balls, Chapter – 6 : Convergence, 6.1 : Definition of Convergence for Sequences, 6.2 : Limits, 6.4 : Convergence in Subspaces and Superspaces, 6.6 : Convergence Criteria for Interior and Closure, 6.7 : Convergence of Subsequences, 6.8 : Cauchy Sequences, , Module – III, , (12 hrs), , Chapter – 7 : Bounds, 7.1 : Bounded Sets, 7.4 : Spaces of Bounded Functions, 7.6 : Convergence and Boundedness, 7.7 : Uniform and Pointwise Convergence, Chapter – 8 : Continuity, 8.1 : Local Continuity, , Page 72 of 115
Page 73 :
72, , 8.3 : Global Continuity, 8.5 : Continuity of Compositions, Chapter – 11 : Connectedness, 11.1 : Connected Metric Spaces, 11.2 : Connected Subsets, 11.3 : Connectedness and Continuity, , References:, 1. E. T. Copson : Metric Spaces Cambridge University Press(1968)ISBN:0-521 35732-2, 2. Irving Kaplansky : Set Theory and Metric Spaces Allyn and Bacon,Inc. Boston(1972), 3. S. Kumaresan : Topology of Metric Spaces Alpha Science International Ltd.(2005) ISBN: 184265-250-8, 4. Wilson A Sutherland : Introduction to Metric and Topological Spaces(2/e) Oxford University, Press(2009)ISBN:978-0-19-956308-1, 5. Mohamed A. Khamsi and William A. Kirk : An Introduction to Metric Spaces and Fixed Point, Theory John Wiley & Sons, Inc(2001) ISBN 0-471-41825-0., , Page 73 of 115
Page 74 :
73, , SEMESTER – VI (Elective), MTS6B14(E03) : MATHEMATICAL, PROGRAMMING WITH PYTHON AND LATEX, 3 Hours/Week, , 2 Credits, , 75 Marks[Int: 15 + Ext : 60], , Aims, Objectives and Outcomes, This course helps the students to understand basis of Python programming, apply Python programming in plotting mathematical functions, apply Python programming in numerical analysis, understands typesetting using Latex and apply Latex in writing equations, , Syllabus, Text, , Python for Education Learning Maths and Physics using Python: Ajith Kumar B.P Inter, University Accelerator Centre 2010, , Course Contents, The course has Theory Part (external evaluation) and Practical Part (only for internal evaluation)., A student has to maintain a practical record of the work. Practical should be carried out in a, GNU/Linux computer system., , Theory, Module – I, , (15 hrs), , Basics of Python Programming, Chapter 2 :, , Programming in Python: Two modes of using Python, Interpreter, Variables and, , Data Types, Operators and their Precedence, Python Strings, Slicing, Python Lists, Mutable and, Immutable Types, Input from the Keyboard, Iteration: while and for loops, Python Syntax, Colon &, Indentation, Syntax of ‘for loops’, Conditional Execution: if, elif and else, Modify loops : break and, continue, Line joining, Functions, Scope of variables, Optional and Named Arguments, More on Strings, and Lists, split and join, Manipulating Lists, Copying Lists, Python Modules and Packages, Different, ways to import, Packages, File Input/Output, The pickle module, Formatted Printing, Exception, Handling, Turtle Graphics., Chapter 3 : Arrays and Matrices: The NumPy Module, Vectorized Functions., (sec. 2.1 to 2.19, 3.1 to 3.2), , Page 74 of 115
Page 75 :
74, , Module – II, , (20 hrs), , Applications of Python Programming, Chapter 4 :, , Data visualization: The Matplotlib Module, Plotting mathematical functions, Fa-, , mous Curves, Power Series, Fourier Series, 2D plot using colors, Meshgrids, 3D Plots, Mayavi, 3D, visualization, Chapter 6 : Numerical methods: Numerical Differentiation, Numerical Integration, Ordinary Differential Equations, Polynomials, Finding roots of an equation, System of Linear Equations, Least, Squares Fitting, Interpolation., (sec. 4.1 to 4.6, 4.8 to 4.10, 6.1 to 6.8), , Module – III, , (13 hrs), , LATEX, Chapter 5 :, , Type setting using LATEX: Document classes, Modifying Text, Dividing the document, Environments, Typesetting Equations, Arrays and matrices, Floating bodies, Inserting Images,, Example, Application, (sec. 5.1 to 5.8), , Practical, A practical examination, based on following topics, should be conducted for the internal assessment, only., Part A: Plotting, 1. Cartesian plot of polynomials showing all zeros, 2. Cartesian plot of quotient of polynomials, 3. Cartesian plot of functions showing asymptotes, 4. Parametric plot of curves, 5. Polar plot of curves, 6. Plot Pi chart, 7. Plot 3D curves, 8. Plot 3D surfaces, Part B: Numerical Analysis, 1. Bisection Method, 2. Newton-Raphson Method, 3. Numerical differentiation, 4. Trapezoidal rule, , Page 75 of 115
Page 76 :
75, , 5. Simpson’s rule, 6. Euler Method to solve ODE, 7. Fourth order RK Method to solve ODE, Part C: LATEX, 1. General documentation, 2. Tables, 3. Writing equations, Mark distribution for, Practical examination as test paper (Total 6 Marks), Part A: 2 marks, Part B: 2 marks, Part C: 2 marks, Practical Record as Assignment: 3 marks, , References:, 1. Saha, Amit : Doing Math with Python: Use Programming to Explore Algebra, Statistics,, Calculus, and More!. No Starch Press, 2015., 2. Nunez-Iglesias, Juan, Stefan van der Walt, and Harriet Dashnow: ”Elegant SciPy : The Art of, Scientific Python.” (2017)., 3. Stewart, John M.: Python for scientists. Cambridge University Press, 2017., 4. Kinder, Jesse M., and Philip Nelson: A student’s guide to Python for physical modeling. Princeton University Press, 2018., 5. McGreggor, Duncan :. Mastering matplotlib. Packt Publishing Ltd, 2015, 6. Lamport, Leslie. LATEX: A Document Preparation System( 2/e) Pearson Education India, 1994., 7. Hahn, Jane: LATEXfor Everyone. Prentice Hall PTR, 1993, 8. Grätzer, George: Math into LATEX. Springer Science & Business Media, 2013, , Page 76 of 115
Page 77 :
., , OPEN COURSES, , Page 77 of 115
Page 78 :
77, , SEMESTER – V (Open Course), (For, , students not having Mathematics as Core Course and, Mathematics and Physics dual Core programme), , MTS5D01 : APPLIED CALCULUS, 3 Hours/Week, , 3 Credits, , 75 Marks[Int: 16 + Ext : 60], , Aims, Objectives and Outcomes, Calculus is the study of how things change. It provides a framework for modeling systems in which, there is change, and a way to deduce the predictions of such models. It provides a way to construct, relatively simple quantitative models of change, and to deduce their consequences. After successful, completion of the course, the student is able to, 1. Identify the independent and dependent variables of a function and compute its domain and, range., 2. Evaluate functions given by formulas at given points, 3. Plot the graphs of straight lines and conics, 4. Compute limits, 5. Check continuity, 6. Compute derivatives and write down the equation of the tangent line, 7. Determine whether the function is increasing or decreasing using derivatives, 8. Compute velocity and acceleration, 9. Compute marginal cost/revenue/profit of production, 10. Compute differential and use it to approximate the error occurred, 11. Perform implicit differentiation, 12. Compute convexity, concavity and points of inflection, 13. Sketch curves, 14. Determine extreme values, 15. Determine the level of elasticity and use it for predicting the behaviour of revenue/cost/profit, 16. Combine the techniques of model building with optimization techniques, 17. Use exponential/logarithmic function to compute compound interest, radioactive decay etc, 18. To compute the area under a curve, average value of a function using integration, 19. Integrate using substitution, 20. To estimate the future and present value of an income flow, 21. To compute the survival and renewal functions, 22. To compute antiderivative, , Page 78 of 115
Page 79 :
78, , 23. To determine population density, 24. To find the area and volume of surface of revolution, , Syllabus, Text, , Discrete Mathematics with Applications : Thomas Koshy, Elsever Academic Press (2004),, ISBN : 0-12-421180-1, , Module – I, , (16 hrs), , Chapter 1 :- Functions, Graphs, and Limits, 1.1 : Functions, 1.2 : The Graph of a Function, 1.3 : Linear Functions, 1.4 : Functional Models, 1.5 : Limits, 1.6 : One sided limits and continuity, Chapter 2 :- Differentiation: Basic Concepts, 2.1 : The Derivative, 2.2 : Techniques of Differentiation, 2.3 : Product and quotient rules: Higher order derivatives [proof of product and quotient rules omitted], 2.4 : The Chain rule [proof of general power rule omitted], , Module –II, , (18 hrs), , 2.5 : Marginal Analysis and Applications using increments, 2.6 : Implicit Differentiation and Related Rates, Chapter 3 :- Additional Applications of Derivative, 3.1 : Increasing and Decreasing Functions; Relative Extrema,, 3.2 : Concavity and Points of Inflection, 3.4 : Optimization; Elasticity of Demand, 3.5 : Additional Applied Optimization, Chapter 4 :- Exponential and Logarithmic Functions, 4.1 : Exponential functions; continuous compounding, , Page 79 of 115
Page 80 :
79, , 4.2 : Logarithmic functions, , Module – III, , (14 hrs), , Chapter 5 :- Integration, 5.1 : Anti differentiation: The Indefinite Integral, 5.2 : Integration by Substitution, 5.3 : The Definite Integral and the Fundamental Theorem of Calculus [only statement of FTC required;, Justification given at the end of the section omitted], 5.5 : Additional Applications to Business and Economics, 5.6 : Additional Applications to the Life and Social Sciences [The derivation of volume formula, omitted; only the formula and its applications required], , References:, 1. Soo T Tan: Applied Calculus for the Managerial, Life, and social sciences (8/e) Cengage Learning (2011) ISBN: 978-0-495-55969-6, 2. Ron Larson : Brief Calculus An Applied Approach(8/e) Houghton Mifflin Company(2009),, ISBN : 978-0-618-95847-4, 3. Stefan Waner, Steven R. Costenoble : Finite Mathematics and Applied Calculus(5/e) Brooks/, Cole Cengage Learning (2011) ISBN : 978-1-4390-4925-9, 4. Frank C. Wilson, Scott Adamson: Applied Calculus Houghton Mifflin Harcourt Publishing, Company (2009), 5. Geoffrey C. Berresford, Andrew M. Rockett: Applied Calculus (7/e) Cengage Learning, (2016),, ISBN : 978-1-305-08531-2, , Page 80 of 115
Page 81 :
80, , SEMESTER – V (Open Course), (For, , students not having Mathematics as Core Course and, Mathematics and Physics dual Core programme), , MTS5D02 : DISCRETE MATHEMATICS FOR BASIC, AND APPLIED SCIENCES, 3 Hours/Week, , 3 Credits, , 75 Marks[Int: 16 + Ext : 60], , Aims, Objectives and Outcomes, The first module of the course discusses the fundamentals of logic, its symbols and rules. This, enables one to think systematically, to express ideas in precise and concise mathematical terms and, also to make valid arguments. How to use logic to arrive at the correct conclusion in the midst of, confusing and contradictory statements is also illustrated., The second module aims to introduce the notion of algebraic structure in Mathematics consisting, of one or more sets together with one or more operations which enable members of the sets to be, combined in some way. What is important about a particular algebraic structure is that many of its, properties are predictable from the characteristics of the operation or operations involved. This means, that we can classify algebraic structures into families whose members have many features in common., Identification of a given algebraic structure as belonging to a particular family of structures allows us, to conclude that it has the properties characteristic of all members of the family., The strong similarity between the algebra of sets and that of propositions and the laws common, to these two systems leads to the introduction of an algebraic structure known as a Boolean algebra, such that the properties which are shared by these systems are common to all Boolean algebras. The, idea of a Boolean algebra was first developed by George Boole in the middle of the nineteenth century., The course aims to introduce Boolean algebra as a significant component of abstract algebra and to, familiarize important applications in the analysis of electronic circuits and electronic control systems., Third module deals with Graph theory which is a branch of Mathematics whose origin traces back, to 17th century with the solution of Konigsberg Bridge problem by Leonhard Euler. The course aims, to provide an introduction to Graph theory and to outline a handful of its applications in various, fields., After successful completion of the course, the students will be able to, • Identify correct and incorrect arguments, • Understand the criteria for the evaluation of arguments, • Understand the scientific way of decision making using the laws of logic, , Page 81 of 115
Page 82 :
81, , • Understand the concept of algebraic structures in Mathematics, • Identify a given algebraic structure as belonging to a particular family of structures and to state, the characteristic properties of the members of the family, • Understand the concept of groups and derive basic theorems on groups, • Define the concept of Boolean algebra as an algebraic structure and list its properties, • Understand the applications of Boolean algebra in switching circuits, • Define a Graph and identify different classes of graphs, • Understand various applications of Graph theory, , Syllabus, Text, , Discrete Mathematics; Proofs, Structures and Applications (3/e) : Rowan Garnier & John, Taylor CRC Press, Taylor & Francis Group (2009), ISBN : 978-1-4398-1280-8 (hardback)/, 978-1-4398-1281-5 (eBook - PDF), , Module – I, , (14 hrs), , Chapter : 1 Logic, 1.1 : Propositions and Truth Values, 1.2 : Logical Connectives and Truth Tables- Disjunction, Conditional Propositions, Bi conditional, Propositions, 1.3 : Tautologies and Contradictions, 1.4 : Logical Equivalence and Logical Implication- More about conditionals, 1.5 : The Algebra of Propositions- The Duality Principle, Substitution Rule, 1.6 : Arguments, 1.7 : Formal Proof of the Validity of Arguments, 1.8 : Predicate Logic - The Universal Quantifier, The Existential Quantifier, Two-Place Predicates,, Negation of Quantified Propositional Functions, 1.9 : Arguments in Predicate Logic- Universal Specification (US), Universal Generalization (UG),, Existential Specification (ES), Existential Generalization (EG), , Module –II, , (16 hrs), , Chapter - 8 : Algebraic Structures, 8.1 : Binary Operations and Their Properties, , Page 82 of 115
Page 83 :
82, , 8.2 : Algebraic Structures- Semigroups, 8.3 : More about Groups, 8.4 : Some Families of Groups- Cyclic Groups, Dihedral Groups, Groups of Permutations, 8.5 : Substructures, 8.6 : Morphisms, Chapter - 10 : Boolean Algebra, 10.1 : Introduction, 10.2 : Properties of Boolean Algebras, 10.3 : Boolean Functions, 10.4 : Switching Circuits, 10.5 : Logic Networks, 10.6 : Minimization of Boolean Expressions, , Module – III, , (18 hrs), , Chapter - 11 : Graph Theory, 11.1 : Definitions and Examples, 11.2 : Paths and Cycles, 11.3 : Isomorphism of Graphs, 11.4 : Trees, 11.5 : Planar Graphs [proof of Euler formula omitted], 11.6 : Directed Graphs, Chapter - 12 : Applications of Graph Theory, 12.2 : Rooted Trees, 12.3 : Sorting, 12.4 : Searching Strategies, , References:, 1. Edward R. Scheinerman :, , Mathematics A Discrete Introduction(3/e) Brooks/ Cole,, , Cengage Learning (2013)ISBN: 978-0-8400-4942-1, 2. Gary Haggard, John Schlipf, Sue White sides : Discrete Mathematics for Computer Science, Thomson Brooks/ Cole(2006) ISBN : 0-534-49601-x, 3. D P Acharjya, Sreekumar : Fundamental Approach to Discrete Mathematics New Age International Publishers(2005) ISBN: 978-81-224-2304-4, , Page 83 of 115
Page 84 :
83, , 4. Gary Chartrand, Ping Zhang : Discrete Mathematics Waveland Press, Inc(2011)ISBN: 978-157766-730-8, 5. Tom Jenkyns, Ben Stephenson : Fundamentals of Discrete Math for Computer Science A, Problem-Solving Primer Springer-Verlag London (2013) ISBN: 978-1-4471-4068-9, 6. Faron Moller, Georg Struth : Modelling Computing Systems Mathematics for Computer Science, Springer-Verlag London (2013) ISBN 978-1-84800-321-7, , Page 84 of 115
Page 85 :
84, , SEMESTER – V (Open Course), (For, , students not having Mathematics as Core Course and, Mathematics and Physics dual Core programme), , MTS5D03 : LINEAR MATHEMATICAL MODELS, 3 Hours/Week, , 3 Credits, , 75 Marks[Int: 16 + Ext : 60], , Aims, Objectives and Outcomes, The aim of this course is to explain the basic concepts of linear functions, solve system of linear, equations using various methods, solve linear programming problems geometrically. And to solve LP, problems more effectively using Simplex algorithm and also explain duality theory., On successful completion of this course, the students will be able to Understand the idea of, slope of the lines, understand to find solution of Linear Systems by the Echelon Method and Gauss, Jordan method. Gets an idea of matrices, understand how to add, subtract and multiplication of, matrices and understand how find the inverse of a matrix. Understand the methods of solving linear, programming problems geometrically and understands the drawbacks of geometric methods and to, solve LP problems more effectively using Simplex method. Understand duality theory, a theory that, establishes relationships between linear programming problems of maximization and minimization., , Syllabus, Text, , Finite Mathematics and Calculus with Applications (9/e) Margaret L. Lial, Raymond N., Greenwell & Nathan P. Ritchey Pearson Education, Inc (2012), ISBN 0-321-74908-1, , Module – I, , (18 hrs), , Chapter - 1 : Linear Functions, 1.1 : Slopes and Equations of Lines, 1.2 : Linear Functions and Applications, 1.3 : The Least Squares Line, Chapter - 2 : Systems of Linear Equations and Matrices, 2.1 : Solution of Linear Systems by the Echelon Method, 2.2 : Solution of Linear Systems by the Gauss-Jordan Method, 2.3 : Addition and Subtraction of Matrices, 2.4 : Multiplication of Matrices, , Page 85 of 115
Page 86 :
85, , 2.5 : Matrix Inverses, 2.6 : Input-Output Models, , Module –II, , (12 hrs), , Chapter - 3: Linear Programming: The Graphical Method, 3.1 : Graphing Linear Inequalities, 3.2 : Solving Linear Programming Problems Graphically, 3.3 : Applications of Linear Programming, , Module – III, , (18 hrs), , Chapter - 4 : Linear Programming: The Simplex Method, 4.1 : Slack Variables and the Pivot, 4.2 : Maximization Problems, 4.3 : Minimization Problems; Duality, 4.4 : Nonstandard Problems, , References:, 1. Soo T Tan : Finite Mathematics For the Managerial, Life, and social sciences (11/e) Cengage, Learning(2015) ISBN: 1-285-46465-6, 2. Ronald J. Harshbarger,, , James J. Reynolds :, , Mathematical Applications for the, , Management, Life, and Social Sciences (9/e) Brooks/ Cole Cengage Learning (2009) ISBN :, 978-0-547-14509-9, 3. Stefan Waner, Steven R. Costenoble : Finite Mathematics and Applied Calculus(5/e) Brooks/Cole, Cengage Learning(2011) ISBN : 978-1-4390-4925-9, 4. Seymour Lipschutz, John J. Schiller, R. Alu Srinivasan : Beginning Finite Mathematics Schaum’s, Outline Series, McGraw-Hill(2005), 5. Howard L. Rolf : Finite Mathematics Enhanced Edition(7/e) Brooks/Cole, Cengage Learning, (2011) ISBN : 978-0-538-49732-9, 6. Michael Sullivan : Finite Mathematics An Applied Approach(11/e) John Wiley & Sons, Inc(2011), ISBN : 978-0470-45827-3, , Page 86 of 115
Page 87 :
86, , SEMESTER – V (Open Course), (For, , students not having Mathematics as Core Course and, Mathematics and Physics dual Core programme), , MTS5 D04 : MATHEMATICS FOR DECISION, MAKING, 3 Hours/Week, , 3 Credits, , 75 Marks[Int: 16 + Ext : 60], , Aims, Objectives and Outcomes, Statistics is the science of learning from data. Various mathematical techniques involved in it, enables to gather, analyze and draw inferences from the data around us, thereby enabling to make, solid decisions. The profound statistical techniques help in evaluating and interpreting both qualitative, and quantitative forms of data. In the given scope of the course, various probability concepts and, probability distributions are introduced to get a wider understanding on the application of statistics, in decision making., The objective of this course is to prepare the students for the core modules in statistical modeling, and analysis. The first module introduces the student to data, describing data and descriptive and, graphical summaries of data. In the later modules, the student is also introduced to probability, concepts and basic probability distributions which are vital for statistical analyses., On successful completion of the course, the students shall acquire the following skills/ knowledge., • The student could understand the classifications of data. Student is also introduced to various, data collection techniques., • Student will learn to visualize various types of data with the use of frequency charts and appropriate graphs., • Student understands concepts like measures of central tendency, measures of variation and, measures of position., • Student gets a clear understanding of basic probability concepts. Student learns conditional, probability, addition rule and other basic theories in probability., • Student will learn various probability distributions of discrete and continuous variables., • Student learns about the normal distribution, which is an important continuous probability, distribution in inferential statistics., • Student understands the standard normal distribution and learns the conversion of normal, variable to standard normal variable., , Page 87 of 115
Page 88 :
87, , Syllabus, Text, , Elementary Statistics: Picturing the World (6/e) Ron Larson & Betsy Farber Pearson, Education, Inc (2015) ISBN : 978-0-321-91121-6, , Module – I, , (14 hrs), , Chapter - 1: Introduction to Statistics, 1.1 : An Overview of Statistics, 1.2 : Data Classification, 1.3 : Data Collection and Experimental Design, Chapter - 2: Descriptive Statistics, 2.1 : Frequency Distributions and their Graphs, 2.2 : More Graphs and Displays, 2.3 : Measures of Central Tendency, 2.4 : Measures of Variation, 2.5 : Measures of Position, , Module –II, , (12 hrs), , Chapter - 3 : Probability, 3.1 : Basic Concepts of Probability and Counting, 3.2 : Conditional Probability and the Multiplication Rule, 3.3 : The Addition Rule, 3.4 : Additional topics in probability and counting, , Module – III, , (22 hrs), , Chapter - 4 : Discrete Probability Distribution, 4.1 : Probability Distributions, 4.2 : Binomial Distributions, 4.3 : More Discrete Probability Distributions, Chapter - 5 : Normal Probability Distribution, 5.1 : Introduction to Normal distributions and Standard Normal Distributions, 5.2 : Normal Distributions: Finding Probabilities, 5.3 : Normal Distributions: Finding Values, , Page 88 of 115
Page 89 :
88, , References:, 1. Mario F. Triola : Elementary Statistics(13/e) : Pearson Education, Inc(2018) ISBN: 978-0-13446245-5, 2. Neil A. Weiss : Elementary Statistics(8/e) Pearson Education, Inc(2012) ISBN: 978-0-32169123-1, 3. Nancy Pfenning : Elementary Statistics : Looking at Big Picture Brooks/Cole Cengage Learning(2011) ISBN: 978-0-495-01652-6, 4. Frederick J Gravetter, Larry B. Wallnau : Statistics for the Behavioral Sciences (10/e) Cengage, Learning(2017) ISBN : 978-1-305-50491-2, 5. Seymour Lipschutz, John J. Schiller, R. Alu Srinivasan : Beginning Finite Mathematics Schaum’s, Outline Series, McGraw-Hill(2005), 6. Michael Sullivan : Finite Mathematics An Applied Approach(11/e) John Wiley & Sons, Inc(2011), ISBN : 978-0470-45827-3, , Page 89 of 115
Page 90 :
., , COMPLEMENTARY COURSES, , Page 90 of 115
Page 91 :
90, , SEMESTER – I, MTS1C01 : MATHEMATICS – 1, 4 Hours/Week, , 3 Credits, , 75 Marks[Int: 15 + Ext : 60], , Aims, Objectives and Outcomes, This course deals with the two branches of calculus, differential calculus and integral calculus, and their, applications. Calculus is a tool for analyzing the physical world around us. The concepts necessary, to explore the relationship between moving objects are provided in calculus. The idea of the definite, integral is defined with the notion of the limit. The first three modules are based on differential calculus, and its applications, and the fourth module is based on integral calculus and its applications. The, Fundamental Theorem of Calculus establishes the connection between the two branches of calculus., After the successful completion of the course, the students learn, • the fundamental ideas of limit, continuity, and differentiability, • increasing and decreasing functions, local maxima, minima, concavity, and inflection points, • how to apply these ideas in drawing the graphs of functions, • to find the solution of maximum-minimum problems using the idea of derivatives, • The Mean Value Theorem and L’Hospital rule, • Riemann sums, • Fundamental Theorem of Calculus and proof, • to solve the area problem, the problem of finding the arc length of a plane curve, and volume, of solids, • Average values and the Mean Value Theorem for integrals, , Syllabus, Text (1), , Calculus I (2/e) : Jerrold Marsden & Alan Weinstein Springer-Verlag New York Inc, (1985) ISBN 0-387-90974-5, , Text (2), , Calculus II (2/e) : Jerrold Marsden & Alan Weinstein Springer-Verlag New York Inc, (1985) ISBN 0-87-90975-3, , Module – I, , (14 hrs), , Page 91 of 115
Page 92 :
91, , 1.1: Introduction to the derivative-instantaneous velocity, slope of tangent line, differentiating simplest functions., 1.2: Limits-Notion of limit, basic properties, derived properties, continuity, continuity of rational, functions, one sided limit, limit involving ±∞., 1.3: The derivative as Limit-formal definition, examples, differentiability and continuity, Leibnitz, notation., 1.4: Differentiating Polynomials-power rule, sum rule etc.., 1.5: Product and quotients-product, quotient, reciprocal & integral power rule, 1.6: Linear Approximation and Tangent Lines-equation of tangent line and linear approximation,, illustrations., , Module – II, , (13 hrs), , 2.1: Rate of change and Second derivative-linear or proportional change, rates of change, second, derivative., 2.2: The Chain Rule-power of a function rule, chain rule., 2.3: Fractional Power & Implicit Differentiation-rational power of a function rule, implicit differentiation., 2.4: Related rates and parametric curves-Related rates, parametric curves, word problems involving, related rates., 2.5: Anti derivatives-anti differentiation and indefinite integrals, anti-differentiation rules., , Module – III, , (18 hrs), , 3.1: Continuity and Intermediate value theorem-IVT: first and second version., 3.2: Increasing and decreasing function-Increasing and decreasing test, critical point test, first derivative test., 3.3: Second derivative and concavity-second derivative test for local maxima, minima and concavity,, inflection points., 3.4: Drawing of Graphs-graphing procedure, asymptotic behaviour., 3.5: Maximum-Minimum Problems-maximum and minimum values on intervals, extreme value theorem, closed interval test, word problems., 3.6: The Mean Value Theorem-The MVT, consequences of MVT-Rolles Theorem, horserace theorem., 11.2: L’Hospital rule-Preliminary version, strengthened version., , Module – IV, , (19 hrs), , 4.1: Summation-summation, distance and velocity, properties of summation, telescoping sum (quick, introduction-relevant ideas only)., , Page 92 of 115
Page 93 :
92, , 4.2: Sums and Areas-step functions, area under graph and its counterpart in distance-velocity problem., 4.3: The definition of Integral-signed area (The counterpart of signed area for our distance-velocity, problem), The integral, Riemann sums., 4.4: The Fundamental Theorem of Calculus-Arriving at FTC intuitively using distance velocity, problem, Fundamental integration Method, proof of FTC, Area under graph, displacements, and velocity., 4.5: Definite and Indefinite integral-indefinite integral test, properties of definite integral, fundamental theorem of calculus: alternative version (interpretation and explanation in terms of areas)., 4.6: Applications of the Integral-Area between graphs, area between intersecting graphs, total changes, from rates of change., 9.1: Volume by slice method-the slice method, volume of solid of revolution by Disk method., 9.3: Average Values and the Mean Value Theorem for Integrals-motivation and definition of average, value, illustration, geometric and physical interpretation, the Mean Value Theorem for Integrals, , References:, 1. Soo T Tan: Calculus Brooks/Cole, Cengage Learning(2010) ISBN: 0-534-46579-X, 2. Gilbert Strang: Calculus Wellesley Cambridge Press(1991) ISBN: 0-9614088-2-0, 3. Ron Larson. Bruce Edwards: Calculus(11/e) Cengage Learning(2018) ISBN: 978-1-337-27534-7, 4. Robert A Adams & Christopher Essex : Calculus Single Variable (8/e) Pearson Education, Canada (2013) ISBN: 0321877403, 5. Joel Hass, Christopher Heil & Maurice D. Weir : Thomas’ Calculus(14/e) Pearson (2018) ISBN:, 0134438981, 6. Jon Rogawski & Colin Adams : Calculus Early Transcendentals (3/e) W. H. Freeman and, Company(2015) ISBN: 1319116450, , Page 93 of 115
Page 94 :
93, , SEMESTER – II, MTS2C02 : MATHEMATICS – 2, 4 Hours/Week, , 3 Credits, , 75 Marks[Int: 15 + Ext : 60], , Aims, Objectives and Outcomes, In this course, polar coordinates are introduced in the first module. Polar coordinates often simplify the equation of curves and surfaces. Polar coordinates are used in navigation as the destination, or direction of travel can be given as an angle and distance from the object being considered. The, relationship between the Cartesian and polar coordinates is specified. Hyperbolic and inverse hyperbolic functions are introduced. Hyperbolic functions are defined in terms of exponential functions., Further applications of integral calculus are demonstrated., In the second module, improper integrals are introduced. Improper integrals find their applications, in probability distributions. Improper integrals enable the study of convergence of series., In the third and fourth module, vector spaces which form the central topic of Linear Algebra are, introduced using several examples. Subspaces, bases, and the dimension of a vector space are covered., A study of matrices and eigen values and eigen vectors is taken up. Properties of determinants are, also dealt with. As diagonal matrices are the matrices with the simplest structure, the diagonalization, of a matrix is introduced., At the end of the course, the students will be able to, • represent points in polar coordinates and convert from one system to another, • do the graphing in polar coordinates, • find the derivatives and anti derivatives of hyperbolic and inverse hyperbolic functions, • find the arc length and surface area of revolution using definite integrals, • find the improper integrals, • find the limit of sequences, • find the integral using the trapezoidal rule and Simpson’s rule, • find the convergence and divergence of series, • solve a system of linear equations using matrix theory, • to find the rank and inverse of a matrix using elementary row transformations, • find the eigen values and the corresponding eigen vectors of a matrix, • to check whether a matrix is diagonalizable or not, , Page 94 of 115
Page 95 :
94, , Syllabus, Text (1), , Calculus I (2/e) : Jerrold Marsden & Alan Weinstein Springer-Verlag New York Inc, (1985) ISBN 0-387-90974-5, , Text (2), , Calculus II (2/e) : Jerrold Marsden & Alan Weinstein Springer-Verlag New York Inc, (1985) ISBN 0-87-90975-3, , Text (3), , Advanced Engineering Mathematics(6/e) : Dennis G Zill Jones & Bartlett Learning,, LLC(2018)ISBN: 978-1-284-10590-2, , Module – I, , Text (1) & (2), , (14 hrs), , 5.1: Polar coordinates and Trigonometry - Cartesian and polar coordinates (Only representation of, points in polar coordinates, relationship between Cartesian and polar coordinates, converting, from one system to another and regions represented by inequalities in polar system are required), 5.3: Inverse functions-inverse function test, inverse function rule, 5.6: Graphing in polar coordinates- Checking symmetry of graphs given in polar equation, drawings,, tangents to graph in polar coordinates, 8.3: Hyperbolic functions- hyperbolic sine, cosine, tan etc., derivatives, anti differentiation formulas, 8.4: Inverse hyperbolic functions- inverse hyperbolic functions (their derivatives and antiderivatives), 10.3: Arc length and surface area- Length of curves, Area of surface of revolution about X and Y, axes, , Module – II, , Text (2), , (17 hrs), , 11.3: Improper integrals- integrals over unbounded intervals, comparison test, integrals of unbounded, functions, 11.4: Limit of sequences and Newton’s method � − N definition, limit of powers, comparison test,, Newton’s method, 11.5: Numerical Integration- Riemann Sum, Trapezoidal Rule, Simpson’s Rule, 12.1: The sum of an infinite series- convergence of series, properties of limit of sequences (statements, only), geometric series, algebraic rules for series, the ith term test, 12.2: The comparison test and alternating series- comparison test, ratio comparison test, alternating, series, alternating series test, absolute and conditional convergence, , Page 95 of 115
Page 96 :
95, , Module – III, , Text (3), , (19 hrs), , 7.6: Vector spaces – definition, examples, subspaces, basis, dimension, span, 7.7: Gram-Schmidt Orthogonalization Process- orthonormal bases for Rn , construction of orthonomal basis of Rn, 8.2: Systems of Linear Algebraic Equations- General form, solving systems, augmented matrix, Elementary row operations, Elimination Methods- Gaussian elimination, Gauss-Jordan elimination,, row echelon form, reduced row echelon form, inconsistent system, networks, homogeneous system, over and underdetermined system, 8.3: Rank of a Matrix- definition, row space, rank by row reduction, rank and linear system, consistency of linear system, 8.4: Determinants- definition, cofactor (quick introduction), 8.5: Properties of determinant- properties, evaluation of determinant by row reducing to triangular, form, , Module – IV, , Text (3), , (14 hrs), , 8.6: Inverse of a Matrix – finding inverse, properties of inverse, adjoint method, row operations, method, using inverse to solve a linear system, 8.8: The eigenvalue problem- Definition, finding eigenvalues and eigenvectors, complex eigenvalues,, eigenvalues and singular matrices, eigenvalues of inverse, 8.9: Powers of Matrices- Cayley-Hamilton theorem, finding the inverse, 8.10: Orthogonal Matrices- symmetric matrices and eigenvalues, inner product, criterion for orthogonal matrix, construction of orthogonal matrix, 8.12: Diagonalization-diagonalizable matrix- sufficient conditions, orthogonal diagonalizability of symmetric matrix, Quadratic Forms, , References:, 1. Soo T Tan: Calculus Brooks/Cole, Cengage Learning(2010) ISBN: 0-534-46579-X, 2. Gilbert Strang: Calculus Wellesley Cambridge Press(1991) ISBN: 0-9614088-2-0, 3. Ron Larson. Bruce Edwards: Calculus(11/e) Cengage Learning(2018) ISBN: 978-1-337-27534-7, 4. Robert A Adams & Christopher Essex : Calculus Single Variable (8/e) Pearson Education, Canada (2013) ISBN: 0321877403, , Page 96 of 115
Page 97 :
96, , 5. Joel Hass, Christopher Heil & Maurice D. Weir : Thomas’ Calculus(14/e) Pearson (2018) ISBN:, 0134438981, 6. Advanced Engineering Mathematics(7/e) Peter V O’Neil: Cengage Learning(2012) ISBN: 9781-111-42741-2, 7. Erwin Kreyszig: Advanced Engineering Mathematics(10/e) John Wiley & Sons(2011) ISBN:, 978-0-470-45836-5, 8. Glyn James: Advanced Modern Engineering Mathematics(4/e) Pearson Education Limited(2011), ISBN: 978-0-273-71923-6, , Page 97 of 115
Page 98 :
97, , SEMESTER – III, MTS3C03 : MATHEMATICS – 3, 5 Hours/Week, , 3 Credits, , 75 Marks[Int: 15 + Ext : 60], , Aims, Objectives and Outcomes, This course comprises the study of vector-valued functions and complex numbers. The ideas, of limit, continuity, derivatives, and integrals of vector-valued functions are introduced. Also, the, concepts of the gradient of a scalar function, curl, and divergence of a vector field is discussed. Line, integral, double integral, and triple integral of vector-valued functions are dealt with and the methods, of evaluation are given using several examples., Complex numbers are introduced in a fashion similar to the calculus of real functions. The study of, analytic functions and their behaviour with respect to the theory of complex calculus is the main focus., The students are enabled to understand the difference between the differentiability and analyticity of, a complex function and the necessary and sufficient conditions for analyticity., The successful completion of the course will enable the students to, • work on the idea of limit, continuity, and derivative of vector-valued functions, • use partial derivatives to find the tangent plane and normal line to a point on a surface, • understand the properties and applications of the gradient of a function, • apply double integral and triple integral to find the mass of a lamina, center of mass, etc., • evaluate curl and divergence of a vector field, • understand line integral, surface integral, and triple integral, • learn the three important theorems: Green’s theorem, Gauss’s theorem, and Stokes’s theorem, and their applications, • learn about harmonic functions and their relation with analytic functions, • understand the definition and evaluation of complex integral, • learn the fundamental results on contour integration such as Cauchy-Goursat Theorem, • understand Cauchy’s integral formula and apply it to derive Liouville’s theorem and the Fundamental Theorem of Algebra, , Page 98 of 115
Page 99 :
98, , Syllabus, Text, , Advanced Engineering Mathematics(6/e) : Dennis G Zill Jones & Bartlett Learning,, LLC(2018)ISBN: 978-1-284-10590-2, , Module – I, , (21 hrs), , 9.1: Vector Functions - Vector Valued Functions, Limits, Continuity, and Derivatives, Geometric, Interpretation of r0 (t), Higher Order Derivatives, Integrals of Vector Functions, Length of a, Space Curve, Arc Length as a Parameter, 9.2: Motion on a Curve - Velocity and Acceleration, Centripetal Acceleration, Curvilinear Motion, in the Plane, 9.3: Curvature and components of Acceleration - definition, Curvature of a Circle, Tangential, and Normal Components of Acceleration, The Binormal, Radius of Curvature, 9.4: Partial Derivatives - Functions of Two Variables, Level Curves, Level Surfaces, Higher Order, and Mixed Derivatives, Functions of Three or More Variables, Chain Rule, Generalizations, 9.5: Directional Derivative - The Gradient of a Function, A Generalization of Partial Differentiation, Method for Computing the Directional Derivative, Functions of Three Variables, Maximum, Value of the Directional Derivative, Gradient Points in Direction of Most Rapid Increase of f, 9.6: Tangent planes and Normal Lines - Geometric Interpretation of the Gradient, Tangent, Plane, Surfaces Given by z = f (x, y), Normal Line, , Module – II, , (24 hrs), , 9.7: Curl and Divergence - Vector Fields, definition of curl and divergence, Physical Interpretations, 9.8: Line Integrals - definition of smooth closed and simple closed curves, Line Integrals in the, Plane, Method of Evaluation - curve as explicit function and curve given parametrically, Line, Integrals in Space, Method of Evaluation, Work, Circulation, 9.9: Independence of Path - Conservative Vector Fields, Path Independence, A Fundamental Theorem, definition of connected, simply connected and multiconnected regions, Integrals Around, Closed Paths, Test for a Conservative Field, Conservative Vector Fields in 3-Space, Conservation, of Energy, 9.10: Double Integral - Integrability, Area, Volume, Properties, Regions of Type I and II, Iterated, Integrals, Evaluation of Double Integrals (Fubini theorem), Reversing the Order of Integration,, Laminas with Variable Density-Center of Mass, Moments of Inertia, Radius of Gyration, , Page 99 of 115
Page 100 :
99, , 9.11: Double Integrals in Polar Coordinates - Polar Rectangles, Change of Variables: Rectangular to Polar Coordinates., 9.12: Green’s Theorem - Line Integrals Along Simple Closed Curves, Green’s theorem in plane,, Region with Holes, 9.13: Surface Integral - Surface Area, Differential of Surface Area, Surface Integral, Method of, Evaluation, Projection of S into Other Planes, Mass of a Surface, Orientable Surfaces, Integrals, of Vector Fields-Flux., 9.14: Stokes’s Theorem - Vector Form of Green’s Theorem, Green’s Theorem in 3-Space Stoke’s, Theorem, Physical Interpretation of Curl, , Module – III, , (21 hrs), , 9.15: Triple Integral - definition, Evaluation by Iterated Integrals, Applications, Cylindrical Coordinates, Conversion of Cylindrical Coordinates to Rectangular Coordinates, Conversion of, Rectangular Coordinates to Cylindrical Coordinates, Triple Integrals in Cylindrical Coordinates,, Spherical Coordinates, Conversion of Spherical Coordinates to Rectangular and Cylindrical Coordinates, Conversion of Rectangular Coordinates to Spherical Coordinates, Triple Integrals in, Spherical Coordinates, 9.16: Divergence Theorem - Another Vector Form of Green’s Theorem, divergence or Gauss’ theorem, (proof omitted), Physical Interpretation of Divergence, 9.17: Change of Variable in Multiple Integral - Double Integrals, Triple Integrals, 17.1: Complex Numbers - definition, arithmetic operations, conjugate, Geometric Interpretation, 17.2: Powers and roots - Polar Form, Multiplication and Division, Integer Powers of z, DeMoivre’s, Formula, Roots, 17.3: Sets in the Complex Plane - neighbourhood, open sets, domain, region etc., 17.4: Functions of a Complex Variable - complex functions, Complex Functions as Flows, Limits, and Continuity, Derivative, Analytic Functions-entire functions, 17.5: Cauchy Riemann Equation - A Necessary Condition for Analyticity, Criteria for analyticity,, Harmonic Functions, Harmonic Conjugate Functions,, 17.6: Exponential and Logarithmic function - (Complex) Exponential Function, Properties, Periodicity, (‘Circuits’ omitted), Complex Logarithm-principal value, properties, Analyticity, 17.7: Trigonometric and Hyperbolic functions - Trigonometric Functions, Hyperbolic Functions,, Properties-Analyticity, periodicity, zeros etc., , Module – IV, , (14 hrs), , Page 100 of 115
Page 101 :
100, , 18.1: Contour integral-definition,, Circulation and Net, , Method, , of, , Evaluation,, , Properties,, , ML, , inequality,, , 18.2: Cauchy-Goursat Theorem- Simply and Multiply Connected Domains, Cauchy’s, Theorem, Cauchy-Goursat theorem, Cauchy-Goursat Theorem for Multiply Connected Domains., 18.3: Independence of Path - Analyticity and path independence, fundamental theorem for contour, integral, Existence of Antiderivative, 18.4: Cauchy’s Integral Formula - First Formula, Second Formula-C.I.F. for derivatives. Liouville’s Theorem, Fundamental Theorem of Algebra, , References:, 1. Soo T Tan: Calculus Brooks/Cole, Cengage Learning(2010 )ISBN 0-534-46579-X, 2. Gilbert Strang: Calculus Wellesley Cambridge Press(1991)ISBN: 0-9614088-2-0, 3. Ron Larson. Bruce Edwards: Calculus(11/e) Cengage Learning(2018) ISBN: 978-1-337-27534-7, 4. Robert A Adams & Christopher Essex : Calculus several Variable (7/e) Pearson Education, Canada (2010) ISBN: 978-0-321-54929-7, 5. Jerrold Marsden & Anthony Tromba : Vector Calculus (6/e) W. H. Freeman and Company, ISBN: 978-1-4292-1508-4, 6. Peter V O’Neil: Advanced Engineering Mathematics(7/e) Cengage Learning(2012)ISBN: 9781-111-42741-2, 7. Erwin Kreyszig: Advanced Engineering Mathematics(10/e) John Wiley & Sons(2011) ISBN:, 978-0-470-45836-5, 8. Glyn James: Advanced Modern Engineering Mathematics(4/e) Pearson Education Limited(2011), ISBN: 978-0-273-71923-6, , Page 101 of 115
Page 102 :
101, , SEMESTER – IV, MTS4C04 : MATHEMATICS – 4, 5 Hours/Week, , 3 Credits, , 75 Marks[Int: 15 + Ext : 60], , Aims, Objectives and Outcomes, In this course, students learn the different methods of solving ordinary and partial differential, equations. The importance of differential equations lies in the fact that even the simplest equations, correspond to useful physical models. The reason for solving a differential equation is to learn about, the underlying physical process. The Laplace method and Fourier series which are valuable tools, in finding the solutions of ordinary and partial differential equations are also dealt with. The heat, equation and wave equation which are the most important partial differential equations are considered, in detail., On successful completion of the course, the students shall acquire the following knowledge., • They learn the major classifications of differential equations., • They learn the conditions for the existence of solution of first and second order Initial Value, Problems., • They learn how to formulate a mathematical model of a physical process., • They learn to solve the first order differential equations that are of linear, separable, exact, and, Bernoulli’s forms., • They learn about the numerical method of solving a differential equation using Euler’s method., • They become familiar with the theory and method of solving second order linear homogeneous, and non-homogeneous equations with constant coefficients., • They learn the method of reduction of order to find a second solution of linear second order, equation by reducing to linear first order equation., • They learn the method of solution of Cauchy Euler equations., • They learn about linear models and Boundary value problems., • They acquire the knowledge of solving a differential equation using the Laplace method, which, is useful to deal with problems in engineering., • They are familiarized with the Fourier series., • They learn the technique of solving partial differential equations using the method of separation, of variables., , Page 102 of 115
Page 103 :
102, , Syllabus, Text, , Advanced Engineering Mathematics(6/e) : Dennis G Zill Jones & Bartlett Learning,, LLC(2018) ISBN: 978-1-284-10590-2, , Module – I, , (21 hrs), , Ordinary Differential Equations, 1.1: Definitions and Terminology - definition, Classification by Type, Classification by Order,, Classification by Linearity, Solution, Interval of Definition, Solution Curve, Explicit and Implicit, Solutions, Families of Solutions, Singular Solution, Systems of Differential Equations, 1.2: Initial Value Problems - First and Second Order IVPs, Existence of solution, 1.3: Differential Equations as Mathematical Models - some specific differential equation models in biology, physics and chemistry., 2.1: Solution Curves without Solution - Direction Fields [‘Autonomous First Order DEs’ omitted], 2.2: Separable Equations - definition. Method of solution, losing a solution, An Integral - Defined, Function, 2.3: Linear Equations - definition, standard form, homogeneous and non homogeneous DE, variation of parameter technique, Method of Solution, General Solution, Singular Points, Piecewise, Linear Differential Equation, Error Function, 2.4: Exact Equations - Differential of a Function of Two Variables, Criteria for an exact differential, Method of Solution, Integrating Factors., 2.5: Solutions by Substitution - Homogeneous Equations, Bernoulli’s Equation, Reduction to, Separation of Variables, 2.6: A Numerical Method - Using the Tangent Line, Euler’s Method [upto and including Example, 2; rest omitted], , Page 103 of 115
Page 104 :
103, , Module – II, , (22 hrs), , Higher Order Differential Equations, 3.1: Theory of Linear Equations - Initial Value and Boundary Value Problems [Existence and, Uniqueness (of solutions), Boundary Value Problem], Homogeneous Equations [Differential Operators, Superposition Principle, Linear Dependence, and Linear Independence, Wronskian], Nonhomogeneous Equations [Complementary Function, Another Superposition Principle], 3.2: Reduction of Order - a general method to find a second solution of linear second order, equation by reducing to linear first order equation, 3.3: Homogeneous Linear Equations with Constant Coefficients - Auxiliary Equation, Distinct Real Roots, Repeated Real Roots, Conjugate Complex Roots, Higher Order Equations,, Rational Roots [‘Use of computer’ part omitted], 3.4: Undetermined Coefficients - Method of Undetermined Coefficients for finding out particular, solution, 3.5: Variation of parameter - General solution using Variation of parameter technique, 3.6: Cauchy Euler Equations - Method of solution, Distinct Real Roots, Repeated Real Roots,, Conjugate Complex Roots, 3.9: Linear Models & Boundary Value Problems - Deflection of a Beam, Eigenvalues and, Eigen functions [upto and including Example 3: the rest is omitted], , Module – III, , (19 hrs), , Laplace Transforms, 4.1: Definition of Laplace Transform - definition, examples, linearity, Transforms of some basic, functions, Sufficient Conditions for Existence of transform, 4.2: Inverse Transform and Transforms of Derivative - Inverse Transforms: A few important, inverse transforms, Linearity, Partial Fractions, Transforms of Derivatives, Solving Linear ODEs, 4.3: Translation Theorems - Translation on the s-axis first translation theorem, its inverse form,, Translation on the t-axis, Unit step function, second translation theorem. Its Inverse form,, Alternative Form of second translation theorem. Beams, 4.4: Additional Operational Properties - Derivatives of Transforms, Transforms of Integrals-convolution, convolution theorem (without proof) and its inverse form, Volterra Integral Equation, Series Circuits [‘Post Script-Green’s Function Redux’ omitted], Transform of a Periodic, Function, 4.5: The Dirac delta Function - Unit Impulse, The Dirac Delta Function and its transform, , Page 104 of 115
Page 105 :
104, , Module – IV, , (18 hrs), , 12.1: Orthogonal Functions - Inner Product, Orthogonal Functions, Orthonormal Sets, Vector, Analogy, Orthogonal Series Expansion, Complete Sets, 12.2: Fourier Series - Trigonometric Series, Fourier Series, Convergence of a Fourier Series, Periodic, Extension, Sequence of Partial Sums, 12.3: Fourier Cosine and Sine Series - Even and Odd Functions., Properties, Cosine and Sine, Series, Gibbs Phenomenon, Half Range Expansions, Periodic Driving Force, 13.1: Separable Partial Differential Equations - Linear Partial Differential Equation, Solution of, a PDE, Separation of Variables (Method), Superposition Principle, Classification of Equations, ( hyperbolic, parabolic, elliptic), 13.2: Classical PDE’s and BVP’s - Heat Equation, Wave Equation, Laplace’s Equation, Initial, Conditions, Boundary Conditions, Boundary Value Problems (‘Variations’ omitted), 13.3: Heat Equation - Solution of the BVP (method of Separation of Variables), , References:, 1. Peter V O’Neil : Advanced Engineering Mathematics(7/e) Cengage Learning(2012) ISBN :, 978-1-111-42741-2, 2. Erwin Kreyszig : Advanced Engineering Mathematics(10/e) John Wiley & Sons(2011) ISBN :, 978-0-470-45836-5, 3. Alan Jeffrey : Advanced Engineering Mathematics Harcourt/Academic Press(2002) ISBN : 012-382592-X, 4. Glyn James: Advanced Modern Engineering Mathematics(4/e) Pearson Education Limited(2011), ISBN: 978-0-273-71923-6, , Page 105 of 115
Page 106 :
., , COMPLEMENTARY COURSE, MATHEMATICAL ECONOMICS, , Page 106 of 115
Page 107 :
106, , SEMESTER – I, MEC1C01 : MATHEMATICAL ECONOMICS, 4 Hours/Week, , 3 Credits, , 75 Marks[Int: 15 + Ext : 60], , Aims, Objectives and Outcomes, The course is intended for students who wish to obtain knowledge of mathematical techniques, suitable for economic analysis. It assumes very little prerequisite knowledge., After the successful completion of the course, the students learn, • Demand and Supply Analysis, • Cost and Revenue Functions, • Theory of Consumer Behaviour, • Economic Applications of Derivatives, , Syllabus, Text (1), , H.L. Ahuja: Principles of Micro Economics, 15th Revised Edition, S. Chand, , Text (2), , Edward T. Dowling: Introduction to Mathematical Economics, Schaum’s Outline Series, Third edition, TMH, , Module – I, , Text(1), , (18 hrs), , Demand and Supply Analysis - Utility and Demand-the meaning of demand and quantity demandedthe law of demand-demand curve-market demand curve-reasons for the law of demand-slope of a, demand curve-shift in demand-demand function and demand curve-the meaning of supply-supply, function-law of supply-slope of a supply curve-shift in supply-market equilibrium-price elasticity of, demand-measurement of price elasticity-arc elasticity of demand-cross elasticity of demand, (relevant sections of chapter 5 and 7), , Module – II, , Text(1), , (13 hrs), , Cost and Revenue Functions - Cost function-Average and marginal cost – short run and long run, costs-shapes of average cost curves in the short run and long run and its explanation-revenue function,, marginal revenue (MR) and average revenue functions (AR), relations between MR, AR and elasticity, of demand, (relevant sections of chapter 19 and 21), , Page 107 of 115
Page 108 :
107, , Module – III, , Text(1), , (13 hrs), , Theory of Consumer Behaviour - Cardinal utility analysis- the law of diminishing marginal utilitythe law of equi-marginal utility- indifference curves-ordinal utiliy-indifference map- marginal rate of, substitution, properties of indifference curves, (Relevant sections of chapter 9 and 11), , Module – IV, , Text(2), , (20 hrs), , Economic Applications of Derivatives - Economic Applications of Derivatives-Marginal, average and total concepts- optimizing economic functions-Functions of several variables and partial, derivatives-rule of partial differentiation, second order partial derivatives, Optimization of multivariable functions, constrained optimization with Lagrange multipliers, significance of Lagrange multiplier,, total and partial derivatives- total derivatives., Marginal productivity, Income determination, multipliers and comparative statics, Income and, cross elasticity of demand, Optimization of multivariable function in Economics, constrained optimization of multivariable function in Economics., (Chap-4: sec. 4.7 & 4.8 ; Chap-5, Chap-6: sec.6.1 to 6.6), , References:, 1. R G D Allen: Mathematical Analysis for Economists Macmillain, 2. Geoff Renshaw: Maths for Economics(3/e) Oxford University Press, N.Y. (2012) ISBN 978-019-960212-4, 3. Mike Rosser: Basic Mathematics for Economists(2/e) Routledge, London (2003) ISBN 0-41526784-6, 4. Taro Yamane: Mathematics for Economists An Elementary Survey Prentice Hall Inc.(1962), 5. Knut Sydsaeter and Peter Hammond: Essential Mathematics for Economic Analysis(4/e) Pearson Education Limited(2012), 6. Henderson & Quandt : Microeconomic Theory A Mathematical Approach (3/e) TMH, , Page 108 of 115
Page 109 :
108, , SEMESTER – II, MEC2C02 : MATHEMATICAL ECONOMICS, 4 Hours/Week, , 3 Credits, , 75 Marks[Int: 15 + Ext : 60], , Aims, Objectives and Outcomes, This is the continuation of previous course. The approach is informal and aims to show students, how to do and apply the mathematics they require for a successful study of economics., At the end of the course, the students will be able to, • understand Inequalities in Income, • understand calculus of several variable, • solve problem related with constrained and unconstrained optimization, • understand input output analysis, , Syllabus, Text (1), , M L Jhingan: Micro Economic Theory(6/e) Vrinda Publications, , Text (2), , Carl P Simon, Lawrence Blume: Mathematics for Economists W. W. Norton & Company, Inc (1994) ISBN 039395733O, , Text (3), , Mehta-Madnani: Mathematics for Economics Revised Edn S Chand, , Module – I, , Text (1), , (9 hrs), , Inequalities in Income - Inequalities in Income-Causes of inequalities, Measures to reduce inequality,, Measurement of inequality of income Lorenz curve, Gini ratio., (Chapter 47), , Module – II, , Text (2), , (18 hrs), , Chapter 14: Calculus of Several Variable: - Directional Derivatives and Gradients, the gradient, vector, Explicit functions from Rn to Rm , Approximation by Differentials, Jacobian derivative, The, Chain rule, Higher Order Derivative. Continuously differentiable functions, Second order derivatives, and Hessians, Young’s theorem, An economic application, , Page 109 of 115
Page 110 :
109, , Chapter 17 Unconstrained Optimization: - Definitions, First Order Conditions, Second Order, Conditions, sufficient conditions, necessary conditions, Global Maxima and Minima, Global Maxima of, Concave Functions, Economic Applications, profit maximizing firm, discriminating monopolist, least, squares analysis, (Sec. 14.6,14.7,14.8, 17.1,17.2,17.3,17.4,17.5), , Module – III, , Text (2), , (18 hrs), , Chapter 18 Constrained Optimization I: First Order Conditions: - Objective function, constraint functions, Examples, Equality Constraints, two variables and one equality constraint, several, equality constraints, inequality constraints, one inequality constraint, several inequality constraints,, Mixed Constraints, Constrained Minimization Problems, Kuhn-Tucker Formulation, Examples and, Applications., (Sec. 18.1,18.2,18.3,18.4,18.5,18.6,18.7), , Module – IV, , Text (3), , (19 hrs), , Input Output Analysis - Introduction - assumption-technological coefficient matrix-closed and, open input output model-coefficient matrix and open model-the Hawkins-Simon conditions -solutions, for two industries -determination of equilibrium of prices - coefficient matrix and closed model-The, Leontief production function - limitation of input output analysis., (sec.19.1 to 19.7, 19.9,19.11,19.13), , References:, 1. A C Chiang & K Wainwright: Fundamentals of Mathematical Economics (4/e) McGraw Hill, 2. R G D Allen: Mathematical Analysis for Economists Macmillain, 3. Urmila Diwekar: Introduction to Applied Optimization(2/e) Springer Science+Business Media,, LLC(2008) ISBN: 9780387766348, 4. Michael D Intriligator: Mathematical Optimization and Economic Theory Classics in Applied, Mathematics, SIAM(2002), 5. Akinson: Distribution and Inequality Measures TMH, , Page 110 of 115
Page 111 :
110, , SEMESTER – III, MEC3C03 : MATHEMATICAL ECONOMICS, 5 Hours/Week, , 3 Credits, , 75 Marks[Int: 15 + Ext : 60], , Aims, Objectives and Outcomes, This is the continuation of previous course. Economic applications are considered although this, course aims to teach the mathematics not the economics., The successful completion of the course will enable the students to, • understand about differential and difference equations, • understand the product function, • understand the Cobb Douglas production function, • understand the Investment Decisions and Analysis of Risks, , Syllabus, Text (1), , Edward T. Dowling: Introduction to Mathematical Economics, Schaum’s Outline Series,, Third edition, TMH, , Text (2), , S P Singh, A P Parashar, H P Singh: Econometrics and Mathematical Economics S., Chand, , Text (3), , C R Kothari: An Introduction to Operation Research (3/e) Vikas Pub. House, , Module – I, , Text (1), , (22 hrs), , Differential and Difference Equations, Differential Equations - definitions and concepts, First Order Linear Differential Equations, Exact differential equations-integrating factors, separation of variables, Economic applications, use of, differential equations in economics., Difference Equations - definitions and concepts, First Order Linear Difference Equations, Economic, applications-the Cobweb model, the Harrod model, (Chapter 16,17), , Module – II, , Text (2), , (18 hrs), , Page 111 of 115
Page 112 :
111, , The Production Function, Meaning and nature of production function, the law of variable proportions-isoquants marginal rate of, technical substitution(MRTs), producer’s equilibrium, Expression path, The elasticity of substitution,, Ridge kines and economic region of production., (Chapter 14 Sec. 14.1 to 14.9 ), , Module – III, , Text (1) & Text (2), , (18 hrs), , Euler’s theorem (statement only), Euler’s theorem and homogeneous production function, Cobb Douglas production function, properties, Economic significance, Limitations, CES production function, properties-advantages-limitations, returns to scale, cobweb theorem, (Chapter 14 Sec. 14.10 to 14.13 of text (2) ), Optimization of Cobb Douglas production function, Optimization of constant elasticity of production, function, (Chapter 6 Sec. 6..9 & 6.10 of text(1) ), , Module – IV, , Text (3), , (22 hrs), , Investment Decisions and Analysis of Risks, Nature of investment decisions, appraisal necessary, Needed information, Appraisal techniques Pay, back method, Average rate of return (ARR) mrthod, Net Present Value (NPV) method, Internal, Rate of Return (IRR) Method, Net Terminal Value Method, Profitability index (P.I.) Analysis of, Risk/Uncertainty; The Risk concept, Risk and Uncertainty situations, Measurement of Risks in precise terms, Incorporating risk in Investment Decisions, Risk adjusted discount rate (RAD) approach,, Certainty Equivalent approach, Probability Distribution approach (The Hillier Models), Decision Trees, Approach, Simulation Approach, (Hertz’s model) Sensitivity analysis., (Chapter 16), , Page 112 of 115
Page 113 :
112, , References:, 1. A C Chiang & K Wainwright: Fundamentals of Mathematical Economics (4/e) McGraw Hill, 2. R G D Allen: Mathematical Analysis for Economists Macmillain, 3. Srinath Baruah: Basic Mathematics and its Applications in Economics Macmillian, 4. Taro Yamane : Mathematics for Economists An Elementary Survey Prentice Hall Inc. (1962), , Page 113 of 115
Page 114 :
113, , SEMESTER – IV, MEC4C04 : MATHEMATICAL ECONOMICS, 5 Hours/Week, , 3 Credits, , 75 Marks[Int: 15 + Ext : 60], , Aims, Objectives and Outcomes, Statistics is a an applied branch of Mathematics, which is an important tool for all social sciences particularly economics. Basics of Statistics and some statistical techniques are discussed in this module., On successful completion of the course, the students shall acquire the following knowledge., • basic idea about econometrics., • the nature of regression analysis., • classical non linear regression model., • Estimation and Hypothesis testing., • extensions of the two variable linear regression model., , Syllabus, Text, , Damodar N Gujarati & Sangeetha : Basic Economics(4/e) TMH Indian Reprint 2008, , Module – I, , (18 hrs), , Introduction to Econometrics - The nature of Regression Analysis -Two variable Regression Analysis., (pages 1 to 59 of Text), , Module – II, , (22 hrs), , Two variable Regression Model, (sec. 3.1 to 3.9 ; pages 60 to 103), , Module – III, , (22 hrs), , Classical normal linear regression model-two variable Regression-Internal Estimation and Hypothesis, testing., , Page 114 of 115
Page 115 :
114, , (sec. 4.1 to 4.5 and 5.1 to 5.13), , Module – IV, , (18 hrs), , Extensions of the two variable linear regression model., (sec. 6.1 to 6.10), , References:, 1. Jeffrey M. Wooldridge :Introductory Econometrics: A Modern Approach (6/e) Cengage Learning(2016), 2. S P Singh, A P Parashar, H P Singh: Econometrics and Mathematical Economics, S. Chand, 3. Douglas C. Montgomery, Elizabeth A. Peck, Geoffrey Vining : Introduction to Linear Regression, Analysis (5/e) John Wiley & Sons (2012), 4. Christopher Dougherty : Introduction to Econometrics(3/e) Oxford University Press(2007), , Page 115 of 115