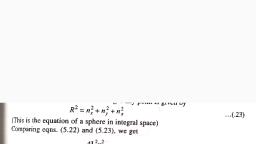Page 1 :
An Introduction to Therm, , , , , , , , , , , -N,K, , at, =In, Vi+V2, , i / s cha, We know that the change in entropy when a gas T) to anther state (volume V, +V/ and temperature /), , T, Vi+V2 ), AS =C, nf 2 | +R nf, , where Cy-and R are respectively, the specific heat at constant volume and universal gas constant,, , case of isothermal change 7) = 7), then the above equation becomes, Vi, +V:, AS = Rin ., 1, A comparison of eqns. (69) and (70) yields, , -N4Ko V, =, in) = Wf), V,+V2 Vi+V2, , ie. N,Ko=R GH), , or Ky = Rk = ® (2), N4, which is the well known Boltzmann constant., Thus Boltzmann theorem gives a statistical interpretation of entropy and it is expressed, mathematically as ;, S=kinW T° (Ba), It was Planck who gave the above explicit formula without any additive constant. This formula, determines the absolute value of the entropy of a given physical system in terms of the total number of, ticrostates accessible to it in conformity with the given macrostate. The zero of the ropy then, _ corresponds to the special state for which only one microstate is accessible (W=1)— - so called, _ “unique configuration”. The statistical approach thus provides a theoretical basis for the th aw of, thermodynamics as well (According to the Planck statement of the third law, the entropy of as er in, equilibrium approaches zero as the temperature approaches zero). Then the system is perfec, , ordered (W = 1 and In W= 0). By using our previous symbol, eqn. (73.i) may also be written as, (ni, , (6), i § lume V; and t, nges from one state (vo! 1 an, , ) is given by, , Ihow, , , , , , S=kinQ, , 14:43 Liouville’s Theorem, Consider an isolated s, , ystem specified classically by f generalized coordinates ¢, M972.) - In a statistical ensemble of such system, let ;, , Plas ps Piss yt} dq ,°*+,dq 7, dpy,--, dp ¢ :, =the number of systems in the ensemble which, at time f, have positions and momenta in the elemet!, , f ns Z, of volume {dq,, dq 5,dp,,---,dp,\ of phase space lying between q, and q, +441» a, 92 +g... p; and Pytdp,., , trea, , Pend, , Eve i = oe 1 motion, Dhician ty system in the ensemble moves in time according to its classical equations of :

Page 2 :
The Statistical Basis of Thermodynamics, , 95, oY p patie, qi ap; ree aq; (74), where H = Hin sO py Ply **y pr} is the Hamiltonian of the system. As a result of this motion the, , . ms in phase space cl in ti ‘, density Of the Systems 1a pace changes in time. We are interested i i i, intof phase space. ed in finding dp/ Of ata given, , Let us focus attention on any given fixed element of volume in phase space located between, g, and q +4915 92 ANd go +g... Py and py +dp, (fig, 4.14),, , The number of systems located in this volume {da,,---,.dq,,.dp, se dp, changes as the, , coordinates and momenta of the system vary in accordance with eqn. (1). In a time df the change in the, number of systems within this volume of phase space is given by Op/dr dt\dq,,---,dp,}. This, , change is due to the number of systems entering and leaving this volume {dq, 7, dp ) in the time, , dt, But the number of systems entering this volume in time df through the “face” q; = constant is just, the number contained in the volume (4, 4t)(dq,---,dp ¢) ie. it is equal to the quantity, , plays»? yst)(ardtdg, --.dp The number of systems leaving through the “face” g,+dq,; =, constant is given by a similar expression except that both p and q,; must be evaluated at 4, +dq,, , instead of at q,., Hence the net number of systems entering the phase-space volume (dq,,---,dp ,) in time dt, , _ through the “faces” q, = constant and q, + dq, = constant is given by, , : ene, pq,dtdq, «dp ¢ -| ea +L cwinrt art “dp y, 1, , o : :, =7 9g, boaalitale dD y @>), 1, , ea tees, Py Gat (di *3q, daat, , a fet, , , , , , , , , , , , , , , , , , Wat dn %, , day, Fig. 4.14: Diagram illustrating a fixed volume element of (two dimensional phase space)

Page 4 :
he statistical Basis of Thermodynamics, , EE ———_., 0q,°Oq 97, oN= eee, | hi, states, where fis the number of degrees of freedom. Acc, , . 0}, ;, ., , rdin, ii) thi, : an : eqn. (79.11) this number will always, se to describe the system. Hence, the, , € like an inc . j, phase, incompressible fluid. Gibbs referred, , le fr iouville’, om Liouville’s theorem. Consider a region, , : pis uniform over i, region are permanently determined by representative points lying in it. ne nae aseieeirad, . The number of elements in this, , region is, , remain the same, irrespective of what coordinat, distribution of representative points moves in the rsp, to this fact as the principle of conservation of dahiRate, We can arrive at yet another important pelt, ev ina phase space, small enough so that the Hanlted,, , ON=poV, In the course of time, each point in this region traces out j ee, . : a tr i, time f, the region OV will have gone to a new region SV’ Wihte chase oe aes a mE, ace. Bot éV', , contain the same number of states and hence, they must hav: i, shapes may be different. This can be proved as follows: ed ela i od, , As no representative point can cross the bound:, ary, nor can i, ee, any point be created or destroyed,, , d d, | = (6N)=—(pdV, ais = ne ), , | 22 Lee, =P. sv + pT (6v)=0 (85), ;, or <(6v)=0 (because #.-0) (86), (87), , c d, , ie. = | Oarer ae, Thus, if a given number of representative points occupy an element of volume SV at a certain time,, volume of equal size at a later time, although the volume element may change, , its shape. This is known as the principle of conservation of extension., , :, , hey will occupy another, . 415 Stirling’s Approximation, }, , Stirling in 1730 gave the following formula for the factorial of large numbers:, lim n!= (zm ntie no, , nite values of n is of the order of +00 Instead of multiplying, , The percent error of this formula for fi, we have merely to calculate the factorial by the use of, , together a large number of integers, a ;, expression(88) by means of a table of logarithms and this involves for fewer operations. :, In order of obtain this formula, let us try 0 estimate the area under the curve = In rus, , curve has the general form depicted in fig. (4.15). If we integrate In (x) by parts,, , 1 Rist, , A, = fin xd = xInx—a =ninn-ntl, 1, , urve shown in figure. If we erect ordinates yi, Yars-» Ym at ¥=*1s, , curve T;, gives, , we obtain the result:, , (89), , 4, is the exact area under the ', *=%X),...,.x=2%,, the traps, , ezoidal rule for the area under the