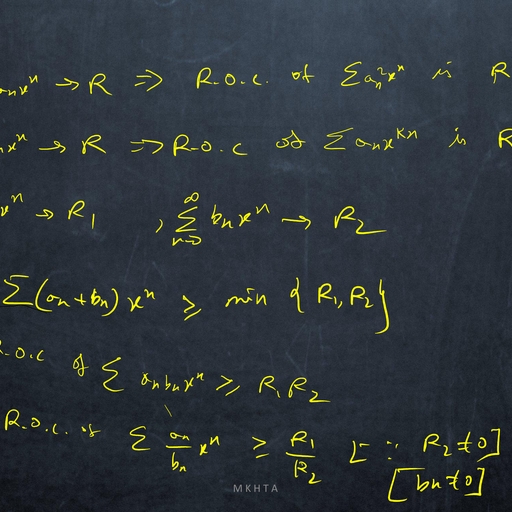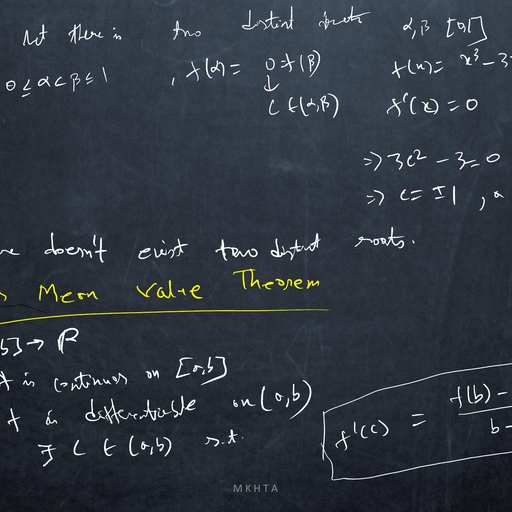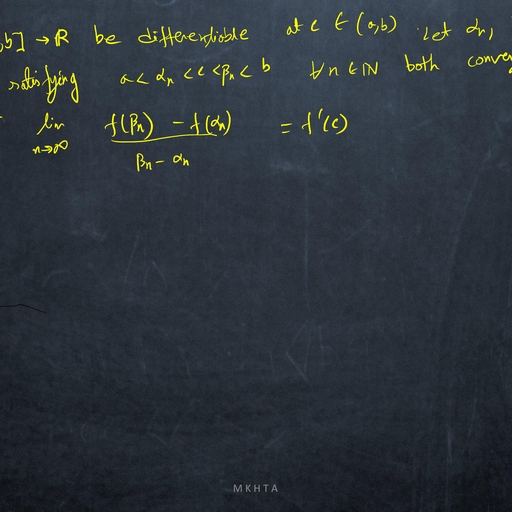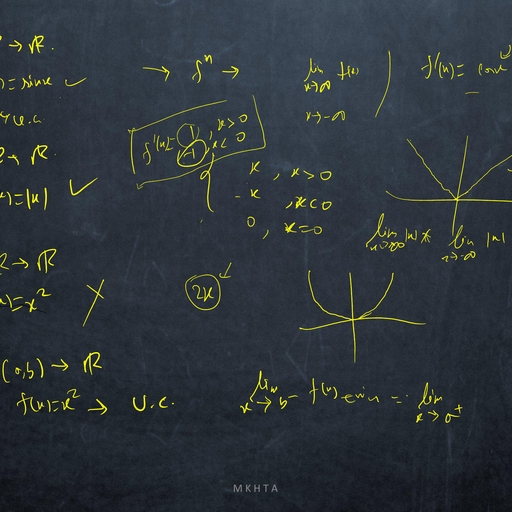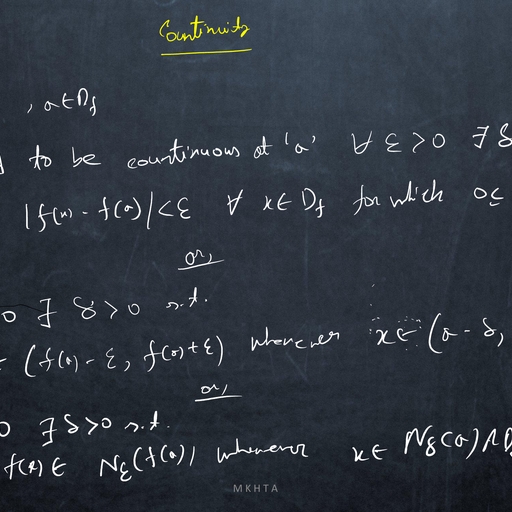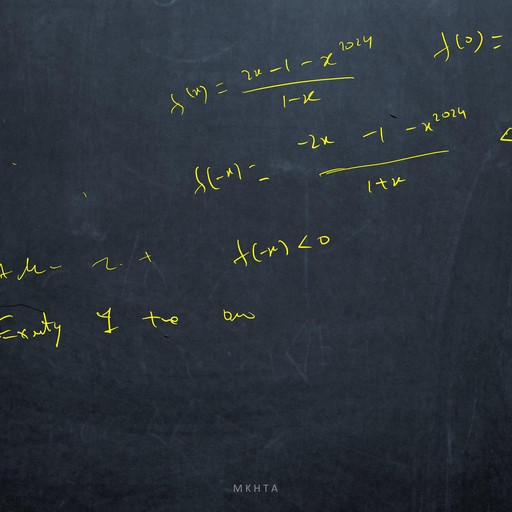Page 1 :
Mathematical Biology, Unit-I, 1, , Introduction, , MKHTA, , Mathematical and theoretical biology is a branch of biology which deals with theoretical analysis, mathematical models and abstractions of the living organisms to investigate the principles that govern the structure,, development and behavior of the systems, as opposed to experimental biology which deals with the conduction, of experiments to prove and validate the scientific theories. The field is sometimes called mathematical biology or biomathematics to stress the mathematical side, or theoretical biology to stress the biological side., Theoretical biology focuses more on the development of theoretical principles for biology while mathematical, biology focuses on the use of mathematical tools to study biological systems, even though the two terms are, sometimes interchanged., , Aims:, , Mathematical biology aims at the mathematical representation and modeling of biological pro-, , cesses, using techniques and tools of applied mathematics and it can be useful in both theoretical and practical, research. Describing systems in a quantitative manner means their behavior can be better simulated, and hence, properties can be predicted that might not be evident to the experimenter. This requires precise mathematical, models., Because of the complexity of the living systems, theoretical biology employs several fields of mathematics,, and has contributed to the development of new techniques., , History:, , Mathematics has been used in biology as early as the 12th century, when Fibonacci used the, , famous Fibonacci series to describe a growing population of rabbits. In the 18th century Daniel Bernoulli, applied mathematics to describe the effect of smallpox on the human population. Thomas Malthus’ 1789 essay, on the growth of the human population was based on the concept of exponential growth. Pierre Francois, Verhulst formulated the logistic growth model in 1836., Fritz Muller described the evolutionary benefits of what is now called Muellerian mimicry in 1879, in an, account notable for being the first use of a mathematical argument in evolutionary ecology to show how powerful, the effect of natural selection would be, unless one includes Malthus’s discussion of the effects of population, growth that influenced Charles Darwin: Malthus argued that growth would be exponential (he uses the word, ”geometric”) while resources (the environment’s carrying capacity) could only grow arithmetically., The term theoretical biology was first used by Johannes Reinke in 1901. One founding text is considered, to be On Growth and Form (1917) by D’Arcy Thompson, and other early pioneers include Ronald Fisher, Hans, Leo Przibram, Nicolas Rashevsky and Vito Volterra., , 1, , MKHTA

Page 2 :
1.1, , Mathematical Meandering, , dx, = f (x), where f does not depends on the variable t explicitly., dt, ?, Definition: The point x is called an equilibrium point (or, fixed point or, critical point or, rest point ), Consider the autonomous system, , if f (x? ) = 0., Definition: An equilibrium point x? is Lyapunov stable if, for any arbitrary small  > 0, there exists, δ > 0 ( depending on ) such that, for all initial conditions x(t0 ) = x0 satisfying |x0 − x? | < δ, we have, |x(t) − x? | < , for all t > t0 ., Definition: An equilibrium point x? is asymptotically stable ( in the sense of Lyapunov ) if it is stable, and if there exists ρ > 0 such that lim |x(t) − x? | < ρ., t→∞, , Thus an equilibrium is asymptotically stable if all sufficiently small initial deviations produce small excursions that eventually returns to the equilibrium., Perturbation: A method for solving a problem by comparing it with a similar one for which the solution, is known. Usually the solution found in this way is approximate., Perturbation variable: To study the stability analysis of an equilibrium x? of a dynamical system, dx, = f (x), we measure the deviation of x from x? by introducing a variable u = x − x? , where |u|  1., dt, Such a variable u is called perturbation variable., du, = f 0 (x? )u, where, Consequently, the non-linear dynamical system is reduced to the linear system, dt, f 0 (x? ) 6= 0, and this linearized system approximately determine the nature of stability of x? of given, system., dx, = f (x) and f is continuously, dt, 0, ?, differentiable function of x. If f (x ) =, 6 0, then the equilibrium point x? is asymptotically stable if, Theorem Let x? be an equilibrium point of the autonomous system, , f 0 (x? ) < 0 and unstable if f 0 (x? ) > 0., Proof Consider the equilibrium point for which f 0 (x? ) < 0. Let u(t) = xt) − x? ., Since f is continuously differentiable function of x, then expanding f (x) about x? , we have, d, {x? + u(t)} = f (x? ) + uf 0 (x? ) + g(u)., dt, Since x? is an equilibrium of given system, then f (x? ) = 0 and consequently we have, du, = uf 0 (x? ) + g(u)., dt, This is a perturbation of first order linear constant coefficient ordinary differential equation, where g(u), consists of higher order terms., Again continuity of g 0 (u) along with g(0) = 0, g 0 (0) = 0, guarantees that for each  > 0 there is a small, neighbourhood of zero such that |g 0 (u)| < . Thus, Z u we have, g(u) =, g 0 (s) ds ≤  |u|., 0, , du, Consequently, it follows that, ≤ u f 0 (x? ) +  |u|., dt, du, Since f 0 (x? ) 6= 0, then for sufficiently small δ and , the higher order terms can not change the sign of, ., dt, ?, Hence sufficiently small perturbations will decay and the equilibrium x is asymptotically stable., Again consider the equilibrium point for which f 0 (x? ) > 0., Proceeding as before we can prove that f 0 (x? ) > 0 implies that the equilibrium x? is unstable., , 2

Page 3 :
Modeling Process, , 2, , In mathematical biology, a model can describe any biological phenomenon. In this, chapter, we focus on dynamical models, which describe how a system changes over, time. Such models are very common in biology as they provide insight into how, various forces act to change a cell, an organism, a population, or an assemblage of, species., Dynamical models are classified into following classes:, • Discrete time model: A discrete time models is a model which describe how, the variables change from one time unit to the next. This type of model tracks, changes to variables in discrete time steps., • Continuous time model: A continuous time model allows variables to change, over any period of time (i.e., time treated as continuous). It is possible for a, change to occur in one small interval of time followed by the same type of change, in the next small interval of time., • Deterministic model: A Deterministic model is the shorthand for the assumption that the future is entirely predicted (determined) by the model., • Stochastic model: A Stochastic model is the shorthand for the assumption that, random (stochastic) events effect the biological system, in which case the model, can only predict the probability of various outcomes in the future., 2.1, , Modeling a Biological Problem, , To construct a dynamical model based on a biological problem, we must follow the, steps described below:, Step 1: Formulate the question, The first step, coming up with a question that what do you want to know?, Describe the model according to the question., Start with the simplest, biologically reasonable description of the problem., Step 2: Determine the basic ingredients, Define the variables in the model and describe any constraints on the variables., Describe any interaction between the variables., Decide whether we treat time as discrete or continuous and choose time scale(i.e.,, 3

Page 4 :
decide what a time step equals in discrete time and specify whether rate will be, measured per second, minute, day, year e.t.c)., Define parameters in the model and describe any constraints on the parameters., Step 3: Qualitatively describe the biological system, Draw a life-cycle diagram for discrete-time models involving multiple events per time, unit., Draw a flow diagram to describe the changes to the variables over time., For models with many possible events, construct a table listing the out comes of every, event., Step 4: Quantitatively describe the biological system, Using the diagrams and tables write down the equations., Check whether the constraints on the variables still met as time passes., Make sure that the units of the right-hand side equal to those on the left-hand side., Think about whether results from the model can address the question., Step 5: Analyze the equations, Use the equations to simulate and graph the changes to the system over time., Choose and perform appropriate analyses and make sure that the analyses can address, the problem., Step 6: Checks and balances, Check the results against data or any known special cases and determine how general, the results are., Consider alternatives to the simplest model., Extend or simplify the model as appropriate., Step 7: Relate the result back to the question Do the results answer the, biological questions?, Are the results counterintuitive?, Interpret the result verbally, and describe conceptually any new insights into the biological process., Describe potential experiments., 3, , Continuous Models, , A continuous system is one in which important activities of the system completes, smoothly without any delay. When a continuous system is modeled mathematically,, 4

Page 5 :
its variables representing the attributes are controlled by continuous functions. If, population density of a single species at time t be denoted by x(t), then x(t) should, be a smooth function of t. Continuous model is the mathematical practice of applying, a model to continuous data. They often use differential equations., A population growth model may be defined as continuous population growth model, if the individuals of a population show continuous breeding season. The populations, grow in size when the birth rate exceeds the death rate. The Malthusian growth model, is a leading of all population models which is written in the book An Essay on the, Principle of Population (1798) by Thomas Robert Malthus. We begin this, section with a simple derivation of the famous exponential growth model., 3.1, , Malthusian Growth Model, , Let N (t) be the population density (number of individuals) at time t of a homogeneous, population. Let b and d be the average per capita birth rate and death rate respectively., Let in time ∆t, the number of births in the population N (t) is b∆t N , and the number, of deaths is d∆t N ., An equation for N (t) at time t + ∆t is then determined to be N (t + ∆t) = N (t) +, b∆tN (t) − d∆tN (t),, N (t + ∆t) − N (t), = (b − d)N (t), ∆t, dN, N (t + ∆t) − N (t), and in the limit ∆t → 0, we have, = lim, = (b − d)N (t);, ∆t→0, dt, ∆t, 1 dN, The per capita growth rate is, of this population. Thus we have,, N dt, which can be rearranged to, , 1 dN, dN, = b − d = r(say) or,, = rN, N dt, dt, , (3.1.1), , The difference between per capita birth and death rates r = b−d, plays an important, role and is known as intrinsic rate of growth., Let N0 = N (0) be the number of individuals at the start of the process. With this, Z N (t), Z t, dN, initial condition the general solution of equation (3.1.1) is obtained as, =, r dt., N, 0, N0, or, N (t) = N0 ert, , (3.1.2), , Which is the Malthusian equation for population growth and it shows that the growth, is exponential in the simple circumstances population. This process is deterministic., , 5

Page 6 :
Stability of equilibrium:, , 140, , Now the equation(3.1.1) has only equi-, , 120, , librium point N ? = 0., , 100, 80, , N(t), , Since there is no immigration or emigration, the population that starts at zero, , r = 0.7 > 0, , 60, 40, , stay at zero., , r=0, , 20, 0, , Again writing the model (3.1.1) as, dN, = f (N ), where f (N ) = rN , we have, dt, f 0 (N ? ) = r., , r = -10, -20, 0, , 0.5, , 1, , 1.5, , 2, , 2.5, , 3, , t, , Figure 1: Malthusian growth curve., , For r > 0, the equilibrium is unstable., After small perturbations, the population moves away from zero., For r < 0, the equilibrium is stable. Small perturbations now decay back to zero., Remarks:, (i) The population grows exponentially for r > 0 i.e., when per capita birth rate is, grater than the capita death rate., (ii) The population decays exponentially for r < 0 i.e., when per capita birth rate is, less than the capita death rate., (iii) The population remains constant for r = 0 i.e., when births balance deaths., Defects of Malthusian Growth Model:, • The model has constant per capita birth and death rates and generates unlimited growth. This is, patently unrealistic., • The model is deterministic; we have ignored chance or stochastic effects. Stochastic effects are, particularly important at small population sizes., • The model ignore lags. The growth rate does not depend on the past. More over the population, responds instantaneously to change the current population size., • We have ignored temporal and spatial variability., , 6, , MKHTA

Page 7 :
3.2, , Logistic Growth Model, , The exponential growth law for population size is unrealistic over long times. Then our main aim is to, find out the factors which can regulate the growth of population. This growth may be regulated by the, over-consumption of resources., We assume that the environment has an intrinsic carrying capacity K, and populations larger than, this size experience high death rates. From a modeling perspective, it is easier to start with density, dependent regulation., Let N (t) be the population density (size) at time t and r, per capita growth rate. To model, population growth with an environmental carrying capacity K, we look for a density dependent equation, dN, of the form,, = rN f (N )., dt, For environmental regulation, the function f (N ) should satisfy:, (i) f (0) = 1 ( the population grows exponentially with growth rate r when N is small)., (ii) f (K) = 0 (the population stops growing at the carrying capacity)., (iii) f (N ) < 0 when N > K (the population decays when it is larger than the carrying capacity)., N, The simplest function f (N ) satisfying these conditions is linear and given by f (N ) = 1 − K, ., The resulting model is the well-known logistic equation,, , , dN, N, = rN 1 −, (3.2.1), dt, K, This equation is also known as Pearl-Verhulst equation. The growth rate of population is now a, quadratic function of population size N ., Let N0 = N (0) be the size of the population at time t = 0. With this initial condition the general, Z N, Z t, K dN, r dt., solution of equation (3.2.1) is obtained as, =, N0 N (K − N ), 0, , Z N , 1, 1, +, dN = rt., or,, N, K −N, N0,  , N, N, or, log, = rt., K − N N0, N0, N, =, ert ., K −N, K − N0, K, , , or, N =, K, 1 + N0 − 1 e−rt, , or,, , (3.2.2), , Which is the exact solution of the logistic equation. The same solution may be obtained by assuming, the equation (3.2.1) as the Bernoulli equation., , Stability of equilibria:, Now the equation(3.2.1) has two equilibria N ? = 0 and N ? = K; at each of these two values, the growth, rate for the population is equal to zero., Consider a new variable x = N − N ? very close to N ? that measures the deviation of N from N ? ., 2, Since xK is small compare to x, for N ? = 0, we have from (3.2.1), dx, rx2, = rx −, ≈ rx, dt, K, For r > 0, small perturbations about N ? = 0 grow exponentially., Hence the equilibrium N ? = 0 is unstable., 7, , (3.2.3)

Page 8 :
2, , N(t), , Since xK is small compare to x, for N ? = K, we have, 120, from (3.2.1), 100, dx, rx2, = −rx −, ≈ −rx, (3.2.4), dt, K, 80, For r > 0, small perturbations about N ? = K decay, 60, exponentially., Hence the equilibrium N ? = K is asymptotically stable., 40, Therefore for r > 0, the solutions to the logistic equation, 20, (3.2.1) are essentially a combination of exponential growth, 0, near N ? = 0 and of exponential decay, close to the carrying, -10, 0, 10, 20, 30, 40, 50, 60, 70, 80, t, capacity K., The equations (3.2.3) and (3.2.4) imply that the solution Figure 2: Logistic growth curve for r =, of the logistic equation is concave upward just above the 0.15 and K = 100., origin and concave downward just below the carrying capacity. Therefore the point of inflexion lies, between the origin and carrying capacity., , , , , d2 N, 2r dN K, 2N dN, Now from the equation (3.2.1), we have, =, −N ., =r 1−, dt2, K, dt, K dt, 2, d2 N, We observe that, = 0 at the point N = K2 ., dt2, d2 N, d2 N, K, K, Also for 0 < N < 2 , we have, > 0 and for 2 < N < K, we have, < 0., dt2, dt2, K, Hence the point of inflexion is at N = 2 ., , Alternative form of solution (3.2.2):, Let at time t = tm , the size of the population is half of the carrying capacity K., , K, K, K, , , =, − 1 = ertm ., , which gives, Therefore from solution (3.2.2), we have, K, 2, N, −rt, 0, 1 + N0 − 1 e m, , , Substituting the value of NK0 − 1 in the equation (3.2.2) we have the alternative form as, N=, , K, 1+, , e−r(t−tm ), , ., , (3.2.5), , Figure-3a shows that the shape of the logistic curve is a S-shaped. This curve is known as Sigmoid, curve., Sigmoid Curve: A sigmoid curve is a S-shaped curve with equation f (x) =, , K, 1+, , e−r(x−xm ), , , where, , (i) xm is the value of x at the middle point of the sigmoid curve,, (ii) K is the maximum value of f (x),, (iii) r is the logistic growth rate or steepness of the curve., Since x ∈ (−∞, ∞), the sigmoid curve looks like the curve in figure-??. It is observed that, lim f (x) = 0 and lim f (x) = K. So the curve has two asymptotes f = 0 and f = K., x→−∞, , x→+∞, , Application: This sigmoid curve or logistic curve, logistic function is applied in the fields, including, Biology ( especially ecology), Biomathematics, Economics, Probability, Statistics, Artificial natural, networks., , 8

Page 9 :
3.3, , Allee Effect, , Professor Wander Clyde Allee (born on 5-th June 1885 near Annapolis, Indiana, in a small Quaker, community) was one of the first ecologist, who gathered sufficient experimental and observational data, to conclude that the evolution of social structures was not only driven by competition, but cooperation, was another, if not the most, fundamental principle in animal species (Allee, 1931). The dynamical, consequences of this importance of animal aggregations directly led to what Odum called in 1953 the, Allee principle, now known as Allee effect., Allee effect: The Allee effect is a phenomenon in biology characterized by a correlation between, population density(or size) and the mean individual fitness (often measured as per capita population, growth rate) of a population or species. This is also termed as depensation in the field of fishery, science., Some related definitions:, Allee threshold: A critical population density(size) below which per capita growth rate becomes, negative., Component Allee effect: A positive relationship between any measurable component of individual, fitness and population density(size)., Demographic Allee effect: A positive relationship between the overall individual fitness, usually, quantified by the per capita population growth rate, and population density(size)., Strong Allee effect: A demographic Allee effect with an Allee threshold., Weak Allee effect: A demographic Allee effect without an Allee threshold., Dormant Allee effect: A component of Allee effect that either does not result in demographic Allee, effect or results in a week Allee effect and which, if interacting with a strong Allee effect, causes, the overall Allee threshold to be higher than the Allee threshold due to the strong Allee effect, alone., Emergent Allee effect: In population models, demographic Allee effects that emerge without treating, an underlying component Allee effect explicitly i.e., without using any component Allee effect, model., Multiple Allee effects: Any situation in which two or more component Allee effects work simultaneously in the same population., Non-additive Allee effect: Multiple Allee effects that give rise to a demographic Allee effect with, an Allee threshold greater or smaller than the algebraic sum of Allee thresholds owing to single, Allee effect., Sub-additive Allee effects: Multiple Allee effects that give rise to a demographic Allee effect with, an Allee threshold smaller than the algebraic sum of Allee thresholds owing to single Allee effect., Super-additive Allee effects: Multiple Allee effects that give rise to a demographic Allee effect with, an Allee threshold greater than the algebraic sum of Allee thresholds owing to single Allee effect., 9

Page 10 :
Mathematical Model, Let N (t) be the population density (size) at time t. Let r be the per capita growth rate and K, the, environmental carrying capacity. Consider the simple cubic growth model,, , , , dN, N, N, = rN, −1, 1−, = f (N ) (say), (3.3.1), dt, A, K, , 60, , 2, , 50, , 1.5, , Stable, , 1, , f(N), , N(t), , 40, , 30, , 20, , Unstable, , 0.5, , 0, , Unstable, , 10, , -0.5, , Stable, 0, , -1, 0, , 2, , 4, , 6, , 8, , 10, , 12, , 14, , 16, , 18, , 20, , 0, , 10, , 20, , t, , 30, , 40, , 50, , 60, , N, , (a) Allee Growth curve., , (b) Stability analysis., , Figure 3: (a) Allee grow for r = 0.02, a = 0.2 and K = 50 and (b) Stability analysis for r = 0.2, a = 4, and K = 50., , , , , 1 dN, N, N, We have, =r, −1, 1−, < 0, for 0 < N < A, [ Since, N < K ], N dt, A, K, Therefore per capita growth rate becomes negative for 0 < N < A. So A is Allee threshold., Now the equation(3.4.1) has three equilibria N ? = 0, N ? = A and N ? = K; at each of these three, values, the growth rate for the population is equal to zero., Consider a new variable x = N − N ? very close to N ? that measures the deviation of N from N ? ., Since x2 and x3 are small compare to x, for N ? = 0, we have from (3.4.1), x, , dx, x, = rx, −1 1−, ≈ −rx, dt, A, K, For r > 0, small perturbations about N ? = 0 decay exponentially., Hence the equilibrium N ? = 0 is stable., Since x2 and x3 are small compare to x, for N ? = A, we have from (3.4.1), , , x, x+A, r, dx, = r(x + A), 1−, ≈ (K − A)x, dt, A, K, K, Since K > A > 0, then for r > 0, small perturbations about N ? = A grow exponentially., Hence the equilibrium N ? = A is unstable., Since x2 and x3 are small compare to x, for N ? = K, we have from (3.4.1), , , , dx, r, x, x, r, = − (K − A)x 1 +, 1+A, ≈ − (K − A)x, dt, A, K, K −A, A, Since K > A > 0, then for r > 0, small perturbations about N ? = K decay exponentially., Hence the equilibrium N ? = K is stable., 10

Page 12 :
Therefore the Gompertz equation (3.4.3) can be expressed as,  , dN, K, = αN log, ,, dt, N, , (3.4.5), , where K is carrying capacity and α is given by r = α log K., , Stability of equilibria:, Now the equation(3.4.5) has two equilibria N ? = 0 and N ? = K., Consider a new variable x = N − N ? very close to N ? that measures the deviation, of N from N ? ., , dx, K, For N ? = 0, we have x = N and from the equation(3.4.5),, = αx log, = f (x)(say), dt, x,
, K, . Therefore f 0 (0+) = lim f 0 (x) > 0., Now f 0 (x) = α log ex, x→0+, , Therefore f is increasing function of x for 0 < x  1., Thus small perturbations about N ? = 0 grow exponentially., Hence N ? = 0 is unstable equilibrium., Since x2 and higher powers of x is small compare to x, for N ? = K, we have from (3.4.5), , , K, dx, = α(K + x) log, ≈ −αx ,, dt, K +x, , Using infinite series expansion of log 1 −, ?, For α > 0, small perturbations about N = K decay exponentially., Hence the equilibrium N ? = K is asymptotically stable., , , dN, K, d2 N, =α, log, ., Again from equation (3.4.5), we have, dt2, dt, eN, d2 N, We observe that, = 0 at the point N = Ke ., 2, dt, d2 N, d2 N, K, >, 0, and, for, < 0., Also for 0 < N < Ke , we have, <, N, <, K,, we, have, e, dt2, dt2, Hence the point of inflexion is at N = Ke ., , (3.4.6), x, K+x, ,
, , ., , So the point of inflexion shifted towards N ? = 0., , 12, , MKHTA

Page 13 :
3.5, , Michaelis-Menten Kinetics, , Enzyme: An enzyme is a substance (protein molecules) that acts as a catalyst in living, , organisms, regulating the rate at which chemical reactions proceed without itself, being altered in the process., Substrate: The substrate is a molecule upon which an enzyme acts., Product: Product is the species formed from chemical reactions. The enzyme converts, , the substrates into different molecules known as products., One of the most basic enzymatic reactions, first proposed by Michaelis and, Menten (1913). In this reaction a substrate S reacts with enzyme E to form a, complex SE which in turn converted into a product P and the enzyme E. We present, this schematically by, k1, , k, , 2, −−, *, S+E), →, P+E, −, − SE −, , (3.5.1), , k−1, , Here k1 , k−1 and k2 are reaction rate constants and the symbol, , indicates the reaction, , is reversible while symbol → indicates reaction is forward (only one way)., This reaction says that one molecule of S combines with one molecules of E to form, one of complex SE, which eventually produces one molecule of P and one molecule of, E again., Let s = [S]= concentration of S, e = [E]= concentration of E, c = [SE]= concentration of SE and p = [P ]= concentration of P ., The law of mass action says that the rate of reaction is proportional to the product, of the concentrations of the reactants. The the mass action law applied to chemical, reaction equation (3.5.1) leads to one equation for each reactant and hence the system, of nonlinear reaction equations, ds, dt, de, dt, dc, dt, dp, dt, , = −k1 es + k−1 c, = −k1 es + (k−1 + k2 )c, = k1 es − (k−1 + k2 )c, , (3.5.2), , = k2 c., , Initially, at the start of the process which convert S to P , we have, s(0) = s0 , e(0) = e0 , c(0) = 0 and p(0) = 0., 13, , (3.5.3)

Page 14 :
The solution of system (3.5.2) with initial conditions (3.5.3) give the concentrations,, and hence rate of reactions, as functions of time t., Note that in any reaction kinetics problem we are only concentrate with nonnegative, concentrations. Therefore s(t) ≥ 0, e(t) ≥ 0, c(t) ≥ 0 and p(t) ≥ 0., The last equation in system (3.5.2) is uncoupled from first three; it gives, Z t, p(t) =, c(t0 ) dt0 ,, , (3.5.4), , 0, , once c(t) has been determined, then we concentrate with analytical solution of first, three equation in system (3.5.2)., In the reaction mechanism in (3.5.1)the enzyme E is a catalyst, which only facilitates the reaction, so its total concentration (free plus combined) is constant. This, conservation law for enzyme also comes immediately from 2nd and 3rd equations in, system (3.5.2) as, de dc, +, = 0 or,, dt dt, , Z, , e(t), , Z, , 0, , c(t), , de(t ) = −, e0, , dc(t0 ), , 0, , or, e(t) + c(t) = e0 ., , (3.5.5), , With the condition (3.5.5), the system of ordinary differential equations (3.5.2), reduces to, ds, = −k1 e0 s + (k1 s + k−1 )c, dt, dc, = k1 e0 s − (k1 s + k−1 + k2 )c, dt, , (3.5.6), , with initial conditions s(0) = s0 and c(0) = 0., It is assumed that the initial stage of the complex, c, formation is very fast after, which it is essentially at equilibrium, that is, , dc, dt, , ≈ 0 in which case from 2nd equation, , of (3.5.6) we get c in terms of s,, c(t) =, , e0 s(t), k−1 + k2, , Km =, ., s(t) + Km, k1, , (3.5.7), , Substituting in the first equation in (3.5.6), we have, ds, k2 e0 s, =−, ,, dt, s + Km, , where Km is called the Michaelis constant., 14, , (3.5.8)

Page 15 :
Since the enzyme is traditionally considered to be present in small amounts compared with the substrate, the assumption is that the substrate concentration effectively, does not change during this initial transient stage. In this case the approximate dynamics is governed by equation (3.5.8) with the initial condition s = s0 . This is known, as the pseudo or quasi-steady state approximation., Solving the equation (3.5.8) with the initial condition s = s0 , we have, s(t) + Km log s(t) = s0 + Km log s0 ., , (3.5.9), , If we now substitute this into equation (3.5.7) we get an expression for the complex, c(t)., But this does not satisfy the initial condition c0 = 0 on c(t). [ Since c0 =, However, perhaps it is reasonable approximation for most of the time., , e 0 s0, 6= 0.], s0 + Km, , There are infect two timescales involved in this system:, (i) initial transient timescale near t = 0 and, (ii) the longer timescale when the substrate changes significantly during which the, enzyme complex, is reasonably approximated by (3.5.7) with s(t) from (3.5.9)., This basic reasoning aries several important questions:, (i) How fast is the initial transient?, (ii) What range of parameters is the approximation (3.5.7) with (3.5.9) ?, (iii) If the enzyme concentration is not small compared with substrate concentration,, how do we deal with it?, At first step we must nondimensionalise the system (3.5.6). A key dimensionless, quantity is the time as the basic assumption depend on the initial transient time., The standard way of doing the quasi-steady state analysis is to introduce dimensionless quantities, τ = k1 e0 t, u(τ ) =, , c(t), k2, k−1 + k2, Km, e0, s(t), , v(τ ) =, , λ=, , K=, =, , =, s0, c0, k1 s0, k1 s0, s0, s0, (3.5.10), , which is reasonable nondimensionalisation if   1., With this substitution the system (3.5.6) transform to the dimensionless system for, , 15, , MKHTA

Page 16 :
quasi-steady state approximation, du, = −u + (u + K − λ)v, dτ, dv, , = u − (u + K)v, dτ, , (3.5.11), , with initial conditions u(0) = 1 and v(0) = 0, where K > λ, Solving the system (3.5.11), we have u(τ ), v(τ ) and hence p(t) and e(t) from (3.5.4), and (3.5.5) respectively., Discussion: From original reaction (3.5.1), which, converts S into a product P , we have the final steady, , 1, 0.9, , state u = 0 and v = 0; that is both the substrate and, is in the time evolution of the reaction; so we need the, solutions of system (3.5.11). But the can not be solved, analytically in a simple closed form., , 0.7, , u, Concentration, , substrate-enzyme concentrations are zero. Since our aim, , 0.8, , 0.6, 0.5, 0.4, , v, , 0.3, 0.2, 0.1, , Near τ = 0 (u = 1, v = 0), we have, decreases from u = 1 and since, , dv, dτ, , du, dτ, , < 0, so u, , 0, 0, , 1, , 2, , 3, , u, u+K ,, , where, , dv, dτ, , =0, , and at that point u still decreasing. After v has reached, , 5, , 6, , 7, , 8, , 9, , 10, , Tau, , > 0, v increases from, , v = 0 and continues to do so until v =, , 4, , Figure 4: Schematic behaviour of, the solution the system (3.5.11)., , maximum it then decreases ultimately to zero as does u, which does so monotonically, for all t., The dimensional enzyme concentration e(t) first decreases from e0 and then increase, to e0 as t → ∞. The solution s are illustrated in figure-4., Transient time estimates and Nondimensionalisation, It is widespread in biology that the remarkable effectiveness of enzymes is reflected in, the small concentrations of the substrate involved. In the Michaelis-Menten model in, e0, dimensionless form (3.5.11) this means  =,  1. However, it not always the case, s0, e0, that  =,  1. Segel(1988) and Segel and Slemrod(1889) extended the traditional, s0, analysis with a new nondimensionalisation which includes this case but which also, e0, covers the situation where, = O(1)., s0, In their analysis they estimated two timescales, the fast transient time tc , and, the longer or slow time ts , during which s(t) changes significantly., 16

Page 17 :
During the initial transient time, the complex c(t) increases rapidly while the sub-, , strate s(t) does not change appreciably so that an estimate of this first timescale is obdc, = k1 e0 s0 − (k1 s0 + k−1 +, tained from the second equation of (3.5.6) with s(t) = s0 , that is, dt, dc, = k1 e0 s0 − k1 (s0 + Km )c, (3.5.12), dt, The solution of this linear equation in c(t) with c(0) = 0 is, n, o, k1 e0 s0, −k1 (s0 +Km ) t, c(t) =, 1−e, k1 (s0 + Km ), , in which the timescale of the exponential is, 1, tc =, k1 (s0 + Km ), , (3.5.13), , To estimate the long timescale ts , in which s(t) changes significantly, ts is defined as, the ratio of the maximum change possible in the substrate, s0 and the size of maximum, rate of change of s(t) setting at s = s0 in (3.5.8). So,, ts ≈, , s0 + Km, s0, ≈, k2 e0, | ds, dt |max, , (3.5.14), , The assumptions on which quasi-steady state approximation is valid are:, (i) the fast initial transient time tc is much smaller than the long time scale ts when, s(t) changes significantly. This means that tc  ts . With the approximations (3.5.13), and (3.5.14), tc  ts requires the parameters to satisfy, k2 e0,  1., k1 (s0 + Km )2, , (3.5.15), , (ii) the initial condition for s(t) can be taken as s(0) = s0 . This means that the, substrate depletion ∆s(t) during the fast transient is only small fraction of s0 ; that is, |∆s(t)|  1. An over estimate of ∆s(t) is given by the maximum rate of depletion, possible from the equation, ds, = −k1 e0 s + (k1 s + k−1 )c, dt, which is k1 e0 s0 multiplied by tc . So, dividing k1 e0 s0 tc by s0 gives the following requirements of parameters,, =, Now from (3.5.15) and Km =, , k−1 +k2, k1 ,, , e0,  1., s0 + Km, , (3.5.16), , we have, , e0, ·, s0 + Km 1 +, , 1, k−1, k2, , 17, , +, , s0 k1, k2, ,  1., , (3.5.17)

Page 19 :
quasi-steady state approximation, ρ, du, =, , −, (1, +, σ)u, +, σuv, +, v,, dτ 0, 1+ρ, dv,  0 = (1 + σ)u − σuv − v, dτ, , (3.5.21), , with initial conditions u(0) = 1 and v(0) = 0., The system we are investigating is (3.5.6). The three dimensionless systems (3.5.11),, (3.5.19) and (3.5.21) are exactly same; they only differ in the way we nondimensionalise, them. All of them have small parameter , but it appears in the equations in different, place. Where a small parameter appear determines the analytical procedure we use., , 19, , MKHTA

Page 20 :
3.6, , Holling type growth, , C. S. Holling was a Canadian ecologist, and one of the conceptual founders of ecological economics. His early work included major contributions to population and, behavioural ecology. In the journal Canadian Entomologist (1959), he published, his classic paper in which he developed the notion of functional response, an idea, that continues to be a linchpin of modern population ecology., He studied predation of small mammals on pine sawflies, and he found that predation rates increased with increasing prey population density. This resulted from two, effects:, (i) each predator increased its consumption rate when exposed to a higher prey density., (ii) predator density increased with increasing prey density., Holling considered these effects as two kinds of responses of predator population to, prey density: (1) the functional response and (2) the numerical response., Functional response: A functional response in ecology is the relationship between, , prey(food) density and the rate at which prey is eaten ( food is consumed)., Numerical response: The numerical response is the reproduction rate of a preda-, , tor(consumer) as a function of prey(food) density., According to Holling, functional responses are generally classified into three types,, which are called Holling’s Type I, Type II, and Type III., Type I functional response: Type I functional response is the linear relationship, between the intake rate of prey (number of prey eaten per predator per unit time), and prey density. The intake rate increases linearly up to a maximum, beyond, which it is constant., The linear increase assumes that the time needed by the consumer (predator) to, process a food item is negligible, or that consuming food does not interfere with, searching for food., If N be the prey density and c be the intake rate, then this type of functional, response φ is given by, φ(N ) = cN., 20, , (3.6.1)

Page 21 :
Type I functional response is found in passive predators like spiders. The number, of flies caught in the net is proportional to fly density. Prey mortality due to, predation is constant., Type-I functional response curve, , 6, , Type-II functional response curve, , 4, , Type III functional response curve, , 3, , 5, , 2.5, 3, , 3, , (N), , 2, (N), , (N), , 4, , 2, , 1.5, , 2, , 1, 1, , 1, , 0.5, , 0, , 0, 0, , 2, , 4, , 6, , 8, , 10, , 12, , 0, 0, , N, , 2, , 4, , 6, , 8, , 10, , 0, , 2, , N, , 4, , 6, , 8, , 10, , N, , Figure 5: Holling type functional response curves, , Type II functional response: Type II functional response is characterized by a decelerating intake rate, which follows from the assumption that the predator (consumer) is limited by its capacity to process food. This is a hyperbolic function, that saturates because of the time it takes to handle prey (processing of food)., This model illustrates that a predator spends its time on two kinds of activities:, (i) Searching for prey, and (ii) Prey handling which includes: chasing, killing,, eating and digesting., Consumption rate of a predator is limited in this model because even if prey are, so abundant that no time is needed for search, a predator still needs to spend time, on prey handling., Total time t equals to the sum of ‘time spent on searching’, ts and ‘time spent on, handling’, th ., t = ts + th ., Let a predator captured on average Na prey during time t. Now the handling time, should be proportional to the number of prey captured. Thus th = th1 Na , where, th1 is time spent on handling of one prey., Capturing prey is assumed to be a random process. Let a predator examines area, A, per time unit (only search time is considered here) and captures all prey that, were found there. The parameter A is often called search rate., After spending time ts for searching, a predator examines the area Ats , and captures Ats N prey where N is prey density per unit area., 21

Page 22 :
Therefore we have, Na = Ats N or, ts =, , Na, ., AN, , tA N, Na, or, Na =, ., AN, 1 + Ath1 N, t, cN, ., and c =, , then Na =, th1, a+N, , Hence we have, t = th1 Na +, Let a =, , 1, Ath1, , cN, ., a+N, Since φ(a) = 2c , then a is called half-saturation constant and c is called capture, Thus the Type II functional response φ(N ) is given by φ(N ) =, , rate., Type III functional response: Type III functional response is similar to type II, functional response at high levels of prey density, saturation occurs. But now, at, low prey density levels, the graphical relationship of number of prey consumed, and the density of the prey population is a more than linearly increasing function, of prey consumed by predators. This accelerating function is largely descriptive,, and often justified by learning time, prey switching, or a combination of both, phenomena, but the type III functional response lacks the rigorous theoretical, underpinning of the type II functional response., , 22, , MKHTA

Page 23 :
3.7, , Bacterial Growth in Chemostat, , Introduction:, , Competition modeling is one of the challenging aspects of mathematical, , biology. The mathematical idea seems quite simple: when one population increases,, the growth rate of other should decreases or at least not increase., Let an ecosystem is modelled by the ordinary differential equation, dyi, = yi fi (y), i = 1, 2, · · · , n,, dt, where fi are continuously differentiable function defined on Rn and y = (y1 , y2 , · · · , yn )., The competition is expressed by the condition, ∂fi, ≤ 0 when i 6= j., ∂yj, The simplest form of such competition occurs when two or more population compete, for the same resource, such as a common food supply or a growth-limiting nutrient., This is called exploitative competition. A simple example of this type of competition, occurs in chemostat., Chemostat: A chemostat (chemical environment is static) or a continuous culture is, a common laboratory apparatus for the culture and growth of microorganism., Bacteria: Bacteria are single celled microorganism and the cell structure is simpler, than that of other organisms. The genetic information is contained in a single, loop of DNA., Reproduction of bacteria: Bacteria reproduce by binary fission. In this process the, bacterium, which is a single cell, divides into two identical daughter cells. Binary, fission begins when the DNA of the bacterium divides into two (replicates). The, bacterial cell then elongates and splits into two daughter cells each with identical, DNA to the parent cell. Each daughter cell is a clone of the parent cell., Bacterial growth in chemostat: The cultures for growth of bacterial populations, are called batch cultures. Bacterial cultures can be maintained in a state of, exponential growth over long periods of time using a system of continuous culture,, designed to relieve the conditions that stop exponential growth in batch cultures., A chemostat can be used to maintain a bacterial population at a constant density., In a chemostat, the growth chamber is connected to a reservoir of sterile medium., 23

Page 24 :
Once growth is initiated, fresh medium is continuously supplied from the reservoir., The volume of fluid in the growth chamber is maintained at a constant level by, some sort of overflow drain. Fresh medium is allowed to enter into the growth, chamber at a rate that limits the growth of the bacteria. The bacteria grow, (cells are formed) at the same rate that bacterial cells (and spent medium) are, removed by the overflow. The rate of addition of the fresh medium determines, the rate of growth because the fresh medium always contains a limiting amount of, an essential nutrient. Thus, the chemostat relieves the insufficiency of nutrients,, the accumulation of toxic substances, and the accumulation of excess cells in the, culture, which are the parameters that initiate the stationary phase of the growth, cycle. The bacterial culture can be grown and maintained at relatively constant, conditions, depending on the flow rate of the nutrients., Derivation of the basic equation of Bacterial Growth in Chemostat, , The apparatus consists of three connected vessels, as shown in figure 6., (i) The left most vessel is called the media reservoir or feed bottle which contains all the nutrients, needed for growth of bacteria - all the nutrients, in excess except for limiting nutrient(a nutrient, essential for growth, present in the medium at a, , Figure 6: A Schematic of simple Chemostat., , limiting concentration)., (ii), , The second vessel is called chemostat vessel or culture vessel to which fresh, , medium is continuously added at constant rate from media reservoir, while culture, liquid containing left over nutrients, metabolic end products and bacteria are continuously removed at the same rate to keep the culture volume constant., (iii), , The third vessel is collection vessel to which the product of the culture vessel, , are collected., Let V denotes the volume of the culture vessel, and F denote the constant volumetric flow rate. The concentration of the input nutrient denoted by S0 , is kept constant., The culture vessel contains a mixture of nutrient and bacteria. It is well stirred, and, all other significant parameters ( for example temperature ) effecting the growth are, kept constant. Now the contents of the media reservoir are pumped at the rate F into, , 24

Page 25 :
the culture vessel, and the contents of the culture vessel are pumped at the same rate, into the collection vessel., Since the output is continuous, the rate of change of nutrient can be expressed as, rate of change = input - washout - consumption., Let S(t) denotes the concentration of nutrient in the culture vessel at time t. Then, V S(t) is the amount of nutrient in the vessel at that time. If there is no bacteria, then, there is no consumption of nutrient., Therefore the rate of change of nutrient per unit time is the difference between the, amount of nutrient pumped into the vessel per unit time and the amount of nutrient, being pumped out of the vessel per unit time. Thus the equation for the nutrient is, d, (V S) = S0 F − SF , where S = S(t)., dt, Since V is constant, then we have, dS, = D(S0 − S),, dt, where the quantity D =, , F, V, , is called the dilution rate or washout rate and has units of 1t ., , Case:1 Let X(t) denotes the concentration of the bacteria and it takes up nutrient, according to simple mass action law, then the evolution equation for nutrient is, dS, m, = D(S0 − S) − SX,, dt, γ, where X = X(t) and m is the growth constant for the bacteria and γ is yield constant, reflecting the conservation of nutrient to the bacteria., The constant γ is dimensionless quantity determined (in batch culture) by measuring, mass of the bacteria formed, ., mass of substrate used, Again since the output is continuous, the rate of change of bacteria can be expressed, as, rate of change = growth - washout., Since the volume V of the culture vessel is constant, then the washout rate of, bacteria will be D. Therefore the evolution equation for bacteria is, dX, = (mS − D)X,, dt, 25

Page 26 :
Thus for bacterial growth in chemostat we have the coupled equation, m, dS, = D(S0 − S) − SX,, dt, γ, dX, = (mS − D)X,, dt, , (3.7.1), , with initial conditions S(0) ≥ 0, X(0) > 0,, where S, X, t are nonnegative variables and S0 , D, m and γ are positive parameters., Mathematical Study:, , There are usual advantages to analyzing dimensionless equations. So we rescale the, all concentrations by S0 and rescale the bacteria by its yield constant γ. Finally, we, treat the reciprocal of the dilution rate as a natural measure of time., Let the dimension less quantities x, y and τ are given by x ≡, , S, S0 ,, , y≡, , X, γS0 , τ, , ≡ Dt., , Therefore the system of equations (3.7.1) transform to the dimensionless system, dx, = 1 − x − axy,, dt, dy, mS0, = axy − y, where a =, ., dt, D, , (3.7.2), (3.7.3), , Adding the equations (3.7.2) and (3.7.3) we have, dx dy, +, = 1 − x − y., dt, dt, , (3.7.4), , Which is a linear ordinary differential equation in x + y., The general solution of the equation (3.7.4) is x(τ ) + y(τ ) = Ae−τ + 1., Lat at τ = 0, the concentrations of rescaled nutrient and bacteria are x0 and y0, respectively., Hence we have the solution of the system of coupled equation (3.7.2) and (3.7.3), x(τ ) + y(τ ) = 1 + (x0 + y0 − 1)e−τ ., , (3.7.5), , It follows that, as τ → ∞ x + y → 1., Therefore the asymptotic behaviour of the equations (3.7.2) and (3.7.3) along the, line x + y = 1., Since our aim is to find the growth of the bacteria, then using x + y = 1, we have, from (3.7.3), , , dy, y, dy, = a(1 − y)y − y or,, = (a − 1)y 1 − a−1, dτ, dt, a, 26, , (3.7.6)

Page 27 :
, dy, y, Comparing the equation (3.7.6) with the logistic equation, = ry 1 −, , we, dτ, K, have, , , D, a, −, 1, = 1−, carrying capacity K = a−1, y(τ ) = K =, ., a and τlim, →∞, a, mS0, In terms of original dimensional units, the effective carrying capacity of bacteria is,
, D, ., K = γ S0 − m, The carrying capacity is defined in terms of measurable quantities γ, m, S0 and D., This carrying capacity increases if γ, m, S0 , D increases and D decreases., , 27, , MKHTA

Page 28 :
Case:2 Let X(t) denotes the concentration of the bacteria and it takes up nutrient, according to Holling type-II functional response. Then the evolution equation for, nutrient is, , m SX, dS, = D(S0 − S) −, ,, dt, γ a+X, where X = X(t), m is the maximal growth constant for the bacteria, a is halfsaturation constant and γ is yield constant reflecting the conservation of nutrient, to the bacteria., The constant γ is dimensionless quantity determined (in batch culture) by measuring, mass of the bacteria formed, ., mass of substrate used, Again since the output is continuous, the rate of change of bacteria can be expressed, as, rate of change = growth - washout., Since the volume V of the culture vessel is constant, then the washout rate of, bacteria will be D. Therefore the evolution equation for bacteria is, , , mS, dX, =, − D X,, dt, a+X, Thus for bacterial growth in chemostat we have the coupled equation, dS, m SX, = D(S0 − S) −, ,, dt, γ a+X, , , dX, mS, =, − D X,, dt, a+X, , (3.7.7), , with initial conditions S(0) ≥ 0, X(0) > 0,, where S, X, t are nonnegative variables and S0 , D, m, a and γ are positive parameters., Mathematical Study:, , There are usual advantages to analyzing dimensionless equations. So we rescale the, all concentrations by S0 and rescale the bacteria by its yield constant γ. Finally, we, treat the reciprocal of the dilution rate as a natural measure of time., Let the dimension less quantities x, y and τ are given by x ≡, , 28, , S, S0 ,, , y≡, , X, γS0 , τ, , ≡ Dt.

Page 29 :
Therefore the system of equations (3.7.7) transform to the dimensionless system, µxy, dx, = 1−x−, ,, dτ, α+x, µxy, a, m, dy, =, − y, where α = , µ = ., dτ, α+x, S0, D, , (3.7.8), (3.7.9), , Adding the equations (3.7.8) and (3.7.9) we have, dx dy, +, = 1 − x − y., dt, dt, , (3.7.10), , Which is a linear ordinary differential equation in x + y., The general solution of the equation (3.7.10) is x(τ ) + y(τ ) = Ae−τ + 1., Lat at τ = 0, the concentrations of rescaled nutrient and bacteria are x0 and y0, respectively., Hence we have the solution of the system of coupled equation (3.7.8) and (3.7.9), x(τ ) + y(τ ) = 1 + (x0 + y0 − 1)e−τ ., , (3.7.11), , It follows that, as τ → ∞ x + y → 1., Therefore the asymptotic behaviour of the equations (3.7.8) and (3.7.9) along the, line x + y = 1., Since our aim is to find the growth of the bacteria, then using x + y = 1, we have, from (3.7.9), , , dy, y, dy, = a(1 − y)y − y or,, = (a − 1)y 1 − a−1, dτ, dt, a, , (3.7.12), , , dy, y, Comparing the equation (3.7.12) with the logistic equation, = ry 1 −, , we, dτ, K, have, , , a−1, D, a−1, ., carrying capacity K = a and lim y(τ ) = K =, = 1−, τ →∞, a, mS0, In terms of original dimensional units, the effective carrying capacity of bacteria is,
, D, K = γ S0 − m, ., The carrying capacity is defined in terms of measurable quantities γ, m, S0 and D., This carrying capacity increases if γ, m, S0 , D increases and D decreases., , 29, , MKHTA