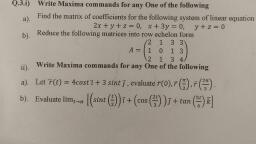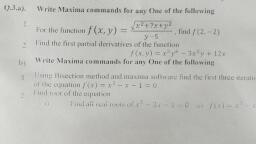Page 2 :
SAVITRIBAI PHULE PUNE UNIVERSITY, PUNE, Board of Studies in Mathematics Syllabus for S. Y. B. Sc, Subject: MATHEMATICS, (With effect from June 2020), , Introduction:, Savitribai Phule Pune University, Pune has decided to change the syllabi of various, faculties from June 2020. Taking into consideration the rapid changes in science and, technology and new approaches in different areas of mathematics and related subjects, Board of studies in Mathematics with concern of teachers of Mathematics from different, colleges affiliated to Savitribai Phule Pune University, Pune has prepared the syllabus of, S.Y.B.Sc. Mathematics. To develop the syllabus the U.G.C. Model curriculum is, followed., Aims:, •, Give the students a sufficient knowledge of fundamental principles, methods and a, clear perception of innumerous power of mathematical ideas and tools and know how, to use them by modeling ,solving and interpreting., •, Reflecting the broad nature of the subject and developing mathematical tools for, continuing further study in various fields of science., •, Enhancing students overall development and to equip them with mathematical, modeling abilities, problem solving skills, creative talent and power of, communication necessary for various kinds of employment ., •, Enabling students to develop a positive attitude towards mathematics as an interesting, and valuable subject of study., Objectives:, •, A student should be able to recall basic facts about mathematics and should be able to, display knowledge of conventions such as notations, terminology and recognize basic, geometrical figures and graphical displays ,state important facts resulting from their, studies., •, A student should get a relational understanding of mathematical concepts and, concerned structures, and should be able to follow the patterns involved, mathematical, reasoning., •, A student should get adequate exposure to global and local concerns that explore them, many aspects of Mathematical Sciences., •, A student be able to apply their skills and knowledge, that is, translate information, presented verbally into mathematical form, select and use appropriate mathematical, formulae or techniques in order to process the information and draw the relevant, conclusion., •, A student should be made aware of history of mathematics and hence of its past,, present and future role as part of our culture., Eligibility: F. Y. B. Sc., as per University rules.
Page 3 :
Structure of the course:, Paper I, Paper II, , Semester - III, Semester -IV, MT-231, Calculus of Several MT-241, Linear Algebra, Variables, MTNumerical Methods MT-242(A), Vector Calculus, 232(A), and Its Applications, Graph Theory, , MT-242(B), , Dynamical Systems, , MT-232(B), Paper III MT-233, , •, •, •, , Mathematics, MT-243, Practical based on, MT - 231 and MT 232, , Mathematics Practical, based on MT - 241 and, MT-242, , All three above courses are compulsory., In Semester-III, select any one from MT-232(A) and MT-232(B)., In Semester-IV, select any one from MT-242(A) and MT-242(B)., , Medium of Instruction: English., Examination:, A) Pattern of examination: Semester., B) Standard of passing: 20 marks out of 50 marks for each papers., But for MT- 231, MT -232(A), MT -232(B), MT -241, MT -242(A), MT -242(B),, MT -233 and MT-243 for passing a student should obtain minimum 14 marks, out of 35 in the theory examination and overall total marks for theory and internal, should be minimum 20., C) Pattern of question papers: For MT- 231, MT -232(A), MT -232(B), MT -241,, MT -242(A), MT -242(B)., Q1. Attempt any 05 out of 07 questions each of 01 marks. [05 Marks], Q2. Attempt any 02 out of 04 questions each of 05 marks. [10 Marks]., Q.3. Attempt any 02 out of 04 questions each of 05 marks. [10 Marks]., Q4. Attempt any 02 out of 04 questions each of 10 marks. [10 Marks]., D) External Students: Not allowed., E) Verification /Revaluation: Allowed for MT- 231, MT -232(A), MT -232(B),, MT -242(A), MT -242(B)., , MT - 241,
Page 4 :
The pattern of question paper for MT -233, MT-243 is given in the detailed syllabus., Equivalence of Previous syllabus along with new syllabus:, Semester-III, , Semester-IV, , New Course, , Old Course, , New Course, , Old Course, , Paper I, , MT-231: Calculus, of Several Variables, , MT-241:Linear, Algebra, , MT-221: Linear, Algebra, , Paper II, , MT-232(A):, Numerical Methods, and Its Applications, , MT-211 :, Multivariable, Calculus-I, MT-212(A):, Discrete, Mathematics, , MT-242(A):, Vector Calculus, , MT-222(A):, Multivariable, Calculus - II, , MT- 212(B):, Laplace, Transform and, Fourier Series, MT-213 :, Mathematics, Practical based, on MT-211 and, MT-212, , MT-242(B):, Dynamical, Systems, , MT-212(B):, Numerical, Analysis, , MT-232(B): Graph, Theory, Paper III, MT-233:, Mathematics, Practical based on, MT-231 and MT232, , MT–223:, MT-243:, Mathematics, Mathematics, Practical based, Practical based on MT-221 and, on MT-241 and MT-222, MT-242, , Qualifications for Teacher: M.Sc. Mathematics (with NET /SET as per existing rules)., ------------------------------------------------------------------------------------------------------------Semester – III, MT-231: Calculus of Several Variables, Unit-1 Limits and Continuity, , [06 lectures], , 1.1 Functions of Several Variables :- Functions of two variables, Domain and Range,, Graphs, Level Curves, Functions of Three or More Variables, 1.2 Limits and Continuity., Unit-2 Partial Derivatives and Differentiability, , [10 lectures], , 2.1 Definition and examples., 2.2 Higher Derivatives, Clairaut’s Theorem (Statement Only) , Partial Differential, Equations, Wave equation.
Page 5 :
2.3 Differentiable function, Differentials, 2.4 Chain Rule, Homogeneous Functions, Euler’s theorem, Unit-3 Extreme Values, , [08 lectures], , 3.1 Extreme values of functions of two variables., 3.2 Necessary conditions for extreme values., 3.3 Second Derivative Test (without proof)., 3.4 Lagrange Multipliers ( with one constraints), Unit-4 Multiple Integrals, , [12 lectures], , 4.1 Iterated Integrals, Fubini’s Theorem (Statement only), 4.2 Double integral over general regions, Change of order of integration for two variables., 4.3 Double integral in Polar coordinates., 4.4 Triple integrals , Evaluation of triple integrals. Triple integrals in spherical coordinates, 4.5 Jacobians , Change of variables in multiple integrals .(Results without proofs), Text book: Multivariable Calculus 7th Edition By James Stewart, Brooks/Cole, Cengage, Learning, 2012, 2008., Unit 1:- Chapter 14: Sec- 14.1, 14.2, Unit 2:- Chapter 14: Sec- 14.3(except the Cobb-Douglas production function), 4.4, (except Tangent Planes and Linear Approximations), Sec-14.5, Unit 3:- Chapter 14: Sec 14.7, 14.8 (except two constraints), Unit 4:- Chapter 15: Sec 15.2, 15.3, 15.4, 15.7 (without Riemann sum and, Application), 15.9, 15.10, Reference Books:, 1. Basic Multivariable Calculus, J. E. Marsden, A. J. Tromba , A. Weinstein, Springer, Verlag (Indian Edition)., 2. Shanti Narayan, R.K. Mittal, A Text-book of Vector Calculus, S.Chand and Company., 3. D.V. Widder, Advanced Calculus (2nd Edition), Prentice Hall of India ,NewDelhi,(1944)., 4. T.M. Apostol , Calculus Vol. II (2nd Edition), John Wiley, New York, (1967)., , MT-232(A): Numerical Methods and It’s Applications, Unit1: Solution of Algebraic and Transcendental Equations, 1.1 Errors and their computations, 1.2 Bisection method., 1.3 The method of False position, 1.4 Newton- Raphson method, Unit 2: Interpolation, , [10 Lectures], , [12 Lectures]
Page 6 :
2.1 Finite Difference Operators and their relations (Forward, Backward, difference and Shift operator)., 2.2 Differences of a polynomial, 2.3 Newton’s Interpolation Formulae (Forward and Backward ), 2.4 Lagrange’s Interpolation Formula, Unit 3: Numerical Differentiation and Integration, [06 Lectures], 3.1 Numerical Differentiation (Derivatives using Newton's forward difference formula), 3.2 Numerical Integration, General quadrature formula., 3.3 Trapezoidal rule., 3.4 Simpsons’s 1/3rd rule., 3.5 Simpsons’s 3/8th rule., Unit 4: Numerical solution of first order ordinary differential equations [08 Lectures], 4.1 Taylor's Series method, 4.2 Picard's method of successive approximations, 4.3 Euler’s method., 4.4 Modified Euler’s methods., 4.5 Runge - Kutta Methods., Text book:, 1. S.S. Sastry, Introductory Methods of Numerical Analysis, 5 th edition, Prentice Hall of, ndia., Unit 1: Chapter 1: section 1.3, Chapter 2: section 2.2, 2.3, 2.5, Unit 2: Chapter 3: section 3.3, 3.5, 3.6, 3.9(3.9.1 only), Unit 3: Chapter 4: section 6.2 (excluding 6.2.1 to 6.2.3), 6.4, Unit 4: Chapter 5: section 8.2, 8.3, 8.4 (excluding 8.4.1)., Reference Books:, 1. C.F. Gerald and O.P. Wheatley, Applied Numerical Analysis, Addison Wesley;, 7thedition (2003)., 2. K.E. Atkinson; An Introduction to Numerical Analysis, Wiley Publications., 3. T. Sauer, Numerical analysis, 3rd edition, Pearson., 4. M. K. Jain, SRK Iyengar and R.K. Jain, Numerical Methods For Scientific & Engg 5e,, New Age International (P) Ltd (2008)., MT-232(B) : Graph Theory, Unit 1. Introduction, 1.1 What is a Graph?, 1.2 Application of Graphs, 1.3 Finite and Infinite Graphs, 1.4 Incidence and Degree, 1.5 Isolated Vertex, Pendant Vertex and Null Graph, Unit 2. Paths and Circuits, , [04 Lectures], , [12 Lectures]
Page 7 :
2.1 Isomorphism, 2.2 Subgraphs, 2.4 Walks, Paths, and Circuits, 2.5 Connected Graphs, Disconnected Graphs, and Components, 2.6 Euler Graphs, 2.7 Operations on Graphs, 2.8 More on Euler Graphs, 2.9 Hamiltonian Paths and Circuits, 2.10 The Traveling Salesman Problem, Unit 3. Trees and Fundamental Circuits, [14 Lectures], 3.1 Trees, 3.2 Some Properties of Trees, 3.3 Pendant Vertices in a Tree, 3.4 Distance and Centers in a Tree, 3.5 Rooted and Binary Trees, 3.6 On Counting Trees, 3.7 Spanning Trees, 3.8 Fundamental Circuits, 3.10 Spanning Trees in a Weighted Graph, Unit 4. Cut-Sets and Cut-Vertices, [06 Lectures], 4.1 Cut-Sets, 4.2 Some Properties of a Cut-Set, 4.3 All Cut-Sets in a Graph, 4.4 Fundamental Circuits and Cut-Sets, 4.5 Connectivity and Separability, Recommended Book :, 1. Narsingh Deo, “Graph Theory with Applications to Engineering and Computer Science”, Printice-Hall, of India Pvt. Lt. New Delhi., Unit 1 : Chapter 1: Sec.1.1 to 1.5, Unit 2: Chapter 2: Sec. 2.1 to 2.10 (Excluding 2.3), Unit 3: Chapter 3: Sec. 3.1 to 3.10 (Excluding 3.9), Unit 4: Chapter 4 : Sec. 4.1 to 4.5, Reference books:, 1. John Clark and Derek Holton, A First Look at Graph Theory (Allied Publishers), 2. Robin J. Wilson, Introduction to Graph Theory, Fourth Edition (low price edition), 3. Introduction to Graph Theory, Douglas West 2nd edition., 4. A Textbook of Graph Theory, Balakrishnan, R., Ranganathan, K., Outcomes of Course:, Upon completion of the course, the students will achieve the following., (i) The mathematical maturity of students in their current and future courses, shall develop.
Page 8 :
(ii) The student develops theoretical, applied and computational skills., (iii) The student gains confidence in proving theorems and solving problems., MT 233: Mathematics Practical, (Practicals based on the applications of articles in MT - 231 and MT - 232), In Semester-III, we should conduct 4 written practical and 2 practical on maxima software for, each paper MT-231 and MT-232., List of Practical, Practical 1 : Problems on Unit 1(Written) from MT-231., Practical 2 : Problems on Unit 2 (Written) from MT-231., Practical 3 : Problems on Unit 3 (Written) from MT-231., Practical 4 : IProblems on Unit 4 (Written) from MT-231., Practical 5 : Problems on unit 1 and unit 2 from MT-231using maxima software., Practical 6 : Problems on Unit 3 and Unit 4 from MT-231using maxima software., Practical 7 : Problems on Unit 1 (Written) from MT-232., Practical 8 :Problems on Unit 2 (Written) from MT-232., Practical 9 : Problems on Unit 3 (Written) from MT-232., Practical 10 : IProblems on Unit 4 (Written) from MT-232., Practical 11 : Problems on unit 1 and unit 2 from MT-232 using maxima software., Practical 12 : Problems on Unit 3 and Unit 4 from MT-2322 using maxima software., Note:, 1. The soft copy of practicals on maxima software will be prepared and provided by the Board of, Studies in mathematics., 2. Practicals on maxima software can be performed on computer only., 3. Practical examination of 25 marks on written problems, 10 marks for problems on maxima, software ( 5 marks for writing syntax and 5 marks to perform the same on computer).
Page 9 :
Semester - IV, MT-241: Linear Algebra, Unit-1: Matrices and System of Linear Equations, , [06 lectures], , 1.1 Row echelon form of a matrix, reduced row echelon form of a matrix., 1.2 Definition of rank of a matrix using row echelon or row reduced echelon form., 1.3 System of linear equations- Introduction, matrix form of linear system, definition, of row equivalent matrices., 1.4 Consistency of homogeneous and non-homogeneous system of linear equations, using rank, condition for consistency., 1.5 Solution of System of Equations: Gauss elimination and Gauss-Jordan elimination, method, examples., Unit-2: Vector Spaces-I, , [10 lectures], , 2.1 Definition and Examples., 2.2 Subspaces., 2.3 Linear Dependence and Independence., 2.4 Basis of Vector Space, Unit-3: Vector Spaces-II, , [08 lectures], , 3.1 Dimension of a Vector Space., 3.2 Row, Column and Null Space of a matrix., 3.3 Rank and nullity., Unit-4: Linear Transformations, , [12 lectures], , 4.1 Definition and Examples, Properties, Equality., 4.2 Kernel and range of a linear Transformation, 4.3 Rank-Nullity theorem., 4.4 Composite and Inverse Transformation., 4.5 Matrices and Linear Transformation., 4.6 Basic Matrix Transformations in R2 and R3, 4.7 Linear Isomorphism., Text Book::, Howard Anton, Chris Rorres, Elementary Linear Algebra, Application Version, Ninth, Edition, Wiley, 11th edition., Unit-1: Chapter-1: Sec. 1.1, 1.2., Unit-2: Chapter- Sec. 4: 4.1 to 4.4., Unit-3: Chapter- Sec. 4: 4.5, 4.7, 4.8
Page 10 :
Unit- 4: Chapter- Sec.8: 8.1 to 8.4, 1.8, 4.9., Reference Books:, (1) K. Hoffman and R. Kunze, Linear Algebra, 2nd edition(2014), Prentice Hall of India, New, Delhi, (2) Steven J. Leon, Linear Algebra with Applications, 4th edition(1994), Prentice Hall of, India. New Delhi, (3) Vivek Sahai, Vikas Bist, Linear Algebra, 4th Reprint 2017, Narosa Publishing House, New, Delhi, (4) Promode Kumar Saikia, Linear Algebra, 2009, Pearson, Delhi, (5) S. Lang, Introduction to Linear Algebra, 2nd edition,1986, Springer-Verlag, New York,, Inc., MT 242(A): Vector Calculus, Unit 1: Vector-Valued Functions, [08 lectures], 1.1 Curves in Space, Limits and Continuity, Derivatives and Motion, Differentiation, Rules for Vector Function, Vector Functions of Constant Length., 1.2 Integrals of Vector Functions., 1.3 Arc Length along a Space Curve, Speed on a Smooth Curve, Unit Tangent, Vector., 1.4 Curvature of a Plane Curve, Circle of Curvature for Plane Curves, Curvature and, Normal Vectors for a Space Curve., Unit 2: Integrals, [12 Lectures], 2.1 Line Integral of Scalar Functions, Additivity, Line integral in the Plane., 2.2 Vector Fields, Gradient Fields, Line Integral of Vector Fields, Line Integrals with, respect to dx, dy, dz ., 2.3 Work done by a Force over a Curve in Space, Flow Integrals and Circulation for, Velocity Fields, Flow across the Simple Closed Plane Curve., 2.4 Path Independence, Conservative and Potential Functions., 2.5 Divergence, Two forms for Green’s Theorem, Green’s Theorem in the Plane, (Proof for special regions),, Unit 3: Surface Integrals, [08 Lectures], 3.1 Parameterizations of Surfaces, Implicit surfaces., 3.2 Surface integrals, Orientation of Surfaces., 3.3 Surface Integrals of Vector Fields., Unit 4: Applications of Integrals, [08 Lectures], 4.1 The Curl Vector Field, Stokes’ Theorem(without proof), Conservative Fields and, Stokes’ Theorem.
Page 11 :
4.2 Divergence in three Dimensions, Divergence Theorem (without proof)., 4.3 Unifying the Integral Theorems., Text Book:, • Thomas’ Calculus (14th Edition) by Hass, Heil, Weir, Pearson Indian Education Services, Pvt. Ltd., Unit 1: Chapter 13: Sec- 13.1, 13.2, 13.3, 13.4, Unit 2: Chapter 16: Sec-16.1, 16.2, 16.3, 16.4, Unit 3: Chapter 16: Sec- 16.5, 16.6, Unit 4: Chapter 16: Sec- 16.7, 16.8, Reference books:, (1) Basic Multivariable Calculus byJ.E.Mardson, A.J.Tromba, A. Weinstein, Sppriger Verlag, (Indian Edition), (2) Advanced Calculus by M.R. Spiegel, Schaum Series., (3) Advanced Calculus (IInd Edition) byD.V. Widder, Prentice Hall of India, New Delhi(1944)., (4) Advanced Calculus by John M. H. Olmsted, Eurasia Publishing House, New Delhi(1970), (5) Calculus Vol. II (IInd Edition) by T.M. Apostol, John Wiley, New York (1967)., , MT-242(B): Dynamical Systems, Unit 1: Eigenvalues and Eigenvectors, 1.1 Eigenvalues and Eigenvectors, 1.2 Diagonalisation(matrices with real and distinct eigenvalues), , [08 Lectures], , Unit 2: First-Order Equations and Planar Linear Systems, 2.1 The Simplest Example, 2.2 The Logistic Population Model, 2.3 Second-Order Differential Equations, 2.4 Planar Systems, 2.5 Preliminaries from Algebra, 2.6 Planar Linear Systems, 2.7 Eigenvalues and Eigenvectors, 2.8 Solving Linear Systems, 2.9 The Linearity Principle., , [12 Lectures], , Unit 3: Phase Portraits for Planar Systems, 3.1 Real Distinct Eigenvalues, 3.2 Complex Eigenvalues, 3.3 Repeated Eigenvalues, 3.4 Changing Coordinates, , [08 Lectures], , Unit 4: Classification of Planar Systems and Exponential of a matrix [08 Lectures]
Page 12 :
4.1 The Trace-Determinant Plane, 4.2 Exponential of a matrix., Textbooks :, 1) Elementary Linear Algebra by Howard Anton and Chris Rorres (9 thedition ),, Applications Version., Unit 1: Chapter 7 : Section 7.1 ( Examples, Theorems with Statements only ) , Section 7.2 ( 2 x 2, and 3 x 3 matrices with real and distinct eigenvalues, Theorems with Statements only ), 2) Differential Equations, Dynamical Systems and An Introduction to Chaos (2 nd edition), by Morris Hirsch, Stephen Smale and Robert Devaney, Academic Press., Unit 2: Chapter 1 : Section - 1.1 to 1.2, Chapter 2 : Section - 2.1 to 2.7., Unit 3: Chapter 3 : Section, 3.1 to 3.4,, Unit 4: Chapter 4 :Section 4.1, Chapter 6 : Section 6.4 ( 2 x 2 matrices with distinct, real, repeated real and complex eigenvalues, 3 x 3 matrices with distinct real, eigenvalues)., Reference Books :, 1. K.B.Datta, Matrix and Linear Algebra, Prentice hall of India Pvt.Ltd, New Delhi 2000., 2. Differential Equations and Dynamical Systems (Third Edition) by Lawrence Perko, Texts in, Applied Mathematics 7, Springer., Outcomes of Course:, Upon completion of the course, the students will achive the following., (i) The mathematical maturity of students in their current and future courses, shall develop., (ii) The student develops theoretical, applied and computational skills., (iii) The student gains confidence in proving theorems and solving problems., MT 243: Mathematics Practical, (Practical based on the applications of articles in MT- 241 and MT -242), In Semester-IV, we should conduct 4 written practical and 2 practical on maxima software for, each paper MT-241 and MT-242., List of Practical, Practical 1 : Problems on Unit 1 (Written) from MT-241., Practical 2 : Problems on Unit 2 (Written) from MT-241., Practical 3 : Problems on Unit 3(Written) from MT-241, Practical 4 : Problems on Unit 4(Written) from MT-241., Practical 5 : Problems on unit 1 and unit 2 from MT-241using maxima software.
Page 13 :
Practical 6 : Problems on Unit 3 and Unit 4 from MT-241 using maxima software., Practical 7 : Problems on Unit 1 (Written) from MT-242., Practical 8 : Problems on Unit 2 (Written) from MT-242., Practical 9 : Problems on Unit 3(Written) from MT-242., Practical 10 : Problems on Unit 4(Written) from MT-242., Practical 11 : Problems on unit 1 and Unit 2 from MT-242 using maxima software., Practical 12 : Problems on Unit 3 and Unit 4 from MT-242 using maxima software., Note:, 1 The soft copy of practical on maxima software will be prepared and provided by the Board of, Studies in mathematics., 2. Practicals on maxima software shall be performed on computer only.., 3.Practical examination 25 marks on written problems, 10 marks for problems on maxima, software ( 5 marks for writing syntax and 5 marks to perform the same on computer only)., Modalities For Conducting The Practical and The Practical Examination:, 1) There will be one 4 hour 10 minutes (250 minutes) practical session for each batch of 15, students per week., 2) The College will conduct the Practical Examination at least 15 days before the, commencement of the Main Theory Examination. The practical examination will consist of, written examination of 20 marks, 10 marks on maxima software and oral examination of 05, marks., 3) There will be external examiner; the practical exam will be of the duration of 3hours., 4) The teacher will set a question paper at the time of paper setting meeting conducted by, Savitribai Phule Pune University, Pune based on pattern as follows, Q1. Any 2 out of 4 each question of 5 marks on paper - I., Q2. Any 2 out of 4 each question of 5 marks on paper - II., Q3. (a) Any 1 out of 2 each question of 5 marks on maxima software from paper – I., (b) Any 1 out of 2 each question of 5 marks on maxima software from paper – II., 5) Each student will maintain a journal to be provided by the college., 7) The internal 15 marks will be given on the basis of journal prepared by student and the, cumulative performance of student at practical., 8) It is recommended that concept may be illustrated using computer software maxima and, graphing calculators wherever possible.
Page 14 :
9) Study tours may be arranged at places having important mathematical institutes or historical, places., 10) Special Instruction:, a) There should be well equipped mathematics practical laboratory of size 20x20, sq. fts containing at least 20 computers., b) Examiners should set separate question papers, solutions and scheme of, marking for each batch and claim the remuneration as per rule., c) Before starting each practical necessary introduction, basic definitions, intuitive, inspiring ideas and prerequisites must be discussed.