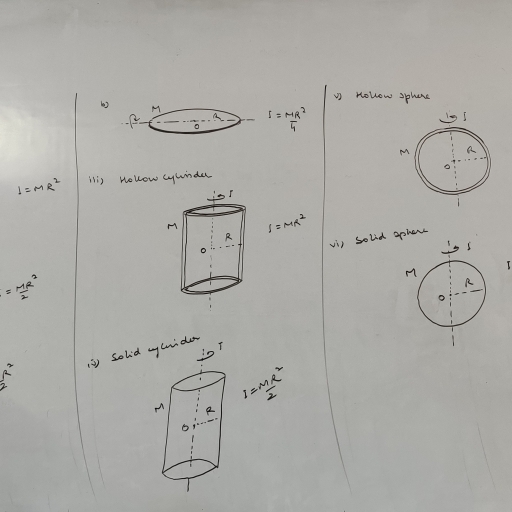
Page 1 :
Fe ., ALTERNATING CURRENTS, , 7/43, , , , a TRANSIENT CURRENTS, , Formulae used., Growth of current in RL circuit, Oe Teller @)4, (i) Decay of current in RL circuit, feat [=he RH!, (iii) Time constant of RL circuit, t= L/R, (iv) Charging of capacitor through resistor,, q=qq(h- HRS), (v) Discharging of capacitor through resistor,, g= (er, (vi) Time constant of R-C circuit is t= RC, ‘Units used. J, Jy in ampere ; R in ohm ; Lin henry, and t, tin seconds., <4 4o in coulomb ; 1, t in sec. ;, Rin ohm and C in farad., , , , (exampte fl When a current of 10 ampere, is flowing through a resistance of 20 ohm and, inductance of 10 henry, the battery is switched off., Find (i) current after 0-4 sec. (ii) the time the, current takes to fall to 60% of its initial value., , Solution. Here, J) = 10 A, R= 202, L= 10H, 1=2,1=0-4 sec., During decay,, Ts Ig e-RD # = 19 ¢-20x 04/10 = 19 ¢-08, logig I = logyg 10 - 0-8 logyg e, , = 1-08 x logyy 2-718 = 1 - 0-8 x 0-4343, logig / = 1 - 03474 = 0-6526, , T= antilog 0-6526 = 4:49 A, , i 60, a = = (|, (i) t=? T= plo Fromi=IpeR)!, , —20, 0 100, , log ig 6 - logyy 10 = - 2 f logyge, 0-7782 — 1-0000 = - 2 t x 0-4343, , or — 0-2218 =~ t x 0-8686, = 02218, , = ——— = 0255s, 0-8686, , \Exampief] A capacitor of capacitance, 05 1. F is discharged through a resistance. Find, the value of resistance if half the charge on, capacitor escapes in one minute., Solution. Here, C = 0-5 p F = 0-5 x 10°F,, R=?, , q= t= 1 min. = 60 sec., , rc. 40, , As q=a¢ i -60/ RC, , =e, , 60, log, 1—log, 2=—7 lobe, , 60, —2303log,, 2=-——x1, 0—2:303 log) RC, 2.303% 0.3010 = ©? _, R(0-5x10~), , e's 60, 0-5x 10 x 2:303x 0-3010, = 1-73 x 108 ohm, , Example f] A 20 mH coil is connected in, , series with a 2 kQ resistor and a 12 V battery., Calculate, , (i) time constant of the circuit,, , (i) time during which current decays to 10%, of its maximum value., , Solution. Here, L = 20 mH = 20 x 103 H,, R=2kQ=2. 103 ohm, V=12V, , , , ; L_ 20x10, () Ti tant == = =10%s, ime constant R 2x102, , -<t, , (ii) For decay of current, J = Ip e L, , I, O_7 410°, ae, , elt =10, , 10° t= 2:303 logig 10, , pe = 2:303 x 10s, 10°, , Scanned with CamScanner
Page 3 :
a, , ALTERNATING CURRENTS, , , , A.C. CIRCUIT CONTAINING, RESISTANCE ONLY, , Mit, , Formulae used. 1. Effective resistance to a.c. = R, | E, she =u, wads = R, 2. No phase change is introduced, i.e., if, E=E sino t, then J = Jp sin wt., , Units used. £, Ep, E, in volt ; J, Io, Jy in ampere ; R, inohm; @ in radian/sec ; tin sec., , , , example f) An alternating voltage given, by V = 140 sin 314 ¢ is connected across a pure, resistor of 50 ohm. Find the rms current through, the resistor. (CBSE 2012), Solution. Here, V= 140 sin 314 t;, R=50Q,1,=2, Compare with standard form : E = Ey sin2 n vt, , Ey _ 140, Ey= 140 V, pay as, , 7-0 145, o= V2 “Ta14 = 198A, Exampte [[]) A light bulb is rated at 100 W, for a 220 V supply. Find, (a) the resistance of the bulb., () the peak voltage of the source, (c) the rms current through the bulb., (CBSE 2012) NCERT Solved Example, Solution. Here, P = 100 W, E, = 220 V,, R=2Ey=21,=?, , E2 E2 220x220, =U Ravi _ 4g4o0, From, P Rik e 100, Ey= 2 Ey = 1-414 x 220 = 311 V, 1 =P 21 ogg a, vE, 220, , , , xarr TH An alternating voltage given, by V= 140 sin 3141 is connected across a pure resistor, of 50 ohm. Find (i) the frequency of the source., (i) the rms current though the resistor., (CBSE 2012), Solution. Here, V = 140 sin 314 1, R = 50 Q,, vs?L=?, , Compare the given equation with the standard, form,, , , , 1, 7145 |, E=E sin wt, Ey= 140 V, = 2 2 = 314,, 314314, On” Ix314 = 50 He |, Ey _140 _14 |, [y= = ==, R 50 5, I 14, == i, v2 5x14 2h., , lExampiefY] A resistance of 40 Q is, connected to an a.c. source of 220 V, 50 Hz. Find, @ the rms current (ii) maximum instantaneous, current in the resistor (iii) time taken by the, current to change from max. value to rms value., , Solution. Here, R = 40 Q, E,, = 220 V, v=50 Hz,, , Ip =V21, = 1-414 x55 =78A, If alternating current is given by, T= I sin qt, then, , : . t, Tg = Jp sin Ot, ; sin wt, = 1 or Wt, =3, , ~, , , , , , and lane = Ig sin @ty, which implies, ot, = 245, paato, 2 4, tt won, @(t, -4)=—+—--==H=, 4) 242 4, 3 tT 1 1, t 4=—= =—=, 4@ 4x2nv 8v 8x50, , = 2:5 x 103 5=2:5 ms, , A.C. CIRCUIT CONTAINING, INDUCTANCE ONLY, , IV’, Formulae used. ‘ Ss, 1, Alternating current through an inductor lags., behind the alt. emf by a phase angle of 90°. If, E= Eo sin ®t; 1= Ip sin (@t—90°) siete bE, 2, Inductive reactance,Xp=@L=2mvL, a x, , I= oe Say, Uv xX, ‘ é, , | Units used. E, Eo, B, in volt ; 7; Jp, f, in e, J, «in henry, X, in ohm ; ¢ in sec ; v in hertz ; @:, - radian/sec, ‘Saois Meaahae, , , , , Scanned with CamScanner
Page 4 :
f AptS TR) Alternating e.m.f. E = 220 sin, 100 7 ¢ is applied to a circuit containing an, , inductance of (3). Write the equation for, n, , instantaneous current through the circuit. What, , will be the reading of a.c. ammeter in the circuit ?, , Solution. Here, E = 220 sin 100 mt, L= L H, ™, , Ey = 220V,, E, Ig = 32-5 -— 220 ' =22A, X, 2mvk agony, Tv, , As current through Z lags behind the applied, e.m.f. through a phase angle of 90°, therefore, instantaneous current through the circuit is, , T= Ig sin (wrt — 1/2) = 2:2 sin (100 nt - 1/2), , A Ty _ 22, Reading of a.c. ammeter = /,, = 2 = ==, v2 2, , =1:556A, , (ExamprefU] A pure inductor of 25-0 mH, is connected to a source of 220 V. Find the, inductive reactance and rms current in the circuit, if the frequency of the source is 50 Hz., , NCERT Solved Example, , Solution. Here, L = 25-0 mH = 25 x 10-3 H,, E, = 220 V, X,= 2,1, =2, v=50 Hz, , Xp=@L=2nvL = 2x2 x50% 25x10, = 7-85 ohm, , jexampie[H A pure inductor of 50 mH is, , 20 V, 50 Hz. Find, ted to an a.c. supply of 220 V,, fon inductive reactance, impedance, rms current, , (Hr, Board 2010), d peak current. r, - Solution. Here, L=50 mH = 50x 10° H, , E, = 220 V, v= 50 Hz, , =a@L=2nvLl, Me eae 3:14 x 50 x 50 X 10°? ohm, , = 15700 x 1073 ohm = 15-7 ohm, z=X,= 15-7 ohm, , ~, , Pradeep’ Fundamental Physics CO a, —a, , 7 a Be 2 229 amp = 140A, v= 7157, , Jy = V2 1, = 1414x140 = 198 A, ni, , Formulae used. |, 1, Through capacitor, alt. current leads the applied, alt. voltage by a phase angle of 90°, ie,, if, E=Epsinwt,then J=/jsin(@t+90) | |, , A.C. CIRCUIT CONTAINING, CONDENSER ONLY, , , , 1 4, 2. Capacitative reactance, X, = oe = = r 34, Vv ;, 1 = Fe, v, Xe, , Units used. E, Eo, E,, in volt ; J, J, ,, in ampere ;C, in farad ; X_ in ohm ; t in sec ; v in hertz and@in, radian/sec. i, , , , Example A 1:5 pF capacitor has a, capacitative reactance of 12 Q. What is the, frequency of the source ? If frequency of source, doubled, what will be the capacitative reactance ?, , Solution. Here, C = 1-5 pF = 1-5 x 10°F,, , , , Xo=12Q, v=?, As x, =. 1, @C 2nve, {Gao 5 1, 2mCXQ -2x314x15x10° x12, v = 8846 Hz, , 1, As XQ ce —, therefore, when vis doubled, X¢, Vv, , becomes half, i.e, 12 =62, 2, , vb (exempts fH] A coil has an inductance of, enry. (a) At what frequency wil it have a, reactance of 3142 ohm ? (b) What honk be the, capacity of a condenser which has the same, reactance at that frequency ?, Solution, (a) Here, L = | henry, v = 2, X,,= 3142 ohms ,, , As X,=o@L=2nve, ~*1 3142, 2nL 2x3142x 1 = 50Ohertz, , Scanned with CamScanner
Page 5 :
(ALTERNATING CURRENTS, , (b) C=2v=500 hertz,, oe), ~@C Inve, , 1 = 1, 2nvXo 23142 500x 3142, __ 106, © (3142)?, , texamprelh] A 15.9 bt F capacitor is, , connected to a 220 V, 50 Hz source. Find the, , capacitative reactance and the current (rms and, , peak) in the circuit. If the frequency is doubled,, , what happens to the capacitative reactance and, , current ? (CBSE 2009), NCERT Solved Example, , Solution. Here, C = 15-0 1 F= 15x 10°F, E, = 220 V, v= 50 Hz,X¢=?, , Xc=X, = 3142 ohm, As Xo, , , , farad = O11pF, , , , , , , , I,=7, Ip =?, eoweh, CoC 2nvCe 2x2 x50x15x10-%, 4, — 7x10" _ 972 ohm, 22x15, 1 = Fv = 21048,, v Xo 212, [y= 21, = 414% 1.04 = 147 A, , When frequency is doubled, dc. halvediand, , current is doubled., pag A.C cIRCUIT CONTAINING R ANDL, , “Vi, , Alternating current in RL circuit, lied alternating e.m,f. by a phase, , RL circuit, = JR? + (OL?, , E, Fy, , Y=T5,y?, al oZ ferxe, , Sa | R, Xpx Zin ohm 5 L in henry ; By in, , Re + XL, , , , , TAT, , , , Exe [) A coil when connected across, a 10 V d.c. supply draws a current of 2 A. When it, is connected across 10 V-50 hz a.c. supply the, same coil draws a current of 1 A. Explain why ?, Hence determine self inductance of the coil., (CBSE Sample Paper 2003), Solution. The coil draws lesser current in 2nd, case because of inductive reactance of the coil., , v_10, =—=—=52, In Ist case, R 7 2, v_10, In second case, Z =7 ae 2108, , Inductive reactance,, X, =Vz2—R? = 102-5? =5V3, InvL=5V3, , 5V3 53., , “ony 2x314x50, , (exampie fl) In an RL circuit, potential, difference across the inductor L is 120 V and pot., diff. across R is 90 V. If rms value of current is, 3 A, what is impedance of the circuit and what is, phase angle between voltage and current ?, , (CBSE 2004), , Solution. Here, V; = 120 V, Vp = 90 V,, , 1,=3A,Z=2,0=?, , As voltages across R and L are 90° out of phase,, , -. resultant voltage,, , V= vv? +V2 . i202 +902 =150V ‘, , = 0-0288 H, , v, za 210 _so0, I,, tang =%L M1 _120_ 155, ar), , = tan"! (1-33) = 534°, In RL circuit, current lags behind the voltage., 121] Following readings were, , obtained in the experiment to determine self, , inductance of a coil. If frequency of a.c. is 50 Hz,, what is the value of self inductance ?, , (Karnataka Board, 2012), , , , Solution. From D.C. Part,, VY. 05, ReleZe =., 1"), 01 5Q, R 012 oc, , Scanned with CamScanner