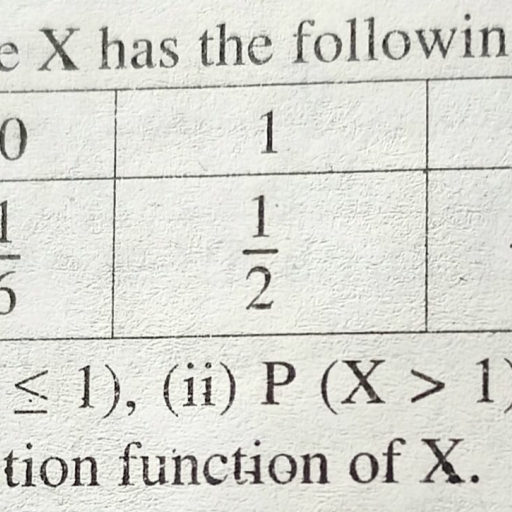Page 1 :
3.3. Uses of Analysis of Time Series, , The process of studying, interpreting and isolating the effects of, various forces (secular trend, seasonal variation, cyclical variation and, Irregular variation) is called the ‘analysis of time series’. The time series, analysis is of great importance not only for businessman or an economist,, but also for people working in various disciplines/subjets, in finance(stock prices, market risk), in economics-(. annual growth, price indices),, in social sciences- ( annual birth rates), in environmental science-( rain, fall), in engineering and medicine- -(brain activities). Some of its uses are, as follows :, , i) It enables us to study the past behaviour of the phenomenon, , under consideration i.e. to determine the type and nature of the variations, in the data.
Page 2 :
ii) The segregation and study of the various Components jg .,, paramount importance for a businessman in the Planning of futy, operations and in the formulation of executive and policy decisions ~, , iii) It helps to compare the actual current performance orm, accomplishments with the expected ones (on the basis of the pall, performances) and analyse the causes of such variations, if any., , iv) It enable us to predict the behaviour of the phenomenon, future, which is very essential for business planning. :, , v) Ithelps us to compare the changes in the values of different, phenomena at different times or places, etc. {
Page 3 :
We or, , wethod of Moving Averages :, 4, , ‘5 The British statistician, , , , , interprete., , The moving average is Charac, constant 'm' known as the period or extent of, moving average. The moving averages of period m, is a series of successive averages (Arithmetic, , Means) of m values at a time, starting with 1s" 24, reginald H. Hooker 34116 and so on. ; an, , Thus, for a time series Yas Yor Vines Yq the moving average (M.A.), values of period m are given by - ;, , terised by a, , st ag +Y,4+, MALS Va teYarcheptetese +Yn),, , 4 ;, 2° MA. = = (Yo + V3 + eee + Yn1) and soon., , In this method, starting from the beginning of the series an, average of period m is calculated. It is placed against the Midvalue of time interval it covers. Keeping the period fixed the process, ‘is repeated by dropping the first yearly figure and adding the figure, of the next year not added before, till the end of the series is reached., , Case i) When period of moving average (m) is Odd :, , Ifthe period of moving average is odd, the moving total and moving, average are placed against mid-value of the time interval it covers. For, example, ifm = 3 then put the first total and average against 2” value, if, m= 5 then put them against 3” value., , Case ii) When period of moving average (m) is Even:, If the period of moving average is even, the moving total and, moving average are placed between two mid-values of the time, , es
Page 4 :
if m = 4 then put the firgt, , rs. For example, ! a, tS ween 94 and 3¢ values. In this case the movin ave a, averag, , igi i i a er, , does not coinside with an Stare Pvorszeby aon ‘ ate, time period, a ot pees Ting averages. 4 mov, ae ec eneunnel by plotting the moving averages, catiae (hecteRIg moving averages On Y - axis and tim, , X-axis) gives trend., , , , , , , , , , , , against time, e Values ont, , period of moving average :, lical fluctuations is known, then moving ave, is calculated by taking the period of moving average equal to the per, cycle. When period of cyclical fluctuations is not known, thena pa |, the actual data is to be drawn and the distance between two Peaks or, depressions of the graph will be taken as period when the cycle is regular., If it is irregular, the average duration of the cycles may be taken as perag, , Itis simple to understand and easy to use as compared tg, , method of least squares. :, , ii) It is superior to graphical method., iii) If the period of moving averages is exactly equal to the period, of the cycle of the data, then cyclical fluctuations can be removed., iv) This method may also be used for measurement of other components., v) In case of a linear-trend, this method can be used for prediction., , Demerits : i) Trend values can not be obtained for all the time periods., ii) The greatest drawback of this method is that the irregular variations —, can not be removed. /, iii) As the period of cyclical variations is not constant, the effect of —, cyclical variations can not be completely removed., iv) In case of non-linear trend, method can not be used for predicting, future values., Remark : For prediction (extend the graph, if required) draw a line, parallel to Y - axis, from the time value (for which prediction is required) t0, , meet the graph, read’y - co-ordinate of the point of intersection. that will, be required value. , Selection of a, if the period of cyc rage, , Od of, , Merits : i)
Page 5 :
3.5.2 Method of Progressive Averages : 3, The method of moving averages can not be used in the early Years, , of an industry because of non-availability of data over a long periog off, , time. At that stage method of progressive averages is useful. Progressivg, , averages are the cumulative averages i.e.an average obtained by dividi, , a cumulative sum by the number of items which makes the sum i.e., , k, =1,.2,3 i..., Progressive Average, P.A. = ze k, , If the time series values are Y,, Yo; Yas Vqee--- the progressive 2, average for the first period is y,, for the seond period it js ‘, (y,ty,)/2, for the third period it is (y,ty,+y,)/3 and so on. Thus to —, calculate the progressive averages we Calculate cumulative sums _, successively and divide the sums by 1,2,3.,........ respectively. 4, , Though it is useful to stdy the trend during the childhood —, of an industry, it suffers from the defect that, these figures are _, not useful as the industry grows up. Hence progressive average —, method should be discontinued as. soon as it is convenient to, do so. 4