Page 2 :
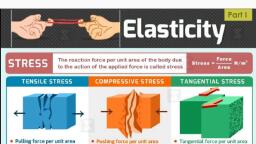
Elasticity, (Overview), , Objective Questions, 1. If a metal wire is stretched a little beyond its, elastic limit (or yield point), and released, it will, (a) lose its elastic property completely, (b) not contract, (c) contract, but its final length will be greater, than its initial length, (d) contract only up to its length at the elastic, limit., 2. A stone weighing 1 kg is tied to a string 1 m, long and whirled in a horizontal circle with a, speed of 2 m/s. If the breaking strength of the, string is 9 N, the maximum speed with which the, stone can be whirled is, (a) 4 m/s (b) 18 m/s, (c) 3 m/s, (d) 6 m/s, 3. Four wires of different materials but the same, area of cross-section are loaded by the same, force. Their lengths and elongations are as, follows. The one whose material’s Young’s, modulus is the largest is, (a) L = 2 m, l = 1 mm (b) L = 1 m, l = 0.25 mm, (c)L = 1.5 m, l = 0.5 mm (d)L = 2.5 m, l = 1.5, mm, 4. A uniform rod of mass m, length L, area of, cross-section A and Young modulus Y hangs, , from the ceiling. Its elongation under its own, weight will be, (a) zero, , (b), , mgL, 2AY, , (c), , mgL, AY, , (d), , 2mgL, AY, , 5. The energy spent in stretching a wire of length L, m and radius r m by 1 m is (Y is the Young’s, modulus of the material of wire), (a), , Yr 2l 2, 2L, , (b), , Yr 2 L, Yr 2 L, Yr 2l, (c), (d), 2l, l, L, , 6. The Young’s modulus of a material is 7x1010, N/m² and its bulk modulus is 11x1010 N/m². It’s, Poisson’s ratio is, (a) 0.17 (b) 0.43 (c) 0.39, (d) 0.26, 7. A metal block is experiencing an atmospheric, pressure of 1x105 N/m². When the same block is, placed in a vacuum chamber, the fractional, change in its volume is (the bulk modulus of, metal is 1.25x1011 N/m²), (a) 4 x 107 (b) 2 x 107 (c) 8 x 107 (d) 1 x 107, 8. One end of a long metallic wire of length L is, tied to the ceiling. The other end is tied to a, massless spring of spring constant k. A mass m, hangs freely from the free end of the spring. The

Page 3 :
3  10 3 kg / m 3 , then the length of the wire, which will break by its own weight will be, (a) 34 m, (b) 30 m, (c) 300 m, (d) 3 m, , area or cross- section and the Young modulus of, the wire are A and Y respectively. If the mass is, slightly pulled down and released, it will, oscillate with a time period T equal to, m, k, mYA, (c) 2, kL, , (a) 2, , m(YA  kL), Yak, mL, (d) 2, YA, , (b) 2, , 9. The length of a metal wire is l1 when the tension, in it is T1 and l2 when the tension is T2. The, natural length of the wire is:, , 10., , (a), , l1T2  l2T1, T2  T1, , (b), , l1T2  l 2 T1, T2  T1, , (c), , l1T2  l 2 T2, T1  T2, , (d), , l1T1  l 2 T2, T1  T2, , 15. If x longitudinal strain is produced in a wire of, Young`s modulus y, then energy stored in the, material of the wire per unit volume is, (a) y x 2, (b) 2y x 2, 1, 1, (c) y 2 x, (d) yx 2, 2, 2, 16., , A wire fixed at the upper end stretches by, length  by applying a force F. The work, done in stretching is, (a) 2F, (b) F, (c) F/2, (d) F/2, , 11. A wire elongates by l when a load W is hanged, from it. If the wire goes over a pulley and two, weights W each are hung at the two ends, the, elongation of the wire will be, (a) l, (b)2 l, (c) zero, (d) l/2, 12. The adjacent graph shows the extension (Δl) of, Δl (x 10-4), a wire of length 1 m, suspended from the top, 4, of a roof at one end and, 3, 2, with a load W connected, 1, to the other end. If the, W(N), cross-sectional area of, 20 40 60 80, the wire is 10-6 m2,, calculate the Young's modulus of the materials, of the wire., (a) 2 × 1011 N/m, (b) 2 × 10-11 N/m, (c) 3 × 10-12 N/m, (d) 2 × 10-13 N/m, 13. Wires A and B are made from the same material, . A has twice the diameter and three times the, length of B . If the elastic limit s are not, reached , when each is stretched by the same, tension , the ratio of energy stored in A to, that in B is, (a) 2:3, (b) 3:4, (c) 3:2, (d) 6:1, 6, , 2, , 14. To break a wire , a force of 10 N / m required, . If the density of the material is, , 17., , One end of a uniform wire of length L and of, weight W is attached rigidly to a point in the, roof and a weight W1 is suspended from its, lower end . If S is the area of cross-section of, the wire , the stress in the wire at a height, 3L/4 from its lower end is, W, W  (W / 4), (a) 1, (b) 1, S, S, W  (3W / 4), W W, (c) 1, (d) 1, S, S, The compressibility of water is 4×10-5 per, atmospheric pressure. The decrease in volume, of 100cm3 of water under a pressure of 100, atmosphere will be, (a) 0.4cm3, (b) 4×10-5cm3, (c) 0.025cm3, (d) 0.004cm3, , 18, , Two wires of made of the same material and, have the same volume. However wire 1 has, cross-sectional area A and wire 2 has crosssectional area 3A. If the length of wire 1, increases by Δx on applying force F, how, much force is needed to stretch wire 2 by the, same amount, (a) F, (b) 4F, (c) 6F, (d) 9F, , 19., , The dimensions of four wire of the same, material are given below. In which wire the, increase in length will be maximum when the, same tension is applied, (a) length 100cm, diameter 1mm, (b) length 200cm, diameter 2mm, (c) length 300cm, diameter 3mm, (d) length 50cm, diameter 0.5mm, , 20., , Two wires of equal lengths are made of the, same, material. Wire A has a diameter that is twice as

Page 4 :
that of wire B. If identical weights are, suspended, from the ends of these wires, the increase in, length, is, (a) Four times for wire A as for wire B, (b) Twice for wire A as for wire B, (c) Half for wire A as for wire B, (d) One-fourth for wire A as for wire B, 21., , 22., , 23., , 24., , A wire elongates by l mm when a load W is, hanged from it. If the wire goes over pulley, and two weights W each are hung at the two, ends, the elongation of the wire will be (in, mm), (a) 21, (b) Zero, (c) ½, (d) l, The breaking stress of a wire depends upon, (a) Length of the wire (b) Radius of the wire, (c) Material of the wire (d) Shape of the cross, section, A wire of length L and radius r is rigidly fixed, at one end. On stretching the other end of the, wire with a force F, the increase in its length is, l. If another wire of same material but of, length 2L and radius 2r is stretched with a, force of 2F, the increase in its length will be, (a)l, (b)2l, (c) ½, (d)1/4, In steel, the young’s modulus and the strain at, the, breaking point are 2×1011Nm-2 and 0.15, respectively. The stress at the breaking point, for steel is therefore, (a)1.33×1011Nm-2, (b)1.33×1012Nm-2, (c) 7.5×10-13Nm-2, (d) 3×1010Nm-2, , 25., , Which one of the following substances, possesses the highest elasticity, (a)Rubber (b)Glass (c)Steel (d) Copper, , 26., , Two wires of the same material have lengths in, the, ratio 1:2 and their radii are in the ratio, 1:√2. If, they are stretched by applying, equal forces, the increase in their lengths will, be in the ratio, (a)2:√2, (b)√2:2, (c)1:1, (d)1:2, , 27., , Which of the following affects the elasticity of, a substance, , (a)Hammering and annealing, (b)Change in temperature, (c)Impurity in substance, (d) All of these, 28., , An iron rod of length 2m and cross section, area of 50 mm2 stretched by 0.5mm, when a, mass of 250kg is hung from its lower end., Young’s modulus of the iron rod is, (a)19.6×1010N/m2, (b)19.6×1015N/m2), (c)19.6×1018N/m2, (d) 19.6×1020N/m2, , 29., , The work done in stretching an elastic wire per, unit volume is or strain energy in a stretched, string is, (a)Stress × Strain, (b) ½ × Stress × Strain, (c) 2 × Strain × Stress (d) Stress/Strain, , 30., , An elastic material of Young’s modulus Y is, subjected to a stress S. The elastic energy, stored per unit volume of the material is, (a)2Y/S2, (b)S2/2Y (c)S/2Y, (d) S2/Y, , 31., , Young’s modulus of the material of a wire is, Y. On pulling the wire by a force F, the, increase in its length is x. The potential energy, of the stretched, wire is, (a)1/2Fx, (b)1/2Yx, 2, (c)1/2Fx, (d)None of these, , 32., , A stretched rubber has, (a) Increased kinetic energy, (b) Increased potential energy, (c) Decreased kinetic energy, (d) Decreased potential energy, , 33., , If a spring extends by x on loading, then the, energystored by the spring is (if T is tension in, the spring and k is spring constant), (a)T2/2x, (b)T2/2k (c)2x/T2, (d) 2T2/k, , 34., , A wire of length L and cross-sectional area A, is made of a material of Young’s modulus Y. It, is stretched by an amount x. The work done(or, energy stored)is, (a)YxA/2L, (b)Yx2A/L, (c) Yx2A/2L, (d) 2Yx2A/L, , 35., , If a rubber ball is taken at the depth of 200m in, a pool, its volume decreases by 0.1%. If the

Page 5 :
density of the water is 1×103kg/m3 and, g=10m/s2, then the volume elasticity in N/m2, will be, (a)108, (b)2×108 (c)109, (d) 2×109, 36., , The isothermal bulk modulus of a gas at, Atmospheric pressure is, (a) 1mm of Hg, (b) 13.6mm of Hg, 5, 2, (c) 1.013×10 N/m, (d) 2.026×105N/m2, , 37., , The Bulk modulus for an incompressible, (a)Zero, (b)Unity, (c)Infinity, (d)Between 0 to 1, , 38., , The graph shows the behaviour of a length of, wire in the region for which the substance, obeys Hooke’s law, P and Q represent, , (a) P = applied force, Q = extension, (b) P = extension, Q = applied force, (c) P = extension, Q = stored elastic energy, (d) P = stored elastic energy, Q = extension, , Steel, , Brass, , 39. A 2 m long light metal rod AB is suspended, from the ceiling horizontally by means of two, vertical wires of equal, length tied to its ends., One wire is of brass, and a has cross-section, C, B, of 0.2x104 m² and the A, other is of steel with, W, 0.1, x, 104, m², crosssection. In order to have equal stresses in, the two wires, a weight is hung from the rod., The position of the weight along the rod from, end A should be, (a) 66.6 cm (b) 133 cm (c) 44.4 cm (d) 155.6 cm, , ….Praveen Gupta