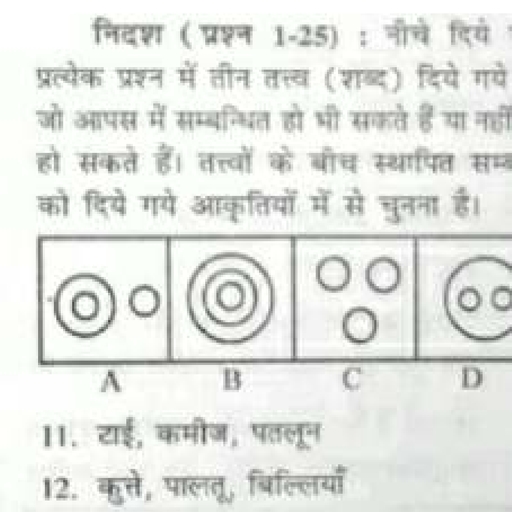
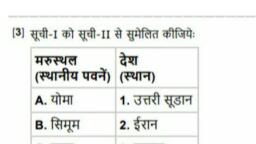
Page 1 :
Mother's Arithmetic Maths * Number System, , Number System Theory, , , , 1. Unit Digit, , it number is called Unit Digit, , , , , unit digit, In This no. 4 is unit digit., , The unit digit of the Resultant value depends upon The unit, digits of all participating numbers., , Unit’s digit when ‘N’ is Raised to a power, unit digit of 0, 1, 5 and 6 has any power (odd or even) no, change, , Rule of 2,3, 7 and8, Unit’s digit when ‘N’ is raised to a power, If the value of power is, , Power, , , , Unit} ; | 2] 3] 4, digit) or | or | or | or, Y | 4net | 4n42| 4n+3| 4n+4, , , , , , , , , , 2 2 4 8 6, 3 3 9 7 Ol, 7 7 c 3 1, 8 8 A 2 6, , , , , , , , , , , , , , , , here n —> Natural No., Ifthose number which uint digit 2. 3,7 and 8 >, all uint digit have cyclicity 4, , 2. Number of Zeroes, , Number of zeroes is an Expression zero:, Zero:- zeor will be formed by 2 and 5, , Ex. 10=2x5, , 100=2?>x ¥, , 1000=2°x §, , = We can say that for ‘n’ number of zero at end of the product., We need exactly ‘n’ combinations of 5 and 2, , Alternate, , Divide successive quotients till we get 0 as the last quotient, , , , wo, , 270, 90 —>, , 30 —, , 10 —>, — 134(add up all the, 3. —> [| quotients), , www, , , , 0 —>, , * Alternate method is easier than first., , 3. Factor, , Factor — A number which divids a given number exactly is, called factor (divisor) of that given number and the given number is called a multiple of that number., , Ex. 1, 2, 4 and 8 are factors of 8 because 8 is perfectly divisible of, 1, 2.4 and8, , Factiors and Multiple, , Ex. Factors of 35 = 1, 5,7, 35, , Ex. Factors of 24 = 1, 2.3, 4, 6, 8, 12. 24, Same,, , Multiple of 2= 2, 4,6, 8, 10........., , Multiple of 7 = 7,14,21,28,35., , * 1 isa factor of every number, , * every number is a factor of itself, , * every number, except | has least 2 factors, * every number has infinite number of its multiples, * every number is a multiple of itself, Number of Factors, , , , , , , , Let N be the number and a, b, c.., , be its prime number and a, b,c..., and p,q. r be the indices (or powers), of a, b,c i.e if N can be expressed as, IN =a?.b4.c*, , then total number of factor of N, (P+)x(qt+h)x@t+h, , If a is even prime factor, b and c are, odd prime factors, , *The numberof even factors, =@)x(qtlx@tl, , *The number of odd factors, =(I)x(qtl)x (r+), , , , , , , , , , Study Center : Jaipur * Gopalpura ¢ Lalkothi * Jnotwara * Ambabari * Alwar + Udaipur a
Page 2 :
Mother's si@aftra + denagla, , quotient 7 is treated as a dividend for the next divisor 3. Thus it, is clear from the above discussion as, , 4. Divisibility, , Rule of Divisibility, , Divisibility by 2 — If the last digit of the number is divisible, by 2, , , , , , sibility by 4 — Iflast two digits of the number are, divisible by 4, , Divisibility by 8 — Iflast three digits of the number are, divisible by 8, , Divisibility by 16 — Iflast four digits of the number are, divisible by 16, , Divisibility by 32 — Iflast five digits of the number are, divisible by 32, , Divisibility of 3 —> All such numbers the sum of whose, digits are divisible by 3, , Divisibility of 9 — All such numbers the sum of whose, digits are divisible by 9, , Divisibility of 6 — A number is divisible by 6 If it is simulta, neously divisible by 2 and 3, , Divisibi of 5 — Iflast digit (0 and 5) is divisible by 5, ‘ibility by 25 — If last two digits of the number are, divisible by 25, , Divisibility of 125 — If last three digits of the number are, divisible by 125, , Divisibility of 11 — The difference of the sum of the digits], in the odd places and the sum of digits in the even places is, ‘0’ of multiple of 11 is divisible, , Divisibility by 3,7, 11, 13, 21,37, and 1001 — If any number, is made by repeating a digit 6 times the number will be divisible, by 3,7, 11, 13, 21, 37 and 100lete., , , , , , Some Important points >, (a) Ifa is divisible by b then ac is also divisible by b., (b) Ifa is divisible by b and b is divisible by c then ais divisible by c., (c) If nis divisible by d and m is divisible by d then (m+n) and, (m-n) are both divisible by d., This has an important implication suppose 48 and 528 are, both divisible by 8., Then (528+48) as well as (528-48) are divisible by 8., , Successive Division :, , If the quotient in a division is further used as a dividend for the, next divisor and again the latest obtained divisor is used as a, dividend for another divisor and so on, then it is called then, “successive division” i.e. if we divide 150 by 4, we get 37 as, quotient and 2 as a remainder then if 37 as quotient and 2 asa, remainder then if 37 ir divided by another divisior say 5 then we, get 7 as a quotient and 2 remainder and again if we divide 7 by, another divisior say 3 we get 2 as quotient and 1 as a remainder, i.e, we can represent it as following, , 4} 150, 37 —> 2, , , , uw, , , , w, , 7 —> 2 ) Remainder, , , , , , 2—1, , , , Now you can see that the quotient obtained in the first division, behaves as a dividend for another divisor 5. Once again the, , , , , , So the 150 is successively divided by 4, 5 and 3 the corresponding remainders are 2,2 and |, , 5. Remainder Theorem, , Ex:- What remainders can be possible when 25 is divided by 7, , “\ ZZ, T, , , , , , +4—> Actual, Remainder, , JR, , 3—> Negative, Remainder, , Remainder is always positive but some times we use negative, remainder for our conveniane if 25 is divided by 7 then actual, remainder will be + 4 but -3 can be used for conveniane for actual, remainder multiple of 7 less, than 25 is 21 hence actual remainder, will be+ 4 and for negative remainder we have to see the multiple, of 7 greater than 25, which is 28 so- 3 will be the remainder., , 6. Arithmetic Progression &, , Geometric Progression, , Arithmetic Progression, A.P. :- Quantities are said to be In arithmetic progression, when they Increases of decrease by a common difference., , Some more examples of Arithmetic Progression are as follows, 1,2,3,4,5, 6,7., , , , 3,7, 11, 15, 19,23., 19,17, 15, 13, 11..., -10, 4,2,8, 14, 20...., , , , 40, 37.5, 35, 32.5, 30.........., 5, 12, 19, 26, 33, , Mh Ms ye, d= Common difference, a,-a,=12-5=7, , a, — First Term, , a, — Second Term, , T, =a+(n-1)d|, , , , T,— nth turm of AP., 1 — First Term of AP., d —> common differecne, , , , HEAD OFFICE : J-7, Himmat Nagar, In front of BIG Bazar, Gopalpura Pulia, Jaipur-302018, 0141-2711689, +91-7073909991 | www.motherseducationhub.org
Page 3 :
Mother's Arithmetic Maths * Number System, , L — Last term/ nth term of AP., Sum of n term., , Sn= plz +(n-1)d], , or, n, Sn=—la+1, “a+, Useful Results, , If the same quantity be added to, or subtracted from, all the, terms ofan AP. the resulting terms will from an AP, but with, the same common difference as before., , If all the terms of an AP be multiplied of divided by the same, quantity, the resulting terms will from an AP, but with a new, common difference, which will be the multiplication/division of, the old common difference. (as the case may be), , Ifa,.a,.a,.a,, a, are in A.P. then, , the arithmetic mean (A.M.), , ap tay tas Pua,, - n, , , , The arithmetic mean (A.M) of odd numbers of consecutive, terms is the middle most term itself., Ifa and b are in AP. then, , A.M. = ——, , If you have to assume 3 terms in AP, assume them as, , a-d, a, atd, of a, atd, at2d, , For assuming 4 terms of an AP we use; a-3d, a-d, atd and a+3d, For assuming 5 terms of an AP, take them as:, , a-2d, a-d, a, atd,a+2d., , Geometric Progression (GP), , GP, , Guantitier are said to be In geometric progression when they, Increase of decrease by a constant factor, , Ex3, 6 12, 24..., , , , |, , a,, Common ratio (r) = ——, a,, , n®termGP—>, , , , , , , , — aml, T, =ar, Where a = First terms of GP, r=common radio, , n— no. of Term., SumofGP, , , , , , ae, , rol, , wherer> 1, , , , , , , , , , or,, , , , , , Ss, -a-r) wherer<1, 1-r, , , , , , Sum of an Infinite geometric progression when r< 1, , , , 5. =, l-r, , , , , , , , Useful Result of GP., , Ifall the terms of a GP be multiplied of divided by the same, quantity. the resulting terms will form a GP with the same, common ratio as before., , Ifa, b, c, d.......are in GP they are also in continued proportion,, since, by definition, a/b = b/c = c/d........= I/r, , Conversely, a series of quantities in continued proportion may, be represented by x, xr, xt”..., , For assuming 3 terms of GP assume them as, , a, arar or a/r, a, ar, , For assuming 4 terms of GP assume them as, , aa 5, 37 at ar, rer, , Tfa,, a,,8,,4,,a,..........a,arein GP, the geometric mean GM., = (a, a),a,,a,,a,. a)!", , , , Ifaandb are two term in GP. then, , GM= Jab, , To find the sum of first n natural numbers, Let the sum be denoted by S; then, $=1+2+3+.....n,is given by, , pote), 2, , To find the sum of the squares if the first n natural numbers, Let the sum be denoted by S; then, , S= 74224374., This is given by:, , se n(n+1)(2n+1), 6, To find the sum of the cubes of the first n natural numbers., , Let the sum be denoted by S: then, STR ZEST ceo +n°, , s= {met, 2, , Thus, the sum of the cubes of the first n natural numbers is, equal to the square of the sum of these numbers., , To find the sum of the first n odd natural numbers., S=14+3+5+.....+Qn-l)5, , To find the sum of the first n even natural numbers., S=2+4+6+2n 5 n (nH), , 7. Power, Indices and Surds, , Before we proceed to exponents (Indices) and surds, it is, proper to learn about Real numbers., , , , Study Center : Jaipur * Gopalpura ¢ Lalkothi * Jnotwara * Ambabari * Alwar + Udaipur Bi
Page 4 :
Mother's si@aftra + denagla, , Number system, Natural Numbers: These are the numbers (1, 2, 3, etc) that are, used for counting. In other words, all positive integers are, natural numbers., The least natural number is | but there is no largest natural, number., The set of natural numbers is denoted by N., Thus, N= {1, 2,3, ......}, , * Whole Numbers : The set of numbers that includes all natural, numbers and the number zero are called whole numbers. The, set of whole numbers is denoted by W., , Thus W = {0, 1, 2, 3..........}, Note: Whole numbers are also called as “Non- negatives, Integers”., Integers: All the natural numbers zero, and the negatives of, natural numbers are called integers., T= f.ccccee3,-2,-1,0, 12,3}, (i Set of negative integers, F212, Bone}, (ii) Set of non-negative integers, (01 DS evccsrah, (iii) Set of Positive integers, 1g, 3 sccm), (iy) Set of non-Positive integers, {0, 1,2, 3..cccc...}, Note: ‘0’ is definately a non- negative integer as well as a nonpositive integer., * Rational Numbers: The numbers which can be expressed in, , P, , the form of qd , Where p and q are integers and g # Oare, , , , , , called rational numbers and their set is denoted by Q., , 12 3 6, . —>—>-—,6| as 6=— fete., a a [ *), are rational numbers., The set of rational numbers encloses the set of integers and, fractions., , Representation of Rational Numbers as Decimals: The, decimal form, ofa rational number is either terminating of non, terminating., , 17 21 . ., Eg = 4.25, z= 4.2 — terminating (or finite) decimal., , 16.52 5, , 3 =53, 3 = 0.6 > Non terminating (of Recurring), , decimal., , Note: If the denomnitor of a rational number has no prime, factors other than 2 or 5, then and only then it is expressible as, aterminating decimal., , * — Irrational numbers : The numbers which when expressed in, decimal form are neither terminating nor repeating decimal are, called “Irrational numbers”., , es. V2, V3,V50, V7, m etc, , 22, Note: The exact value of 7 is not ~, , , , 22 22, , as z is rational while 7¢ is irrational 7 is the approcimate, , value of 7 . Similarly 3.14 is not an exact value of 70 ., , * Real numbers: All rational and irrational numbers together, form the set of real numbers, denoted by R., Thus every natural number every whole number, every in, together, every rational number and every irrational number is, areal number., , Note :(i) The Sum (or difference) of a rational and an irrational, number is irrational., 3, Eg. (++¥3),(2-5)3-s2). 7+ etc., are all irrational., , (ii) The product of a rational and an irrational number is irrational,, , e.g. 43 5 995 etc. are all irrational., , Even and Odd numbers: Integers divisible by 2 are called even, numbers, while those which are not divisible by 2 are known, as odd integers., , Thus........-6, -4, -2, 0.2.4.6... etc are even integers, , And -5, -3, -1, 1,3, 5....... etc are odd integers, , * Prime numbers: A number greater than Lis called a prime, number, ifit has exactly two factors, namely | and itself., , E.g: 2.3, 5,7, 11, 13, 17, 19, 23,29, 31,37, 41, 43, 47, 53, 59, 61, etc., , — 2 isthe only even number which is prime., , * Composite numbers:- Composite numbers are the numbers are, the numbers are the numbers greater than 1 which are not, prime., , e.g. 4. 6,9, 14, 15, etc., Note: | is neither prime nor composite., There are 25 prime numbers 1 & 100., Test for prime numbers : Let x be a given number and let k be, , an integer very near to vx Stk> Vx, If x is not divisible by any prime number less than k, then x is, prime, otherwise. it is not prime., , E.g. Check whether 571 is prime or not?, , Clearly, 24> 4/571, , So, we divide 571 by each prime number less than 24 which are, 2,3,5,7, 9, 11, 17, 19, and 23, we find that 571 is not divisible by any of them. So, 571 isa, prime number., * — Co-Prime Number: Two numbers are co-prime, if their H.C.F., (Highest common factor) is 1, E.g. (2,3), (3,13), (5.7) etc are co-prime number., * Perfect Numbers: If the sum of the divisors of a number excluding N itself is equal to N, then N is called a perfect number., E.g, 6,28,496,8128 etc., For 6, divisors are 1, 2 and 3., 6:142+3=6, 28:14+2+4+7+14=28, Note: The sum of the reciprocals of the divisors of a perfect number, including that of its own is always equal to 2, E.g, For 6, divisors are 1, 2, and 3., 1,1,1,1_6+34+2+1_ 12, <+24+—4+—=——__ = — =2, 12 3 6 6 6, , , , 7°, , HEAD OFFICE : J-7, Himmat Nagar, In front of BIG Bazar, Gopalpura Pulia, Jaipur-302018, 0141-2711689, +91-7073909991 | www.motherseducationhub.org