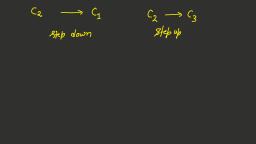Page 1 :
Chemical Kinetics, Recap Notes, Chemical kinetics : It is the branch of, chemistry which deals with the study of, reaction rates and their mechanisms., Rate of a reaction : The rate of a reaction, can be defined as the change in concentration, of a reactant or a product in unit time. For, the reaction,, ∆[ R ], ∆[ P ], P, Rate = –, or +, R, ∆t, ∆t, Units of rate : Concentration time–1 i.e.,, mol L–1 s–1 or atm s–1 for gaseous reactions., Average rate of reaction : It is the average, value during a large time interval., rav =, , − ∆[ R ] + ∆[ P ], =, ∆t, ∆t, , Instantaneous rate of reaction : It is the, rate of a reaction at a particular instant of, time i.e., when Dt approaches zero., rinst =, , − d[ R] + d[ P ], =, dt, dt, , Factors influencing rate of a reaction :, X Concentration, :, Greater, the, concentrations of the reactants, faster is, the rate of reaction., X Physical state of reactants : Reactions, involving gaseous reactants are faster, than reactions containing solid and liquid, reactants., X Temperature : The rate of reaction, increases with increase of temperature., For most of the reactions, rate of reaction, becomes almost double with 10° C rise of, temperature., , X, X, , X, , X, , Presence of catalyst : A catalyst, generally increases the speed of a reaction., Surface area of reactants : For a, reaction involving a solid reactant or, catalyst, the greater is the surface area,, the faster is the reaction., Presence of light : Photochemical, reactions take place in the presence of, light only., Activation energy : Lower the activation, energy faster is the reaction., , Rate law and rate constant : The equation, that correlates the rate of reaction with, concentration of reactants is known as rate, law., X For a simple reaction, A + B → C + D, Rate = k[A][B] where k is the rate constant, which is equal to the rate of reaction when, concentration of each of the reactant is, unity., X For a simple reaction, aA + bB → cC + dD, Rate = k[A]x[B]y and order of reaction =, x+y, Difference between order and molecularity, Order and molecularity :, Molecularity of, reaction, It is the total, number of species, taking part in a, chemical reaction., It is a theoretical, concept., , Order of, reaction, It is the sum of, the powers of the, concentration terms of, reacting species in the, rate law equation., It is an experimental, quantity.

Page 2 :
It is derived from, the mechanism of, reaction., It can neither be, zero nor fractional., It is always a whole, number., , It is derived from the, rate expression., , It is applicable, It is applicable to, only to elementary, elementary as well as, reactions. The, complex reactions., overall molecularity, of a complex reaction, has no significance., , It may be zero,, fractional or an, integer (may range, from 0 to 3)., , Half life of reaction : The time in which the concentration of a reactant is reduced to one, half of its initial concentration is called half life of the reaction., 1, t1 / 2 ∝, ; where n is the order of the reaction., n −1, a, , Rate law, integrated rate law, half-life, units of rate constant and graph for the reactions, of different orders :, Order, , Rate law, , Integrated rate, law, , 0, , Rate = k[A]0, , 1, , Rate = k[A], , 1, , 2, , Rate = k[A], , 2, , 2, , Rate = k[A] [B], , kt =, , n, , Rate = k[A]n, , ( n − 1) kt =, , [A]t = –kt + [A]0, , s, , ln[A]t = –kt + ln [A]0 t1/2 = 0.693/k, 1/[A]t = kt + 1/[A]0, , t1/2 = 1/k [A]0, , [ B ]0 [ A ], 1, ln, [ A ]0 − [ B ]0, [ A ]0 [ B ], 1, n −1, , [ A], , −, , 1, n −1, , [ A0 ], , t1 / 2 =, , CH3COOC2H5 + H2O, , H+, , CH3COOH, + C2H5OH, , –1, , L mol, , Graph, [A] vs t; slope = –k, ln[A] vs t; slope = –k, , –1, , s, , –1, , 1/[A] vs t; slope = k, , L mol–1 s–1, , –, , Acid hydrolysis of ethyl acetate :, , , mol L–1 s–1, , t1/2 = [A]0/2k, , Pseudo first order reactions : Those, reactions which are not truly of the first, order but under certain conditions become, reactions of the first order are called pseudo, first order reactions. e.g.,, X, , Units of rate, constant, , Half-life, , 2n −1 − 1, , n −1, , k ( n − 1) [ A ]0, , (mol L–1 )1–n s–1, , –, 1, [ A ]n−1, , vs t; slope = k, , Rate = k′[CH3COOC2H5][H2O], X, , = k[CH3COOC2H5] where, k = k′[H2O], Acid catalysed inversion of cane, sugar :, H+, C12H22O11 + H2O, C6H12O6, Cane sugar        Glucose, , + C6H12O6,                Fructose, Rate = k[C12H22O11]

Page 3 :
Practice Time, OBJECTIVE TYPE QUESTIONS, , 1. The decomposition of dimethyl ether is a, fractional order reaction. The rate of reaction is, given by rate = k(pCH3COCH3)3/2. If the pressure, is measured in bar and time in minutes, then, what are the units of rate and rate constant, respectively?, (a) bar min–1, bar2 min–1, (b) bar min–1, bar–1/2 min–1, (c) bar–1/2 min–1, bar2 min–1, (d) bar min–1, bar1/2 min–1, 2. The rate of a gaseous reaction is given by the, expression k[A]2[B]3. The volume of the reaction, vessel is reduced to one half of the initial volume., What will be the reaction rate as compared to, the original rate a?, 1, 1, a, (b), (a), a, 2, 8, (c) 2a, (d) 32a, 3. For a reaction P + Q → 2R + S. Which of the, following statements is incorrect?, (a) Rate of disappearance of P = Rate of, appearance of S, (b) Rate of disappearance of Q = 2 × Rate of, appearance of R, (c) Rate of disappearance of P = Rate of, disappearance of Q, 1, (d) Rate of disappearance of Q =, × Rate of, 2, appearance of R, 4. Which of the following statements for order, of reaction is not correct?, (a) Order can be determined experimentally., (b) Order of reaction is equal to the sum of, powers of concentration terms in rate law, expression., (c) Order cannot be fractional., (d) Order is not affected by stoichiometric, coefficient of the reactants., , 5. The half-life of the reaction X → Y, following, first order kinetics, when the initial concentration, of A is 0.01 mol L –1 and initial rate is, 0.00352 mol L–1 min–1 will be, (a) 19.69 min, (b) 1.969 min, (c) 7.75 min, (d) 77.5 min, 6. The reaction 2X → Y + Z would be zero order, reaction when, (a) rate remains unchanged at any concentration, of Y and Z, (b) rate of reaction doubles if concentration of, Y is doubled., (c) rate of reaction remains same at any, concentration of X, (d) rate of reaction is directly proportional to, square of concentration of X., 7. The rate constant of a first order reaction is, 15 × 10–3 s–1. How long will 5.0 g of this reactant, take to reduce to 3.0 g?, (a) 34.07 s, (b) 7.57 s, (c) 10.10 s, (d) 15 s, 8. The decomposition of a substance follows, first order kinetics. If its concentration is, reduced to 1/8 of its initial value in 12 minutes,, the rate constant of the decomposition system, is, 1,  2.303,  2.303, , (a) , log  min −1 (b) , log 8 min −1,  12,  12, , 8,  0.693 , min −1, (c) ,  12 , ,  1, , (d)  log 8 min −1,  12, , , 9. Which of the following statements is not, correct?, (a) For a zero order reaction, t1/2 is proportional, to initial concentration., 1, (b) For a reaction t1 / 2 ∝, , where n is order, n −1, a, of the reaction.

Page 4 :
(c) The unit of rate constant for a reaction is, mol1 – n Ln – 1 s–1 where n is order of the, reaction., (d) The unit of rate of reaction changes with, order of reaction., 10. Consider the reaction, 2N2O5, 4NO2 + O2., In the reaction NO2 is being formed at the rate, of 0.0125 mol L–1 s–1. What is the rate of reaction, at this time?, (a) 0.0018 mol L–1 s–1, , (b) 0.0031 mol L–1 s–1, , (c) 0.0041 mol L–1 s–1, , (d) 0.050 mol L–1 s–1, , 11. C o n s i d e r t h e r e a c t i o n P → Q . T h e, concentration of both the reactants and the, products varies exponentially with time. Which, of the following figures correctly describes, the change in concentration of reactants and, products with time?, , (b), [P], , Concentration, , Concentration, , (a), , [Q ], , [Q ], , Time, [Q ], , (d), [P], , [P], , Concentration, , (c), , Concentration, , Time, , [P], , Time, , [Q ], Time, , 12. The number of molecules of the reactants, taking part in a single step of the reaction is, indicative of, (a) order of a reaction, (b) molecularity of a reaction, (c) fast step of the mechanism of a reaction, (d) half-life of the reaction., 13. For a reversible reaction, A + B, C + D,, the graph for rate of reaction with time is given, below., , Rate, , (p), (r), , (q), Time, , Mark the terms (p), (q) and (r)., , (a) (p) - rate of backward reaction, (q) - rate of, forward reaction, (r) - equilibrium, (b) (p) - rate of forward reaction, (q) - rate of, backward reaction, (r) - equilibrium, (c) (p) - concentration of products, (q) concentration of reactants, (r) - rate of, reaction, (d) (p) - instantaneous rate of reaction, (q) variation of rate, (r) - average rate of reaction, 14. For the reaction, 2N 2O5, 4NO2 + O2,, the rate of reaction can be expressed in terms, of time and concentration by the expression:, d[ N2 O5 ], , =−, , 1 d[ NO2 ] 1 d[ O2 ], =, 4, dt, 2 dt, , 1 d[ N2 O5 ], =, 4, dt, 1 d[ N2 O5 ], (d) Rate = −, =, 2, dt, , 1 d[ NO2 ] d[ O2 ], =, 2, dt, dt, 1 d[ NO2 ] 1 d[ O2 ], =, 2, dt, 2 dt, , (a) Rate = −, , dt, 1 d[ N2 O5 ] 1 d[ NO2 ] d[ O2 ], =, =, (b) Rate = −, 2, 4, dt, dt, dt, , (c) Rate = −, , 15. In a reaction 2HI → H2 + I2, the concentration, of HI decreases from 0.5 mol L–1 to 0.4 mol L–1 in, 10 minutes. What is the rate of reaction during, this interval?, (a) 5 × 10–3 M min–1, (b) 2.5 × 10–3 M min–1, –2, –1, (c) 5 × 10 M min, (d) 2.5 × 10–2 M min–1, 16., for, (a), (b), (c), (d), , The unit of rate and rate constant are same, a, zero order reaction, first order reaction, second order reaction, third order reaction., , 17. In pseudo unimolecular reactions,, (a) both the reactants are present in low, concentration, (b) both the reactants are present in same, concentration, (c) one of the reactants is present in excess, (d) one of the reactants is non-reactive, 18. For a reaction R → P, the concentration of, a reactant changes from 0.05 M to 0.04 M in, 30 minutes. What will be the average rate of, reaction in minutes?, (a) 4 × 10–4 M min–1, , (b) 8 × 10–4 M min–1, , (c) 3.3 × 10–4 M min–1 (d) 2.2 × 10–4 M min–1

Page 5 :
Conc. of X, , 19. For a general reaction, Y, the plot of conc., X, of X vs time is given in, the figure. What is the, order of the reaction and, what are the units of rate, Time, constant?, (b) First, mol L–1 s–1, (a) Zero, mol L–1 s–1, –1, (c) First, s, (d) Zero, L mol–1 s–1, 20. Which of the following is an example of a, fractional order reaction?, (a) NH4NO2 → N2 + 2H2O, (b) NO + O3 → NO2 + O2, (c) 2NO + Br2 → 2NOBr, (d) CH3CHO → CH4 + CO, 21. The value of rate of a pseudo first order, reaction depends upon, (a) the concentration of both the reactants, present in the reaction, (b) the concentration of the reactant present in, small amount, (c) the concentration of the reactant present in, excess, (d) the value of DH of the reaction., 22. The rate law for a reaction,, A + B → C + D is given by the expression k[A]., The rate of reaction will be, (a) doubled on doubling the concentration of B, (b) halved on reducing the concentration of A, to half, (c) decreased on increasing the temperature of, the reaction, (d) unaffected by any change in concentration, or temperature., 23. Nitrogen dioxide (NO 2 ) dissociates into, nitric oxide (NO) and oxygen (O2) as follows:, 2NO2 → 2NO + O2, If the rate of decrease of concentration of NO2, is 6.0 × 10–12 mol L–1 s–1, what will be the rate, of increase of concentration of O2?, (a) 3 × 10–12 mol L–1 s–1, (b) 6 × 10–12 mol L–1 s–1, (c) 1 × 10–12 mol L–1 s–1, (d) 1.5 × 10–12 mol L–1 s–1, 24. For the reaction 4NH3 + 5O2, 4NO + 6H2O,, if the rate of disappearance of NH 3 is, 3.6 × 10 –3 mol L –1 s –1 , what is the rate of, formation of H2O?, , (a), (b), (c), (d), , 5.4, 3.6, 4×, 0.6, , × 10–3 mol L–1 s–1, × 10–3 mol L–1 s–1, 10–4 mol L–1 s–1, × 10–4 mol L–1 s–1, , 25. The rate constant for the reaction,, 2N2O5 → 4NO2 + O2 is 2 × 10–5 s–1. If rate of, reaction is 1.4 × 10–5 mol L–1 s–1, what will be, the concentration of N2O5 in mol L–1?, (a) 0.8, (b) 0.7, (c) 1.2, (d) 1, 26. When a chemical reaction takes place,, during the course of the reaction the rate of, reaction, (a) keeps on increasing with time, (b) remains constant with time, (c) keeps on decreasing with time, (d) shows irregular trend with time., 27. For a unimolecular reaction,, (a) the order and molecularity of the slowest, step are equal to one, (b) molecularity of the reaction can be zero, one, or two, (c) more than one reacting species are involved, in one step, (d) molecularity of the reaction can be, determined only experimentally., 28. In a reaction 2X → Y, the concentration of X, decreases from 3.0 moles/litre to 2.0 moles/litre, in 5 minutes. The rate of reaction is, (a) 0.1 mol L–1 min–1 (b) 5 mol L–1 min–1, (c) 1 mol L–1 min–1, (d) 0.5 mol L–1 min–1, 29. The chemical reaction, 2O3 → 3O2 proceeds, as, (fast), O3  O2 + [O], (slow), , [O] + O3 → 2O2, The rate law expression will be, (a) Rate = k[O][O3], (b) Rate = k[O3]2 [O2]–1, 2, (c) Rate = k[O3], (d) Rate = k[O2][O], 30., (a), (b), (c), (d), , Radioactive disintegration is an example of, zero order reaction, first order reaction, second order reaction, third order reaction., , 31. In a first order reaction the concentration, of reactant decreases from 400 mol L –1 to, 25 mol L–1 in 200 seconds. The rate constant for, the reaction is

Page 6 :
(a) 1.01386 s–1, (c) 1.386 × 10–2 s–1, , (b) 2 × 10–4 s–1, (d) 3.4 × 10–4 s–1, , (c) First order and zero order, (d) None of these, , 32. What will be the rate equation for the, reaction 2X + Y → Z, if the order of the reaction, is zero?, (a) Rate = k[X][Y], (b) Rate = k, (d) Rate = k[X][Y]0, (c) Rate = k[X]0[Y], 33. The following data were obtained during the, first order thermal decomposition of SO2Cl2 at, a constant volume., SO2Cl2(g) → SO2(g) + Cl2(g), Experiment Time/s–1 Total pressure/atm, , 1, 0, 0.5, , 2, 100, 0.6, What is the rate of reaction when total pressure, is 0.65 atm?, (a) 0.35 atm s–1, (b) 2.235 × 10–3 atm s–1, (c) 7.8 × 10–4 atm s–1, (d) 1.55 × 10–4 atm s–1, 34. A first order reaction is 20% complete in 10, minutes. What is the specific rate constant for, the reaction?, (b) 0.009 min–1, (a) 0.0970 min–1, –1, (c) 0.0223 min, (d) 2.223 min–1, 35. In a pseudo first order hydrolysis of ester in, water, the following results were obtained., , t /s, Ester/mol L–1, , 0, , 30, , 60, , 90, , 0.55, , 0.31, , 0.17, , 0.085, , What will be the average rate of reaction between, the time interval 30 to 60 seconds?, (a) 1.91 × 10–2 s–1, , 38. The expression to calculate time required, for completion of zero order reaction is, [R ], (a) t = 0, (b) t = [R] – [R0], k, [ R ] − [ R], k, (d) t = 0, (c) t =, [ R0 ], [ R0 ], 39. For the reaction 2NH3 → N2 + 3H2, if, d[ NH3 ], , d[ N2 ], = k1 [ NH3 ],, = k2 [ NH3 ],, dt, dt, d[ H2 ], = k3 [ NH3 ], dt, then the relation between k1, k2 and k3 is, (b) k1 = 3k2 = 2k3, (a) k1 = k2 = k3, −, , (c) 1.5k1 = 3k2 = k3, , At t = 800 s, [N2O5] = 1.45 mol L–1, , (c) 2.84 × 10, , (d) 2.07 × 10–2 s–1, 36. Two plots are shown below between, concentration and time t. Which of the given, orders are shown by the graphs respectively?, slope = –k, , ln(a – x), , t, , (a) Zero order and first order, (b) First order and first order, , (d) 2k1 = k2 = 3k3., , 40. The decomposition of dinitrogen pentoxide, (N2O5) follows first order rate law. What will be, the rate constant from the given data?, , (a) 3.12 × 10–4 s–1, , (c) 1.98 × 10–3 s–1, , slope = –k, , 1 d[ H2 ], 1 d[ NH3 ], =+, 2 dt, 3, dt, 1 d[ H2 ], 1 d[ NH3 ], (c) +, =−, 2 dt, 3, dt, 1 d[ H2 ], 1 d[ NH3 ], (d) +, =−, 3 dt, 2, dt, , (b) −, , At t = 1600 s, [N2O5] = 0.88 mol L–1, , (b) 4.67 × 10–3 mol L–1 s–1, , At, , 37. For the reaction N2 + 3H2 → 2NH3, how are, the rate of reaction expressions inter-related, d[ NH3 ], d[ H2 ], and, ?, dt, dt, 1 d[ H2 ], 1 d[ NH3 ], =+, (a) −, 3 dt, 2, dt, , t, , –4, , s, , –1, , (b) 6.24 × 10–4 s–1, (d) 8.14 × 10–4 s–1, , 41. The overall rate of a reaction is governed by, (a) the rate of fastest intermediate step, (b) the sum total of the rates of all intermediate, steps, (c) the average of the rates of all the intermediate, steps, (d) the rate of slowest intermediate step., 42. Rate of reaction is the change in concentration, of any one of the reactants or products per unit, time.

Page 7 :
For a hypothetical reaction, A → B, ∆[ A] ∆[ B], =, Rate of reaction = −, dt, dt, In a reaction, A + 2B → 3C + 2D, the concentration, of A decreases from 0.5 mol/L to 0.35 mol/L in, 15 seconds. Then a student Ajinkya calculated, following rates :, I. Rate of formation of C is 0.03 mol/L-s., II. Rate of formation of D is 0.025 mol/L-s., III. Rate of disappearance of B is 0.02 mol/L-s., Which is/are incorrect statement(s)?, (a) I only, (b) II only, (c) II & III both, (d) I & III both, –kt, , 43. For a first order reaction, [A] = [A] 0 e, concentration of reactant decreases exponentially, with time., 0.693, and t1 / 2 =, k, This relation shows that half-life is independent, of concentration and t 1/2 decreases with the, increase of temperature, For first order reaction,, 2N2O5(g), 4NO2(g) + O2(g), The reaction proceeds to 99.6% completion in, (a) 2 half lives, (b) 6 half lives, (c) 8 half lives, (d) 5 half lives, 44. A student of class-12, Jayesh did few, experiments for the reaction,, 2N2O5(g), 2N2O4(g) + O2(g), and he plotted time against total pressure, 0.530, 0.523, , 0.520, 0.512, , Pt 0.510, 0.5, 0, , 100, t, , 200, , If this reaction follows first order kinetics, value, of rate constant k is, (b) 4.98 × 10–4 s–1, (a) 5.96 × 10–3 s–1, (c) 4.13 × 10–3 s–1, (d) 5.85 × 10–4 s–1, 45. Priyanshi after learning chemical kinetics, chapter in class, she made notes for zero order, and first order reactions as given below:, Differential Integral StraRate, Rate law ight, Line, law, [II], plot, [I], [III], , Zero, order, , d [ R], = −k, dt, , Half Units, Life, [V], [IV], , kt = [R]0 ln[R] [Ro]/k mol, L–1 s–1, – [R], vs t, , First d [ R], [R] =, order dt = − k[ R] [R]0e–kt, , [R], vs t, , ln 2k, , s–1, , But the made few mistakes. Identify the wrong, listed equations., (a) Only I and III, (b) Only I and II, (c) Only IV, (d) III and IV, C, 46. For the reaction, A + B, following data has been observed, From the following data for the reaction between A, and B., Exp., [A],, No. mol L–1, 2.5 × 10, , –4, , 5.0 × 10, , –4, , III 1.0 × 10, , –3, , I, II, , initial rate, mole L–1 s–1 at, , [B],, mol L–1, 3.0 × 10, , –5, , 6.0 × 10, , –5, , 6.0 × 10, , –5, , 300 K, , 320 K, , 5.0 × 10, , –4, , 2.0 × 10–3, , 4.0 × 10, , –3, , —, , 1.6 × 10, , –2, , —, , The incorrect option about this reaction is, (a) the order of reaction with respect to A is 2, (b) the order of reaction with respect to B is 1, (c) the rate constant for the given reaction is, 2.67 × 105 mol–2 L2 s–1, (d) none of these., , Case I : Read the following and answer the, questions from 47 to 51 given below., The half-life of a reaction is the time required for, the concentration of reactant to decrease by half,, i.e., [ A ]t = 1 [ A ], 2, 0.693, For first order reaction, t1 / 2 =, k, , this means t1/2 is independent, of initial concentration., Figure shows that typical, variation of concentration, of reactant exhibiting first, order kinetics. It may be, noted that though the major, , Concentration, , Case Based MCQs, , 0, , 1 2 3 4, Number of half-life

Page 8 :
portion of the first order kinetics may be over in, a finite time, but the reaction will never cease as, the concentration of reactant will be zero only at, infinite time., 47. A first order reaction has a rate constant, k = 3.01 × 10 –3 /s. How long it will take to, decompose half of the reactant?, (a) 2.303 s, (b) 23.03 s, (c) 230.3 s, (d) 2303 s, 48. The rate constant for a first order reaction is, 7.0 × 10–4 s–1. If initial concentration of reactant, is 0.080 M, what is the half life of reaction?, (a) 990 s, (b) 79.2 s, (c) 12375 s, (d) 10.10 × 10–4 s, 49. For the half-life period of a first order, reaction, which one of the following statements, is generally false?, (a) It is independent of initial concentration., (b) It is dependent on rate of the reaction., (c) At t1/2, the concentration of the reactant is, reduced by half., (d) None of these., 50. The rate of a first order reaction is, 0.04 mol L–1 s–1 at 10 minutes and 0.03 mol L–1 s–1, at 20 minutes after initiation. The half-life of, the reaction is, (a) 4.408 min, (b) 44.086 min, (c) 24.086 min, (d) 2.408 min, 51. The plot of t1/2 vs initial concentration [A]0, for a first order reaction is given by, , (a) t1/2, , (b) t1/2, [A]0, , (c) t1/2, , [A]0, , (d) t1/2, [A]0, , [A]0, , Case II : Read the following and answer the, questions from 52 to 55 given below., For a first order reaction, A → Products,, a, 2.303, k =, log, , where a is the initial, t, a−x, concentration of A and (a–x) is the concentration, of A after time t. k is rate constant. Its value, is constant at constant temperature for a, , reaction. The time in which half of the reactant, is consumed is called half-life period. Half-life, period of a first order reaction is constant. Its, value is independent of initial concentration or, any other external conditions., In the following questions (Q. No. 52-55), a, statement of assertion followed by a statement, of reason is given. Choose the correct answer, out of the following choices on the basis of the, above passage., (a) Assertion and reason both are correct, statements and reason is correct explanation, for assertion., (b) Assertion and reason both are correct, statements but reason is not correct, explanation for assertion., (c) Assertion is correct statement but reason is, wrong statement., (d) Assertion is wrong statement but reason is, correct statement., 52. Assertion : Rate of reaction doubles when, concentration of reactant is doubled if it is a first, order reaction., Reason : Rate constant also doubles., 53. Assertion : For the first order reaction,, 2.303, half-life period is expressed as t1/2 =, log 2., k, Reason : The half-life time of a first order, reaction is not always constant and it depends, upon the initial concentration of reactants., 54. Assertion : For a first order reaction,, the concentration of the reactant decreases, exponentially with time., Reason : Rate of reaction at any time depends, upon the concentration of the reactant at that, time., 55. Assertion : Half-life period for a first order, reaction is independent of initial concentration, of the reactant., 0.693, Reason : For a first order reaction, t1/2 =, ,, k, where k is rate constant., Case III : Read the following and answer the, questions from 56 to 59 given below., Number of molecules which must collide, simultaneously to give product is called, molecularity. It is equal to sum of coefficients, of reactants present in stoichiometric chemical, equation., For reaction, m1A + m2B → Product

Page 9 :
Molecularity = [m1 + m2], In complex reaction each step has its own, molecularity which is equal to the sum of, coefficients of reactants present in a particular, step. Molecularity is a theoretical property., Its value is any whole number. Number of, concentration terms on which rate of reaction, depends is called order of reaction or sum of, powers of concentration terms present in the, rate equation is called order of reaction., , Case IV : Read the following and answer the, questions from 60 to 64 given below., For the reaction : 2NO(g) + Cl2(g) → 2NOCl(g),, the following data were collected. All the, measurements were taken at 263 K., Experiment, No., , Initial, [NO], (M), , 1., , 0.15, , 0.15, , 0.60, , 2., , 0.15, , 0.30, , 1.20, , Then order of reaction = m1 + m2., , 3., , 0.30, , 0.15, , 2.40, , In simple reaction, order and molecularity are, same., In complex reaction, order of slowest step is the, order of over all reaction. This step is known as, rate determining step. Order is an experimental, property. Its value may be zero, fractional or, negative., , 4., , 0.25, , 0.25, , ?, , m, m, If rate equation of reaction is : Rate = k ⋅ C A1 ⋅ C B 2, , 60., (a), 61., (a), , Initial Initial rate of, [Cl2] disapp. of Cl2, (M), (M/min), , The molecularity of the reaction is, 1, (b) 2, (c) 3, (d) 4, The expression for rate law is, r = k[NO][Cl2], (b) r = k[NO]2[Cl2], , (c) r = k[NO][Cl2]2, , (d) r = k[NO]2[Cl2]2, , 56. The rate of reaction, A + 2B → products, is, d[ A ], = k[ A ][ B ]2, given by the following equation: −, dt, , 62. The overall order of the reaction is, (a) 2, (b) 0, (c) 1, (d) 3, , If B is present in large excess, the order of the, reaction is, (a) zero, (b) first, (c) second, (d) third., , 63. The value of rate constant is, (a) 150.32 M–2 min–1 (b) 200.08 M–1 min–1, (c) 177.77 M–2 min–1 (d) 155.75 M–1 min–1, , 57. The molecularity of the reaction :, 6FeSO4 + 3H2SO4 + KClO3 →, , (a) 6, (c) 10, , KCl + 3Fe2(SO4)3 + 3H2O is, (b) 3, (d) 7, , 58. Which of the following statements is false, in the following?, (a) Order of a reaction may be even zero., (b) Molecularity of a reaction is always a whole, number., (c) Molecularity and order always have same, values for a reaction., (d) Order of a reaction depends upon the, mechanism of the reaction., 59. The rate of the reaction, A + B + C → products,, d[ A ], is given by r = −, =k[ A ]1 / 2 [ B ]1 / 3 [ C ]1 / 4 . The, dt, order of the reaction is, 13, 1, 1, 1, (b), (c), (d), (a), 12, 3, 2, 4, , 64. The initial rate of disappearance of Cl2 in, experiment 4 is, (a) 1.75 M min–1, (b) 3.23 M min–1, (c) 2.25 M min–1, (d) 2.77 M min–1, Case V : Read the following and answer the, questions from 65 to 69 given below., A reaction is said to be of the first order if the rate, of the reaction depends upon one concentration, term only. For a first order reaction of the type, A → Products, the rate of the reaction is given as :, rate = k[A]. The differential rate law is given as :, dA, = –k[A]. The integrated rate law is :, dt, [ A], = –kt, where [A] is the concentration, ln, [ A ]0, of reactant left at time t and [A]0 is the initial, concentration of the reactant, k is the rate, constant., , 65. The unit of rate constant for a first order, reaction is, (a) s–1, (b) mol L–1 s–1, –1 –1, (c) L mol s, (d) L2 mol–2 s–1

Page 10 :
66. Half-life period of a first order reaction is, 10 min. Starting with initial concentration, 12 M, the rate after 20 min is, (a) 0.693 × 3 M min–1, , (b) 0.0693 × 4 M min–1, , (c) 0.0693 M min–1, , (d) 0.0693 × 3 M min–1, , 67. 50% of a first order reaction is complete in, 23 minutes. Calculate the time required to, complete 90% of the reaction., (a) 70.4 minutes, (b) 76.4 minutes, (c) 38.7 minutes, (d) 35.2 minutes, , 68. For a first order reaction, (A) → products,, the concentration of A changes from 0.1 M to, 0.025 M in 40 minutes. The rate of reaction, when the concentration of A is 0.01 M, is, (a) 3.47 × 10–4 M/min (b) 3.47 × 10–5 M/min, (c) 1.73 × 10–4 M/min (d) 1.73 × 10–5 M/min, 69. The half-life period of a 1st order reaction is, 60 minutes. What percentage will be left over, after 240 minutes?, (a) 6.25%, (b) 4.25%, (c) 5%, (d) 6%, , Assertion & Reasoning Based MCQs, For question numbers 70-80, a statement of assertion followed by a statement of reason is given. Choose, the correct answer out of the following choices., (a) Assertion and reason both are correct statements and reason is correct explanation for assertion., (b) Assertion and reason both are correct statements but reason is not correct explanation for assertion., (c) Assertion is correct statement but reason is wrong statement., (d) Assertion is wrong statement but reason is correct statement., 70. Assertion : The rate of the reaction is the, rate of change of concentration of a reactant or, a product., Reason : Rate of reaction remains constant, during the complete reaction., 71. Assertion : The rate law equation can be, found only by experiment., Reason : It can be written from stoichiometric, equation., 72. Assertion : The order of the reaction, CH3COOC2H5 + H2O → CH3COOH + C2H5OH, is 1., Reason : The molecularity of this reaction is 2., 73. Assertion : For the reaction,, 2N2O5 → 4NO2 + O2, Rate = k [N2O5], Reason : Rate of decomposition of N 2 O 5 is, determined by slow step., , Reason : Nature of reactants, concentration of, reactants, products and catalyst affect the rate, of reaction., 76. Assertion : Formation of HI is a bimolecular, reaction., Reason : Two molecules of reactants are involved, in this reaction., 77. Assertion : Hydrolysis of cane sugar is a, pseudo first order reaction., Reason : Water is present in large excess during, hydrolysis., 78. Assertion : Rate of reaction can be, expressed as rate of change in partial pressure, of the gaseous reactants or products., Reason : Partial pressure of a gas is equal to, its concentration., , 74. Assertion : Half-life period of a reaction of, first order is independent of initial concentration., Reason : The time taken for completion of 75%, of a first order reaction is equivalent to two half, lives., , 79. Assertion : The decomposition of NH3 on, finely divided platinum surface is first order, when the concentration is low, however at higher, concentration, the reaction becomes zero order., Reason : In first order reaction, the rate of, reaction is proportional to the first power of the, concentration of the reactant., , 75. Assertion : Chemical kinetics deals with, the rate of reaction, the factors affecting the rate, of the reaction and the mechanism by which the, reaction proceeds., , 80. Assertion : Instantaneous rate of reaction, is equal to dx/dt., Reason : It is the rate of reaction at any, particular instant of time.

Page 11 :
SUBJECTIVE TYPE QUESTIONS, , Very Short Answer Type Questions (VSA), 1. Distinguish between molecularity and order, of a reaction., 2., , Define the half-life period of reaction (t½)., , 3. For a reaction R, P, half-life (t 1/2) is, observed to be independent of the initial, concentration of reactants. What is the order of, reaction?, , 6. Express the rate of the following reaction in, terms of the formation of ammonia., N2(g) + 3H2(g), 2NH3(g), 7. If the rate constant of reaction is k = 3 × 10–4s–1,, then identify the order of the reaction., , 4. If half-life period of a first order reaction is, x and 3/4th life period of the same reaction is y,, how are x and y related to each other?, , For the reaction 3H2(g) + N2(g) → 2NH3(g),, −d[H2 ], how are the rate of reaction, expression, dt, d[NH3 ], interrelated?, and, dt, 9. Define elementary step in a reaction., , 5. Draw a graph between concentration and, time for a zero order reaction., , 10. Distinguish between ‘rate expression’ and, ‘rate constant’ of a reaction., , 8., , Short Answer Type Questions (SA-I), 11. For a reaction A + B → P, the rate law is given, by, r = k[A]1/2 [B]2, What is the order of this reaction?, 12. For a chemical reaction R → P,, the variation in the concentration, [R] vs. time (t) plot is given as, (i) Predict the order of the reaction., (ii) What is the slope of the curve?, 13. For a reaction, I−, alkaline medium, , 2H2 O2 , → 2H2 O + O2, , the proposed mechanism is as given below :, (1) H2 O2 + I − → H2 O + IO − (slow), (2) H2 O2 + IO − → H2 O + I − +O2 (fast), (i) Write rate law for the reaction., (ii) Write the overall order of reaction., (iii) Out of steps (1) and (2), which one is rate, determining step?, 14. For a first order reaction, the time taken, to reduce initial concentration by a factor of, 1/4 is 10 minutes. What will be the time required, to reduce initial concentration by a factor of, 1/16?, , 15. For a first order reaction, show that time, required for 99% completion is twice the time, required for the completion of 90% of reaction., 16. What is meant by rate of reaction? Differentiate, between average rate and instantaneous rate, of reaction., 17. For a reaction A + B, P, the rate is given, by Rate = k[A][B]2, (i) How is the rate of reaction affected if the, concentration of B is doubled?, (ii) What is the overall order of reaction if A is, present in large excess?, 18. The thermal decomposition of HCO2H is, a first order reaction with a rate constant of, 2.4 × 10–3 s–1 at a certain temperature. Calculate, how long will it take for three-fourth of initial, quantity of HCO2H to decompose., (log 0.25 = – 0.6021), 19. For a reaction : 2NH3(g), N2(g) + 3H2(g) ;, Rate = k, (i) Write the order and molecularity of this, reaction., (ii) Write the unit of k., 20. For the reaction, 2N2O5(g), , 4NO2(g) + O2(g),, , the rate of formation of NO2(g) is 2.8 × 10–3 M s–1., Calculate the rate of disappearance of N2O5(g).

Page 12 :
Short Answer Type Questions (SA-II), 21. What do you understand by the ‘order of a, reaction’? Identify the reaction order from each, of the following units of reaction rate constant :, (i) L–1 mol s–1, (ii) L mol–1 s–1, 22. For a chemical reaction, R → P, the variation in the, ln [R], ln, concentration, ln [R] vs. time (s), plot is given as, t(s), (i) Predict the order of the reaction., (ii) What is the slope of the curve?, (iii) Write the unit of the rate constant for this, reaction., 23. For a reaction, the rate law is :, Rate = k [A][B] 1/2 . Can this reaction be an, elementary reaction?, 24. A reaction is first order in A and second, order in B., (i) Write differential rate equation., (ii) How is rate affected when concentration of, B is tripled?, (iii) How is rate affected when concentration of, both A and B is doubled?, (iv) What is molecularity of a reaction?, 25. In a pseudo first order hyrolysis of ester in, water, the following results are obtained :, t in seconds, , [Ester]M, , 0, , 30, , 60, , 90, , 0.55, , 0.31, , 0.17, , 0.085, , (i) Calculate the average rate of reaction, between the time interval 30 to 60 seconds., (ii) Calculate the pseudo first order rate constant, for the hydrolysis of ester., 26. The rate of decomposition of ammonia is, found to depend upon the concentration of NH3, d[ NH3 ], k1 [ NH3 ], according to the equation −, =, dt, 1 + k2 [ NH3 ], What will be the order of reaction when, (i) concentration of NH3 is very high?, (ii) concentration of NH3 is very low?, 27. A certain reaction takes 5 minutes for initial, concentration 0.5 mol L–1 to become 0.25 mol L–1, and another 5 minutes to becomes 0.125 mol L–1., What is the order and specific rate constant of, the reaction?, , 28. Following data are obtained for the reaction :, N2O 5, , 2NO2 +, , 1, O2, 2, , t/s, , 0, , 300, , 600, , [N2O5]/, mol L–1, , 1.6 × 10–2, , 0.8 × 10–2, , 0.4 × 10–2, , (a) Show that it follows first order reaction., (b) Calculate the half-life., (Given : log 2 = 0.3010, log 4 = 0.6021), 29. A first order reaction takes 160 minutes time, for 20% completion. Calculate time required for, half completion of reaction., 30. Hydrogen peroxide, H2O2(aq) decomposes to, H2O(l) and O2(g) in a reaction that is first order in, H2O2 and has a rate constant k = 1.06 × 10–3 min–1., (i) How long will it take for 15% of a sample of, H2O2 to decompose?, (ii) How long will it take for 85% of the sample, to decompose?, 31. When inversion of sucrose is studied at pH = 5,, the half-life period is always found to be 500, minutes irrespective of any initial concentration, but when it is studied at pH = 6, the half-life, period is found to be 50 minutes. Derive the rate, law expression for the inversion of sucrose., 32. What will be the rate of decomposition, of N 2 O 5 and rate of formation of NO 2 and, O 2 when [N 2 O 5 ] = 0.40 M for the reaction, 2N2O5 → 4NO2 + O2. The rate constant for this, reaction is 3.1 × 10–4 min–1., 33. The following data were obtained during the, first order thermal decomposition of SO2Cl2 at, a constant volume :, SO2Cl2(g), , SO2(g) + Cl2(g), , Experiment Time/s Total pressure/atm, 1, 0, 0.4, 2, 100, 0.7, Calculate the rate constant., (Given : log 4 = 0.6021, log 2 = 0.3010)

Page 13 :
34. From the data given below, calculate order, of reaction., S.No., , [A](M), , [B](M), , Rate (M s–1), , 1., , 1.0, , 0.20, , 0.10, , 2., , 2.0, , 0.20, , 0.20, , 3., , 2.0, , 0.40, , 0.80, , 35. For the first order thermal decomposition, reaction, the following data were obtained :, C2H4(g) + HCl(g), C2H5Cl(g), Time/sec, 0, 300, , Total pressure/atm, 0.30, 0.50, , Calculate the rate constant., (Given : log 2 = 0.301, log 3 = 0.4771, log 4 =, 0.6021), , Long Answer Type Questions (LA), 36. Calculate the order of the reaction and the, rate constant for the decomposition of N2O5 at, 30°C from the following rate data., Rate of, reaction, (Mol L–1 hr–1), , Concentration of, N 2O 5, (Mol L–1), , 1., , 0.10, , 0.34, , 2., , 0.20, , 0.68, , 3., , 0.40, , 1.36, , S.No., , reaction, as the concentration of water, remains constant., (ii) Calculate the average rate of reaction, between the time interval 30 to 60 seconds., (Given : log 2 = 0.3010, log 4 = 0.6021), 39. For a homogeneous gas phase reaction, A (g) → B (g) + C (g) + D (g) , the pressure of the, reaction mixture increases by 40% in 20 minute., Calculate rate constant of a reaction., , 37. The half-life period of a first order reaction is, 30 minutes. Calculate the specific reaction rate, of the reaction. What fraction of the reactant, remains after 70 minutes?, , 40. The following results have been obtained, during the kinetic studies of the reaction :, Experiment, No., , [CH3COOCH3]/mol L–1, , 0, 0.60, , 30, 0.30, , 60, 0.15, , (i) Show that it follows pseudo first order, , OBJECTIVE TYPE QUESTIONS, 1. (b) : In terms of pressure, Rate = k(pCH3COCH3)3/2, Units of rate = bar min–1, rate, Units of rate constant =, ( pCH 3OCH 3 )3/2, , , =, , bar min−1, bar, , 3/2, , = bar −1/2 min− 1, , [A], , [B], , Initial rate of, formation of D, , 3., , 0.1 M 0.1 M 6.0 × 10–3 M min–1, 0.3 M 0.2 M 7.2 × 10–2 M min–1, 0.3 M 0.4 M 2.88 × 10–1 M min–1, , 4., , 0.4 M 0.1 M 2.40 × 10–2 M min–1, , 1., , 38. For the hydrolysis of methyl acetate in, aqueous solution, the following results were, obtained :, t/s, , C+D, , 2A + B, , 2., , Calculate the rate of formation of D when, [A] = 0.5 mol L–1 and [B] = 0.2 mol L–1., , 2. (d) : Rate = k[A]2 [B]3 = a, When volume is reduced to one half then conc. of reactants, will be doubled., Rate = k[2A]2 [2B]3 = 32 k[A]2 [B]3 = 32a, 1, 3. (b) : Rate of disappearance of Q =, × rate of, 2, appearance of R, 4., , (c) : Order of reaction can be zero, fractional or negative.

Page 14 :
dx, = k [X ] (For a first order reaction), dt, 0.00352 = k × 0.01 ⇒ k = 0.352, 0.693 0.693, t1/2 =, =, = 1.969 min, k, 0.352, 6. (c) : Rate of a zero order reaction is independent of the, concentration of reactants., 2.303  a , 2.303, 5 , log , or t =, log   = 34.07 s, 7. (a) : t =,  a − x , k, 15 × 10 −3  3 , 5., , 8., , (b) :, , (b) : k =, , 2.303  a , log ,  a − x , t, , (for first order), , 20. (d) : CH3CHO → CH4 + CO, Rate = k[CH3CHO]3/2, 21. (b) : If one of the reactant is present in excess, the, reaction becomes independent of the concentration of that, reactant hence it becomes pseudo first order reaction., Thus, rate of pseudo first order reaction depends upon the, concentration of the reactant present in small amount., 22. (b) : The rate of reaction depends upon concentration of, only A., 23. (a) : For the reaction, 2NO2 → 2NO + O2, , 2.303, 1  2.303, , k=, =, log, log 8  min−1, , 12, 1 / 8  12, , −, , 1 d [NO2 ] 1 d [NO] d [O2 ], =, =, 2 dt, 2 dt, dt, , 9. (d) : The unit of rate of reaction is mol L–1 s–1. It does, not change with order., , −, , d [NO2 ], = 6 × 10−12 mol L−1 s−1, dt, , 1 d [NO2 ] 1, 10. (b) : Rate =, = × 0.0125 = 0.0031 mol L–1 s–1, 4 dt, 4, 11. (b) : In a reaction P → Q, concentration of reactant, decreases as concentration of product increases during the, course of a reaction., 12. (b) : The number of molecules of the reactants taking, part in a single step of the reaction tells about molecularity, of the reaction., 13. (b) : Rate of forward reaction decreases and rate, of backward reaction increases with passage of time. At, equilibrium both the rates become equal., 14. (b) : For 2N2O5 → 4NO2 + O2, the rate of reaction can, be expressed as, 1 d [N2O5 ] 1 d [NO2 ] d [O2 ], =, =, 2 dt, 4 dt, dt, 1 ∆[R ], 1 0.4 − 0.5, =− ×, 15. (a) : Average rate = −, 2 ∆t, 2, 10, 1 0.1, −3, −1, = 5 × 10 M min, = ×, 2 10, −, , 16. (a) : For a zero order reaction, rate = k[A]0 = k, Units = mol L–1 s–1, 17. (c) : When one of the reactants is in excess the reaction, behaves as a first order reaction., 18. (c) : Average rate = −, =−, , (0.04 − 0.05), 30, , =, , ([R ]2 − [R ]1 ), ∆[R ], =−, ∆t, t 2 − t1, , 0.01, = 3.3 × 10−4 M min−1, 30, , 19. (a) : For a zero order reaction, rate = k =, Units of k = mol L–1 s–1, , d [O2 ], = 3 × 10−12 mol L−1 s−1, dt, 1 d [NH3 ], 1 d [H2O], 24. (a) : −, =+, 4 dt, 6 dt, d [H2O] 6, = × 3.6 × 10−3 = 5.4 × 10−3 mol L−1 s−1, 4, dt, 25. (b) : Rate = k[N2O5] (first order as unit of rate constant, is s–1), [N2O 5 ] =, , Rate 1.4 × 10 −5 mol L−1 s −1, =, = 0.7 mol L−1, k, 2 × 10 −5 s −1, , 26. (c) : Rate of reaction ∝ conc. of reactants, As the reaction proceeds, concentration of the reactants, decreases hence the rate also keeps on decreasing with time., 27. (a) : For a unimolecular reaction, both order and, molecularity are one in rate determining step., 28. (a) : Rate = −, , 1 ∆[X ], 1 (2 − 3), =−, = − 0.1 mol L−1 min−1, 2 ∆t, 2 5, , k1, , , 29. (b) : O3 , ,  O2 + [O], k, −1, , (fast), , k, , 2, → 2O2 (slow), [O] + O3 , , Rate of reaction is determined by slow step hence,, Rate = k2[O][O3], [O] is unstable intermediate so substitute the value of [O] in, above equation., Rate of forward reaction = k1[O3], Rate of backward reaction = k–1[O2][O], , dx, dt, , At equilibrium,, Rate of forward reaction = Rate of backward reaction, k1[O3] = k–1[O2][O]

Page 15 :
[O ] =, , k 1[ O 3 ], k −1[O 2 ], , k [O 3 ]2,  k [O ] , Rate = k 2  1 3  [O 3 ] ; Rate =, [O 2 ],  k −1[O 2 ] , 30. (b) : Radioactive disintegration is an example of first, order reaction., k =, , 2.303  N 0 , log  ,  Nt , t, , =, , 37. (a) : For the reaction N2 + 3H2, −, , 2.303  a  2.303  400 , log , log , =,  a − x  200,  25 , t, , 38. (a) : [R] = [R]0 – kt, For completion of reaction [R] = 0, , d [N2 ] 1 d [H2 ], 1 d [NH3 ], =, =, 2 dt, 3 dt, dt, 1, 1, k [NH ] = k 2 [NH3 ] = k 3 [NH3 ], 2 1 3, 3, , Pressure at time t, , SO2Cl2 → SO2 + Cl2, p0, , 0, , 0, , p0 – p, , p, , p, , Let initial pressure p0 ∝ R0, Pressure at time t, Pt = p0 – p + p + p = p0 + p, Pressure of reactants at time t, p0 – p = 2p0 – Pt ∝ R, 2.303  p0 , k=, log ,  2p0 − Pt , t, =, , 2.303 , 0.5,  2.303, log , log1.25, =, , 100, 2 × 0.5 − 0.6  100, , = 2.2318 × 10–3 s–1, Pressure of SO2Cl2 at time t (pSO2Cl2), = 2p0 – Pt = 2 × 0.50 – 0.65 atm = 0.35 atm, Rate at that time = k × pSO2Cl2, , = (2.2318 × 10–3) × (0.35) = 7.8 × 10–4 atm s–1, , 34. (c) : a − x =, k=, , 80, × a = 0.8a , t = 10 min, 100, , 2.303  a  2.303  a , log , =, log ,  a − x ,  0.8a , 10, t, , 10, = 0.2303(1 − 0.9030), 8,   = 0.2303 × 0.0970 = 0.0223 min–1, k = 0.2303log, , 35. (b) : Average rate during the time interval 30-60 s., C −C, (0.17 − 0.31) 0.14, =, Rate = − 2 1 = −, t 2 − t1, 60 − 30, 30, = 4.67 × 10–3 mol L–1 s–1, , N2 + 3H2, , Rate = −, , 32. (b) : Rate = k[X]0 [Y]0 or rate = k, Initial pressure, , [R ]0, k, , 39. (c) : 2NH3, , 2.303, × 1.204 = 0.01386 s−1 = 1.386 × 10−2 s−1, 200, , 33. (c) :, , 2NH3,, , 1 d [H2 ], 1 d [NH3 ], =+, 3 dt, 2 dt, , or t =, , 31. (c) : For first order reaction,, k=, , 36. (a) : Linear plots are obtained in the graph of, A t vs t for zero order reaction and ln a – x vs t for first order, reaction., , 1.5k1 = 3k2 = k3, 40. (b) : k =, k=, , [A ], 2.303, log 1, (t 2 − t1 ) [A2 ], , 2.303, 1.45 2.303, log, =, × 0.2169, (1600 − 800) 0.88 800, , = 6.24 × 10–4 s–1, 41. (d) : The slowest step is rate determining step., 42. (b) :, =, , 1 [C ] 1 d [D ] − d [ A ], 1 d [B ], =, =, =−, 3 dt 2 dt, dt, 2 dt, , − d [A ], (0.035 − 0.5) 0.15, =−, =, = 0.01 mol / L - s, dt, 15, 15, , − d [B ], = 0.02 mol / L - s, dt, d [C ], = 3 × 0.01 = 0.03 mol / L - s, dt, d [D ], = 2 × 0.01 = 0.02 mol / L - s, dt, 43. (c) : For 99.6% completion,, Let a = 100, x = 99.6, a – x = 0.4, k=, , 2.303 100 2.303, =, log, log 250, t 99.6, 0.4 t 99.6, , 2.303, log 250, k, 0.693, k=, t1/ 2, , t 99.6% =, , From equation (i) & (ii), , ...(i), ...(ii)

Page 16 :
t 99.6% =, , Dividing equation (ii) by equation (i),, , 2.303, × 2.4 × t1/ 2 = 8t1/ 2, 0.693, , (Rate)2, , 44. (b) : The following data were obtained during the, first order thermal decomposition of N2O5(g) at constant, volume :, 2N2O4(g) + O2(g), 2N2O5(g), S.No., Time/s, Total Pressure/(atm), 1., 0, 0.5, 2., 100, 0.512, Let the pressure of N2O5(g) decrease by 2x atm. As two moles, of N2O5 decompose to give two moles of N2O4(g) and one, mole of O2 (g), the pressure of N2O4(g) increases by 2x atm, and that of O2(g) increases by x atm., 2N2O4(g) + O2(g), , 2N2O4(g), Start t = 0 , At time t , , 0.5 atm, (0.5 – 2x) atm, , 0 atm, 2x atm, , 0 atm, x atm, , (Rate)1, , or k =, , \, , 2.303, × 0.0216 = 4.98 × 10 −4 s −1, 100, [R ]0, ., 2k, , For first order reaction ln [R] vs t gives straight line plot and, ln2, half life =, k, 46. (c) : (i) Rate law can be written as follows:, Rate = k [A]p [B]q, From experiments I, II and III, (Rate)1 = k [2.5 × 10–4]p [3.0 × 10–5]q = 5.0 × 10–4 ...(i), , (Rate)2 = k [5.0 × 10–4]p [6.0 × 10–5]q = 4.0 × 10–3 ...(ii), , (Rate)3 = k [1.0 × 10–3]p [6.0 × 10–5]q = 1.6 × 10–2 ...(iii), Dividing equation (iii) by equation (ii),, (Rate)2, , or, , (1.0 × 10 −3 ) p, , 1.6 × 10 −2, =, (5.0 × 10 −4 ) p 4.0 × 10 −3, , 2p = 4 or 2p = 22 i. e. p = 2, , t1/2 =, , 0.693, 3.01 × 10−3, , = 230.3 s, , 49. (b) : For a first order reaction t1/2 =, , 45. (d) : For zero order reaction,, , =, , (2.5×10 −4 )2 (3.0×10 −5 ), , 48. (a) : Half life (t1/2) of a first order reaction is given as :, 0.693, 0.693, t 1/2 =, =, = 990 s, k, 7.0 × 10−4, , p, 2.303, 2.303, 0.5 atm, log t =0 =, log, t, pt =100, 100, 0.476 atm, , (Rate)3, , 5.0×10 −4 (mol L−1)3, , 47. (c) : For a first order reaction :, 0.693, , k = 3.01 × 10–3 s–1, t1/2 =, k, , We know that,, , [R] vs t is a straight line plot and half life t1/2 =, , 4.0 × 10 −3, =, −4, (2.5 × 10 −4 ) p (3.0 × 10 −5 )q 5.0 × 10, , = 2.67 × 108 mol−2 L 2 s −1, , = (0.5 – 2x) + 2x + x = 0.5 + x, x = pt – 0.5, pN2O5 = 0.5 – 2x, = 0.5 – 2 (pt – 0.5) = 1.5 – 2pt, At t = 100 s; pt = 0.512 atm, pN2O5 = 1.5 – 2 × 0.512 = 0.476 atm, , =, , (5.0 × 10 −4 ) p (6.0 × 10 −5 )q, , or 2p. 2q = 8 or 22. 2q = 8, or 2q = 8/22 or 2q = 21 or q = 1, Thus the rate equation is Rate = k[A]2 [B], ∴ Order of reaction with respect to A = 2, Order of reaction with respect to B = 1, (ii) Rate constant (k) at 300 K :, From experiment 1, we have, Rate = k (2.5 × 10–4)2 (3.0 × 10–5), or 5.0 × 10–4 mol L–1, = k (2.5 × 10–4 mol L–1)2 (3.0 × 10–5 mol L–1), , p t = p N2O5 + p N2O4 + p O2, , k=, , =, , 0.693, k, , therefore t1/2 depends solely on k., 50. (c) : Let the concentrations of the reactant after, 10 min and 20 min be C1 and C2 respectively., \, , Rate after 10 min = 0.04 × 60 mol L–1min–1 = k.C1, , and rate after 20 min = 0.03 × 60 mol L–1min–1 = k.C2, ∴, , C 1 0.04 × 60 4, =, =, C 2 0.03 × 60 3, , Let the reaction starts after 10 minutes., 2.303 C1 2.303 4, k=, log =, log = 0.02878, 10, 10, 3, C2, 0.6932 0.6932, =, = 24.086 min, 0.02878, k, 51. (b) : For a first order reactions, t1/2 = k[A]00 = k. Thus t1/2, is independent of initial concentration. Hence plot of t1/2 vs, [A]0 will be a horizontal line., ∴ t1/2 =

Page 17 :
52. (c) : For first order reaction, Rate1 = k[A1], According to question, [A2] = [2A1], \ Rate2 = k[2A1] ⇒ Rate2 = 2 Rate1, For a given reaction, rate constant is constant and independent, of the concentration of reactant., 2.303, a, 53. (c) : For a first order reaction k =, log, t, a−x, 2.303, a, 2.303, a 2.303, k=, log, =, log, =, log 2, a /2, t1/2, a − a /2, t1/2, t1/2, , 62. (d) : As the order w.r.t. NO is 2 and order w.r.t. Cl2, is 1, hence the overall order is 3., , 2.303, log 2., k, Thus t1/2 is independent of initial concentration of reactant, for first order reaction., , 65. (a) : Unit of rate constant for a reaction of nth order =, (conc.)1–n time–1, For a first order reaction, n = 1, Unit of rate constant = (mol L–1)1 – 1 s–1 = s–1, , Therefore half-life period t1/2 =, , 54. (b) : For a first order reaction, [A] = [A]0e–kt…(i), According to eq. (i), concentration of reactant decreases, exponentially., 55. (a) : For a first order reaction, t1/2 is inversely proportional, to k, it does not depend on the initial concentration of the, reactant., 56. (b) : From the expression, d [A ], −, = k [A][B ]2, dt, when B is present in large excess, rate will be independent, upon the change in conc. of B, therefore order of reaction, will be one., 57. (c) : The total number of reactant molecules participating, in a chemical reaction is known as its molecularity, hence the, molecularity = 6 + 3 + 1 = 10., 58. (c) : Molecularity may or may not be equal to the order, of a reaction., 1 1 1 6 + 4 + 3 13, =, 59. (d) : Order of reaction = + + =, 2 3 4, 12, 12, 60. (c) : 2NO(g) + Cl2(g) → 2NOCl(g), Molecularity = 3, 61. (b) : Let the rate of this reaction, r = k[NO]m[Cl2]n, then, , r1 0.60 k (0.15)m (0.15)n, =, =, r2 1.20 k (0.15)m (0.30)n, n, , 1  1, or,, =   ⇒ n =1, 2 2, r 1.20 k (0.15)m (0.30)n, =, Again from 2 =, r3 2.40 k (0.30)m (0.15)n, m, , 1  1 2, 1  1, =  ⋅, = , or, , , 2, 2, 1, 4 2, Hence, expression for rate law is, r = k[NO]2 [Cl2]1, or, , m, , ⇒ m =2, , 63. (c) : Substituting the values of experiment 1 in rate law, expression, 0.60 M min–1 = k(0.15 M)2 (0.15 M)1, or k =, , 0.60 M min−1, 0.0225 × 0.15 M3, , = 177.77 M−2 min−1, , 64. (d) : r = 177.7 M –2 min –1 × (0.25 M) 2 (0.25 M), = 2.77 M min–1, , t /2, /2, 66. (d) : 12 M t1, → 6 M 1, → 3M, Initial conc., , t1/2 = 10 min, 0.693, k=, = 0.0693 min−1, 10, As t1/2 is 10 min, after 20 minutes the concentration will, be 3 M., Hence, Rate = 0.0693 × 3 M min–1, 67. (b) : t1/2 = 23 minutes, 0.693, 0.693, 0.693, t1/2 =, ⇒ k=, ⇒ k=, min−1, k, 23, t1/2, For 90% completion,, 2.303  a , 2.303 × 23  100 , ;, t=, log ,  a − x  t = 0.693 log  100 − 90 , k, t = 76.4 minutes, 68. (a) : For the first order reaction, k =, , 2.303  a , log ,  a − x , t, , a = 0.1 M, a – x = 0.025 M, t = 40 min, 2.303, 0.1 2.303, k=, log, =, log 4 = 0.0347 min–1, 40, 0.025, 40, [A] → product, Thus, rate = k[A], rate = 0.0347 × 0.01 M min–1 = 3.47 × 10–4 M min–1, 69. (a) : t1/2 =, , 0.693 0.693, 0.693, ⇒, =k ⇒, =k, k, t1/2, 60, , k = 0.01155 min–1, k=, , 2.303  a , log ,  a − x , t, , Let the initial amount (a) be 100., 0.01155 min–1 =, , 2.303,  100 , log , , 240 min  a − x 

Page 18 :
0.01155 min−1 × 240 min,  100 , = log ,  a − x , 2.303, 1.204 = log 100 – log (a – x), 1.204 = 2 – log (a – x), log (a – x) = 2 – 1.204 = 0.796, (a – x) = 6.25%, 70. (c) : Rate of reaction does not remain constant during, the complete reaction because rate depends upon the, concentration of reactants which decreases with time., 71. (c) : The rate law equation cannot be written from, stoichiometric equation., 72. (b) : During hydrolysis of ester, water is always present, in high concentration, thus there is very little change in its, concentration and it practically remains constant. Thus, the, order of reaction is 1 (pseudo first order reaction)., 73. (a) : Rate of any reaction is equal to the rate of its, slowest step and here rate of given reaction = k [N 2O 5], because the slowest step has only N2O5 molecule involved., 74. (b) , , 75. (b), , 76. (a) : A bimolecular reaction may involve combination, of two molecules or exchange of atoms or groups of atoms, between the two reactant molecules., 77. (a) : Hydrolysis of cane sugar is pseudo first order, reaction. Since, water is always in excess, rate of reaction, does not depend appreciably on its concentration, thus it is, an example of pseudo unimolecular reactions., 78. (c) : For a gaseous reaction at constant T, concentration, is directly proportional to the partial pressure of the species., Thus, the rate of reaction can be expressed in terms of partial, pressure for gaseous reactants or products., 79. (b) : In a heterogeneous system, the reactant is, absorbed on the surface of a solid catalyst. The fraction, of the surface of the catalyst covered by the reactant is, proportional to its concentration at low values and the rate, of reaction is first order. However at higher concentration,, the surface of catalyst is fully covered and the reaction rate, becomes independent of concentration and it becomes zero, order reaction., 80. (b) : Instantaneous rate of a reaction is equal to small, change in concentration (dx) during a small interval of time, (dt) at that particular instant of time divided by the time, interval., , SUBJECTIVE TYPE QUESTIONS, 1., Order of a reaction Molecularity of a reaction, 1. It is the sum of powers 1. It is the number of reacting, of the concentration, species (atoms, ions or, of the reactants in the, molecules) taking part in an, rate law expression., elementary reaction which, must collide simultaneously, in, order to bring about a, chemical reaction., 2. It can be zero or even 2. It is always a whole number., a fraction., Generally, in a complex reaction the order of reaction is equal, to the molecularity of the slowest step., 2. The time taken for half of the reaction to complete, i.e.,, the time in which the concentration of a reactant is reduced, to half of its original value is called half-life period of the, reaction., [R ], t = t1/2 when [R ] = 0, 2, 3. Half-life of first order reaction is independent of the, initial concentration of reactants., 0.693, t1/2 =, k, 0.693 0.693, =, t1/2, x, , 4., , For a first order reaction, k =, , For, , 3, 3, 1, th life period, a − x = a − a = a, 4, 4, 4, , \, , k=, , 0.693 2.303, a, 2.303, a, =, log, ;, log, a /4, x, y, (a − x ), y, , 0.693 2.303, 0.693 0.693 × 2, 2log2 ;, =, =, x, y, x, y, y = 2x, 5., , [R] = –k0t + [R]0, , 6., , N2(g) + 3H2(g), , 2NH3(g), , −d [N2 ], 1 d [H2 ], 1 d [NH3 ], =−, =+, dt, 3 dt, 2 dt

Page 19 :
7. First order reaction has s –1 as the unit of the rate, constant., 1 d [H2 ], 1 d [NH3 ], =+, 3 dt, 2 dt, 9. Elementary step : Each step of a complex reaction is, called an elementary step., , 8., , −, , 10. Rate expression is a way of expressing rate of reaction, in terms of concentration of reactants, e.g., for a general, reaction, aA + bB, cC + dD, x, Rate = k[A] [B]y, Rate constant (k) is equal to the rate of reaction when molar, concentration of reactant is unity. Its units depends upon, the order of reaction., 11. Rate law, r = k[A]1/2 [B]2, Order of reaction is sum of the powers of concentration terms,, 1, 5, \ Order of reaction = + 2 = = 2.5, 2, 2, 12. (i) The reaction is of zero order., d [R ], (ii) Slope of the curve = − k =, dt, 13. (i) Rate = k[H2O2][I–], (ii) Overall order of reaction is 2., (iii) Step (1) being the slow step is the rate determining step, of the reaction., 14. Let initial concentration (a) = 1, then, final concentration (a – x) = 1/4, 2.303, 1, ∴ t1/ 4 =, log, ...(i), k, 1/ 4, 2.303, 1, ...(ii), log, k, 1 / 16, Dividing equation (ii) by (i), t1/16 log 16, 1.204, = 20 minutes, =, ⇒ t1/16 = 10 ×, 10, 0.6021, log 4, Similarly, t1/16 =, , 15. For first order reaction, t =, , [R ], 2.303, log 0, k, [Rt ], , For 99% completion of reaction, t = t0.99, [R]0 = 1, [R]t = (1 – 0.99) = 0.01 = 10–2, 2.303, 1, 2.303, 2.303, log −2 =, log 102 =, × 2 ...(i), k, k, k, 10, For 90% completion of reaction, t = t0.90, [R]0 = 1, [R]t = (1–0.9) = 0.1 = 10–1, 2.303, 1, 2.303, 2.303 ...(ii), t 0.90 =, log −1 =, log 10 =, k, k, k, 10, Comparing equations (i) and (ii),, t0.99 = 2 × t0.90, t 0.99 =, , 16. Change in concentration i.e., either (decrease in, concentration of reactant or increase in concentration of, product) per unit time is called rate of reaction., C − C ∆C, Rate of reaction = 2 1 =, ∆t, t 2 − t1, The ratio of change of concentration of reactants to the time, consumed in that change is called average rate of reaction., ∆x, C − C1, rav =, =− 2, ∆t, t 2 − t1, The rate of reaction at a particular instant (time) is called, instantaneous rate of reaction., rins =, , dx, dt, , dx = small change in concentration, dt = small time interval, 17. (i) From the rate law equation, order of reaction w.r.t. B, is 2. Hence, if concentration of B is doubled, rate will become, four times., (ii) If A is present in large excess, rate of reaction will, be independent of concentration of A and hence, order of, reaction will be 2., 18. For a first order reaction, t =, , [R ], 2.303, log 0, k, [R ], , Given k = 2.4 × 10–3 s–1, [R ], [R ] = 0 , t = ?, 4, Substituting these values in the equation, we get, t=, t=, , 2.303, 2.4 × 10, , −3 −1, , s, , 2.303, 2.4 × 10, , −3 −1, , s, , log, , [R ]0, [R ], , log 4 =, , 2.303, 2.4 × 10 −3, , × 0.6021 s, , t = 577.7 s = 578 s, 19. (i) The decomposition of gaseous ammonia on a hot, platinum surface is a zero order reaction at high pressure., In this reaction, platinum metal acts as a catalyst. At high, pressure, the metal surface gets saturated with gas molecules., So, a further change in reaction conditions is unable to alter, the amount of ammonia on the surface of the catalyst making, rate of the reaction independent of its concentration., However, two molecules of ammonia react to give products, thus, the molecularity is two., (ii) For a zero order reaction, unit of rate constant is, mol L–1 s–1., d [NO2 ], = 2.8 × 10 −3 M s −1, dt, According to rate law expression,, , 20. Given,

Page 20 :
\, , −, , 1 d [N2O5 ] 1 d [NO2 ] d [O2 ], =, =, 2, dt, 4 dt, dt, , −, , 1 d [N2O5 ] 1, = × 2.8 × 10 −3, 2 dt, 4, , −d [N2O5 ] 1, = × 2.8 × 10 −3 = 1.4 × 10 −3 M s −1, dt, 2, 21. Order of a reaction : It is the sum of the power of, reactant in the rate law expression., (i) L–1 mol s–1 – Zero order reaction, (ii) s–1 , – First order reaction, 22. (i) The reaction is of 1st order., (ii) For first order reaction, ln[R] = –kt + ln [R]0, comparing eqn. y = m × x + c, we get a straight line with slope = –k and intercept equal, to ln[R]0., (iii) Unit of rate constant for first order reaction, mol L−1, 1, ×, = s −1, s, (mol L−1)1, 23. For an elementary reaction, order should be equal to, molecularity and further molecularity should be integral. For, the given reaction, order of reaction = 1 + 1/2 = 3/2. Since, molecularity cannot be fractional, therefore, for the given, reaction, order is not equal to molecularity. Hence given, reaction cannot be an elementary reaction., 24. (i) Differential rate equation of reaction is, dx, = k [A ]1[B ]2 = k [A ][B ]2, dt, (ii) When conc. of B is tripled, it means conc. of B becomes, [3 × B], dx ′, = k [A][3B ]2, \ New rate of reaction,, dt,  dx , = 9k[A][B]2 = 9  ,  dt , i.e., the rate of reaction will become 9 times., (iii) When conc. of A is doubled and that of B is also doubled,, then conc. of A becomes [2A] and that of B becomes [2B]., dx ′, = k [2A ][2B ]2 = 8k [A][B]2, \ Now rate of reaction,, dt, i.e., the rate of reaction will become 8 times., (iv) Molecularity of a reaction is the number of reacting, particles which collide simultaneously to bring about the, chemical change. It is a theoretical concept., 25. (i) Average rate of reaction between the time interval, 30 to 60 seconds is, , rav =, , −[0.17 − 0.31] 0.14, =, 60 − 30, 30, , = 4.67 × 10–3 s–1 [Taking only difference], 2.303 [R ]0, log, t, [R ], At t = 30 s,, 2.303 0.55 2.303, k=, =, × 0.249 = 1.91 × 10 −2 s −1, log, 30, 0.31, 30, At t = 60 s,, 2.303 0.55 2.303, k=, log, =, × 0.5099 = 1.96 × 10 −2 s −1, 60, 0.17, 60, (ii) k =, , At t = 90 s, 2.303, 0.55, k=, log, 90, 0.085, 2.303, × 0.8109 = 2.07 × 10 −2 s −1, 90, \ Average value of k, k=, , =, , 1.91 × 10 −2 + 1.96 × 10 −2 + 2.07 × 10 −2, = 1.98 × 10 −2s −1, 3, , 26. The given rate law equation can be written as, d [NH3 ], k1, −, =, 1 / [NH3 ] + k 2, dt, If [NH3] is very high, 1/[NH3] becomes negligible, d [NH3 ] k1, ∴ −, = =k, dt, k2, , (i), , i.e., rate becomes independent of concentration. Hence, it is, of zero order., (ii) If [NH 3] is is very small, 1/[NH 3] will be very large, (>>k 2 ), so that k 2 can be neglected in comparison to, d [NH3 ], k1, =, = k1[NH3 ], 1/[NH3]. Hence −, dt, 1 / [NH3 ], Thus, reaction is of 1st order., 27. The given data is, 5 min, , 5 min, , 0.5 molL−1  , → 0.25 molL−1  , → 0.125 molL−1, Half life period is independent of initial concentration of the, reactant, hence reaction is of first order., For first order reaction, k=, , 0.693 0.693, =, = 0.138 min−1, t1/2, 5 min, , 28. (a) The formula of rate constant for first order reaction, is, 2.303 [A ]0, k=, log, [A ]t, t

Page 21 :
k1 =, , 2.303 (1.6 × 10 −2 ) mol L−1, = 2.3 × 10 −3 s −1, log, 300 s (0.8 × 10 −2 ) mol L−1, , −2, −1, Similarly, k 2 = 2.303 log (1.6 × 10 ) mol L, 2, −, 600 s (0.4 × 10 ) mol L−1, , , = 2.3 × 10–3 s–1, Unit and magnitude of rate constant shows the given reaction, is of first order., (b) The formula for half-life for first order reaction is, 0.693, 0.693, t1/2 =, =, = 301.30 s, k, 2.3 × 10 −3 s −1, 29. Given : [R]0 = 1, [R] = 0.80, t = 160 min, t1/2 = ?, [R ]0, 2.303, For first order reaction, k =, log10, [R ], t, 2.303, 2.303, 1, × log 1.25, log10, or, k =, 160 min, 160, 0.8, 2.303 × 0.0969, or, k =, = 1.39 × 10 −3 min−1, 160 min, 0.693, 0.693, =, = 498 min, Again t1/2 =, k, 1.39 × 10 −3, or,, , k=, , 2.303 [A ]0, log, 30. (i) t =, [A ], k, Given k = 1.06 × 10–3 min–1,, , [A ]0 100, =, 85, [A ], , 2.303, , 100, log, t=, −3, −1, 85, 1.06 × 10 min, 2303, [2 log10 − log 85]min, 1.06, 2303 × 0.0706, 2303, [2 × 1 − 1.9294] =, t=, 1.06, 1.06, t = 153.39 min = 153.4 min., t=, , [A]0 100, =, [A] 15, 2.303, 100 2303, log, [2 log10 − log15]min, =, t=, −3, −1, 15, 1.06, 1.06 × 10 min, (ii) Given k = 1.06 × 10–3 min–1,, , 2303, 2303 × 0.8239, [2 ×1−1.1761] =, min = 1790 min, 1.06, 1.06, 31. At pH = 5, as half-life period is found to be independent, of initial concentration of sucrose, this means with respect to, sucrose, it is a reaction of first order, i.e., Rate = k[Sucrose]., If n is the order with respect to H+ ion, t1/2 ∝[H+]1–n,, i.e., 500 ∝ (10–5)1 – n [pH = 5 means [H+] = 10–5 M] ...(i), ...(ii), and 50 ∝ (10–6)1 – n [pH = 6 means [H+] = 10–6M], =, , Dividing (i) by (ii), 10 = (10)1 – n i.e. 1 – n = 1 or n = 0, i.e.,, order with respect to H+ ion = 0. Hence, overall rate law is, Rate = k [Sucrose] [H+]0., 32. The given reaction is 2N2O5 → 4NO2 + O2, Unit of rate constant suggests that rate of reaction is first, order., Hence, rate of reaction = k[N2O5], , = 3.1 × 10–4 min–1 × 0.40 M, , = 1.24 × 10–4 M min–1, Rate of reaction,, 1 d [N2O5 ], 1 d [NO2 ], d [O2 ], =−, =+, =+, 2 dt, 4 dt, dt, d [N2O5 ], = 1.24 × 10 −4 M min−1 × 2, dt, , = 2.48 × 10–4 M min–1, −, , ∴, , Similarly, , +, , d [NO2 ], = 4 × 1.24 × 10 −4 M min−1, dt, = 4.96 × 10–4 M min–1, , d [O2 ], = 1.24 × 10 −4 M min−1, dt, , 33. The given reaction is, SO2Cl2(g), At t = 0   , At time t, , SO2(g) + Cl2(g), 0.4 atm      0     0, , (0.4 – x) atm     x atm  , , x atm, , Total pressure at time t will be, Pt = (0.4 – x) + x + x = 0.4 + x, x = (Pt – 0.4), Pressure of SO2Cl2 at time t will be, pSO2Cl2 = 0.4 – x = 0.4 – (Pt – 0.4) = 0.8 – Pt, At time t = 100 s, Pt = 0.7 atm, \ pSO2Cl2 = 0.8 – 0.7 = 0.1 atm, According to first order kinetic equation, p SO2Cl2 (initial), 2.303, k=, log, t, p SO2Cl2 (after reaction), =, , 2.303  0.4 , log   = 1.3 × 10 −2 s −1,  0.1 , 100, , 34. Let rate of reaction r = k[A]a[B]b, From the data, r1 = 0.10 M s–1 = k(1.0 M)a (0.20 M)b, r2 = 0.20 M s–1 = k(2.0 M)a (0.20 M)b, r3 = 0.80 M s–1 = k(2.0 M)a (0.40 M)b, Dividing eqn. (i) by (ii), r1 0.10 Ms −1 k (1.0 M)a (0.20 M)b, =, =, r2 0.20 Ms −1 k (2.0 M)a (0.20 M)b, , ... (i), ... (ii), ... (iii)

Page 22 :
a, , 1  1, =   or a = 1, 2 2, Dividing eqn. (ii) by eqn. (iii), , \, , or,, , b, , 1  1, r2 0.20 Ms −1 k (2.0)a (0.20)b, or,, =   or, b = 2, =, =, 4 2, r3 0.80 Ms −1 k (2.0)a (0.40)b, Hence, order of reaction = 1 + 2 = 3, 35. The given reaction is, , C2H5Cl(g), At time t = 0, At time t = 300 sec, , C2H4(g) + HCl(g), , 0.30 atm, 0.30 – x, , 0, , 0, , x, , x, , Total pressure = 0.30 – x + x + x = 0.50, or 0.30 + x = 0.50, \ x = 0.50 – 0.30 = 0.20, \ Initial pressure, P0 = 0.30 atm, Pressure of C2H5Cl after 300 sec,, Pt = 0.30 – 0.20 = 0.10 atm, Using formula for first order reaction,, 2.303  P0 , k=, log  ,  Pt , t, k=, , 2.303  0.30 , log ,  0.10 , 300, , k=, , 2.303, 2.303 × 0.4771, log 3 =, = 3.66 × 10–3 sec–1, 300, 300, , 36. (i) Let rate of reaction, ∴, , d [N2O5 ], = k [N2O5 ]n, dt, , r1 = 0.10 mol L–1 hr–1 = k × (0.34 mol L–1)n, r2 = 0.20 mol L–1 hr–1 = k × (0.68 mol L–1)n, r3 = 0.40 mol L–1 hr–1 = k × (1.36 mol L–1)n, r1 0.10 mol L−1 hr −1 k (0.34 mol L−1)n, =, =, r2 0.20 mol L−1 hr −1 k (0.68 molL−1)n,  1,  , 2, , n, , or, , 1, =, 2, , (ii), ∴, , Rate = k⋅[N2O5], 0.10 mol L–1 hr–1 = k × 0.34 mol L–1, , or, , k=, , \n=1, , 0.10 mol L−1 hr −1 or k = 2.9 × 10–1 hr–1, 0.34 mol L−1, , 37. For a first order reaction, 0.6932 0.6932, k=, =, = 0.0231min−1, t1/2, 30, Suppose the reaction is,    , A, t = 0    a    , t = 70 min (a – x)   , , Products, 0, x, , Fraction of the reactant remains unreacted =, , Now, k =, , (a − x ), a, , 2.303  a , 2.303  a , log ,  a − x  or 0.0231 = 70 log  a − x , t, ,  a  0.0231 × 70, =, log , = 0.7021,  a − x , 2.303, or, \, , a, = antilog 0.7021 = 5.036, a−x, a−x, 1, =, = 0.1985 ≈ 0.2, a, 5.036, , 38. (i) For a first order reaction,, 2.303 [A ]0, k=, log, [A ], t, When t = 30 s, 2.303  0.60  2.303, =, × 0.3010 = 0.0231 s–1, log ,  0.30 , 30, 30, When t = 60 s, k=, , 2.303  0.60  2.303, =, × 0.602 = 0.0231 s–1, log ,  0.15 , 60, 60, As the value of k is constant at different time intervals, the, reaction is first order w.r.t. ester when [H2O] is constant., Hence, it is pseudo first order reaction., C − C −(0.15 − 0.30), (ii) Average rate = − 2 1 =, t 2 − t1, 60 − 30, k=, , 0.15, = 5 × 10 −3 mol L−1s −1, 30, 39. The given reaction is, , A(g) →, B(g) +, C(g) +, =, , Initial pressure, Po, After 20 min. Po – x, , 0, x, , 0, x, , Total pressure = Po – x + x + x + x = Po + 2x, 40 2x Po, Po + 2x = Po + Po ×, =, ;, or Po = 5x, 100, 1 2.5, Po, ∴ x =, 5, Now,, [R]0 = Po, P, [R ] = Po − x = Po − o = 0.8 Po, 5, [R ], 2.303, log10 0, Using formula, k =, [R ], t, Po, 2.303, or, k =, log10, 20 min, 0.8 Po, or,, , k=, , 2.303, log 1.25, 20 min, , or, k =, , k = 1.115 × 10–2 min–1, , 2.303 × 0.0969, 20 min, , D(g), 0, x

Page 23 :
40. Suppose order with respect to A is m and with respect, to B is n. Then the rate law will be, Rate = k[A]m[B]n, Substituting the value of experiments 1 to 4, we get, Expt. 1 : Rate = 6.0 × 10, , –3, , m, , n, , = k (0.1) (0.1) ...(i), , Expt. 2 : Rate = 7.2 × 10–2 = k (0.3)m (0.2)n...(ii), Expt. 3 : Rate = 2.88 × 10, , –1, , m, , n, , = k (0.3) (0.4) ...(iii), , –2, , = k (0.4)m (0.1)n...(iv), Expt. 4 : Rate = 2.4 × 10, Comparing equation (i) and equation (iv),, \, , or,, \, , (Rate)1 6.0 × 10 −3 k (0.1)m (0.1)n, =, =, (Rate) 4 2.4 × 10 −2 k (0.4)m (0.1)n, 1 (0.1)m  1 , =, = , 4 (0.4)m  4 , m=1, , m, , Comparing equation (ii) and equation (iii), , (Rate)2 7.2 × 10 −2, k (0.3)m (0.2)n, =, =, (Rate)3 2.88 × 10 −1 k (0.3)m (0.4)n, or,, , 2, , (0.2)n  1 ,  1, = ,   =, 2, (0.4)n  2 , , n, , \ n=2, , Rate law expression is : Rate = k[A][B]2, The rate constant can be calculated from the given data of, any experiment using expression :, Rate, k=, [A ][B ]2, 6.0 × 10 −3, From expt. 1, k =, = 6.0, 0.1 × (0.1)2, \, , Rate constant k = 6.0 mol–2 L2 min–1, dx, Unit of k,, = k [A ]1[B ]2 = 6.0[0.5][0.2]2, dt, = 6 × 5 × 4 × 10–3 = 1.2 × 10–1 mol L–1 min–1, \, , 