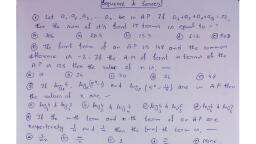Page 1 :
Chapter, HARMONIC PROGRESSION, DEFINITION, The numbers, whose reciprocals are in A.P., are said to be in Harmonic Progression (H.P.) e.g., 1 1 1, are in H.P., 258, as 2, 5, 8, ..are in A.P., nTH TERM OF H.P., If a be the first term and b be the second term of a H.P., then, nth term (Tn) =, 1, ab, 1, + (n- 1), a -b b+(n- 1) (a – b), a, ab, 1 1, +(n, a, a - b, 1), ab, as, a b, are in A.P., Where Common difference =, 1, 1, a - b, b., a, ab, Note : n numbers are in A.P., G.P. and H.P. if they all are equal ie., a = a2 = a3 =...= an., Then for A.P. Common difference d = 0, and for G.P. Common ratio r= 1., Ilustration 1, Find the ninth term of the series :, 2. 4, 1, 9., 17, 4****, Solution, 17, 9., 1 4, 17, 1, Here, 4, 4 1, 4, 4, 17, 9 4, 17, 4, 2 1, 4, 9 17 4, are in A.P., 4, 1**, 9th term of A.P. = a+ (n – 1)d =, + (9 – 1), 9 8, 10, 5, 18-8, 4, %3D, 4, 2, .. 9th te iP., 1, +....., =, 4, 17, 1

Page 2 :
44, SBPD Publications Harmonic Progression, Illustration 2, Find the 14th term of the series 1,.., 6., *...., 5, Solution, 5, 7, Let 14th term of H.P. be x then its corresponding A.P. is, 1,, 6', x', 5 1, d =1-, 6., Here, 6., 1, 14th term =, + (14 - 1) x [Formula : nth term a+ (n -1) d], 6., 5., 13, 18, = 3, 6., %3D, +, %3D, 1, : Required 14th term of H.P., x =, 3, Illustration 3, 7, 1, and, 26, Find the H. P. whose fifth and eighth terms are -, 8°, Solution, 1, 1, 1, Let, a' a +d a + 2d... are in H.P., 7, 5th term = -, 26, 1, 26, = a+ 4d =-, %3D, a + 4d, 1, and, 8th term = -, 1, 8., a + 7d, → a +7d = -8, On Subtracting,, 26, 3d =-8+, 56+ 26, -30, 7, 7, 7, 10, d=-, 7, 26, a + 4d = -, 7, Now,, 26, 4 x 10, = +, 7, 26 40-26· 14, = 2, a =- 4d -, %3D, 7, 7, :. Required H.P. is,, 1, 1, 1, 2, 10, 20, 2 -, 2 -, 1 7, 2' 4', i.e.,, Illustration 4, 3, 5, x, are in H.P. then find the value of x., If, Solution, 3, 2x, 82, 8, 3, 1, 3, 13 13, 8 2, 8

Page 3 :
Harmonic Progression, 45, Illustration 5, 11 1, 5' 9' 13', Write down the seventh term of, Solution, Reciprocal the given terms are 5, 9, 13, ., Its first term 5, Conimon difference 9-5, which are in H.P., = 4, n = 7, Tn = d+ (n - 1) d, T1 = 5+ (7 – 1) 4, T7 = 29 is in A.P., 1, is in H.P., 29, Thus,, Illustration 6, 8, +5+.., 13, Papeh, Find the nth term of the series 4 +4 +4-, Solution, · The given, 30, H.P. is 4 +, 7, 60, +5+...., 13, 1, 13, +., 30, 7, The corresponding A.P. is +, 1, +....., 4, 60, 7, d =, 30, Here, a =, 4', 4, 14 15, %3D, 60, 60, nth term, = a + (n -, !n, 1)d, (n, 60, 15-n+ 1, 60, 1, n-1, 16-n, %3D, %3D, 4, 60, 60, 1, 1, 60, Hence,, nth term of H.P. =, nth term of A.P., 16-n, 16-n, 60, Illustration 7, Find the 9th term of H.P. 6, 4, 3, Solution, The given H.P. is 6, 4, 3 ., 11 1, The corresponding A.P. is, ....., 6' 4' 3, Here, 6., 1, d =, 4, %3D, 12, n =9, 3

Page 4 :
SBPD Publications Harmonic Progression, 46, Tn = a+ (n- 1)d, 1, T9= 6, D+ (9, 12, 1+4 5, 6., is in H.P., 1, 2, is in A.P. or, %3D, %3D, 6 3, 6., SUM OF n TERMS OF H. P., There is no formula to find the sum of n terms of H.P., Illustration 8, 111 1, Find the sum of the harmonic progression 5 3 8' 11", Solution, 1, 1, 1, 1, +-+, 5, S4 =, 11, 2, 403, 220 + 88 + 55 +40, 5 x 8 x 11, %3D, 440, Illustration 9, 33, and first term is, 40, 1, 2, Find the progression., The sum of first three terms of a H. P. is, Solution, 1, First term of H.P. =, .. First term of corresponding A.P. = 2, A.P. be 2, 2+ d, 2+2d,..., Let, Then, 1, H.P. is, 1, 1, 2+ d' 2+ 2d"*, 1, 1, 33, (Given), Sum of First three terms =, 2+d, 2+ 2d 40, 1, 1, 33, 1, 2+d' 2+2d 40, 40, 4+3d, 13, (2 +d) (2 + 2d) 40, 40 (4 + 3d) = 13 (2 + d) (1 + d) x 2, 20 (4 + 3d) = 13(2 + 3d + d), 80 + 60d = 26+ 39d + 13d, 13d + 39d - 60d + 26 - 80=0, 13d - 21d- 54 = 0, 13d-39d + 18d-54 0, 13d(d- 3) + 18(d- 3) = 0, (d-3) (13d+ 18) = 0, 18, d= 3 or d=-, 13, 4, 1239

Page 5 :
Harmonic Progression, 47, Case 1. d = 3, 1, H.P. :, 1, 1, 2 2+3 2+6", 1 1 1, 2 5 8, i.e.,, ....., 18, Case 2. d =-, 13, 1, 1, H.P. :, 18, 36, 2., 13, 2 -, 13, 1 13, 2 8, 13, ie.,, 10', HARMONIC MEAN, If three numbers a, H, b are in harmonic progression then H is called the harmonic mean of a, and b., a, H, b are in H.P., 1 1, 1, are in A.P., ань, 1, 1, 1, 1, H, b, H, 1, a, 1, %3D, b., a, 2, a +b, ab, H, 2ab, H =, a +b, i.e., "Harmonic mean is the reciprocal of Arithmetic mean of reciprocals.", More than one (say n) harmonic means can be inserted between two numbers such that the, series becomes a H.P. of (n+2) term., Let a and b be two numbers and n number x1, x2..., Xn be inserted betwcen them such that,, a, X1, x2.., Xn, b are in H.P., 11 1, 1 1, are in A.P., a xi x2, Xn b, If d = Common difference, (n+2)th term =, 1, + (n + 1) d, a, a-b, (n + 1) d =, a, ab, (a-b), ab (n + 1), a -b, 2 (a - b), ab (n + 1)', 1, 1, 1, 1, %3D, ab (n + 1)' x2, a, a, 1, (а-b), 2 (a - b), ab (n + 1), ab (n + 1), a, 1 : : :