Page 1 :
IKAT Academy, 109,1stFloor,PratapComplex,NearMunirkaMetroGateNo3, , CLASS 11 - PHYSICS, Short Length Test: MOTION IN A PLANE, Time Allowed: 1 hour and 30 minutes, , Maximum Marks: 35, , General Instructions:, IKAT Academy, , This is a short length test based on the chapter- Motion In A Plane., There are total 50 questions., All questions are compulsory., Total time allotted is 90 minutes., Please give the test honestly and seriously., All the best!!, , Section A, 1., , If Ax , Ay, a), c), , 2., , and Az, , are x, y and z components of a vector then its magnitude is, , −, −−−−−−−−−−, −, 2, , 2, , 2, , √Ax + 2 Ay + Az, , −, −−−−−−−−−−, −, 2, , 2, , 2, , √3 Ax + Ay + Az, , b), d), , [1], , −, −−−−−−−−−, −, 2, , 2, , 2, , √Ax + Ay + Az, , −, −−−−−−−−−, −, 2, , 2, , 3, , √Ax + Ay + Az, , A cricketer hits a cricket ball from the ground so that it goes directly upwards. If the ball takes, [1], 10 s to return to the ground, determine its maximum height., , 3., , a) 112.5 m, , b) 132.5 m, , c) 152.5 m, , d) 122.5 m, , A batter hits a baseball so that it leaves the bat at speed v0 = 37.0 m/s at an angle a = 53.1o., , [1], , Find the time when the ball reaches the highest point of its flight, and its height h at this time?, , 4., , 5., , a) 3.02 s, 44.7 m, , b) 3.32 s, 41.7 m, , c) 3.12 s, 43.7 m, , d) 3.22 s, 42.7 m, , Which of the following physical quantities is a vector?, a) temperature, , b) impulse, , c) charge, , d) gravitational potential, , Vector addition is, a) asymmetric, , [1], , [1], b) commutative, , Contact No. 9555561066, 9142935757, , 1/7
Page 2 :
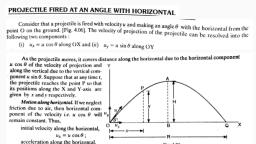
c) non-commutative, 6., , d) intransitive, , An arbitrary vector A⃗ in a plane can be expressed in terms of its x and y components by the, , [1], , equation, , 7., , a), , ⃗, ^, ^, A = Ax i − Ay j, , b), , ⃗, A = Ax + Ay, , c), , ⃗, ^, ^, A = Ax i + Ay j, , d), , ⃗, A = Ax − Ay, , The horizontal range of a projectile fired at an angle of 15° is 50 m. If it is fired with the same, , [1], , speed at an angle of 45°, its range will be, , 8., , 9., , a) 100 m, , b) 141 m, , c) 71 m, , d) 60 m, , A body is projected with a velocity of 20ms-1 at 50° to the horizontal. Find time of flight., a) 4.2 s, , b) 3.5 s, , c) 5.1 s, , d) 3.1 s, , The position of a particle is given by r ⃗ =, , 2^, ^, ^, 3.0t i + 2.0 t j + 4.0 k, , . Find the magnitude and, , [1], , [1], , direction of the velocity of the particle at t = 2.0 s., a) 8.84 m s−1 , 75∘ with x-axis, , b) 6.54 m s−1 , 74∘ with x-axis, , c) 7.54 m s−1 , 72 with x-axis, , d) 8.54 m s−1 , 70 with x-axis, , ∘, , 10., , ∘, , A man stands on the roof of a 15.0 m tall building and throws a rock with a velocity of, , [1], , magnitude 30.0 m/s at an angle of 33.0° above the horizontal. You can ignore air resistance., Calculate the magnitude of the velocity of the rock just before it strikes the ground., , 11., , a) 30.6 m/s, , b) 29.6 m/s, , c) 32.6 m/s, , d) 34.6 m/s, , Passengers on a carnival ride move at constant speed in a horizontal circle of radius 5.0 m,, , [1], , making a complete circle in 4.0 s. What is their acceleration?, , 12., , a) 14 m s−2, , b) 16 m s−2, , c) 12 m s−2, , d) 15 m s−2, −, −, , The speed of a projectile when it is at its greatest height is √ 25 times its speed at half the, , [1], , maximum height. What is the angle of projection?, , 13., , a), , 60, , ∘, , b), , 90, , c), , 15, , ∘, , d), , 45, , ∘, , ∘, , A swimmer wishes to cross a 500 m wide river flowing at 5 km/hr. His speed with respect to, , [1], , water is 3 km/hr. If he heads in the direction making an angle θ with the flow, find the time he, takes to cross the river?, a), c), 14., , 10, cosθ, 10, sinθ, , minutes, , b), , minutes, , d), , 10, sinθ, 10, cosθ, , seconds, seconds, , To find the sum of vectors A⃗ and B⃗ , we place vector B⃗ so that its, , Contact No. 9555561066, 9142935757, , [1], , 2/7
Page 3 :
a) tail is at the tail of the vector A⃗, , b) direction is the same as that of, vector A⃗, , c) tail is at the head of the vector A⃗, 15., , d) head is at the head of the vector A⃗, , In a two dimensional motion, instantaneous speed v0 is a positive constant. Then which of the, , [1], , following are necessarily true?, a) Displacements in equal time, , b) Average acceleration must always, , intervals are equal., c) The average velocity is not zero at, , vanish., d) Equal path lengths are traversed in, , any time., 16., , equal intervals., , A cyclist is riding with a speed of 27 km/h. As he approaches a circular turn on the road of, , [1], , radius 80 m, he applies brakes and reduces his speed at the constant rate of 0.50 m/s every, second. What is the magnitude and direction of the net acceleration of the cyclist on the, circular turn?, a) 0.84 m s−2 , 58.5o with the direction, , b) 0.82 m s−2 , 59.5o with the direction, , of velocity, , of velocity, , c) 0.85 m s−2 , 56.5∘ with the direction, , d) 0.86 m s−2 , 54.5o with the direction, , of velocity, 17., , of velocity, , A projectile is fired a velocity of 150 meters per second at an angle of 30 degrees with the, , [1], , horizontal. What is the magnitude of the vertical component of the velocity at the time the, projectile is fired?, , 18., , 19., , a) 225 m/s, , b) 75 m/s, , c) 150 m/s, , d) 130 m/s, , It is found that |A + B| = |A|.This necessarily implies,, a) B = 0, , b) A.B ≤ 0, , c) A, B are perpendicular, , d) A, B are antiparallel, , Multiplying a vector v ⃗ by a negative real number λ, a), , gives a vector, , →, ′, , v, , = λv ⃗ in a direction, , opposite to v ⃗, , b), , gives a vector, , [1], →, ′, , v, , = λv ⃗ in the same, , direction as v ⃗, , c) gives a scalar that is λ times the, magnitude of v ⃗, 20., , [1], , d) gives a scalar that is λ times the, polar angle of v ⃗, , An elevator is descending with uniform acceleration. A person in the elevator drops a marble, , [1], , at the moment the elevator starts to measure the acceleration of the elevator. The marble is 2, m above the floor when it is dropped. It takes 1.2 s to reach the floor of the elevator. What is, the acceleration of the floor? Take g = 10 ms-2., a) 8.18 ms−2, , b) 6.58 ms−2, , c) 7.2 ms−2, , d) 6.08 ms−2, , Contact No. 9555561066, 9142935757, , 3/7
Page 4 :
21., , 22., , Vectors are added by, , [1], , a) adding the magnitudes of the vectors, , b) adding the angles of the vectors, , c) parallelogram law of addition, , d) translating the two vectors, , An airplane’s compass indicates that it is headed due north, and its airspeed indicator shows, , [1], , that it is moving through the air at 240 km/h. If there is a 100-km/h wind from west to east. In, what direction should the pilot head to travel due north? What will be her velocity relative to, the earth?, , 23., , a) 35o W of N, 198 km/h, , b) 28o W of N, 260 km/h, , c) 23o W of N, 260 km/h, , d) 29o W of N, 200 km/h, , A man can swim with a speed of 4.0 km/h in still water. How long does he take to cross a river, , [1], , 1.0 km wide if the river flows steadily at 3.0 km/h and he makes his strokes normal to the river, current? How far down the river does he go when he reaches the other bank?, , 24., , 25., , a) 13 min, 700 m, , b) 16 min, 650 m, , c) 15 min, 750 m, , d) 19 min, 500 m, , As a ball rises, the vertical component of its velocity, a) Can't be determined, , b) Remains constant, , c) Increase, , d) Decrease, , Null vector or a zero vector has a magnitude, , [1], , [1], , a) greater than zero, , b) of complex nature, , c) equal to zero, , d) less than zero, Section B, , 26., , Assertion (A): Two similar trains are moving along the equatorial line with the same speed, , [1], , but in opposite direction. They will exert equal pressure on the rails., Reason (R): In uniform circular motion, the magnitude of acceleration remains constant but, the direction continuously changes., a) Both A and R are true and R is the, correct explanation of A., c) A is true but R is false., 27., , b) Both A and R are true but R is not the, correct explanation of A., d) A is false but R is true., , Assertion (A): When range of a projectile is maximum, its angle of projection may be 45o or, , [1], , 135o., Reason (R): Whether θ is 45o or 135o, value of range remains the same, only the sign changes., a) Both A and R are true and R is the, correct explanation of A., c) A is true but R is false., 28., , b) Both A and R are true but R is not the, correct explanation of A., d) A is false but R is true., , Assertion (A): In projectile motion, the angle between the instantaneous velocity and, , [1], , acceleration at maximum height is 180o., Reason (R): At the maximum height, velocity of projectile is in horizontal direction only., , Contact No. 9555561066, 9142935757, , 4/7
Page 5 :
a) Both A and R are true and R is the, correct explanation of A., c) A is true but R is false., 29., , b) Both A and R are true but R is not the, correct explanation of A., d) A is false but R is true., , Assertion (A): If a physical quantity is a vector, it must have direction., , [1], , Reason (R): Current has a direction therefore it is a vector quantity., a) Both A and R are true and R is the, correct explanation of A., c) A is true but R is false., 30., , b) Both A and R are true but R is not the, correct explanation of A., d) A is false but R is true., , Assertion (A): Two equal vectors have their resultant equal to three fourth of either of them., , [1], , The angle between them is 136o., Reason (R): The minimum number of numerically equal vectors whose sum can be zero is, three., a) Both A and R are true and R is the, correct explanation of A., c) A is true but R is false., , b) Both A and R are true but R is not the, correct explanation of A., d) A is false but R is true., Section C, , Question No. 31 to 35 are based on the given text. Read the text carefully and answer the, questions:, While treating the topic of projectile motion, it is assumed that the air resistance has no effect on, the motion of the projectile., Friction, force due to viscosity, air resistance are all dissipative forces. In the presence of any of, such force opposing motion, any object will lose some part of its initial energy and consequently,, momentum too. Thus, a projectile that traverses a parabolic path will certainly show deviation, from its idealised trajectory in the presence of air resistance. It will not hit the ground with the, same speed with which was projected from it., In the absence of air resistance, the x-component of the velocity remains constant and it is only the, y-component that undergoes a continuous change. However, in the presence of air resistance, both, , [5], , of these will get affected. That means that the range will be less than the value calculated from, equation, R=, , 2, , u, , sin 2θ0, g, , Maximum height attained will also be less than the value predicted by the equation, Hmax =, , (u sin θ0 ), , 2, , 2g, , In order to avoid air resistance, we will have to perform the experiment in vacuum or under low, pressure., 31., , In presence of air resistance, a projectile, a) Both Loses its energy and, , b) Loses its energy, , momentum, c) Loses its momentum, , d) Loses its acceleration, , Contact No. 9555561066, 9142935757, , 5/7
Page 6 :
32., , In the absence of air resistance,, i. the x-component of the velocity remains constant and it is only the y-component that undergoes, a continuous change, ii. the y-component of the velocity remains constant and it is only the x-component that undergoes, a continuous change, iii. the x-component and y-component of the velocity both remain constant, iv. the x-component and y-component of the velocity both vary continuously, , 33., , a) Option (iv), , b) Option (i), , c) Option (ii), , d) Option (iii), , In presence of air resistance,, i. Range and maximum height both will remain same as calculated from the standard equations., ii. Range and maximum height both will be less than the values calculated from the standard, equations., iii. Range and maximum height both will be more than the values calculated from the standard, equations., iv. Range will be more but maximum height will be less than the values calculated from the, standard equations., , 34., , a) Option (iv), , b) Option (ii), , c) Option (i), , d) Option (iii), , Following chart shows the acceleration due to gravity of different planets., Planet, , Acceleration due to gravity, g, , Mercury, , 3.59, , Venus, , 8.87, , Earth, , 9.81, , Mars, , 3.77, , Jupiter, , 25.95, , Saturn, , 11.08, , Which one of the following statement is correct?, i. Range and maximum height of a projectile with same initial velocity and angle of projection, will be same in each planet., ii. Range and maximum height of a projectile with same initial velocity and angle of projection, will be maximum at Jupiter., iii. Range and maximum height of a projectile with same initial velocity and angle of projection, will be minimum at Mercury., iv. Range and maximum height of a projectile with same initial velocity and angle of projection, will be minimum at Jupiter., a) Option (iii), , b) Option (ii), , Contact No. 9555561066, 9142935757, , 6/7
Page 7 :
c) Option (i), 35., , d) Option (iv), , Which of the following diagram correctly depicts the path of a projectile in presence and absence, of air resistance?, a), , b), , c), , d), , Contact No. 9555561066, 9142935757, , 7/7