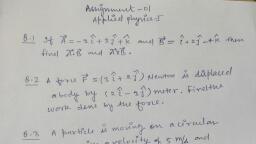Question 1 :
In uniform circular motion, the velocity vector and acceleration vector are:
Question 2 :
(1):In uniform circular motion, tangential acceleration is zero.<div>(2) : In uniform circular motion, velocity is constant.<br/></div>
Question 3 :
State whether True or False :<br/>A cyclist while going around a curve on a horizontal track has to bend himself a little from his vertical position in order to avoid overturning.
Question 4 :
When a bus turns a corner sharply, the passengers tend to fall
Question 5 :
A merry go round has a radius of $4\ m$ and completes a revolution in $2\ s$. Then acceleration of a point on its rim will be:<br/>
Question 6 :
An aeroplane is moving in a circular path with a speed of $200m/s$. If the mass of the plane is $1500kg$, and the force acting on it is equal to $120kN$, then find the radius of the circle of motion.
Question 8 :
(1) : When a rigid body is rotating about its own axis, all particles of that body have the same angular velocity.<br/> (2) : All particles of the body have the same time period.<br/>
Question 9 :
The angular displacement of a particle is given by $\theta =t^{3}+t^{2}+t+1$ then, its angular velocity at $t = 2$ sec is _____ $rads^{-1}$ :<br/>
Question 12 :
A particle is in circular motion in a horizontal plane. It has angular velocity of $ 10 \pi \ rad/s $ at the end of 2 s and angular velocity $ 15 \pi\ rad/s $ at the end of 4 s. The angular acceleration of particle is
Question 13 :
A body of mass $40kg$ is moving in a circle of radius $20m$ with a speed of $2m/s$. Find the centripetal force acting on the body.
Question 14 :
An athlete completes one round of a circular track of radius $R$ in $40$ seconds. What will be his displacement at the end of $2$ minute $20$ seconds?
Question 15 :
Which one of the following is most probably not a case of uniform circular motion?
Question 16 :
If a body of mass $2kg$ requires a centripetal force of $10N$ to keep it moving in a circle of radius $5m$, then find the speed at which the body is moving.
Question 17 :
(1) : If a body moving in a circular path has a constant speed, then there is no force acting on it.<br/> (2) : The direction of the velocity vector of a body moving in a circular path is changing.<br/>
Question 18 :
If the speed of body moving in circle is doubled and the radius is halved, its centripetal acceleration becomes<p></p>
Question 19 :
A ball tied to a string is swung in a vertical circle. Which of the following remains constant?
Question 20 :
Two particles $p$ and $q$ are located at distances $r_{p}$ and $r_{q}$ respectively from the centre of a rotating disc such that $r_{p}$ >$r_{q}$. Then:<br/>
Question 21 :
In a uniform circular motion, the direction of radial acceleration is always
Question 22 :
A $0.5 kg$ ball moves in a circle of radius $0.4 m$ at a velocity of $4 { m }/{ s }$. The centripetal force on the ball is:
Question 23 :
Starting from rest the fly wheel of a motor attains an angular velocity of $60 rad/s$ in $5\ s$, the angular acceleration of the fly wheel is:<br/>
Question 24 :
A point size body is moving along a circle at an angular velocity of $2.8\ rads^{-1}$. If the centripetal acceleration of the body is $7\ ms^{-2 }$, then its speed is:<br/>
Question 26 :
When a particle is in uniform circular motion it does not have:
Question 27 :
A satellite is orbiting round the earth. If both gravitational force and centripetal force on the satellite is $'F'$ then net force acting on the satellite to revolve round the earth is<br/>
Question 28 :
A small bucket containing water is rotated in a vertical circle of radius $R$ by means of a rope. $v$ is velocity of bucket at highest point. Then water does not fall down if:<br/>
Question 29 :
A stationary wheel starts rotating about its own axis at uniform angular acceleration $ 8\ rad / s^{2}$ . The time taken by it to complete $77$ rotations is:<br/>
Question 30 :
A fly-over bridge is a part of a vertical circle of radius $80\ m$ and a vehicle is travelling on it. The vehicle does not leave the surface of bridge at its highest point, if maximum speed of vehicle is:<br/>
Question 32 :
At turns, slopes are made on the road in order to
Question 33 :
If a particle tied to the end of a string is set in a circular motion, then the tension of the string is:<br/>
Question 34 :
(1) : In uniform circular motion the kinetic energy of the body is constant.<br/> (2) : In uniform circular motion the tangential force is zero.<br/>
Question 35 :
In order to cause something to move in a circular path, we must apply
Question 36 :
A simple pendulum with bob of mass $m$ and length $x$ is held in position at an angle $1$ and then angle $2$ with the vertical. When released from these positions, speeds with which it passes the lowest positions are ${v}_{1}$ and ${v}_{2}$ respectively. Then, $\cfrac { { v }_{ 1 } }{ { v }_{ 2 } } $ is
Question 37 :
Let $a_r$ and $a_t$ represents radial and tangential acceleration. The motion of a particle may be circular if
Question 38 :
A body of mass, $m$, is rotated in a vertical circle of radius, $R$, by means of a light string. If the velocity of body is $\sqrt{5gR}$ at the lowest point of vertical circle, then tension in the string is:<br/>
Question 39 :
When a cyclist bends in order to take a turn, which of the following provide the extra centripetal force required?
Question 40 :
A particle is moving around a circular path with uniform angular speed $(\omega)$. The radius of the circular path is $(r)$. The acceleration of the particle is
Question 41 :
A particle of mass $m$ is observed from an inertial frame of reference and is found to move in a circle of radius $r$ with a uniform speed $v$. The centrifugal force on it is
Question 42 :
The angle through which a cyclist has to bend himself to take a safe turn is given by :
Question 43 :
What is the centripetal acceleration of the ball if the instantaneous velocity of the ball is doubled?
Question 45 :
In order to keep a body moving in a circle, there exists a force on it that is directed toward center of circle. This force is known as
Question 46 :
A particle is moving at a uniform speed of $2\ {ms}^{-1}$ in a circle of radius $0.5$ m. The centripetal acceleration of the particle is:<br/>
Question 47 :
Uniform circular motion is called continuously accelerated motion mainly because its :
Question 48 :
A ball experiences a centripetal acceleration of constant magnitude $9 m/s^2$ when it moving in circular path of radius $0.25$ m. Calculate the angular speed of ball if mass is $0.5$ kg.<br/>
Question 49 :
A small stone tied to an inextensible string of negligible mass is rotated in a circle of radius $2 m$ in a vertical plane. Find the speed at a horizontal point on the circle. (in $m/s$)
Question 50 :
The order of magnitude of revolution period of the earth around the sun is
Question 51 :
A road bridge is in the form of a circular arc of radius $18 m$. What is the limiting speed with which a car can traverse the bridge without losing contact at the highest point if the centre of gravity of the car is $0.4 m$ above the ground? (in $m/s$)<br/>
Question 52 :
The magnitude of the acceleration revolving in a circular path of a given radius is directly proportional to____.
Question 53 :
A satellite is orbiting round the earth. The centripetal force acting on the satellite is $F$. The force of the satellite on the earth is also $ F $. The net force on the satellite is :
Question 54 :
A car is moving on a straight road at a speed of 50 km/h and a truck is ahead of the car and having a large plane mirror fixed vertically on the back of truck. Truck is running at a speed of 70 km/h. For a stationary observer standing between car and truck. What is the speed of image of car in the mirror?
Question 55 :
A particle of mass, $m$, is tied to a light string and rotated with a speed, $v$, along a circular path of radius, $r$. If $T=$ tension in the string and $mg =$ gravitational force on the particle, then the actual forces acting on the particle are<br/>
Question 56 :
Two satellites $P$ and $Q$ are in the same circular orbit round the earth. The mass of $P$ is greater than that of $Q$. It follows that
Question 57 :
Velocity of a particle at any instant is given by the equation $\vec {v} = (2 t \hat {i} + 3 t^2 \hat {j})\ m/s$, and radius of the curvature of the path is $2\ m$. Centripetal acceleration of the particle at $t = 2\ s$ is:
Question 58 :
A 500 Kg car takes turn of radius 50mwith a velocity of 36 Kmph. The centripetal force required is
Question 59 :
If the radii of circular paths of two particles of same masses are in the ratio of 1 : 2, then in order to have same centripetal force, their speeds should be in the ratio of
Question 60 :
A wheel is subjected to uniform angular acceleration about its axis. Initially its angular velocity is zero. In the first two seconds it rotates through angle $\theta_1$. In the next two seconds it rotates through angle $\theta_2$. What is the ratio $\theta_2 / \theta_1$?<br>
Question 61 :
Instantaneous power of constant force acting on a particle moving in a straight line under the action of this force
Question 62 :
What happens to centripital force of a revolving body if you double the orbital speed v and halve the angular velocity $ \omega $ :-
Question 63 :
A bag containing tea and some air bubbles, sealed at both the ends are taken to a space station and rotated rapidly in the gravity free environment, What will happen to the air bubbles
Question 64 :
A weightless thread can bear tension up to $30N$. A stone of mass $500\ g$ is tied to it and revolved in a circular path of radius $2m$ in a vertical plane. If $g=10{ms}^{-2}$, then the maximum angular velocity of the stone will be:
Question 65 :
A wheel has angular acceleration of $3.0\ rad/s^2$ and an intial angular speed of $2.00\ rad/s$. In a time of $2s$ it has rotated through an angle (in radians) of:
Question 66 :
A small mass lying at the top of a smooth convex hemisphere is just pushed horizontally. The angle with the vertical where it looses contact with surface is:<br/>
Question 67 :
A stone of mass $1kg$ is tied to the end of a string of $1m$ length. It is whirled in a vertical circle. If the velocity of the stone at the top be $4m/s$. What is the tension in the string (at that instant)?
Question 69 :
A body of mass m is moving in a circle of radius r with uniform speed V. The force on the body is $mV^{2}/r$ and is directed towards the centre, what is the work done by this force in moving the body over half the circumference of the circle?
Question 70 :
A body moving with a constant speed describes a circular path whose radius vector is given by $\overrightarrow {r}= 15 (cos pt\hat{i}+ sin pt \hat{j})m$, where is in rad/ s, and t is second. What is its centripetal acceleration at t=3 s?
Question 71 :
A simple pendulum is oscillating with an angular amplitude $90^{0}$. If the direction of resultant acceleration of the bob is horizontal at a point where angle made by the string with vertical is:<br>
Question 72 :
Certain neutron stars are believed to be rotating at about $1$rev/s. If such a star has a radius of $20$km, the acceleration of an object on the equator of the star will be.
Question 73 :
A body of mass $0.1\ kg$ when rotated in a circular path of diameter $1.0\ m$ on a frictionless horizontal plane by means of string, makes $10$ revolutions in $31.4$ seconds. The centripetal force acting on the body will be
Question 74 :
A point size mass $100\ g$ is rotated in a vertical circle using a cord of length $20\ cm$. When the string makes an angle $60^o$ with the vertical, the speed of the mass is $1.5\ m/s$. The tangential accelaration of the mass in that position is:<br/>
Question 75 :
The real force 'F' acting on a particle of mass 'm' performing circular motion acts along the radius of circle 'r' and is directed towards the centre of circle. The square root of magnitude of such force is? (T$=$ periodic time)
Question 76 :
If a cycle moves in a circle of radius $10m$, moving with a speed of $5m/s$ and making an angle of $76^o$ with the horizontal. Find $g$ at that place.
Question 77 :
The angular velocity of a wheel increases from $100\ m/s$ to $300\ m/s$ in $10\ s$. The revolutions made during that time is:
Question 78 :
A simple pendulum of length $50 cm$ is suspended from a fixed point $O$ and a nail is fixed at a point $P$ which is vertically below $O$ at some distance. The bob is released when string is horizontal. The bob reaches lowest position then it describes vertical circle whose centre coincides with point $P$. The minimum distance between $O$ and $P$ is:<br/>
Question 79 :
A wheel rotates with a constant acceleration of $ 2 \ \ rads^{-2}$. If the wheel starts from rest, how many revolution will it make in the first $10$ seconds?
Question 80 :
Dynamics of circular motion ,A particle is moving in a circle :<br>
Question 81 :
A van is moving with a speed of 72 km h$^{-1}$ on a level road, where the coefficient of friction between its tyres and road is 0.5. The minimum radius of curvature, the road mush for safe driving of van is (g = 10 m s$^{-2}$). <br>
Question 82 :
A nail is fixed at a point $P$ vertically below the point of suspension '$O$' of a simple pendulum of length $1m$. The bob is released when the string of pendulum makes an angle $30^{0}$ with horizontal. The bob reaches lowest point then describes vertical circle whose centre coincides with $P$. The least distance of $P$ from $O$ is:<br/>
Question 83 :
A fighter plane is pulling out for drive at $900\ km/h$ in a vertical circle of radius $2\ km$. Its mass is $5000\ kg$. Find the force exerted by the air on it at the lowest point.<br/>
Question 84 :
Assertion: In circular motion, work done by centripetal force is zero.
Reason: In circular motion centripetal force is perpendicular to the displacement.
Question 85 :
A stone of mass $1\ kg$ is tied of the end of a string $1\ m$ long. It is whirled in a vertical circle. If the velocity of stone at the top is $4\ m/s$. What is the tension in the string at the lowest point? <div>Take $g = 10\ m/s^{2}$<br/></div>
Question 86 :
A body of mass m is rotated in a vertical circle with help of light string such that velocity of body at a point is equal to critical velocity at that point. If $T_{1},T_{2}$ be the tensions in the string when the body is crossing the highest and the lowest points of vertical circle respectively, then which of the following relation is correct?<br/>
Question 87 :
The maximum time period of a bucket full of water whirled in a vertical circle of radius $2.5\ m$ so that water does not fall is $(g=10\ ms^{-2})$:<br>
Question 88 :
A person who is standing on the Equator flew away by the effect of the centrifugal force? The Earth equatorial radius is 6378 km, its angular velocity is $7.29 \times 10^{-5} rad/s$. Assume that the person weighs 80 kg.
Question 89 :
A disc is rotating in a room. A boy standing near the rim of the disc of radius $R$ finds the water droplet falling from the ceiling is always falling on his head. As one drop hits his head, other one starts from the ceiling. If height of the roof above his head is $H$, then angular velocity of the disc is
Question 90 :
A sphere is suspended by a thread of length, $L$. What minimum horizontal velocity has to be imparted to the ball for it to reach the height of suspension?<br/>
Question 91 :
A body is tied at the end of a string of length L and revolved in a vertical circle. The string is just taut when the body is at the highest position. Velocity of the body when the string is horizontal is<br/>
Question 92 :
If the speed of a particle in circular motion is doubled and its radius is halved, then the centripetal force will
Question 93 :
When a ceiling fan is switched off, its angular velocity reduces to half its initial value after it completes $36$ rotations. The number of rotations it will make further before coming to rest is Assuming angular retardation to be uniform
Question 94 :
A body is revolving with a constant speed along a circular path. Which of the following statements are true regarding that body?<br/>
Question 95 :
A particle of mass , is moving with velocity v in horizontal circle under a centripetal force $-\frac{k}{r^{2}}$. What is the energy of the particle if r is radius?
Question 96 :
A car is moving on a circular path and takes a turn. if ${ R }_{ 1 }$ and ${ R }_{ 2 }$, be the reactions on the inner and outer wheels respectively, then
Question 97 :
A car goes around uniform circular track of radius $R$ at a uniform speed $v$ once in every $T$ seconds. The magnitude of the centripetal acceleration is $a_C$. If the car now goes uniformly around a larger circular track of radius $2R$ and experiences a centripetal acceleration of magnitude $8a_c$, then its time period is
Question 98 :
A pendulum bob is raised to a height, $h$, and released from rest. At what height will it attain half of its maximum speed?
Question 99 :
The formula that torque equals the rate of change of angular momentum is true in following general cases:<b></b>
Question 100 :
When a ceilling fan is switched off its angular velocity reduces to $50\%$ while it makes $36$ rotations. How many more rotation will it make before coming to rest (Assume uniform angular retardation):
Question 101 :
A particle of mass m is moving in a circular path of constant radius r such that its centripetal acceleration $a_c$ is varying with time t as $a_c=k^2rt^2$ where k is a constant. The power delivered to the particle by the forces acting on it, is?
Question 102 :
A particle is kept at rest at the top of a sphere of diameter $42m$. When disturbed slightly, it slides down. At what height $h$ from the bottom, the particle will leave the sphere.
Question 103 :
A body is revolving with a constant speed along a circle. If its direction of motion is reversed but the speed remains the same then?<br>(a) the centripetal force will not suffer any change in magnitude<br>(b) the centripetal force will have its direction reversed<br>(c) the centripetal force will not suffer any change in direction<br>(d) the centripetal force is doubled.<br>
Question 104 :
Assertion: A solid sphere is rolling on a rough horizontal surface. Acceleration of contact point is zero.
Reason: A solid sphere can roll on the smooth surface.
Question 105 :
if a certain car,going with speed $v_1$,rounds a level curve with a radius $R_1$ it is just on the verge of skidding.if its speed is now doubled, the radius of the tightest curve on the same road tht it can round without skidding is:
Question 106 :
An airplane flying at $100\ m/sec $ dives in a vertical plane along the circle of radius $200\ m.$ The mass of the pilot is $75\ kg $ What will be the force exerted by the pilot on his seat when the airplane is at the maximum height?
Question 107 :
On horizontal smooth surface a mass of $2 kg$ is whirled in a horizontal circle by means of a string at an initial angular speed of $5\ rpm$. Keeping the radius constant the tension in the string is doubled. The new angular speed is near by
Question 108 :
A body is moving along a circle of radius $r$ under the influence of centripetal force $F$. Its total energy is<br/>
Question 109 :
A particle moves along a circle of radius $(20/\pi)m$ with constant tangential acceleration. If the velocity of the particle is $80m/s$ at the end of the second revolution after motion has began, the tangential acceleration is
Question 110 :
A car of mass $1000 kg $ is moving with a speed of $40 ms^{-1} $ on a circular path of radius $400 m. $ If its speed is increasing at the rate of $3ms^{-1} $ the total force acting on the car is :
Question 111 :
A mass $m$ is revolving in a vertical circle at the end of a string of length $20\ cm$. By how much times does the tension of the string at the lowest point exceed the tension at the topmost point-
Question 112 :
A body attached to a string of length describes a vertical circle such that it is just able to cross the highest point. Find the minimum velocity at the bottom of the circle.
Question 113 :
The diameter of a flywheel is $1.2 m$ and it makes 900 revolutions per minute. Calculate the acceleration at a point on its rim.
Question 114 :
A car moves along a horizontal circular road of radius r with constant speed v. The coefficient of friction between the wheels and the road is $ \mu $. which of the following statements is not true ?
Question 115 :
A thin circular wire of radius R rotates about its vertical diameter with an angular frequency $\displaystyle \omega .$ Show that a small bead on the wire remains at its lowermost point $\displaystyle \omega \leq \sqrt{g\:l\:R}.$ What is angle made by the radius vector joining the centre to the bead with the vertical downward direction for $\displaystyle \omega = \sqrt{2g\:l\:R}?$ Neglect friction.
Question 116 :
A body of mass $500g$ is revolving in a horizontal circle of radius $0.49m$. The centripetal force acting on it (if its period is $11sec$) will be
Question 117 :
A tube of length $l$ is filled completely with an incompressible liquid of mass $m$ and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity $\omega$. The force exerted by the liquid at the other end is:<br/>
Question 118 :
A uniform disc of mass $M$ and radius $R$ is mounted on an axle supported in frictionless bearings. A light cord is wrapped around the rim of the disc and a steady downward pull $T$ is exerted on the cord. The tangential acceleration of a point on the rim is
Question 120 :
A disc has 'M' and radius 'R'. How much tangential force should be applied to the rim of the disc so as to rotate with angular velocity '\omega' in time 't'?
Question 122 :
A particle moves in a circle of the radius $25cm$ at two revolutions per second. The acceleration of the particle in $m/{sec}^{2}$ is
Question 123 :
On being churned the butter separates out of milk due to __________.
Question 124 :
A wheel is making Revolution about axis with uniform angular acceleration, Starting from rest, it reaches $100\ rev/sec$ in $4\ seconds$. Find the angular rotated during these four seconds.
Question 125 :
A particle of mass $m$ is observed from an inertial frame of reference and is a circle of radius $r$ with a uniform speed $v$. The centrifugal force on it is:
Question 126 :
A mass attached to once end of a string crosses top-most point on a vertical circle with critical speed. Its centripetal acceleration when string becomes horizontal will be (g = gravitational acceleration)
Question 127 :
A particle moves in a circle of radius $2.0 cm$ at a speed given by $v = 4 t$, where $v$ is in cm/s and $t$ is in seconds. Find total acceleration at $t = 1s$.
Question 128 :
A particle moves along a circle of radius $\left (\displaystyle \frac{20}{\pi} \right )m$ with tangential acceleration of constant magnitude. If the speed of the particle is $80 m/s$ at the end of the Second revolution after motion has begun, the tangential acceleration is<br>
Question 129 :
A $62 kg $ woman is a passenger in a "rotor ride" at an amusement park. A d$5.0 m$ is spun with an angular velocity of $25 rpm $ . The woman is pressed against the wall of the rotating drum. While the drum rotates, the floor is lowered. A vertical static friction force supports the woman's weight. What must the coefficient of friction be to support her weight?
Question 130 :
A particle slides on surface of a fixed smooth sphere starting from topmost point. The angle rotated by the radius through the particle, when it leaves contact with the sphere, is
Question 131 :
Find the acceleration $w^\prime $of the particle relative to the disc.
Question 132 :
Two identical trains A and B move with equal speeds on parallel tracks along the equator. A moves from east to west and B, from west to east. Which train will exert greater force on the tracks?
Question 133 :
A satellite is in a circular orbit round the earth at an altitude $R$ above the earth's surface, where $R$ is the radius of the earth. If $g$ is the acceleration due to gravity of the earth the speed of the satellite is
Question 134 :
The centripetal force required for a $1000 kg$ car traveling at $36 kmph $ to take a turn by $90^o $ in traveling along an arc of length $628 m $ is
Question 135 :
A disc rotates about its axis with a constant angular acceleration of $4$ rad$/s^2$. Find the radius tangential accelerations of a particle at a distance of $1$ cm from the axis at the end of the second after the disc starts rotating.
Question 136 :
When a particle moves along a straight path, then the particle has
Question 137 :
A particle moving along a circular path with the uniform angular velocity $\omega$ is under the action of a force $F$ directed towards the center of the circular path. If the radius of the circular path is doubled without changing the linear velocity, the centripetal force acting on the body would be<br/>
Question 138 :
A particle starts rotating from rest. Its angular dispalcement is expressed by the following equation $\theta = 0.025t^2 - 0.1t$ where $\theta$ is in radian and $t$ is seconds. The angular acceleration of the particle is
Question 139 :
A merry-go-round, made of a ring-like platform of radius R and mass M. is revolving with angular speed $\omega$? A person of mass M is standing on it. At one instant., the person jumps off the<br>round, radially away from the center of the round (as seen from the round). The speed of the round afterwards is:
Question 140 :
A wheel has moment of inertia $10^{-2} kg-m^2$ and is making 10 rps. The torque required to stop it in 5 secs is
Question 141 :
A motor car is traveling at $30 m/s$ on a circular road of radius $500 m$. It is increasing its speed at the rate of $2 \ m/s^2$. What is its acceleration?
Question 142 :
If the equation for the displacement of a particle moving on a circular path is given by $(\theta)=2t^3+0.5$, where $\theta$ is in radians and $t$ in seconds, then the angular velocity of the particle after $2s$ from its start is
Question 143 :
When a force $F_1$ acts on a particle, frequency $6$Hz and when a force $F_2$ acts, frequency is 8 Hz. What is the frequency when both the force act simultaneously in same direction?
Question 144 :
A ball tied to the end of the string swings in a vertical circle under the influence of gravity.
Question 145 :
A weightless thread can bear tension upto $37 N$. A stone of mass $500 g$ is tied to it and revolved in a circular path of radius $4 m$ in a vertical plane. If $g=10 {ms}^{-2}$, then the maximum angular velocity of the stone will be:
Question 146 :
A particle moves along a circle of radius $\left(\dfrac{20}{\pi}\right)$m with constant tangential acceleration. If the speed of the particle is $80$m/s at the end of the second revolution after motion has begun, the tangential acceleration is?
Question 147 :
A particle is moving in a circle of radius $R$ in such a way that at any instant the normal and tangential component of its acceleration are equal. If its speed at $t=0$ is $\displaystyle v_{0}.$ The time taken to complete the first revolution is
Question 148 :
An aeroplane flying at constant speed $105\ m/s$ towards East, makes a gradual turn following a circular path to fly South. The turn takes $15$ seconds to complete. The magnitude of the centripetal acceleration during the turn is<br/>
Question 149 :
A rod of length $l$ and mass $m$ fixed at one end, it hanging vertically. The other end is now raised so that the rod makes an angle ${30}^{o}$ with horizontal line. The work done in this process will be:
Question 150 :
A car moves horizontally with a constant acceleration of $3 m/s^2 . $ A ball is suspended by a string from the ceiling of the car. The ball does not swing, being at rest with respect to the car. What angle does the string make with the vertical?