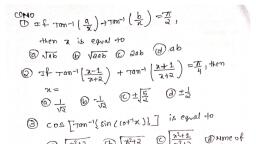Page 1 :
Date:-06-02-2022, , , , , , , , (3 Elevate Institute Chandrapur, , , , , , , , , , , , , , , , , , MHT-CET Time : 1.30 Hrs., TEST-1 Marks: 100, MATHEMATICS, 3 9 ;, 1. Ifsin @= 7 and tan 0= — , then cos @ is 10. If sin (a ~ fl) = Sand cos (a+ p)= 1, where, 1 8 27 15 ; ,, (eo — op ££ @q.= a.and § are positive acute angles, then, “) 6 ®) 27 © 8 © 4 (A) a=45°,B=15° (B) a=15°, p= 452, C) a=6°,B=15 =15°, B= 60°, 2 If sin® =3, then <O*U0E i equal to © « p ©).'0 B, ae : UL Iftan = 2, then cos 8 is equal to, (A) a ®) 4 €) 2. @® 2 20 1, (A) +— jw) +—, 3. sin® + cosh 1 Pe, “ J=cot@ 1-tan0— © += @) +=, fA) 0 (B) 1 29 21, ; = si ind ~, (C) cosé ae (D) cos 6+ sin i mee on anit @ lies: in ‘the, 4. Ifsin @=——L and tan 0 = 1, then @ lies in 10, Nz quadrant, then sec @=, (A) _ first quadrant (B) second quadrant (A) is _(B) -1, (C) third quadrant = (D) _ fourth quadrant vin Vin, 5. Itsin@=~ + and.cos @= ~ then ies in © ia (0) “iq, (A) 1* quadrant (B) 0” quadrant 1 5, (C) Hi quadrant = (D) TV" quadrant 13. If tan 0 = and 0 lies in the I* quadrant,, 6. When x= © then tan 2 is nee i, (A) 1 (B) 0 (A) TE (B) “FE, 1, ©) {D) not defined v5 V5, Cc = D) B © % ©) -%, 4, sin? = + cos? © — tan? = = uN, - ‘ 4 14. If sin @ = 5 and 0 Mes in the ‘second, A > ®.-7 © 8 ©) 1 quadrant, then the value of seo 0 + tan 0 is, 2 5 2 5, = * 60° cosec 30° A= @ = © -= =, 8. Ifxsind5 008 60 ae then x= A; OB 7, O-3;O +, (A) 2 (@) 4 © 8 @® 16 15. Which of the following is true?, 9, If sin @= V3 cos 0, then 0 is equal to CA) tae 6 ~sinl Gm ton! Ose’, , (A) 45° (@B) 30°, (Cc) 75° (D) 60°, , , , , , , , (B) sec’ 0 cosec? 0 = sec? 6 —coscc’ O, (C) cosec? @+ cot” @= cosec* 6 cot’ @, (D) none of these

Page 2 :
16,, , 17., , 18., , 19., , cot x+ tanx =, , (A) cot 2x (8) 2cofx, (C) sec x cosec x (D) cot® 2x, Tis veoniet sin’ 20°+cos* 20°, , sin* 20°+cos* 20°, wo ® + OL M2, Ifx=acos’ 4, y= b sin’ 8, then, , wo (ff » Gh, , oF o Fes, , Which one of the following is incorrect?, , (A) sino=~ 2 (8) césO=1, (c) sec 0= 5 (D) tan6=20, Which of the following is possible?, , 2 a8, (A) cos 6 ; @) an O=.5, (C) sc0=+ ) tmo=45, , The value of cos* 6 + sec’ @ is always, (A) _ less than I, , (B) equal to 1, , (C) greater than 1, but less than 2, (D) greater than or equal to 2, , Ifcos A= Buen tan 34 =, (A) 0 (B) ;, cc) 1 (D) not defined, , ies A= 2, cos B= Sand Fea<o,, , i = <B <0, then the value of, , 2sinAt+4sin B=, (4) 4 (@) 2 © + @) 0, , if tan 6+ sec6= V3 and 0<0 <2, then 0 is, equal to, , x 2x se, 6, , wot OOF O, , x an : pico, If —<0<— i, 2 < ean. thine is equal to, , (A) secO-tan@ = (B)_ sec, + tan O, (©) tan8—sec8 (D) sec? 6 + tan? @, , , , , , , , 3., , If 6 lies in the second quadrant, then the value, , 1-sin@ I+sin®) ,, of (#8) « isnt) is equal to, , , , , , (A) 2s0c0 (B) -2sec 6, {C) 2 cosec 6 (D) 2¢os6, If n<a<>®, then fiscosa , [ltcosee, 2 l+cosa Vi-cosa, w= e —, sina sina, 1 1, © Fina “ina, , If A lies in the second quadrant and, 3 tam A + 4 = 0, then the value of, 2 cot A—5 cos A+sin A is equal to, , ‘ -53 -7, A) <5. () 10, 7 23, , © F (D) tp, , If sec @ ~ tan @= +, then @ lies in the, , (A) first quadrant (B) second quadrant, (C) third quadrant (D) fourth quadrant, , Ifcos 6 + sin @= V2 cos , then, , cos O- sin B=, (A) V2 sin® (B) 2sin6, (©) -V2sin6@ =D) V2 cos, , Ifsinx + cos-x = a, then |sin x— cos x{ equals, , (A) ¥2-8? (B) V2+a?, (©) va?-2 @) ve-4, , If 3 sin 6 + 4 cos 0 = 5, then the value of, 3 cos 0 = 4 sin @ is equal to, , , , , , (A) 0 (B) -5, © Ss. (D) 4, Ifsec 0~ tan 0 = ***, then cos 0 =, a’ +1 a’-1, oO v-1 ® a, 2a 2a, © a’sl ©) a’-l, , The value of — the expression, 2sin @tan Of] ~ tan@) + 2sinGsec” O is, , , , , , (i+tanoy, sin@ 2sinO, “ 1+tan@ ®) 1+ tan, 2sin0 sin@ © (1+tan ey ©) (i+tan6)?

Page 3 :
4., , Jf A is an obtuse angle, then, sin’ A—cos’ A | sinA, , n 2 tan A cot A, sin A—cosA 1+ tan? A, is equal to, (A) 1 @®) -!, (Cc) .2 ; @) 2, The equation (a + b)* = dab sin’ @ is possible, only when ,, (A) 2a=b (B) a-b, (C) a=2b (D) a=-b, 1f5 tan. = 4, then 28100 3c080, Ssin8+ 2cos6, wo mt OL Ms, If sin 6 + cosec 6 = 2, then sin® @ + cosec’@ =, A 1 @® 3 © 2 @ 4, sin 200° + cos 200° is, (A) ‘negative {B) positive, (C) zero (D) zero ar positive, gos 1*,cos 2°. cos 3° ..... cos 179° =, Ao ®t © -;M 4, If sin 6 — cos @ = 1, then the value of, ‘sin’0 — cos’@ is equal to, (A) 1 (B) -l, «) 0 (D) 2, Iftan 0 = =, then sin 0 =, (A) —4/5 but not 4/5, (B) —4/5 or 4/5, (C) 4/5 but not — 4/5, ‘ 4 4, (D) Neither Znor =, If sin 9 == and 6 lis in the second quadrant,, , then sec 6 + tan 6 =, (A) -3 (B) -5 (©) -7 (D) -9, , 47., , 2t, , If sin © = or and 6 lies in the second, quadrant, then cos 6 is equal to, , 1-? e-1, a ® ie, , ofat let?, © Te © 1-r|, If cosec 6 — cot 6 = 2017, then quadrant in, which 6 lies is, “A! @®wv Om ou, , Ireotee A+ cot A= +2, then tan A =, , 21 15 44 17, A): = a. Pee, (A) 2 (B) Ts (Cc) 117 (D) 3, , If tan 6 + sec 0 = e*, then cos 6 equals, , , , (e* +e") 2, “ 2 ®) {e" +e"), (c'-e") (ef -e"), (« 2 (D) ("+e"), , If 2y cos® = x sin® and 2x secO ~ y cosec6 = 3,, then. + 4y?=, {A) 4, , (c) -2, , (B) -4, (D) 2, , {secA +tanA = 1)(secA -tanA + 1)- 2 tanA =, , (A) stcA (B) 2secA, , (Cc) 0 @) 1, , sin 6 + cos® 0 + 3 sin” Geos" O =, , (A) 0 @) -1, , «cy 1 (D) None of these, , The value of cos 105° is, 341 1, , (A, , » wa © 22, V3+1 1-3, , (Cc) ra nd (D) ae

Page 4 :
61., , 62,, , tan 15° =, a) 5 @) -2, (Cc) 2-v3 (DP) 24+ 3, , cos 38° cos 8° + sin 38° sin 8° is equal to, , (A) cos 30° (B) cos 60°, (C) cos 45° (D) cos 38°, + (WBeos23° ~ sin 23° ) =, (A) cos 43° (B) cos 7°, 1, © yo 53° (D) cos 53°, ‘The value of tan SA — tan 3A ~ tan 2A is, equal to, (A) tan SA tan 3A tan 2A, (B) —1tan SA tan 3A tan 2A, (Cc) 0, (Dp) 1, The value of, ‘tan 57° — tan 12° — tan 57° tan 12° is, (A) tan 69° (B) tan 45°, (c) 0 (D) ten 57°, cos 10° +sin 10" _, cos 10° ~sin 10°, (A) tan S5° (B) cot 55°, (C) -tan35° {D) — cot 35°, cost —sin8. |, au, (A) tan 53° (B) tan 37°, (C) tan 82° (D) tan 62°, IFtan A= —*— and tin B= =, then the, value of A + Bis, r tT, x, (A) 0 @® 2 («) 3 @) 4, Iftan A — tan B = x and cot B- cotA = y,, then cot (A — B) =, (a) 4+y @ J, ay, dla 442, (c) zy (D) ">, The value of tan (-945°) is, (A) -1 (B) -2, (Cc) -3 (D) -4, sin ()sin(3*)10, 1 -1 1, As ® >OG (D) 1, , , , , , 67., , sin 15° + cos 105° =, (A) 0, , (B) 2 sin 15°, , (C) cos 15° + sin 15°, (D) sin 15° — cos 15°, , If ABCD is a cyclic quadrilateral, then, cos A + cos B is equal to, , (A) 0, , (B) cos C + cos D, , (C) = (cos C + cos D), , (D) cos C-cosD, , eots4? tan 20° _, The value of 36° aaa cot 70, {A) 0 (B) 2, (Cc) 3 (@D) 1, Ifsin A + cos A= 1, then sin 2A is equal to, at @®2 © Ms, 2+ J2+200840 =, (A) cos@ (B). sind, (C) 2cosd (D) 2sin8, 1 + cos? 2A is equal to, (A) sin’ A+ cos A, (B) sin’ 2A, , (c) 2 (cos! NA+ sin’ A), (D) 2 (cos A—sin' A), , , , The largest value of sin 8 cos 0 is, 1 i 3, , A) 1 = ¢ =, (A) (B) 2 (c) = (D) 2, cos 20° cos 40° cos 80° =, , 1 1 el 1, A) = = ae, (A) 7 8 7.9 >. ® ;, sinO+sin20, 1+c0s0 + cos 20, (A) Stan 6 (B) Feot 0 7, (C) tan@ (D) cord, iftan A= 3 then tan 3A =, , 9 1 7 1, a) 5 ®. > © 5 @) -3, Iftan Sat, then ie = is equal to, {A) cos @ (B) sin@, (C) sec (D) cos 26

Page 5 :
74., , Iftan4 = 3 hen LrcosA, , 2..2 1-cosA, , , , , , 9 4, @ 35-8) 5 O Fos,, tan * is equal o, l—sin A l+sinA, A): yan ®) A, cos A l+cosA, Ooi coa )-Vi=cosa, , Itsin a =4 and cos B= ~12, where A and B, , lie in first and third quadrant respectively, then, cos (A +B) =, , 36 : 56, (A) 3 (B) “er, 16 16, © Ss (@) “55, , 1 1, IfsinA = and sin B = ~~, where A and, sin Te sin ye, B are positive acute angles, then A + B=, , Tr Bid x, , B) — = (A) x ® z>O 7 OF, If cos @ = 5 and’ ties in the 1 quadrant,, then the value of, cos (30° + 6} +cos (45° — 8) + cos (120° ~ 0), , eh, (B) Bg], , (a) #3, , 7 2, , © Hey, , @) eS-4), , IA+B= =, then (1 + tan A) (I +tan B)=, , (A) 1 @) 2, CC) ® ~ @) -2 °, tan 3A — tan 2A — tan A=, , (A) tan 3A tan 2A tan A, , (B) =tan3A tan 2A tanA, , (C) tan A tan 2A - tan 2A tan 3A, (D) tan 2A tan 3A ~tan A tan 2A, , , , tan 20° + tan 40° + V3 tan 20° tan 40° =, , (A) i @) V3, 1, ) = D) -v3, © -z (py -v3, If tan A = 2 tan B + cot B, then 2 tan (A — B), is equal to, (A) tanB @) 2tanB, (C) cotB (D) 2cotB, oa, tan3A~tanA cot3A-cotA, (A) tanA (B) tan 2A, (C) cota (D) cot2A, The value of, tan 81° — tan 63° — tan 27° + tan 9° is equal to, (A) 1 (B) 2, « 3 (D) 4, x 6);, tan £40 an (3+-0)is gua vo, (ay -2 (B) -1, © 1 @) 0, tan 100° + tan 125° + tan 100° tan 125°=, (A) 0 @) +, © -1 (D) 1, tan (¥+0]-tan (¥-0)~, _ (A) 2 tan 20 (B) 2cot26, (C) tan 20 (D) cot 20, tan (60° + A) tan (60° A) is equal to, 20052 A+1, “@ 2cos2A-1, 2cos2A-1, ®) 2cos2A+1, cos 2A +21, © cos 2A~1, cos 2A—1, ©) ‘cos 2A +21, , sin2A _cosA _, 1+cos2A ‘1+c08A, , A A, (A) tan (B) as, (c) sec (D) cosee—, , 2 2