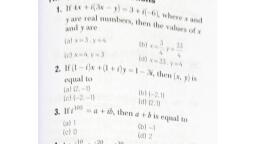Question 1 :
Let N denote the set of all natural numbers and R a relation on $$N\times N$$. Which of the following is an equivalence relation?
Question 2 :
$$N$$ is the set of positive integers. The relation $$R$$ is defined on N x N as follows: $$(a,b) R (c,d)\Longleftrightarrow ad=bc$$ Prove that
Question 3 :
If $$f:\mathbb{N} \rightarrow \mathbb{N}$$ and $$f(x) = x^{2}$$ then the function is<br/>
Question 4 :
The true set of real value of $$x$$ for which the function, $$f(x)=x\ \mathrm{ln}\ x-x+1$$ is positive is
Question 5 :
Let $$f:R\rightarrow R$$ be defined as $$f(x)=x^{3}+2x^{2}+4x+\sin \left(\dfrac{\pi}{2}\right)$$ and $$g(x)$$ be the inverse function of $$f(x)$$, then $$g'(8)$$ is equal to
Question 7 :
Let $$f: N\rightarrow R$$ such that $$f(x)=\dfrac{2x-1}{2}$$ and $$g: Q\rightarrow R$$such that $$g(x)=x+2$$ be two function. Then $$(gof)\left(\dfrac{3}{2}\right)$$ is equal to
Question 8 :
Which one of the following relations on R (set of real numbers) is an equivalence relation
Question 9 :
The number of reflexive relation in set A = {a, b, c} is equal to
Question 10 :
Let $$T$$ be the set of all triangles in the Euclidean plane, and let a relation $$R$$ on $$T$$ be defined as $$aRb$$, if $$a$$ is congruent to $$b$$ for all $$a,b\in T$$. Then, $$R$$ is
Question 11 :
Let $$A=\left\{ 2,3,4,5,....,17,18 \right\} $$. Let $$\simeq $$ be the equivalence relation on $$A\times A$$, cartesian product of $$A$$ with itself, defined by $$(a,b)\simeq (c,d)$$, iff $$ad=bc$$. The the number of ordered pairs of the equivalence class of $$(3,2)$$ is
Question 12 :
If $$A=\left\{ 1,2,3 \right\} $$, then a relation $$R=\left\{ \left( 2,3 \right) \right\} $$ on $$A$$ is
Question 14 :
Find number of all such functions $$y = f(x)$$ which are one-one?
Question 15 :
Let $$A = \left\{ {1,2,3} \right\}$$ and $$R = \left\{ {\left( {1,1} \right),\left( {1,3} \right),\left( {3,1} \right),\left( {2,2} \right),\left( {2,1} \right),\left( {3,3} \right)} \right\}$$, then the relation $$R$$ and $$A$$ is
Question 16 :
If $$A=\left\{ a,b,c \right\} $$, then the relation $$R=\left\{ \left( b,c \right) \right\} $$ on $$A$$ is
Question 17 :
The relation $$R=\left\{ \left( 1,1 \right) ,\left( 2,2 \right) \left( 3,3 \right)  \right\} $$ on the set $$A=\left\{ 1,2,3 \right\} $$ is
Question 18 :
If the relation is defined on $$R-\left\{ 0 \right\} $$ by $$\left( x,y \right) \in S\Leftrightarrow xy>0$$, then $$S$$ is ________
Question 19 :
Let $$A=\left\{ 1,2,3 \right\} $$. Then, the number of equivalence relations containing $$(1,2)$$ over set A is
Question 20 :
The number of reflexive relations of a set with four elements is equal to
Question 22 :
Let $$f(x,y)=xy^{2}$$ if $$x$$ and $$y$$ satisfy $$x^{2}+y^{2}=9$$ then the minimum value of $$f(x,y)$$ is
Question 23 :
If $$A=\left\{ a,b,c,d \right\} $$, then a relation $$R=\left\{ \left( a,b \right) ,\left( b,a \right) ,\left( a,a \right) \right\} $$ on $$A$$ is
Question 24 :
Let E = {1, 2, 3, 4} and F {1, 2}. Then the number of onto functions from E to F is
Question 25 :
Let A={ 1, 2, 3, 4} and R= {( 2, 2), (3, 3), (4, 4), (1, 2)} be a relation on A. Then R is
Question 26 :
Let $$L$$ denote the set of all straight lines in a plane, Let a relation $$R$$ be defined by $$lRm$$, iff $$l$$ is perpendicular to $$m$$ for all $$l \in L$$. Then, $$R$$ is
Question 27 :
On the set $$N$$ of all natural numbers define the relation $$R$$ by $$a R b$$ if and only if the G.C.D. of $$a$$ and $$b$$ is $$2$$. Then $$R$$ is:
Question 28 :
Which of the following is not an equivalence relation on $$Z$$?
Question 29 :
For real number $$x$$ and $$y$$, define $$xRy$$ iff $$x-y+\sqrt{2}$$ is an irrational number. Then the relation $$R$$ is
Question 30 :
Assertion: Domain of $$f(x)$$ is singleton.
Reason: Range of $$f(x)$$ is singleton.