Question 1 :
Let {tex} g ( x ) = x f ( x ) , {/tex} where {tex} f ( x ) = \left\{ \begin{array} { c c } { x \sin \frac { 1 } { x } , } & { x \neq 0 } \\ { 0 } & { , x = 0 } \end{array} . \text { At } x = 0 \right. {/tex}

Question 3 :
If $x_{1}$ and $x_{2}$ are the real and distinct roots of $ax^2+bx+c=0$, then <br/>${ e }^{ \displaystyle \lim _{ x\rightarrow x_1 }{ \displaystyle \frac { (1+\sin { (a{ x }^{ 2 }+bx+c))-1 } }{ x-{ x }_{ 1 } } } }$ is equal to:<br/>

Question 4 :
If $\displaystyle l=\lim_{x\rightarrow 0}\frac{\sin ax-\sin x-x}{x^3}$ exists, and is finite, then the values of '$l$' and '$a$' are respectively equal to

Question 5 :
Arrange the following limits in the ascending order.<br>a) $\displaystyle\lim_{x\rightarrow 0}\displaystyle \frac{\tan^{4}x-\sin^{4}x}{\mathrm{x}^{6}}$<br><br>b) $\displaystyle\lim_{x\rightarrow 0}\displaystyle \frac{\tan^{8}x-\sin^{8}x}{x^{5}\tan x^{5}}$<br><br>c) $\displaystyle\lim_{x\rightarrow 0}\displaystyle \frac{\tan^{3}x-\sin^{3}x}{x\sin^{4}x}$<br><br>d) $\displaystyle\lim_{x\rightarrow 0}\displaystyle \frac{\tan^{5}x-\mathrm{\sin}^{5}x}{x^{2}.\sin^{3}x\tan^{2}x}$

Question 6 :
In {tex} [ 0,1 ] {/tex} Lagranges Mean Value theorem is NOT applicable to

Question 7 :
The normal to the curve {tex} x = a ( \cos \theta + \theta \sin \theta ) {/tex}, {tex} y = a ( \sin \theta - \theta \cos \theta ) {/tex} at any point {tex} ^ { \prime } \theta ^ { \prime } {/tex} is such that

Question 8 :
The triangle formed by the tangent to the curve {tex} f ( x ) = x ^ { 2 } + b x {/tex} {tex} - b {/tex} at the point {tex} ( 1,1 ) {/tex} and the coordinate axes, lies in the first quadrant. If its area is {tex} 2 , {/tex} then the value of {tex} b {/tex} is

Question 9 :
Let {tex} f ( x ) = \left( 1 + b ^ { 2 } \right) x ^ { 2 } + 2 b x + 1 {/tex} and let {tex} m ( b ) {/tex} be the minimum value of {tex} f ( x ) . {/tex} As {tex} b {/tex} varies, the range of {tex} m ( b ) {/tex} is

Question 10 :
If {tex} y ^ { 2 } = P ( x ) , {/tex} a polynomial of degree {tex} 3 , {/tex} then {tex} 2 \frac { d } { d x } \left( y ^ { 3 } \frac { d ^ { 2 } y } { d x ^ { 2 } } \right) {/tex} equals

Question 11 :
If {tex} f ( x ) = x ^ { \alpha } \log x {/tex} and {tex} f ( 0 ) = 0 , {/tex} then the value of {tex} \alpha {/tex} for which Rolle's theorem can be applied in {tex} [ 0,1 ] {/tex} is

Question 12 :
The minimum value of {tex} f ( x ) = | 3 - x | + | 2 + x | + | 5 - x | {/tex} is

Question 13 :
If {tex} y = ( \sin x ) ^ { \tan x } , {/tex} then {tex} \frac { d y } { d x } {/tex} is equal to

Question 14 :
The total number of local maxima and local minima of the function <br>{tex} f ( x ) = \left\{ \begin{array} { l } { ( 2 + x ) ^ { 3 } , - 3 < x \leq - 1 } \\ { x ^ { 2 / 3 } , - 1 < x < 2 } \end{array} \right. {/tex} is

Question 15 :
If {tex} y = a \ln x + b x ^ { 2 } + x {/tex} has its extremum values at {tex} x = - 1 {/tex} and {tex} x = 2 , {/tex} then

Question 16 :
If {tex} f ( x ) = x ^ { 3 } + b x ^ { 2 } + c x + d {/tex} and {tex} 0 < b ^ { 2 } < c , {/tex} then {tex} \operatorname { in } ( - \infty , \infty ) {/tex}

Question 17 :
Let {tex} f ( x ) = \{ \begin{array} { l l } { | x | , } & { \text { for } \quad 0 < | x | \leq 2 } \\ { 1 , } & { \text { for } x = 0 } \end{array} \text { then at } x = 0 , f {/tex} has

Question 18 :
Let the function {tex} g: ( - \infty , \infty ) \rightarrow \left( - \frac { \pi } { 2 } , \frac { \pi } { 2 } \right) {/tex} be given by {tex} g ( u ) = 2 \tan ^ { - 1 } \left( e ^ { u } \right) - \frac { \pi } { 2 } . {/tex} Then, {tex} \mathrm { g } {/tex} is<br>

Question 19 :
On the interval {tex} [ 0,1 ] {/tex} the function {tex} x ^ { 25 } ( 1 - x ) ^ { 75 } {/tex} takes its maximum value at the point

Question 20 :
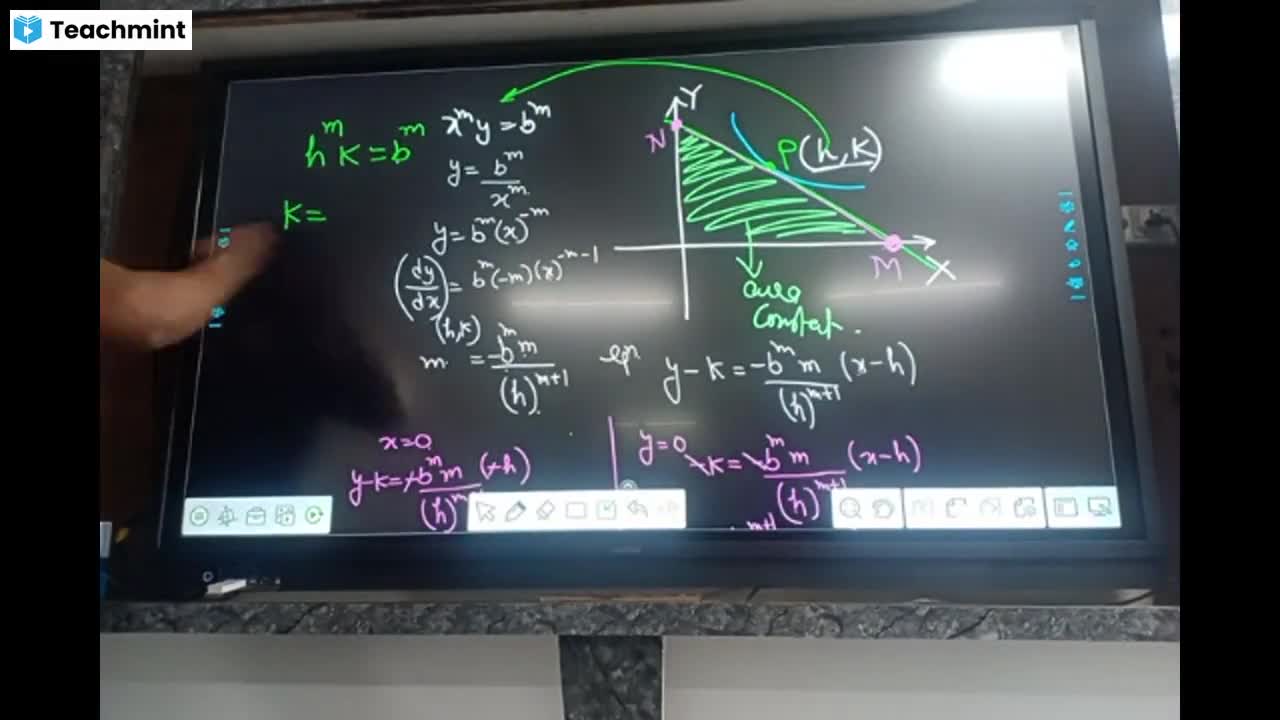
A given right circular cone has a volume {tex} p , {/tex} and the largest right circular cylinder that can be inscribed in the cone has a volume {tex} q . {/tex} Then {tex} p: q {/tex} is

Question 21 :
The point(s) on the curve {tex} y ^ { 3 } + 3 x ^ { 2 } = 12 y {/tex} where the tangent is vertical, is (are)

Question 22 :
For all {tex} \mathrm { x } \in ( 0,1 ) {/tex}

Question 23 :
If the normal to the curve {tex} y = f ( x ) {/tex} at the point {tex} ( 3,4 ) {/tex} makes an angle {tex} \frac { 3 \pi } { 4 } {/tex} with the positive {tex} x {/tex} -axis, then {tex} f ^ { \prime } ( 3 ) = {/tex}

Question 24 :
If {tex} f ( x ) = \{ \begin{array} { l r } { 3 x ^ { 2 } + 12 x - 1 , } & { - 1 \leq x \leq 2 } \\ { 37 - x } & { 2 < x \leq 3 } \end{array} {/tex} then:

Question 25 :
The slope of the tangent to a curve {tex} y = f ( x ) {/tex} at {tex} [ x , f ( x ) ] {/tex} is {tex} 2 x + 1 . {/tex} If the curve passes through the point {tex} ( 1,2 ) , {/tex} then the area bounded by the curve, the {tex} x {/tex} -axis and the line {tex} x = 1 {/tex} is