Page 1 :
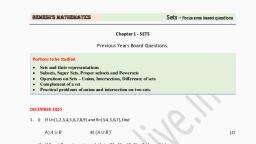
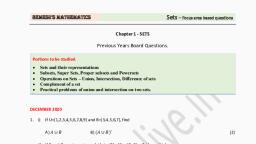
TERM-1 (MOCK TEST), SUB-MATH, , 1. If n (A) = 3 and n (B) = 6 and A ⊆ B, then, the number of elements in A ∩ B is equal to, (a) 9, (b) 3, (c) 6, (d) 0, 2. The cardinality of the power set of {0, 1, 2 ., . ., 10} is ______., (a) 1024, (b) 1023, (c) 2048, (d) 2043, 3. If A = {0,1,5, 4, 7}. Then the total number, subsets of A are, (a) 32, (b) 64, (c) 40, (d) None of these, 4. What is the cardinality of the set of odd, positive integers less than 10?, (a) 10, (b) 5, (c) 3, (d) 20, 5. Which of the following sets are null sets, (a) {x: |x |< -4, x ∈ N}, (b) 2 and 3, (c) Set of all prime numbers between 15, and 19, (d) {x: x < 5, x > 6}, 6. Which of the following statements is true?, (a) {3} ∈ {1, 3, 5}, (b) {1} ∈ {1, 3, 5}, (c) {3, 5} ∈ {1, 3, 5}, (d) 3 ∈ {1, 3, 5}, 7., Empty set is a?, (a) Finite Set, (b) Invalid Set, (c) None of the above, (d) Infinite Set, 8. Which set is the subset of all given sets?, (a) {1}, (b) {0}, (c) { }, (d) {1, 2, 3, 4}, 9. Which of the following two sets are equal?, (a) A = {1, 2} and B = {1}, (b) A = {1, 2} and B = {1, 2, 3}, , CLASS-XI, , TOPIC- SET THEORY, , (c) A = {1, 2, 3} and B = {2, 1, 3}, (d) A = {1, 2, 4} and B = {1, 2, 3}, 10. If A, B, C be any three sets such that A ∪ B, = A ∪ C and A ∩ B = A ∩ C, then, (a) A = C, (b) A = B, (c) A = B = C, (d) B = C, 11. Given the sets A = {1, 2, 3}, B = {3 , 4}, C, = {4 , 5, 6}, then A ∪ (B ∩ C) is, (a) {3}, (b) {1, 2 ,3 , 4, 5, 6}, (c) {1, 2 , 3 , 4}, (d) None of these, 12. If 𝑋 = {8𝑛 − 7𝑛 − 1: 𝑛 ∈ 𝑁} and 𝑌 =, {49𝑛 − 49: 𝑛 ∈ 𝑁}. Then,, (a) 𝑋 ⊂ 𝑌, (b) 𝑌 ⊂ 𝑋, (c) 𝑋 = 𝑌, (d) 𝑋 ∩ 𝑌 = 𝜑, 13. If 𝐴 = {(𝑥, 𝑦): 𝑥 2 + 𝑦 2 = 25} and 𝐵 =, {(𝑥, 𝑦): 𝑥 2 + 9𝑦 2 = 144}, then 𝐴 ∩ 𝐵, contains, (a) 1 points, (b) 2 points, (c) 3 points, (d) 4 points, 14. If A and B are two sets, then 𝐴 ∩ (𝐴 ∪ 𝐵), equals to, (a) A, (b) B, (c) 𝜑, (d) 𝐴 ∩ 𝐵, 15. If 𝑆 = {𝑥 : 𝑥 𝑖𝑠 𝑎 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑒 𝑜𝑓 3 𝑎𝑛𝑑 𝑥 <, 100} and, 𝑃=, { 𝑥 : 𝑥 𝑖𝑠 𝑎 𝑝𝑟𝑖𝑚𝑒 𝑛𝑢𝑚𝑏𝑒𝑟 𝑙𝑒𝑠𝑠 𝑡h𝑎𝑛 20}., Then 𝑛(𝑆) + 𝑛(𝑃)., (a) 34, (b) 31, (c) 33, (d) 41

Page 2 :
TERM-1 (MOCK TEST), SUB-MATH, , CLASS-XI, , 16. Total number of elements in the power set of, A containing 15 elements is, (a) 215, (b) 152, (c) 215−1, (d) 215 − 1, 17. If 𝐴 = 𝑃({1, 2}), where P denotes the power, set, then which one of the following is, correct ?, (a) {1, 2} ⊂ 𝐴, (b) 1 ∈ 𝐴, (c) 𝜑 ∉ 𝐴, (d) {1, 2} ∈ 𝐴, 18. If a set is denoted as 𝐴 = 𝜑, then number of, elements in A is, (a) 1, (b) 0, (c) 2, (d) 3, 19. The set of all natural numbers 𝑥 such that, 4𝑥 + 9 < 50 in roster form is, (a) {1, 2, 4, 6, 8, 10}, (b) {1, 3, 5, 7, 9}, (c) {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, (d) None of the above, 20. Two finite sets have m and n elements. The, number of subsets of the first set is 112, more than that of the second set. The values, of m and n are, respectively, (a) 4, 7, (b) 7, 4, (c) 4, 4, (d) 7, 7, , TOPIC- SET THEORY