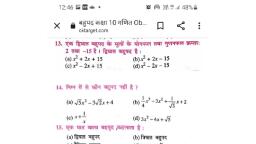
Question 1 :
If $2$ is one of roots of ${ x }^{ 2 }-4x+k=0$ then $k=$
Question 2 :
If $\alpha, \beta, \gamma$ be the zeroes of the polynomial $ax^3+bx^2+cx+d$, then the value of $\alpha \beta+\beta \gamma+\gamma \alpha$ is-
Question 3 :
If $\alpha $ and $\beta $ are zeros of the quadratic polynomial $2x^2+3x-6$, then find the values of :<br/>$\alpha^2+\beta^2$<br/>
Question 4 :
$\alpha, \beta$ & $\gamma$ are the zeroes of cubic polynomial $P(x) = ax^3 + bx^2 + cx + d, (a \neq 0)$ then product of their zeroes $[\alpha . \beta . \gamma] = $ .................
Question 5 :
If the sum of the squares of zeroes of the polynomial $5x^2 + 3x + k = 0$ is $\displaystyle \frac{-11}{25}$, find the value of k.<span><br></span>
Question 8 :
If a polynomial $p(x)$ is divided by $x - a$ then remainder is<br/>
Question 9 :
Choose the correct answer from the alternatives given.<br>If the expression $2x^2$ + 14x - 15 is divided by (x - 4). then the remainder is
Question 10 :
If 1 is one of the zeroes of the polynomial $x^2 - x + k$, then the value of k is _________.
Question 11 :
If $\alpha$ and $\beta$ are the zeroes of the polynomial $f(x) = x^2 - px + q$, then the polynomial having $\displaystyle \frac{1}{\alpha}$ and $\displaystyle \frac{1}{\beta}$ as its zeroes is __________.
Question 13 :
$ax^3 + bx^2 + cx + d = 0$ is said to be cubic polynomial if _________.
Question 14 :
Apply the division algorithm to find the remainder on dividing $p(x) = x^4 -3x^2 + 4x + 5$ by $g(x)= x^2 +1 -x.$
Question 15 :
What is the remainder, when <br>$(4{x^3} - 3{x^2} + 2x - 1)$ is divided by (x+2)?<br>
Question 16 :
The remainder when $4{a^3} - 12{a^2} + 14a - 3$ is divided by $2a-1$, is
Question 17 :
If $ \alpha , \beta , \gamma $ are roots of $x^3 -1 = 0, $ then product of roots $ \alpha , \beta , \gamma $ is :
Question 20 :
A cubic polynomial with sum of its zeroes, sum of the product of its zeroes taken two at a time and the product of its zeroes as 2, -7, -14 respectively, is __________.
Question 21 :
$\alpha$ and $\beta$ are the zeros of a polynomial, such that $\alpha + \beta = 6$ and $\alpha \beta = 4$. Identify the polynomial.
Question 23 :
What is the remainder when $\left( 2{ x }^{ 2 }+3x+7 \right) $ is divided by $\left( x+2 \right) $?
Question 24 :
If $\alpha$ and $\beta$ are the zeroes of the polynomial $ 5x^{2}-7x+2$, then, the sum of their reciprocals is :<br/>
Question 26 :
Factorise the expressions and divide them as directed.$5pq(p^2 - q^2)\div 2p(p + q)$
Question 27 :
<span>Work out the following divisions.</span><div>$10y(6y + 21) \div 5(2y + 7)$<br/></div>
Question 28 :
The product of the zeroes of the cubic polynomial $p(x)$ is ...............
Question 29 :
If $\alpha,\beta$ are the roots of the quadratic equation ${ x }^{ 2 }-\left( { 3+2 }^{ \sqrt { \log _{ 2 }{ 3 }  }  }-{ 3 }^{ \sqrt { \log _{ 3 }{ 2 }  }  } \right) x-2\left( { 3 }^{ \log _{ 3 }{ 2 }  }-{ 2 }^{ \log _{ 2 }{ 3 }  } \right) =0$, then the value of ${\alpha},{\beta}$ is.
Question 31 :
The difference of roots of the quadratic equation $4y^2 - 4y + 1 = 0$ is _________.
Question 33 :
<span>The value of $\lambda $ for which the expression $x^3 + x^2 - 5x + \lambda $ wiI1 be divisible by $(x - 2)$ is:</span>
Question 34 :
Let $\alpha$ , $\beta$ be the zeros of the polynomial $x^2-px+r$ and $\large{\frac{\alpha}{2}}$, $2\beta$ be the zeros of $x^2-qx+r$. Then the value of $r$ is
Question 35 :
Apply division algorithm to find the quotient q(x) and remainder r(x) on dividing $f(x) =10x^4 +17x^3-62x^2+30x -3$ by $g(x) =2x^2-x+1$
Question 36 :
If $\beta$ and $\dfrac{1}{\beta}$ are zeroes of polynomial $6x^2-24x+(a-12)$. Find $a$.<br/>
Question 37 :
If $f(x)=2{x}^{3}+3{x}^{2}+cx+8$, where $c$ is a constant. The graph of $f$ intersects the x-axis at the three points $(-4,0)(\cfrac{1}{2},0)$ and $(p,0)$. Find the value of $c$.
Question 38 :
If 1 is zero of the polynomial $p\left (x \right ) = ax^{2}-3\left (a-1 \right ) x-1$, then the value of 'a' is<br>
Question 39 :
If $\alpha$ and $\dfrac{1}{\alpha}$ are zeroes of polynomial $3x^2+13x+(12-p)$. What is the value of $p$?<br/>
Question 40 :
If $\alpha, \beta$ are zeros of the polynomial $f(x)=x^2-c(x+1)-c$, then $(\alpha+1)(\beta+1)=$<br>
Question 41 :
If $\alpha, \beta, \gamma$ be the zeroes of the cubic polynomial $ax^3 + bx^2 + 4x + 7 = 0$, then the value of $\alpha \beta + \beta \gamma + \gamma \alpha =$ ________.
Question 42 :
If $p(x)$ is a polnomial such that $p(x^{2}+1)=\left\{p(x)\right\}^{2}+1$ and $p(0)=0$ then $p^{1}(o)$ is equal to
Question 43 :
If $\alpha $ and $\beta $ are zeros of the polynomial $2x^2-4x +5$, find the values of $\alpha^2+\beta^2$<br/>
Question 45 :
If $\alpha ,\beta$ and $\gamma$ are the zeroes of the polynomial ${ 2x }^{ 3 }+{ x }^{ 2 }-13x+6$ then $\alpha \beta \gamma$=
Question 46 :
The number of different possible values for the sum $x+y+z$, where $x,y,z$ are real numbers such that ${x}^{4}+4{y}^{4}+16{z}^{4}+64=32xyz$ is
Question 47 :
The number of integers $n$ for which $3x^3-25x+n=0$ has three real roots is$?$<br/>
Question 48 :
Suppose $\alpha ,\beta .\gamma $ are roots of ${ x }^{ 3 }+{ x }^{ 2 }+2x+3=0$. If $f(x)=0$ is a cubic polynomial equation whose roots are $\alpha +\beta ,\beta +\gamma ,\gamma +\alpha $ then $f(x)=$
Question 49 :
If $\alpha ,\beta .\gamma $ are roots of ${ x }^{ 3 }-5x+4=0$ then ${ \left( { \alpha }^{ 3 }+{ \beta }^{ 3 }+{ \gamma }^{ 3 } \right) }^{ 2 }=$
Question 50 :
Total number of polynomials of the form ${ x }^{ 3 }+a{ x }^{ 2 }+bx+c$ that are divisible by ${ x }^{ 2 }+1$, where $a,b,c\in \left\{ 1,2,3,......10 \right\} $ is equal to