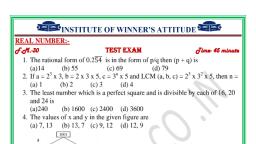
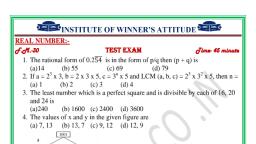
Question 1 :
$\dfrac{1}{3}x - \dfrac{1}{6}y = 4$<br/>$6x - ay = 8$<br/>In the system of equations above, $a$ is a constant. If the system has no solution, what is the value of $a$
Question 2 :
If x and y are positive with $x-y=2$ and $xy=24$ , then $ \displaystyle \frac{1}{x}+\frac{1}{y}$   is equal to
Question 3 :
The survey of a manufacturing company producing a beverage and snacks was done. It was found that it sells orange drinks at $ $1.07$ and choco chip cookies at $ $0.78$ the maximum. Now, it was found that it had sold $57$ food items in total and earned about $ $45.87 $ of revenue. Find out the equations representing these two. 
Question 4 :
If $2x + y = 5$, then $4x + 2y$ is equal to _________.
Question 5 :
Equation of a straight line passing through the point $(2,3)$ and inclined at an angle of $\tan^{-1}\dfrac{1}{2}$ with the line $y+2x=5$, is:
Question 6 :
The graph of the linear equation $2x -y = 4$ cuts x-axis at
Question 8 :
The solution of the simultaneous equations $\displaystyle \frac{x}{2}+\frac{y}{3}=4\: \: and\: \: x+y=10 $ is given by
Question 9 :
What is the equation of the line through (1, 2) so that the segment of the line intercepted between the axes is bisected at this point ?
Question 10 :
Two perpendicular lines are intersecting at $(4,3)$. One meeting coordinate axis at $(4,0)$, find the coordinates of the intersection of other line with the cordinate axes.
Question 12 :
The unit digit of a number is $x$ and its tenth digit is $y$ then the number will be 
Question 14 :
Let PS be the median of the triangle with vertices $P\left( 2,2 \right), Q\left( 6,-1 \right), R\left( 7,3 \right).$The equation of the line passing through $\left( 1,-1 \right)$and parallel to PS is
Question 15 :
If the system of equation, ${a}^{2}x-ay=1-a$ & $bx+(3-2b)y=3+a$ possesses a unique solution $x=1$, $y=1$ then:
Question 16 :
A line which passes through (5, 6) and (-3. -4) has an equation of
Question 17 :
The solution of the equation $2x - 3y = 7$ and $4x - 6y = 20$ is
Question 19 :
If the equations $4x + 7y = 10 $ and $10x + ky = 25$ represent coincident lines, then the value of $k$ is
Question 20 :
Equation of a straight line passing through the origin and making an acute angle with $x-$axis twice the size of the angle made by the line $y=(0.2)\ x$ with the $x-$axis, is: