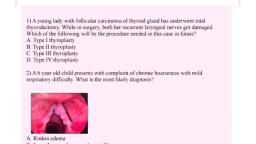
Question 1 :
Two supplementary angles are in the ratio 4 : 5. The angles are<br>

Question 2 :
State the following statement is True or False<br>If two parallel lines are cut by transversal, then the pair of alternate interior angles are not equal

Question 5 :
If two supplementary angles differ by $44^o$, then one of the angles is ___________.

Question 10 :
State true or false.The sum of interior angles of a triangle is ${ 180 }^{ \circ&#160; }$.

Question 11 :
If two angles are complementary and in the ratio $17:13$. Find the measure of angles.

Question 14 :
The supplement angleof the complement of$\displaystyle { 30 }^{ o }$ is

Question 15 :
Two supplementary angles are in ratio $4:5$. Find the measure of greater angle.

Question 16 :
Find the equation of a line, which has the y intercept 4, and is parallel to the line $\displaystyle 2x-3y=7$. Find the co-ordinates of the point, where it cuts the x-axis.

Question 17 :
If two line $L_1$ and $L_2$ in space,are defined by<br>$\begin{array}{l}{L_1} = \left\{ {x = \sqrt \lambda y + \left( {\sqrt \lambda - 1} \right),z = \left( {\sqrt \lambda - 1} \right)y + \sqrt \lambda } \right\}and\\{L_2} = \left\{ {x = \sqrt \mu y + \left( {1 - \sqrt \mu } \right),z = \left( {1 - \sqrt \mu } \right)y + \sqrt \mu } \right\}\end{array}$, <br>then $L_1$ is perpendicular to $L_2$ for all non-negative reals $\lambda $ and $\mu $, such that:<br><br>

Question 20 :
<br/>Two supplementary angles are in the ratio $3:2$. The smaller angle measures?

Question 21 :
Find the measure of an angle, if seven times its complement is $10^{\circ}$ less than three times its supplement

Question 22 :
Two angles are adjacent and form an angle of $100^\circ$. The larger is $20^{\circ}$ less than five times the smaller. The larger angle is

Question 25 :
The number of rational values of $m$ for which the $y$-coordinate of the point of intersection of the lines $3x+2y=10$ and $x=my+2$ is an integer is