Test Details

Matrices

Test

Nov 03, 11:00 AM

30 minutes

Nov 04, 5:00 PM

40.0 marks

MCQ

20 questions

Er. Dipesh Tripathi Sir

I have completed bachelor of engineering in mechanical branch from University of Mumbai. I have experience of teaching maths subject of all streams.

Class Details

Applied mathematics

Xllth Commerce

Applied mathematics

More from Er. Dipesh Tripathi Sir

(13)

Lecture

Lecture 2021-07-01

b-com

Appliedmathematics

0 Likes

6 Views

Er. Dipesh Tripathi Sir

Jul 01, 2021

Lecture

Lecture 2021-06-30

b-com

Appliedmathematics

0 Likes

13 Views

Er. Dipesh Tripathi Sir

Jun 30, 2021

Lecture

Lecture 2021-03-02

b-sc

Maths

0 Likes

34 Views

Er. Dipesh Tripathi Sir

Mar 02, 2021

Lecture

Lecture 2021-03-01

b-sc

Maths

0 Likes

24 Views

Er. Dipesh Tripathi Sir

Mar 01, 2021

Lecture

Lecture 2021-02-27

class-10th

Mathematicsandstatistics

0 Likes

35 Views

Er. Dipesh Tripathi Sir

Feb 27, 2021

Lecture

Lecture 2021-02-26

b-sc

Maths

0 Likes

25 Views

Er. Dipesh Tripathi Sir

Feb 26, 2021

Lecture

Lecture 2021-02-15

b-sc

Maths

0 Likes

16 Views

Er. Dipesh Tripathi Sir

Feb 15, 2021

Lecture

Lecture 2021-02-09

b-sc

Maths

0 Likes

18 Views

Er. Dipesh Tripathi Sir

Feb 09, 2021

Lecture

Lecture 2021-02-07

b-sc

Maths

0 Likes

4 Views

Er. Dipesh Tripathi Sir

Feb 07, 2021

Lecture

Lecture 2021-01-19

b-sc

Maths

0 Likes

10 Views

Er. Dipesh Tripathi Sir

Jan 19, 2021

Lecture

Lecture 2021-01-17

b-sc

Maths

0 Likes

7 Views

Er. Dipesh Tripathi Sir

Jan 17, 2021

Lecture

Lecture 2021-01-13

b-sc

Maths

0 Likes

14 Views

Er. Dipesh Tripathi Sir

Jan 13, 2021

Lecture

Lecture 2021-01-04

b-sc

Mathematicsandstatistics

0 Likes

30 Views

Er. Dipesh Tripathi Sir

Jan 04, 2021

Recommended Content

(20)

Test

Matrices,Determinants

b-com

Mathematics

0 Likes

12 Views

Sunit Kumar

Jan 28, 2022

Test

Matrices

naveengowda

Maths

0 Likes

7 Views

Naveen

Jan 08, 2022

Homework

Matrices

secondsemester

Appliedmathematics

0 Likes

11 Views

Amita Tripathi

Jan 22, 2022

Test

Matrices,Determinants

b-com

Maths

0 Likes

1 Views

VK Maurya sir

Jan 28, 2022

Test

Matrices

b-sc

Mathematics

0 Likes

28 Views

NAVIN KUMAR JAISWAL

Dec 10, 2021

Test

Statistics

b-com

Appliedmathematics

0 Likes

23 Views

Kulkarni Sir

Dec 01, 2021

Test

Matrices

b-com

Mathematics

0 Likes

5 Views

sourav ghosh

Oct 23, 2021

Test

Matrices

b-sc

Mathspaperiu-Mat-138

0 Likes

17 Views

Mahesh Sahebrao Wavare

Jan 14, 2022

Test

Matrices

b-com

Maths

0 Likes

3 Views

Mangal Sonone

Feb 28, 2022

Test

Matrices

b-com

Math100100

0 Likes

8 Views

Vinay Sir

Dec 15, 2021

Test

Matrices

b-com

Computer

0 Likes

11 Views

Deepak pandit

Dec 11, 2021

Test

Matrices

b-com

Maths

0 Likes

16 Views

MR. SHIVSHANKAR YADAV

Nov 22, 2021

Homework

Matrices

b-com

Physicalchemistry

0 Likes

5 Views

Manish Verma

Jan 20, 2022

Test

Matrices

b-com

Computer

0 Likes

6 Views

Jagdish S. Prajapati

Jan 09, 2022

Test

Matrices

b-com

Mathematics

0 Likes

1 Views

Mayur Sir

Jan 08, 2022

Test

Matrices

b-com

Mathematics

0 Likes

1 Views

Mayur Sir

Jan 12, 2022

Test

Matrices

b-com

Maths

0 Likes

19 Views

T.N. NIMBHORKAR

Jan 18, 2022

Test

Matrices

b-com

Maths

0 Likes

2 Views

Mangal Sonone

Mar 12, 2022

Test

Matrices

b-com

Businessmathematics

0 Likes

0 Views

somnath Vedpathak

Mar 18, 2022

Test

Matrices

b-com

Mathematics

0 Likes

3 Views

Bishu sir

Jan 09, 2022

Question Text

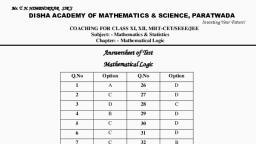
Question 1 :
If $A=\begin{bmatrix} \alpha & 2\\ 2 & \alpha \end{bmatrix}$ and $|A^3|=125$, then $\alpha=$ _____.

Question 3 :
Let $\alpha$ be a root of the equation $x^2+x+1=0$ and the matrix $A=\dfrac{1}{\sqrt{3}}\begin{bmatrix} 1& 1& 1 \\ 1& \alpha& \alpha^2\\ 1& \alpha^2& \alpha^4\end{bmatrix}$ then the matrix $A^{31}$ is equal to :

Question 4 :
If  $A=\begin{bmatrix} 2 & 1 \\ 1 & 3 \end{bmatrix}$ , $B=\begin{bmatrix} 3 & 2 & 0 \\ 1 & 0  & 4  \end{bmatrix}$, then $AB=$ is

Question 5 :
If $\displaystyle \:A= \left [ \begin{matrix}2 &0 &-3 \\4 &3 &1 \\-5 &7 &2 \end{matrix} \right ]$ is expressed as the sum of a symmetric and skew-symmetric matrix, then the symmetric matrix is

Question 6 :
Say true or false: If A & B are symmetric matrices of same order then $AB - BA$ is symmetric.

Question 7 :
Let $\mathrm{A} =\left[\begin{array}{ll} 1 & -1\\ 2 & -1 \end{array}\right],\ \mathrm{B}=\left[\begin{array}{ll} x & 1\\ y & -1 \end{array}\right]$, if $(\mathrm{A}+\mathrm{B})^{2}=\mathrm{A}^{2}+\mathrm{B}^{2}$, find  $(x,y)$ is equal to

Question 8 :
If $A$ and $B$ are two non-zero square matrices of the same order such that the product $AB=0$, then

Question 9 :
If $A = \begin{bmatrix}1 &3 \\ 3 & 4\end{bmatrix}$ and $A^{2} - kA - 5I_{2} = 0$, then the value of $k$ is

Question 10 :
If $\left[\begin{array}{lll}  1 &  3 &  0\\  1 &  0 & -2\\ -4 & -4 &  4 \end{array}\right] =\mathrm{A}+\mathrm{B}$ where $\mathrm{A}$ is symmetric matrix and $\mathrm{B}$ is skew-symmetric, then $\mathrm{A}-\mathrm{B}$ is equal to

Question 11 :
If $A=\begin{bmatrix} \alpha & 0 \\ 1 & 1 \end{bmatrix}$ and $B=\begin{bmatrix} 1 & 0 \\ 5 & 1 \end{bmatrix}$, then value of $\alpha$ for which ${A}^{2}=B$, is

Question 12 :
If $A = \begin{bmatrix} 2& 3\\ -1 & 2\end{bmatrix}$, then $A^{3} + 3A^{2} - 4A + 1$ is equal to

Question 13 :
Under what condition is the matrix equation $A^2-B^2=(A-B)(A+B)$ is true ?

Question 14 :
If $A=\begin{bmatrix} 4 & x+2\\ 2x-3 & x+1\end{bmatrix}$ is symmetric, then what is x equal to?

Question 15 :
If A and B are symmetric and commute , then which of the following is /are symmetric ?

Question 16 :
lf the value of a third order determinant is 11, then the value of the determinant of $A^{-1}=$

Question 17 :
$\begin{bmatrix} 1 & 6\\ 7 & 2 \end{bmatrix}$ = P + Q, where P is a symmetric & Q is a skew-symmetric, then P =

Question 18 :
Let A be a square matrix, then $AA^T $ and $A^TA$ are 

Question 19 :
If $A$ and $B$ are two matrices of the same order, then $A-B=B-A$.

Question 20 :
lf the order of $\mathrm{A}$ is  $\mathrm4\times3$, the order of $\mathrm{B}$ is $\mathrm4\times5$ and the order of $\mathrm{C}$ is $\mathrm7\times3$, then the order of $(\mathrm{A}^{T}\mathrm{B})^{T}\mathrm{C}^{T}$ is

More from Er. Dipesh Tripathi Sir

Recommended Content

Learn from Anywhere on Any Device